Study on Anisotropic Strange Stars in
f
(
T
,
T
)
Gravity
Abstract
1. Introduction
2. Basic Mathematical Formalism of Gravity and the Einstein Field Equations
3. Explicit Stellar Equations in Gravity under the Einsteinian Spacetime
4. Solution to the Einstein Field Equations in Gravity for Stellar Modeling
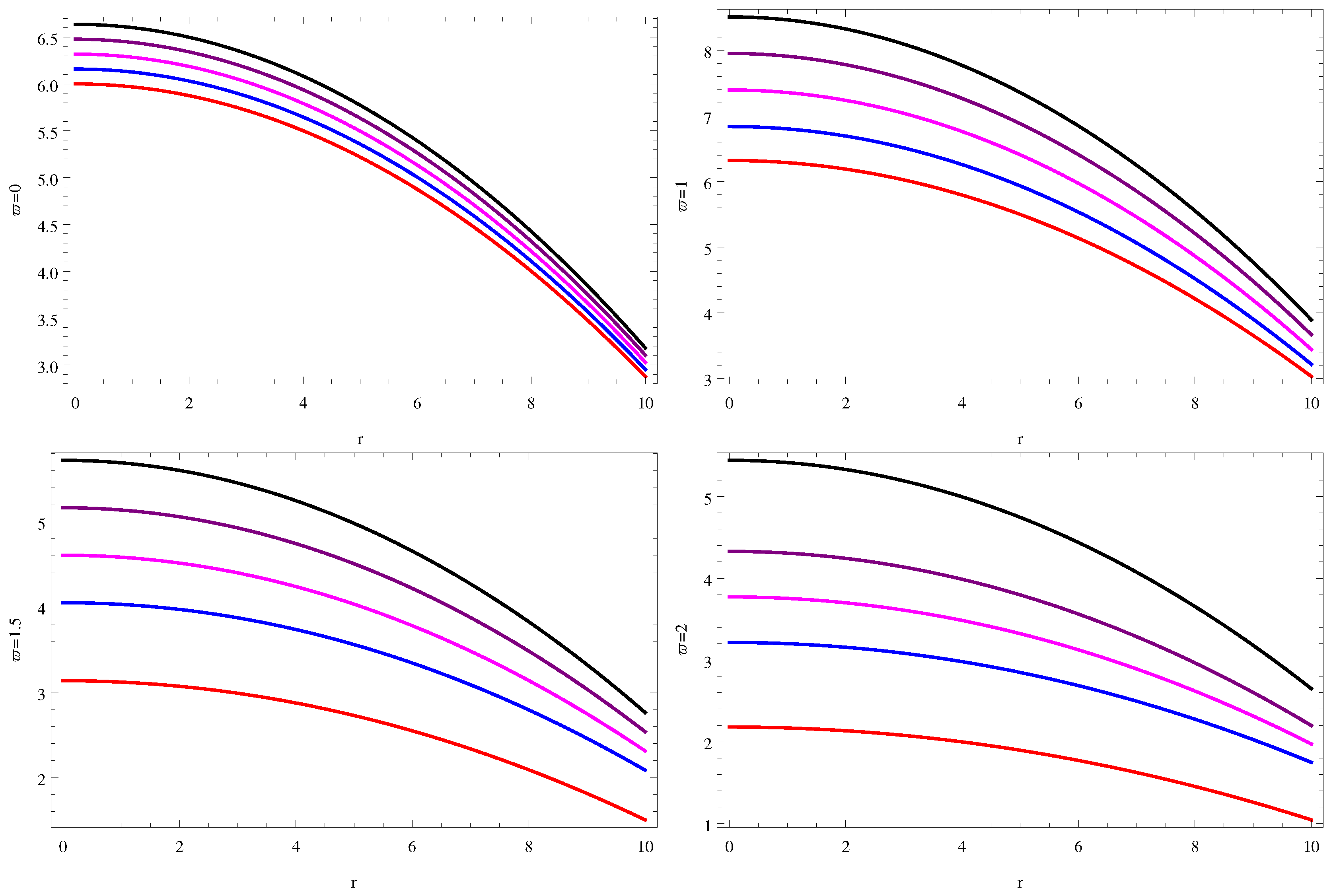
5. Physical Features of Strange (Quark) Stars in Gravity
5.1. Energy Conditions
5.2. Mass–Radius Relation
5.3. Stability of the Stellar Model
5.3.1. Modified TOV Equation in Gravity Theory
5.3.2. Principle of Causality
5.4. Cracking Condition
Adiabatic Index
5.5. Compactification Factor and Redshift
6. A Comparison Study Between gravity and Standard GR
7. Discussions and Conclusion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bodmer, A.R. Collapsed nuclei. Phys. Rev. D 1971, 4, 1601–1606. [Google Scholar] [CrossRef]
- Terazawa, H. Super-Hypernuclei in the Quark-Shell Model. II. J. Phys. Soc. Japan 1989, 58, 4388–4393. [Google Scholar] [CrossRef]
- Witten, E. Cosmic separation of phases. Phys. Rev. D 1984, 30, 272–285. [Google Scholar] [CrossRef]
- Baade, W.; Zwicky, F. Remarks on super-novae and cosmic rays. Phys. Rev. 1934, 46, 76–77. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. The physics of neutron stars. Science 2004, 304, 536–542. [Google Scholar] [CrossRef] [PubMed]
- Steiner, A.W.; Prakash, M.; Lattimer, J.M.; Ellis, P.J. Isospin asymmetry in nuclei and neutron stars. Phys. Rep. 2005, 410, 325–375. [Google Scholar] [CrossRef]
- Bombaci, I.; Parenti, I.; Vidana, I. Quark deconfinement and implications for the radius and the limiting mass of compact stars. Astrophy. J. 2004, 614, 314–325. [Google Scholar] [CrossRef]
- Staff, J.; Ouyed, R.; Bagchi, M. A three-stage model for the inner engine of gamma-ray bursts: Prompt emission and early afterglow. Astrophy. J. 2007, 667, 340–350. [Google Scholar] [CrossRef]
- Herzog, M.; Röpke, F.K. Three-dimensional hydrodynamic simulations of the combustion of a neutron star into a quark star. Phys. Rev. D 2011, 84, 083002. [Google Scholar] [CrossRef]
- Schwarzschild, K. Uber das gravitationsfeld eines massenpunktesnach der Einsteinschen Theorie. Sitzungsber. Preuß. Akad. Wissenschaften Berlin Phys. Math. Kl 1916, 189–196. [Google Scholar]
- Schwarzschild, K. Uber das Gravitationsfeld einer Kugel ausin kompressibler Flüssigkeitnach der Einsteinschen Theorie. Sitzungsberichte KöNiglich Preuss. Akad. Wiss. Berl. Phys.-Math. Klasse 1916, 424–434. [Google Scholar]
- Ruderman, R. Pulsars: Structures and dynamics. Ann. Rev. Astron. Astrophys. 1972, 10, 427–476. [Google Scholar] [CrossRef]
- Herrera, L.; Santos, N.O. Local anisotropy in self-gravitating systems. Phys. Rep. 1997, 286, 53–130. [Google Scholar] [CrossRef]
- Hewish, A.; Bell, S.J.; Pilkington, J.D.H.; Scott, P.F.; Collins, R.A. Observation of a rapidly pulsating radio source. Nature 1968, 217, 709–713. [Google Scholar] [CrossRef]
- Hossein, S.M.; Rahaman, F.; Naskar, J.; Kalam, M.; Ray, S. Anisotropic compact stars with variable cosmological constant. Int. J. Mod. Phys. D 2012, 21, 1250088. [Google Scholar] [CrossRef]
- Kalam, M.; Rahaman, F.; Molla, S.; Hossein, S.M. Anisotropic quintessence stars. Astrophys. Space Sci. 2014, 349, 865–871. [Google Scholar] [CrossRef]
- Krori, K.D.; Barua, J. A singularity-free solution for a charged fluid sphere in general relativity. J. Phys. A Math. Gen. 1975, 8, 508–511. [Google Scholar] [CrossRef]
- Kalam, M.; Rahaman, F.; Ray, S.; Hossein, M.; Karar, I.; Naskar, J. Anisotropic strange star with de Sitter spacetime. Eur. Phys. J. C 2012, 72, 2248. [Google Scholar] [CrossRef]
- Paul, B.C.; Deb, R. Relativistic solutions of anisotropic compact objects. Astrophys. Space Sci. 2014, 354, 421–430. [Google Scholar] [CrossRef]
- Cheng, K.S.; Dai, Z.G.; Lu, T. Strange stars and related astrophysical phenomena. Int. J. Mod. Phys. D 1998, 7, 139–176. [Google Scholar] [CrossRef]
- Bhar, P. Singularity-free anisotropic strange quintessence star. Astrophys. Space Sci. 2015, 356, 309–318. [Google Scholar] [CrossRef]
- Abbas, G.; Zubair, M.; Mustafa, G. Anisotropic strange quintessence stars in f(R) gravity. Astrophys. Space Sci. 2015, 358, 26. [Google Scholar] [CrossRef]
- Rahaman, F.; Chakraborty, K.; Kuhfittig, P.K.F.; Shit, G.C.; Rahman, M. A new deterministic model of strange stars. Eur. Phys. J. C 2014, 74, 3126. [Google Scholar] [CrossRef]
- Arbañil, J.D.V.; Malheiro, M. Radial stability of anisotropic strange quark stars. J. Cosmol. Astropart. Phys. 2016, 11, 012. [Google Scholar] [CrossRef]
- Murad, M.H. Some analytical models of anisotropic strange stars. Astrophys. Space Sci. 2016, 361, 20. [Google Scholar] [CrossRef]
- Mak, M.K.; Harko, T. Quark stars admitting a one-parameter group of conformal motions. Int. J. Mod. Phys. D 2004, 13, 149–156. [Google Scholar] [CrossRef]
- Abbas, G. Cardy-Verlinde Formula of Non-Commutative Schwarzschild Black Hole. Adv. High Energy Phys. 2014, 2014, 306256. [Google Scholar] [CrossRef]
- Abbas, G. Collapse and expansion of anisotropic plane symmetric source. Astrophys. Space Sci. 2014, 350, 307–311. [Google Scholar] [CrossRef]
- Abbas, G.; Sabiullah, U. Geodesic study of regular Hayward black hole Geodesic study of regular Hayward black hole. Astrophys. Space Sci. 2014, 352, 769–774. [Google Scholar] [CrossRef]
- Abbas, G. Phantom Energy Accretion onto a Black hole in Hořava-Lifshitz Gravity. Sci. China Phys. Mech. Astron. 2014, 57, 604–607. [Google Scholar] [CrossRef]
- Abbas, G. Effects of electromagnetic field on the collapse and expansion of anisotropic gravitating source. Astrophys. Space Sci. 2014, 352, 955–961. [Google Scholar] [CrossRef]
- Abbas, G.; Kanwal, A.; Zubair, M. Anisotropic Compact Stars in f(T) Gravity. Astrophys. Space Sci. 2015, 357, 109. [Google Scholar] [CrossRef]
- Abbas, G.; Nazeer, S.; Meraj, M.A. Cylindrically Symmetric Models of Anisotropic Compact Objects. Astrophys. Space Sci. 2014, 354, 449–455. [Google Scholar] [CrossRef]
- Abbas, G.; Momeni, D.; Ali, M.A.; Myrzakulov, R.; Qaisar, S. Anisotropic Compact Stars in f(G) Gravity. Astrophys. Space Sci. 2015, 357, 158. [Google Scholar] [CrossRef]
- Deb, D.; Ghosh, S.; Maurya, S.K.; Khlopov, M.; Ray, S. Anisotropic compact stars in f(T) gravity under Karmarkar condition. Tech Vistas 2018, 1, 1–20. [Google Scholar]
- Das, A.; Ghosh, S.; Deb, D.; Rahaman, F.; Ray, S. Study of gravastars under f(T) gravity. Nucl. Phys. B 2020, 954, 114986. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified Gauss–Bonnet theory as gravitational alternative for dark energy. Phys. Lett. B 2005, 631, 1–6. [Google Scholar] [CrossRef]
- Abbas, G.; Qaisar, S.; Jawad, A. Strange stars in f(T) gravity with MIT bag model. Astrophys. Space Sci. 2015, 359, 57. [Google Scholar] [CrossRef]
- Oliveira, A.M.; Velten, H.E.S.; Fabris, J.C.; Casarini, L. Neutron stars in Rastall gravity. Phys. Rev. D 2015, 92, 044020. [Google Scholar] [CrossRef]
- Abbas, G.; Shahzad, M.R. A new model of quintessence compact stars in the Rastall theory of gravity. Eur. Phys. J. A 2018, 54, 211. [Google Scholar] [CrossRef]
- Abbas, G.; Shahzad, M.R. Models of anisotropic compact stars in the Rastall theory of gravity. Astrophys. Space Sci. 2019, 364, 50. [Google Scholar] [CrossRef]
- Mota, C.E.; Santos, L.C.N.; Grams, G.; da Silva, F.M.; Menezes, D.P. Combined Rastall and rainbow theories of gravity with applications to neutron stars. Phys. Rev. D 2019, 100, 024043. [Google Scholar] [CrossRef]
- Mota, C.E.; Santos, L.C.N.; da Silva, F.M.; Flores, C.V.; da Silva, T.J.N.; Menezes, D.P. Anisotropic Compact Stars in Rastall-Rainbow Gravity. arXiv 2019, arXiv:1911.03208 [astro-ph.HE]. [Google Scholar]
- Rizaldy, R.; Sulaksono, A. Deformation of a magnetized quark star in Rastall gravity. J. Phys. Conf. Ser. 2019, 1321, 022016. [Google Scholar] [CrossRef]
- Shahzad, M.R.; Abbas, G. Strange stars with MIT bag model in the Rastall theory of gravity. Int. J. Geom. Meth. Mod. Phys. 2019, 16, 1950132. [Google Scholar] [CrossRef]
- Nazar, H.; Abbas, G. Charged anisotropic collapsing stars with heat flux in f(R) gravity. Chin. J. Phys. 2020, 63, 436–447. [Google Scholar] [CrossRef]
- Sharif, M.; Waseem, A. Anisotropic quark stars in f(R,T) gravity. Eur. Phys. J. C 2018, 78, 868. [Google Scholar] [CrossRef]
- Maurya, S.K.; Tello-Ortiz, F. Charged anisotropic strange stars in general relativity. Eur. Phys. J. C 2019, 79, 33. [Google Scholar] [CrossRef]
- Maurya, S.K.; Banerjee, A.; Jasim, M.K.; Kumar, J.; Prasad, A.K.; Pradhan, A. Anisotropic compact stars in the Buchdahl model: A comprehensive study. Phys. Rev. D 2019, 99, 044029. [Google Scholar] [CrossRef]
- Maurya, S.K.; Tello-Ortiz, F. Generalized relativistic anisotropic compact star models by gravitational decoupling. Eur. Phys. J. C 2019, 79, 85. [Google Scholar] [CrossRef]
- Prasad, A.K.; Kumar, J.; Maurya, S.K.; Dayanandan, B. Relativistic model for anisotropic compact stars using Karmarkar condition. Astrophys. Space Sci. 2019, 364, 66. [Google Scholar] [CrossRef]
- Saha, P.; Debnath, U. Anisotropic Quintessence Strange Stars in f(T) Gravity with Modified Chaplygin Gas. Adv. High Energy Phys. 2018, 3901790. [Google Scholar] [CrossRef]
- Saha, P.; Debnath, U. Study of anisotropic compact stars with quintessence field and modified chaplygin gas in f(T) gravity. Eur. Phys. J. C 2019, 79, 919. [Google Scholar] [CrossRef]
- Deb, D.; Rahaman, F.; Ray, S.; Guha, B.K. Anisotropic strange stars under simplest minimal matter-geometry coupling in the f(R,T) gravity. Phys. Rev. D 2018, 97, 084026. [Google Scholar] [CrossRef]
- Deb, D.; Rahaman, F.; Ray, S.; Guha, B.K. Strange stars in gravity. J. Cosmol. Astropart. Phys. 2018, 3, 44. [Google Scholar] [CrossRef]
- Biswas, S.; Ghosh, S.; Ray, S.; Rahaman, F.; Guha, B.K. Strange stars in Krori-Barua space-time under gravity. Ann. Phys. 2019, 401, 1. [Google Scholar] [CrossRef]
- Moraes, P.H.R.S.; Arbañil, J.D.V.; Malheiro, M. Stellar equilibrium configurations of compact stars in theory of gravity. J. Cosmol. Astropart. Phys. 2016, 06, 005. [Google Scholar] [CrossRef]
- Das, A.; Ghosh, S.; Guha, B.K.; Das, S.; Rahaman, F.; Ray, S. Gravastars in gravity. Phys. Rev. D 2017, 95, 124011. [Google Scholar] [CrossRef]
- Deb, D.; Ketov, S.V.; Khlopov, M.; Ray, S. Study on charged strange stars in gravity. J. Cosmol. Astropart. Phys. 2019, 10, 070. [Google Scholar] [CrossRef]
- Deb, D.; Ketov, S.V.; Maurya, S.K.; Khlopov, M.; Moraes, P.H.R.S..; Ray, S. Exploring physical features of anisotropic strange stars beyond standard maximum mass limit in gravity. Mon. Not. R. Astron. Soc. 2019, 485, 5652–5665. [Google Scholar] [CrossRef]
- Biswas, S.; Shee, D.; Ray, S.; Guha, B.K. Anisotropic strange star with Tolman–Kuchowicz metric under f(R,T) gravity. Eur. Phys. J. C 2020, 80, 175. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Otalora, G.; Saridakis, E.N. gravity and cosmology. J. Cosmol. Astropart. Phys. 2014, 12, 021. [Google Scholar] [CrossRef]
- Momeni, D.; Myrzakulov, R. Cosmological reconstruction of gravity. Int. J. Geom. Methods Mod. Phys. 2014, 11, 1450077. [Google Scholar] [CrossRef]
- Nassur, S.B.; Houndjo, M.J.S.; Rodrigues, M.E.; Kpadonou, A.V.; Tossa, J. From the early to the late time universe within gravity. Astrophys. Space Sci. 2015, 360, 60. [Google Scholar] [CrossRef]
- Salako, I.G.; Jawad, A.; Chattopadhyay, S. Holographic dark energy reconstruction in gravity. Astrophys. Space Sci. 2015, 358, 13. [Google Scholar] [CrossRef]
- Ganiou, M.G.; Salako, I.G.; Houndjo, M.J.S.; Tossa, J. cosmological models in phase space. Astrophys. Space Sci. 2016, 361, 57. [Google Scholar] [CrossRef]
- Ganiou, M.G.; Salako, I.G.; Houndjo, M.J.S.; Tossa, J. Geodesic Deviation Equation in ΛCDM Gravity. Int. J. Theor. Phys. 2016, 55, 3954–3972. [Google Scholar] [CrossRef]
- Junior, E.L.B.; Rodrigues, M.E.; Salako, I.G.; Houndjo, M.J.S. Reconstruction, thermodynamics and stability of the ΛCDM model in gravity. Class. Quantum Gravity 2016, 33, 125006. [Google Scholar] [CrossRef]
- Sáez-Gómez, D.; Carvalho, C.S.; Lobo, F.S.N.; Tereno, I. Constraining gravity models using type Ia supernovae. Phys. Rev. D 2016, 94, 024034. [Google Scholar] [CrossRef]
- Farrugia, G.; Said, J.L. Growth factor in gravity. Phys. Rev. D 2016, 94, 124004. [Google Scholar] [CrossRef]
- Rezaei, T.M.; Amani, A. Stability and interacting gravity with modified Chaplygin gas. Can. J. Phys. 2017, 95, 1068–1073. [Google Scholar] [CrossRef]
- Arouko, M.Z.; Salako, I.G.; Kanfon, A.D.; Houndjo, M.J.S.; Baffou, E. Rip cosmologies, Wormhole Solutions and Big Trip in the theory of gravity. arXiv 2020, arXiv:2004.06000 [gr-qc]. [Google Scholar] [CrossRef]
- Ghosh, S.; Kanfon, A.D.; Das, A.; Houndjo, M.J.S.; Salako, I.G.; Ray, S. Gravastars in gravity. Int. J. Mod. Phys. A 2020, 35, 2050017. [Google Scholar] [CrossRef]
- Pace, M.; Said, J.L. Quark stars in -gravity. Eur. Phys. J. C 2017, 77, 62. [Google Scholar] [CrossRef]
- Pace, M.; Said, J.L. A perturbative approach to neutron stars in -gravity. Eur. Phys. J. C 2017, 77, 283. [Google Scholar] [CrossRef]
- Gangopadhyay, T.; Ray, S.; Li, X.-D.; Dey, J.; Dey, M. Strange star equation of state fits the refined mass measurement of 12 pulsars and predicts their radii. Mon. Not. R. Astron. Soc. 2013, 431, 3216–3221. [Google Scholar] [CrossRef]
- Deb, D.; Roy Chowdhury, S.; Guha, B.K.; Ray, S. Can strange stars mimic dark energy stars? arXiv 2016, arXiv:1611.02253. [Google Scholar]
- Maluf, J.W.; Ulhoa, S.C. On the gravitational angular momentum of rotating sources. Gen. Rel. Gravit. 2009, 41, 1233–1247. [Google Scholar] [CrossRef][Green Version]
- Maluf, J.W.; Faria, F.F.; Ulhoa, S.C. On reference frames in spacetime and gravitational energy in freely falling frames. Class. Quantum Gravity 2007, 24, 2743–2754. [Google Scholar] [CrossRef]
- Maluf, J.W.; Ulhoa, S.C.; da Rocha-Neto, J.F. Gravitational pressure on event horizons and thermodynamics in the teleparallel framework. Phys. Rev. D 2012, 85, 044050. [Google Scholar] [CrossRef]
- Daouda, M.H.; Rodrigues, M.E.; Houndjo, M.J.S. New static solutions in f(T) theory. Eur. Phys. J. C 2011, 71, 1817. [Google Scholar] [CrossRef]
- Daouda, M.H.; Rodrigues, M.E.; Houndjo, M.J.S. Static anisotropic solutions in f(T) theory. Eur. Phys. J. C 2012, 72. [Google Scholar] [CrossRef]
- Xu, R.X.; Tao, D.J.; Yang, Y. The superflares of soft Γ -ray repeaters: Giant quakes in solid quark stars? Mon. Not. R. Astron. Soc. 2006, 373, L85–L89. [Google Scholar] [CrossRef]
- Canuto, V. Neutron Stars: General Review Solvay Conf. on Astrophysics and Gravitation, Brussels, Belgium, 1973.
- Bowers, R.L.; Liang, E.P.T. Anisotropic spheres in general relativity. Class. Astrophys. J. 1974, 188, 657–665. [Google Scholar] [CrossRef]
- Sawyer, R.F. Condensed π− Phase in Neutron-Star Matter. Phys. Rev. Lett. 1972, 29, 382–385. [Google Scholar] [CrossRef]
- Sokolov, A.I. Phase transformations in a superfluid neutron liquid. J. Exp. Theor. Phys. 1980, 79, 1137–1140. [Google Scholar]
- Kippenhahn, R.; Weigert, A. Stellar Structure and Evolution; Springer: Berlin, Germany, 1990. [Google Scholar]
- Ivanov, B.V. Maximum bounds on the surface redshift of anisotropic stars. Phys. Rev. D 2002, 65, 104011. [Google Scholar] [CrossRef]
- Varela, V.; Rahaman, F.; Ray, S.; Chakraborty, K.; Kalam, M. Charged anisotropic matter with linear or nonlinear equation of state. Phys. Rev. D 2010, 82, 044052. [Google Scholar] [CrossRef]
- Rahaman, F.; Ray, S.; Jafry, A.K.; Chakraborty, K. Singularity-free solutions for anisotropic charged fluids with Chaplygin equation of state. Phys. Rev. D 2010, 82, 104055. [Google Scholar] [CrossRef]
- Rahaman, F.; Kuhfittig, P.K.F.; Kalam, M.; Usmani, A.A.; Ray, S. A comparison of Hořava-Lifshitz gravity and Einstein gravity through thin-shell wormhole construction. Class. Quantum Gravity 2011, 28, 155021. [Google Scholar] [CrossRef]
- Rahaman, F.; Maulick, R.; Yadav, A.K.; Ray, S.; Sharma, R. Singularity-free dark energy star. Gen. Relat. Gravit. 2012, 44, 107–124. [Google Scholar] [CrossRef]
- Shee, D.; Rahaman, F.; Guha, B.K.; Ray, S. Anisotropic stars with non-static conformal symmetry. Astrophys. Space Sci. 2016, 361, 167. [Google Scholar] [CrossRef]
- Maurya, S.K.; Gupta, Y.K.; Ray, S.; Deb, D. Generalised model for anisotropic compact stars. Eur. Phys. J. C 2016, 76, 693. [Google Scholar] [CrossRef]
- Maurya, S.K.; Deb, D.; Ray, S.; Kuhfittig, P.K.F. Compact stars: A generalized model. arXiv 2018, arXiv:1703.08436. [Google Scholar]
- Deb, D.; Roy Chowdhury, S.; Ray, S.; Rahaman, F.; Guha, B.K. Relativistic model for anisotropic strange stars. Ann. Phys. 2017, 387, 239–252. [Google Scholar] [CrossRef]
- Chodos, A.; Jaffe, R.L.; Johnson, K.; Thorn, C.B.; Weisskopf, V.F. New extended model of hadrons. Phys. Rev. D 1974, 9, 3471–3495. [Google Scholar] [CrossRef]
- Zdunik, J.L.; Bulik, T.; Kluzniak, W.; Haensel, P.; Gondek-Rosinska, D. On the mass of moderately rotating strange stars in the MIT bag model and LMXBs. Astron. Astrophys. 2000, 359, 143–147. [Google Scholar]
- Maieron, C.; Baldo, M.; Burgio, G.F.; Schulze, H.-J. Hybrid stars with the color dielectric and the MIT bag models. Phys. Rev. D 2004, 70, 043010. [Google Scholar] [CrossRef]
- Nicotra, O.E.; Baldo, M.; Burgio, G.F.; Schulze, H.-J. Hybrid protoneutron stars with the MIT bag mode. Phys. Rev. D 2006, 74, 123001. [Google Scholar] [CrossRef]
- Bao, T.; Liu, G.-Z.; Zhu, M.-F. Properties of hybrid stars in an extended MIT bag model. Chin. Phys. C 2009, 33, 340–344. [Google Scholar]
- Uechi, S.T.; Uechi, H. Hardon-quark hybrid stars constructed by the nonlinear σ-ω-ρ mean-field model and MIT-bag model. arXiv 2010, arXiv:1003.4815. [Google Scholar] [CrossRef]
- Isayev, A.A. Stability of magnetized strange quark matter in the MIT bag model with a density dependent bag pressure. Phys. Rev. C 2015, 91, 015208. [Google Scholar] [CrossRef]
- Cardoso, P.H.G.; da Silva, T.N.; Deppman, A.; Menezes, D.P. Quark matter revisited with non-extensive MIT bag model. Eur. Phys. J. A 2017, 53, 191. [Google Scholar] [CrossRef]
- Joshi, S.; Sau, S.; Sanyal, S. Quark cores in extensions of the MIT Bag model. arXiv 2002, arXiv:2002.07647 [nucl-th]. [Google Scholar]
- Mak, M.K.; Harko, T. Anisotropic stars in general relativity. Proc. Roy. Soc. Lond. A 2003, 459, 393–408. [Google Scholar] [CrossRef]
- Moraes, P.H.R.S.; Correa, R.A.C.; Lobato, R.V. Analytical general solutions for static wormholes in f(R,T) gravity. J. Cosmol. Astropart. Phys. 2017, 1707, 029. [Google Scholar] [CrossRef]
- De León, J.P. Limiting configurations allowed by the energy conditions. Gen. Rel. Gravit. 1993, 25, 1123–1137. [Google Scholar] [CrossRef]
- Shuryak, E.V. Quantum chromodynamics and the theory of superdense matter. Phys. Rep. 1980, 61, 71–158. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Evidence for quark-matter cores in massive neutron stars. Nature Phys. 2020, 16, 907–910. [Google Scholar] [CrossRef]
- Tolman, R.C. Static solutions of Einstein’s field equations for spheres of fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On massive neutron cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Herrera, L. Cracking of self-gravitating compact objects. Phys. Lett. A 1992, 165, 206–210. [Google Scholar] [CrossRef]
- Abreu, H.; Hernández, H.; Núñez, L.A. Sound speeds, cracking and stability of self-gravitating anisotropic compact objects. Class. Quantum Gravity 2007, 24, 4631–4645. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Dynamical Instability of Gaseous Masses Approaching the Schwarzschild Limit in General Relativity. Astrophys. J. 1964, 12, 114–116. [Google Scholar]
- Heintzmann, H.; Hillebrandt, W. Neutron stars with an anisotropic equation of state - mass, redshift and stability. Astron. Astrophys. 1975, 38, 51–55. [Google Scholar]
- Hillebrandt, W.; Steinmetz, K.O. Anisotropic neutron star models-Stability against radial and nonradial pulsations. Astron. Astrophys. 1976, 53, 283–287. [Google Scholar]
- Bombaci, I. The maximum mass of a neutron star. Astron. Astrophys. 1996, 305, 871–877. [Google Scholar]
- Andréasson, H. Sharp bounds on the critical stability radius for relativistic charged spheres. Commun. Math. Phys. 2009, 288, 715–730. [Google Scholar] [CrossRef]
- Bondi, H. The contraction of gravitating spheres. Proc. R. Soc. Lond. A 1964, 281, 39–48. [Google Scholar]
- Chan, R.; Herrera, L.; Santos, N.O. Dynamical instability for radiating anisotropic collapse. Mon. Not. R. Astron. Soc. 1993, 265, 533–544. [Google Scholar] [CrossRef]
- Barraco, D.E.; Hamity, V.H. Maximum mass of a spherically symmetric isotropic star. Phys. Rev. D 2002, 65, 124028. [Google Scholar] [CrossRef]
- Böhmer, C.G.; Harko, T. Bounds on the basic physical parameters for anisotropic compact general relativistic objects. Class. Quantum Gravity 2006, 23, 6479–6491. [Google Scholar] [CrossRef]
- Aziz, A.; Ray, S.; Rahaman, F.; Khlopov, M.; Guha, B.K. Constraining values of bag constant for strange star candidates. Int. J. Mod. Phys. D 2019, 28, 1941006. [Google Scholar] [CrossRef]
- Itoh, N. Hydrostatic equilibrium of hypothetical quark stars. Progr. Theor. Phys. 1970, 44, 291–292. [Google Scholar] [CrossRef]
- Haensel, P.; Zdunik, J.; Schaeffer, R. Strange quark stars. Astron. Astrophys. 1986, 160, 121–128. [Google Scholar]
- Alcock, C.; Farhi, E.; Olinto, A. Strange stars. Astrophys. J. 1986, 310, 261–272. [Google Scholar] [CrossRef]
- Pagliara, G.; Herzog, M.; Röpke, F.K. Combustion of a neutron star into a strange quark star: The neutrino signal. Phys. Rev. D 2013, 87, 103007. [Google Scholar] [CrossRef]
- Bauswein, A.; Janka, H.T.; Oechslin, R.; Pagliara, G.; Sagert, I.; Schaffner-Bielich, J.; Hohle, M.M.; Neuhäuser, R. Mass ejection by strange star mergers and observational implications. Phys. Rev. Lett. 2009, 103, 011101. [Google Scholar] [CrossRef]
- Bauswein, A.; Oechslin, R.; Janka, H.-T. Discriminating strange star mergers from neutron star mergers by gravitational-wave measurements. Phys. Rev. D 2010, 81, 024012. [Google Scholar] [CrossRef]
- Llanes-Estrada, P.J. Constraining gravity with hadron physics: Neutron stars, modified gravity and gravitational waves. EPJ Web Conf. 2017, 137, 01013. [Google Scholar] [CrossRef]
- Motohashi, H.; Minamitsuji, M. General Relativity solutions in modified gravity. Phys. Lett. B 2018, 781, 728–734. [Google Scholar] [CrossRef]
- Berti, E.; Yagi, K.; Yang, H.; Yunes, N. Extreme gravity tests with gravitational waves from compact binary coalescences: (II) ringdown. Gen. Relat. Gravit. 2018, 50, 49. [Google Scholar] [CrossRef]
- Yamada, K.; Narikawa, T.; Tanaka, T. Testing massive-field modifications of gravity via gravitational waves. Prog. Theor. Exp. Phys. 2019, 2019, 103E01. [Google Scholar] [CrossRef]









© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salako, I.G.; Khlopov, M.; Ray, S.; Arouko, M.Z.; Saha, P.; Debnath, U.
Study on Anisotropic Strange Stars in
Salako IG, Khlopov M, Ray S, Arouko MZ, Saha P, Debnath U.
Study on Anisotropic Strange Stars in
Salako, Ines G., M. Khlopov, Saibal Ray, M. Z. Arouko, Pameli Saha, and Ujjal Debnath.
2020. "Study on Anisotropic Strange Stars in
Salako, I. G., Khlopov, M., Ray, S., Arouko, M. Z., Saha, P., & Debnath, U.
(2020). Study on Anisotropic Strange Stars in





