Thin-Shell Wormholes in Einstein and Einstein–Gauss–Bonnet Theories of Gravity
Abstract
:1. Introduction
1.1. Einstein–Rosen Bridge
- (a)
- Photons and initially are in the lower sheet. They go to the center . The values and correspond to and , respectively. The vertical bold line is the curvature singularity . At this moment, the singularity is in between two quasi-Euclidean spaces.
- (b)
- Both photons go to the center. A throat is going to appear.
- (c)
- The throat just opened. The circumference of the throat is smaller than .
- (d)
- The maximal throat, . The photon has passed though the throat.
- (e)
- The throat is shrinking. Both photons have passed though the throat.
- (f)
- The moment of the throat closing. In this stage, both photons are still in the upper sheet, while the photon approaches the central singularity.
- (g)
- Photon is just caught. Then, disappears in the singularity and stops existing.
- (h)
- Photon keeps escaping to the null infinity of the upper sheet.
1.2. Wormhole Properties in Brief
1.2.1. Embedding Wormholes and Asymptotic Flatness
1.2.2. Flaring-Out Condition
1.2.3. Absence of the Horizon
1.2.4. Magnitude of the Tension at the Throat
1.2.5. Exotic Matter
1.2.6. Other Properties
1.3. Simple Exact Solutions and Their Stability
2. Thin-Shell Wormholes
2.1. Junction Conditions
2.2. Construction
2.3. Equation of Motion for the Shell
2.4. Simplest Thin-Shell Wormhole
2.5. Stability
2.5.1. Global Stability
2.5.2. Local Stability
- (1)
- There are stable solutions in or .
- (2)
- No solution in is stable.
- (3)
- The solution at is unstable regardless of the value of .
2.5.3. Pure Tension
3. Generalized Thin-Shell Wormholes
3.1. Charged Generalization
3.2. Presence of a Cosmological Constant
3.2.1. Schwarzschild–de Sitter Thin-Shell Wormhole:
3.2.2. Schwarzschild–Anti de Sitter Thin-Shell Wormhole:
3.2.3. (Anti) de Sitter Thin-Shell Wormhole
3.3. Non- Symmetric Case
3.4. In Higher Dimensions
4. Pure Tension Wormholes in Einstein Gravity
4.1. Einstein Gravity
4.2. Advantage of Use of Pure Tension
4.3. Pure Tension Wormholes in Einstein Gravity
4.4. Effective Potential
4.5. Static Solutions and Stability Criterion
5. Pure Tension Wormholes in Einstein–Gauss–Bonnet Gravity
5.1. Einstein–Gauss–Bonnet Gravity
5.2. Pure Tension Wormholes in Einstein–Gauss–Bonnet Gravity
5.3. Bulk Solution
5.4. Equation of Motion for a Thin-Shell
5.5. Effective Potential for the Shell
5.6. Negative Energy Density of the Shell
5.7. Static Solutions
5.8. Stability Criterion
5.8.1. Einstein Gravity
5.8.2. Einstein–Gauss–Bonnet Gravity
5.9. Effect of the Gauss–Bonnet Term on the Stability
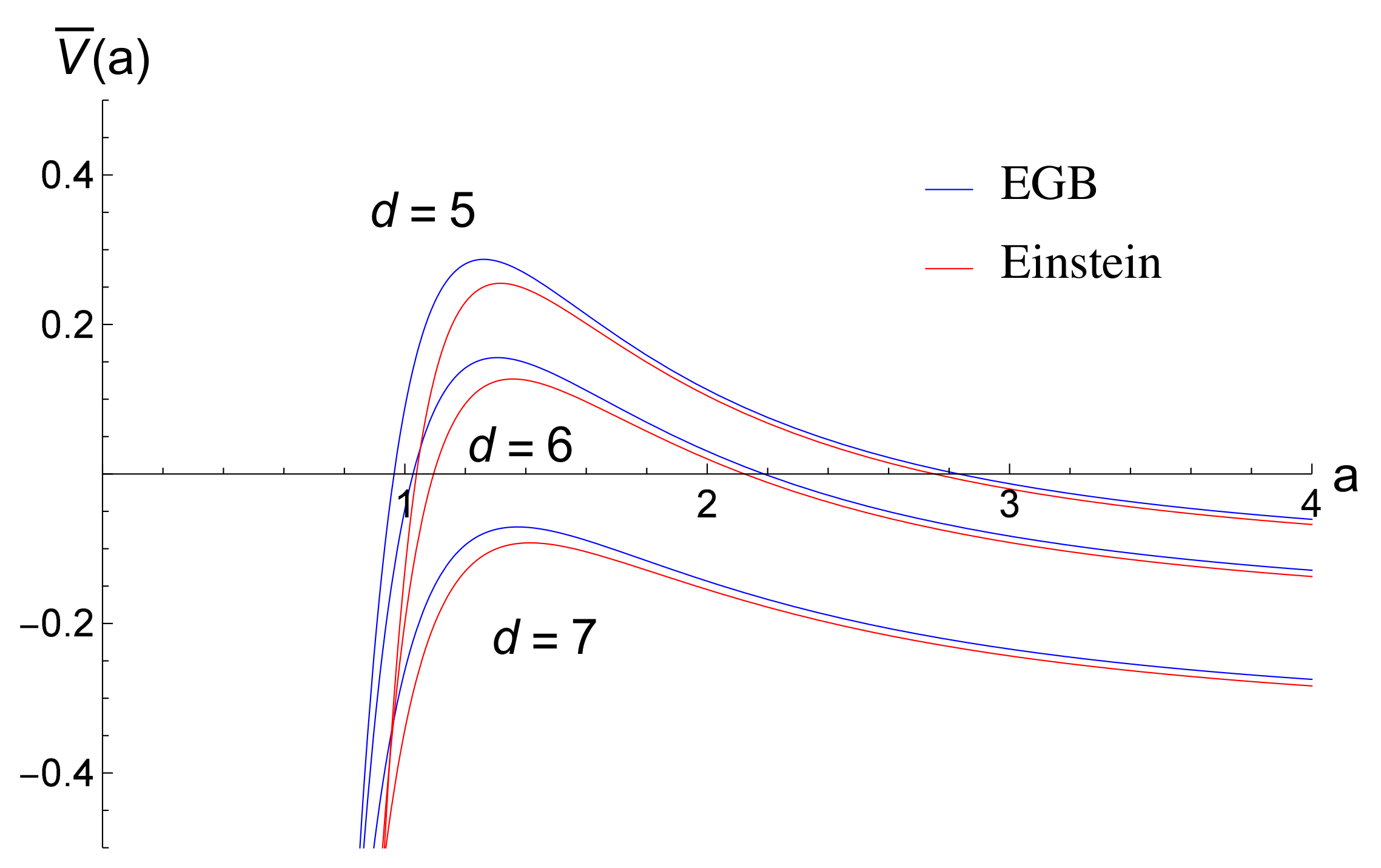
5.10. Stability Analysis
6. Conclusions
6.1. In Einstein Gravity
6.2. In Einstein–Gauss–Bonnet Gravity
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Morris, M.S.; Thorne, K.S.; Yurtsever, U. Wormholes, Time Machines, and the Weak Energy Condition. Phys. Rev. Lett. 1988, 61, 1446. [Google Scholar] [CrossRef] [Green Version]
- Flamm, L. Beiträge zur Einsteinschen Gravitationstheorie. Phys. Z. 1916, 17, 448. [Google Scholar]
- Einstein, A.; Rosen, N. The Particle Problem in the General Theory of Relativity. Phys. Rev. 1935, 48, 73. [Google Scholar] [CrossRef]
- Kokubu, T.; Harada, T. Negative tension branes as stable thin-shell wormholes. Class. Quantum Grav. 2015, 32, 205001. [Google Scholar] [CrossRef] [Green Version]
- Kokubu, T.; Maeda, H.; Harada, T. Does the Gauss–Bonnet term stabilize wormholes? Class. Quantum Grav. 2015, 32, 235021. [Google Scholar] [CrossRef] [Green Version]
- Fuller, R.; Wheeler, J. Causality and Multiply Connected Space-Time. Phys. Rev. 1962, 128, 919. [Google Scholar] [CrossRef]
- Morris, M.S.; Thorne, K.S. Wormholes in space-time and their use for interstellar travel: A tool for teaching general relativity. Am. J. Phys. 1988, 56, 395. [Google Scholar] [CrossRef] [Green Version]
- Ellis, H.G. Ether flow through a drainhole—A particle model in general relativity. J. Math. Phys. 1973, 14, 104. [Google Scholar] [CrossRef]
- Bronnikov, K.A. Scalar-tensor theory and scalar charge. Acta Phys. Polon. B 1973, 4, 251. [Google Scholar]
- Kodama, T. General Relativistic Nonlinear Field: A Kink Solution in a Generalized Geometry. Phys. Rev. D 1978, 18, 3529. [Google Scholar] [CrossRef]
- Armendariz-Picon, C. On a class of stable, traversable Lorentzian wormholes in classical general relativity. Phys. Rev. D 2002, 65, 104010. [Google Scholar] [CrossRef] [Green Version]
- Shinkai, H.; Hayward, S.A. Fate of the first traversible wormhole: Black hole collapse or inflationary expansion. Phys. Rev. D 2002, 66, 044005. [Google Scholar] [CrossRef] [Green Version]
- González, J.A.; Guzman, F.S.; Sarbach, O. Instability of wormholes supported by a ghost scalar field. I. Linear stability analysis. Class. Quantum Grav. 2009, 26, 015010. [Google Scholar] [CrossRef] [Green Version]
- González, J.A.; Guzman, F.S.; Sarbach, O. Instability of wormholes supported by a ghost scalar field. II. Nonlinear evolution. Class. Quantum Grav. 2009, 26, 015011. [Google Scholar] [CrossRef]
- González, J.A.; Guzman, F.S.; Sarbach, O. On the instability of charged wormholes supported by a ghost scalar field. Phys. Rev. D 2009, 80, 024023. [Google Scholar] [CrossRef] [Green Version]
- Torii, T.; Shinkai, H. Wormholes in higher dimensional space-time: Exact solutions and their linear stability analysis. Phys. Rev. D 2013, 88, 064027. [Google Scholar] [CrossRef] [Green Version]
- Visser, M. Traversable wormholes from surgically modified Schwarzschild space-times. Nucl. Phys. B 1989, 328, 203. [Google Scholar] [CrossRef] [Green Version]
- Visser, M. Lorentzian Wormholes; AIP Press: New York, NY, USA, 1996. [Google Scholar]
- Visser, M. Traversable wormholes: Some simple examples. Phys. Rev. D 1989, 39, 3182. [Google Scholar] [CrossRef] [Green Version]
- Poisson, E.; Visser, M. Thin shell wormholes: Linearization stability. Phys. Rev. D 1995, 52, 7318. [Google Scholar] [CrossRef] [Green Version]
- Eiroa, E.F.; Romero, G.E. Linearized stability of charged thin shell wormholes. Gen. Rel. Grav. 2004, 36, 651. [Google Scholar] [CrossRef] [Green Version]
- Eiroa, E.F. Stability of thin-shell wormholes with spherical symmetry. Phys. Rev. D 2008, 78, 024018. [Google Scholar] [CrossRef] [Green Version]
- Ishak, M.; Lake, K. Stability of transparent spherically symmetric thin shells and wormholes. Phys. Rev. D 2002, 65, 044011. [Google Scholar] [CrossRef] [Green Version]
- Lobo, F.S.N.; Crawford, P. Linearized stability analysis of thin shell wormholes with a cosmological constant. Class. Quantum Grav. 2004, 21, 391–404. [Google Scholar] [CrossRef] [Green Version]
- Eiroa, E.F.; Simeone, C. Cylindrical thin shell wormholes. Phys. Rev. D 2004, 70, 044008. [Google Scholar] [CrossRef] [Green Version]
- Bejarano, C.; Eiroa, E.F.; Simeone, C. Thin-shell wormholes associated with global cosmic strings. Phys. Rev. D 2007, 75, 027501. [Google Scholar] [CrossRef] [Green Version]
- Eiroa, E.F.; Simeone, C. Some general aspects of thin-shell wormholes with cylindrical symmetry. Phys. Rev. D 2010, 81, 084022. [Google Scholar] [CrossRef] [Green Version]
- Mazharimousavi, S.H.; Halilsoy, M.; Amirabi, Z. Stability of generic cylindrical thin shell wormholes. Phys. Rev. D 2014, 89, 084003. [Google Scholar] [CrossRef] [Green Version]
- Eiroa, E.F.; Simeone, C. Brans-Dicke cylindrical wormholes. Phys. Rev. D 2010, 82, 084039. [Google Scholar] [CrossRef] [Green Version]
- Richarte, M.G. Cylindrical wormholes in DGP gravity. Phys. Rev. D 2013, 87, 067503. [Google Scholar] [CrossRef] [Green Version]
- Garcia, N.M.; Lobo, F.S.N.; Visser, M. Generic spherically symmetric dynamic thin-shell traversable wormholes in standard general relativity. Phys. Rev. D 2012, 86, 044026. [Google Scholar] [CrossRef] [Green Version]
- Dias, G.A.S.; Lemos, J.P.S. Thin-shell wormholes in dd-dimensional general relativity: Solutions, properties, and stability. Phys. Rev. D 2010, 82, 084023. [Google Scholar] [CrossRef] [Green Version]
- Mustafa, G.; Hussain, I.; Farasat Shamir, M. Stable Wormholes in the Background of an Exponential f(R) Gravity. Universe 2020, 6, 48. [Google Scholar] [CrossRef] [Green Version]
- Mustafa, G.; Abbas, G.; Xia, T. Wormhole solutions in F(T, TG) gravity under Gaussian and Lorentzian non-commutative distributions with conformal motions. Chin. J. Phys. 2019, 60, 362–378. [Google Scholar] [CrossRef]
- Mustafa, G.; Waheed, S.; Zubair, M.; Xia, T. Non-commutative Wormholes Exhibiting Conformal Motion in Rastall Gravity. Chin. J. Phys. 2020, 33, 2050035. [Google Scholar] [CrossRef]
- Konoplya, R.; Zhidenko, A. Wormholes versus black holes: Quasinormal ringing at early and late times. J. Cosmol. Astropart. Phys. 2016, 2016, 43. [Google Scholar] [CrossRef] [Green Version]
- Cardoso, V.; Hopper, S.; Macedo, C.F.B.; Palenzuela, C.; Pani, P. Gravitational-wave signatures of exotic compact objects and of quantum corrections at the horizon scale. Phys. Rev. D 2016, 94, 084031. [Google Scholar] [CrossRef] [Green Version]
- Deng, H.; Garriga, J.; Vilenkin, A. Primordial black hole and wormhole formation by domain walls. J. Cosmol. Astropart. Phys. 2017, 2017, 50. [Google Scholar] [CrossRef]
- Smirnov, A.L. Traversable intra-Universe wormholes and timeholes in General Relativity: Two new solutions. Class. Quantum Grav. 2016, 33, 225005. [Google Scholar] [CrossRef] [Green Version]
- Cardoso, V.; Franzin, E.; Maselli, A.; Pani, P.; Raposo, G. Testing strong-field gravity with tidal Love numbers. Phys. Rev. D 2017, 95, 084014. [Google Scholar] [CrossRef] [Green Version]
- Akai, Y.; Nakao, K.I. Nonlinear stability of a brane wormhole. Phys. Rev. D 2017, 96, 024033. [Google Scholar] [CrossRef] [Green Version]
- Tsukamoto, N.; Kokubu, T. Linear stability analysis of a rotating thin-shell wormhole. Phys. Rev. D 2018, 98, 044026. [Google Scholar] [CrossRef] [Green Version]
- Konoplya, R.A.; Stuchlík, Z.; Zhidenko, A. Echoes of compact objects: New physics near the surface and matter at a distance. Phys. Rev. D 2019, 99, 024007. [Google Scholar] [CrossRef] [Green Version]
- Li, A.C.; Xu, W.L.; Zeng, D.F. Linear Stability Analysis of Evolving Thin Shell Wormholes. J. Cosmol. Astropart. Phys. 2019, 2019, 16. [Google Scholar] [CrossRef] [Green Version]
- Lobo, F.S.N.; Simpson, A.; Visser, M. Dynamic thin-shell black-bounce traversable wormholes. Phys. Rev. D 2020, 101, 124035. [Google Scholar] [CrossRef]
- Koga, Y. Photon surfaces as pure tension shells: Uniqueness of thin shell wormholes. Phys. Rev. D 2020, 101, 104022. [Google Scholar] [CrossRef]
- Poisson, E. A Relativist’s Toolkit; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Barrabés, C.; Bressange, G.F. Singular hypersurfaces in scalar - tensor theories of gravity. Class. Quantum Grav. 1997, 14, 805. [Google Scholar] [CrossRef]
- Ruban, V. Generalized Birkhoff’s theorem (GBT) for Einstein-Maxwell fields (Λ ≠ 0). In Proceedings of the 8th International Conference on General Relativity and Gravitation, Waterloo, ON, Canada, 7–12 August 1977; p. 303. [Google Scholar]
- Bronnikov, K.; Kovalchuk, M. On a generalisation of Birkhoff’s theorem. J. Phys. A. Math. Gen. 1980, 13, 187. [Google Scholar] [CrossRef]
- Bronnikov, K.; Melnikov, V. The Birkhoff theorem in multidimensional gravity. Gen. Rel. Grav. 1995, 27, 465. [Google Scholar] [CrossRef] [Green Version]
- Goenner, H. Lorentz-invariant gravitational perturbations and the evaluation of generalized green’s functions. Commun. Math. Phys. 1970, 16, 34–47. [Google Scholar] [CrossRef]
- Sato, H.; Kodama, H. Ippan Sotaisei Riron; Iwanami Shoten: Tokyo, Japan, 1992. [Google Scholar]
- Barceló, C.; Visser, M. Brane surgery: Energy conditions, traversable wormholes, and voids. Nucl. Phys. B 2000, 584, 415–435. [Google Scholar] [CrossRef] [Green Version]
- Kaluza, T. Zum Unitätsproblem der Physik. Sitzungsber. Preuss. Akad. Wiss. 1921, 96, 69. [Google Scholar]
- Klein, O. Quantum Theory and Five-Dimensional Theory of Relativity. Eur. Phys. J. A 1926, 37, 895. [Google Scholar]
- Maldacena, J. The Large N Limit of Superconformal Field Theories and Supergravity. Adv. Theor. Math. Phys. 1998, 2, 231. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. A Large mass hierarchy from a small extra dimension. Phys. Rev. Lett. 1999, 83, 3370. [Google Scholar] [CrossRef] [Green Version]
- Bronnikov, K.; Rubin, S.G. Black Holes, Cosmology and Extra Dimensions; World Scientific: Singapore, 2013; p. 184. [Google Scholar]
- Eiroa, E.F.; Simeone, C. Thin-shell wormholes in dilaton gravity. Phys. Rev. D 2005, 71, 127501. [Google Scholar] [CrossRef] [Green Version]
- Rahaman, F.; Kalam, M.; Chakraborti, S. Thin shell wormhole in heterotic string theory. Int. J. Mod. Phys. D 2007, 16, 1669. [Google Scholar] [CrossRef] [Green Version]
- Richarte, M.G.; Simeone, C. Wormholes in Einstein-Born-Infeld theory. Phys. Rev. D 2009, 80, 104033. [Google Scholar] [CrossRef]
- Richarte, M.G. Wormholes and solitonic shells in five-dimensional DGP theory. Phys. Rev. D 2010, 82, 044021. [Google Scholar] [CrossRef] [Green Version]
- Usmani, A.A.; Hasan, Z.; Rahaman, F.; Rakib, S.A.; Ray, S.; Kuhfittig, P.K.F. Thin-shell wormholes from charged black holes in generalized dilaton-axion gravity. Gen. Rel. Grav. 2010, 42, 2901. [Google Scholar] [CrossRef]
- Rahaman, F.; Kuhfittig, P.K.F.; Kalam, M.; Usmani, A.A.; Ray, S. A comparison of Horava-Lifshitz gravity and Einstein gravity through thin-shell wormhole construction. Class. Quantum Grav. 2011, 28, 155021. [Google Scholar] [CrossRef] [Green Version]
- Mazharimousavi, S. Habib; Halilsoy, M.; Amirabi, Z. d-dimensional non-asymptotically flat thin-shell wormholes in Einstein-Yang-Mills-Dilaton gravity. Phys. Lett. A 2011, 375, 231–236. [Google Scholar] [CrossRef] [Green Version]
- Dehghani, M.H.; Mehdizadeh, M.R. Lovelock thin-shell wormholes. Phys. Rev. D 2012, 85, 024024. [Google Scholar] [CrossRef] [Green Version]
- Kozyrev, S.M. Stability of composite vacuum Heckmann wormholes in Brans-Dicke theory. arXiv 2014, arXiv:1401.6662. [Google Scholar]
- Kanti, P.; Kleihaus, B.; Kunz, J. Wormholes in Dilatonic Einstein-Gauss-Bonnet Theory. Phys. Rev. Lett. 2011, 107, 271101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kanti, P.; Kleihaus, B.; Kunz, J. Stable Lorentzian Wormholes in Dilatonic Einstein-Gauss-Bonnet Theory. Phys. Rev. D 2012, 85, 044007. [Google Scholar] [CrossRef] [Green Version]
- Gross, D.J.; Witten, E. Superstring Modifications Of Einstein’s Equations. Nucl. Phys. 1986, B277, 1. [Google Scholar] [CrossRef]
- Gross, D.J.; Sloan, J.H. The Quartic Effective Action For The Heterotic String. Nucl. Phys. 1987, B291, 41. [Google Scholar] [CrossRef]
- Metsaev, R.R.; Tseytlin, A.A. Two Loop Beta Function For The Generalized Bosonic Sigma Model. Phys. Lett. B 1987, 191, 354. [Google Scholar] [CrossRef]
- Zwiebach, B. Curvature Squared Terms And String Theories. Phys. Lett. B 1985, 156, 315. [Google Scholar] [CrossRef]
- Metsaev, R.R.; Tseytlin, A.A. Order Alpha-Prime (Two Loop) Equivalence Of The String Equations Of Motion And The Sigma Model Weyl Invariance Conditions: Dependence On The Dilaton And The Antisymmetric Tensor. Nucl. Phys. 1987, B293, 385. [Google Scholar] [CrossRef]
- Cuyubamba, M.A.; Konoplya, R.A.; Zhidenko, A. No stable wormholes in Einstein-dilaton-Gauss-Bonnet theory. Phys. Rev. D 2018, 98, 044040. [Google Scholar] [CrossRef] [Green Version]
- Thibeault, M.; Simeone, C.; Eiroa, E.F. Thin-shell wormholes in Einstein-Maxwell theory with a Gauss-Bonnet term. Gen. Rel. Grav. 2006, 38, 1593. [Google Scholar] [CrossRef]
- Richarte, M.G.; Simeone, C. Thin-shell wormholes supported by ordinary matter in Einstein-Gauss-Bonnet gravity. Phys. Rev. D 2007, 76, 087502, Erratum in 2008, 77, 089903. [Google Scholar] [CrossRef] [Green Version]
- Garraffo, C.; Giribet, G.; Gravanis, E.; Willison, S. Gravitational solitons and C0 vacuum metrics in five-dimensional Lovelock gravity. J. Math. Phys. 2008, 49, 042502. [Google Scholar] [CrossRef] [Green Version]
- Bandyopadhyay, T.; Chakraborty, S. Thin-shell wormholes in Einstein-Yang-Mills-Gauss-Bonnet theory. Class. Quantum Grav. 2009, 26, 085005. [Google Scholar] [CrossRef]
- Mazharimousavi, S.H.; Halilsoy, M.; Amirabi, Z. Stability of thin-shell wormholes supported by ordinary matter in Einstein-Maxwell-Gauss-Bonnet gravity. Phys. Rev. D 2010, 81, 104002. [Google Scholar] [CrossRef] [Green Version]
- Simeone, C. Addendum to Thin-shell wormholes supported by ordinary matter in Einstein-Gauss-Bonnet gravity. Phys. Rev. D 2011, 83, 087503. [Google Scholar] [CrossRef] [Green Version]
- Amirabi, Z.; Halilsoy, M.; Mazharimousavi, S.H. Effect of the Gauss-Bonnet parameter in the stability of thin-shell wormholes. Phys. Rev. D 2013, 8, 124023. [Google Scholar] [CrossRef] [Green Version]
- Boulware, D.G.; Deser, S. String Generated Gravity Models. Phys. Rev. Lett. 1985, 55, 2656. [Google Scholar] [CrossRef] [Green Version]
- Wheeler, J.T. Symmetric solutions to the Gauss-Bonnet extended Einstein equations. Nucl. Phys. 1986, B268, 737. [Google Scholar] [CrossRef]
- Lorenz-Petzold, D. Higher Dimensional Gauss-Bonnet Cosmologies. Mod. Phys. Lett. 1988, A3, 827. [Google Scholar] [CrossRef]
- Cai, R.-G. Gauss-Bonnet black holes in AdS spaces. Phys. Rev. D 2002, 65, 084014. [Google Scholar] [CrossRef] [Green Version]
- Cai, R.-G.; Guo, Q. Gauss-Bonnet black holes in dS spaces. Phys. Rev. D 2004, 69, 104025. [Google Scholar] [CrossRef] [Green Version]
- Torii, T.; Maeda, H. Spacetime structure of static solutions in Gauss-Bonnet gravity: Neutral case. Phys. Rev. D 2005, 71, 124002. [Google Scholar] [CrossRef] [Green Version]
- Wiltshire, D.L. Spherically Symmetric Solutions of Einstein-Maxwell Theory With a Gauss-Bonnet Term. Phys. Lett. 1986, 169B, 36. [Google Scholar] [CrossRef]
- Myers, R.C. Higher Derivative Gravity, Surface Terms and String Theory. Phys. Rev. D 1987, 36, 392. [Google Scholar] [CrossRef] [PubMed]
- Davis, S.C. Israel conditions for the Gauss-Bonnet theory and the Friedmann equation on the brane universe. Phys. Rev. D 2003, 67, 024030. [Google Scholar] [CrossRef] [Green Version]
- Gravanis, E.; Willison, S. Israel conditions for the Gauss-Bonnet theory and the Friedmann equation on the brane universe. Phys. Lett. 2013, B562, 118. [Google Scholar] [CrossRef] [Green Version]
- Bronnikov, K.; Lipatova, L.N.; Novikov, I.D.; Shatskiy, A.A. Example of a Stable Wormhole in General Relativity. Gravit. Cosmol. 2013, 19, 269. [Google Scholar] [CrossRef] [Green Version]
- Gerlach, U.H.; Sengupta, U.K. Gauge invariant perturbations on most general spherically symmetric space-times. Phys. Rev. D 1979, 19, 2268. [Google Scholar] [CrossRef]
- Gerlach, U.H.; Sengupta, U.K. Junction conditions for odd parity perturbations on most general spherically symmetric space-times. Phys. Rev. D 1979, 20, 3009. [Google Scholar] [CrossRef]
- Gerlach, U.H.; Sengupta, U.K. Even parity junction conditions for perturbations on most general spherically symmetric space-times. J. Math. Phys. 1979, 20, 2540. [Google Scholar] [CrossRef]
- Gerlach, U.H.; Sengupta, U.K. Gauge invariant coupled gravitational, acoustical, and electromagnetic modes on most general spherical space-times. Phys. Rev. D 1980, 22, 1300. [Google Scholar] [CrossRef]
- Kodama, H.; Ishihara, H.; Fujiwata, Y. Does a domain wall emit gravitational waves? General-relativistic perturbative analysis of a simple case. Phys. Rev. D 1994, 50, 7292. [Google Scholar] [CrossRef] [PubMed]
| 1. | Recently, the instability of the present wormhole was reported by [76]. |
















| Static Solution | Horizon Avoidance | Stability | |
|---|---|---|---|
| Satisfied | Marginally stable | ||
| None | – | – |
| Static Solution | Horizon Avoidance | Stability | ||
|---|---|---|---|---|
| Unstable | ||||
| : Stable | ||||
| : Unstable | ||||
| Unstable | ||||
| None | – | – | ||
| None | – | – | ||
| Static Solution | Horizon Avoidance | Stability | ||
|---|---|---|---|---|
| None | – | – | ||
| Stable | ||||
| None | – | – | ||
| Marginally | ||||
| Satisfied | stable | |||
| None | – | – | ||
| Static Solution | Horizon Avoidance | Stability | ||
|---|---|---|---|---|
| None | – | – | ||
| Stable | ||||
| Stable | ||||
| Stable | ||||
| None | – | – | ||
| Stable | ||||
| Existence | Possible Range of | Stability | ||
|---|---|---|---|---|
| Unstable | ||||
| Unstable | ||||
| None | – | – | ||
| Marginally stable | ||||
| None | – | – | ||
| Stable |
| Static Solutions Exist? | Stability | ||
|---|---|---|---|
| Yes | U | ||
| No | – | ||
| : No | – | ||
| : Yes | M | ||
| No | – | ||
| No | – | ||
| : No | – | ||
| : Yes | S | ||
| : Yes | S or M | ||
| with : Yes | S or M | ||
| with : Yes | S, M, or U |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kokubu, T.; Harada, T. Thin-Shell Wormholes in Einstein and Einstein–Gauss–Bonnet Theories of Gravity. Universe 2020, 6, 197. https://doi.org/10.3390/universe6110197
Kokubu T, Harada T. Thin-Shell Wormholes in Einstein and Einstein–Gauss–Bonnet Theories of Gravity. Universe. 2020; 6(11):197. https://doi.org/10.3390/universe6110197
Chicago/Turabian StyleKokubu, Takafumi, and Tomohiro Harada. 2020. "Thin-Shell Wormholes in Einstein and Einstein–Gauss–Bonnet Theories of Gravity" Universe 6, no. 11: 197. https://doi.org/10.3390/universe6110197
APA StyleKokubu, T., & Harada, T. (2020). Thin-Shell Wormholes in Einstein and Einstein–Gauss–Bonnet Theories of Gravity. Universe, 6(11), 197. https://doi.org/10.3390/universe6110197





