Black Holes and Wormholes in Extended Gravity
Abstract
:1. Introduction
2. Dilatonic (Einstein–Maxwell–)Gauss–Bonnet Gravity
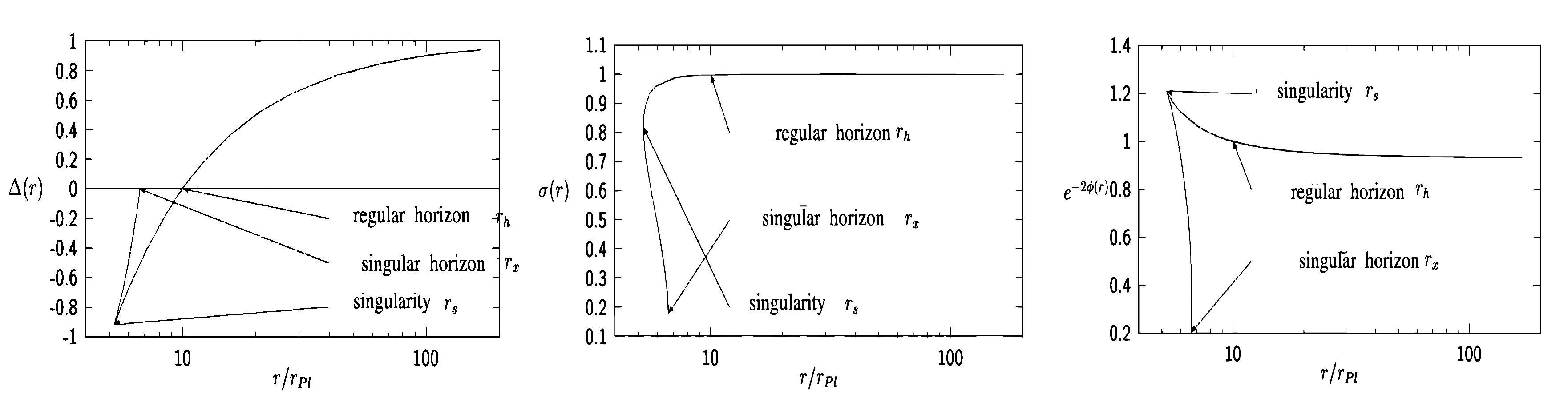
2.1. 4D Black Hole Solutions in Gauss–Bonnet Gravity
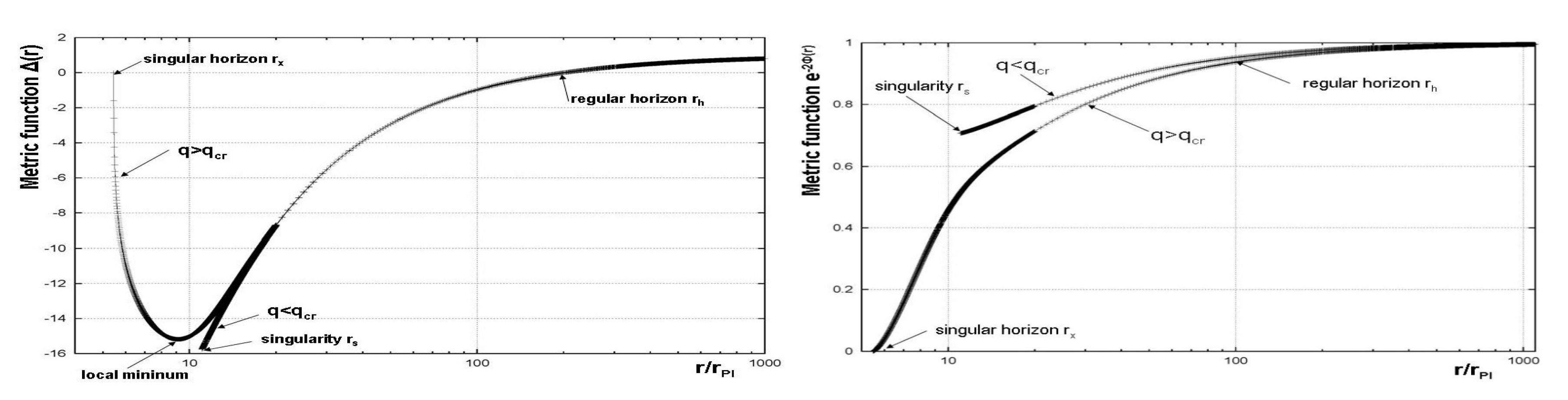
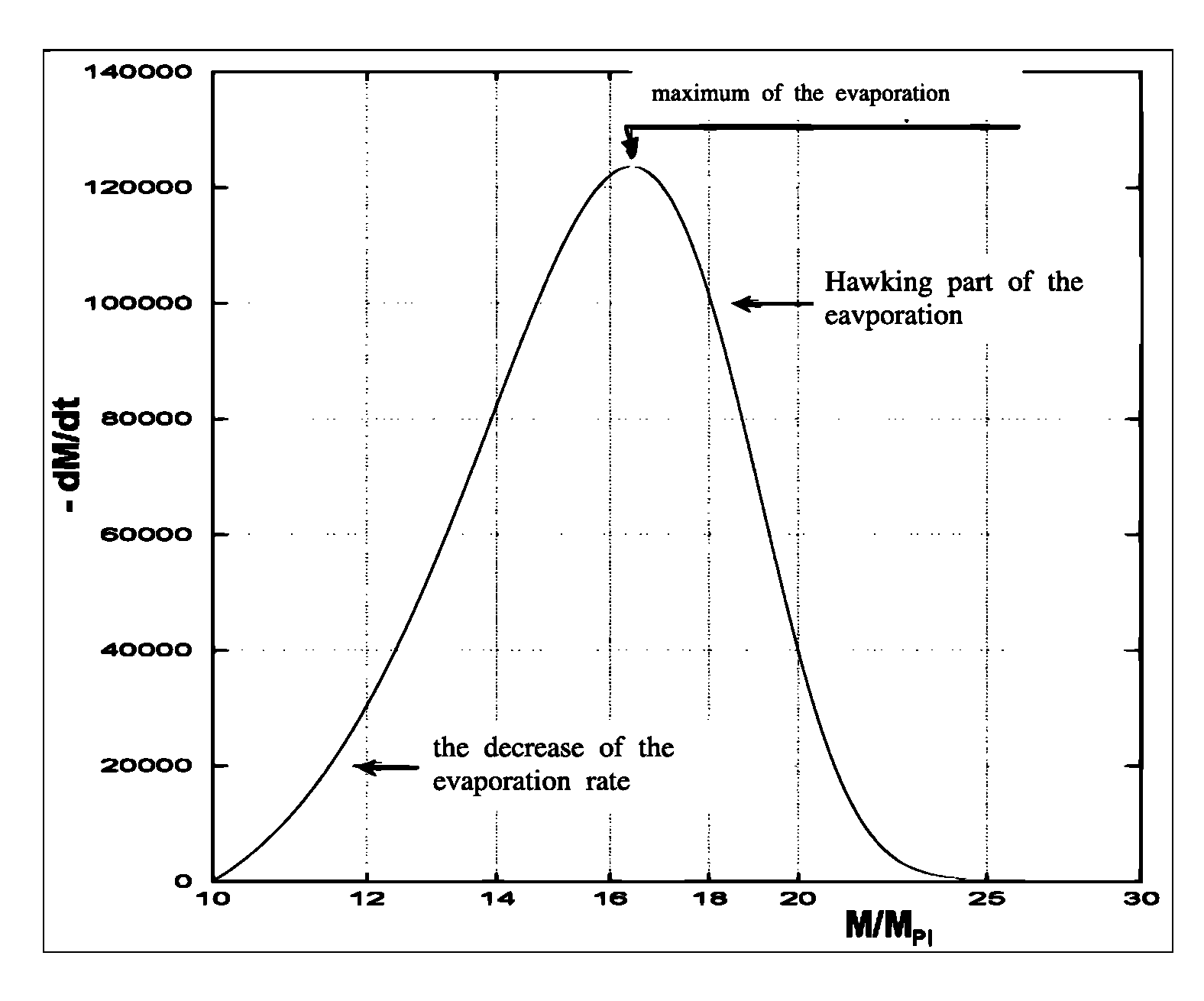
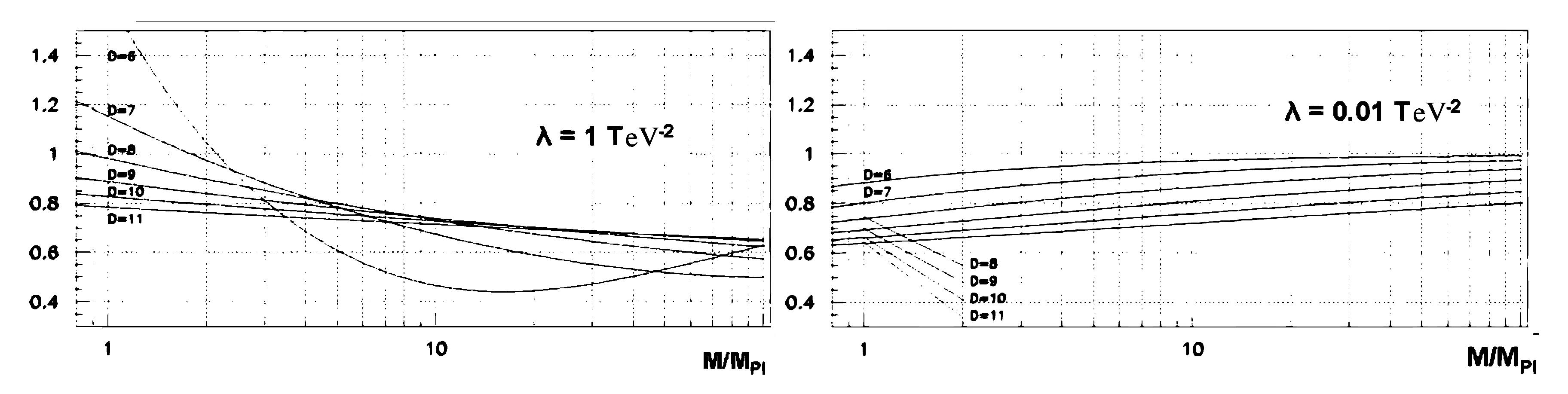
2.2. Multidimensional Non-Rotating Black Hole Solutions in Gauss–Bonnet Gravity
2.3. Dadhich–Molina 6D-Solution
3. Black Hole with the Tidal Charge
4. Brans–Dicke Theory
4.1. Brans–Dicke Spherically-Symmetric Wormhole
4.2. Wormhole Embedded in a de Sitter Universe Solution
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tamaki, T.; Maeda, K.; Torii, T. Non-Abelian black holes in Brans-Dicke theory. Phys. Rev. D 1998, 57, 4870–4884. [Google Scholar] [CrossRef] [Green Version]
- Novikov, I.D.; Frolov, V.P. Physics of Black Holes; Springer: Dordrecht, The Netherlands, 1989; Volume 27. [Google Scholar]
- Lovelock, D. The Einstein tensor and its generalizations. J. Math. Phys. 1971, 12, 498–501. [Google Scholar] [CrossRef]
- Lanczos, C. A Remarkable property of the Riemann-Christoffel tensor in four dimensions. Ann. Math. 1938, 39, 842–850. [Google Scholar] [CrossRef] [Green Version]
- Higgs, P.W. Quadratic lagrangians and general relativity. Nuovo Cim. 1959, 11, 816–820. [Google Scholar] [CrossRef]
- Zwiebach, B. Curvature Squared Terms and String Theories. Phys. Lett. B 1985, 156, 315–317. [Google Scholar] [CrossRef]
- Alexeev, S.O.; Pomazanov, M.V. Black hole solutions with dilatonic hair in higher curvature gravity. Phys. Rev. D 1997, 55, 2110–2118. [Google Scholar] [CrossRef] [Green Version]
- Kanti, P.; Mavromatos, N.E.; Rizos, J.; Tamvakis, K.; Winstanley, E. Dilatonic black holes in higher curvature string gravity. Phys. Rev. D 1996, 54, 5049–5058. [Google Scholar] [CrossRef] [Green Version]
- Wiltshire, D.L. Spherically Symmetric Solutions of Einstein-maxwell Theory With a Gauss–Bonnet Term. Phys. Lett. B 1986, 169, 36–40. [Google Scholar] [CrossRef]
- Mignemi, S.; Wiltshire, D.L. Black holes in higher derivative gravity theories. Phys. Rev. D 1992, 46, 1475–1506. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mignemi, S.; Stewart, N.R. Charged black holes in effective string theory. Phys. Rev. D 1993, 47, 5259–5269. [Google Scholar] [CrossRef] [Green Version]
- Alexeyev, S.O.; Rannu, K.A. Gauss-bonnet black holes and possibilities for their experimental search. J. Exp. Theor. Phys. 2012, 114, 406–427. [Google Scholar] [CrossRef]
- Alekseev, S.O.; Sazhin, M.V. Four-dimensional dilatonic black holes in Gauss–Bonnet extended string gravity. Gen. Rel. Grav. 1998, 30, 1187–1201. [Google Scholar]
- Bakopoulos, A.; Antoniou, G.; Kanti, P. Novel Black-Hole Solutions in Einstein-Scalar-Gauss–Bonnet Theories with a Cosmological Constant. Phys. Rev. D 2019, 99, 064003. [Google Scholar] [CrossRef] [Green Version]
- Alexeyev, S.; Mignemi, S. Black holes and naked singularities in low-energy limit of string gravity with modulus field. Class. Quant. Grav. 2001, 18, 4165–4178. [Google Scholar] [CrossRef] [Green Version]
- Alexeyev, S.; Monong, Y. Additional Constraints on Coupling Functions for String Gravity with Second Order Curvature Corrections; Nova Science: Hauppauge, NY, USA, 2017; pp. 219–226. [Google Scholar]
- Alexeyev, S.; Barrau, A.; Rannu, K.A. Internal structure of a Maxwell-Gauss–Bonnet black hole. Phys. Rev. D 2009, 79, 067503. [Google Scholar] [CrossRef]
- Garfinkle, D.; Horowitz, G.T.; Strominger, A. Charged black holes in string theory. Phys. Rev. D 1991, 43, 3140. [Google Scholar] [CrossRef] [PubMed]
- Alexeyev, S.; Barrau, A.; Boudoul, G.; Khovanskaya, O.; Sazhin, M. Black hole relics in string gravity: Last stages of Hawking evaporation. Class. Quant. Grav. 2002, 19, 4431–4444. [Google Scholar] [CrossRef] [Green Version]
- Minamitsuji, M.; Ikeda, T. Scalarized black holes in the presence of the coupling to Gauss–Bonnet gravity. Phys. Rev. D 2019, 99, 044017. [Google Scholar] [CrossRef] [Green Version]
- Doneva, D.D.; Yazadjiev, S.S. New Gauss–Bonnet Black Holes with Curvature-Induced Scalarization in Extended Scalar-Tensor Theories. Phys. Rev. Lett. 2018, 120, 131103. [Google Scholar] [CrossRef] [Green Version]
- Doneva, D.D.; Staykov, K.V.; Yazadjiev, S.S. Gauss–Bonnet black holes with a massive scalar field. Phys. Rev. D 2019, 99, 104045. [Google Scholar] [CrossRef] [Green Version]
- Antoniou, G.; Bakopoulos, A.; Kanti, P. Black-Hole Solutions with Scalar Hair in Einstein-Scalar-Gauss–Bonnet Theories. Phys. Rev. D 2018, 97, 084037. [Google Scholar] [CrossRef] [Green Version]
- Antoniou, G.; Bakopoulos, A.; Kanti, P. Evasion of No-Hair Theorems and Novel Black-Hole Solutions in Gauss–Bonnet Theories. Phys. Rev. Lett. 2018, 120, 131102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bakopoulos, A.; Kanti, P.; Pappas, N. On the Existence of Solutions with a Horizon in Pure Scalar-Gauss–Bonnet Theories. arXiv 2019, arXiv:1910.14637. [Google Scholar] [CrossRef] [Green Version]
- Alekseev, S.O.; Khovanskaya, O.S. Additional study of a restriction on the minimum black hole mass in string gravity. Grav. Cosmol. 2000, 6, 14–18. [Google Scholar]
- Aguilar-Pérez, G.; Cruz, M.; Lepe, S.; Moran-Rivera, I. Hairy black hole stability under odd parity perturbations in the Einstein-Gauss–Bonnet model. arXiv 2019, arXiv:1907.06168. [Google Scholar]
- Myung, Y.S.; Zou, D.C. Black holes in Gauss–Bonnet and Chern–Simons-scalar theory. arXiv 2019, arXiv:1903.08312. [Google Scholar] [CrossRef] [Green Version]
- Blázquez-Salcedo, J.L.; Doneva, D.D.; Kunz, J.; Yazadjiev, S.S. Radial perturbations of the scalarized Einstein-Gauss–Bonnet black holes. Phys. Rev. D 2018, 98, 084011. [Google Scholar] [CrossRef] [Green Version]
- Cai, R.G. Gauss–Bonnet black holes in AdS spaces. Phys. Rev. D 2002, 65, 084014. [Google Scholar] [CrossRef] [Green Version]
- Barrau, A.; Grain, J.; Alexeyev, S.O. Gauss–Bonnet black holes at the LHC: Beyond the dimensionality of space. Phys. Lett. B 2004, 584, 114. [Google Scholar] [CrossRef] [Green Version]
- Alexeyev, S.; Popov, N.; Startseva, M.; Barrau, A.; Grain, J. Kerr-Gauss–Bonnet Black Holes: Exact Analytical Solution. J. Exp. Theor. Phys. 2008, 106, 709–713. [Google Scholar] [CrossRef] [Green Version]
- Page, D.N. Particle Emission Rates from a Black Hole. 2. Massless Particles from a Rotating Hole. Phys. Rev. D 1976, 14, 3260–3273. [Google Scholar] [CrossRef]
- Maeda, H.; Dadhich, N. Kaluza-Klein black hole with negatively curved extra dimensions in string generated gravity models. Phys. Rev. D 2006, 74, 021501. [Google Scholar] [CrossRef] [Green Version]
- Maeda, H.; Dadhich, N. Matter without matter: Novel Kaluza-Klein spacetime in Einstein-Gauss–Bonnet gravity. Phys. Rev. D 2007, 75, 044007. [Google Scholar] [CrossRef] [Green Version]
- Dadhich, N.; Maeda, H. Origin of matter out of pure curvature. Int. J. Mod. Phys. D 2008, 17, 513–518. [Google Scholar] [CrossRef] [Green Version]
- Molina, A.; Dadhich, N. On Kaluza-Klein spacetime in Einstein-Gauss–Bonnet gravity. Int. J. Mod. Phys. D 2009, 18, 599–611. [Google Scholar] [CrossRef] [Green Version]
- Alexeyev, S.O.; Petrov, A.N.; Latosh, B.N. Maeda-Dadhich Solutions as Real Black Holes. Phys. Rev. D 2015, 92, 104046. [Google Scholar] [CrossRef] [Green Version]
- Dadhich, N.; Maartens, R.; Papadopoulos, P.; Rezania, V. Black holes on the brane. Phys. Lett B. 2000, 487, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Pugliese, D.; Quevedo, H.; Ruffini, R. Circular motion of neutral test particles in Reissner–Nordstrom spacetime. Phys. Rev. D 2011, 83, 024021. [Google Scholar] [CrossRef] [Green Version]
- Doeleman, S.S.; Fish, V.L.; Schenck, D.E.; Beaudoin, C.; Blundell, R.; Bower, G.C.; Broderick, A.E.; Chamberlin, R.; Freund, R.; Friberg, P.; et al. Jet Launching Structure Resolved Near the Supermassive Black Hole in M87. Science 2012, 338, 355–358. [Google Scholar] [CrossRef] [Green Version]
- Hawking, S.W. Particle Creation by Black Holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Shankaranarayanan, S.; Padmanabhan, T.; Srinivasan, K. Hawking radiation in different coordinate settings: Complex paths approach. Class. Quant. Grav. 2002, 19, 2671–2688. [Google Scholar] [CrossRef] [Green Version]
- Randall, L.; Sundrum, R. An Alternative to compactification. Phys. Rev. Lett. 1999, 83, 4690–4693. [Google Scholar] [CrossRef] [Green Version]
- Shiromizu, T.; Maeda, K.i.; Sasaki, M. The Einstein equation on the 3-brane world. Phys. Rev. D 2000, 62, 024012. [Google Scholar] [CrossRef] [Green Version]
- Alexeyev, S.O.; Starodubtseva, D.A. Black holes in models with noncompact extra dimensions. J. Exp. Theor. Phys. 2010, 111, 576–581. [Google Scholar] [CrossRef]
- Cherepashchuk, A.M. Black holes in binary stellar systems and galactic nuclei. Phys. Usp. 2014, 57, 359–376. [Google Scholar] [CrossRef]
- Zakharov, A.F. Constraints on a charge in the Reissner–Nordstrom metric for the black hole at the Galactic Center. Phys. Rev. D 2014, 90, 062007. [Google Scholar] [CrossRef] [Green Version]
- Alexeyev, S.O.; Latosh, B.N.; Prokopov, V.A.; Emtsova, E.D. Phenomenological Extension for Tidal Charge Black Hole. J. Exp. Theor. Phys. 2019, 128, 720–726. [Google Scholar] [CrossRef] [Green Version]
- Brans, C.; Dicke, R.H. Mach’s principle and a relativistic theory of gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Bertotti, B.; Iess, L.; Tortora, P. A test of general relativity using radio links with the Cassini spacecraft. Nature 2003, 425, 374–376. [Google Scholar] [CrossRef]
- Hrycyna, O.; Szydlowski, M. Brans–Dicke theory and the emergence of ΛCDM model. Phys. Rev. D 2013, 88, 064018. [Google Scholar] [CrossRef] [Green Version]
- Campanelli, M.; Lousto, C.O. Are black holes in Brans–Dicke theory precisely the same as a general relativity? Int. J. Mod. Phys. D 1993, 2, 451–462. [Google Scholar] [CrossRef] [Green Version]
- Agnese, A.G.; La Camera, M. Wormholes in the Brans–Dicke theory of gravitation. Phys. Rev. D 1995, 51, 2011–2013. [Google Scholar] [CrossRef] [PubMed]
- Bhadra, A.; Sarkar, K. On static spherically symmetric solutions of the vacuum Brans–Dicke theory. Gen. Relativ. Gravit. 2005, 37, 2189–2199. [Google Scholar] [CrossRef]
- Elizalde, E.; Nojiri, S.; Odintsov, S.D. Late-time cosmology in (phantom) scalar-tensor theory: Dark energy and the cosmic speed-up. Phys. Rev. D 2004, 70, 043539. [Google Scholar] [CrossRef] [Green Version]
- Xiao, X.G.; Zhu, J.Y. Wormhole solution in vacuum Brans–Dicke theory with cosmological constant. Chin. Phys. Lett. 1996, 13, 405–408. [Google Scholar] [CrossRef]
- Alexeyev, S.O.; Rannu, K.A.; Gareeva, D.V. Possible observation sequences of Brans–Dicke wormholes. J. Exp. Theor. Phys. 2011, 113, 628–636. [Google Scholar] [CrossRef] [Green Version]
- Tretyakova, D.A.; Latosh, B.N.; Alexeyev, S.O. Wormholes and naked singularities in Brans–Dicke cosmology. Class. Quant. Grav. 2015, 32, 18500. [Google Scholar] [CrossRef] [Green Version]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.-K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First, M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar]
- Goddi, C.; Crew, G.; Impellizzeri, V.; Martí-Vidal, I.; Matthews, L.D.; Messias, H.; Rottmann, H.; Alef, W.; Blackburn, L.; Bronzwaer, T.; et al. First, M87 Event Horizon Telescope Results and the Role of ALMA. Messenger 2019, 177, 25. [Google Scholar]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 509, 167–321. [Google Scholar] [CrossRef] [Green Version]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alexeyev, S.; Sendyuk, M. Black Holes and Wormholes in Extended Gravity. Universe 2020, 6, 25. https://doi.org/10.3390/universe6020025
Alexeyev S, Sendyuk M. Black Holes and Wormholes in Extended Gravity. Universe. 2020; 6(2):25. https://doi.org/10.3390/universe6020025
Chicago/Turabian StyleAlexeyev, Stanislav, and Maxim Sendyuk. 2020. "Black Holes and Wormholes in Extended Gravity" Universe 6, no. 2: 25. https://doi.org/10.3390/universe6020025
APA StyleAlexeyev, S., & Sendyuk, M. (2020). Black Holes and Wormholes in Extended Gravity. Universe, 6(2), 25. https://doi.org/10.3390/universe6020025



