Localization of Energy and Momentum in an Asymptotically Reissner-Nordström Non-Singular Black Hole Space-Time Geometry
Abstract
1. Introduction
2. The Asymptotically Reissner-Nordström Non-Singular Black Hole Space-Time Geometry
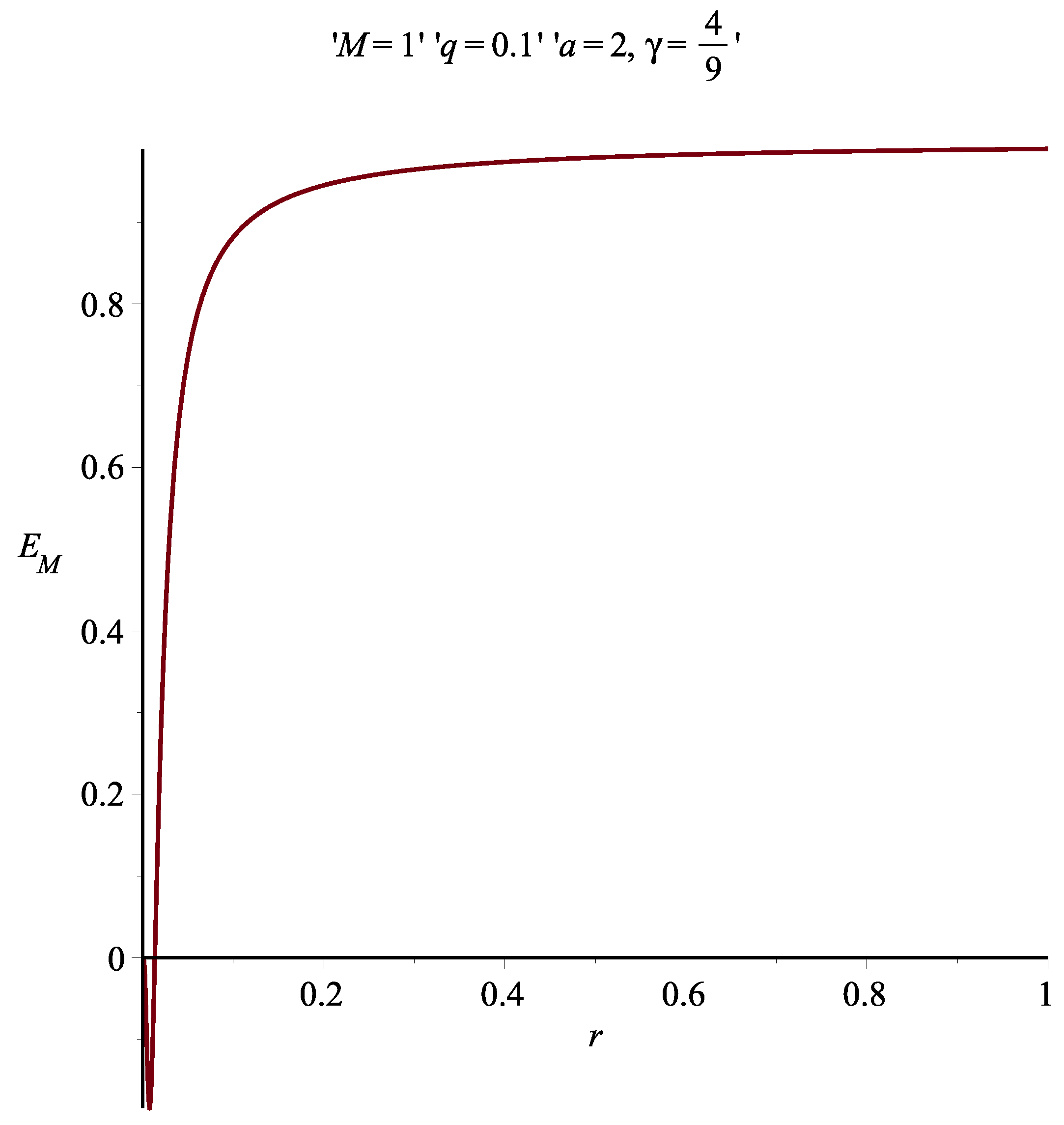
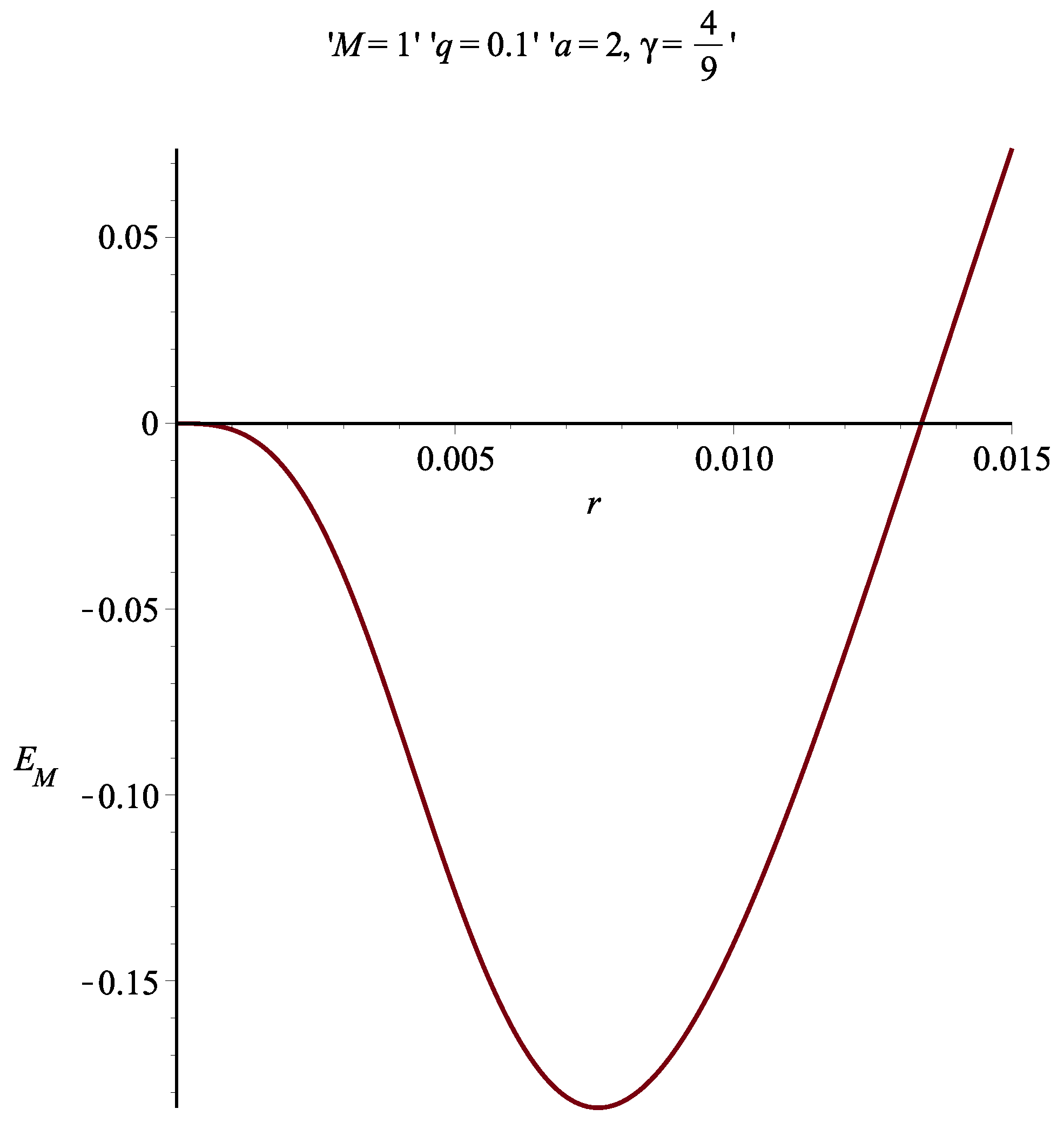
3. Einstein Prescription and the Energy Distribution of the Asymptotically Reissner-Nordström Non-Singular Black Hole
4. Landau-Lifshitz Energy-Momentum Complex and the Energy Distribution of the Asymptotically Reissner-Nordström Non-Singular Black Hole
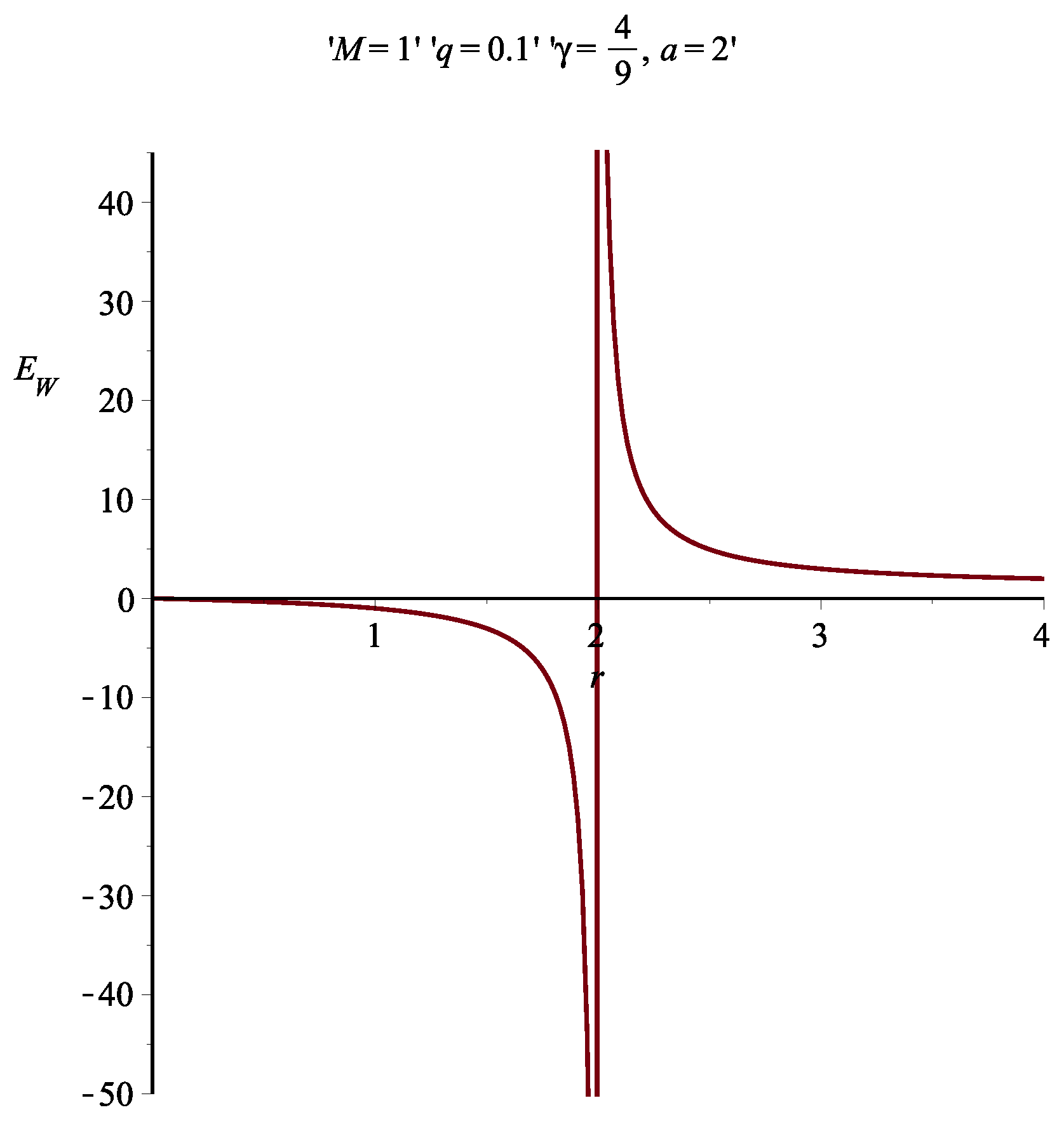
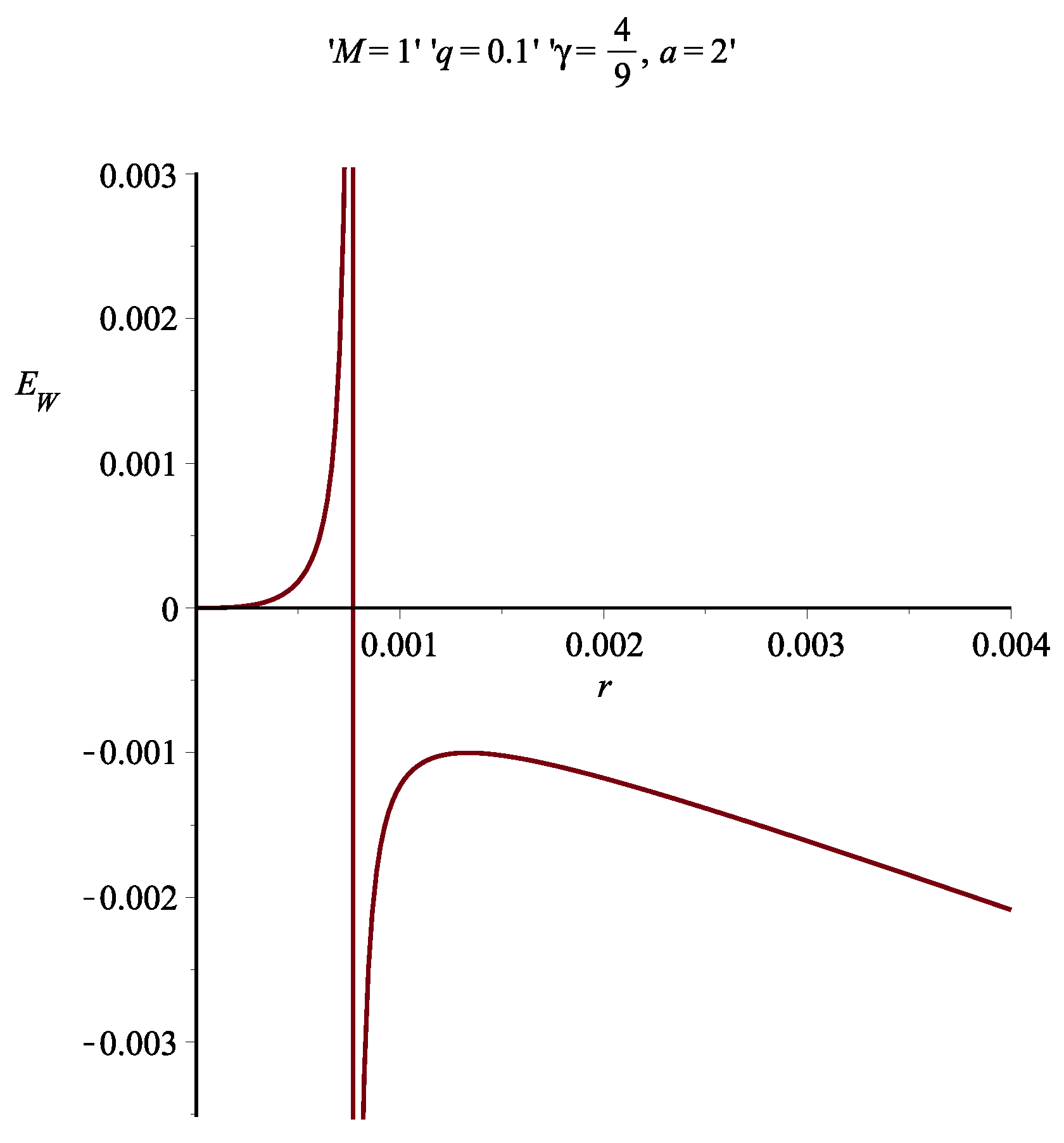
5. Weinberg Prescription and the Energy Distribution of the Asymptotically Reissner-Nordström Non-Singular Black Hole
6. Møller Prescription and the Energy Distribution of the Asymptotically Reissner-Nordström Non-Singular Black Hole
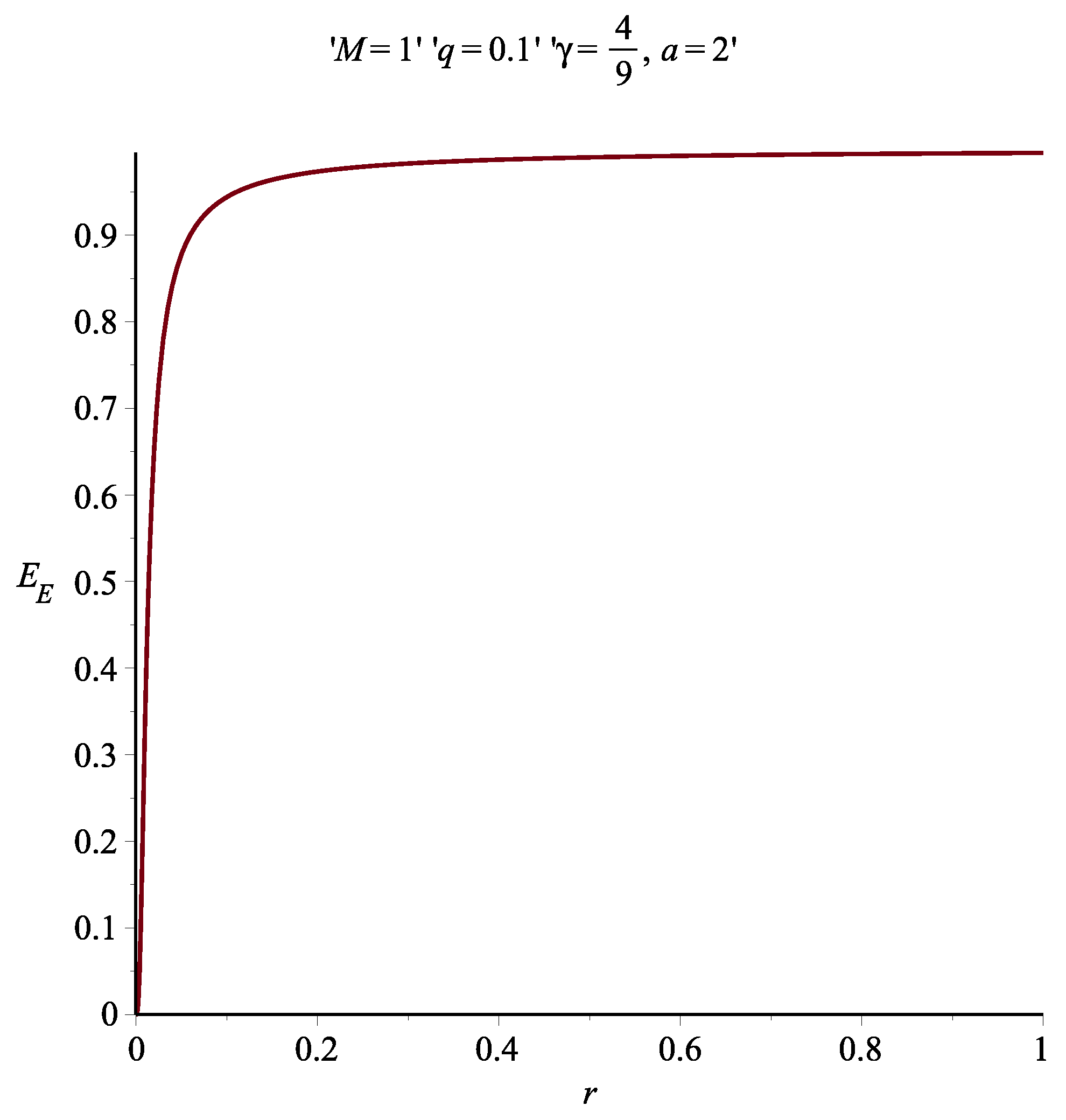
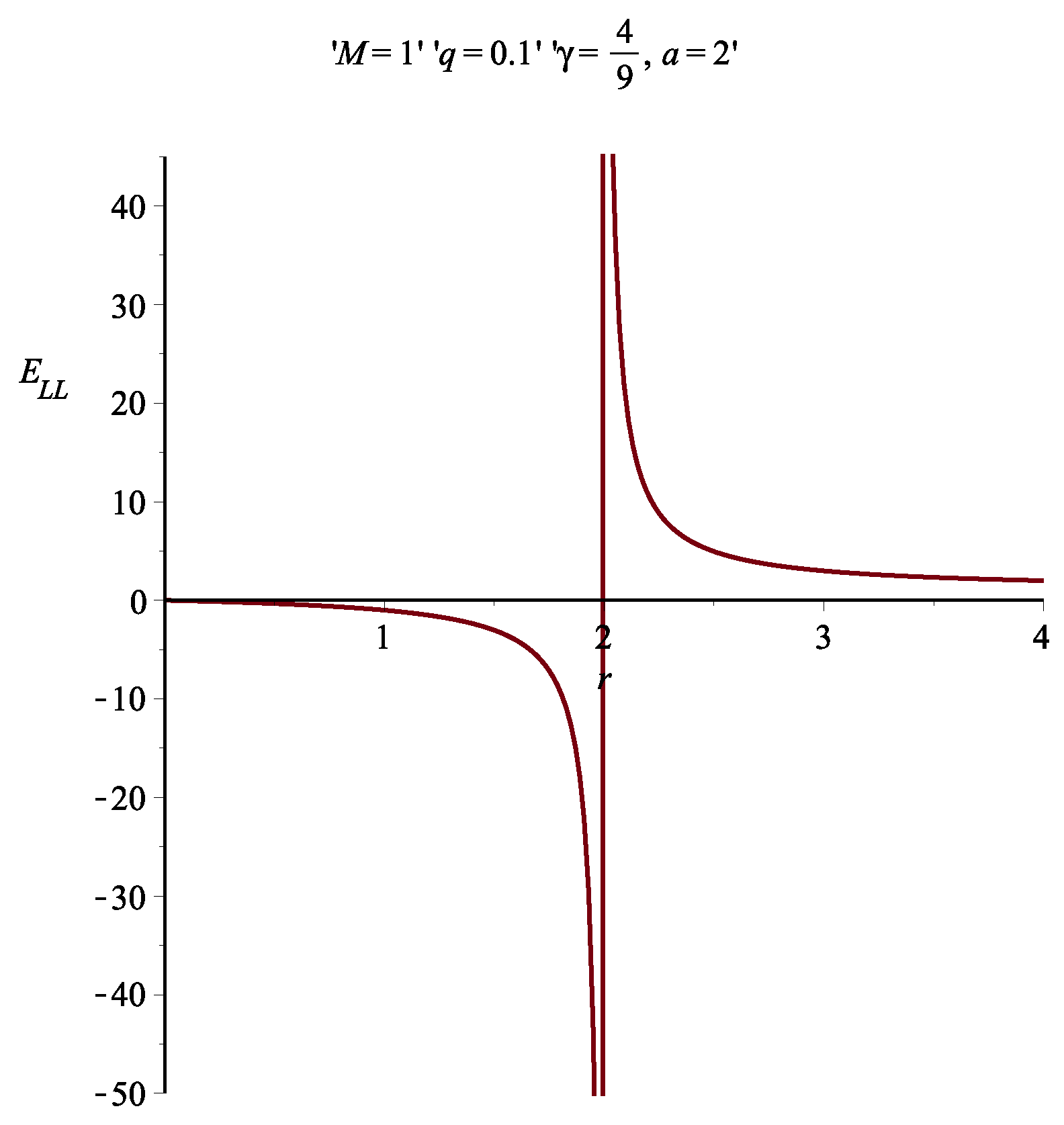
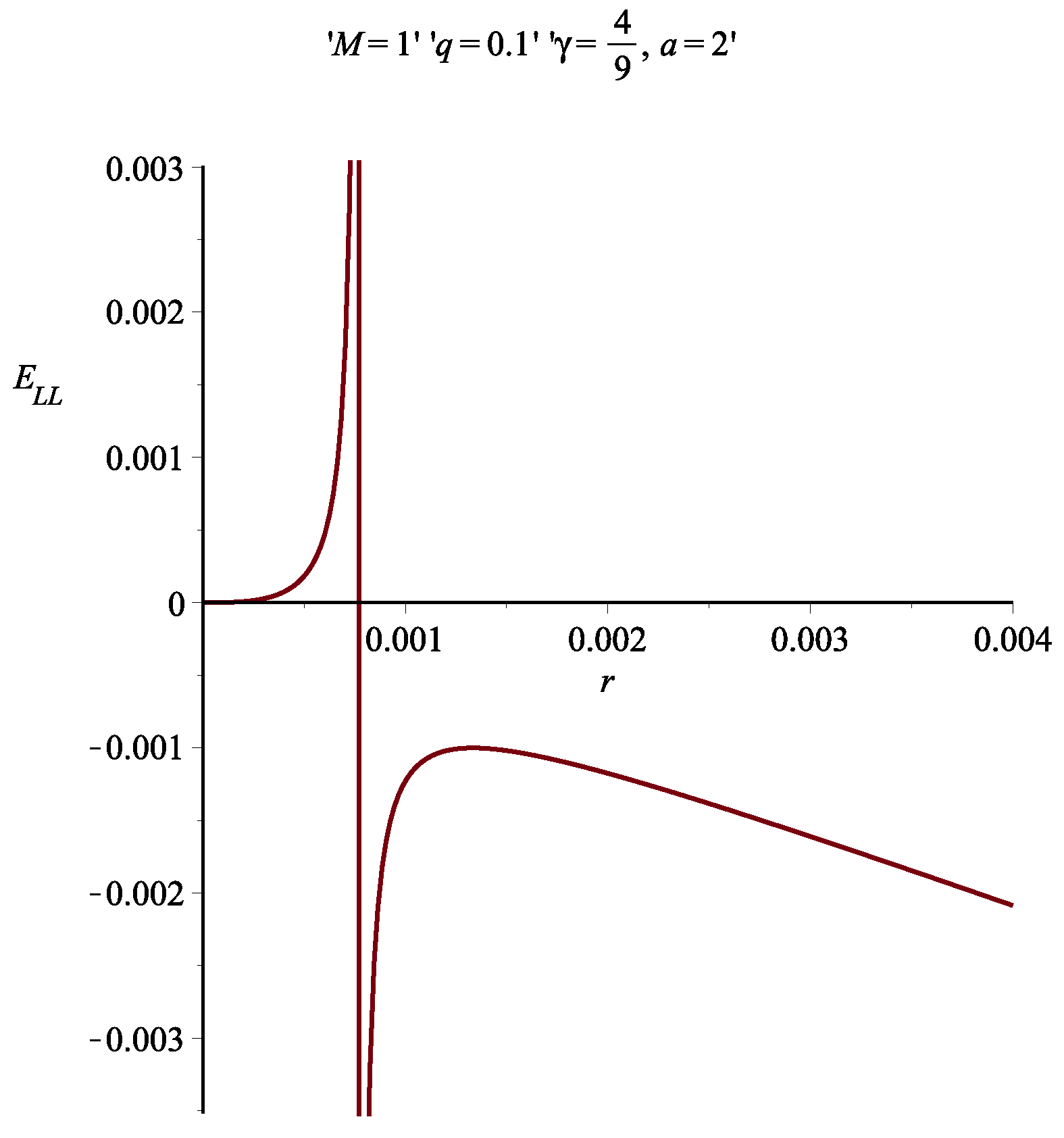
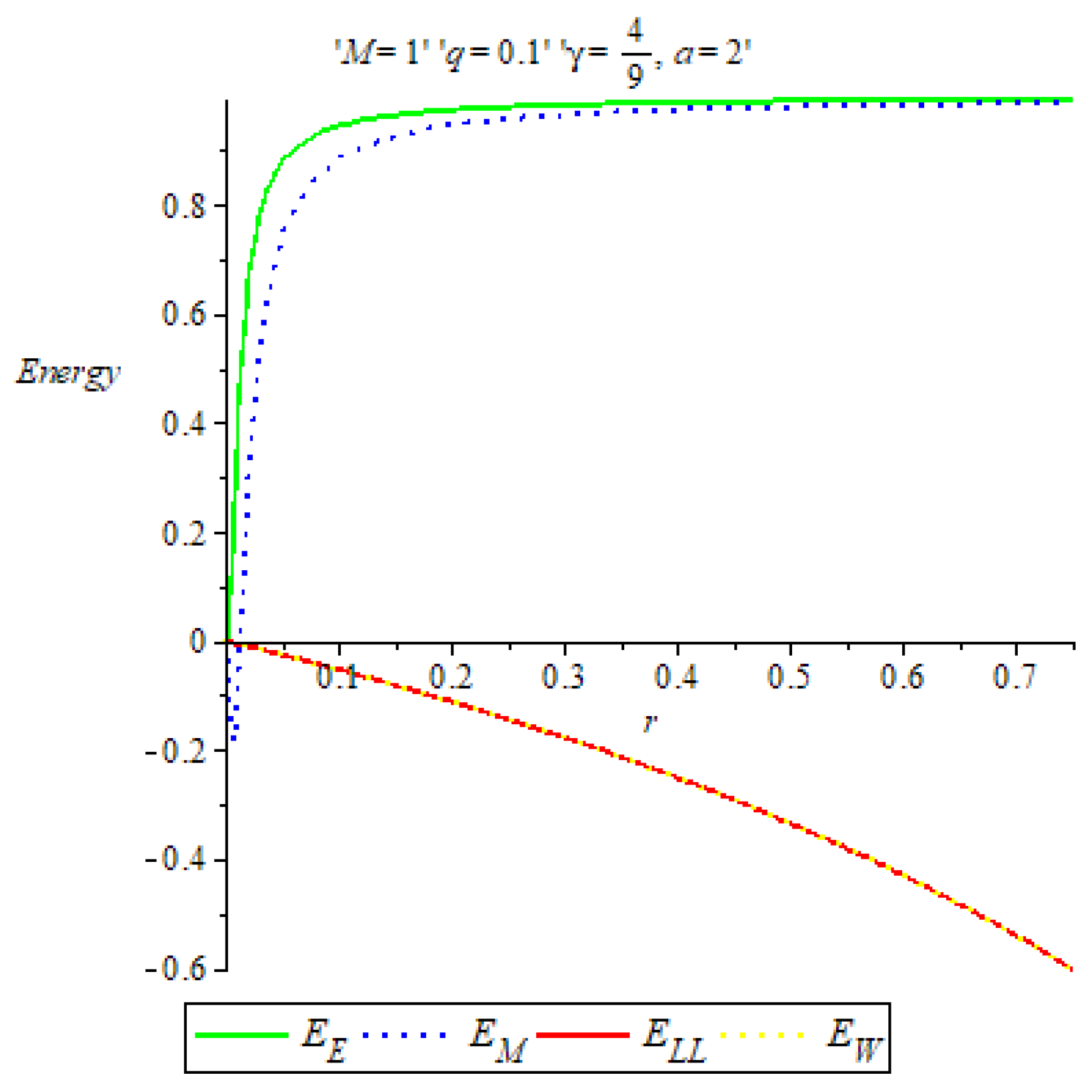
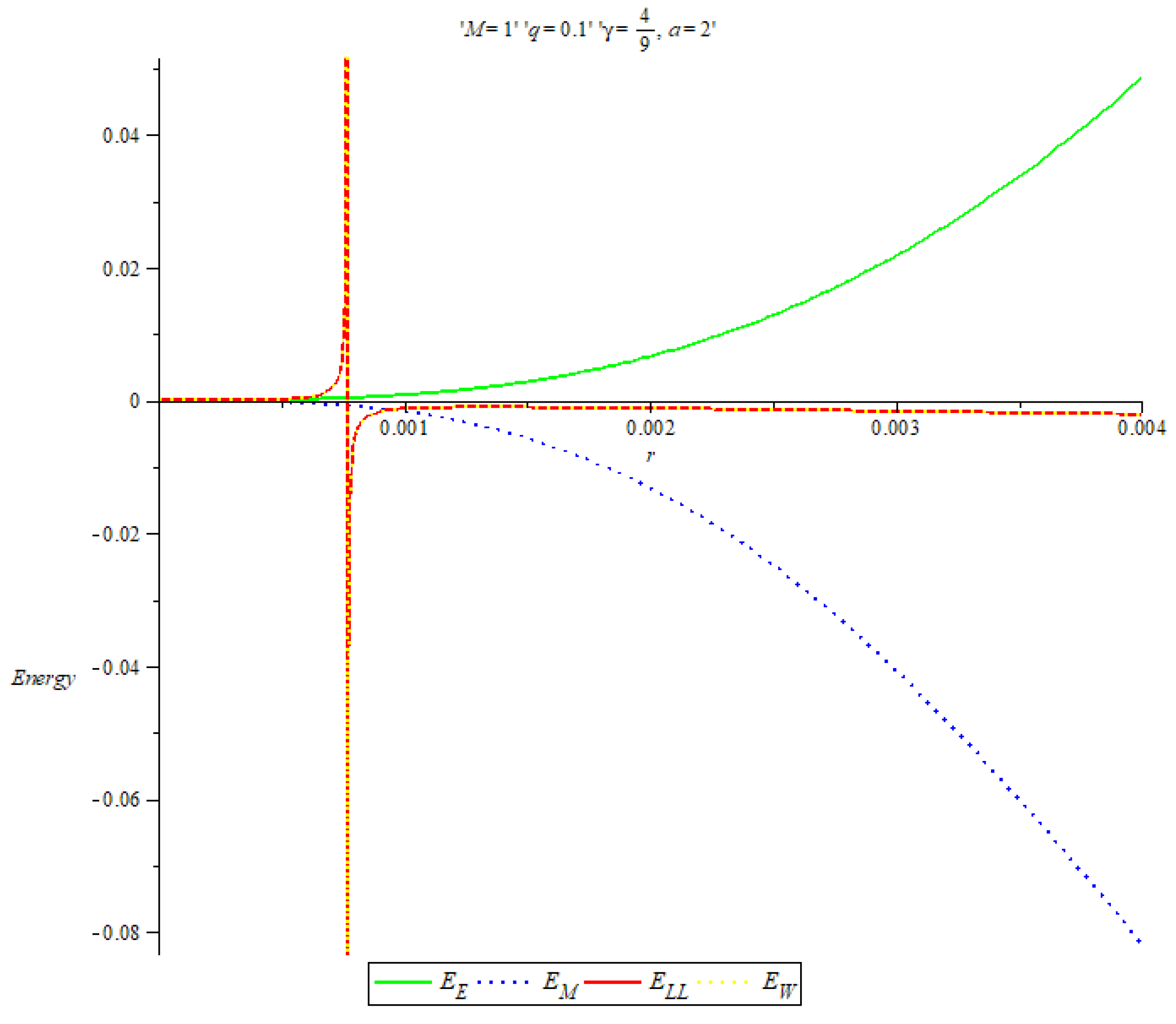
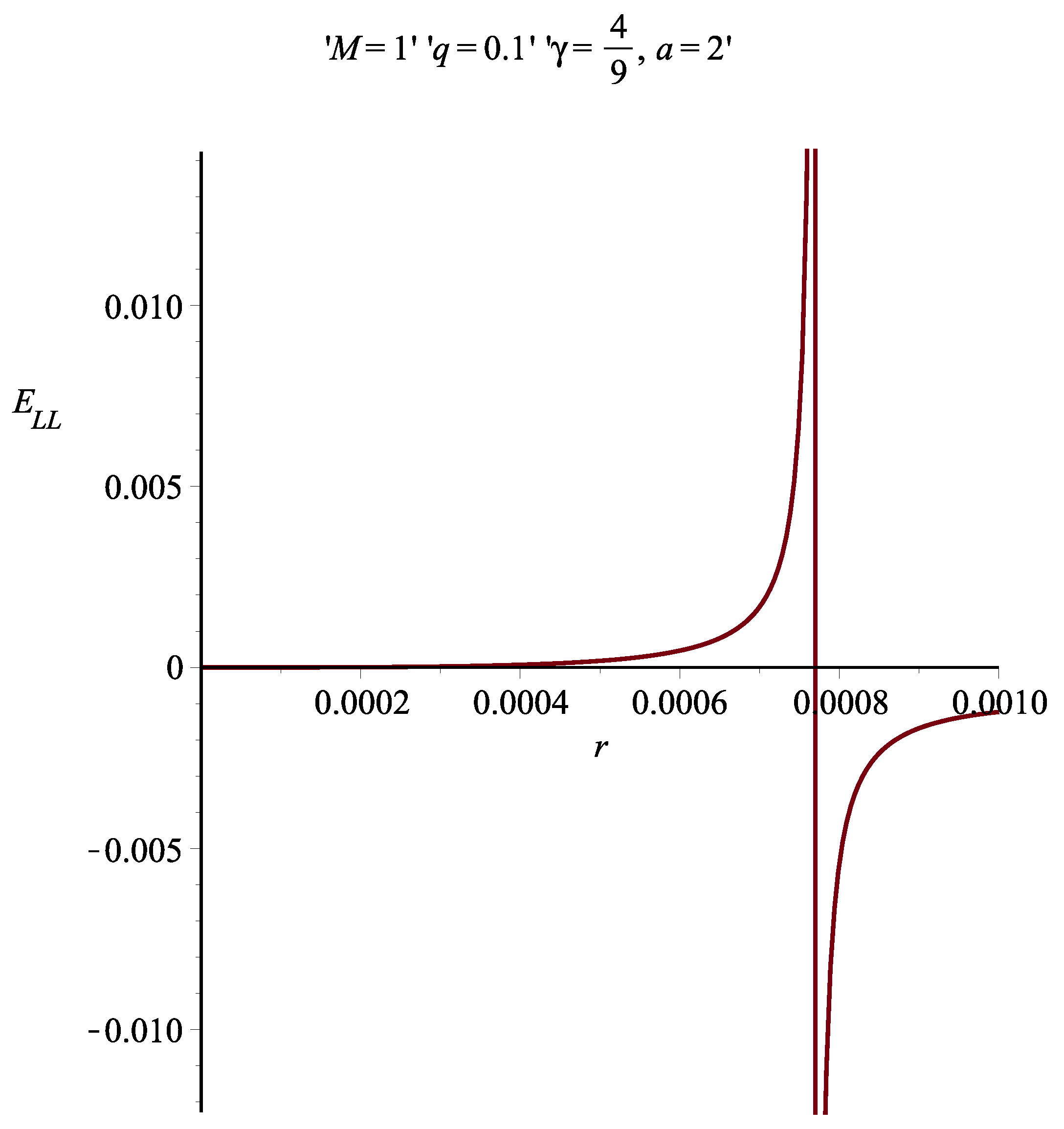
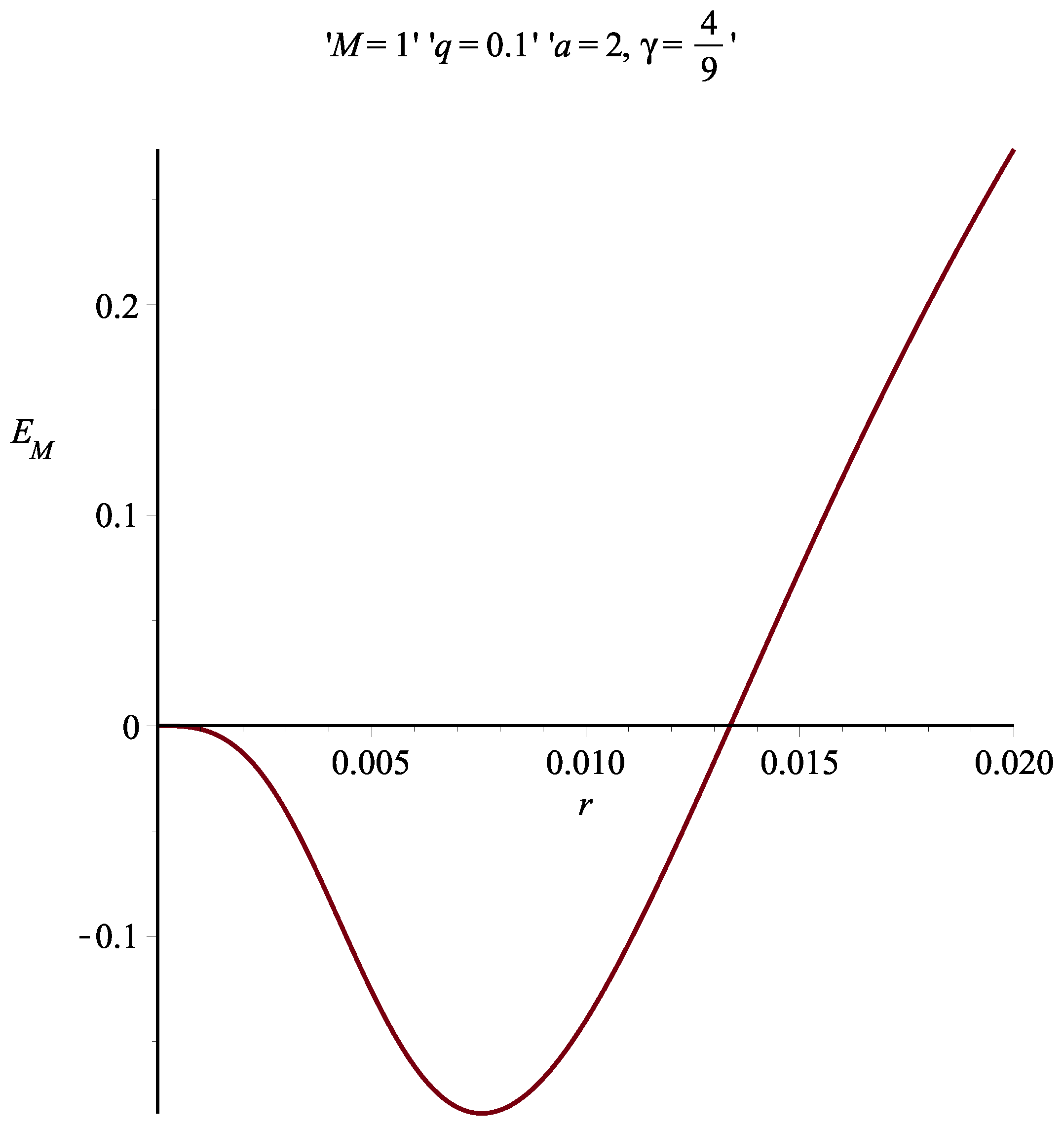
7. Results and Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bel, L. Définition d’une densité d’énergie et d’un état de radiation totale généralisée. Comptes Rendus de l’Académie des Sciences 1958, 246, 3015–3018. [Google Scholar]
- Bonilla, M.Á.; Senovilla, J.M. Some properties of the Bel and Bel-Robinson tensors. Gen. Relativ. Gravit. 1997, 29, 91–116. [Google Scholar] [CrossRef]
- Senovilla, J.M. The universal ‘energy’operator. Class. Quantum Gravity 2006, 23, 7143. [Google Scholar] [CrossRef]
- Brown, J.D.; York, J.W., Jr. Quasilocal energy and conserved charges derived from the gravitational action. Phys. Rev. D 1993, 47, 1407. [Google Scholar] [CrossRef]
- Hayward, S.A. Quasilocal gravitational energy. Phys. Rev. D 1994, 49, 831. [Google Scholar] [CrossRef]
- Chen, C.M.; Nester, J.M. Quasilocal quantities for general relativity and other gravity theories. Class. Quantum Gravity 1999, 16, 1279. [Google Scholar] [CrossRef]
- Lui, C.C.M.; Yau, S.T. Positivity of quasilocal mass. Phys. Rev. Lett. 2003, 90, 231102. [Google Scholar] [CrossRef] [PubMed]
- Balart, L. Quasilocal energy, Komar charge and horizon for regular black holes. Phys. Lett. B 2010, 687, 280–285. [Google Scholar] [CrossRef]
- Einstein, A. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften. 1915. Available online: https://einsteinpapers.press.princeton.edu/vol6-doc/ (accessed on 2 April 2020).
- Trautman, A. Conservation laws in general relativity. In Gravitation: An Introduction to Current Research; Witten, L., Ed.; John Wiley & Sons: New York, NY, USA, 1962; p. 169. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Pergamon Press: New York, NY, USA, 1987; p. 280. [Google Scholar]
- Papapetrou, A. Equations of motion in general relativity. Proc. Phys. Soc. Sect. A 1951, 64, 57. [Google Scholar] [CrossRef]
- Bergmann, P.G.; Thomson, R. Spin and angular momentum in general relativity. Phys. Rev. 1953, 89, 400. [Google Scholar] [CrossRef]
- Møller, C. On the localization of the energy of a physical system in the general theory of relativity. Ann. Phys. 1958, 4, 347–371. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of General Theory of Relativity; John Wiley & Sons: New York, NY, USA, 1972; p. 165. [Google Scholar]
- Vagenas, E.C. Energy distribution in a BTZ black hole spacetime. Int. J. Mod. Phys. D 2005, 14, 573. [Google Scholar] [CrossRef]
- Multamäki, T.; Putaja, A.; Vilja, I.; Vagenas, E.C. Energy–momentum complexes in f (R) theories of gravity. Class. Quantum Gravity 2008, 25, 075017. [Google Scholar] [CrossRef]
- Rosen, N.; Virbhadra, K.S. Energy and momentum of cylindrical gravitational waves. Gen. Relativ. Gravit. 1993, 25, 429. [Google Scholar] [CrossRef]
- Aygün, S.; Tarhan, I. Energy momentum localization for Bianchi type-IV Universe in general relativity and teleparallel gravity. Pramana 2012, 78, 531–548. [Google Scholar] [CrossRef]
- Radinschi, I. Energy associated with the Bianchi type VI0 Universe. Chin. J. Phys. 2001, 39, 393. [Google Scholar]
- Sahoo, P.K.; Mahanta, K.L.; Goit, D.; Sinha, A.K.; Xulu, S.S.; Das, U.R.; Prasad, A.; Prasad, R. Einstein energy-momentum complex for a phantom black hole metric. Chin. Phys. Lett. 2015, 32, 020402. [Google Scholar] [CrossRef][Green Version]
- Tripathy, S.K.; Mishra, B.; Pandey, G.K.; Singh, A.K.; Kumar, T.; Xulu, S.S. Energy and Momentum of Bianchi Type Universes. Adv. High Energy Phys. 2015, 2015, 705262. [Google Scholar] [CrossRef]
- Radinschi, I.; Rahaman, F.; Banerjee, A. The energy distribution of Hořava-Lifshitz black hole solutions. Int. J. Theor. Phys. 2012, 51, 1425–1434. [Google Scholar] [CrossRef]
- Radinschi, I.; Grammenos, T. Møller’s energy-momentum complex for a spacetime geometry on a noncommutative curved D3-brane. Int. J. Theor. Phys. 2008, 47, 1363–1372. [Google Scholar] [CrossRef]
- Aguirregabiria, J.M.; Chamorro, A.; Virbhadra, K.S. Energy and angular momentum of charged rotating black holes. Gen. Relativ. Gravit. 1996, 28, 1393. [Google Scholar] [CrossRef]
- Xulu, S.S. Bergmann–Thomson Energy-Momentum Complex for Solutions More General than the Kerr–Schild Class. Int. J. Theor. Phys. 2007, 46, 2915–2922. [Google Scholar] [CrossRef]
- Virbhadra, K.S. Naked singularities and Seifert’s conjecture. Phys. Rev. D 1999, 60, 104041. [Google Scholar] [CrossRef]
- Yang, I.C.; Lin, C.L.; Radinschi, I. The energy of regular black hole in general relativity coupled to nonlinear electrodynamics. Int. J. Theor. Phys. 2009, 48, 248–255. [Google Scholar] [CrossRef]
- Radinschi, I.; Rahaman, F.; Ghosh, A. On the energy of charged black holes in generalized dilaton-axion gravity. Int. J. Theor. Phys. 2010, 49, 943–956. [Google Scholar] [CrossRef][Green Version]
- Radinschi, I.; Rahaman, F.; Banerjee, A. On the Energy of Hořava–Lifshitz Black Holes. Int. J. Theor. Phys. 2011, 50, 2906–2916. [Google Scholar] [CrossRef]
- Sahoo, P.K.; Radinschi, I.; Mahanta, K.L. Energy–momentum distribution in general relativity for a phantom black hole metric. Indian J. Phys. 2019. [Google Scholar] [CrossRef]
- Abdel-Megied, M.; Gad, R.M. Møller’s energy in the Kantowski-Sachs space-time. Adv. High Energy Phys. 2010, 2010, 379473. [Google Scholar] [CrossRef]
- Sharif, M.; Azam, M. Energy–momentum distribution: Some examples. Int. J. Mod. Phys. A 2007, 22, 1935. [Google Scholar] [CrossRef]
- Vagenas, E.C. Energy distribution in 2D stringy black hole backgrounds. Int. J. Mod. Phys. A 2003, 18, 5781. [Google Scholar] [CrossRef]
- Dogru, M.U.; Varlikli, N.; Baykal, D.; Kiy, G.; Taser, D.; Çaglar, H.; Gunduz, E. Energy and momentum of higher dimensional black holes. Int. J. Theor. Phys. 2012, 51, 1545–1554. [Google Scholar] [CrossRef]
- Vagenas, E.C. Energy distribution in the dyadosphere of a Reissner-Nordstrom black hole in Møller’s prescription. Mod. Phys. Lett. A 2006, 21, 1947. [Google Scholar] [CrossRef]
- Balart, L. Energy distribution of (2+1)-dimensional black holes with nonlinear electrodynamics. Mod. Phys. Lett. A 2009, 24, 2777. [Google Scholar] [CrossRef]
- Ragab, M.G.; Fouad, A. Energy and Momentum Distributions of Kantowski and Sachs Space-time. Astrophys. Space Sci. 2007, 310, 135–140. [Google Scholar]
- Matyjasek, J. Some remarks on the Einstein and Møller pseudotensors for static and spherically-symmetric configurations. Mod. Phys. Lett. A 2008, 23, 591. [Google Scholar] [CrossRef]
- Nashed, G.G.L. Energy distribution of Kerr spacetime using Moller energy momentum complex. Nuovo Cimento 2004, B119, 967–974. [Google Scholar]
- Dogru, M.U.; Baykal, D.; Kiy, G.; Taser, D.; Caglar, H.; Varlikli, N. Energy-momentum distributions of five-dimensional homogeneous-anisotropic universes. Int. J. Mod. Phys. D 2012, 21, 1250078. [Google Scholar] [CrossRef]
- Nester, J.M.; So, L.L.; Vargas, T. Energy of homogeneous cosmologies. Phys. Rev. D 2008, 78, 044035. [Google Scholar] [CrossRef]
- Nashed, G.G. Energy of spherically symmetric space-times on regularizing teleparallelism. Int. J. Mod. Phys. A 2010, 25, 2883. [Google Scholar] [CrossRef]
- Sharif, M.; Jawad, A. Energy contents of some well-known solutions in teleparallel gravity. Astrophys. Space Sci. 2011, 331, 257–263. [Google Scholar] [CrossRef]
- Maluf, J.W.; Veiga, M.V.O.; da Rocha-Neto, J.F. Regularized expression for the gravitational energy-momentum in teleparallel gravity and the principle of equivalence. Gen. Relativ. Gravit. 2007, 39, 227. [Google Scholar] [CrossRef]
- Mourad, M.F. Gravitational energy–momentum and gravitational flux of cylindrically rotating solution in the teleparallel gravity. Indian J. Phys. 2019, 93, 1233–1239. [Google Scholar] [CrossRef]
- Aygün, S.; Baysal, H.; Aktaş, C.; Yılmaz, I.; Sahoo, P.K.; Tarhan, I. Teleparallel energy–momentum distribution of various black hole and wormhole metrics. Int. J. Mod. Phys. A 2018, 33, 1850184. [Google Scholar] [CrossRef]
- Ganiou, M.G.; Houndjo, M.J.S.; Tossa, J. f (T) gravity and energy distribution in Landau–Lifshitz prescription. Int. J. Mod. Phys. D 2018, 27, 1850039. [Google Scholar] [CrossRef]
- Penrose, R. Quasi-local mass and angular momentum in general relativity. Proc. R. Soc. Lond. A Math. Phys. Sci. 1982, 381, 53–63. [Google Scholar]
- Tod, K.P. Some examples of Penrose’s quasi-local mass construction. Proc. R. Soc. Lond. A. Math. Phys. Sci. 1983, 388, 457–477. [Google Scholar]
- Wang, M.T.; Yau, S.T. Quasilocal mass in general relativity. Phys. Rev. Lett. 2009, 102, 021101. [Google Scholar] [CrossRef]
- Wang, M.T.; Yau, S.T. Isometric embeddings into the Minkowski space and new quasi-local mass. Commun. Math. Phys. 2019, 288, 919–942. [Google Scholar] [CrossRef]
- Chen, C.M.; Liu, J.L.; Nester, J.M. Gravitational energy is well defined. Int. J. Mod. Phys. D 2018, 27, 1847017. [Google Scholar] [CrossRef]
- Chen, C.M.; Liu, J.L.; Nester, J.M. Quasi-local energy from a Minkowski reference. Gen. Relativ. Gravit. 2018, 50, 158. [Google Scholar] [CrossRef]
- Balart, L.; Vagenas, E.C. Regular black holes with a nonlinear electrodynamics source. Phys. Rev. D 2014, 90, 124045. [Google Scholar] [CrossRef]
- Ayon-Beato, E.; Garcia, A. Regular black hole in general relativity coupled to nonlinear electrodynamics. Phys. Rev. Lett. 1998, 80, 5056–5059. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Capozziello, S. Magnetic black holes in Weitzenböck geometry. Gen. Relativ. Gravit. 2019, 51, 50. [Google Scholar] [CrossRef]
- Nashed, G.G.L.; Capozziello, S. Charged spherically symmetric black holes in f(R) gravity and their stability analysis. Phys. Rev. D 2019, 19, 104018. [Google Scholar] [CrossRef]
- Abedi, H.; Abbassi, A.M.; Capozziello, S. Cosmological perturbations in gravitational energy-momentum complex. Ann. Phys. 2019, 405, 54. [Google Scholar] [CrossRef]
- Virbhadra, K.S.; Ellis, G.F. Schwarzschild black hole lensing. Phys. Rev. D 2000, 62, 084003. [Google Scholar] [CrossRef]
- Claudel, C.M.; Virbhadra, K.S.; Ellis, G.F. The geometry of photon surfaces. J. Math. Phys. 2000, 42, 818–838. [Google Scholar] [CrossRef]
- Virbhadra, K.S. Relativistic images of Schwarzschild black hole lensing. Phys. Rev. D 2009, 79, 083004. [Google Scholar] [CrossRef]
- Radinschi, I.; Grammenos, T.; Rahaman, F.; Spanou, A.; Islam, S.; Chattopadhyay, S.; Pasqua, A. Energy-momentum for a charged nonsingular black hole solution with a nonlinear mass function. Adv. High Energy Phys. 2017, 2017, 7656389. [Google Scholar] [CrossRef]
- Radinschi, I.; Rahaman, F.; Grammenos, T.; Islam, S. Einstein and Møller energy-momentum complexes for a new regular black hole solution with a nonlinear electrodynamics source. Adv. High Energy Phys. 2016, 2016, 9049308. [Google Scholar] [CrossRef]
- Capozziello, S.; Capriolo, M.; Transirico, M. The gravitational energy-momentum pseudo-tensor of higher-order theories of gravity. Ann. Phys. 2017, 529, 1600376. [Google Scholar] [CrossRef]
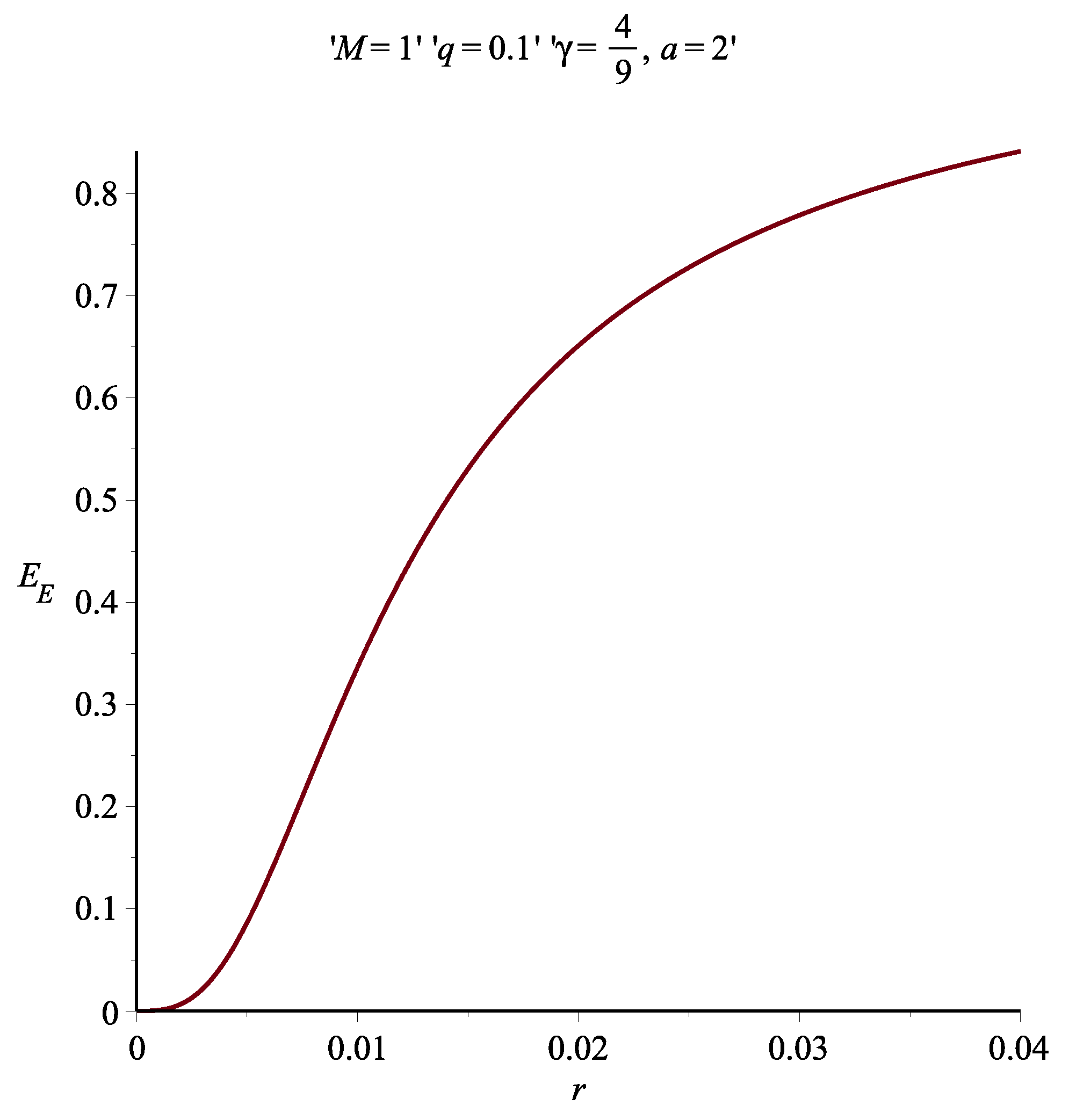
| Case | |||
| Einstein | 0 | M | M |
| Landau-Lifshitz | 0 | M | |
| Weinberg | 0 | M | |
| Møller | 0 | M | M |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radinschi, I.; Sahoo, P.K.; Grammenos, T.; Chattopadhyay, S.; Cazacu, M.-M. Localization of Energy and Momentum in an Asymptotically Reissner-Nordström Non-Singular Black Hole Space-Time Geometry. Universe 2020, 6, 69. https://doi.org/10.3390/universe6050069
Radinschi I, Sahoo PK, Grammenos T, Chattopadhyay S, Cazacu M-M. Localization of Energy and Momentum in an Asymptotically Reissner-Nordström Non-Singular Black Hole Space-Time Geometry. Universe. 2020; 6(5):69. https://doi.org/10.3390/universe6050069
Chicago/Turabian StyleRadinschi, Irina, Pradyumn Kumar Sahoo, Theophanes Grammenos, Surajit Chattopadhyay, and Marius-Mihai Cazacu. 2020. "Localization of Energy and Momentum in an Asymptotically Reissner-Nordström Non-Singular Black Hole Space-Time Geometry" Universe 6, no. 5: 69. https://doi.org/10.3390/universe6050069
APA StyleRadinschi, I., Sahoo, P. K., Grammenos, T., Chattopadhyay, S., & Cazacu, M.-M. (2020). Localization of Energy and Momentum in an Asymptotically Reissner-Nordström Non-Singular Black Hole Space-Time Geometry. Universe, 6(5), 69. https://doi.org/10.3390/universe6050069









