High-Order Multipole and Binary Love Number Universal Relations
Abstract
:1. Introduction
2. Methods
- Causality of the maximum mass NS is preserved (i.e., the maximum sound speed is less than the speed of light c below the maximum stable central density);
- The maximum stable mass of a non-rotating NS, , is greater than , and
- for the NS.
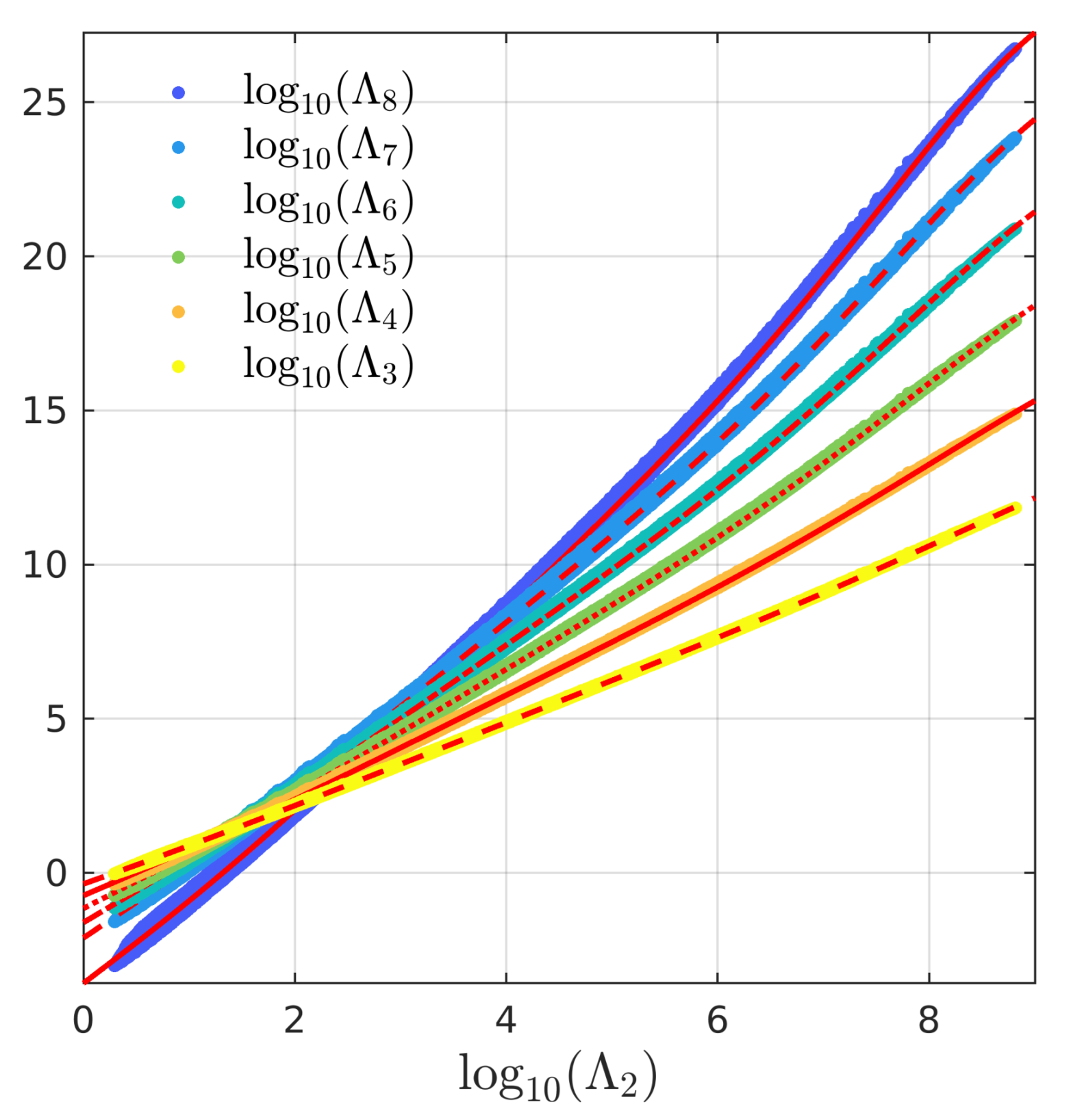
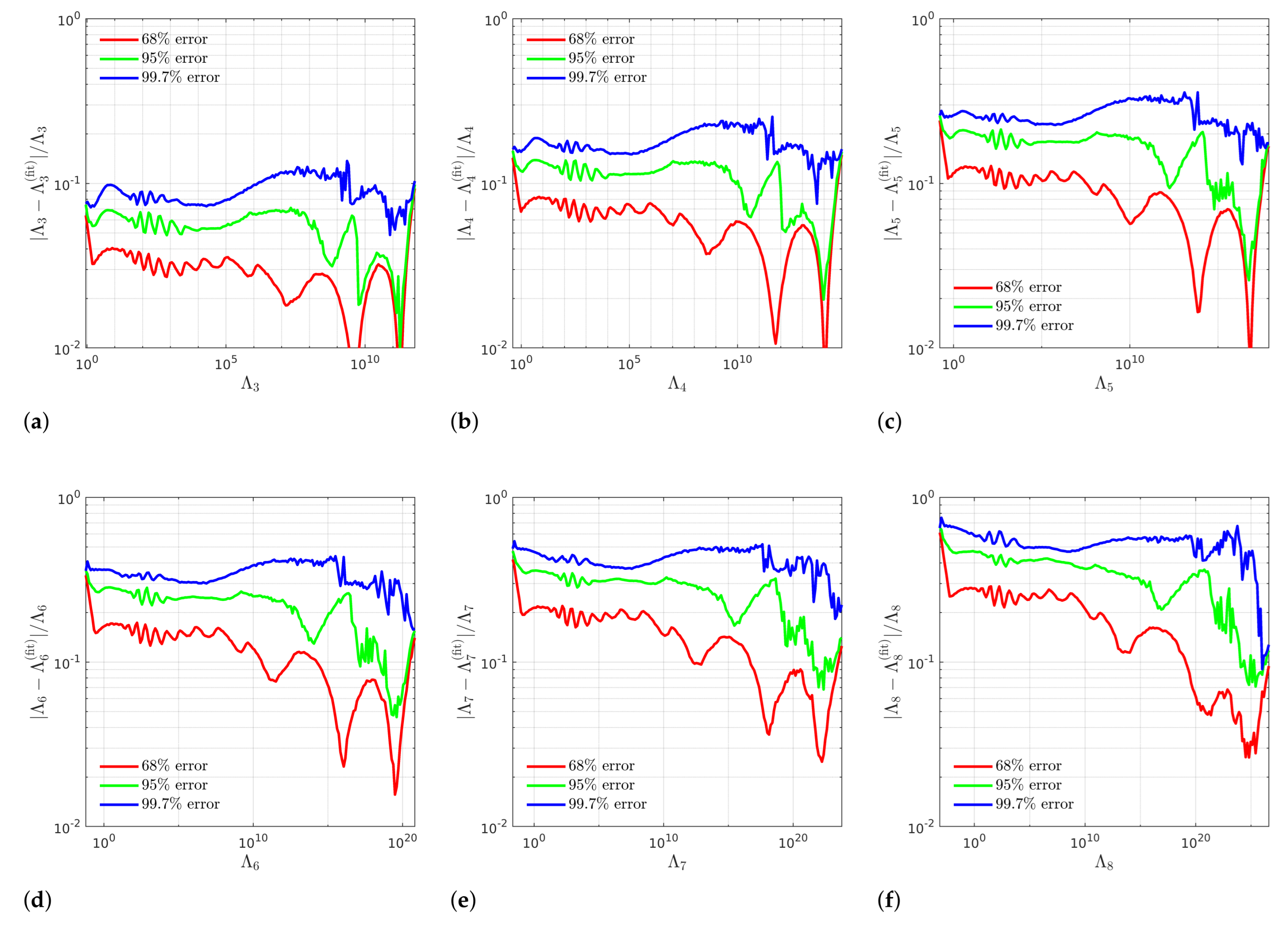
3. High-Order Multipole Relations
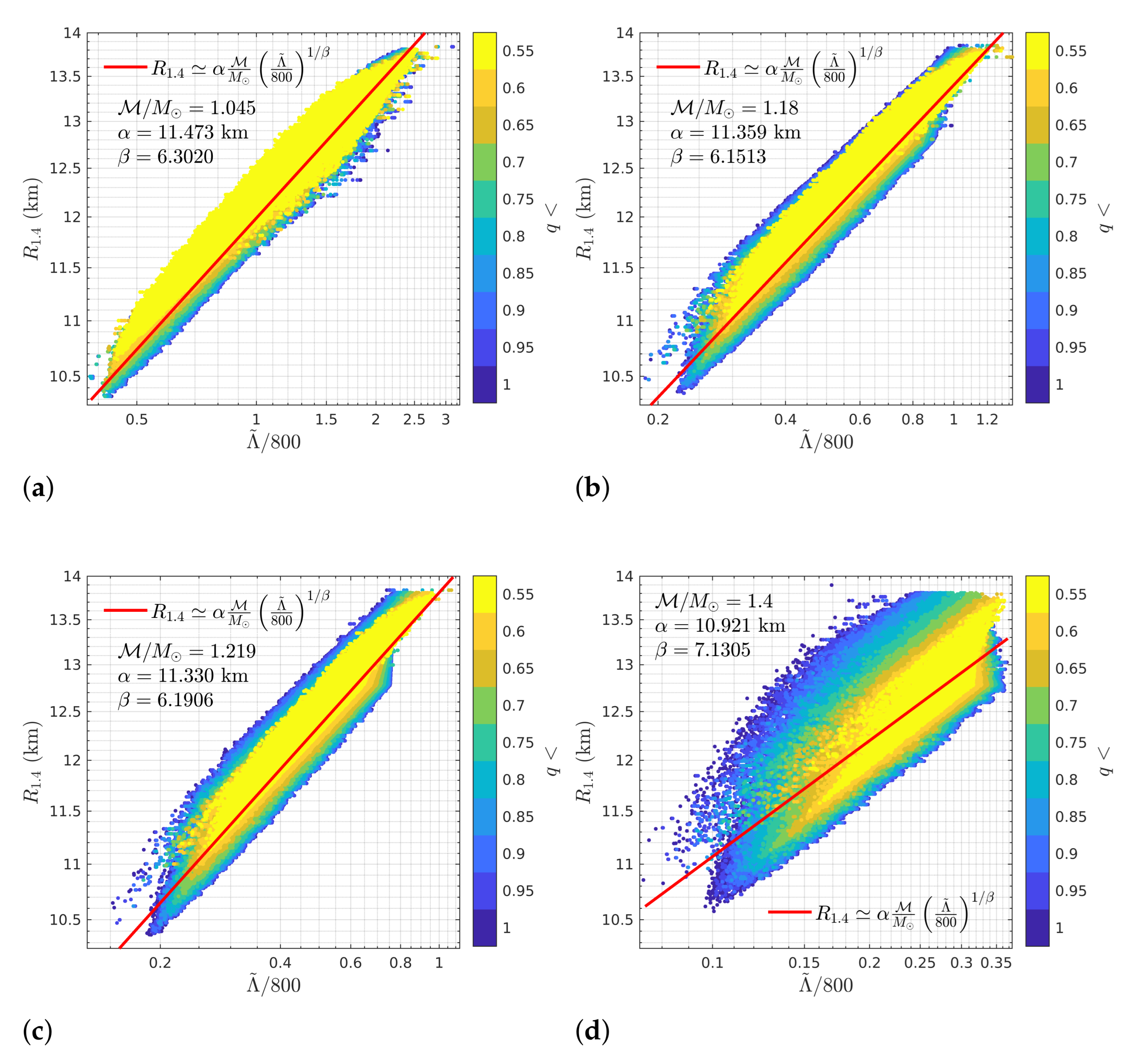
4. - Relation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EOS | Equation of state |
| NS | Neutron star |
| BNS | Binary neutron star |
| GW | Gravitational wave |
| MCMC | Markov chain Monte Carlo |
| TOV | Tolman-Oppenheimer-Volkoff |
References
- Andersson, N.; Kokkotas, K.D. Gravitational Waves and Pulsating Stars: What Can We Learn from Future Observations? Phys. Rev. Lett. 1996, 77, 4134–4137. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Andersson, N.; Kokkotas, K.D. Towards gravitational wave asteroseismology. Mon. Not. R. Astron. Soc. 1998, 299, 1059–1068. [Google Scholar] [CrossRef] [Green Version]
- Benhar, O.; Berti, E.; Ferrari, V. The imprint of the equation of state on the axial w-modes of oscillating neutron stars. Mon. Not. R. Astron. Soc. 1999, 310, 797–803. [Google Scholar] [CrossRef] [Green Version]
- Benhar, O.; Ferrari, V.; Gualtieri, L. Gravitational wave asteroseismology reexamined. Phys. Rev. D 2004, 70, 124015. [Google Scholar] [CrossRef]
- Tsui, L.K.; Leung, P.T. Universality in quasi-normal modes of neutron stars. Mon. Not. R. Astron. Soc. 2005, 357, 1029–1037. [Google Scholar] [CrossRef] [Green Version]
- Lau, H.K.; Leung, P.T.; Lin, L.M. Inferring Physical Parameters of Compact Stars from their f-mode Gravitational Wave Signals. Astrophys. J. 2010, 714, 1234–1238. [Google Scholar] [CrossRef] [Green Version]
- Bejger, M.; Haensel, P. Moments of inertia for neutron and strange stars: Limits derived for the Crab pulsar. Astron. Astrophys. 2002, 396, 917–921. [Google Scholar] [CrossRef] [Green Version]
- Lattimer, J.M.; Schutz, B.F. Constraining the Equation of State with Moment of Inertia Measurements. Astophys. J. 2005, 629, 979–984. [Google Scholar] [CrossRef] [Green Version]
- Urbanec, M.; Miller, J.C.; Stuchlík, Z. Quadrupole moments of rotating neutron stars and strange stars. Mon. Not. R. Astron. Soc. 2013, 433, 1903–1909. [Google Scholar] [CrossRef] [Green Version]
- Yagi, K.; Yunes, N. I-Love-Q: Unexpected Universal Relations for Neutron Stars and Quark Stars. Science 2013, 341, 365–368. [Google Scholar] [CrossRef] [Green Version]
- Yagi, K.; Yunes, N. I-Love-Q relations in neutron stars and their applications to astrophysics, gravitational waves, and fundamental physics. Phys. Rev. D 2013, 88, 023009. [Google Scholar] [CrossRef] [Green Version]
- Yagi, K. Multipole Love relations. Phys. Rev. D 2014, 89, 043011. [Google Scholar] [CrossRef] [Green Version]
- Yagi, K.; Stein, L.C.; Pappas, G.; Yunes, N.; Apostolatos, T.A. Why I-Love-Q: Explaining why universality emerges in compact objects. Phys. Rev. D 2014, 90, 063010. [Google Scholar] [CrossRef] [Green Version]
- Godzieba, D.A.; Gamba, R.; Radice, D.; Bernuzzi, S. Updated universal relations for tidal deformabilities of neutron stars from phenomenological equations of state. Phys. Rev. D 2021, 103, 063036. [Google Scholar] [CrossRef]
- Hinderer, T.; Lackey, B.D.; Lang, R.N.; Read, J.S. Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys. Rev. D 2010, 81, 123016. [Google Scholar] [CrossRef] [Green Version]
- Hinderer, T. Tidal Love Numbers of Neutron Stars. Astrophys. J. 2008, 677, 1216–1220. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A. Relativistic tidal properties of neutron stars. Phys. Rev. D 2009, 80, 084035. [Google Scholar] [CrossRef] [Green Version]
- Nagar, A.; Messina, F.; Rettegno, P.; Bini, D.; Damour, T.; Geralico, A.; Akcay, S.; Bernuzzi, S. Nonlinear-in-spin effects in effective-one-body waveform models of spin-aligned, inspiralling, neutron star binaries. Phys. Rev. D 2019, 99, 044007. [Google Scholar] [CrossRef] [Green Version]
- Zhao, T.; Lattimer, J.M. Tidal deformabilities and neutron star mergers. Phys. Rev. D 2018, 98, 063020. [Google Scholar] [CrossRef] [Green Version]
- Yagi, K.; Yunes, N. Approximate universal relations for neutron stars and quark stars. Phys. Rep. 2017, 681, 1–72. [Google Scholar] [CrossRef] [Green Version]
- Gamba, R.; Breschi, M.; Bernuzzi, S.; Agathos, M.; Nagar, A. Waveform systematics in the gravitational-wave inference of tidal parameters and equation of state from binary neutron star signals. arXiv 2020, arXiv:2009.08467. [Google Scholar]
- Adhikari, R.X. Gravitational radiation detection with laser interferometry. Rev. Mod. Phys. 2014, 86, 121–151. [Google Scholar] [CrossRef]
- Einstein Telescope. Available online: http://www.et-gw.eu/ (accessed on 29 September 2021).
- Hild, S.; Chelkowski, S.; Freise, A. Pushing towards the ET sensitivity using ’conventional’ technology. arXiv 2008, arXiv:0810.0604. [Google Scholar]
- Reitze, D.; Adhikari, R.X.; Ballmer, S.; Barish, B.; Barsotti, L.; Billingsley, G.; Brown, D.A.; Chen, Y.; Coyne, D.; Eisenstein, R.; et al. Contribution to Gravitational-Wave Astronomy beyond LIGO. Bull. Am. Astron. Soc. 2019, 51, 35. [Google Scholar]
- Flanagan, É.É.; Hinderer, T. Constraining neutron-star tidal Love numbers with gravitational-wave detectors. Phys. Rev. D 2008, 77, 021502. [Google Scholar] [CrossRef] [Green Version]
- Damour, T.; Nagar, A.; Villain, L. Measurability of the tidal polarizability of neutron stars in late-inspiral gravitational-wave signals. Phys. Rev. D 2012, 85, 123007. [Google Scholar] [CrossRef] [Green Version]
- De, S.; Finstad, D.; Lattimer, J.M.; Brown, D.A.; Berger, E.; Biwer, C.M. Tidal Deformabilities and Radii of Neutron Stars from the Observation of GW170817. Phys. Rev. Lett. 2018, 121, 091102. [Google Scholar] [CrossRef] [Green Version]
- Postnikov, S.; Prakash, M.; Lattimer, J.M. Tidal Love numbers of neutron and self-bound quark stars. Phys. Rev. D 2010, 82, 024016. [Google Scholar] [CrossRef] [Green Version]
- Yagi, K.; Yunes, N. Binary Love relations. Class. Quantum Gravity 2016, 33, 13LT01. [Google Scholar] [CrossRef] [Green Version]
- Maselli, A.; Cardoso, V.; Ferrari, V.; Gualtieri, L.; Pani, P. Equation-of-state-independent relations in neutron stars. Phys. Rev. D 2013, 88, 023007. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef] [Green Version]
- Essick, R.; Landry, P.; Holz, D.E. Nonparametric inference of neutron star composition, equation of state, and maximum mass with GW170817. Phys. Rev. D 2020, 101, 063007. [Google Scholar] [CrossRef] [Green Version]
- Read, J.S.; Lackey, B.D.; Owen, B.J.; Friedman, J.L. Constraints on a phenomenologically parametrized neutron-star equation of state. Phys. Rev. D 2009, 79, 124032. [Google Scholar] [CrossRef] [Green Version]
- Bernuzzi, S.; Nagar, A. Gravitational waves from pulsations of neutron stars described by realistic Equations of State. Phys. Rev. 2008, D78, 024024. [Google Scholar] [CrossRef] [Green Version]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. Shapiro Delay Measurement of A Two Solar Mass Neutron Star. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef]
- Fonseca, E. The NANOGrav Nine-year Data Set: Mass and Geometric Measurements of Binary Millisecond Pulsars. Astrophys. J. 2016, 832, 167. [Google Scholar] [CrossRef]
- Arzoumanian, Z. The NANOGrav 11-year Data Set: High-precision timing of 45 Millisecond Pulsars. Astrophys. J. Suppl. 2018, 235, 37. [Google Scholar] [CrossRef] [Green Version]
- Antoniadis, J. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 6131. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cromartie, H.T. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2019, 4, 72–76. [Google Scholar] [CrossRef] [Green Version]
- Linares, M.; Shahbaz, T.; Casares, J. Peering into the dark side: Magnesium lines establish a massive neutron star in PSR J2215+5135. Astrophys. J. 2018, 859, 54. [Google Scholar] [CrossRef]
- Margalit, B.; Metzger, B.D. Constraining the Maximum Mass of Neutron Stars From Multi-Messenger Observations of GW170817. Astrophys. J. Lett. 2017, 850, L19. [Google Scholar] [CrossRef]
- Shibata, M.; Fujibayashi, S.; Hotokezaka, K.; Kiuchi, K.; Kyutoku, K.; Sekiguchi, Y.; Tanaka, M. Modeling GW170817 based on numerical relativity and its implications. Phys. Rev. 2017, D96, 123012. [Google Scholar] [CrossRef] [Green Version]
- Rezzolla, L.; Most, E.R.; Weih, L.R. Using gravitational-wave observations and quasi-universal relations to constrain the maximum mass of neutron stars. Astrophys. J. Lett. 2018, 852, L25. [Google Scholar] [CrossRef]
- Ruiz, M.; Shapiro, S.L.; Tsokaros, A. GW170817, General Relativistic Magnetohydrodynamic Simulations, and the Neutron Star Maximum Mass. Phys. Rev. 2018, D97, 021501. [Google Scholar] [CrossRef] [Green Version]
- Shibata, M.; Zhou, E.; Kiuchi, K.; Fujibayashi, S. Constraint on the maximum mass of neutron stars using GW170817 event. Phys. Rev. 2019, D100, 023015. [Google Scholar] [CrossRef] [Green Version]
- Godzieba, D.A.; Radice, D.; Bernuzzi, S. On the Maximum Mass of Neutron Stars and GW190814. Astrophys. J. 2021, 908, 122. [Google Scholar] [CrossRef]
- Martinez, J.G.; Stovall, K.; Freire, P.C.C.; Deneva, J.S.; Jenet, F.A.; McLaughlin, M.A.; Bagchi, M.; Bates, S.D.; Ridolfi, A. Pulsar J0453+1559: A Double Neutron Star System with a Large Mass Asymmetry. Astrophys. J. 2015, 812, 143. [Google Scholar] [CrossRef] [Green Version]
- Suwa, Y.; Yoshida, T.; Shibata, M.; Umeda, H.; Takahashi, K. On the minimum mass of neutron stars. Mon. Not. R. Astron. Soc. 2018, 481, 3305–3312. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B.P. Prospects for observing and localizing gravitational-wave transients with Advanced LIGO, Advanced Virgo and KAGRA. Living Rev. Relativ. 2020, 23, 3. [Google Scholar] [CrossRef]
- Danielewicz, P.; Lacey, R.; Lynch, W.G. Determination of the Equation of State of Dense Matter. Science 2002, 298, 1592–1596. [Google Scholar] [CrossRef] [Green Version]
- Reed, B.T.; Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J. Implications of PREX-2 on the Equation of State of Neutron-Rich Matter. Phys. Rev. Lett. 2021, 126, 172503. [Google Scholar] [CrossRef]
- Steiner, A.W.; Lattimer, J.M.; Brown, E.F. The Equation of State from Observed Masses and Radii of Neutron Stars. Astrophys. J. 2010, 722, 33–54. [Google Scholar] [CrossRef]
- Lattimer, J.M. The Nuclear Equation of State and Neutron Star Masses. Annu. Rev. Nucl. Part. Sci. 2012, 62, 485–515. [Google Scholar] [CrossRef] [Green Version]
- Özel, F.; Freire, P. Masses, Radii, and the Equation of State of Neutron Stars. Ann. Rev. Astro. Astrophys. 2016, 54, 401–440. [Google Scholar] [CrossRef] [Green Version]
- Annala, E.; Gorda, T.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Evidence for quark-matter cores in massive neutron stars. Nat. Phys. 2020, 16, 907–910. [Google Scholar] [CrossRef]
- Godzieba, D.A.; Radice, D.; Bernuzzi, S. Phenomenological EOS Data Set. Zenodo 2020. [Google Scholar] [CrossRef]
| Relation | |||||||
|---|---|---|---|---|---|---|---|
| – | |||||||
| – | |||||||
| – | |||||||
| – | |||||||
| – | |||||||
| – |
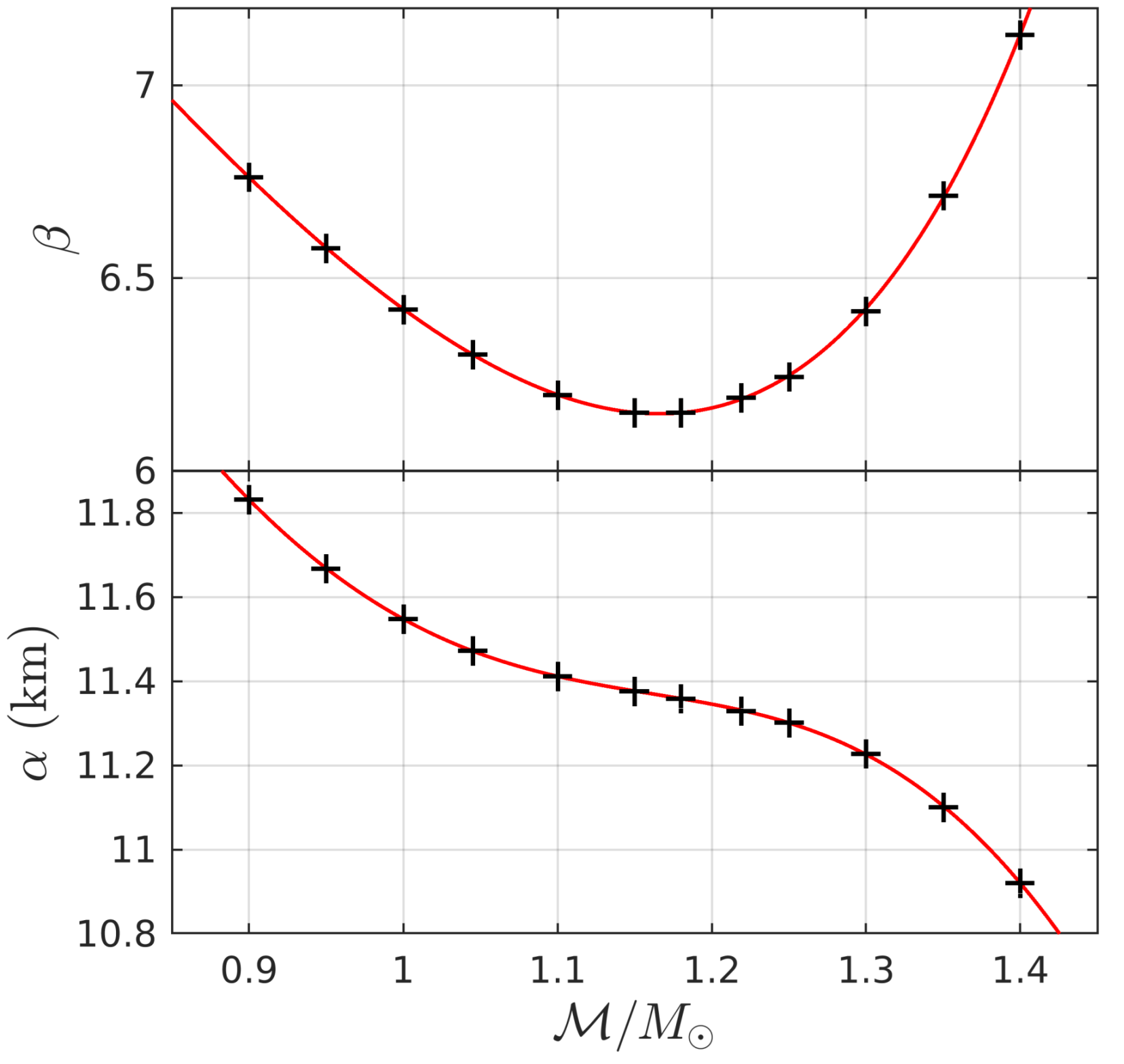
| (km) | ||
|---|---|---|
| 0.900 | 11.832 | 6.7621 |
| 0.950 | 11.668 | 6.5775 |
| 1.000 | 11.548 | 6.4189 |
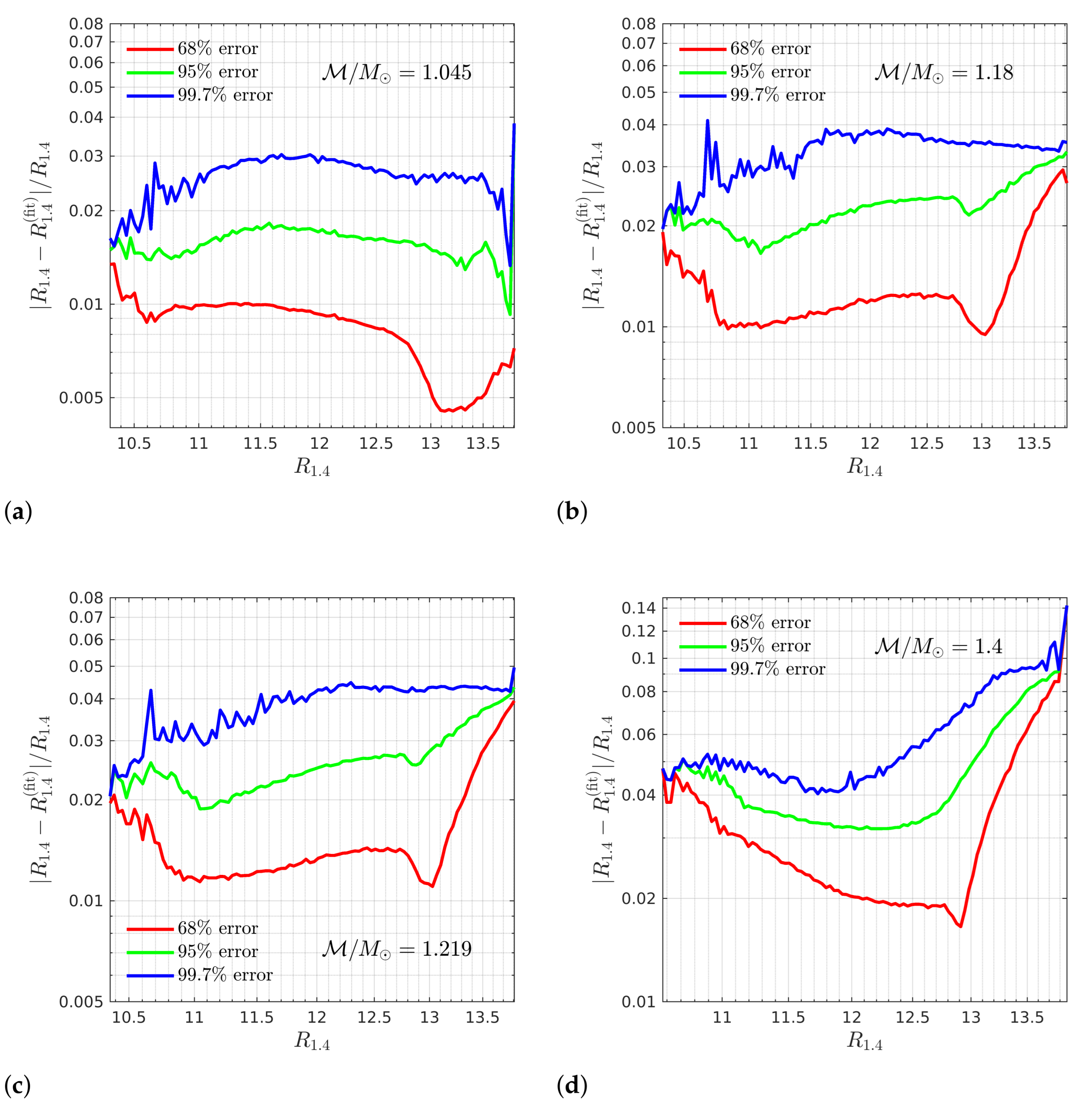
| 1.045 | 11.473 | 6.3020 |
| 1.100 | 11.412 | 6.1972 |
| 1.150 | 11.377 | 6.1515 |
| 1.180 | 11.359 | 6.1513 |
| 1.219 | 11.330 | 6.1906 |
| 1.250 | 11.302 | 6.2441 |
| 1.300 | 11.228 | 6.4147 |
| 1.350 | 11.102 | 6.7139 |
| 1.400 | 10.921 | 7.1305 |
| 1.4 | - | 1 | ||||||
| 1 | ||||||||
| 1.5 | - | 1 | ||||||
| 1 | ||||||||
| 1.6 | - | 1 | ||||||
| 1 | ||||||||
| 1.7 | - | 1 | ||||||
| 1 | ||||||||
| 1.8 | - | 1 | ||||||
| 1 | ||||||||
| 1.9 | - | 1 | ||||||
| 1 | ||||||||
| 2 | 63,061 | - | 1 | |||||
| 1 | ||||||||
| 2.14 | 93,209 | - | 12,686 | 1 | ||||
| 58,353 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Godzieba, D.A.; Radice, D. High-Order Multipole and Binary Love Number Universal Relations. Universe 2021, 7, 368. https://doi.org/10.3390/universe7100368
Godzieba DA, Radice D. High-Order Multipole and Binary Love Number Universal Relations. Universe. 2021; 7(10):368. https://doi.org/10.3390/universe7100368
Chicago/Turabian StyleGodzieba, Daniel A., and David Radice. 2021. "High-Order Multipole and Binary Love Number Universal Relations" Universe 7, no. 10: 368. https://doi.org/10.3390/universe7100368
APA StyleGodzieba, D. A., & Radice, D. (2021). High-Order Multipole and Binary Love Number Universal Relations. Universe, 7(10), 368. https://doi.org/10.3390/universe7100368






