Abstract
We analyze the effects of gravity on neutrino wave packet decoherence. As a specific example, we consider the gravitational field of a spinning spherical body described by the Lense–Thirring metric. By working in the weak-field limit and employing Gaussian wave packets, we show that the characteristic coherence length of neutrino oscillation processes is nontrivially affected, with the corrections being dependent on the mass and angular velocity of the gravity source. Possible experimental implications are finally discussed.
1. Introduction
Neutrinos are among the elementary particles in the Standard Model (SM) of fundamental interactions. In spite of this, their essential nature has not yet been fully revealed, and has become even more puzzling after Pontecorvo’s pioneering idea of neutrino mass and mixing [,,] and the subsequent discovery of flavor oscillations [,,,]. Further studies in Quantum Field Theory (QFT) have highlighted the shortcomings of the standard quantum mechanical (QM) predictions by pointing out the unitary inequivalence between the Fock spaces for definite flavor fields and definite mass fields [,,]. Phenomenological implications of this inequivalence have been investigated in a variety of contexts, ranging from vacuum effects [,,,,] to particle decays [,,,] and apparent violations of the weak equivalence principle [].
Neutrino mixing and oscillations are typically analyzed in the plane wave approximation. However, a more realistic treatment that accounts for neutrinos being localized particles should involve the use of wave packets (WPs), which introduce decoherence among the mass eigenstates. The first WP approach was developed in [], showing the existence of a coherence length beyond which the interference between massive neutrinos becomes negligible. This effect arises from the different group velocities of the different mass states, which leads WPs to spread over macroscopic sizes and separate during the propagation. Wave packet models of neutrino oscillations were later developed within the framework of QM [,,] and QFT [,,,], both in vacuum and matter [,,] (see [] for a review). In particular, in dense environments, decoherence through WP separation was shown to depend on the model chosen for the adiabaticity violation of WP evolution [,].
All of the above investigations were performed in flat spacetime. The effects of gravity on neutrino decoherence were addressed in [] by considering a static and spherically symmetric field described by the Schwarzschild metric. By adopting the density matrix formalism [] with Gaussian WPs and exploiting previous achievements of [,,], neutrino decoherence was quantified by a coherence coordinate distance and a proper time. As a result, it was shown that these quantities are nontrivially modified with respect to the flat case, with the corrections being, in principle, sizable. Aspects of gravitational decoherence were also explored in neutrino lensing in Schwarzschild [] and [] spacetime.
The Schwarzschild solution provides a first useful approximation to describe the spacetime metric around many astronomical objects, including the Earth and Sun. However, it does not account for the rotation of the source. In this work, we take a further step forward by studying neutrino decoherence in the gravitational field of a spinning spherical body of constant density and in the weak-field regime (Lense–Thirring metric) []. Following [], we resort to the density matrix approach and evaluate the coherence length in terms of the neutrino local energy, which is the energy actually measured by an inertial observer at rest at a finite radius in the gravitational field. In this sense, our calculation differs from that of [], where the final result is exhibited as a function of the asymptotic energy of neutrinos. We show that it is possible to extract a separate gravitational contribution depending on the mass and angular velocity of the source. Experimental implications of our finding are preliminarily discussed at the end.
The layout of the paper is as follows: In Section 2, we review the density matrix approach to describing neutrino WP decoherence in flat spacetime. For this purpose, we follow [,]. The above considerations are then extended to curved spacetime in Section 3. As a specific example, we consider neutrino propagation in the Lense–Thirring metric. The conclusions and outlook are summarized in Section 4. Throughout the entire manuscript, we use natural units and the metric with the conventional mostly negative signature .
2. WP Decoherence in Flat Spacetime: The Density Matrix Approach
In the SM, it is a well-established fact that neutrinos interact in weak eigenstates that are superpositions of mass eigenstates through Pontecorvo transformation [,,]:
where () denotes the flavor (mass) index and is the generic element of the Pontecorvo mixing matrix1. The time-dependent neutrino state with three-momentum is the solution of the Schrödinger-like equation , where H is the Hamiltonian governing the time evolution. In astrophysical environments, the Hamiltonian may include different contributions, such as the vacuum term, the matter interactions, and self-interactions. However, following [], in our analysis, we neglect matter effects and neutrino self-interactions outside the compact object. We are then left with , where is the free energy eigenvalue of the i-th mass eigenstate.
In the coordinate space, the i-th neutrino state is given by the 3-dimensional Fourier expansion
To streamline the notation, henceforth, we denote the momentum integration by . At this stage, it is worth emphasizing that we are neglecting the spin structure of neutrinos. This is, in principle, not relevant for our purposes of studying gravitational effects on neutrino flavor oscillations and decoherence. In passing, we mention that effects of gravity–spin coupling on neutrinos have been largely addressed in the literature (see, e.g., [,,]).
In the standard treatment of flavor oscillations, the mass eigenstates are typically described by plane waves. To account for the localization of neutrinos to a finite region, a formalism based on WPs should be used. This has been considered in [,,,,,,,,,,]. In the WP approach, the neutrino flavor state (1) turns out to be a superposition of mass eigenstate WPs, each centered around the momentum with distribution amplitude . At the initial time , the i-th WP component satisfies
where and
The explicit form of the WP distribution will be given below.
Now, by using Equation (2), the i-th mass state in the coordinate space can be written as
where the wave function in the coordinate space is the Fourier transform of the corresponding momentum-dependent wave function, i.e.,
Therefore, the flavor state takes the form
Starting from the above premises, let us employ the density matrix formalism to describe the WP decoherence effects. In flat spacetime, the one-body density matrix for the neutrino state (7) is defined, as usual, by []
Flavor vacuum oscillations occur due to the interference between different massive neutrinos. Thus, in the WP approach, the condition to be satisfied to detect oscillations at a given point is that the mass eigenstate WPs still overlap sufficiently to produce interference in that point (see Figure 1). To account for this, one introduces the coherence length , which is defined as the distance travelled by neutrinos beyond which the WPs corresponding to different propagation eigenstates composing the produced neutrino flavor state separate by more than the WP size . Recalling that the decoherence is generated by the different group velocities of the different mass eigenstate WPs, the coherence length can be estimated heuristically as [], where is the average group velocity of the WPs and is the difference between the group velocities of the mass eigenstate WPs. For relativistic neutrinos, we have [,]
where and is the average energy between the interfering mass eigenstates. Clearly, in the plane wave approximation, we have because of the infinite spatial extension of plane waves.
The above relation is to be compared with the characteristic oscillation length in the plane wave formalism, which is
Thus, the central role of the finite WP-width assumption in producing decoherence between the different neutrino eigenstate WPs is evident.
It is worth noting that, in the presence of three neutrino generations, one should define a coherence length for each pair of propagation eigenstates. In that case, complete decoherence occurs when the distance travelled by neutrinos is higher than all of the coherence lengths. As remarked in [], partial decoherence may also be of interest in some physical contexts.
We now aim at deriving the coherence length (10) more rigorously by using the density matrix approach. As we shall see in the next section, this formalism is also well suited for extension to curved spacetime. Toward this end, we need to specify the explicit form of WPs. There exist in the literature several examples of WPs, such as square or sech WPs. Here, we resort to the most common Gaussian WPs of momentum width
for which the (normalized) distribution amplitude reads
Notice that the plane wave limit is recovered for (i.e., for ), which yields , where V is the normalization volume.
We have assumed equal dispersion for the mass eigenstate WPs.
The integrals in Equation (14) can be computed by expanding the neutrino energy around the WP central momentum according to []
(and similarly for ), where and is the group velocity of the j-th mass eigenstate. The relation (14) then becomes
Through the explicit calculation of the Gaussian integrals, we get
where
Let us now evaluate the density matrix averaged over time
which is the typical quantity of interest in oscillation experiments. Tedious but straightforward calculations lead to
where
The first term does not affect oscillations. The second one is the oscillation term with the extra factor , where we have set and . The last factor is the damping term, which is actually responsible for decoherence. In passing, we remark that the above averaged density matrix can be alternatively calculated as a function of time by integrating Equation (19) over space coordinates. This was done in [], obtaining a similar expression for the decoherence term through the identification .
From Equation (25), we can now estimate the coherence length between the mass eigenstate WPs as the distance at which the density matrix is suppressed by a factor . This gives []
which agrees with the heuristic estimate in Equation (10), up to a numerical factor.
In the next section, we show how the density matrix formalism is modified when extended to curved spacetime. In particular, we consider the case of the Lense–Thirring metric and evaluate gravity-induced corrections to the coherence length (26).
3. Gravitational Effects on WP Decoherence: The Lense–Thirring Metric Example
Gravitational effects on neutrino oscillations have been extensively analyzed in the literature by using several approaches, e.g., the plane wave method [,] or geometric formalisms [,], and in different metrics, such as the Schwarzschild [,], Kerr [,], Friedmann–Robertson–Walker [,], and Lense–Thirring [] metrics, among others. Recently, nontrivial results were obtained in extended theories of gravity [], quantum gravity scenarios [,], and in QFT in a curved background [,].
The first systematic WP treatment of decoherence in neutrino oscillations was developed in [] by relying on Stodolsky’s covariant generalization of the quantum mechanical phase shift in Equation (15) []. By way of illustration, calculations were explicitly performed for Schwarzschild geometry.
In curved spacetime, a neutrino flavor state produced at the point is described by . During the propagation to the detection point , the i-th mass eigenstate evolves according to
where the QM phase in its covariant form is given by []
Here, () is the canonical four-momentum conjugated to the coordinate ,
satisfying the generalized mass–shell relation
where is the metric tensor and is the line element along the trajectory described by the i-th neutrino state. In the approximation of relativistic neutrinos, it is reasonable to assume that this trajectory is close to a null-geodesic. Clearly, the detection point D is such that the mass eigenstate WPs can still interfere in it (see Figure 1).
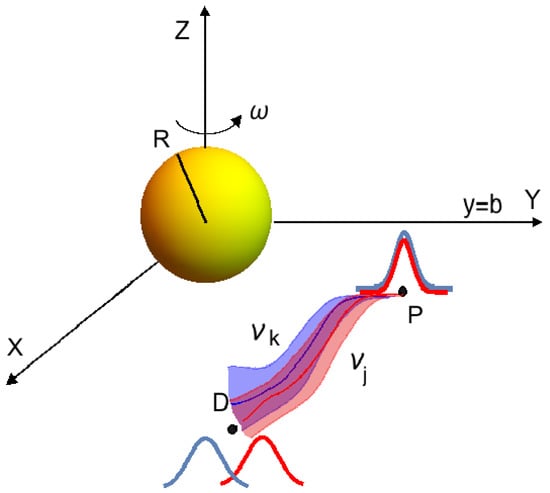
Figure 1.
Pictorial representation of a neutrino propagating in the gravitational field of a spinning spherical body from the production point to the detection point , where the WPs can still interfere. We are assuming that each eigenstate WP follows a trajectory close to null-geodesics. The (online) colored widths represent the distribution of the trajectories due to the WP finite extension.
The relation (27) along with the definition (28) of the QM phase generalize Equation (2) to an arbitrary curved space. For equal to Minkowski tensor, it is easy to check that the standard evolution in flat spacetime is recovered.
The Lense–Thirring Metric Example
The Lense–Thirring metric describes the gravitational field around a spinning spherical source of constant density. Let us denote by M and R the mass and radius of the central source, respectively. By assuming the neutrino propagation to be confined to the equatorial plane (), the line element in the (linearized) weak-field limit can be written in cartesian coordinates as
where
and is the angular velocity of the source, which is supposed to be constant and oriented along the z axis. The gravitational potential is defined by
where, for simplicity, we have denoted the radial distance in the equatorial plane by r.
Equation (31) provides the metric typically employed to describe gravitomagnetic frame-dragging effects [,]. Moreover, in [], it was used to compute gravity corrections to the Mandelstam–Tamm time–energy uncertainty relation for oscillations.
In the above setting, it is easy to show that the only nontrivial components of the four-momentum are
where we have neglected higher-order terms in the potential .
Following [,], we can now consider a first approximation in which the neutrinos propagate along a direction parallel to the x-axis with impact parameter (Figure 1). This implies that in Equations (34) and (36). Furthermore, since the metric (31) does not depend on t, the component is a constant of motion, corresponding to the neutrino energy as measured by an inertial observer at rest at infinity (asymptotic energy). The local energy, which is the quantity actually measured by an observer at rest at finite radius in the gravitational field [,,], is related to through the transformation law that connects the local Lorentz frame to the general frame
where are the vierbein fields, and we have used the standard convention of denoting general coordinates and local Lorentz frame indexes by Greek and hatted Latin letters, respectively. With reference to the metric (31), the relevant tetrad components are []
From Equation (37), it is a matter of calculation to show that the local and asymptotic energies are related by []:
where the subscript L stands for “local” and we have omitted the space- and momentum-dependence of for simplicity.
A comment is now in order: In [], all of the quantities are expressed in terms of the asymptotic energy . To make the comparison with the formulas of [] easier, in what follows, we retain the dependence on and implement the substitution (39) only at the end.
With our assumptions, the mass–shell relation (30) takes the form
where r must now be intended as . From Equation (34), along with , we derive
which can be substituted into (40) to give
Here, we have exploited the condition of relativistic neutrinos at infinity, which ensures that they are even more relativistic for , according to Equation (39). Without loss of generality, we assume that neutrinos propagate toward increasing values of x as s increases, so the solution with the positive sign must be considered.
Let us now consider the covariant phase in Equation (28). Combining Equations (34)–(36), (41), and (42), for the integral argument, one gets
The covariant phase then reads
where, for brevity, we have defined , , and
with
Clearly, for a non-rotating source, . In this case, Equation (44) reproduces the linearized result of [] for the Schwarzschild metric up to a global sign due to the different signature convention adopted for the metric.
From Equation (44), the phase difference of the mass eigenstate WPs reads
By using the first-order expansion (17), this becomes
where we have used Equation (20) and introduced the shorthand notation
Let us now evaluate the one-body density matrix describing the neutrino mass eigenstates as (non-covariant) Gaussian WPs. This is given by the generalization of Equation (14) with the QM phase being given by Equation (49), i.e.,
where we have used the tilde to distinguish the density matrix in curved spacetime from the corresponding flat expression. The normalization is defined in Equation (16).
As in Section 2, the averaged density matrix is obtained by integrating over the coordinate time. In this case, the resulting expression can also be factorized into the product of three terms as follows:
in order to compare with the corresponding flat result (22). The amplitude is independent of the travelled distance and exhibits the same expression as in Minkowski spacetime (see Equation (23)). The second term, which is responsible for flavor oscillations, is given by
Finally, the damping term reads
which, for relativistic neutrinos, becomes
Here, E is the average energy between the mass eigenstates, as defined below Equation (10).
We notice that Equation (55) is formally the same as the damping term found in [] in the Schwarzschild metric. As argued in [], to make the dependence on M and explicit, should be recast in terms of the local (rather than asymptotic) energy (39). By implementing the transformation (39) in Equation (55), we are led to
where the local energy must be considered as being evaluated at the detection point D.
In analogy with the flat-spacetime case, one can now define the proper coherence length as the distance at which the density matrix is suppressed by the factor . We then obtain
We remark that in the limit, Equation (26) is straightforwardly recovered, since . This is indeed the expected outcome in the absence of a gravitational field. Therefore, with respect to the flat case, the coherence length in the linearized Lense–Thirring metric turns out to be decreased by acquiring some nontrivial corrections. Specifically, the second term in the brackets is a constant factor that only depends on the source mass and the detection point. The presence of this correction could somehow be expected, since the spacetime metric is no longer translation-invariant. The third term is the genuinely Lense–Thirring imprint, as it carries the information about the rotational velocity of the central object and the impact parameter b of the neutrino’s trajectory.
It would be interesting to estimate the gravity corrections in Equation (57). For this purpose, we study the case of neutrinos in the gravitational field of the Sun. Then, by assuming the mass of the Sun and its rotational frequency and setting , , we obtain the following estimate for the relative difference between the coherence length (57) and the corresponding flat-spacetime expression
Predictably, this shows that the impact of the Sun’s gravity on decoherence effects is negligible, at least with the current experimental technology. On the other hand, for neutrinos in astrophysical environments, such as supernova neutrinos or neutrinos propagating in the field of massive compact objects, we expect these effects to be significantly improved, as shown in [] for the case of the Schwarzschild geometrical background. However, a more rigorous analysis of decoherence effects in the strong-field regime would require us to go beyond the linearized approximation. This study is under active investigation and will be presented elsewhere.
Finally, in order to compare Equation (56) with the result of [], we need to express the coordinate distance in terms of the proper distance between the production and detection points. Under our assumptions, it is possible to show that these two quantities are related by []:
where and are defined in Equation (47). By plugging into Equation (56), the averaged density matrix takes the form
which gives rise to the modified coherence length
For vanishing spinning velocity , it is easy to check that the above formula reproduces the coherence length obtained in [] for the case of a non-rotating Schwarzschild source2. By comparison with Equation (57), it follows that acquires a further correction with the same logarithmic behavior as in Schwarzschild spacetime []. We plan to further investigate the physical meaning of Equation (61) in order to understand how to express the quantities in terms of proper distance in a more consistent way.
4. Discussion and Conclusions
The influence of gravity on neutrino decoherence was investigated within the framework of the density matrix with Gaussian WPs. As a specific background, we considered the gravitational field around a spinning spherical body described by the Lense–Thirring metric. By working in the weak field, we derived the effective coherence length for relativistic neutrinos, showing that it is nontrivially modified with respect to the flat case. A rough estimation of gravity corrections highlighted that they are below the sensitivity of current experiments for neutrinos propagating in the gravitational field of the Sun. However, significant deviations from the standard result are expected in strong-field regimes, e.g., in the case of neutron stars formed from a core-collapse supernova [,] or in the presence of supermassive black holes. This is in line with []. In this regard, we need to emphasize that our comparison with the result of [] has to be seen as more qualitative than quantitative. Indeed, a direct comparison with [] is prevented due to the fact that the analysis of [] did not rely on the weak-field approximation. This allowed the authors of [] to test gravity in stronger regimes than in our case. We are currently working on the extension of our formalism beyond the weak-field approximation. This will be presented elsewhere as an upgrade of the present study.
We remark that our study relies on some preliminary assumptions. For instance, we neglected matter and neutrino self-interactions outside the central compact object. As claimed in [], these effects can be embedded by using a similar procedure involving the use of the matter eigenstate basis instead of the mass one. This investigation turns out to be necessary in order to explore whether WP decoherence suppresses flavor oscillations and its impact on the supernova dynamics and r-process nucleosynthesis. Furthermore, we considered rectilinear propagation of mass eigenstate WPs. In a more general treatment, bending effects should also be contemplated. To give a rough estimation of the correction we neglected, let us think of neutrinos as nearly massless particles. In this case, we can refer to [,], where it was shown that the magnitude of the bending angle for a light ray in the Lense–Thirring metric and in the equatorial plane turns out to be
where is the angular momentum of the source and is a unit vector in the direction of the angular momentum of light about the center of the source-body. The term outside the parenthesis provides the pure Schwarzschild correction. For instance, in the case of the Sun, the relative correction to the pure mass term is of the order of , which, in principle, justifies our assumption.
Apart from their intrinsic relevance, let us emphasize that decoherence effects on neutrino oscillations are also studied to constrain quantum gravity models [,,]. In particular, in [], quantum gravitational analogues of the MSW effect and of foam models endowed with stochastic fluctuations of the background were presented as possible alternative sources of decoherence in neutrino oscillations. A similar analysis was recently developed in [], where the influence of quantum gravity on neutrino propagation and decoherence was investigated with a focus on the case of neutrino interactions with virtual black holes produced by spacetime fluctuations. The study of the above aspects is quite demanding and will be the object of future work.
Author Contributions
Conceptualization, G.G.L.; Writing—original draft, G.G.L.; Writing—review & editing, M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
This manuscript has no associated data.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| QFT | Quantum Field Theory |
| QM | Quantum Mechanics |
| WP | Wave packet |
| SM | Standard Model |
Notes
| 1 | We consider a simplified model involving only two generations of neutrinos. The same considerations and results hold in the case of three flavors. |
| 2 | Strictly speaking, the second term in the square brackets is found with the opposite sign with respect to [] due to a possible mistake therein. |
References
- Pontecorvo, B. Mesonium and anti-mesonium. Zh. Eksp. Teor. Fiz. 1957, 33, 549. [Google Scholar]
- Pontecorvo, B. Inverse beta processes and nonconservation of lepton charge. Zh. Eksp. Teor. Fiz. 1957, 34, 247. [Google Scholar]
- Pontecorvo, B. Neutrino Experiments and the Problem of Conservation of Leptonic Charge. Zh. Eksp. Teor. Fiz. 1967, 53, 1717. [Google Scholar]
- Fukuda, Y.; Hayakawa, T.; Ichihara, E.; Inoue, K.; Ishihara, K.; Ishino, H.; Itow, Y.; Kajita, T.; Kameda, J.; Kasuga, S.; et al. Evidence for Oscillation of Atmospheric Neutrinos. Phys. Rev. Lett. 1998, 1562, 81. [Google Scholar] [CrossRef] [Green Version]
- Abe, K.; Hayato, Y.; Iida, T.; Iyogi, K.; Kameda, J.; Koshio, Y.; Kozuma, Y.; Marti, L.; Miura, M.; Moriyama, S.; et al. Evidence for the Appearance of Atmospheric Tau Neutrinos in Super-Kamiokande. Phys. Rev. Lett. 2013, 110, 181802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ahmad, Q.R.; Allen, R.C.; Andersen, T.C. Measurement of the Rate of νe + d → p + p + e− Interactions Produced by 8B Solar Neutrinos at the Sudbury Neutrino Observatory. Phys. Rev. Lett. 2001, 87, 071301. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, Q.R.; Allen, R.C.; Andersen, T.C.; Anglin, J.D.; Barton, J.C.; Beier, E.W.; Bercovitch, M.; Bigu, J.; Biller, S.D.; Black, R.A.; et al. Direct Evidence for Neutrino Flavor Transformation from Neutral-Current Interactions in the Sudbury Neutrino Observatory. Phys. Rev. Lett. 2002, 89, 011301. [Google Scholar] [CrossRef]
- Blasone, M.; Vitiello, G. Quantum field theory of fermion mixing. Annals Phys. 1995, 244, 283. [Google Scholar] [CrossRef] [Green Version]
- Blasone, M.; Capolupo, A.; Romei, O.; Vitiello, G. Quantum field theory of boson mixing. Phys. Rev. D 2001, 63, 125015. [Google Scholar] [CrossRef] [Green Version]
- Ji, C.R.; Mishchenko, Y. General Quantum Field Theory of Flavor Mixing and Oscillations. Universe 2021, 7, 51. [Google Scholar] [CrossRef]
- Blasone, M.; Luciano, G.G.; Petruzziello, L.; Smaldone, L. Casimir effect for mixed fields. Phys. Lett. B 2018, 278, 786. [Google Scholar] [CrossRef]
- Blasone, M.; Lambiase, G.; Luciano, G.G. Nonthermal signature of the Unruh effect in field mixing. Phys. Rev. D 2017, 96, 025023. [Google Scholar] [CrossRef] [Green Version]
- Capolupo, A.; Lambiase, G.; Quaranta, A. Neutrinos in curved spacetime: Particle mixing and flavor oscillations. Phys. Rev. D 2020, 101, 095022. [Google Scholar] [CrossRef]
- Luciano, G.G.; Blasone, M. q-generalized Tsallis thermostatistics in Unruh effect for mixed fields. Phys. Rev. D 2021, 104, 045004. [Google Scholar] [CrossRef]
- Luciano, G.G.; Blasone, M. Nonextensive Tsallis statistics in Unruh effect for Dirac neutrinos. arXiv 2021, arXiv:2107.11402. [Google Scholar]
- Blasone, M.; Lambiase, G.; Luciano, G.G.; Petruzziello, L. Role of neutrino mixing in accelerated proton decay. Phys. Rev. D 2018, 97, 105008. [Google Scholar] [CrossRef] [Green Version]
- Blasone, M.; Lambiase, G.; Luciano, G.G.; Petruzziello, L. Neutrino oscillations in Unruh radiation. Phys. Lett. B 2020, 800, 135083. [Google Scholar] [CrossRef]
- Blasone, M.; Lambiase, G.; Luciano, G.G.; Petruzziello, L. On the β-decay of the accelerated proton and neutrino oscillations: A three-flavor description with CP violation. Eur. Phys. J. C 2020, 80, 130. [Google Scholar] [CrossRef]
- Lee, C.Y. Interactions and oscillations of coherent flavor eigenstates in beta decay. Mod. Phys. Lett. A 2020, 29, 2030015. [Google Scholar] [CrossRef]
- Blasone, M.; Jizba, P.; Lambiase, G.; Petruzziello, L. Non-relativistic neutrinos and the weak equivalence principle apparent violation. Phys. Lett. B 2020, 811, 135883. [Google Scholar] [CrossRef]
- Nussinov, S. Solar Neutrinos and Neutrino Mixing. Phys. Lett. B 1976, 63, 201. [Google Scholar] [CrossRef]
- Giunti, C.; Kim, C.W.; Lee, U.W. When do neutrinos really oscillate? Quantum mechanics of neutrino oscillations. Phys. Rev. D 1991, 44, 3635. [Google Scholar] [CrossRef]
- Giunti, C.; Kim, C.W. Coherence of neutrino oscillations in the wave packet approach. Phys. Rev. D 1998, 58, 017301. [Google Scholar] [CrossRef] [Green Version]
- Dolgov, A.D. Neutrinos in cosmology. Phys. Rept. 2002, 370, 333. [Google Scholar] [CrossRef] [Green Version]
- Kiers, K.; Weiss, N. Neutrino oscillations in a model with a source and detector. Phys. Rev. D 1998, 57, 3091. [Google Scholar] [CrossRef] [Green Version]
- Cardall, C.Y. Coherence of neutrino flavor mixing in quantum field theory. Phys. Rev. D 2000, 61, 073006. [Google Scholar] [CrossRef] [Green Version]
- Beuthe, M. Towards a unique formula for neutrino oscillations in vacuum. Phys. Rev. D 2002, 66, 013003. [Google Scholar] [CrossRef] [Green Version]
- Giunti, C. Neutrino wave packets in quantum field theory. J. High Energy Phys. 2002, 11, 017. [Google Scholar] [CrossRef] [Green Version]
- Giunti, C.; Kim, C.W.; Lee, U.W. Coherence of neutrino oscillations in vacuum and matter in the wave packet treatment. Phys. Lett. B 1992, 274, 87. [Google Scholar] [CrossRef]
- Kersten, J.; Smirnov, A.Y. Decoherence and oscillations of supernova neutrinos. Eur. Phys. J. C 2016, 76, 339. [Google Scholar] [CrossRef] [Green Version]
- Akhmedov, E.; Kopp, J.; Lindner, M. Collective neutrino oscillations and neutrino wave packets. J. Cosmol. Astropart. Phys. 2017, 9, 017. [Google Scholar] [CrossRef] [Green Version]
- Giunti, C. Coherence and wave packets in neutrino oscillations. Found. Phys. Lett. 2004, 17, 103. [Google Scholar] [CrossRef] [Green Version]
- Chatelain, A.; Volpe, M.C. Neutrino decoherence in presence of strong gravitational fields. Phys. Lett. B 2020, 801, 135150. [Google Scholar] [CrossRef]
- Stodolsky, L. 36 On the Treatment of Neutrino Oscillations in a Thermal Environment. Phys. Rev. D 1987, 36, 2273. [Google Scholar] [CrossRef] [PubMed]
- Cardall, C.Y.; Fuller, G.M. Neutrino oscillations in curved space-time: An Heuristic treatment. Phys. Rev. D 1997, 55, 7960. [Google Scholar] [CrossRef] [Green Version]
- Fornengo, N.; Giunti, C.; Kim, C.W.; Song, J. Gravitational effects on the neutrino oscillation. Phys. Rev. D 1997, 56, 1895. [Google Scholar] [CrossRef] [Green Version]
- Swami, H.; Lochan, K.; Patel, K.M. Aspects of gravitational decoherence in neutrino lensing. arXiv 2021, arXiv:2106.07671. [Google Scholar]
- Chakrabarty, H.; Borah, D.; Abdujabbarov, A.; Malafarina, D.; Ahmedov, B. Effects of gravitational lensing on neutrino oscillation in γ-spacetime. arXiv 2021, arXiv:2109.02395. [Google Scholar]
- Lense, J.; Thirring, H. Über die Einfluss der Eigenrotation der Zentralkörper auf die Bewegung der Planeten und Monde nach der Einsteinschen Gravitationstheorie (trad. On the influence of the proper rotation of a central body on the motion of the planets and the moon, according to Einstein’s theory of gravitation). Z. Phys. 1918, 19, 156. [Google Scholar]
- Cai, Y.C.; Papini, G. Neutrino helicity flip from gravity spin coupling. Phys. Rev. Lett. 1991, 1259, 66. [Google Scholar] [CrossRef]
- Dvornikov, M. Spin effects in neutrino gravitational scattering. Phys. Rev. D 2020, 056018, 101. [Google Scholar] [CrossRef] [Green Version]
- Mastrototaro, L.; Lambiase, G. Neutrino spin oscillations in conformally gravity coupling models and quintessence surrounding a black hole. Phys. Rev. D 2021, 024021, 104. [Google Scholar]
- Konno, K.; Kasai, M. General relativistic effects of gravity in quantum mechanics: A case of ultra-relativistic, spin 1/2 particles. Prog. Theor. Phys. 1998, 100, 1145. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.H.; Li, X.Q. Three-generation neutrino oscillations in curved spacetime. Nucl. Phys. B 2016, 911, 563. [Google Scholar] [CrossRef] [Green Version]
- Ahluwalia, D.V.; Burgard, C. Gravitationally Induced Neutrino-Oscillation Phases. Gen. Rel. Grav. 1996, 28, 1161. [Google Scholar] [CrossRef]
- Wudka, J. Mass dependence of the gravitationally induced wave-function phase. Phys. Rev. D 2001, 64, 065009. [Google Scholar] [CrossRef] [Green Version]
- Visinelli, L. Neutrino flavor oscillations in a curved space-time. Gen. Rel. Grav. 2015, 47, 62. [Google Scholar] [CrossRef]
- Khalifeh, A.R.; Jimenez, R. Distinguishing Dark Energy Models with Neutrino Oscillations. arXiv 2021, arXiv:2105.07973. [Google Scholar]
- Lambiase, G.; Papini, G.; Punzi, R.; Scarpetta, G. Neutrino optics and oscillations in gravitational fields. Phys. Rev. D 2005, 71, 073011. [Google Scholar] [CrossRef] [Green Version]
- Buoninfante, L.; Luciano, G.G.; Petruzziello, L.; Smaldone, L. Neutrino oscillations in extended theories of gravity. Phys. Rev. D 2020, 101, 024016. [Google Scholar] [CrossRef] [Green Version]
- Mavromatos, N.E.; Meregaglia, A.; Rubbia, A.; Sakharov, A.; Sarkar, S. Quantum-Gravity Decoherence Effects in Neutrino Oscillations: Expected Constraints From CNGS and J-PARC. Phys. Rev. D 2008, 77, 053014. [Google Scholar] [CrossRef] [Green Version]
- Sprenger, M.; Nicolini, P.; Bleicher, M. Quantum Gravity signals in neutrino oscillations. Int. J. Mod. Phys. E 2011, 20S2, 1. [Google Scholar] [CrossRef]
- Ruggiero, M.L.; Tartaglia, A. Gravitomagnetic effects. Nuovo Cim. B 2002, 117, 743. [Google Scholar]
- Ciufolini, I. Dragging of inertial frames. Nature 2007, 449, 41. [Google Scholar] [CrossRef]
- Blasone, M.; Lambiase, G.; Luciano, G.G.; Petruzziello, L.; Smaldone, L. Time-energy uncertainty relation for neutrino oscillations in curved spacetime. Class. Quant. Grav. 2020, 37, 155004. [Google Scholar] [CrossRef]
- Petruzziello, L. Comment on “Neutrino decoherence in presence of strong gravitational fields”. Phys. Lett. B 2020, 809, 135784. [Google Scholar] [CrossRef]
- Cohen, J.M.; Brill, D.R. Further Examples of <<Machian>> Effects of Rotating Bodies in General Relativity. Il Nuovo Cimento B 1968, 56, 209. [Google Scholar]
- Luciano, G.G.; Petruzziello, L. Testing gravity with neutrinos: From classical to quantum regime. Int. J. Mod. Phys. D 2020, 29, 2043002. [Google Scholar] [CrossRef]
- Stuttard, T.; Jensen, M. Neutrino decoherence from quantum gravitational stochastic perturbations. Phys. Rev. D 2020, 102, 115003. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).