Nuclear Equation of State in the Relativistic Point-Coupling Model Constrained by Excitations in Finite Nuclei
Abstract
1. Introduction
2. Relativistic Point-Coupling Functionals for Studies of the Symmetry Energy
3. Results
3.1. Nuclear Matter Properties and Equation of State
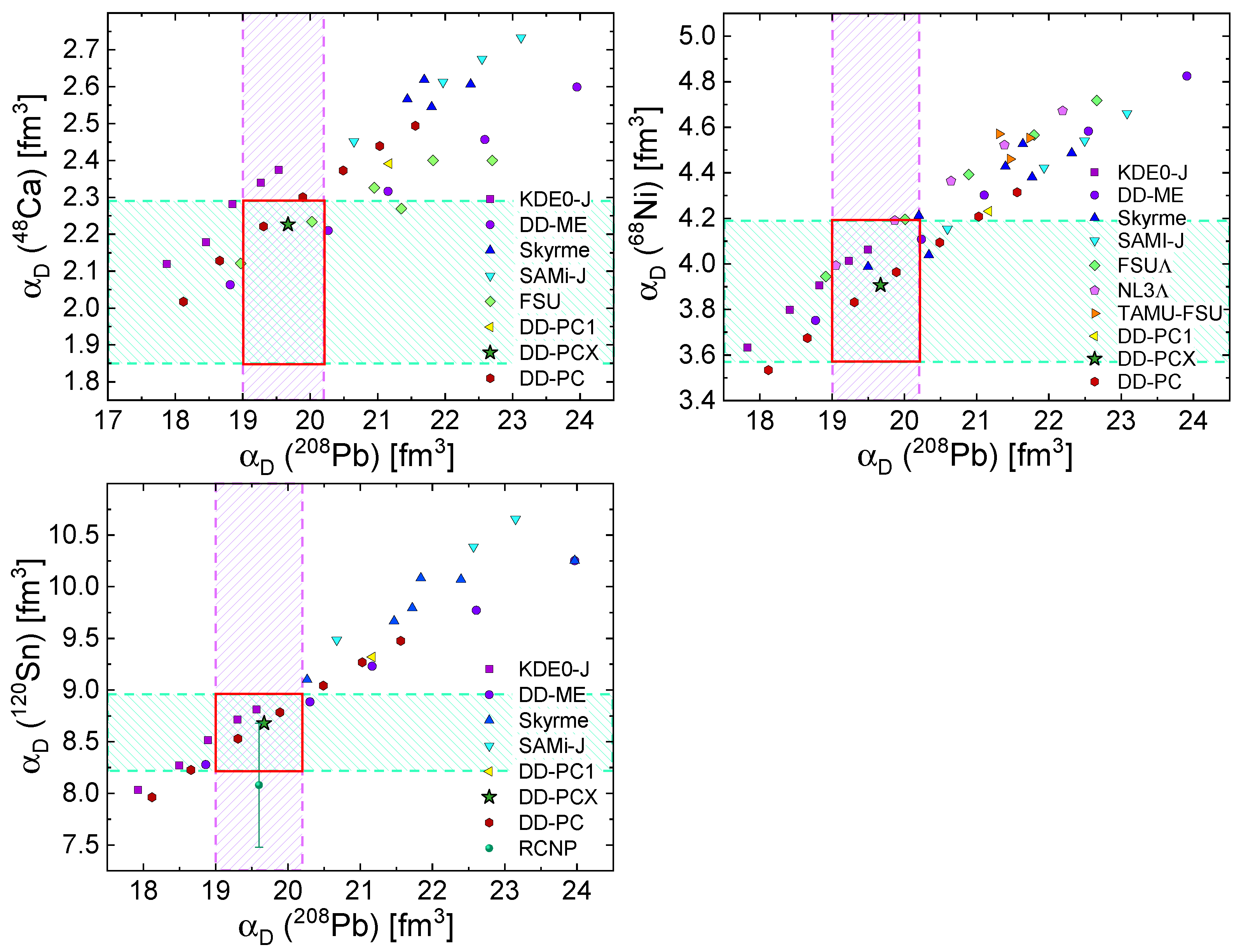
3.2. Dipole Polarizability and Neutron Skin
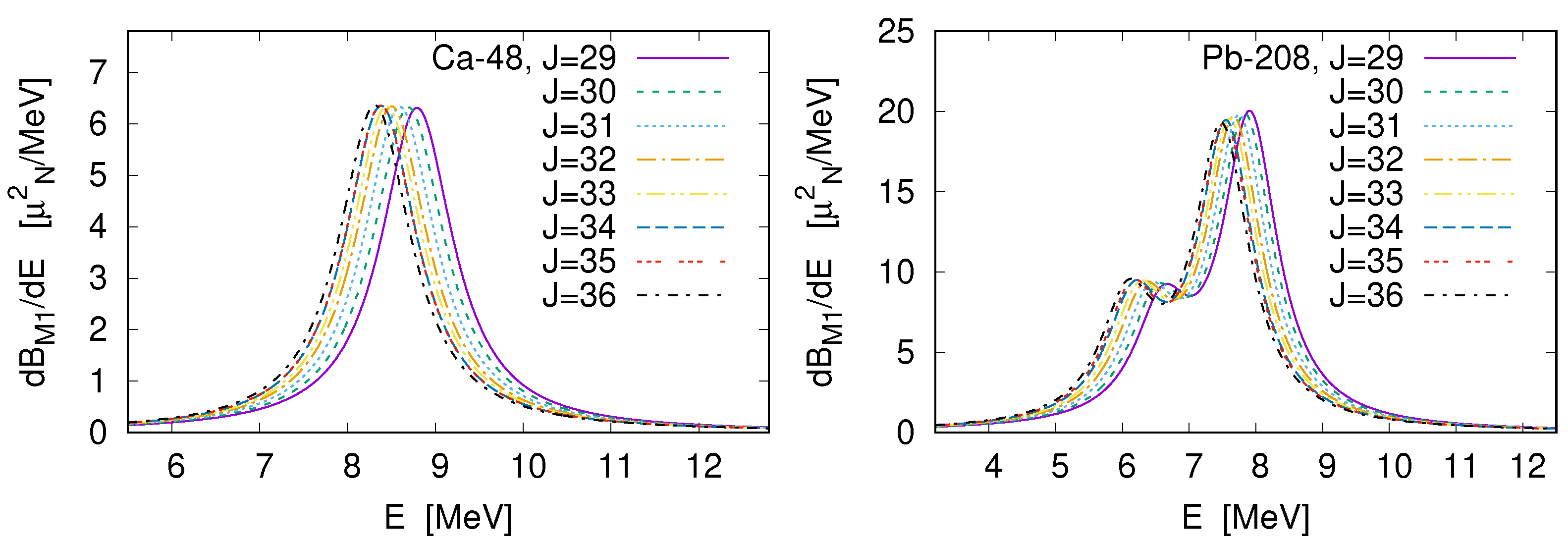
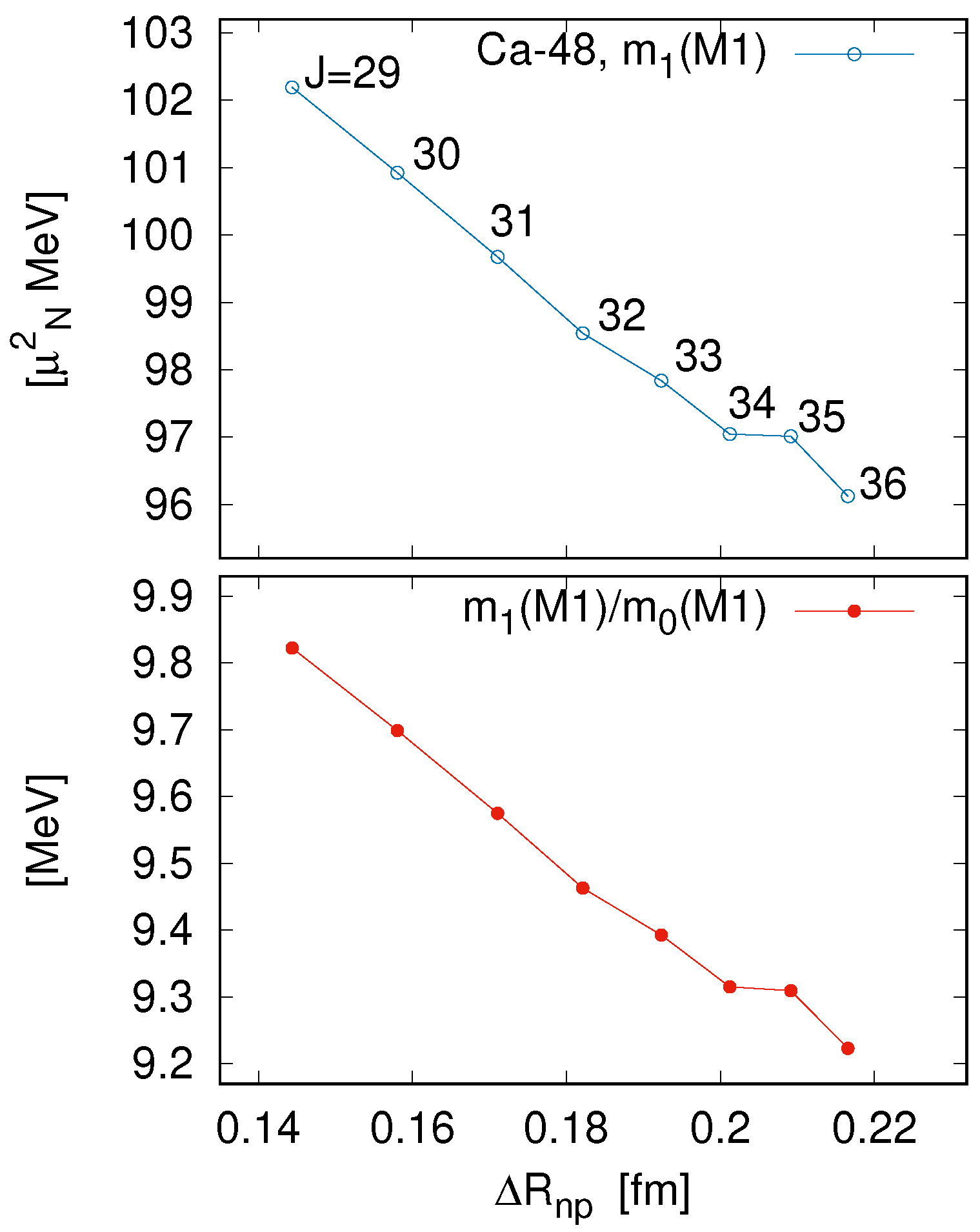
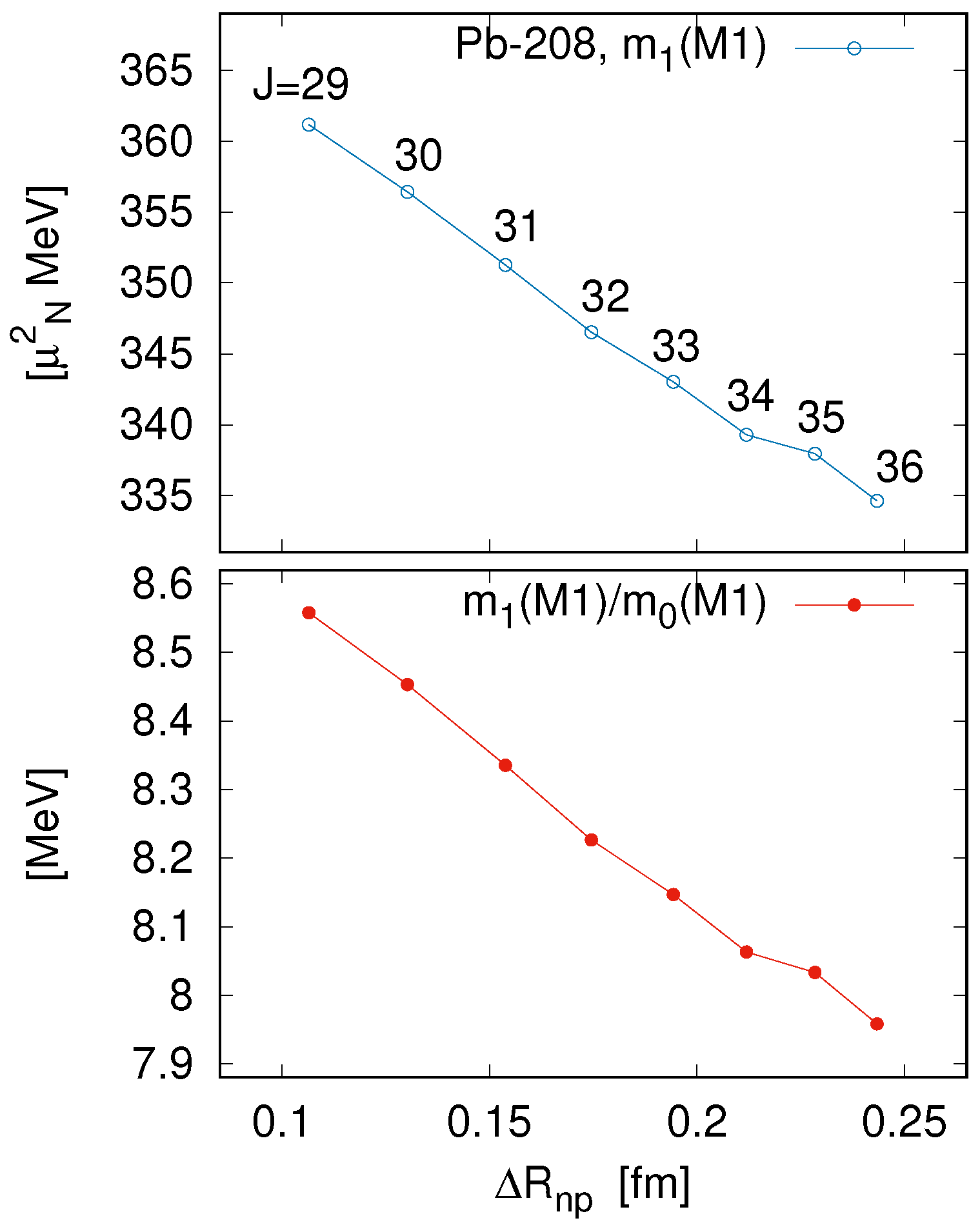
3.3. Sensitivity of Magnetic-Dipole Excitation to Symmetry Energy
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EDF | Energy density functional |
| RHB | Relativistic Hartree–Bogoliubov |
| QRPA | Quasiparticle random phase approximation |
| EoS | Equation of state |
References
- Lattimer, J.M. The Nuclear Equation of State and Neutron Star Masses. Annu. Rev. Nucl. Part. Sci. 2012, 62, 485–515. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Nikšić, T.; Vretenar, D.; Ring, P. New relativistic mean-field interaction with density-dependent meson-nucleon couplings. Phys. Rev. C 2005, 71, 024312. [Google Scholar] [CrossRef]
- Nikšić, T.; Vretenar, D.; Ring, P. Relativistic nuclear energy density functionals: Adjusting parameters to binding energies. Phys. Rev. C 2008, 78, 034318. [Google Scholar] [CrossRef]
- Chen, W.C.; Piekarewicz, J.; Centelles, M. Giant monopole energies from a constrained relativistic mean-field approach. Phys. Rev. C 2013, 88, 024319. [Google Scholar] [CrossRef]
- Chen, W.C.; Piekarewicz, J. Building relativistic mean field models for finite nuclei and neutron stars. Phys. Rev. C 2014, 90, 044305. [Google Scholar] [CrossRef]
- Kortelainen, M.; Lesinski, T.; Moré, J.; Nazarewicz, W.; Sarich, J.; Schunck, N.; Stoitsov, M.V.; Wild, S. Nuclear energy density optimization. Phys. Rev. C 2010, 82, 024313. [Google Scholar] [CrossRef]
- Kortelainen, M.; McDonnell, J.; Nazarewicz, W.; Reinhard, P.G.; Sarich, J.; Schunck, N.; Stoitsov, M.V.; Wild, S.M. Nuclear energy density optimization: Large deformations. Phys. Rev. C 2012, 85, 024304. [Google Scholar] [CrossRef]
- Kortelainen, M.; McDonnell, J.; Nazarewicz, W.; Olsen, E.; Reinhard, P.G.; Sarich, J.; Schunck, N.; Wild, S.M.; Davesne, D.; Erler, J.; et al. Nuclear energy density optimization: Shell structure. Phys. Rev. C 2014, 89, 054314. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Paar, N. Nuclear equation of state from ground and collective excited state properties of nuclei. Prog. Part. Nucl. Phys. 2018, 101, 96–176. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Lim, Y. Constraining the symmetry parameters of the nuclear interaction. Astrophys. J. 2013, 771, 51. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Brown, E.F.; Kim, Y.; Lynch, W.G.; Michaels, R.; Ono, A.; Piekarewicz, J.; Tsang, M.B.; Wolter, H.H. A way forward in the study of the symmetry energy: Experiment, theory, and observation. J. Phys. G Nucl. Part. Phys. 2014, 41, 093001. [Google Scholar] [CrossRef]
- Tsang, M.B.; Stone, J.R.; Camera, F.; Danielewicz, P.; Gandolfi, S.; Hebeler, K.; Horowitz, C.J.; Lee, J.; Lynch, W.G.; Kohley, Z.; et al. Constraints on the symmetry energy and neutron skins from experiments and theory. Phys. Rev. C 2012, 86, 015803. [Google Scholar] [CrossRef]
- Centelles, M.; Roca-Maza, X.; Viñas, X.; Warda, M. Nuclear Symmetry Energy Probed by Neutron Skin Thickness of Nuclei. Phys. Rev. Lett. 2009, 102, 122502. [Google Scholar] [CrossRef] [PubMed]
- Garg, U.; Colò, G. The compression-mode giant resonances and nuclear incompressibility. Prog. Part. Nucl. Phys. 2018, 101, 55–95. [Google Scholar] [CrossRef]
- Stone, J.R.; Stone, N.J.; Moszkowski, S.A. Incompressibility in finite nuclei and nuclear matter. Phys. Rev. C 2014, 89, 044316. [Google Scholar] [CrossRef]
- Danielewicz, P.; Lacey, R.; Lynch, W.G. Determination of the Equation of State of Dense Matter. Science 2002, 298, 1592–1596. [Google Scholar] [CrossRef]
- Baldo, M.; Burgio, G. The nuclear symmetry energy. Prog. Part. Nucl. Phys. 2016, 91, 203–258. [Google Scholar] [CrossRef]
- Abrahamyan, S.; Ahmed, Z.; Albataineh, H.; Aniol, K.; Armstrong, D.S.; Armstrong, W.; Averett, T.; Babineau, B.; Barbieri, A.; Bellini, V.; et al. Measurement of the Neutron Radius of 208Pb through Parity Violation in Electron Scattering. Phys. Rev. Lett. 2012, 108, 112502. [Google Scholar] [CrossRef]
- Adhikari, D.; Albataineh, H.; Androic, D.; Aniol, K.; Armstrong, D.S.; Averett, T.; Barcus, S.; Bellini, V.; Beminiwattha, R.S.; Benesch, J.F.; et al. An Accurate Determination of the Neutron Skin Thickness of 208Pb through Parity-Violation in Electron Scattering. arXiv 2021, arXiv:2102.10767. [Google Scholar]
- Piekarewicz, J.; Agrawal, B.K.; Colò, G.; Nazarewicz, W.; Paar, N.; Reinhard, P.G.; Roca-Maza, X.; Vretenar, D. Electric dipole polarizability and the neutron skin. Phys. Rev. C 2012, 85, 041302. [Google Scholar] [CrossRef]
- Danielewicz, P.; Lee, J. Symmetry energy II: Isobaric analog states. Nucl. Phys. A 2014, 922, 1–70. [Google Scholar] [CrossRef]
- Vretenar, D.; Paar, N.; Nikšić, T.; Ring, P. Spin-Isospin Resonances and the Neutron Skin of Nuclei. Phys. Rev. Lett. 2003, 91, 262502. [Google Scholar] [CrossRef] [PubMed]
- Krasznahorkay, A.; Paar, N.; Vretenar, D.; Harakeh, M. Anti-analog giant dipole resonances and the neutron skin of nuclei. Phys. Lett. B 2013, 720, 428–432. [Google Scholar] [CrossRef]
- Cao, L.G.; Roca-Maza, X.; Colò, G.; Sagawa, H. Constraints on the neutron skin and symmetry energy from the anti-analog giant dipole resonance in 208Pb. Phys. Rev. C 2015, 92, 034308. [Google Scholar] [CrossRef]
- Yüksel, E.; Marketin, T.; Paar, N. Optimizing the relativistic energy density functional with nuclear ground state and collective excitation properties. Phys. Rev. C 2019, 99, 034318. [Google Scholar] [CrossRef]
- Paar, N.; Ring, P.; Nikšić, T.; Vretenar, D. Quasiparticle random phase approximation based on the relativistic Hartree-Bogoliubov model. Phys. Rev. C 2003, 67, 034312. [Google Scholar] [CrossRef]
- Klüpfel, P.; Reinhard, P.G.; Bürvenich, T.J.; Maruhn, J.A. Variations on a theme by Skyrme: A systematic study of adjustments of model parameters. Phys. Rev. C 2009, 79, 034310. [Google Scholar] [CrossRef]
- Nikšić, T.; Paar, N.; Vretenar, D.; Ring, P. DIRHB—A relativistic self-consistent mean-field framework for atomic nuclei. Comput. Phys. Commun. 2014, 185, 1808–1821. [Google Scholar] [CrossRef]
- Paar, N.; Vretenar, D.; Ring, P. Proton Electric Pygmy Dipole Resonance. Phys. Rev. Lett. 2005, 94, 182501. [Google Scholar] [CrossRef]
- Paar, N.; Niu, Y.F.; Vretenar, D.; Meng, J. Isoscalar and Isovector Splitting of Pygmy Dipole Structures. Phys. Rev. Lett. 2009, 103, 032502. [Google Scholar] [CrossRef] [PubMed]
- Niu, Y.F.; Niu, Z.M.; Paar, N.; Vretenar, D.; Wang, G.H.; Bai, J.S.; Meng, J. Pairing transitions in finite-temperature relativistic Hartree-Bogoliubov theory. Phys. Rev. C 2013, 88, 034308. [Google Scholar] [CrossRef]
- Niu, Y.; Paar, N.; Vretenar, D.; Meng, J. Low-energy monopole and dipole response in nuclei at finite temperature. Phys. Lett. B 2009, 681, 315–319. [Google Scholar] [CrossRef]
- Khan, E.; Paar, N.; Vretenar, D. Low-energy monopole strength in exotic nickel isotopes. Phys. Rev. C 2011, 84, 051301. [Google Scholar] [CrossRef]
- Yüksel, E.; Paar, N.; Colò, G.; Khan, E.; Niu, Y.F. Gamow-Teller excitations at finite temperature: Competition between pairing and temperature effects. Phys. Rev. C 2020, 101, 044305. [Google Scholar] [CrossRef]
- Kružić, G.; Oishi, T.; Vale, D.; Paar, N. Magnetic dipole excitations based on the relativistic nuclear energy density functional. Phys. Rev. C 2020, 102, 044315. [Google Scholar] [CrossRef]
- Paar, N.; Vretenar, D.; Marketin, T.; Ring, P. Inclusive charged-current neutrino-nucleus reactions calculated with the relativistic quasiparticle random-phase approximation. Phys. Rev. C 2008, 77, 024608. [Google Scholar] [CrossRef]
- Samana, A.R.; Krmpotić, F.; Paar, N.; Bertulani, C.A. Neutrino and antineutrino charge-exchange reactions on 12C. Phys. Rev. C 2011, 83, 024303. [Google Scholar] [CrossRef]
- Fantina, A.F.; Khan, E.; Colò, G.; Paar, N.; Vretenar, D. Stellar electron-capture rates on nuclei based on a microscopic Skyrme functional. Phys. Rev. C 2012, 86, 035805. [Google Scholar] [CrossRef]
- Vale, D.; Rauscher, T.; Paar, N. Hybrid method to resolve the neutrino mass hierarchy by supernova (anti)neutrino induced reactions. J. Cosmol. Astropart. Phys. 2016, 2016, 007. [Google Scholar] [CrossRef]
- Petković, J.; Marketin, T.; Martínez-Pinedo, G.; Paar, N. Self-consistent calculation of the reactor antineutrino spectra including forbidden transitions. J. Phys. G Nucl. Part. Phys. 2019, 46, 085103. [Google Scholar] [CrossRef]
- Nikšić, T.; Vretenar, D.; Finelli, P.; Ring, P. Relativistic Hartree-Bogoliubov model with density-dependent meson-nucleon couplings. Phys. Rev. C 2002, 66, 024306. [Google Scholar] [CrossRef]
- Tian, Y.; Ma, Z.y.; Ring, P. Axially deformed relativistic Hartree Bogoliubov theory with a separable pairing force. Phys. Rev. C 2009, 80, 024313. [Google Scholar] [CrossRef]
- Finelli, P.; Kaiser, N.; Vretenar, D.; Weise, W. Relativistic nuclear model with point-couplings constrained by QCD and chiral symmetry. Nucl. Phys. A 2004, 735, 449–481. [Google Scholar] [CrossRef]
- Bender, M.; Rutz, K.; Reinhard, P.G.; Maruhn, J.A. Pairing gaps from nuclear mean-field models. Eur. Phys. J. A 2000, 8, 59–75. [Google Scholar] [CrossRef]
- Huang, W.; Audi, G.; Wang, M.; Kondev, F.G.; Naimi, S.; Xu, X. The AME2016 atomic mass evaluation (I). Evaluation of input data; and adjustment procedures. Chin. Phys. C 2017, 41, 030002. [Google Scholar] [CrossRef]
- Wang, M.; Audi, G.; Kondev, F.G.; Huang, W.; Naimi, S.; Xu, X. The AME2016 atomic mass evaluation (II). Tables, graphs and references. Chin. Phys. C 2017, 41, 030003. [Google Scholar] [CrossRef]
- Angeli, I.; Marinova, K. Table of experimental nuclear ground state charge radii: An update. At. Data Nucl. Data Tables 2013, 99, 69–95. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Paar, N.; Colò, G. Covariance analysis for energy density functionals and instabilities. J. Phys. G Nucl. Part. Phys. 2015, 42, 034033. [Google Scholar] [CrossRef]
- Klähn, T.; Blaschke, D.; Typel, S.; van Dalen, E.N.E.; Faessler, A.; Fuchs, C.; Gaitanos, T.; Grigorian, H.; Ho, A.; Kolomeitsev, E.E.; et al. Constraints on the high-density nuclear equation of state from the phenomenology of compact stars and heavy-ion collisions. Phys. Rev. C 2006, 74, 035802. [Google Scholar] [CrossRef]
- Drischler, C.; Furnstahl, R.J.; Melendez, J.A.; Phillips, D.R. How Well Do We Know the Neutron-Matter Equation of State at the Densities Inside Neutron Stars? A Bayesian Approach with Correlated Uncertainties. Phys. Rev. Lett. 2020, 125, 202702. [Google Scholar] [CrossRef] [PubMed]
- Paar, N.; Vretenar, D.; Khan, E.; Colò, G. Exotic modes of excitation in atomic nuclei far from stability. Rep. Prog. Phys. 2007, 70, 691–793. [Google Scholar] [CrossRef]
- Trzcińska, A.; Jastrzȩbski, J.; Lubiński, P.; Hartmann, F.J.; Schmidt, R.; von Egidy, T.; Kłos, B. Neutron Density Distributions Deduced from Antiprotonic Atoms. Phys. Rev. Lett. 2001, 87, 082501. [Google Scholar] [CrossRef] [PubMed]
- Świątecki, W.J.; Trzcińska, A.; Jastrzębski, J. Difference of the root-mean-square sizes of neutron and proton distributions in nuclei: Comparison of theory with data. Phys. Rev. C 2005, 71, 047301. [Google Scholar] [CrossRef]
- Birkhan, J.; Miorelli, M.; Bacca, S.; Bassauer, S.; Bertulani, C.A.; Hagen, G.; Matsubara, H.; von Neumann-Cosel, P.; Papenbrock, T.; Pietralla, N.; et al. Electric Dipole Polarizability of 48Ca and Implications for the Neutron Skin. Phys. Rev. Lett. 2017, 118, 252501. [Google Scholar] [CrossRef]
- Rossi, D.M.; Adrich, P.; Aksouh, F.; Alvarez-Pol, H.; Aumann, T.; Benlliure, J.; Böhmer, M.; Boretzky, K.; Casarejos, E.; Chartier, M.; et al. Measurement of the Dipole Polarizability of the Unstable Neutron-Rich Nucleus 68Ni. Phys. Rev. Lett. 2013, 111, 242503. [Google Scholar] [CrossRef]
- Hashimoto, T.; Krumbholz, A.M.; Reinhard, P.G.; Tamii, A.; von Neumann-Cosel, P.; Adachi, T.; Aoi, N.; Bertulani, C.A.; Fujita, H.; Fujita, Y.; et al. Dipole polarizability of 120Sn and nuclear energy density functionals. Phys. Rev. C 2015, 92, 031305. [Google Scholar] [CrossRef]
- Bassauer, S.; von Neumann-Cosel, P.; Reinhard, P.G.; Tamii, A.; Adachi, S.; Bertulani, C.; Chan, P.; Colò, G.; DÁlessio, A.; Fujioka, H.; et al. Evolution of the dipole polarizability in the stable tin isotope chain. Phys. Lett. B 2020, 810, 135804. [Google Scholar] [CrossRef]
- Tamii, A.; Poltoratska, I.; von Neumann-Cosel, P.; Fujita, Y.; Adachi, T.; Bertulani, C.A.; Carter, J.; Dozono, M.; Fujita, H.; Fujita, K.; et al. Complete Electric Dipole Response and the Neutron Skin in 208Pb. Phys. Rev. Lett. 2011, 107, 062502. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Viñas, X.; Centelles, M.; Agrawal, B.K.; Colò, G.; Paar, N.; Piekarewicz, J.; Vretenar, D. Neutron skin thickness from the measured electric dipole polarizability in 68Ni, 120Sn, and 208Pb. Phys. Rev. C 2015, 92, 064304. [Google Scholar] [CrossRef]
- De Vries, H.; De Jager, C.; De Vries, C. Nuclear charge-density-distribution parameters from elastic electron scattering. At. Data Nucl. Data Tables 1987, 36, 495–536. [Google Scholar] [CrossRef]
- Fricke, G.; Bernhardt, C.; Heilig, K.; Schaller, L.; Schellenberg, L.; Shera, E.; Dejager, C. Nuclear Ground State Charge Radii from Electromagnetic Interactions. At. Data Nucl. Data Tables 1995, 60, 177–285. [Google Scholar] [CrossRef]
- Zumbro, J.D.; Shera, E.B.; Tanaka, Y.; Bemis, C.E.; Naumann, R.A.; Hoehn, M.V.; Reuter, W.; Steffen, R.M. E2 and E4 Deformations in 233,234,235,238U. Phys. Rev. Lett. 1984, 53, 1888–1892. [Google Scholar] [CrossRef]
- Zumbro, J.; Naumann, R.; Hoehn, M.; Reuter, W.; Shera, E.; Bemis, C.; Tanaka, Y. E2 and E4 deformations in 232Th and 239,240,242Pu. Phys. Lett. B 1986, 167, 383–387. [Google Scholar] [CrossRef]
- Ray, L. Neutron isotopic density differences deduced from 0.8 GeV polarized proton elastic scattering. Phys. Rev. C 1979, 19, 1855–1872. [Google Scholar] [CrossRef]
- Krasznahorkay, A.; Akimune, H.; van den Berg, A.; Blasi, N.; Brandenburg, S.; Csatloś, M.; Fujiwara, M.; Gulyaś, J.; Harakeh, M.; Hunyadi, M.; et al. Neutron-skin thickness in neutron-rich isotopes. Nucl. Phys. A 2004, 731, 224–234. [Google Scholar] [CrossRef]
- Krasznahorkay, A.; Fujiwara, M.; van Aarle, P.; Akimune, H.; Daito, I.; Fujimura, H.; Fujita, Y.; Harakeh, M.N.; Inomata, T.; Jänecke, J.; et al. Excitation of Isovector Spin-Dipole Resonances and Neutron Skin of Nuclei. Phys. Rev. Lett. 1999, 82, 3216–3219. [Google Scholar] [CrossRef]
- Klimkiewicz, A.; Paar, N.; Adrich, P.; Fallot, M.; Boretzky, K.; Aumann, T.; Cortina-Gil, D.; Pramanik, U.D.; Elze, T.W.; Emling, H.; et al. Nuclear symmetry energy and neutron skins derived from pygmy dipole resonances. Phys. Rev. C 2007, 76, 051603. [Google Scholar] [CrossRef]
- Terashima, S.; Sakaguchi, H.; Takeda, H.; Ishikawa, T.; Itoh, M.; Kawabata, T.; Murakami, T.; Uchida, M.; Yasuda, Y.; Yosoi, M.; et al. Proton elastic scattering from tin isotopes at 295 MeV and systematic change of neutron density distributions. Phys. Rev. C 2008, 77, 024317. [Google Scholar] [CrossRef]
- Oishi, T.; Kružić, G.; Paar, N. Role of residual interaction in the relativistic description of M1 excitation. J. Phys. G Nucl. Part. Phys. 2020, 47, 115106. [Google Scholar] [CrossRef]
- Ring, P.; Schuck, P. The Nuclear Many-Body Problems; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Fujita, Y.; Rubio, B.; Gelletly, W. Spin-isospin excitations probed by strong, weak and electro-magnetic interactions. Prog. Part. Nucl. Phys. 2011, 66, 549–606. [Google Scholar] [CrossRef]
- Von Neumann-Cosel, P.; Poves, A.; Retamosa, J.; Richter, A. Magnetic dipole response in nuclei at the N = 28 shell closure: A new look1Work supported by the DFG under Contract Ri 242/12-1 and by research grants from the DGES (Spain), Nos. PB96-53 and PB96-604.1. Phys. Lett. B 1998, 443, 1–6. [Google Scholar] [CrossRef]
- Vesely, P.; Kvasil, J.; Nesterenko, V.O.; Kleinig, W.; Reinhard, P.G.; Ponomarev, V.Y. Skyrme random-phase-approximation description of spin-flip M1 giant resonance. Phys. Rev. C 2009, 80, 031302. [Google Scholar] [CrossRef]
- Nesterenko, V.O.; Kvasil, J.; Vesely, P.; Kleinig, W.; Reinhard, P.G.; Ponomarev, V.Y. Spin-flip M1 giant resonance as a challenge for Skyrme forces. J. Phys. G Nucl. Part. Phys. 2010, 37, 064034. [Google Scholar] [CrossRef]
- Oishi, T.; Paar, N. Magnetic dipole excitation and its sum rule in nuclei with two valence nucleons. Phys. Rev. C 2019, 100, 024308. [Google Scholar] [CrossRef]
- Birkhan, J.; Matsubara, H.; von Neumann-Cosel, P.; Pietralla, N.; Ponomarev, V.Y.; Richter, A.; Tamii, A.; Wambach, J. Electromagnetic M1 transition strengths from inelastic proton scattering: The cases of 48Ca and 208Pb. Phys. Rev. C 2016, 93, 041302. [Google Scholar] [CrossRef]
- Tompkins, J.R.; Arnold, C.W.; Karwowski, H.J.; Rich, G.C.; Sobotka, L.G.; Howell, C.R. Measurements of the 48Ca(γ,n) reaction. Phys. Rev. C 2011, 84, 044331. [Google Scholar] [CrossRef]
- Mathy, M.; Birkhan, J.; Matsubara, H.; von Neumann-Cosel, P.; Pietralla, N.; Ponomarev, V.Y.; Richter, A.; Tamii, A. Search for weak M1 transitions in 48Ca with inelastic proton scattering. Phys. Rev. C 2017, 95, 054316. [Google Scholar] [CrossRef]
- Laszewski, R.M.; Rullhusen, P.; Hoblit, S.D.; LeBrun, S.F. Giant M1 Resonance in Pb. Phys. Rev. Lett. 1985, 54, 530–533. [Google Scholar] [CrossRef]
- Laszewski, R.M.; Alarcon, R.; Dale, D.S.; Hoblit, S.D. Distribution of M1 Transitions in 208Pb. Phys. Rev. Lett. 1988, 61, 1710–1712. [Google Scholar] [CrossRef]

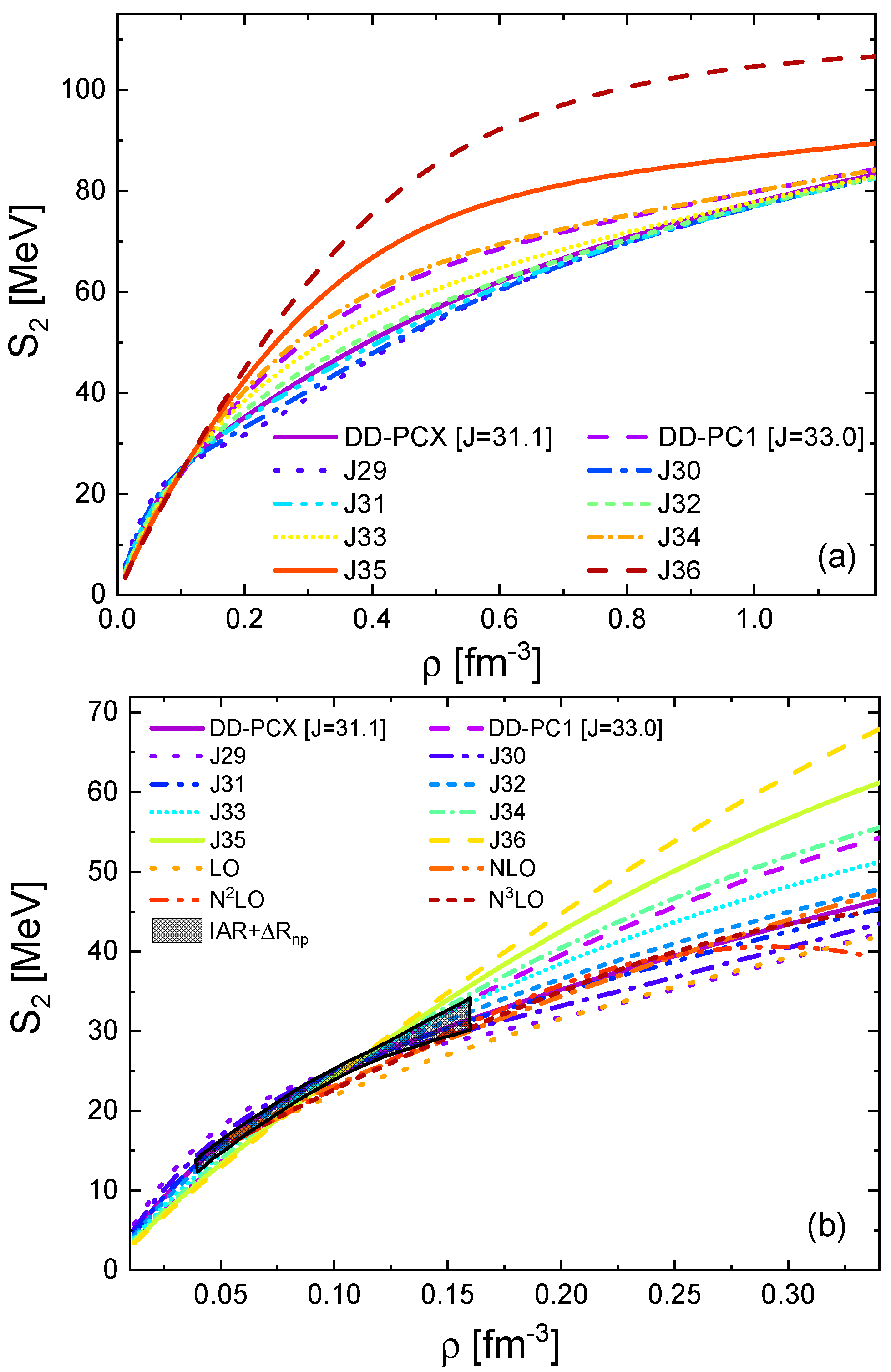
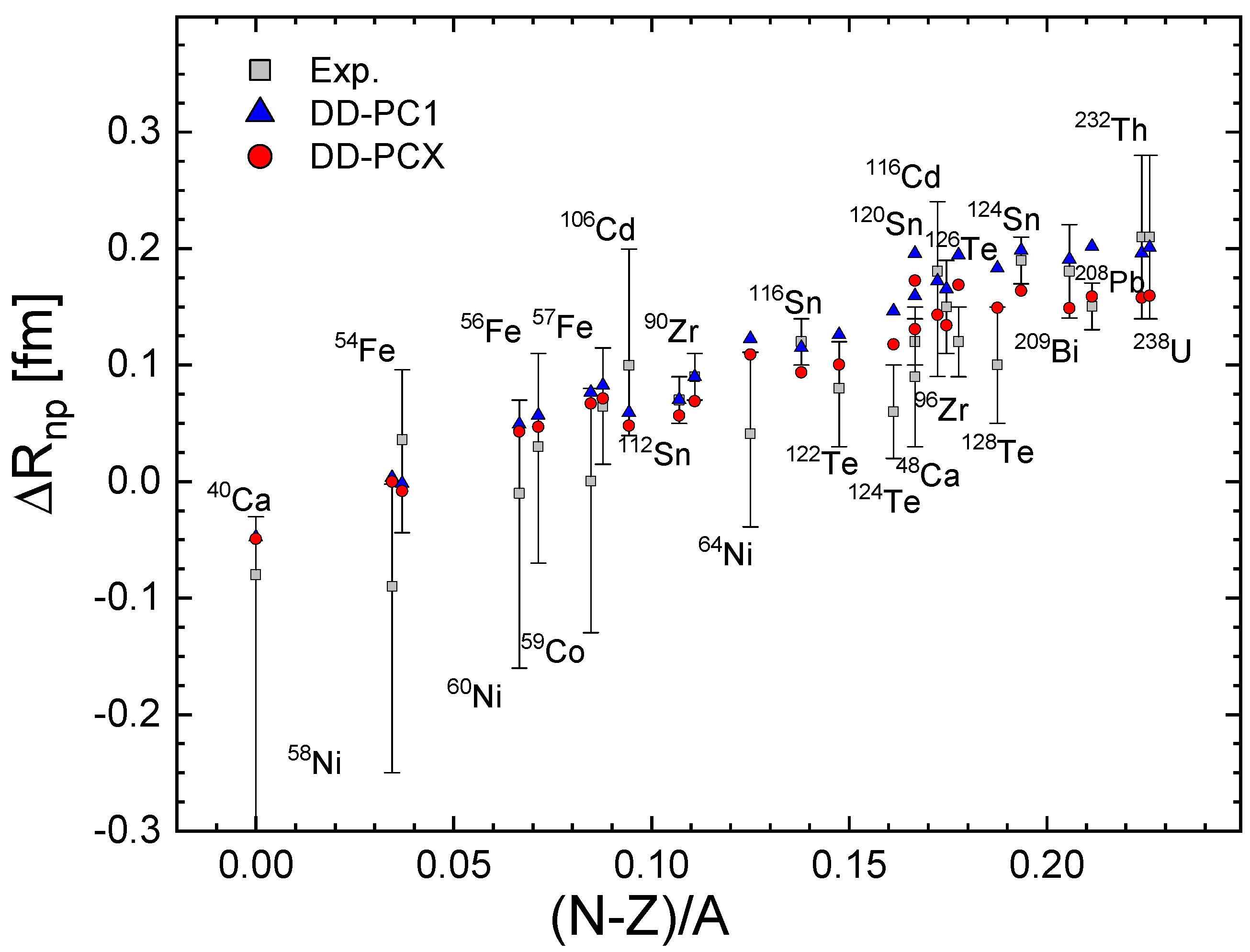
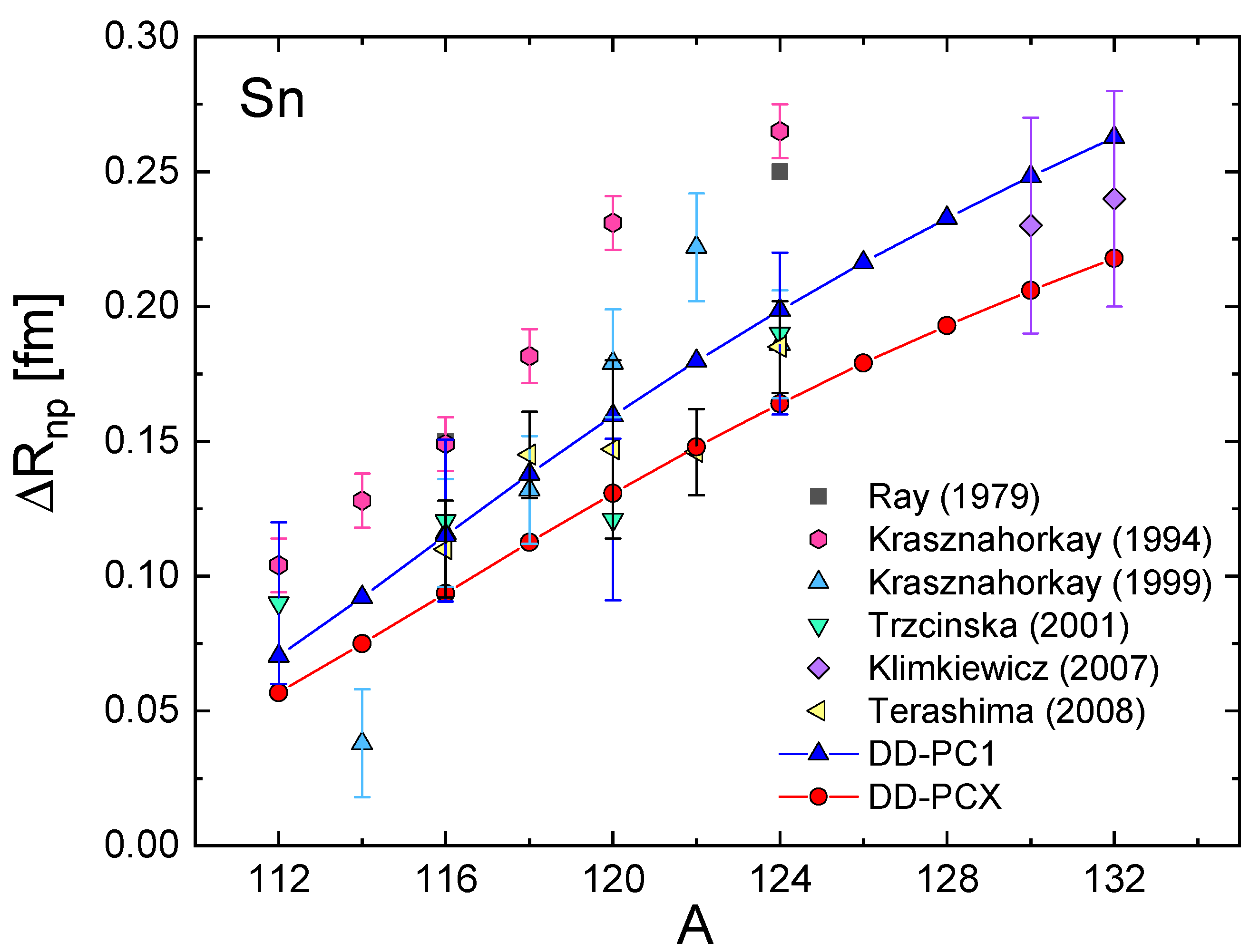
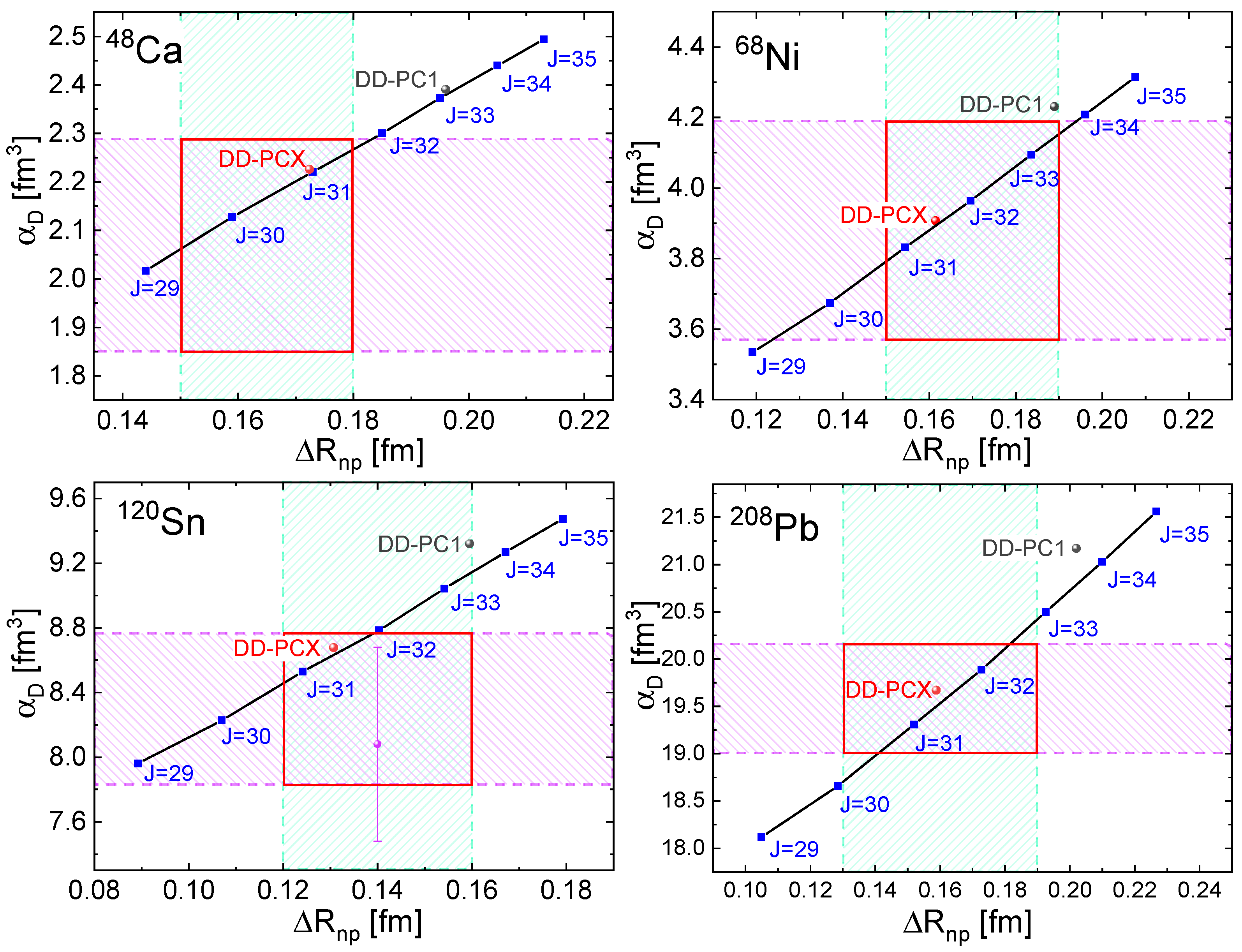
| Nucleus | B.E. | |||||
|---|---|---|---|---|---|---|
| (±0.15 MeV) | (±0.15 MeV) | (±1 MeV) | (±0.02 fm) | (±0.05 fm) | (±0.05 fm) | |
| O | −127.619 (2) | 2.777 (1) | ||||
| O | −139.807 (1) | |||||
| O | −151.371 (1) | |||||
| O | −162.026 (1) | |||||
| Ne | −132.142 (1) | |||||
| Mg | −134.479 (1) | |||||
| Si | −283.428 (1) | |||||
| S | 1.52 (1) | −308.714 (1) | 3.299 (1) | 3.577 (1) | 0.994 (2) | |
| Ar | 1.44 (1) | −327.342 (1) | 3.404 (1) | |||
| Ca | −281.371 (1) | |||||
| Ca | −313.121 (1) | |||||
| Ca | −342.052 (2) | 3.485 (2) | 3.831 (2) | 0.978 (2) | ||
| Ca | 1.68 (1) | −361.895 (1) | 3.513 (2) | 3.876 (2) | 0.999 (2) | |
| Ca | 1.70 (1) | −380.959 (1) | 3.523 (3) | 3.912 (1) | 0.975 (2) | |
| Ca | 1.49 (1) | −398.772 (1) | 3.502 (1) | |||
| Ca | −416.001 (1) | 3.484 (1) | 3.936 (1) | 0.881 (1) | ||
| Ca | −427.508 (1) | |||||
| Ti | −346.888 (1) | |||||
| Ti | −437.784 (1) | |||||
| Cr | −456.350 (1) | 3.642 (1) | 4.173 (1) | 0.924 (1) | ||
| Fe | −471.763 (1) | 3.693 (5) | 4.258 (5) | 0.900 (5) | ||
| Ni | −483.994 (1) | |||||
| Ni | −590.407 (1) | |||||
| Ni | −613.455 (1) | |||||
| Se | −727.338 (1) | |||||
| Kr | −749.234 (1) | |||||
| Sr | −768.468 (1) | 4.220 (1) | 4.994 (1) | 0.923 (1) | ||
| Zr | −783.898 (1) | 4.272 (1) | 5.040 (1) | 0.957 (1) | ||
| Mo | 1.40 (1) | −796.510 (1) | 4.315 (1) | 5.104 (1) | 0.950 (1) | |
| Ru | −806.864 (1) | |||||
| Pd | −815.040 (1) | |||||
| Cd | −821.072 (1) | |||||
| Sn | −825.297 (2) | |||||
| Sn | −893.795 (1) | |||||
| Sn | −914.654 (1) | |||||
| Sn | 1.41 (1) | −953.526 (1) | 4.596 (1) | 5.477 (2) | ||
| Sn | 1.26 (3) | −971.570 (1) | 4.610 (1) | 5.509 (2) | 0.948 (2) | |
| Sn | 1.21 (3) | −988.681 (1) | 4.626 (1) | 5.541 (1) | 0.945 (1) | |
| Sn | 1.34 (1) | −1004.951 (1) | 4.640 (1) | 5.571 (1) | 0.931 (1) | |
| Sn | 1.39 (1) | −1020.539 (1) | 5.591 (1) | |||
| Sn | 1.37 (1) | −1035.524 (1) | ||||
| Sn | 1.31 (1) | −1049.960 (1) | 4.674 (1) | 5.640 (1) | ||
| Sn | 1.26 (1) | −1063.883 (1) | ||||
| Sn | 1.22 (1) | −1077.373 (1) | ||||
| Sn | 1.17 (3) | −1090.286 (1) | ||||
| Sn | −1102.840 (1) | |||||
| Sn | −1108.871 (1) | |||||
| Te | 0.81 (1) | −1123.410 (1) | ||||
| Xe | 0.98 (1) | −1141.881 (1) | ||||
| Ba | 1.12 (1) | −1158.292 (1) | 4.834 (1) | 5.868 (2) | 0.900 (1) | |
| Ce | 1.21 (1) | −1172.687 (1) | 4.877 (1) | |||
| Nd | 1.23 (1) | −1185.136 (1) | 4.915 (1) | 5.876 (3) | 0.989 (3) | |
| Sm | 1.25 (1) | −1195.729 (1) | ||||
| Gd | 1.42 (1) | −1204.427 (1) | 4.984 (1) | |||
| Dy | 1.49 (1) | −1210.773 (1) | 5.046 (1) | |||
| Er | −1215.329 (1) | 5.076 (2) | ||||
| Yb | −1218.396 (1) | |||||
| Hg | −1621.048 (1) | 5.485 (1) | ||||
| Pb | −1560.018 (1) | 5.450 (2) | ||||
| Pb | −1576.361 (1) | 5.459 (2) | ||||
| Pb | −1592.193 (1) | 5.474 (1) | ||||
| Pb | −1607.505 (1) | 5.483 (1) | 6.749 (1) | 0.918 (1) | ||
| Pb | 0.59 (1) | −1622.323 (1) | 5.494 (1) | 6.766 (1) | 0.921 (1) | |
| Pb | −1636.429 (1) | 5.505 (1) | 6.806 (1) | 0.900 (1) | ||
| Pb | 0.66 (1) | −1645.552 (1) | 5.523 (1) | |||
| Pb | −1654.514 (1) | 5.542 (1) | ||||
| Pb | −1663.290 (1) | 5.562 (1) | ||||
| Po | 0.81 (1) | −1645.212 (1) | 5.534 (1) | |||
| Rn | 0.88 (1) | −1652.496 (1) | 5.555 (2) | |||
| Ra | 0.96 (1) | −1658.322 (1) | 5.571 (3) | |||
| Th | −1662.694 (1) | |||||
| U | −1665.659 (1) |
| Parameters | J = 29 | J = 30 | J = 31 | J = 32 | J = 33 | J = 34 | J = 35 | J = 36 |
|---|---|---|---|---|---|---|---|---|
| (fm) | −10.418334630 | −10.384498639 | −10.390657606 | −10.389488800 | −10.387142700 | −10.386956740 | −10.384414509 | −10.387781497 |
| (fm) | −9.163612956 | −9.202629009 | −9.189174805 | −9.197715907 | −9.215314920 | −9.208074838 | −9.215072973 | −9.218990127 |
| (fm) | −4.968064171 | −5.014345965 | −5.031326770 | −5.030638408 | −5.021597419 | −5.023220520 | −5.012403311 | −5.019048957 |
| 1.348374834 | 1.351382727 | 1.352967739 | 1.352329476 | 1.351064617 | 1.352262229 | 1.350836047 | 1.352173708 | |
| (fm) | 6.591051202 | 6.583857817 | 6.584374904 | 6.584425799 | 6.584907238 | 6.587404662 | 6.583350394 | 6.585576629 |
| (fm) | 8.366192199 | 8.380745134 | 8.363054275 | 8.358949669 | 8.366666526 | 8.350225226 | 8.361167422 | 8.359267286 |
| 0.737531721 | 0.742903470 | 0.740865993 | 0.739885318 | 0.740096759 | 0.740274812 | 0.740322161 | 0.740857140 | |
| (fm) | 4.370433886 | 3.630253620 | 3.017651110 | 2.581533741 | 2.200070930 | 1.913161650 | 1.654675062 | 1.474609051 |
| 1.845561631 | 1.570350651 | 1.301516924 | 1.067071385 | 0.836496499 | 0.629569428 | 0.426269288 | 0.252072712 | |
| (fm) | −0.823980938 | −0.828843122 | −0.835583928 | −0.841884906 | −0.846057419 | −0.849721556 | −0.849999864 | −0.859856552 |
| (MeV.fm) | −829.99300 | −829.32779 | −826.75466 | −825.97419 | −820.16793 | −820.80162 | −818.64718 | −818.82887 |
| (MeV.fm) | −770.15586 | −769.51970 | −769.92950 | −769.75826 | −771.71259 | −771.63793 | −772.34643 | −773.77497 |
| E/A (MeV) | (MeV) | J (MeV) | L (MeV) | |
|---|---|---|---|---|
| DD-PC-J29 | −16.019 | 230.0 | 29.0 | 29.0 |
| DD-PC-J30 | −16.043 | 230.0 | 30.0 | 35.6 |
| DD-PC-J31 | −16.055 | 230.0 | 31.0 | 43.8 |
| DD-PC-J32 | −16.067 | 230.0 | 32.0 | 52.3 |
| DD-PC-J33 | −16.076 | 230.0 | 33.0 | 62.0 |
| DD-PC-J34 | −16.087 | 230.0 | 34.0 | 72.1 |
| DD-PC-J35 | −16.096 | 230.0 | 35.0 | 83.2 |
| DD-PC-J36 | −16.123 | 230.0 | 36.0 | 94.1 |
| DD-PC1 | −16.061 | 230.0 | 33.0 | 70.0 |
| DD-PCX | −16.026 | 213.0 | 31.1 | 46.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yüksel, E.; Oishi, T.; Paar, N. Nuclear Equation of State in the Relativistic Point-Coupling Model Constrained by Excitations in Finite Nuclei. Universe 2021, 7, 71. https://doi.org/10.3390/universe7030071
Yüksel E, Oishi T, Paar N. Nuclear Equation of State in the Relativistic Point-Coupling Model Constrained by Excitations in Finite Nuclei. Universe. 2021; 7(3):71. https://doi.org/10.3390/universe7030071
Chicago/Turabian StyleYüksel, Esra, Tomohiro Oishi, and Nils Paar. 2021. "Nuclear Equation of State in the Relativistic Point-Coupling Model Constrained by Excitations in Finite Nuclei" Universe 7, no. 3: 71. https://doi.org/10.3390/universe7030071
APA StyleYüksel, E., Oishi, T., & Paar, N. (2021). Nuclear Equation of State in the Relativistic Point-Coupling Model Constrained by Excitations in Finite Nuclei. Universe, 7(3), 71. https://doi.org/10.3390/universe7030071






