Casimir Effect for Fermion Condensate in Conical Rings
Abstract
:1. Introduction
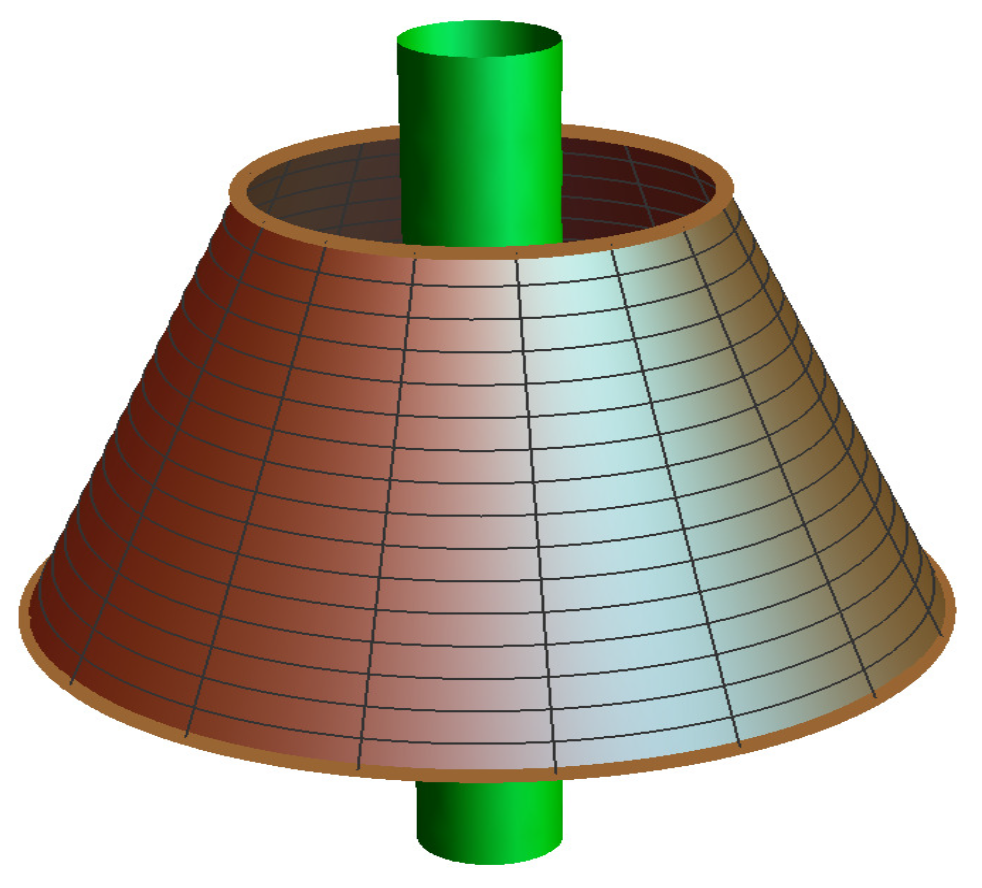
2. Geometry and the Field Modes
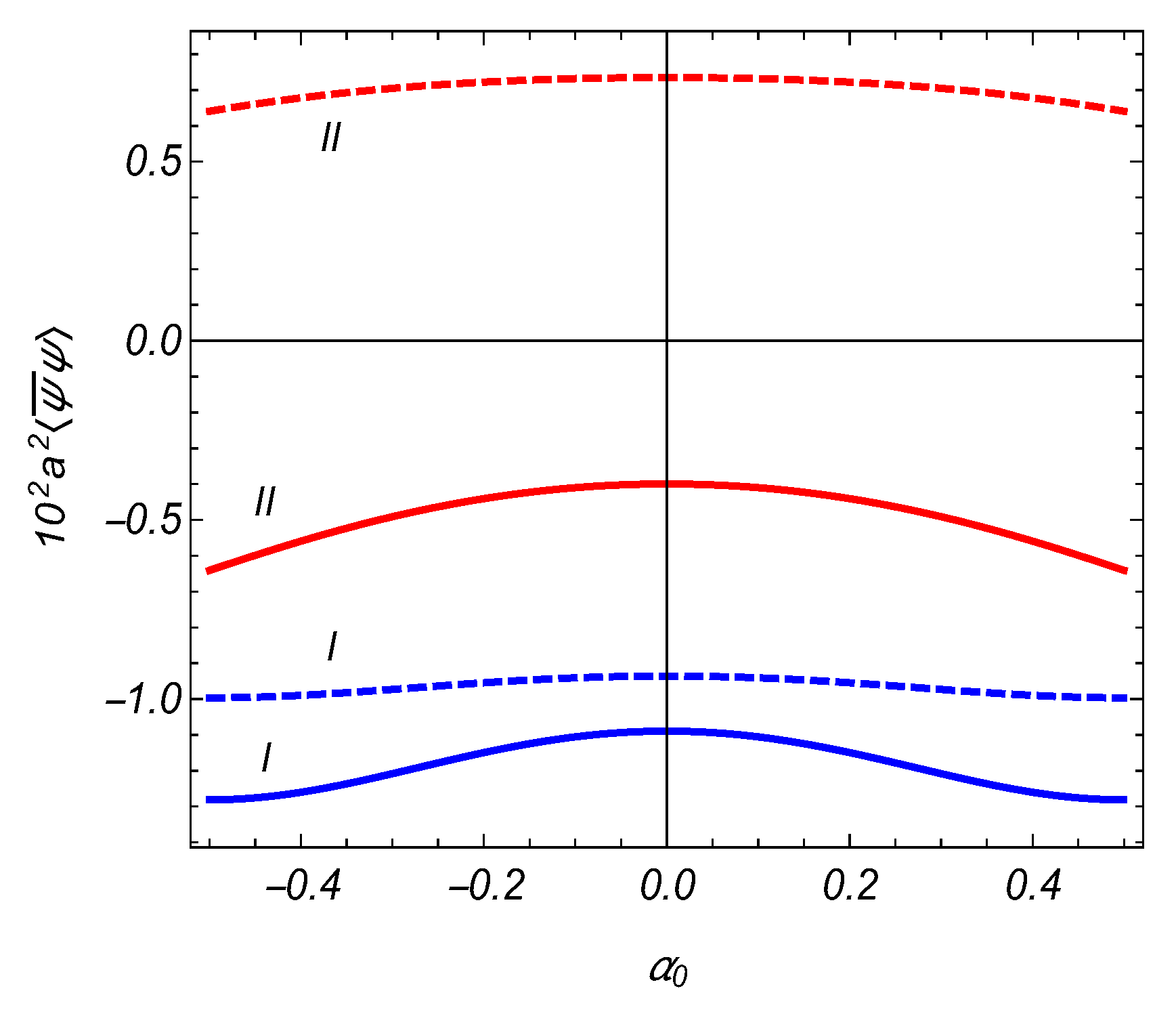
3. Fermion Condensate
4. Fermion Condensate in P- and T-Symmetric Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fradkin, E. Field Theories of Condensed Matter Physics; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Marino, E.C. Quantum Field Theory Approach to Condensed Matter Physics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Gusynin, V.P.; Sharapov, S.G.; Carbotte, J.P. AC Conductivity of Graphene: From Tight-Binding Model to 2+1-Dimensional Quantum Electrodynamics. Int. J. Mod. Phys. B 2007, 21, 4611. [Google Scholar] [CrossRef] [Green Version]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef] [Green Version]
- Qi, X.-L.; Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef] [Green Version]
- Mostepanenko, V.M.; Trunov, N.N. The Casimir Effect and Its Applications; Clarendon Press: Oxford, UK, 1997. [Google Scholar]
- Elizalde, E.; Odintsov, S.D.; Romeo, A.; Bytsenko, A.A.; Zerbini, S. Zeta Regularization Techniques with Applications; World Scientific: Singapore, 1994. [Google Scholar]
- Milton, K.A. The Casimir Effect: Physical Manifestation of Zero-Point Energy; World Scientific: Singapore, 2002. [Google Scholar]
- Bordag, M.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Advances in the Casimir Effect; Oxford University Press: New York, NY USA, 2009. [Google Scholar]
- Dalvit, D.; Milonni, P.; Roberts, D.; da Rosa, F. (Eds.) Casimir Physics; Lecture Notes in Physics; Springer: Berlin, Germany, 2011; Volume 834. [Google Scholar]
- Bordag, M.; Fialkovsky, I.V.; Gitman, D.M.; Vassilevich, D.V. Casimir interaction between a perfect conductor and graphene described by the Dirac model. Phys. Rev. B 2009, 80, 245406. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Santos, G. Thermal van der Waals interaction between graphene layers. Phys. Rev. B 2009, 80, 245424. [Google Scholar] [CrossRef] [Green Version]
- Drosdoff, D.; Woods, L.M. Casimir forces and graphene sheets. Phys. Rev. B 2010, 82, 155459. [Google Scholar] [CrossRef] [Green Version]
- Fialkovsky, I.V.; Marachevsky, V.N.; Vassilevich, D.V. Finite-temperature Casimir effect for graphene. Phys. Rev. B 2011, 84, 035446. [Google Scholar] [CrossRef] [Green Version]
- Sernelius, B.E. Casimir interactions in graphene systems. Europhys. Lett. 2011, 95, 57003. [Google Scholar] [CrossRef] [Green Version]
- Phan, A.D.; Woods, L.M.; Drosdoff, D.; Bondarev, I.V.; Viet, N.A. Temperature dependent graphene suspension due to thermal Casimir interaction. Appl. Phys. Lett. 2012, 101, 113118. [Google Scholar] [CrossRef] [Green Version]
- Chaichian, M.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Tureanu, A. Thermal Casimir-Polder interaction of different atoms with graphene. Phys. Rev. A 2012, 86, 012515. [Google Scholar] [CrossRef] [Green Version]
- Bordag, M.; Klimchitskaya, G.L.; Mostepanenko, V.M. Thermal Casimir effect in the interaction of graphene with dielectrics and metals. Phys. Rev. B 2012, 86, 165429. [Google Scholar] [CrossRef] [Green Version]
- Sernelius, B.E. Retarded interactions in graphene systems. Phys. Rev. B 2012, 85, 195427. [Google Scholar] [CrossRef] [Green Version]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Van der Waals and Casimir interactions between two graphene sheets. Phys. Rev. B 2013, 87, 075439. [Google Scholar] [CrossRef] [Green Version]
- Phan, A.D.; Phan, T. Casimir interactions in strained graphene systems. Phys. Status Solid RRL 2014, 8, 1003. [Google Scholar] [CrossRef] [Green Version]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Theory of the Casimir interaction from graphene-coated substrates using the polarization tensor and comparison with experiment. Phys. Rev. B 2014, 89, 115419. [Google Scholar] [CrossRef] [Green Version]
- Dobson, J.F.; Gould, T.; Vignale, G. How Many-Body Effects Modify the van der Waals Interaction between Graphene Sheets. Phys. Rev. X 2014, 4, 021040. [Google Scholar] [CrossRef] [Green Version]
- Bordag, M.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Petrov, V.M. Quantum field theoretical description for the reflectivity of graphene. Phys. Rev. D 2015, 91, 045037. [Google Scholar] [CrossRef] [Green Version]
- Sernelius, B.E. Casimir effects in systems containing 2D layers such as graphene and 2D electron gases. J. Phys. Condens. Matter 2015, 27, 214017. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bordag, M.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Petrov, V.M. Erratum: Quantum field theoretical description for the reflectivity of graphene [Phys. Rev. D 91, 045037 (2015)]. Phys. Rev. D 2016, 93, 089907. [Google Scholar] [CrossRef] [Green Version]
- Khusnutdinov, N.; Kashapov, R.; Woods, L.M. Casimir-Polder effect for a stack of conductive planes. Phys. Rev. A 2016, 94, 012513. [Google Scholar] [CrossRef] [Green Version]
- Drosdoff, D.; Bondarev, I.V.; Widom, A.; Podgornik, R.; Woods, L.M. Charge-Induced Fluctuation Forces in Graphitic Nanostructures. Phys. Rev. X 2016, 6, 011004. [Google Scholar] [CrossRef] [Green Version]
- Inui, N. Casimir effect on graphene resonator. J. Appl. Phys. 2016, 119, 104502. [Google Scholar] [CrossRef]
- Bimonte, G.; Klimchitskaya, G.L.; Mostepanenko, V.M. How to observe the giant thermal effect in the Casimir force for graphene systems. Phys. Rev. A 2017, 96, 012517. [Google Scholar] [CrossRef] [Green Version]
- Bordag, M.; Fialkovsky, I.; Vassilevich, D. Casimir interaction of strained graphene. Phys. Lett. A 2017, 381, 2439. [Google Scholar] [CrossRef] [Green Version]
- Martinez, J.C.; Chen, X.; Jalil, M.B.A. Casimir effect and graphene: Tunability, scalability, Casimir rotor. AIP Adv. 2018, 8, 015330. [Google Scholar] [CrossRef]
- Derras-Chouk, A.; Chudnovsky, E.M.; Garanin, D.A.; Jaafar, R. Graphene cantilever under Casimir force. J. Phys. D Appl. Phys. 2018, 51, 195301. [Google Scholar] [CrossRef] [Green Version]
- Khusnutdinov, N.; Woods, L.M. Casimir Effects in 2D Dirac Materials (Scientific Summary). JETP Lett. 2019, 110, 183. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. The Casimir force between real materials: Experiment and theory. Rev. Mod. Phys. 2009, 81, 1827. [Google Scholar] [CrossRef] [Green Version]
- Woods, L.M.; Dalvit, D.A.R.; Tkatchenko, A.; Rodriguez-Lopez, P.; Rodriguez, A.W.; Podgornik, R. Materials perspective on Casimir and van der Waals interactions. Rev. Mod. Phys. 2016, 88, 045003. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Casimir and Casimir-Polder forces in graphene systems: Quantum field theoretical description and thermodynamics. Universe 2020, 6, 150. [Google Scholar] [CrossRef]
- Rodriguez-Lopez, P.; Kort-Kamp, W.J.M.; Dalvit, D.A.R.; Woods, L.M. Casimir force phase transitions in the graphene family. Nat. Commun. 2017, 8, 14699. [Google Scholar] [CrossRef] [Green Version]
- Elizalde, E.; Leseduarte, S.; Odintsov, S.D. Chiral symmetry breaking in the Nambu-Jona-Lasinio model in curved spacetime with a nontrivial topology. Phys. Rev. D 1994, 49, 5551. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Inagaki, T.; Muta, T.; Odintsov, S.D. Dynamical Symmetry Breaking in Curved Spacetime. Prog. Theor. Phys. Suppl. 1997, 127, 93. [Google Scholar] [CrossRef] [Green Version]
- Flachi, A. Interacting fermions, boundaries, and finite size effects. Phys. Rev. D 2012, 86, 104047. [Google Scholar] [CrossRef] [Green Version]
- Flachi, A. Dual fermion condensates in curved space. Phys. Rev. D 2013, 88, 085011. [Google Scholar] [CrossRef] [Green Version]
- Flachi, A.; Nitta, M.; Takada, S.; Yoshii, R. Sign Flip in the Casimir Force for Interacting Fermion Systems. Phys. Rev. Lett. 2017, 119, 031601. [Google Scholar] [CrossRef] [Green Version]
- Flachi, A.; Vitagliano, V. Symmetry breaking and lattice kirigami: Finite temperature effects. Phys. Rev. D 2019, 99, 125010. [Google Scholar] [CrossRef] [Green Version]
- Bellucci, S.; Saharian, A.A. Fermionic Casimir densities in toroidally compactified spacetimes with applications to nanotubes. Phys. Rev. D 2009, 79, 085019. [Google Scholar] [CrossRef] [Green Version]
- Bellucci, S.; Saharian, A.A.; Bardeghyan, V.M. Induced fermionic current in toroidally compactified spacetimes with applications to cylindrical and toroidal nanotubes. Phys. Rev. D 2010, 82, 065011. [Google Scholar] [CrossRef] [Green Version]
- Bellucci, S.; Bezerra de Mello, E.R.; Saharian, A.A. Finite temperature fermionic condensate and currents in topologically nontrivial spaces. Phys. Rev. D 2014, 89, 085002. [Google Scholar] [CrossRef] [Green Version]
- Bellucci, S.; Saharian, A.A. Fermionic Casimir effect for parallel plates in the presence of compact dimensions with applications to nanotubes. Phys. Rev. D 2009, 80, 105003. [Google Scholar] [CrossRef] [Green Version]
- Elizalde, E.; Odintsov, S.D.; Saharian, A.A. Fermionic condensate and Casimir densities in the presence of compact dimensions with applications to nanotubes. Phys. Rev. D 2011, 83, 105023. [Google Scholar] [CrossRef] [Green Version]
- Bellucci, S.; Saharian, A.A. Fermionic current from topology and boundaries with applications to higher-dimensional models and nanophysics. Phys. Rev. D 2013, 87, 025005. [Google Scholar] [CrossRef] [Green Version]
- Bezerra de Mello, E.R.; Saharian, A.A. Casimir Effect in Hemisphere Capped Tubes. Int. J. Theor. Phys. 2016, 55, 1167. [Google Scholar] [CrossRef] [Green Version]
- Bellucci, S.; Saharian, A.A.; Vardanyan, V. Fermionic currents in AdS spacetime with compact dimensions. Phys. Rev. D 2017, 96, 065025. [Google Scholar] [CrossRef] [Green Version]
- Bellucci, S.; Saharian, A.A.; Simonyan, D.H.; Vardanyan, V. Fermionic currents in topologically nontrivial braneworlds. Phys. Rev. D 2018, 98, 085020. [Google Scholar] [CrossRef] [Green Version]
- Bellucci, S.; Saharian, A.A.; Sargsyan, H.G.; Vardanyan, V. Fermionic vacuum currents in topologically nontrivial braneworlds: Two-brane geometry. Phys. Rev. D 2020, 101, 045020. [Google Scholar] [CrossRef] [Green Version]
- Kolesnikov, D.V.; Osipov, V.A. Field-theoretical approach to the description of electronic properties of carbon nanostructures. Phys. Part. Nucl. 2009, 40, 502. [Google Scholar] [CrossRef]
- Vozmediano, M.A.H.; Katsnelson, M.I.; Guinea, F. Gauge fields in graphene. Phys. Rep. 2010, 496, 109. [Google Scholar] [CrossRef] [Green Version]
- Iorio, A.; Lambiase, G. Quantum field theory in curved graphene spacetimes, Lobachevsky geometry, Weyl symmetry, Hawking effect, and all that. Phys. Rev. D 2014, 90, 025006. [Google Scholar] [CrossRef] [Green Version]
- Morresi, T. Exploring event horizons and Hawking radiation through deformed graphene membranes. 2D Mater. 2020, 7, 041006. [Google Scholar] [CrossRef]
- Bellucci, S.; Brevik, I.; Saharian, A.A.; Sargsyan, H.G. The Casimir effect for fermionic currents in conical rings with applications to graphene ribbons. Eur. Phys. J. C 2020, 80, 281. [Google Scholar] [CrossRef] [Green Version]
- Krishnan, A. Graphitic cones and the nucleation of curved carbon surfaces. Nature 1997, 388, 451. [Google Scholar] [CrossRef]
- Charlier, J.-C.; Rignanese, G.-M. Electronic Structure of Carbon Nanocones. Phys. Rev. Lett. 2001, 86, 5970. [Google Scholar] [CrossRef]
- Naess, S.N.; Elgsaeter, A.; Helgesen, G.; Knudsen, K.D. Carbon nanocones: Wall structure and morphology. Sci. Technol. Adv. Mater. 2009, 10, 065002. [Google Scholar] [CrossRef]
- Lammert, P.E.; Crespi, V.H. Topological Phases in Graphitic Cones. Phys. Rev. Lett. 2000, 85, 5190. [Google Scholar] [CrossRef] [Green Version]
- Osipov, V.A.; Kochetov, E.A. Dirac fermions on graphite cones. JETP Lett. 2001, 73, 562. [Google Scholar] [CrossRef]
- Lammert, P.E.; Crespi, V.H. Graphene cones: Classification by fictitious flux and electronic properties. Phys. Rev. B 2004, 69, 035406. [Google Scholar] [CrossRef]
- Cortijo, A.; Vozmediano, M.A.H. Effects of topological defects and local curvature on the electronic properties of planar graphene. Nucl. Phys. B 2007, 763, 293–308. [Google Scholar] [CrossRef]
- Sitenko, Y.A.; Vlasii, N.D. Electronic properties of graphene with a topological defect. Nucl. Phys. B 2007, 787, 241–259. [Google Scholar] [CrossRef] [Green Version]
- Sitenko, Y.A.; Vlasii, N.D. On the possible induced charge on a graphitic nanocone at finite temperature. J. Phys. A Math. Theor. 2008, 41, 164034. [Google Scholar] [CrossRef]
- Furtado, C.; Moraes, F.; Carvalho, A.M.M. Geometric phases in graphitic cones. Phys. Lett. A 2008, 372, 5368–5371. [Google Scholar] [CrossRef] [Green Version]
- Chakraborty, B.; Gupta, K.S.; Sen, S. Effect of topology on the critical charge in graphene. Phys. Rev. B 2011, 83, 115412. [Google Scholar] [CrossRef] [Green Version]
- Sitenko, Y.A.; Vlasii, N.D. Vacuum polarization in graphene with a topological defect. Low Temp. Phys. 2008, 34, 826. [Google Scholar] [CrossRef] [Green Version]
- Sitenko, Y.A.; Gorkavenko, V.M. Properties of the ground state of electronic excitations in carbon-like nanocones. Low Temp. Phys. 2018, 44, 1261. [Google Scholar] [CrossRef] [Green Version]
- Sitenko, Y.A.; Gorkavenko, V.M. Induced vacuum magnetic flux in quantum spinor matter in the background of a topological defect in two-dimensional space. Phys. Rev. D 2019, 100, 085011. [Google Scholar] [CrossRef] [Green Version]
- Bellucci, S.; Bezerra de Mello, E.R.; Saharian, A.A. Fermionic condensate in a conical space with a circular boundary and magnetic flux. Phys. Rev. D 2011, 83, 085017. [Google Scholar] [CrossRef] [Green Version]
- Bezerra de Mello, E.R.; Bezerra, V.; Saharian, A.A.; Bardeghyan, V.M. Fermionic current densities induced by magnetic flux in a conical space with a circular boundary. Phys. Rev. D 2010, 82, 085033. [Google Scholar] [CrossRef] [Green Version]
- Bezerra de Mello, E.R.; Moraes, F.; Saharian, A.A. Fermionic Casimir densities in a conical space with a circular boundary and magnetic flux. Phys. Rev. D 2012, 85, 045016. [Google Scholar] [CrossRef] [Green Version]
- Bellucci, S.; Bezerra de Mello, E.R.; Bragança, E.; Saharian, A.A. Finite temperature fermion condensate, charge and current densities in a (2+1)-dimensional conical space. Eur. Phys. J. C 2016, 76, 350. [Google Scholar] [CrossRef] [Green Version]
- Saharian, A.A.; Bezerra de Mello, E.R.; Saharyan, A.A. Finite temperature fermionic condensate in a conical space with a circular boundary and magnetic flux. Phys. Rev. D 2019, 100, 105014. [Google Scholar] [CrossRef] [Green Version]
- Chu, C.-S.; Miao, R.-X. Fermion condensation induced by the Weyl anomaly. Phys. Rev. D 2020, 102, 046011. [Google Scholar] [CrossRef]
- Chu, C.-S.; Miao, R.-X. Weyl anomaly induced Fermi condensation and holography. J. High Energy Phys. 2020, 2008, 134. [Google Scholar] [CrossRef]
- Bellucci, S.; Saharian, A.A.; Grigoryan, A.K. Induced fermionic charge and current densities in two-dimensional rings. Phys. Rev. D 2016, 94, 105007. [Google Scholar] [CrossRef] [Green Version]
- Johnson, K. The MIT bag model. Acta Phys. Polonica 1975, B6, 865–892. [Google Scholar]
- Berry, M.V.; Mondragon, R.J. Neutrino billiards: Time-reversal symmetry-breaking without magnetic fields. Proc. R. Soc. A 1987, 412, 53–74. [Google Scholar] [CrossRef]
- McCann, E.; Fal’ko, V.I. Symmetry of boundary conditions of the Dirac equation for electrons in carbon nanotubes. J. Phys. Condens. Matter 2004, 16, 2371–2379. [Google Scholar] [CrossRef]
- Brey, L.; Fertig, H.A. Electronic states of graphene nanoribbons studied with the Dirac equation. Phys. Rev. B 2006, 73, 235411. [Google Scholar] [CrossRef] [Green Version]
- Akhmerov, A.R.; Beenakker, C.W.J. Boundary conditions for Dirac fermions on a terminated honeycomb lattice. Phys. Rev. B 2008, 77, 085423. [Google Scholar] [CrossRef] [Green Version]
- Beneventano, C.G.; Santangelo, E.M. Boundary Conditions in the Dirac Approach to Graphene Devices. Int. J. Mod. Phys. Conf. Series 2012, 14, 240–249. [Google Scholar] [CrossRef] [Green Version]
- Sitenko, Y.A. Casimir effect with quantized charged spinor matter in background magnetic field. Phys. Rev. D 2015, 91, 085012. [Google Scholar] [CrossRef] [Green Version]
- Araújo, A.L.; Maciel, R.P.; Dornelas, R.G.F.; Varjas, D.; Ferreira, G.J. Interplay between boundary conditions and Wilson’s mass in Dirac-like Hamiltonians. Phys. Rev. B 2019, 100, 205111. [Google Scholar] [CrossRef] [Green Version]
- Bezerra de Mello, E.R.; Saharian, A.A. Spinor Casimir effect for concentric spherical shells in the global monopole spacetime. Class. Quantum Grav. 2006, 23, 4673–4691. [Google Scholar] [CrossRef] [Green Version]
- Saharian, A.A. The Generalized Abel-Plana Formula with Applications to Bessel Functions and Casimir Effect; Report No. ICTP/2007/082; Yerevan State University Publishing House: Yerevan, RA, USA, 2008. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions; Dover: New York, NY, USA, 1972. [Google Scholar]
- Miransky, V.A.; Shovkovy, I.A. Quantum field theory in a magnetic field: From quantum chromodynamics to graphene and Dirac semimetals. Phys. Rept. 2015, 576, 1–209. [Google Scholar] [CrossRef] [Green Version]
- Shifman, M.A.; Vainshtein, A.I.; Zakharov, V.I. QCD and resonance physics. Theoretical foundations. Nucl. Phys. B 1979, 147, 385–447. [Google Scholar] [CrossRef]
- Saharian, A.A.; Kotanjyan, A.S.; Sargsyan, H.G. Electromagnetic field correlators and the Casimir effect for planar boundaries in AdS spacetime with application in braneworlds. Phys. Rev. D 2020, 102, 105014. [Google Scholar] [CrossRef]
- Klimenko, K.G. Phase structure of generalized Gross-Neveu models. Z. Phys. C 1988, 37, 457–463. [Google Scholar] [CrossRef]
- Rosenstein, B.; Warr, B.J.; Park, S.H. Thermodynamics of (2+1)-dimensional four-fermion models. Phys. Rev. D 1989, 39, 3088–3092. [Google Scholar] [CrossRef]
- Rosenstein, B.; Warr, B.J.; Park, S.H. Four-fermion theory is renormalizable in 2+1 dimensions. Phys. Rev. Lett. 1989, 62, 1433–1436. [Google Scholar] [CrossRef]
- Semenoff, G.W.; Wijewardhana, L.C.R. Dynamical mass generation in 3D four-fermion Theory. Phys. Rev. Lett. 1989, 63, 2633–2636. [Google Scholar] [CrossRef]
- Semenoff, G.W.; Wijewardhana, L.C.R. Dynamical violation of parity and chiral symmetry in three-dimensional four-Fermi theory. Phys. Rev. D 1992, 45, 1342–1354. [Google Scholar] [CrossRef] [PubMed]
- Ebert, D.; Klimenko, K.G.; Kolmakov, P.B.; Zhukovsky, V.C. Phase transitions in hexagonal, graphene-like lattice sheets and nanotubes under the influence of external conditions. Ann. Phys. 2016, 371, 254–286. [Google Scholar] [CrossRef] [Green Version]
- Ebert, D.; Blaschke, D. Thermodynamics of a generalized graphene-motivated (2+1)D Gross-Neveu model beyond the mean field within the Beth-Uhlenbeck approach. Prog. Theor. Exp. Phys. 2019, 123I01. [Google Scholar] [CrossRef]
- Drut, J.E.; Son, D.T. Renormalization group flow of quartic perturbations in graphene: Strong coupling and large-N limits. Phys. Rev. B 2008, 77, 075115. [Google Scholar] [CrossRef] [Green Version]
- Juričić, V.; Herbut, I.F.; Semenoff, G.W. Coulomb interaction at the metal-insulator critical point in graphene. Phys. Rev. B 2009, 80, 081405. [Google Scholar] [CrossRef] [Green Version]
- Herbut, I.F.; Juričić, V.; Vafek, O. Relativistic Mott criticality in graphene. Phys. Rev. B 2009, 80, 075432. [Google Scholar] [CrossRef]
- Vitale, P. Temperature-induced phase transitions in four-fermion models in curved space-time. Nucl. Phys. B 1999, 551, 490–510. [Google Scholar] [CrossRef] [Green Version]
- Ebert, D.; Klimenko, K.G.; Tyukov, A.V.; Zhukovsky, V.C. Finite size effects in the Gross-Neveu model with isospin chemical potential. Phys. Rev. D 2008, 78, 045008. [Google Scholar] [CrossRef] [Green Version]
- Abreu, L.M.; Malbouisson, A.P.C.; Malbouisson, J.M.C.; Santana, A.E. Finite-size effects on the chiral phase diagram of four-fermion models in four dimensions. Nucl. Phys. B 2009, 819, 127–138. [Google Scholar] [CrossRef] [Green Version]
- Ebert, D.; Klimenko, K.G. Cooper pairing and finite-size effects in a Nambu–Jona-Lasinio-type four-fermion model. Phys. Rev. D 2010, 82, 025018. [Google Scholar] [CrossRef] [Green Version]
- Khanna, F.C.; Malbouisson, A.P.C.; Malbouisson, J.M.C.; Santana, A.E. Phase transition in the massive Gross-Neveu model in toroidal topologies. Phys. Rev. D 2012, 85, 085015. [Google Scholar] [CrossRef] [Green Version]
- Zahed, I.; Brown, G.E. The Skyrme model. Phys. Rep. 1986, 142, 1–102. [Google Scholar] [CrossRef]
- Hosaka, A.; Hiroshi, T. Chiral bag model for the nucleon. Phys. Rep. 1996, 277, 65–188. [Google Scholar] [CrossRef]
- Novak, M.A.; Rho, M.; Zahed, I. Chiral Nuclear Dynamics; World Scientific: Singapore, 1996. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saharian, A.; Petrosyan, T.; Hovhannisyan, A. Casimir Effect for Fermion Condensate in Conical Rings. Universe 2021, 7, 73. https://doi.org/10.3390/universe7030073
Saharian A, Petrosyan T, Hovhannisyan A. Casimir Effect for Fermion Condensate in Conical Rings. Universe. 2021; 7(3):73. https://doi.org/10.3390/universe7030073
Chicago/Turabian StyleSaharian, Aram, Tigran Petrosyan, and Arshak Hovhannisyan. 2021. "Casimir Effect for Fermion Condensate in Conical Rings" Universe 7, no. 3: 73. https://doi.org/10.3390/universe7030073
APA StyleSaharian, A., Petrosyan, T., & Hovhannisyan, A. (2021). Casimir Effect for Fermion Condensate in Conical Rings. Universe, 7(3), 73. https://doi.org/10.3390/universe7030073






