1. Introduction
According to the Cosmological Principle, the Universe, when seen on a sufficiently large scale (beyond a few hundred Mpc), should appear isotropic, without any preferred directions, to a co-moving observer in the expanding Universe. Such an observer is at rest with respect to the Universe at large and the angular distribution of sources in the sky should appear statistically to be similar in all directions. However, if relative to the co-moving coordinates the observer has a motion, called a peculiar motion, then because of the Doppler boosting as well as aberration effects, the observer will find the sky brightness as well as the number counts of distant extragalactic objects to manifest a dipole anisotropy, proportional to the peculiar velocity of the observer. The Cosmic Microwave Background Radiation (CMBR), shows such a dipole anisotropy that, when ascribed to the peculiar motion of the solar system, yields for the peculiar velocity a value 370 km s
along right ascension (RA)
, declination (Dec)
or in galactic coordinates,
[
1,
2,
3].
On the other hand, our peculiar velocity has also been determined in recent years from the anisotropy observed in the sky distribution of large samples of discrete radio sources. The NRAO VLA Sky Survey (NVSS), comprising 1.8 million radio sources [
4], showed a statistically significant dipole asymmetry corresponding to a velocity ∼4 times the CMBR value [
5], something that was not only unexpected, but appeared initially almost preposterous, however, confirmed subsequently by many independent groups [
6,
7,
8,
9]. Further, in the TIFR GMRT Sky Survey (TGSS) [
10], comprising 0.62 million sources [
11], a very significant (>
) dipole anisotropy, amounting to a velocity ∼10 times the CMBR value, was detected [
9,
12]. However, equally surprising, the direction of motion in both cases has turned out to be along the CMBR dipole. Recently, a homogeneously selected DR12Q sample of 103,245 distant quasars has shown a redshift dipole along the CMBR dipole direction, implying a velocity ∼
times though in a direction directly opposite to, but nonetheless parallel to, the CMBR dipole [
13]. A more recent determination of the peculiar motion from a sample of quasars derived from the Wide-field Infrared Survey Explorer (WISE), has shown an amplitude over twice as large the CMBR value [
14]. Now a genuine solar peculiar velocity cannot vary from one set of measurements to another and such discordant dipoles could imply that the explanation for the genesis of these dipoles, including that of the CMBR, might lie elsewhere. At the same time a common direction for all these dipoles, determined from completely independent surveys by different groups, using independent computational routines, does indicate that the differences in the dipoles are not merely random fluctuations or due to some systematics in data or procedures, otherwise their directions too would be different. Instead, it might suggest a preferred direction in the Universe implying a genuine anisotropy, which would violate the Cosmological Principle, the core of the modern cosmology. As a result of the huge impact on the cosmological models any genuine variations in the dipole magnitudes may impart, further independent determinations of the dipole vectors are warranted.
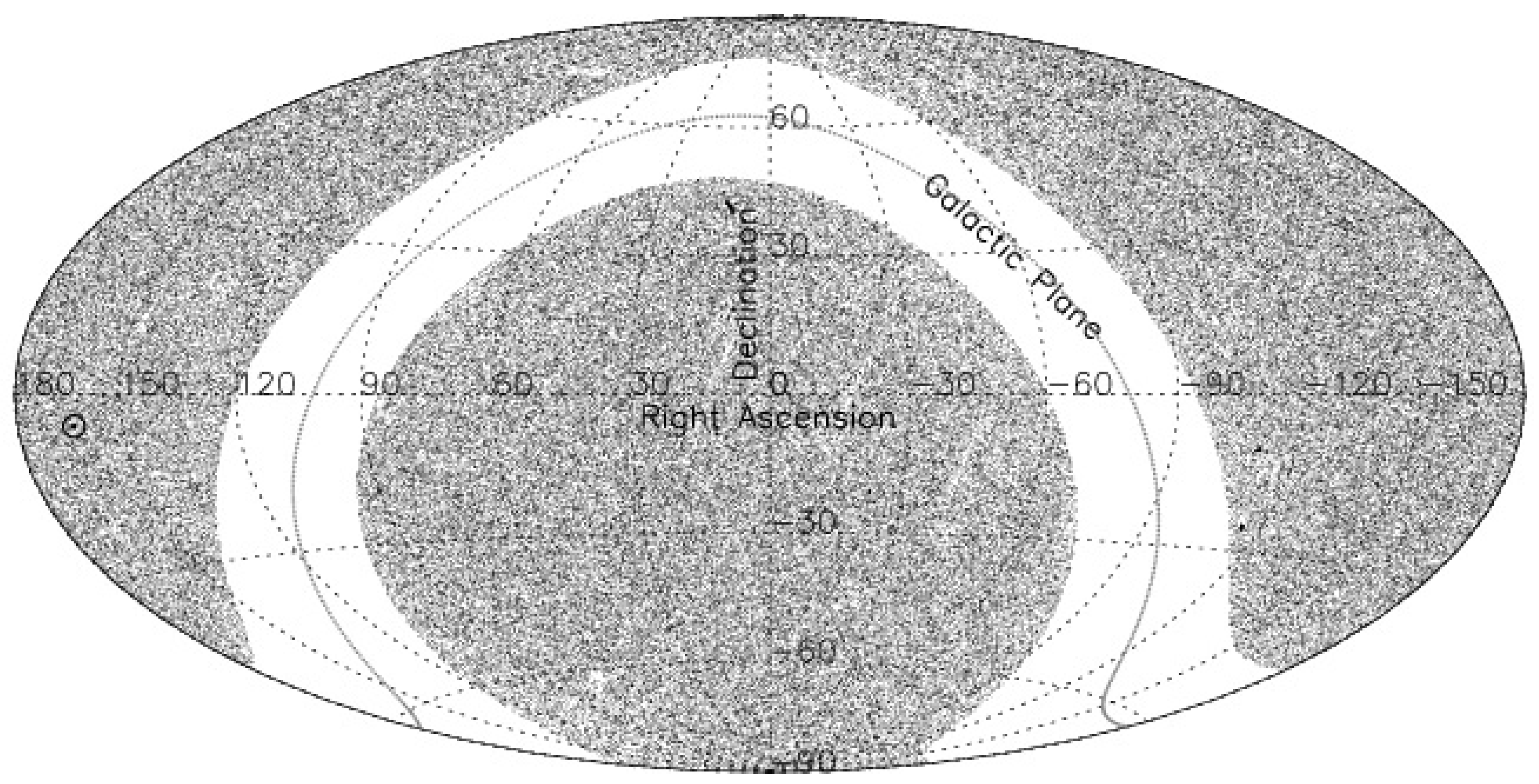
Here we determine our peculiar motion from a sample of 0.28 million AGNs (
Figure 1), selected from the Mid Infra Red Active Galactic Nuclei (MIRAGN) sample comprising more than a million sources [
15]. A preliminary account of these results was presented in proceedings of the 1st Electronic Conference on the Universe [
16], where the genesis of a dipole anisotropy in the number density, owing to the observer’s peculiar motion, in an otherwise isotropic distribution of sources in the sky, and how one could estimate the peculiar velocity vector from the observed dipole anisotropy and the sample selected by us for this purpose, were discussed. Here we pursue and explore these findings in a greater detail, discussing any possible pitfalls in the sample selection and the techniques employed. Further, we exploit another alternate method to extract the dipole, and do a comparison of our derived results vis-à-vis the peculiar velocity information previously available in the literature, and point out their cosmological implications.
2. Dipole Vector Due to the Motion of the Observer
Due to the assumed isotropy of the Universe—à la Cosmological Principle—an observer stationary with respect to the comoving coordinates of the cosmic fluid should find the average number densities of distant AGNs as well as their flux densities to be distributed uniformly over the sky. However, an observer moving with a velocity
v relative to the cosmic fluid, will find a source along an angle
with respect to the direction of motion, to appear brighter due to Doppler boosting by a factor
[
17], where
is the Doppler factor and
is the spectral index defined by
, with
S being the flux density of the source at the frequency
of the observing instrument. Here we have used the non-relativistic formula for the Doppler factor as all previous observations indicate that
. As the integral source counts of the extragalactic source population usually follow a power law,
[
17], the number of sources observed by a telescope of a given sensitivity will be higher by a factor
, due to the Doppler boosting [
17]. Additionally, due to the aberration of light, the apparent position of a source will shift toward the direction of motion by a value,
, thereby changing the number density by another factor
[
17]. Thus, as a combined effect of Doppler boosting and aberration, the observed number counts will vary with direction as
, which, for
, can be expressed as a dipole anisotropy,
[
5,
17,
18], with an amplitude
Let
be the position vector of the
ith source, then a stationary observer, due to the assumed isotropy of the Universe, should find
. However, for a moving observer,
will yield a net vector along the direction of motion [
18]. Then the peculiar speed
v of the observer could be obtained from [
5,
12]
where
is the polar angle of the
ith source with respect to the dipole direction of motion [
18] and
N is the total number of sources in the sample.
Thus, exploiting the angular positions of extragalactic sources in a large survey that covers the whole sky and is complete in the sense that it comprises all sources above a certain flux-density limit, we can determine our peculiar motion. It should be noted that exclusions of strips like the galactic plane,
(
Figure 1), which affect the forward and backward measurements identically, do not have systematic effects on the determined direction of the peculiar motion [
5,
17].
3. Our Sample of MIRAGNs
The sample of AGNs used in this study is selected from a publicly made available larger all-sky sample of 1.4 million active galactic nuclei (AGNs) [
15], in turn derived from the Wide-field Infrared Survey Explorer final catalog release (AllWISE), that incorporates data from the WISE Full Cryogenic, 3-Band Cryo and NEOWISE Post-Cryo survey [
19,
20]. The WISE survey is an all-sky mid-IR survey at 3.4, 4.6, 12 and 22 m (W1, W2, W3 and W4) with angular resolutions 6.1, 6.4, 6.5 and 12 arcsec, respectively. AllWISE comprises data for almost 748 million objects, out of these about 1.4 million objects met a two-color infrared photometric selection criteria for AGNs, that formed the original MIRAGN sample [
15].
For our purpose, we have restricted the MIRAGN sample to an upper limit of magnitude, W1
, mainly because of a differential increase in the number density for weaker sources in various regions of the sky, due to deeper WISE coverage. However, due to the completeness of the basic survey at strong source levels, the number density distribution in the sky at low infrared magnitudes remains unaffected as a deeper coverage adds only fainter sources, which are at higher infrared magnitudes. From a detailed examination of the original MIRAGN sample data in small-range magnitude slices at different W1 levels, we find that from W1 ≈ 15.5 onward, there is a non-uniform distribution in sky that increases rapidly at higher magnitudes, i.e., for weaker sources.
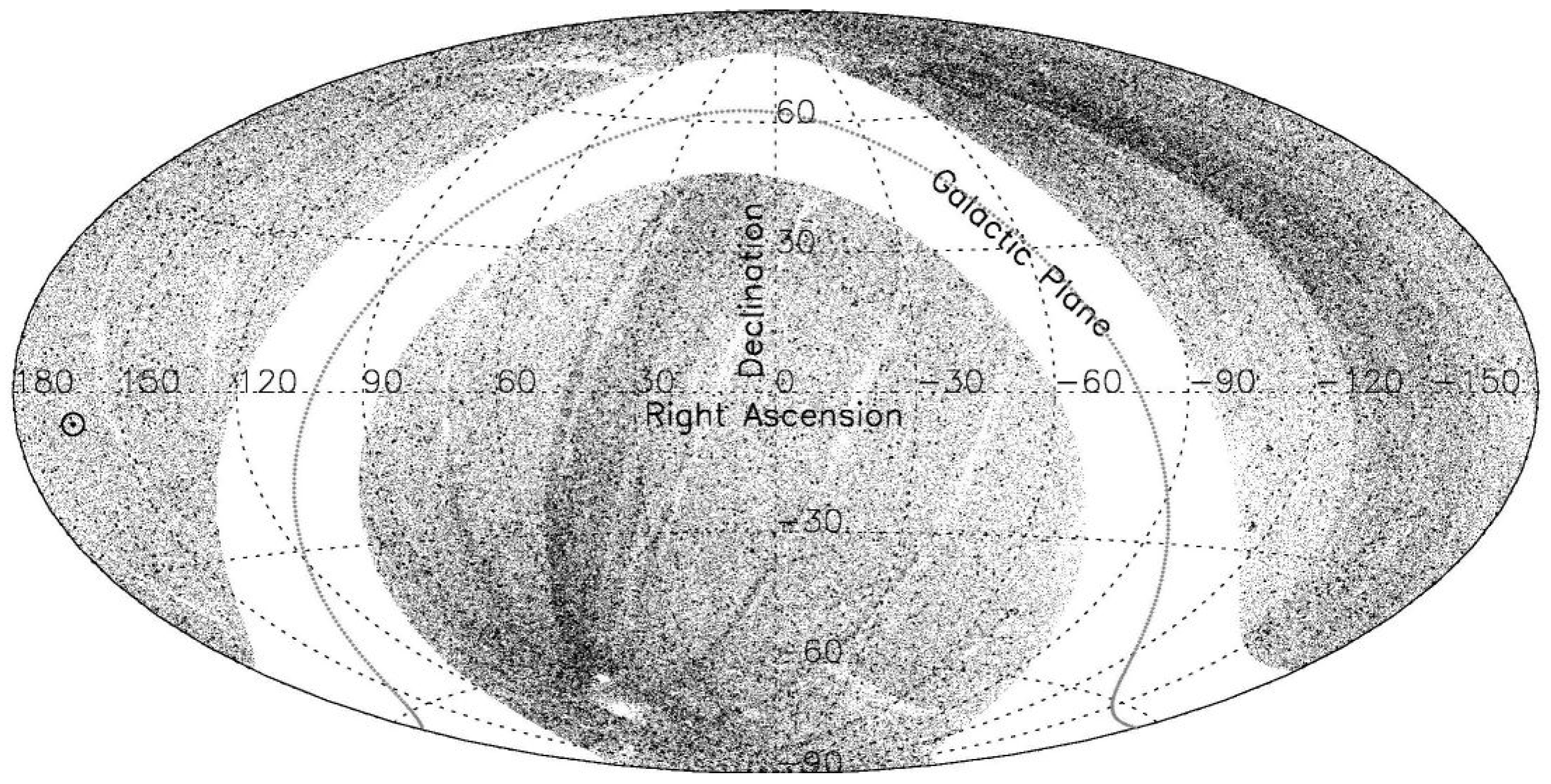
Figure 2 and
Figure 3 show the increasing non-uniformity for magnitude levels W1
. Accordingly, we have chosen W1 = 15.0 to be our upper magnitude limit. On the lower side, we have restricted our sample to W1
. This is only to minimize the effects of the local bulk flows which will affect sources at low redshifts,
, corresponding to W1 < 12. In any case, the number of sources for W1
is relatively very small and their inclusion or exclusion hardly affects the results. Further, we have also excluded all sources in the galactic plane with
to avoid contamination by galactic sources [
15]. Our final sample then comprises 279,139 AGNs.
Figure 1 shows the sky distribution of sources in our sample. The distribution seems to be quite uniform across the sky, except for the gap seen in the
wide strip about the galactic plane.
5. Discussion
The view that the solar system peculiar motion is 370 km s, as given by the CMBR dipole, seems to be widely accepted. However, one needs to keep an open mind about it, without sticking rigidly to the conventional view that only the CMBR provides a reference frame which, somehow, is to be considered as more fundamental than the other ones, e.g., AGNs, for establishing the peculiar motion of the solar system. While the CMBR refers to the radiation era (), AGNs represent the much later matter era (). A common direction for the two dipoles, determined from completely independent data, does indicate that these dipole amplitudes differ not because of random statistical fluctuations, or due to some systematics in the observations or in the data analysis, otherwise even their directions would have turned out to be different, and that the difference in their amplitudes might be a pointer to some occurrence of cosmological significance.
In
Figure 3, we saw that there are large scale inhomogeneities in the sky distribution of the MIRAGN number densities at W1
levels. In fact, even at somewhat brighter levels,
W1
, such large scale inhomogeneities in the sky distribution are present (
Figure 2), though at a reduced level. How can we be sure that such large scale inhomogeneities in the sky distribution are not present in our sample at W1
levels? Although we may not be able to discern them from
Figure 1 with our eyes, how can we make sure of the lack of their underlying presence in our data, at least at levels which could have influenced our intended determination of the dipole significantly? In other words, could such large scale inhomogeneities or even some large scale statistical fluctuations in certain directions be the cause of our observed dipole being much larger than the CMBR dipole?
For one thing, such non-uniformities would have to be distributed over various sky regions in such a way that these make the resulting excess in the dipole amplitude to occur in the same direction as the CMBR dipole. Moreover, these also have to be spread all across the magnitude band of our MIRAGN sample, as our three bins, selected with no overlap in the magnitude band, yield very similar dipole vectors. In fact, one can verify that it is a genuine dipole distribution in the number densities and not merely a result of some systematics in the data. From Equation (
3), we see that
yields a component of the dipole along
. We can verify this
dependence of
, by making cumulative counts of
and
in two opposite hemispheres,
and
, for various
values.
Figure 8 shows a plot of the
, computed for our MIRAGN sample using Equation (
3), as a function of
, the angle with respect to the determined dipole direction, RA
, Dec
. The dotted curve shows
, calculated from cumulative counts, has the best fit by a
dipole curve, with
km s
. We have also plotted the error bars, calculated for a random (binomial) distribution, at some representative points. The larger fluctuations seen for
, although still within statistical uncertainties, are because of a smaller dipole component (
) vis-à-vis the relatively larger statistical fluctuations in a binomial distribution due to a lesser number of sources in the reduced sky zones. Additionally shown is the expected curve for the peculiar velocity,
km s
derived from the CMBR dipole, which lies way below the dipole components estimated from the MIRAGNs data.
A vectorial summation of sky positions of all sources, as determined in
Table 1, in itself does not guarantee that the resultant vector is necessarily a dipole, after all we will always get some resulting RA, Dec and
from such a summation, and whatever might be the statistical uncertainties. However, a systematic variation pattern of dipole amplitudes over the sky, as seen in
Figure 5, where the pole position
M from
Table 1 is right in the middle of the darkest region, while the corresponding antipole position
A lies in the lighter most region, indicates the genuine nature of the dipole. Moreover, the dashed curve, representing the zero amplitude of the dipole, overlaps the great circle, at
from the poles at
M and
A, added to the fact that we obtained the same particulars for the dipole from the hemisphere method, where not only the direction of the dipole from the brute force method (
Table 3) turned out to be the same as was determined in
Table 1, even the amplitude of the dipole, where various sources, depending upon their sky positions get different weights, gave the same value, confirming that it is a genuine dipole. More so because of the
pattern seen in
Figure 8, as would be expected only for a dipole. Only in a rather contrived scenario would one expect the differential number counts in two opposite hemispheres in the sky, to follow the
behavior, unless it were the result of a genuine dipole in the number density distribution, irrespective of the ultimate cause of the dipole.
Though spectroscopic redshifts are not available for most of the sources in the sample, however, from the sources where redshifts are available [
15], as well as from the previous information in the literature, AGNs are known to lie mostly at redshifts between 0.5 and 3 and are, in fact, the most distant discrete objects seen in the Universe. Therefore, the dipole anisotropy seen among them is not a local effect, and has a genuine bearing on the Cosmological Principle.
For a comparison with some earlier dipole determinations from the radio data on AGNs [
12], in
Figure 9 we show the plots of the
for both TGSS and NVSS data as a function of
, measured with respect to the CMBR dipole direction. It should be noted that the conversion factor from
to peculiar velocity
v in
Figure 9 is somewhat different in comparison with that in
Figure 7, because of the difference in indices
x and
between the radio and Infra red populations. It does seem that the peculiar velocity of the solar system estimated from the TGSS data is much higher than the NVSS data [
12], the latter in agreement with the MIRAGN dipole in
Figure 8.
A recent determination of the peculiar motion of the solar system from a dipole anisotropy in the redshift distribution of distant quasars has also yielded discrepant value of
km s
along the direction of the CMBR dipole [
13], implying a solar peculiar motion in a direction opposite to that derived from all other previous dipoles. Nevertheless, it is evident that all AGN dipoles have much larger amplitudes than the CMBR dipole, even though various AGN dipole directions in the sky may be lying parallel to the CMBR dipole.
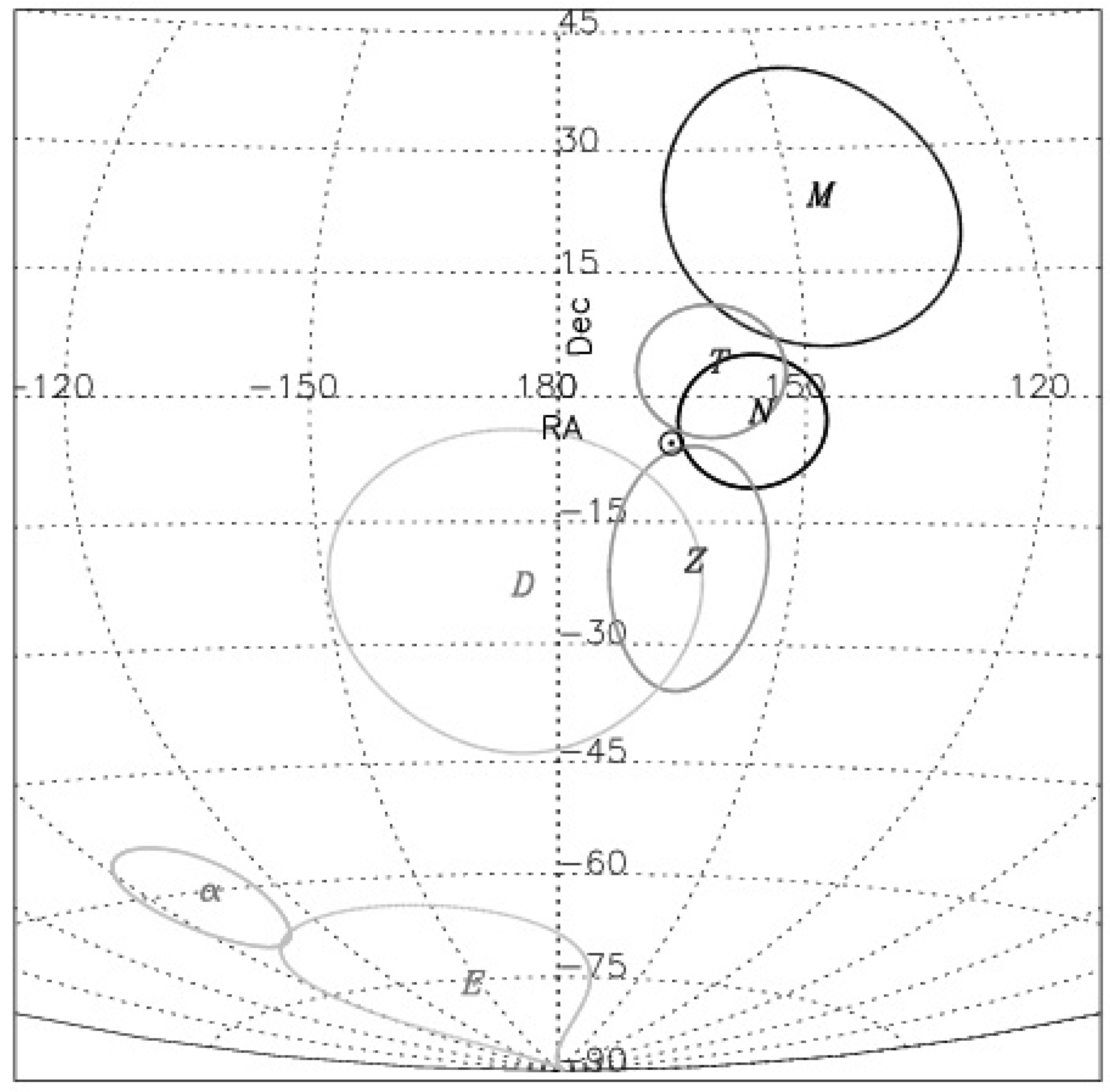
In
Figure 10, the sky position of our MIRAGN pole is shown by M, along with the
error ellipse, while the CMBR pole position is indicated by ⊙, which has negligible errors [
1,
2,
3]. Additionally plotted are the various other determined pole positions, N for the NVSS dipole, T for the TGSS dipole and D for the DR12Q dipole, along with their
error ellipses [
5,
12,
13]. From
Figure 10, it does seem that various AGN dipoles are within ∼
, except for the MIRAGN pole which is at
, of the CMBR pole, from which we can surmise that the various AGN dipoles are pointing along the same direction as the CMBR dipole.
Here it may be pointed out that a recent determination of the dipole [
14] from a flux-limited, all-sky sample of 1.36 million quasars observed by the Wide-field Infrared Survey Explorer (WISE) gave the direction of the dipole to be similar,
(RA=
, Dec=
, about
from the CMBR pole. However, the amplitude of the peculiar velocity (
km s
) was over twice as large as the CMBR value (
km s
), while we find the peculiar velocity (
km s
) to be over four times the CMBR value. This mysterious factor of two difference in the peculiar velocity values, estimated from these two Mid Infra Red AGN samples, needs to be explored further, whether it is due to a difference in the basic samples themselves or is it arising from the differences in the excluded zones, e.g., the galactic latitudes, or caused by some other, as yet unknown, reason. Nevertheless, one thing is clear, both the peculiar velocity estimates are inconsistent with the CMBR peculiar velocity value, though the direction estimate in each individual case does appear consistent with the CMBR dipole direction, within statistical uncertainties.
Since the peculiar velocity of the solar system should not be dependent upon the specific data or technique used to determine it, one obvious inference from the discordant values of the inferred peculiar motion from observed dipoles for the CMBR and the AGNs could be that there is a large relative motion between various cosmic reference frames. Otherwise, one has to take the view point that the observed discordant dipoles (including the CMBR), contrary to the conventional wisdom, do not reflect a motion of the observer (or a peculiar velocity of the solar system), and that we should instead look for some other possible cause for the genesis of these dipoles, including that of the CMBR. However, one has to then explain the existence of a preferred direction of all the dipoles and that what is so special about this particular direction A not-too-far-fetched inference drawn could be that a common direction for the dipoles, including of the CMBR, is a pointer toward the presence of an inherently preferred cosmic direction (axis!), implying perhaps an anisotropic Universe [
5] in conflict with the Cosmological Principle.
There are also other dipoles seen at cosmological scales. For instance, the “dark flow” dipole, which is a statistically significant dipole found at the position of galaxy clusters in filtered maps of the CMBR temperature anisotropies, implies the existence of a primordial CMBR dipole of non-kinematic origin, presenting itself as an effective motion across the entire cosmological horizon [
21,
22,
23,
24]. The CMBR dipole measurements are also consistent with some dynamical contributions to the CMBR dipole, resulting possibly from an SU(2) gauge principle [
25,
26,
27]. The detection of a dipole in the spatial variation of the fine-structure constant,
, based on study of quasar absorption systems has also been reported [
28,
29,
30,
31]. These spatial variations of the fine structure constant can be constrained using clusters of galaxies [
32,
33]. It seems that the fine structure constant cosmic dipole is aligned with the corresponding dark energy dipole within 1
uncertainties [
34,
35]. In
Figure 10, we have plotted positions of some of these poles to show their correlation, if any, with the CMBR dipole as well as various AGN dipoles. Here
D (Dark Flow) [
23],
(Fine Structure constant) [
29,
33] and
E (Dark Energy) [
34] are shown along with their quoted error ellipses. While the direction of dark flow dipole could be correlating with the direction of the CMBR dipole, the fine structure constant cosmic dipole and the dark energy dipole seem to be pointing quite away from the direction of the CMBR dipole. At the same time, because of large statistical uncertainties, the direction of dark flow dipole being in the same direction as the dark energy dipole cannot be ruled out. Further, there is a preference seen at significant levels for odd multipoles in the large scale anisotropies of the CMB temperature, a parity asymmetry, to be strongly aligned with the CMBR dipole [
36,
37,
38].
If the CMBR dipole is of kinematic origin due to the solar system peculiar motion, something resulting from the distribution of matter at local scales, in contrast to dipoles originating at cosmic scales, these observed correlations in the directions of various dipoles and asymmetries give rise to doubts about whether the CMBR dipole is really caused by our peculiar motion. If the CMBR dipole is due to some intrinsic asymmetry at cosmic scales, suggested by an order of magnitude difference in the dipole magnitudes as inferred from various AGN datasets, even though all appear to be in the same direction as the CMBR dipole, it gives rise to a larger question of the ultimate reliability of the Cosmological Principle, a cornerstone of the modern cosmology.