Abstract
The Langmuir–Landau-Centrifugal Drive (LLCD), which can effectively “convert” gravitational energy into particles, is explored as a driving mechanism responsible for the extreme thermal luminosity acquired by some active galactic nuclei (AGN). For this purpose, we consider equations governing the process of heating of AGN magnetospheres. In particular, we examine the Fourier components of the momentum equation, the continuity equation and the Poisson equation in the linear approximation and estimate the growth rate of the centrifugally excited electrostatic waves and the increment of the Langmuir collapse. It is shown that the process of energy pumping is composed of three stages: in the first stage the energy is efficiently transferred from rotation to the electrostatic modes. In due course of time, the second regime-the Langmuir collapse-occurs, when energy pumping is even more efficient. This process is terminated by the Landau damping, when enormous energy is released in the form of heat. We show that the magnetospheres of the supermassive black holes with luminosities of the order of erg/s can be heated up to K.
1. Introduction
Rotating magnetospheres, with relatively strong magnetic fields, surrounding active galactic nuclei (AGN), are believed to be the regions where cosmic rays might originate [1,2]. These particles are highly relativistic and one of the open problems in modern astrophysics is how do they attain such high energies.
Several mechanisms have been suggested to explain acceleration of leptons or hadrons to ultra-high energies. In particular, in the so-called Fermi class (and its modifications) of processes [3,4,5], the acceleration occurs in relatively strong magnetic fields in the magnetospheres of astrophysical objects. The Fermi processes, it turns out, are efficient only if the particles are already relativistic. For overall efficiency, therefore, some kind of a pre-acceleration is desirable [1].
In this paper, however, we explore the Langmuir-Landau-Centrifugal Drive (LLCD) mechanism that makes use of the plasma collective phenomena manifested though the Langmuir wave that will serve as a conduit for transferring gravitational energy in the rotating magnetosphere of an AGN to particle kinetic /thermal energy. Although LLCD has been discussed and developed in several papers [2,6,7,8], we will summarize its salient qualitative features in the introduction.
Since in the AGN magnetospheres magnetic fields are of the order of G, the charged particle flows will follow co-rotating magnetic field lines (frozen-in condition), experiencing very strong relativistic centrifugal force in the light cylinder (LC) zone (area where the linear velocity of rotation exactly equals the speed of light) [9]. If the plasma number density is high enough to provide the screening of longitudinal (along the magnetic field lines) electric field up to the LC area, the centrifugal mechanism becomes very efficient [10]. The strong relativistic differential centrifugal force leads to several consequences, for instance, the direct acceleration of electrons to very high energies (Lorentz factors of the order of ) [1,11]. Although the LLCD mechanism has been shown to accelerate particles to even higher energies, we in this paper emphasize its possible role in heating of the magnetosphere.
The first step in the LLCD process is the parametric excitation of Langmuir waves through charge separation caused by differential rotation of different charge species (electrons and protons ) endowed with different Lorentz factors. This process, examined for millisecond pulsars [12] and AGN [13], proves to be very effective in pumping enormous energy (from rotation, which in turn is gravitationally driven) into what could be called centrifugally driven electrostatic waves.
In the second stage of LLCD, the electrostatic waves Landau damp and transfer energy from centrifugally amplified modes to particle kinetic energy. The efficacy of this wave-particle energy transfer has been demonstrated for millisecond and newly born pulsars [8,14]; it was shown that LLCD could energize particles to the tune of eV.
In the study of the role of LLCD in the AGN magnetospheres [2], and SgrA (located in the center of the Milky Way) [7], we found that the parametrically amplified Langmuir waves, before undergoing standard Landau damp, go through another intermediate boosting via Langmuir collapse. One learns from the classical work by [15] that the Langmuir turbulence in the non-linear regime creates unstably excited caverns or the low-density regions. As a result, the high frequency pressure pulls the particles from the cavern, which in turn, provokes highly unstable collapse leading to fast amplification of the electrostatic field. The corresponding problem has been studied for three-dimensional geometry by [16] considering spectra of Langmuir turbulence. The termination by means of the Landau damping of the collapse process has been numerically studied by [17]. This last stage is the most important one in energy pumping process, because the whole energy of Langmuir waves transfers to particle kinetic energies. Applying this process to AGN [2] and the central black hole of our galaxy [7], it has been found that protons might achieve extremely high energies of the order of (in AGNs) and (in SgrA).
A principal consequence of Langmuir collapse might be not only the particle acceleration in a particular direction but also the efficient heating of the sustaining plasma. It is this heating that is posited here to be the cause of the observed intrinsic brightness (high temperatures K) of some AGNs [18].
2. The Theoretical Model of LLCD
The plasma under consideration lies in the magnetosphere of a supermassive black hole of typical mass ( g is the solar mass), and corresponding angular velocity of rotation
where c is the speed of light, dyne-cm/g is the gravitational constant and and are respectively dimensionless mass and a dimensionless parameter measuring the rate of rotation.
If the plasma in the near vicinity of a supermassive black hole is anchored by a magnetic field strong enough to maintain frozen-in condition, i.e., the charged particles will follow the field lines. In our model, we assume that the AGN radiation energy density and magnetic field energy density are of the same orders of magnitude (approximate equipartition). Then, on the light cylinder surface, where the relativistic effects of rotation are the most efficient, the strength of magnetic field is given by [11],
where is the light cylinder radius and is the dimensionless luminosity. As has been explained in detail by [1], the charged particles co-rotate with the field lines until the Lorentz factor reaches its maximum value, (here is the proton’s mass). Due accretion, the nearby area of AGN contains soft thermal photons which, by means of the IC scattering, might affect the process of acceleration. IC operates primarily on electrons while it is strongly suppressed for protons (by a factor ) and does not limit the maximum energy protons may acquire. In the framework of our approach the magnetic field lines almost up to the LC are supposed to be approximately straight. In the rotating magnetosphere this means that the particles in the rotating frame of reference move along straight trajectories.
However, it has been shown that on the LC itself the field lines are swept back, lagging behind the rotation [19] but up to the mentioned zone the field lines are quasi straight.
The original content of the LLCD mechanism, the parametric generation of centrifugally driven Langmuir waves, is contained in the set of linearized fluid equations (in Fourier space) coupled to the Poisson equation [2,8,14]:
where Equation (3) is the equation of motion in the presence of a centrifugal force, Equation (4) represents the continuity equation, and Equation (5) is the Poisson equation for the electric field E. In the preceding equations, is the species index (either electrons or protons), is the first order dimensionless momentum (), k represents the wave number of the excited mode, is the zeroth order velocity and is the radial coordinate [2], is the particle’s charge and and are, respectively the perturbed and unperturbed Fourier components of the number density.
The first term on the righthand side of Equation (3) represents the relativistic analogue of the centrifugal force. Since the centrifugal force differentiates between different species (electrons and protons), the resulting charge separation excites the Langmuir instability.
Notice that due to the time dependence of the centrifugal force, the preceding system cannot be “mode analyzed” by the standard techniques. However, we can extract almost as much information from the system as in a typical system, by the method developed in [14]. The ansatz
converts the aforementioned set of governing equations to a pair of coupled equations (time dependence is left only in )
where is the relativistic plasma frequency of the corresponding specie, is the Lorentz factor, , and .
A quasi “dispersion relation” for the electrostatic wave is derived after a formal Fourier transform (For the detailed derivation please see the paper by [14] of Equations (7) and (8)
where is the Bessel function. For resonant modes, , , we find that the effective dispersion relation is contained in
that is readily solved to yield the instability growth rate
where .
3. Discussion
Let us now examine the relevance of this instability as an agent for energy transfer in the AGN context. Since this instability is driven by differential rotation between the electron and ion fluids, it falls in the general class of two stream instabilities. We now show that for the magnetospheric plasma, consisting of relativistic electrons and protons, the instability growth rates are “large” implying that Langmuir wave generation is very efficient.
From Equation (10), one can straightforwardly show that for electrons with Lorentz factors , and protons with the same value , the timescale of energy pumping from rotation to electrostatic waves, ∼, varies in the range 600–2000 s. On the other hand, the kinematic timescale (escape timescale) of co-rotating particles (electrons and protons) equals s. As is evident, the instability timescale is much less than the kinematic timescale, indicating extremely high efficiency of centrifugally driven electrostatic waves.
These relatively high amplitude Langmuir waves will, now, induce high frequency pressure pushing the particles out from the perturbed zone [15]. In the resulting flow density areas (caverns), the penetrating waves will amplify pressure, which in turn, augments the process of pulling out of the particles resulting in the Langmuir collapse.
We assume that the kinetic and potential energies of plasmons inside the caverns are of the same orders of magnitude [20]
where is the Debye length scale, erg K is the Boltzmann constant and is the temperature provided by the accretion process. Since the perturbation density is much less than the unperturbed density, , energy of plasmons is almost constant
It is useful to recognize that k defines the system length scale (k∼). Equation (13), then, implies that the electrostatic energy density behaves as where q denotes the dimensionality of the process. Coupled with Equation (12), we find that the high frequency pressure, [20], suppresses the thermal pressure, only for three-dimensional geometry. Inside the magnetosphere, however, the effective geometry is one-dimensional () since the particles are in the frozen-in condition and follow the field lines. In this region, thus, the collapse is impossible (∼l and ∼l); it can be realized only in the outer regions of the magnetospheres, for distances exceeding the LC radius.
Zakharov showed that for three-dimensional geometry, , the driven electrostatic field and the corresponding length scale of the cavern behave as [15]
where is the time when the electric field fully collapses, and is the electrostatic field before the collapse starts (the initial field amplified by means of the electrostatic instability) and represents a length scale in the LC zone where the process of energy pumping occurs [2] and we have taking into account that the escape time of particles equals [21]. It is clear from the preceding equations that in due course of time, the length scale of the cavern goes to zero, whereas the electrostatic field asymptotically increases.
This process is terminated by means of Landau damping, when l reaches the dissipation length scale, ,20]. From Equations (14) and (15) one can show that the electrostatic field will be boosted by the factor . Correspondingly, a certain fraction, , of the electrical energy converts to heat, increasing the temperature of the ambient plasma,
where (in the framework of the equipartition approach) it has been assumed that the energy pumped by means of the collapse nearby the LC zone in a thin layer, (being of the order of cm), is uniformly distributed in a cylindrical area with typical radius, ; the energy is emitted away as a black body radiation. Here we assume that the typical heated radius is of the order of 0.01 pc (an approximate outer radius of the accretion disc for the given mass of the BH [22], and H represents the height of the corresponding cylinder. From Equation (16) one can, straightforwardly, obtain the increased temperature of the AGN ambient
The proposed heating mechanism is efficient, if the corresponding temperature exceeds that of the accretion disk temperature, which is estimated as [22]
where is the Schwarzschild radius of the supermassive black hole, is the accretion rate and describes efficiency of the accretion process.
In Figure 1 we show the dependance of and T on the bolometric luminosity of AGN. The set of parameters is: , , , , , , and pc. As is evident from the plots, the centrifugally driven heating mechanism becomes efficient for highly luminous AGN. In particular, for AGN with erg/s the temperature becomes much higher than the initial value (∼10 K) acquired in the accretion processes. On the other hand, one can straightforwardly check that the heating process is not sensitive with the rotation rate, which is a direct result of the power (see Equation (17)). Here we assumed the equipartition distribution of energy: half of the pumped energy goes to acceleration and half-to the heating process.
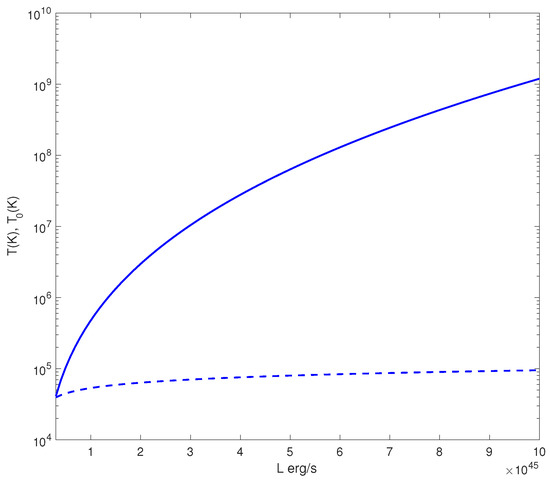
Figure 1.
Behavior of T (solid line) and (dashed line) with respect to the bolometric luminosity of AGN. The set of parameters is: , , , , , and pc.
The heating mechanism considered in the present work is so efficient that it can heat the system to blackbody radiation temperatures K, which have been observed in the X-ray corona of AGNs [18].
It is worth noting that during the acceleration the particles might lose energy by means of the several cooling mechanisms. This problem is considered in detail by [2]. The synchrotron process almost from the very beginning of motion becomes insignificant because the corresponding radiation is so efficient that the particles very soon transit to the ground Landau level, follow the magnetic field lines and do not emit any more in the synchrotron regime.
The curvature radiation does not impose any significant constraints as well. In particular, on the last stage of LLCD the particles achieve such high energies that the magnetic field becomes dependent on plasma energy density, the particles move along straight trajectories and as a result the curvature radiation is terminated.
The inverse Compton (IC) scattering for the considered energies occurs in the Klein–Nishina regime, when the corresponding timescale is a continuously increasing function of the proton energy [23], therefore this mechanism does not limit maximum achievable energies.
Another mechanism, which potentially might limit the process of proton acceleration is the photo-pion energy losses. The corresponding timescale is a continuously decreasing function of energy and for the extremely high values eV is of the order of s. On the other hand, the timescale of energy pumping into Langmuir waves is by several orders of magnitude less than the aforementioned value. The collapse in turn, since characterized by blowing up (see Equations (14) and (15)) is even more efficient than any other mechanisms. Therefore, the photo-pion cooling does not impose any constraints on proton acceleration and consequently on the heating process.
4. Summary
By examining the LLCD mechanism we have considered the system of equations composed by the Euler equation, continuity equation and the Poisson equation respectively. It has been shown that by means of the centrifugal force, the Langmuir waves parametrically amplify. As a result, the excited electrostatic waves efficiently pump energy from rotation.
Amplification of electrostatic field on the next stage is provided by means of the Langmuir collapse, which terminates on the Debye length-scales, resulting in the heating of the surrounding medium. It has been shown that for luminosities greater than erg/s the mentioned process can provide temperatures in the following interval K.
Author Contributions
Z.O. and S.M. developed the analytical model, obtained the results and wrote the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are available in the article and can be accessed via a DOI link.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LLCD | The Langmuir-Landau-Centrifugal Drive |
| AGN | active galactic nuclei |
| LC | Light cylinder |
| IC | inverse Compton |
References
- Rieger, F.M.; Mannheim, K. Particle acceleration by rotating magnetospheres in active galactic nuclei. Astron. Astrophys. 2000, 353, 473. [Google Scholar]
- Osmanov, Z.; Mahajan, S.; Machabeli, S.; Chkheidze, N. Extremely efficient Zevatron in rotating AGN magnetospheres. Mon. Not. R. Astron. Soc. 2014, 445, 4155–4160. [Google Scholar] [CrossRef]
- Fermi, E. On the Origin of the Cosmic Radiation. Phys. Rev. 1949, 75, 1169. [Google Scholar] [CrossRef]
- Bell, A.R. The acceleration of cosmic rays in shock fronts—I. Mon. Not. R. Astron. Soc. 1978, 182, 147–156. [Google Scholar] [CrossRef]
- Bell, A.R. The acceleration of cosmic rays in shock fronts—II. Mon. Not. R. Astron. Soc. 1978, 182, 443–455. [Google Scholar] [CrossRef]
- Osmanov, Z. Relativistic Effects of Rotation in γ-ray Pulsars—Invited Review. arXiv 2021, arXiv:2101.05584. [Google Scholar]
- Osmanov, Z.; Mahajan, S.; Machabeli, S. On the Rotationally Driven Pevatron in the Center of the Milky Way. Astrophys. J. 2017, 835, 164. [Google Scholar] [CrossRef]
- Osmanov, Z.; Mahajan, S.; Machabeli, S.; Chkheidze, N. Millisecond newly born pulsars as efficient accelerators of electrons. Nat. Sci. Rep. 2015, 5, 14443. [Google Scholar] [CrossRef] [PubMed]
- Gold, T. Rotating Neutron Stars and the Nature of Pulsars. Nature 1969, 221, 25. [Google Scholar] [CrossRef]
- Rieger, F.M. Nonthermal Processes in Black Hole-Jet Magnetospheres. Int. J. Mod. Phys. D 2011, 20, 1547–1596. [Google Scholar] [CrossRef]
- Osmanov, Z.; Rogava, A.S.; Bodo, G. On the efficiency of particle acceleration by rotating magnetospheres in AGN. Astron. Astrophys. 2007, 470, 395–400. [Google Scholar] [CrossRef][Green Version]
- Machabeli, G.; Osmanov, Z.; Mahajan, S. Parametric mechanism of the rotation energy pumping by a relativistic plasma. Phys. Plasmas 2005, 12, 062901. [Google Scholar] [CrossRef]
- Osmanov, Z. Centrifugally driven electrostatic instability in extragalactic jets. Phys. Plasmas 2008, 15, 032901. [Google Scholar] [CrossRef]
- Mahajan, S.; Machabeli, G.; Osmanov, Z.; Chkheidze, N. Ultra High Energy Electrons Powered by Pulsar Rotation. Nat. Sci. Rep. 2013, 3, 1262. [Google Scholar] [CrossRef] [PubMed]
- Zakharov, V.E. Collapse of Langmuir Waves. Sov. J. Exp. Theory Phys. 1972, 35, 908–914. [Google Scholar]
- Galeev, A.A.; Sagdeev, R.Z.; Shapiro, V.D.; Shevchenko, V.I. Langmuir turbulence and dissipation of high-frequency energy. Sov. J. Exp. Theory Phys. 1977, 46, 711. [Google Scholar]
- Degtiarev, L.M.; Zakharov, V.E.; Rudakov, L.I. Dynamics of Langmuir collapse. Sov. J. Plasma Phys. 1976, 2, 240–246. [Google Scholar]
- Beckmann, V.; Shrader, C. Active Galactic Nuclei; Wiley-Vch: New York, NY, USA, 2012. [Google Scholar]
- Osmanov, Z. Efficiency of the centrifugally induced curvature drift instability in AGN winds. Astron. Astrophys. 2008, 490, 487–492. [Google Scholar] [CrossRef][Green Version]
- Artsimovich, L.A.; Sagdeev, R.Z. Plasma Physics for Physicists; Atomizdat: Moscow, Russia, 1979. [Google Scholar]
- Machabeli, G.Z.; Rogava, A.D. Centrifugal force: A gedanken experiment. Phys. Rev. A 1994, 50, 98. [Google Scholar] [CrossRef] [PubMed]
- Carroll, B.W.; Ostlie, D.A. An Introduction to Modern Astrophysics and Cosmology; Pearson: San Francisco, CA, USA, 2010. [Google Scholar]
- Blumenthal, G.R.; Gould, R.J. Bremsstrahlung, Synchrotron Radiation, and Compton Scattering of High-Energy Electrons Traversing Dilute Gases. Rev. Mod. Phys. 1970, 42, 237. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).