Measurement of the Casimir Force between 0.2 and 8 μm: Experimental Procedures and Comparison with Theory
Abstract
1. Introduction
2. Materials, Methods and Results
2.1. Sample Preparation and Characterization
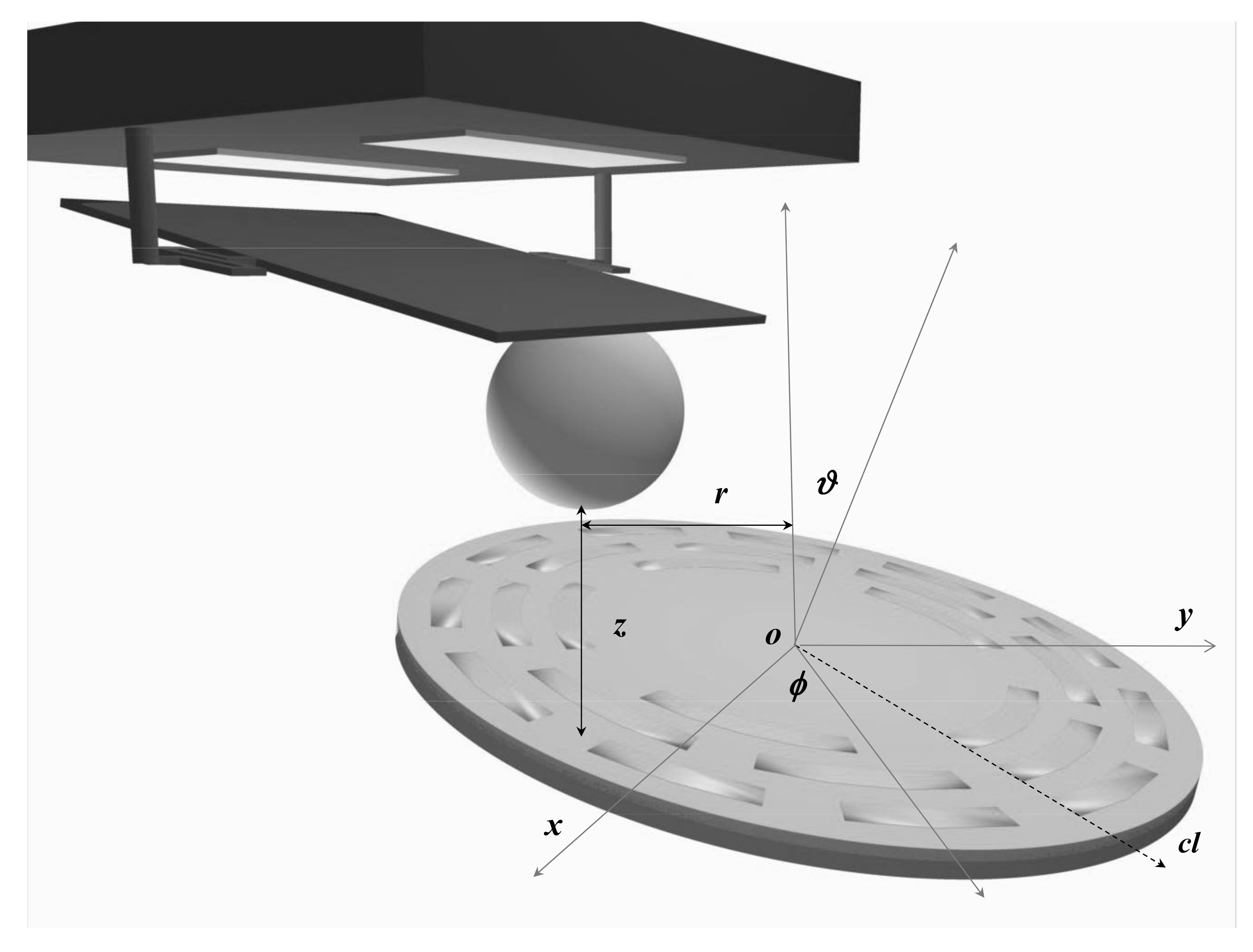
2.2. Oscillators
2.3. Electrostatic Calibration and Separation Determination
2.4. Results
3. Systematic Errors and Edge Effects
3.1. Contributions to the Systematic Error
3.2. Investigation of Edge Effects
4. Exact Evaluation of the Casimir Force in Sphere-Plate Geometry Using the Scattering Formula
4.1. Plane-Wave Representation
4.2. Zero-Frequency Limit
4.3. Numerical Application
5. Computation of the Casimir Force in Sphere-Plate Geometry Based on the Derivative Expansion
6. Total Errors and the Comparison between Experiment and Theory
6.1. Random and Total Experimental Errors
6.2. Two Methods of Comparison between Experiment and Theory
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Casimir, H.B.G. On the attraction between two perfectly conducting plates. Proc. K. Ned. Akad. Wet. B 1948, 51, 793–795. [Google Scholar]
- Lamoreaux, S.K. Demonstration of the Casimir Force in the 0.6 to 6 μm Range. Phys. Rev. Lett. 1997, 78, 5–8. [Google Scholar] [CrossRef]
- Lifshitz, E.M. The theory of molecular attractive forces between solids. Zh. Eksp. Teor. Fiz. 1955, 29, 94–110, Translated: Sov. Phys. JETP 1956, 2, 73–83. [Google Scholar]
- Dzyaloshinskii, I.E.; Lifshitz, E.M.; Pitaevskii, L.P. The general theory of van der Waals forces. Usp. Fiz. Nauk 1961, 73, 381–422, Translated: Adv. Phys. 1961, 10, 165–209. [Google Scholar] [CrossRef]
- Mohideen, U.; Roy, A. Precision Measurement of the Casimir Force from 0.1 to 0.9 μm. Phys. Rev. Lett. 1998, 81, 4549–4552. [Google Scholar] [CrossRef]
- Chan, H.B.; Aksyuk, V.A.; Kleiman, R.N.; Bishop, D.J.; Capasso, F. Quantum mechanical actuation of microelectromechanical system by the Casimir effect. Science 2001, 291, 1941–1944. [Google Scholar] [CrossRef] [PubMed]
- Chan, H.B.; Aksyuk, V.A.; Kleiman, R.N.; Bishop, D.J.; Capasso, F. Nonlinear Micromechanical Casimir Oscillator. Phys. Rev. Lett. 2001, 87, 211801. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Fischbach, E.; Krause, D.E. Measurement of the Casimir Force between Dissimilar Metals. Phys. Rev. Lett. 2003, 91, 050402. [Google Scholar] [CrossRef] [PubMed]
- Decca, R.S.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; López, D.; Mostepanenko, V.M. Improved tests of extra-dimensional physics and thermal quantum field theory from new Casimir force measurements. Phys. Rev. D 2003, 68, 116003. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Precise comparison of theory and new experiment for the Casimir force leads to stronger constraints on thermal quantum effects and long-range interactions. Ann. Phys. 2005, 318, 37–80. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Tests of new physics from precise measurements of the Casimir pressure between two gold-coated plates. Phys. Rev. D 2007, 75, 077101. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Novel constraints on light elementary particles and extra-dimensional physics from the Casimir effect. Eur. Phys. J. C 2007, 51, 963–975. [Google Scholar] [CrossRef]
- Palik, E.D. (Ed.) Handbook of Optical Constants of Solids; Academic Press: New York, NY, USA, 1985. [Google Scholar]
- Chang, C.C.; Banishev, A.A.; Castillo-Garza, R.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Gradient of the Casimir force between Au surfaces of a sphere and a plate measured using an atomic force microscope in a frequency-shift technique. Phys. Rev. B 2012, 85, 165443. [Google Scholar] [CrossRef]
- Banishev, A.A.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Demonstration of the Casimir Force between Ferromagnetic Surfaces of a Ni-Coated Sphere and a Ni-Coated Plate. Phys. Rev. Lett. 2013, 110, 137401. [Google Scholar] [CrossRef] [PubMed]
- Banishev, A.A.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Casimir interaction between two magnetic metals in comparison with nonmagnetic test bodies. Phys. Rev. B 2013, 88, 155410. [Google Scholar] [CrossRef]
- Bimonte, G. Hide It to See It Better: A Robust Setup to Probe the Thermal Casimir Effect. Phys. Rev. Lett. 2014, 112, 240401. [Google Scholar] [CrossRef] [PubMed]
- Bimonte, G.; López, D.; Decca, R.S. Isoelectronic determination of the thermal Casimir force. Phys. Rev. B 2016, 93, 184434. [Google Scholar] [CrossRef]
- Xu, J.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Reducing detrimental electrostatic effects in Casimir-force measurements and Casimir-force-based microdevices. Phys. Rev. A 2018, 97, 032501. [Google Scholar] [CrossRef]
- Liu, M.; Xu, J.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Examining the Casimir puzzle with an upgraded AFM-based technique and advanced surface cleaning. Phys. Rev. B 2019, 100, 081406(R). [Google Scholar] [CrossRef]
- Liu, M.; Xu, J.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Precision measurements of the gradient of the Casimir force between ultraclean metallic surfaces at larger separations. Phys. Rev. A 2019, 100, 052511. [Google Scholar] [CrossRef]
- Sushkov, A.O.; Kim, W.J.; Dalvit, D.A.R.; Lamoreaux, S.K. Observation of the thermal Casimir force. Nat. Phys. 2011, 7, 230–233. [Google Scholar] [CrossRef]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M.; Romero, C. Impact of surface imperfections on the Casimir force for lenses of centimeter-size curvature radii. Phys. Rev. B 2011, 83, 075417. [Google Scholar] [CrossRef]
- Bordag, M.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Observation of the thermal Casimir force is open to question. Int. J. Mod. Phys. A 2011, 26, 3918–3929. [Google Scholar]
- Chen, Y.-J.; Tham, W.K.; Krause, D.E.; López, D.; Fischbach, E.; Decca, R.S. Stronger limits on hypothetical Yukawa interactions in the 30—8000 nm range. Phys. Rev. Lett. 2016, 116, 221102. [Google Scholar] [CrossRef] [PubMed]
- Behunin, R.O.; Intravaia, F.; Dalvit, D.A.R.; Maia Neto, P.A.; Reynaud, S. Modeling electrostatic patch effects in Casimir force measurements. Phys. Rev. A 2012, 85, 012504. [Google Scholar] [CrossRef]
- Spreng, B.; Hartmann, M.; Henning, V.; Maia Neto, P.A.; Ingold, G.-L. Proximity force approximation and specular reflection: Application of the WKB limit of Mie scattering to the Casimir effect. Phys. Rev. A 2018, 97, 062504. [Google Scholar] [CrossRef]
- Henning, V.; Spreng, B.; Hartmann, M.; Ingold, G.-L.; Maia Neto, P.A. Role of diffraction in the Casimir effect beyond the proximity force approximation. J. Opt. Soc. Am. B 2019, 36, C77–C87. [Google Scholar] [CrossRef]
- Spreng, B.; Maia Neto, P.A.; Ingold, G.-L. Plane-wave approach to the exact van der Waals interaction between colloid particles. J. Chem. Phys. 2020, 153, 024115. [Google Scholar] [CrossRef]
- Fosco, C.D.; Lombardo, F.C.; Mazzitelli, F.D. Proximity force approximation for the Casimir energy as a derivative expansion. Phys. Rev. D 2011, 84, 105031. [Google Scholar] [CrossRef]
- Bimonte, G.; Emig, T.; Kardar, M. Material dependence of Casimir force: Gradient expansion beyond proximity. Appl. Phys. Lett. 2012, 100, 074110. [Google Scholar] [CrossRef]
- Bimonte, G.; Emig, T.; Jaffe, R.L.; Kardar, M. Casimir forces beyond the proximity force approximation. Europhys. Lett. 2012, 97, 50001. [Google Scholar] [CrossRef]
- López, D.; Decca, R.S.; Fischbach, E.; Krause, D.E. MEMS-Based Force Sensor Design and Applications. Bell Labs. Tech. J. 2005, 10, 61–80. [Google Scholar] [CrossRef]
- Lärmer, F.; Schilp, A. Method of Anisotropically Etching Silicon. DE Patent 4241045, US Patent 5501893 and EP Patent 625285 1996. [Google Scholar]
- Kolb, P.W.; Decca, R.S.; Drew, H.D. Capacitive sensor for micropositioning in two dimensions. Rev. Sci. Instrum. 1998, 69, 310–312. [Google Scholar] [CrossRef]
- Simpson, W.; Leonhardt, U. (Eds.) Forces of the Quantum Vacuum: An Introduction to Casimir Physics; World Scientific: Singapore, 2015; Chapter 4. [Google Scholar]
- Decca, R.S.; López, D. Measurement of the Casimir force using a microelectromechanical torsional oscillator: Electrostatic calibration. Int. J. Mod. Phys. A 2009, 24, 1748–1756. [Google Scholar] [CrossRef]
- Chen, F.; Mohideen, U.; Klimchitskaya, G.L.; Mostepanenko, V.M. Experimental test for the conductivity properties from the Casimir force between metal and semiconductor. Phys. Rev. A 2006, 74, 022103. [Google Scholar] [CrossRef]
- Behunin, R.O.; Dalvit, D.A.R.; Decca, R.S.; Genet, C.; Jung, I.W.; Lambrecht, A.; Liscio, A.; López, D.; Reynaud, S.; Schnoering, G.; et al. Kelvin probe force microscopy of metallic surfaces used in Casimir force measurements. Phys. Rev. A 2014, 90, 062115. [Google Scholar] [CrossRef]
- Behunin, R.O.; Zeng, Y.; Dalvit, D.A.R.; Reynaud, S. Electrostatic patch effects in Casimir-force experiments performed in the sphere-plane geometry. Phys. Rev. A 2012, 86, 052509. [Google Scholar] [CrossRef]
- Bulgac, A.; Magierski, P.; Wirzba, A. Scalar Casimir effect between Dirichlet spheres or a plate and a sphere. Phys. Rev. D 2006, 73, 025007. [Google Scholar] [CrossRef]
- Emig, T.; Jaffe, R.L.; Kardar, M.; Scardicchio, A. Casimir Interaction between a Plate and a Cylinder. Phys. Rev. Lett. 2006, 96, 080403. [Google Scholar] [CrossRef]
- Bordag, M. Casimir effect for a sphere and a cylinder in front of a plane and corrections to the proximity force theorem. Phys. Rev. D 2006, 73, 125018. [Google Scholar] [CrossRef]
- Lambrecht, A.; Maia Neto, P.A.; Reynaud, S. The Casimir effect within scattering theory. New J. Phys. 2008, 78, 012115. [Google Scholar] [CrossRef]
- Rahi, S.J.; Emig, T.; Graham, N.; Jaffe, R.L.; Kardar, M. Scattering theory approach to electromagnetic Casimir forces. Phys. Rev. D 2009, 80, 085021. [Google Scholar] [CrossRef]
- Maia Neto, P.A.; Lambrecht, A.; Reynaud, S. Casimir energy between a plane and a sphere in electromagnetic vacuum. Phys. Rev. A 2008, 78, 012115. [Google Scholar] [CrossRef]
- Emig, T. Fluctuation-induced quantum interactions between compact objects and a plane mirror. J. Stat. Mech. 2008, 2008, P04007. [Google Scholar] [CrossRef]
- Canaguier-Durand, A.; Maia Neto, P.A.; Lambrecht, A.; Reynaud, S. Thermal Casimir Effect in the Plane-Sphere Geometry. Phys. Rev. Lett. 2010, 104, 040403. [Google Scholar] [CrossRef]
- Hartmann, M.; Ingold, G.-L.; Maia Neto, P.A. Plasma versus Drude Modeling of the Casimir Force: Beyond the Proximity Force Approximation. Phys. Rev. Lett. 2017, 119, 043901. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley-VCH: Weinheim, Germany, 2004; Chapter 4. [Google Scholar]
- Olver, F.W.J.; Daalhuis, A.B.; Lozier, D.W.; Schneider, B.I.; Boisvert, R.F.; Clark, C.W.; Miller, B.R.; Saunders, B.V.; Cohl, H.S.; McClain, M.A. (Eds.) NIST Digital Library of Mathematical Functions. Release 1.1.1 of 2021–03-15. Available online: http://dlmf.nist.gov/ (accessed on 6 April 2021).
- Canaguier-Durand, A. Multipolar Scattering Expansion for the Casimir Effect in the Sphere-Plane Geometry. Ph.D. Thesis, Université Pierre et Marie Curie—Paris VI, Paris, France, 2011. [Google Scholar]
- Schoger, T.; Ingold, G.-L. Classical Casimir free energy for two Drude spheres of arbitrary radii: A plane-wave approach. arXiv 2020, arXiv:2009.14090. [Google Scholar]
- Bornemann, F. On the numerical evaluation of Fredholm determinants. Math. Comp. 2012, 79, 871–915. [Google Scholar] [CrossRef]
- Boyd, J.P. Exponentially convergent Fourier-quadrature schemes on bounded and infinite intervals. J. Sci. Comput. 1987, 2, 99–109. [Google Scholar] [CrossRef]
- Bordag, M.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Advances in the Casimir Effect; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Fosco, C.D.; Lombardo, F.C. Mazzitelli, F.D. Derivative expansion for the Casimir effect at zero and finite temperature in d+1 dimwnsions. Phys. Rev. D 2012, 86, 045021. [Google Scholar] [CrossRef]
- Fosco, C.D.; Lombardo, F.C. Mazzitelli, F.D. Derivative-expansion approach to the interaction between close surfaces. Phys. Rev. A 2014, 89, 062120. [Google Scholar] [CrossRef]
- Bimonte, G. Going beyond PFA: A precise formula for the sphere-plate Casimir force. Europhys. Lett. 2017, 118, 20002. [Google Scholar] [CrossRef]
- Bimonte, G. Beyond-proximity-force-approximation Casimir force between two spheres at finite temperature. II. Plasma versus Drude modeling, grounded versus isolated spheres. Phys. Rev. D 2018, 98, 105004. [Google Scholar] [CrossRef]
- Bimonte, G.; Emig, T. Exact Results for Classical Casimir Interactions: Dirichlet and Drude Model in the Sphere-Sphere and Sphere-Plane Geometry. Phys. Rev. Lett. 2012, 109, 160403. [Google Scholar] [CrossRef]
- Canaguier-Durand, A.; Ingold, G.-L.; Jaekel, M.-T.; Lambrecht, A.; Maia Neto, P.A.; Reynaud, S. Classical Casimir interaction in the plane-sphere geometry. Phys. Rev. A 2012, 85, 052501. [Google Scholar] [CrossRef]
- Bimonte, G. Classical Casimir interaction of a perfectly conducting sphere and plate. Phys. Rev. D 2017, 95, 065004. [Google Scholar] [CrossRef]
- Rabinovich, S.G. Measurement Errors and Uncertainties: Theory and Practice; Springer: New York, NY, USA, 2000. [Google Scholar]
- Launer, R.L.; Wilkinson, G.N. (Eds.) Robustness in Statistics; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. The Casimir force between real materials: Experiment and theory. Rev. Mod. Phys. 2009, 81, 1827–1885. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. An alternative response to the off-shell quantum fluctuations: A step forward in resolution of the Casimir puzzle. Eur. Phys. J. C 2020, 80, 900. [Google Scholar] [CrossRef]















| [nm] | [nm] | Flatness of wafer [nm] | |
|---|---|---|---|
| Separation | 0.6 | 0.2 | 1.2 |
| Detection [fN] | Calibration [fN] | Measurement [fN] | |
| Force | 0.6 | 0.2 | [85, 0.5] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bimonte, G.; Spreng, B.; Maia Neto, P.A.; Ingold, G.-L.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Decca, R.S. Measurement of the Casimir Force between 0.2 and 8 μm: Experimental Procedures and Comparison with Theory. Universe 2021, 7, 93. https://doi.org/10.3390/universe7040093
Bimonte G, Spreng B, Maia Neto PA, Ingold G-L, Klimchitskaya GL, Mostepanenko VM, Decca RS. Measurement of the Casimir Force between 0.2 and 8 μm: Experimental Procedures and Comparison with Theory. Universe. 2021; 7(4):93. https://doi.org/10.3390/universe7040093
Chicago/Turabian StyleBimonte, Giuseppe, Benjamin Spreng, Paulo A. Maia Neto, Gert-Ludwig Ingold, Galina L. Klimchitskaya, Vladimir M. Mostepanenko, and Ricardo S. Decca. 2021. "Measurement of the Casimir Force between 0.2 and 8 μm: Experimental Procedures and Comparison with Theory" Universe 7, no. 4: 93. https://doi.org/10.3390/universe7040093
APA StyleBimonte, G., Spreng, B., Maia Neto, P. A., Ingold, G.-L., Klimchitskaya, G. L., Mostepanenko, V. M., & Decca, R. S. (2021). Measurement of the Casimir Force between 0.2 and 8 μm: Experimental Procedures and Comparison with Theory. Universe, 7(4), 93. https://doi.org/10.3390/universe7040093








