Scaling Properties of Galaxy Groups
Abstract
1. Introduction
1.1. Galaxy Groups and Astrophysics
1.2. Galaxy Groups and Cosmology
1.3. This Review
2. X-ray Scaling Relations
2.1. Theoretical Expectations
2.2. Observed Scaling Relations
3. Optical Scaling Relations
3.1. Velocity Dispersion
3.2. The Luminosity-Velocity Dispersion Relation
3.3. The Velocity Dispersion-Temperature Relation
3.4. Low Velocity Dispersion Groups
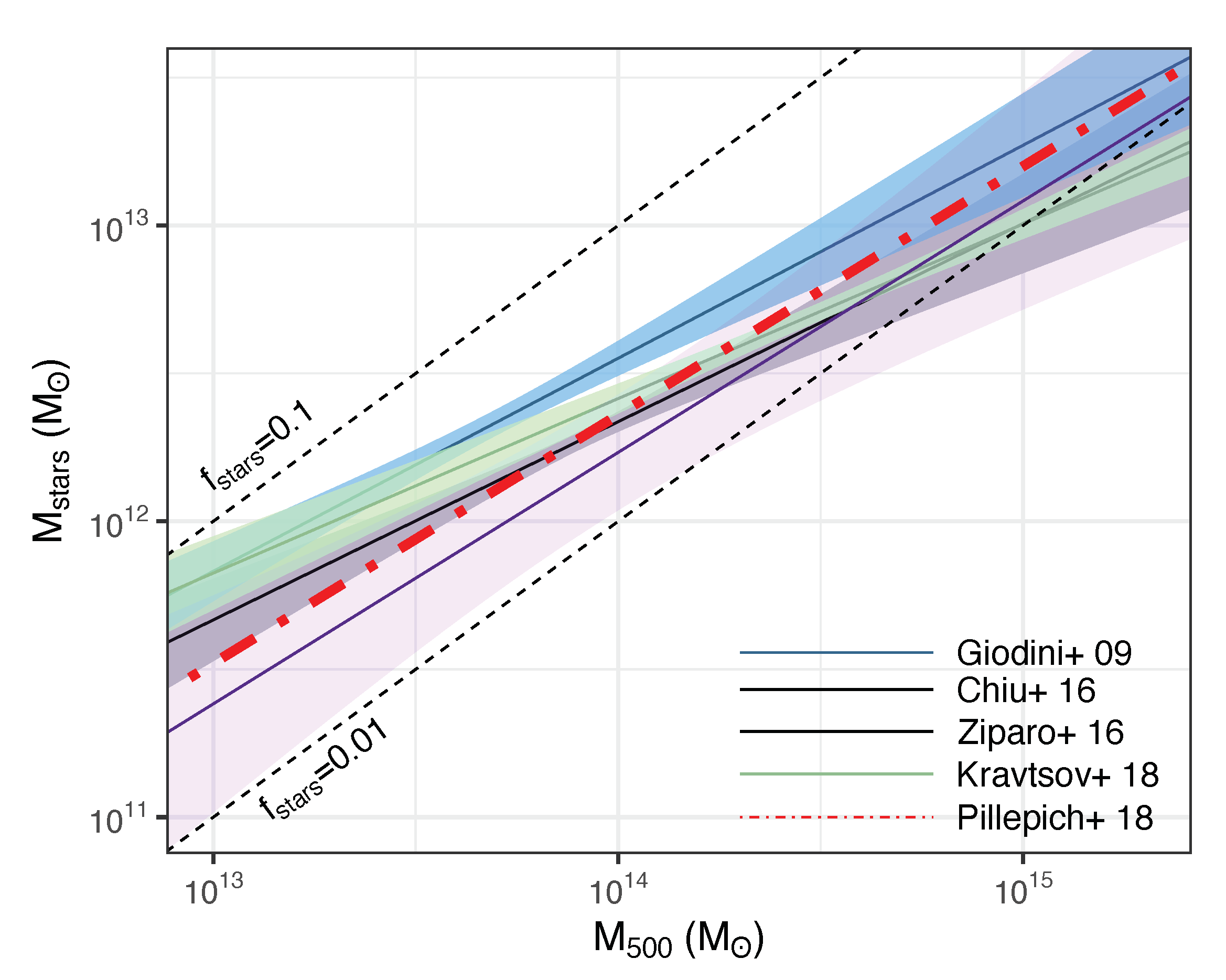
3.5. Stellar Gas Content of Galaxy Groups
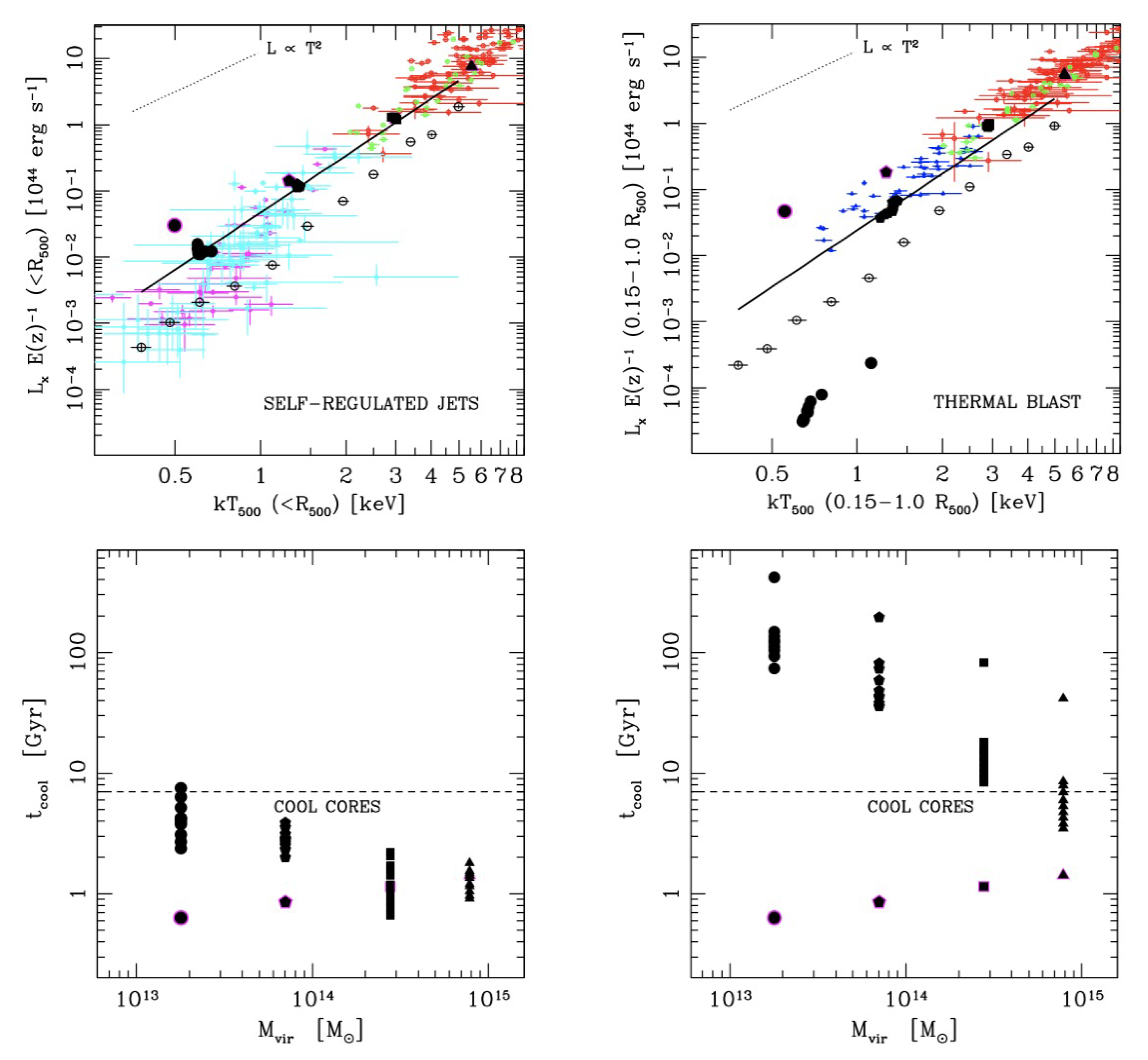
4. The Role of SMBHs: Observed Scaling Relations and Predictions via HD Simulations
5. Galaxy Groups with the Next-Generation Instruments
6. Final Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eke, V.R.; Baugh, C.M.; Cole, S.; Frenk, C.S.; Norberg, P.; Peacock, J.A.; Baldry, I.K.; Bland-Hawthorn, J.; Bridges, T.; Cannon, R.; et al. Galaxy groups in the 2dFGRS: The group-finding algorithm and the 2PIGG catalogue. MNRAS 2004, 348, 866–878. [Google Scholar] [CrossRef]
- Giodini, S.; Pierini, D.; Finoguenov, A.; Pratt, G.W.; Boehringer, H.; Leauthaud, A.; Guzzo, L.; Aussel, H.; Bolzonella, M.; Capak, P.; et al. Stellar and Total Baryon Mass Fractions in Groups and Clusters Since Redshift 1. ApJ 2009, 703, 982–993. [Google Scholar] [CrossRef]
- Eigenthaler, P.; Zeilinger, W.W. The Search for Fossil Groups of Galaxies. Astron. Nachr. 2007, 328, 699. [Google Scholar]
- Nolthenius, R.; White, S.D.M. Groups of galaxies in the CfA survey and in cold dark matter universes. MNRAS 1987, 225, 505–530. [Google Scholar] [CrossRef]
- Hickson, P. Systematic properties of compact groups of galaxies. ApJ 1982, 255, 382–391. [Google Scholar] [CrossRef]
- Jones, L.R.; Ponman, T.J.; Horton, A.; Babul, A.; Ebeling, H.; Burke, D.J. The nature and space density of fossil groups of galaxies. MNRAS 2003, 343, 627–638. [Google Scholar] [CrossRef]
- Helsdon, S.F.; Ponman, T.J. Are X-ray properties of loose groups different from those of compact groups? MNRAS 2000, 319, 933–938. [Google Scholar] [CrossRef]
- Ponman, T.J.; Cannon, D.B.; Navarro, J.F. The thermal imprint of galaxy formation on X-ray clusters. Nature 1999, 397, 135–137. [Google Scholar] [CrossRef]
- Sanderson, A.J.R.; Ponman, T.J.; Finoguenov, A.; Lloyd-Davies, E.J.; Markevitch, M. The Birmingham-CfA cluster scaling project—I. Gas fraction and the M-TX relation. MNRAS 2003, 340, 989–1010. [Google Scholar] [CrossRef]
- Despali, G.; Giocoli, C.; Angulo, R.E.; Tormen, G.; Sheth, R.K.; Baso, G.; Moscardini, L. The universality of the virial halo mass function and models for non-universality of other halo definitions. MNRAS 2016, 456, 2486–2504. [Google Scholar] [CrossRef]
- Tully, R.B. Nearby Groups of Galaxies. II. an All-Sky Survey within 3000 Kilometers per Second. ApJ 1987, 321, 280. [Google Scholar] [CrossRef]
- Fukugita, M.; Hogan, C.J.; Peebles, P.J.E. The Cosmic Baryon Budget. ApJ 1998, 503, 518–530. [Google Scholar] [CrossRef]
- Brighenti, F.; Mathews, W.G. Heated Cooling Flows. ApJ 2002, 573, 542–561. [Google Scholar] [CrossRef][Green Version]
- McCarthy, I.G.; Schaye, J.; Ponman, T.J.; Bower, R.G.; Booth, C.M.; Dalla Vecchia, C.; Crain, R.A.; Springel, V.; Theuns, T.; Wiersma, R.P.C. The case for AGN feedback in galaxy groups. MNRAS 2010, 406, 822–839. [Google Scholar] [CrossRef]
- Gaspari, M.; Brighenti, F.; Temi, P. Mechanical AGN feedback: Controlling the thermodynamical evolution of elliptical galaxies. MNRAS 2012, 424, 190–209. [Google Scholar] [CrossRef]
- Hudson, D.S.; Mittal, R.; Reiprich, T.H.; Nulsen, P.E.J.; Andernach, H.; Sarazin, C.L. What is a cool-core cluster? a detailed analysis of the cores of the X-ray flux-limited HIFLUGCS cluster sample. Astron. Astrophys. 2010, 513, A37. [Google Scholar] [CrossRef]
- Bharadwaj, V.; Reiprich, T.H.; Schellenberger, G.; Eckmiller, H.J.; Mittal, R.; Israel, H. Intracluster medium cooling, AGN feedback, and brightest cluster galaxy properties of galaxy groups. Five properties where groups differ from clusters. Astron. Astrophys. 2014, 572, A46. [Google Scholar] [CrossRef][Green Version]
- O’Sullivan, E.; Ponman, T.J.; Kolokythas, K.; Raychaudhury, S.; Babul, A.; Vrtilek, J.M.; David, L.P.; Giacintucci, S.; Gitti, M.; Haines, C.P. The Complete Local Volume Groups Sample—I. Sample selection and X-ray properties of the high-richness subsample. MNRAS 2017, 472, 1482–1505. [Google Scholar] [CrossRef]
- Bogdán, Á.; Lovisari, L.; Volonteri, M.; Dubois, Y. Correlation between the Total Gravitating Mass of Groups and Clusters and the Supermassive Black Hole Mass of Brightest Galaxies. ApJ 2018, 852, 131. [Google Scholar] [CrossRef]
- Gaspari, M.; Eckert, D.; Ettori, S.; Tozzi, P.; Bassini, L.; Rasia, E.; Brighenti, F.; Sun, M.; Borgani, S.; Johnson, S.D.; et al. The X-Ray Halo Scaling Relations of Supermassive Black Holes. ApJ 2019, 884, 169. [Google Scholar] [CrossRef]
- Lakhchaura, K.; Truong, N.; Werner, N. Correlations between supermassive black holes, hot atmospheres, and the total masses of early-type galaxies. MNRAS 2019, 488, L134–L142. [Google Scholar] [CrossRef]
- Sijacki, D.; Springel, V.; Di Matteo, T.; Hernquist, L. A unified model for AGN feedback in cosmological simulations of structure formation. MNRAS 2007, 380, 877–900. [Google Scholar] [CrossRef]
- Puchwein, E.; Sijacki, D.; Springel, V. Simulations of AGN Feedback in Galaxy Clusters and Groups: Impact on Gas Fractions and the LX-T Scaling Relation. ApJ 2008, 687, L53–L56. [Google Scholar] [CrossRef]
- Fabjan, D.; Borgani, S.; Tornatore, L.; Saro, A.; Murante, G.; Dolag, K. Simulating the effect of active galactic nuclei feedback on the metal enrichment of galaxy clusters. MNRAS 2010, 401, 1670–1690. [Google Scholar] [CrossRef]
- Le Brun, A.M.C.; McCarthy, I.G.; Schaye, J.; Ponman, T.J. Towards a realistic population of simulated galaxy groups and clusters. MNRAS 2014, 441, 1270–1290. [Google Scholar] [CrossRef]
- Planelles, S.; Borgani, S.; Fabjan, D.; Killedar, M.; Murante, G.; Granato, G.L.; Ragone-Figueroa, C.; Dolag, K. On the role of AGN feedback on the thermal and chemodynamical properties of the hot intracluster medium. MNRAS 2014, 438, 195–216. [Google Scholar] [CrossRef]
- Gaspari, M.; Brighenti, F.; Temi, P.; Ettori, S. Can AGN Feedback Break the Self-similarity of Galaxies, Groups, and Clusters? ApJ 2014, 783, L10. [Google Scholar] [CrossRef]
- Truong, N.; Rasia, E.; Mazzotta, P.; Planelles, S.; Biffi, V.; Fabjan, D.; Beck, A.M.; Borgani, S.; Dolag, K.; Gaspari, M.; et al. Cosmological hydrodynamical simulations of galaxy clusters: X-ray scaling relations and their evolution. MNRAS 2018, 474, 4089–4111. [Google Scholar] [CrossRef]
- Markevitch, M. The LX-T Relation and Temperature Function for Nearby Clusters Revisited. ApJ 1998, 504, 27–34. [Google Scholar] [CrossRef]
- Pratt, G.W.; Croston, J.H.; Arnaud, M.; Böhringer, H. Galaxy cluster X-ray luminosity scaling relations from a representative local sample (REXCESS). Astron. Astrophys. 2009, 498, 361–378. [Google Scholar] [CrossRef]
- Mittal, R.; Hicks, A.; Reiprich, T.H.; Jaritz, V. The LX - Tvir relation in galaxy clusters: Effects of radiative cooling and AGN heating. Astron. Astrophys. 2011, 532, A133. [Google Scholar] [CrossRef]
- Bharadwaj, V.; Reiprich, T.H.; Lovisari, L.; Eckmiller, H.J. Extending the LX - T relation from clusters to groups. Impact of cool core nature, AGN feedback, and selection effects. Astron. Astrophys. 2015, 573, A75. [Google Scholar] [CrossRef][Green Version]
- Mantz, A.B.; Allen, S.W.; Morris, R.G.; von der Linden, A.; Applegate, D.E.; Kelly, P.L.; Burke, D.L.; Donovan, D.; Ebeling, H. Weighing the giants- V. Galaxy cluster scaling relations. MNRAS 2016, 463, 3582–3603. [Google Scholar] [CrossRef]
- Lovisari, L.; Schellenberger, G.; Sereno, M.; Ettori, S.; Pratt, G.W.; Forman, W.R.; Jones, C.; Andrade-Santos, F.; Randall, S.; Kraft, R. X-Ray Scaling Relations for a Representative Sample of Planck-selected Clusters Observed with XMM-Newton. ApJ 2020, 892, 102. [Google Scholar] [CrossRef]
- Eckert, D.; Molendi, S.; Paltani, S. The cool-core bias in X-ray galaxy cluster samples. I. Method and application to HIFLUGCS. Astron. Astrophys. 2011, 526, A79. [Google Scholar] [CrossRef]
- Reiprich, T.H.; Böhringer, H. The Mass Function of an X-Ray Flux-limited Sample of Galaxy Clusters. ApJ 2002, 567, 716–740. [Google Scholar] [CrossRef]
- Allen, S.W.; Rapetti, D.A.; Schmidt, R.W.; Ebeling, H.; Morris, R.G.; Fabian, A.C. Improved constraints on dark energy from Chandra X-ray observations of the largest relaxed galaxy clusters. MRAS 2008, 383, 879–896. [Google Scholar] [CrossRef]
- Vikhlinin, A.; Kravtsov, A.V.; Burenin, R.A.; Ebeling, H.; Forman, W.R.; Hornstrup, A.; Jones, C.; Murray, S.S.; Nagai, D.; Quintana, H.; et al. Chandra Cluster Cosmology Project III: Cosmological Parameter Constraints. ApJ 2009, 692, 1060–1074. [Google Scholar] [CrossRef]
- Rozo, E.; Wechsler, R.H.; Rykoff, E.S.; Annis, J.T.; Becker, M.R.; Evrard, A.E.; Frieman, J.A.; Hansen, S.M.; Hao, J.; Johnston, D.E.; et al. Cosmological Constraints from the Sloan Digital Sky Survey maxBCG Cluster Catalog. ApJ 2010, 708, 645–660. [Google Scholar] [CrossRef]
- Mantz, A.B.; von der Linden, A.; Allen, S.W.; Applegate, D.E.; Kelly, P.L.; Morris, R.G.; Rapetti, D.A.; Schmidt, R.W.; Adhikari, S.; Allen, M.T.; et al. Weighing the giants—IV. Cosmology and neutrino mass. MNRAS 2015, 446, 2205–2225. [Google Scholar] [CrossRef]
- de Haan, T.; Benson, B.A.; Bleem, L.E.; Allen, S.W.; Applegate, D.E.; Ashby, M.L.N.; Bautz, M.; Bayliss, M.; Bocquet, S.; Brodwin, M.; et al. Cosmological Constraints from Galaxy Clusters in the 2500 Square-degree SPT-SZ Survey. ApJ 2016, 832, 95. [Google Scholar] [CrossRef]
- Planck Collaboration Planck 2015 results. XXIV. Cosmology from Sunyaev-Zeldovich cluster counts. Astron. Astrophys. 2016, 594, A24. [CrossRef]
- Böhringer, H.; Chon, G.; Fukugita, M. The extended ROSAT-ESO Flux-Limited X-ray Galaxy Cluster Survey (REFLEX II). VII. The mass function of galaxy clusters. Astron. Astrophys. 2017, 608, A65. [Google Scholar] [CrossRef]
- Schellenberger, G.; Reiprich, T.H. HICOSMO: Cosmology with a complete sample of galaxy clusters—II. Cosmological results. MNRAS 2017, 471, 1370–1389. [Google Scholar] [CrossRef]
- Pacaud, F.; Pierre, M.; Melin, J.B.; Adami, C.; Evrard, A.E.; Galli, S.; Gastaldello, F.; Maughan, B.J.; Sereno, M.; Alis, S.; et al. The XXL Survey. XXV. Cosmological analysis of the C1 cluster number counts. Astron. Astrophys. 2018, 620, A10. [Google Scholar] [CrossRef]
- Bocquet, S.; Dietrich, J.P.; Schrabback, T.; Bleem, L.E.; Klein, M.; Allen, S.W.; Applegate, D.E.; Ashby, M.L.N.; Bautz, M.; Bayliss, M.; et al. Cluster Cosmology Constraints from the 2500 deg2 SPT-SZ Survey: Inclusion of Weak Gravitational Lensing Data from Magellan and the Hubble Space Telescope. ApJ 2019, 878, 55. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Abdalla, F.B.; Alarcon, A.; Aleksić, J.; Allam, S.; Allen, S.; Amara, A.; Annis, J.; Asorey, J.; Avila, S.; et al. Dark Energy Survey year 1 results: Cosmological constraints from galaxy clustering and weak lensing. Phys. Rev. D 2018, 98, 043526. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Aguena, M.; Alarcon, A.; Allam, S.; Allen, S.; Annis, J.; Avila, S.; Bacon, D.; Bechtol, K.; Bermeo, A.; et al. Dark Energy Survey Year 1 Results: Cosmological constraints from cluster abundances and weak lensing. Phys. Rev. D 2020, 102, 023509. [Google Scholar] [CrossRef]
- McClintock, T.; Varga, T.N.; Gruen, D.; Rozo, E.; Rykoff, E.S.; Shin, T.; Melchior, P.; DeRose, J.; Seitz, S.; Dietrich, J.P.; et al. Dark Energy Survey Year 1 results: Weak lensing mass calibration of redMaPPer galaxy clusters. MNRAS 2019, 482, 1352–1378. [Google Scholar] [CrossRef]
- Farahi, A.; Chen, X.; Evrard, A.E.; Hollowood, D.L.; Wilkinson, R.; Bhargava, S.; Giles, P.; Romer, A.K.; Jeltema, T.; Hilton, M.; et al. Mass variance from archival X-ray properties of Dark Energy Survey Year-1 galaxy clusters. MNRAS 2019, 490, 3341–3354. [Google Scholar] [CrossRef]
- Mulchaey, J.S. X-ray Properties of Groups of Galaxies. Annu. Rev. Astron. Astrophys. 2000, 38, 289–335. [Google Scholar] [CrossRef]
- Sun, M. Hot gas in galaxy groups: Recent observations. New J. Phys. 2012, 14, 045004. [Google Scholar] [CrossRef]
- Kaiser, N. Evolution and clustering of rich clusters. MNRAS 1986, 222, 323–345. [Google Scholar] [CrossRef]
- Kitayama, T.; Suto, Y. Semianalytic Predictions for Statistical Properties of X-Ray Clusters of Galaxies in Cold Dark Matter Universes. ApJ 1996, 469, 480. [Google Scholar] [CrossRef]
- Bryan, G.L.; Norman, M.L. Statistical Properties of X-Ray Clusters: Analytic and Numerical Comparisons. ApJ 1998, 495, 80–99. [Google Scholar] [CrossRef]
- Voit, G.M. Tracing cosmic evolution with clusters of galaxies. Rev. Mod. Phys. 2005, 77, 207–258. [Google Scholar] [CrossRef]
- Maughan, B.J.; Jones, L.R.; Ebeling, H.; Scharf, C. The evolution of the cluster X-ray scaling relations in the Wide Angle ROSAT Pointed Survey sample at 0.6 < z < 1.0. MNRAS 2006, 365, 509–529. [Google Scholar] [CrossRef]
- Borgani, S.; Diaferio, A.; Dolag, K.; Schindler, S. Thermodynamical Properties of the ICM from Hydrodynamical Simulations. Space Sci. Rev. 2008, 134, 269–293. [Google Scholar] [CrossRef][Green Version]
- Böhringer, H.; Dolag, K.; Chon, G. Modelling self-similar appearance of galaxy clusters in X-rays. Astron. Astrophys. 2012, 539, A120. [Google Scholar] [CrossRef]
- Ettori, S. The generalized scaling relations for X-ray galaxy clusters: The most powerful mass proxy. MNRAS 2013, 435, 1265–1277. [Google Scholar] [CrossRef]
- Giodini, S.; Lovisari, L.; Pointecouteau, E.; Ettori, S.; Reiprich, T.H.; Hoekstra, H. Scaling Relations for Galaxy Clusters: Properties and Evolution. Space Sci. Rev. 2013, 177, 247–282. [Google Scholar] [CrossRef]
- Maughan, B.J. PICACS: Self-consistent modelling of galaxy cluster scaling relations. MNRAS 2014, 437, 1171–1186. [Google Scholar] [CrossRef]
- Ettori, S. The physics inside the scaling relations for X-ray galaxy clusters: Gas clumpiness, gas mass fraction and slope of the pressure profile. MNRAS 2015, 446, 2629–2639. [Google Scholar] [CrossRef]
- Ettori, S.; Lovisari, L.; Sereno, M. From universal profiles to universal scaling laws in X-ray galaxy clusters. Astron. Astrophys. 2020, 644, A111. [Google Scholar] [CrossRef]
- Sarazin, C.L. X-ray emission from clusters of galaxies. Rev. Mod. Phys. 1986, 58, 1–115. [Google Scholar] [CrossRef]
- Peterson, J.R.; Fabian, A.C. X-ray spectroscopy of cooling clusters. Phys. Rep. 2006, 427, 1–39. [Google Scholar] [CrossRef]
- Kaastra, J.S.; Paerels, F.B.S.; Durret, F.; Schindler, S.; Richter, P. Thermal Radiation Processes. Space Sci. Rev. 2008, 134, 155–190. [Google Scholar] [CrossRef]
- Böhringer, H.; Werner, N. X-ray spectroscopy of galaxy clusters: Studying astrophysical processes in the largest celestial laboratories. Astron. Astrophys. Rev. 2010, 18, 127–196. [Google Scholar] [CrossRef]
- Smith, R.K.; Brickhouse, N.S.; Liedahl, D.A.; Raymond, J.C. Collisional Plasma Models with APEC/APED: Emission-Line Diagnostics of Hydrogen-like and Helium-like Ions. ApJ 2001, 556, L91–L95. [Google Scholar] [CrossRef]
- Arnaud, K.A. XSPEC: The First Ten Years. In Astronomical Data Analysis Software and Systems V; Astronomical Society of the Pacific Conference Series; Jacoby, G.H., Barnes, J., Eds.; NASA/GSFC: Greenbelt, MD, USA, 1996; Volume 101, p. 17. [Google Scholar]
- Asplund, M.; Grevesse, N.; Sauval, A.J.; Scott, P. The Chemical Composition of the Sun. Annu. Rev. Astron. Astrophys. 2009, 47, 481–522. [Google Scholar] [CrossRef]
- Vikhlinin, A.; Kravtsov, A.; Forman, W.; Jones, C.; Markevitch, M.; Murray, S.S.; Van Speybroeck, L. Chandra Sample of Nearby Relaxed Galaxy Clusters: Mass, Gas Fraction, and Mass-Temperature Relation. ApJ 2006, 640, 691–709. [Google Scholar] [CrossRef]
- Gonzalez, A.H.; Zaritsky, D.; Zabludoff, A.I. A Census of Baryons in Galaxy Clusters and Groups. ApJ 2007, 666, 147–155. [Google Scholar] [CrossRef]
- Gastaldello, F.; Buote, D.A.; Humphrey, P.J.; Zappacosta, L.; Bullock, J.S.; Brighenti, F.; Mathews, W.G. Probing the Dark Matter and Gas Fraction in Relaxed Galaxy Groups with X-Ray Observations from Chandra and XMM-Newton. ApJ 2007, 669, 158–183. [Google Scholar] [CrossRef]
- Dai, X.; Bregman, J.N.; Kochanek, C.S.; Rasia, E. On the Baryon Fractions in Clusters and Groups of Galaxies. ApJ 2010, 719, 119–125. [Google Scholar] [CrossRef]
- Gonzalez, A.H.; Sivanandam, S.; Zabludoff, A.I.; Zaritsky, D. Galaxy Cluster Baryon Fractions Revisited. ApJ 2013, 778, 14. [Google Scholar] [CrossRef]
- Lovisari, L.; Reiprich, T.H.; Schellenberger, G. Scaling properties of a complete X-ray selected galaxy group sample. Astron. Astrophys. 2015, 573, A118. [Google Scholar] [CrossRef]
- Eckert, D.; Ettori, S.; Coupon, J.; Gastaldello, F.; Pierre, M.; Melin, J.B.; Le Brun, A.M.C.; McCarthy, I.G.; Adami, C.; Chiappetti, L.; et al. The XXL Survey. XIII. Baryon content of the bright cluster sample. Astron. Astrophys. 2016, 592, A12. [Google Scholar] [CrossRef]
- Zou, S.; Maughan, B.J.; Giles, P.A.; Vikhlinin, A.; Pacaud, F.; Burenin, R.; Hornstrup, A. The X-ray luminosity-temperature relation of a complete sample of low-mass galaxy clusters. MNRAS 2016, 463, 820–831. [Google Scholar] [CrossRef]
- Rasmussen, J.; Ponman, T.J. Temperature and abundance profiles of hot gas in galaxy groups—I. Results and statistical analysis. MNRAS 2007, 380, 1554–1572. [Google Scholar] [CrossRef]
- Sun, M.; Voit, G.M.; Donahue, M.; Jones, C.; Forman, W.; Vikhlinin, A. Chandra Studies of the X-Ray Gas Properties of Galaxy Groups. ApJ 2009, 693, 1142–1172. [Google Scholar] [CrossRef]
- Mernier, F.; de Plaa, J.; Kaastra, J.S.; Zhang, Y.Y.; Akamatsu, H.; Gu, L.; Kosec, P.; Mao, J.; Pinto, C.; Reiprich, T.H.; et al. Radial metal abundance profiles in the intra-cluster medium of cool-core galaxy clusters, groups, and ellipticals. Astron. Astrophys. 2017, 603, A80. [Google Scholar] [CrossRef]
- Lovisari, L.; Reiprich, T.H. The non-uniformity of galaxy cluster metallicity profiles. MNRAS 2019, 483, 540–557. [Google Scholar] [CrossRef]
- Grevesse, N.; Sauval, A.J. Standard Solar Composition. Space Sci. Rev. 1998, 85, 161–174. [Google Scholar] [CrossRef]
- Lodders, K.; Palme, H.; Gail, H.P. Abundances of the Elements in the Solar System. arXiv 2009, arXiv:0901.1149. [Google Scholar]
- Anders, E.; Grevesse, N. Abundances of the elements: Meteoritic and solar. Geochim. Cosmochim. Acta 1989, 53, 197–214. [Google Scholar] [CrossRef]
- Lloyd-Davies, E.J.; Ponman, T.J.; Cannon, D.B. The entropy and energy of intergalactic gas in galaxy clusters. MNRAS 2000, 315, 689–702. [Google Scholar] [CrossRef]
- Ponman, T.J.; Sanderson, A.J.R.; Finoguenov, A. The Birmingham-CfA cluster scaling project—III. Entropy and similarity in galaxy systems. MNRAS 2003, 343, 331–342. [Google Scholar] [CrossRef]
- Finoguenov, A.; Ponman, T.J.; Osmond, J.P.F.; Zimer, M. XMM-Newton study of 0.012 < z < 0.024 groups—I. Overview of the IGM thermodynamics. MNRAS 2007, 374, 737–760. [Google Scholar] [CrossRef]
- Johnson, R.; Ponman, T.J.; Finoguenov, A. A statistical analysis of the Two-Dimensional XMM-Newton Group Survey: The impact of feedback on group properties. MNRAS 2009, 395, 1287–1308. [Google Scholar] [CrossRef]
- Panagoulia, E.K.; Fabian, A.C.; Sanders, J.S. A volume-limited sample of X-ray galaxy groups and clusters—I. Radial entropy and cooling time profiles. MNRAS 2014, 438, 2341–2354. [Google Scholar] [CrossRef]
- Helsdon, S.F.; Ponman, T.J. The intragroup medium in loose groups of galaxies. MNRAS 2000, 315, 356–370. [Google Scholar] [CrossRef]
- Xue, Y.J.; Wu, X.P. The LX-T, LX-σ, and σ-T Relations for Groups and Clusters of Galaxies. ApJ 2000, 538, 65–71. [Google Scholar] [CrossRef]
- Osmond, J.P.F.; Ponman, T.J. The GEMS project: X-ray analysis and statistical properties of the group sample. MNRAS 2004, 350, 1511–1535. [Google Scholar] [CrossRef]
- Shang, C.; Scharf, C. A Low-Redshift Galaxy Cluster X-Ray Temperature Function Incorporating Suzaku Data. ApJ 2009, 690, 879–890. [Google Scholar] [CrossRef]
- Eckmiller, H.J.; Hudson, D.S.; Reiprich, T.H. Testing the low-mass end of X-ray scaling relations with a sample of Chandra galaxy groups. Astron. Astrophys. 2011, 535, A105. [Google Scholar] [CrossRef]
- Ikebe, Y.; Reiprich, T.H.; Böhringer, H.; Tanaka, Y.; Kitayama, T. A new measurement of the X-ray temperature function of clusters of galaxies. Astron. Astrophys. 2002, 383, 773–790. [Google Scholar] [CrossRef]
- Stanek, R.; Evrard, A.E.; Böhringer, H.; Schuecker, P.; Nord, B. The X-Ray Luminosity-Mass Relation for Local Clusters of Galaxies. ApJ 2006, 648, 956–968. [Google Scholar] [CrossRef]
- Pacaud, F.; Pierre, M.; Adami, C.; Altieri, B.; Andreon, S.; Chiappetti, L.; Detal, A.; Duc, P.A.; Galaz, G.; Gueguen, A.; et al. The XMM-LSS survey: The Class 1 cluster sample over the initial 5 deg2 and its cosmological modelling. MNRAS 2007, 382, 1289–1308. [Google Scholar] [CrossRef]
- Schellenberger, G.; Reiprich, T.H. HICOSMO—Cosmology with a complete sample of galaxy clusters—I. Data analysis, sample selection and luminosity-mass scaling relation. MNRAS 2017, 469, 3738–3761. [Google Scholar] [CrossRef]
- Kettula, K.; Giodini, S.; van Uitert, E.; Hoekstra, H.; Finoguenov, A.; Lerchster, M.; Erben, T.; Heymans, C.; Hildebrandt, H.; Kitching, T.D.; et al. CFHTLenS: Weak lensing calibrated scaling relations for low-mass clusters of galaxies. MNRAS 2015, 451, 1460–1481. [Google Scholar] [CrossRef]
- Rasmussen, J.; Ponman, T.J.; Mulchaey, J.S.; Miles, T.A.; Raychaudhury, S. First results of the XI Groups Project: Studying an unbiased sample of galaxy groups. MNRAS 2006, 373, 653–665. [Google Scholar] [CrossRef]
- Anderson, M.E.; Gaspari, M.; White, S.D.M.; Wang, W.; Dai, X. Unifying X-ray scaling relations from galaxies to clusters. MNRAS 2015, 449, 3806–3826. [Google Scholar] [CrossRef]
- Andreon, S.; Serra, A.L.; Moretti, A.; Trinchieri, G. The amazing diversity in the hot gas content of an X-ray unbiased massive galaxy clusters sample. Astron. Astrophys. 2016, 585, A147. [Google Scholar] [CrossRef]
- Valtchanov, I.; Pierre, M.; Gastaud, R. Comparison of source detection procedures for XMM-Newton images. Astron. Astrophys. 2001, 370, 689–706. [Google Scholar] [CrossRef]
- Šuhada, R.; Song, J.; Böhringer, H.; Mohr, J.J.; Chon, G.; Finoguenov, A.; Fassbender, R.; Desai, S.; Armstrong, R.; Zenteno, A.; et al. The XMM-BCS galaxy cluster survey. I. The X-ray selected cluster catalog from the initial 6 deg2. Astron. Astrophys. 2012, 537, A39. [Google Scholar] [CrossRef]
- Xu, W.; Ramos-Ceja, M.E.; Pacaud, F.; Reiprich, T.H.; Erben, T. A new X-ray-selected sample of very extended galaxy groups from the ROSAT All-Sky Survey. Astron. Astrophys. 2018, 619, A162. [Google Scholar] [CrossRef]
- Miniati, F.; Finoguenov, A.; Silverman, J.D.; Carollo, M.; Cibinel, A.; Lilly, S.J.; Schawinski, K. The X-Ray Zurich Environmental Study (X-ZENS). II. X-Ray Observations of the Diffuse Intragroup Medium in Galaxy Groups. ApJ 2016, 819, 26. [Google Scholar] [CrossRef]
- Pearson, R.J.; Ponman, T.J.; Norberg, P.; Robotham, A.S.G.; Babul, A.; Bower, R.G.; McCarthy, I.G.; Brough, S.; Driver, S.P.; Pimbblet, K. Galaxy And Mass Assembly: Search for a population of high-entropy galaxy groups. MNRAS 2017, 469, 3489–3504. [Google Scholar] [CrossRef]
- Migkas, K.; Schellenberger, G.; Reiprich, T.H.; Pacaud, F.; Ramos-Ceja, M.E.; Lovisari, L. Probing cosmic isotropy with a new X-ray galaxy cluster sample through the LX-T scaling relation. Astron. Astrophys. 2020, 636, A15. [Google Scholar] [CrossRef]
- Schellenberger, G.; Reiprich, T.H.; Lovisari, L.; Nevalainen, J.; David, L. XMM-Newton and Chandra cross-calibration using HIFLUGCS galaxy clusters. Systematic temperature differences and cosmological impact. Astron. Astrophys. 2015, 575, A30. [Google Scholar] [CrossRef]
- Sereno, M. A Bayesian approach to linear regression in astronomy. MNRAS 2016, 455, 2149–2162. [Google Scholar] [CrossRef]
- Kettula, K.; Nevalainen, J.; Miller, E.D. Cross-calibration of Suzaku/XIS and XMM-Newton/EPIC using galaxy clusters. Astron. Astrophys. 2013, 552, A47. [Google Scholar] [CrossRef]
- Umetsu, K.; Sereno, M.; Lieu, M.; Miyatake, H.; Medezinski, E.; Nishizawa, A.J.; Giles, P.; Gastaldello, F.; McCarthy, I.G.; Kilbinger, M.; et al. Weak-lensing Analysis of X-Ray-selected XXL Galaxy Groups and Clusters with Subaru HSC Data. ApJ 2020, 890, 148. [Google Scholar] [CrossRef]
- Sereno, M.; Umetsu, K.; Ettori, S.; Eckert, D.; Gastaldello, F.; Giles, P.; Lieu, M.; Maughan, B.; Okabe, N.; Birkinshaw, M.; et al. XXL Survey groups and clusters in the Hyper Suprime-Cam Survey. Scaling relations between X-ray properties and weak lensing mass. MNRAS 2020, 492, 4528–4545. [Google Scholar] [CrossRef]
- Nevalainen, J.; David, L.; Guainazzi, M. Cross-calibrating X-ray detectors with clusters of galaxies: An IACHEC study. Astron. Astrophys. 2010, 523, A22. [Google Scholar] [CrossRef]
- Colafrancesco, S.; Giordano, F. Structure and evolution of magnetized clusters: Entropy profiles, S - T and LX - T relations. Astron. Astrophys. 2007, 466, 421–435. [Google Scholar] [CrossRef]
- Mahdavi, A.; Finoguenov, A.; Böhringer, H.; Geller, M.J.; Henry, J.P. XMM-Newton and Gemini Observations of Eight RASSCALS Galaxy Groups. ApJ 2005, 622, 187–204. [Google Scholar] [CrossRef]
- Pratt, G.W.; Arnaud, M.; Piffaretti, R.; Böhringer, H.; Ponman, T.J.; Croston, J.H.; Voit, G.M.; Borgani, S.; Bower, R.G. Gas entropy in a representative sample of nearby X-ray galaxy clusters (REXCESS): Relationship to gas mass fraction. Astron. Astrophys. 2010, 511, A85. [Google Scholar] [CrossRef]
- Mantz, A.B.; Allen, S.W.; Morris, R.G.; Schmidt, R.W. Cosmology and astrophysics from relaxed galaxy clusters—III. Thermodynamic profiles and scaling relations. MNRAS 2016, 456, 4020–4039. [Google Scholar] [CrossRef]
- Mantz, A.B.; Allen, S.W.; Morris, R.G.; von der Linden, A. Centre-excised X-ray luminosity as an efficient mass proxy for future galaxy cluster surveys. MNRAS 2018, 473, 3072–3079. [Google Scholar] [CrossRef]
- Bulbul, E.; Chiu, I.N.; Mohr, J.J.; McDonald, M.; Benson, B.; Bautz, M.W.; Bayliss, M.; Bleem, L.; Brodwin, M.; Bocquet, S.; et al. X-Ray Properties of SPT-selected Galaxy Clusters at 0.2 < z < 1.5 Observed with XMM-Newton. ApJ 2019, 871, 50. [Google Scholar] [CrossRef]
- Leauthaud, A.; Finoguenov, A.; Kneib, J.P.; Taylor, J.E.; Massey, R.; Rhodes, J.; Ilbert, O.; Bundy, K.; Tinker, J.; George, M.R.; et al. A Weak Lensing Study of X-ray Groups in the Cosmos Survey: Form and Evolution of the Mass-Luminosity Relation. ApJ 2010, 709, 97–114. [Google Scholar] [CrossRef]
- Pierre, M.; Pacaud, F.; Adami, C.; Alis, S.; Altieri, B.; Baran, N.; Benoist, C.; Birkinshaw, M.; Bongiorno, A.; Bremer, M.N.; et al. The XXL Survey. I. Scientific motivations—XMM-Newton observing plan—Follow-up observations and simulation programme. Astron. Astrophys. 2016, 592, A1. [Google Scholar] [CrossRef]
- Schaye, J.; Dalla Vecchia, C.; Booth, C.M.; Wiersma, R.P.C.; Theuns, T.; Haas, M.R.; Bertone, S.; Duffy, A.R.; McCarthy, I.G.; van de Voort, F. The physics driving the cosmic star formation history. MNRAS 2010, 402, 1536–1560. [Google Scholar] [CrossRef]
- Semboloni, E.; Hoekstra, H.; Schaye, J.; van Daalen, M.P.; McCarthy, I.G. Quantifying the effect of baryon physics on weak lensing tomography. MNRAS 2011, 417, 2020–2035. [Google Scholar] [CrossRef]
- Finoguenov, A.; Reiprich, T.H.; Böhringer, H. Details of the mass-temperature relation for clusters of galaxies. Astron. Astrophys. 2001, 368, 749–759. [Google Scholar] [CrossRef]
- Kettula, K.; Finoguenov, A.; Massey, R.; Rhodes, J.; Hoekstra, H.; Taylor, J.E.; Spinelli, P.F.; Tanaka, M.; Ilbert, O.; Capak, P.; et al. Weak Lensing Calibrated M-T Scaling Relation of Galaxy Groups in the COSMOS Fieldsstarf. ApJ 2013, 778, 74. [Google Scholar] [CrossRef]
- Spitzer, L. Physics of Fully Ionized Gases; Courier Corporation: North Chelmsford, MA, USA, 1962. [Google Scholar]
- Kravtsov, A.V.; Vikhlinin, A.; Nagai, D. A New Robust Low-Scatter X-Ray Mass Indicator for Clusters of Galaxies. ApJ 2006, 650, 128–136. [Google Scholar] [CrossRef]
- Jeltema, T.E.; Mulchaey, J.S.; Lubin, L.M.; Rosati, P.; Böhringer, H. X-Ray Properties of Intermediate-Redshift Groups of Galaxies. ApJ 2006, 649, 649–660. [Google Scholar] [CrossRef][Green Version]
- Alshino, A.; Ponman, T.; Pacaud, F.; Pierre, M. Evolution of the X-ray profiles of poor clusters from the XMM-LSS survey. MNRAS 2010, 407, 2543–2556. [Google Scholar] [CrossRef]
- Beers, T.C.; Flynn, K.; Gebhardt, K. Measures of Location and Scale for Velocities in Clusters of Galaxies—A Robust Approach. AJ 1990, 100, 32. [Google Scholar] [CrossRef]
- Ruel, J.; Bazin, G.; Bayliss, M.; Brodwin, M.; Foley, R.J.; Stalder, B.; Aird, K.A.; Armstrong, R.; Ashby, M.L.N.; Bautz, M.; et al. Optical Spectroscopy and Velocity Dispersions of Galaxy Clusters from the SPT-SZ Survey. ApJ 2014, 792, 45. [Google Scholar] [CrossRef]
- Quintana, H.; Melnick, J. The correlation between X-ray luminosity and velicity dispersion in clusters of galaxies. AJ 1982, 87, 972–979. [Google Scholar] [CrossRef]
- Mulchaey, J.S.; Zabludoff, A.I. The Properties of Poor Groups of Galaxies. II. X-Ray and Optical Comparisons. ApJ 1998, 496, 73–92. [Google Scholar] [CrossRef]
- Mahdavi, A.; Geller, M.J. The LX-σ Relation for Galaxies and Clusters of Galaxies. ApJ 2001, 554, L129–L132. [Google Scholar] [CrossRef]
- Ortiz-Gil, A.; Guzzo, L.; Schuecker, P.; Böhringer, H.; Collins, C.A. The X-ray luminosity-velocity dispersion relation in the REFLEX cluster survey. MNRAS 2004, 348, 325–332. [Google Scholar] [CrossRef][Green Version]
- Zhang, Y.Y.; Andernach, H.; Caretta, C.A.; Reiprich, T.H.; Böhringer, H.; Puchwein, E.; Sijacki, D.; Girardi, M. HIFLUGCS: Galaxy cluster scaling relations between X-ray luminosity, gas mass, cluster radius, and velocity dispersion. Astron. Astrophys. 2011, 526, A105. [Google Scholar] [CrossRef]
- Nastasi, A.; Böhringer, H.; Fassbender, R.; de Hoon, A.; Lamer, G.; Mohr, J.J.; Padilla, N.; Pratt, G.W.; Quintana, H.; Rosati, P.; et al. Kinematic analysis of a sample of X-ray luminous distant galaxy clusters. The LX-σv relation in the z > 0.6 universe. Astron. Astrophys. 2014, 564, A17. [Google Scholar] [CrossRef]
- Kirkpatrick, C.C.; Clerc, N.; Finoguenov, A.; Damsted, S.; Ider Chitham, J.; Kukkola, A.E.; Gueguen, A.; Furnell, K.; Rykoff, E.; Comparat, J.; et al. SPIDERS: An overview of the largest catalogue of spectroscopically confirmed x-ray galaxy clusters. MNRAS 2021, 503, 5763–5777. [Google Scholar] [CrossRef]
- Ponman, T.J.; Bourner, P.D.J.; Ebeling, H.; Böhringer, H. A ROSAT survey of Hickson’s compact galaxy groups. MNRAS 1996, 283, 690–708. [Google Scholar] [CrossRef][Green Version]
- Sohn, J.; Geller, M.J.; Zahid, H.J. A Spectroscopic Census of X-Ray Systems in the COSMOS Field. ApJ 2019, 880, 142. [Google Scholar] [CrossRef]
- Connelly, J.L.; Wilman, D.J.; Finoguenov, A.; Hou, A.; Mulchaey, J.S.; McGee, S.L.; Balogh, M.L.; Parker, L.C.; Saglia, R.; Henderson, R.D.E.; et al. Exploring the Diversity of Groups at 0.1 < z < 0.8 with X-Ray and Optically Selected Samples. ApJ 2012, 756, 139. [Google Scholar] [CrossRef]
- Carlberg, R.G.; Yee, H.K.C.; Morris, S.L.; Lin, H.; Sawicki, M.; Wirth, G.; Patton, D.; Shepherd, C.W.; Ellingson, E.; Schade, D. The CNOC2 field galaxy redshift survey. Philos. Trans. R. Soc. Lond. Ser. A 1999, 357, 167. [Google Scholar] [CrossRef][Green Version]
- Finoguenov, A.; Guzzo, L.; Hasinger, G.; Scoville, N.Z.; Aussel, H.; Böhringer, H.; Brusa, M.; Capak, P.; Cappelluti, N.; Comastri, A.; et al. The XMM-Newton Wide-Field Survey in the COSMOS Field: Statistical Properties of Clusters of Galaxies. ApJS 2007, 172, 182–195. [Google Scholar] [CrossRef]
- Scoville, N.; Aussel, H.; Brusa, M.; Capak, P.; Carollo, C.M.; Elvis, M.; Giavalisco, M.; Guzzo, L.; Hasinger, G.; Impey, C.; et al. The Cosmic Evolution Survey (COSMOS): Overview. ApJS 2007, 172, 1–8. [Google Scholar] [CrossRef]
- George, M.R.; Leauthaud, A.; Bundy, K.; Finoguenov, A.; Tinker, J.; Lin, Y.T.; Mei, S.; Kneib, J.P.; Aussel, H.; Behroozi, P.S.; et al. Galaxies in X-Ray Groups. I. Robust Membership Assignment and the Impact of Group Environments on Quenching. ApJ 2011, 742, 125. [Google Scholar] [CrossRef]
- Vajgel, B.; Jones, C.; Lopes, P.A.A.; Forman, W.R.; Murray, S.S.; Goulding, A.; Andrade-Santos, F. X-Ray-selected Galaxy Groups in Boötes. ApJ 2014, 794, 88. [Google Scholar] [CrossRef]
- Murray, S.S.; Kenter, A.; Forman, W.R.; Jones, C.; Green, P.J.; Kochanek, C.S.; Vikhlinin, A.; Fabricant, D.; Fazio, G.; Brand, K.; et al. XBootes: An X-Ray Survey of the NDWFS Bootes Field. I. Overview and Initial Results. ApJS 2005, 161, 1–8. [Google Scholar] [CrossRef]
- Wilson, S.; Hilton, M.; Rooney, P.J.; Caldwell, C.; Kay, S.T.; Collins, C.A.; McCarthy, I.G.; Romer, A.K.; Bermeo, A.; Bernstein, R.; et al. The XMM Cluster Survey: Evolution of the velocity dispersion-temperature relation over half a Hubble time. MNRAS 2016, 463, 413–428. [Google Scholar] [CrossRef][Green Version]
- Romer, A.K.; Viana, P.T.P.; Liddle, A.R.; Mann, R.G. A Serendipitous Galaxy Cluster Survey with XMM: Expected Catalogue Properties and Scientific Applications. Astrophys. J. 1999. [Google Scholar]
- Farahi, A.; Guglielmo, V.; Evrard, A.E.; Poggianti, B.M.; Adami, C.; Ettori, S.; Gastaldello, F.; Giles, P.A.; Maughan, B.J.; Rapetti, D.; et al. The XXL Survey: XXIII. The Mass Scale of XXL Clusters from Ensemble Spectroscopy. Astron. Astrophys. 2018, 620, A8. [Google Scholar] [CrossRef]
- Adami, C.; Giles, P.; Koulouridis, E.; Pacaud, F.; Caretta, C.A.; Pierre, M.; Eckert, D.; Ramos-Ceja, M.E.; Gastaldello, F.; Fotopoulou, S.; et al. The XXL Survey. XX. The 365 cluster catalogue. Astron. Astrophys. 2018, 620, A5. [Google Scholar] [CrossRef]
- Mamon, G. Dynamical Theory of groups and Clusters of Galaxies. arXiv 1993, arXiv:astro-ph/9308032. [Google Scholar]
- Mamon, G.A.; Biviano, A.; Boué, G. MAMPOSSt: Modelling Anisotropy and Mass Profiles of Observed Spherical Systems—I. Gaussian 3D velocities. MNRAS 2013, 429, 3079–3098. [Google Scholar] [CrossRef]
- Goulding, A.D.; Greene, J.E.; Ma, C.P.; Veale, M.; Bogdan, A.; Nyland, K.; Blakeslee, J.P.; McConnell, N.J.; Thomas, J. The MASSIVE Survey. IV. The X-ray Halos of the Most Massive Early-type Galaxies in the Nearby Universe. ApJ 2016, 826, 167. [Google Scholar] [CrossRef]
- Ma, C.P.; Greene, J.E.; McConnell, N.; Janish, R.; Blakeslee, J.P.; Thomas, J.; Murphy, J.D. The MASSIVE Survey. I. A Volume-limited Integral-field Spectroscopic Study of the Most Massive Early-type Galaxies within 108 Mpc. ApJ 2014, 795, 158. [Google Scholar] [CrossRef]
- Le Brun, A.M.C.; McCarthy, I.G.; Schaye, J.; Ponman, T.J. The scatter and evolution of the global hot gas properties of simulated galaxy cluster populations. MNRAS 2017, 466, 4442–4469. [Google Scholar] [CrossRef]
- Farahi, A.; Evrard, A.E.; McCarthy, I.; Barnes, D.J.; Kay, S.T. Localized massive halo properties in BAHAMAS and MACSIS simulations: Scalings, lognormality, and covariance. MNRAS 2018, 478, 2618–2632. [Google Scholar] [CrossRef]
- Kar Chowdhury, R.; Chatterjee, S.; Lonappan, A.I.; Khandai, N.; Di Matteo, T. Cosmological Simulation of Galaxy Groups and Clusters. I. Global Effect of Feedback from Active Galactic Nuclei. ApJ 2020, 889, 60. [Google Scholar] [CrossRef]
- Helsdon, S.F.; Ponman, T.J.; Mulchaey, J.S. Chandra Observations of Low Velocity Dispersion Groups. ApJ 2005, 618, 679–691. [Google Scholar] [CrossRef]
- Mantz, A.; Allen, S.W.; Ebeling, H.; Rapetti, D.; Drlica-Wagner, A. The observed growth of massive galaxy clusters—II. X-ray scaling relations. MNRAS 2010, 406, 1773–1795. [Google Scholar] [CrossRef]
- Giles, P.A.; Maughan, B.J.; Dahle, H.; Bonamente, M.; Landry, D.; Jones, C.; Joy, M.; Murray, S.S.; van der Pyl, N. Chandra measurements of a complete sample of X-ray luminous galaxy clusters: The luminosity-mass relation. MNRAS 2017, 465, 858–884. [Google Scholar] [CrossRef]
- Ettori, S.; Morandi, A.; Tozzi, P.; Balestra, I.; Borgani, S.; Rosati, P.; Lovisari, L.; Terenziani, F. The cluster gas mass fraction as a cosmological probe: A revised study. Astron. Astrophys. 2009, 501, 61–73. [Google Scholar] [CrossRef]
- Mantz, A.B.; Allen, S.W.; Morris, R.G.; Rapetti, D.A.; Applegate, D.E.; Kelly, P.L.; von der Linden, A.; Schmidt, R.W. Cosmology and astrophysics from relaxed galaxy clusters—II. Cosmological constraints. MNRAS 2014, 440, 2077–2098. [Google Scholar] [CrossRef]
- Lin, Y.T.; Mohr, J.J.; Stanford, S.A. Near-Infrared Properties of Galaxy Clusters: Luminosity as a Binding Mass Predictor and the State of Cluster Baryons. ApJ 2003, 591, 749–763. [Google Scholar] [CrossRef]
- Behroozi, P.S.; Conroy, C.; Wechsler, R.H. A Comprehensive Analysis of Uncertainties Affecting the Stellar Mass-Halo Mass Relation for 0 < z < 4. ApJ 2010, 717, 379–403. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Laganá, T.F.; Pierini, D.; Puchwein, E.; Schneider, P.; Reiprich, T.H. Star-formation efficiency and metal enrichment of the intracluster medium in local massive clusters of galaxies. Astron. Astrophys. 2011, 535, A78. [Google Scholar] [CrossRef]
- Leauthaud, A.; George, M.R.; Behroozi, P.S.; Bundy, K.; Tinker, J.; Wechsler, R.H.; Conroy, C.; Finoguenov, A.; Tanaka, M. The Integrated Stellar Content of Dark Matter Halos. ApJ 2012, 746, 95. [Google Scholar] [CrossRef]
- Laganá, T.F.; Martinet, N.; Durret, F.; Lima Neto, G.B.; Maughan, B.; Zhang, Y.Y. A comprehensive picture of baryons in groups and clusters of galaxies. Astron. Astrophys. 2013, 555, A66. [Google Scholar] [CrossRef]
- Chiu, I.; Mohr, J.J.; McDonald, M.; Bocquet, S.; Desai, S.; Klein, M.; Israel, H.; Ashby, M.L.N.; Stanford, A.; Benson, B.A.; et al. Baryon content in a sample of 91 galaxy clusters selected by the South Pole Telescope at 0.2 < z < 1.25. MNRAS 2018, 478, 3072–3099. [Google Scholar] [CrossRef]
- Decker, B.; Brodwin, M.; Abdulla, Z.; Gonzalez, A.H.; Marrone, D.P.; O’Donnell, C.; Stanford, S.A.; Wylezalek, D.; Carlstrom, J.E.; Eisenhardt, P.R.M.; et al. The Massive and Distant Clusters of WISE Survey. VI. Stellar Mass Fractions of a Sample of High-redshift Infrared-selected Clusters. ApJ 2019, 878, 72. [Google Scholar] [CrossRef]
- Vikhlinin, A.; McNamara, B.R.; Forman, W.; Jones, C.; Quintana, H.; Hornstrup, A. A Catalog of 200 Galaxy Clusters Serendipitously Detected in the ROSAT PSPC Pointed Observations. ApJ 1998, 502, 558–581. [Google Scholar] [CrossRef]
- Lilly, S.J.; Le Fèvre, O.; Renzini, A.; Zamorani, G.; Scodeggio, M.; Contini, T.; Carollo, C.M.; Hasinger, G.; Kneib, J.P.; Iovino, A.; et al. zCOSMOS: A Large VLT/VIMOS Redshift Survey Covering 0 < z < 3 in the COSMOS Field. ApJS 2007, 172, 70–85. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Structure of Cold Dark Matter Halos. ApJ 1996, 462, 563. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. A Universal Density Profile from Hierarchical Clustering. ApJ 1997, 490, 493–508. [Google Scholar] [CrossRef]
- Chiu, I.; Saro, A.; Mohr, J.; Desai, S.; Bocquet, S.; Capasso, R.; Gangkofner, C.; Gupta, N.; Liu, J. Stellar mass to halo mass scaling relation for X-ray-selected low-mass galaxy clusters and groups out to redshift z ≈ 1. MNRAS 2016, 458, 379–393. [Google Scholar] [CrossRef]
- Liu, J.; Mohr, J.; Saro, A.; Aird, K.A.; Ashby, M.L.N.; Bautz, M.; Bayliss, M.; Benson, B.A.; Bleem, L.E.; Bocquet, S.; et al. Analysis of Sunyaev-Zel’dovich effect mass-observable relations using South Pole Telescope observations of an X-ray selected sample of low-mass galaxy clusters and groups. MNRAS 2015, 448, 2085–2099. [Google Scholar] [CrossRef]
- Kravtsov, A.V.; Vikhlinin, A.A.; Meshcheryakov, A.V. Stellar Mass—Halo Mass Relation and Star Formation Efficiency in High-Mass Halos. Astron. Lett. 2018, 44, 8–34. [Google Scholar] [CrossRef]
- Pillepich, A.; Nelson, D.; Hernquist, L.; Springel, V.; Pakmor, R.; Torrey, P.; Weinberger, R.; Genel, S.; Naiman, J.P.; Marinacci, F.; et al. First results from the IllustrisTNG simulations: The stellar mass content of groups and clusters of galaxies. MNRAS 2018, 475, 648–675. [Google Scholar] [CrossRef]
- Ziparo, F.; Smith, G.P.; Mulroy, S.L.; Lieu, M.; Willis, J.P.; Hudelot, P.; McGee, S.L.; Fotopoulou, S.; Lidman, C.; Lavoie, S.; et al. The XXL Survey. X. K-band luminosity—Weak-lensing mass relation for groups and clusters of galaxies. Astron. Astrophys. 2016, 592, A9. [Google Scholar] [CrossRef][Green Version]
- Muzzin, A.; Yee, H.K.C.; Hall, P.B.; Lin, H. Near-Infrared Properties of Moderate-Redshift Galaxy Clusters. II. Halo Occupation Number, Mass-to-Light Ratios, and Ωm. ApJ 2007, 663, 150–163. [Google Scholar] [CrossRef]
- Gaspari, M.; Ruszkowski, M.; Oh, S.P. Chaotic cold accretion on to black holes. MNRAS 2013, 432, 3401–3422. [Google Scholar] [CrossRef]
- Prasad, D.; Sharma, P.; Babul, A. Cool Core Cycles: Cold Gas and AGN Jet Feedback in Cluster Cores. ApJ 2015, 811, 108. [Google Scholar] [CrossRef]
- Voit, G.M.; Meece, G.; Li, Y.; O’Shea, B.W.; Bryan, G.L.; Donahue, M. A Global Model for Circumgalactic and Cluster-core Precipitation. ApJ 2017, 845, 80. [Google Scholar] [CrossRef]
- Temi, P.; Amblard, A.; Gitti, M.; Brighenti, F.; Gaspari, M.; Mathews, W.G.; David, L. ALMA Observations of Molecular Clouds in Three Group-centered Elliptical Galaxies: NGC 5846, NGC 4636, and NGC 5044. ApJ 2018, 858, 17. [Google Scholar] [CrossRef]
- Tremblay, G.R.; Combes, F.; Oonk, J.B.R.; Russell, H.R.; McDonald, M.A.; Gaspari, M.; Husemann, B.; Nulsen, P.E.J.; McNamara, B.R.; Hamer, S.L.; et al. A Galaxy-scale Fountain of Cold Molecular Gas Pumped by a Black Hole. ApJ 2018, 865, 13. [Google Scholar] [CrossRef]
- Gaspari, M.; McDonald, M.; Hamer, S.L.; Brighenti, F.; Temi, P.; Gendron-Marsolais, M.; Hlavacek-Larrondo, J.; Edge, A.C.; Werner, N.; Tozzi, P.; et al. Shaken Snow Globes: Kinematic Tracers of the Multiphase Condensation Cascade in Massive Galaxies, Groups, and Clusters. ApJ 2018, 854, 167. [Google Scholar] [CrossRef]
- Rose, T.; Edge, A.C.; Combes, F.; Gaspari, M.; Hamer, S.; Nesvadba, N.; Peck, A.B.; Sarazin, C.; Tremblay, G.R.; Baum, S.A.; et al. Constraining cold accretion on to supermassive black holes: Molecular gas in the cores of eight brightest cluster galaxies revealed by joint CO and CN absorption. MNRAS 2019, 489, 349–365. [Google Scholar] [CrossRef]
- Storchi-Bergmann, T.; Schnorr-Müller, A. Observational constraints on the feeding of supermassive black holes. Nat. Astron. 2019, 3, 48–61. [Google Scholar] [CrossRef]
- Tombesi, F.; Cappi, M.; Reeves, J.N.; Nemmen, R.S.; Braito, V.; Gaspari, M.; Reynolds, C.S. Unification of X-ray winds in Seyfert galaxies: From ultra-fast outflows to warm absorbers. MNRAS 2013, 430, 1102–1117. [Google Scholar] [CrossRef]
- Sa̧dowski, A.; Gaspari, M. Kinetic and radiative power from optically thin accretion flows. MNRAS 2017, 468, 1398–1404. [Google Scholar] [CrossRef]
- Fiore, F.; Feruglio, C.; Shankar, F.; Bischetti, M.; Bongiorno, A.; Brusa, M.; Carniani, S.; Cicone, C.; Duras, F.; Lamastra, A.; et al. AGN wind scaling relations and the co-evolution of black holes and galaxies. Astron. Astrophys. 2017, 601, A143. [Google Scholar] [CrossRef]
- McNamara, B.R.; Nulsen, P.E.J. Mechanical feedback from active galactic nuclei in galaxies, groups and clusters. New J. Phys. 2012, 14, 055023. [Google Scholar] [CrossRef]
- Fabian, A.C. Observational Evidence of Active Galactic Nuclei Feedback. Annu. Rev. Astron. Astrophys. 2012, 50, 455–489. [Google Scholar] [CrossRef]
- Gitti, M.; Brighenti, F.; McNamara, B.R. Evidence for AGN Feedback in Galaxy Clusters and Groups. Adv. Astronomy 2012, 2012, 1–24. [Google Scholar] [CrossRef]
- Brighenti, F.; Mathews, W.G.; Temi, P. Hot Gaseous Atmospheres in Galaxy Groups and Clusters Are Both Heated and Cooled by X-Ray Cavities. ApJ 2015, 802, 118. [Google Scholar] [CrossRef]
- Gaspari, M. Shaping the X-ray spectrum of galaxy clusters with AGN feedback and turbulence. MNRAS 2015, 451, L60–L64. [Google Scholar] [CrossRef]
- Liu, W.; Sun, M.; Nulsen, P.; Clarke, T.; Sarazin, C.; Forman, W.; Gaspari, M.; Giacintucci, S.; Lal, D.V.; Edge, T. AGN feedback in galaxy group 3C 88: Cavities, shock, and jet reorientation. MNRAS 2019, 484, 3376–3392. [Google Scholar] [CrossRef]
- Yang, H.Y.K.; Gaspari, M.; Marlow, C. The Impact of Radio AGN Bubble Composition on the Dynamics and Thermal Balance of the Intracluster Medium. ApJ 2019, 871, 6. [Google Scholar] [CrossRef]
- Wittor, D.; Gaspari, M. Dissecting the turbulent weather driven by mechanical AGN feedback. MNRAS 2020, 498, 4983–5002. [Google Scholar] [CrossRef]
- Voit, G.M.; Bryan, G.L.; Prasad, D.; Frisbie, R.; Li, Y.; Donahue, M.; O’Shea, B.W.; Sun, M.; Werner, N. A Black Hole Feedback Valve in Massive Galaxies. ApJ 2020, 899, 70. [Google Scholar] [CrossRef]
- Kormendy, J.; Ho, L.C. Coevolution (Or Not) of Supermassive Black Holes and Host Galaxies. Annu. Rev. Astron. Astrophys. 2013, 51, 511–653. [Google Scholar] [CrossRef]
- Saglia, R.P.; Opitsch, M.; Erwin, P.; Thomas, J.; Beifiori, A.; Fabricius, M.; Mazzalay, X.; Nowak, N.; Rusli, S.P.; Bender, R. The SINFONI Black Hole Survey: The Black Hole Fundamental Plane Revisited and the Paths of (Co)evolution of Supermassive Black Holes and Bulges. ApJ 2016, 818, 47. [Google Scholar] [CrossRef]
- Bondi, H. On spherically symmetrical accretion. MNRAS 1952, 112, 195. [Google Scholar] [CrossRef]
- Narayan, R.; Fabian, A.C. Bondi flow from a slowly rotating hot atmosphere. MNRAS 2011, 415, 3721–3730. [Google Scholar] [CrossRef]
- Voit, G.M. A Role for Turbulence in Circumgalactic Precipitation. ApJ 2018, 868, 102. [Google Scholar] [CrossRef]
- Olivares, V.; Salome, P.; Combes, F.; Hamer, S.; Guillard, P.; Lehnert, M.D.; Polles, F.L.; Beckmann, R.S.; Dubois, Y.; Donahue, M.; et al. Ubiquitous cold and massive filaments in cool core clusters. Astron. Astrophys. 2019, 631, A22. [Google Scholar] [CrossRef]
- Bassini, L.; Rasia, E.; Borgani, S.; Ragone-Figueroa, C.; Biffi, V.; Dolag, K.; Gaspari, M.; Granato, G.L.; Murante, G.; Taffoni, G.; et al. Black hole mass of central galaxies and cluster mass correlation in cosmological hydro-dynamical simulations. Astron. Astrophys. 2019, 630, A144. [Google Scholar] [CrossRef]
- Truong, N.; Pillepich, A.; Werner, N. Correlations between supermassive black holes and hot gas atmospheres in IllustrisTNG and X-ray observations. MNRAS 2021, 501, 2210–2230. [Google Scholar] [CrossRef]
- Gaspari, M.; Tombesi, F.; Cappi, M. Linking macro-, meso- and microscales in multiphase AGN feeding and feedback. Nature Astronomy 2020, 4, 10–13. [Google Scholar] [CrossRef]
- Kravtsov, A.V.; Borgani, S. Formation of Galaxy Clusters. Annu. Rev. Astron. Astrophys. 2012, 50, 353–409. [Google Scholar] [CrossRef]
- Tremmel, M.; Karcher, M.; Governato, F.; Volonteri, M.; Quinn, T.R.; Pontzen, A.; Anderson, L.; Bellovary, J. The Romulus cosmological simulations: A physical approach to the formation, dynamics and accretion models of SMBHs. MNRAS 2017, 470, 1121–1139. [Google Scholar] [CrossRef]
- Babyk, I.V.; McNamara, B.R.; Nulsen, P.E.J.; Russell, H.R.; Vantyghem, A.N.; Hogan, M.T.; Pulido, F.A. A Universal Entropy Profile for the Hot Atmospheres of Galaxies and Clusters within R 2500. ApJ 2018, 862, 39. [Google Scholar] [CrossRef]
- Planelles, S.; Fabjan, D.; Borgani, S.; Murante, G.; Rasia, E.; Biffi, V.; Truong, N.; Ragone-Figueroa, C.; Granato, G.L.; Dolag, K.; et al. Pressure of the hot gas in simulations of galaxy clusters. MNRAS 2017, 467, 3827–3847. [Google Scholar] [CrossRef]
- Weinberger, R.; Springel, V.; Pakmor, R.; Nelson, D.; Genel, S.; Pillepich, A.; Vogelsberger, M.; Marinacci, F.; Naiman, J.; Torrey, P.; et al. Supermassive black holes and their feedback effects in the IllustrisTNG simulation. MNRAS 2018, 479, 4056–4072. [Google Scholar] [CrossRef]
- Mulchaey, J.S.; Davis, D.S.; Mushotzky, R.F.; Burstein, D. An X-Ray Atlas of Groups of Galaxies. ApJS 2003, 145, 39–64. [Google Scholar] [CrossRef]
- Maughan, B.J.; Giles, P.A.; Randall, S.W.; Jones, C.; Forman, W.R. Self-similar scaling and evolution in the galaxy cluster X-ray luminosity-temperature relation. MNRAS 2012, 421, 1583–1602. [Google Scholar] [CrossRef]
- Predehl, P.; Andritschke, R.; Arefiev, V.; Babyshkin, V.; Batanov, O.; Becker, W.; Böhringer, H.; Bogomolov, A.; Boller, T.; Borm, K.; et al. The eROSITA X-ray telescope on SRG. arXiv 2020, arXiv:2010.03477. [Google Scholar] [CrossRef]
- Clerc, N.; Ramos-Ceja, M.E.; Ridl, J.; Lamer, G.; Brunner, H.; Hofmann, F.; Comparat, J.; Pacaud, F.; Käfer, F.; Reiprich, T.H.; et al. Synthetic simulations of the extragalactic sky seen by eROSITA. I. Pre-launch selection functions from Monte-Carlo simulations. Astron. Astrophys. 2018, 617, A92. [Google Scholar] [CrossRef]
- Käfer, F.; Finoguenov, A.; Eckert, D.; Clerc, N.; Ramos-Ceja, M.E.; Sanders, J.S.; Ghirardini, V. Toward the low-scatter selection of X-ray clusters. Galaxy cluster detection with eROSITA through cluster outskirts. Astron. Astrophys. 2020, 634, A8. [Google Scholar] [CrossRef]
- Merloni, A.; Predehl, P.; Becker, W.; Böhringer, H.; Boller, T.; Brunner, H.; Brusa, M.; Dennerl, K.; Freyberg, M.; Friedrich, P.; et al. eROSITA Science Book: Mapping the Structure of the Energetic Universe. arXiv 2012, arXiv:1209.3114. [Google Scholar]
- Pillepich, A.; Porciani, C.; Reiprich, T.H. The X-ray cluster survey with eRosita: Forecasts for cosmology, cluster physics and primordial non-Gaussianity. MNRAS 2012, 422, 44–69. [Google Scholar] [CrossRef]
- Borm, K.; Reiprich, T.H.; Mohammed, I.; Lovisari, L. Constraining galaxy cluster temperatures and redshifts with eROSITA survey data. Astron. Astrophys. 2014, 567, A65. [Google Scholar] [CrossRef]
- Zandanel, F.; Fornasa, M.; Prada, F.; Reiprich, T.H.; Pacaud, F.; Klypin, A. MultiDark clusters: Galaxy cluster mock light-cones, eROSITA, and the cluster power spectrum. MNRAS 2018, 480, 987–1005. [Google Scholar] [CrossRef]
- Pillepich, A.; Reiprich, T.H.; Porciani, C.; Borm, K.; Merloni, A. Forecasts on dark energy from the X-ray cluster survey with eROSITA: Constraints from counts and clustering. MNRAS 2018, 481, 613–626. [Google Scholar] [CrossRef]
- Pointecouteau, E.; Reiprich, T.H.; Adami, C.; Arnaud, M.; Biffi, V.; Borgani, S.; Borm, K.; Bourdin, H.; Brueggen, M.; Bulbul, E.; et al. The Hot and Energetic Universe: The evolution of galaxy groups and clusters. arXiv 2013, arXiv:1306.2319. [Google Scholar]
- Ettori, S.; Pratt, G.W.; de Plaa, J.; Eckert, D.; Nevalainen, J.; Battistelli, E.S.; Borgani, S.; Croston, J.H.; Finoguenov, A.; Kaastra, J.; et al. The Hot and Energetic Universe: The astrophysics of galaxy groups and clusters. arXiv 2013, arXiv:1306.2322. [Google Scholar]
- Croston, J.H.; Sanders, J.S.; Heinz, S.; Hardcastle, M.J.; Zhuravleva, I.; Bîrzan, L.; Bower, R.G.; Brüggen, M.; Churazov, E.; Edge, A.C.; et al. The Hot and Energetic Universe: AGN feedback in galaxy clusters and groups. arXiv 2013, arXiv:1306.2323. [Google Scholar]
- Cucchetti, E.; Pointecouteau, E.; Peille, P.; Clerc, N.; Rasia, E.; Biffi, V.; Borgani, S.; Tornatore, L.; Dolag, K.; Roncarelli, M.; et al. Athena X-IFU synthetic observations of galaxy clusters to probe the chemical enrichment of the Universe. Astron. Astrophys. 2018, 620, A173. [Google Scholar] [CrossRef]
- Roncarelli, M.; Gaspari, M.; Ettori, S.; Biffi, V.; Brighenti, F.; Bulbul, E.; Clerc, N.; Cucchetti, E.; Pointecouteau, E.; Rasia, E. Measuring turbulence and gas motions in galaxy clusters via synthetic Athena X-IFU observations. Astron. Astrophys. 2018, 618, A39. [Google Scholar] [CrossRef]
- Mernier, F.; Cucchetti, E.; Tornatore, L.; Biffi, V.; Pointecouteau, E.; Clerc, N.; Peille, P.; Rasia, E.; Barret, D.; Borgani, S.; et al. Constraining the origin and models of chemical enrichment in galaxy clusters using the Athena X-IFU. Astron. Astrophys. 2020, 642, A90. [Google Scholar] [CrossRef]
- Marchesi, S.; Gilli, R.; Lanzuisi, G.; Dauser, T.; Ettori, S.; Vito, F.; Cappelluti, N.; Comastri, A.; Mushotzky, R.; Ptak, A.; et al. Mock catalogs for the extragalactic X-ray sky: Simulating AGN surveys with ATHENA and with the AXIS probe. Astron. Astrophys. 2020, 642, A184. [Google Scholar] [CrossRef]
- Benson, B.A.; Ade, P.A.R.; Ahmed, Z.; Allen, S.W.; Arnold, K.; Austermann, J.E.; Bender, A.N.; Bleem, L.E.; Carlstrom, J.E.; Chang, C.L.; et al. SPT-3G: A next-generation cosmic microwave background polarization experiment on the South Pole telescope. In Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VII; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; Holland, W.S., Zmuidzinas, J., Eds.; International Society for Optics and Photonics: London, UK, 2014; Volume 9153. [Google Scholar] [CrossRef]
- Sartoris, B.; Biviano, A.; Fedeli, C.; Bartlett, J.G.; Borgani, S.; Costanzi, M.; Giocoli, C.; Moscardini, L.; Weller, J.; Ascaso, B.; et al. Next generation cosmology: Constraints from the Euclid galaxy cluster survey. MNRAS 2016, 459, 1764–1780. [Google Scholar] [CrossRef]
- Finoguenov, A.; Merloni, A.; Comparat, J.; Nandra, K.; Salvato, M.; Tempel, E.; Raichoor, A.; Richard, J.; Kneib, J.P.; Pillepich, A.; et al. 4MOST Consortium Survey 5: eROSITA Galaxy Cluster Redshift Survey. Messenger 2019, 175, 39–41. [Google Scholar] [CrossRef]
- Driver, S.P.; Liske, J.; Davies, L.J.M.; Robotham, A.S.G.; Baldry, I.K.; Brown, M.J.I.; Cluver, M.; Kuijken, K.; Loveday, J.; McMahon, R.; et al. 4MOST Consortium Survey 7: Wide-Area VISTA Extragalactic Survey (WAVES). Messenger 2019, 175, 46–49. [Google Scholar] [CrossRef]
- Zheng, Y.L.; Shen, S.Y. Compact Groups of Galaxies in Sloan Digital Sky Survey and LAMOST Spectral Survey. II. Dynamical Properties of Isolated and Embedded Groups. ApJ 2021, 911, 105. [Google Scholar] [CrossRef]
- Balestra, I.; Tozzi, P.; Ettori, S.; Rosati, P.; Borgani, S.; Mainieri, V.; Norman, C.; Viola, M. Tracing the evolution in the iron content of the intra-cluster medium. Astron. Astrophys. 2007, 462, 429–442. [Google Scholar] [CrossRef]
| 1 | Three main processes contribute to the X-ray emission: thermal bremsstrahlung (due to the deflection of a free electron by the electric field of a ion), recombination (due to the capture of an electron by an ion), and two-photon decay (due to the changing of the quantum level of an electron in an ion). See details in the reviews from, e.g., Sarazin [65], Peterson and Fabian [66], Kaastra et al. [67], and Böhringer and Werner [68]. |
| 2 | http://www.mpe.mpg.de/erosita/, accessed on 3 May 2021. |
| 3 | https://www.the-athena-x-ray-observatory.eu/, accessed on 3 May 2021. |
| 4 | https://www.lynxobservatory.com/, accessed on 3 May 2021. |
| 5 | http://axis.astro.umd.edu, accessed on 3 May 2021. |
| 6 | https://pole.uchicago.edu/, accessed on 3 May 2021. |
| 7 | https://www.euclid-ec.org/, accessed on 3 May 2021. |
| 8 | https://roman.gsfc.nasa.gov/, accessed on 3 May 2021. |
| 9 | https://www.lsst.org, accessed on 3 May 2021. |
| 10 | https://www.4most.eu/cms/, accessed on 3 May 2021. |
| 11 | https://www.darkenergysurvey.org/, accessed on 3 May 2021. |
| 12 | https://www.darkenergysurvey.org/, accessed on 3 May 2021. |

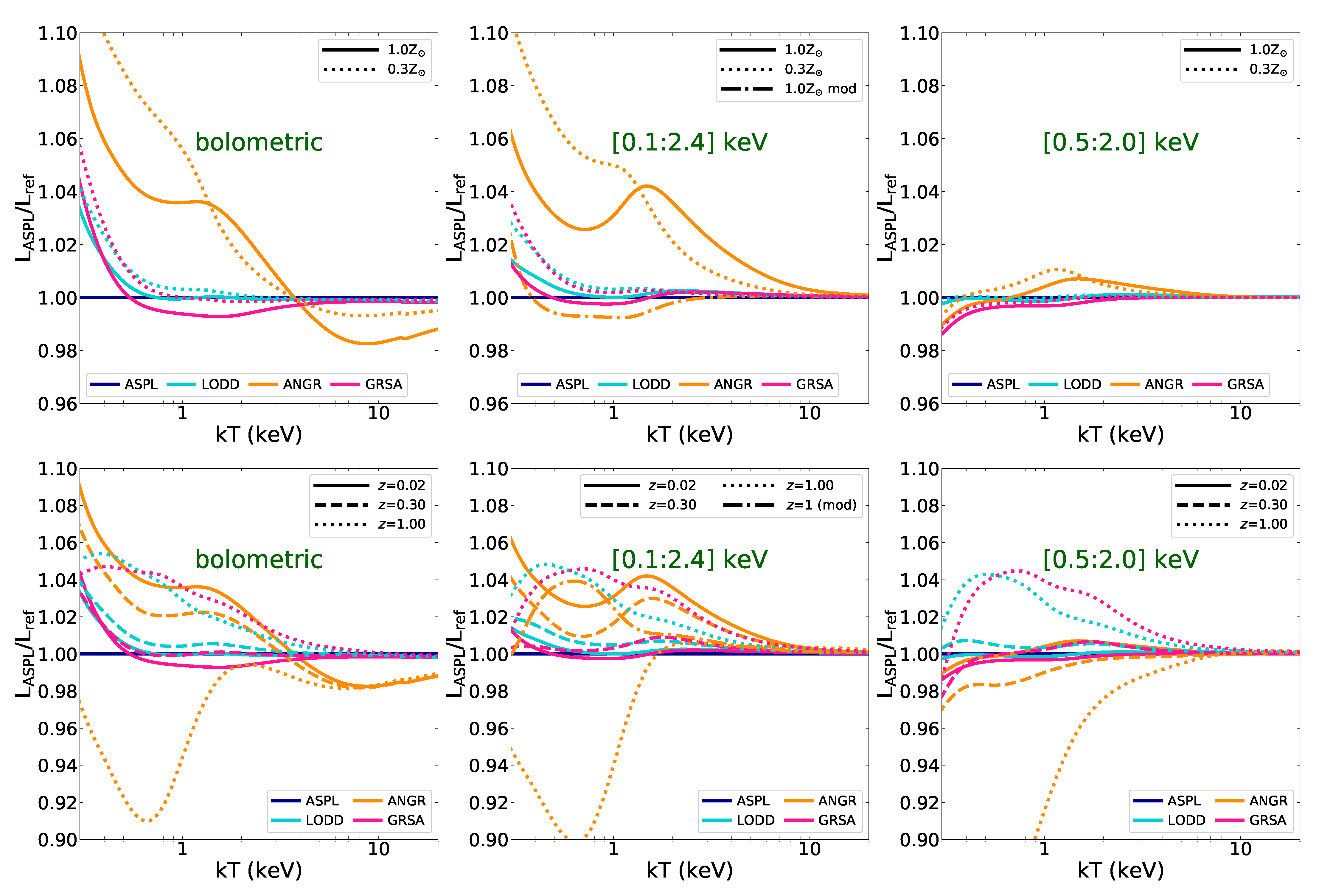

| E Band | T Range | Slope (Z = 0.3Z) | Slope (Z = 0.5Z) | Slope (Z = 1.0Z) |
|---|---|---|---|---|
| bol | 0.4−0.7 | +0.20 | +0.16 | +0.11 |
| 0.4–2.0 | −0.00 | −0.14 | −0.34 | |
| 0.4–3.0 | +0.06 | −0.07 | −0.26 | |
| 0.4–10.0 | +0.20 | +0.11 | −0.03 | |
| 0.7–2.0 | −0.11 | −0.30 | −0.58 | |
| 0.7–3.0 | +0.01 | −0.15 | −0.40 | |
| 0.7–10.0 | +0.20 | +0.10 | −0.06 | |
| 2.0–10.0 | +0.40 | +0.36 | +0.28 | |
| 3.0–10.0 | +0.43 | +0.41 | +0.35 | |
| 0.1–2.4 | 0.4−0.7 | +0.44 | +0.42 | +0.39 |
| 0.4–2.0 | −0.04 | −0.19 | −0.42 | |
| 0.4–3.0 | −0.04 | −0.18 | −0.39 | |
| 0.4–10.0 | −0.06 | −0.16 | −0.31 | |
| 0.7–2.0 | −0.29 | −0.52 | −0.84 | |
| 0.7–3.0 | −0.22 | −0.40 | −0.68 | |
| 0.7–10.0 | −0.16 | −0.27 | −0.45 | |
| 2.0–10.0 | −0.08 | −0.12 | −0.20 | |
| 3.0–10.0 | −0.10 | −0.12 | −0.17 | |
| 0.5–2 | 0.4−0.7 | +0.63 | +0.56 | +0.50 |
| 0.4–2.0 | −0.03 | −0.23 | −0.48 | |
| 0.4–3.0 | −0.02 | −0.21 | −0.45 | |
| 0.4–10.0 | −0.04 | −0.17 | −0.35 | |
| 0.7–2.0 | −0.38 | −0.65 | –1.00 | |
| 0.7–3.0 | −0.27 | −0.50 | −0.81 | |
| 0.7–10.0 | −0.18 | −0.32 | −0.52 | |
| 2.0–10.0 | −0.06 | −0.11 | −0.22 | |
| 3.0–10.0 | −0.07 | −0.11 | −0.18 |
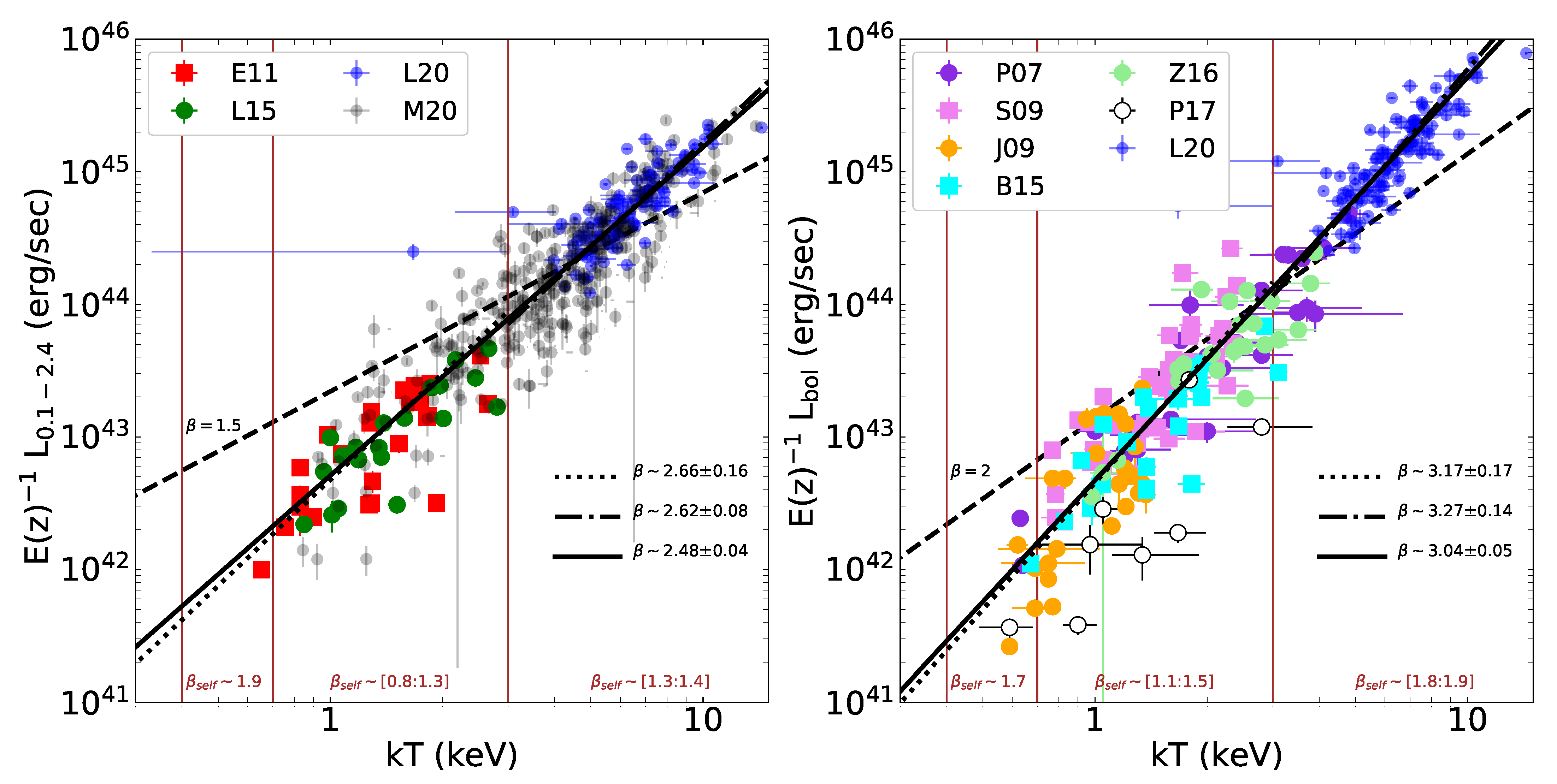
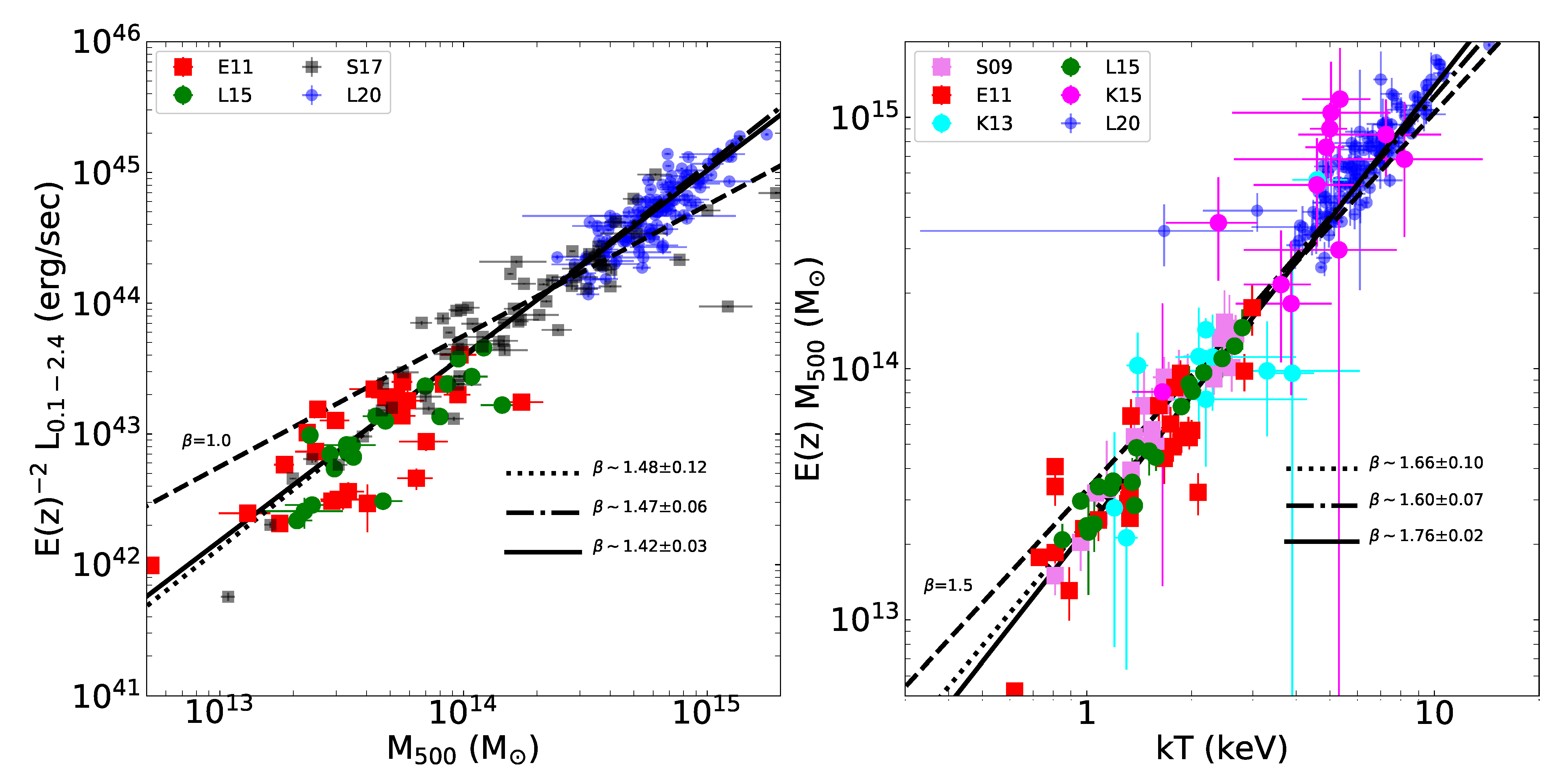
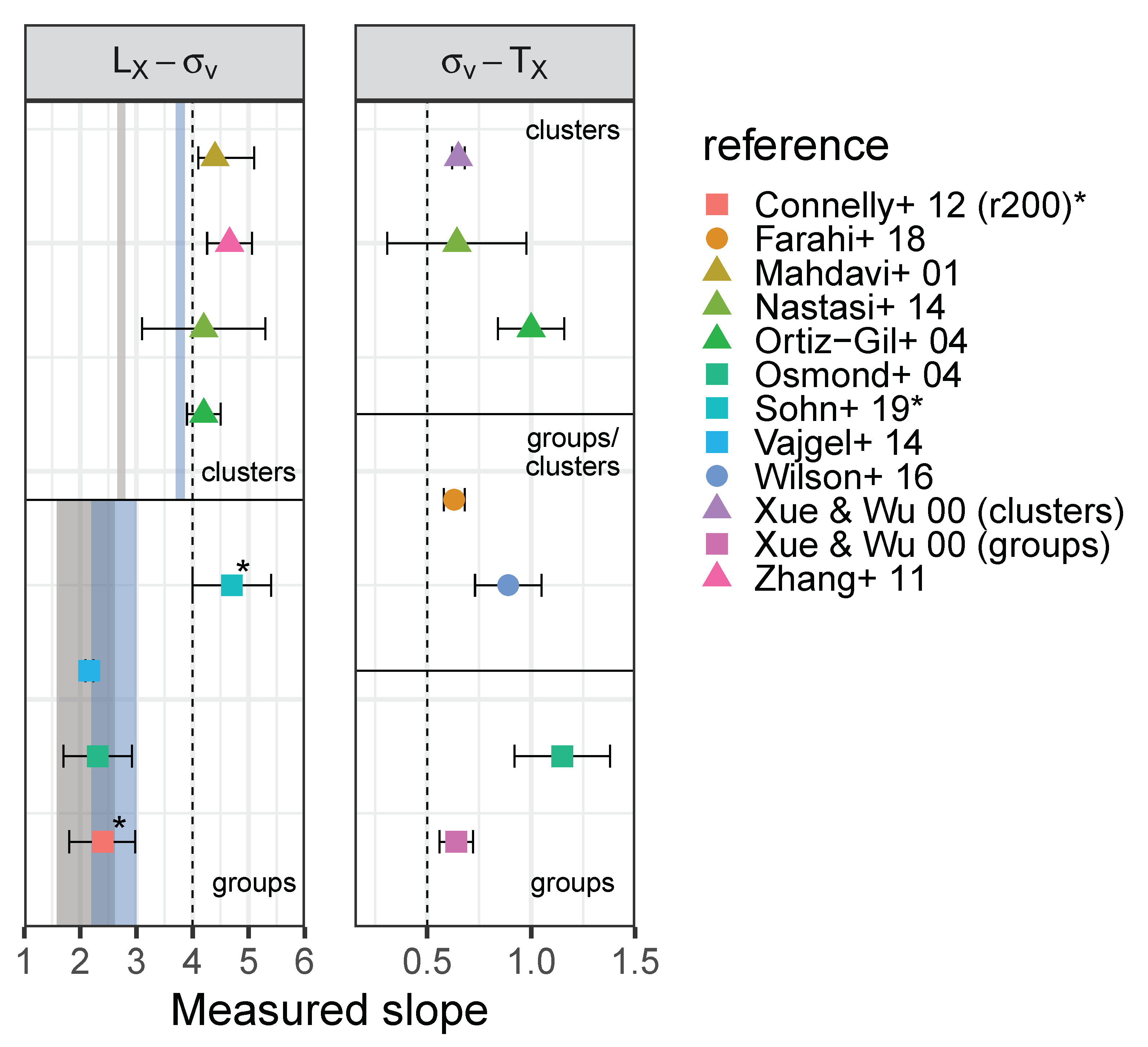
| Relation | N | kT (keV) | z Range | slope | slope | slope | Reference | Note |
|---|---|---|---|---|---|---|---|---|
| L–T | 26 | 0.6–3.0 | 0.012–0.049 | [0.9:1.1] | 2.25 ± 0.21 | 3.27 ± 0.26 | E11 | a†☐⇈ |
| L–T BC | 20 | 0.9–2.8 | 0.012–0.034 | [0.7:1.2] | 2.86 ± 0.29 | - | L15 | a†☐⇊ |
| L–T | 20 | 0.9–2.8 | 0.012–0.034 | [0.7:1.2] | 2.05 ± 0.32 | 2.90 ± 0.36 | L15 | a†☐⇊ |
| L–T BC | 12 | 1.7–8.2 | 0.1–0.47 | [1.3:1.5] | 2.52 ± 0.17 | - | K15 | a‡∆⇊ |
| L–T | 12 | 1.7–8.2 | 0.1–0.47 | [1.3:1.5] | 2.65 ± 0.17 | 2.47 ± 1.23 | K15 | a‡∆⇊ |
| L–T BC | 26 | 0.6–3.6 | 0.012–0.049 | [1.2:1.6] | 3.20 ± 0.26 | - | B15 | c†☐⇈ |
| L–T | 26 | 0.6–3.6 | 0.012–0.049 | [1.2:1.6] | 2.17 ± 0.26 | 3.11 ± 0.54 | B15 | c†☐⇈ |
| L–T BC | 23 | 1.0–3.9 | 0.03–0.147 | [0.8:1.3] | 2.79 ± 0.33 | - | Z16 | b‡◇⇈ |
| L–T BC | 23 | 1.0–3.9 | 0.03–0.147 | [1.2:1.6] | 3.29 ± 0.33 | - | Z16 | c‡◇⇈ |
| L–T | 23 | 1.0–3.9 | 0.03–0.147 | [1.2:1.6] | 3.28 ± 0.33 | 2.92 ± 0.25 | Z16 | c‡⇈ |
| L–T | 23 | 1.0–3.9 | 0.03–0.147 | [1.2:1.6] | 3.81 ± 0.46 | 3.46 ± 0.45 | Z16 | c‡◇⇈ |
| L–M | 26 | 0.6–3.0 | 0.012–0.049 | [0.4:0.8] | 1.34 ± 0.18 | 1.47 ± 0.43 | E11 | a†⇈ |
| L–M BC | 20 | 0.9–2.8 | 0.012–0.034 | [0.2:0.7] | 1.66 ± 0.22 | - | L15 | a†⇊ |
| L–M | 20 | 0.9–2.8 | 0.012–0.034 | [0.2:0.7] | 1.32 ± 0.24 | 1.68 ± 0.32 | L15 | a†⇊ |
| L–M | 12 | 1.7–8.2 | 0.1–0.47 | [0.8:0.9] | 1.43 ± 0.16 | 1.52 ± 0.73 | K15 | a‡⇊ |
| L–M BC | 105 | 0.6–6.0 | 0.054–1.033 | [0.4:0.8] | 1.07 ± 0.37 | - | S20 | b‡⇊ |
| M–T | 43 | 0.7–2.7 | 0.012–0.122 | 1.5 | 1.67 ± 0.15 | 1.75 ± 0.14 | S09 | ◇⇈ |
| M–T | 26 | 0.6–3.0 | 0.012–0.049 | 1.5 | 1.68 ± 0.20 | 1.87 ± 0.37 | E11 | ☐⇈ |
| M–T | 10 | 1.2–4.6 | 0.124–0.834 | 1.5 | 1.71 ± 0.49 | 1.46 ± 0.58 | K13 | ⊚⇊ |
| M–T | 20 | 0.9–2.8 | 0.012–0.034 | 1.5 | 1.65 ± 0.07 | 1.61 ± 0.10 | L15 | ☐⇊ |
| M–T BC | 12 | 1.7–8.2 | 0.1–0.47 | 1.5 | 1.52 ± 0.17 | - | K15 | ∆⇊ |
| M–T | 12 | 1.7–8.2 | 0.1–0.47 | 1.5 | 1.68 ± 0.17 | 1.22 ± 0.82 | K15 | ∆⇊ |
| M–T | 76 | 0.6–6.0 | 0.044–1.002 | 1.5 | 1.33 ± 0.75 | 1.14 ± 0.32 | U20 | ⊠⇊ |
| M–Y | 43 | 0.7–2.7 | 0.012–0.122 | 0.6 | 0.56 ± 0.03 | 0.71 ± 0.24 | S09 | ⇈ |
| M–Y | 26 | 0.6–3.0 | 0.012–0.049 | 0.6 | 0.53 ± 0.06 | 0.58 ± 0.19 | E11 | ⇈ |
| M–Y | 20 | 0.9–2.8 | 0.012–0.034 | 0.6 | 0.60 ± 0.03 | 0.58 ± 0.04 | L15 | ⇊ |
| M–M | 43 | 0.7–2.7 | 0.012–0.122 | 1 | 1.14 ± 0.03 | 0.97 ± 0.21 | S09 | ⇈ |
| M–M | 26 | 0.6–3.0 | 0.012–0.049 | 1 | 1.38 ± 0.18 | 1.22 ± 0.44 | E11 | ⇈ |
| M–M | 20 | 0.9–2.8 | 0.012–0.034 | 1 | 1.09 ± 0.08 | 1.11 ± 0.10 | L15 | ⇊ |
| M–M | 118 | 0.6–6.0 | 0.054–1.033 | 1 | 1.35 ± 0.30 | - | S20 | ⇊ |
| K–T | 43 | 0.7–2.7 | 0.012–0.122 | 1 | 0.83 ± 0.20 | - | S09 | ◇⇈ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lovisari, L.; Ettori, S.; Gaspari, M.; Giles, P.A. Scaling Properties of Galaxy Groups. Universe 2021, 7, 139. https://doi.org/10.3390/universe7050139
Lovisari L, Ettori S, Gaspari M, Giles PA. Scaling Properties of Galaxy Groups. Universe. 2021; 7(5):139. https://doi.org/10.3390/universe7050139
Chicago/Turabian StyleLovisari, Lorenzo, Stefano Ettori, Massimo Gaspari, and Paul A. Giles. 2021. "Scaling Properties of Galaxy Groups" Universe 7, no. 5: 139. https://doi.org/10.3390/universe7050139
APA StyleLovisari, L., Ettori, S., Gaspari, M., & Giles, P. A. (2021). Scaling Properties of Galaxy Groups. Universe, 7(5), 139. https://doi.org/10.3390/universe7050139







