Firewall from Effective Field Theory
Abstract
:1. Introduction
2. Back-Reacted Geometry
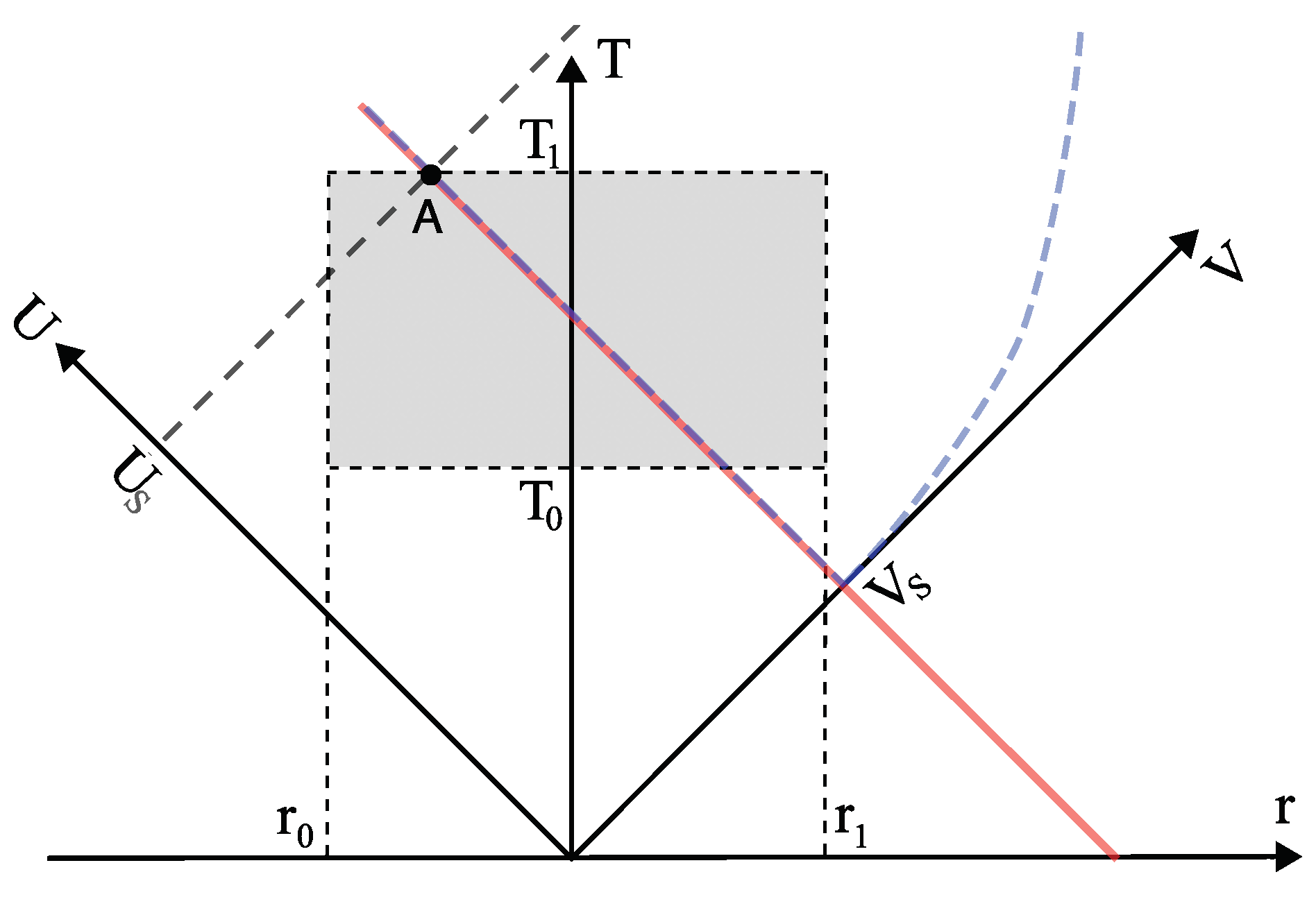
2.1. Near-Horizon Region and Uneventful Condition
2.2. Solution of
2.3. Solution of
2.4. Near-Horizon Geometry
3. Breakdown of Effective Theory
3.1. Free-Field Quantization in the Near-Horizon Region
3.2. Transition Amplitude
3.3. Comments on the Amplitude
3.3.1. Amplitudes in the Static Background
3.3.2. Large Amplitudes in Dynamical Background
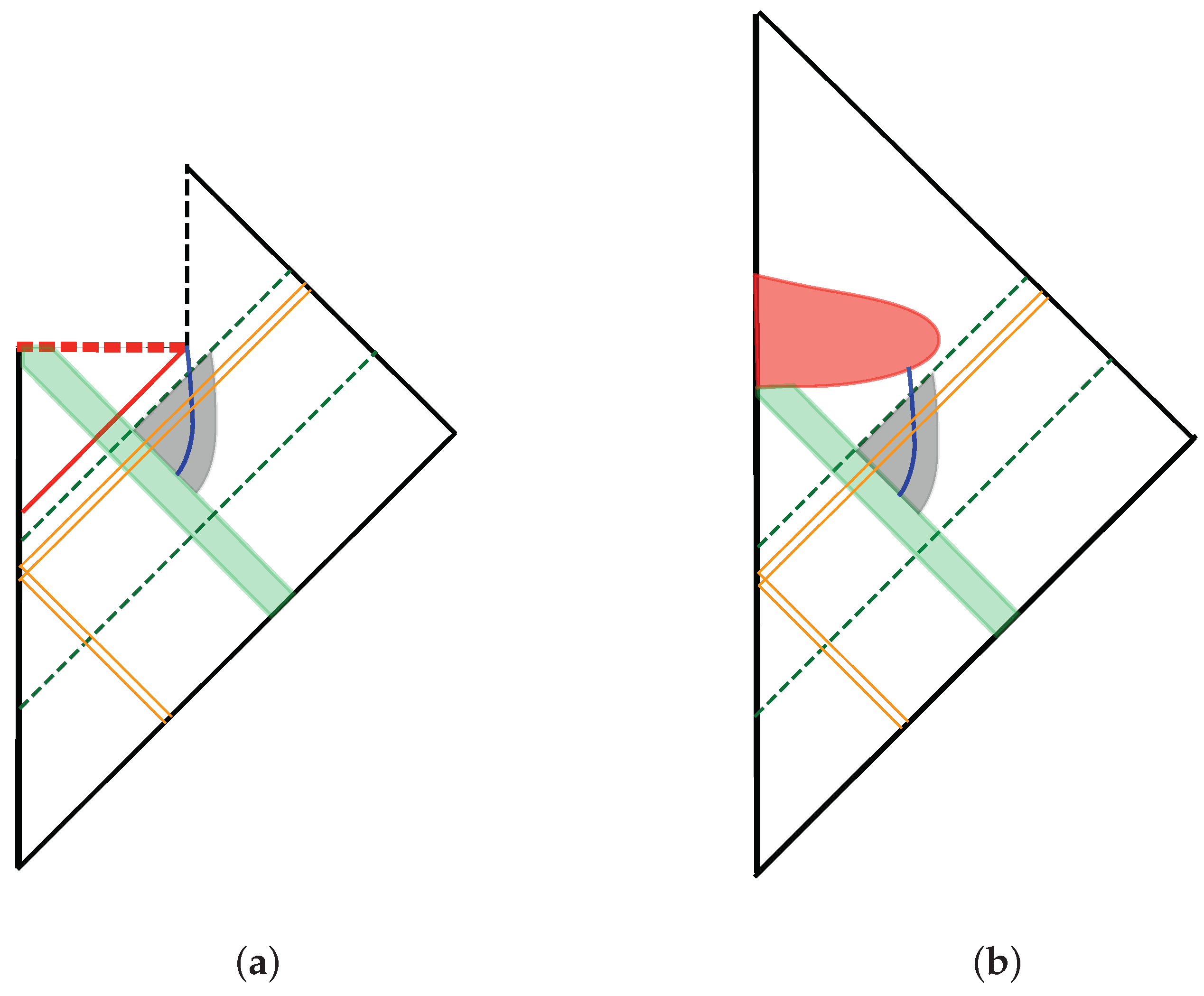
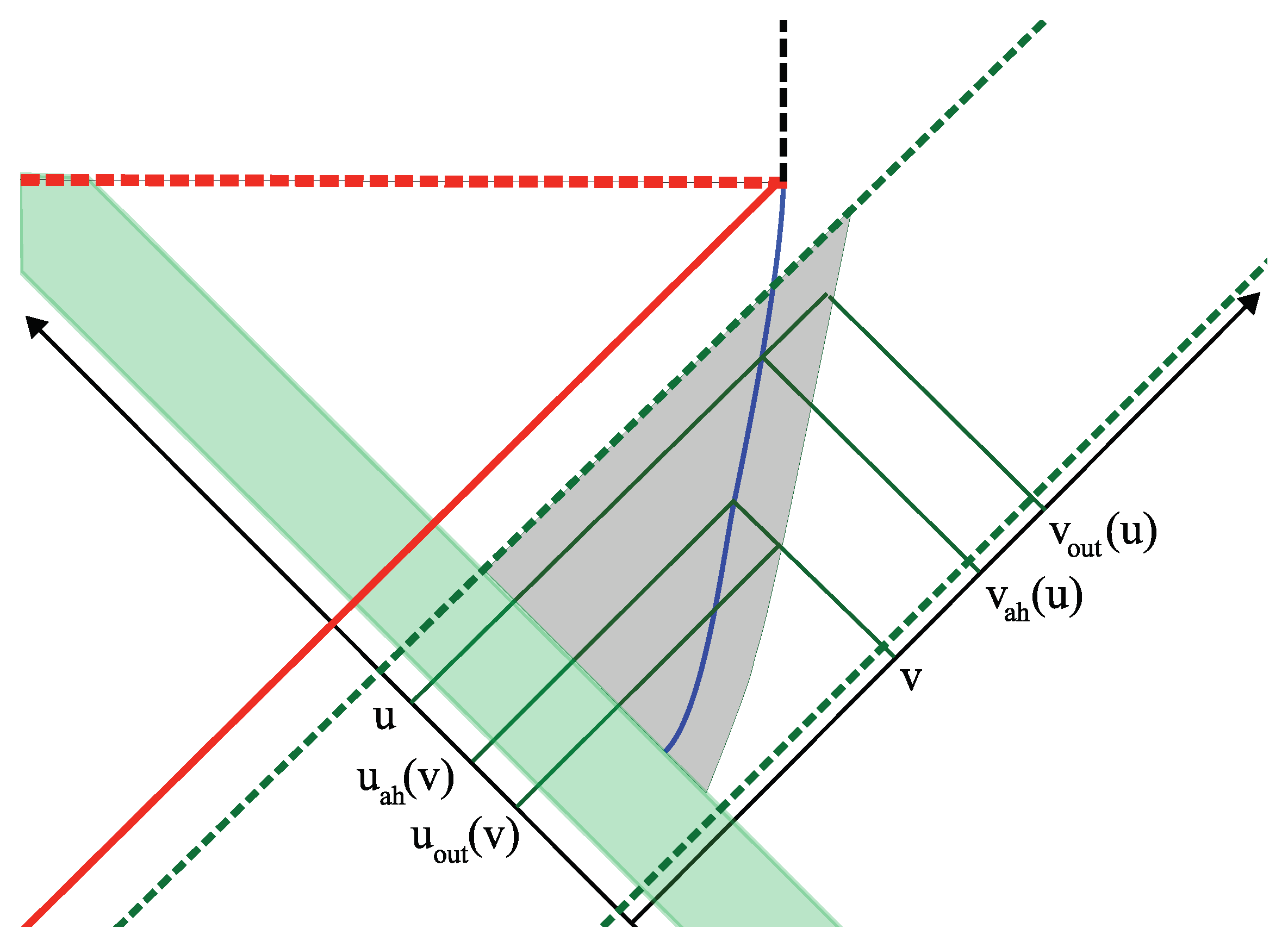
3.4. Example: Thin Shell and
3.5. Firewall
3.6. Viewpoint of Freely Falling Observers
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. Ingoing Vaidya Metric
Appendix B. Relation between a(u) and
Appendix C. Order-of-Magnitude of the First Term in Equation (23)
Appendix D. Calculation of
| 1 | |
| 2 | A “high-energy event” refers to a physical observable at an energy scale higher than the cutoff energy of the low-energy effective theory. |
| 3 | There is no clear inconsistency in a unitary evaporation without high-energy events [16] if there are no small particles like nuclei. However, we will show below that a firewall still arises under general assumptions. |
| 4 | |
| 5 | |
| 6 | It is equally natural to use the condition instead of Equation (5). This different choice would not make any essential difference in the discussion below. |
| 7 | |
| 8 | If the collapsing shell is not thin, it only introduces negligible corrections to the relation between U and u in the near-horizon region. |
| 9 | See, for example, Ref. [46]. |
| 10 | There may be other factors of C to a positive power in the calculation of the amplitude, but we will see that, generically, with a sufficiently large order of derivatives, the amplitude involves a negative power of C. |
| 11 | It was pointed out in Ref. [49] that a large matrix element is obtained (for an operator without higher derivatives) when only the space outside the event horizon is integrated over, but it is merely an artifact of the boundary condition at the event horizon, and this large contribution is cancelled by the space inside the event horizon. Here, we take to cover the four different regions (i)–(iv) to rule out the possibility that the matrix element becomes large due to an artificial boundary condition. |
| 12 | For large n, the amplitude is further enhanced by other factors in Equation (96). |
| 13 | The potential cancellation between the contribution from the time-dependent matter distribution and that from the time-dependent vacuum geometry generically requires fine tuning (see Appendix D for more discussion). |
| 14 | For a freely falling observer comoving with the collapsing matter, the v-coordinate of the observer in this frame is roughly constant. The coordinates suitable for the observer are given by Equations (63) and (72), and the transition amplitude increases with the retarded time u mostly due to the increase in rather than that in . |
| 15 |
References
- Hawking, S.W. Breakdown of Predictability in Gravitational Collapse. Phys. Rev. D 1976, 14, 2460. [Google Scholar] [CrossRef]
- Mathur, S.D. The Information paradox: A Pedagogical introduction. Class. Quant. Grav. 2009, 26, 224001. [Google Scholar] [CrossRef] [Green Version]
- Marolf, D. The Black Hole information problem: Past, present, and future. Rept. Prog. Phys. 2017, 80, 092001. [Google Scholar] [CrossRef] [PubMed]
- Hawking, S.W. Particle Creation by Black Holes. Commun. Math. Phys. 1975, 43, 199. [Google Scholar] [CrossRef]
- Hawking, S.W. Black Holes and Thermodynamics. Phys. Rev. D 1976, 13, 191. [Google Scholar] [CrossRef]
- Hawking, S.W. Information Preservation and Weather Forecasting for Black Holes. arXiv 2015, arXiv:1401.5761. [Google Scholar]
- Hawking, S.W. The Information Paradox for Black Holes. arXiv 2014, arXiv:1509.01147. [Google Scholar]
- Saini, A.; Stojkovic, D. Radiation from a collapsing object is manifestly unitary. Phys. Rev. Lett. 2015, 114, 111301. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Cai, Q.Y.; You, L.; Zhan, M.S. Hidden Messenger Revealed in Hawking Radiation: A Resolution to the Paradox of Black Hole Information Loss. Phys. Lett. B 2009, 675, 98. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Cai, Q.Y.; Zhan, M.S.; You, L. Entropy is Conserved in Hawking Radiation as Tunneling: A Revisit of the Black Hole Information Loss Paradox. Ann. Phys. 2011, 326, 350. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Cai, Q.Y.; Zhan, M.S.; You, L. Towards experimentally testing the paradox of black hole information loss. Phys. Rev. D 2013, 87, 044006. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Cai, Q.Y.; Zhan, M.S.; You, L. Information conservation is fundamental: Recovering the lost information in Hawking radiation. Int. J. Mod. Phys. D 2013, 22, 1341014. [Google Scholar] [CrossRef] [Green Version]
- Penington, G. Entanglement Wedge Reconstruction and the Information Paradox. J. High Energy Phys. 2020, 2020, 1–84. [Google Scholar] [CrossRef]
- Almheiri, A.; Engelhardt, N.; Marolf, D.; Maxfield, H. The entropy of bulk quantum fields and the entanglement wedge of an evaporating black hole. J. High Energy Phys. 2019, 1912, 63. [Google Scholar] [CrossRef] [Green Version]
- Almheiri, A.; Mahajan, R.; Maldacena, J.; Zhao, Y. The Page curve of Hawking radiation from semiclassical geometry. arXiv 2019, arXiv:1908.10996. [Google Scholar] [CrossRef] [Green Version]
- Hutchinson, J.; Stojkovic, D. Icezones instead of firewalls: Extended entanglement beyond the event horizon and unitary evaporation of a black hole. Class. Quant. Grav. 2016, 33, 135006. [Google Scholar] [CrossRef] [Green Version]
- Almheiri, A.; Marolf, D.; Polchinski, J.; Sully, J. Black Holes: Complementarity or Firewalls? J. High Energy Phys. 2013, 1302, 62. [Google Scholar] [CrossRef] [Green Version]
- Lunin, O.; Mathur, S.D. AdS/CFT duality and the black hole information paradox. Nucl. Phys. B 2002, 623, 342. [Google Scholar] [CrossRef] [Green Version]
- Lunin, O.; Mathur, S.D. Statistical interpretation of Bekenstein entropy for systems with a stretched horizon. Phys. Rev. Lett. 2002, 88, 211303. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Braunstein, S.L. Black hole entropy as entropy of entanglement, or it’s curtains for the equivalence principle. arXiv 2009, arXiv:0907.1190v1. [Google Scholar]
- Braunstein, S.L.; Pirandola, S.; Życzkowski, K. Better Late than Never: Information Retrieval from Black Holes. Phys. Rev. Lett. 2013, 110, 101301. [Google Scholar] [CrossRef] [PubMed]
- Dodelson, M.; Silverstein, E. String-theoretic breakdown of effective field theory near black hole horizons. Phys. Rev. D 2017, 96, 066010. [Google Scholar] [CrossRef] [Green Version]
- Weinberg, S. The Quantum Theory of Fields; Cambridge University Press: Cambridge, UK, 1995; Volume 1. [Google Scholar]
- Sekino, Y.; Susskind, L. Fast Scramblers. J. High Energy Phys. 2008, 10, 65. [Google Scholar] [CrossRef] [Green Version]
- Nurmagambetov, A.J.; Park, I.Y. Quantum-induced trans-Planckian energy near horizon. J. High Energy Phys. 2018, 5, 167. [Google Scholar] [CrossRef] [Green Version]
- Nurmagambetov, A.J.; Park, I.Y. Quantum-gravitational trans-Planckian energy of a time-dependent black hole. Symmetry 2019, 11, 1303. [Google Scholar] [CrossRef] [Green Version]
- Nurmagambetov, A.J.; Park, I.Y. Quantum-gravitational trans-Planckian radiation by a rotating black hole. arXiv 2020, arXiv:2007.06070. [Google Scholar]
- Ho, P.M.; Matsuo, Y.; Yokokura, Y. An Analytic Description of Semi-Classical Black-Hole Geometry. arXiv 2020, arXiv:1912.12855. [Google Scholar]
- Ho, P.M.; Matsuo, Y.; Yokokura, Y. Distance between collapsing matter and trapping horizon in evaporating black holes. arXiv 2019, arXiv:1912.12863. [Google Scholar]
- Hiscock, W.A. Models of Evaporating Black Holes. {II}. Effects of the Outgoing Created Radiation. Phys. Rev. D 1981, 23, 2823–2827. [Google Scholar] [CrossRef]
- Ashtekar, A. Black Hole evaporation: A Perspective from Loop Quantum Gravity. Universe 2020, 6, 21. [Google Scholar] [CrossRef] [Green Version]
- Visser, M. Essential and inessential features of Hawking radiation. Int. J. Mod. Phys. D 2003, 12, 649–661. [Google Scholar] [CrossRef] [Green Version]
- Barcelo, C.; Liberati, S.; Sonego, S.; Visser, M. Quasi-particle creation by analogue black holes. Class. Quant. Grav. 2006, 23, 5341–5366. [Google Scholar] [CrossRef]
- Barcelo, C.; Liberati, S.; Sonego, S.; Visser, M. Hawking-like radiation does not require a trapped region. Phys. Rev. Lett. 2006, 97, 171301. [Google Scholar] [CrossRef] [Green Version]
- Ho, P.M.; Matsuo, Y. Trapping Horizon and Negative Energy. J. High Energy Phys. 2019, 1906, 57. [Google Scholar] [CrossRef] [Green Version]
- Ho, P.M.; Matsuo, Y. Static Black Holes With Back Reaction From Vacuum Energy. Class. Quant. Grav. 2018, 35, 065012. [Google Scholar] [CrossRef] [Green Version]
- Ho, P.M.; Matsuo, Y. Static Black Hole and Vacuum Energy: Thin Shell and Incompressible Fluid. J. High Energy Phys. 2018, 1803, 96. [Google Scholar] [CrossRef]
- Ho, P.M.; Matsuo, Y. On the Near-Horizon Geometry of an Evaporating Black Hole. J. High Energy Phys. 2018, 1807, 47. [Google Scholar] [CrossRef] [Green Version]
- Ho, P.M.; Kawai, H.; Matsuo, Y.; Yokokura, Y. Back Reaction of 4D Conformal Fields on Static Geometry. J. High Energy Phys. 2018, 1811, 56. [Google Scholar] [CrossRef] [Green Version]
- Davies, P.; Fulling, S.; Unruh, W. Energy Momentum Tensor Near an Evaporating Black Hole. Phys. Rev. D 1976, 13, 2720–2723. [Google Scholar] [CrossRef] [Green Version]
- Fulling, S.A. Radiation and Vacuum Polarization Near a Black Hole. Phys. Rev. D 1977, 15, 2411. [Google Scholar] [CrossRef]
- Christensen, S.M.; Fulling, S.A. Trace Anomalies and the Hawking Effect. Phys. Rev. D 1977, 15, 2088. [Google Scholar] [CrossRef] [Green Version]
- Parentani, R.; Piran, T. The Internal geometry of an evaporating black hole. Phys. Rev. Lett. 1994, 93, 2805–2808. [Google Scholar] [CrossRef] [Green Version]
- Frolov, V.; Novikov, I. Black hole physics: Basic concepts and new developments. Fundam. Theor. Phys. 1998, 96. [Google Scholar] [CrossRef]
- Barcelo, C.; Liberati, S.; Sonego, S.; Visser, M. Hawking-like radiation from evolving black holes and compact horizonless objects. J. High Energy Phys. 2011, 1102, 3. [Google Scholar] [CrossRef] [Green Version]
- Brout, R.; Massar, S.; Parentani, R.; Spindel, P. A Primer for black hole quantum physics. Phys. Rept. 1995, 260, 329. [Google Scholar] [CrossRef] [Green Version]
- Unruh, W.G. Origin of the Particles in Black Hole Evaporation. Phys. Rev. D 1997, 15, 365. [Google Scholar] [CrossRef]
- Unruh, W. Notes on black hole evaporation. Phys. Rev. D 1976, 14, 870. [Google Scholar] [CrossRef] [Green Version]
- Giddings, S.B. Black hole information, unitarity, and nonlocality. Phys. Rev. D 2006, 74, 106005. [Google Scholar] [CrossRef] [Green Version]
- Hooft, G.T. On the Quantum Structure of a Black Hole. Nucl. Phys. B 1985, 256, 727. [Google Scholar] [CrossRef]
- Kawai, H.; Yokokura, Y. Black Hole as a Quantum Field Configuration. Universe 2020, 6, 77. [Google Scholar] [CrossRef]
- Jacobson, T. Black hole evaporation and ultrashort distances. Phys. Rev. D 1991, 44, 1731. [Google Scholar] [CrossRef] [PubMed]
- Unruh, W.G. Sonic analog of black holes and the effects of high frequencies on black hole evaporation. Phys. Rev. D 1995, 51, 2827. [Google Scholar] [CrossRef] [Green Version]
- Brout, R.; Massar, S.; Parentani, R.; Spindel, P. Hawking radiation without transPlanckian frequencies. Phys. Rev. D 1995, 52, 4559. [Google Scholar] [CrossRef] [Green Version]
- Helfer, A.D. Do black holes radiate? Rept. Prog. Phys. 2003, 66, 943. [Google Scholar] [CrossRef] [Green Version]
- Lafrance, R.; Myers, R.C. Gravity’s rainbow. Phys. Rev. D 1995, 51, 2584–2590. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hooft, G.T. The Firewall Transformation for Black Holes and Some of Its Implications. Found. Phys. 2017, 47, 1503–1542. [Google Scholar] [CrossRef] [Green Version]
- Hooft, G.T. The quantum black hole as a theoretical lab, a pedagogical treatment of a new approach. arXiv 2019, arXiv:1902.10469. [Google Scholar]
- Kawai, H.; Matsuo, Y.; Yokokura, Y. A Self-consistent Model of the Black Hole Evaporation. Int. J. Mod. Phys. A 2013, 28, 1350050. [Google Scholar] [CrossRef] [Green Version]
- Kawai, H.; Yokokura, Y. Phenomenological Description of the Interior of the Schwarzschild Black Hole. Int. J. Mod. Phys. A 2015, 30, 1550091. [Google Scholar] [CrossRef] [Green Version]
- Ho, P.M. Comment on Self-Consistent Model of Black Hole Formation and Evaporation. J. High Energy Phys. 2018, 1508, 96. [Google Scholar] [CrossRef]
- Kawai, H.; Yokokura, Y. Interior of Black Holes and Information Recovery. Phys. Rev. D 2016, 93, 044011. [Google Scholar] [CrossRef] [Green Version]
- Ho, P.M. The Absence of Horizon in Black-Hole Formation. Nucl. Phys. B 2016, 906, 394. [Google Scholar] [CrossRef] [Green Version]
- Ho, P.M. Asymptotic Black Holes. Class. Quant. Grav. 2017, 34, 085006. [Google Scholar] [CrossRef] [Green Version]
- Kawai, H.; Yokokura, Y. A Model of Black Hole Evaporation and 4D Weyl Anomaly. Universe 2017, 3, 51. [Google Scholar] [CrossRef] [Green Version]
- Ho, P.M.; Matsuo, Y.; Yang, S.J. Asymptotic States of Black Holes in KMY Model. arXiv 2020, arXiv:1903.11499. [Google Scholar] [CrossRef] [Green Version]
- Ho, P.M.; Matsuo, Y.; Yang, S.J. Vacuum Energy at Apparent Horizon in Conventional Model of Black Holes. arXiv 2019, arXiv:1904.01322. [Google Scholar]
- Mathur, S.D. The VECRO hypothesis. arXiv 2020, arXiv:2001.11057. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ho, P.-M.; Yokokura, Y. Firewall from Effective Field Theory. Universe 2021, 7, 241. https://doi.org/10.3390/universe7070241
Ho P-M, Yokokura Y. Firewall from Effective Field Theory. Universe. 2021; 7(7):241. https://doi.org/10.3390/universe7070241
Chicago/Turabian StyleHo, Pei-Ming, and Yuki Yokokura. 2021. "Firewall from Effective Field Theory" Universe 7, no. 7: 241. https://doi.org/10.3390/universe7070241
APA StyleHo, P.-M., & Yokokura, Y. (2021). Firewall from Effective Field Theory. Universe, 7(7), 241. https://doi.org/10.3390/universe7070241





