GEMS Embeddings of Schwarzschild and RN Black Holes in Painlevé-Gullstrand Spacetimes
Abstract
1. Introduction
2. GEMS Embedding of the Schwarzschild Black Hole in the PG Spacetime
2.1. GEMS Embedding of the Schwarzschild Black Hole in the Spherically Symmetric Spacetime
2.2. GEMS of the Schwarzschild Black Hole in the PG Spacetime
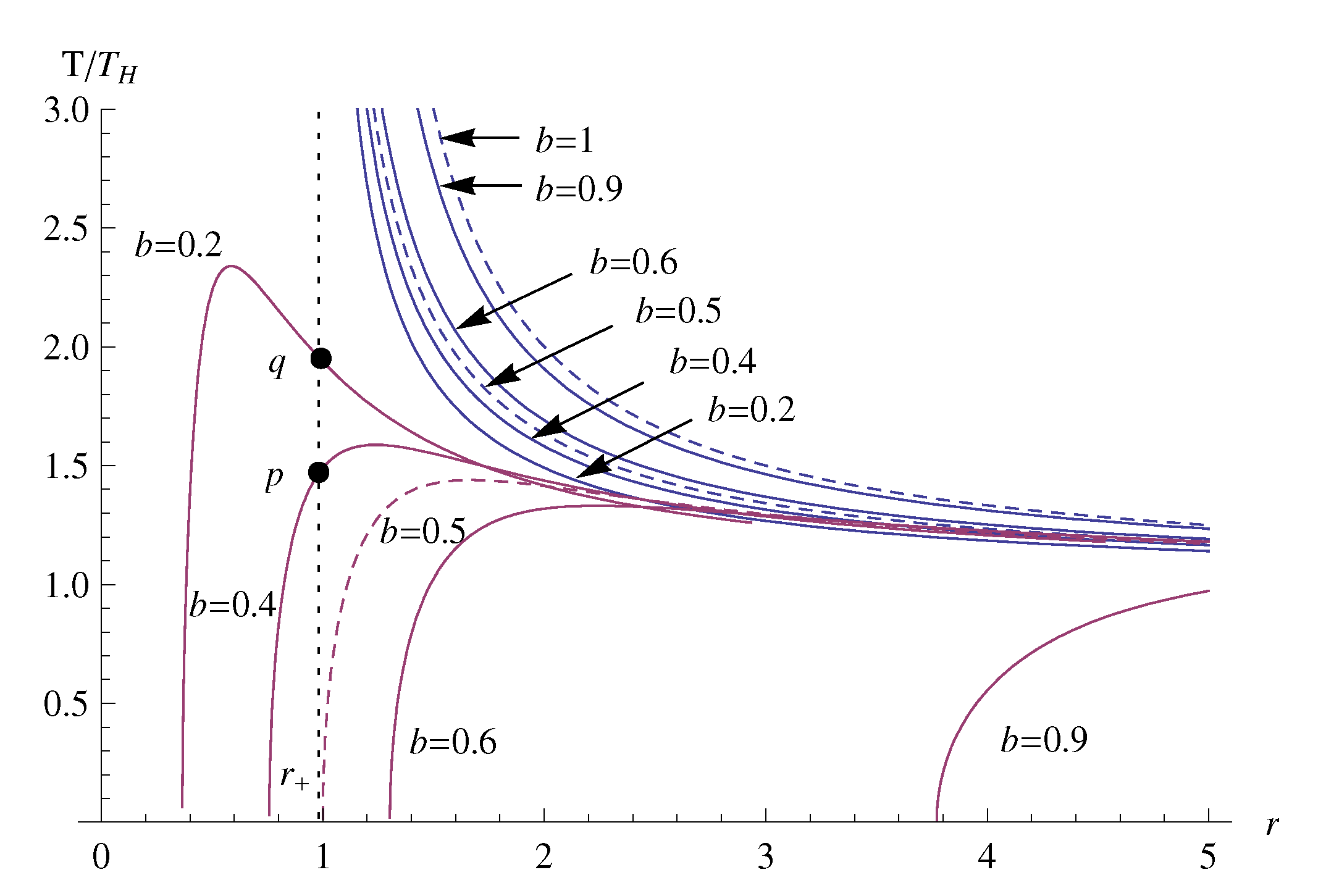
3. GEMS of the RN Black Hole in the PG Spacetime
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Fronsdal, C. Completion and Embedding of the Schwarzschild Solution. Phys. Rev. 1959, 116, 778–781. [Google Scholar] [CrossRef]
- Rosen, J. Embedding of Various Relativistic Riemannian Spaces in Pseudo-Euclidean Spaces. Rev. Mod. Phys. 1965, 37, 204–214. [Google Scholar] [CrossRef]
- Goenner, H.F. Local isometric embedding of Riemannian manifolds and Einstein’s theory of gravitation. In General Relativity and Gravitation: One Hundred Years after the Birth of Albert Einstein; Held, A., Ed.; Plenum: New York, NY, USA, 1980; Volume 1, pp. 441–468. [Google Scholar]
- Hawking, S.W. Particle Creation by Black Holes. Commun. Math. Phys. 1975, 43, 199–220, Erratum in Commun. Math. Phys. 1976, 46, 206. [Google Scholar] [CrossRef]
- Unruh, W.G. Notes on black hole evaporation. Phys. Rev. D 1976, 14, 870–892. [Google Scholar] [CrossRef]
- Deser, S.; Levin, O. Accelerated detectors and temperature in (anti)-de Sitter spaces. Class. Quant. Grav. 1997, 14, L163–L168. [Google Scholar] [CrossRef]
- Deser, S.; Levin, O. Equivalence of Hawking and Unruh temperatures through flat space embeddings. Class. Quant. Grav. 1998, 15, L85–L87. [Google Scholar] [CrossRef]
- Deser, S.; Levin, O. Mapping Hawking into Unruh thermal properties. Phys. Rev. D 1999, 59, 064004. [Google Scholar] [CrossRef]
- Hong, S.-T.; Kim, Y.-W.; Park, Y.-J. Higher dimensional flat embeddings of (2 + 1)-dimensional black holes. Phys. Rev. D 2000, 62, 024024. [Google Scholar] [CrossRef]
- Kim, Y.-W.; Park, Y.-J.; Soh, K.-S. Reissner-Nordström AdS black hole in the GEMS approach. Phys. Rev. D 2000, 62, 104020. [Google Scholar] [CrossRef]
- Hong, S.-T. Complete higher dimensional global embedding structures of various black holes. Gen. Rel. Grav. 2004, 36, 1919–1929. [Google Scholar] [CrossRef]
- Chen, H.Z.; Tian, Y.; Gao, Y.H.; Song, X.C. The GEMS approach to stationary motions in the spherically symmetric spacetimes. J. High Energy Phys. 2004, 410, 11. [Google Scholar] [CrossRef]
- Santos, N.L.; Dias, O.J.C.; Lemos, J.P.S. Global embedding of D-dimensional black holes with a cosmological constant in Minkowskian spacetimes: Matching between Hawking temperature and Unruh temperature. Phys. Rev. D 2004, 70, 124033. [Google Scholar] [CrossRef]
- Banerjee, R.; Majhi, B.R. A New Global Embedding Approach to Study Hawking and Unruh Effects. Phys. Lett. B 2010, 690, 83–86. [Google Scholar] [CrossRef]
- Cai, R.G.; Myung, Y.S. Hawking temperature for constant curvature black bole and its analogue in de Sitter space. Phys. Rev. D 2011, 83, 107502. [Google Scholar] [CrossRef]
- Hu, B.; Li, H.F. Mapping Hawking temperature in the spinning constant curvature black hole spaces into Unruh temperature. Mod. Phys. Lett. A 2012, 27, 1250002. [Google Scholar]
- Hong, S.-T.; Kim, W.T.; Kim, Y.-W.; Park, Y.-J. Global embeddings of scalar-tensor theories in (2+1)-dimensions. Phys. Rev. D 2000, 62, 064021. [Google Scholar] [CrossRef]
- Hong, S.-T.; Kim, W.T.; Oh, J.J.; Park, Y.-J. Higher dimensional flat embeddings of black strings in (2+1) dimensions. Phys. Rev. D 2001, 63, 127502. [Google Scholar] [CrossRef]
- Hong, S.-T. Thermodynamics of (1+1) dilatonic black holes in global flat embedding scheme. Phys. Lett. B 2005, 623, 135–140. [Google Scholar] [CrossRef]
- Hong, S.-T. SO(3,2)/Sp(2) symmetries in BTZ black holes. Phys. Lett. B 2004, 578, 187–194. [Google Scholar] [CrossRef]
- Hong, S.-T.; Kim, S.-W. Can wormholes have negative temperatures? Mod. Phys. Lett. A 2006, 21, 789–794. [Google Scholar] [CrossRef]
- Paston, S.A.; Sheykin, A.A. Global Embedding of the Reissner-Nordström Metric in the Flat Ambient Space. SIGMA 2014, 10, 3. [Google Scholar] [CrossRef]
- Paston, S.A. Hawking into Unruh mapping for embeddings of hyperbolic type. Class. Quant. Grav. 2015, 32, 145009. [Google Scholar] [CrossRef][Green Version]
- Sheykin, A.A.; Solovyev, D.P.; Paston, S.A. Global embeddings of BTZ and Schwarzschild-AdS type black holes in a flat space. Symmetry 2019, 11, 841. [Google Scholar] [CrossRef]
- Paston, S.A.; Sheykin, A.A. From the Embedding Theory to General Relativity in a result of inflation. Int. J. Mod. Phys. D 2012, 21, 1250043. [Google Scholar] [CrossRef]
- Paston, S.A.; Sheykin, A.A. Embedding theory as new geometrical mimetic gravity. Eur. Phys. J. C 2018, 78, 989. [Google Scholar] [CrossRef]
- Paston, S.A. Dark matter from non-relativistic embedding gravity. Mod. Phys. Lett. A 2021, 36, 2150101. [Google Scholar] [CrossRef]
- Paston, S.A. Non-Relativistic Limit of Embedding Gravity as General Relativity with Dark Matter. Universe 2020, 6, 163. [Google Scholar] [CrossRef]
- Brynjolfsson, E.J.; Thorlacius, L. Taking the Temperature of a Black Hole. J. High Energy Phys. 2008, 809, 66. [Google Scholar] [CrossRef]
- Kim, Y.-W.; Choi, J.; Park, Y.-J. Local free-fall temperature of a RN-AdS black hole. Int. J. Mod. Phys. A 2010, 25, 3107–3120. [Google Scholar] [CrossRef]
- Kim, Y.-W.; Choi, J.; Park, Y.-J. Local free-fall temperature of Gibbons-Maeda-Garfinkle-Horowitz-Strominger black holes. Phys. Rev. D 2014, 89, 044004. [Google Scholar] [CrossRef]
- Kim, Y.-W.; Park, Y.-J. Local free-fall Temperature of modified Schwarzschild black hole in rainbow spacetime. Mod. Phys. Lett. A 2016, 31, 1650106. [Google Scholar] [CrossRef]
- Hong, S.-T. Free fall temperature of Schwarzschild-Tangherlini-AdS black hole. arXiv 2015, arXiv:1510.05511. [Google Scholar]
- Hong, S.-T.; Kim, Y.-W.; Park, Y.-J. Local free-fall temperatures of charged BTZ black holes in massive gravity. Phys. Rev. D 2019, 99, 024047. [Google Scholar] [CrossRef]
- Hong, S.-T.; Kim, Y.-W.; Park, Y.-J. GEMS embeddings and freely falling temperatures of Schwarzschild(-AdS) black holes in massive gravity. Phys. Lett. B 2020, 800, 135116. [Google Scholar] [CrossRef]
- Taylor, E.; Wheeler, J.A. Exploring Black Holes: Introduction to General Relativity; Addison Wesley Longman: San Francisco, CA, USA, 2000. [Google Scholar]
- Painlevé, P. La mécanique classique et la théorie de la relativité. C. R. Acad. Sci. 1921, 173, 677–680. [Google Scholar]
- Gullstrand, A. Allgemeine Lösung des statischen Einkörperproblems in der Einsteinschen Gravitationstheorie. Ark. Mat. Astron. Fys. 1922, 16, 1–15. [Google Scholar]
- Kraus, P.; Wilczek, F. Some applications of a simple stationary line element for the Schwarzschild geometry. Mod. Phys. Lett. A 1994, 9, 3713–3719. [Google Scholar] [CrossRef]
- Parikh, M.K.; Wilczek, F. Hawking radiation as tunneling. Phys. Rev. Lett. 2000, 85, 5042–5045. [Google Scholar] [CrossRef]
- Parikh, M.K. A Secret tunnel through the horizon. Int. J. Mod. Phys. D 2004, 13, 2351–2354. [Google Scholar] [CrossRef]
- Martel, K.; Poisson, E. Regular coordinate systems for Schwarzschild and other spherical space-times. Am. J. Phys. 2001, 69, 476–480. [Google Scholar] [CrossRef]
- Francis, M.R.; Kosowsky, A. Geodesics in the generalized Schwarzschild solution. Am. J. Phys. 2004, 72, 1204–1209. [Google Scholar] [CrossRef]
- Hamilton, A.J.S.; Lisle, J.P. The River model of black holes. Am. J. Phys. 2008, 76, 519–532. [Google Scholar] [CrossRef]
- Finch, T.K. Coordinate families for the Schwarzschild geometry based on radial timelike geodesics. Gen. Rel. Grav. 2015, 47, 56. [Google Scholar] [CrossRef]
- Unruh, W.G. Experimental black hole evaporation. Phys. Rev. Lett. 1981, 46, 1351–1353. [Google Scholar] [CrossRef]
- Visser, M. Acoustic black holes: Horizons, ergospheres, and Hawking radiation. Class. Quant. Grav. 1998, 15, 1767–1791. [Google Scholar] [CrossRef]
- Volovik, G.E. The Universe in a Helium Droplet; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Barcelo, C.; Liberati, S.; Visser, M. Analogue gravity. Living Rev. Rel. 2005, 8, 12, Living Rev. Rel.2011, 14, 3. [Google Scholar] [CrossRef]
- Kanai, Y.; Siino, M.; Hosoya, A. Gravitational collapse in Painlevé-Gullstrand coordinates. Prog. Theor. Phys. 2011, 125, 1053–1065. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Snyder, H. On Continued Gravitational Contraction. Phys. Rev. 1939, 56, 455–459. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Pinceton University Press: Princeton, NJ, USA; Oxford, UK, 2017. [Google Scholar]
- Visser, M. Heuristic approach to the Schwarzschild geometry. Int. J. Mod. Phys. D 2005, 14, 2051–2068. [Google Scholar] [CrossRef]
- Perez-Roman, I.; Breton, N. The region interior to the event horizon of the Regular Hayward Black Hole. Gen. Rel. Grav. 2018, 50, 64. [Google Scholar] [CrossRef]
- Faraoni, V.; Vachon, G. When Painlev/’e-Gullstrand coordinates fail. Eur. Phys. J. C 2020, 80, 771. [Google Scholar] [CrossRef] [PubMed]
- Baines, J.; Berry, T.; Simpson, A.; Visser, M. Unit-lapse versions of the Kerr spacetime. Class. Quant. Grav. 2021, 38, 055001. [Google Scholar] [CrossRef]
- Wald, R.M. General Relativity; University of Chicago: Chicago, IL, USA, 1984. [Google Scholar]
- Hong, S.-T.; Kim, Y.-W.; Park, Y.-J. Tidal effects in Schwarzschild black hole in holographic massive gravity. Phys. Lett. B 2020, 811, 135967. [Google Scholar] [CrossRef]
- Lin, C.Y.; Soo, C. Generalized Painlevé-Gullstrand metrics. Phys. Lett. B 2009, 671, 493–495. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, S.-T.; Kim, Y.-W.; Park, Y.-J. GEMS Embeddings of Schwarzschild and RN Black Holes in Painlevé-Gullstrand Spacetimes. Universe 2022, 8, 15. https://doi.org/10.3390/universe8010015
Hong S-T, Kim Y-W, Park Y-J. GEMS Embeddings of Schwarzschild and RN Black Holes in Painlevé-Gullstrand Spacetimes. Universe. 2022; 8(1):15. https://doi.org/10.3390/universe8010015
Chicago/Turabian StyleHong, Soon-Tae, Yong-Wan Kim, and Young-Jai Park. 2022. "GEMS Embeddings of Schwarzschild and RN Black Holes in Painlevé-Gullstrand Spacetimes" Universe 8, no. 1: 15. https://doi.org/10.3390/universe8010015
APA StyleHong, S.-T., Kim, Y.-W., & Park, Y.-J. (2022). GEMS Embeddings of Schwarzschild and RN Black Holes in Painlevé-Gullstrand Spacetimes. Universe, 8(1), 15. https://doi.org/10.3390/universe8010015




