Lensing Magnification Seen by Gravitational Wave Detectors
Abstract
:1. Introduction
2. Lens Modeling
2.1. Basic Strong Lensing Quantities
2.2. Optical Depth and Lensing Probability
3. Inclusion of Lensing Selection Effects
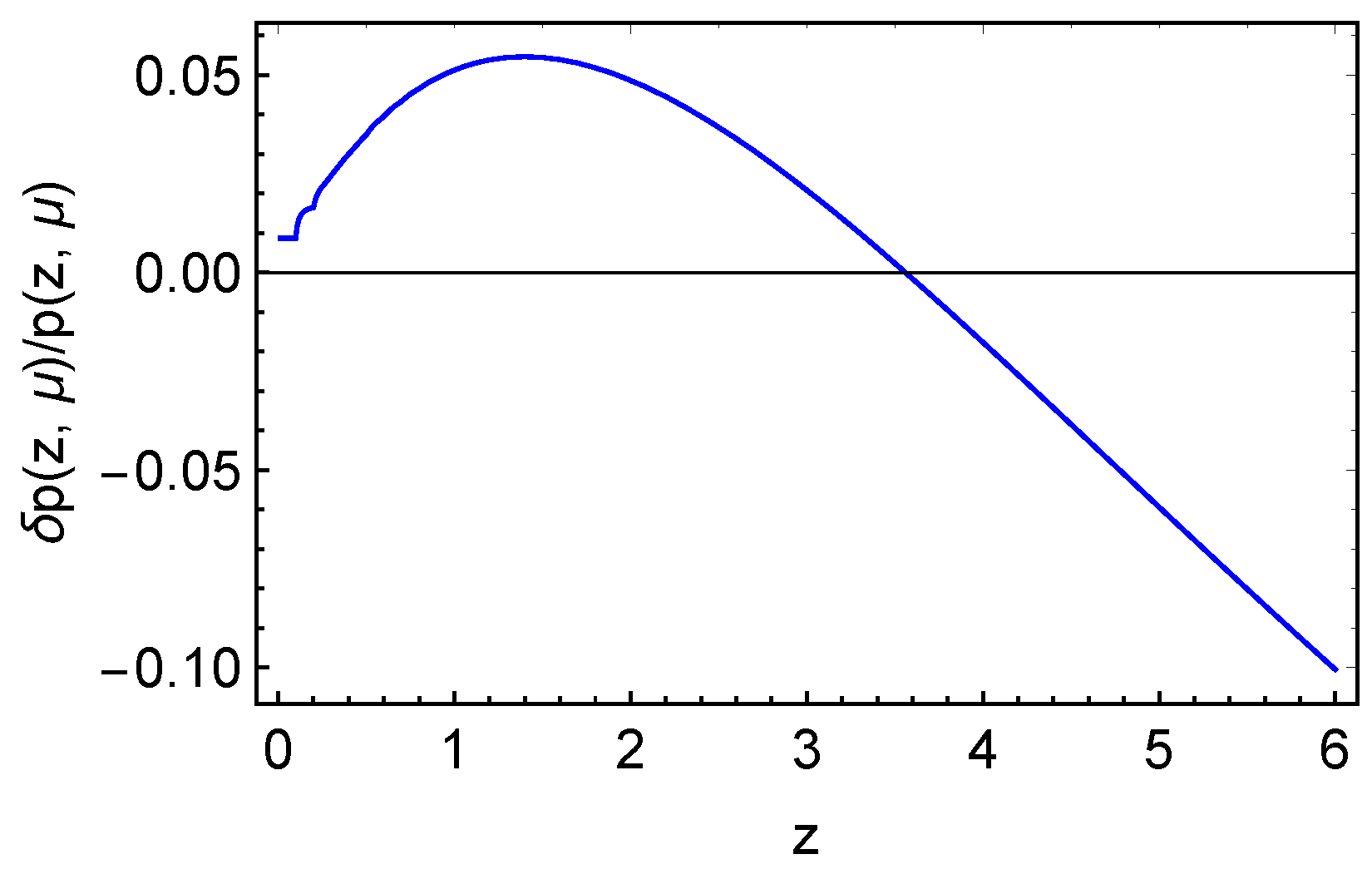
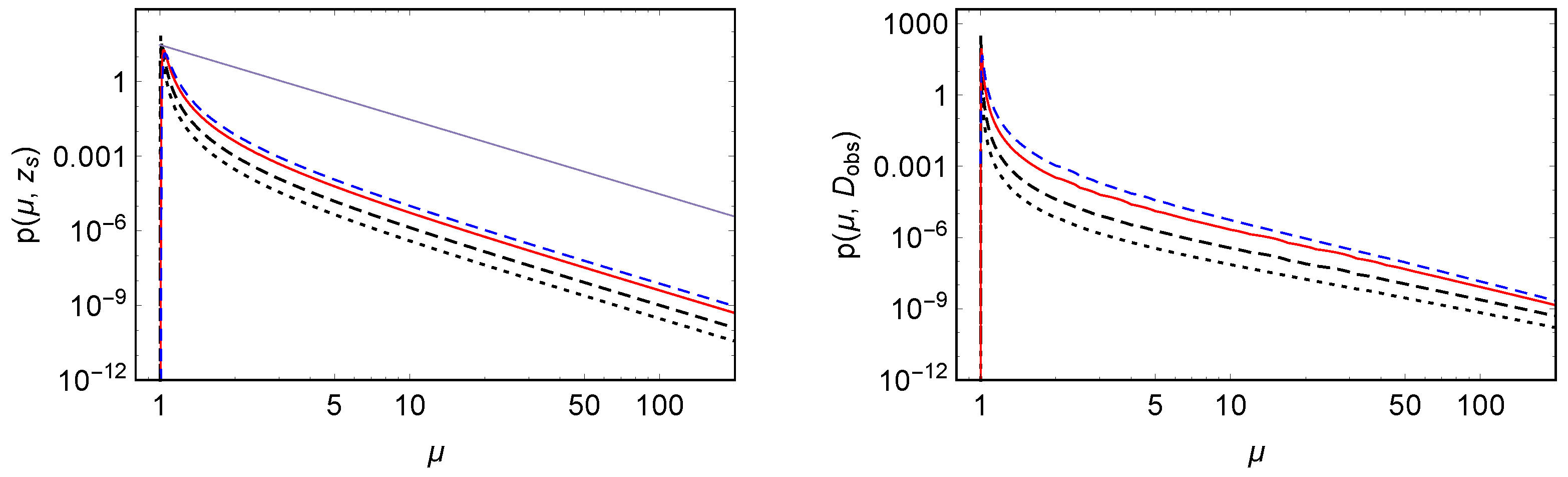
3.1. Magnification Distribution as Function of Redshift
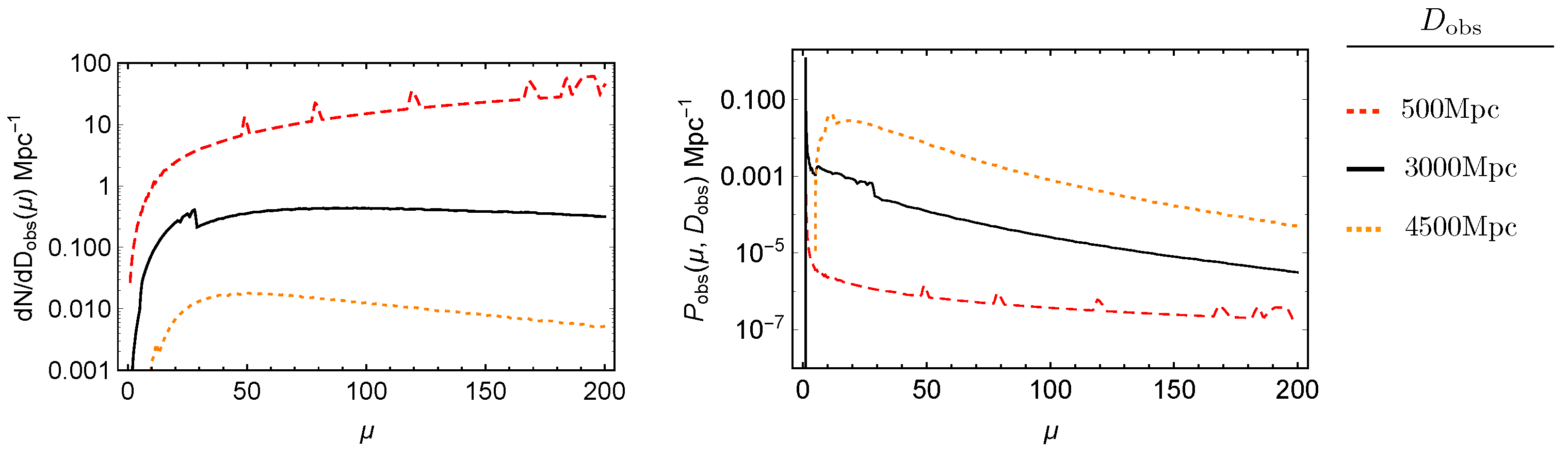
3.2. Magnification Distribution as Function of Observed Distance
4. Numerical Results
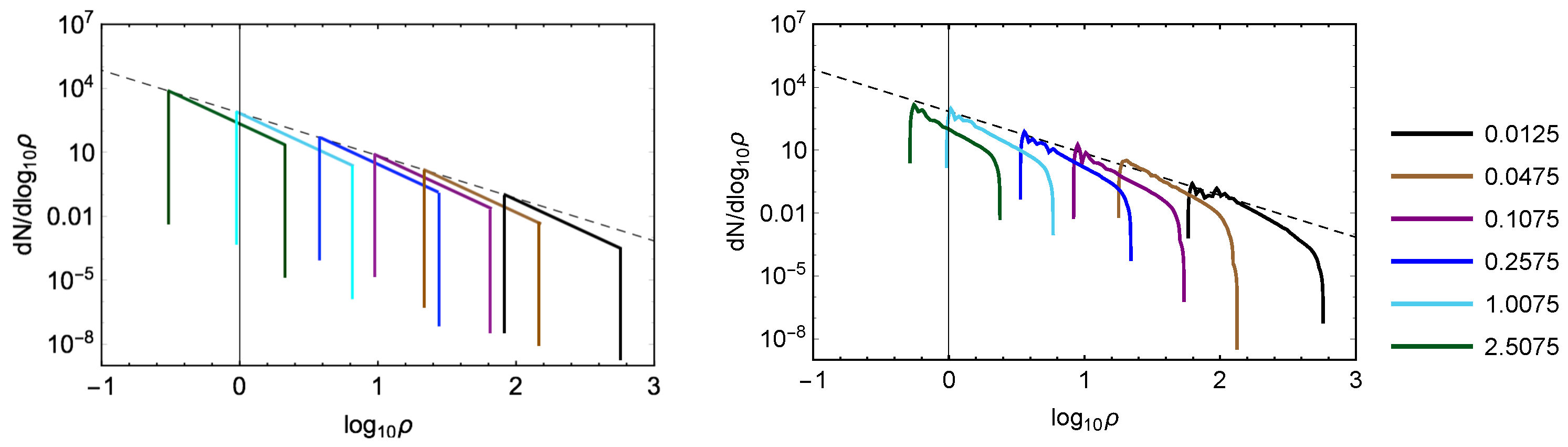
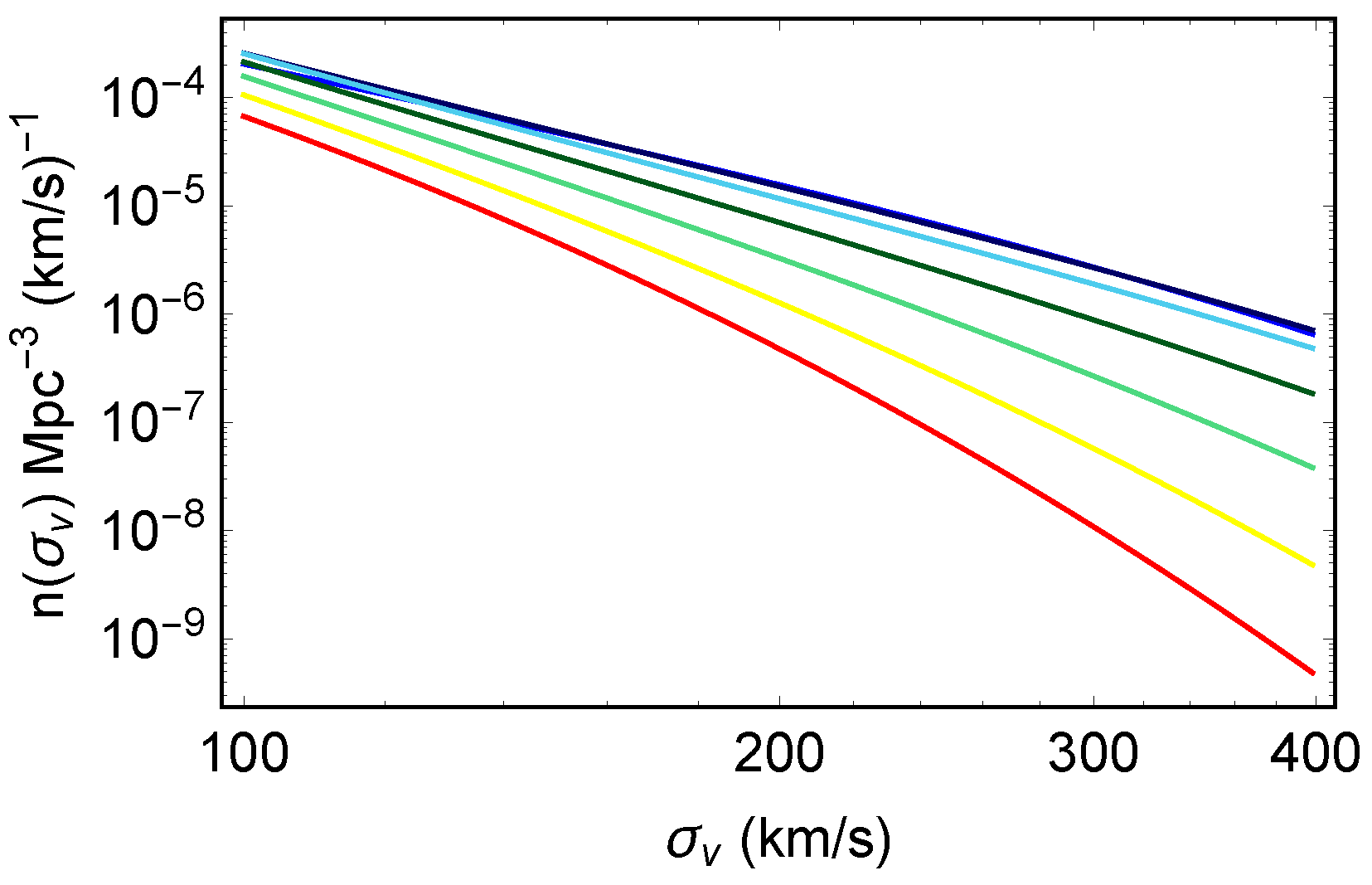
4.1. The Lens Distribution
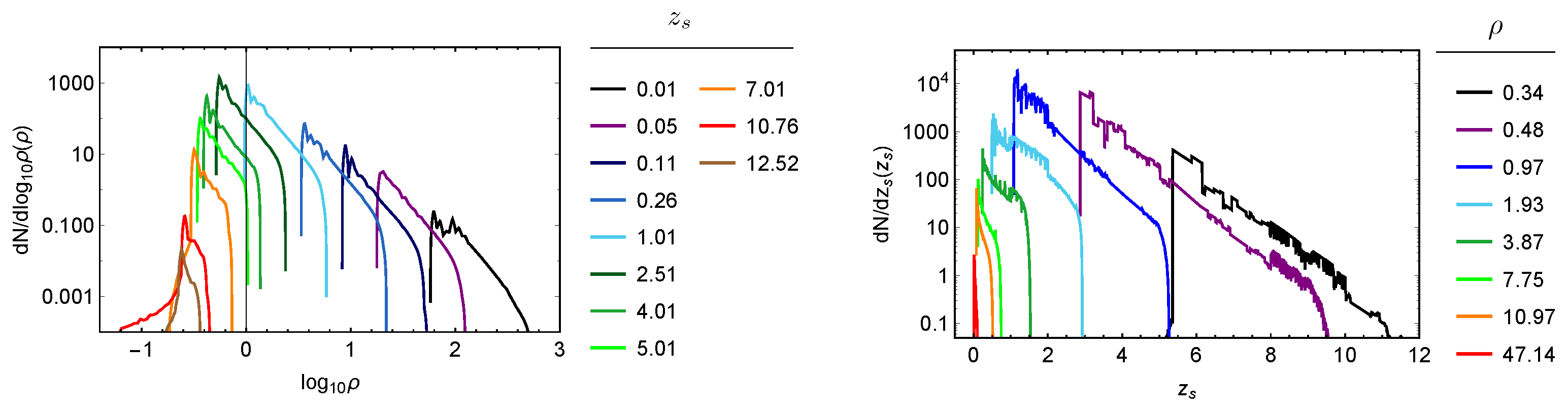
4.2. Results for Magnification Probability Density
4.3. Compact Binary Population
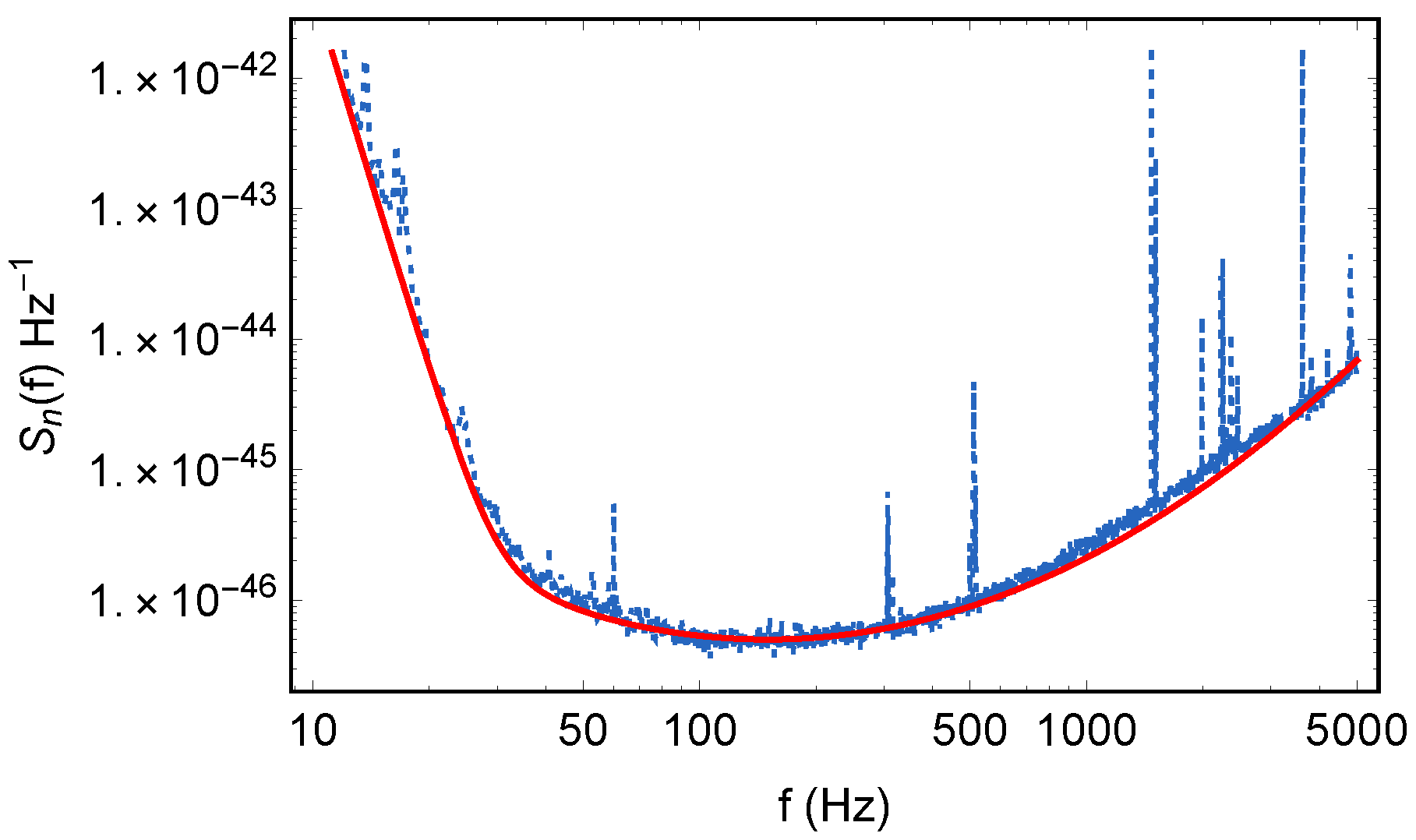
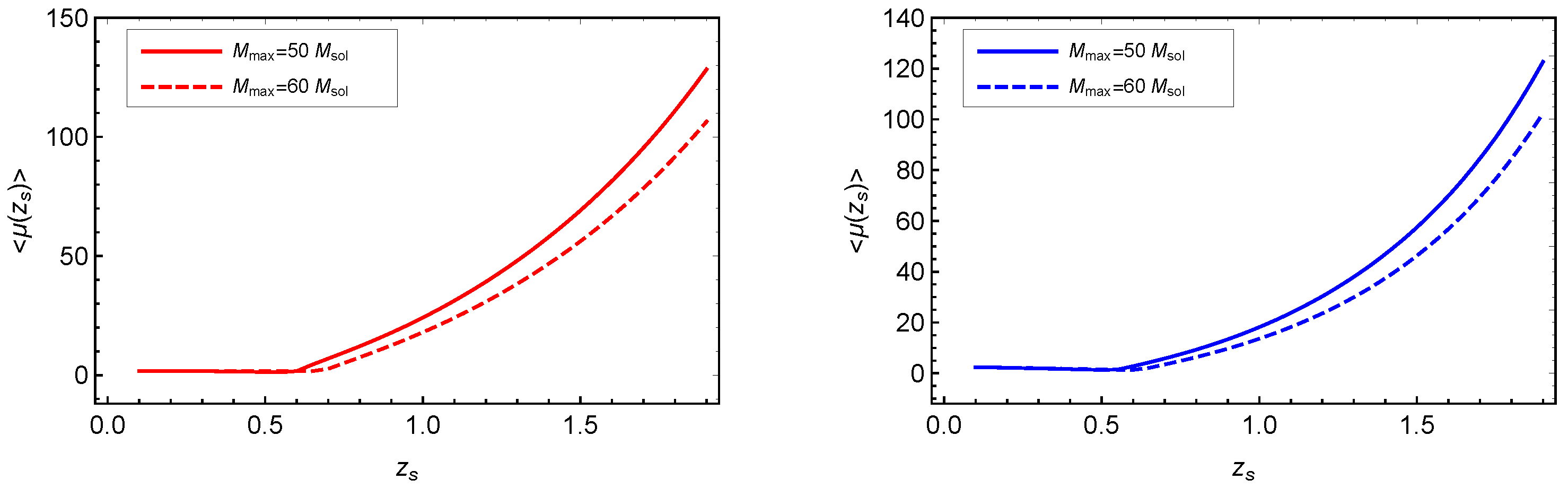
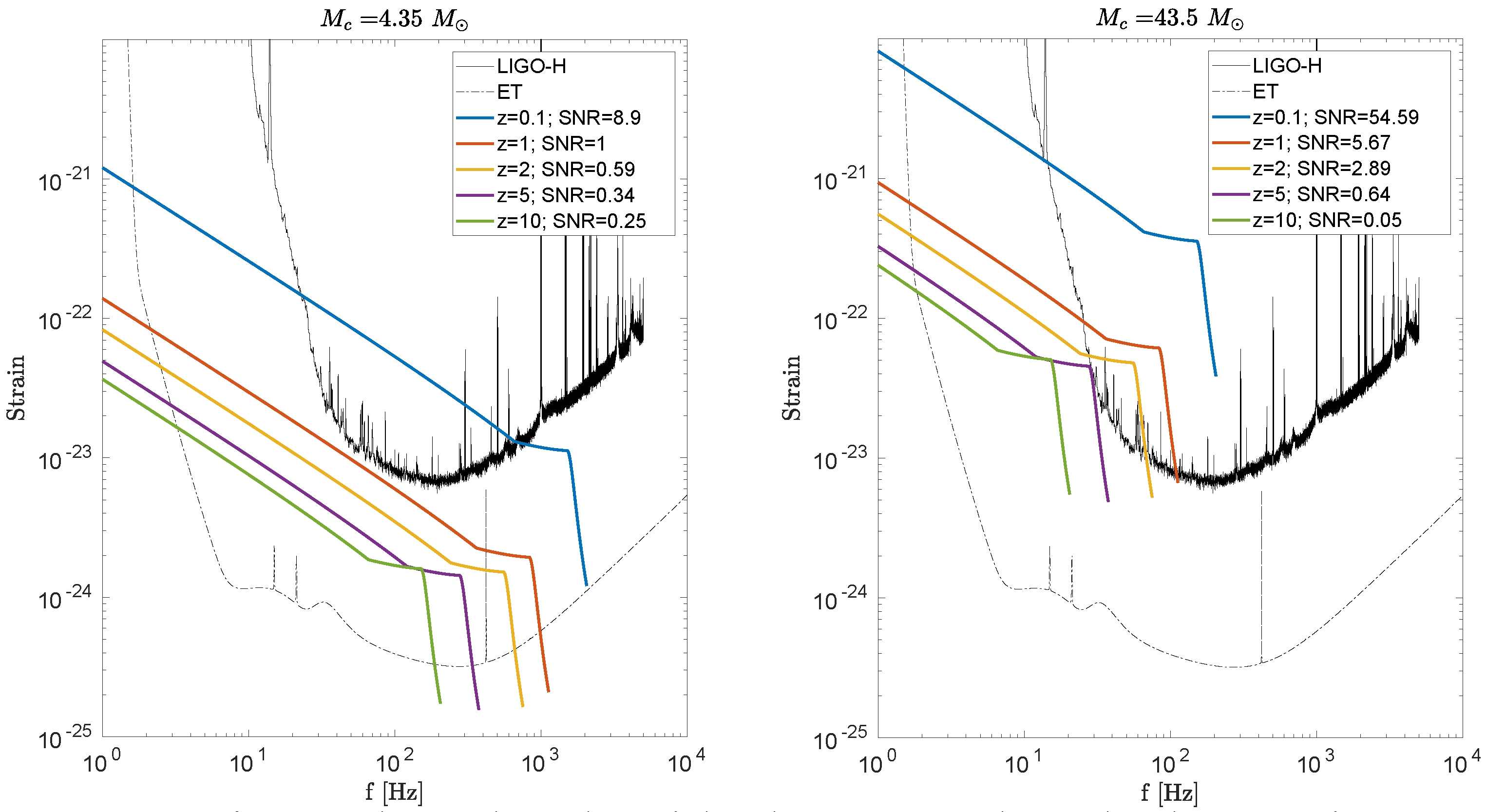
4.4. Probability of Strong Lensing for LIGO/Virgo Events
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. Fit to the Illustris Simulation
| 7.391498 | 5.729400 | −1.120552 | |
| −6.863393 | −5.273271 | 1.104114 | |
| 2.852083 | 1.255696 | −0.286638 | |
| 0.067032 | −0.048683 | 0.007648 |
Appendix B. Analytic Description of Lens Distribution
Appendix C. Analytical Description of BBH Population
Appendix D. Analytic Derivation of the Average Magnification
Appendix E. Analytical Results for the LIGO Detector(s)
References
- Abbott, B.P. et al. [LIGO Scientific Collaboration and Virgo Collaboration] Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [LIGO Scientific Collaboration and Virgo Collaboration] GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [LIGO Scientific Collaboration and Virgo Collaboration] Binary Black Hole Mergers in the first Advanced LIGO Observing Run. Phys. Rev. 2016, X6, 041015. [Google Scholar] [CrossRef]
- Abbott, B.P. t al. [LIGO Scientific Collaboration and Virgo Collaboration]. GW170608: Observation of a 19-solar-mass Binary Black Hole Coalescence. Astrophys. J. 2017, 851, L35. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [LIGO Scientific Collaboration and Virgo Collaboration] GW170814: A Three-Detector Observation of Gravitational Waves from a Binary Black Hole Coalescence. Phys. Rev. Lett. 2017, 119, 141101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abbott, B.P. et al. [LIGO Scientific and Virgo Collaboration] GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abbott, B.P. et al. [LIGO Scientific Collaboration and Virgo Collaboration] GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abbott, B.P. et al. [LIGO Scientific Collaboration and Virgo Collaboration] GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs. Phys. Rev. 2019, X9, 031040. [Google Scholar] [CrossRef] [Green Version]
- Abbott, R. et al. [LIGO Scientific Collaboration and Virgo Collaboration] GWTC-2: Compact Binary Coalescences Observed by LIGO and Virgo during the First Half of the Third Observing Run. Phys. Rev. X 2021, 11, 021053. [Google Scholar] [CrossRef]
- Abbott, R. et al. [LIGO Scientific Collaboration, Virgo Collaboration, and KAGRA Collaboration] Observation of Gravitational Waves from Two Neutron Star–Black Hole Coalescences. Astrophys. J. Lett. 2021, 915, L5. [Google Scholar] [CrossRef]
- Abbott, R. et al. [LIGO Scientific Collaboration, Virgo Collaboration, and KAGRA Collaboration] GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo During the Second Part of the Third Observing Run. arXiv 2021, arXiv:2111.03606. [Google Scholar]
- Oguri, M. Effect of gravitational lensing on the distribution of gravitational waves from distant binary black hole mergers. Mon. Not. R. Astron. Soc. 2018, 480, 3842–3855. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Stebbins, A.; Turner, E.L. Gravitational Lensing of Gravitational Waves from Merging Neutron Star Binaries. Phys. Rev. Lett. 1996, 77, 2875–2878. [Google Scholar] [CrossRef]
- Sereno, M.; Sesana, A.; Bleuler, A.; Jetzer, P.; Volonteri, M.; Begelman, M.C. Strong Lensing of Gravitational Waves as Seen by LISA. Phys. Rev. Lett. 2010, 105, 251101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ng, K.K.Y.; Wong, K.W.K.; Broadhurst, T.; Li, T.G.F. Precise LIGO Lensing Rate Predictions for Binary Black Holes. Phys. Rev. 2018, D97, 023012. [Google Scholar] [CrossRef] [Green Version]
- Broadhurst, T.; Diego, J.M.; Smoot, G. Reinterpreting Low Frequency LIGO/Virgo Events as Magnified Stellar-Mass Black Holes at Cosmological Distances. arXiv 2018, arXiv:1802.05273. [Google Scholar]
- Broadhurst, T.; Diego, J.M.; Smoot, G.F. Twin LIGO/Virgo Detections of a Viable Gravitationally-Lensed Black Hole Merger. arXiv 2019, arXiv:1901.03190. [Google Scholar]
- Haris, K.; Mehta, A.K.; Kumar, S.; Venumadhav, T.; Ajith, P. Identifying strongly lensed gravitational wave signals from binary black hole mergers. arXiv 2018, arXiv:1807.07062. [Google Scholar]
- Cao, Z.; Li, L.F.; Wang, Y. Gravitational lensing effects on parameter estimation in gravitational wave detection with advanced detectors. Phys. Rev. D 2014, 90, 062003. [Google Scholar] [CrossRef] [Green Version]
- Dai, L.; Venumadhav, T. On the waveforms of gravitationally lensed gravitational waves. arXiv 2017, arXiv:1702.04724. [Google Scholar]
- Dai, L.; Li, S.S.; Zackay, B.; Mao, S.; Lu, Y. Detecting Lensing-Induced Diffraction in Astrophysical Gravitational Waves. Phys. Rev. D 2018, 98, 104029. [Google Scholar] [CrossRef] [Green Version]
- Dai, L.; Venumadhav, T.; Sigurdson, K. Effect of lensing magnification on the apparent distribution of black hole mergers. Phys. Rev. D 2017, 95, 044011. [Google Scholar] [CrossRef] [Green Version]
- Jung, S.; Shin, C.S. Gravitational-Wave Fringes at LIGO: Detecting Compact Dark Matter by Gravitational Lensing. Phys. Rev. Lett. 2019, 122, 041103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lai, K.H.; Hannuksela, O.A.; Herrera-Martín, A.; Diego, J.M.; Broadhurst, T.; Li, T.G.F. Discovering intermediate-mass black hole lenses through gravitational wave lensing. Phys. Rev. D 2018, 98, 083005. [Google Scholar] [CrossRef] [Green Version]
- Smith, G.P.; Jauzac, M.; Veitch, J.; Farr, W.M.; Massey, R.; Richard, J. What if LIGO’s gravitational wave detections are strongly lensed by massive galaxy clusters? Mon. Not. R. Astron. Soc. 2018, 475, 3823–3828. [Google Scholar] [CrossRef]
- Shan, X.; Wei, C.; Hu, B. Lensing magnification: Gravitational waves from coalescing stellar-mass binary black holes. arXiv 2020, arXiv:2012.08381. [Google Scholar] [CrossRef]
- Diego, J.M.; Broadhurst, T.; Smoot, G. Evidence for lensing of gravitational waves from LIGO-Virgo. arXiv 2021, arXiv:2106.06545. [Google Scholar] [CrossRef]
- Pagano, G.; Hannuksela, O.A.; Li, T.G.F. lensingGW: A Python package for lensing of gravitational waves. Astron. Astrophys. 2020, 643, A167. [Google Scholar] [CrossRef]
- Mukherjee, S.; Wandelt, B.D.; Silk, J. Probing the theory of gravity with gravitational lensing of gravitational waves and galaxy surveys. Mon. Not. R. Astron. Soc. 2020, 494, 1956–1970. [Google Scholar] [CrossRef]
- Chung, K.W.; Li, T.G.F. Lensing of Gravitational Waves as a Novel Probe of Graviton Mass. arXiv 2021, arXiv:2106.09630. [Google Scholar] [CrossRef]
- Urrutia, J.; Vaskonen, V. Lensing of gravitational waves as a probe of compact dark matter. arXiv 2021, arXiv:2109.03213. [Google Scholar] [CrossRef]
- Cremonese, P.; Mota, D.F.; Salzano, V. Characteristic features of gravitational wave lensing as probe of lens mass model. arXiv 2021, arXiv:2111.01163. [Google Scholar]
- Hannuksela, O.A.; Haris, K.; Ng, K.K.Y.; Kumar, S.; Mehta, A.K.; Keitel, D.; Li, T.G.F.; Ajith, P. Search for gravitational lensing signatures in LIGO-Virgo binary black hole events. Astrophys. J. 2019, 874, L2. [Google Scholar] [CrossRef] [Green Version]
- Oguri, M. Strong gravitational lensing of explosive transients. Rept. Prog. Phys. 2019, 82, 126901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Diego, J.M. Constraining the abundance of primordial black holes with gravitational lensing of gravitational waves at LIGO frequencies. arXiv 2019, arXiv:1911.05736. [Google Scholar] [CrossRef]
- Broadhurst, T.; Diego, J.M.; Smoot, G.F. Interpreting LIGO/Virgo “Mass-Gap” events as lensed Neutron Star-Black Hole binaries. arXiv 2020, arXiv:2006.13219. [Google Scholar]
- Gavazzi, R.; Treu, T.; Rhodes, J.D.; Koopmans, L.V.; Bolton, A.S.; Burles, S.; Massey, R.; Moustakas, L.A. The Sloan Lens ACS Survey. 4. The mass density profile of early-type galaxies out to 100 effective radii. Astrophys. J. 2007, 667, 176–190. [Google Scholar] [CrossRef]
- Robertson, A.; Smith, G.P.; Massey, R.; Eke, V.; Jauzac, M.; Bianconi, M.; Ryczanowski, D. What does strong gravitational lensing? The mass and redshift distribution of high-magnification lenses. arXiv 2020, arXiv:2002.01479. [Google Scholar] [CrossRef]
- Belczynski, K.; Holz, D.E.; Bulik, T.; O’Shaughnessy, R. The first gravitational-wave source from the isolated evolution of two 40–100 Msun stars. Nature 2016, 534, 512. [Google Scholar] [CrossRef] [Green Version]
- Eldridge, J.J.; Stanway, E.R. BPASS predictions for Binary Black-Hole Mergers. Mon. Not. R. Astron. Soc. 2016, 462, 3302–3313. [Google Scholar] [CrossRef] [Green Version]
- Wysocki, D.; Gerosa, D.; O’Shaughnessy, R.; Belczynski, K.; Gladysz, W.; Berti, E.; Kesden, M.; Holz, D.E. Explaining LIGO’s observations via isolated binary evolution with natal kicks. Phys. Rev. D 2018, 97, 043014. [Google Scholar] [CrossRef] [Green Version]
- Dvorkin, I.; Uzan, J.P.; Vangioni, E.; Silk, J. Exploring stellar evolution with gravitational-wave observations. Mon. Not. R. Astron. Soc. 2018, 479, 121–129. [Google Scholar] [CrossRef] [Green Version]
- Kruckow, M.U.; Tauris, T.M.; Langer, N.; Kramer, M.; Izzard, R.G. Progenitors of gravitational wave mergers: Binary evolution with the stellar grid-based code ComBinE. Mon. Not. R. Astron. Soc. 2018, 481, 1908–1949. [Google Scholar] [CrossRef]
- Spera, M.; Mapelli, M.; Giacobbo, N.; Trani, A.A.; Bressan, A.; Costa, G. Merging black hole binaries with the SEVN code. Mon. Not. R. Astron. Soc. 2019, 485, 889–907. [Google Scholar] [CrossRef] [Green Version]
- Mapelli, M.; Giacobbo, N.; Santoliquido, F.; Artale, M.C. The properties of merging black holes and neutron stars across cosmic time. Mon. Not. R. Astron. Soc. 2019, 487, 2–13. [Google Scholar] [CrossRef]
- Rodriguez, C.L.; Zevin, M.; Amaro-Seoane, P.; Chatterjee, S.; Kremer, K.; Rasio, F.A.; Ye, C.S. Black holes: The next generation—Repeated mergers in dense star clusters and their gravitational-wave properties. Phys. Rev. D 2019, 100, 043027. [Google Scholar] [CrossRef] [Green Version]
- Stevenson, S.; Sampson, M.; Powell, J.; Vigna-Gómez, A.; Neijssel, C.J.; Szécsi, D.; Mandel, I. The impact of pair-instability mass loss on the binary black hole mass distribution. Astrophys. J. 2019, 882, 121. [Google Scholar] [CrossRef]
- Fragione, G.; Leigh, N.; Perna, R. Black hole and neutron star mergers in Galactic Nuclei: The role of triples. Mon. Not. R. Astron. Soc. 2019, 488, 2825–2835. [Google Scholar] [CrossRef] [Green Version]
- Woosley, S.E.; Heger, A. The Pair-Instability Mass Gap for Black Holes. Astrophys. J. Lett. 2021, 912, L31. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [LIGO Scientific Collaboration and Virgo Collaboration] Binary Black Hole Population Properties Inferred from the First and Second Observing Runs of Advanced LIGO and Advanced Virgo. Astrophys. J. 2019, 882, L24. [Google Scholar] [CrossRef] [Green Version]
- Turner, E.L.; Ostriker, J.P.; Gott, J. Richard, I. The Statistics of gravitational lenses: The Distributions of image angular separations and lens redshifts. Astrophys. J. 1984, 284, 1–22. [Google Scholar] [CrossRef]
- Fukugita, M.; Futamase, T.; Kasai, M.; Turner, E.L. Statistical Properties of Gravitational Lenses with a Nonzero Cosmological Constant. Astrophys. J. 1992, 393, 3. [Google Scholar] [CrossRef]
- Oguri, M.; Marshall, P.J. Gravitationally lensed quasars and supernovae in future wide-field optical imaging surveys. Mon. Not. R. Astron. Soc. 2010, 405, 2579–2593. [Google Scholar] [CrossRef] [Green Version]
- Hilbert, S.; White, S.D.; Hartlap, J.; Schneider, P. Strong lensing optical depths in a LambdaCDM universe. Mon. Not. R. Astron. Soc. 2007, 382, 121–132. [Google Scholar] [CrossRef] [Green Version]
- Hilbert, S.; White, S.D.; Hartlap, J.; Schneider, P. Strong lensing optical depths in a LCDM Universe. 2. The influence of the stellar mass in galaxies. Mon. Not. R. Astron. Soc. 2008, 386, 1845–1854. [Google Scholar] [CrossRef] [Green Version]
- Schneider, P.; Ehlers, J.; Falco, E.E. Gravitational Lenses; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar] [CrossRef]
- Finn, L.S.; Chernoff, D.F. Observing binary inspiral in gravitational radiation: One interferometer. Phys. Rev. 1993, D47, 2198–2219. [Google Scholar] [CrossRef] [Green Version]
- Maggiore, M. Gravitational Waves. Vol. 1: Theory and Experiments; Oxford Master Series in Physics; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Torrey, P.; Wellons, S.; Machado, F.; Griffen, B.; Nelson, D.; Rodriguez-Gomez, V.; McKinnon, R.; Pillepich, A.; Ma, C.P.; Vogelsberger, M.; et al. An analysis of the evolving comoving number density of galaxies in hydrodynamical simulations. Mon. Not. R. Astron. Soc. 2015, 454, 2770–2786. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Genel, S.; Springel, V.; Torrey, P.; Sijacki, D.; Xu, D.; Snyder, G.F.; Nelson, D.; Hernquist, L. Introducing the Illustris Project: Simulating the coevolution of dark and visible matter in the Universe. Mon. Not. R. Astron. Soc. 2014, 444, 1518–1547. [Google Scholar] [CrossRef] [Green Version]
- Vogelsberger, M.; Genel, S.; Springel, V.; Torrey, P.; Sijacki, D.; Xu, D.; Snyder, G.F.; Bird, S.; Nelson, D.; Hernquist, L. Properties of galaxies reproduced by a hydrodynamic simulation. Nature 2014, 509, 177–182. [Google Scholar] [CrossRef] [Green Version]
- Genel, S.; Vogelsberger, M.; Springel, V.; Sijacki, D.; Nelson, D.; Snyder, G.; Rodriguez-Gomez, V.; Torrey, P.; Hernquist, L. Introducing the Illustris Project: The evolution of galaxy populations across cosmic time. Mon. Not. R. Astron. Soc. 2014, 445, 175–200. [Google Scholar] [CrossRef]
- Torrey, P.; (Department of Astronomy, University of Florida, Gainesville, FL, USA). Personal communication, 2019.
- Takahashi, R.; Sato, M.; Nishimichi, T.; Taruya, A.; Oguri, M. Revising the Halofit Model for the Nonlinear Matter Power Spectrum. Astrophys. J. 2012, 761, 152. [Google Scholar] [CrossRef] [Green Version]
- Vangioni, E.; Olive, K.A.; Prestegard, T.; Silk, J.; Petitjean, P.; Mandic, V. The Impact of Star Formation and Gamma-Ray Burst Rates at High Redshift on Cosmic Chemical Evolution and Reionization. Mon. Not. R. Astron. Soc. 2015, 447, 2575. [Google Scholar] [CrossRef] [Green Version]
- Ajith, P.; Hannam, M.; Husa, S.; Chen, Y.; Brügmann, B.; Dorband, N.; Müller, D.; Ohme, F.; Pollney, D.; Reisswig, C.; et al. Inspiral-merger-ringdown waveforms for black-hole binaries with non-precessing spins. Phys. Rev. Lett. 2011, 106, 241101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Collaboration, L.S. H1 Calibrated Sensitivity Spectra June 10 2017; Technical Report; LIGO Scientific Collaboration: Cascina, Italy, 2017. [Google Scholar]
- Collaboration, L.S. L1 Calibrated Sensitivity Spectra Aug 06 2017; Technical Report; LIGO Scientific Collaboration: Cascina, Italy, 2017. [Google Scholar]
- Collaboration, L.S. Unofficial Sensitivity Curves for Various Detector Configurations Used in ISWP 2016; Technical Report; LIGO Scientific Collaboration: Cascina, Italy, 2016. [Google Scholar]
- Cusin, G.; Tamanini, N. Characterization of lensing selection effects for LISA massive black hole binary mergers. Mon. Not. R. Astron. Soc. 2021, 504, 3610–3618. [Google Scholar] [CrossRef]
- LIGO-Virgo. 2019. Available online: https://dcc.ligo.org/LIGO-P1900011/public (accessed on 16 November 2019).




| Symbol | Definition |
|---|---|
| (cosmological) source redshift | |
| (cosmological) lens redshift | |
| luminosity distance to the source | |
| luminosity distance to the lens | |
| angular diameter distance to the source | |
| angular diameter distance to the lens | |
| angular diameter distance from the lens to the source | |
| observed source redshift (inferred from standard CDM assuming no magnification) | |
| galaxy velocity dispersion | |
| magnification | |
| time-delay between multiple images | |
| lensing cross-section | |
| optical depth for magnification by at least for source at | |
| probability density of magnification for source at | |
| probability of magnification by at least for source at | |
| limiting flux of a given observatory | |
| limiting signal-to-noise ratio (corresponding to ) | |
| # sources observed with liming flux in a bin around | |
| # sources observed with liming flux in a bin around | |
| # sources that we see with liming flux in a bin around , if the magnification is | |
| # sources that we see with liming flux in a bin around , if the magnification is | |
| probability density that an observed source at (cosmological) redshift z is magnified by | |
| probability density that an observed source at observed redshift is magnified by |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cusin, G.; Durrer, R.; Dvorkin, I. Lensing Magnification Seen by Gravitational Wave Detectors. Universe 2022, 8, 19. https://doi.org/10.3390/universe8010019
Cusin G, Durrer R, Dvorkin I. Lensing Magnification Seen by Gravitational Wave Detectors. Universe. 2022; 8(1):19. https://doi.org/10.3390/universe8010019
Chicago/Turabian StyleCusin, Giulia, Ruth Durrer, and Irina Dvorkin. 2022. "Lensing Magnification Seen by Gravitational Wave Detectors" Universe 8, no. 1: 19. https://doi.org/10.3390/universe8010019
APA StyleCusin, G., Durrer, R., & Dvorkin, I. (2022). Lensing Magnification Seen by Gravitational Wave Detectors. Universe, 8(1), 19. https://doi.org/10.3390/universe8010019






