k-Essence Inflation Evading Swampland Conjectures and Inflationary Parameters

Abstract

In this paper, we study the inflationary scenario in the realm of k-essence model and swampland conjectures. Taking into account three models of Chaplygin gas, such as generalized, modified, and generalized cosmic Chaplygin gas models, we discuss the equation of state (EoS) parameter $\omega$, slow roll parameters $(ϵ(\varphi ),\eta (\varphi ))$, curvature perturbation $(P_s)$, tensor to scalar ratio $(r)$, and scalar spectral index $(n_s)$. As regards the k-essence model, the coupling function as a function of scalar field $L(\varphi )$ is used. We investigate the swampland conjecture and then find the value of $\zeta (\varphi )$, i.e., bound of second conjecture for these three models by unifying swampland conjecture and k-essence. We plot the EoS parameter $\omega$, inflationary parameters plane $r-n_s$ and bound of swampland conjecture $\zeta (\varphi )-\varphi$, which determine that the values of $\omega <-1$ for each model, r, are $r<0.0094,r\le 0.0065,r\le 0.0067$, and ranges for $n_s$ are $[0.934,0.999],[0.9,0.999],[0.9,0.992]$ for generalized, modified, and generalized cosmic Chaplygin gas models, respectively, and compare their compatibility with the Planck data from 2018. Furthermore, we determine the bound for swampland conjecture as $\zeta (\varphi )\le 0.992,\zeta (\varphi )\le 0.964,\zeta (\varphi )\le 0.964$ for generalized, modified and generalized cosmic Chaplygin gas models, respectively.

1. Introduction

The big bang model is used to describe the evolution of the universe, but this model failed to describe the formation of large scale structures, cosmic microwave background radiations, and anisotropy [1,2]. Aside from these problems, big bang is unable to give the solution of an initial value problem such as horizon flatness and monopole problems, defined as smoothness of cosmic microwave background radiations, flatness of the universe and single pole of a magnet, respectively. To solve these problems, Guth [3] proposed the model of inflation which gives the answer to these questions and inflation also gave answer to horizon, flatness and monopole problems. The universe is now in accelerating phase of expansion and the origin of this acceleration is generally attributed to dark energy (DE), an exotic type of fluid with negative pressure. Observations revealed conclusively that this unknown ingredient fills roughly $70\%$ of the Universe [4]. Several DE models are developed among which one is k-essence model with the ability to produce a DE component with a sound speed slower than the speed of light which is another intriguing feature of this model [5]. Chaplygin gas (CG) model is a DE model which is used to unify dark matter and DE [6]. The phantom era, in which the universe expands exponentially and give the possibility of DE with the EoS approximately equal to $-1$ [7]. Some more DE models are quintessence [8], cosmological constant [9], tachyon [10], quintom [11], holographic DE [12,13], etc.

Exponential expansion of the universe is called inflation.The first idea of inflation was given by Alan Guth [3]. Inflation provides an answer to the horizon and flatness problem and clarifies the large scale structure [3]. Inflation consists of two eras, i.e., slow roll and reheating, according to these eras in which we differentiate between the types of inflation. Inflation is divided into two categories: cold inflation and warm inflation. Cold inflation consists of two phases: first is the slow roll in which accelerated expansion takes place; second, there is a reheating phase after which the energy density of inflation is converted into matter [14,15]. Warm inflation in this type of inflation reheating is avoided at the end of inflation because reheating take place during the slow roll process. Another difference between cold inflation and warm inflation is initial fluctuation which is very important for the formation of large scale structures [16].

In string theory, swampland conjectures are very important as they replaced the cosmological constant $\Lambda$ with a time-dependent scalar-field quintessence with constrained parameters. Kehagias and Riotto [17] provided some comments discussing the constraints on the inflationary models inferred from the two swampland criteria which have been recently proposed. Kinney and Vagnozzi [18] consider string-motivated swampland conjectures with single-field inflation, suggesting that effective scalar field theories with a consistent ultraviolet completion must have field excursion in combination with a sufficiently steep potential. Achúcarro and Palma [19] showed that the two conditions rule out inflationary backgrounds that follow geodesic trajectories in field space, but not those following curved, non-geodesic, trajectories (which are parameterized by a non-vanishing bending rate $\Omega$ of the multi-field trajectory). Oikonomou [20] consider a fiber inflation model and super gravity $\alpha$-attractor model of the inflation and found inflationary phenomenology of the models viable. Moreover, with same values of the free parameters satisfying inflationary viability satisfy swampland conjecture criteria too. Oikonomou et al. [21] studied a class of $f(R,\varphi )$ gravity models which during the inflationary era, which is the large curvature regime, resulting in an effective inflationary Lagrangian that contains a rescaled Einstein–Hilbert term in the presence of a canonical minimally coupled scalar field. The dimensionless parameter is chosen to take values in the range $0<\alpha <1$.

CG is an exotic type of fluid, which gained attention due to negative pressure. The CG model explains the evolution of cosmos from dust-like particles to DE [22,23]. We can describe the nature of DE with the help of the negative pressure of CG which has positive energy density. To fit the cosmological data more accurately, we can make amendments in the CG model and can devise new models; generalized CG is one of those. The pure CG, also known as the generalized CG, is a perfect fluid that initially behaves like a pressureless and then like a cosmological constant. Benaoum [6], discussed the modified CG model, which describes radiation in the initial phase. CG does not meet the energy criteria, yet it nevertheless represents consistency based on evidence from several cosmic probes, e.g., Wilkinson microwave anisotropy probe (WMAP) and Hubble space telescope. To understand observational data better, different CG models were presented by adding some parameters in EoS. Bento et al. [23], used generalized CG to unify accelerated expansion with dark matter-energy. A more refined form of generalized CG is generalized cosmic CG, which was first presented by González-Díaz [24]. The advantage of this model is that it is free from instabilities and any un-physical behavior, even phantom energy condition satisfied in a vacuum fluid. Guo and Zhang [25] showed that in terms of background evolution the variable CG model is similar to an interaction model between DE and dark matter. Debnath [26] proposed a model of variable modified CG and demonstrated its role in the universe’s accelerating phase. He indicated that EoS for this model is valid from the radiation era to the quintessence phase. Herrera et al. [27] used generalized CG to study warm intermediate inflationary universe and using a generalized form of the dissipative coefficient, they investigated the model in weak and strong dissipative regimes. Jawad et al. [28] studied modified CG in framework of brane-world for inflationary universe using standard and tachyon scalar fields. After these models, to obtain more accurate results, researchers refined these models by adding new parameters. Sharif and Nawazish [29] used fluid cosmology and scalar field to study inflation for the model of homogenous and anisotropic universe in $f(R)$ gravity. Saleem [30] explored inflation during oscillations using the system of non-minimal derivative coupling and reconstructed the oscillatory inflation’s formalism by the use of anisotropic background.

Moradpour et al. [31] studied inflation in the framework of R$\acute{e}$ny entropy and found that correction to the Friedmann equations can explain both inflationary and accelerated phases. Nojiri et al. [32] studied inflation by adding a kinetic term to the action of the vacuum $f(R)$ gravity, which is k-essence $f(R)$ gravity, and examined inflationary parameters with the result that the theory is compatible with observational data. Furthermore, they discussed the existence of inflationary attractors for the slow roll inflation. Saleem and Zubair [33] used slow roll approximation and tachyon field to study the inflation using Hamiltonian–Jacobian equations. Pareek and Nautiyal [34] used quadratic and exponential potentials to discuss k-inflation constraints with kinetic term of DBI and power law from reheating. Bamba et al. [35] used inflation to study the generation of magnetic fields. When the electromagnetic field’s conformal invariance breaks down further, they found constraints of EoS parameter on the reheating equation. Moreover, many authors investigated the warm inflation in various alternatives as well as modified theories of gravity [36,37,38,39,40,41,42,43,44,45,46].

The k-essence model can be used to study cosmic inflation. In this model, Lagrangian is a function of scalar field and kinetic term. We also discuss these models to study inflation [47,48]. The k-essence models are developed from k-inflation [49] that can be used to study DE and the unification of dark matter and DE. Kinetic k-essence is a model in which only kinetic factor contained in Lagrangian and independent to the field itself. Quintessence is special case of k-essence whose Lagrangian contains non-canonical kinetic term [50,51,52,53]. Alternatively, in order to understand the evolution of early universe, we need a consistent embedding of model of early universe in quantum theory. Herrera [1] unify the k-essence and attractor using coupling parameter $L(\varphi )$ and potential $V(\varphi )$ given by $n_s(N)$ together with slow roll parameter $ϵ(N)$ (where $n_s$ and $ϵ$ both are function of number of e-folds N).

In this paper, we consider CG, modified CG, and generalized CG, in the framework of k-essence scalar field as a candidate for inflation. In Section 2, we find slow roll parameters as a function of scalar field $\varphi$ that is coupled with some coupling function $L(\varphi )$. We discuss the relation between number of e-folds N and scalar field $\varphi$, scalar and tensor perturbation. With the help of these parameters, we find tensor to scalar ratio and scalar spectral index. In Section 3, we discuss $r-n_s$ planes and analyze the compatibility of models with Planck data 2018. In Section 4, we use swampland conjectures to find the bounds for these models. We plot $\zeta (\varphi )-\varphi$ planes to find the bound of swampland constraints. In Section 5, we summarize our results.

2. General Formalism

The k-essence models are the scalar field theories for which Lagrangian is the function of kinetic term X and scalar field $\varphi$. The action term for k-essence is given as [54]

$$S=\int \sqrt{-g}{d}^{4}x\left(\frac{1}{2}R+\mathcal{L}(\varphi ,X)\right).$$

(1)

Here g is determinant of space–time metric $g_{ab},R$ represents Ricci scalar $X=\frac{-g^{ab}}{2}\frac{\partial \varphi }{\partial x^a}\frac{\partial \varphi }{\partial x^b}$ is kinetic energy of the scalar field and $\mathcal{L}(\varphi ,X)$ corresponds to Lagrangian density depends upon scalar field $\varphi$ and kinetic energy X. For the perfect fluid the pressure and density of Einstein–Hilbert action in Equation (1) can be determined by [34]

$$\begin{array}{ccc}\hfill p(\varphi ,X)& =& \mathcal{L}(\varphi ,X),\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill \rho (\varphi ,X)& =& 2X\frac{\partial \mathcal{L}(\varphi ,X)}{\partial X}-\mathcal{L}(\varphi ,X),\hfill \end{array}$$

(3)

respectively. Lagrangian density can be specifically given as $\mathcal{L}(\varphi ,X)=X-V(\varphi ),$ where $V(\varphi )$ is potential depends on scalar field. Here we use the Lagrangian density given as

$$\mathcal{L}(\varphi ,X)=2L(\varphi )X+X-V(\varphi ),$$

(4)

where $L(\varphi )$ is coupling function depends on $\varphi$ which can be defined as

$$L=h{\varphi }^p.$$

(5)

where h and p are real constants. When $L\to 0$ then we get the standard general relativity. The EoS parameter is an important cosmological parameter which classify the various phases of universe ($\omega <-1$ indicates phantom era also called inflationary era, $\omega =-1$ describes vacuum phase, $-1<\omega <-\frac{1}{3}$ presents quintessence era, $\omega =0$ identifies cold dark matter phase, $0<\omega <\frac{1}{3}$ depict the radiation phase) and mathematically given as [55]

$$\omega =\frac{p}{\rho }.$$

(6)

From Equations (2)–(4), the EoS parameter becomes

$$\omega =\frac{2XL(\varphi )+X-V(\varphi )}{2XL(\varphi )+X+V(\varphi )},$$

(7)

where

$$X=-\frac{{\dot{\varphi }}^2}{2}=-\frac{{(V^{\prime })}^2}{18H^2{(1+2L)}^2}.$$

(8)

Thus, the EoS parameter in simplified form can be given as

$$\omega =-\frac{18V(\varphi )(1+2L)H^2+{(V^{\prime })}^2}{18V(\varphi )(1+2L)H^2-{(V^{\prime })}^2}.$$

(9)

To study the inflationary models, we take the FRW metric for flat universe which is given as

$${(ds)}^2=-{(dt)}^2+a^2(t)\left(\frac{{(dr)}^2}{1-k{r}^2}+r^2{(d\theta )}^2+r^2{sin}^2\theta {(d\phi )}^2\right),$$

(10)

where $a(t)$ is scale factor and $k\in \{0,-1,1\}$ is spatial curvature defines the geometry of universe. We consider a homogeneous scalar field depending on $\varphi$ such that $\varphi =\varphi (t)$. For flat FRW metric (10), the Friedmann equation becomes

$$3H^2=\rho .$$

(11)

Now consider the equation of continuity for perfect fluid which is

$$\dot{\rho }+3H(p+\rho )=0.$$

(12)

Using Equations (2)–(4), we can write Equation (12) as

$$\ddot{\varphi }+3H\dot{\varphi }+\frac{V^{\prime }+L^{\prime }{\dot{\varphi }}^2}{1+2L}=0.$$

(13)

Equation (11) can also be described as

$$3H^2=V+\frac{{\dot{\varphi }}^2}{2}+L{\dot{\varphi }}^2.$$

(14)

Combining Equations (13) and (14), we have

$$3H^2+2\dot{H}+\frac{1}{2}{\dot{\varphi }}^2-V+L^{\prime }{\dot{\varphi }}^2=0.$$

(15)

Now we introduce slow roll parameters, which can be given as

$$\begin{array}{c}\hfill {ϵ}_1=-\frac{\dot{H}}{H^2}.\end{array}$$

(16)

$$\begin{array}{c}\hfill {ϵ}_2=-\frac{\ddot{H}}{H\dot{H}}.\end{array}$$

(17)

The above Equation (17) can also be written as

$${ϵ}_2=-\frac{\ddot{\varphi }}{H\dot{\varphi }}.$$

(18)

Some more slow roll parameters involving the coupling function can be described as

$$\begin{array}{ccc}\hfill {ϵ}_3& =& -\frac{LX}{H^2},\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill {ϵ}_4& =& -\frac{2L^{\prime }X}{V^{\prime }},\hfill \end{array}$$

(20)

where H is a Hubble parameter. The conditions resulted in the inflationary scenario, the slow roll parameters ${ϵ}_1,{ϵ}_2,{ϵ}_3,{ϵ}_4$ should be less than 1. Using the slow roll conditions from Equations (16)–(20), we can rewrite the Friedmann Equation (11) as

$$3H^2=V.$$

(21)

Equation (13) can be reduced as

$$3H\dot{\varphi }(1+2L)=-V^{\prime }.$$

(22)

Now we will discuss the inflationary parameters, but first we define inflation as exponential expansion of universe which occurs ${10}^{-32}$ s after the big bang explosion. There are various models presented defining inflation in different contexts, such as chaotic inflation, slow roll inflation, and the Staronbisky $R^2$-model. The first inflationary parameter is about slow roll, which is a phenomenon in which the scalar field is changing slowly with time. There are some basic parameters for slow roll which are given in Equations (16)–(20). Moreover, the logarithmic amount of expansion is called amount of inflation is generally called the number of e-folds and is denoted by N. We can define the number of e-folds as,

$$N={\int }_{t_f}^{t_i}Hdt,$$

(23)

where $t_f,t_i$ are final and initial time of inflation. We required at least 50 e-folds to meet the requirement of horizon problem [56]. The other important inflationary parameters are those which involves perturbation that originate from the quantum fluctuation in the inflation field. The results of CMB reveals that there were quantum fluctuations of gravity during inflation which were the seed of our universe. Despite the fact that any field can cause cosmological perturbations, we only consider scalar and tensor fluctuations [57]. The power spectrum for scalar perturbation yields

$$P_s=\frac{H^4}{4{\pi }^2{\dot{\varphi }}^2},$$

(24)

and the power spectrum for tensor perturbation is given as

$$P_t=\frac{2H^2}{{\pi }^2}.$$

(25)

The tensor to scalar ratio r is another important parameter in inflationary scenario, which is the ratio between tensor perturbation and scalar perturbation called the tensor to scalar ratio and mathematically given as [58]

$$r=\frac{P_t}{P_s}.$$

(26)

The scalar spectral index $n_s$ is another important inflationary parameter, which represents the rate of change of scalar perturbation with respect to the wave number and is given as

$$n_s=1+\frac{d\ln P_s}{\ln k},$$

(27)

where k is the wave number given as $d\ln k=-dN$. The scalar spectral index can also be represented as

$$n_s=1+2\eta -6ϵ,$$

(28)

where $\eta ,ϵ$ are slow roll parameters. If $n_s-1$ becomes fewer than one, then the power spectrum varies very slowly in slow roll inflation [59]. The other parameter is the running spectral index which can be defined as the first order derivative of spectral index and always has values less then 0, its mathematical formalism is given by [60]

$$\frac{d{n}_s}{d\ln k}=\frac{d}{d\ln k}(1+2\eta -6ϵ).$$

(29)

In an upcoming work, we will use power law potential, the power law plateau type of potential can be represented as

$$V=\frac{M^4{\varphi }^2}{m^2+{\varphi }^2},$$

(30)

where $m,M$ is sub-Planckian and GUT scale masses. Generically this potential can be represented as

$$V=V_0{\left(\frac{{\varphi }^n}{m^n+{\varphi }^n}\right)}^q.$$

(31)

Here $V_o$ is inflationary scale $\varphi ,m$ is real field and mass, respectively, and $n,q\in \mathbb{R}$ [61,62]. For plateau inflation $\varphi \ge m$ otherwise it will be identical to monomial inflation which contracts the observations.

3. Inflationary Parameters of k-Essence and Chaplygin Gas Models

There are many models used to describe DE among which the CG model is one that is used to describe DE because of its negative pressure and positive energy density. Del Campo and Herrera [63] proposed the warm CG model for which the EoS for CG is defined as

$$P=-\frac{l}{\rho },$$

(32)

where $\rho$ is positive density and l is positive constant.

3.1. Generalized Chaplygin Gas

Kammshchick [64] looked at the FRW universe made up of CG and demonstrated that it agrees with current observations of cosmic acceleration. Another model is studied, which is the generalized CG model with two free parameters with EoS as

$$P=-\frac{c}{{\rho }^{\alpha }},$$

(33)

where $\alpha \in (0,1]$ and $c>0$ is constant. The energy density of generalized CG is

$$\rho =c+\frac{A}{a^{3(1+\alpha )}},$$

(34)

where A is integration constant and a is a scale factor. The equation for $\rho$ that we obtain by extrapolation can be expressed as

$$\rho ={(c+{\rho }_{\phi }^{1+\alpha })}^{\frac{1}{1+\alpha }}.$$

(35)

The energy density corresponding to the scalar field has been in the order of potential throughout the inflationary era, hence assume that ${\rho }_{\phi }\approx V$. Now for our simplicity, suppose that $\alpha =1$ which gives

$$\rho ={(c+{\rho }_{\phi }^2)}^{\frac{1}{2}}.$$

(36)

The Friedmenn equation for Equation (36) takes the form

$$H^2=\frac{1}{3}\sqrt{c+V^2}.$$

(37)

Substituting all concerned values in Equation (9), we can find the simplified form of EoS parameter for generalized CG model as

$$\omega =-\frac{6{\varphi }^2\left(2h{\varphi }^n+1\right){\left(m^n+{\varphi }^n\right)}^2\sqrt{V_0^2{\left(\frac{{\varphi }^n}{m^n+{\varphi }^n}\right)}^{2q}+c}+V_0{n}^2{q}^2{m}^{2n}{\left(\frac{{\varphi }^n}{m^n+{\varphi }^n}\right)}^q}{6{\varphi }^2\left(2h{\varphi }^n+1\right){\left(m^n+{\varphi }^n\right)}^2\sqrt{V_0^2{\left(\frac{{\varphi }^n}{m^n+{\varphi }^n}\right)}^{2q}+c}-V_0{n}^2{q}^2{m}^{2n}{\left(\frac{{\varphi }^n}{m^n+{\varphi }^n}\right)}^q}.$$

(38)

The outcomes from Figure 1 show that $\omega <-1$ which depicts the phantom phase of the universe, also called the inflationary era, which confirms that k-essence generalized CG models exhibits inflationary era. Thus, k-essence models have a direct effect on the duration of the inflationary era.

We use slow roll approximation ${(\dot{\varphi })}^2<V$ and suppose that $V^{\prime }=\frac{\partial V}{\partial \varphi }$ and $V^{″}=\frac{{\partial }^{2}V}{\partial {\varphi }^2}$. For flatness condition, the slow roll parameters must be less than one [65,66,67]. First, we examine the first slow roll parameter ${ϵ}_1$ given in Equation (16) which yields

$${ϵ}_1=-\frac{H^{\prime }\dot{\varphi }}{H^2}\Rightarrow {ϵ}_1=\frac{3VV{}^{\prime }{}^2}{6(1+2L){(c+V^2)}^{\frac{3}{2}}}.$$

(39)

When $L\to 0$ then we will obtain ${ϵ}_1\to ϵ$

$$ϵ=\frac{3VV{}^{\prime }{}^2}{6{(c+V^2)}^{\frac{3}{2}}}.$$

(40)

Here $ϵ$ is standard slow roll parameter. On comparing Equations (39) and (40)

$${ϵ}_1=\frac{1}{1+2L}ϵ.$$

(41)

The parameter ${ϵ}_2$ in Equation (17) is given as

$${ϵ}_2=-\frac{H^{″}\dot{\varphi }}{H{H}^{\prime }}\Rightarrow {ϵ}_2=\frac{V^{″}}{(1+2L)\sqrt{c+V^2}}.$$

(42)

When $L\to 0$ then we obtain ${ϵ}_2\to \eta$

$$\eta =\frac{V^{″}}{\sqrt{c+V^2}}.$$

(43)

Here $\eta$ is standard slow roll parameter. To measure the amount of expansion of inflationary models we device a formula for number of e-folds which is

$$N={\int }_{{\varphi }_i}^{{\varphi }_f}\sqrt{c+V^2}\frac{1+2L}{V^{\prime }}d{\varphi }^{\prime },$$

(44)

where ${\varphi }_f$ is scalar field at the final stage of inflation and ${\varphi }_i$ is the scalar field at the start of inflation. The spectrum of scalar perturbation is

$$P_s=\frac{H^4}{4\pi \dot{\varphi }(1+2L)}=\frac{{(c+V^2)}^{\frac{3}{2}}(1+2L)}{12{\pi }^{2}V{}^{\prime }{}^2}.$$

(45)

The spectrum of tensor perturbation is not modified for k-essence, it is the same as in our study of general relativity [1], and can be seen in Equation (25). The spectrum of tensor to scalar ratio r for k-essence model can be given as

$$r=\frac{8V{}^{\prime }{}^2}{(1+2L)(c+V^2)}.$$

(46)

Scalar spectral index in terms of slow roll parameters in the framework of k-essence model can be given using Equation (27) as

$$n_s-1=\frac{1}{1+2L}\left[2\eta -6ϵ-\frac{2L^{\prime }{V}^{\prime }}{(1+2L)\sqrt{c+V^2}}\right].$$

(47)

Figure 2 shows the variation in $n_s$ with respect to r compared to the contours of Planck data 2018 for the schemes TT+lowE+lensing, TT,TE,EE+lowE+lensing and TT,TE,EE+ lowE+lensing+BK15+BAO. To plot $n_s-r$, we consider $n=-4.5$ for which the tensor to scalar ratio $r<0.0094$ and $n_s$ lies between ($0.934,0.999$). The graphical outcome confirms the compatibility of results with the recent Planck data.

$$\begin{array}{ccc}\hfill \frac{d{n}_s}{d\ln k}& =& \frac{-1}{{(1+2L)}^2}[\frac{2V^{\prime }{V}^{‴}}{c+V^2}-\frac{8V{(V^{\prime })}^2{V}^{″}+3{(V^{\prime })}^4}{{(c+V^2)}^2}+\frac{9V^2{(V^{\prime })}^4}{{(c+V^2)}^3}\hfill \\ \hfill & -& \frac{1}{(1+2L)}\left(\frac{2{(V^{\prime })}^2{L}^{″}}{(c+V^2)}+\frac{6V^{\prime }{V}^{″}{L}^{\prime }}{(c+V^2)}\right)+\frac{8{(V^{\prime }{L}^{\prime })}^2}{{(1+2L)}^2(c+V^2)}\hfill \\ \hfill & +& \frac{8V{(V^{\prime })}^3{L}^{\prime }}{(1+2L){(c+V^2)}^2}]\hfill \end{array}$$

(48)

3.2. Modified Chaplygin Gas

The modified CG model in the framework of FRW universe is a good candidate to explain the DE, since the strong oscillation of power spectrum and structure formation cannot be explained by CG model. So modified CG is used for such a purpose. We can modify CG because the results from CG models are similar to the $\Lambda$CDM model [68]. The EoS for modified CG is

$$P=\mu \rho -\frac{l_1}{{\rho }^{\lambda }},$$

(49)

where $\mu \in (0,\frac{1}{3}),\lambda \in (0,1]$ and $l_1$ positive constant. When $\mu =0$ then modified CG will be converted into generalized CG. The energy density of modified CG is given in the following

$$\rho ={\left(B+\frac{e}{a^{3(1+\lambda )(1+\mu )}}\right)}^{(1+\lambda )}.$$

(50)

Here $B>0,B=\frac{l_1}{1+\mu }$ and e is constant of integration. The equation of flat FRW universe in the case of modified CG is obtained from Equation (50)

$$H^2=\frac{1}{3}{(B+V^{(1+\lambda )(1+\mu )})}^{\frac{1}{1+\lambda }}.$$

(51)

Inserting the values of $H^2,V$ and L in Equation (9), some simplifications lead to the mathematical value of EoS parameter for modified CG model as

$$\omega =-\frac{6{\varphi }^2\left(2h{\varphi }^n+1\right){\left(m^n+{\varphi }^n\right)}^2{\left({\left(V_0{\left(\frac{{\varphi }^n}{m^n+{\varphi }^n}\right)}^q\right)}^{(\lambda +1)(\mu +1)}+B\right)}^{\frac{1}{\lambda +1}}+V_0{n}^2{q}^2{m}^{2n}{\left(\frac{{\varphi }^n}{m^n+{\varphi }^n}\right)}^q}{6{\varphi }^2\left(2h{\varphi }^n+1\right){\left(m^n+{\varphi }^n\right)}^2{\left({\left(V_0{\left(\frac{{\varphi }^n}{m^n+{\varphi }^n}\right)}^q\right)}^{(\lambda +1)(\mu +1)}+B\right)}^{\frac{1}{\lambda +1}}-V_0{n}^2{q}^2{m}^{2n}{\left(\frac{{\varphi }^n}{m^n+{\varphi }^n}\right)}^q}.$$

(52)

In Figure 3 it can be shown that for different values of n mentioned in the panel, the EoS parameter $\omega <-1$ which exhibits the phantom phase (inflationary era) of the universe which gives a confirmation that k-essence modified CG models are compatible with the inflationary era of the universe and thus k-essence models have a direct effect on the duration of the inflationary era.

The first slow roll parameter for modified CG can be derived for Equation (51)

$${ϵ}_1=\frac{{(V^{\prime })}^2(1+\mu )V^{(1+\lambda )(1+\mu )}}{2(1+2L){(B+V^{(1+\lambda )(1+\mu )})}^{\frac{2+\lambda }{1+\lambda }}},$$

(53)

when $L\to 0$ then we will obtain ${ϵ}_1\to ϵ$

$$ϵ=\frac{{(V^{\prime })}^2(1+\mu )V^{(1+\lambda )(1+\mu )}}{2{(B+V^{(1+\lambda )(1+\mu )})}^{\frac{2+\lambda }{1+\lambda }}},$$

(54)

from Equations (53) and (54) we have

$${ϵ}_1=\frac{1}{1+2L}ϵ.$$

(55)

Now second slow roll parameter can be determined as

$${ϵ}_2=\frac{V^{″}}{(1+2L){(B+V^{(1+\lambda )(1+\mu )})}^{\frac{1}{1+\lambda }}}.$$

(56)

For the standard slow roll parameter $\eta$ putting $L=0$ we get

$$\eta =\frac{V^{″}}{{(B+V^{(1+\lambda )(1+\mu )})}^{\frac{1}{1+\lambda }}}.$$

(57)

For the occurrence of inflationary scenario, these slow roll parameters should be less then one. Under slow roll condition number of e-folds for modified CG is

$$N={\int }_{{\varphi }_f}^{{\varphi }_i}{(B+V^{(1+\lambda )(1+\mu )})}^{\frac{1}{1+\lambda }}\frac{(1+2L)}{V^{\prime }}d{\varphi }^{\prime }.$$

(58)

The power spectrum for scalar perturbation in case of modified CG is given as

$$P_s=\frac{{(B+V^{(1+\lambda )(1+\mu )})}^{\frac{3}{1+\lambda }}(1+2L)}{12{\pi }^{2}V{}^{\prime }{}^2}.$$

(59)

The tensor to scalar ratio is given as

$$r=\frac{8{(V^{\prime })}^2}{{(B+V^{(1+\lambda )(1+\mu )})}^{\frac{2}{1+\lambda }}(1+2L)}.$$

(60)

Scalar spectral index in terms of slow roll parameter in framework of k-essence model for modified CG is given as

$$n_s-1=\frac{1}{1+2L}\left[2\eta -6ϵ-\frac{2L^{\prime }{V}^{\prime }}{(1+2L){(B+V^{(1+\lambda )(1+\mu )})}^{\frac{1}{1+\lambda }}}\right].$$

(61)

Figure 4 demonstrates the change of $n_s$ with respect to r for $n=0.27$ along with the direct confrontation against the Planck $n_s-r$ plot. We found that the value of tensor to scalar ratio remains less then 0.0065 and scalar spectral index $n_s\in [0.9,0.999]$. The Planck data 2018 contours justify the obtained results are compatible with the recent Planck data.

Running of scalar spectral index is

$$\begin{array}{ccc}\hfill \frac{d{n}_s}{d\ln k}& =& \frac{-1}{{(1+2L)}^2}[\frac{2V^{\prime }{V}^{‴}}{{(B+V^{(1+\lambda )(1+\mu )})}^{\frac{2}{1+\lambda }}}-\frac{8(1+\mu ){(V^{\prime })}^2{V}^{″}}{{(B+V^{(1+\lambda )(1+\mu )})}^{\frac{3+\lambda }{1+\lambda }}}\hfill \\ \hfill & \times & V^{\mu +\lambda +\mu \lambda }-\frac{3(1+\mu )(\mu +\lambda +\mu \lambda )V{}^{\prime }{}^4}{{(B+V^{(1+\lambda )(1+\mu )})}^{\frac{3+\lambda }{1+\lambda }}}+3{(1+\mu )}^2(2+\lambda )V{}^{\prime }{}^4\hfill \\ \hfill & \times & \frac{V^{2(\mu +\lambda +\mu \lambda )}}{{(B+V^{(1+\lambda )(1+\mu )})}^{\frac{4+2\lambda }{1+\lambda }}}-\frac{2V{}^{\prime }{}^2{L}^{″}-6V^{\prime }{V}^{″}{L}^{\prime }}{(1+2L){(B+V^{(1+\lambda )(1+\mu )})}^{\frac{2}{1+\lambda }}}\hfill \\ \hfill & +& \frac{8{(L^{\prime }{V}^{\prime })}^2}{{(1+2L)}^2{(B+V^{(1+\lambda )(1+\mu )})}^{\frac{2}{1+\lambda }}}+\frac{8(1+\mu )V{}^{\prime }{}^3{L}^{\prime }{V}^{\mu +\lambda +\mu \lambda }}{(1+2L)}\hfill \\ \hfill & \times & \frac{1}{{(B+V^{(1+\lambda )(1+\mu )})}^{\frac{3+\lambda }{1+\lambda }}}]\hfill \end{array}$$

(62)

3.3. Generalized Cosmic Chaplygin Gas

A more refined form of generalized CG is generalized cosmic CG which was first presented by González-Díaz [24]. The advantage of this model is that it is free from instabilities and any un-physical behavior even if phantom energy condition satisfied in vacuum fluid. EoS of generalized cosmic CG is given as

$$P=-{\rho }^{-\alpha }\left[D+{({\rho }^{1+\alpha }-D)}^{-\nu }\right],$$

(63)

where $D=\frac{F}{1+\nu }-1,\alpha >0$ and $\nu$ are some constants, here F can be positive or negative and $\nu \in (-j,0),j>1$. We can obtain energy density by solving continuity equation which is

$$\rho ={\left(D+{(1+\frac{f}{a^{3(1+\nu )(1+\alpha )}})}^{\frac{1}{1+\nu }}\right)}^{\frac{1}{1+\alpha }}.$$

(64)

Here f is integration constant. The Friedmenn equation for flat FRW universe in case of generalized cosmic CG for Equation (64) is given as

$$H^2=\frac{1}{3}{(D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }})}^{\frac{1}{1+\alpha }}.$$

(65)

Inserting the concerned values such as $L,V(\varphi )$ and $H^2$ in Equation (9), simplifications yields

$$\omega =-\frac{18{\varphi }^2\left(2h{\varphi }^n+1\right){\left(m^n+{\varphi }^n\right)}^2{\left({\left({\left(V_0{\left(\frac{{\varphi }^n}{m^n+{\varphi }^n}\right)}^q\right)}^{(\alpha +1)(\nu +1)}+D+1\right)}^{\frac{1}{\nu +1}}\right)}^{\frac{1}{\alpha +1}}+V_0{n}^2{q}^2{m}^{2n}{\left(\frac{{\varphi }^n}{m^n+{\varphi }^n}\right)}^q}{18{\varphi }^2\left(2h{\varphi }^n+1\right){\left(m^n+{\varphi }^n\right)}^2{\left({\left({\left(V_0{\left(\frac{{\varphi }^n}{m^n+{\varphi }^n}\right)}^q\right)}^{(\alpha +1)(\nu +1)}+D+1\right)}^{\frac{1}{\nu +1}}\right)}^{\frac{1}{\alpha +1}}-V_0{n}^2{q}^2{m}^{2n}{\left(\frac{{\varphi }^n}{m^n+{\varphi }^n}\right)}^q}.$$

(66)

The EoS parameter for k-essence generalized cosmic CG model is plotted in Figure 5 which depicts that for various values of n, $\omega <-1$ which demonstrate the phantom era (inflationary phase) of the universe confirming that k-essence modified CG models are compatible with the inflationary era of the universe and thus k-essence models have a direct impact on the duration of the inflationary phase. Dimensionless slow roll parameters for the generalized cosmic CG model are given as

$${ϵ}_1=\frac{{(V^{\prime })}^2{V}^{\alpha +\nu +\alpha \nu }}{2(1+2L){(1+V^{(1+\alpha )(1+\nu )})}^{\frac{\nu }{1+\nu }}{(D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }})}^{\frac{2+\alpha }{1+\alpha }}},$$

(67)

when $L\to 0$ then we will obtain ${ϵ}_1\to ϵ$

$$ϵ=\frac{{(V^{\prime })}^2{V}^{\alpha +\nu +\alpha \nu }}{2{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{\nu }{1+\nu }}{(D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }})}^{\frac{2+\alpha }{1+\alpha }}}.$$

(68)

Second slow roll parameter is obtained as

$${ϵ}_2=\frac{V^{″}}{(1+2L){(D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }})}^{\frac{1}{1+\alpha }}}.$$

(69)

The value of parameter $\eta$ can be obtained by substituting $L=0$, which is

$$\eta =\frac{V^{″}}{{(D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }})}^{\frac{1}{1+\alpha }}}.$$

(70)

The number of e-folds for generalized cosmic CG is

$$N={\int }_{{\varphi }_f}^{{\varphi }_i}{(D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }})}^{\frac{1}{1+\alpha }}\frac{1+2L}{V^{\prime }}d{\varphi }^{\prime }.$$

(71)

The power spectrum of scalar and tensor perturbation for generalized cosmic CG is given as

$$P_s=\frac{{(D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }})}^{\frac{3}{1+\alpha }}(1+2L)}{12{\pi }^{2}V{}^{\prime }{}^2}.$$

(72)

Tensor to scalar ratio can be determined by using Equations (25) and (72) as

$$r=\frac{8V{}^{\prime }{}^2}{(1+2L){(D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }})}^{\frac{2}{1+\alpha }}}.$$

(73)

Scalar spectral index for generalized cosmic CG is given as

$$n_s-1=\frac{1}{1+2L}\left[2\eta -6ϵ-\frac{2L^{\prime }{V}^{\prime }}{(1+2L){(D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }})}^{\frac{1}{1+\alpha }}}\right].$$

(74)

Figure 6 shows the variation in tensor to scalar ratio r with respect to the scalar spectral index $n_s$, which we plotted for $n=0.16$ along with the contours of Planck data from 2018 for different schemes. The outcomes depicted that tensor to scalar ratio $r<0.0067$ while the scalar spectral index $0.9\le n_s\le 0.992$. Planck’s data contours and the plotted trajectory depicts that model is compatible with the different schemes of the recent Planck data.

$$\begin{array}{ccc}\hfill \frac{d{n}_s}{d\ln k}& =& \frac{-1}{{(1+2L)}^2}[\frac{2V^{\prime }{V}^{‴}}{{(D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }})}^{\frac{2}{1+\alpha }}}\hfill \\ \hfill & -& \frac{8{(V^{\prime })}^2{V}^{″}{V}^{\alpha +\nu +\alpha \nu }}{{(D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }})}^{\frac{3+\alpha }{1+\alpha }}}\hfill \\ \hfill & \times & \frac{1}{{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{\nu }{1+\nu }}}-\frac{3(\alpha +\nu +\alpha \nu ){(V^{\prime })}^4}{{(D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }})}^{\frac{3+\alpha }{1+\alpha }}}\hfill \\ \hfill & \times & \frac{V^{\alpha +\nu +\alpha \nu -1}}{{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{\nu }{1+\nu }}}+\frac{3\nu (1+\alpha ){(V^{\prime })}^4}{{(D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }})}^{\frac{3+\alpha }{1+\alpha }}}\hfill \\ \hfill & \times & \frac{V^{2(\alpha +\nu +\alpha \nu )}}{{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1+2\nu }{1+\nu }}}+\frac{3(2+\alpha ){(V^{\prime })}^4}{{(D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }})}^{\frac{4+2\alpha }{1+\alpha }}}\hfill \\ \hfill & \times & \frac{V^{2(\alpha +\nu +\alpha \nu )}}{{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{2\nu }{1+\nu }}}-\frac{2{(V^{\prime })}^2{L}^{″}{(1+2L)}^{-1}}{{(D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }})}^{\frac{2}{1+\alpha }}}\hfill \\ \hfill & -& \frac{6L^{\prime }{V}^{\prime }{V}^{″}}{(1+2L){(D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }})}^{\frac{2}{1+\alpha }}}\hfill \\ \hfill & +& \frac{8{(L^{\prime }{V}^{\prime })}^2}{{(1+2L)}^2{[D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }}]}^{\frac{2}{1+\alpha }}}\hfill \\ \hfill & +& \frac{8L^{\prime }{(V^{\prime })}^3{V}^{\alpha +\nu +\alpha \nu }}{(1+2L){(1+V^{(1+\alpha )(1+\nu )})}^{\frac{\nu }{1+\nu }}}\hfill \\ \hfill & \times & \frac{1}{{(D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }})}^{\frac{3+\alpha }{1+\alpha }}}].\hfill \end{array}$$

(75)

4. Swampland Conjectures of k-Essence and Chaplygin Gas Models

Super-string theory is a theory that unifies all forces of nature and has strict constraints called the Swampland constraints or conjectures. There are two conjectures. The first is about the range of inflationary field which is less then the Planckian mass, i.e., $\Delta \varphi <M_p$ and the second is related to the slope of scalar potential which is

$$\frac{\nabla V}{V}\ge \frac{\zeta }{M_p},$$

(76)

where ∇ is gradient in space of field [69], V is the scalar potential $\nabla V$ is slope of scalar potential. We can use entropy arguments to find the bound that is given in Equation (76), we assume that $\varphi$ is increasing function and with increase in $\varphi$, M($\varphi$) of effective degrees of freedom increase and will enter in low energy effective field theory [69] such that

$$M\sim nexp(b\varphi ),$$

(77)

where n is monotonic function depending upon $\varphi$ and we have photons with masses

$$m\sim exp(-a\Delta \varphi ),$$

(78)

where $a,b$ are constant. Since n is monotone so

$$\frac{dn}{d\varphi }>0.$$

(79)

We have the Hubble horizon as $R=\frac{1}{H}$ and in Equation (77) we define tower state entropy as

$$S_t(M,R)=M^{\gamma }{(R)}^{\delta },$$

(80)

where $\gamma ,\delta$ are constants and Gibbons-Hawking entropy is stated below

$$M^{\gamma }{(R)}^{\delta }\le 8{\pi }^2{R}^2.$$

(81)

4.1. Generalized Chaplygin Gas

To find the bound of swampland constraint, substitute the value of H from Equation (37), we have

$$\frac{c+V^2}{9}\le {(\frac{8{\pi }^2}{M^{\gamma }})}^{\frac{4}{2-\delta }}.$$

(82)

Taking the logarithm and derivative of the above inequality, we obtain

$$\frac{V{V}^{\prime }}{c+V^2}\le -\frac{2\gamma {(\ln M)}^{\prime }}{2-\delta }.$$

(83)

In Equation (83) the left hand side of Equation (76) implies

$$\frac{V^{\prime }}{V}\ge (1+\frac{c}{V^2})\frac{2\gamma {(\ln M)}^{\prime }}{2-\delta }.$$

(84)

Using Equation (77) in Equation (84)

$$\frac{V^{\prime }}{V}\ge (1+\frac{c}{V^2})\frac{2\gamma }{2-\delta }(b+\frac{n^{\prime }}{n})>(1+\frac{c}{V^2})\frac{2b\gamma }{2-\delta }.$$

(85)

Comparing Equation (85) with Equation (76), we obtain

$$\zeta =(1+\frac{c}{V^2})\frac{2b\gamma }{2-\delta }$$

(86)

Figure 7 represents the change in bound of second swampland conjecture with respect to scalar field. The behavior of all the three trajectories shows the value of $\zeta (\varphi )$ is less than 1. For $n=1$ trajectory is different than $n=2,3$ and near $\varphi =0.3$ these two trajectories coincide.

4.2. Modified Chaplygin Gas

To find the bound for modified CG model, substituting the value of H in Equation (81), simplification leads to the relation

$$\frac{{(B+V^{(1+\lambda )(1+\mu )})}^{\frac{1}{1+\lambda }}}{3}\le {(\frac{8{\pi }^2}{M^{\gamma }})}^{\frac{1}{1-\frac{\delta }{2}}}.$$

(87)

Taking the log and differentiating Equation (87), we have

$$\frac{(1+\mu )V^{\prime }{V}^{\mu +\lambda +\mu \lambda }}{B+V^{(1+\lambda )(1+\mu )}}\ge \frac{2\gamma {(\ln M)}^{\prime }}{2-\delta }.$$

(88)

From Equation (88), the left hand side of inequality (76) becomes

$$\frac{V^{\prime }}{V}\ge \frac{2\gamma b}{(1+\mu )(2-\delta )}(1+\frac{B}{V^{(1+\lambda )(1+\mu )}}).$$

(89)

By comparing Equation (89) and Equation (76), we have

$$\zeta =\frac{2\gamma b}{(1+\mu )(2-\delta )}(1+\frac{B}{V^{(1+\lambda )(1+\mu )}}).$$

(90)

Figure 8 represents the variation in lower bound of swampland second conjecture with scalar field. The plot of all the three trajectories shows that the value of $\zeta (\varphi )$ is less than 1. For $n=1$ trajectory is distinct then $n=2,3$ and after $\varphi =0.25$ these two trajectories overlapped.

4.3. Generalized Cosmic Chaplygin Gas

The bound for generalized cosmic CG can be determined by putting the value of H in Equation (37), we obtain

$$\frac{{(D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }})}^{\frac{1}{1+\alpha }}}{3}\le {(\frac{8{\pi }^2}{N^{\gamma }})}^{\frac{1}{1-\frac{\delta }{2}}},$$

(91)

By taking the derivative of logarithm of Equation (91) we have

$$\frac{V^{\alpha +\nu +\alpha \nu }{V}^{\prime }}{{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{\nu }{1+\nu }}(D+{(1+V^{(1+\alpha )(1+\nu )})}^{\frac{1}{1+\nu }})}\ge \frac{2\gamma {(\ln N)}^{\prime }}{2-\delta }$$

(92)

Simplifying Equation (92) to obtain the left side of Equation (76)

$$\frac{V^{\prime }}{V}\ge {(1+\frac{1}{V^{(1+\alpha )(1+\nu )}})}^{\frac{\nu }{1+\nu }}(\frac{D}{V^{1+\alpha }}+{(1+\frac{1}{V^{(1+\alpha )(1+\nu )}})}^{\frac{1}{1+\nu }}\frac{2b\gamma }{(2-\delta )})$$

(93)

By comparing Equation (93) and Equation (76) we obtain the value of $\zeta$ as

$$\zeta ={(1+\frac{1}{V^{(1+\alpha )(1+\nu )}})}^{\frac{\nu }{1+\nu }}(\frac{D}{V^{1+\alpha }}+{(1+\frac{1}{V^{(1+\alpha )(1+\nu )}})}^{\frac{1}{1+\nu }}\frac{2b\gamma }{(2-\delta )})$$

(94)

Figure 9 demonstrates the variation in bound of second swampland conjecture with respect to scalar field. The behavior of all the three trajectories shows the value of $\zeta (\varphi )$ is less than 1. For $n=1$ trajectory is different than $n=2,3$ and after $\varphi =0.25$ these two trajectories coincide.

5. Concluding Remarks

In this paper, we studied CG models, such as generalized CG, modified CG and generalized cosmic CG in inflationary scenario for FRW universe taking into account scalar field setup. We used the Friedmann equation to find the EoS parameter and parameters of inflation, i.e., slow roll, scalar perturbation, tensor perturbation, tensor to scalar ratio, and scalar spectral index. We determined all these parameters as a function of scalar field $\varphi$. We plotted the EoS parameter and $n_s-r$ planes along with their contours of Planck data 2018 for all the three models to check their compatibility with the recent Planck data.

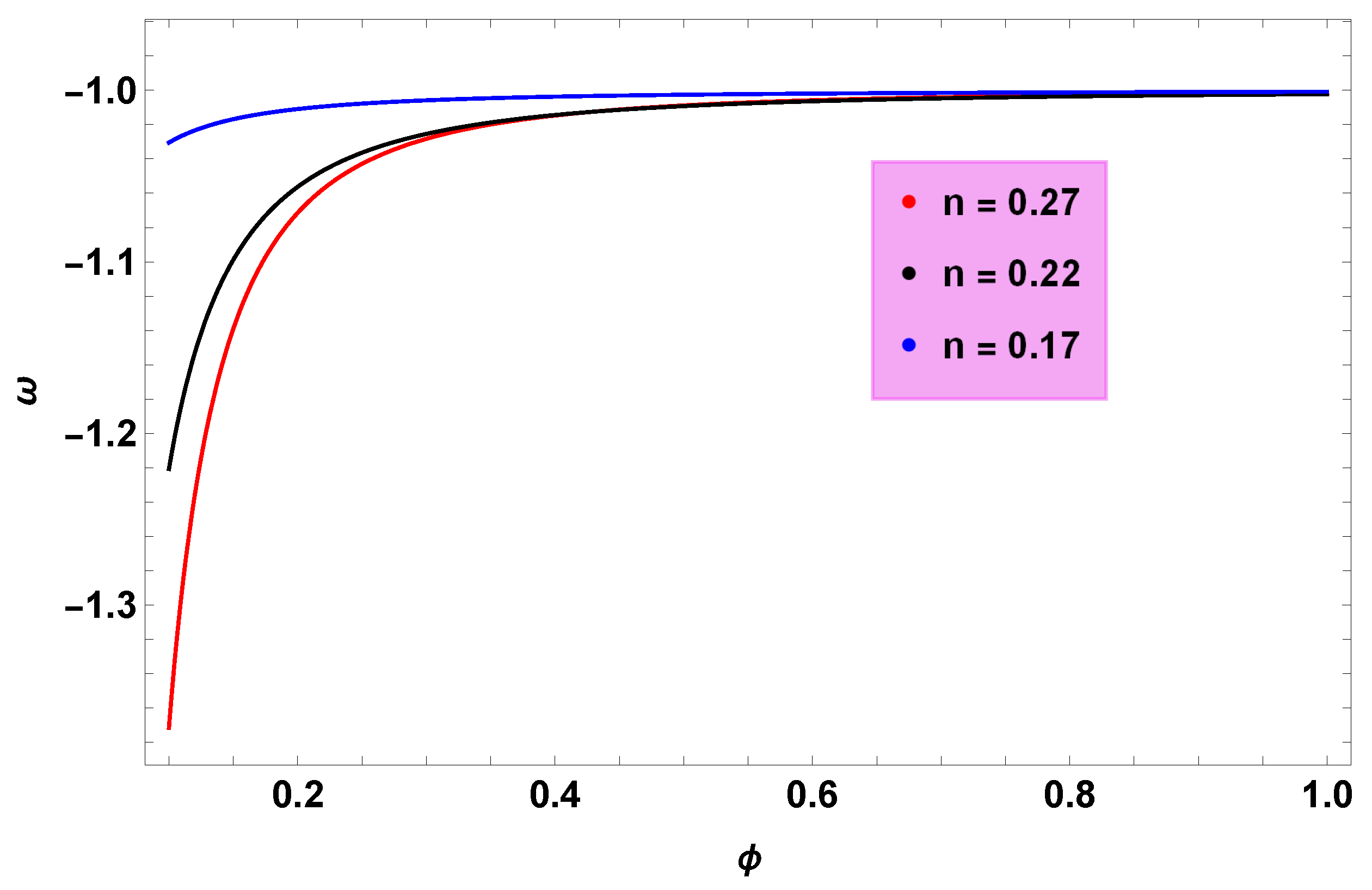
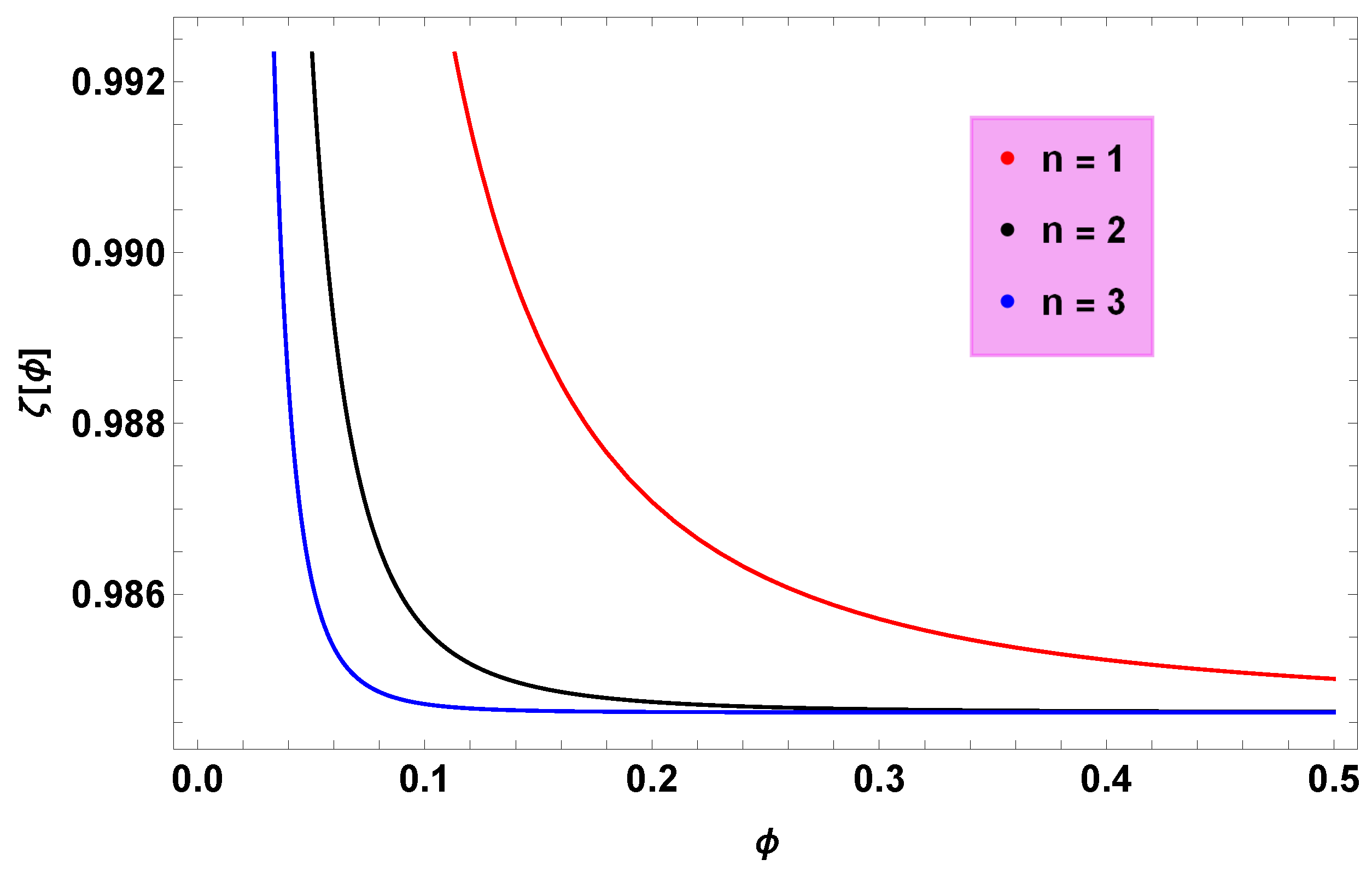
• In generalized CG, we found from Figure 1 that $\omega <-1$ depicts the phantom phase (inflationary era) of the universe justifying that k-essence models have a direct effect on the duration of the inflationary era.
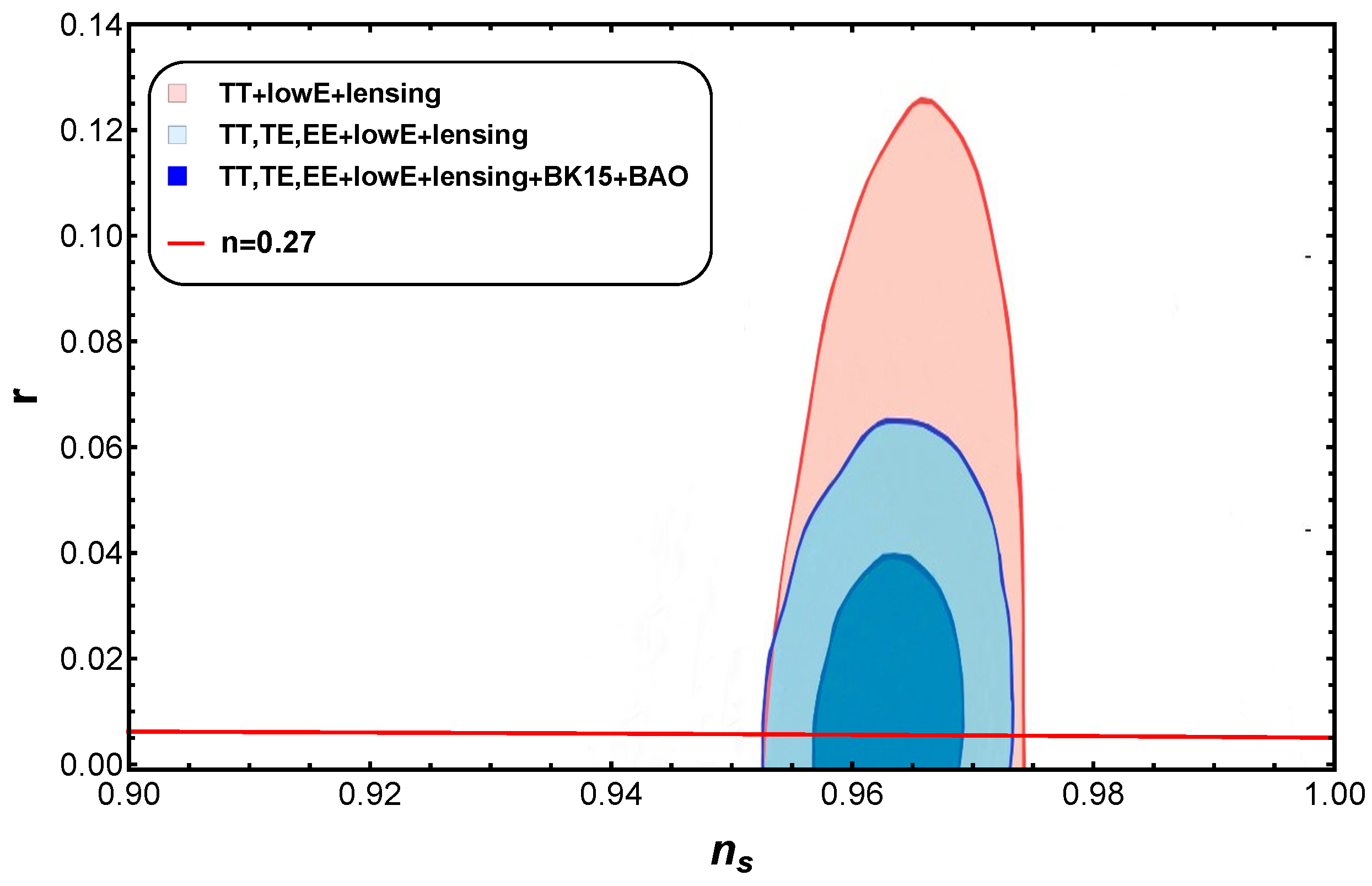
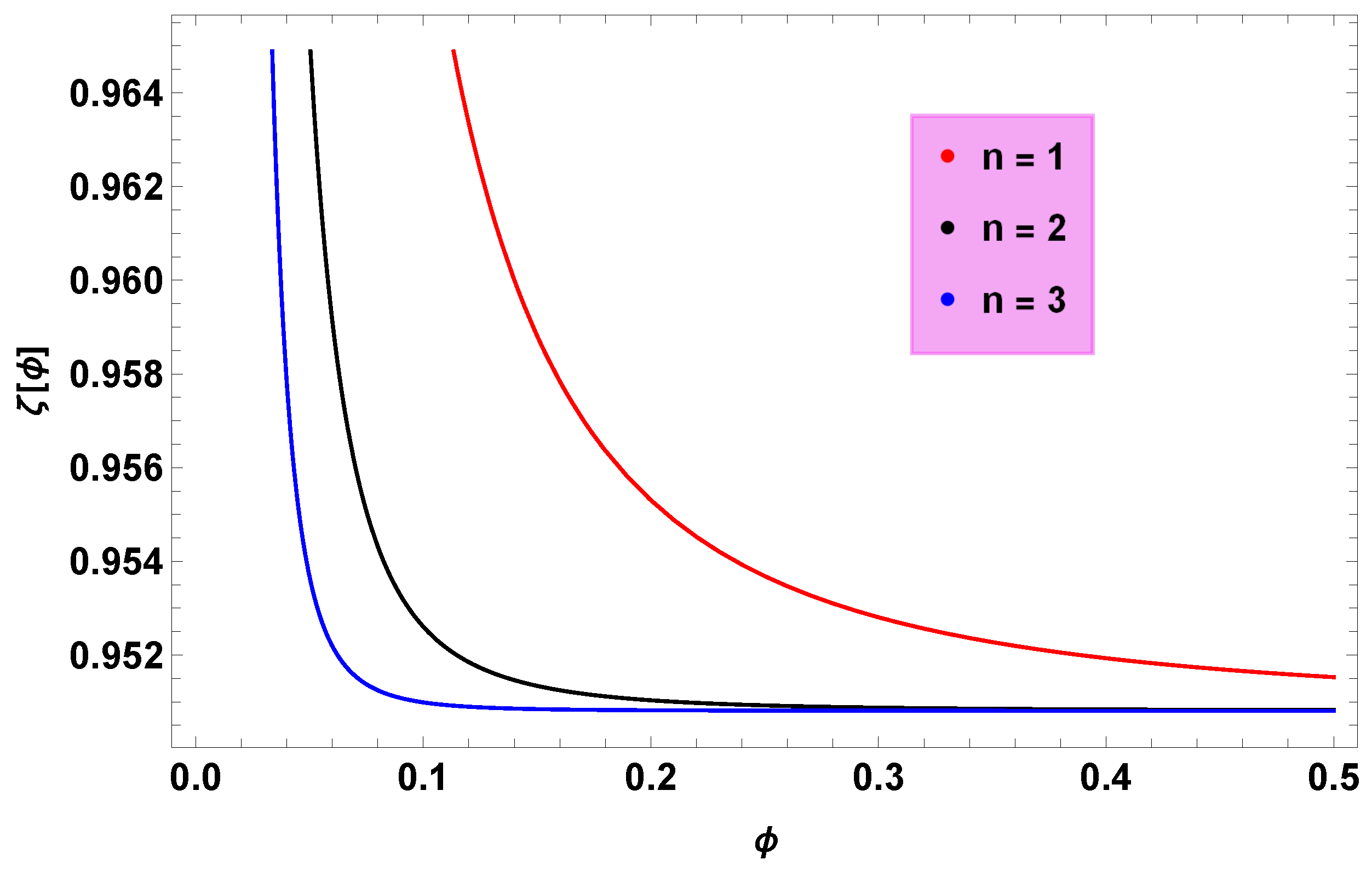
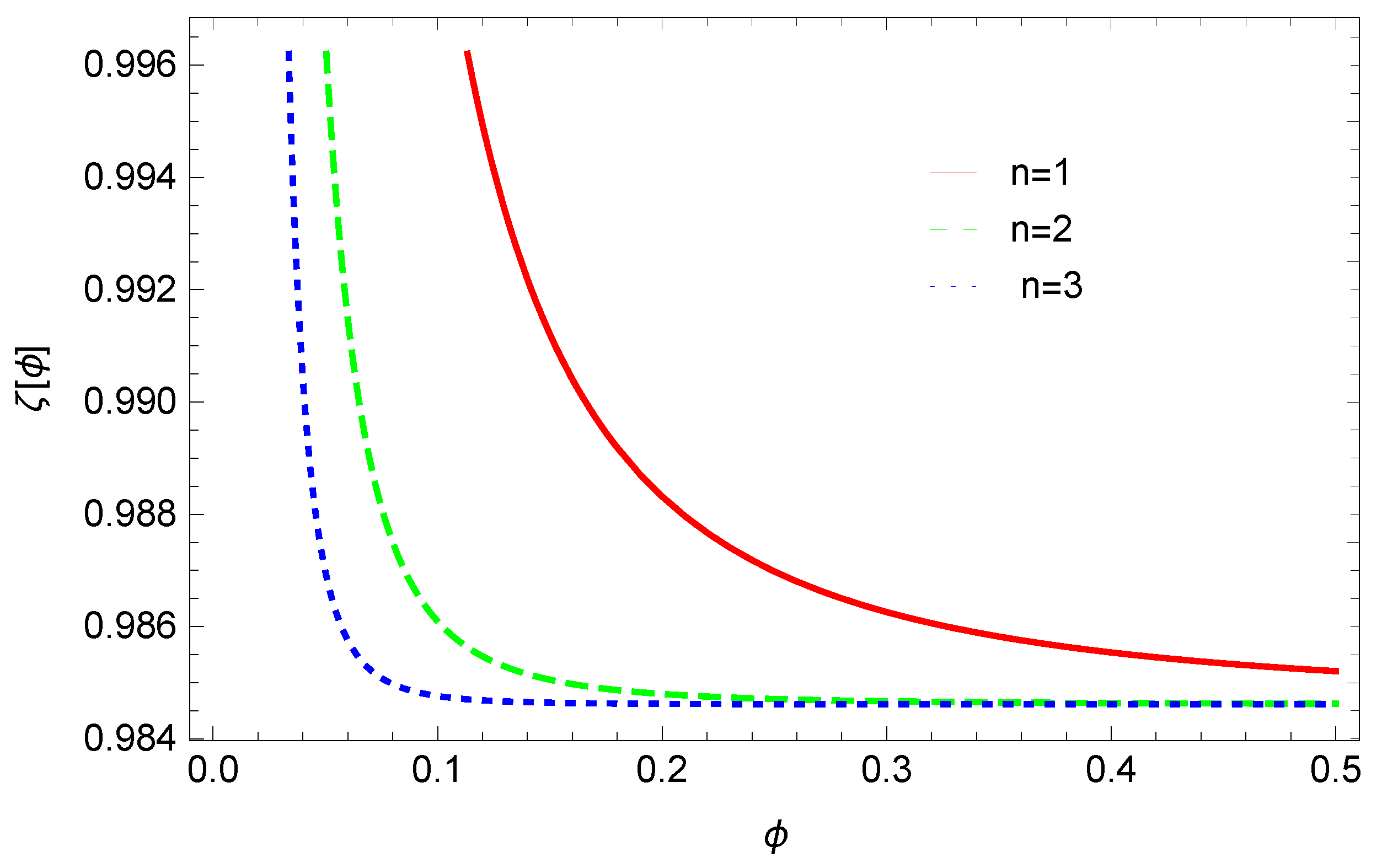
• In generalized CG, we observed that for Figure 2, $n_s$ lies in the range $[0.934,0.999]$ and $r<0.0094$ which is compatible with Planck’s 2018 data.
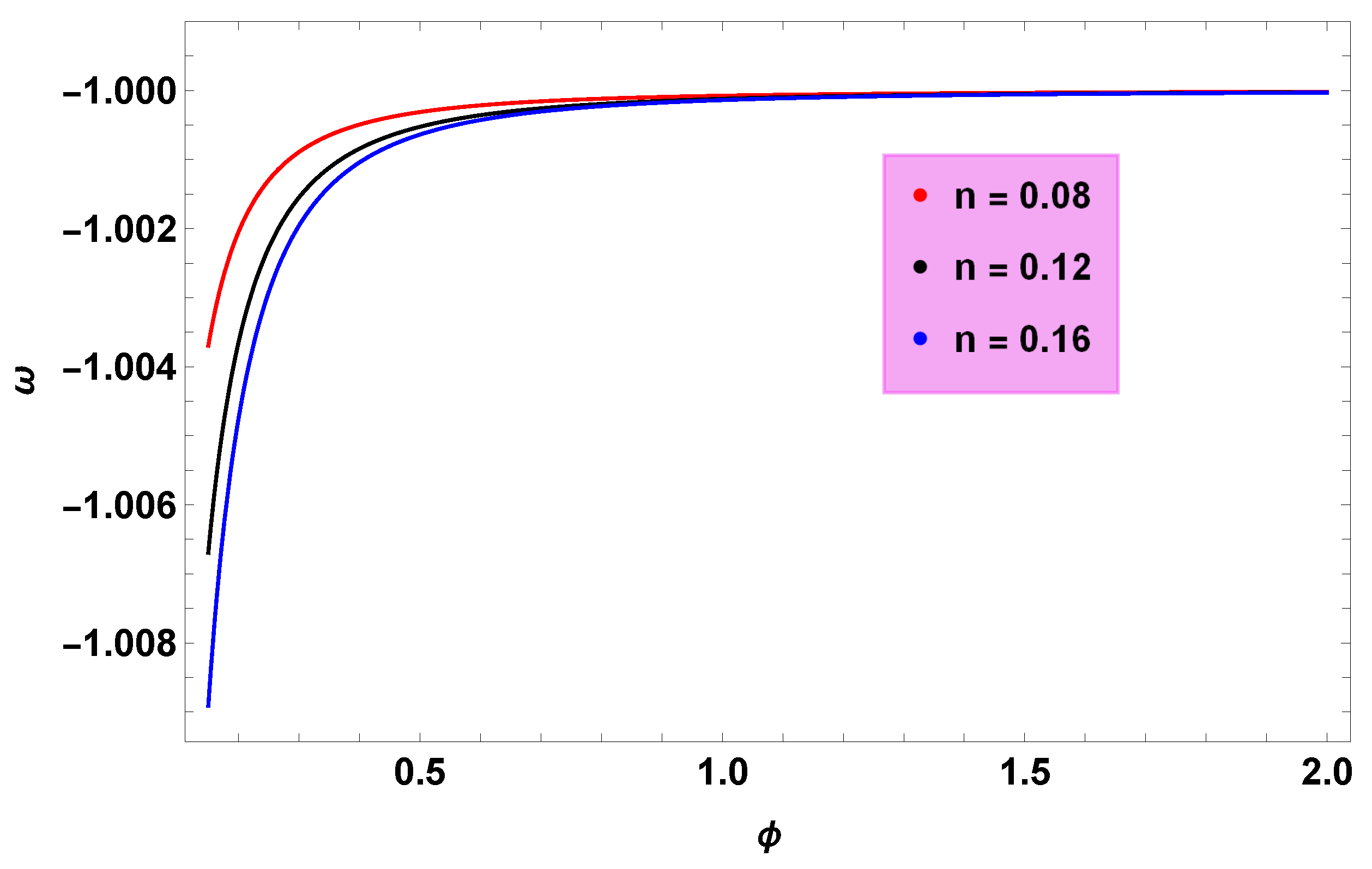
• In modified CG, we observed from Figure 3 that $\omega <-1$ results in the phantom era (inflationary phase) of the universe which justify the direct effect on the duration of the inflationary era by k-essence modified CG models.
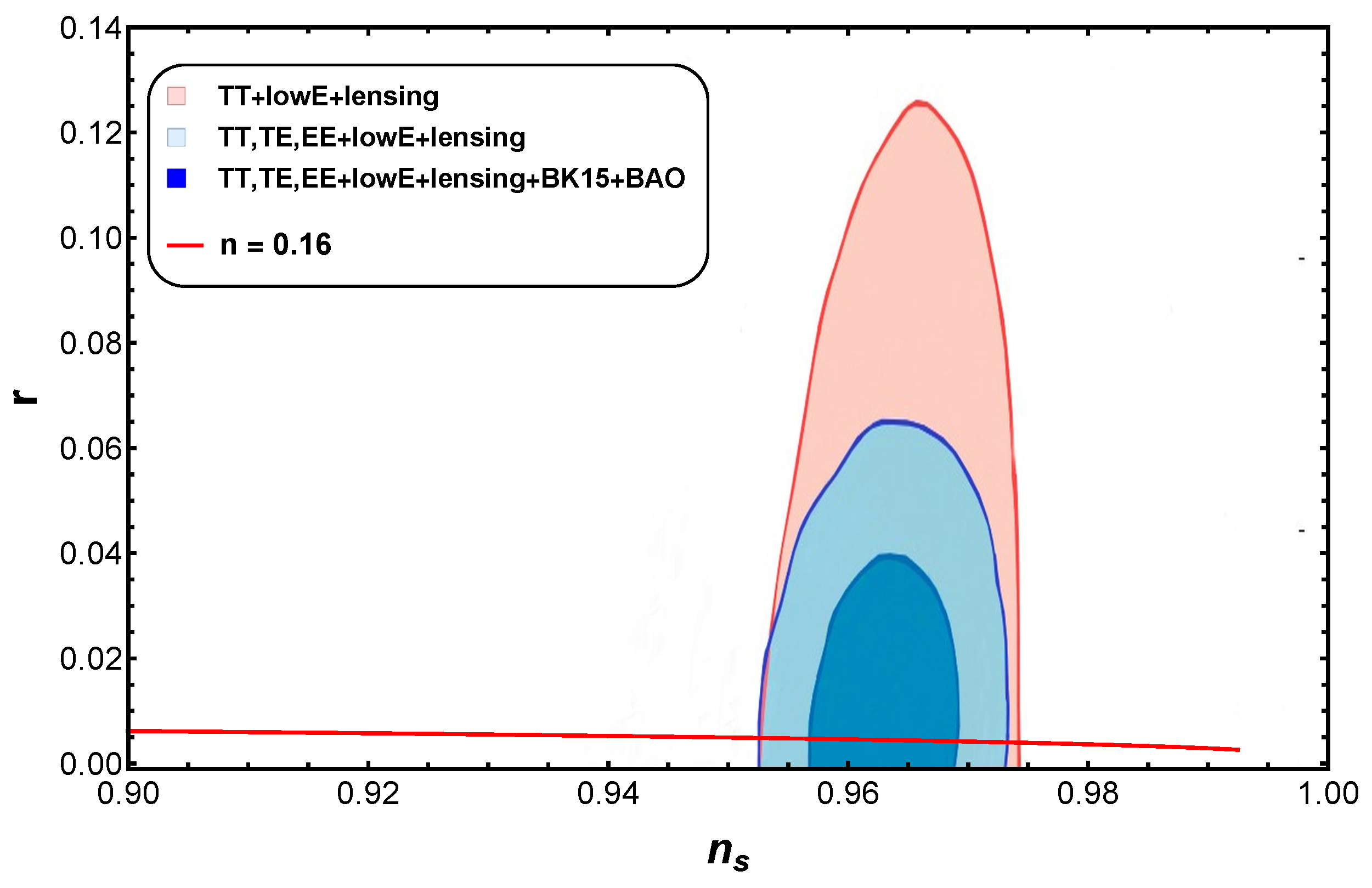
• For modified CG, we noticed in Figure 4 that $n_s$ lies in the range $[0.9,0.999]$ and $r\le 0.0065$ which is comparable with Planck data from 2018.
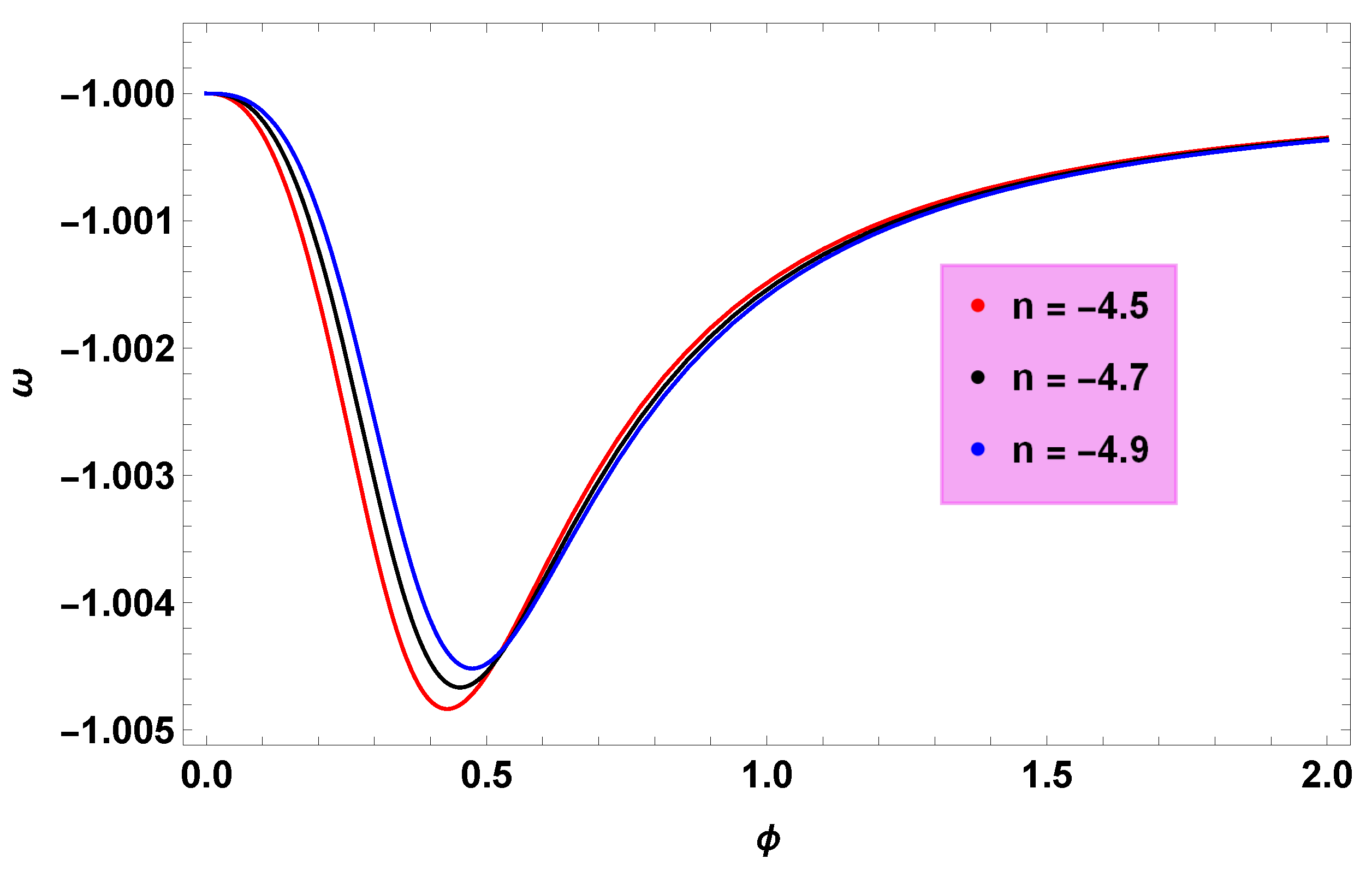
• Figure 5 show that EoS parameter $\omega <-1$ describing the phantom era of the universe which is a justification of the direct effect on the duration of the inflationary era by k-essence generalized cosmic CG models.
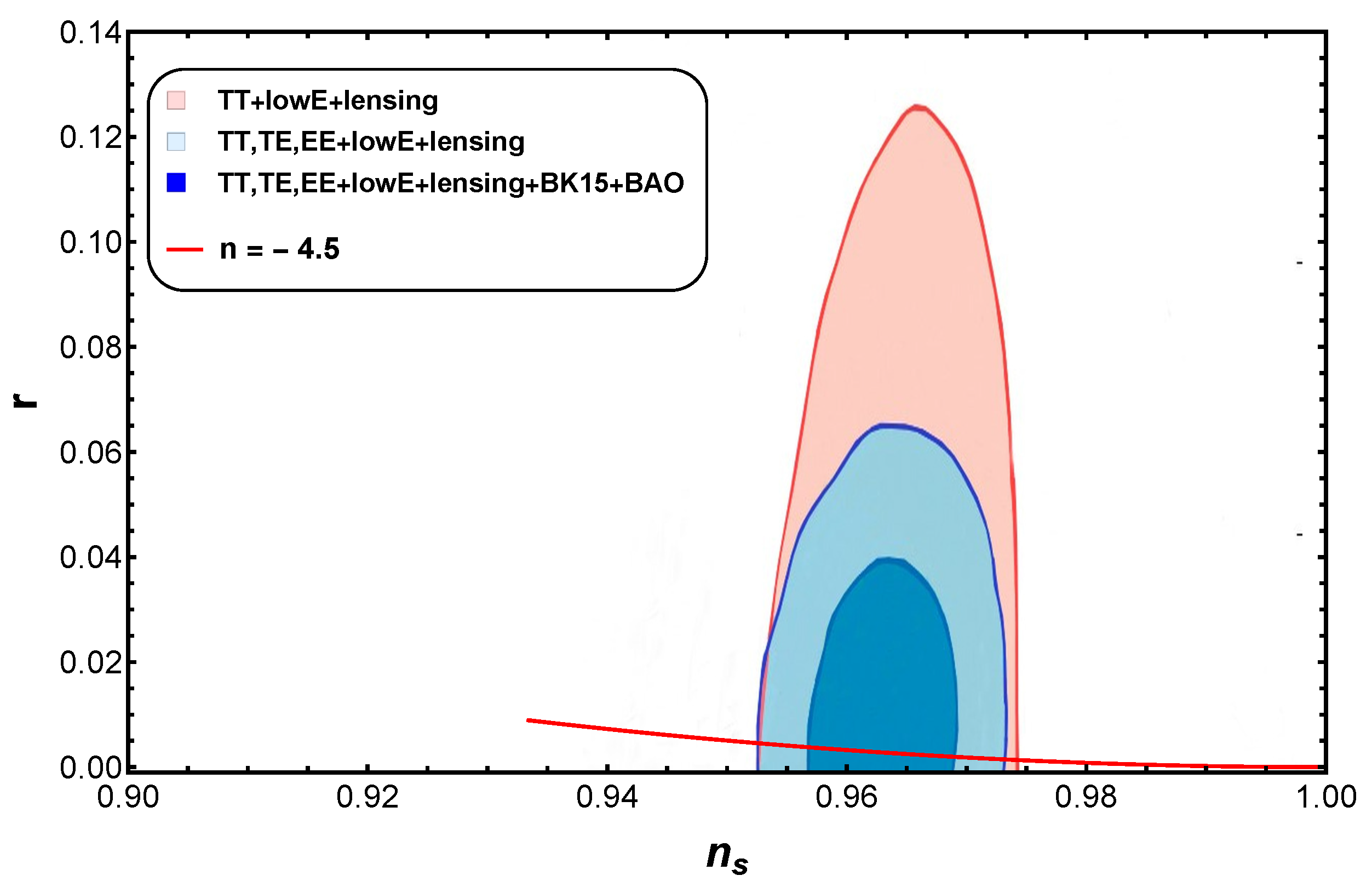
• Using generalized cosmic CG, we observed that in Figure 6, $n_s$ is in the range $[0.9,0.992]$ and $r\le 0.0067$ which is compatible with Planck data from 2018.

The Planck data [70] given as

Table 1. Observational Scheme of Planck 2018.

Parameters	TT+lowE	TT,TE,EE+lowE	TT,TE,EE+lowE+lensing
$n_s$	$0.9626\pm 0.0057$	$0.9649\pm 0.0044$	$0.9649\pm 0.0042$
r	<0.102	<0.107	<0.101

:

After calculating inflationary parameters, we unified the k-essence with swampland conjecture to find to bounds of swampland for CG gas models in k-essence frame. We used the entropy argument and effective field theories to find the bounds of swampland conjecture for all the three models. Then we plot $\zeta (\varphi )-\varphi$ planes for all CG gas models.

• Figure 7 represent the plot for generalized CG in which we demonstrated that for $\varphi \in (0,0.5),\zeta (\varphi )\le 0.992.$
• Figure 8 is the graph for modified CG in which we showed that for $\varphi \in (0,0.5)$, we have $\zeta (\varphi )\le 0.964.$
• Figure 9 is the plot for generalized cosmic CG in which we demonstrated that for $\varphi \in (0,0.5)$, we have $\zeta (\varphi )\le 0.964$

Hence, we have shown that the value of the constant, i.e., the bound of swampland conjecture, must be of order 1.