Afterglow Light Curves from Off-Axis GRB Jets in Stratified Circumburst Medium
Abstract
:1. Introduction
2. The Analytical Light Curves from an Off-Axis Jet in the Stratified Medium
2.1. Coasting Phase
2.2. Deceleration Phase
2.3. Late Afterglow
3. The Numerical Calculation of Afterglow Light Curves
3.1. Dynamic Evolution of the Afterglow Jet
3.2. Flux Calculation
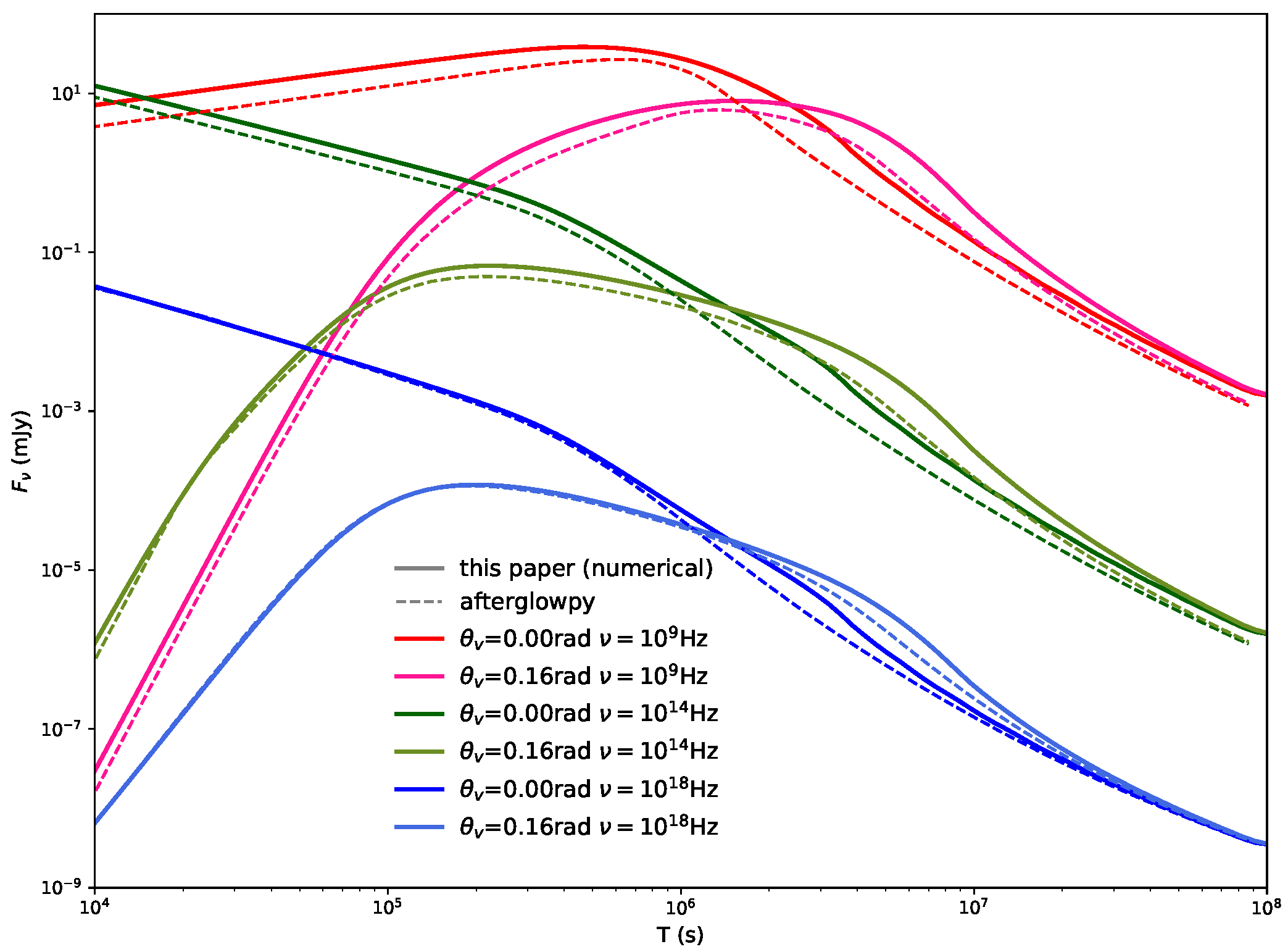
3.3. Code Verification
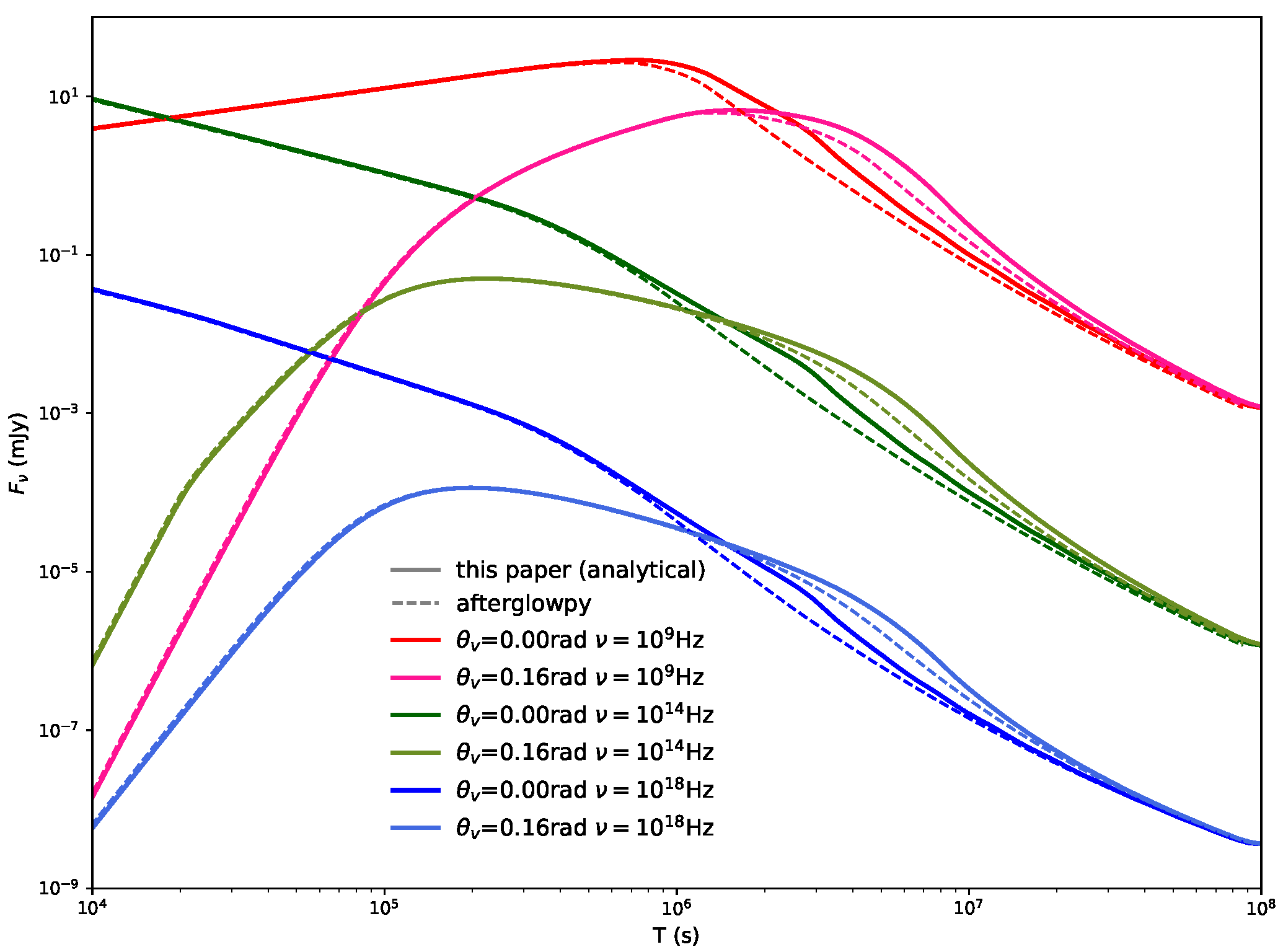
3.4. Comparison with the Analytical Results
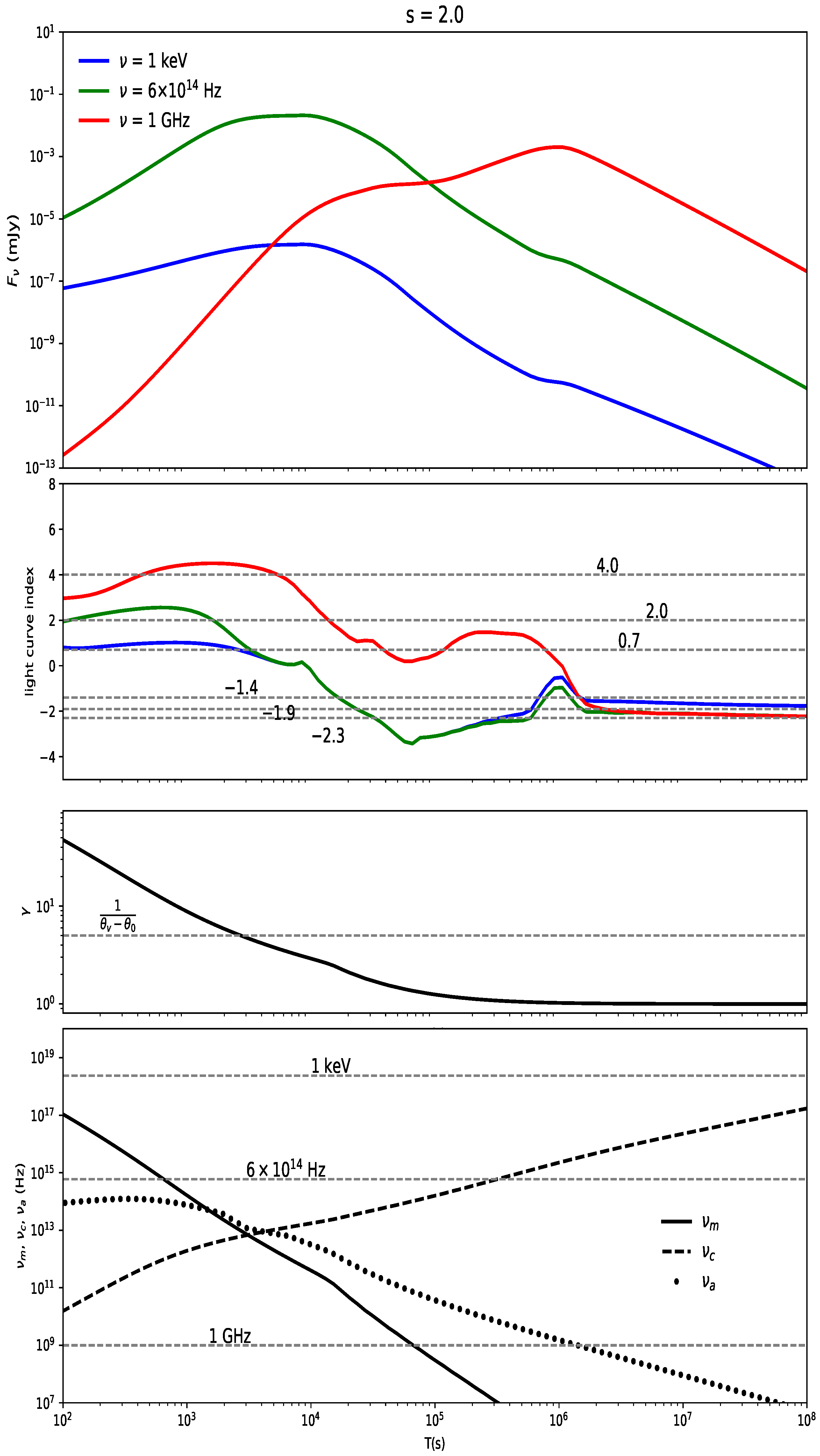
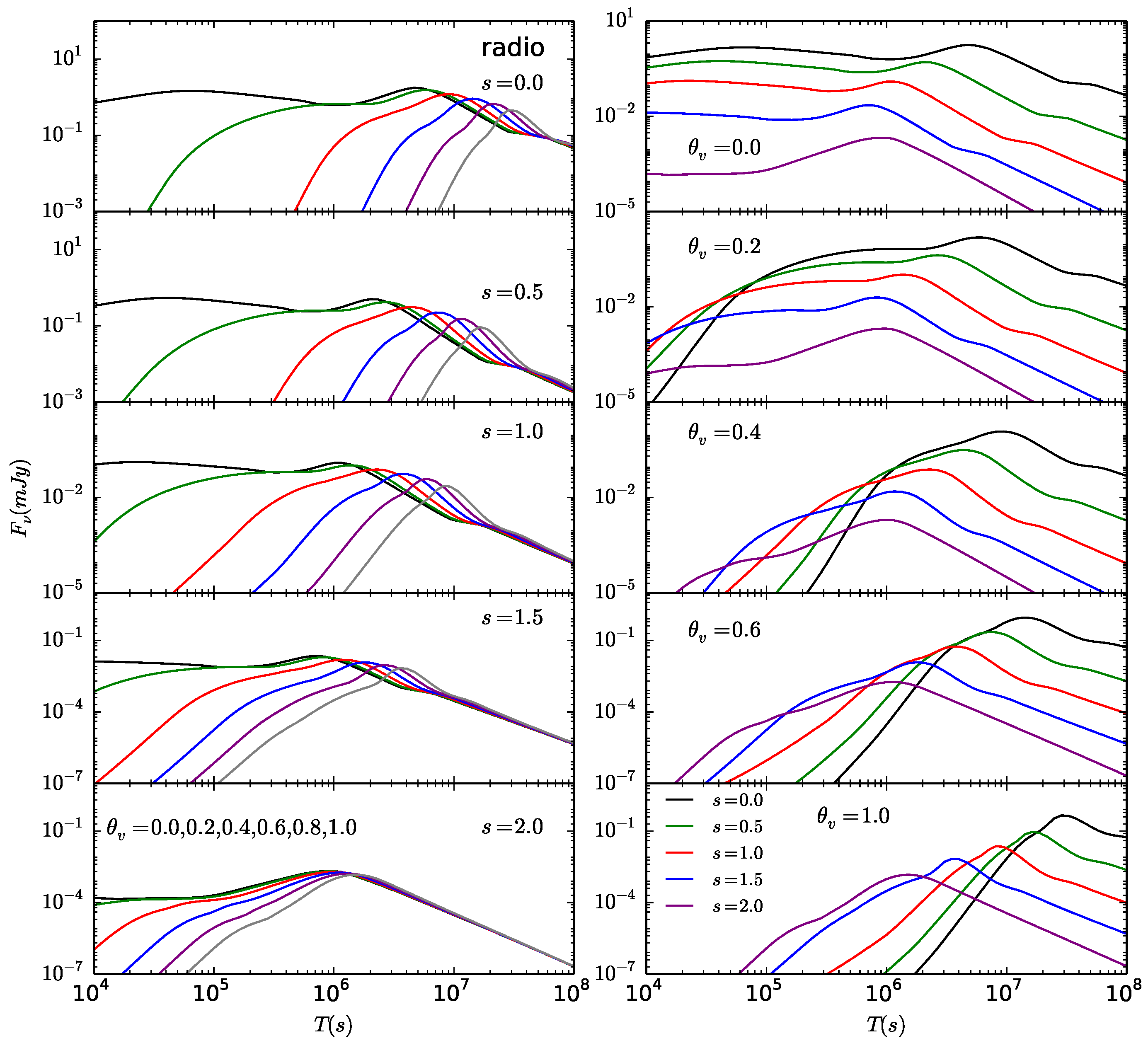
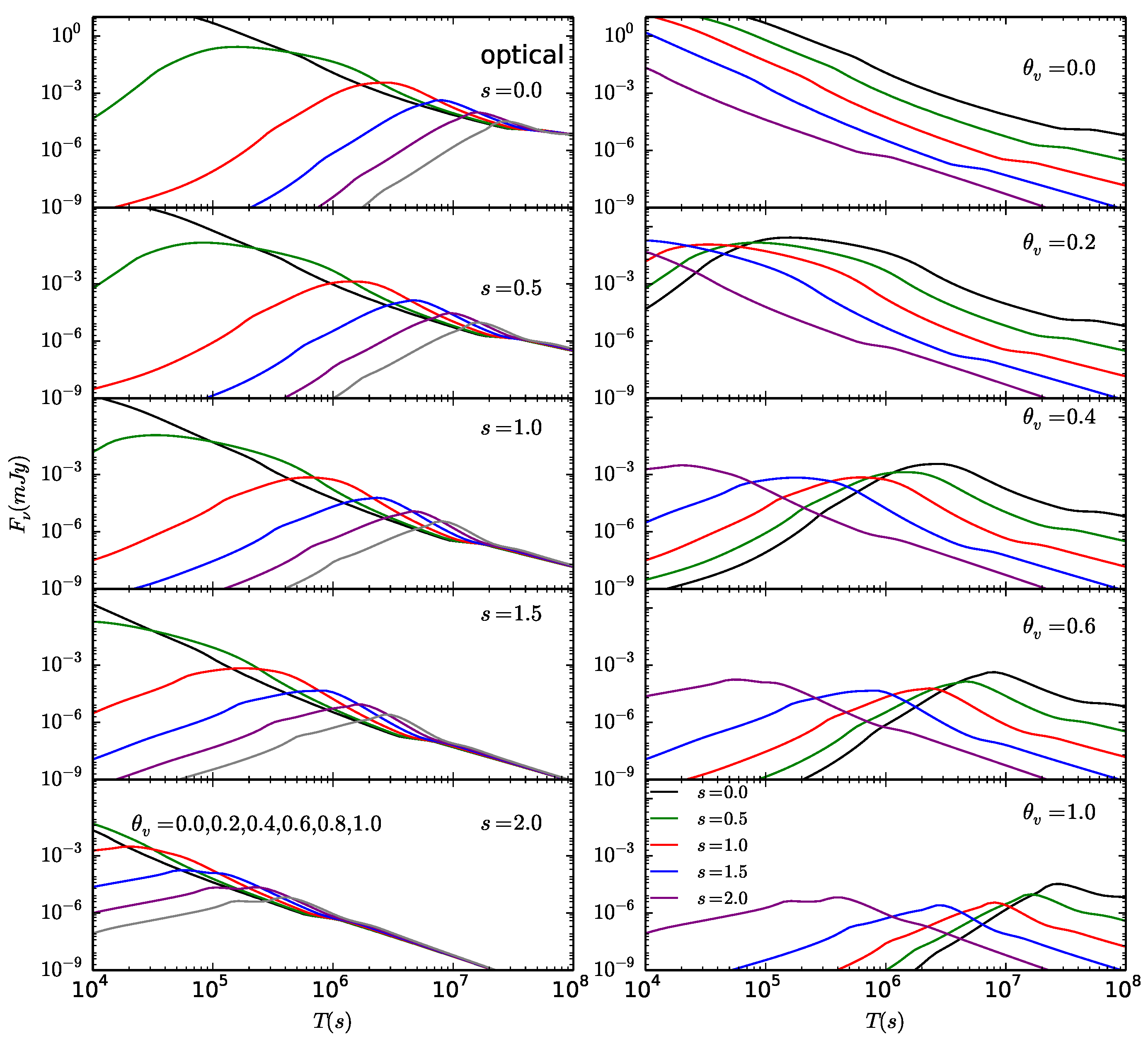
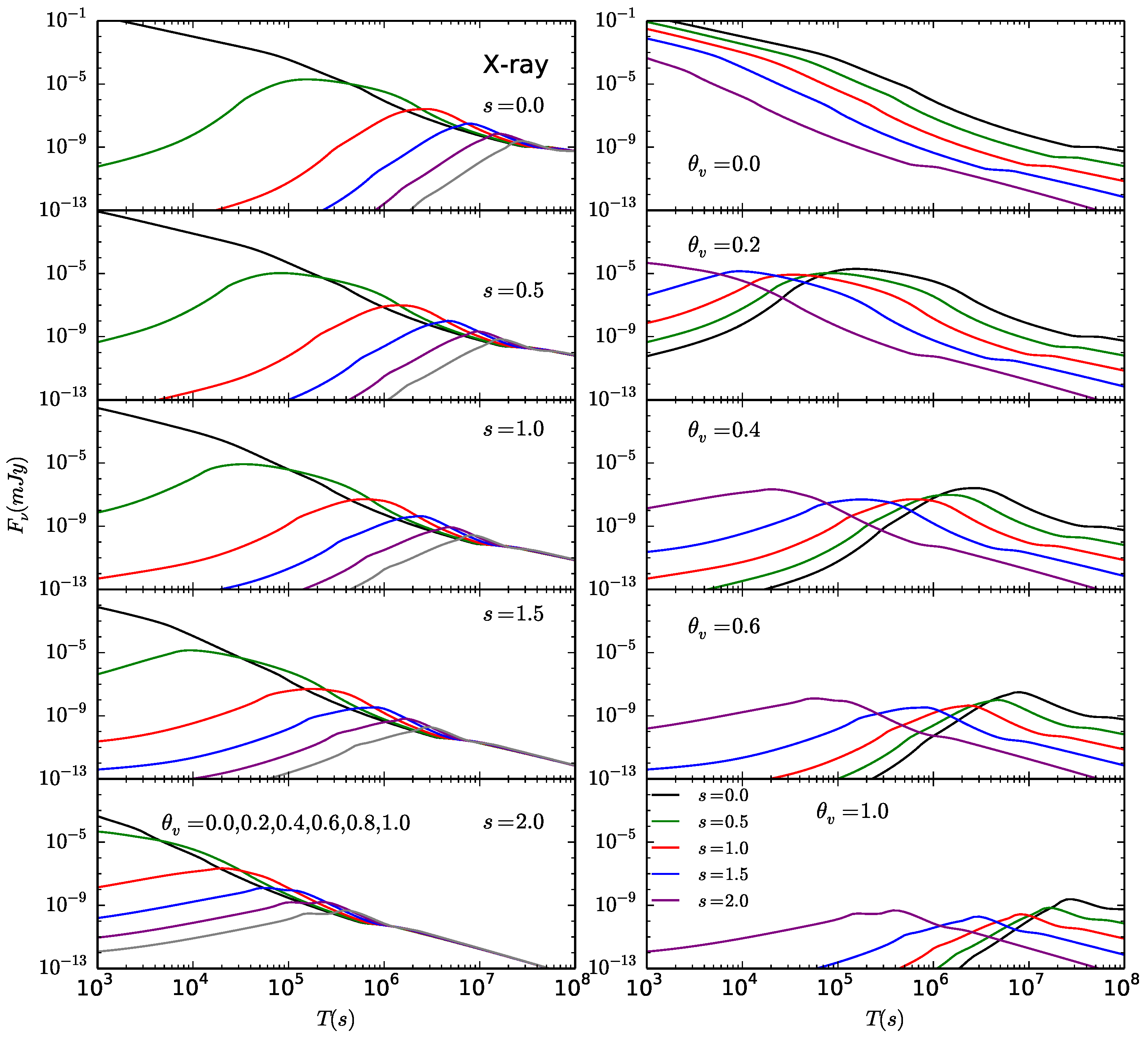
3.5. Typical Off-Axis Light Curves in a Stratified Medium
4. Summary and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Off-Axis Afterglow Light Curves for νm < νa < νc, νc < νa < νm, νa > max(νc, νm)
References
- Katz, J.I. Low-Frequency Spectra of Gamma-Ray Bursts. Astrophys. J. 1994, 432, L107–L109. [Google Scholar] [CrossRef]
- Mészáros, P.; Rees, M.J. Optical and Long-Wavelength Afterglow from Gamma-Ray Bursts. Astrophys. J. 1997, 476, 232–237. [Google Scholar] [CrossRef] [Green Version]
- Blandford, R.D.; McKee, C.F. Fluid dynamics of relativistic blast waves. Phys. Fluids 1976, 19, 1130–1138. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T.; Narayan, R. Spectra and Light Curves of Gamma-Ray Burst Afterglows. Astrophys. J. 1998, 497, L17–L20. [Google Scholar] [CrossRef]
- Harrison, F.A.; Bloom, J.S.; Frail, D.A.; Sari, R.; Kulkarni, S.R.; Djorgovski, S.G.; Axelrod, T.; Mould, J.; Schmidt, B.P.; Wieringa, M.H.; et al. Optical and Radio Observations of the Afterglow from GRB 990510: Evidence for a Jet. Astrophys. J. 1999, 523, L121–L124. [Google Scholar] [CrossRef] [Green Version]
- Kulkarni, S.R.; Djorgovski, S.G.; Odewahn, S.C.; Bloom, J.S.; Gal, R.R.; Koresko, C.D.; Harrison, F.A.; Lubin, L.M.; Armus, L.; Sari, R.; et al. The afterglow, redshift and extreme energetics of the γ-ray burst of 23 January 1999. Nature 1999, 398, 389–394. [Google Scholar] [CrossRef] [Green Version]
- Rhoads, J.E. The Dynamics and Light Curves of Beamed Gamma-Ray Burst Afterglows. Astrophys. J. 1999, 525, 737–749. [Google Scholar] [CrossRef] [Green Version]
- Sari, R.; Piran, T.; Halpern, J.P. Jets in Gamma-Ray Bursts. Astrophys. J. 1999, 519, L17–L20. [Google Scholar] [CrossRef] [Green Version]
- Heise, J.; Zand, J.I.; Kippen, R.M.; Woods, P.M. Gamma-Ray Bursts in the Afterglow Era; Costa, E., Frontera, F., Hjorth, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; p. 16. [Google Scholar]
- Yamazaki, R.; Ioka, K.; Nakamura, T. X-ray Flashes from Off-Axis Gamma-Ray Bursts. Astrophys. J. 2002, 571, L31–L35. [Google Scholar] [CrossRef]
- Zhang, B.; Dai, X.; Lloyd-Ronning, N.M.; Mészáros, P. Quasi-universal Gaussian Jets: A Unified Picture for Gamma-Ray Bursts and X-Ray Flashes. Astrophys. J. 2004, 601, L119–L122. [Google Scholar] [CrossRef]
- Ghirlanda, G.; Burlon, D.; Ghisellini, G.; Salvaterra, R.; Bernardini, M.G.; Campana, S.; Covino, S.; D’Avanzo, P.; D’Elia, V.; Melandri, A.; et al. GRB Orphan Afterglows in Present and Future Radio Transient Surveys. Publ. Astron. Soc. Aust. 2014, 31, 22. [Google Scholar] [CrossRef] [Green Version]
- Granot, J.; Panaitescu, A.; Kumar, P.; Woosley, S.E. Off-Axis Afterglow Emission from Jetted Gamma-Ray Bursts. Astrophys. J. 2002, 570, L61–L64. [Google Scholar] [CrossRef]
- Huang, Y.F.; Dai, Z.G.; Lu, T. Failed gamma-ray bursts and orphan afterglows. Mon. Not. R. Astron. Soc. 2002, 332, 735–740. [Google Scholar] [CrossRef] [Green Version]
- Lamb, G.P.; Tanaka, M.; Kobayashi, S. Transient survey rates for orphan afterglows from compact merger jets. Mon. Not. R. Astron. Soc. 2018, 476, 4435–4441. [Google Scholar] [CrossRef]
- Levinson, A.; Ofek, E.O.; Waxman, E.; Gal-Yam, A. Orphan Gamma-Ray Burst Radio Afterglows: Candidates and Constraints on Beaming. Astrophys. J. 2002, 576, 923–931. [Google Scholar] [CrossRef]
- Nakar, E.; Piran, T.; Granot, J. The Detectability of Orphan Afterglows. Astrophys. J. 2002, 579, 699–705. [Google Scholar] [CrossRef] [Green Version]
- Totani, T.; Panaitescu, A. Orphan Afterglows of Collimated Gamma-Ray Bursts: Rate Predictions and Prospects for Detection. Astrophys. J. 2002, 576, 120–134. [Google Scholar] [CrossRef] [Green Version]
- Zou, Y.C.; Wu, X.F.; Dai, Z.G. Estimation of the detectability of optical orphan afterglows. Astron. Astrophys. 2007, 461, 115–119. [Google Scholar] [CrossRef]
- van Eerten, H.; Zhang, W.; MacFadyen, A. Off-axis Gamma-ray Burst Afterglow Modeling Based on a Two-dimensional Axisymmetric Hydrodynamics Simulation. Astrophys. J. 2010, 722, 235–247. [Google Scholar] [CrossRef] [Green Version]
- Ho, A.Y.Q.; Perley, D.A.; Yao, Y.; Svinkin, D.; Postigo, A.d.; Perley, R.A.; Kann, D.A.; Burns, E.; Andreoni, I.; Bellm, E.C.; et al. Cosmological Fast Optical Transients with the Zwicky Transient Facility: A Search for Dirty Fireballs. arXiv 2022, arXiv:2201.12366. [Google Scholar] [CrossRef]
- Granot, J.; De Colle, F.; Ramirez-Ruiz, E. Off-axis afterglow light curves and images from 2D hydrodynamic simulations of double-sided GRB jets in a stratified external medium. Mon. Not. R. Astron. Soc. 2018, 481, 2711–2720. [Google Scholar] [CrossRef] [Green Version]
- Moderski, R.; Sikora, M.; Bulik, T. On Beaming Effects in Afterglow Light Curves. Astrophys. J. 2000, 529, 151–156. [Google Scholar] [CrossRef] [Green Version]
- Rossi, E.; Lazzati, D.; Rees, M.J. Afterglow light curves, viewing angle and the jet structure of r-ray bursts. Mon. Not. R. Astron. Soc. 2002, 332, 945–950. [Google Scholar] [CrossRef] [Green Version]
- Salafia, O.S.; Ghisellini, G.; Pescalli, A.; Ghirlanda, G.; Nappo, F. Light curves and spectra from off-axis gamma-ray bursts. Mon. Not. R. Astron. Soc. 2016, 461, 3607–3619. [Google Scholar] [CrossRef] [Green Version]
- MacFadyen, A.I.; Woosley, S.E. Collapsars: Gamma-Ray Bursts and Explosions in “Failed Supernovae”. Astrophys. J. 1999, 524, 262–289. [Google Scholar] [CrossRef] [Green Version]
- Paczyński, B. Gamma-ray bursts as hypernovae. AIP Conf. Proc. 1998, 428, 783–787. [Google Scholar]
- Woosley, S.E. Gamma-Ray Bursts from Stellar Mass Accretion Disks around Black Holes. Astrophys. J. 1993, 405, 273. [Google Scholar] [CrossRef]
- Chevalier, R.A.; Li, Z.-Y. Gamma-Ray Burst Environments and Progenitors. Astrophys. J. 1999, 520, L29–L32. [Google Scholar] [CrossRef] [Green Version]
- Chevalier, R.A.; Li, Z.-Y. Wind Interaction Models for Gamma-Ray Burst Afterglows: The Case for Two Types of Progenitors. Astrophys. J. 2000, 536, 195–212. [Google Scholar] [CrossRef] [Green Version]
- Dai, Z.G.; Lu, T. Gamma-ray burst afterglows: Effects of radiative corrections and non-uniformity of the surrounding medium. Mon. Not. R. Astron. Soc. 1998, 298, 87–92. [Google Scholar] [CrossRef] [Green Version]
- Ramirez-Ruiz, E.; Dray, L.M.; Madau, P.; Tout, C.A. Winds from massive stars: Implications for the afterglows of r-ray bursts. Mon. Not. R. Astron. Soc. 2001, 327, 829–840. [Google Scholar] [CrossRef]
- Fong, W.; Berger, E.; Margutti, R.; Zauderer, B.A. A Decade of Short-duration Gamma-Ray Burst Broadband Afterglows: Energetics, Circumburst Densities, and Jet Opening Angles. Astrophys. J. 2015, 815, 102. [Google Scholar] [CrossRef] [Green Version]
- Nicuesa Guelbenzu, A.; Klose, S.; Greiner, J.; Kann, D.A.; Krühler, T.; Rossi, A.; Schulze, S.; Afonso, P.M.J.; Elliott, J.; Filgas, R.; et al. Multi-color observations of short GRB afterglows: 20 events observed between 2007 and 2010. Astron. Astrophys. 2012, 548, A101. [Google Scholar] [CrossRef]
- Yi, S.-X.; Wu, X.-F.; Dai, Z.-G. Early afterglows of gamma-ray bursts in a stratified medium with a power-law density distribution. Am. Astron. Soc. 2013, 776, 120. [Google Scholar] [CrossRef]
- Yi, S.-X.; Wu, X.-F.; Zou, Y.-C.; Dai, Z.-G. The Bright Reverse Shock Emission in the Optical Afterglows of Gamma-Ray Bursts in a Stratified Medium. Astrophys. J. 2020, 895, 94. [Google Scholar] [CrossRef]
- LIGO Scientific Collaboration and Virgo Collaboration. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [Green Version]
- Gill, R.; Granot, J. Afterglow imaging and polarization of misaligned structured GRB jets and cocoons: Breaking the degeneracy in GRB 170817A. Mon. Not. R. Astron. Soc. 2018, 478, 4128–4141. [Google Scholar] [CrossRef]
- Granot, J.; Guetta, D.; Gill, R. Lessons from the Short GRB 170817A: The First Gravitational-wave Detection of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 850, L24. [Google Scholar] [CrossRef] [Green Version]
- Granot, J.; Gill, R.; Guetta, D.; De Colle, F. Off-axis emission of short GRB jets from double neutron star mergers and GRB 170817A. Mon. Not. R. Astron. Soc. 2018, 481, 1597–1608. [Google Scholar] [CrossRef] [Green Version]
- Lamb, G.P.; Kobayashi, S. Electromagnetic counterparts to structured jets from gravitational wave detected mergers. Mon. Not. R. Astron. Soc. 2017, 472, 4953–4964. [Google Scholar] [CrossRef]
- Lazzati, D.; Perna, R.; Morsony, B.J.; Lopez-Camara, D.; Cantiello, M.; Ciolfi, R.; Giacomazzo, B.; Workman, J.C. Kuramoto Model for Excitation-Inhibition-Based Oscillations. Phys. Rev. Lett. 2018, 120, 241103. [Google Scholar] [CrossRef] [PubMed]
- Mooley, K.P.; Deller, A.T.; Gottlieb, O.; Nakar, E.; Hallinan, G.; Bourke, S.; Frail, D.A.; Horesh, A.; Corsi, A.; Hotokezaka, K. Superluminal motion of a relativistic jet in the neutron-star merger GW170817. Nature 2018, 561, 355–359. [Google Scholar] [CrossRef] [PubMed]
- Ryan, G.; Eerten, H.v.; Piro, L.; Troja, E. Gamma-Ray Burst Afterglows in the Multimessenger Era: Numerical Models and Closure Relations. Astrophys. J. 2020, 896, 166. [Google Scholar] [CrossRef]
- Troja, E.; Piro, L.; van Eerten, H.; Wollaeger, R.T.; Im, M.; Fox, O.D.; Butler, N.R.; Cenko, S.B.; Sakamoto, T.; Fryer, C.L.; et al. The X-ray counterpart to the gravitational-wave event GW170817. Nature 2017, 551, 71–74. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, S.; Zhang, B. The onset of gamma-ray burst afterglow. Astrophys. J. 2007, 655, 973. [Google Scholar] [CrossRef]
- Sari, R.; Piran, T. Predictions for the very early afterglow and the optical flash. Astrophys. J. 1999, 520, 641. [Google Scholar] [CrossRef] [Green Version]
- Sari, R.; Piran, T. Hydrodynamic Timescales and Temporal Structure of Gamma-Ray Bursts. Astrophys. J. Lett. 1995, 455, L143. [Google Scholar] [CrossRef]
- Panaitescu, A.; Kumar, P. Analytic light curves of gamma-ray burst afterglows: Homogeneous versus wind external media. Astrophys. J. 2000, 543, 66. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.F.; Dai, Z.G.; Huang, Y.F.; Lu, T. Optical flashes and very early afterglows in wind environments. Mon. Not. R. Astron. Soc. 2003, 342, 1131–1138. [Google Scholar] [CrossRef] [Green Version]
- Nakar, E.; Piran, T. Implications of the radio and X-ray emission that followed GW170817. Mon. Not. R. Astron. Soc. 2018, 478, 407–415. [Google Scholar] [CrossRef] [Green Version]
- Panaitescu, A.; Vestrand, W.T. Taxonomy of gamma-ray burst optical light curves: Identification of a salient class of early afterglows. Mon. Not. R. Astron. Soc. 2008, 387, 497–504. [Google Scholar] [CrossRef]
- Dai, Z.G.; Lu, T. The Afterglow of GRB 990123 and a Dense Medium. Astrophys. J. 1999, 519, L155–L158. [Google Scholar] [CrossRef] [Green Version]
- Frail, D.A.; Waxman, E.; Kulkarni, S.R. A 450 Day Light Curve of the Radio Afterglow of GRB 970508: Fireball Calorimetry. Astrophys. J. 2000, 537, 191–204. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.F.; Gou, L.J.; Dai, Z.G.; Lu, T. Overall evolution of jetted gamma-ray burst ejecta. Astrophys. J. 2000, 543, 90. [Google Scholar] [CrossRef] [Green Version]
- Livio, M.; Waxman, E. Toward a Model for the Progenitors of Gamma-Ray Bursts. Astrophys. J. 2000, 538, 187–191. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; MacFadyen, A. The dynamics and afterglow radiation of gamma-ray bursts. I. Constant density medium. Astrophys. J. 2009, 698, 1261. [Google Scholar] [CrossRef] [Green Version]
- Draine, B.T. Physics of the Interstellar and Intergalactic Medium by Bruce T. Draine; Princeton University Press: Princeton, FL, USA, 2011; ISBN 978-0-691-12214-4. [Google Scholar]
- Granot, J.; Ramirez-Ruiz, E.; Taylor, G.B.; Eichler, D.; Lyubarsky, Y.E.; Wijers, R.A.M.J.; Gaensler, B.M.; Gelfand, J.D.; Kouveliotou, C. Diagnosing the Outflow from the SGR 1806-20 Giant Flare with Radio Observations. Astrophys. J. 2006, 638, 391–396. [Google Scholar] [CrossRef] [Green Version]
- Sironi, L.; Giannios, D. A Late-time Flattening of Light Curves in Gamma-Ray Burst Afterglows. Astrophys. J. 2013, 778, 107. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Li, Z. Persistent X-Ray Emission from ASASSN-15lh: Massive Ejecta and Pre-SLSN Dense Wind? Astrophys. J. 2018, 859, 123. [Google Scholar] [CrossRef] [Green Version]
- Duffell, P.C.; Laskar, T. On the Deceleration and Spreading of Relativistic Jets. I. Jet Dynamics. Astrophys. J. 2018, 865. [Google Scholar] [CrossRef] [Green Version]
- Granot, J.; Piran, T. On the lateral expansion of gamma-ray burst jets. Mon. Not. R. Astron. Soc. 2012, 421, 570–587. [Google Scholar] [CrossRef]
- Wygoda, N.; Waxman, E.; Frail, D.A. Relativistic jet dynamics and calorimetry of gamma-ray bursts. Astrophys. J. Lett. 2011, 738, L23. [Google Scholar] [CrossRef] [Green Version]
- Granot, J.; Piran, T.; Sari, R. Images and Spectra from the Interior of a Relativistic Fireball. Astrophys. J. 1999, 513, 679–689. [Google Scholar] [CrossRef] [Green Version]
- Finke, J.D.; Dermer, C.D.; Böttcher, M. Synchrotron Self-Compton Analysis of TeV X-Ray-Selected BL Lacertae Objects. Astrophys. J. 2008, 686, 181. [Google Scholar] [CrossRef]
- Rybicki, G.B.; Lightman, A.P. Radiative Processes in Astrophysics; Wiley: New York, NY, USA, 1979. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in FORTRAN; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- De Colle, F.; Ramirez-Ruiz, E.; Granot, J.; Lopez-Camara, D. Simulations of Gamma-Ray Burst Jets in a Stratified External Medium: Dynamics, Afterglow Light Curves, Jet Breaks, and Radio Calorimetry. Astrophys. J. 2012, 751, 57. [Google Scholar] [CrossRef]
- Liang, E.W.; Li, L.; Gao, H.; Zhang, B.; Liang, Y.F.; Wu, X.F.; Yi, S.X.; Dai, Z.G.; Tang, Q.W.; Chen, J.M.; et al. A Comprehensive Study of Gamma-Ray Burst Optical Emission. II. Afterglow Onset and Late Re-brightening Components. Astrophys. J. 2013, 774, 13. [Google Scholar] [CrossRef]
- Kouveliotou, C.; Granot, J.; Racusin, J.L.; Bellm, E.; Vianello, G.; Oates, S.; Fryer, C.L.; Boggs, S.E.; Christensen, F.E.; Craig, W.W.; et al. NuSTAR observations of Grb 130427A establish a single component synchrotron afterglow origin for the late optical to multi-GeV emission. Astrophys. J. Lett. 2013, 779, L1. [Google Scholar] [CrossRef] [Green Version]
- Ghirlanda, G.; Salafia, O.S.; Paragi, Z.; Giroletti, M.; Yang, J.; Marcote, B.; Blanchard, J.; Agudo, I.; An, T.; Bernardini, M.G.; et al. Compact radio emission indicates a structured jet was produced by a binary neutron star merger. Science 2019, 363, 968. [Google Scholar] [CrossRef] [Green Version]
- Kasliwal, M.M.; Nakar, E.; Singer, L.P.; Kaplan, D.L.; Cook, D.O.; Van Sistine, A.; Lau, R.M.; Fremling, C.; Gottlieb, O.; Jencson, J.E.; et al. Illuminating gravitational waves: A concordant picture of photons from a neutron star merger. Science 2017, 358, 1559. [Google Scholar] [CrossRef] [Green Version]
- Yuan, W.; Zhang, C.; Feng, H.; Zhang, S.N.; Ling, Z.X.; Zhao, D.; Deng, J.; Qiu, Y.; Osborne, J.P.; O’Brien, P.; et al. Einstein Probe-a small mission to monitor and explore the dynamic X-ray Universe. arXiv 2015, arXiv:1506.07735. [Google Scholar]
- LSST Science Collaboration; Abell, P.A.; Allison, J.; Anderson, S.F.; Andrew, J.R.; Angel, J.R.P.; Armus, L.; Arnett, D.; Asztalos, S.J.; Axelrod, T.S.; et al. Lsst science book, version 2.0. arXiv 2009, arXiv:0912.0201. [Google Scholar]
- Kobayashi, S.; Mészáros, P.; Zhang, B. GRB 090313 and the origin of optical peaks in gamma-ray burst light curves: Implications for lorentz factors and radio flares. Astrophys. J. 2004, 601, L13. [Google Scholar] [CrossRef]
- Ghisellini, G.; Guilbert, P.W.; Svensson, R. The Synchrotron Boiler. Astrophys. J. 1988, 334, L5. [Google Scholar] [CrossRef]

| Acronym List | |
|---|---|
| CBM | circumburst medium |
| GRB | gamma-ray burst |
| IGM | intergalactic medium |
| ISM | interstellar medium |
| LOS | line of sight |
| SSA | synchrotron self-absorption |
| s | Fast Cooling () | |||
| s | s+1 | (11-6s)/3 | (8-3s)/4 | [8-(p+2)s]/4 |
| 0 | 1 | 3.7 | 2 | 2 |
| 0.5 | 1.5 | 2.7 | 1.6 | |
| 1 | 2 | 1.7 | 1.3 | |
| 1.5 | 2.5 | 0.7 | 0.9 | |
| 2 | 3 | −0.3 | 0.5 | |
| s | Slow Cooling () | |||
| s | 2 | (9-4s)/3 | [12-(p+5)s]/4 | [8-(p+2)s]/4 |
| 0 | 2 | 3 | 3 | 2 |
| 0.5 | 2 | 2.3 | ||
| 1 | 2 | 1.7 | 1.2 | |
| 1.5 | 2 | 1 | 0.3 | |
| 2 | 2 | 0.3 | −0.7 | |
| s | For () | |||
| s | 4 | (17-8s)/3 | (26-9s)/4 | (32-6p-10s+ps)/4 |
| 0 | 4 | 5.7 | 6.5 | |
| 0.5 | 4 | 4.3 | 5.4 | |
| 1 | 4 | 3.0 | 4.3 | |
| 1.5 | 4 | 1.7 | 3.1 | |
| 2 | 4 | 0.3 | 2.0 | |
| s | For () | |||
| s | 4 | (14-s)/4 | (26-9s)/4 | (32-6p-10s+ps)/4 |
| 0 | 4 | 3.5 | 6.5 | |
| 0.5 | 4 | 3.4 | 5.4 | |
| 1 | 4 | 3.3 | 4.3 | |
| 1.5 | 4 | 3.1 | 3.1 | |
| 2 | 4 | 3.0 | 2.0 | |
| s | For () | |||
| s | 2 | 7-8s/3 | (30-6p-11s+ps)/4 | (32-6p-10s+ps)/4 |
| 0 | 2 | 7.0 | ||
| 0.5 | 2 | 5.7 | ||
| 1 | 2 | 4.3 | ||
| 1.5 | 2 | 3.0 | ||
| 2 | 2 | 1.7 | ||
| s | For () | |||
| s | 2 | (14-s)/4 | (30-6p-11s+ps)/4 | (32-6p-10s+ps)/4 |
| 0 | 2 | 3.5 | ||
| 0.5 | 2 | 3.4 | ||
| 1 | 2 | 3.3 | ||
| 1.5 | 2 | 3.1 | ||
| 2 | 2 | 3.0 | ||
| s | Sideways Expansion Dominated Phase | Newtonian Phase | Deep Newtonian Phase | ||
|---|---|---|---|---|---|
| s | [4s(p-2)-15p+21]/2(5-s) | [2s(2p-3)-15p+20]/2(5-s) | 3(p+1)/2(s-5) | (3p-2s+4)/2(s-5) | |
| 0 | |||||
| 0.5 | |||||
| 1 | |||||
| 1.5 | |||||
| 2 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.-H.; Cheng, K.-F. Afterglow Light Curves from Off-Axis GRB Jets in Stratified Circumburst Medium. Universe 2022, 8, 588. https://doi.org/10.3390/universe8110588
Zhao X-H, Cheng K-F. Afterglow Light Curves from Off-Axis GRB Jets in Stratified Circumburst Medium. Universe. 2022; 8(11):588. https://doi.org/10.3390/universe8110588
Chicago/Turabian StyleZhao, Xiao-Hong, and Kang-Fa Cheng. 2022. "Afterglow Light Curves from Off-Axis GRB Jets in Stratified Circumburst Medium" Universe 8, no. 11: 588. https://doi.org/10.3390/universe8110588
APA StyleZhao, X.-H., & Cheng, K.-F. (2022). Afterglow Light Curves from Off-Axis GRB Jets in Stratified Circumburst Medium. Universe, 8(11), 588. https://doi.org/10.3390/universe8110588









