Effective Field Theory Description of Horizon-Fluid Determines the Scrambling Time
Abstract
:1. Introduction
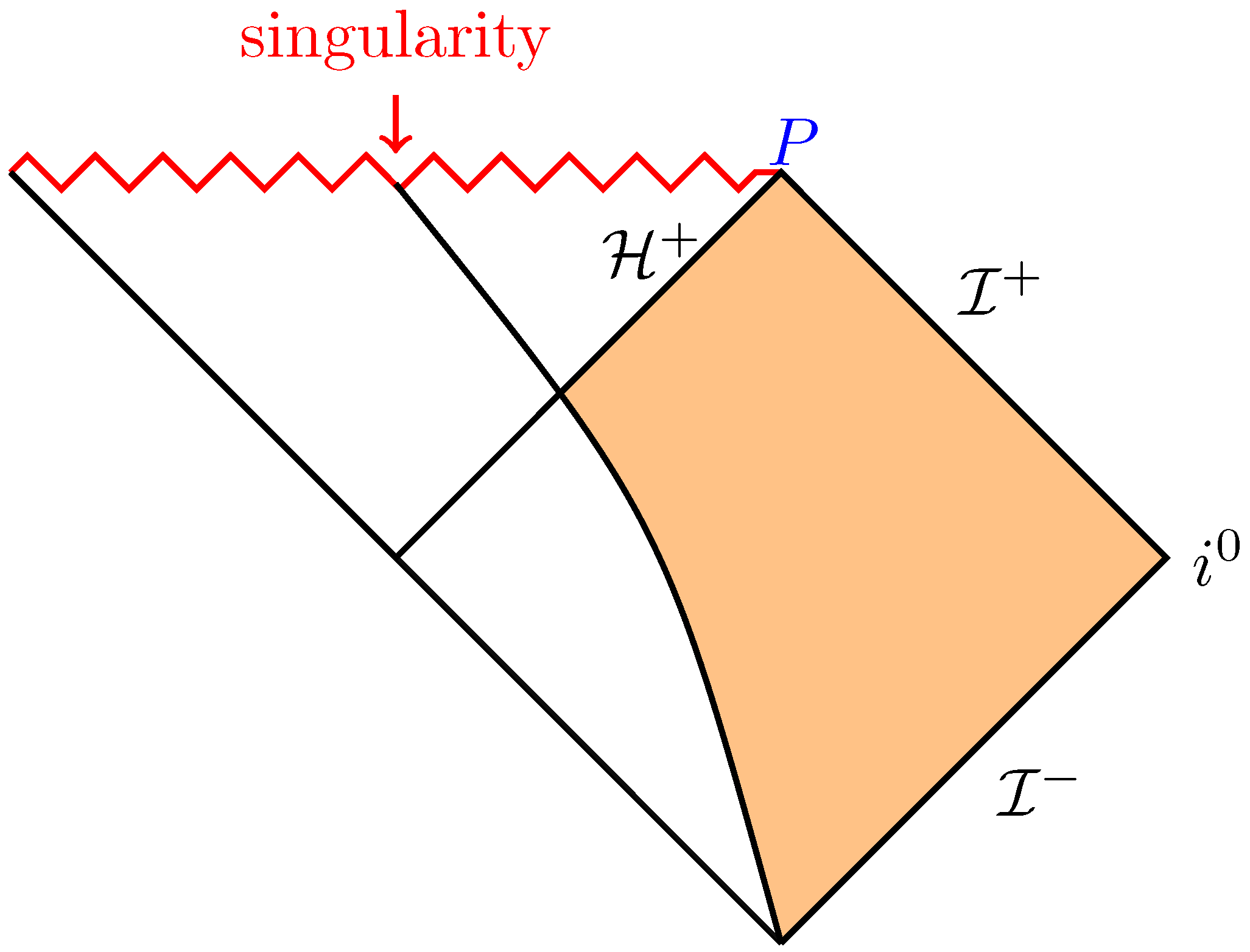
2. Effective Field Theory Description of the Dynamical Horizon
- 1.
- Associate the process of the perturbed black hole to a stationary black hole as a critical phenomenon.
- 2.
- Use the Ginzburg–Landau formalism to phenomenologically describe this process.
- 3.
- 4.
- Identify the function with the effective scalar field Hamiltonian (2).
2.1. Associate the Process with Critical Phenomena
2.2. Phenomenological Description of the Process Using Ginzburg–Landau Formalism
2.3. Associate the Ginzburg–Landau Functional to the Entropy Functional of the Horizon-Fluid
2.4. Identify the Functional with the Effective Scalar Field Hamiltonian
3. Bulk Viscosity from Effective Field Theory
3.1. Obtain Energy-Momentum-Stress Tensor for the Effective Scalar Field Action
3.2. Modify Jeon’s Procedure for the Horizon-Fluid
3.3. Obtain the Correlation Function Corresponding to the Homogeneous Perturbations
3.4. Fix the Constant by Mapping to the Macroscopic Physics
4. Thermalization Rate from Effective Field Theory
4.1. Thermalization Follows from the Horizon-Fluid
- 1.
- After mixing, the entire gas system moves to a state away from the thermal equilibrium.
- 2.
- After some time, the entire gas system thermalizes to a new thermal equilibrium with a lower temperature.
- A
- Cold gas is brought into contact with hot gas in many uniform steps. At each step, only a minimal amount of cold gas gets mixed into the gas system.
- B
- This small amount of cold gas is allowed to thermalize with the gas system at each step. Further, let us impose the condition that more cold gas only comes in contact with the part of the preceding cold gas thermalized in the last step 2.
4.2. Thermalization Rate and Bulk-Viscosity
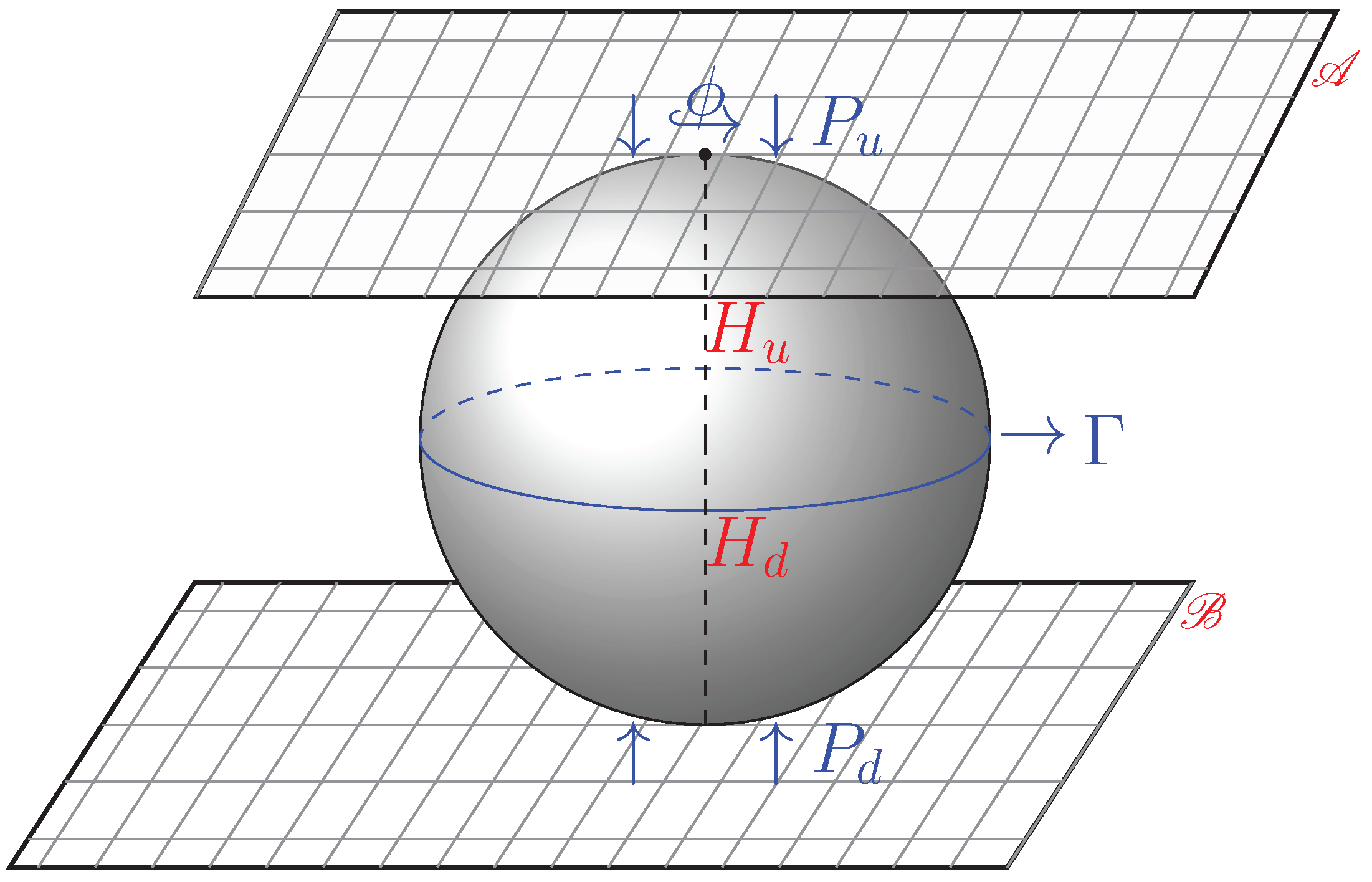
5. Microscopic Toy Model Corresponding to Effective Field Theory
- 1.
- Adopt the Baxter model for the black hole horizon. This is achieved by the projection of two planes onto the surface of a sphere.
- 2.
- Show that the eight-vertex Baxter model incorporates diffeomorphism symmetry.
- 3.
- Show that in the continuum limit, the microscopic toy model leads to effective Hamiltonian (2).
5.1. Adopting the Baxter Model for Black Hole Horizon
5.2. Eight-Vertex Model and Deformed CFT
5.3. Continuum Limit and Effective Field Theory
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Coefficient of Bulk Viscosity from Linear Response Theory
Appendix B. Teleological Boundary Condition
Appendix C. Explicit Evaluation of Bulk Viscosity
| 1 | The conformal anomaly gives rise to the central term in the Virasoro algebra. |
| 2 | This is an artificial step and unlikely to occur in terrestrial experiments. |
| 3 | Since we only consider homogeneous perturbations, the spatial derivatives vanish |
References
- Wald, R.M. The thermodynamics of black holes. Living Rev. Rela. 2001, 4, 6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jacobson, T.; Parentani, R. Horizon entropy. Found. Phys. 2003, 33, 323–348. [Google Scholar] [CrossRef]
- Carlip, S. Black Hole Thermodynamics and Statistical Mechanics. Lect. Notes Phys. 2009, 769, 89–123. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Carter, B.; Hawking, S.W. The Four laws of black hole mechanics. Commun. Math. Phys. 1973, 31, 161–170. [Google Scholar] [CrossRef]
- Jacobson, T. Thermodynamics of space-time: The Einstein equation of state. Phys. Rev. Lett. 1995, 75, 1260–1263. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Padmanabhan, T. Thermodynamical aspects of gravity: New insights. Rep. Prog. Phys. 2010, 73, 046901. [Google Scholar] [CrossRef] [Green Version]
- Padmanabhan, T. Distribution Function of the Atoms of Spacetime and the Nature of Gravity. Entropy 2015, 17, 7420–7452. [Google Scholar] [CrossRef] [Green Version]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Das, S.; Shankaranarayanan, S. Where are the black hole entropy degrees of freedom? Class. Quant. Grav. 2007, 24, 5299–5306. [Google Scholar] [CrossRef] [Green Version]
- Romatschke, P.; Romatschke, U. Relativistic Fluid Dynamics In and Out of Equilibrium; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef]
- Damour, T. Surface Effects in Black-Hole Physics. In Proceedings of the Marcel Grossmann Meeting: General Relativity; Ruffini, R., Ed.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Price, R.H.; Thorne, K.S. Membrane viewpoint on black holes: Properties and evolution of the stretched horizon. Phys. Rev. D 1986, 33, 915–941. [Google Scholar] [CrossRef] [Green Version]
- Thorne, K.S.; Price, R.H.; Macdonald, D.A. The Membrane Paradigm; Yale University Press: New Haven, CT, USA, 1986; Volume 19, p. 379. [Google Scholar]
- Tessarotto, M.; Cremaschini, C. Background Independence and Gauge Invariance in General Relativity Part 1: The Classical Theory. Symmetry 2022, 14, 2083. [Google Scholar] [CrossRef]
- Tessarotto, M.; Cremaschini, C. Background Independence and Gauge Invariance in General Relativity Part 2—Covariant Quantum Gravity. Symmetry 2022, 14, 2229. [Google Scholar] [CrossRef]
- Hamber, H.W. Quantum Gravity on the Lattice. Gen. Rel. Grav. 2009, 41, 817–876. [Google Scholar] [CrossRef] [Green Version]
- Wetterich, C. Lattice diffeomorphism invariance. Phys. Rev. D 2012, 85, 104017. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharya, S.; Shankaranarayanan, S. Fluctuations in horizon-fluid lead to negative bulk viscosity. Phys. Rev. D 2016, D93, 064030. [Google Scholar] [CrossRef] [Green Version]
- Cropp, B.; Bhattacharya, S.; Shankaranarayanan, S. Hints of quantum gravity from the horizon fluid. Phys. Rev. D 2017, D95, 024006. [Google Scholar] [CrossRef] [Green Version]
- Sekino, Y.; Susskind, L. Fast Scramblers. J. High Energy Phys. 2008, 10, 065. [Google Scholar] [CrossRef] [Green Version]
- Baxter, R.J. Eight-vertex model in lattice statistics. Phys. Rev. Lett. 1971, 26, 832. [Google Scholar] [CrossRef]
- Baxter, R.; Wu, F. Exact solution of an Ising model with three-spin interactions on a triangular lattice. Phys. Rev. Lett. 1973, 31, 1294. [Google Scholar] [CrossRef]
- Baxter, R.J. Corner transfer matrices of the eight-vertex model. I. Low-temperature expansions and conjectured properties. J. Stat. Phys. 1976, 15, 485–503. [Google Scholar] [CrossRef]
- Baxter, R.J. Corner transfer matrices of the eight-vertex model. II. The Ising model case. J. Stat. Phys. 1977, 17, 1–14. [Google Scholar] [CrossRef]
- Baxter, R.J. Variational approximations for square lattice models in statistical mechanics. J. Stat. Phys. 1978, 19, 461–478. [Google Scholar] [CrossRef]
- Baxter, R.J. Exactly Solved Models in Statistical Mechanics; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Jeon, S. Hydrodynamic transport coefficients in relativistic scalar field theory. Phys. Rev. D 1995, 52, 3591–3642. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Burgess, C. Quantum gravity in everyday life: General relativity as an effective field theory. Living Rev. Rel. 2004, 7, 5–56. [Google Scholar] [CrossRef] [Green Version]
- Penco, R. An introduction to effective field theories. arXiv 2020, arXiv:2006.16285. [Google Scholar]
- Bhattacharya, S.; Shankaranarayanan, S. How Emergent is Gravity? Int. J. Mod. Phys. 2015, D24, 1544005. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharya, S.; Shankaranarayanan, S. Is there an upper bound on the size of a black-hole? Int. J. Mod. Phys. 2018, D27, 1847011. [Google Scholar] [CrossRef]
- Kaul, R.K.; Majumdar, P. Quantum black hole entropy. Phys. Lett. 1998, B439, 267–270. [Google Scholar] [CrossRef] [Green Version]
- Kaul, R.K.; Majumdar, P. Schwarzschild horizon dynamics and SU(2) Chern-Simons theory. Phys. Rev. 2011, D83, 024038. [Google Scholar] [CrossRef] [Green Version]
- Koga, J.i. Asymptotic symmetries on Killing horizons. Phys. Rev. D 2001, D64, 124012. [Google Scholar] [CrossRef]
- Hotta, M.; Sasaki, K.; Sasaki, T. Diffeomorphism on horizon as an asymptotic isometry of Schwarzschild black hole. Class. Quant. Grav. 2001, 18, 1823–1834. [Google Scholar] [CrossRef] [Green Version]
- Hotta, M. Holographic charge excitations on horizontal boundary. Phys. Rev. 2002, D66, 124021. [Google Scholar] [CrossRef] [Green Version]
- Carlip, S. Black hole entropy from conformal field theory in any dimension. Phys. Rev. Lett. 1999, 82, 2828. [Google Scholar] [CrossRef] [Green Version]
- Carlip, S. Effective Conformal Descriptions of Black Hole Entropy. Entropy 2011, 13, 1355–1379. [Google Scholar] [CrossRef] [Green Version]
- Barnich, G.; Troessaert, C. Symmetries of asymptotically flat 4 dimensional spacetimes at null infinity revisited. Phys. Rev. Lett. 2010, 105, 111103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Donnay, L.; Giribet, G.; Gonzalez, H.A.; Pino, M. Supertranslations and Superrotations at the Black Hole Horizon. Phys. Rev. Lett. 2016, 116, 091101. [Google Scholar] [CrossRef] [Green Version]
- Bondi, H.; van der Burg, M.G.J.; Metzner, A.W.K. Gravitational waves in general relativity. 7. Waves from axisymmetric isolated systems. Proc. Roy. Soc. Lond. 1962, A269, 21–52. [Google Scholar] [CrossRef]
- Sachs, R.K. Gravitational waves in general relativity. 8. Waves in asymptotically flat space-times. Proc. Roy. Soc. Lond. 1962, A270, 103–126. [Google Scholar] [CrossRef]
- Strominger, A. Lectures on the Infrared Structure of Gravity and Gauge Theory; Princeton University Press: Princeton, NJ, USA, 2017. [Google Scholar]
- Compére, G. The Kerr/CFT correspondence and its extensions. Living Rev. Rel. 2012, 15, 11. [Google Scholar] [CrossRef] [Green Version]
- Averin, A. Schwarzschild/CFT from soft black hole hair? J. High Energy Phys. 2019, 2019, 1–24. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Zamolodchikov, A. Higher-order integrals of motion in two-dimensional models of the field theory with a broken conformal. JETP Lett. 1987, 46, 129. [Google Scholar]
- Zamolodchikov, A.B. Integrable field theory from conformal field theory. In Integrable Systems and Quantum Field Theory; Elsevier: Amsterdam, The Netherlands, 1989; pp. 641–674. [Google Scholar]
- Penrose, O.; Fife, P.C. Thermodynamically consistent models of phase-field type for the kinetic of phase transitions. Phys. D 1990, 43, 44–62. [Google Scholar] [CrossRef]
- López, J.L.; Bhattacharya, S.; Shankaranarayanan, S. Statistical modeling of the fluid dual to Boulware-Deser black hole. Phys. Rev. D 2016, 94, 024029. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharya, S.; Shankaranarayanan, S. Negative specific heat of black-holes from fluid-gravity correspondence. Classical and Quantum Gravity 2017, 34, 075005. [Google Scholar] [CrossRef]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; Addison-Wesley: Boston, MA, USA, 1995. [Google Scholar]
- Kubo, R. The fluctuation-dissipation theorem. Rep. Prog. Phys. 1966, 29, 255–284. [Google Scholar] [CrossRef] [Green Version]
- Bekenstein, J.D. The quantum mass spectrum of the Kerr black hole. Lettere al Nuovo Cimento (1971–1985) 1974, 11, 467–470. [Google Scholar] [CrossRef]
- Lashkari, N.; Stanford, D.; Hastings, M.; Osborne, T.; Hayden, P. Towards the Fast Scrambling Conjecture. J. High Energy Phys. 2013, 4, 022. [Google Scholar] [CrossRef] [Green Version]
- Casher, A.; Englert, F.; Itzhaki, N.; Massar, S.; Parentani, R. Black hole horizon fluctuations. Nucl. Phys. 1997, B484, 419–434. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, M.; Shankaranarayanan, S. Back-reaction of matter fluctuations in asymptotically non-flat black-hole space-times. Ann. Phys. 2022, 440, 168829. [Google Scholar] [CrossRef]
- Ropotenko, K. Fast scrambling as brownian motion in a fluid with negative viscosity. arXiv 2017, arXiv:1704.04444. [Google Scholar]
- Hayden, P.; Preskill, J. Black holes as mirrors: Quantum information in random subsystems. J. High Energy Phys. 2007, 09, 120. [Google Scholar] [CrossRef] [Green Version]
- Susskind, L. Addendum to Fast Scramblers. arXiv 2011, arXiv:1101.6048. [Google Scholar]
- Hartnoll, S.A.; Hofman, D.M. Locally Critical Resistivities from Umklapp Scattering. Phys. Rev. Lett. 2012, 108, 241601. [Google Scholar] [CrossRef]
- Kadanoff, L.P.; Wegner, F.J. Some critical properties of the eight-vertex model. Phys. Rev. B 1971, 4, 3989. [Google Scholar] [CrossRef] [Green Version]
- Itoyama, H.; Thacker, H.B. Lattice Virasoro Algebra and Corner Transfer Matrices in the Baxter Eight Vertex Model. Phys. Rev. Lett. 1987, 58, 1395. [Google Scholar] [CrossRef] [PubMed]
- Thacker, H. Corner transfer matrices and Lorentz invariance on a lattice. Phys. D Nonlinear Phenom. 1986, 18, 348–359. [Google Scholar] [CrossRef]
- Itoyama, H.; Thacker, H.B. Integrability and Virasoro Symmetry of the Noncritical Baxter-Ising Model. Nucl. Phys. 1989, B320, 541–590. [Google Scholar] [CrossRef]
- Sutherland, B. Two-Dimensional Hydrogen Bonded Crystals without the Ice Rule. J. Math. Phys. 1970, 11, 3183–3186. [Google Scholar] [CrossRef]
- Gervais, J.L. Infinite family of polynomial functions of the Virasoro generators with vanishing Poisson brackets. Phys. Lett. B 1985, 160, 277–278. [Google Scholar] [CrossRef]
- Polyakov, A.M. Gauge Fields and Strings; Contemporary Concepts in Physics; Taylor & Francis: London, UK, 1987. [Google Scholar]
- Evans, D.J.; Searles, D.J. Causality, response theory, and the second law of thermodynamics. Phys. Rev. E 1996, 53, 5808–5815. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhattacharya, S.; Shankaranarayanan, S. Effective Field Theory Description of Horizon-Fluid Determines the Scrambling Time. Universe 2022, 8, 603. https://doi.org/10.3390/universe8110603
Bhattacharya S, Shankaranarayanan S. Effective Field Theory Description of Horizon-Fluid Determines the Scrambling Time. Universe. 2022; 8(11):603. https://doi.org/10.3390/universe8110603
Chicago/Turabian StyleBhattacharya, Swastik, and S. Shankaranarayanan. 2022. "Effective Field Theory Description of Horizon-Fluid Determines the Scrambling Time" Universe 8, no. 11: 603. https://doi.org/10.3390/universe8110603
APA StyleBhattacharya, S., & Shankaranarayanan, S. (2022). Effective Field Theory Description of Horizon-Fluid Determines the Scrambling Time. Universe, 8(11), 603. https://doi.org/10.3390/universe8110603






