Large-Scale Solar Wind Phenomena Affecting the Turbulent Cascade Evolution behind the Quasi-Perpendicular Bow Shock
Abstract
:1. Introduction
2. Data and Methods
2.1. Spacecraft Measurements Used
2.2. Tracking of the Plasma Volume
2.3. Fourier Analysis
2.4. Turbulence Evolution between the L1 and the Bow Shock
2.5. Determination of the BS Type
2.6. Data Selection
2.7. Taylor Hypothesis
3. Results
3.1. Undisturbed Solar Wind
3.2. Disturbed Compressed SW Flow
3.3. Disturbed SW Flow Associated with ICMEs
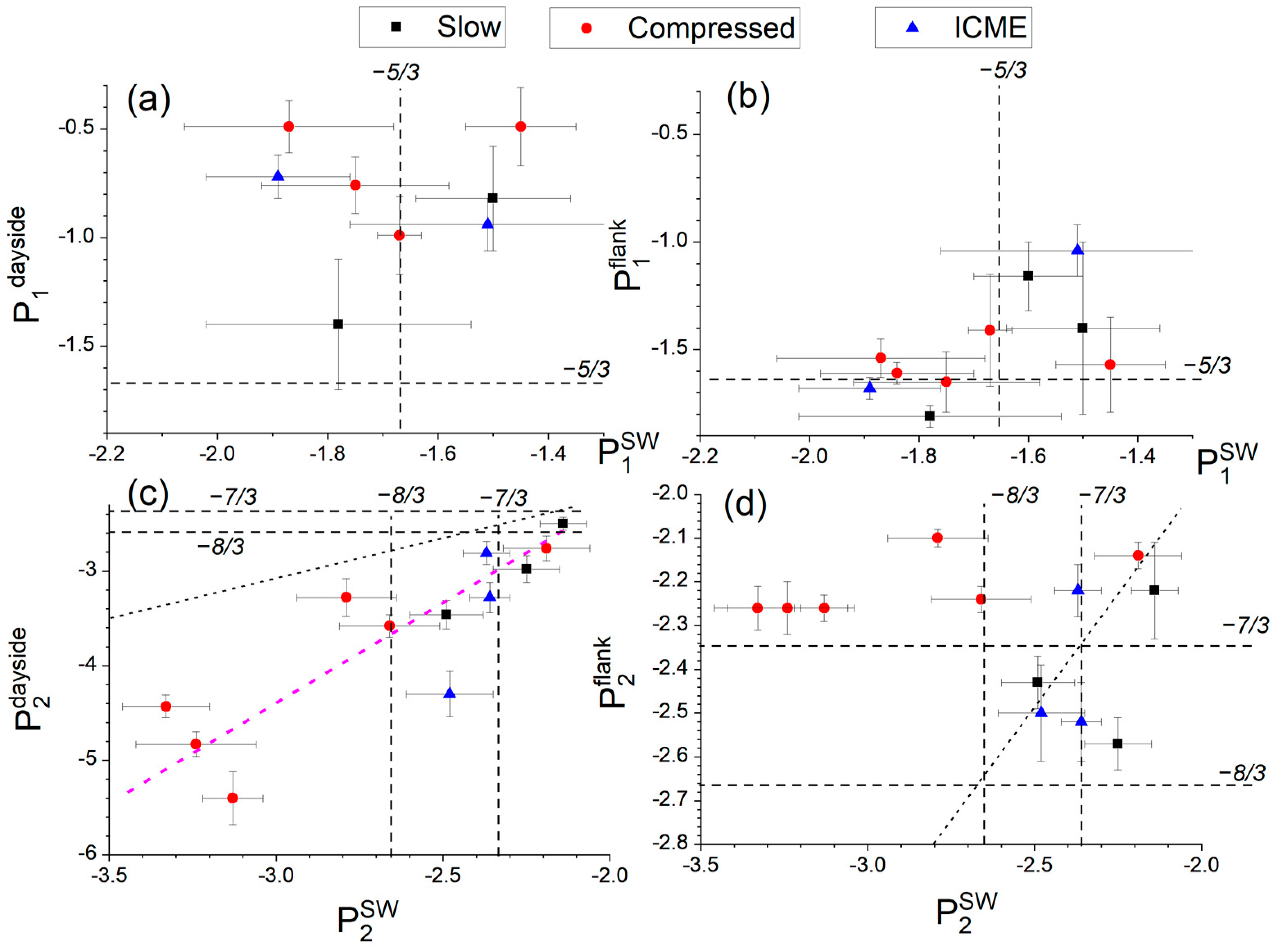
4. Relation between the Spectra Properties in Different Regions of the Near-Earth Space
5. Discussion and Summary
- During the slow undisturbed SW streams, the fluctuation spectrum may be modified in different ways at the MHD scales in the dayside MSH and tends to restore Kolmogorov scaling at the flanks; at the kinetic scales, slight steepening of the spectrum occurs at the dayside MSH with the restoration of the initial SW slope at the flanks;
- During disturbed SW streams, substantial deviation from the Kolmogorov scaling occurs at the MHD scales in the dayside MSH; at the flanks, the Kolmogorov scaling is typically restored except for the cases in particular vicinity of the BS;
- Steepening of the spectra behind the BS occurs for all types of the SW; the compressed SW streams are characterized by slightly steeper spectra than typically observed in the SW, which become untypically steep in the dayside MSH;
- Steepening of the spectra in the dayside MSH at the kinetic scales seems to be controlled by the level of plasma compression in the dayside MSH, with steeper spectra presenting during the more compressed plasma;
- Turbulent cascade embedded to the compressed SW streams evolves in the MSH in a specific way that results in untypically flat spectra at the flanks; specific redistribution of the energy through the cascade when plasma propagates away from the BS is likely to be a feature of these SW streams.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yermolaev, Y.I.; Lodkina, I.G.; Nikolaeva, N.S.; Yermolaev, M.Y. Dynamics of large-scale solar wind streams obtained by the double superposed epoch analysis. J. Geophys. Res. Space Phys. 2015, 120, 7094–7106. [Google Scholar] [CrossRef] [Green Version]
- Petrukovich, A.A.; Malova, H.V.; Popov, V.Y.; Maiewski, E.V.; Izmodenov, V.V.; Katushkina, O.A.; Vinogradov, A.A.; Riazantseva, M.; Rakhmanova, L.S.; Podladchikova, T.V.; et al. Modern view of the solar wind from micro to macro scales. Physics-Uspekhi 2020, 63, 801–811. [Google Scholar] [CrossRef]
- Spreiter, J.R.; Summers, A.L.; Alksne, A.Y. Hydromagnetic flow around the magnetosphere. Planet. Space Sci. 1966, 14, 223–253. [Google Scholar] [CrossRef] [Green Version]
- Spreiter, J.R.; Stahara, S.S. A new predictive model for determining solar wind-terrestrial planet interactions. J. Geophys. Res. 1980, 85, 6769–6777. [Google Scholar] [CrossRef]
- Kartalev, M.; Nikolova, V.; Kamenetsky, V.; Mastikov, I. On the self-consistent determination of dayside magnetopause shape and position. Planet. Space Sci. 1996, 44, 1195–1208. [Google Scholar] [CrossRef]
- Tóth, G.; Sokolov, I.; Gombosi, T.; Chesney, D.R.; Clauer, C.R.; De Zeeuw, D.; Hansen, K.C.; Kane, K.J.; Manchester, W.B.; Oehmke, R.C.; et al. Space Weather Modeling Framework: A new tool for the space science community. J. Geophys. Res. Space Phys. 2005, 110, A12226. [Google Scholar] [CrossRef] [Green Version]
- Zastenker, G.; Nozdrachev, M.; Němeček, Z.; Šafránková, J.; Paularena, K.; Richardson, J.; Lepping, R.; Mukai, T. Multispacecraft measurements of plasma and magnetic field variations in the magnetosheath: Comparison with Spreiter models and motion of the structures. Planet. Space Sci. 2002, 50, 601–612. [Google Scholar] [CrossRef]
- Hayosh, M.; Safrankova, J.; Němeček, Z. MHD-modelling of the magnetosheath ion plasma flow and magnetic field and their comparison with experiments. Adv. Space Res. 2006, 37, 507–514. [Google Scholar] [CrossRef]
- Schwartz, S.; Burgess, D.; Moses, J.J. Low-frequency waves in the Earth’s magnetosheath: Present status. Ann. Geophys. 1996, 14, 1134–1150. [Google Scholar] [CrossRef] [Green Version]
- Lucek, E.A.; Constantinescu, D.; Goldstein, M.L.; Pickett, J.; Pinçon, J.L.; Sahraoui, F.; Treumann, R.A.; Walker, S.N. The Magnetosheath. Space Sci. Rev. 2005, 118, 95–152. [Google Scholar] [CrossRef]
- Karimabadi, H.; Roytershteyn, V.; Vu, H.X.; Omelchenko, Y.A.; Scudder, J.; Daughton, W.; Dimmock, A.; Nykyri, K.; Wan, M.; Sibeck, D.; et al. The link between shocks, turbulence, and magnetic reconnection in collisionless plasmas. Phys. Plasmas 2014, 21, 062308. [Google Scholar] [CrossRef] [Green Version]
- Palmroth, M.; Ganse, U.; Pfau-Kempf, Y.; Battarbee, M.; Turc, L.; Brito, T.; Grandin, M.; Hoilijoki, S.; Sandroos, A.; von Alfthan, S. Vlasov methods in space physics and astrophysics. Living Rev. Comput. Astrophys. 2018, 4, 1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, Q.; Wang, H.; Wang, X.; Lu, S.; Wang, R.; Gao, X.; Wang, S.; Lin, Y. Turbulence-Driven Magnetic Reconnection in the Magnetosheath Downstream of a Quasi-Parallel Shock: A Three-Dimensional Global Hybrid Simulation. Geophys. Res. Lett. 2020, 47, e2019GL085661. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. R. Soc. A 1941, 434, 9–13. [Google Scholar]
- Goldreich, P.; Sridhar, S. Toward a theory of interstellar turbulence. II: Strong alfvenic turbulence. Astrophys. J. 1995, 438, 763–775. [Google Scholar] [CrossRef]
- Schekochihin, A.A.; Cowley, S.C.; Dorland, W.; Hammett, G.; Howes, G.G.; Quataert, E.; Tatsuno, T. Astrophysical gyrokinetics: Kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys. J. Suppl. Ser. 2009, 182, 310–377. [Google Scholar] [CrossRef] [Green Version]
- Boldyrev, S.; Perez, J.C. Spectrum of kinetic-alfvén turbulence. Astrophys. J. Lett. 2012, 758, L44. [Google Scholar] [CrossRef] [Green Version]
- Sahraoui, F.; Hadid, L.; Huang, S. Magnetohydrodynamic and kinetic scale turbulence in the near-Earth space plasmas: A (short) biased review. Rev. Mod. Plasma Phys. 2020, 4, 4. [Google Scholar] [CrossRef]
- Rakhmanova, L.; Riazantseva, M.; Zastenker, G. Plasma and Magnetic Field Turbulence in the Earth’s Magnetosheath at Ion Scales. Front. Astron. Space Sci. 2021, 7, 616635. [Google Scholar] [CrossRef]
- Stawarz, J.E.; Eastwood, J.P.; Phan, T.D.; Gingell, I.L.; Shay, M.A.; Burch, J.L.; Ergun, R.E.; Giles, B.L.; Gershman, D.J.; Le Contel, O.; et al. Properties of the Turbulence Associated with Electron-only Magnetic Reconnection in Earth’s Magnetosheath. Astrophys. J. Lett. 2019, 877, L37. [Google Scholar] [CrossRef] [Green Version]
- Vörös, Z.; Yordanova, E.; Khotyaintsev, Y.V.; Varsani, A.; Narita, Y. Energy Conversion at Kinetic Scales in the Turbulent Magnetosheath. Front. Astron. Space Sci. 2019, 6, 60. [Google Scholar] [CrossRef]
- Yordanova, E.; Vörös, Z.; Raptis, S.; Karlsson, T. Current Sheet Statistics in the Magnetosheath. Front. Astron. Space Sci. 2020, 7, 2. [Google Scholar] [CrossRef] [Green Version]
- Alexandrova, O.; Lacombe, C.; Mangeney, A. Spectra and anisotropy of magnetic fluctuations in the Earth’s magnetosheath: Cluster observations. Ann. Geophys. 2008, 26, 3585–3596. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.Y.; Sahraoui, F.; Deng, X.H.; He, J.S.; Yuan, Z.G.; Zhou, M.; Pang, Y.; Fu, H.S. Kinetic turbulence in the terrestrial magnetosheath: Cluster observations. Astrophys. J. Lett. 2014, 789, L28. [Google Scholar] [CrossRef] [Green Version]
- Rakhmanova, L.; Riazantseva, M.; Zastenker, G. Plasma fluctuations at the flanks of the Earth’s magnetosheath at ion kinetic scales. Ann. Geophys. 2016, 34, 1011–1018. [Google Scholar] [CrossRef] [Green Version]
- Matteini, L.; Alexandrova, O.; Chen, C.H.K.; Lacombe, C. Electric and magnetic spectra from MHD to electron scales in the magnetosheath. Mon. Not. R. Astron. Soc. 2017, 466, 945–951. [Google Scholar] [CrossRef]
- Denskat, K.U.; Beinroth, H.J.; Neubauer, F.M. Interplanetary magnetic field power spectra with frequencies from 2.4 × 10−5 Hz to 470 Hz from HELIOS-observations during solarminimum conditions. J. Geophys. 1983, 54, 60–67. [Google Scholar]
- Riazantseva, M.O.; Budaev, V.; Zelenyi, L.M.; Zastenker, G.N.; Pavlos, G.P.; Šafránková, J.; Němeček, Z.; Prech, L.; Nemec, F. Dynamic properties of small-scale solar wind plasma fluctuations. Philos. Trans. R. Soc. Ser. A 2015, 373, 20140146. [Google Scholar] [CrossRef] [Green Version]
- Alexandrova, O.; Jagarlamudi, V.K.; Hellinger, P.; Maksimovic, M.; Shprits, Y.; Mangeney, A. Spectrum of kinetic plasma turbulence at 0.3–0.9 astronomical units from the Sun. Phys. Rev. E 2021, 103, 063202. [Google Scholar] [CrossRef]
- Alexandrova, O.; Saur, J.; Lacombe, C.; Mangeney, A.; Mitchell, J.; Schwartz, S.; Robert, P. Universality of Solar-Wind Turbulent Spectrum from MHD to Electron Scales. Phys. Rev. Lett. 2009, 103, 165003. [Google Scholar] [CrossRef] [Green Version]
- Alexandrova, O.; Lacombe, C.; Mangeney, A.; Grappin, R.; Maksimovic, M. Solar wind turbulent spectrum at plasma kinetic scales. Astrophys. J. 2012, 760. [Google Scholar] [CrossRef] [Green Version]
- Lion, S.; Alexandrova, O.; Zaslavsky, A. Coherent events and spectral shape at ion kinetic scales in the fast solar wind turbulence. Astrophys. J. 2016, 824, 47. [Google Scholar] [CrossRef]
- Sahraoui, F.; Belmont, G.; Rezeau, L.; Cornilleau-Wehrlin, N.; Pinçon, J.L.; Balogh, A. Anisotropic Turbulent Spectra in the Terrestrial Magnetosheath as Seen by the Cluster Spacecraft. Phys. Rev. Lett. 2006, 96, 075002. [Google Scholar] [CrossRef]
- Yordanova, E.; Vaivads, A.; André, M.; Buchert, S.C.; Vörös, Z. Magnetosheath Plasma Turbulence and Its Spatiotemporal Evolution as Observed by the Cluster Spacecraft. Phys. Rev. Lett. 2008, 100, 205003. [Google Scholar] [CrossRef]
- Rakhmanova, L.S.; Riazantseva, M.O.; Zastenker, G.N.; Yermolaev, Y.I. High-frequency plasma fluctuations in the middle magnetosheath and near its boundaries: Spektr-R observations. J. Plasma Phys. 2017, 83, 705830204. [Google Scholar] [CrossRef]
- Huang, S.Y.; Hadid, L.Z.; Sahraoui, F.; Yuan, Z.G.; Deng, X.H. On the Existence of the Kolmogorov Inertial Range in the Terrestrial Magnetosheath Turbulence. Astrophys. J. Lett. 2017, 836, L10. [Google Scholar] [CrossRef] [Green Version]
- Shevyrev, N.; Zastenker, G. Some features of the plasma flow in the magnetosheath behind quasi-parallel and quasi-perpendicular bow shocks. Planet. Space Sci. 2005, 53, 95–102. [Google Scholar] [CrossRef]
- Czaykowska, A.; Bauer, T.M.; Treumann, R.A.; Baumjohann, W. Magnetic field fluctuations across the Earth’s bow shock. Ann. Geophys. 2001, 19, 275–287. [Google Scholar] [CrossRef] [Green Version]
- Breuillard, H.; Matteini, L.; Argall, M.R.; Sahraoui, F.; Andriopoulou, M.; Le Contel, O.; Retinò, A.; Mirioni, L.; Huang, S.Y.; Gershman, D.J.; et al. New Insights into the Nature of Turbulence in the Earth’s Magnetosheath Using Magnetospheric MultiScale Mission Data. Astrophys. J. 2018, 859, 127. [Google Scholar] [CrossRef]
- Rakhmanova, L.; Riazantseva, M.; Zastenker, G.; Yermolaev, Y.; Lodkina, I. Dynamics of Plasma Turbulence at Earth’s Bow Shock and through the Magnetosheath. Astrophys. J. 2020, 901, 30. [Google Scholar] [CrossRef]
- Horbury, T.S.; Forman, M.A.; Oughton, S. Spacecraft observations of solar wind turbulence: An overview. Plasma Phys. Control. Fusion 2005, 47, B703–B717. [Google Scholar] [CrossRef] [Green Version]
- Anderson, B.J.; Fuselier, S.A.; Gary, S.P.; Denton, R.E. Magnetic spectral signatures in the Earth’s magnetosheath and plasma depletion layer. J. Geophys. Res. 1994, 99, 5877–5891. [Google Scholar] [CrossRef]
- Lacombe, C.; Belmont, G.; Hubert, D.; Harvey, C.C.; Mangeney, A.; Russell, C.T.; Gosling, J.T.; Fuselier, S.A. Density and magnetic field fluctuations observed by ISEE 1–2 in the quiet magnetosheath. Ann. Geophys. 1995, 13, 343–357. [Google Scholar] [CrossRef]
- Czaykowska, A.; Bauer, T.M.; Treumann, R.A.; Baumjohann, W. Mirror waves downstream of the quasi-perpendicular bow shock. J. Geophys. Res. 1998, 103, 4747–4752. [Google Scholar] [CrossRef]
- Hellinger, P.; Trávníček, P.; Mangeney, A.; Grappin, R. Hybrid simulations of the magnetosheath compression: Marginal stability path. Geophys. Res. Lett. 2003, 30, 1959. [Google Scholar] [CrossRef] [Green Version]
- Alexandrova, O.; Mangeney, A.; Maksimovic, M.; Bosqued, J.-M.; Andre, M.; Cornilleau-Wehrlin, N. Alfvén vortex filaments observed in magnetosheath downstream of a quasi-perpendicular bow shock. J. Geophys. Res. 2006, 111, A12208. [Google Scholar] [CrossRef] [Green Version]
- Alexandrova, O. Solar wind vs magnetosheath turbulence and Alfvén vortices. Nonlinear Process. Geophys. 2008, 15, 95–108. [Google Scholar] [CrossRef]
- Roberts, O.W.; Li, X.; Alexandrova, O.; Li, B. Observation of an MHD Alfvén vortex in the slow solar wind. J. Geophys. Res. Space Phys. 2016, 121, 3870–3881. [Google Scholar] [CrossRef] [Green Version]
- Perrone, D.; Alexandrova, O.; Roberts, O.W.; Lion, S.; Lacombe, C.; Walsh, A.; Maksimovic, M.; Zouganelis, I. Coherent Structures at Ion Scales in Fast Solar Wind: Cluster Observations. Astrophys. J. 2017, 849, 49. [Google Scholar] [CrossRef] [Green Version]
- Rakhmanova, L.; Riazantseva, M.; Zastenker, G.; Verigin, M. Kinetic-Scale Ion Flux Fluctuations behind the Quasi-Parallel and Quasi-Perpendicular Bow Shock. J. Geophys. Res. Space Phys. 2018, 123, 5300–5314. [Google Scholar] [CrossRef]
- Rakhmanova, L.S.; Riazantseva, M.O.; Zastenker, G.N.; Verigin, M.I. Effect of the Magnetopause and Bow Shock on Characteristics of Plasma Turbulence in the Earth’s Magnetosheath. Geomagn. Aeron. 2018, 58, 718–727. [Google Scholar] [CrossRef]
- Li, H.; Jiang, W.-C.; Wang, C.; Verscharen, D.; Zeng, C.; Russell, C.T.; Giles, B.; Burch, J.L. Evolution of the Earth’s Magnetosheath Turbulence: A Statistical Study Based on MMS Observations. Astrophys. J. 2020, 898, L43. [Google Scholar] [CrossRef]
- Rakhmanova, L.S.; Riazantseva, M.O.; Zastenker, G.N.; Yermolaev, Y.I.; Lodkina, I.G. Dependence of the Properties of a Turbulent Cascade behind the Bow Shock on the Dynamics of the Solar Wind Parameters. Cosm. Res. 2020, 58, 478–486. [Google Scholar] [CrossRef]
- Borovsky, J.E.; Denton, M.H.; Smith, C.W. Some Properties of the Solar Wind Turbulence at 1 AU Statistically Examined in the Different Types of Solar Wind Plasma. J. Geophys. Res. Space Phys. 2019, 124, 2406–2424. [Google Scholar] [CrossRef]
- Riazantseva, M.O.; Rakhmanova, L.S.; Yermolaev, Y.I.; Lodkina, I.G.; Zastenker, G.N.; Chesalin, L.S. Characteristics of Turbulent Solar Wind Flow in Plasma Compression Regions. Cosm. Res. 2020, 58, 468–477. [Google Scholar] [CrossRef]
- Koller, F.; Temmer, M.; Preisser, L.; Plaschke, F.; Geyer, P.; Jian, L.K.; Roberts, O.W.; Hietala, H.; LaMoury, A.T. Magnetosheath Jet Occurrence Rate in Relation to CMEs and SIRs. J. Geophys. Res. Space Phys. 2022, 127, e2021JA030124. [Google Scholar] [CrossRef]
- Ala-Lahti, M.; Dimmock, A.P.; Pulkkinen, T.I.; Good, S.W.; Yordanova, E.; Turc, L.; Kilpua, E.K.J. Transmission of an ICME Sheath into the Earth’s Magnetosheath and the Occurrence of Traveling Foreshocks. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029896. [Google Scholar] [CrossRef]
- Zelenyi, L.M.; Zastenker, G.N.; Petrukovich, A.A.; Chesalin, L.S.; Nazarov, V.N.; Prokhorenko, V.I.; Larionov, E.I. Plasma-F experiment onboard the Spectr-R satellite. Cosm. Res. 2013, 51, 73–77. [Google Scholar] [CrossRef]
- Angelopoulos, V. The THEMIS Mission. Space Sci. Rev. 2008, 141, 5–34. [Google Scholar] [CrossRef]
- Lepping, R.P.; Acũna, M.H.; Burlaga, L.F.; Farrell, W.M.; Slavin, J.A.; Schatten, K.H.; Mariani, F.; Ness, N.F.; Neubauer, F.M.; Whang, Y.C.; et al. The WIND magnetic field investigation. Space Sci. Rev. 1995, 71, 207–229. [Google Scholar] [CrossRef]
- Auster, H.U.; Glassmeier, K.H.; Magnes, W.; Aydogar, O.; Baumjohann, W.; Constantinescu, D.; Fischer, D.A.; Fornacon, K.H.; Georgescu, E.; Harvey, P.M.; et al. The THEMIS Fluxgate Magnetometer. Space Sci. Rev. 2008, 141, 235–264. [Google Scholar] [CrossRef]
- Šafránková, J.; Němeček, Z.; Prech, L.; Zastenker, G.; Cermak, I.; Chesalin, L.; Komárek, A.; Vaverka, J.; Beránek, M.; Pavlu, J.; et al. Fast Solar Wind Monitor (BMSW): Description and First Results. Space Sci. Rev. 2013, 175, 165–182. [Google Scholar] [CrossRef]
- Zastenker, G.N.; Šafránková, J.; Němeček, Z.; Prech, L.; Cermak, I.; Vaverka, J.; Komárek, A.; Voita, J.; Chesalin, L.S.; Karimov, B.T.; et al. Fast measurements of parameters of the Solar Wind using the BMSW instrument. Cosm. Res. 2013, 51, 78–89. [Google Scholar] [CrossRef]
- Neugebauer, M.; Wu, C.S.; Huba, J.D. Plasma fluctuations in the solar wind. J. Geophys. Res. 1978, 83, 1027–1034. [Google Scholar] [CrossRef]
- Pitňa, A.; Šafránková, J.; Němeček, Z.; Goncharov, O.; Nemec, F.; Prech, L.; Chen, C.H.K.; Zastenker, G.N. Density fluctuations upstream and downstream of interplanetary shocks. Astrophys. J. 2016, 819, 41. [Google Scholar] [CrossRef]
- Chen, C.H.K.; Boldyrev, S. Nature of Kinetic Scale Turbulence in the Earth’s Magnetosheath. Astrophys. J. 2017, 842, 122. [Google Scholar] [CrossRef]
- Roberts, O.W.; Narita, Y.; Li, X.; Escoubet, C.P.; Laakso, H. Multipoint analysis of compressive fluctuations in the fast and slow solar wind. J. Geophys. Res. Space Phys. 2017, 122, 6940–6963. [Google Scholar] [CrossRef]
- He, J.; Zhu, X.; Verscharen, D.; Duan, D.; Zhao, J.; Wang, T. Spectra of Diffusion, Dispersion, and Dissipation for Kinetic Alfvénic and Compressive Turbulence: Comparison between Kinetic Theory and Measurements from MMS. Astrophys. J. 2020, 898, 43. [Google Scholar] [CrossRef]
- Ogilvie, K.W.; Chornay, D.J.; Fritzenreiter, R.J.; Hunsaker, F.; Keller, J.; Lobell, J.; Miller, G.; Scudder, J.D.; Sittler, E.C.; Torbert, R.B.; et al. SWE, a comprehensive plasma instrument for the wind spacecraft. Space Sci. Rev. 1995, 71, 55–77. [Google Scholar] [CrossRef]
- Lin, R.P.; Anderson, K.A.; Ashford, S.; Carlson, C.; Curtis, D.; Ergun, R.; Larson, D.; McFadden, J.; McCarthy, M.; Parks, G.K.; et al. A three-dimensional plasma and energetic particle investigation for the wind spacecraft. Space Sci. Rev. 1995, 71, 125–153. [Google Scholar] [CrossRef]
- McFadden, J.P.; Carlson, C.W.; Larson, D.J.; Ludlam, M.; Abiad, R.; Elliott, B.J.; Turin, P.; Marckwordt, M.; Angelopoulos, V. The THEMIS ESA Plasma Instrument and In-flight Calibration. Space Sci. Rev. 2008, 141, 277–302. [Google Scholar] [CrossRef]
- Rakhmanova, L.; Riazantseva, M.; Zastenker, G. Correlation level between solar wind and magnetosheath plasma and magnetic field parameters. Adv. Space Res. 2016, 58, 157–165. [Google Scholar] [CrossRef]
- Richardson, J.D.; Paularena, K.I. Plasma and magnetic field correlations in the solar wind. J. Geophys. Res. 2001, 106, 239–251. [Google Scholar] [CrossRef]
- Yermolaev, Y.I.; Nikolaeva, N.S.; Lodkina, I.G.; Yermolaev, M.Y. Catalog of large-scale solar wind phenomena during 1976–2000. Cosm. Res. 2009, 47, 81–94. [Google Scholar] [CrossRef]
- Wu, C.-C.; Lepping, R.P. Comparisons of characteristics of magnetic clouds and cloud-like structures during 1995–2012. Sol. Phys. 2015, 290, 1243–1269. [Google Scholar] [CrossRef]
- Taylor, G.I. The Spectrum of Turbulence. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1938, 164, 476–490. [Google Scholar] [CrossRef] [Green Version]
- Howes, G.G.; Klein, K.; Tenbarge, J.M. Validity of the taylor hypothesis for linear kinetic waves in the weakly collisional solar wind. Astrophys. J. 2014, 789, 106. [Google Scholar] [CrossRef] [Green Version]
- Klein, K.; Howes, G.G.; Tenbarge, J.M. The violation of the taylor hypothesis in measurements of solar wind turbulence. Astrophys. J. Lett. 2014, 790, L20. [Google Scholar] [CrossRef] [Green Version]
- Vörös, Z.; Yordanova, E.; Graham, D.B.; Khotyaintsev, Y.V.; Narita, Y. MMS Observations of Whistler and Lower Hybrid Drift Waves Associated with Magnetic Reconnection in the Turbulent Magnetosheath. J. Geophys. Res. Space Phys. 2019, 124, 8551–8563. [Google Scholar] [CrossRef] [Green Version]
- Lacombe, C.; Alexandrova, O.; Matteini, L.; Santolík, O.; Cornilleau-Wehrlin, N.; Mangeney, A.; de Conchy, Y.; Maksimovic, M. Whistler mode waves and the electron heat flux in the solar wind: Cluster observations. Astrophys. J. 2014, 796, 5. [Google Scholar] [CrossRef] [Green Version]
- Celnikier, L.M.; Harvey, C.C.; Jegou, R.; Moricet, P.; Kemp, M. A determination of the electron density fluctuation spectrum in the solar wind, using the ISEE propagation experiment. Astron. Astrophys. 1983, 126, 293–298. [Google Scholar]
- Šafránková, J.; Němeček, Z.; Nemec, F.; Prech, L.; Pitňa, A.; Chen, C.H.K.; Zastenker, G.N. Solar wind density spectra around the ion spectral break. Astrophys. J. 2015, 803, 107. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.H.K.; Wicks, R.; Horbury, T.S.; Schekochihin, A. Interpreting power anisotropy measurements in plasma turbulence. Astrophys. J. Lett. 2010, 711, L79. [Google Scholar] [CrossRef]
- Chen, C.H.K.; Mallet, A.; Yousef, T.A.; Schekochihin, A.A.; Horbury, T.S. Anisotropy of Alfv’enic turbulence in the solar wind and numerical simulations. Mon. Not. R. Astron. Soc. 2011, 415, 3219–3226. [Google Scholar] [CrossRef] [Green Version]
- Rakhmanova, L.S.; Riazantseva, M.O.; Zastenker, G.N.; Yermolaev, Y.I.; Lodkina, I.G.; Chesalin, L.S. Turbulent Cascade in the Magnetosheath Affected by the Solar Wind’s Plasma Turbulence. Cosm. Res. 2020, 57, 443–450. [Google Scholar] [CrossRef]
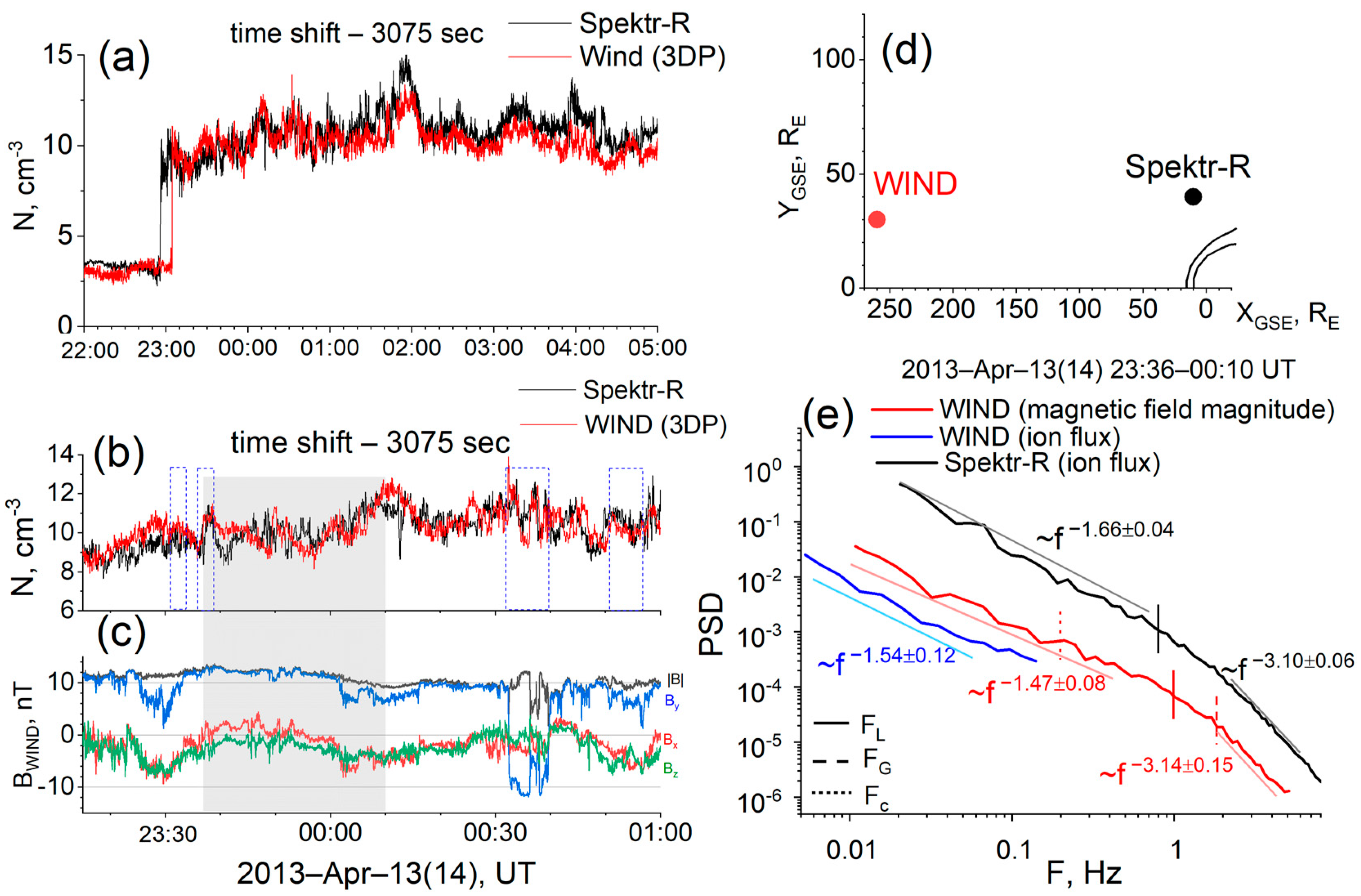

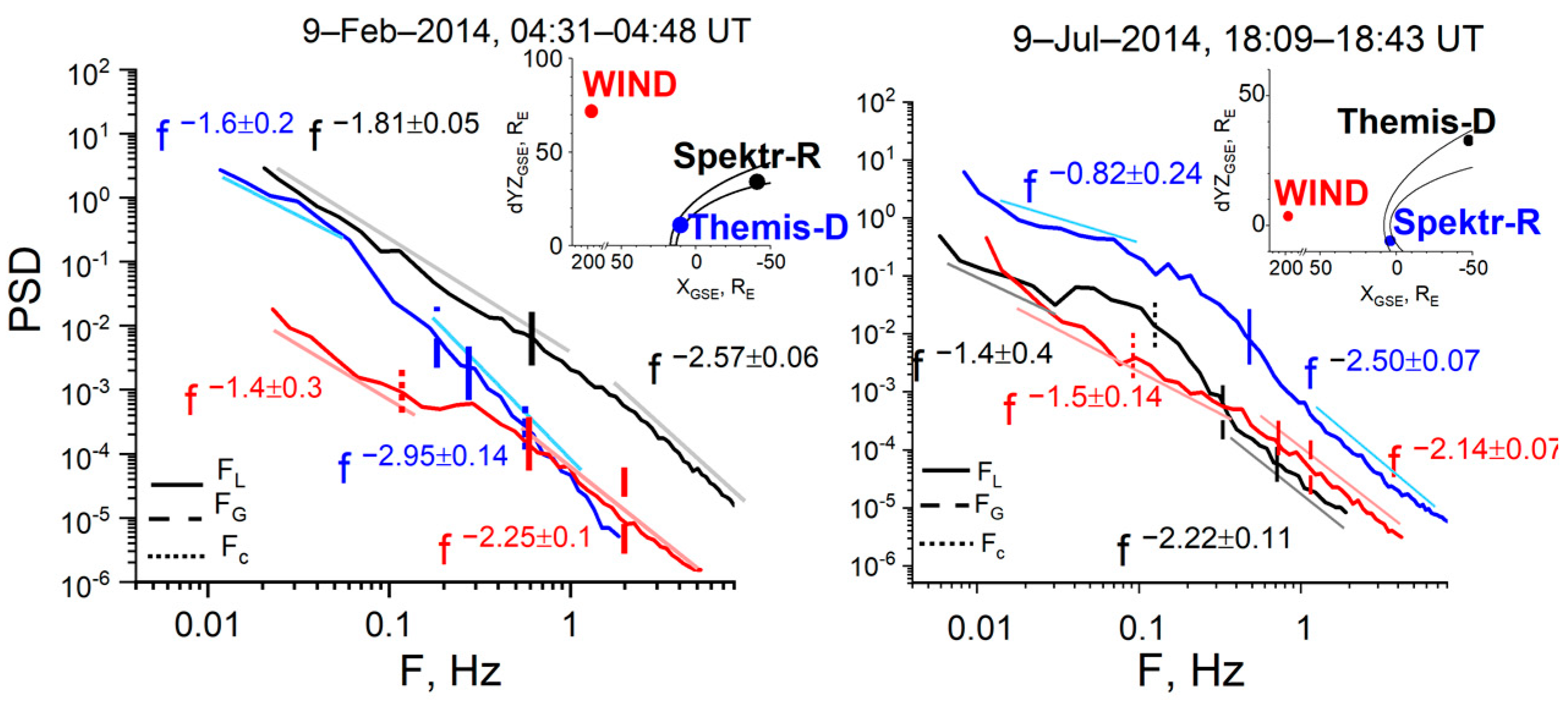
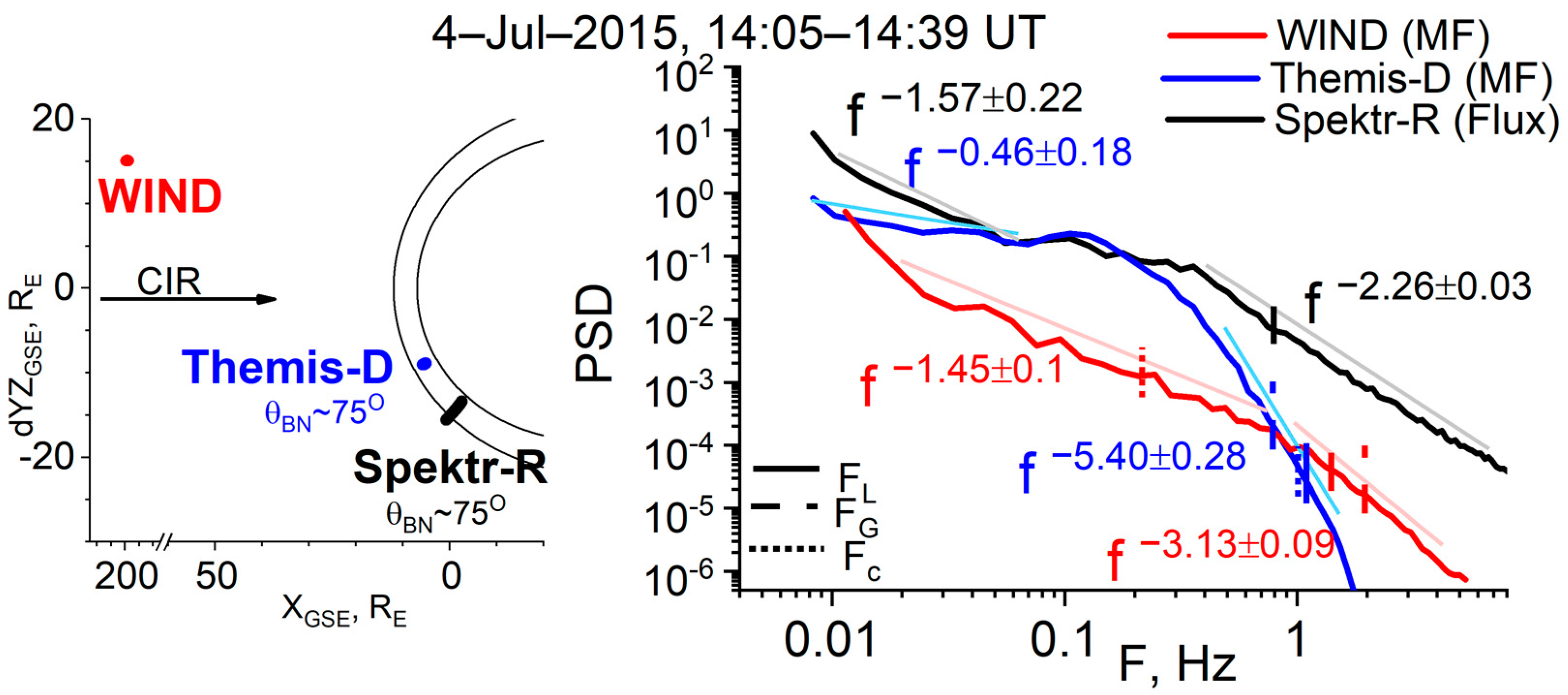
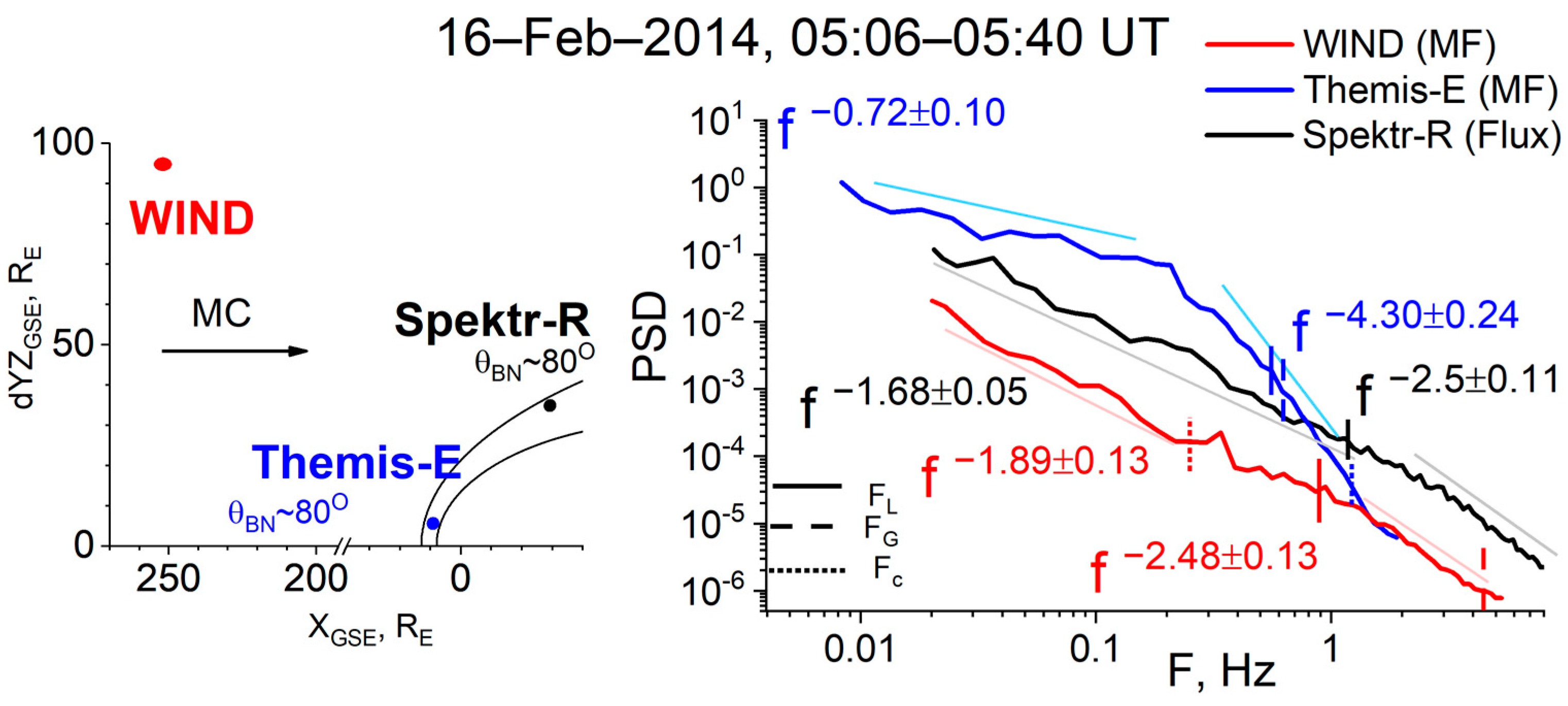

| № | Date | SW Type | Dayside MSH Parameters | SW Parameters | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| V/VA | βp | α(V,B), ° | N, cm−3 | V, km/s | |B|, nT | Tp, eV | βp | α(V,B), ° | |||
| 1 | 2014-02-08 | Ejecta | 0.4 | 0.7 | 75 | 6.1 | 459 | 11.7 | 8.4 | 0.15 | 61 |
| 2 | 2014-02-09 | SLOW | 0.5 | 2.6 | 150 | 4.3 | 431 | 7.0 | 2.9 | 0.10 | 119 |
| 3 | 2014-02-16 | MC | 0.5 | 0.7 | 64 | 9.4 | 405 | 17.0 | 3.0 | 0.04 | 78 |
| 4 | 2014-02-27 | SLOW | 0.8 | 4.3 | 55 | 17.4 | 353 | 4.7 | 3.2 | 1.01 | 121 |
| 5 | 2014-02-27 | CIR | 0.7 | 2.0 | 82 | 21.2 | 472 | 14.3 | 21.3 | 0.89 | 88 |
| 6 | 2014-07-09 | SLOW | -- | -- | -- | 8.4 | 351 | 6.2 | 4.6 | 0.40 | 82 |
| 7 | 2015-03-17 | SHEATH | 1.7 | 3.5 | 151 | 24.2 | 545 | 21.4 | 67.1 | 1.43 | 136 |
| 8 | 2015-03-17 | MC | 0.5 | 1.5 | 84 | 9.7 | 563 | 18.4 | 5.6 | 0.06 | 62 |
| 9 | 2015-07-04 | CIR | 1.2 | 2.2 | 75 | 30.5 | 365 | 14.5 | 7.7 | 0.45 | 87 |
| 10 | 2016-05-21 | CIR | 1.9 | 6.2 | 109 | 10.4 | 493 | 8.9 | 8.6 | 0.46 | 123 |
| 11 | 2017-11-15 | CIR | 1.0 | 3.5 | 81 | 27.9 | 425 | 9.7 | 2.6 | 0.32 | 102 |
| 12 | 2017-12-04 | CIR | 2.2 | 3.8 | 97 | 31.8 | 326 | 4.9 | 2.5 | 1.34 | 82 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rakhmanova, L.S.; Riazantseva, M.O.; Zastenker, G.N.; Yermolaev, Y.I. Large-Scale Solar Wind Phenomena Affecting the Turbulent Cascade Evolution behind the Quasi-Perpendicular Bow Shock. Universe 2022, 8, 611. https://doi.org/10.3390/universe8120611
Rakhmanova LS, Riazantseva MO, Zastenker GN, Yermolaev YI. Large-Scale Solar Wind Phenomena Affecting the Turbulent Cascade Evolution behind the Quasi-Perpendicular Bow Shock. Universe. 2022; 8(12):611. https://doi.org/10.3390/universe8120611
Chicago/Turabian StyleRakhmanova, Liudmila S., Maria O. Riazantseva, Georgy N. Zastenker, and Yuri I. Yermolaev. 2022. "Large-Scale Solar Wind Phenomena Affecting the Turbulent Cascade Evolution behind the Quasi-Perpendicular Bow Shock" Universe 8, no. 12: 611. https://doi.org/10.3390/universe8120611
APA StyleRakhmanova, L. S., Riazantseva, M. O., Zastenker, G. N., & Yermolaev, Y. I. (2022). Large-Scale Solar Wind Phenomena Affecting the Turbulent Cascade Evolution behind the Quasi-Perpendicular Bow Shock. Universe, 8(12), 611. https://doi.org/10.3390/universe8120611







