Top Quark Asymmetries

Abstract

The production of top quark pairs (t$\overline{t}$) via the quark-antiquark initial state is not symmetric under the exchange of top quark and antiquark. Calculations of this next-to-leading order effect predict asymmetries of about one to a few percent, depending on the centre-of-mass energy and the selected phase space. Experimentally, this charge asymmetry of t$\overline{t}$ production manifests itself in differences in angular distributions between top quarks and antiquarks. Sensitive observables are the rapidities of the produced top quarks and antiquarks as well as their energies. In dileptonic t$\overline{t}$ events, the asymmetry of the t$\overline{t}$ system is reflected in a similar asymmetry in the system of the produced lepton pair, with the crucial advantage of a simpler reconstruction procedure. In this article we review the measurements of this effect in different final states and using different observables by the ATLAS and CMS Collaborations in LHC collisions at three different centre-of-mass energies.

1. Introduction

Symmetry is a well known principle in Nature and has also a significant impact on our every-day-life, where symmetric states are considered “right” or “beautiful”, be it in arts, architecture, or other fields of our life. Moreover, symmetry is a powerful concept of the mathematical description of the world we live in and many of the great achievements in humankind’s endeavour to understand and formally describe the underlying principles of physics have been made thanks to symmetries. A prominent example is the standard model of particle physics (SM) being based on gauge symmetries. “Asymmetry” on the other hand is—according to the Merriam-Webster dictionary—defined as “the lack or absence of symmetry” [1], while this—on the first glance—sounds like a shortcoming of something that fails to be symmetric, a deeper look reveals that asymmetry as a principle of Nature is as important as symmetry. Just think of the asymmetry between matter and antimatter in our Universe that makes the Universe and life possible in the first place. Asymmetries in elementary particle physics often shape the way towards a deeper understanding of the fundamental objects and their interactions. One well-known example for such an asymmetry in particle physics is the asymmetry between top quarks and top antiquarks in the production of t$\overline{t}$ pairs. When produced via the charge symmetric fusion of two gluons, top quark (t) and antiquark ($\overline{t}$) behave symmetrically, while they loose this symmetry when produced from quark-antiquark-annihilation, as the top quark is tied to the incoming quark and the top antiquark is connected to the incoming antiquark, hence defining preferred directions for the production of top quarks and top antiquarks.

The fact that the production of top quark-antiquark pairs (t$\overline{t}$) from quark-antiquark initial states is not symmetric under exchange of top quark and antiquark when looking at cross sections as functions of angular variables was described and predicted already more than thirty years ago [2,3], followed by first measurements at the Fermilab Tevatron by the CDF [4] and D0 [5] Collaborations in 2008. Initially, the CDF results [6] have been a bit large in value with respect to the prediction and caused some stir in the physics community at that time. Triggered by the observed discrepancy between SM predictions and experimental results, several attempts have been made to explain the experimental findings with BSM physics, see for example Refs. [7,8,9,10]. However, in the following, updated theory calculations including further corrections and superseding new experimental results from the Tevatron experiments came closer [11], calming down the excitement that has been raised by the first experimental results.

In the meanwhile, data taking at the LHC started with the first proton-proton collisions in 2009 and the top quark and its properties came also in focus of the LHC experiments. Differences in angular distributions of top quarks and antiquarks could also be measured at the LHC, although under less favorable conditions, reducing the measurable size of the effect significantly. The challenging environment is partially compensated by the vast amount of t$\overline{t}$ candidate events produced in LHC collisions with the effect of a reduced statistical component of the measurement’s uncertainty.

In this article, we summarize the most recently published results by the ATLAS and CMS Collaborations on different manifestations of this t$\overline{t}$ production asymmetry, derived at three different centre-of-mass energies, and evaluate what we have learned from them concerning the top quark and potential indications for physics from beyond the standard model in the top quark sector.

2. Phenomenology and Theory Overview

When produced from the annihilation of a quark and an antiquark, the top quark and top antiquark interact with the colour fields of the incoming partons. This interaction leads to a correlation of the directions of motion of the outgoing top quark and of the incoming quark and of the directions of motion of the outgoing top antiquark and of the incoming antiquark, yielding differences in angular distributions of top quark and antiquark. This charge asymmetry, i.e., an asymmetry between top quark and antiquark, can also be calculated quantitatively. It occurs at next-to-leading-order (NLO) perturbation theory as an effect of the interference of initial-state (ISR) and final-state (FSR) radiation diagrams and of the interference of the Born and box diagrams for quark-antiquark initial states. While the ISR-FSR interference contributes negatively to the asymmetry, the contribution from the Born-box interference is positive. As the gluon-gluon initial state is charge symmetric, no asymmetry is present in these events. The t$\overline{t}$ processes (without extra additional jets) with a quark-gluon initial state feature a very small asymmetry, which - compared to the asymmetry from quark-antiquark initial states- can be neglected in most of the cases.

On parton level, the $t\overline{t}$ charge asymmetry can be defined as as a forward-backward asymmetry ($A_{\mathrm{FB}}$):

$$A_{\mathrm{FB}}=\frac{\sigma (x>0)-\sigma (x<0)}{\sigma (x>0)+\sigma (x<0)},$$

(1)

where x can be any observable (for example (pseudo-)rapidity) that defines two hemispheres with $x>0$ defining the hemisphere of “forward” direction and $x<0$ the hemisphere of “backward” direction and the $\sigma$s are the corresponding t$\overline{t}$ production cross sections for production in either of the two hemispheres.

How this parton level asymmetry actually manifests itself on particle level and how big the measurable effect is, depends on the colliding particles and their energy.

At the Tevatron collider at Fermilab protons and antiprotons were collided at a centre-of-mass energy of 1.96 TeV. Given the parton distribution functions (PDFs) of proton and antiproton at this energy, a valid assumption is, that the direction of the proton beam is also the direction of the incoming initial-state valence quark, while the direction of the antiproton beam defines the direction of the initial-state valence antiquark: “the charge asymmetry will be reflected not only in the partonic rest frame but also in the center-of-mass system of the proton and antiproton” [3]. The asymmetry is thus visible in the ratios of produced top quarks to top antiquarks in the two hemispheres. The experimental observable that has been used for the Tevatron analyses is $\Delta \eta$, the difference of the pseudorapidities of top quark and top antiquark in each event.

A t$\overline{t}$ forward-backward asymmetry can also be defined at the LHC, although not as straight-forward as for the Tevatron. While at the Tevatron, as discussed above, the “forward” direction is simply given by the proton beam direction, such a “global” definition of a preferred spatial direction for all events is not possible, because of the charge symmetric proton-proton collisions at the LHC. Here, it is a priori not clear whether the incoming (anti)quark comes from a proton from the clockwise injected beam or from the anti-clockwise injected beam. The parton level definition of “forward” and “backward” hemispheres is therefore only valid for single events. Consequently also on particle level the forward and backward directions can only be defined for single events. Therefore one needs to exploit a reconstructable observable that is sensitive to the forward direction as defined on parton level. The longitudinal momentum of the produced t$\overline{t}$ system is suited for that purpose as the incoming quark parton has on average a higher momentum fraction of the proton compared to the antiquark parton and the t$\overline{t}$ system is thus on average boosted along the direction of motion of the incoming quark.

However, also without making the effort to define forward and backward directions in LHC collisions, one can still identify a difference in angular distributions between top quark and top antiquark. The interacting quarks in proton-proton collisions can be valence quarks or sea quarks, while the interacting antiquarks are always sea quarks. Thus, the initial state quarks carry on average a higher momentum fraction of the proton compared to initial state antiquarks. This difference in average momentum together with the already mentioned correlation of the momentum of the incoming (anti-)quark with that of the produced top (anti-)quark, results in higher momenta on average of the produced top quarks, while the top antiquarks are produced more centrally. Experimentally this effect can be observed through the difference in the widths of the rapidity (y) distributions of top quarks compared to the one of top antiquarks.

Finally, in t$\overline{t}$ events with an additional high-p_T jet, where the quark gluon initial state ($qg\to t\overline{t}j$) plays the dominating role, exists an asymmetry in the scattering angles between top quarks and top antiquarks with respect to the direction of motion of the additional jet. Energy and momentum conservation connects the asymmetry of the top quark and antiquark scattering angles in the $t\overline{t}j$ rest frame to an observable energy difference of top quark and antiquark, ΔE. Hence this effect is named energy asymmetry [12]. Exploiting the boost of the outgoing quark-jet in the direction of the incoming valence quark one can define ΔE differentially and thus maximise the statistical sensitivity to the energy asymmetry.

In the SM, the positive contributions from the Born-box interference outweigh the negative contributions from the ISR-FSR interference and the predicted asymmetry values from theoretical calculations lie in the range of very few percent (see for example Refs. [13,14,15]). The actual values depend on the colliding hadrons, on the centre-of-mass energy, on the examined phase-space, on the exploited observable, and on the terms and corrections included in the calculation. Although the asymmetry occurs at NLO precision in QCD calculations, it has been shown that electroweak (EW) contributions as well as next-to-next-to-leading order (NNLO) QCD contributions are of significant size [13,15]. However, the analyses described in this review make in general use of the state-of-the-art NLO-QCD Monte Carlo generators for the simulation of the t$\overline{t}$ signal. Predictions from these generators are therefore in general smaller than predictions from theory calculations including higher order QCD effects and EW contributions. For that reason, in the analyses described in this review wherever possible the experimental results are compared to predictions from calculations rather than to predictions from simulation. Physics contributions from beyond the SM (BSM) could however significantly enhance the asymmetry between top quark and antiquark while sustaining other boundary conditions like the total t$\overline{t}$ production cross section or other kinematic distributions of the produced top(anti)quarks. As the top quark plays a special role among all quarks of the SM due to its large mass and correspondingly its Yukawa coupling being close to unity, it is believed to be particularly sensitive to new physics contributions. Depending on the mass scale of hypothetical new particles, different approaches are used in the theory calculations to predict the impact on the t$\overline{t}$ charge asymmetry. Assuming the new physics being very heavy and out of reach of the LHC collisions, an effective field theory (EFT) ansatz is used to identify those operators [16,17] that could have a significant impact on the t$\overline{t}$ charge asymmetry while keeping the predictions for various kinematic distributions and cross sections in agreement with observations. Potential light new particles could be exchanged via s, t, or u channel. Prominent examples of such additional new particles are a colour-octet vector G, a neutral $Z^{\prime }$ boson, a charged $W^{\prime }$ boson, a colour-triplet scalar $\omega$, or a colour-sextet scalar Ω [18].

3. Measurements of the t$\overline{t}$ Charge Asymmetry at the LHC

The ATLAS and CMS Collaborations have measured the t$\overline{t}$ charge asymmetry at three different centre-of-mass energies at the LHC, at 7, 8, and 13 TeV. t$\overline{t}$ candidate events with either two charged leptons (dilepton channel) or one charged lepton (lepton+jets channel) are analyzed. In the analyses of both collaborations, "lepton" refers to electrons and muons, while tau leptons are only considered indirectly through their decay products (electrons or muons) when decaying leptonically. The difference of the absolute values of the rapidity of the top quarks and antiquarks serves as the observable sensitive to the t$\overline{t}$ charge asymmetry,

$$A_{\mathrm{C}}^{t\overline{t}}=\frac{N(\Delta |y|>0)-N(\Delta |y|<0)}{N(\Delta |y|>0)+N(\Delta |y|<0)},$$

(2)

where $\Delta \left|y\right|=|y_t|-|y_{\overline{t}}|$.

In order to construct this observable, the t$\overline{t}$ system needs to be fully reconstructed. For this purpose different approaches are used in the different analyses. The common property of all these reconstruction methods is that the reconstructed fourvectors of top quarks and antiquarks as well as the resulting kinematic observable are always diluted with respect to their true values and they need to be corrected for. The impacts from a $\Delta \left|y\right|$ dependent detector efficiency and resolution effects of the kinematic reconstruction are rectified in the different analyses by deploying unfolding methods.

For events in the dilepton channel, it is also possible to measure directly $\Delta \left|\eta \right|$ between the positively and the negatively charged lepton from the top quark decays: $\Delta \left|\eta \right|=|{\eta }_{{\ell }^{+}}|-|{\eta }_{{\ell }^{-}}|$. As the leptons from the top quark decay inherit the direction of motion of the mother top quark, a similar asymmetry is expected also for this lepton based $\Delta \left|\eta \right|$ observable,

$$A_{\mathrm{C}}^{\ell \ell }=\frac{N(\Delta |\eta |>0)-N(\Delta |\eta |<0)}{N(\Delta |\eta |>0)+N(\Delta |\eta |<0)}.$$

(3)

However, the direction of motion of the leptons is not fully identical to that of the mother top (anti)quarks, as a result the predicted asymmetry is smaller by about 40% compared to the asymmetry of top quark and antiquark. This disadvantage is compensated for by the advantage that no reconstruction of the t$\overline{t}$ system is required and thus no diluting effects from the reconstruction resolution have to be considered when analysing the asymmetry of the leptons. Only the detector acceptance needs to be corrected for in the unfolding, making this procedure simpler and reducing the impact on the result from the chosen unfolding method.

It is also interesting to measure $A_{\mathrm{C}}^{t\overline{t}}$ differentially as a function of kinematic variables of the t$\overline{t}$ system that are sensitive to the t$\overline{t}$ charge asymmetry. Suited for this purpose are the transverse momentum $p_{\mathrm{T}}^{t\overline{t}}$, the rapidity $y_{t\overline{t}}$, and the invariant mass $m_{t\overline{t}}$ of the t$\overline{t}$ system. Furthermore, the boost in z direction of the t$\overline{t}$ system, ${\beta }_{z,t\overline{t}}$, is used in differential measurements. The transverse momentum of the t$\overline{t}$ system gives a handle on the ratio of the positive contribution to the total asymmetry from the interference between Born and box diagrams and the negative contribution from the interference between ISR and FSR. Events with additional hard radiation feature on average also a higher transverse momentum of the t$\overline{t}$ system, thus for t$\overline{t}$ events at high transverse momentum the negative contribution from the ISR-FSR interference dominates [13]. As t$\overline{t}$ pairs produced via $q\overline{q}$ annihilation are most often found at large rapidities, while the charge symmetric production via gluon fusion is dominant in the central region, one can expect an enhancement of the charge asymmetry with increasing $|y_{t\overline{t}}|$ [13]. This is because of the on average higher momentum of the valence quarks with respect to the momentum of the sea antiquarks, resulting in a boost of the t$\overline{t}$ system in the z direction. For the very same reason, also the boost of the t$\overline{t}$ system in z direction is a powerful observable to enhance the size of the asymmetry. Finally, the invariant mass of the t$\overline{t}$ system is also sensitive to production mechanism with an enhanced fraction of $q\overline{q}$ produced t$\overline{t}$ pairs at high values of $m_{t\overline{t}}$ and thus also enhanced values for the asymmetry. In addition, the effect of new contributions from BMS physics is expected to be stronger for events with high $m_{t\overline{t}}$ values or with large values of the z coordinate of the velocity of the t$\overline{t}$ system [19].

In order to correct for efficiency and resolution effects in these differential measurements, sophisticated multidimensional unfolding procedures need to be deployed as not only the $\Delta \left|y\right|$ distribution but also the values of the kinematic variables of the t$\overline{t}$ system need to be corrected at the same time.

The following sections summarize the t$\overline{t}$ charge asymmetry measurements at 7, 8, and 13 TeV in the dilepton and lepton+jets channels, carried out by the ATLAS and CMS Collaborations.

3.1. Measurements at 7 TeV Centre-of-Mass Energy

The ATLAS and CMS Collaborations have both explored the full dataset of collisions at 7 TeV centre-of-mass energy to measure the t$\overline{t}$ charge asymmetry in the dilepton and lepton+jets channels. The dataset collected by the ATLAS experiment corresponds to an integrated luminosity of 4.6 fb⁻¹, while the CMS dataset corresponds to 5 fb⁻¹. The t$\overline{t}$ charge asymmetry $A_{\mathrm{C}}^{t\overline{t}}$ is measured in both channels while the lepton asymmetry $A_{\mathrm{C}}^{\ell \ell }$ is an exclusive observable of the dilepton channel. Theory calculations at NLO QCD including mixed QCD-QED and QCD-weak interaction corrections [14] predict for the SM at a centre-of-mass energy of 7 TeV values of

$$\begin{array}{c}\hfill A_{\mathrm{C}}^{t\overline{t}}=0.0123\pm 0.0005\left(\mathrm{scale}\right),\end{array}$$

(4)

$$\begin{array}{c}\hfill A_{\mathrm{C}}^{\ell \ell }=0.0070\pm 0.0003\left(\mathrm{scale}\right).\end{array}$$

(5)

The quoted scale uncertainties consider variation of the renormalization and factorization scales by factors of 0.5 and 2 with respect to the reference value, set to the top quark mass. Another calculation, differing in few technical aspects like the central value of the renormalization and factorization scales being set to the partonic centre-of-mass energy and the usage of a leading order parton distribution function instead of a next-to-leading order one, yields a similar value for the t$\overline{t}$ charge asymmetry, $A_{\mathrm{C}}^{t\overline{t}}=0.0115\pm 0.0006\left(\mathrm{scale}\right)$ [13].

These predictions are made for inclusive t$\overline{t}$ production without any constraints on the phase space of the process. Hence, the asymmetries measured experimentally in a certain phase space region, as defined by the event selection requirements of the analyses, need to be extrapolated to the full phase space of t$\overline{t}$ production to be directly comparable to the predictions. For this purpose, corrections are applied to the reconstructed distributions of the sensitive observables.

In this chapter, the measurements of $A_{\mathrm{C}}^{t\overline{t}}$ and $A_{\mathrm{C}}^{\ell \ell }$ at $\sqrt{s}=7$ TeV by the ATLAS and CMS Collaborations are summarized.

3.1.1. Measurements of the t$\overline{t}$ and Lepton Charge Asymmetry in the Dilepton Channel by ATLAS

The ATLAS Collaboration measured the lepton and t$\overline{t}$ charge asymmetry in the 7 TeV dataset in the dilepton channel [20]. Electrons, muons, and jets, reconstructed using the anti-$k_{\mathrm{T}}$ algorithm with a distance parameter of $R=0.4$, are considered in the analysis. To suppress backgrounds from fake and non-prompt leptons, the electrons and muons are required to be isolated from any other activity in the detector around their tracks. Exactly two, oppositely charged, isolated leptons are required and according to the flavour of the leptons, the selected dataset is divided into three channels: $ee$, $e\mu$, $\mu \mu$. To suppress background events from Drell-Yan and Z boson production, in the $ee$ and $\mu \mu$ channels, the invariant mass of the lepton pair needs to be larger than 15 GeV and needs to fall outside a window of 20 GeV width centered on the Z boson mass. In addition, the missing transverse energy $E_{\mathrm{T}}^{\mathrm{miss}}$ of candidate events needs to be larger than 60 GeV in these channels.

8125 candidate events remain in the selected dataset, with about six times more signal than background expected. The main background contribution comes from the electroweak production of single top quarks, followed by diboson production. The two backgrounds from Z boson production and fake or non prompt leptons are efficiently reduced by the requirements mentioned above and comprise the smallest contribution to the background considered in this analysis.

The sensitive observable of the measurement of the lepton charge asymmetry, the difference in pseudorapidity of the two charged leptons $\Delta \left|\eta \right|$, is directly accessible from the fourvectors of the selected leptons. For the difference of the rapidity of the two top quarks $\Delta \left|y\right|$, the sensitive observable of the measurement of the t$\overline{t}$ charge asymmetry, a kinematic reconstruction of the t$\overline{t}$ system needs to be applied, starting from the objects measured in the detector and imposing energy conservation at each decay vertex. The resulting kinematic equations are underconstrained due to the two neutrinos present in the signal process. For that reason further assumptions are made on the reconstructed top quark and W boson masses and a scan over all possible hypotheses for the two final state neutrinos is performed. Every hypothesis gets a weight that reflects the degree of agreement between the $E_{\mathrm{T}}^{\mathrm{miss}}$ calculated from the reconstructed neutrinos and the $E_{\mathrm{T}}^{\mathrm{miss}}$ as observed in the event. In addition, all possible associations of jets and leptons are considered where the jet energies are allowed to float within their resolutions. For each event the hypothesis with the best neutrino weight is used in the further analysis chain. Studies on simulated t$\overline{t}$ events show that with this method, solutions for 80% of all events can be found, while for 20% of the events the method does not produce a valid solution. Consequently, the events without solution of the kinematic reconstruction are not considered for the analysis.

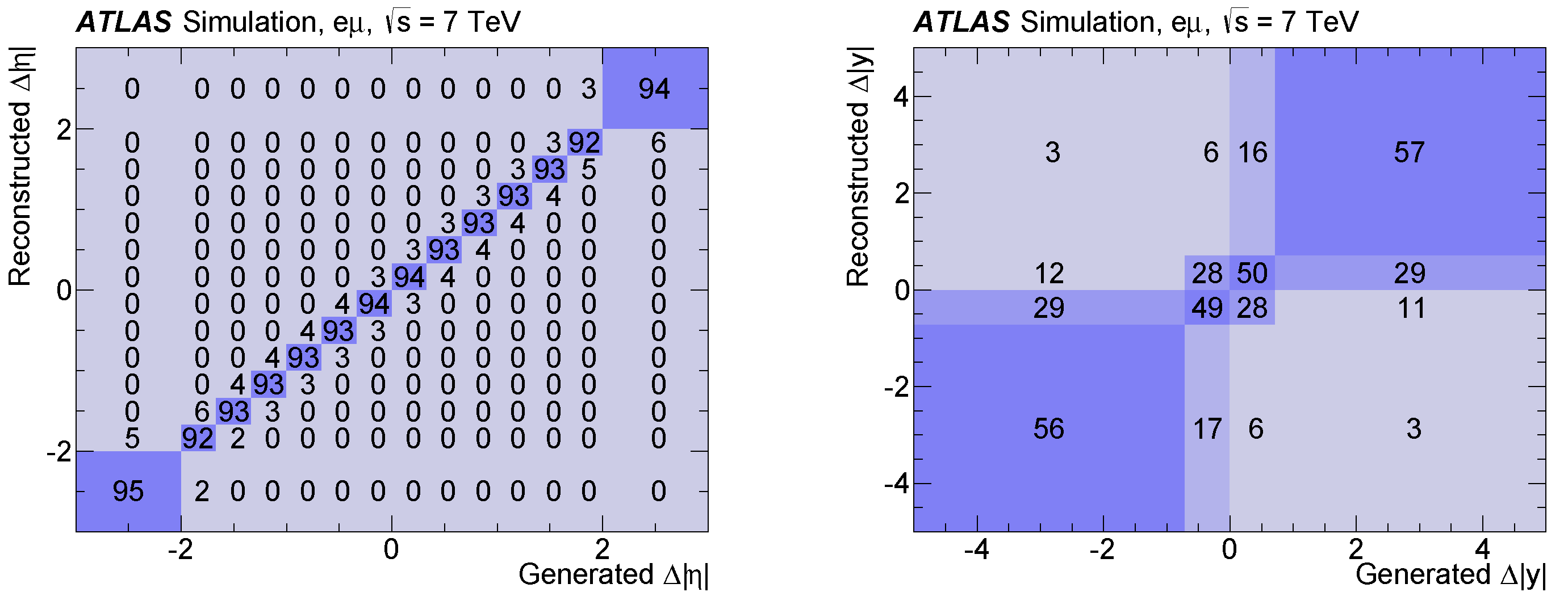
Figure 1 shows the reconstructed values of $\Delta \left|\eta \right|$ between the two leptons (left) and $\Delta \left|y\right|$ between top quark and antiquark (right) over their generated true values. This response matrix describes the resolution of the reconstruction and how likely migrations between different bins of true and reconstructed values of the sensitive observable are. The response matrix for the lepton asymmetry is dominated by the diagonal elements with each being larger than 90%, thus showing a very good resolution of the reconstruction. Hence, the main correction needed in this analysis is the correction of the acceptance effects.

Acceptance effects and the small migration effects are corrected for by bin-by-bin correction factors, which are applied to the background subtracted numbers of selected data events in each bin. The correction factors are derived from simulation and are given by the ratio of predicted signal events from the true distribution in a certain bin divided by the predicted signal events from the reconstructed distribution in the same bin.

As can be seen from Figure 1 (right), the resolution of the observable relying on the t$\overline{t}$ system reconstruction is worse with respect to that of the lepton based observable. Hence, instead of bin-wise correction factors, the fully Bayesian unfolding (FBU, [21]) is applied to correct for detector resolution effects. For that purpose, the response matrix as shown in Figure 1 (right), describing the detector resolution effects, is derived from the nominal simulated t$\overline{t}$ sample from generated and reconstructed values of the sensitive observable. By applying this matrix to the true distribution and adding a background model, the total expected yield of events in the selected phase space can be expressed and compared via a maximum likelihood estimator to the number of observed events per bin. Within the FBU, the maximum likelihood estimator is regularized with an additional curvature based regularization function that dampens statistical fluctuations. On top of the FBU additional acceptance correction factors are applied on the unfolded distribution. The total corrections to the bins of the $\Delta \left|y\right|$ distribution depend on the actual bin and channel and vary between 10 and 100.

For both measurements, the linearity of the applied methods is checked using samples of simulated t$\overline{t}$ events, reweighted such that they exhibit different true asymmetries and comparing the results with the true asymmetry. The impacts of various sources of systematic uncertainties vary for the different channels with the overall tendency that the lepton based measurement is dominated by the uncertainties in the lepton reconstruction and the uncertainty in the modeling of the non prompt and fake leptons in the case of the $ee$ channel, while for the t$\overline{t}$ charge asymmetry measurement several sources of uncertainty are of similar importance, including uncertainties in the reconstruction of leptons, jets, and missing transverse energy, as well uncertainties in the modeling of the non prompt and fake leptons background component.

Figure 2 shows the normalized $\Delta \left|\eta \right|$ and $\Delta \left|y\right|$ distributions in the $e\mu$ channel after the described corrections have been applied.

The asymmetries are measured individually in the three channels and are later on combined using the best linear unbiased estimator (BLUE) method [22,23]. The individual results and their combination are listed in

Table 1. Results for the lepton-based asymmetry $A_{\mathrm{C}}^{\ell \ell }$ and the $t\overline{t}$ asymmetry $A_{\mathrm{C}}^{t\overline{t}}$ after correcting for detector, resolution, and acceptance effects. The values in the $ee$, $e\mu$, and $\mu \mu$ channels as well as the combined value are presented with their statistical and systematic uncertainties [20].

Channel	${\mathit{A}}_{\mathbf{C}}^{\mathbf{\ell }\mathbf{\ell }}$	${\mathit{A}}_{\mathbf{C}}^{\mathit{t}\overline{\mathit{t}}}$
$ee$	$0.101\pm 0.052\pm 0.021$	$0.025\pm 0.069\pm 0.027$
$e\mu$	$0.009\pm 0.019\pm 0.009$	$0.007\pm 0.032\pm 0.018$
$\mu \mu$	$0.047\pm 0.030\pm 0.012$	$0.043\pm 0.045\pm 0.013$
Combined	$0.024\pm 0.015\pm 0.009$	$0.021\pm 0.025\pm 0.017$

. For both measurements the result from the $e\mu$ channel contributes with the largest weight to the combination, while the result from the $ee$ channel plays in both cases only a minor role. The combined results are comparable with the predictions for the SM, but also with zero asymmetry, as can be seen in Figure 3.

3.1.2. Measurements of the t$\overline{t}$ and Lepton Charge Asymmetry in the Dilepton Channel by CMS

Lepton and t$\overline{t}$ charge asymmetry were also measured by the CMS Collaboration in the 7 TeV dataset [24]. In addition to the inclusive results for both asymmetries, the lepton charge asymmetry was measured differentially as function of the invariant mass, absolute value of the rapidity, and transverse momentum of the t$\overline{t}$ system. Similar requirements are made to the recorded events as in the ATLAS analysis discussed above to select a dataset enriched in t$\overline{t}$ dilepton candidate events and to suppress the dominant background contributions. Exactly two isolated charged leptons are required and at least one of the two or more jets, reconstructed using the $k_{\mathrm{T}}$ algorithm with a distance parameter of $R=0.5$, needs to be identified as stemming from the hadronization of a b quark, using the Combined Secondary Vertex Tagger (CSV) [25]. CMS employs the particle flow technique [26] to reconstruct jets and the missing transverse momentum.

The selected dataset consists of 9824 candidate events with an estimated signal to background ratio of about 13, thus the dataset in the CMS analysis is slightly larger compared to that of the ATLAS analysis and features a two times higher purity in terms of t$\overline{t}$ dilepton events. The main background contributions come from the production of single top quarks and t$\overline{t}$ events without dileptonic decays, followed by diboson production. In this analysis, no separate measurements are performed in the three lepton flavour channels $ee$, $e\mu$, and $\mu \mu$, instead the events of the three channels are added up and the resulting distributions are then fitted.

In order to resolve the ambiguity of the missing transverse momentum and the two neutrinos present in the events and the ambiguity in combining the b tagged jets with the charged leptons for the reconstruction of the t$\overline{t}$ system, the Analytical Matrix Weighting Technique (AMWT) [27] is employed. This technique finds the most probable solution for a top quark mass of 172.5 GeV out of the up to eight possible solutions for the reconstruction of the t$\overline{t}$ system. The momenta of jets and the missing transverse momentum are allowed to float within their respective uncertainties to reduce the fraction of events with no analytic solution. The about 14% of events for which the AMWT fails to find a solution are only considered in the inclusive lepton charge asymmetry measurement and omitted for all measurements that involve reconstructed quantities of the t$\overline{t}$ system.

As in the ATLAS analysis, the reconstructed distributions of $\Delta \left|\eta \right|$ and $\Delta \left|y\right|$ need to be corrected for acceptance and migration effects. The smearing matrix with generated and reconstructed $\Delta \left|\eta \right|$ ($\Delta \left|y\right|$) values, derived from simulated t$\overline{t}$ events and a matrix with acceptance times efficiency on the diagonal elements are used to correct the reconstructed distributions via a regularized unfolding algorithm based on singular-value decomposition (SVD) [28]. In the CMS analysis, for the correction of both observables, the same unfolding technique is employed.

For the differential measurements of the lepton charge asymmetry as functions of $m_{t\overline{t}}$, $|y_{t\overline{t}}|$, and $p_{\mathrm{T}}^{t\overline{t}}$, two-dimensional distributions of reconstructed values need to be unfolded, using the same unfolding technique as for the inclusive measurements. In order to not amplify statistical uncertainties, the number of bins in $\Delta \left|\eta \right|$ and $\Delta \left|y\right|$ is reduced to two, while three bins are used for the $m_{t\overline{t}}$, $|y_{t\overline{t}}|$, and $p_{\mathrm{T}}^{t\overline{t}}$ distributions.

The performance of the applied unfolding method is checked using samples of simulated t$\overline{t}$ events, reweighted such that they feature asymmetries between −0.2 and 0.2, and comparing the resulting asymmetry measurement with the true asymmetry of the respective sample. The impact of various experimental and theoretical sources of systematic uncertainties are evaluated. For the measurement of the lepton asymmetry, the by far dominating contribution to the overall systematic uncertainty is the uncertainty in the factorization and renormalization scales of the used simulation. In the case of the t$\overline{t}$ charge asymmetry factorization and renormalization scale uncertainties are also the dominant contribution together with the uncertainty in the jet energy scale.

Figure 4 shows the distributions of $\Delta \left|\eta \right|$ and $\Delta \left|y\right|$ after background subtraction and unfolding, compared to the distributions predicted by MC@NLO. The resulting asymmetry values of the inclusive measurements, listed in

Table 2. Results for the lepton-based asymmetry $A_{\mathrm{C}}^{\ell \ell }$ and the t$\overline{t}$ asymmetry $A_{\mathrm{C}}^{t\overline{t}}$ after correcting for detector, resolution, and acceptance effects. The values are presented with their statistical and systematic uncertainties [24].

Channel	${\mathit{A}}_{\mathbf{C}}^{\mathbf{\ell }\mathbf{\ell }}$	${\mathit{A}}_{\mathbf{C}}^{\mathit{t}\overline{\mathit{t}}}$
$\ell \ell$	$0.009\pm 0.010\pm 0.006$	$-0.010\pm 0.0017\pm 0.008$

, are comparable with the predictions by the SM but are within their uncertainties also comparable with zero asymmetry.

The dependence of the measured lepton asymmetry on three kinematic variables of the t$\overline{t}$ system are shown in Figure 5. Within their relatively large uncertainties also the differential results are comparable with the predictions of the simulation.

3.1.3. Measurement of the t$\overline{t}$ Charge Asymmetry in the Lepton+Jets Channel by ATLAS

The ATLAS Collaboration measured the t$\overline{t}$ charge asymmetry in the 7 TeV dataset also for events with a single lepton signature (lepton+jets channel) [29]. Exactly one isolated high-p_T electron or muon, missing transverse momentum, and at least four jets are required. On top of this “pretag” selection, at least one of the selected jets needs to be identified as stemming from the hadronization of a b quark for the event to enter the “tag” selection. For the purpose of identifying jets from b quarks, a combination of three different b-tagging algorithms is used [30,31].

From the 111,817 events passing the criteria of the “pretag” selection, 59,497 events feature in addition at least one identified b jet. The estimated signal to background ratio in the “tag” selection dataset is about 4. The dominant background contribution comes from the production of W bosons in association with jets, followed by single top quark production and the production of QCD multijets.

As the production cross section for positively charged W bosons is larger than that for negatively charged W bosons, the asymmetry in the numbers of selected events with positively and negatively charged leptons can be used to estimate the background contribution from W+jets production directly from the data. This estimation is done in the pretag selected dataset and then extrapolated to the tag selection by applying tagging efficiencies derived from simulated W+jets events. As the flavour composition of the jets accompanying the W bosons is not well predicted in the simulation, the flavour fractions are derived in data and applied to the simulation. The amount of multijet production from QCD processes is determined using the matrix method, which, based on tight and more loosely defined lepton samples, estimates the efficiency for leptons from multijet background to pass the tight selection criteria of the event selection applied in this analysis.

The t$\overline{t}$ system is reconstructed by applying a kinematic fit based on likelihood determination for the different reconstruction options for each event [32]. While for the inclusive measurement all t$\overline{t}$ candidate events are used, the differential measurements are only carried out for events with a likelihood value above a certain threshold to reject events that are not reconstructed well.

As for the analysis in the dilepton channel, again the FBU method is used to correct the reconstructed distributions for acceptance and resolution effects. As the number of selected events is larger compared to that of the dilepton analysis, four bins instead of only two are used for the $\Delta \left|y\right|$ distribution, in the inclusive measurement as well as in the differential measurement.

Several sources of systematic uncertainty are considered as nuisance parameters in the likelihood function used for the unfolding and the systematic uncertainty of the measurement is then determined by means of a marginalization procedure applied to this likelihood. The dominating contributions come from the uncertainty in the energy scale and resolution of leptons and jets, and from the missing transverse momentum and pileup modeling.

The measured asymmetry values are summarized in

Table 3. Measured inclusive charge asymmetry values for the electron and muon channels combined after unfolding for the full phase space, for events with ${\beta }_{z,t\overline{t}}>0.6$, and for events with $m_{t\overline{t}}>600$ GeV [29], along with the respective predictions [14]. The uncertainties of the measurements include statistical and systematic components.

Phase Space	Measured ${\mathit{A}}_{\mathbf{C}}^{\mathit{t}\overline{\mathit{t}}}$	SM prediction for ${\mathit{A}}_{\mathbf{C}}^{\mathit{t}\overline{\mathit{t}}}$
Full	$0.006\pm 0.010$	$0.0123\pm 0.0005$
$m_{t\overline{t}}>600$ GeV	$0.018\pm 0.022$	$0.{0175}_{-0.0004}^{+0.0005}$
${\beta }_{z,t\overline{t}}>0.6$	$0.011\pm 0.018$	$0.{020}_{-0.007}^{+0.006}$

. In addition to the inclusive result for the full phase space, also the asymmetries for events with $m_{t\overline{t}}>600$ GeV and for events with ${\beta }_{z,t\overline{t}}>0.6$, i.e., for events from phase space regions where an enhanced asymmetry is predicted, are measured separately and compared to the SM predictions. The quoted uncertainty for the measured values represents the total uncertainty including statistical and systematic components. Figure 6 shows the results of the differential measurements. All measured values are within their uncertainties comparable to SM predictions as well as to zero asymmetry.

3.1.4. Measurement of the t$\overline{t}$ Charge Asymmetry in the Lepton+Jets Channel by CMS

The charge asymmetry was also measured inclusively and differentially in the lepton+jets channel by the CMS Collaboration [33]. After the typical event selection requirements of exactly one isolated electron or muon, at least four jets, of which at least one has to be tagged as b jet, and substantial missing transverse momentum, 57,687 events remain for the measurement. About 20% of the selected events come from background processes, with the biggest contribution coming from the production of W bosons in association with jets, followed by the electroweak production of single top quarks and multijet production.

The leptonically decaying top quark is reconstructed from the fourvector of the electron or muon and from the transverse momentum vector. All assignments of selected jets to the final state quarks in a t$\overline{t}$ event are considered and the hypothesis with the highest probability to correctly describe the t$\overline{t}$ system is chosen for each event. It is worth mentioning that all events are considered in the analysis and no restriction is made on the quality of the event reconstruction. Disturbing effects from event selection and detector and reconstruction method resolution are corrected for by employing a regularized generalized matrix inversion unfolding. For the differential measurements not only the $\Delta \left|y\right|$ distribution is unfolded but also the kinematic variables of the t$\overline{t}$ system. As the binning schemes in $\Delta \left|y\right|$ differ depending on the bin of the kinematic t$\overline{t}$ variable, a non trivial definition of “neighboring bin” had to be found to correctly consider the influence of adjacent bins in the regularization procedure.

The dominating source of systematic uncertainty comes from the dependency of the asymmetry on the three kinematic t$\overline{t}$ variables and its impact on the used unfolding method and from the uncertainty in the selection and identification of the leptons. Depending on the actual bin, also uncertainties in the jet energy scale contribute significantly to the differential measurements.

Figure 7 (top left) shows the unfolded $\Delta \left|y\right|$ spectrum. From this distribution, the inclusive t$\overline{t}$ charge asymmetry is measured to be $A_{\mathrm{C}}^{t\overline{t}}=0.004\pm 0.010\left(\mathrm{stat}\right)\pm 0.011\left(\mathrm{syst}\right)$. The $A_{\mathrm{C}}^{t\overline{t}}$ values as functions of $m_{t\overline{t}}$, $|y_{t\overline{t}}|$, and $p_{\mathrm{T}}^{t\overline{t}}$ are shown in Figure 7 (top right and bottom). All results are consistent with predictions for the SM, but are also consistent with zero asymmetry.

3.1.5. Combination of the Inclusive Measurements of the t$\overline{t}$ Charge Asymmetry in the Lepton+Jets Channel by ATLAS and CMS

The results of the inclusive $A_{\mathrm{C}}^{t\overline{t}}$ measurements in the lepton+jets channel at 7 TeV by the ATLAS and CMS Collaborations have been combined within the LHC working group for top quark physics (LHC$top$WG) [35]. The BLUE technique with the method implemented in Ref. [36] is used to find the combination of the two results with the smallest total uncertainty. Most systematic uncertainties are considered uncorrelated in the combination, except for the uncertainty in the modeling of the t$\overline{t}$ signal and the W+jets background (both 50% correlated between ATLAS and CMS) and the uncertainty in the used PDFs (100% correlated between ATLAS and CMS).

The result of the combination of the two measurements in the lepton+jets channel at 7 TeV is $A_C^{t\overline{t}}=0.005\pm 0.007\left(\mathrm{stat}\right)\pm 0.006\left(\mathrm{syst}\right)$, with the ATLAS result contributing with a weight of 0.65 and the CMS result with a weight of 0.35. The ${\chi }^2$ with one degree of freedom of the combination is 0.012, corresponding to a p-value of 0.91. The improvement in the total uncertainty of the combined results with respect to the individual results is 18% for the ATLAS measurement and 40% for the CMS analysis.

Figure 8 summarizes all ATLAS and CMS measurements of $A_{\mathrm{C}}^{t\overline{t}}$ and $A_{\mathrm{C}}^{\ell \ell }$ at 7 TeV centre-of-mass energy and their compatibility with theory calculations for the standard model.

3.2. Measurements at 8   Centre-of-Mass Energy

The ATLAS and CMS Collaborations performed various top quark asymmetry measurements using the LHC dataset at $\sqrt{s}=8$ TeV of around 20 fb⁻¹ in the dilepton and lepton+jets channels. As for the 7 TeV measurements, the t$\overline{t}$ charge asymmetry $A_{\mathrm{C}}^{t\overline{t}}$ is measured in both channels while the lepton asymmetry is measured exclusively in the dilepton channel. At 8 TeV centre-of-mass energy, the SM prediction computed at NLO QCD including mixed QCD-QED and QCD-weak interaction corrections [14] is slightly smaller than at 7 TeV:

$$\begin{array}{c}\hfill A_{\mathrm{C}}^{t\overline{t}}=0.0111\pm 0.0004\left(\mathrm{scale}\right),\end{array}$$

(6)

$$\begin{array}{c}\hfill A_{\mathrm{C}}^{\ell \ell }=0.0064\pm 0.0003\left(\mathrm{scale}\right).\end{array}$$

(7)

The quoted scale uncertainties consider variation of the renormalization and factorization scales by factors of 0.5 and 2 with respect to the reference value, set to the top quark mass, as well as PDF uncertainties. As for 7 TeV, another calculation at NLO, using a different PDF set and setting the renormalizaton and factorization scales to a different value is available [13], yielding a similar result for the t$\overline{t}$ charge asymmetry, $A_{\mathrm{C}}^{t\overline{t}}=0.0102\pm 0.0005\left(\mathrm{scale}\right)$. These two predictions are derived by evaluating the asymmetry in powers of the strong and electroweak couplings at NLO only in the numerator and evaluating the denominator using the LO matrix element. In a third calculation, at NNLO [15], both, the numerator and the denominator are calculated at full QCD NNLO precision without any expansion in powers of strong and electroweak couplings. Furthermore, dynamical factorization and renormalization scales and an NNLO PDF are used to derive the t$\overline{t}$ charge asymmetry prediction of $A_{\mathrm{C}}^{t\overline{t}}=0.{0095}_{-0.0007}^{+0.0005}\left(\mathrm{scale}\right)$.

In this chapter, we summarize the ATLAS and CMS results in the dilepton and lepton+jets channel at 8 TeV.

3.2.1. Measurements of the t$\overline{t}$ and Lepton Charge Asymmetry in the Dilepton Channel by ATLAS

As at 7 TeV, the ATLAS Collaboration measurement in the dilepton channel at 8 TeV studied both the lepton and the t$\overline{t}$ charge asymmetry [38]. Three different final states are considered in this analysis: events with two electrons ($ee$), with one electron and one muon ($e\mu$), and with two muons ($\mu \mu$). Exactly two of these leptons, isolated and of opposite electric charge, should be present in the final state. At least two reconstructed jets are also required. In the same-flavour channels, the invariant mass of the two leptons must lie outside the Z boson mass window. In these channels, it is also required that $E_{\mathrm{T}}^{\mathrm{miss}}>30$ GeV and that at least one of the jets is b-tagged to further suppress Drell-Yan and Z boson production as well as diboson background. In the $e\mu$ channel, the background suppression is achieved by requiring that the scalar sum of the p_T of the two leading lets and leptons to be larger than 130 GeV. After this selection, the selected number of events in the $ee$, $\mu \mu$, and $e\mu$ channels, respectively, are: 12,785; 14,453; and 42,363. The background from Z+jets, single top, and diboson production are evaluated using simulated events. Because of possible mismodeling of the $E_{\mathrm{T}}^{\mathrm{miss}}$ distribution in Z bosons production in association with heavy-flavour jets, the normalisation of the inclusive and heavy-flavour component of the Drell-Yan background in the same-flavour channels is computed using data from control regions and applied afterwards to correct the simulated events. For the background coming from fake or non-prompt leptons the shape of distributions of kinematic observables is taken from simulation where at least one of the leptons is required not to be matched to the generated ones. Scale factors to adjust the normalisation are derived from data in a specific control region requiring two leptons with the same electric charge.

The lepton charge asymmetry $A_{\mathrm{C}}^{\ell \ell }$ is obtained directly from the pseudorapidity of the leptons while $A_{\mathrm{C}}^{t\overline{t}}$ requires the reconstruction of the top quarks. This kinematic reconstruction is performed by solving the system of equations that relates the particle momenta at the decay vertices. The system is underconstrained because of the presence of two neutrinos escaping detection. The system is hence solved numerically using the kinematic (KIN) method [39,40]. The experimental uncertainties of the measured jets and $E_{\mathrm{T}}^{\mathrm{miss}}$ are taken into account by sampling the phase space according to their resolution. For each of the sampling points up to four solutions can be found. The KIN method chooses the solution that leads to the lowest reconstructed mass of the t$\overline{t}$ system. There is also an ambiguity in the assignment of the lepton with the b-tagged jet. The assignment is chosen that has the most reconstructed trials. The performance of the KIN method is quantified by evaluating the efficiency of reconstructing t$\overline{t}$ events and the probability of reconstructing the correct sign of $\Delta \left|y\right|$. These probabilities are found to be 90% and 76%.

The ATLAS measurements are performed inclusively and differentially as a function of the invariant mass of the t$\overline{t}$ system, of the transverse momentum of the t$\overline{t}$ system, and the boost in z direction of the t$\overline{t}$ system. The measurements are performed in the full phase space after correcting for reconstruction and acceptance effects to parton level, as well as in a fiducial region after correction to particle level. The fiducial region is defined to closely match the region accessed by the ATLAS detector. Such fiducial results allow to reduce the dependency to MC generators and avoid large extrapolation to the full phase space. The fiducial volume definition closely follows the requirements applied on the reconstructed objects but using particle level objects. Using these particle objects, the top quark reconstruction is performed using the pseudotop algorithm described in Ref. [41]. As for the 7 TeV results, the correction for detector resolution and acceptance effects is performed using the FBU technique. The migration matrix is obtained from the nominal t$\overline{t}$ simulated sample. The combination between the $ee$, $e\mu$, and $\mu \mu$ channels is performed by mapping the reconstructed distributions of the three channels to the same corrected distribution. The systematic uncertainties are treated as nuisance parameters in the maximum likelihood estimation. For each differential measurement, the choice of binning for $\Delta \left|\eta \right|$ or $\Delta \left|y\right|$ is optimized by minimizing the expected statistical uncertainty. For the optimized binning choices, more than 50% of the events are found to lie within the diagonal bins of the migration matrix for $\Delta \left|y\right|$, and more than 97% for $\Delta \left|\eta \right|$.

Various sources of systematic uncertainties affect the measurements. The statistical uncertainty gives the largest contribution followed by the uncertainties on kinematic reconstruction and signal modeling uncertainties. Figure 9 summarizes the results in the full phase space, which appear to be compatible with the SM predictions. Figure 10 shows the unfolded distributions of $\Delta \left|\eta \right|$ and $\Delta \left|y\right|$ for the inclusive measurements in the fiducial phase space compared to NLO MC generator predictions [42].

The inclusive results for $A_{\mathrm{C}}^{\ell \ell }$ and $A_{\mathrm{C}}^{t\overline{t}}$ in the full phase space are compared in Figure 11 to the SM predictions and to two BSM predictions compatible with the Tevatron results. One model contains a light octet with mass below the t$\overline{t}$ production threshold, while the other one introduces a heavy octet with mass beyond the LHC reach [43]. In this figure the correlation between $A_{\mathrm{C}}^{\ell \ell }$ and $A_{\mathrm{C}}^{t\overline{t}}$ is taken into account and is found to be 48%. The results are compatible with the SM but do not exclude the two BSM models considered.

3.2.2. Measurements of the t$\overline{t}$ and Lepton Charge Asymmetry in the Dilepton Channel by CMS

The CMS Collaboration also performed the inclusive and differential measurements of both the leptonic and t$\overline{t}$ asymmetries at 8 TeV [44]. The analysis requires events with exactly two isolated, oppositely charged leptons with p_T $>20$ GeV and with an invariant mass of the dilepton system above 20 GeV and outside the Z boson mass window. At least two jets with p_T $>30$ GeV are required with one of them identified as coming from a b quark. High missing transverse momentum ($p_{\mathrm{T}}^{\mathrm{miss}}>40$ GeV) is required to suppress the Drell-Yan background in the channel with same-flavour leptons. In total, 43,898 events are selected with these requirements with an estimated background contribution of about 9%. In the t$\overline{t}$ system reconstruction method of this analysis, the solutions for the neutrino momenta are found analytically assuming a top quark mass of 172.5 GeV. Each of the events can have up to eight possible solutions. To choose the most probable one, the matrix weighting technique [27] is used as in the 7 TeV measurement. The signs of $\Delta \left|\eta \right|$ and $\Delta \left|y\right|$ are correctly reconstructed in 99.5% and 74.9% of the selected t$\overline{t}$ events, respectively. In about 16% of all events, no solution for the reconstruction of the t$\overline{t}$ system exists and these events are consequently only used for the inclusive measurement of the lepton charge asymmetry.

Samples of simulated events are used to evaluate the background contamination in the selected sample. Several data control regions are used to correct the normalisation of the Z+jets background and the background coming from fake or non-prompt leptons. After subtraction of the background, the distributions are corrected for detector acceptance, event selection efficiency, and finite detector resolution at parton level using an unfolding technique. In this process the binning of each of the distributions is adjusted according to the observable resolution. The unfolding is performed using the Tunfold package [45] using regularization based on the curvature of the simulated signal distributions. The optimized regularisation strength is found to be relatively weak.

The differential measurements are performed as a function of the invariant mass of the t$\overline{t}$ system, as well as the absolute rapidity and transverse momentum of the t$\overline{t}$ system in the laboratory frame. Three bins are used for each of these differential distributions.

Several sources of systematic uncertainties are considered in the measurements. The ones that impact the most the inclusive $A_{\mathrm{C}}^{t\overline{t}}$ and $A_{\mathrm{C}}^{\ell \ell }$ results are the uncertainty in the unfolding procedure coming from the limited number of simulated t$\overline{t}$ events, as well as the uncertainty from the t$\overline{t}$ modeling coming from variation of the renormalization and factorization scales, while the differential measurements are largely limited by the statistical component of the uncertainty.

The unfolded $\Delta \left|\eta \right|$ and $\Delta \left|y\right|$ distributions at parton level are shown in Figure 12, compared to the SM predictions at NLO+EW level [14] as well as to predictions from the NLO MC@NLO generator [46]. The resulting inclusive values for $A_{\mathrm{C}}^{t\overline{t}}$ and $A_{\mathrm{C}}^{\ell \ell }$ are given in

Table 4. Results for the lepton-based asymmetry $A_{\mathrm{C}}^{\ell \ell }$ and the t$\overline{t}$ asymmetry $A_{\mathrm{C}}^{t\overline{t}}$ after correcting for detector, resolution, and acceptance effects. The values are presented with their statistical and systematic uncertainties [44].

Channel	${\mathit{A}}_{\mathbf{C}}^{\mathbf{\ell }\mathbf{\ell }}$	${\mathit{A}}_{\mathbf{C}}^{\mathit{t}\overline{\mathit{t}}}$
$\ell \ell$	$0.003\pm 0.006\pm 0.003$	$0.011\pm 0.011\pm 0.007$

. The results are compatible with the SM expectations as well as with zero asymmetry.

The differential results as a function of $m_{t\overline{t}}$, $|y_{t\overline{t}}|$, and $p_{\mathrm{T}}^{t\overline{t}}$ are presented in Figure 13 and show also reasonable agreement with the predictions.

3.2.3. Measurement of the t$\overline{t}$ Charge Asymmetry in the Lepton+Jets Channel by ATLAS

The ATLAS Collaboration has performed two types of measurements in the lepton+jets channel at 8 TeV. The first one measured inclusively and differentially the t$\overline{t}$ asymmetry $A_{\mathrm{C}}^{t\overline{t}}$ in the full phase space [47]. The second measurement focused on the t$\overline{t}$ asymmetry in events where the top-quark pair is produced with a large invariant mass. i.e., highly boosted top-quark pair production [48]. The boosted channel is expected to have a higher sensitivity to the expected SM asymmetry due to a higher fraction of quark-antiquark initiated processes.

The standard analysis (so called resolved channel [47]) selects exactly one electron or muon candidate and at least four jets with p_T  $>25$ GeV. The selected events are separated according to the number of b-tagged jets they contain (zero, one or at least two). In order to suppress the background from multijet and Z+jets backgrounds in events with zero or one b-tagged jet, further requirements are applied $E_{\mathrm{T}}^{\mathrm{miss}}$ on and on the reconstructed transverse mass of the W boson from the hadronically decaying top quark. After the event selection, 216,465 and 193,418 events remain in the two signal regions with either one or at least two b tagged jets, with approximated background contributions of about 34% and 11%, respectively. The main background comes from W+jets events. The shape of the distributions of kinematic observables for this background is estimated using simulated events while its normalisation is adjusted using data exploiting the difference in production cross sections between $W^{+}$ and $W^{-}$. This adjustment is used in situ and embedded in the unfolding procedure that corrects for detector acceptance and efficiency. The multijet background is also estimated from data using the matrix method [47]. The other minor backgrounds coming from single-top quark, Z+jets or diboson production are evaluated using simulation.

As in the other channels, to measure the t$\overline{t}$ asymmetry inclusively and differentially, the full t$\overline{t}$ system needs to be reconstructed. This reconstruction is achieved applying a kinematic fit [49] using at most five jets. The average correct-sign fraction is estimated to be around 72% for events with exactly one b-tagged jets and 75% for events with at least two b-tagged jets. The lepton charge is used to determine the flavour (quark or antiquark) of the semilaptonically decaying top quark candidate.

The measurements are corrected for acceptance and detector resolution effects to parton level by unfolding using the FBU technique. The asymmetry is determined from maximizing the FBU extended likelihood where the events are separated based on the lepton charge and the b-tagged jet multiplicity (zero, one, at least two). The $\Delta \left|y\right|$ distribution is split in four bins, also for each differential measurement. The calibration of the W+jets prediction is achieved by adjusting in the fit the flavour components of the jets associated with the W boson. The b-tagged jet multiplicity provides information about the heavy and light-flavour composition of the W+jets background while the lepton charge asymmetry is used to determine the normalisation of each component. Various sources of systematic uncertainties are included as nuisance parameters. The dominant source is found to come from the uncertainty in jet energy scale and resolution.

The resulting inclusive t$\overline{t}$ asymmetry is measured to be $A_C^{t\overline{t}}=0.009\pm 0.005(\mathrm{stat}+\mathrm{syst})$, compatible with the SM prediction. The measurement is limited by the statistical uncertainty. The differential measurements of the charge asymmetry at parton level as a function of the invariant t$\overline{t}$ mass, the boost of the t$\overline{t}$ system, and the transverse momentum of this system are shown in Figure 14 compared with the SM prediction and with two benchmark BSM scenarios. The results are compatible with the SM and are not able to distinguish between SM and these two BSM scenarios within the quoted uncertainties.

The ATLAS measurement using highly boosted top quark pairs [48] focuses on lepton+jets events where the hadronic top-quark decay is reconstructed as a single large-radius jet (R = 1.0) and tagged as coming from an actual top quark using jet substructure variables. The leptonic top-quark decay is reconstructed from a standard small-radius jet (R = 0.4), a charged lepton (electron or muon), and missing transverse momentum from the escaping neutrino. The longitudinal component of the neutrino momentum is calculated using a constraint on the W boson mass and solving a quadratic equation. The selected large-radius jet should have p_T $>300$ GeV and must be separated from both the charged lepton and the small-radius jet. A substructure analysis of the large-radius jet is used to tag the boosted top quark. At least one of the small-radius jets associated with the leptonically decaying top quark must be b-tagged. The selected events yield a good efficiency and resolution for the t$\overline{t}$ invariant mass of around 6% for $m_{t\overline{t}}\sim 1$ TeV. The background is estimated using simulation except for the normalisation of the W+jets background and heavy flavour fractions that are adjusted from data and the multijet background that is fully estimated from data using the matrix method.

For electron and muon channel combined, 7741 events are selected, with about 13% background contribution. This number of observed events is found to be approximately 10% less than the number predicted by the simulation, a result of the known mismodeling of the top quark p_T spectrum in the simulation. Since the asymmetry is computed as a ratio, it is not sensitive to the absolute cross section. The difference in shape has been tested to have a negligible impact. The $\Delta \left|y\right|$ distribution as a function of $m_{t\overline{t}}$ is corrected for acceptance and detector effects to parton level using FBU, as in the resolved analysis, in the phase space: $m_{t\overline{t}}>750$ GeV and $-2<\Delta \left|y\right|<2$.

The $A_{\mathrm{C}}^{t\overline{t}}$ values from the unfolded distribution in four $m_{t\overline{t}}$ bins are shown in Figure 15. The measurement generally agrees with the SM prediction. The largest observed difference reaches $1.6\sigma$ in the third bin. In the measured phase space, $m_{t\overline{t}}>750$ GeV and $|\Delta |y\left|\right|<2$, the inclusive asymmetry is $A_{\mathrm{C}}^{t\overline{t}}=0.042\pm 0.032$, where the dominant uncertainty is coming from modeling uncertainty and the statistical component. The result agrees well with the SM prediction.

3.2.4. Measurement of the t$\overline{t}$ Charge Asymmetry in the Lepton+Jets Channel by CMS

The CMS Collaboration has performed two types of measurements in the lepton+jets channel at 8 TeV using different techniques to access the asymmetry. The first analysis measured inclusively and differentially the t$\overline{t}$ asymmetry $A_{\mathrm{C}}^{t\overline{t}}$ at parton level after applying an unfolding technique [50]. For the second measurement, the same dataset was analyzed to get the inclusive t$\overline{t}$ asymmetry value but using a template technique based on a parametrization of the SM [51]. This second analysis also differs in selecting more events.

The analysis using an unfolding technique [50] measured $A_{\mathrm{C}}^{t\overline{t}}$ inclusively and as functions of $m_{t\overline{t}}$, $|y_{t\overline{t}}|$, and $p_{\mathrm{T}}^{t\overline{t}}$. The measurements are performed at parton level both in a fiducial phase space that emulates the restriction of the detector phase space and also extrapolated to the full phase space.

The event selection requires one electron or one muon and four or more jets with at least one of them being b-tagged. In total, 362,244 events are selected with about 20% contribution from background processes. The fiducial region is defined using particle objects with a selection mimicking the selection applied at reconstruction level. It contains around 10% of the events of the full phase space and roughly 50% of the events in the fiducial region pass the reconstruction level selection.

The distributions of kinematic observables for the background processes are modelled using simulated events while their rates are estimated using a simultaneous fit of the transverse mass of the W boson from the hadronic top quark decay and of the invariant mass of the combination of three jets that have the largest vectorial p_T sum. The multijet background is modelled using data in a control region with non isolated leptons. The top quark reconstruction is performed using the same likelihood method as in the 7 TeV analysis.

After background subtraction, the distributions corrected for acceptance and detector effects are determined through unfolding using a generalized matrix inversion method. Regularization is applied to limit the statistical uncertainties due to the unfolding procedure. It is implemented by minimizing the statistical correlations between bins in the unfolding spectrum. The correctness of the unfolding procedure has been verified using pseudo-experiments. The unfolded $\Delta \left|y\right|$ distributions in the fiducial and full phase spaces are shown in Figure 16 compared with SM predictions [13,14]. The measured inclusive t$\overline{t}$ asymmetry in the fiducial and full phase space, respectively, are summarized in

Table 5. Results of the inclusive t$\overline{t}$ charge asymmetry measurements in the fiducial and full phase space [50], compared to the respective SM predictions [13,14,52].

Phase Space	Measured ${\mathit{A}}_{\mathbf{C}}^{\mathit{t}\overline{\mathit{t}}}$	Calculated ${\mathit{A}}_{\mathbf{C}}^{\mathit{t}\overline{\mathit{t}}}$
fiducial	$-0.0035\pm 0.0072\left(\mathrm{stat}\right)\pm 0.0031\left(\mathrm{syst}\right)$	$0.0101\pm 0.0010$
full	$0.0010\pm 0.0068\left(\mathrm{stat}\right)\pm 0.037\left(\mathrm{syst}\right)$	$0.0111\pm 0.0004$
		$0.0102\pm 0.0005$

. In both cases the experimental results are a bit low with respect to the predictions for the SM [13,14,52], especially in the fiducial region. However, the deviation is below two standard deviations.

The differential measurements as a function of $m_{t\overline{t}}$, $|y_{t\overline{t}}|$, and $p_{\mathrm{T}}^{t\overline{t}}$ in the full phase space are displayed in Figure 17. The result of the asymmetry as a function of $m_{t\overline{t}}$ is shown with two different binnings. The distributions agree with the SM prediction and are also compared to a model containing an effective axial-vector coupling of the gluon [53,54].

The other CMS measurement in the lepton+jets channel is based on a template technique [51] using the bounded observable Y${}_{t\overline{t}}$ defined as Y${}_{t\overline{t}}$ = $tanh\Delta \left|y\right|$. The Y${}_{t\overline{t}}$ distribution can be translated as a linear combination of the symmetric and asymmetric components of the probability distribution $\rho \left(\mathrm{Y}{}_{t\overline{t}}\right)$ (see Figure 18). The asymmetry $A_{\mathrm{C}}^{t\overline{t}}$ corresponds then to the level of asymmetric component that best fits the observed data distribution.

The selected events contain one isolated electron or muon and at least four jets among which at least one is b-tagged. In total, 667,096 events are selected, of which about 35% are estimated to come from background processes. The top quarks are reconstructed using the most likely assignment of the jets to the t$\overline{t}$ decay partons. For each assignment the four-momenta of the jets are corrected according to the partons that are assigned to using flavour-dependent scale factors derived from t$\overline{t}$ simulation. The chosen assignment is determined using a likelihood criterion taking into account the b-tagging information and the constraints from the reconstruction hadronically decaying W boson and top quark. The energy resolution of the jets for the chosen assignment is further improved using a kinematic fit under the W boson and top quark mass constraints.

The amount of t$\overline{t}$, W+jets, and multijet events after selection is determined using a likelihood discriminant built from the hadronically decaying W boson transverse mass and from the probability that at least one of the possible jet-parton assignments is the correct one. The other minor backgrounds are estimated using simulated events.

After the determination of the sample composition, another likelihood fit on the Y${}_{t\overline{t}}$ distribution is performed to measure $A_{\mathrm{C}}^{t\overline{t}}$. The performance of the method is checked on simulated samples showing negligible bias. The antisymmetric component of the Y${}_{t\overline{t}}$ distribution is shown in Figure 19 for data and for the fit model in the e+jets and $\mu$+jets channels. The measured t$\overline{t}$ asymmetry is found to be $A_{\mathrm{C}}^{t\overline{t}}=0.0033\pm 0.0026\left(\mathrm{stat}\right)+0.0033\left(\mathrm{syst}\right)$. This result is compatible with the SM and with the result from the other CMS measurement, though more precise. The template method incorporates more information from the model than the analysis using unfolding leading to a reduced statistical uncertainty but at the expense of greater model dependence. The dominant source of systematic uncertainty is coming from the statistical uncertainty in the templates.

3.2.5. Combination of the Measurements of the t$\overline{t}$ Charge Asymmetry in the Lepton+Jets Channel by ATLAS and CMS

The results of the inclusive $A_{\mathrm{C}}^{t\overline{t}}$ measurements in the lepton+jets channel at 8 TeV by the ATLAS and CMS Collaborations have been combined [35] using the same machinery as for the combination of the 7 TeV results. From the two CMS analyses in the lepton+jets channel, the one with the the smaller total uncertainty, the analysis based on a template method, is used for the combination with the result from the ATLAS Collaboration. With respect to the combination of the 7 TeV results, the treatment of the correlations of the systematic uncertainties between the two analyses is more fine grained. Especially the uncertainty in the jet energy scale is split into various sources that are grouped into four categories depending on the assumed correlation between the experiments, while again, most uncertainty sources are found to be uncorrelated, some of the signal and background modelling uncertainties are found to be correlated. The uncertainty in the chosen MC event generator, the uncertainty in the simulation of ISR and FSR, as well as the chosen PDF model are treated as fully correlated in the combination. The same applies to the uncertainty in the background contributions from single top quark production and the production of Z bosons in association with jets. As already mentioned, the individual sources of the jet energy uncertainty are grouped together into four categories. One category includes all jet energy related uncertainties that are considered uncorrelated, one category includes all uncertainties that are found to be partially correlated, using 50% as correlation parameter in the combination, and two categories contain the mostly and fully correlated uncertainties, which both enter with a 100% correlation assumption the combination.

The result of the combination of the two measurements in the lepton+jets channel at 8 TeV is $A_{\mathrm{C}}^{t\overline{t}}=0.0055\pm 0.0023\left(\mathrm{stat}\right)\pm 0.0025\left(\mathrm{syst}\right)$, with the ATLAS result contributing with a weight of 0.39 and the CMS result with a weight of 0.61. The ${\chi }^2$ with one degree of freedom of the combination is 0.88, corresponding to a p-value of 0.35. The improvement in the total uncertainty of the combined results with respect to the individual results is 32% for the ATLAS measurement and 17% for the CMS analysis.

Figure 20 shows the allowed regions in the two dimensional plane spanned by the LHC charge asymmetry at 8 TeV and the Tevatron forward backward asymmetry for the SM and several BSM theories, together with the LHC combined $A_{\mathrm{C}}^{t\overline{t}}$ value and $A_{\mathrm{FB}}$ results from the Tevatron. The combined $A_{\mathrm{C}}^{t\overline{t}}$ value puts strong constraints on the parameter space of several BSM scenarios, including models with a charged $W^{\prime }$ boson with right-handed couplings, heavy colour-octet vector gluons ${\mathrm{G}}_{\mu }$ with axial couplings, colour-singlet Higgs boson models like isodoublets $\varphi$, colour-triplet scalars ${\omega }^4$, and colour-sextet scalars ${\Omega }^4$ with right-handed flavour-violating $tu$ couplings (for more details on the BMS models, see Refs. [10,56]).

Figure 21 summarizes the inclusive $A_{\mathrm{C}}$ measurements by the ATLAS and CMS Collaborations at 8 TeV in the dilepton and lepton+jets channels and the combination of the latter and compares the experimental results with theory predictions. Within the quoted uncertainties, the results are well comparable with the predictions.

In a second combination, the differential measurements of $A_{\mathrm{C}}^{t\overline{t}}$ as a function of the invariant mass of the t$\overline{t}$ system of the ATLAS [47] and CMS [50] Collaborations are combined [35]. In both analyses, six bins are used for the $m_{t\overline{t}}$ distribution, with the same value ranges for the different bins. Although the same tools as for the combination of the inclusive measurements are used, the way how the correlations between the analyses are taken into account differs significantly. First of all, for the combination of the differential measurements the second CMS analysis is used, the one based on an unfolding method. As a result, two correlation assumptions need to be adjusted: the correlation of the parton shower and hadronization uncertainty is assumed to be 100% (was treated not correlated in the combination of inclusive results) and the uncertainty in the single top and Z+jets background modeling is considered uncorrelated (was assumed 100% correlated in the combination of the inclusive results).

However, the conceptual difference in the treatment of the uncertainty correlation is the additional consideration of bin-to-bin correlations. The correlation assumptions described above are strictly speaking only valid to describe the correlations between the same bins in two analyses (for instance between bin 2 of the ATLAS analysis and bin 2 of the CMS analysis). Two further categories of correlations need to be taken into account to describe the correlation model of differential measurements correctly. Within an analysis, the different bins are correlated with each other, which makes up the first category of bin-to-bin correlations. The same is true across experiments, making up the second category of bin-to-bin correlations. The above mentioned correlations between the same bins in two analyses are a special case of this second category. In contrast to these diagonal elements in a matrix of ATLAS versus CMS correlations, for the off-diagonal elements, the correlation assumption needs to be modified by the bin-to-bin uncertainties within the two analyses. This non-trivial treatment of correlations is detailed in Ref. [35].

The individual t$\overline{t}$ charge asymmetry values as a function of the invariant mass of the t$\overline{t}$ system along with the combined values can be found in Figure 22 (left). Depending on the bin, the ATLAS result contributes with weights between 0.22 and 0.59 to the combined value, while the weights of the CMS results vary between 0.41 and 0.78. The overall tendency is that the ATLAS result dominates the low mass region, while the CMS result dominates the high mass region. The total ${\chi }^2$ of the combination with six degrees of freedom is 4.01 and corresponds to a p-value of 0.69. The improvement in precision ranges, again depending on the bin, between 20 and 52% for the ATLAS analysis and between 9 and 31% for the CMS analysis. In Figure 22, (right), the resulting combined charge asymmetry as function of $m_{t\overline{t}}$ is compared to two theory predictions for the SM, calculated at NLO [14] and NNLO [57,58,59], respectively, and to two versions of a colour-octet model [43]. The latter is chosen as its prediction for $A_{\mathrm{FB}}$ is in agreement with the Tevatron results and its deviations with respect to the SM prediction for $A_{\mathrm{C}}^{t\overline{t}}$ are—for the heavy version—on the order of the measurement uncertainty. Within this uncertainty the combined values are comparable with the SM prediction as well as with both BSM scenarios.

3.3. Measurements at 13 TeV Centre-of-Mass Energy

The fraction of $q\overline{q}$ initiated top quark pair production decreases with increasing centre-of-mass energy, and so does the t$\overline{t}$ charge asymmetry. To compensate for the decreasing size of the effect to be measured, one needs to define regions of phase space in which the $q\overline{q}\to t\overline{t}$ process is enhanced with respect to the overall phase space for top quark pair production. As discussed earlier, events with high values of the reconstructed invariant mass of the t$\overline{t}$ system or with a large boost of the t$\overline{t}$ system in z direction feature enhanced fractions of $q\overline{q}$ initiated t$\overline{t}$ production and thus larger values of the predicted t$\overline{t}$ charge asymmetry. The additional advantage is that these phase space regions are also sensitive to contributions from new physics. Consequently, the ATLAS and CMS Collaborations measured the t$\overline{t}$ charge asymmetry at 13 TeV in samples of events with boosted t$\overline{t}$ candidates, i.e., events with high values of the reconstructed invariant mass of the t$\overline{t}$ system or events with large boosts in z direction. Depending on the actual definition of the phase space used for the measurement, the predictions for $A_{\mathrm{C}}^{t\overline{t}}$ span one order of magnitude and vary between around 0.001 and 0.015.

The following two sections summarize the $A_{\mathrm{C}}^{t\overline{t}}$ measurements by the ATLAS and CMS Collaborations at $\sqrt{s}=13$ TeV.

3.3.1. Measurement of the t$\overline{t}$ Charge Asymmetry in Lepton+Jets and Dilepton Events by ATLAS

The ATLAS Collaboration measured the t$\overline{t}$ and the lepton charge asymmetry using the full Run 2 dataset of 139 fb⁻¹ at 13 TeV [60]. The $A_{\mathrm{C}}^{t\overline{t}}$ measurement is performed in the lepton+jets channel both in the resolved and boosted topologies. It is also measured using dilepton events in the resolved topology. The measurements are performed inclusively and differentially as a function of $m_{t\overline{t}}$, ${\beta }_{z,t\overline{t}}>0.6$, and $p_{\mathrm{T}}^{t\overline{t}}$. The $A_{\mathrm{C}}^{\ell \ell }$ measurement is performed only in the resolved channel inclusively and differentially as a function of the following kinematic quantities of the dilepton pair: $m_{\ell \ell }$, ${\beta }_{z,\ell \ell }$, and $p_{\mathrm{T}}^{\ell \ell }$.

A common event selection is applied in the lepton+jets channel for both the resolved and boosted topologies requiring exactly one isolated lepton and at least one small-radius jet that has to be b-tagged. Further requirements on $E_{\mathrm{T}}^{\mathrm{miss}}$ and on the reconstructed transverse mass of the W boson are applied to reduce the fake lepton background. The in total 4,126,511 selected events are classified based on their topologies (resolved or boosted) and on their number of b-tagged jets. The resolved topology is requiring at least four small-radius jets with p_T $>25$ GeV. The assignment of the jets to the corresponding partons from the decaying top quarks is assessed using a BDT that aims to discriminant signal from the combinatorial background, separately for events with one or two b-tagged jets. This BDT combines kinematic variables and b-tagging information with weights from the kinematic likelihood fit [49] used for the lepton+jets measurement at 8 TeV. The best permutation in each event is required to have a BDT score higher than 0.3. This represents 50% of correctly assigned jets for t$\overline{t}$ signal events that pass the selection. The boosted topology requires, together with the b-tagged small-radius jet, at least one large-radius jet with p_T $>350$ GeV. This large jet should be tagged as coming from the decay of a boosted top quark using an operating point with 80% efficiency. Additional requirements are applied on the separation of the large-radius jet with the lepton and with the small-radius jet since the two top quarks are expected to be produced back to back. The fourvector of the hadronically decaying top quark is taken to be the one of the large-radius jet. The semileptonically decaying top quark fourvector is reconstructed from the lepton kinematic, the small-radius jet and calculating the neutrino fourvector from a W boson mass constrain. The invariant mass of the t$\overline{t}$ system is requested to be larger than 500 GeV, which separates the resolved and boosted channel. The lepton+jets channel features an estimated background contribution of about 14%. Dilepton events are required to have at least two small-radius jets with p_T  $>25$ GeV, among which at least one is b-tagged, and two opposite-charge leptons. For events with same-flavour leptons, the invariant mass of the dilepton system is required to be outside the Z boson mass window and an $E_{\mathrm{T}}^{\mathrm{miss}}$ cut is applied. The top quark kinematics is reconstructed using the neutrino weighting algorithm [61]. The 837,177 selected events are classified in four regions according to their lepton flavour ($e\mu$ and $ee+\mu \mu$) and b-tagged jet multiplicity (1 exclusive b-tagged jet, 2 inclusive b-tagged jets). The background contamination is estimated to be about 6%.

All signal and background processes are modelled using samples of simulated events except the non-prompt lepton and fake-lepton backgrounds, which are estimated using data-driven methods. The matrix method is used in the lepton+jets channel. In the dilepton channel, the fake background in the simulation is scaled by the data over simulation ratio computed in a control region with same sign leptons, separately for the $\mu \mu$ channel and for the $ee$ and $e\mu$ channels, where an additional correction due to charge misidentification is also applied. Scaling factors are also applied to the Z+jets background in the dilepton channel, to allow for significant theoretical uncertainties in the modelling of Z boson production with heavy-flavour jets.

The differential $\Delta \left|y\right|$ distributions are corrected for acceptance and detector effects using the FBU technique where systematic uncertainties that affect the measurements are treated as nuisance parameters. In this process the t$\overline{t}$ signal normalisation is kept as a free parameter common to all bins and the lepton+jets and dilepton regions are combined. The number of bins is chosen as a compromise between the statistical uncertainty on the measured asymmetries and the bias in the measurements. Several assumptions about the correlations of the systematic uncertainties are made when combining the different regions. The experimental uncertainties are treated as fully correlated across all regions. For the signal and background modelling uncertainties several decorrelation schemes are studied. The modelling uncertainties are assumed to be correlated among the regions unless they are constrained by more than 30% in the FBU marginalisation. For a small number of them where the decorrelation scheme is increasing the total uncertainty by 5% to 20%, the more conservative scheme is chosen. The leading sources of systematic uncertainties come from the signal and background modelling uncertainties.

The combined inclusive $A_{\mathrm{C}}^{t\overline{t}}$ asymmetry from single lepton and dilepton events is measured to be $0.0068\pm 0.0015$ in agreement with the SM calculation at NNLO accuracy in the strong coupling with NLO electroweak corrections of $0.{0064}_{-0.0006}^{+0.0005}$ [15]. The quoted SM uncertainties include renormalization and factorization scale variations and PDF uncertainties, while the measurement uncertainty includes both the statistical and systematic uncertainties of 0.0010 each. The SM computation is performed by expanding the numerator and denominator at a given order in perturbation theory. The measurement differs from zero by 4.7 standard deviations, providing strong evidence for t$\overline{t}$ charge asymmetry at the LHC. Figure 23 (left) shows the $A_{\mathrm{C}}^{t\overline{t}}$ differential measurement as a function of $m_{t\overline{t}}$ which is also consistent with the NNLO expectation.

The $A_{\mathrm{C}}^{\ell \ell }$ asymmetry is measured in the dilepton channel only and gives $0.0054\pm 0.0012\left(\mathrm{stat}\right)\pm 0.0023\left(\mathrm{syst}\right)$, while the SM calculation at NLO in QCD, including NLO EW corrections predicts $0.{0040}_{-0.0001}^{+0.0002}$ [14], where the uncertainties come from renormalization and factorization scale variations and PDF uncertainties. The $A_{\mathrm{C}}^{\ell \ell }$ differential measurement as a function of $m_{\ell \ell }$ is shown in Figure 23 (right).

The combined $A_{\mathrm{C}}^{t\overline{t}}$ results are interpreted within an SM effective field theory (SMEFT) using new operators connecting four quarks with different chiralities. Such operators could be the sign of new particles or interactions extending the SM [16,62,63]. For the interpretation of these results, dimension-six operators are considered. If Λ represents the characteristic new-physics scale, contributions to a given observable of Λ⁻² come from the interference of the dimension-six operators with the SM amplitudes. The squares of dimension-six operators lead to contributions of order Λ⁻⁴ . Higher order contributions are neglected. 15 dimension-six operators are considered: eight $q\overline{q}t\overline{t}$ operators with left-handed left-handed (LL) or right-handed right-handed (RR) structure, six other $q\overline{q}t\overline{t}$ operators with LR structure and one tensor that modifies the top-gluon interaction. The relation between operators and the charge asymmetry is determined at NLO accuracy and parameterised with analytic function. Fits are performed either retaining only the Λ⁻² contributions or including both Λ⁻² and Λ⁻⁴ contributions. The limits on individual coefficients are derived using a ${\chi }^2$ minimisation combining all results of the differential measurement as a function of $m_{t\overline{t}}$. They are shown on Figure 24. The limits that include both Λ⁻² and Λ⁻⁴ contributions are generally about a factor two stronger than the bounds derived from the inclusive measurement because of the enhanced sensitivity at large $m_{t\overline{t}}$. The sensitivity of this analysis is also compared to the one of the energy asymmetry described in Section 5 performed using t$\overline{t}$+jet events. Due to the extra jet in these type of events, the QCD structure of the energy asymmetry is not the same as for $A_{\mathrm{C}}^{t\overline{t}}$. So it appears that these two asymmetry observables probe different directions in chiral and colour space.

3.3.2. Measurement of the t$\overline{t}$ Charge Asymmetry in Lepton+Jets Events with Large Values of the Invariant Mass of the t$\overline{t}$ System by CMS

The CMS Collaboration analyzed the full Run-2 dataset corresponding to $138$ fb⁻¹ and measured the t$\overline{t}$ charge asymmetry in the lepton+jets channel for events with high values of the invariant mass of the t$\overline{t}$ system [64]. For events with boosted top quarks and top antiquarks, the decay products of the top (anti)quark are collimated and depending on the decay mode and the transverse momentum partially or fully merged. At the leptonic decay leg, the charged lepton from the leptonically decaying W boson is close to the b jet from the top quark decay, thus no isolation requirement is applied on the leptons in the event selection. For the hadronic decay leg, depending on the transverse momentum of the top (anti)quark, three possible topologies exist. For very large $p_{\mathrm{T}}$ values, the decay products end up reconstructed in a single, large-radius jet (“boosted” topology), while for low $p_{\mathrm{T}}$ values the three final state quarks give rise to three individual jets, the so-called “resolved” topology. For $p_{\mathrm{T}}$ values in between, the two quarks from the hadronically decaying W boson are reconstructed as one single jet, while the b jet from the top quark decay is resolved from the W boson jet, the so-called “semi-resolved” category. Using large-radius jet reconstruction and jet substructure techniques, the above mentioned topologies are experimentally examined, and the large-radius jets are either identified as the collimated decay products of a hadronically decaying top (anti)quark (t tag) or as collimated decay products of a hadronically decaying W boson (W tag). Events with one t tag and no W tag fall in the “boosted” category, events with one W tag and no t tag belong to the “semi-resolved” category, and events with neither t nor W tag are considered as “resolved” events. Events with more than one t or W tag are discarded.

Depending on the topology of the t$\overline{t}$ event candidate, the reconstruction of the fourvectors of top quark and antiquark differs. For events with a boosted topology, the t tagged large-radius jet is assigned to the hadronically decaying top quark, and the small-radius jets with $\Delta R>0.8$ from the hadronically decaying top quark are considered for the leptonically decaying top quark. In events with a “semi-resolved” topology, the large-radius jet with the W tag is assigned to the hadronically decaying W boson and all small-radius jets with $\Delta R>0.8$ from the hadronically W boson are considered for either the b jet from the hadronically decaying top quark or the b jet from the leptronically decaying top quark. For events in the “resolved” category all small-radius jets are considered for assigning them to the final state quarks from the two decaying top quarks. For each event the hypothesis with the best ${\chi }^2$, a measure for how close the masses of the two reconstructed top quarks are to each other and to the value determined simulation, is chosen and a cut on this variable is applied to suppress background events.

A binned maximum likelihood fit is performed simultaneously to the $\Delta \left|y\right|$ distributions in twelve channels (two lepton flavours, three data taking periods, two $m_{t\overline{t}}$ regions) to extract the t$\overline{t}$ charge asymmetry from the selected data set. The migration between true and generated values is taken into account when constructing the likelihood. The fit is performed for the fiducial volume as well as for the full phase space. For the latter one, additional corrections for acceptance and event selection efficiency are applied to the numbers of events in the twelve bins. For events with an invariant mass of the reconstructed t$\overline{t}$ system of $m_{t\overline{t}}>750$ GeV, the measured value for the t$\overline{t}$ charge asymmetry in the full phase space of t$\overline{t}$ production is $A_{\mathrm{C}}^{t\overline{t}}={0.69}_{-0.69}^{+0.65}$, where the uncertainty represents the total uncertainty. The corresponding theoretical prediction at NNLO in QCD perturbation theory with NLO electroweak corrections, calculated using the methods documented in Ref. [15] is $A_{\mathrm{C}}^{t\overline{t}}={0.94}_{-0.07}^{+0.05}$. The experimental results for different $m_{t\overline{t}}$ ranges in the fiducial region as well as in the full phase space are summarized in Figure 25. The results are within their uncertainties comparable with the SM predictions but also with zero asymmetry. Despite of the limited statistical significance of the results, they nevertheless demonstrate the potential to measure top quark properties in boosted event topologies.

4. Measurement of the Forward-Backward Asymmetry at the LHC

To date, the LHC measurements of the charge asymmetry $A_{\mathrm{C}}$ have been discussed, where top quark and antiquark yield different widths of the rapidity distributions as a result of the underlying physics that are different for top quarks and antiquarks. Historically, the t$\overline{t}$ production asymmetry was described [3] and measured [4,5] as a forward-backward asymmetry. As discussed earlier, also at LHC forward and backward directions can be defined, and thus also a forward-backward asymmetry can be predicted and observed. Because of the charge symmetric proton-proton collision, the definition of forward and backward hemispheres is, however, only possible for individual events and needs to be indirectly accessed by the longitudinal momentum of the t$\overline{t}$ system.

In this chapter, we describe an $A_{\mathrm{FB}}$ measurement by the CMS Collaboration, using data from LHC collisions at $\sqrt{s}=13$ TeV corresponding to an integrated luminosity of 35.9 fb⁻¹ [65]. Candidate t$\overline{t}$ events with a lepton+jets signature are selected. The idea is to measure the forward-backward asymmetry in $q\overline{q}\to t\overline{t}$ events, by exploiting observables that have the power to discriminate the $q\overline{q}$ initial state for t$\overline{t}$ production from $gg$ and $gq$ initial states as well as from non-t$\overline{t}$ backgrounds, and are sensitive to the forward and backward direction of the produced top quark and antiquark.

The observable used to define whether the top quark is produced in forward or backward direction is the cosine of the angle between the top quark and the direction of motion of the incoming quark in the centre-of-mass frame of the t$\overline{t}$ system, $c^{*}$. The differential cross section for the $q\overline{q}\to t\overline{t}$ process as a function of $c^{*}$ can be written as

$$\frac{d\sigma }{d{c}^{*}}\approx f_{\mathrm{sym}}\left(c^{*}\right)+\left[{\int }_{-1}^1{f}_{\mathrm{sym}}\left(x\right)dx\right]c^{*}{A}_{\mathrm{FB}}^{\left(1\right)}\left(m_{t\overline{t}}\right),$$

(8)

a linear combination of symmetric and antisymmetric functions of the production angle $c^{*}$ with $A_{\mathrm{FB}}^{\left(1\right)}$ being a parameter. From this definition of the differential cross section and Equation (1) follows that the forward-backward asymmetry $A_{\mathrm{FB}}\approx A_{\mathrm{FB}}^{\left(1\right)}$, the linearized forward-backward asymmetry. A comparison between fitted $A_{\mathrm{FB}}^{\left(1\right)}$ values and $A_{\mathrm{FB}}$ values determined from the numbers of events with top quarks produced in forward direction and events with top quarks produced in backward direction in generated signal events shows that the above approximation is valid.

The proton-proton collisions at LHC confront the analysers with two main challenges: Firstly, the production of t$\overline{t}$ pairs is dominated by the charge symmetric $gg$ process, followed by the $qg$ subprocess, which features only a tiny asymmetry and secondly, the forward and backward directions cannot be defined globally but need to be defined event by event. To overcome this challenge, the analysis exploits observables that help to discriminate the $q\overline{q}\to t\overline{t}$ process not only from non-t$\overline{t}$ backgrounds but also from t$\overline{t}$ production from $gg$ and $gq$ initial states, and that are sensitive to the direction of the incoming quark parton. The observables of choice are the invariant mass of the t$\overline{t}$ system, $m_{t\overline{t}}$, the scaled longitudinal momentum of the t$\overline{t}$ system in the laboratory frame, $x_{\mathrm{F}}=2p_{\mathrm{L}}/\sqrt{s}$, and $c^{*}$.

Distributions of these three observables are shown in Figure 26, for simulated t$\overline{t}$ events, separately for $q\overline{q}$, $gg$, and $qg$ initial states. The events have been generated using the POWHEG Monte Carlo generator [66]. In all three distributions a differentiation between the $q\overline{q}$ initial state and the other two is clearly visible, while the distributions from $gg$ and $qg$ initial states are very similar. For that reason, the latter two are treated as one single, combined process in the analysis. The parton distribution function of the proton leads to a—on average—higher momentum fractions of the incoming quark with respect to the incoming antiquark and thus the longitudinal momentum of the t$\overline{t}$ system in the laboratory frame is correlated with the direction of the incoming quark in $q\overline{q}$ initial states. Figure 26, lower right, shows the performance of choosing the longitudinal direction of the t$\overline{t}$ system in the laboratory frame as the direction of the initial state quark, based on the dilution factor D, defined as the difference between the number of correctly assigned quark directions and incorrectly assigned quark directions, normalized to the sum of both numbers, as a function of $|x_{\mathrm{F}}|$. As can be seen, especially for the region with higher $|x_{\mathrm{F}}|$, which is dominated by $q\overline{q}$ initial states, the efficiency for the choice of the quark direction based in the longitudinal direction of motion of the t$\overline{t}$ system is very high.

In order to construct the reconstructed versions of the observables discussed above, the candidate t$\overline{t}$ system in each event needs to be reconstructed from the objects detected by the detector. As contributions from potential new, massive particles are expected for large values of $m_{t\overline{t}}$, and as the fraction of $q\overline{q}$ initial states increases with increasing momentum of the t$\overline{t}$ system, it makes sense to group the events in categories according to the Lorentz boost of the event and thus the mass and momentum of the candidate t$\overline{t}$ pair. The analyzers define two “boosted” categories with high Lorentz boost of the event, where the decay products of the hadronically decaying top quark or top antiquark are all merged into one single fat jet that is identified as originating from a top quark, “top tagged”, (type-1), or where these decay products are fully or partially merged into a fat jet that is not top tagged (type-2). The third category, containing most of the t$\overline{t}$ events, is defined as events, where all decay products are distinguishable, thus also called “resolved” category.

The reconstruction of the kinematic quantities of the t$\overline{t}$ pair is done via a maximum likelihood fit, in which the momenta of the decay products are allowed to vary within their resolution, and all combinations of jets are considered. Owing to the different event topologies in the three categories introduced above, the constraints for the assignment of the selected jets to the final state quarks differ. While for type-2 and type-3 events all jet-quark assignments are considered to reconstruct the leptonic and hadronic top quark candidates, for type-1 events, the top tagged jet is chosen to represent the hadronically decaying top quark. In addition, the selected lepton and the missing transverse momentum enter the reconstruction of the leptonic part of the t$\overline{t}$ candidate in all three cases. From the reconstructed t$\overline{t}$ candidates, the observables relevant for the analysis can then be constructed. The reconstructed observables are named $m_{\mathrm{r}}$, $x_{\mathrm{r}}$, and $c_{\mathrm{r}}^{*}$. As discussed above, the direction of the incoming quark (needed for the calculation of $c_{\mathrm{r}}^{*}$), is chosen according to the longitudinal momentum direction of the reconstructed t$\overline{t}$ system.

For the extraction of $A_{\mathrm{FB}}$, a three-dimensional (in the three dimensions $m_{\mathrm{r}}$, $x_{\mathrm{r}}$, $c_{\mathrm{r}}^{*}$) distribution function, being the sum of individual distribution functions for the signal and several background processes, each scaled with the corresponding scaling parameter, is used. t$\overline{t}$ dilepton and full hadronic, single top quark, and $Z+$jets background contributions are considered using a single background template, W+jets events are considered using another background template. The third background template used in the fit, is constructed from side-band data and represents the QCD mutlijet production. In order to construct the signal template for this fit, a fourth observable, the lepton charge Q, is exploited. Assuming a charge-parity symmetry of the detector with respect to the acceptance for events with negatively charged leptons and events with positively charged leptons, the charge of the lepton can be used to construct symmetric and antisymmetric distributions for the signal $q\overline{q}\to t\overline{t}$ process. The parameter $A_{\mathrm{FB}}^{\left(1\right)}$ enters the fit function as linear parameter with the antisymmetric part of the signal template. The data are fitted in twelve different channels in total—3 categories (type-1, type-2, type-3), 2 flavours (electron, muon), 2 lepton charges—simultaneously. The systematic uncertainties are taken into account as nuisance parameters of the fit. Using 1000 sets of pseudo data for each value of $A_{\mathrm{FB}}^{\left(1\right)}$, generated from the template models with the corresponding $A_{\mathrm{FB}}^{\left(1\right)}$ input value, a Neyman construction is derived and the final result can be read off this construction. Figure 27 shows the Neyman construction, with the actual fit result drawn in as horizontal line and the corresponding true $A_{FB}^{\left(1\right)}$ value with uncertainties, projected on the x axis.

The resulting forward-backward asymmetry of $A_{\mathrm{FB}}^{\left(1\right)}=0.{048}_{-0.087}^{+0.095}{\left(\mathrm{stat}\right)}_{-0.029}^{+0.020}\left(\mathrm{syst}\right)$ is well comparable with the expectations from the standard model.

5. Measurement of the t$\overline{t}$ Energy Asymmetry at the LHC

Another way to study the t$\overline{t}$ charge asymmetry is to use an observable linked to the energy difference between the top quarks and antiquarks: $\Delta =e_t-E_{\overline{t}}$. The energy asymmetry [12] mainly occurs through the $qg\to t\overline{t}q$ process which is more abundant than the $gg\to t\overline{t}$ process at the LHC. It is therefor expected to be larger than asymmetries based on rapidity. The presence of an additional jet allows us to investigate QCD effects at leading order (LO) while the asymmetry in $q\overline{q}\to t\overline{t}$ is only appearing at NLO. The energy difference ΔE is connected to the angle of the final-state particles $(t,\overline{t},j)$ by energy and momentum conservation and could be interpreted as an asymmetry of the top quark and antiquark scattering angles with respect to the jet direction. In the process $pp\to t\overline{t}j$, the energy asymmetry can be defined as a function of the jet angle θ_j as [12]:

$$A_E\left({\theta }_j\right)=\frac{{\sigma }_{t\overline{t}j}\left({\theta }_j\right|\Delta E>0)-{\sigma }_{t\overline{t}j}\left({\theta }_j\right|\Delta E<0)}{{\sigma }_{t\overline{t}j}\left({\theta }_j\right|\Delta E>0)+{\sigma }_{t\overline{t}j}\left({\theta }_j\right|\Delta E<0)},$$

(9)

where ${\sigma }_{t\overline{t}j}\left({\theta }_j\right)$ is the differential cross section as a function of ${\theta }_j$. Both ΔE and θ_j are defined in the $t\overline{t}j$ rest frame, which corresponds to the partonic centre-of-mass frame in tree-level processes. The energy asymmetry can be formulated without involving the direction of the incoming quark. The outgoing quark-jet is boosted in the direction of the incoming valence quark. This boost translates into the rapidity of the $t\overline{t}j$ system in the laboratory frame: $yt\overline{t}j$. Hence it is possible to optimise the definition of the energy asymmetry in Equation (9) by associating the forward $yt\overline{t}j>0$ and backward $yt\overline{t}j<0$ final state with the forward θ_j and backward $\pi -{\theta }_j$ scattered jet [67,68]:

$$\begin{array}{c}\hfill {\sigma }^{\mathrm{opt}}\left({\theta }_j\right)=\sigma \left({\theta }_j\right|yt\overline{t}j>0)+\sigma (\pi -{\theta }_j|yt\overline{t}j<0){\theta }_j,{\theta }_j\in [0,\pi ].\end{array}$$

(10)

Equation (9) can then be redefined as:

$$A_E\left({\theta }_j\right)=\frac{{\sigma }^{\mathrm{opt}}\left({\theta }_j\right|\Delta E>0)-{\sigma }^{\mathrm{opt}}\left({\theta }_j\right|\Delta E<0)}{{\sigma }^{\mathrm{opt}}\left({\theta }_j\right|\Delta E>0)+{\sigma }^{\mathrm{opt}}\left({\theta }_j\right|\Delta E<0)}$$

(11)

to maximise the statistical sensitivity to the energy asymmetry.

The ATLAS Collaboration has performed a measurement of this energy asymmetry using 139 fb⁻¹ of proton-proton collision data of the LHC at $\sqrt{s}=13$ TeV [69]. The energy asymmetry is measured in $t\overline{t}j$ production in a fiducial phase space defined at particle level. The analysis is performed in the semileptonic t$\overline{t}$ decay channel where one of the top quarks is leading to a W boson that decays leptonically (leptonic top quark). The hadronic decay products of the other top quark are required to be collimated in one large-radius jet, which characterizes a top quark with large momentum. This phase space is also referred to as the boosted regime. In this boosted regime, it is easier to identify the additional jet not coming from the hadronically decaying top quark.

Events are selected requiring an isolated electron or a muon with $p_T > 27$ with no other high momentum leptons. The hadronic top quark candidate is selected as a large-radius jet with $p_T > 350$ GeV separated from the lepton. This large-radius jet is required to be tagged as a top quark candidate. Such top-tagging is performed with a DNN that relies on jet substructure variable inputs [70] and has a efficiency of 80% for a large-radius jet matched to a truth top quark. The jet from the leptonic top quark candidate is defined as a small-radius jet close to the lepton but isolated from the hadronic top quark candidate. The additional jet produced with the t$\overline{t}$ event is requested to be a small-radius jet with $p_T > 100$ GeV separated from the large-radius jet and from the lepton and different from the leptonic top quark candidate. This p_T cut was chosen as a trade-off between statistical precision and increase of the energy asymmetry for high-p_T values. One of the small-radius jets is requested to be tagged as coming from a b quark. It should be either the jet of the leptonic top quark candidate or it should be within the hadronic top quark candidate. The missing transverse momentum is used as an estimation of the transverse momentum of the neutrino momentum coming from the W boson decay from the leptonic top quark. The leptonic top quark four-momentum is defined as the sum of the four-vectors of the lepton, the neutrino, and the jet assigned to the letponic top quark candidate. The charge of the leptonic top quark is assessed using the lepton charge, while the opposite charge is assigned to the hadronic top quark candidate.

The $t\overline{t}j$ process has been generated using the POWHEG-BOX generator [66] while MADGRAPH5_aMC@NLO [71] was used for the interpretation of the results in terms of SMEFT. The first main source of background to $t\overline{t}j$ production in the semileptonic channel comes from events with a prompt electron or muon from a W or Z boson decay ($tW$, s-channel single top production, W/Z+jets, diboson production, or $t\overline{t}W/Z/H$). This background is estimated from simulation. The production of W bosons in association with jets is the main contribution corresponding to 5% of the events in the signal region, followed by t events corresponding to roughly 3%. The second main source, contributing to 2% in the signal region, is coming from events with fake or non-prompt leptons. This background is evaluated using a data-driven method, the matrix method [72].

The asymmetry is extracted by computing the ratio defined in Equation (11) using the number of events $N^{\mathrm{opt}}\left({\theta }_j\right)$ in three bins of θ_j: $[0,\pi /3,3/5\pi ,\pi ]$, each divided into four bins (two bins with $\Delta E < 0$ and two bins with $\Delta E > 0$). The number of events observed at the detector level is corrected for detector effects to particle level in a fiducial phase space using the FBU technique. Experimental and theoretical systematic uncertainties are included through nuisance parameters that are marginalized. The unfolding has been found to be robust against the inclusion of standard model Effective Field Theory operators within their current limits (see below). The data distributions at detector level input to the unfolding are found to be in agreement with the SM expectations.

The uncertainty on the measurement is dominated by the statistical component. The largest systematic uncertainties are the uncertainty in jet energy resolution, in t$\overline{t}$ modelling, and in the fake background estimation. The results are shown in Figure 28. The measurement is found to be in good agreement with the SM expectation with a p-value of 0.80. In the first bin the measured asymmetry differs from zero by 2.1 standard deviations.

The sensitivity of the energy asymmetry to new physics at a high energy scale is investigated in the SMEFT framework. The operators considered in this interpretation are of dimension six, while higher-dimensional operators are neglected. The analysis also assumes CP invariance so that all coefficient are considered real. In the Warsaw basis [73], 15 dimension-six operators can affect $t\overline{t}j$ production at tree level [17]. The energy asymmetry is particularly sensitive to the chirality and colour charges of the involved operators. To illustrate this sensitivity, a selection of six four-quark operators involving different chiral structures (LL, RR, LR) and colour structure (singlet or octet) are chosen. To assess the sensitivity of the energy asymmetry to the Wilson coefficients of these operators, a ${\chi }^2$ is built between the measured asymmetry and the SMEFT predictions in the three measured jet-angle bins taking into account the correlations among the measurements and among the predictions. The obtained bounds on individual Wilson coefficients are summarized in Figure 29. Overall the energy asymmetry is sensitive to the operator range $[-2,2]$ at 95% C.L. Bounds for several pairs of operators are also derived. These show complementary constraints between the asymmetry built using rapidity and the energy asymmetry probing different directions in chiral and colour space. The energy asymmetry is then able to resolve nearly blind directions left by other top-quark observables and so will provide useful additional information in global EFT fits.

6. Measurement of the Charge Asymmetry at the LHC

As discussed above, t$\overline{t}$ production at the LHC is dominated by the gluon fusion process which is charge symmetric. On the other hand, the production of a t$\overline{t}$ pair in association with a W boson referred to as $t\overline{t}W$ is initiated at LO by a $q{\overline{q}}^{\prime }$ initial state, while the quark-gluon channels open up at NLO. The gluon fusion initial state does not contribute until NNLO. The $t\overline{t}W$ production can then serve as an interesting tool to measure the t$\overline{t}$ charge asymmetry. Indeed the charge asymmetry in $t\overline{t}W$ events is expected to be larger than in t$\overline{t}$ production [74,75]. In addition the W boson in such process can be radiated from the $q{\overline{q}}^{\prime }$ initial state and then serves as a polariser of $q{\overline{q}}^{\prime }$ and thus of t$\overline{t}$. This polarisation further enhances the asymmetry between the decay products of the top quarks and top antiquarks, leading to an enhanced leptonic asymmetry when looking at leptonically decaying top and antitop quarks. The SM NLO QCD prediction of the leptonic asymmetry in the full phase space at $\sqrt{s}=13$ TeV [74,75] is $-0.{1316}_{+0.0112}^{-0.0081}$ where the quoted uncertainties are coming from scale variations.

The drawback of the $t\overline{t}W$ process is however its much smaller cross section (around 0.6 pb) compared to t$\overline{t}$ production (around 830 pb). Besides being a rare process, making predictions for the $t\overline{t}W$ cross section is also challenging, as large corrections arise from higher powers of both the strong and weak couplings [76]. Hence $t\overline{t}W$ measurements represent sensitive tests of QCD predictions connected with the electroweak sector.

The ATLAS Collaboration has performed a search for the leptonic charge asymmetry in $t\overline{t}W$ production using 139 fb⁻¹ of proton-proton collision data of the LHC at $\sqrt{s}=13$ TeV [77]. The measurement is performed in the trilepton channel both at detector level and at particle level after unfolding. Events are selected with exactly three isolated light leptons (electrons or muons) with p_T larger than 30, 20, and 15 GeV. At least two jets and one b jet is required. The selected events are then classified into four signal regions according to their jet and b-jet multiplicity as well as their amount of $E_{\mathrm{T}}^{\mathrm{miss}}$. Four control regions are also defined in order to fit the dominant backgrounds simultaneously with the signal. Because two of the leptons are expected to come from the decays of the top quarks and antiquarks, the sum of the three lepton charges is required to be $\pm 1$. The invariant mass of the opposite sign same flavour lepton pair is required to be higher than 30 GeV and outside the Z boson peak region (except for the control region for the $t\overline{t}Z$ background where such mass should be around 90 GeV). Two control regions are used to evaluate the amount of non-prompt electrons or muons arising from heavy-flavour hadron decays. These regions are defined by requiring that the third lepton fails the isolation criteria. A last control region is targeting the estimation of $\gamma$ conversions by requiring that at least one of the leptons is an electron failing the material conversion rejection criteria.

In order to compute $\Delta \left|\eta \right|=|{\eta }_{{\ell }^{+}}|-|{\eta }_{{\ell }^{-}}|$ and then $A_{\mathrm{C}}^{\ell \ell }$, the two opposite sign leptons that are coming from the t$\overline{t}$ decay need to be separated from the one coming from the W decay. This is addressed using a BDT that takes five variables as input. They are defined as the masses and $\Delta R$ of the systems formed by the leptons and the closest or second closest b jets. The fraction of events in which the lepton with the highest BDT score originates from a top quark or top antiquark decay is estimated to be 71%, using simulation. The second lepton needed to compute $\Delta \left|\eta \right|$ is taken to be the lepton with the opposite charge from the lepton selected by the BDT.

A profile-likelihood fit is used to extract the signal as well as the normalisation for the most relevant background processes: i.e., $t\overline{t}Z$, non-prompt electrons and muons as well as electrons from $\gamma$-conversions. The template shapes for these backgrounds are taken from simulated events. Each of the four signal regions are separated into $\Delta \left|\eta \right|>0$ and $\Delta \left|\eta \right|\le 0$. Separate normalisation factors in the $\Delta \left|\eta \right|>0$ and $\Delta \left|\eta \right|\le 0$ regions are allowed to float freely in the fit to avoid any bias from an assumption of SM asymmetries for these processes. The post-fit predictions and data yields for $\Delta \left|\eta \right|>0$ and $\Delta \left|\eta \right|\le 0$ in the four signal region are shown in Figure 30. Tests using MC have been performed to validate that the extracted asymmetry value is not biased by the absolute normalisation of the $t\overline{t}W$ process.

The leptonic charge asymmetry in event is measured to be: $A_{\mathrm{C}}^{\ell \ell }\left(t\overline{t}W\right)=-0.123\pm 0.136\left(\mathrm{stat}\right)\pm 0.051\left(\mathrm{syst}\right)$ in $t\overline{t}W$ agreement with the predictions from Sherpa simulation [78] in this phase space: $-0.{084}_{-0.003}^{+0.005}\left(\mathrm{scale}\right)\pm 0.006\left(\mathrm{MCstat}\right)$. The measurement is statistically limited. The leading systematic uncertainty is coming from the comparison of the fit performed with separated control regions for $\Delta \left|\eta \right|>0$ and $\Delta \left|\eta \right|\le 0$ (as in the default case) with an alternative fit performed where each background is normalised with a single normalisation factor (i.e., not separated between $\Delta \left|\eta \right|>0$ and $\Delta \left|\eta \right|\le 0$). Other important sources of systematic uncertainties are coming from the $t\overline{t}W$ and $t\overline{t}Z$ modelling uncertainties.

To obtain the charge asymmetry at particle level in a specific fiducial phase space close to the reconstructed one, an unfolding procedure is performed to correct for detector and acceptance effects. For this result, a simpler method is adopted to associate the leptons to the top quarks. A lepton is chosen to come from a top quark if the mass of the system formed by this lepton and the closest b jet is the closest to the most probable mass value according to the $t\overline{t}W$ simulation. This procedure has an efficiency of approximately 65% to identify the correct leptons. The unfolding procedure is based on a profile-likelihood approach as in Ref. [79]. In this approach, each bin in the particle-level distribution is folded through the response matrix, resulting in the bins at detector level. The normalisations for the main backgrounds and the analysis regions are split into $\Delta \left|\eta \right|>0$ and $\Delta \left|\eta \right|\le 0$ in the same way as for the detector-level results. An injection test is performed to verify that charge asymmetries potentially deviating from the SM prediction can be recovered in the unfolding procedure. The charge asymmetry value unfolded to particle level in the fiducial phase space is found to be: $A_{\mathrm{C}}^{\ell \ell }\left(t\overline{t}W\right)=-0.112\pm 0.170\left(\mathrm{stat}\right)\pm 0.055\left(\mathrm{syst}\right)$ compared to the SM prediction from Sherpa [78]: $-0.{063}_{-0.004}^{+0.007}\left(\mathrm{scale}\right)\pm 0.004\left(\mathrm{MCstat}\right)$. The leading sources of systematic uncertainties are the same as for the detector level result. As both results are limited by the statistical uncertainty, the potential of $t\overline{t}W$ events to measure the charge asymmetry is promising in the years to come.

7. Conclusions

The ATLAS and CMS Collaborations have performed several measurements of t$\overline{t}$ asymmetries using LHC collision events with either a single lepton or exactly two leptons, collected at 7, 8, and 13 TeV centre-of-mass energy. The fact that t$\overline{t}$ production via quark antiquark annihilation is not invariant under exchange of top quark and top antiquark manifests itself in different asymmetries. Both collaborations measured the lepton and t$\overline{t}$ charge asymmetries. The CMS Collaboration analyzed in addition the forward-backward asymmetry of t$\overline{t}$ events, while the ATLAS Collaboration investigated the t$\overline{t}$ energy asymmetry and the charge asymmetry in t$\overline{t}$ events where an additional W boson is produced. The measured asymmetries are typically corrected for efficiency and acceptance effects and thus extrapolated to either a fiducial or the full phase space. In addition both collaborations dedicated analyses to investigate the t$\overline{t}$ charge asymmetry in events with a boosted topology. While inclusive asymmetry measurements were performed at 7 TeV, the increase of the dataset available at 8 and 13 TeV allowed to perform differential measurements in phase spaces where asymmetries are predicted to be enhanced. Hence the expected asymmetry decrease with increased centre-of-mass energy could be compensated. The corrections of the reconstructed distributions required the application of unfolding methods where especially for the differential measurements and their combination significant development work was needed in order to make the existing algorithms applicable. The results of the presented analyses have shown that the t$\overline{t}$ charge asymmetry—although smaller in size compared to the effect at the Tevatron—is also measureable at the LHC, even differentially as function of suited kinematic variables of the t$\overline{t}$ system. The LHC measurements yield no significant hint of contributions from physics beyond the standard model.

Although the precision for some of the analyses is—especially given the small size of the effect—quite impressive, it is apparent that the analyses are dominated by statistical uncertainties in the phase spaces where the asymmetries are expected to be enhanced. Their sensitivity thus is limited by the size of the selected dataset. Given that the data taking periods at 7, 8, and 13 TeV are over, a reduction of the statistical component of the measurements will only be possible by analyzing the data of the recently started Run 3 and the future high luminosity LHC phase. The to be expected larger samples of selected t$\overline{t}$ candidate events will enable measurements to focus on the interesting regions in phase space with enhanced t$\overline{t}$ charge asymmetry, e.g., mainly events with boosted topologies. Furthermore, the vast amount of available t$\overline{t}$ signal events will facilitate multi-differential measurements of the t$\overline{t}$ charge asymmetry and will thus help to increase our knowledge of this property and the nature of the top quark itself. Higher collision energies on the contrary will not bring further advantage as the size of the effect decreases with increasing centre-of-mass energy.

Looking beyond the future LHC extensions, the next particle collider will most probably be an electron-positron machine. Assuming the centre-of-mass energy of the collider exceeds the t$\overline{t}$ production threshold, it will be able to study pairwise top-quark production via electron-positron annihilation for the first time. The interaction of the produced top quarks and antiquarks with the electric fields of the incoming electron and positron will also result in preferred spatial directions for the production of top (anti)quarks, thus giving rise to an asymmetry between top quark and antiquark. The thorough analysis of this asymmetry in top quark pair production through electron-positron annihilation will complement the information collected by analyzing the mostly QCD-induced charge asymmetry in t$\overline{t}$ production from quark-antiquark annihilation, as discussed in this review.

Thus, the future of t$\overline{t}$ production asymmetries remains interesting. Incoming measurements with increased precision will help to improve the level of details under which the standard model of particle physics is scrutinized and the search for new physics beyond what is currently known.