Scalar Field Models of Barrow Holographic Dark Energy in f(R,T) Gravity
Abstract
:1. Introduction
2. Barrow Holographic Dark Energy
3. Assessment of Gravitational Field Equations of Theory
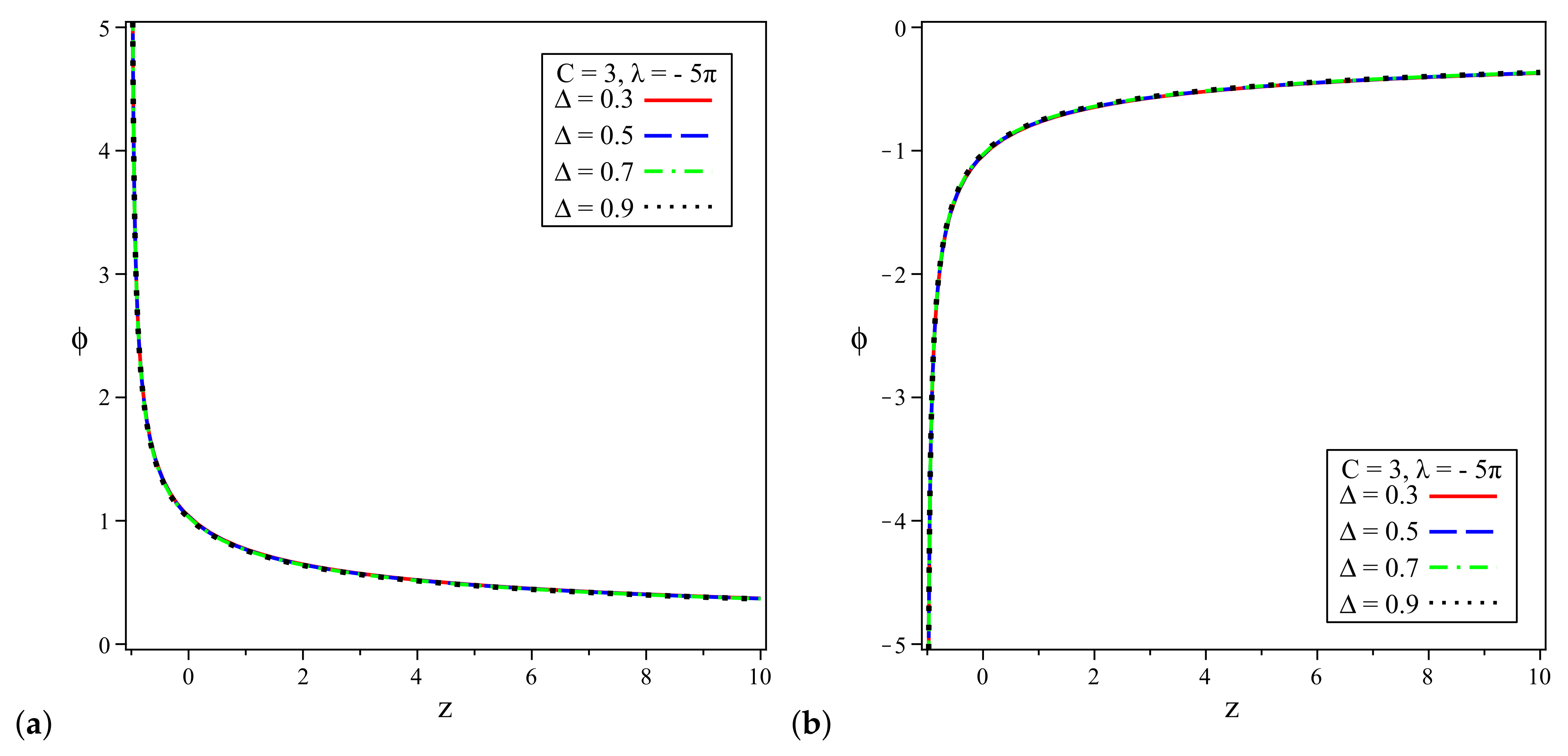
4. The Cosmological Model
5. Correspondence with Scalar Field Models
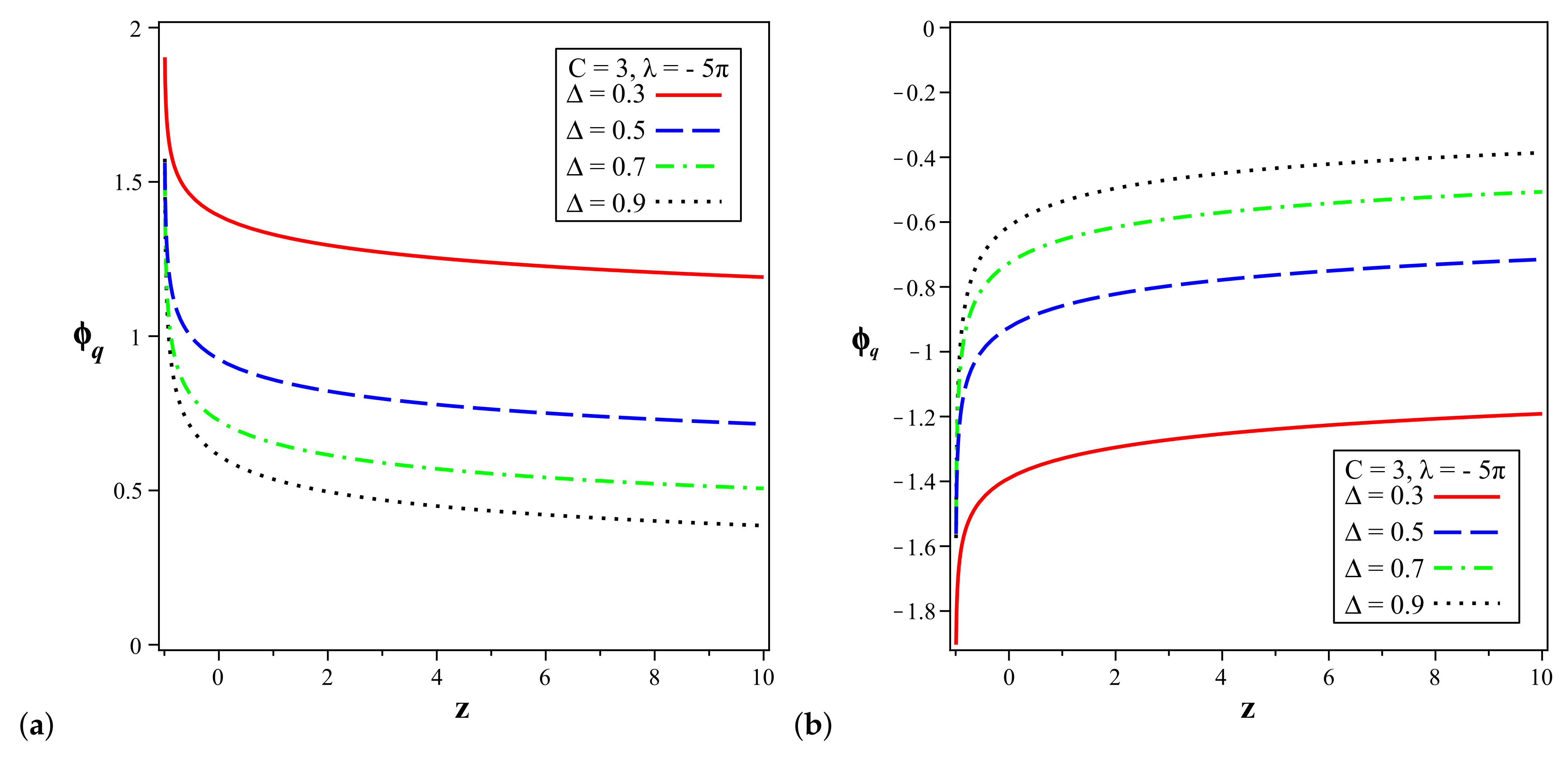
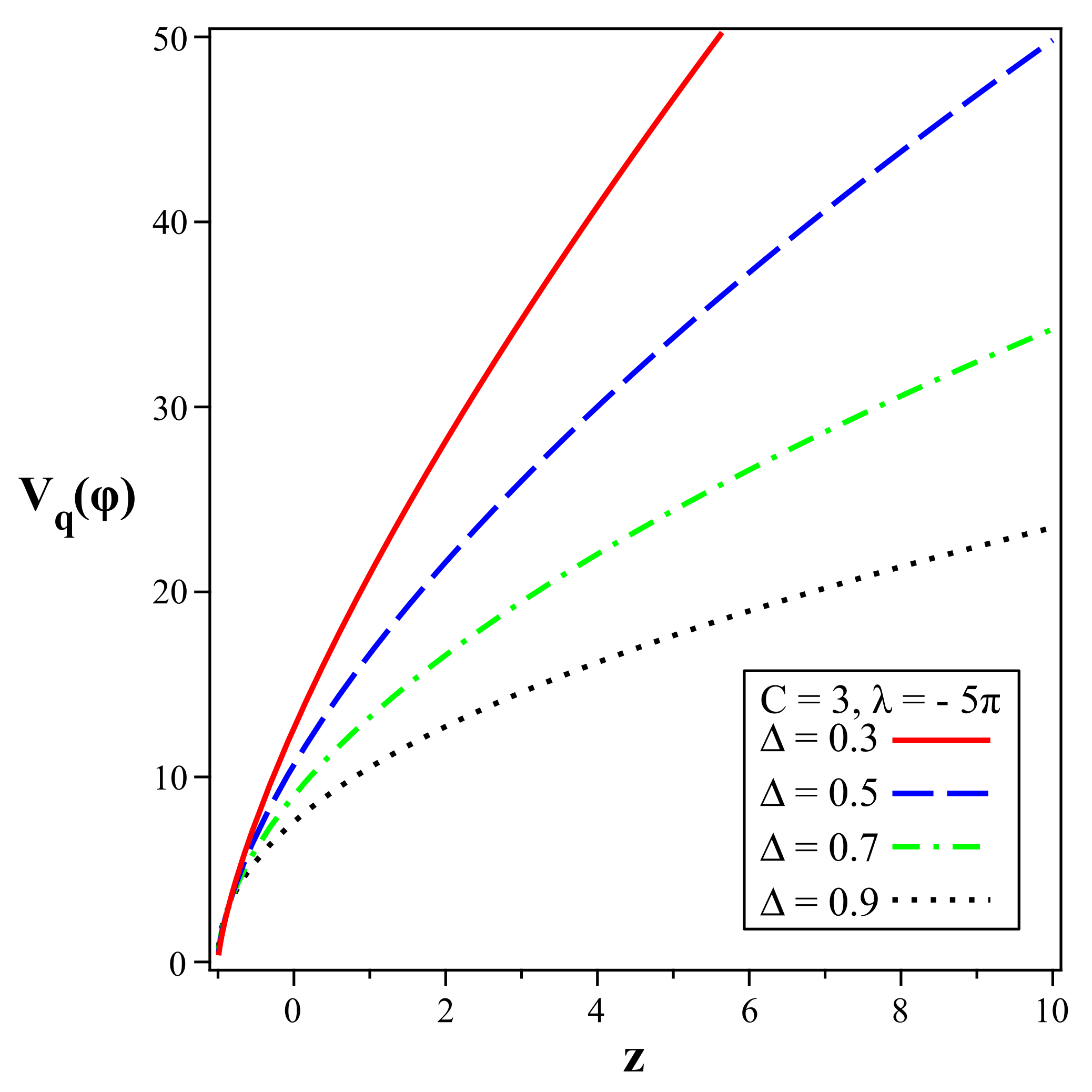
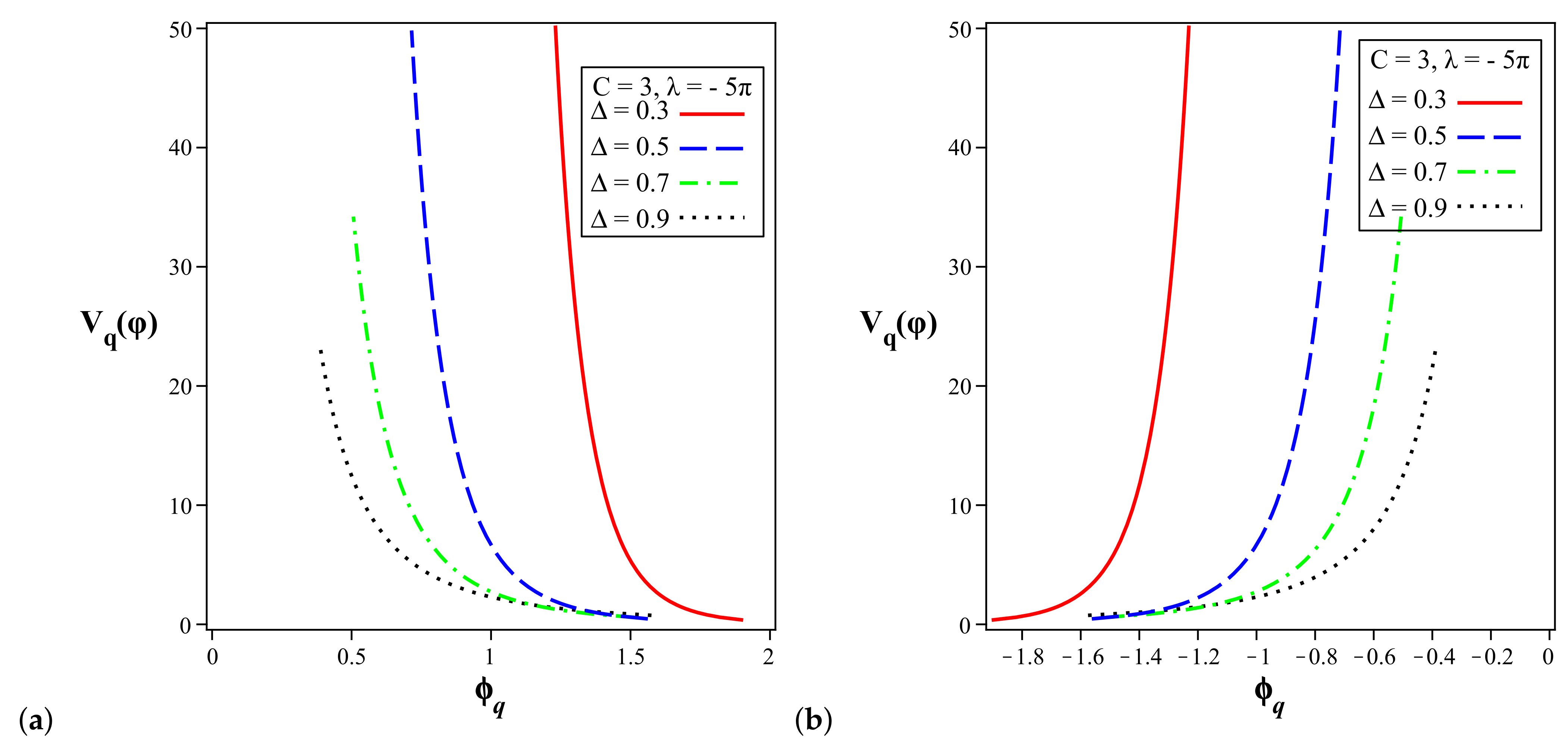
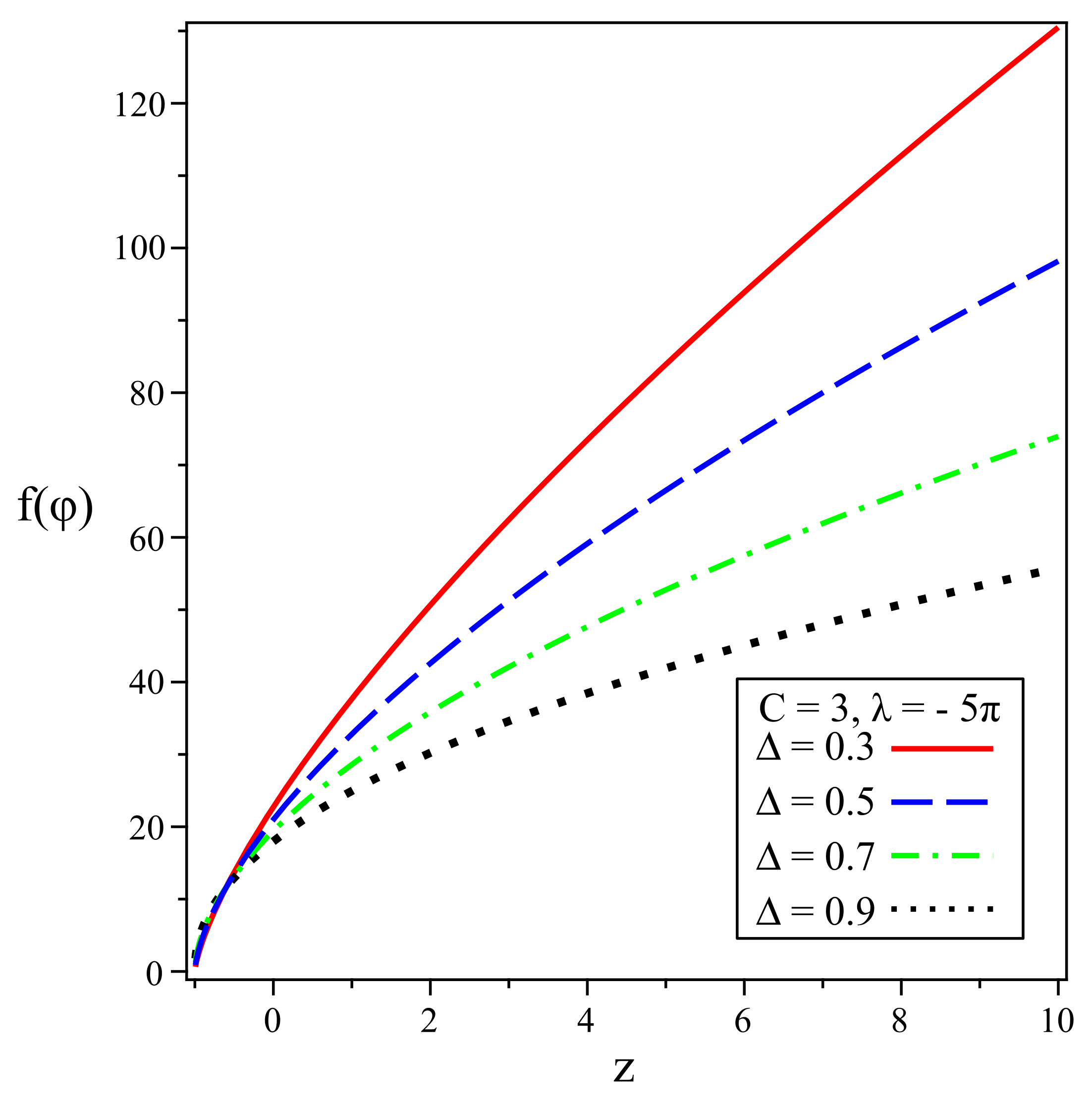
5.1. Quintessence Model for Barrow Hologaphic Dark Energy
5.2. k-Essence Model for Barrow Holographic Dark Energy
5.3. Dilation Model for Barrow Holographic Dark Energy
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Capozziello, S.; Cardone, V.F.; Troisi, A. Dark energy and dark matter as curvature effects. J. Cosmol. Astropart. Phys. 2006, 8, 001. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Visinelli, L.; Brax, P.; Davis, A.C.; Sakstein, J. Direct detection of dark energy: The XENON1T excess and future prospects. Phys. Rev. D 2021, 104, 063023. [Google Scholar] [CrossRef]
- Capozziello, S.; Cardone, V.F.; Troisi, A. Reconciling dark energy models with f(R) theories. Phys. Rev. D 2005, 71, 043503. [Google Scholar] [CrossRef]
- Ferlito, F.; Vagnozzi, S.; Mota, D.F.; Baldi, M. Cosmological direct detection of dark energy: Non-linear structure formation signatures of dark energy scattering with visible matter. Mon. Not. Roy. Astron. Soc. 2022, 512, 1885–1905. [Google Scholar]
- Capozziello, S.; Nojiri, S.; Odintsov, S.D. Unified phantom cosmology: Inflation, dark energy and dark matter under the same standard. Phys. Lett. B 2006, 632, 597–604. [Google Scholar] [CrossRef] [Green Version]
- Valentino, E.D.; Gariazzo, S.; Mena, O.; Vagnozzi, S. Soundness of Dark Energy properties. J. Cosmol. Astropart. Phys. 2020, 07, 045. [Google Scholar] [CrossRef]
- Capozziello, S.; Cardone, V.F.; Elizalde, E.; Nojiri, S.; Odintsov, S.D. Observational constraints on dark energy with generalized equations of state. Phys. Rev. D 2006, 73, 043512. [Google Scholar] [CrossRef] [Green Version]
- Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy: The Equation of state description versus scalar-tensor or modified gravity. Phys. Lett. B 2006, 634, 93–100. [Google Scholar] [CrossRef] [Green Version]
- Peebles, P.J.E.; Ratra, B. The Cosmological Constant and Dark Energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef] [Green Version]
- Frieman, J.; Turner, M.; Huterer, D. Dark Energy and the Accelerating Universe. Ann. Rev. Astron. Astrophys. 2008, 46, 385–432. [Google Scholar] [CrossRef] [Green Version]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Cardone, V.F.; Troisi, A.; Capozziello, S. Unified dark energy models: A Phenomenological approach. Phys. Rev. D 2004, 69, 083517. [Google Scholar] [CrossRef] [Green Version]
- Paliathanasis, A.; Leon, G. Dynamics of a two scalar field cosmological model with phantom terms. Class. Quant. Grav. 2021, 38, 075013. [Google Scholar] [CrossRef]
- Garg, S.K.; Krishnan, C. Bounds on Slow Roll and the de Sitter Swampland. J. High Energy Phys. 2019, 11, 075. [Google Scholar] [CrossRef] [Green Version]
- Bravo, R.; Palma, G.A.; Riquelme, S. A Tip for Landscape Riders: Multi-Field Inflation Can Fulfill the Swampland Distance Conjecture. J. Cosmol. Astropart. Phys. 2020, 2, 4. [Google Scholar] [CrossRef] [Green Version]
- Achúcarro, A.; Palma, G.A. The string swampland constraints require multi-field inflation. J. Cosmol. Astropart. Phys. 2019, 02, 041. [Google Scholar] [CrossRef] [Green Version]
- Hooft, G. Dimensional reduction in quantum gravity. Conf. Proc. C 1993, 930308, 284–296. [Google Scholar]
- Susskind, L. The World as a hologram. J. Math. Phys. 1995, 36, 6377. [Google Scholar] [CrossRef] [Green Version]
- Witten, E. Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 1998, 2, 253–291. [Google Scholar] [CrossRef] [Green Version]
- Bousso, R. The Holographic principle. Rev. Mod. Phys. 2002, 74, 825–874. [Google Scholar] [CrossRef] [Green Version]
- Li, M. A Model of holographic dark energy. Phys. Lett. B 2004, 603, 1. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Y.; Li, M. Holographic Dark Energy. Phys. Rept. 2017, 696, 1–57. [Google Scholar] [CrossRef] [Green Version]
- Pavon, D.; Zimdahl, W. Holographic dark energy and cosmic coincidence. Phys. Lett. B 2005, 628, 206–210. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D. Unifying phantom inflation with late-time acceleration: Scalar phantom-non-phantom transition model and generalized holographic dark energy. Gen. Rel. Grav. 2006, 38, 1285. [Google Scholar] [CrossRef] [Green Version]
- Saridakis, E.N. Ricci-Gauss-Bonnet holographic dark energy. Phys. Rev. D 2018, 97, 064035. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Saridakis, E.N.; Setare, M.R.; Xu, L. Observational constraints on holographic dark energy with varying gravitational constant. J. Cosmol. Astropart. Phys. 2010, 03, 31. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D.; Paul, T. Different Faces of Generalized Holographic Dark Energy. Symmetry 2021, 13, 928. [Google Scholar] [CrossRef]
- Horvat, R. Holographic bounds and Higgs inflation. Phys. Lett. B 2011, 699, 174–176. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Saridakis, E.N. Holographic inflation. Phys. Lett. B 2019, 797, 134829. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Saridakis, E.N. Holographic bounce. Nucl. Phys. B 2019, 949, 114790. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K.; Paul, T. Unifying Holographic Inflation with Holographic Dark Energy: A Covariant Approach. Phys. Rev. D 2020, 102, 023540. [Google Scholar] [CrossRef]
- Barrow, J.D. The Area of a Rough Black Hole. Phys. Lett. B 2020, 808, 135643. [Google Scholar] [CrossRef]
- Saridakis, E.N. Barrow holographic dark energy. Phys. Rev. D 2020, 102, 123525. [Google Scholar] [CrossRef]
- Srivastava, S.; Sharma, U.K. Barrow holographic dark energy with Hubble horizon as IR cutoff. Int. J. Geom. Meth. Mod. Phys. 2021, 18, 2150014. [Google Scholar] [CrossRef]
- Sarkar, A.; Chattopadhyay, S. The Barrow holographic dark energy-based reconstruction of f(R) gravity and cosmology with Nojiri–Odintsov cutoff. Int. J. Geom. Meth. Mod. Phys. 2021, 18, 2150148. [Google Scholar] [CrossRef]
- Barrow, J.D.; Basilakos, S.; Saridakis, E.N. Big Bang Nucleosynthesis constraints on Barrow entropy. Phys. Lett. B 2021, 815, 136134. [Google Scholar] [CrossRef]
- Jusufi, K.; Azreg-Aïnou, M.; Jamil, M.; Saridakis, E.N. Constraints on Barrow Entropy from M87* and S2 Star Observations. Universe 2022, 8, 102. [Google Scholar] [CrossRef]
- Mamon, A.A.; Paliathanasis, A.; Saha, S. Dynamics of an Interacting Barrow Holographic Dark Energy Model and its Thermodynamic Implications. Eur. Phys. J. Plus 2021, 136, 134. [Google Scholar] [CrossRef]
- Adhikary, P.; Das, S.; Basilakos, S.; Saridakis, E.N. Barrow holographic dark energy in a nonflat universe. Phys. Rev. D 2021, 104, 123519. [Google Scholar] [CrossRef]
- Pradhan, A.; Dixit, A.; Bhardwaj, V.K. Barrow HDE model for Statefinder diagnostic in FLRW Universe. Int. J. Mod. Phys. A 2021, 36, 2150030. [Google Scholar] [CrossRef]
- Anagnostopoulos, F.K.; Basilakos, S.; Saridakis, E.N. Observational constraints on Barrow holographic dark energy. Eur. Phys. J. C 2020, 80, 826. [Google Scholar] [CrossRef]
- Saridakis, E.N. Modified cosmology through spacetime thermodynamics and Barrow horizon entropy. J. Cosmol. Astropart. Phys. 2020, 7, 031. [Google Scholar] [CrossRef]
- Jawad, A.; Rani, S.; Ashraf, S.; Azhar, N. Barrow holographic dark energy in deformed Hořava–Lifshitz gravity. Int. J. Geom. Meth. Mod. Phys. 2022, 19, 2250112. [Google Scholar] [CrossRef]
- Bhardwaj, V.K.; Dixit, A.; Pradhan, A. Statefinder hierarchy model for the Barrow holographic dark energy. New Astron. 2021, 88, 101623. [Google Scholar] [CrossRef]
- Sheykhi, A. Barrow Entropy Corrections to Friedmann Equations. Phys. Rev. D 2021, 103, 123503. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Paul, T. Early and late universe holographic cosmology from a new generalized entropy. Phys. Lett. B 2022, 831, 137189. [Google Scholar] [CrossRef]
- Farsi, B.; Sheykhi, A. Growth of Perturbations in Tsallis and Barrow Cosmology. arXiv 2022, arXiv:2205.04138. [Google Scholar]
- Pradhan, A.; Bhardwaj, V.K.; Garg, P.; Krishnannair, S. FRW cosmological models with Barrow holographic dark energy in Brans–Dicke theory. Int. J. Geom. Meth. Mod. Phys. 2022, 19, 2250106. [Google Scholar] [CrossRef]
- Asghari, M.; Sheykhi, A. Observational constraints of the modified cosmology through Barrow entropy. Eur. Phys. J. C 2022, 82, 388. [Google Scholar] [CrossRef]
- Oliveros, A.; Sabogal, M.A.; Acero, M.A. Barrow holographic dark energy with Granda–Oliveros cutoff. Eur. Phys. J. Plus 2022, 137, 783. [Google Scholar] [CrossRef] [PubMed]
- Sharma, U.K.; Kumar, M. Barrow holographic phantom. Int. J. Geom. Meth. Mod. Phys. 2022, 19, 2250066. [Google Scholar] [CrossRef]
- Remya, A.; Pankaj; Sharma, U.K. Cosmological parameters in Barrow holographic dark energy. Int. J. Geom. Meth. Mod. Phys. 2022, 19, 2250082. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Paul, T. Barrow entropic dark energy: A member of generalized holographic dark energy family. Phys. Lett. B 2022, 825, 136844. [Google Scholar] [CrossRef]
- Sharma, U.K.; Varshney, G.; Dubey, V.C. Barrow agegraphic dark energy. Int. J. Mod. Phys. D 2021, 30, 2150021. [Google Scholar] [CrossRef]
- Huang, H.; Huang, Q.; Zhang, R. Phase Space Analysis of Barrow Agegraphic Dark Energy. Universe 2022, 8, 467. [Google Scholar] [CrossRef]
- Rani, S.; Azhar, N. Braneworld Inspires Cosmological Implications of Barrow Holographic Dark Energy. Universe 2021, 7, 268. [Google Scholar] [CrossRef]
- Buchdahl, H.A. Non-linear Lagrangians and cosmological theory. Mon. Not. Roy. Astron. Soc. 1970, 150, 1. [Google Scholar] [CrossRef] [Green Version]
- Felice, A.D.; Tsujikawa, S. f(R) theories. Living Rev. Rel. 2010, 13, 3. [Google Scholar]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified Gravity and Cosmology. Phys. Rept. 2012, 513, 1. [Google Scholar]
- Bamba, K.; Capozziello, S.; Nojiri, S.; Odintsov, S.D. Dark energy cosmology: The equivalent description via different theoretical models and cosmography tests. Astrophys. Space Sci. 2012, 342, 155. [Google Scholar] [CrossRef] [Green Version]
- Sotiriou, T.P.; Faraoni, V. f(R) Theories Of Gravity. Rev. Mod. Phys. 2010, 82, 451. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59. [Google Scholar]
- Harko, T.; Lobo, F.S.N.; Nojiri, S.; Odintsov, S.D. f(R,T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef] [Green Version]
- Shamir, M.F.; Raza, Z. Cylindrically symmetric solutions in f(R,T) gravity. Astrophys. Space Sci. 2015, 356, 111. [Google Scholar] [CrossRef] [Green Version]
- Alvarenga, F.G.; Cruz-Dombriz, A.d.; Houndjo, M.J.S.; Rodrigues, M.E.; Sáez-Gómez, D. Dynamics of scalar perturbations in f(R,T) gravity. Phys. Rev. D 2013, 87, 103526, Erratum in: Phys. Rev. D 2013, 87, 129905. [Google Scholar] [CrossRef]
- Harko, T. Thermodynamic interpretation of the generalized gravity models with geometry - matter coupling. Phys. Rev. D 2014, 90, 044067. [Google Scholar] [CrossRef] [Green Version]
- Josset, T.; Perez, A.; Sudarsky, D. Dark Energy from Violation of Energy Conservation. Phys. Rev. Lett. 2017, 118, 021102. [Google Scholar] [CrossRef] [Green Version]
- Taser, D.U. Conformally symmetric Friedmann–Robertson–Walker metric in f(R,T) gravity. Mod. Phys. Lett. A 2020, 35, 2050067. [Google Scholar] [CrossRef]
- Sharif, M.; Rani, S.; Myrzakulov, R. Analysis of F(R,T) gravity models through energy conditions. Eur. Phys. J. Plus 2013, 128, 123. [Google Scholar] [CrossRef] [Green Version]
- Zubair, M.; Durrani, L.R. Exploring tsallis holographic dark energy scenario in f(R,T) gravity. Chin. J. Phys. 2021, 69, 153–171. [Google Scholar] [CrossRef]
- Fisher, S.B.; Carlson, E.D. Reexamining f(R,T) gravity. Phys. Rev. D 2019, 100, 064059. [Google Scholar] [CrossRef] [Green Version]
- Barrientos, J.; Rubilar, G.F. Comment on f(R,T) gravity. Phys. Rev. D 2014, 90, 028501. [Google Scholar] [CrossRef]
- Setare, M.R. Holographic tachyon model of dark energy. Phys. Lett. B 2007, 653, 116. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zhang, X.; Liu, H. Holographic tachyon model. Phys. Lett. B 2007, 651, 84. [Google Scholar] [CrossRef] [Green Version]
- Granda, L.N. Reconstructing the potentials for the quintessence and tachyon dark energy, from the holographic principle. Int. J. Mod. Phys. D 2009, 18, 1749. [Google Scholar] [CrossRef]
- Acikgoz, I.; Binbay, F.; Salti, M.; Aydogdu, O. Ghost DBI-essence in fractal geometry. Eur. Phys. J. Plus 2016, 131, 157. [Google Scholar] [CrossRef]
- Debnath, U.; Jamil, M. Correspondence between DBI-essence and Modified Chaplygin Gas and the Generalized Second Law of Thermodynamics. Astrophys. Space Sci. 2011, 335, 545. [Google Scholar] [CrossRef]
- Yang, W.Q.; Wu, Y.B.; Song, L.M.; Su, Y.Y.; Li, J.; Zhang, D.D.; Wang, X.G. Reconstruction of new holographic scalar field models of dark energy in Brans-Dicke Universe. Mod. Phys. Lett. A 2011, 26, 191. [Google Scholar]
- Chattopadhyay, S.; Pasqua, A.; Khurshudyan, M. New holographic reconstruction of scalar field dark energy models in the framework of chameleon Brans-Dicke cosmology. Eur. Phys. J. C 2014, 74, 3080. [Google Scholar] [CrossRef] [Green Version]
- Karami, K.; Fahimi, K. Interacting viscous ghost tachyon, k-essence and dilaton scalar field models of dark energy. Class. Quant. Grav. 2013, 30, 065018. [Google Scholar] [CrossRef] [Green Version]
- Karami, K.; Fehri, J. New holographic scalar field models of dark energy in non-flat universe. Phys. Lett. B 2020, 684, 61. [Google Scholar] [CrossRef] [Green Version]
- Varshney, G.; Sharma, U.K.; Pradhan, A. Reconstructing the k-essence and the dilation field models of the THDE in f(R,T) gravity. Eur. Phys. J. Plus 2020, 135, 541. [Google Scholar] [CrossRef]
- Sharma, U.K. Reconstruction of quintessence field for the THDE with swampland correspondence in f(R,T) gravity. Int. J. Geom. Methods Mod. Phys. 2021, 18, 2150031. [Google Scholar] [CrossRef]
- Varshney, G.; Sharma, U.K.; Pradhan, A.; Kumar, N. Reconstruction of Tachyon, Dirac-Born-Infeld-essence and Phantom model for Tsallis holographic dark energy in f(R,T) gravity. Chin. J. Phys. 2021, 73, 56–73. [Google Scholar] [CrossRef]
- Pradhan, A.; Varshney, G.; Sharma, U.K. The scalar field models of Tsallis holographic dark energy with Granda–Oliveros cutoff in modified gravity. Can. J. Phys. 2021, 99, 866–874. [Google Scholar] [CrossRef]
- Sharma, U.K. Reconstructing Tsallis holographic phantom. Pramana 2022, 96, 210. [Google Scholar] [CrossRef]
- Granda, L.N.; Oliveros, A. New infrared cut-off for the holographic scalar fields models of dark energy. Phys. Lett. B 2009, 671, 199. [Google Scholar] [CrossRef] [Green Version]
- Sheykhi, A. Holographic Scalar Fields Models of Dark Energy. Phys. Rev. D 2011, 84, 107302. [Google Scholar] [CrossRef] [Green Version]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Butterworth-Heinemann: Oxford, UK, 1998. [Google Scholar]
- Adhav, K.S. LRS Bianchi type-I cosmological model in f(R,T) theory of gravity. Astrophys. Space Sci. 2012, 339, 365–369. [Google Scholar] [CrossRef]
- Samanta, G.C. Universe Filled with Dark Energy (DE) from a Wet Dark Fluid (WDF) in f(R,T) Gravity. Int. J. Theor. Phys. 2013, 52, 2303–2315. [Google Scholar] [CrossRef]
- Samanta, G.C.; Dhal, S.N. Higher Dimensional Cosmological Models Filled with Perfect Fluid in f(R,T) Theory of Gravity. Int. J. Theor. Phys. 2013, 52, 1334–1344. [Google Scholar] [CrossRef] [Green Version]
- Shamir, M.F. Bianchi type-I cosmology in f(R,T) gravity. J. Exp. Theor. Phys. 2014, 119, 242–250. [Google Scholar] [CrossRef]
- Chaubey, R.; Shukla, A.K. A new class of Bianchi cosmological models in f(R,T) gravity. Astrophys. Space Sci. 2013, 343, 415–422. [Google Scholar] [CrossRef]
- Ahmed, N.; Pradhan, A.; Fekry, M.; Alamri, S.Z. V cosmological models in f (R, T) modified gravity with Λ(T) by using generation technique. Nriag J. Astron. Geophys. 2016, 5, 35–47. [Google Scholar] [CrossRef] [Green Version]
- Pradhan, A.; Jaiswal, R. Magnetized string cosmological models of accelerated expansion of the Universe in f(R,T) theory of gravity. Int. J. Geom. Meth. Mod. Phys. 2018, 15, 1850076. [Google Scholar] [CrossRef]
- Das, K.; Bharali, J. Interacting Anisotropic Ghost Dark Energy Model in f(R,T) Theory of Gravity. Grav. Cosmol. 2021, 27, 68–77. [Google Scholar] [CrossRef]
- Poplawski, N.J. A Lagrangian description of interacting dark energy. arXiv 2006, arXiv:gr-qc/0608031. [Google Scholar]
- Armendariz-Picon, C.; Mukhanov, V.F.; Steinhardt, P.J. Essentials of k essence. Phys. Rev. D 2001, 63, 103510. [Google Scholar] [CrossRef]
- Piazza, F.; Tsujikawa, S. Dilatonic ghost condensate as dark energy. J. Cosmol. Astropart. Phys. 2004, 07, 4. [Google Scholar] [CrossRef]
- Granda, L.N.; Oliveros, A. Holographic reconstruction of the k-essence and dilaton models. arXiv 2009, arXiv:0901.0561. [Google Scholar]
- Guo, Z.K.; Ohta, N.; Zhang, Y.Z. Parametrization of quintessence and its potential. Phys. Rev. D 2005, 72, 023504. [Google Scholar] [CrossRef] [Green Version]
- Armendariz-Picon, C.; Damour, T.; Mukhanov, V.F. k-inflation. Phys. Lett. B 1999, 458, 209–218. [Google Scholar] [CrossRef] [Green Version]
- Tsujikawa, S.; Sami, M. A Unified approach to scaling solutions in a general cosmological background. Phys. Lett. B 2004, 603, 113–123. [Google Scholar] [CrossRef] [Green Version]
- Carroll, S.M.; Hoffman, M.; Trodden, M. Can the dark energy equation-of-state parameter w be less than -1? Phys. Rev. D 2003, 68, 023509. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, U.K.; Kumar, M.; Varshney, G. Scalar Field Models of Barrow Holographic Dark Energy in f(R,T) Gravity. Universe 2022, 8, 642. https://doi.org/10.3390/universe8120642
Sharma UK, Kumar M, Varshney G. Scalar Field Models of Barrow Holographic Dark Energy in f(R,T) Gravity. Universe. 2022; 8(12):642. https://doi.org/10.3390/universe8120642
Chicago/Turabian StyleSharma, Umesh Kumar, Mukesh Kumar, and Gunjan Varshney. 2022. "Scalar Field Models of Barrow Holographic Dark Energy in f(R,T) Gravity" Universe 8, no. 12: 642. https://doi.org/10.3390/universe8120642
APA StyleSharma, U. K., Kumar, M., & Varshney, G. (2022). Scalar Field Models of Barrow Holographic Dark Energy in f(R,T) Gravity. Universe, 8(12), 642. https://doi.org/10.3390/universe8120642










