The Contribution of Charged Bosons with Right-Handed Neutrinos to the Muon g − 2 Anomaly in the Twin Higgs Models

Abstract

We examine the charged boson and right-handed neutrino contribution to the muon $g-2$ anomaly in twin Higgs models with joint constraints of Higgs global fit data, precision electroweak data, leptonic flavor-changing decay $\mu \to e\gamma$, and the mass requirement of heavy-gauge bosons. It comes with the conclusion that some parameters, such as the coupling of charged Higgs to the lepton $y_{\mu }$, the top Yukawa $y_t$, and heavy-gauge boson coupling to the lepton $V_{\mu }$ are constrained roughly in the range of $0.12\lesssim y_{\mu }\lesssim 0.4$, $0.4\lesssim y_t\lesssim 0.9$, and $0.47\lesssim V_{\mu }\lesssim 1$, respectively.

1. Introduction

The long-standing puzzle of the muon anomalous magnetic moment $a_{\mu }\equiv {(g-2)}_{\mu }/2$ was measured by the E989 muon $g-2$ anomaly experiment in Fermilab (FNAL) [1] and the Brookheaven National Laboratory (BNL) [2,3],

$$a_{\mu }^{\mathrm{FNAL}+\mathrm{BNL}}=(11659206.1\pm 4.1)\times {10}^{-10}$$

(1)

which has a $4.2\sigma$ deviation from the prediction of the SM [1,4,5]

$$\Delta a_{\mu }^{\mathrm{FNAL}+\mathrm{BNL}}=(25.1\pm 5.9)\times {10}^{-10}.$$

(2)

It may hint at the existence of a new physics beyond the SM. The difference between the experimental data and the SM prediction determines that there is room for new physics. Various new physics scenarios try to explain the muon $g-2$ excess. For recent works, see, e.g., refs. [6,7,8,9,10,11,12].

So-called twin Higgs (TH) models can be realized by extending the SM with discrete twin symmetry [13] and are quite appealing. First, the discrete symmetry in them connects SM fields with extended ones. Second, more importantly, the extended fields are uncharged under SM gauge groups, i.e., they will appear as singlets, and “show” in upcoming experiments purely as missing energy, escaping from the current constraints of the LHC to new particles [14].

In TH models, the extra charged gauge bosons and charged scalars [15,16] may have leptonic and the quark flavor-changing couplings, which will contribute to a muon anomalous magnetic moment. Since there is not any signal of the twin top and twin gauge bosons in the experiments, their masses may be very heavy, and the phenomenological signatures are suppressed. Therefore, the main contribution to the muon anomaly comes not from heavy twin top and twin gauge bosons, but from the charged Higgs via its Yukawa couplings to SM quarks and leptons.

However, TH models have encountered difficulties in cosmological considerations. In the simplest realization of TH [13] models, the twin particles will eventually transfer their entropies into those of SM photons and neutrinos, which results in deviations from the observations [17,18], greatly increasing the value of $N_{eff}$, which is the effective number of (light) neutrino species [19,20].

Various modifications are proposed to reduce the $N_{eff}$ value in TH models. See, e.g., refs. [20,21,22,23,24,25,26,27]. Type I seesaw [28,29,30,31] is one of the mechanisms to provide tiny neutrino masses by involving the exchange of right-handed neutrinos, and is also one to lower the effective degrees of freedom contributed by the twin sector when it is embedded into TH models [23]. Typical lepton flavor-changing couplings will appear via this mechanism, leading to interesting phenomenological consequences.

Flavor-changing couplings can contribute to the muon anomalous magnetic moment not only at the one-loop level, but also via the two-loop diagrams. Since the quarks are much heavier than the leptons, the phase space suppression may be surpassed by the mass enhancement. Therefore, the two-loop Barr–Zee diagrams [32] may contribute much more largely than that from the one-loop ones, if only the Higgs bosons are not too light [33,34]. Thus, in the following, we will calculate the contributions from both the one-loop and two-loop levels. We will examine the relevant parameter space of TH models by considering the joint effects from the theory, the precision electroweak data, the 125 GeV Higgs signal data and the muon $g-2$ anomaly.

This paper is organized as follows. In Section 2, we simply present TH models and the relevant couplings. In Section 3, we discuss the rough constraints of the relevant parameters in TH models. In Section 4, we calculate the muon anomalous magnetic moment $g-2$ at the one-loop level. The analytic expressions for the two-loop muon $g-2$ anomaly and the Higgs global fit are given in Section 5. In Section 6, we calculate the contributions of the Barr–Zee diagrams and the total constraints. Finally, the conclusion is drawn in Section 7.

2. The TH Models and the Relevant Couplings

The hierarchy problem [35,36,37], which is induced by the disparity between the electroweak scale and the Planck scale, is one of the most outstanding problems in particle physics (see, e.g., [38]). Both supersymmetry [39] and the compositeness of the Higgs [40,41], even the strong breaking models [42,43,44,45,46,47,48,49], where the electroweak scale originates from a supersymmetry breaking scale or a composite scale, or even abandoning the idea of the Higgs as the origin of the electroweak symmetry breaking, have attempted to address the issue.

However, in the new physics models mentioned above, the solutions to the hierarchy problem generically contain the top quark partners that have SM-colored charge with the mass at the electroweak scale. Such particles have very rich phenomenological possibilities, which are easily found at the Large Hadron Collider (LHC). However, so far, there is not any signal of this kind of particle, which constrains their masses severely: typically, larger than 1 TeV [19,50,51,52,53]. To satisfy the bounds of this kind, the parameters in these theories need to be fine-tuned to fix the electroweak scale.

One solution to the above problem is to assume that the Higgs mass is protected by a $Z_2$ discrete symmetry that copies the SM particles. Therefore, the new particles associated with this symmetry do not have the SM color charge, which is called the twin Higgs (TH) model [13]. This situation makes the new particle states much more difficult to produce and detect at the LHC.

In the original TH framework, the SM particles and their copies are related to discrete $Z_2$ twin symmetry. To contain a residual custodial symmetry, the global symmetry of the Higgs sector in the simplest realization can be taken as $SO\left(8\right)$ or $SO\left(7\right)$ [15,16,54,55]. The SM Higgs doublet is a part of the pseudo-Nambu–Goldstone boson (pNGB), which arises from the spontaneous breaking of the global $SO\left(8\right)$($SO\left(7\right)$) symmetry into $SO\left(7\right)$($G_2$). The neutral Higgs mass, under the joint action of global symmetry and discrete twin symmetry, is protected from one-loop quadratic divergence.

This mechanism can stabilize the Higgs mass up to the energy scale at the order of 5–10 TeV, and solve the so-called “little hierarchy” problem [14]. A lot of models of this kind [13,56,57,58,59,60,61,62,63,64], have been proposed. TH [13] realization is one of the best-known examples. After the twin Higgs obtains a vacuum expectation value f, the SM Higgs has appeared as a pseudo-Nambu–Goldstone (pNG) boson, preventing the Higgs mass from quantum corrections up to the scale ${\Lambda }_{TH}\sim 4\pi f$ because of the twin symmetry between the top and the colorless top partner.

Ref [13] gives the Higgs contributed by the new gauge bosons and extra fermions and estimates the fine tunings. For example, the contribution of the top partners to the Higgs potential is given as

$$m_h^2=\frac{3}{8{\pi }^2}\frac{y^2{M}^2}{M^2-y^2{f}^2}\left(M^{2}ln\frac{m_{T_A}^2}{m_{T_B}^2}-y^2{f}^{2}ln\frac{m_{m_{T_A}^2}^2}{m_{t_B}^2}\right),$$

(3)

where y is Yukawa coupling, $yH{Q}_L{T}_R+h.c.$, and $m_{T_A}^2=M^2+y^2{f}^2$, $m_{T_B}^2=M^2$, $m_{t_B}^2=y^2{f}^2$. The reference finally suggests that, for the limit $M\to \Lambda$, with $f=800$ GeV, $\Lambda \sim 4\pi f\approx 10$ TeV, from Equation (3), the Higgs mass is 166 GeV and the fine tuning is $11\%$ (1 in 9), which is acceptable. The Higgs mass is 153 GeV and the fine tuning is $31\%$ (1 in 3) for $f=500$ GeV, $\Lambda \approx 6$ TeV. Therefore, for scale up to the order of 5–10 TeV, the pseudo-Goldstone Higgs mass will be protected against radiative corrections, and one can refer to the original paper [13] for details.

2.1. The Charged Higgses and the Yukawa Couplings to the Third Generation in Twin Higgs Models

Since the minimal coset $U\left(4\right)/U\left(3\right)$ does not contain a residual custodial symmetry, and in the non-linear case the twin mechanism is not realized in the gauge sector within this global group, while $SO\left(8\right)/SO\left(7\right)$ prevents a large custodial breaking in composite models of the twin mechanism, the global symmetry-breaking pattern of the simplest original TH model can be $SO\left(8\right)/SO\left(7\right)$ or $SO\left(7\right)/G_2$ [15,16,54,55]. Therefore, there are 7 pNGBs after the breaking and 6 of them are eaten by the ordinary and twin gauge bosons, meaning that there will be only one neutral scalar left.

Besides the SM-like neutral Higgs, there would be charged Higgses. Some TH models introduce extra scalars for different goals. For example, to provide suitable neutrino masses via couplings to the right-handed neutrinos, a $SU{\left(2\right)}_L$ singlet charged scalar $S^{+}$ was introduced in [65], while [24,25] add a new scalar $\varphi$ to have a similar effect in couplings with leptons.

Extra charged scalars may also appear in the particle list due to the enlarging breaking mode. The aim of the economical breaking choices mentioned above is to keep breaking smallest, but it can be otherwise. For example, it can be $SO\left(8\right)\to G_2$ or $SO\left(2N\right)\to SO\left(N\right)\times SO\left(N\right)$ [66] (the former N is for the SM sector and the latter for the twin sector).

In the following, we assume the global breaking is $SO\left(8\right)\to G_2$ as an example. After the six gauge bosons obtain masses, the left eight PNGBs can be written as $\Pi$ matrix

$$\Pi =\sqrt{2}{\pi }^{\widehat{a}}{T}^{\widehat{a}},\widehat{a}=1,\cdots ,7,$$

(4)

where $T^{\widehat{a}}$ are the broken generators, defined as

$$T_{ij}^{\widehat{a}}=-\frac{i}{\sqrt{2}}{t}_{ij}^{\widehat{a}8},\widehat{a}=1,\dots ,7.$$

(5)

Here, $t_{ij}^{ab}={\delta }_i^a{\delta }_j^b-{\delta }_j^a{\delta }_i^b$, and ${\pi }^{\widehat{a}}$ are the Goldstone fields.

Therefore, the 8 scalar degrees of freedom may be packaged into an 8 of $SO\left(8\right)$

$$\varphi =expi\frac{\Pi }{f}.$$

(6)

The first 4 components would comprise the Higgs multiplet, and the latter N the twin Higgs. They can also be parameterized via the decomposition $\mathbf{8}=(\mathbf{2},\mathbf{1},\mathbf{2})+(\mathbf{1},\mathbf{2},\mathbf{2})$ under $SU{\left(2\right)}_L\times SU{\left(2\right)}_{\tilde{L}}\times SU{\left(2\right)}_{\widehat{R}}$ as

$$(\mathbf{2},\mathbf{1},\mathbf{2}):H=\frac{f}{\sqrt{2}}\left(\begin{array}{c}{\pi }_2+i{\pi }_1\\ {\pi }_4-i{\pi }_3\end{array}\right),(\mathbf{1},\mathbf{2},\mathbf{2}):\tilde{H}=\frac{f}{\sqrt{2}}\left(\begin{array}{c}{\pi }_6+i{\pi }_5\\ \sigma -i{\pi }_7\end{array}\right),$$

(7)

where $\frac{f}{\sqrt{2}}({\pi }_2+i{\pi }_1)$ can identified as the charged scalar $H^{\pm }$. In some situations, ${\tilde{\omega }}^{\pm }\equiv f({\pi }_6\pm i{\pi }_5)/\sqrt{2}$ and ${\tilde{\omega }}_0\equiv f{\pi }_7$ can also be taken as the long-lived particles.

At low energies, the representations of SO(8) of the third-generation quarks $q_L$ and ${\tilde{q}}_L$ can be written as

$$\begin{array}{ccc}\hfill Q_L& =& v_b{b}_L+v_t{t}_L=\frac{1}{\sqrt{2}}{\left(\begin{array}{cccccccc}i{b}_L& b_L& i{t}_L& -t_L& 0& 0& 0& 0\end{array}\right)}^T,\hfill \\ \hfill {\tilde{Q}}_L& =& {\tilde{v}}_b{\tilde{b}}_L+{\tilde{v}}_t{\tilde{t}}_L=\frac{1}{\sqrt{2}}{\left(\begin{array}{cccccccc}0& 0& 0& 0& i{\tilde{b}}_L& {\tilde{b}}_L& i{\tilde{t}}_L& -{\tilde{t}}_L\end{array}\right)}^T,\hfill \end{array}$$

(8)

while those of $t_R$ and ${\tilde{t}}_R$ are singlets. Thus, the top Yukawa couplings are written as

$$y_{t}f{\overline{t}}_R{\Sigma }^{†}{Q}_L+{\tilde{y}}_{t}f{\overline{\tilde{t}}}_R{\Sigma }^{†}{\tilde{Q}}_L+\mathrm{h}.\mathrm{c}.=-y_t{\overline{q}}_{L}H{t}_R-{\tilde{y}}_t{\overline{\tilde{t}}}_R\tilde{H}{\tilde{q}}_L+\mathrm{h}.\mathrm{c}.+...,$$

(9)

where $q_L=(b,t),{\tilde{q}}_L=(\tilde{b},\tilde{t})$.

A $Z_2$ symmetry $q_L,t_R\leftrightarrow {\tilde{q}}_L,{\tilde{t}}_R$ leads to $y_t={\tilde{y}}_t$. The masses of the rest of the fermions (including twin fermions) are obtained in a similar manner. Due to ${\tilde{y}}_{\psi }\ll y_t$, the associated contribution to the Higgs potential of the light fermions will be negligible. Therefore, it is not necessary to enforce the approximate equality $y_{\psi }={\tilde{y}}_{\psi }$.

2.2. Flavor-Changing Couplings of Leptons in TH Models

In the seesaw type I model [28,29,30,31], to realize the seesaw mechanism, right-handed neutrinos are introduced, and they are singlets under the SM gauge group $SU{\left(3\right)}_C\times SU{\left(2\right)}_L\times U{\left(1\right)}_Y$ [67]. We denote ${\nu }_i$s as the ordinary tiny neutrinos, and ${\nu }_{iR}$s as the heavy right-handed neutrinos. The masses of the neutrinos can be described by the following Lagrangian terms

$$\mathcal{L}\supset -Y_j{\overline{\nu }}_R{H}^{+}{p}_L{\ell }_j-y_j\overline{\nu }{H}^{+}{p}_L{\ell }_j+\mathrm{h}.\mathrm{c}.+...,$$

(10)

In the mass eigenstate basis, the gauge interactions with ${\nu }_R$ are given by [68,69],

$$\begin{array}{ccc}\hfill \mathcal{L}& \supset & -\frac{g}{\sqrt{2}}\left({\overline{l}}_{jL}{\gamma }^{\mu }{V}_{PMNS}{\nu }_{iL}{W}_{\mu }^{-}+{\overline{l}}_{jL}{\gamma }^{\mu }{V}_{l\nu }{\left({\nu }_{iR}\right)}_{L}N{W}_{\mu }^{-}+h.c.\right)\hfill \\ & \to & V_j{\overline{\nu }}_R{W}_{\mu }^{+}{\gamma }^{\mu }{P}_L{\ell }_j+h.c.+...\hfill \end{array}$$

(11)

Please note that in the second lines of Equations (10) and (11) and following calculation, we assume that the right-handed neutrinos are degenerate, i.e., ${\nu }_{1R}={\nu }_{2R}={\nu }_{3R}={\nu }_R$, which means that there is only one flavor of the heavy neutrino (the same case for the ordinary neutrinos). Therefore, the couplings will be simply written as $V_j$, $Y_j$ and $y_j$, respectively, where j can be e, $\mu$, and $\tau$.

Please note that the $3\times 3$ Maki–Nakagawa–Sakata (MNS) matrix $U_{MNS}$ [70,71] elements in the above flavor-changing couplings are also absorbed into the couplings and their effects are actually neglected.

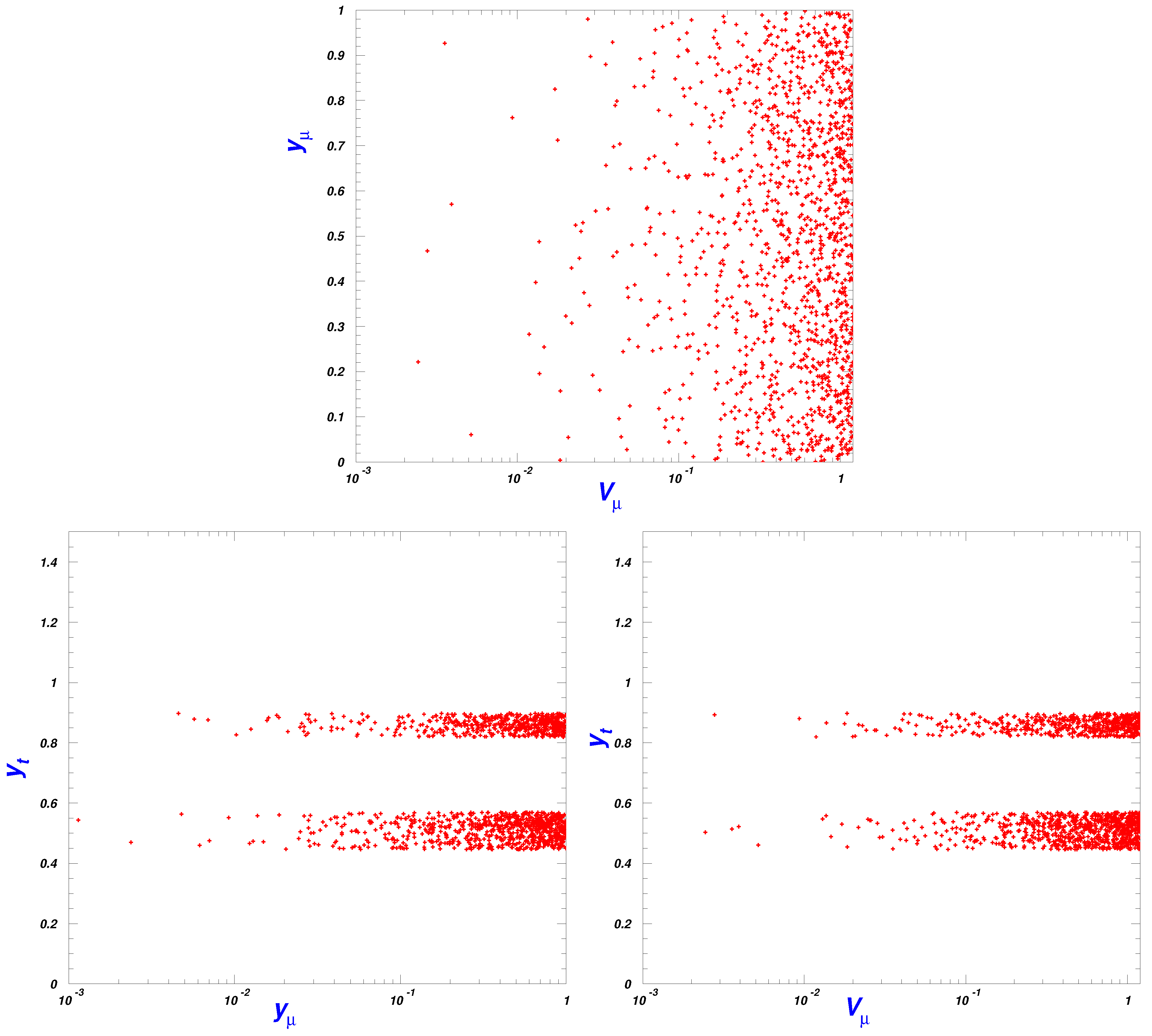
3. The Rough Ranges of the Relevant Parameters in TH Models

In this paper, we take the light CP-even Higgs h as the SM-like Higgs, $m_h=125.5$ GeV. The mass difference between the charged Higgs boson and the neutral heavy Higgs boson should be less than 300 GeV, i.e., $|m_{H^{\pm }}-m_0|\le 300$ GeV, and in general, the mass of the neutral heavy Higgs boson is larger than that of the SM-like Higgs [72,73]. We here, however, just roughly scan over the charged Higgs mass $m_{H^{\pm }}$ in the following ranges:

$$100\mathrm{GeV}<m_{H^{\pm }}<1000\mathrm{GeV}.$$

(12)

In the following, we will simply discuss the constraints on the parameters:

(1)

The first constraint comes from the signal data of the 125 GeV Higgs, which is important, since the couplings of the SM-like Higgs with the fermions and the bosons in TH models can deviate from the SM largely and the production and decay modes of the SM-like Higgs may be modified severely. In the paper, we will perform the calculation of ${\chi }_h^2$ for the signal strengths of the 125 GeV Higgs, which will be shown in Section 5 and Section 6.

(2)

The constraints on parameter f come from the joint effects of the Z-pole precision measurements, the low-energy neutral current process, and the high-energy precision measurements off the Z-pole indirectly, and according to all these data, f should be larger than 500–600 GeV [74]. On the other hand, to control in a mild fine tuning, f should not be too large, since the fine tuning is more severe for large f. The constraints for f can also come from the flavor-changing decay $\mu \to e\gamma$: With the experimental constraints, [75,76], $\mathrm{BR}(\mu \to e\gamma )<4.2\times {10}^{-13}$, the flavor-changing decay $\mu \to e\gamma$ will give $f\sim [0.6–2]$ TeV.

So after we take the above constraints from the electroweak precision measurements and the LHC data into account, we can assume that $500\le f\le 2000$ GeV. In our numerical evaluations, however, we have not taken f as a free parameter. Instead, we assume the characteristic mass and coupling of the composite resonances is set by m and g, respectively, which are related by the symmetry-breaking order parameter, f, as $m=gf$.

(3)

In the present experiments, $m_{W_H^{\pm }}$ has been constrained stringently [77,78,79]. The ATLAS experiment has presented the first search for dilepton resonances based on the full Run 2 data-set [77,79] and set limits on the $W^{\prime }$ production cross-section times branching fraction in the process

$$\sigma (pp\to W^{\prime }X)\times BR(W^{\prime }\to \nu \ell )$$

(13)

for $M_W^{\prime }$ in the $0.15$ TeV–7 TeV range, correspondingly. Recently, similar searches have also been presented by the CMS Collaboration using 140 fb${}^{-1}$ of data recorded at $\sqrt{s}=13$ TeV [78]. The most stringent limits on the mass of $W^{\prime }$ boson to date come from the searches in the above process by the ATLAS and CMS collaborations using data taken at $\sqrt{s}=13$ TeV in Run 2 and set a 95% confidence level (CL) lower limit on the $W^{\prime }$ mass of 6.0 TeV [79].

This analysis, however, is based on the simplest models [80] such as the sequential standard model proposed by Altarelli et al. [81], which is usually taken as a convenient benchmark in the experiments. In the simplest models, the gauge particles are considered to be the copies of the SM gauge bosons, and their couplings to fermions are in the same mode as those of the SM gauge bosons, but they miss trilinear couplings such as $W^{\prime }WZ$ and $Z^{\prime }WW$, etc. Therefore, the situation that the sequential standard model [81] has acted as a reference for experimental extended gauge boson searches may be changed, and the results may be re-interpreted in the context of other new physics models [82]. In the following computation, we will check the sensitivity of the charged heavy-gauge boson with the mass range $1\le m_{W_H^{\pm }}\le 20$ TeV.

(4)

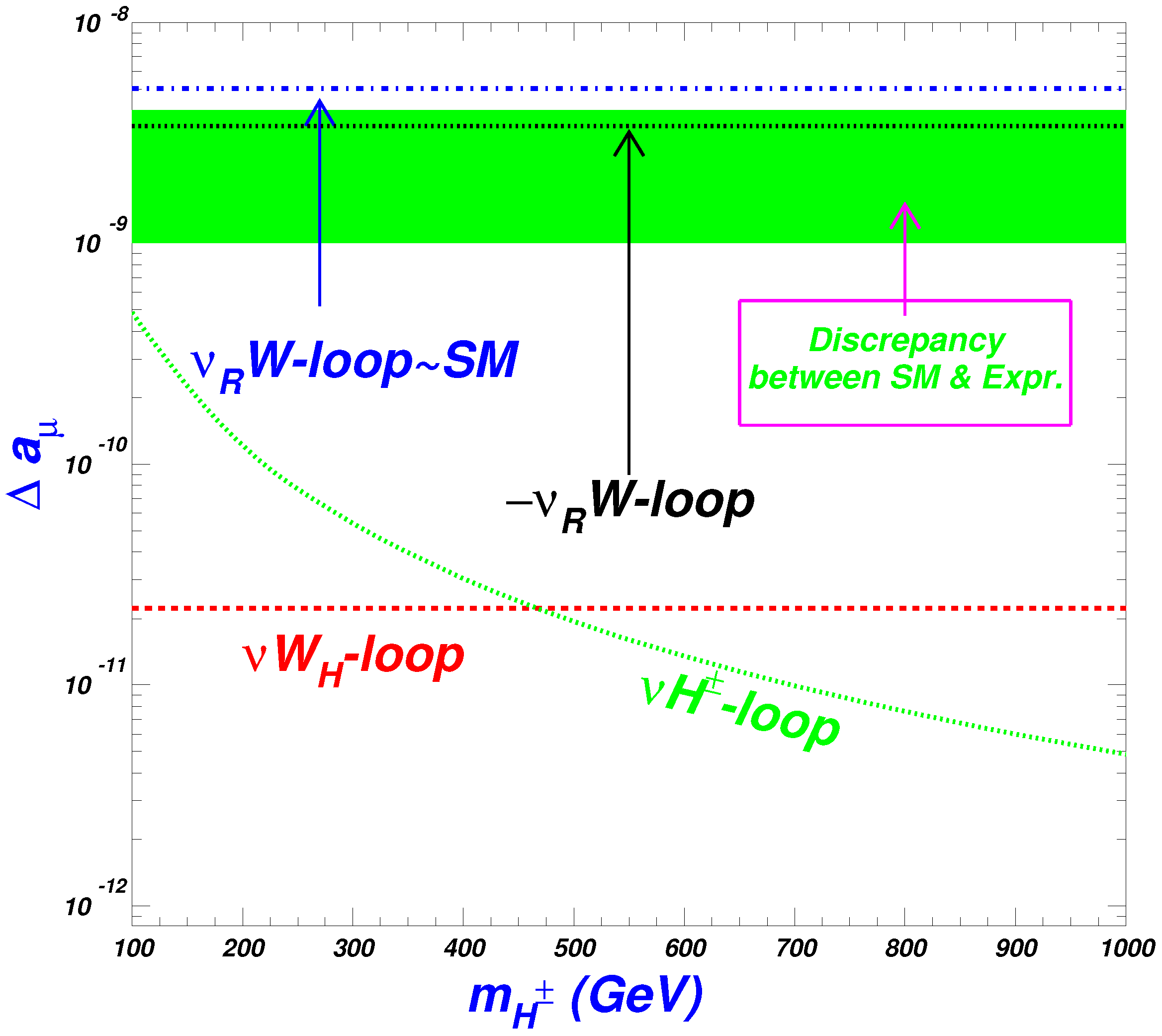
Regarding the top Yukawa $y_t$, at the EW scale, it should be the same as that in the SM, but at the higher scale, each will be different. Since in general, we assume that the top quark is connected to electroweak symmetry breaking and sensitive to new physics models, we scan the top Yukawa $y_t$ from zero to $1.5$ times of the SM top Yukawa $y_t^{SM}$. The heavy-gauge boson couplings to the lepton $V_{\mu }$ is also from zero to $1.5$ times of the SM couplings $V_{\mu }^{SM}$.

From the relationship of the masses of the ordinary neutrino and the right-handed neutrino, $m_{\nu }$∼$\frac{Y_{\mu }^2{v}^2}{m_{{\nu }_R}}$ [20], we can estimate the Yukawa coupling $Y_{\mu }$ is roughly ${10}^{-5}$–${10}^{-3}$ when the right-handed neutrino masses are taken in the order of TeV and the ordinary neutrino masses are assumed as ${10}^{-3}$–${10}^{-1}$ eV. Or, if the right-handed mass $m_{{\nu }_R}$ is free, this relationship may serve as a constraint on $Y_{\mu }$.

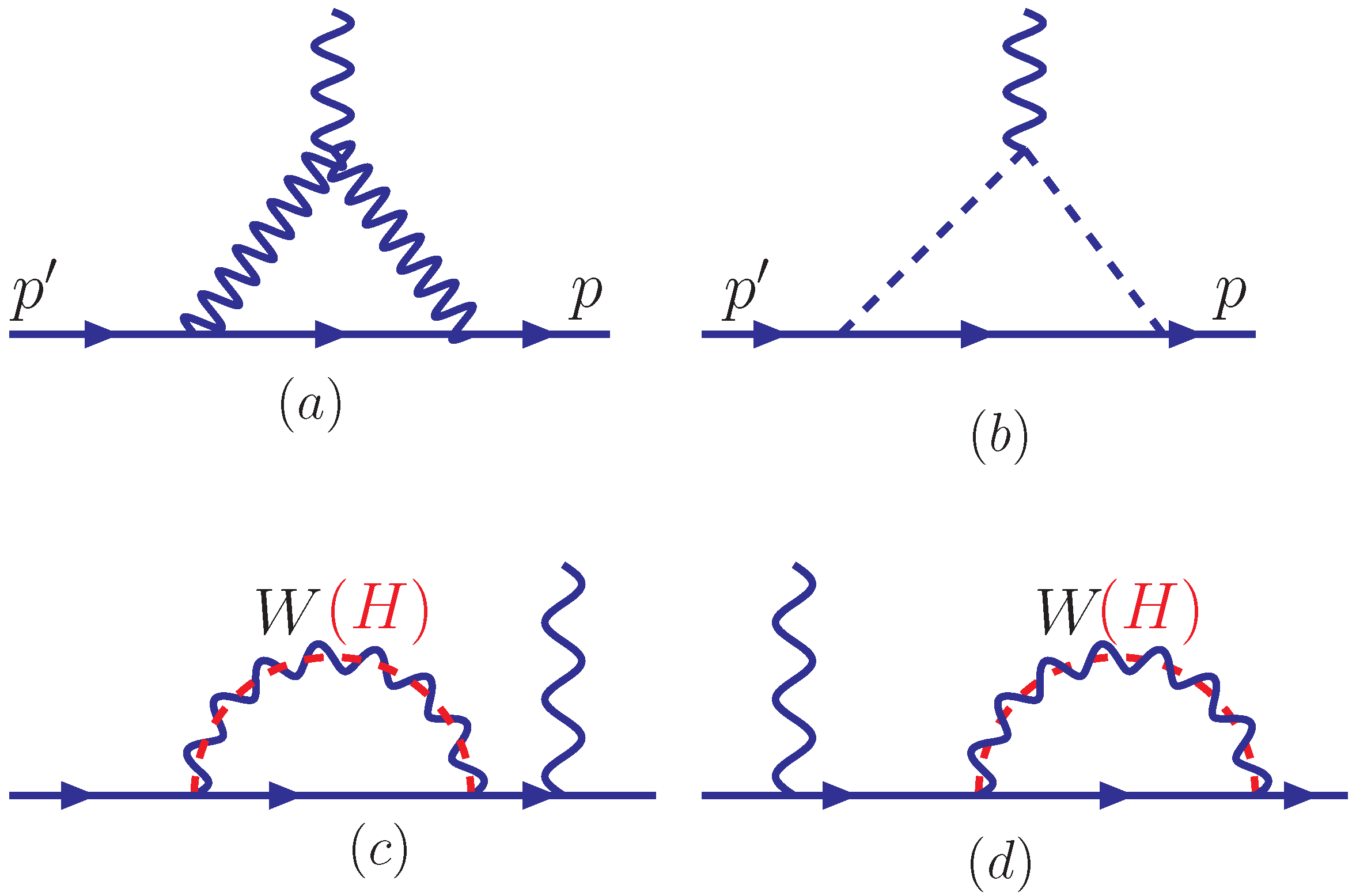
4. The One-Loop Muon Anomalous Magnetic Moment $\mathit{g}-\mathbf{2}$

From the couplings of Equations (10) and (11), one can easily calculate the new contributions to the muon anomalous magnetic moment, which are generated by one-loop diagrams involving the exchange of $W_{\mu }$ gauge boson and charged scalar $H^{\pm }$ with heavy neutrino, as shown in Figure 1.

Please note that the contributions from Figure 1c,d contain self-energy of the fermions, which is proportional to ${\gamma }^{\lambda }$, and they do not contribute to the muon anomalous moment. That is because, when the Lorentz structure is written as the matrix element of the electromagnetic current between incoming and outgoing fermion states of momentum and spin $\{p,s\}$ and $\{p^{\prime },s^{\prime }\}$, respectively,

$$<p,s|J_{\lambda }^{em}|p^{\prime },s^{\prime }>={\overline{\mu }}_e(p,s)\{F_1\left(Q^2\right){\gamma }_{\lambda }+\frac{F_2\left(Q^2\right)}{2m}·\frac{i}{2}[{\gamma }_{\lambda },{\gamma }_{\nu }]·q^{\nu }\}{\mu }_p(p^{\prime },s^{\prime }),$$

(14)

the second term, $F_2\left(0\right)=\frac{g-2}{2}\equiv a_{\mu }$ ($Q=p^{\prime }-p$ ), while the first term, i.e., Figure 1c,d does not contribute the muon anomalous magnetic moment.

The one-loop contribution to the muon anomalous magnetic moment can be written as [83,84,85]:

$$\Delta a_{\mu }^{TH}=\Delta a_{\mu }^{{\nu }_{R}W}+\Delta a_{\mu }^{{\nu }_{R}H}+\Delta a_{\mu }^{\nu H}+\Delta a_{\mu }^{\nu W_H}.$$

(15)

$$\Delta a_{\mu }^{{.}_{\mathrm{R}}\mathrm{W}}\left(1-\mathrm{loop}\right)=V_{\mu }^2\frac{m_{\mu }^2}{8{\pi }^2}{\int }_0^{1}dx\frac{x^2(1+x)-x(1-x)\frac{m_{{\nu }_R}^2}{m_W^2}}{m_W^{2}x+m_{{\nu }_R}^2(1-x)},$$

(16)

$$\Delta a_{\mu }^{.{\mathrm{W}}_{\mathrm{H}}}\left(1-\mathrm{loop}\right)={\left(\frac{g}{\sqrt{2}}\right)}^2\frac{m_{\mu }^2}{8{\pi }^2}{\int }_0^{1}dx\frac{x^2(1+x)}{m_{W_H}^{2}x+m_{\nu }^2(1-x)},$$

(17)

$$\Delta a_{\mu }^{{.}_{\mathrm{R}}\mathrm{H}}\left(1-\mathrm{loop}\right)=Y_{\mu }^2\frac{m_{\mu }^2}{16{\pi }^2}{\int }_0^{1}dx\frac{x^3-x^2}{m_H^{2}x+m_{{\nu }_R}^2(1-x)},$$

(18)

$$\Delta a_{\mu }^{.\mathrm{H}}\left(1-\mathrm{loop}\right)=y_{\mu }^2\frac{m_{\mu }^2}{16{\pi }^2}{\int }_0^{1}dx\frac{x^3-x^2}{m_H^{2}x+m_{\nu }^2(1-x)},$$

(19)

where $\frac{g}{\sqrt{2}}$ is the $W\left(W_H\right)$ boson couplings to the leptons, similar to that in the SM.

Figure 2 shows that the contributions of the charged Higgs, the heavy charged bosons and the heavy neutrino at one-loop level, and we find that the contributions from $\nu W_H,\nu H^{\pm }$ loop are quite small, about ∼${10}^{-11}$, which cannot explain the discrepancy between the experiments and the theoretical prediction. Due to the heavy neutrino mass suppression, the ${\nu }_R{H}^{\pm }$ loop is even smaller, about ${10}^{-31}$, which is too small and does not show in Figure 2.

When $m_{{\nu }_R}$ is very small, the ${\nu }_{R}W$ loop contribution given as Equation (16) is large, just as that in [7,86], $\Delta a_{\mu }^{{.}_{\mathrm{R}}\mathrm{W}}$ approximatively equals to the one-loop contribution predicted by the SM, $\Delta a_{\mu }^{{.}_{\mathrm{R}}\mathrm{W}}\sim {10}^{-9}$. Please note that the contribution is positive. However, in our case, $m_{{\nu }_R}\sim Y_{\mu }^2{v}^2/m_{\nu }\gg m_W$, from Equation (16), the ${\nu }_{R}W$ contribution can be approximately given as $\frac{-V_{\mu }^2{m}_{\mu }^2}{16{\pi }^2{m}_W^2}\sim -{10}^{-9}$, which is negative and widens the discrepancy between theory and experiment. This further constrains the mixing matrix element $V_{\mu }$, which will have to be significantly suppressed. Therefore, in our parameter space, the total contribution of the one-loop contribution is negative, which makes it impossible to arrive at the required order of the experiments.

Therefore, we can conclude that in the twin Higgs models, the one-loop contribution cannot remedy the discrepancy between the experiments and the theoretical calculation. Since in the two-loop Barr–Zee contribution, the large mass ratio of quarks to leptons may surpass the phase suppression compared to that at the one-loop level, and perhaps more parameters contribute to the muon anomalous magnetic moment, it will be of importance to consider the two-loop level calculation.

5. The Analytic Expressions for the Two-Loop Muon $\mathit{g}-\mathbf{2}$ Anomaly and the 125 GeV Higgs Global Fit in TH Models

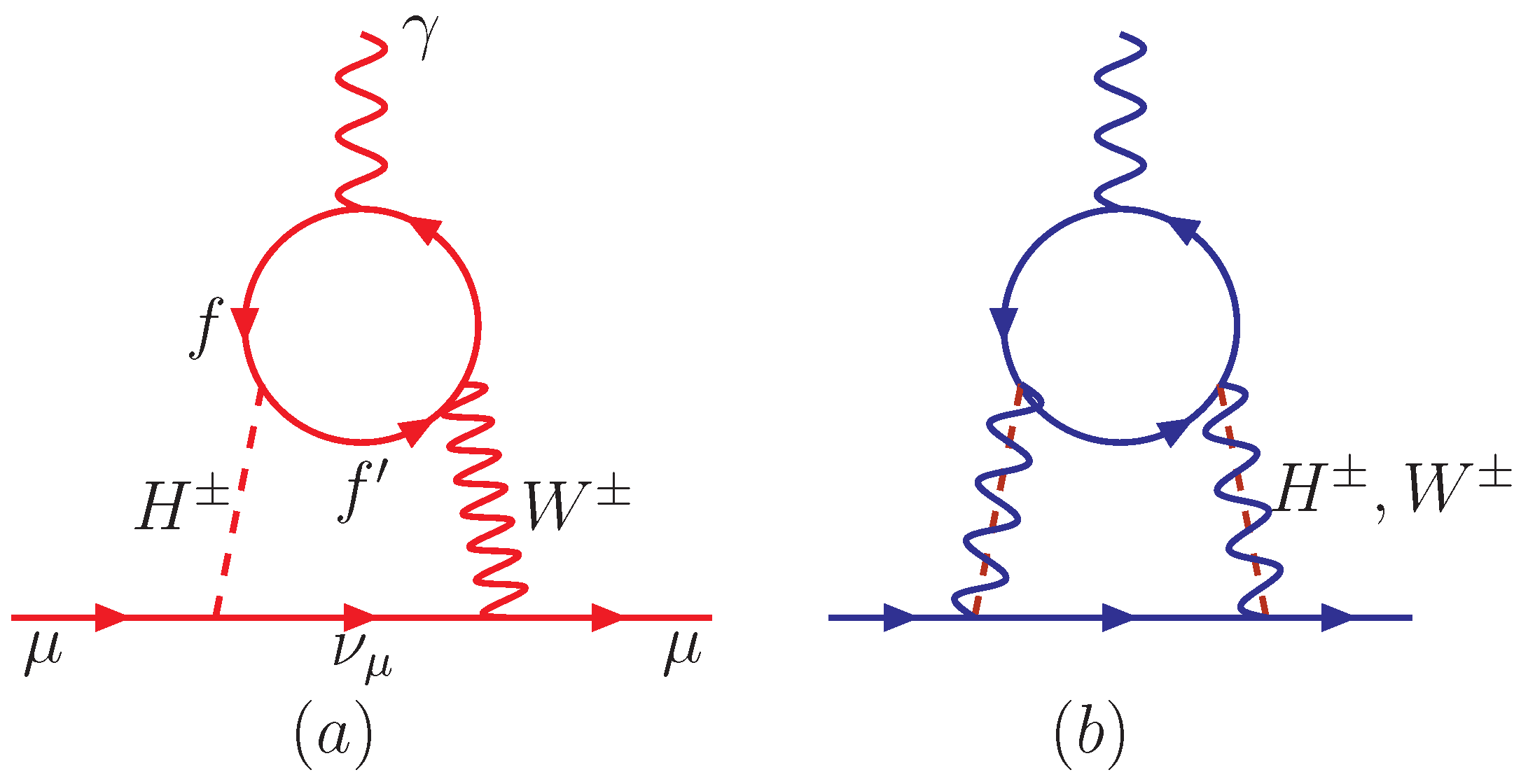
5.1. The Analytic Expressions for Two-Loop Barr–Zee Muon $g-2$

In TH models, the two-loop Barr–Zee muon $g-2$ anomaly contributions are mediated by the charged Higgs $H^{\pm }$ and the gauge boson with the fermions. The large enhancement factor $m_q^2/m_{\mu }^2$ may surpass the loop suppression phase space factor $\alpha /\pi$; therefore, the two-loop contributions could be more important than one-loop ones. Since the couplings $H^0\mu \overline{\mu }$, proportional to $m_{\mu }/v$, is too small to have large contribution in the two-loop diagrams, and due to the discrete symmetry, it is usually difficult to form couplings such as $WZ{H}^{+}$, $W\gamma H^{+}$, $W{h}^0{H}^{+}$ etc., [87], and the heavy-gauge boson mass suppression, we will just consider the diagrams given in Figure 3.

Please note that, in the Barr–Zee two-loop diagrams, there are no two scalars or two $W^{\pm }$ charged bosons connect to the triangle loop simultaneously due to the helicity constraints. Since between the two charged particles in the quark loop, the fermion is the bottom quark, the slash momentum terms must vanish undergoing a single $\gamma$ matrix because of the much smaller mass of the bottom quark compared to the top quark, shown in Figure 3b. Thus, the only contribution comes from Figure 3a.

In Figure 3a, the fermion loop can consist of not only top and bottom quark $ttb$, $bbt$, but also the lepton with the right-handed neutrino $\ell \ell v_R$, since the neutrino mass might be quite large. The Barr–Zee two-loop contribution from quark loop can be written as [11,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103],

$$\begin{array}{ccc}\hfill \Delta a_{\mu }\left(ttb+bbt\right)& =& 4m_{\mu }^2·\frac{g{V}_{tb}}{\sqrt{2}}·\frac{g}{\sqrt{2}}·\frac{1}{512{\pi }^4}\frac{N_t^c}{m_{H^{+}}^2-m_W^2}\hfill \\ & & {\int }_0^{1}dx[Q_{t}x+Q_b(1-x)]\left[G\left(\frac{m_t^2}{m_{H^{+}}^2},\frac{m_b^2}{m_{H^{+}}^2}\right)-G\left(\frac{m_t^2}{m_W^2},\frac{m_b^2}{m_W^2}\right)\right]\hfill \\ & \times & \left({{\Gamma }_{tb}^{H^{+},R}}^{*}{\Gamma }_{{\nu }_{\mu }\mu }^{H^{+}}\right)\left[\frac{m_t}{m_{\mu }}x(1+x)\right]\hfill \end{array}$$

(20)

where ${\Gamma }_{tb}^{H^{+},R}=i{y}_t,{\Gamma }_{\nu \mu }^{H^{+}}=i{y}_{\mu }$ are the couplings of $H^{+}\overline{t}b$ and $H^{+}\overline{\nu }\mu$, respectively, and $P_{R,L}=\frac{1}{2}(1\pm {\gamma }^5)$. The loop function is defined as,

$$\begin{array}{c}\hfill G(r^a,r^b)=\frac{ln\left(\frac{r^{a}x+r^b(1-x)}{x(1-x)}\right)}{x(1-x)-r^{a}x-r^b(1-x)}.\end{array}$$

(21)

For the $\ell \ell {\nu }_R$ loop when the heavy neutrinos enter the loop, the contribution can be obtained by replacing $m_t$, $m_b$, $Q_t$ and $Q_b$ by $m_{{\nu }_R}$, $m_{\ell }$, $Q_{{\nu }_R}=0$ and $Q_{\ell }=-1$, respectively, in Equation (20), which can be written explicitly as

$$\begin{array}{ccc}\hfill \Delta a_{\mu }\left(\ell \ell {\nu }_R\right)& =& 4m_{\mu }^2·\frac{g}{\sqrt{2}}·V_{\mu }·\frac{1}{512{\pi }^4}\frac{1}{m_{H^{+}}^2-m_W^2}\hfill \\ & & {\int }_0^{1}dx{Q}_l(1-x)\left[G\left(\frac{m_{{\nu }_R}^2}{m_{H^{+}}^2},\frac{m_{\ell }^2}{m_{H^{+}}^2}\right)-G\left(\frac{m_{{\nu }_R}^2}{m_W^2},\frac{m_{\ell }^2}{m_W^2}\right)\right]\hfill \\ & \times & \left({{\Gamma }_{{\nu }_R\ell }^{H^{+},R}}^{*}{\Gamma }_{{\nu }_{\mu }\mu }^{H^{+}}\right)\left[\frac{m_{{\nu }_R}}{m_{\mu }}x(1+x)\right]\hfill \end{array}$$

(22)

where ${\Gamma }_{{\nu }_R\ell }^{H^{+},R}=i{Y}_{\mu }$.

5.2. Global Fit of the 125 GeV Higgs

We will perform a global fit to the 125 GeV Higgs signal data and a large number of observables. For the given neutral SM-like scalar-field h and its couplings, the ${\chi }_h^2$ function can be defined as

$$\begin{array}{c}\hfill {\chi }_h^2=\sum _k\frac{{\left({\mu }_k-{\widehat{\mu }}_k\right)}^2}{{\sigma }_k^2},\end{array}$$

(23)

where k runs over the different production(decay) channels considered, and ${\mu }_k$ is the corresponding theoretical predictions for the TH parameters. ${\widehat{\mu }}_k$ and ${\sigma }_k$ denote the measured Higgs signal strengths and their one-sigma errors, respectively, and their choices in this work appear in [104,105,106], though the data and the references listed are not complete.

The Higgs signal strengths, employed in the experimental data on Higgs searches, measure the observable cross-sections compared to the corresponding SM predictions. At the LHC, the SM-like Higgs particle is generated by the following production procedures: gluon fusion ($gg\to H$), vector boson fusion ($q{q}^{\prime }\to q{q}^{\prime }VV\to q{q}^{\prime }H$), associated production with a vector boson ($q{\overline{q}}^{\prime }\to WH/ZH$), and the associated production with a $t\overline{t}$ pair ($q\overline{q}/gg\to t\overline{t}H$). Meanwhile, the Higgs decay channels are $\gamma \gamma$, $Z{Z}^{(*)}$, $W{W}^{(*)}$, $b\overline{b}$ and ${\tau }^{+}{\tau }^{-}$. The expressions of the Higgs signal strengths have been shown in [11] and we will not repeat them here.

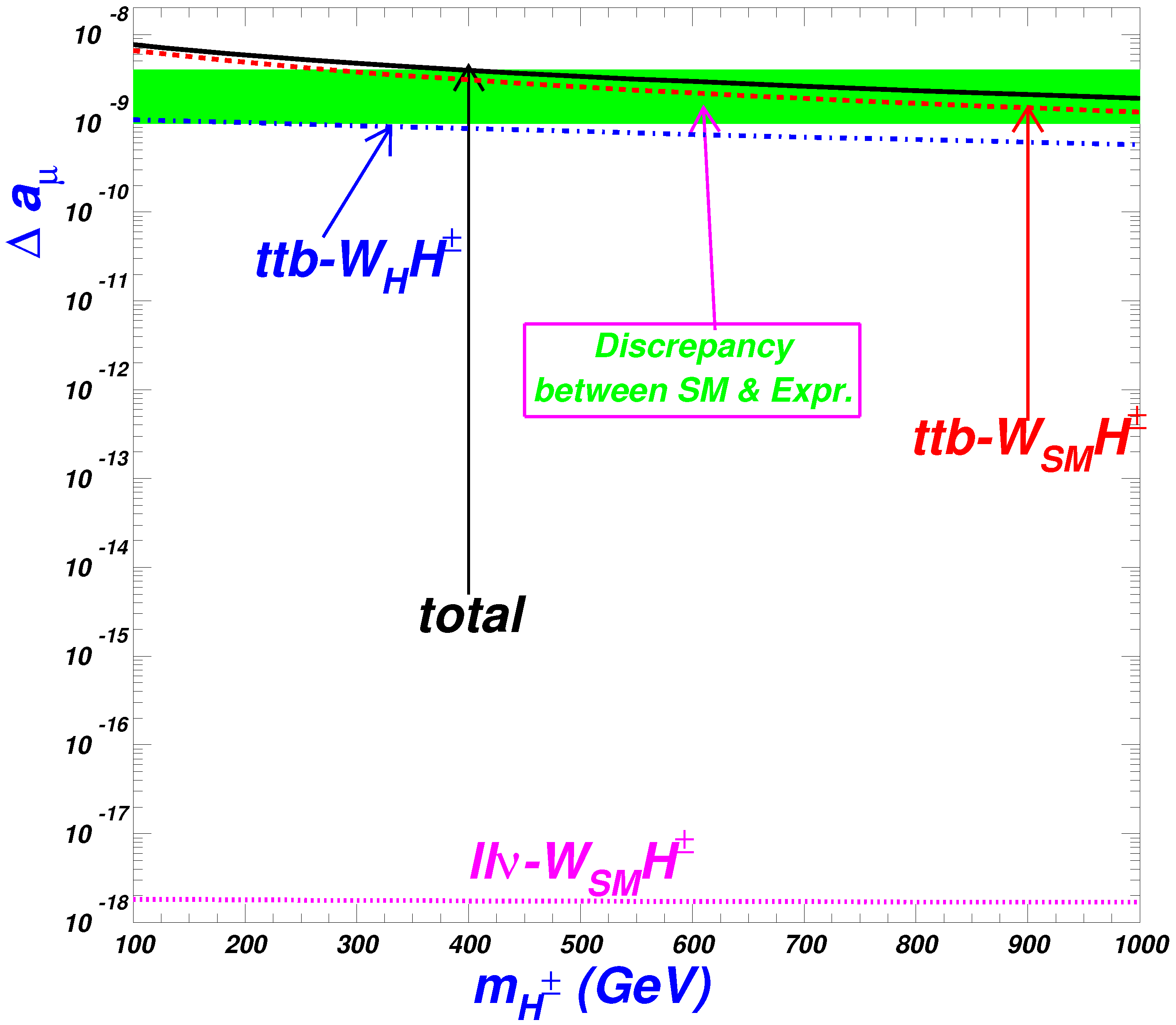
6. The Calculation of the Barr–Zee Diagrams and the Final Total Constraints from the One- and Two-Loop Contribution

Though in Equations (10) and (11), the LFV couplings are induced by the SM gauge bosons, we here still consider the twin, i.e., heavy-gauge bosons, which have the same LFV couplings, but the heavy-gauge bosons are quite heavier, about 1 TeV or more, just as the discussion above.

In Figure 4, we give the comparison of the contribution at the two-loop level between the inner lines of the SM charged gauge bosons and the TH heavy charged boson and that from the right-handed neutrino loop with the SM charged leptons. The green shadow area in the figure shows the discrepancy between the SM and the measurement for the anomalous magnetic moment $\Delta a_{\mu }$.

From Figure 4 we can see the heavy mass of the gauge boson suppressing the contribution, and the contribution is smaller than that of the SM gauge boson, which can be seen from the blue and red curves. We also consider the lepton $\ell \ell {\nu }_R$ loop contribution with the charged Higgs and the SM $W^{\pm }$, which is shown via the bottom curve in Figure 4, and it is much smaller than the other contributions. Hence, the total two-loop contribution comes from not only the SM $W^{\pm }$, but also from the heavy $W_H^{\pm }$, together with both quark loop and lepton loop, and not the same as those in the one-loop, the contributions are all positive in the parameter spaces under consideration.

Please note that the coupling $Y_{\mu }$ is related to the ordinary neutrino masses and the heavy neutrino mass $m_{{\nu }_R}$, just as shown in Section 3 (4), $m_{\nu }$∼$\frac{Y_{\mu }^2{v}^2}{m_{{\nu }_R}}$, or $m_{{\nu }_R}$∼$\frac{Y_{\mu }^2{v}^2}{m_{\nu }}$. Since the upper bound of the heavy neutrino mass is not provided in the experiments, we here just assume the mass is a parameter determined by the coupling $Y_{\mu }$ and the ordinary neutrino mass. With larger couplings and the tiny neutrino mass, the heavy neutrino mass is quite large, so the contribution to the two-loop muon anomalous magnetic moment will be very small due to the mass depression, as shown in Figure 4.

Moreover, from Equation (22) and Figure 4, we know that the contribution from the $\ell \ell {\nu }_R$ loop is so small that the only coupling $Y_{\mu }$ related to it is not important in determining the $g-2$ calculation, and at the same time, $Y_{\mu }$ has nothing to do with other processes. Therefore, we here take it as a fixed value: $Y_{\mu }=0.004$.

However, the contributions in Figure 4 are given for the parameters only varying with the charged Higgs mass and without including one-loop ones. Therefore, in Figure 5, we will show the tendency of the total contribution, including not only at the two-loop but also at the one-loop level, along with the other parameters. From Figure 5 we can see that $\Delta a_{\mu }$ increases with the increasing couplings $y_{\mu }$ and $y_t$ but decreases with the increasing $V_{\mu }$, which is because the largest one-loop process to $\Delta a_{\mu }$ is from ${\nu }_{R}W$ loop with a negative value, and when $V_{\mu }$ increases, it will be larger towards the negative direction. Under current parameter conditions, when $V_{\mu }=0.7$, the total contribution begins to be positive, and the experiments require $V_{\mu }$ in the range of $0.47\lesssim V_{\mu }\lesssim 0.66$. For $y_{\mu }$ and $y_t$, to arrive at the discrepancy level, relatively large values are required: $y_{\mu }\gtrsim 0.52$ and $0.43\lesssim y_t\lesssim 0.65$. From Figure 4 and Figure 5, we can see that the total contribution can arrive at the required range in some parameter spaces.

Next, we scan the anomalous magnetic moment and the Higgs global fit by taking 10,000 random points, so the more the points are left, the higher the possibility of the event is to be probed in the experiments. We restate the parameter ranges: $100\le m_{H^{\pm }}\le 1000$ GeV, $0\le y_t\le 1.5$, $0\le V_{\mu }\le 1.2$ and $0\le y_{\mu }\le 0.5$.

Since ${\chi }_h^2$ fits to the 125 GeV Higgs decay signal data, and we here assume that the neutral Higgs in TH models does not mix with the charged Higgs, the masses of the charged Higgs and the heavy neutrinos contribute little to the Higgs strength ${\chi }_h^2$, and at the same time, they will hardly be constricted by it, too. On the other hand, due to the quite large top mass, the top Yukawa coupling contributes to the ${\chi }_h^2$ value much more than those from the others. Therefore, in Figure 6, we will show the surviving samples only on the planes of the couplings: $y_{\mu }\sim V_{\mu }$, $y_t\sim y_{\mu }$ and $y_t\sim V_{\mu }$, for the Higgs strengthen in the 3$\sigma$ confidence level. Figure 6 shows that ${\chi }_h^2$ favors large $y_t$, while it is not sensitive to the other couplings.

In Figure 7, we further impose the two-loop $g-2$ anomaly constraints on the surviving sample points of ${\chi }_h^2$ within 3$\sigma$ possibility on the planes of $y_t\sim m_{H^{\pm }}$, $y_t\sim V_{\mu }$, $V_{\mu }\sim y_{\mu }$, and $y_t\sim y_{\mu }$. From the first figure in Figure 7, we can see that the charged Higgs mass is not constrained too much, but the surviving samples favor a larger $y_t$.

We also see from Equation (20) that the $g-2$ anomaly varies with the top Yukawa coupling $y_t$, so coupling $y_t$ should matter a lot, which can be seen from the other figures in Figure 7. This relevance will constrain $y_t$ greatly, and it can grossly read as $0.4\lesssim y_t\lesssim 0.9$. Another parameter which receives strong constraint is $y_{\mu }$ in TH models, and from Equation (20) we know if the quark loops contribute greatly that the $g-2$ anomaly is also relevant to the parameter $y_{\mu }$ and favors a large value of $y_{\mu }$. Therefore, in Figure 7 we give the allowed ranges of both with all the constraints, from which we can grossly obtain $0.12\lesssim y_{\mu }\lesssim 0.4$. However, the two-loop $g-2$ anomaly is not sensitive to the coupling $V_{\mu }$, and it is mainly contributed by a TTB-induced loop, given in Equation (20), which can be seen in Figure 4. Therefore, even with the negative one-loop ${\nu }_{R}W$-mediated process contribution, the total $\Delta a_{\mu }$ does not constrain so stringently as that in the second diagram of Figure 5: $0.47\lesssim V_{\mu }\lesssim 0.66$. For example, in the the right-upper diagram of Figure 7, $V_{\mu }$ can even be larger than 1 in extreme cases.

7. Conclusions

We consider the charged Higgs contribution to the muon $g-2$ anomaly in TH models with the joint constraints of Higgs global fit data. After imposing various relevant theoretical and experimental constraints, we perform the scan over the parameter space of this model to identify the ranges in favor of the muon $g-2$ explanation. We find that the muon $g-2$ anomaly can be explained in TH models in some parameter spaces. The Higgs direct search limits from LHC contribute most largely to all the constraints. With the joint constraints from the 125 GeV Higgs signal data, the precision electroweak data, and the leptonic decay, we find that the muon $g-2$ anomaly constrains the coupling of charged Higgs to the lepton $y_{\mu }$, the top Yukawa $y_t$, and the heavy-gauge boson coupling to the lepton $V_{\mu }$ roughly as $0.12\lesssim y_{\mu }\lesssim 0.4$, $0.4\lesssim y_t\lesssim 0.9$, and $0.47\lesssim V_{\mu }\lesssim 1$.