Analogous Hawking Effect: S-Matrix and Thermofield Dynamics

Abstract

We consider the full S-matrix in the scattering giving rise to analogous Hawking radiation in dispersive media. We show the general structure of the scattering in the weak dispersion approximation and discuss some unnoticed features of the primary process, with a possible generalization of the phenomenology of the Hawking effect. In particular, we stress that the Hawking particle and its antiparticle partner a priori could also be produced with different rates. We provide a general parameterization of the S-matrix, adopting the Iwasawa decomposition for the matrix itself. Then, we assume that a perturbative structure in a suitable sense is allowed and display the corresponding expansion. In connection with the general structure of the S-matrix at the leading order, we also consider the thermofield dynamics (TFD) framework and show that the TFD picture is still available, with a doubling of the degrees of freedom emerging in a natural way, as for the astrophysical black hole case. Furthermore, we show that particles on the thermal vacuum can be identified with real particles appearing in the scattering.

1. Introduction

In [1,2] we proposed a fourth-order ordinary differential equation as a master equation allowing to deal with the analogous Hawking effect in condensed matter systems in a systematic way, in the approximation of weak dispersive effects. Systems between the most studied and relevant ones, such as Bose–Einstein condensates (BEC), dielectric media, and water are encompassed in our picture. The only change is in the identification of the weak dispersion parameter $ϵ$ appearing in the master equation.

Herein, we take into consideration the full structure of the S-matrix, which is associated with the analogous Hawking effect in condensed matter. The S-matrix has been discussed previously in the literature, see, e.g., [3,4,5,6,7], for BEC, water, and for the Corley model [8]. In particular, in a general picture encompassing the previously discussed ones, we show that the S-matrix, at the leading order in $ϵ$, is very simplified with respect to the original complexity of the complete scattering process, due to the fact that two modes participating in the scattering substantially decouple, at least as far as the primary process, i.e., the pair-creation process, is concerned (they still can interact at the level of subsequent scattering with respect to the primary process). The manifest advantage of the proposed framework [1,2] consists in the fact that a unified picture for many interesting cases occurring in the physical literature can be provided, and this is true also at the level of the structure of the S-matrix. Moreover, by our analysis it is also clear that, whenever a direct participation of the aforementioned modes in the primary process would occur, one could maintain thermality for the spectrum of the particles detected at infinity. However, there would occur a difference in the number of created particles, to be identified with the Hawking particles, and the would be Hawking partners (would-be anti-particles, where “would be” stresses their possible different production ratio w.r.t. particles), and then a generalization of the Hawking process would occur, with a thermal spectrum but separate behavior between the Hawking particle and its would-be partner. This is also a feature that could be a very interesting subject of experimental verification. In particular, a joint measurement of the Hawking particle could represent in any case a corroboration of the general picture for the analog Hawking effect.

Further, we take into account a series expansion of the S-matrix, as we are interested in looking for corrections to the leading structure S-matrix due to subleading processes. After a naive approach, we adopt a rigorous picture involving the Iwasawa decomposition of the unitary group associated with the S-matrix itself, by means of which we can corroborate the aforementioned naive approach. The proposed Iwasawa decomposition represents a novel tool in the analysis of the S-matrix and will be the subject of further analysis.

As an interesting consequence of the above-mentioned picture involving decoupling of the two modes, we show that also in the analog Hawking effect there exists still the possibility to associate a thermofield dynamics framework for the primary process. One can again show that the doubling of the number of degrees of freedom, with the introduction of a (would-be fictitious) Hilbert space, arises in a natural way, as in the case of astrophysical black holes, as Israel pointed out [9]. Furthermore, we show that particles over the thermal vacuum can also be identified with real particles appearing in the scattering and detectable in the final scattering states, as far as the white hole situation is concerned. For the black hole case, they still appear as ingoing states, and we point out that experiments involving stimulated Hawking radiation in the black hole case have been performed in [10].

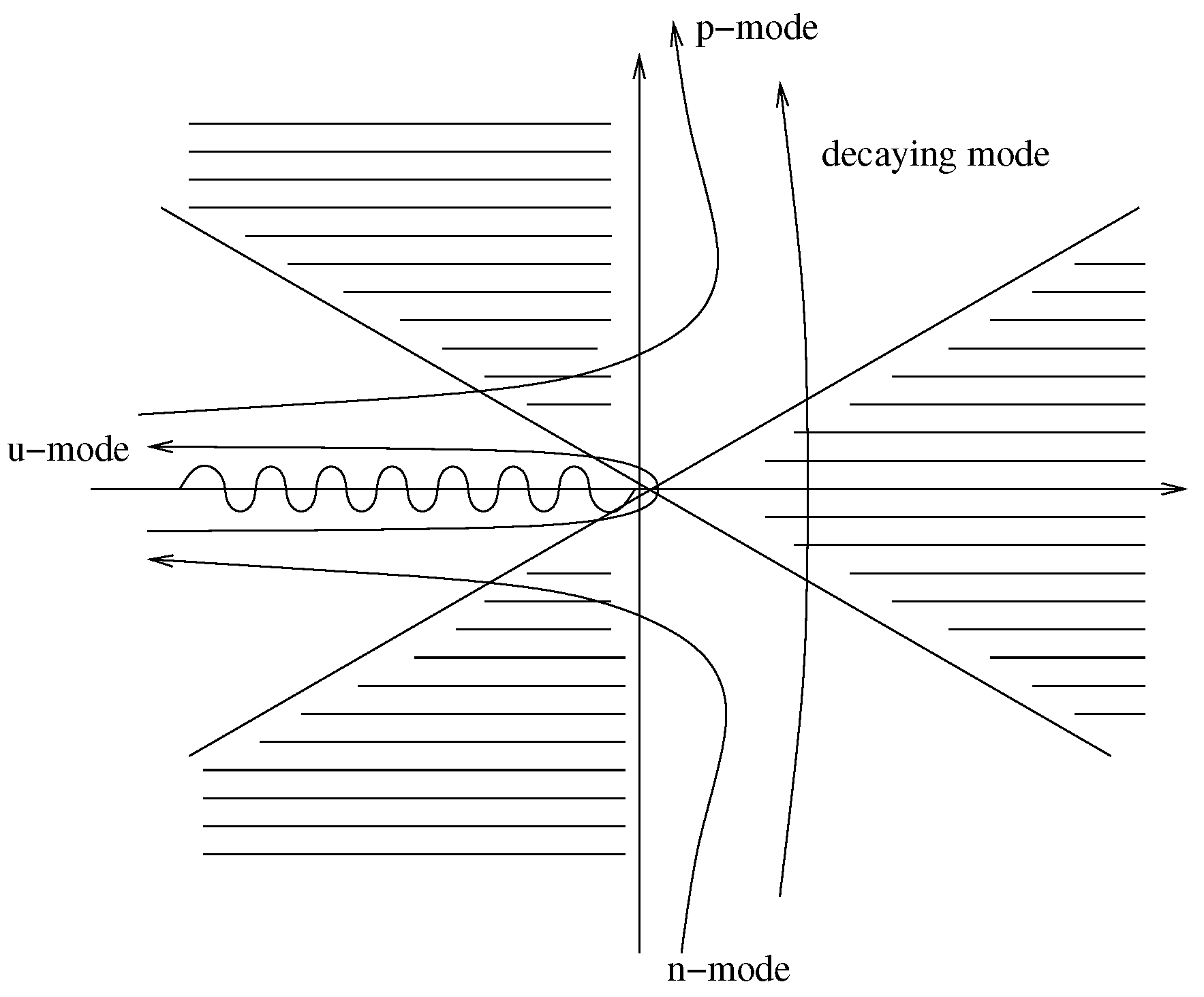
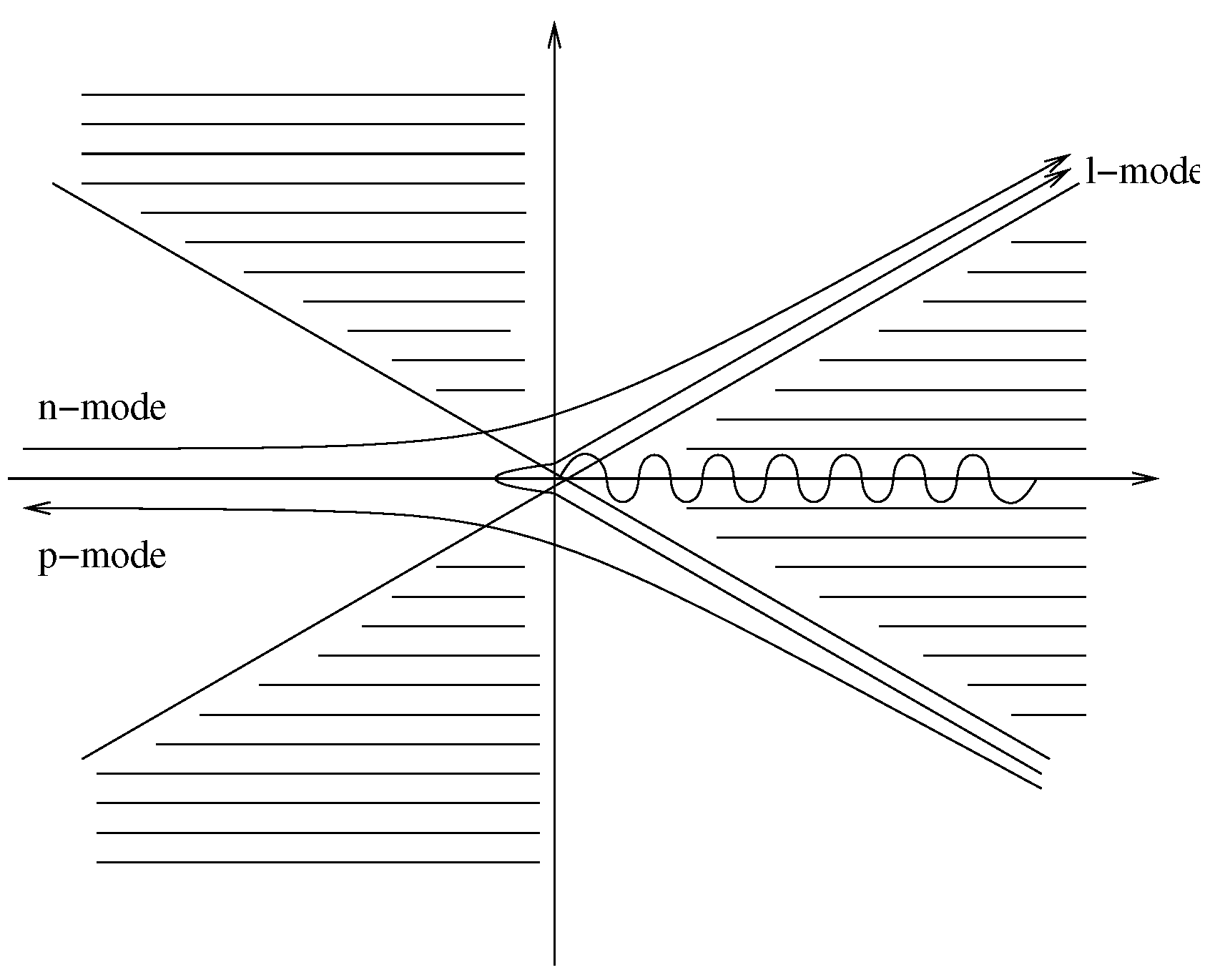
2. The Master Equation: An Orr–Sommerfeld Type Fourth-Order Equation

Three significant cases of wave equations in dispersive analogue gravity can be reconduced to the equation

$${ϵ}^2\frac{d^4\mathrm{\Phi }}{d{x}^4}\pm \left[p_3(x,ϵ)\frac{d^2\mathrm{\Phi }}{d{x}^2}+p_2(x,ϵ)\frac{d\mathrm{\Phi }}{dx}+p_1(x,ϵ)\mathrm{\Phi }\right]=0,$$

(1)

where the upper sign occurs in the case of subluminal dispersion and the lower one in the case of superluminal dispersion. The latter case is considered in Nishimoto’s works (see, e.g., [11] and references therein). Furthermore,

$$p_i(x,ϵ)=\sum _{n=0}^{\infty }{p}_{in}\left(x\right){ϵ}^n,$$

(2)

is assumed. As $ϵ\to 0$, one finds the reduced equation

$$p_{30}\left(x\right)\frac{d^2\mathrm{\Phi }}{d{x}^2}+p_{20}\left(x\right)\frac{d\mathrm{\Phi }}{dx}+p_{10}\left(x\right)\mathrm{\Phi }=0.$$

(3)

Solutions of

$$p_{30}\left(x\right)=0$$

(4)

define the turning points (TPs) of the equation, and in the analysis of the reduced equation, the behavior of solutions in the neighborhood of the TPs is of utmost relevance for the scattering problem we mean to delve into. In the following, we limit ourselves to the case of a single TP, which can be identified with $x=0$ without loss of generality. In [11], it is assumed that the reduced equation displays a Fuchsian singularity at the TP (nothing actually prevents the general equation in itself to admit a regular behavior).

It can be shown [11] that near the TP $x=a$ the original equation is replaced by the fourth-order differential equation

$$\frac{d^{4}w}{d{z}^4}\pm \left(z\frac{d^{2}w}{d{z}^2}+\lambda \frac{dw}{dz}\right)=0,$$

(5)

where, as discussed at length in [1], $w\left(z\right)$ represents the (rescaled [1]) wave-function in the near horizon approximation, to be then matched in the linear region, with WKB solutions that hold far from the turning point. We refer the reader to [1] for further details. In (5), the upper sign is for the subluminal case, and the lower one is for the superluminal one, and

$$z={\left(p_{30}^{\prime }\left(a\right)\right)}^{1/3}{ϵ}^{-2/3}(x-a),$$

(6)

and

$$\lambda =\frac{p_{20}\left(a\right)}{p_{30}^{\prime }\left(a\right)}.$$

(7)

Solutions to Equation (5) are found by means of Laplace integrals

$$w_j\left(z\right)=\frac{1}{2\pi i}{\int }_{C_j}dt{t}^{\lambda -2}exp(zt\pm \frac{1}{3}{t}^3),$$

(8)

with a suitable choice for the paths $C_j$ in the complex t-plane. Of course, there is also a constant solution, which appears to be a Dirac delta in the space of the Laplace transform. This further solution is fundamental in order to obtain a complete basis for the scattering problem also in the region near the TP (i.e., near the horizon). As we discussed in [1,2], Equation (5) is universal in form and is at the root of the analogous Hawking effect in dispersive media, as far as they are governed by the above Orr–Sommerfeld-like equation. In the following, we shall limit ourselves to the explicit discussion of the subluminal case. For the superluminal one, we refer the reader to [2] for further details. See also the following section. For the specific case of dielectric media, see also [12].

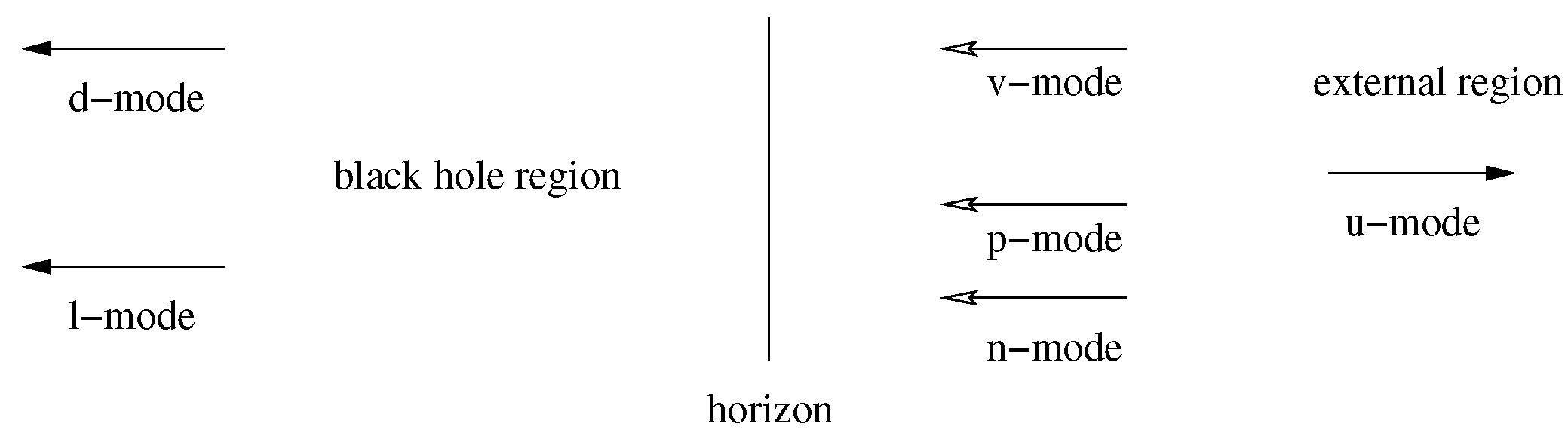
3. The $\mathbf{S}$-Matrix in Presence of Dispersion

As known, the spectator mode v does not participate in the process at the turning point, at least as far as the weak dispersion limit $0<ϵ\ll 1$ is assumed, where $ϵ$ is the parameter involved in the weak dispersion approximation, with $ϵ=0$ indicating the absence of dispersion. One may construct the straddling mode, which is obtained by analytic continuation of the Hawking mode in the black hole region, to be identified with the l-mode. The analytic continuation is unique and involves also the choice of the branch, i.e., of the sheet of the Riemannian surface related to the logarithmic branch point associated with the solutions of the differential equation governing the scattering process.

To be more precise: let us first individuate the OUT modes of the scattering, and in particular let us call the u-mode the Hawking mode in the external region, the l-mode its partner in the black hole region, and d-mode the (regular) mode again in the black hole region. The l-mode has a negative norm (antiparticle). As far as the IN modes are concerned, let us call the p-mode and the n-mode the high wave-number modes entering the black hole, where the n-mode is a negative norm one. Last, but not least, we call v-mode the (regular) mode entering the black hole. See Figure 1 for a pictorial representation.

As we have discussed in [1,2], at least at the leading order in the weak dispersion approximation, the v-mode substantially decouples from the other ones, leaving a very simple structure for the S-matrix, which will be discussed in the following subsection.

3.1. The Complete S-Matrix

The following scattering operator is taken into account in literature (see, e.g., [6] for the subluminal case): if one considers as $IN$-modes the ones moving towards the TP and as $OUT$-modes the ones moving towards infinity (i.e., $x\to \pm \infty$), one may write

$${\mathrm{\Phi }}^{OUT}=S{\mathrm{\Phi }}^{IN}$$

(9)

where

$${\mathrm{\Phi }}^{IN}:=\left(\begin{array}{c}{\varphi }_p\\ {\varphi }_n\\ {\varphi }_v\end{array}\right),$$

(10)

and

$${\mathrm{\Phi }}^{OUT}:=\left(\begin{array}{c}{\varphi }_u\\ {\varphi }_l\\ {\varphi }_d\end{array}\right).$$

(11)

One has

$$S=\left(\begin{array}{ccc}{\sigma }_{up}& {\sigma }_{un}& {\sigma }_{uv}\\ {\sigma }_{lp}& {\sigma }_{ln}& {\sigma }_{lv}\\ {\sigma }_{dp}& {\sigma }_{dn}& {\sigma }_{dv}\end{array}\right).$$

(12)

In order to allow a better visualization of the overall process, we represent schematically in Figure 1 the modes participating to the scattering. In particular, we display the subluminal case for the black hole scattering. The IN modes are traveling towards the horizon, whereas the OUT ones are traveling towards the asymptotic regions ($x\to \infty$ in the asymptotic external region and $x\to -\infty$ in the deep black hole region). In the superluminal case, the only change occurring is that the p-mode and the n-mode travel towards the horizon from the black hole region.

One obtains, by taking into account that $S\in U(1,-1,1)$,

$$\begin{array}{ccc}& & |{\sigma }_{up}{|}^2-|{\sigma }_{un}{|}^2+{\left|{\sigma }_{uv}\right|}^2=1,\hfill \end{array}$$

(13)

$$\begin{array}{ccc}& & |{\sigma }_{lp}{|}^2-|{\sigma }_{ln}{|}^2+{\left|{\sigma }_{lv}\right|}^2=-1,\hfill \end{array}$$

(14)

$$\begin{array}{ccc}& & |{\sigma }_{dp}{|}^2-|{\sigma }_{dn}{|}^2+{\left|{\sigma }_{dv}\right|}^2=1.\hfill \end{array}$$

(15)

The above formulas amount to current conservations. As it is evident, there are three current conservations occurring for the processes at hand. The first formula amounts to the current conservation (13) for the Hawking process. As discussed in [1,2], in the near-horizon approximation one can individuate for the Hawking process a diagram in the Laplace transform space where the particles involved in the aforementioned current conservation appear. One should expect that also for the other processes involved in the other two current conservations where analogous diagrams can be drawn. As we noticed in [1], for the Hawking process the v-mode is not enabled to participate in the process directly, i.e., at the level of the near-horizon process. For the sake of completeness, we also present in Figure 2 the diagram involved in the Hawking process in the subluminal case, which was called Corley’s diagram in [1]. See [8] and also [4,13]. For the superluminal case, there are only little changes. See [2,4,8,13].

For the Hawking mode at frequency $\omega$, one obtains (cf. [1])

$$w_u\left(z\right)\simeq -\frac{1}{i\pi }{\left|z\right|}^{i\frac{\omega }{k}}\mathrm{\Gamma }\left(-i\frac{\omega }{\kappa }\right)sinh\left(\frac{\pi \omega }{\kappa }\right),$$

(16)

where $\kappa$ corresponds to the surface gravity for the analogous black hole one is considering (see [1,2]), whereas for the n-mode and the p-mode one has [1]

$$\begin{array}{cc}\hfill w_p\left(z\right)\simeq & \frac{1}{2\sqrt{\pi }}{e}^{-\frac{3}{4}\pi i}{e}^{\frac{\pi \omega }{2\kappa }}{\left|z\right|}^{-\frac{i\omega }{2\kappa }-\frac{3}{4}}{e}^{i\frac{2}{3}{\left|z\right|}^{3/2}},\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill w_n\left(z\right)\simeq & \frac{1}{2\sqrt{\pi }}{e}^{\frac{1}{4}\pi i}{e}^{-\frac{\pi \omega }{2\kappa }}{\left|z\right|}^{-\frac{i\omega }{2\kappa }-\frac{3}{4}}{e}^{-i\frac{2}{3}{\left|z\right|}^{3/2}}.\hfill \end{array}$$

(18)

3.2. The Hawking Partner

One may obtain the Hawking partner by choosing a suitable analytical continuation for $x<0$. It turns out that, by choosing the branch where $-1=e^{-i\pi }$, for the further solution one obtains

$$w_l\left(z\right):\simeq -\frac{1}{i\pi }{e}^{\pi \frac{\omega }{\kappa }}{z}^{i\frac{\omega }{k}}\mathrm{\Gamma }\left(-i\frac{\omega }{\kappa }\right)sinh\left(\frac{\pi \omega }{\kappa }\right).$$

(19)

As to the latter mode, the second line (14) represents the process involving the Hawking partner, i.e., the l-mode, which is specular with respect to the one for the Hawking particle (u-mode). As to the associated diagram, there are some subtleties that can be suitably pointed out. Of course, as the number of Hawking modes can be obtained by considering the ratio

$$|{\beta }_{\omega }{|}^2:=\frac{|J_x^n|}{|J_x^u|},$$

(20)

for the l-mode, to be identified with the Hawking partner, one must get

$$|{\beta }_{\omega }^{partner}{|}^2:=\frac{|J_x^{npartner}|}{|J_x^l|},$$

(21)

and this expression must coincide with the former one, if the identification is correct.

According to the discussion in [13], in order to maintain the same ratio between the two currents in the two latest equations, it is necessary to exchange the roles of the n-mode and the p-mode, and this can be obtained by shifting the cut on the positive real axis. See Figure 3.

We follow a different strategy, as we maintain the identification of the Hawking partner with the mode that is obtained by analytic continuation at $z<0$ from the Hawking mode, as indicated above [1] (where we chose $-1=e^{-i\pi }$). Being an antiparticle, its relation is with the conjugate solutions corresponding to the p-mode and to the n-mode (so that the former is in its antiparticle state and the latter in the particle one). Then, one obtains

$$\begin{array}{cc}\hfill w_p^{*}\left(z\right)\propto & e^{-\frac{\pi \omega }{2\kappa }}{\left|z\right|}^{\frac{i\omega }{2\kappa }-\frac{3}{4}}{e}^{i\frac{2}{3}{\left|z\right|}^{3/2}},\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill w_n^{*}\left(z\right)\propto & e^{\frac{\pi \omega }{2\kappa }}{\left|z\right|}^{\frac{i\omega }{2\kappa }-\frac{3}{4}}{e}^{-i\frac{2}{3}{\left|z\right|}^{3/2}}.\hfill \end{array}$$

(23)

As a consequence, one is able to maintain the same ratio for (20) and for (21).

We can also obtain the same result with a different choice. It is straightforward to show that the l-mode can be obtained simply by taking into account a different leaf of the logarithm $log\left(z\right)$ (or, equivalently of the power function $z^a$, with a being non-rational):

$$log\left(z\right)=log\left|z\right|+iarg\left(z\right)+i2\pi m,m\in \mathbb{Z}.$$

(24)

The principal branch is given by $m=0$. Let us consider the branch $m=-1$. We check if the same Corley diagram as in Figure 2, but this time with the path around the cut representing the Hawking particle with $x<0$, can represent the right physical situation, now on the branch $m=-1$. This time, we choose $-1=e^{i\pi }$, and it is easy to show that we get again (23) for the Hawking partner. What happens in the case of the p-mode and n-mode? They coincide with the ones indicated in (22) and (23), respectively, and then the ratio in (20) and (21) is the same. From the physical point of view, one would wonder if there is the necessity to pass to the different leaf as we did. In a certain sense, given that in the non-dispersive Hawking process the Hawking particle and its partner are pair-created, one would expect the same diagram for both the modes in the dispersive case, at least as far as u-modes and l-modes can be considered as the partners of a pair. This gives a nice support to the picture involving the $m=-1$ branch. At the same time, one can also interpret the particles appearing in that branch as belonging to the would-be fictitious Hilbert space involved in the TFD picture of the phenomenon. See also the following section.

3.3. Generalized Hawking Effect in Analogue Gravity

There is also a nice consequence to be immediately pointed out: let us write the number of created particles for the two aforementioned cases, by taking into account that the signal of thermality for the Hawking process is in general assumed to be given by

$$|{\sigma }_{up}{|}^2=exp\left({\beta }_h\omega \right){\left|{\sigma }_{un}\right|}^2,$$

(25)

where ${\beta }_h:=2\pi /\kappa$ is the inverse of the analogous Hawking temperature, and, analogously, also for the Hawking partner one must expect

$$|{\sigma }_{ln}{|}^2=exp\left({\beta }_h\omega \right){\left|{\sigma }_{lp}\right|}^2.$$

(26)

One obtains

$$\begin{array}{ccc}\hfill |{\sigma }_{un}{|}^2& =& \frac{1-|{\sigma }_{uv}{|}^2}{exp\left({\beta }_h\omega \right)-1},\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill |{\sigma }_{lp}{|}^2& =& \frac{1+|{\sigma }_{lv}{|}^2}{exp\left({\beta }_h\omega \right)-1},\hfill \end{array}$$

(28)

respectively. A first interesting consequence is that, at the level of particle creation, the identification of the l-mode as the Hawking partner, which is then created at the same rate as the Hawking mode, requires that

$${\sigma }_{uv}=0={\sigma }_{lv},$$

(29)

at least for what concerns the primary process, i.e., we mean the process of pair-creation regardless of any subsequent scattering depleting the flux of the particles arriving at infinity: It might happen that subsequent scattering is able to deplete the flux of Hawking particles at infinity, still leaving unaltered the above balance for the primary pair-creation process.

This is a very interesting consequence of the overall picture concerning the analogous Hawking effect in dispersive media. Indeed, the above considerations are model-independent, as they hold true in general for a dispersion relation like the one emerging for any model that is governed by a fourth-order ordinary differential equation, and, as far as (25) and (26) are assumed to be implemented, as it is commonly done at least in the weak dispersion approximation, any deviation from pure thermality at the level of the primary process would clearly be of hindrance to the identification of the l-mode as the Hawking partner, as a different rate of creation would occur. To some extent, this is not a tricky problem, as the thermality one is interested in would still be ensured. However, it is remarkable that one should also stress that a process where the aforementioned difference in the rate of particle creation occurs would be a generalized Hawking effect. It is remarkable also that the Hawking effect discussed, e.g., in [14,15] is (probably?) to be ascribed to the latter generalization, as a grey-body factor arises at the level of the primary process.

3.4. The Third Process

One has further interesting consequences for the third process for the third current. Additionally, the d-mode cannot participate in the process (it corresponds to the constant solution in the near-horizon approximation [1]), as well as the v-mode itself. There is no chance to draw a diagram involving also the modes $p,n$ involved in the third current conservation. As a consequence, one must also find at the leading order

$${\sigma }_{dp}=0={\sigma }_{dn},$$

(30)

which implies also

$$|{\sigma }_{dv}|=1.$$

(31)

3.5. The S-Matrix

As a consequence of the weak dispersion ansatz discussed in [1], one obtains at the leading order in $ϵ$ a trivial decoupling of the S-matrix:

$$S=\left(\begin{array}{ccc}{\sigma }_{up}& {\sigma }_{un}& 0\\ {\sigma }_{lp}& {\sigma }_{ln}& 0\\ 0& 0& 1\end{array}\right).$$

(32)

It is easy to show that,

$$|{\sigma }_{up}{|}^2=exp\left({\beta }_h\omega \right)|{\sigma }_{un}{|}^2=:{\left|{\alpha }_{\omega }\right|}^2,$$

(33)

and then, at the leading order,

$$|{\sigma }_{un}{|}^2=\frac{1}{exp\left({\beta }_h\omega \right)-1}=:{\left|{\beta }_{\omega }\right|}^2.$$

(34)

Analogously, one finds

$$|{\sigma }_{ln}{|}^2=exp\left({\beta }_h\omega \right)|{\sigma }_{lp}{|}^2={\left|{\alpha }_{\omega }\right|}^2,$$

(35)

and then, at the leading order,

$$|{\sigma }_{lp}{|}^2=\frac{1}{exp\left({\beta }_h\omega \right)-1}={\left|{\beta }_{\omega }\right|}^2.$$

(36)

As already noticed in the literature, the above S-matrix satisfies the equation

$$S^{†}US=U=SU{S}^{†},$$

(37)

where

$$U=\mathrm{diag}(1,-1,1).$$

(38)

This condition arises from the following considerations: we are actually considering the Bogoliubov transformation $\mathcal{B}$ from the initial scattering state to the final one. As is well-known (see, e.g., [16,17]) in the case of a scalar field one has

$$\mathcal{B}q{\mathcal{B}}^{-1}={\mathcal{B}}^{-1}q\mathcal{B}=q,$$

(39)

where one defines the operator

$$q:=P_{+}-P_{-},$$

(40)

and where $P_{\pm }$ are the projectors on the positive/negative norm solutions, respectively. This condition is easily seen to be equivalent to (37).

It may be noted that, from the point of view of quantum field theory (QFT), the S-matrix discussed above is different from the usual S-matrix of the standard QFT, albeit there is a direct relation between them. In QFT, there is usually another definition of S-matrix:

$${\widehat{\varphi }}^{out}\left(x\right)={\mathcal{S}}^{-1}{\widehat{\varphi }}^{in}\left(x\right)\mathcal{S},$$

(41)

where we have indicated with $\mathcal{S}$ the scattering operator of QFT. As well-known, it has to be an unitary operator: ${\mathcal{S}}^{†}\mathcal{S}=\mathcal{S}{\mathcal{S}}^{†}=I$, such that $|0,out\rangle =\mathcal{S}|0,in\rangle$ holds, which is ensured if a finite number of particles is created in the transition between the two aforementioned vacua [16,18,19].

3.6. A Perturbative Approach to the S-Matrix

For simplicity of notation, henceforth we shift to a more standard writing of the scattering matrix. The S-matrix has entries $s_{ij}$. Condition (37) leads to the following six equations:

$$\begin{array}{ccc}& & |s_{11}{|}^2-|s_{12}{|}^2+{\left|s_{13}\right|}^2=1,\hfill \end{array}$$

(42)

$$\begin{array}{ccc}& & |s_{21}{|}^2-|s_{22}{|}^2+{\left|s_{23}\right|}^2=-1,\hfill \end{array}$$

(43)

$$\begin{array}{ccc}& & |s_{31}{|}^2-|s_{32}{|}^2+{\left|s_{33}\right|}^2=1,\hfill \end{array}$$

(44)

$$\begin{array}{ccc}& & s_{12}{s}_{11}-s_{22}{s}_{21}-s_{32}{s}_{31}=0,\hfill \end{array}$$

(45)

$$\begin{array}{ccc}& & s_{13}{s}_{11}-s_{23}{s}_{21}-s_{33}{s}_{31}=0,\hfill \end{array}$$

(46)

$$\begin{array}{ccc}& & s_{12}{s}_{13}-s_{22}{s}_{23}-s_{32}{s}_{33}=0.\hfill \end{array}$$

(47)

One may explore the next-to-leading-order correction in $ϵ$ by assuming an analytic behavior of the S-matrix in the parameter $ϵ$. This might be a non-trivial assumption, as our analysis is involved with quantum field theory in external fields, where $ϵ$ enters in a non-trivial way. Then, we still maintain an expansion parameter, say ${ϵ}^{\prime }$, leaving open the problem to find out the relation between $ϵ$ and ${ϵ}^{\prime }$. Indeed, in our case, our fourth-order equation of the Orr–Sommerfeld kind is involved in a singular perturbation theory problem, as higher-order derivatives appear in the perturbation itself, and this represents a nontrivial mathematical problem. It is, e.g., not easy to determine in a complete way the first correction to the wave functions in the near-horizon region. As to general difficulties occurring in the case of singular perturbation theory, see, e.g., Examples 1.19 and 1.20, pp. 435–436 in [20]. We proceed as in [21], with the difference that our expansion parameter is ${ϵ}^{\prime }$:

$$S=S^{\left(0\right)}+\sum _{k=1}^{\infty }{{ϵ}^{\prime }}^k{S}^{\left(k\right)}=S^{\left(0\right)}+{ϵ}^{\prime }{S}^{\left(1\right)}+{{ϵ}^{\prime }}^2{S}^{\left(2\right)}+\dots$$

(48)

We put:

$$\begin{array}{ccc}& & s_{11}^{\left(0\right)}={\alpha }_{\omega }=s_{22}^{\left(0\right)},\hfill \end{array}$$

(49)

$$\begin{array}{ccc}& & s_{12}^{\left(0\right)}={\beta }_{\omega }=s_{21}^{\left(0\right)}.\hfill \end{array}$$

(50)

It is supposed that $s_{13},s_{23}$ are at least order of ${ϵ}^{\prime }$, i.e., are small (cf. [21]). With simple algebraic manipulations of Equations (46) and (47) we get the following equations:

$$\begin{array}{ccc}\hfill ({\alpha }_{\omega }-1)s_{13}^{\left(1\right)}& =& {\beta }_{\omega }{s}_{23}^{\left(1\right)},\hfill \end{array}$$

(51)

$$\begin{array}{ccc}\hfill ({\alpha }_{\omega }+1)s_{23}^{\left(1\right)}& =& {\beta }_{\omega }{s}_{13}^{\left(1\right)},\hfill \end{array}$$

(52)

and then we obtain, as in [21],

$$\frac{s_{13}}{s_{23}}=\frac{{\beta }_{\omega }}{{\alpha }_{\omega }-1}=\frac{{\alpha }_{\omega }+1}{{\beta }_{\omega }}=:r,$$

(53)

i.e., $s_{13}^{\left(1\right)}=r{s}_{23}^{\left(1\right)}$.

From Equations (42) and (43), at order ${ϵ}^{\prime }$, we obtain

$$\frac{s_{11}^{\left(1\right)}}{s_{12}^{\left(1\right)}}=\frac{{\beta }_{\omega }}{{\alpha }_{\omega }}=\frac{s_{22}^{\left(1\right)}}{s_{12}^{\left(1\right)}},$$

(54)

and then $s_{11}^{\left(1\right)}=s_{22}^{\left(1\right)}$. Furthermore, Equation (44) at order ${ϵ}^{\prime }$ provides $s_{33}^{\left(1\right)}=0$. As a consequence, we get

$$S=\left(\begin{array}{ccc}{\alpha }_{\omega }& {\beta }_{\omega }& 0\\ {\beta }_{\omega }& {\alpha }_{\omega }& 0\\ 0& 0& 1\end{array}\right)+{ϵ}^{\prime }\left(\begin{array}{ccc}{s}_{11}^{\left(1\right)}& \frac{{\alpha }_{\omega }}{{\beta }_{\omega }}{s}_{11}^{\left(1\right)}& r{s}_{23}^{\left(1\right)}\\ \frac{{\alpha }_{\omega }}{{\beta }_{\omega }}{s}_{11}^{\left(1\right)}& s_{11}^{\left(1\right)}& s_{23}^{\left(1\right)}\\ r{s}_{23}^{\left(1\right)}& s_{23}^{\left(1\right)}& 0\end{array}\right)+O\left({{ϵ}^{\prime }}^2\right).$$

(55)

A less-naive approach to the parameterization of the S-matrix is presented in the following subsection. As to the meaning of the parameters $s_{11}^{\left(1\right)}$ and $s_{23}^{\left(1\right)}$, it is better to go back to the previous notation: one has $s_{11}^{\left(1\right)}={\sigma }_{uv}^{\left(1\right)}$, which corresponds to the amplitude, at the first order, of conversion of an initial v-mode to a final u-mode (Hawking particle), whereas $s_{23}^{\left(1\right)}={\sigma }_{lv}^{\left(1\right)}$ corresponds to the amplitude, at the first order, of conversion of an initial v-mode to a final l-mode (Hawking partner). We recall that we indicated the l-mode as would-be Hawking partner because of the possibility to find a different amplitude of production of the l-mode with respect to the amplitude of production of the u-mode, as previously discussed. This difference does not arise in our framework of $ϵ$-expansion. This is obviously also true in the above expansion in ${ϵ}^{\prime }$. A relation (yet-unknown) ${ϵ}^{\prime }=h\left(ϵ\right)$, where h is a function to be determined, is expected.

3.7. A General Parametrization of the S-Matrix

As we said, the S-matrix constructed above is an element of the group $U(1,-1,1)$, a real form of $U(3,\mathbb{C})$ preserving the quadratic Hermitian form $\eta :=$ diag$(1,-1,1)$ in ${\mathbb{C}}^3$. Its general element depends on nine real parameters and can be realized by means of the Iwasawa parametrization [22,23]. It means that the generic form of S can be put in the following form:

$$\begin{array}{c}\hfill S=KAN\end{array}$$

(56)

where K is a generic element of the maximal compact subgroup; A is a maximal non-compact abelian subgroup; and N is the exponentiation of the nilpotent generated by the positive roots associated to A. Let us do it in detail, starting from the associated Lie algebra $\mathfrak{u}(1,-1,1)$. It consists of the 33 matrices A that satisfy

$$\begin{array}{c}\hfill A^{†}\eta +\eta A=0,\end{array}$$

(57)

which gives

$$\begin{array}{c}\hfill \left(\begin{array}{ccc}{a}_{11}^{*}& a_{21}^{*}& a_{31}^{*}\\ a_{12}^{*}& a_{22}^{*}& a_{32}^{*}\\ a_{13}^{*}& a_{23}^{*}& a_{33}^{*}\end{array}\right)=\left(\begin{array}{ccc}-a_{11}& a_{12}& -a_{13}\\ a_{21}& -a_{22}& a_{23}\\ -a_{31}& a_{32}& -a_{33}\end{array}\right).\end{array}$$

(58)

Accordingly, we choose the following basis for the Lie algebra:

$$\begin{array}{cc}\hfill {\mu }_1& =\left(\begin{array}{ccc}0& 0& -i\\ 0& 0& 0\\ -i& 0& 0\end{array}\right),{\mu }_2=\left(\begin{array}{ccc}0& 0& -1\\ 0& 0& 0\\ 1& 0& 0\end{array}\right),{\mu }_3=\left(\begin{array}{ccc}-i& 0& 0\\ 0& 0& 0\\ 0& 0& i\end{array}\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mu }_4& =\left(\begin{array}{ccc}0& 0& 0\\ 0& -i& 0\\ 0& 0& 0\end{array}\right),{\mu }_5=\left(\begin{array}{ccc}-i& 0& 0\\ 0& -i& 0\\ 0& 0& -i\end{array}\right),{\mu }_6=\left(\begin{array}{ccc}0& 1& 0\\ 1& 0& 0\\ 0& 0& 0\end{array}\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mu }_7& =\left(\begin{array}{ccc}0& -i& 0\\ i& 0& 0\\ 0& 0& 0\end{array}\right),{\mu }_8=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 1\\ 0& 1& 0\end{array}\right),{\mu }_9=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& -i\\ 0& i& 0\end{array}\right).\hfill \end{array}$$

(59)

Notice that they are trace orthogonal but not uniformly normalized. This choice simplifies the expressions we need. The first 5 matrices are compact (their squares have negative trace) and generate the maximal compact subgroup K. It is a $U\left(2\right)U\left(1\right)$: the first four matrices generate $U\left(2\right)$, of which the first three generate $SU\left(2\right)$, and the fifth matrix generates the $U\left(1\right)$. The quotient $U(1,-1,1)/\left(U\right(2\left)U\right(1\left)\right)$ has rank 1, so there is only one generator for A. We choose ${\mu }_6$. Finally, we have to determine the eigenmatrices of the adjoint action of ${\mu }_6$ corresponding to positive roots. These are easily obtained by computing the commutators $[{\mu }_6,{\mu }_j]$, $j=7,8,9$. We get

$$\begin{array}{c}\hfill N_1=\left(\begin{array}{ccc}i& -i& 0\\ i& -i& 0\\ 0& 0& 0\end{array}\right),N_2=\left(\begin{array}{ccc}0& 0& -1\\ 0& 0& 1\\ 1& 1& 0\end{array}\right),N_3=\left(\begin{array}{ccc}0& 0& -i\\ 0& 0& -i\\ -i& i& 0\end{array}\right).\end{array}$$

(60)

Parametrizing the subgroup $SU\left(2\right)$ à la Euler, we get

$$\begin{array}{c}\hfill S[\overrightarrow{x};y;\overrightarrow{z}]\equiv K[\overrightarrow{x}]A\left[y\right]N[\overrightarrow{z}],\end{array}$$

(61)

with

$$\begin{array}{cc}\hfill K[\overrightarrow{x}]=& e^{x_1{\mu }_3}{e}^{x_2{\mu }_2}{e}^{x_3{\mu }_3}{e}^{x_4{\mu }_4}{e}^{x_5{\mu }_5},\hfill \end{array}$$

(62)

$$\begin{array}{cc}\hfill A\left[y\right]=& e^{y{\mu }_6},\hfill \end{array}$$

(63)

$$\begin{array}{cc}\hfill N[\overrightarrow{z}]=& e^{z_1{N}_1}{e}^{z_2{N}_2}{e}^{z_3{N}_3}.\hfill \end{array}$$

(64)

More explicitly

$$\begin{array}{cc}\hfill K[\overrightarrow{x}]=& e^{-i{x}_5}\left(\begin{array}{ccc}{e}^{-i{x}_1}& 0& 0\\ 0& 1& 0\\ 0& 0& e^{i{x}_1}\end{array}\right)\left(\begin{array}{ccc}cos{x}_2& 0& -sin{x}_2\\ 0& 1& 0\\ sin{x}_2& 0& cos{x}_2\end{array}\right)\left(\begin{array}{ccc}{e}^{-i{x}_3}& 0& 0\\ 0& 1& 0\\ 0& 0& e^{i{x}_3}\end{array}\right)\left(\begin{array}{ccc}1& 0& 0\\ 0& e^{-i{x}_4}& 0\\ 0& 0& 1\end{array}\right),\hfill \end{array}$$

(65)

$$\begin{array}{cc}\hfill A[y]=& \left(\begin{array}{ccc}coshy& sinhy& 0\\ sinhy& coshy& 0\\ 0& 0& 1\end{array}\right),\hfill \end{array}$$

(66)

$$\begin{array}{cc}\hfill N[\overrightarrow{z}]=& \left(\begin{array}{ccc}1+i{z}_1& -i{z}_1& 0\\ i{z}_1& 1-i{z}_1& 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{ccc}1-\frac{z_2^2}{2}& -\frac{z_2^2}{2}& -z_2\\ \frac{z_2^2}{2}& 1+\frac{z_2^2}{2}& z_2\\ z_2& z_2& 1\end{array}\right)\left(\begin{array}{ccc}1-\frac{z_3^2}{2}& \frac{z_3^2}{2}& -i{z}_3\\ -\frac{z_3^2}{2}& 1+\frac{z_3^2}{2}& -i{z}_3\\ -i{z}_3& i{z}_3& 1\end{array}\right).\hfill \end{array}$$

(67)

The range of the parameter to cover the whole group is

$$\begin{array}{c}\hfill x_1,x_4\in [0,\pi ],x_2\in [0,\pi /2],x_3,x_5\in [0,2\pi ],y,z_1,z_2,z_3\in \mathbb{R}.\end{array}$$

(68)

Exploiting all the products would provide us the most general parametrization for coefficients of S. However, for several analyses it may be convenient to keep the terms factorized. As an example, let us consider again the case of a perturbative deviation from (32). To this end, we can write

$$\begin{array}{c}\hfill S^{\left(0\right)}=S[\overrightarrow{0},y_{\omega },\overrightarrow{0}]=\left(\begin{array}{ccc}cosh{y}_{\omega }& sinh{y}_{\omega }& 0\\ sinh{y}_{\omega }& cosh{y}_{\omega }& 0\\ 0& 0& 1\end{array}\right),\end{array}$$

(69)

with $sinh{y}_{\omega }={\beta }_{\omega }$. We could compute the most general first-order correction, but we want now to limit ourselves to consider only real corrections, so we keep $x_1=x_3=x_4=x_5=z_1=z_3=0$, set

$$\begin{array}{c}\hfill x_2=a{ϵ}^{\prime },y=y_{\omega }+b{ϵ}^{\prime },z_2=c{ϵ}^{\prime },\end{array}$$

(70)

and keep the first order in ${ϵ}^{\prime }$. This gives $S=S^{\left(0\right)}+{ϵ}^{\prime }{S}^{\left(1\right)}+\cdots$, with

$$\begin{array}{c}\hfill S^{\left(1\right)}=\left(\begin{array}{ccc}{\beta }_{\omega }b& {\alpha }_{\omega }b& -a-c({\alpha }_{\omega }-{\beta }_{\omega })\\ {\alpha }_{\omega }b& {\beta }_{\omega }b& c({\alpha }_{\omega }-{\beta }_{\omega })\\ a{\alpha }_{\omega }+c& a{\beta }_{\omega }+c& 0\end{array}\right).\end{array}$$

(71)

This expression is more general than (55). While the first 22 block coincides with the previous one, the last row and column are more general, since they are not forced to be symmetric, and so we have three independent parameters in place of just two. Notice that imposing $S_{23}^{\left(1\right)}=S_{32}^{\left(1\right)}$ in (71) automatically gives symmetry and reproduces exactly (55). We stress that, while the comparison we have just done seems to suggest a direct identification ${ϵ}^{\prime }=ϵ$, such a conclusion would be too naive as one has to determine the final identification in the full quantum field theory framework.

Our parametrization allows to include easily also the corrections due to the non-real terms (by switching on $x_1,x_3,x_4,x_5,z_1,z_3$) or to extend the perturbation at any given order or to provide exact general expressions, after relating the generalized Iwasawa parameters with the physical ones.

4. Thermofield Dynamics and Thermality

From the origins of the Hawking effect and of the thermofield dynamics (TFD) framework for describing thermal equilibrium, there exists a fine relation between thermal emission by black holes [9] and thermofield formalism [24,25,26,27]. As discovered by Werner Israel, the thermal vacuum of TFD coincides with the Hartle–Hawking state, sometimes also indicated as a Hartle–Hawking–Israel state in tribute of Israel’s finding [9]. See also [13,28,29]. Our possibility to show that the p-modes and n-modes correspond to the particle/antiparticle states of the thermal vacuum, i.e., as particles of the Hartle–Hawking–Israel vacuum, is a noticeable consequence of the aforementioned scheme.

4.1. A Summary of TFD

Thermofield dynamics are introduced with the aim of describing quantum field theory at a finite temperature. The key idea is to set up a formalism where the ensemble average of any operator at thermal equilibrium is replaced by an expectation value of the same operator with respect to a thermal vacuum:

$${\langle A\rangle }_{\beta }=\frac{1}{Z\left(\beta \right)}Tr(exp(-\beta H)A)=:\langle 0\left(\beta \right)\left|A\right|0\left(\beta \right)\rangle .$$

(72)

In the previous equation, $Z\left(\beta \right)$ is the partition function, and H is the Hamiltonian operator for the system at hand; $\left|0\right(\beta )\rangle$ is the thermal vacuum, and $\beta$ is the inverse temperature, as usual. It is not possible to obtain that $\left|0\right(\beta )\rangle$ stays in the same Hilbert space $\mathcal{H}$ as the bosonic theory at hand, but, in order to implement the above mapping, it is necessary to duplicate the degrees of freedom by introducing a fictitious copy $\tilde{\mathcal{H}}$ of the original Hilbert space, with associated creation and annihilation operators. The thermal state $\left|0\right(\beta )\rangle$ can be arranged for in the tensor product $\mathcal{H}\otimes \tilde{\mathcal{H}}$. Let us introduce in the vacuum states $|0\rangle$ and $|\tilde{0}\rangle$, with corresponding annihilator operators $a_l,{\tilde{a}}_l$ and $b_l,{\tilde{b}}_l$ for particles and antiparticles, respectively. A physical (fictitious) n–particle state whose energy is $E_n$ is denoted by $|n\rangle$ ($|\tilde{n}\rangle$) and $|n,\tilde{n}\rangle =|n\rangle |\tilde{n}\rangle$ is the n–particle tensor product state.

The vacuum state in the extended Hilbert state is

$$|0\left(\beta \right)\rangle =\frac{1}{\sqrt{Z\left(\beta \right)}}\sum _n{e}^{-\beta E_n/2}|n,\tilde{n}\rangle ;$$

(73)

$Z\left(\beta \right)$ is a normalization.

In the calculation of (72), one has to sum over all the fictitious states $\tilde{n}$; the result is

$$\langle A\rangle =\langle 0\left(\beta \right)\left|A\right|0\left(\beta \right)\rangle =\frac{1}{Z\left(\beta \right)}\sum _n{e}^{-\beta E_n}\langle n\left|A\right|n\rangle .$$

(74)

One can also introduce thermal-state operators, according to the standard constructions in thermofield dynamics, and introduce the thermal state $\left|0\right(\beta )\rangle$ and thermal-state annihilation operators $a_l\left(\beta \right),{\tilde{a}}_l\left(\beta \right),b_l\left(\beta \right),{\tilde{b}}_l\left(\beta \right)$, which are such that

$$a_l\left(\beta \right)|0\left(\beta \right)\rangle ={\tilde{a}}_l\left(\beta \right)|0\left(\beta \right)\rangle =b_l\left(\beta \right)|0\left(\beta \right)\rangle ={\tilde{b}}_l\left(\beta \right)|0\left(\beta \right)\rangle =0.$$

(75)

Let us recall that, for bosons, we have $E_n=n\omega$. We are mainly interested in the following Bogoliubov relations:

$$\begin{array}{ccc}\hfill a_l& =& c_l{a}_l\left(\beta \right)-s_l{\tilde{a}}_l^{†}\left(\beta \right),\hfill \end{array}$$

(76)

$$\begin{array}{ccc}\hfill a_l^{†}& =& c_l{a}_l^{†}\left(\beta \right)-s_l{\tilde{a}}_l\left(\beta \right),\hfill \end{array}$$

(77)

and the analogous ones for b-operators (which correspond to operators for antiparticles, i.e., for negative frequency states; cf. [24]), with

$$\begin{array}{ccc}\hfill c_l:& =& \frac{1}{\sqrt{1-exp(-\beta \omega )}},\hfill \end{array}$$

(78)

$$\begin{array}{ccc}\hfill s_l:& =& \frac{exp(-\frac{1}{2}\beta \omega )}{\sqrt{1-exp(-\beta \omega )}}.\hfill \end{array}$$

(79)

4.2. Analogue Hawking Effect and TFD

In the framework of analogue gravity, one may show that particle of the thermal vacuum can be identified with particles appearing in the spectrum of the analogous system displaying the analogous Hawking effect. In agreement with the leading term in the S-matrix we discussed above, we have ${\mathrm{\Gamma }}_{\omega }=1$, where ${\mathrm{\Gamma }}_{\omega }$ stays for the grey-body factor (see (85) below), and we have restored its standard notation for the Hawking effect itself. The decoupling of the modes $v,d$ at the leading order, as discussed the previous section, is fundamental in order to allow a thermofield dynamics picture also in analogue gravity, as we show below. Indeed, as a consequence of such a decoupling, we can write

$$a_{\omega }^u={\alpha }_{\omega }{a}_{\omega }^p+{\beta }_{\omega }{a}_{\omega }^{n†},$$

(80)

to be compared with the thermofield formula

$$a_{\omega }=u_{\omega }\left({\beta }_h\right)a_{\omega }\left({\beta }_h\right)+v_{\omega }\left({\beta }_h\right){\tilde{a}}_{\omega }^{†}\left({\beta }_h\right),$$

(81)

where

$$a_{\omega }\left({\beta }_h\right)|0\left({\beta }_h\right)\rangle =0={\tilde{a}}_{\omega }\left({\beta }_h\right)|0\left({\beta }_h\right)\rangle .$$

(82)

The fictitious Hilbert space of TFD is instead populated by the Hawking partner:

$$a_{\omega }^{l†}={\beta }_{\omega }{a}_{\omega }^p+{\alpha }_{\omega }{a}_{\omega }^{n†},$$

(83)

to be compared with the thermofield formula

$${\tilde{a}}_{\omega }^{†}=u_{\omega }\left({\beta }_h\right){\tilde{a}}_{\omega }^{†}\left({\beta }_h\right)+v_{\omega }\left({\beta }_h\right)a_{\omega }\left({\beta }_h\right).$$

(84)

As a consequence, we can claim that the p-modes and the n-modes correspond to particle states associated with the thermal vacuum, to be compared with the Hawking mode (u-mode) and the Hawking partner (l-mode), which are states of the “standard” (i.e., non-thermal) vacuum, and belong to the Hilbert space and to the would-be fictitious Hilbert space, respectively. Further, we note that, in the case t of a white hole, modes $p,n$ are outgoing scattering states; in the black hole case, modes $p,n$ are ingoing scattering states, which can be associated with vacuum fluctuations (as far as the spontaneous process is concerned) and real particles in the stimulated case. Then, it is worth mentioning that, in both the white hole case and the black hole one, $p,n$ may be experimentally measured, and so we have also a physical measure of the aforementioned particles excited over the thermal vacuum. This happens only in the case of analogue-gravity models, where a nontrivial dispersion appears. Furthermore, we can also interpret the fictitious part of the Hilbert space involving the Hawking partner as associated with the $m=-1$ branch of the analytic function we discussed in the previous section.

We also think that the above picture would be of strong interest also for theoreticians of TFD, as the particles of the thermal vacuum appear in the present case as real particles, which can actually be measured, as discussed above (e.g., in the case of a white hole configuration of a nonlinear dielectric medium, one may detect photons corresponding to the $p,n$ states in a suitable photon detector). See also [10].

One may wonder if it is possible to extend our considerations also to the case where ${\mathrm{\Gamma }}_{\omega }<1$ because of a depletion process of the actually created particles. This means that ${\sigma }_{uv}\ne 0$, and then

$${\mathrm{\Gamma }}_{\omega }=1-{\left|{\sigma }_{uv}\right|}^2<1.$$

(85)

As discussed in [1], one maintains the relation (33), and then one obtains

$$|{\sigma }_{un}{|}^2=\frac{{\mathrm{\Gamma }}_{\omega }}{exp\left({\beta }_h\omega \right)-1}=:{\left|{\beta }_{\omega }\right|}^2.$$

(86)

A very naive ansatz would be the following: the picture concerning states $u,l$ and states $p,n$ proceeds as above, with the difference that the depletion of Hawking particles (u-modes) at infinity because of the backscattering (v-modes) is such that

$$u_{\omega }\left({\beta }_h\right)=\sqrt{\frac{{\mathrm{\Gamma }}_{\omega }}{1-exp(-\beta \omega )}},$$

(87)

and

$$v_{\omega }\left({\beta }_h\right)=\sqrt{\frac{{\mathrm{\Gamma }}_{\omega }}{exp\left(\beta \omega \right)-1}}.$$

(88)

Still, one has to remark that the effects of depletion not only can but even must in principle act in a different way in the case of the Hawking mode and in the case of the Hawking partner, as Equations (27) and (28) show, disrupting the standard TFD picture and maybe leaving room for a generalization of the standard formalism. We do not delve into this problem herein.

5. Conclusions

We took into account the general structure of the Hawking scattering process in analogue gravity with weak dispersion. We discussed in detail the process involving the Hawking partner, and we showed that, in general, one could expect different creation rates for the Hawking particle and the (would-be) Hawking partner, unless a weak dispersion takes place, as in the framework of the generalized Orr–Sommerfeld equation we discussed in [1,2], encompassing the framework introduced in [4,8], at least at the leading order in the weak expansion parameter $ϵ$. Including higher-order correction in $ϵ$ in general may be tricky. Therefore, in order to show which kind of general form the further corrections one must expect at the subleading order for the S-matrix operator, we proposed a general method based on a rigorous Iwasawa decomposition of the group $U(1,-1,1)$ in order to prescribe the general form of the S-matrix. In principle, this method allows to describe any possible modification of the S-matrix, perturbative or not, and it makes easily controllable any expansion with respect to an infinitesimal parameter ${ϵ}^{\prime }$, once the latter is related to the physical perturbation parameter $ϵ$. We did not try to propose here a direct relation between ${ϵ}^{\prime }$ and $ϵ$, since in general it is made tricky by technical subtleties; quantum field theory does not allow to just make naive identifications. A direct perturbative expansion in $ϵ$ requires in general further assumptions (as a reasonable smallness of some non-diagonal entries of the S-matrix, see [21]). We leave this delicate question to a future work devoted to a full investigation of the potentiality of the Iwasawa parameterization approach.

We think that the analysis we presented here, together with the ones in [1,2], provides the possibility to improve our knowledge of the analog Hawking effect on the theoretical side, but also on the experimental one, as it is made possible in line with principles a more-accurate black hole spectroscopy (albeit probably only in a semi-analytical way for what concerns actual calculations of higher-order corrections to the S-matrix). Furthermore, we took into account the thermofield dynamics framework, and we have showed that, at least at the leading order, it maintains its performability also in the dispersive analogue-gravity framework, with the (apparently unnoticed before) further bonus that particles on the thermal vacuum can be identified with the modes p and n, and then it becomes experimentally measurable, as discussed in the previous section. The TFD framework is instead jeopardized by the presence of grey-body factors for the Hawking particle and the would-be Hawking partner at the leading order, as different rates no more allow to define a thermal vacuum in the standard way.