The Equation of State of Neutron-Rich Matter at Fourth Order of Chiral Effective Field Theory and the Radius of a Medium-Mass Neutron Star
Abstract
:1. Introduction
2. General Aspects of Neutron Stars
3. Description of the Calculation
3.1. The Two-Nucleon Force
3.2. The Three-Nucleon Force
3.3. Equation of State for Stellar Matter
3.4. Polytropic Extrapolation
3.5. Mass-Radius Relation
4. Results and Discussion
4.1. Chiral Uncertainty
4.2. Results
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | The equations of state utilized in this work can be obtained contacting the corresponding author at the provided email address. |
References
- Abbott, B.P. [LIGO Scientific Collaboration and Virgo Collaboration]. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Sammarruca, F.; Millerson, R. The radius of the canonical-mass neutron star and chiral effective field theory. J. Phys. G Nucl. Part. Phys. 2019, 46, 24001. [Google Scholar] [CrossRef] [Green Version]
- Weinberg, S. Three-body interactions among nucleons and pions. Phys. Lett. B 1992, 295, 114. [Google Scholar] [CrossRef] [Green Version]
- Weinberg, S. Nuclear forces from chiral lagrangians. Phys. Lett. B 1990, 251, 288. [Google Scholar] [CrossRef]
- Sammarruca, F.; Millerson, R. Analysis of the neutron matter equation of state and the symmetry energy up to fourth order of chiral effective field theory. Phys. Rev. C 2021, 104, 034308. [Google Scholar] [CrossRef]
- Sammarruca, F.; Millerson, R. Overview of symmetric nuclear matter properties from chiral interactions up to fourth order of the chiral expansion. Phys. Rev. C 2021, 104, 064312. [Google Scholar] [CrossRef]
- Reed, B.T.; Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J. Implications of PREX-II on the equation of state of neutron-rich matter. arXiv 2021, arXiv:2101.03193. [Google Scholar]
- Burrows, A. Perspectives on Core-Collapse Supernova Theory. Rev. Mod. Phys. 2013, 85, 245. [Google Scholar] [CrossRef] [Green Version]
- Chadwick, J. Possible Existance of a Neutron. Nature 1932, 129, 312. [Google Scholar] [CrossRef]
- Baade, W.; Zwicky, F. On Super-Novae. Proc. Nat. Acad. Sci. USA 1934, 20, 254. [Google Scholar] [CrossRef] [Green Version]
- Baade, W.; Zwicky, F. Remarks on Super-Novae and Cosmic Rays. Phys. Rev. 1934, 46, 76. [Google Scholar] [CrossRef]
- Tolmann, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. C 1939, 55, 364. [Google Scholar] [CrossRef] [Green Version]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. C 1939, 55, 374. [Google Scholar] [CrossRef]
- Cameron, A.G.W. Pyconuclear Reactions and Nova Explosions. Astrophys. J. 1959, 130, 916. [Google Scholar] [CrossRef]
- Ambartsumyan, V.A.; Saakyan, G.S. The degenerate Superdense Gas of Elementary Particles. Astron. Zhurnal 1960, 37, 193. [Google Scholar]
- Salpeter, E.E. Matter at high densities. Ann. Phys. (N. Y.) 1960, 11, 393. [Google Scholar] [CrossRef]
- Ivanenko, D.; Kurdgelaidze, D.F. Hypothesis on quark star. Astrofizika 1965, 1, 479. [Google Scholar]
- Tsuruta, S.; Cameron, A.G.W. Cooling and detectability of neutron stars. Can. J. Phys. 1966, 44, 1863. [Google Scholar] [CrossRef] [Green Version]
- Migdal, A.B. Stability of Vacuum and Limiting Fields. Zh. Eksp. Teor. Fiz. 1971, 61, 2209. [Google Scholar] [CrossRef]
- Sawyer, R.F. Condensed π- Phase in Neutron-Star Matter. Phys. Rev. Lett. 1972, 29, 382. [Google Scholar] [CrossRef]
- Sawyer, R.F.; Scalapino, D.J. Pion Condensation in Superdense Nuclear Matter. Phys. Rev. D 1972, 7, 953. [Google Scholar] [CrossRef] [Green Version]
- Kaplan, D.B.; Nelson, A.E. Strange goings on in dense nucleonic matter. Phys. Lett. B 1986, 175, 57. [Google Scholar] [CrossRef]
- Ivanenko, D.; Kurdgelaidze, D.F. Remarks on Quark Stars. Lett. Nuovo Cimento 1969, 2, 13. [Google Scholar] [CrossRef]
- Chiu, H.-Y. Supernovae, neutrinos, and neutron stars. Ann. Phys. 1964, 26, 364. [Google Scholar] [CrossRef]
- Yakovlev, D.G.; Levenfish, K.P.; Shibanov, Y.A. Cooling of neutron stars and superfluidity in their core. Phys. Usp. 1999, 42, 737. [Google Scholar] [CrossRef] [Green Version]
- Pacini, F. Energy emission from a neutron star. Nature 1967, 216, 567. [Google Scholar] [CrossRef]
- Hewish, A.; Bell, S.J.; Pilkington, J.D.H.; Scott, P.F.; Collins, R.A. Observation of a Rapidly Pulsating Radio Source. Nature 1968, 217, 709. [Google Scholar] [CrossRef]
- Gold, T. Rotating Neutron Stars as the Origin of the Pulsating Radio Sources. Nature 1968, 218, 731. [Google Scholar] [CrossRef]
- Large, M.I.; Vaughan, A.E.; Mills, B.Y. A Pulsar Supernova Association? Nature 1968, 220, 340. [Google Scholar] [CrossRef]
- Reifenstein, E.C.; Brundage, W.D.; Staelin, D.H. Crab Nebula Pulsar NPO527. Phys. Rev. Lett. 1969, 22, 311. [Google Scholar] [CrossRef]
- Glendenning, N.K. Compact Stars, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Manchester, R.N. 50 Years of Pulsars! IOP Conf. Ser. J. Phys. 2017, 932, 012001. [Google Scholar] [CrossRef]
- Hulse, R.A.; Taylor, J.H. Discovery of a pulsar in a binary system. Astrophys. J. 1975, 195, L51. [Google Scholar] [CrossRef]
- Johnston, S.; Manchester, R.N.; Lyne, A.G.; Bailes, M.; Kaspi, V.M.; Qiao, G.; Amico, N.D. PSR 1259-63: A Binary Radio Pulsar with a Be Star Companion. Astrophys. J. 1992, 387, L37. [Google Scholar] [CrossRef]
- Lyne, A.G.; Brinklow, A.; Middleditch, J.; Kulkarni, S.R.; Backer, D.C.; Clifton, T.R. The discovery of a millisecond pulsar in the globular cluster M28. Nature 1987, 328, 399. [Google Scholar] [CrossRef]
- Wolszczan, A.; Frail, D.A. A planetary system around the millisecond pulsar PSR1257+12. Nature 1992, 355, 145. [Google Scholar] [CrossRef]
- McLaughlin, M.A.; Lyne, A.G.; Lorimer, D.R.; Kramer, M.; Faulkner, A.J.; Manchester, R.N.; Cordes, J.M.; Camilo, F.; Possenti, A.; Stairs, I.H.; et al. Transient radio bursts from rotating neutron stars. Nature 2006, 439, 817. [Google Scholar] [CrossRef]
- van Paradijs, J.; Taam, R.E.; van den Heuvel, E.P.J. On the nature of the ‘anomalous’ 6-s X-ray pulsars. Astron. Astrophys. 1995, 299, L41. [Google Scholar]
- Martinez, J.G.; Stovall, K.; Freire, P.C.C.; Deneva, J.S.; Jenet, F.A.; McLaughlin, M.A.; Bagchi, M.; Bates, S.D.; Ridolfi, A. Pulsar J0453+1559: A double neutron star system with a large mass asymmetry. Astrophys. J. 2015, 812, 143. [Google Scholar] [CrossRef] [Green Version]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nature Astro. 2020, 4, 72. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.M.; Wang, J.; Zhao, Y.H.; Yin, H.X.; Song, L.M.; Menezes, D.P.; Wickramasinghe, D.T.; Ferrario, L.; Chardonnet, P. Study of measured pulsar masses and their possible conclusions. Astron. Astrophys. 2011, 527, A83. [Google Scholar] [CrossRef] [Green Version]
- Tauris, T.M.; Sanyal, D.; Yoon, S.-C.; Langer, N. Evolution towards and beyond accretion-induced collapse of massive white dwarfs and formation of millisecond pulsars. Astron. Astrophys. 2013, 558, A39. [Google Scholar] [CrossRef] [Green Version]
- Schwab, J.; Quataert, E.; Bildsten, L. Thermal runaway during the evolution of ONeMg cores towards accretion-induced collapse. Mon. Not. R. Astron. Soc. 2015, 453, 2. [Google Scholar] [CrossRef] [Green Version]
- Ruiter, A.J.; Ferrario, L.; Belczynski, K.; Seitenzahl, I.R.; Crocker, R.M.; Karakas, A.I. On the formation of neutron stars via accretion-induced collapse in binaries. Mon. Not. R. Astron. Soc. 2019, 484, 1. [Google Scholar] [CrossRef] [Green Version]
- Steiner, A.W.; Lattimer, J.M.; Brown, E.F. The neutron star mass-radius relation and the equation of state of dense matter. Astrophys. J. 2013, 765, L5. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Vuorinen, A. Gravitational-Wave Constraints on the Neutron-Star-Matter Equation of State. Phys. Rev. Lett. 2018, 120, 172703. [Google Scholar] [CrossRef] [Green Version]
- Cackett, E.M.; Bhattacharyya, S.; Grindley, J.E.; van der Klis, M.; Strohmayer, T.E.; Miller, J.M.; Homan, J.; Miller, M.C.; Wijnands, R. Relativistic Iron Emission Lines in Neutron Star Low-Mass X-Ray Binaries as Probes of Neutron Star Radii. Astrophys. J. 2008, 674, 1. [Google Scholar] [CrossRef] [Green Version]
- Lattimer, J.M.; Steiner, A.W. Neutron Star Masses and radii from quiescent Low-Mass X-ray Binaries. Astrophys. J. 2014, 784, 123. [Google Scholar] [CrossRef] [Green Version]
- Newton, W.G.; Gearheart, M.; Hooker, J.; Li, B.A. Neutron Star Crust; Bertulani, C.A., Piekarewicz, J., Eds.; Nova Science Pub. Inc.: Hauppauge, NY, USA, 2011; Chapter 12. [Google Scholar]
- Tsang, M.B.; Stone, J.R.; Camera, F.; Danielewicz, P.; Gandolfi, S.; Hebeler, K.; Horowitz, C.J.; Lee, J.; Lynch, W.G.; Kohley, Z.; et al. Constraints on the symmetry energy and neutron skins from experiment and theory. Phys. Rev. C 2012, 86, 015803. [Google Scholar] [CrossRef] [Green Version]
- Lattimer, J.M.; Lim, Y. Constraining the symmetry parameters of the nuclear interaction. Astrophys. J. 2013, 771, 51. [Google Scholar] [CrossRef] [Green Version]
- Steiner, A.W.; Gandolfi, S. Connecting Neutron Star Observations to Three-Body Forces in Neutron Matter and to the Nuclear Symmetry Energy. Phys. Rev. Lett. 2012, 108, 081102. [Google Scholar] [CrossRef]
- Hebeler, K.; Lattimer, J.M.; Pethick, C.J.; Schwenk, A. Equation of state and neutron star properties constrained by nuclear physics and observation. Astrophys. J. 2013, 773, 11. [Google Scholar] [CrossRef] [Green Version]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Burgio, G.F.; Vidana, I. The Equation of State of Nuclear Matter: From Finite Nuclei to Neutron Stars. Universe 2020, 6, 119. [Google Scholar] [CrossRef]
- Vidana, I. A short walk through the physics of neutron stars. arXiv 2018, arXiv:1805.00837. [Google Scholar] [CrossRef]
- Blaschke, D.; Schaffner-Bielich, J.; Schulze, H.J. Topical issue on exotic matter in neutron stars. Eur. Phys. J. A 2016, 52, 71. [Google Scholar] [CrossRef] [Green Version]
- Rhoades, C.D.; Ruffini, R. Maximum mass of a neutron star. Phys. Rev. Lett. 1974, 32, 324. [Google Scholar] [CrossRef] [Green Version]
- Coraggio, L.; Holt, J.W.; Itaco, N.; Machleidt, R.; Marcucci, L.E.; Sammarruca, F. Nuclear-matter equation of state with consistent two- and three-body perturbative chiral interactions. Phys. Rev. C 2014, 89, 044321. [Google Scholar] [CrossRef]
- Entem, D.R.; Machleidt, R.; Nosyk, Y. High-quality two-nucleon potentials up to fifth order of the chiral expansion. Phys. Rev. C 2017, 96, 024004. [Google Scholar] [CrossRef]
- Entem, D.R.; Machleidt, R. Accurate charge-dependent nucleon-nucleon potential at fourth order of chiral perturbation theory. Phys. Rev. C 2003, 68, 041001(R). [Google Scholar] [CrossRef] [Green Version]
- Hoferichter, M.; de Elvira, J.R.; Kubis, B.; Meissner, U.-G. Matching Pion-Nucleon Roy-Steiner Equations to Chiral Perturbation Theory. Phys. Rev. Lett. 2016, 115, 192301, Roy-Steiner-equation analysis of pion-nucleon scattering. Phys. Rep. 2016, 625, 1.. [Google Scholar] [CrossRef] [PubMed]
- Hoppe, J.; Drischler, C.; Furnstahl, R.J.; Hebeler, K.; Schwenk, A. Weinberg eigenvalues for chiral nucleon-nucleon interactions. Phys. Rev. C 2017, 96, 054002. [Google Scholar] [CrossRef] [Green Version]
- Drischler, C.; Hebeler, K.; Schwenk, A. Chiral interactions up to next-to-next-to-next-to-leading order and nuclear saturation. Phys. Rev. Lett. 2019, 122, 042501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Epelbaum, E.; Nogga, A.; Glöckle, W.; Kamada, H.; Meißner, U.-G.; Witala, H. Three nucleon forces from chiral effective field theory. Phys. Rev. C 2002, 66, 064001. [Google Scholar] [CrossRef] [Green Version]
- Hebeler, K.; Schwenk, A. Chiral three-nucleon forces and neutron matter. Phys. Rev. C 2010, 82, 014314. [Google Scholar] [CrossRef] [Green Version]
- Holt, J.W.; Kaiser, N.; Weise, W. Chiral three-nucleon interaction and the 14C-dating β decay. Phys. Rev. C 2009, 79, 054331. [Google Scholar] [CrossRef] [Green Version]
- Holt, J.W.; Kaiser, N.; Weise, W. Density-dependent effective nucleon-nucleon interaction from chiral three-nucleon forces. Phys. Rev. C 2010, 81, 024002. [Google Scholar] [CrossRef] [Green Version]
- Bernard, V.; Epelbaum, E.; Krebs, H.; Meißner, U.-G. Subleading contributions to the chiral three-nucleon force: Long-range terms. Phys. Rev. C 2008, 77, 064004. [Google Scholar] [CrossRef] [Green Version]
- Bernard, V.; Epelbaum, E.; Krebs, H.; Meißner, U.-G. Subleading contributions to the chiral three-nucleon force. II. Short-range terms and relativistic corrections. Phys. Rev. C 2011, 84, 054001. [Google Scholar] [CrossRef]
- Tews, I.; Krüger, T.; Hebeler, K.; Schwenk, A. Neutron Matter at Next-to-Next-to-Next-to-Leading Order in Chiral Effective Field Theory. Phys. Rev. Lett. 2013, 110, 032504. [Google Scholar] [CrossRef] [Green Version]
- Drischler, C.; Carbone, A.; Hebeler, K.; Schwenk, A. Neutron matter from chiral two- and three-nucleon calculations up to N3LO. Phys. Rev. C 2016, 94, 054307. [Google Scholar] [CrossRef] [Green Version]
- Hebeler, K.; Krebs, H.; Epelbaum, E.; Golak, J.; Skibinski, R. Efficient calculation of chiral three-nucleon forces up to N3LO for ab initio studies. Phys. Rev. C 2015, 91, 044001. [Google Scholar] [CrossRef] [Green Version]
- Kaiser, N.; Singh, B. Density-dependent NN interaction from subleading chiral three-nucleon forces: Long-range terms. Phys. Rev. C 2019, 100, 014002. [Google Scholar] [CrossRef] [Green Version]
- Kaiser, N. Density-dependent nn-potential from subleading chiral three-neutron forces: Long-range terms. arXiv 2020, arXiv:2010.02739v4. [Google Scholar]
- Kaiser, N.; Niessner, V. Density-dependent NN interaction from subleading chiral 3N forces: Short-range terms and relativistic corrections. Phys. Rev. C 2018, 98, 054002. [Google Scholar] [CrossRef] [Green Version]
- Treuer, L. Density-Dependent Neutron-Neutron Interaction from Subleading Chiral Three-Neutron Forces. arXiv 2009, arXiv:2009.11104. [Google Scholar]
- Krebs, H.; Gasparyan, A.; Epelbaum, E. Chiral three-nucleon force at N4LO: Longest-range contributions. Phys. Rev. C 2012, 85, 054006. [Google Scholar] [CrossRef] [Green Version]
- Read, J.S.; Lackey, B.D.; Owen, B.J.; Friedman, J.L. Constraints on a phenomenologically parameterized neutron-star equation of state. Phys. Rev. D 2009, 79, 124032. [Google Scholar] [CrossRef] [Green Version]
- Weber, F. Pulsars as Astrophysical Laboratories for Nuclear and Particle Physics; Institute of Physics Publishing: Bristol, UK, 1999. [Google Scholar]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. arXiv 2021, arXiv:2105.06979. [Google Scholar] [CrossRef]
- Harrison, B.K.; Wheeler, J.A. Gravitational Theory and Gravitational Collapse; University of Chicago: Chicago, IL, USA, 1965. [Google Scholar]
- Negele, J.W.; Vautherin, D. Neutron star matter at sub-nuclear densities. Nucl. Phys. 1973, A207, 298. [Google Scholar] [CrossRef]
- Epelbaum, E.; Krebs, H.; Meißner, U.-G. Improved chiral nucleon-nucleon potential up to next-to-next-to-next-to-leading order. Eur. Phys. J. A 2015, 51, 53. [Google Scholar] [CrossRef] [Green Version]
- Drischler, C.; Holt, J.W.; Wellenhofer, C. Chiral Effective Field Theory and the High-Density Nuclear Equation of State. Annu. Rev. Nucl. Part. Sci. 2021, 71, 403. [Google Scholar] [CrossRef]
- Hebeler, K.; Lattimer, J.; Pethick, C.; Schwenk, A. Constraints on Neutron Star Radii Based on Chiral Effective Field Theory Interactions. Phys. Rev. Lett. 2010, 105, 161102. [Google Scholar] [CrossRef] [PubMed]
- Dickhoff, W.H.; Barbieri, C. Self-consistent Green’s function method for nuclei and nuclear matter. Prog. Part. Nucl. Phys. 2004, 52, 377. [Google Scholar] [CrossRef] [Green Version]
- Rios, A. Green’s Function Techniques for Infinite Nuclear Systems. Front. Phys. 2020, 8, 387. [Google Scholar] [CrossRef]
- Tews, I.; Gandolfi, S.; Gezerlis, A.; Schwenk, A. Quantum Monte Carlo calculations of neutron matter with chiral three-body forces. Phys. Rev. C 2016, 93, 024305. [Google Scholar] [CrossRef]
- Lonardoni, D.; Tews, I.; Gandolfi, S.; Gezerlis, A.; Carlson, J. Nuclear and neutron-star matter from local chiral interactions. Phys. Rev. Res. 2020, 2, 022033. [Google Scholar] [CrossRef]
- Lynn, J.E.; Tews, I.; Carlson, J.; Gandolfi, S.; Gezerlis, A.; Schmidt, K.E.; Schwenk, A. Chiral Three-Nucleon Interactions in Light Nuclei, Neutron-α scattering, and Neutron Matter. Phys. Rev. Lett. 2016, 116, 062501. [Google Scholar] [CrossRef] [Green Version]
- Lim, Y.; Holt, J. Bayesian modeling of the nuclear equation of state for neutron star tidal deformabilities and GW170817. Eur. Phys. J. A 2019, 55, 209. [Google Scholar] [CrossRef]
- Tews, I.; Carlson, J.; Gandolfi, S.; Reddy, S. Constraining the Speed of Sound inside Neutron Stars with Chiral Effective Field Theory Interactions and Observations. Astrophys. J. 2018, 860, 149. [Google Scholar] [CrossRef]
- Poisson, E.; Will, C.M. Gravity: Newtonian, Post-Newtonian, Relativistic; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- De, S.; Finstad, D.; Lattimer, J.M.; Brown, A.D.; Berger, E.; Biwer, C.M. Tidal Deformabilities and Radii of Neutron Stars from the Observation of GW170817. Phys. Rev. Lett. 2018, 121, 091102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Capano, C.D.; Tews, I.; Brown, S.M.; Margalit, B.; De, S.; Kumar, S.; Brown, D.A.; Krishnan, B.; Reddy, S. Stringent constraints on neutron-star radii from multimessanger observations and nuclear theory. Nat. Astron. 2020, 4, 625. [Google Scholar] [CrossRef]
- Tews, I.; Margueron, J.; Reddy, S. Confronting gravitational-wave observations with modern nuclear physics constraints. Eur. Phys. J. 2019, 55, 97. [Google Scholar] [CrossRef] [Green Version]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. arXiv 2019, arXiv:1912.05702, arXiv:1912.05702. [Google Scholar]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef] [Green Version]
- Mann, A. The golden age of neutron-star physics has arrived. Nature 2020, 579, 20. [Google Scholar] [CrossRef] [Green Version]

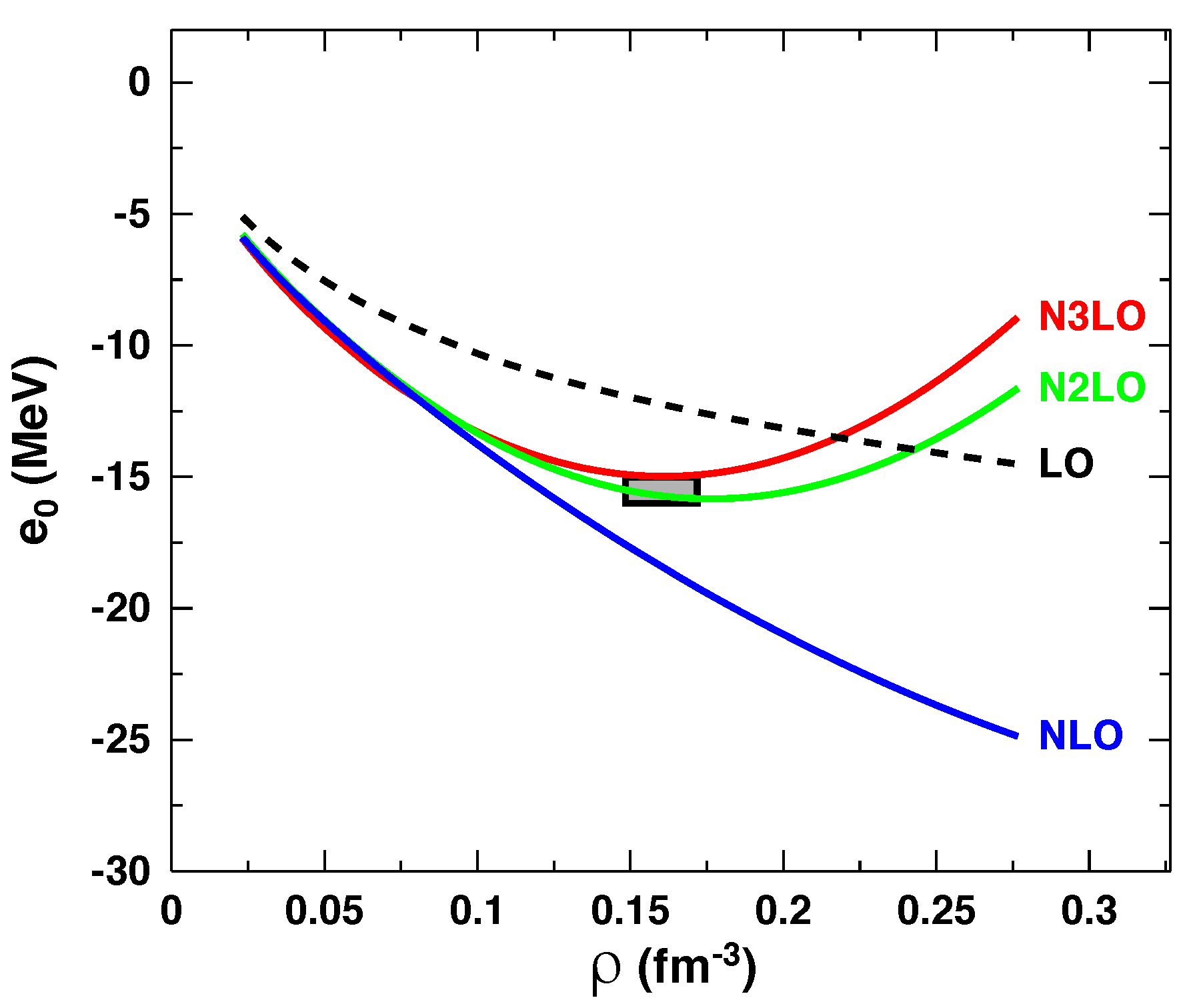
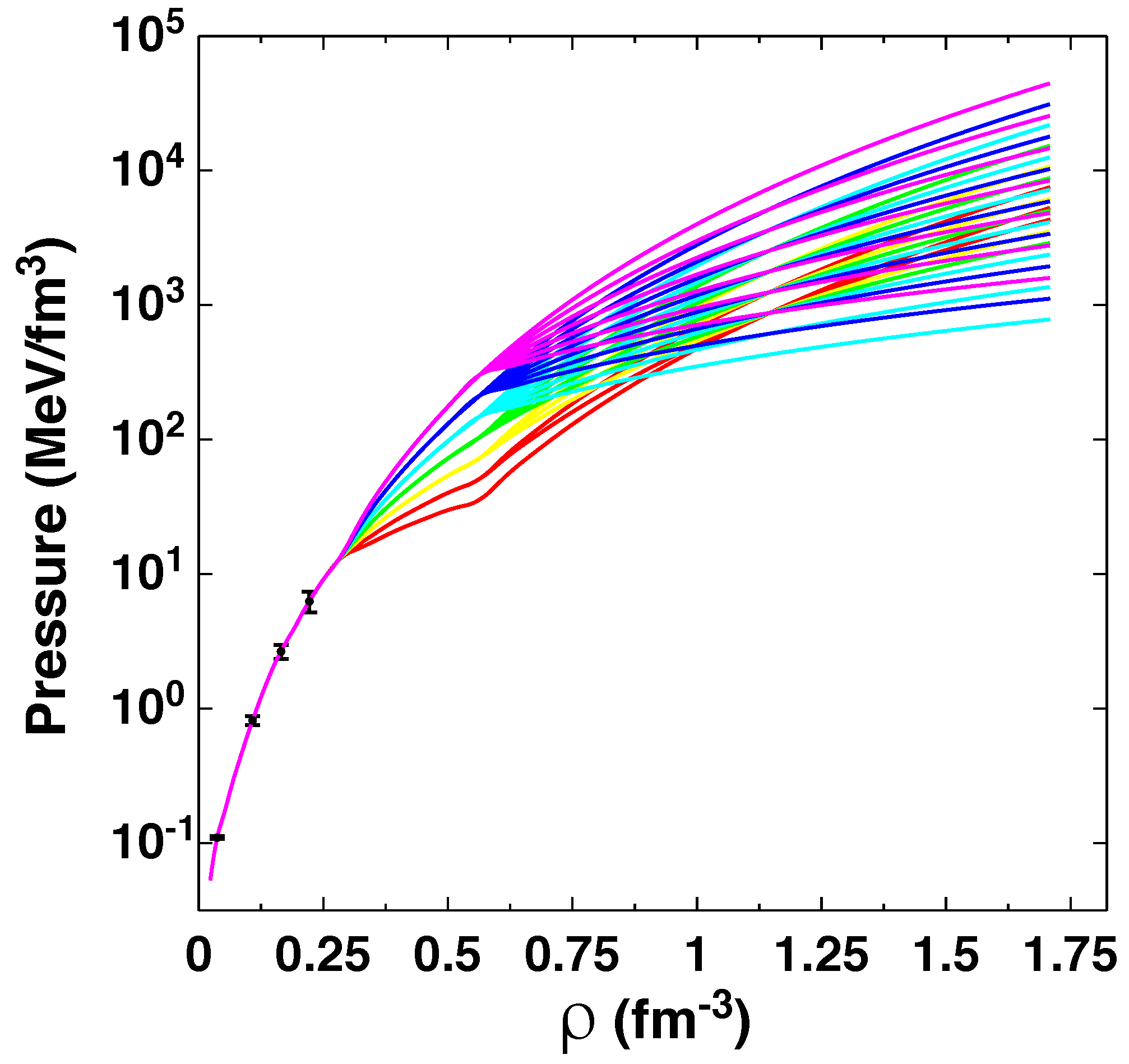
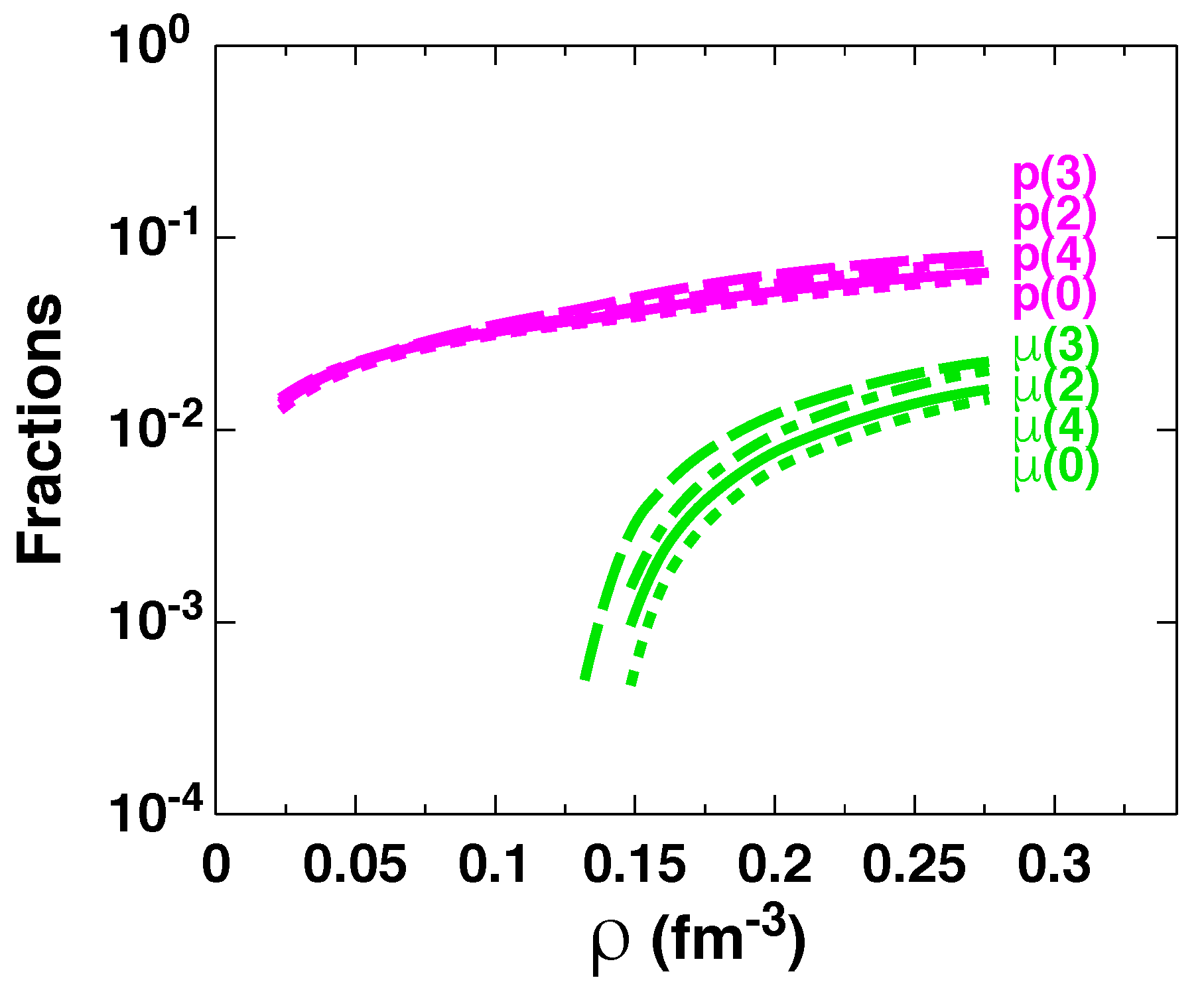

| (MeV) | ||||||||
|---|---|---|---|---|---|---|---|---|
| NLO | 450 | −0.74 | −3.61 | 2.44 | 2.75 | 0.13 | −0.013000 | −0.000283 |
| NLO | 450 | −1.07 | −5.32 | 3.56 | 0.50 | −1.25 | −0.011828 | −0.000010 |
| (MeV) | (MeV) | |
|---|---|---|
| 0.16 | 31.3 ± 0.8 | 52.6 ± 4.0 |
| R (km) | (fm) | |||
|---|---|---|---|---|
| 1.5 | 4.5 | 10.05 | 0.82 | 0.90 |
| 2 | 4 | 10.64 | 0.74 | 0.81 |
| 4.5 | 10.70 | 0.71 | 0.86 | |
| 2.5 | 3.5 | 11.34 | 0.63 | 0.71 |
| 4 | 11.34 | 0.62 | 0.78 | |
| 4.5 | 11.35 | 0.61 | 0.84 | |
| 3 | 3 | 11.87 | 0.51 | 0.62 |
| 3.5 | 11.87 | 0.51 | 0.63 | |
| 4 | 11.87 | 0.51 | 0.63 | |
| 4.5 | 11.87 | 0.51 | 0.63 | |
| 3.5 | any | 12.15 | 0.45 | 0.67 |
| 4 | any | 12.29 | 0.41 | 0.71 |
| 4.5 | any | 12.39 | 0.39 | 0.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sammarruca, F.; Millerson, R. The Equation of State of Neutron-Rich Matter at Fourth Order of Chiral Effective Field Theory and the Radius of a Medium-Mass Neutron Star. Universe 2022, 8, 133. https://doi.org/10.3390/universe8020133
Sammarruca F, Millerson R. The Equation of State of Neutron-Rich Matter at Fourth Order of Chiral Effective Field Theory and the Radius of a Medium-Mass Neutron Star. Universe. 2022; 8(2):133. https://doi.org/10.3390/universe8020133
Chicago/Turabian StyleSammarruca, Francesca, and Randy Millerson. 2022. "The Equation of State of Neutron-Rich Matter at Fourth Order of Chiral Effective Field Theory and the Radius of a Medium-Mass Neutron Star" Universe 8, no. 2: 133. https://doi.org/10.3390/universe8020133
APA StyleSammarruca, F., & Millerson, R. (2022). The Equation of State of Neutron-Rich Matter at Fourth Order of Chiral Effective Field Theory and the Radius of a Medium-Mass Neutron Star. Universe, 8(2), 133. https://doi.org/10.3390/universe8020133





