PBH Formation from Spherically Symmetric Hydrodynamical Perturbations: A Review
Abstract
1. Introduction
2. Basics of PBH Formation
3. The Abundance of PBHs
4. Cosmological Setup for PBH Formation
4.1. Misner–Sharp Equations
4.2. The Gradient Expansion Approximation, Initial Conditions, and Compaction Function
4.3. Horizon Formation
- Surface (A–B): In this region, we have a transition between and (normal region) to and . This horizon, moves inwards of the computational domain, which eventually will encounter a singularity at ;
- Surface (B–C): In this region, we have a transition between and to and (normal region). This horizon, typically called “the apparent horizon”, moves outwards of the computational domain. Actually, this horizon and the previous one emerge from a single marginally trapped surface. During the evolution, the motion of the horizon can be followed to obtain the PBH mass , where is the location of the outer horizon in time. At the final stage of the gravitational collapse for very late times, this horizon will become static, i.e., ;
- Surface (C–D): In the last region, we have a transition between and (normal region) to and . This case corresponds to an anti-trapped surface, which corresponds to the cosmological horizon, moving outwards. We should mention that this horizon does not correspond to the cosmological horizon from the FLRW background, since the perturbed medium (deviating from the FLRW solution) affects the evolution of the cosmological horizon.
4.4. PBH Mass and Accretion
5. Numerical Techniques
5.1. Pseudospectral Methods
5.2. Numerical Procedure
- Create the different grid points for the different subdomains with a given number of points , and compute the different Chebyshev differentiation matrices . Introduce also the initial time step , which usually is enough to ensure stability;
- Specify a lower and an upper limit in of the bisection. The maximum value can be chosen for the upper limit, and for the lower bound, (which corresponds to the threshold estimation using a Jeans length criteria). To reduce the computational time, a closer domain to can be chosen if such a domain is known;
- A value is taken once the bisection starts. From that, the curvature profiles or can be built, and the location of the compaction function peak can be found, , using Equations (51) and (53) respectively. Subsequently, compute the perturbations of the hydrodynamical variables following Equations (40) and (41);
- To distinguish numerically the formation of an apparent horizon or not, we used the peak value of the compaction function in time. When the peak approaches , this implies the formation of the apparent horizon 3. In this case, the value of chosen would imply the formation of a black hole, i.e., , and therefore, a lower value closer to must be found modifying the bound of the bisection in such way that . In the opposite case, when decreases continuously for some time, this will imply the dispersion of the perturbation, and the bisection bound should be modified as ;
- The previous steps are iterated until the difference between and is lower than the desired resolution, i.e., . From that, the threshold value is defined as . When approaches the critical value, in some cases, the grid resolution initially set up is not enough to follow the evolution; if so, then is shifted according to to avoid being close to . Another alternative would be the dynamical inclusion of more subgrids in the desired region where gradients start to be large.
5.3. Numerical Estimation of the Final PBH Mass
6. Numerical Results
6.1. Curvature Fluctuations
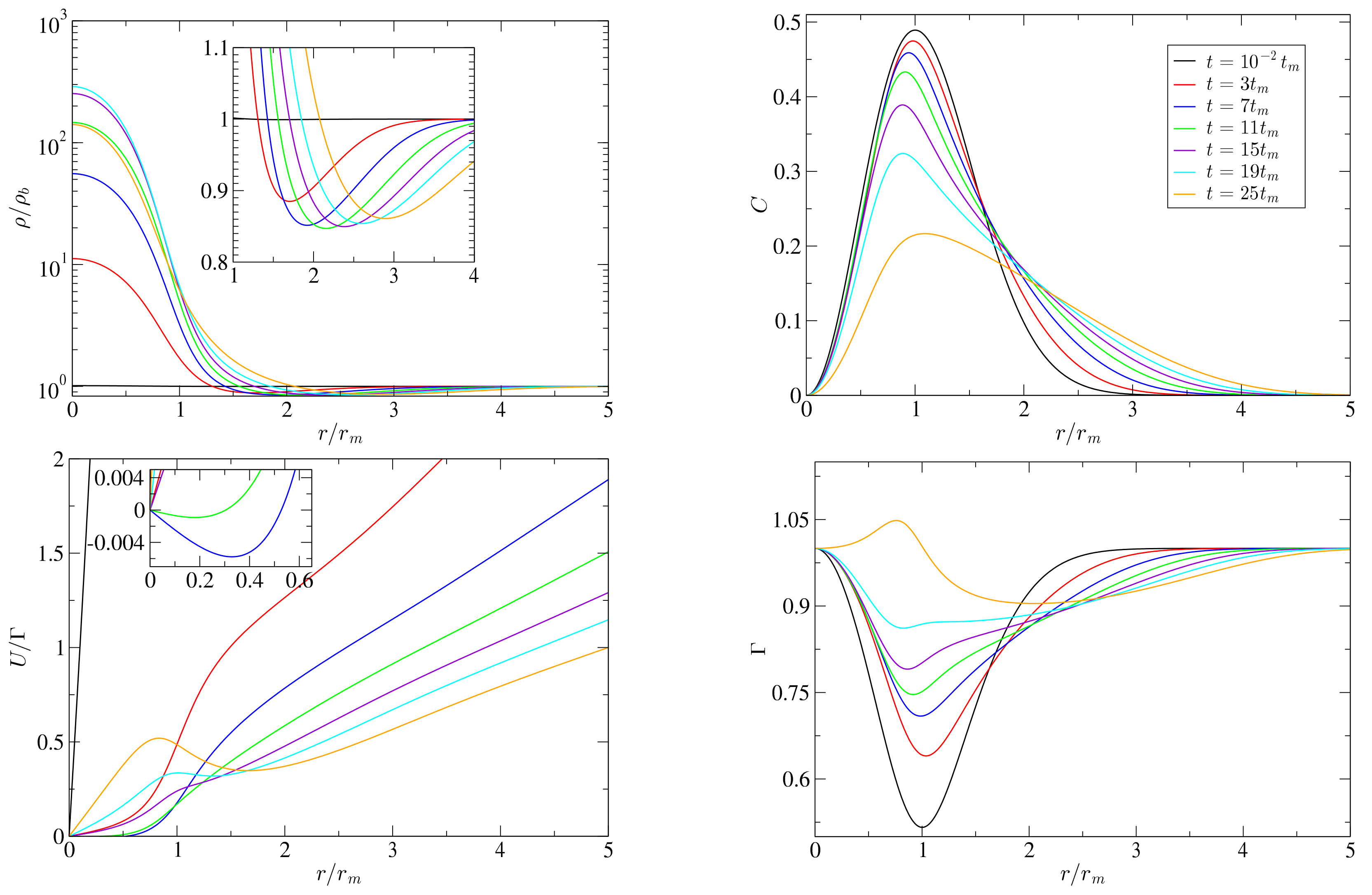
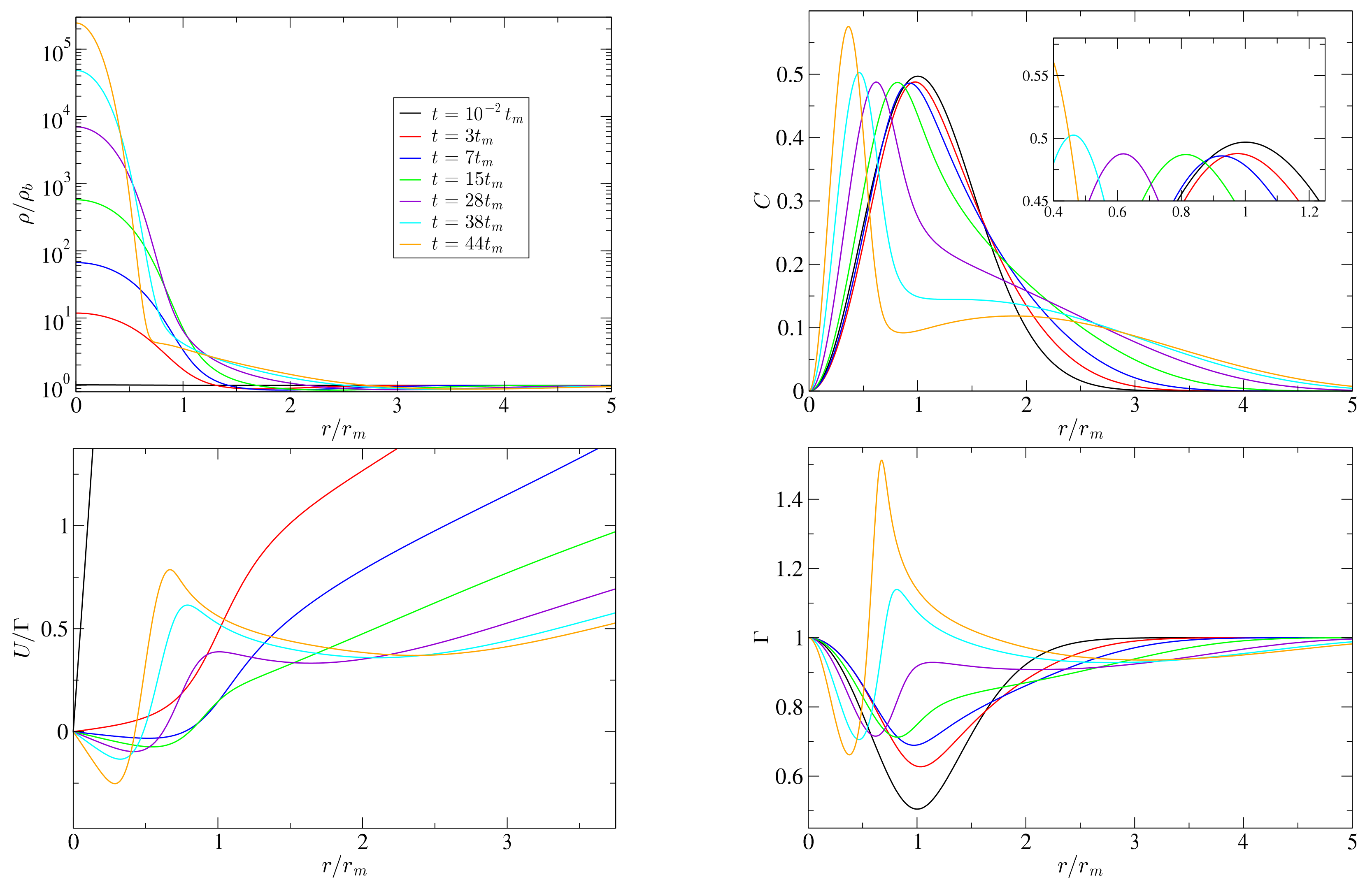
6.2. Non-Linear Behaviour of the Gravitational Collapse
6.3. Thresholds for PBH Formation
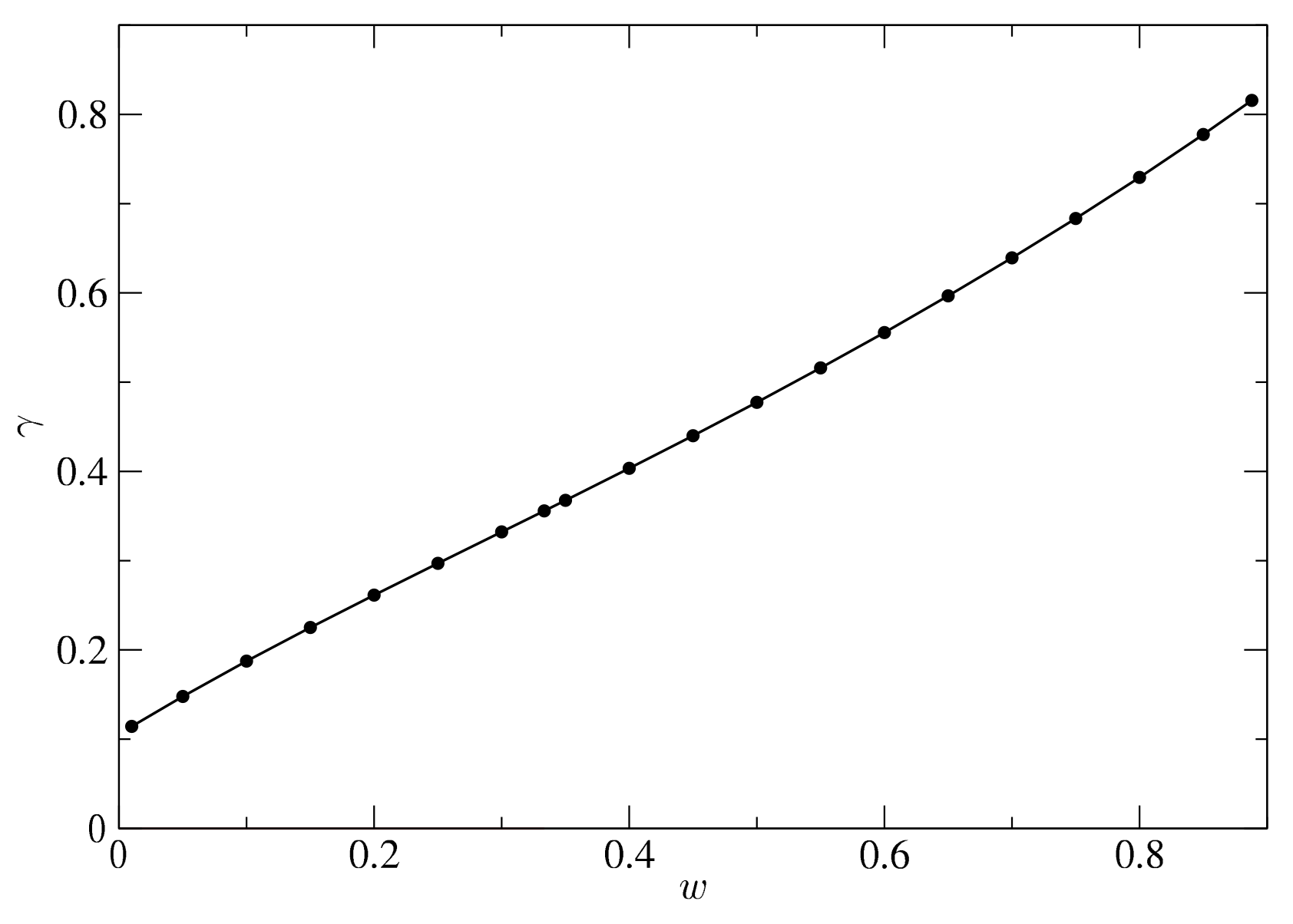
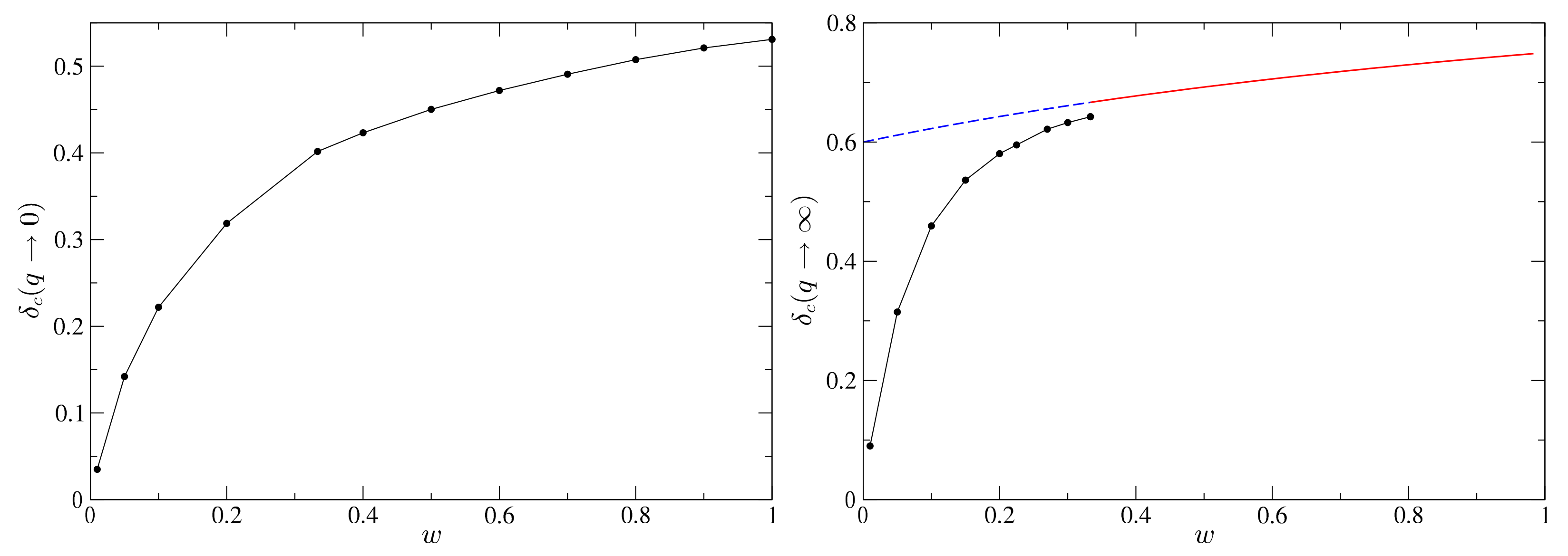
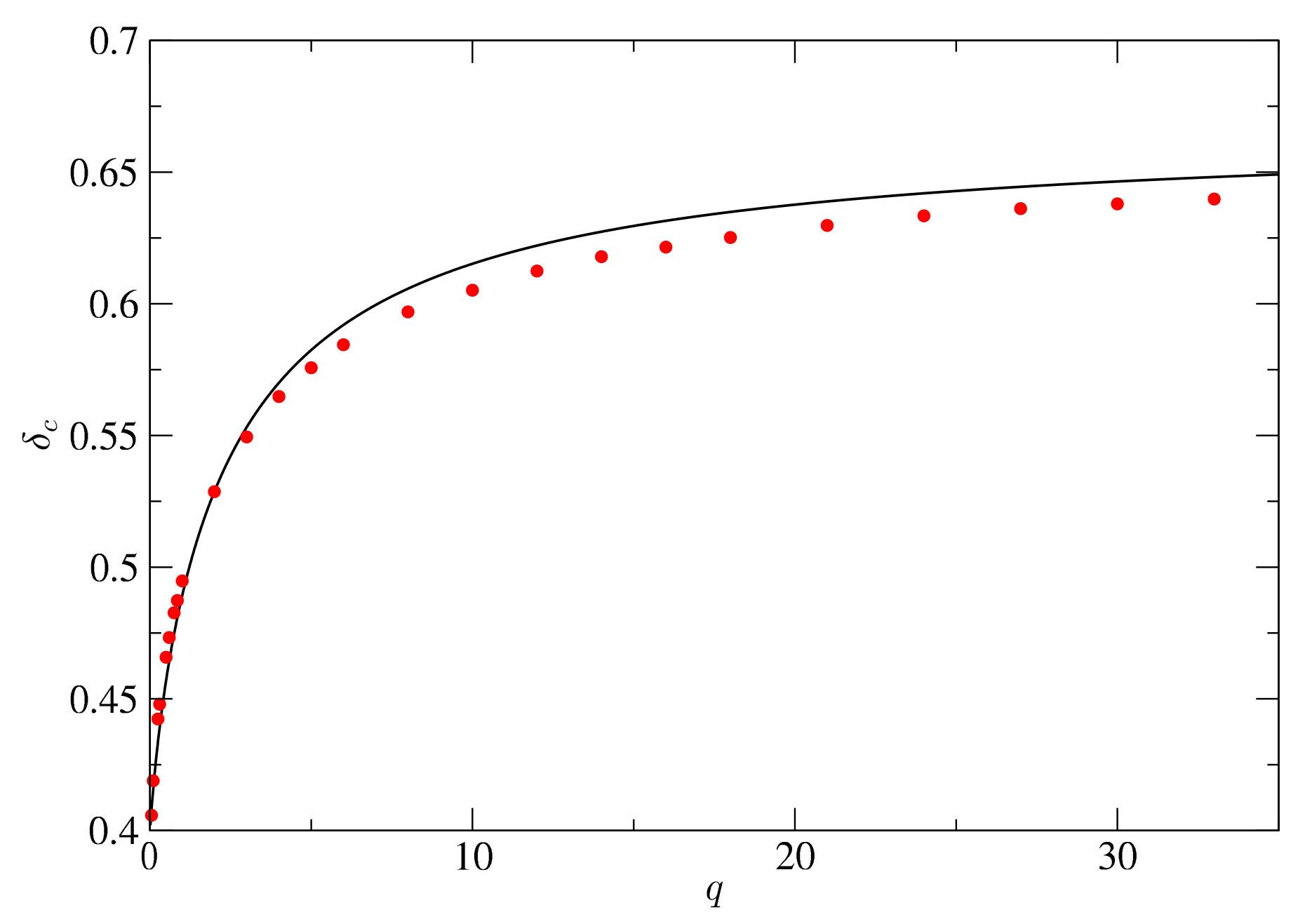
- The case corresponds to a that becomes approximately constant over a wide range of scales. Simulations, in this case, become difficult due to the presence of conical singularities [84]. To solve this issue, in [84], a modified profile of Equation (82) was used to subtract the mass excess beyond and fulfil that at the boundaries, the FLRW background is recovered. In Figure 14 are shown the numerical values of in terms of w, which show a strong dependence on w. As expected, for , the threshold ;
- The case of large corresponds to the case of a sharply peaked profile for the compaction function. For this kind of profile, the pressure gradients acting against the gravitational collapse are maximal, and hence, the compaction function should be maximal as well. Analytically, this is shown by Equation (50) that (at super-horizon scales). As was proven numerically in [79], in the case of radiation . The intuition is that the saturation should persist to larger values of w because larger values of w also imply larger pressures that fight against the collapse. Therefore, for , the compaction function of a peaked profile must also saturate the bound . This was verified numerically in [80]. This behaviour is no longer true for , something obvious in the case of dust , since , but always for any profile. This is shown in the left panel of Figure 14. It should be taken into account that beyond , the simulations do not obtain the threshold with enough resolution. This is the reason why the numerical value of the threshold for does not exactly coincide with . One expects that in the asymptotic limit, the threshold for should match with , as was pointed out in [79] with the same argument.
6.4. PBH Masses
7. Analytical Estimation for the Threshold of PBH Formation
7.1. Shape-Dependent Analytical Estimation of the Threshold for Radiation Fluid
7.2. Generalisation of the Analytical Threshold beyond the Radiation Fluid
7.3. A Comparison between Analytical Estimates
8. Other Scenarios of PBH Formation
9. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PBHs | Primordial Black Holes |
| DM | Dark Matter |
| FLRW | Friedman–Lemaître–Robertson–Walker |
| GR | General Relativity |
| CMB | Cosmic Microwave Background |
| LIGO | Laser Interferometer Gravitational-Wave Observatory |
| BH | Black Hole |
| PDE | Partial Differential Equation |
| AMR | Adaptive Mesh Refinement |
| NANOGrav | North American Nanohertz Observatory for Gravitational Waves |
| 1 | The confluent hypergeometric function is defined as . |
| 2 | The erf function is defined as . |
| 3 | Technically, the condition of the formation of the apparent horizon is given when . However, for computationally efficiency, ot is easier to check whatever , since , which avoids finding the cosmological horizon. |
| 4 | The gamma function is defined as . |
| 5 | The incomplete gamma function is defined as . |
| 6 | The hypergeometric function is defined as . |
References
- Particle Data Group. Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D. History of dark matter. Rev. Mod. Phys. 2018, 90, 045002. [Google Scholar] [CrossRef]
- Carr, B.; Kohri, K.; Sendouda, Y.; Yokoyama, J. Constraints on Primordial Black Holes. Rep. Prog. Phys. 2021, 84, 116902. [Google Scholar] [CrossRef] [PubMed]
- Carr, B.; Kuhnel, F. Primordial Black Holes as Dark Matter Candidates. arXiv 2021, arXiv:2110.02821. [Google Scholar]
- Carr, B.; Kuhnel, F.; Visinelli, L. Black holes and WIMPs: All or nothing or something else. Mon. Not. R. Astron. Soc. 2021, 506, 3648–3661. [Google Scholar] [CrossRef]
- Carr, B.; Kuhnel, F.; Visinelli, L. Constraints on Stupendously Large Black Holes. Mon. Not. R. Astron. Soc. 2021, 501, 2029–2043. [Google Scholar] [CrossRef]
- Carr, B.J.; Kohri, K.; Sendouda, Y.; Yokoyama, J. New cosmological constraints on primordial black holes. Phys. Rev. D 2010, 81, 104019. [Google Scholar] [CrossRef]
- Keith, C.; Hooper, D.; Blinov, N.; McDermott, S.D. Constraints on Primordial Black Holes From Big Bang Nucleosynthesis Revisited. Phys. Rev. D 2020, 102, 103512. [Google Scholar] [CrossRef]
- Carr, B.J.; Hawking, S.W. Black Holes in the Early Universe. Mon. Not. R. Astron. Soc. 1974, 168, 399–415. [Google Scholar] [CrossRef]
- Hawking, S. Gravitationally Collapsed Objects of Very Low Mass. Mon. Not. R. Astron. Soc. 1971, 152, 75–78. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Novikov, I.D. The Hypothesis of Cores Retarded during Expansion and the Hot Cosmological Model. Sov. Astron. 1967, 10, 602. [Google Scholar]
- Carr, B.; Kühnel, F.; Sandstad, M. Primordial black holes as dark matter. Phys. Rev. D 2016, 94, 083504. [Google Scholar] [CrossRef]
- García-Bellido, J.; Linde, A.; Wands, D. Density perturbations and black hole formation in hybrid inflation. Phys. Rev. D 1996, 54, 6040–6058. [Google Scholar] [CrossRef]
- Khlopov, M.Y. Primordial black holes. Res. Astron. Astrophys. 2010, 10, 495–528. [Google Scholar] [CrossRef]
- Sasaki, M.; Suyama, T.; Tanaka, T.; Yokoyama, S. Primordial black holes—perspectives in gravitational wave astronomy. Class. Quantum Gravity 2018, 35, 063001. [Google Scholar] [CrossRef]
- Inomata, K.; Kawasaki, M.; Mukaida, K.; Tada, Y.; Yanagida, T.T. Inflationary primordial black holes as all dark matter. Phys. Rev. D 2017, 96, 043504. [Google Scholar] [CrossRef]
- Georg, J.; Watson, S. A preferred mass range for primordial black hole formation and black holes as dark matter revisited. J. High Energy Phys. 2017, 2017, 138. [Google Scholar] [CrossRef]
- Carr, B.; Silk, J. Primordial black holes as generators of cosmic structures. Mon. Not. R. Astron. Soc. 2018, 478, 3756–3775. [Google Scholar] [CrossRef]
- Bird, S.; Cholis, I.; Muñoz, J.B.; Ali-Haïmoud, Y.; Kamionkowski, M.; Kovetz, E.D.; Raccanelli, A.; Riess, A.G. Did LIGO Detect Dark Matter? Phys. Rev. Lett. 2016, 116, 201301. [Google Scholar] [CrossRef]
- Ali-Haimoud, Y.E. Electromagnetic probes of primordial black holes as dark matter. arXiv 2019, arXiv:1903.04424. [Google Scholar]
- Clesse, S.; García-Bellido, J. The clustering of massive Primordial Black Holes as Dark Matter: Measuring their mass distribution with Advanced LIGO. Phys. Dark Univ. 2017, 15, 142–147. [Google Scholar] [CrossRef]
- Luis Bernal, J.; Bellomo, N.; Raccanelli, A.; Verde, L. Cosmological implications of Primordial Black Holes. J. Cosmol. Astropart. Phys. 2017, 10, 052. [Google Scholar] [CrossRef]
- Clesse, S.; García-Bellido, J. Massive Primordial Black Holes from Hybrid Inflation as Dark Matter and the seeds of Galaxies. Phys. Rev. D 2015, 92, 023524. [Google Scholar] [CrossRef]
- Clesse, S.; García-Bellido, J.; Orani, S. Detecting the Stochastic Gravitational Wave Background from Primordial Black Hole Formation. arXiv 2018, arXiv:1812.11011. [Google Scholar]
- Tada, Y.; Yokoyama, S. Primordial black hole tower: Dark matter, earth-mass, and LIGO black holes. Phys. Rev. D 2019, 100, 023537. [Google Scholar] [CrossRef]
- Atal, V.; Sanglas, A.; Triantafyllou, N. NANOGrav signal as mergers of Stupendously Large Primordial Black Holes. J. Cosmol. Astropart. Phys. 2021, 06, 022. [Google Scholar] [CrossRef]
- Atal, V.; Sanglas, A.; Triantafyllou, N. LIGO/Virgo black holes and dark matter: The effect of spatial clustering. J. Cosmol. Astropart. Phys. 2020, 11, 036. [Google Scholar] [CrossRef]
- De Luca, V.; Franciolini, G.; Pani, P.; Riotto, A. Primordial Black Holes Confront LIGO/Virgo data: Current situation. J. Cosmol. Astropart. Phys. 2020, 06, 044. [Google Scholar] [CrossRef]
- Bartolo, N.; De Luca, V.; Franciolini, G.; Peloso, M.; Racco, D.; Riotto, A. Testing primordial black holes as dark matter with LISA. Phys. Rev. D 2019, 99, 103521. [Google Scholar] [CrossRef]
- Clesse, S.; García-Bellido, J. Seven Hints for Primordial Black Hole Dark Matter. Phys. Dark Univ. 2018, 22, 137–146. [Google Scholar] [CrossRef]
- Ezquiaga, J.M.; García-Bellido, J.; Vennin, V. The exponential tail of inflationary fluctuations: Consequences for primordial black holes. J. Cosmol. Astropart. Phys. 2020, 03, 029. [Google Scholar] [CrossRef]
- Takhistov, V. Primordial Black Hole Dark Matter and Ways to Find It. In Proceedings of the 40th International Conference on High Energy Physics, Prague, Czech Republic, 30 July–5 August 2020; p. 610. [Google Scholar] [CrossRef]
- Jedamzik, K. Primordial Black Hole Dark Matter and the LIGO/Virgo observations. J. Cosmol. Astropart. Phys. 2020, 09, 022. [Google Scholar] [CrossRef]
- Vallejo-Peña, S.A.; Romano, A.E. Are primordial black holes produced by entropy perturbations in single field inflationary models? J. Cosmol. Astropart. Phys. 2019, 11, 015. [Google Scholar] [CrossRef]
- Kashlinsky, A. LIGO gravitational wave detection, primordial black holes and the near-IR cosmic infrared background anisotropies. Astrophys. J. Lett. 2016, 823, L25. [Google Scholar] [CrossRef]
- Kashlinsky, A.; Arendt, R.G.; Atrio-Barandela, F.; Cappelluti, N.; Ferrara, A.; Hasinger, G. Looking at cosmic near-infrared background radiation anisotropies. Rev. Mod. Phys. 2018, 90, 025006. [Google Scholar] [CrossRef]
- Kashlinsky, A. Cosmological Advection Flows in the Presence of Primordial Black Holes asDark Matter and Formation of First Sources. Phys. Rev. Lett. 2021, 126, 011101. [Google Scholar] [CrossRef]
- Pi, S.; Zhang, Y.l.; Huang, Q.G.; Sasaki, M. Scalaron from R2-gravity as a heavy field. J. Cosmol. Astropart. Phys. 2018, 05, 042. [Google Scholar] [CrossRef]
- Carr, B.; Kuhnel, F. Primordial Black Holes as Dark Matter: Recent Developments. Ann. Rev. Nucl. Part. Sci. 2020, 70, 355–394. [Google Scholar] [CrossRef]
- Bean, R.; Magueijo, J.A. Could supermassive black holes be quintessential primordial black holes? Phys. Rev. D 2002, 66, 063505. [Google Scholar] [CrossRef]
- Bernal, J.L.; Raccanelli, A.; Verde, L.; Silk, J. Signatures of primordial black holes as seeds of supermassive black holes. J. Cosmol. Astropart. Phys. 2018, 05, 017, Erratum in J. Cosmol. Astropart. Phys. 2020, 01, E01. [Google Scholar] [CrossRef]
- Meszaros, P. Primeval black holes and galaxy formation. Astron. Astrophys. 1975, 38, 5–13. [Google Scholar]
- Carr, B.J. Pregalactic black hole accretion and the thermal history of the Universe. Mon. Not. R. Astron. Soc. 1981, 194, 639–668. [Google Scholar] [CrossRef]
- Abbott, B.P.E.A. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Sasaki, M.; Suyama, T.; Tanaka, T.; Yokoyama, S. Primordial Black Hole Scenario for the Gravitational-Wave Event GW150914. Phys. Rev. Lett. 2016, 117, 061101, Erratum in Phys. Rev. Lett. 2018, 121, 059901. [Google Scholar] [CrossRef] [PubMed]
- Franciolini, G.; Baibhav, V.; De Luca, V.; Ng, K.K.Y.; Wong, K.W.K.; Berti, E.; Pani, P.; Riotto, A.; Vitale, S. Quantifying the evidence for primordial black holes in LIGO/Virgo gravitational-wave data. arXiv 2021, arXiv:2111.12693. [Google Scholar]
- Sasaki, M.; Takhistov, V.; Vardanyan, V.; Zhang, Y.l. Establishing the Non-Primordial Origin of Black Hole-Neutron Star Mergers. arXiv 2021, arXiv:2110.09509. [Google Scholar]
- Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, N.; Bouffanais, Y. Search for subsolar-mass binaries in the first half of Advanced LIGO and Virgo’s third observing run. arXiv 2021, arXiv:2109.12197. [Google Scholar]
- Chen, Z.C.; Yuan, C.; Huang, Q.G. Confronting the primordial black hole scenario with the gravitational-wave events detected by LIGO-Virgo. arXiv 2021, arXiv:2108.11740. [Google Scholar]
- De Luca, V.; Desjacques, V.; Franciolini, G.; Pani, P.; Riotto, A. GW190521 Mass Gap Event and the Primordial Black Hole Scenario. Phys. Rev. Lett. 2021, 126, 051101. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Baker, P.T.; Blumer, H.; Bécsy, B.; Brazier, A.; Brook, P.R.; NANOGrav Collaboration. The NANOGrav 12.5 yr Data Set: Search for an Isotropic Stochastic Gravitational-wave Background. Astrophys. J. Lett. 2020, 905, L34. [Google Scholar] [CrossRef]
- Vaskonen, V.; Veermäe, H. Did NANOGrav see a signal from primordial black hole formation? Phys. Rev. Lett. 2021, 126, 051303. [Google Scholar] [CrossRef]
- De Luca, V.; Franciolini, G.; Riotto, A. NANOGrav Data Hints at Primordial Black Holes as Dark Matter. Phys. Rev. Lett. 2021, 126, 041303. [Google Scholar] [CrossRef]
- Kohri, K.; Terada, T. Solar-Mass Primordial Black Holes Explain NANOGrav Hint of Gravitational Waves. Phys. Lett. B 2021, 813, 136040. [Google Scholar] [CrossRef]
- Bian, L.; Cai, R.G.; Liu, J.; Yang, X.Y.; Zhou, R. Evidence for different gravitational-wave sources in the NANOGrav dataset. Phys. Rev. D 2021, 103, L081301. [Google Scholar] [CrossRef]
- Sugiyama, S.; Takhistov, V.; Vitagliano, E.; Kusenko, A.; Sasaki, M.; Takada, M. Testing Stochastic Gravitational Wave Signals from Primordial Black Holes with Optical Telescopes. Phys. Lett. B 2021, 814, 136097. [Google Scholar] [CrossRef]
- Domènech, G.; Pi, S. NANOGrav Hints on Planet-Mass Primordial Black Holes. arXiv 2020, arXiv:2010.03976. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Mohanty, S.; Parashari, P. Implications of the NANOGrav result on primordial gravitational waves in nonstandard cosmologies. Phys. Rev. D 2021, 103, 063532. [Google Scholar] [CrossRef]
- Inomata, K.; Kawasaki, M.; Mukaida, K.; Yanagida, T.T. NANOGrav Results and LIGO-Virgo Primordial Black Holes in Axionlike Curvaton Models. Phys. Rev. Lett. 2021, 126, 131301. [Google Scholar] [CrossRef]
- Germani, C.; Musco, I. Abundance of Primordial Black Holes Depends on the Shape of the Inflationary Power Spectrum. Phys. Rev. Lett. 2019, 122, 141302. [Google Scholar] [CrossRef]
- Nadezhin, D.K.; Novikov, I.D.; Polnarev, A.G. The hydrodynamics of primordial black hole formation. Sov. Astron. 1978, 22, 129–138. [Google Scholar]
- Niemeyer, J.C.; Jedamzik, K. Near-Critical Gravitational Collapse and the Initial Mass Function of Primordial Black Holes. Phys. Rev. Lett. 1998, 80, 5481–5484. [Google Scholar] [CrossRef]
- Niemeyer, J.C.; Jedamzik, K. Dynamics of primordial black hole formation. Phys. Rev. D 1999, 59, 124013. [Google Scholar] [CrossRef]
- Hawke, I.; Stewart, J.M. The dynamics of primordial black-hole formation. Class. Quantum Gravity 2002, 19, 3687–3707. [Google Scholar] [CrossRef]
- Musco, I.; Miller, J.C.; Polnarev, A.G. Primordial black hole formation in the radiative era: Investigation of the critical nature of the collapse. Class. Quantum Gravity 2009, 26, 235001. [Google Scholar] [CrossRef]
- Koike, T.; Hara, T.; Adachi, S. Critical Behaviour in Gravitational Collapse of Radiation Fluid: A Renormalization Group (Linear Perturbation) Analysis. Phys. Rev. Lett. 1995, 74, 5170–5173. [Google Scholar] [CrossRef] [PubMed]
- Maison, D. Nonuniversality of critical behaviour in spherically symmetric gravitational collapse. Phys. Lett. B 1996, 366, 82–84. [Google Scholar] [CrossRef]
- Evans, C.R.; Coleman, J.S. Critical phenomena and self-similarity in the gravitational collapse of radiation fluid. Phys. Rev. Lett. 1994, 72, 1782–1785. [Google Scholar] [CrossRef]
- May, M.M.; White, R.H. Stellar Dynamics and Gravitational Collapse. Methods Comput. Phys. 1967, 7, 219–258. [Google Scholar]
- Misner, C.W.; Sharp, D.H. Relativistic Equations for Adiabatic, Spherically Symmetric Gravitational Collapse. Phys. Rev. 1964, 136, B571–B576. [Google Scholar] [CrossRef]
- Hernandez, W.C., Jr.; Misner, C.W. Observer Time as a Coordinate in Relativistic Spherical Hydrodynamics. Astrophys. J. 1966, 143, 452. [Google Scholar] [CrossRef]
- Baumgarte, T.W.; Shapiro, S.L.; Teukolsky, S.A. Computing supernova collapse to neutron stars and black holes. Astrophys. J. 1995, 443, 717–734. [Google Scholar] [CrossRef]
- Musco, I.; Miller, J.C.; Rezzolla, L. Computations of primordial black-hole formation. Class. Quantum Gravity 2005, 22, 1405–1424. [Google Scholar] [CrossRef]
- Carr, B.J. The primordial black hole mass spectrum. Astrophys. J. 1975, 201, 1–19. [Google Scholar] [CrossRef]
- Harada, T.; Yoo, C.M.; Kohri, K. Threshold of primordial black hole formation. Phys. Rev. D 2013, 88, 084051. [Google Scholar] [CrossRef]
- Harada, T.; Yoo, C.M.; Nakama, T.; Koga, Y. Cosmological long-wavelength solutions and primordial black hole formation. Phys. Rev. D 2015, 91, 084057. [Google Scholar] [CrossRef]
- Shibata, M.; Sasaki, M. Black hole formation in the Friedmann universe: Formulation and computation in numerical relativity. Phys. Rev. D 1999, 60, 084002. [Google Scholar] [CrossRef]
- Nakama, T. The double formation of primordial black holes. J. Cosmol. Astropart. Phys. 2014, 10, 040. [Google Scholar] [CrossRef]
- Musco, I. Threshold for primordial black holes: Dependence on the shape of the cosmological perturbations. Phys. Rev. D 2019, 100, 123524. [Google Scholar] [CrossRef]
- Escrivà, A. Simulation of primordial black hole formation using pseudospectral methods. Phys. Dark Universe 2020, 27, 100466. [Google Scholar] [CrossRef]
- Hidalgo, J.C.; Polnarev, A.G. Probability of primordial black hole formation and its dependence on the radial profile of initial configurations. Phys. Rev. D 2009, 79, 044006. [Google Scholar] [CrossRef]
- Nakama, T.; Harada, T.; Polnarev, A.; Yokoyama, J. Identifying the most crucial parameters of the initial curvature profile for primordial black hole formation. J. Cosmol. Astropart. Phys. 2014, 2014, 037. [Google Scholar] [CrossRef]
- Escrivà, A.; Germani, C.; Sheth, R.K. Universal threshold for primordial black hole formation. Phys. Rev. D 2020, 101, 044022. [Google Scholar] [CrossRef]
- Escrivà, A.; Germani, C.; Sheth, R.K. Analytical thresholds for black hole formation in general cosmological backgrounds. J. Cosmol. Astropart. Phys. 2021, 01, 030. [Google Scholar] [CrossRef]
- Gundlach, C. Critical phenomena in gravitational collapse. Living Rev. Rel. 1999, 2, 4. [Google Scholar] [CrossRef]
- Harada, T.; Carr, B.J. Upper limits on the size of a primordial black hole. Phys. Rev. D 2005, 71, 104009. [Google Scholar] [CrossRef]
- Escrivà, A.; Romano, A.E. Effects of the shape of curvature peaks on the size of primordial black holes. J. Cosmol. Astropart. Phys. 2021, 05, 066. [Google Scholar] [CrossRef]
- Green, A.M.; Kavanagh, B.J. Primordial Black Holes as a dark matter candidate. J. Phys. Nucl. Part. Phys. 2021, 48, 043001. [Google Scholar] [CrossRef]
- Yuan, C.; Huang, Q.G. A topic review on probing primordial black hole dark matter with scalar induced gravitational waves. arXiv 2021, arXiv:2103.04739. [Google Scholar] [CrossRef]
- Villanueva-Domingo, P.; Mena, O.; Palomares-Ruiz, S. A brief review on primordial black holes as dark matter. Front. Astron. Space Sci. 2021, 8, 87. [Google Scholar] [CrossRef]
- Domènech, G. Scalar induced gravitational waves review. Universe 2021, 7, 398. [Google Scholar] [CrossRef]
- Allahverdi, R. The First Three Seconds: A Review of Possible Expansion Histories of the Early Universe. arXiv 2020, arXiv:2006.16182. [Google Scholar] [CrossRef]
- Neilsen, D.W.; Choptuik, M.W. Critical phenomena in perfect fluids. Class. Quant. Grav. 2000, 17, 761–782. [Google Scholar] [CrossRef]
- Musco, I.; Miller, J.C. Primordial black hole formation in the early universe: Critical behaviour and self-similarity. Class. Quantum Gravity 2013, 30, 145009. [Google Scholar] [CrossRef]
- Germani, C.; Sheth, R.K. Nonlinear statistics of primordial black holes from Gaussian curvature perturbations. Phys. Rev. D 2020, 101, 063520. [Google Scholar] [CrossRef]
- De Luca, V.; Franciolini, G.; Kehagias, A.; Peloso, M.; Riotto, A.; Ünal, C. The Ineludible non-Gaussianity of the Primordial Black Hole Abundance. J. Cosmol. Astropart. Phys. 2019, 07, 048. [Google Scholar] [CrossRef]
- Kalaja, A.; Bellomo, N.; Bartolo, N.; Bertacca, D.; Matarrese, S.; Musco, I.; Raccanelli, A.; Verde, L. From Primordial Black Holes Abundance to Primordial Curvature Power Spectrum (and back). J. Cosmol. Astropart. Phys. 2019, 10, 031. [Google Scholar] [CrossRef]
- Erfani, E.; Kameli, H.; Baghram, S. Primordial Black Holes in the Excursion Set Theory. Mon. Not. R. Astron. Soc. 2021, 505, 1787–1793. [Google Scholar] [CrossRef]
- Wu, Y.P. Peak statistics for the primordial black hole abundance. Phys. Dark Univ. 2020, 30, 100654. [Google Scholar] [CrossRef]
- De Luca, V.; Franciolini, G.; Riotto, A. On the Primordial Black Hole Mass Function for Broad Spectra. Phys. Lett. B 2020, 807, 135550. [Google Scholar] [CrossRef]
- Young, S.; Musso, M. Application of peaks theory to the abundance of primordial black holes. J. Cosmol. Astropart. Phys. 2020, 11, 022. [Google Scholar] [CrossRef]
- Yoo, C.M.; Harada, T.; Hirano, S.; Kohri, K. Abundance of Primordial Black Holes in Peak Theory for an Arbitrary Power Spectrum. Prog. Theor. Exp. Phys. 2021, 2021, 013E02. [Google Scholar] [CrossRef]
- Yoo, C.M.; Gong, J.O.; Yokoyama, S. Abundance of primordial black holes with local non-Gaussianity in peak theory. J. Cosmol. Astropart. Phys. 2019, 09, 033. [Google Scholar] [CrossRef]
- Gow, A.D.; Byrnes, C.T.; Cole, P.S.; Young, S. The power spectrum on small scales: Robust constraints and comparing PBH methodologies. J. Cosmol. Astropart. Phys. 2021, 02, 002. [Google Scholar] [CrossRef]
- Young, S. The primordial black hole formation criterion re-examined: Parametrisation, timing and the choice of window function. Int. J. Mod. Phys. D 2019, 29, 2030002. [Google Scholar] [CrossRef]
- Young, S.; Musco, I.; Byrnes, C.T. Primordial black hole formation and abundance: Contribution from the non-linear relation between the density and curvature perturbation. J. Cosmol. Astropart. Phys. 2019, 11, 012. [Google Scholar] [CrossRef]
- Young, S.; Byrnes, C.T. Primordial black holes in non-Gaussian regimes. J. Cosmol. Astropart. Phys. 2013, 08, 052. [Google Scholar] [CrossRef]
- Young, S.; Byrnes, C.T.; Sasaki, M. Calculating the mass fraction of primordial black holes. J. Cosmol. Astropart. Phys. 2014, 07, 045. [Google Scholar] [CrossRef]
- Yoo, C.M.; Harada, T.; Garriga, J.; Kohri, K. PBH abundance from random Gaussian curvature perturbations and a local density threshold. arXiv 2018, arXiv:1805.03946. [Google Scholar]
- Suyama, T.; Yokoyama, S. A novel formulation of the primordial black hole mass function. Prog. Theor. Exp. Phys. 2020, 2020, 023E03. [Google Scholar] [CrossRef]
- Ando, K.; Inomata, K.; Kawasaki, M. Primordial black holes and uncertainties in the choice of the window function. Phys. Rev. D 2018, 97, 103528. [Google Scholar] [CrossRef]
- Zaballa, I.; Green, A.M.; Malik, K.A.; Sasaki, M. Constraints on the primordial curvature perturbation from primordial black holes. J. Cosmol. Astropart. Phys. 2007, 03, 010. [Google Scholar] [CrossRef]
- Yokoyama, J. Cosmological constraints on primordial black holes produced in the near critical gravitational collapse. Phys. Rev. D 1998, 58, 107502. [Google Scholar] [CrossRef]
- Tada, Y.; Vennin, V. Statistics of coarse-grained cosmological fields in stochastic inflation. arXiv 2021, arXiv:2111.15280. [Google Scholar]
- Press, W.H.; Schechter, P. Formation of galaxies and clusters of galaxies by selfsimilar gravitational condensation. Astrophys. J. 1974, 187, 425–438. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Bond, J.R.; Kaiser, N.; Szalay, A.S. The Statistics of Peaks of Gaussian Random Fields. Astrophys. J. 1986, 304, 15. [Google Scholar] [CrossRef]
- Green, A.M.; Liddle, A.R.; Malik, K.A.; Sasaki, M. A New calculation of the mass fraction of primordial black holes. Phys. Rev. D 2004, 70, 041502. [Google Scholar] [CrossRef]
- Yoo, C.M.; Harada, T.; Garriga, J.; Kohri, K. Primordial black hole abundance from random Gaussian curvature perturbations and a local density threshold. Prog. Theor. Exp. Phys. 2018, 2018, 123E01. [Google Scholar] [CrossRef]
- Carr, B.; Raidal, M.; Tenkanen, T.; Vaskonen, V.; Veermäe, H. Primordial black hole constraints for extended mass functions. Phys. Rev. D 2017, 96, 023514. [Google Scholar] [CrossRef]
- Tokeshi, K.; Inomata, K.; Yokoyama, J. Window function dependence of the novel mass function of primordial black holes. J. Cosmol. Astropart. Phys. 2020, 12, 038. [Google Scholar] [CrossRef]
- Salopek, D.S.; Bond, J.R. Nonlinear evolution of long-wavelength metric fluctuations in inflationary models. Phys. Rev. D 1990, 42, 3936–3962. [Google Scholar] [CrossRef]
- Polnarev, A.G.; Musco, I. Curvature profiles as initial conditions for primordial black hole formation. Class. Quantum Gravity 2007, 24, 1405–1431. [Google Scholar] [CrossRef]
- Arnowitt, R.L.; Deser, S.; Misner, C.W. The Dynamics of general relativity. Gen. Rel. Grav. 2008, 40, 1997–2027. [Google Scholar] [CrossRef]
- Arnowitt, R.; Deser, S.; Misner, C.W. Dynamical Structure and Definition of Energy in General Relativity. Phys. Rev. 1959, 116, 1322–1330. [Google Scholar] [CrossRef]
- Tanaka, Y.; Sasaki, M. Gradient expansion approach to nonlinear superhorizon perturbations. II. A Single scalar field. Prog. Theor. Phys. 2007, 118, 455–473. [Google Scholar] [CrossRef]
- Lyth, D.H.; Malik, K.A.; Sasaki, M. A General proof of the conservation of the curvature perturbation. J. Cosmol. Astropart. Phys. 2005, 05, 004. [Google Scholar] [CrossRef]
- Sugiyama, N.S.; Komatsu, E.; Futamase, T. δN formalism. Phys. Rev. D 2013, 87, 023530. [Google Scholar] [CrossRef]
- Romano, A.E.; Sasaki, M.; Starobinsky, A.A. Effects of inhomogeneities on apparent cosmological observables: ‘Fake’ evolving dark energy. Eur. Phys. J. C 2012, 72, 2242. [Google Scholar] [CrossRef]
- Polnarev, A.G.; Nakama, T.; Yokoyama, J. Self-consistent initial conditions for primordial black hole formation. J. Cosmol. Astropart. Phys. 2012, 09, 027. [Google Scholar] [CrossRef]
- Kopp, M.; Hofmann, S.; Weller, J. Separate Universes Do Not Constrain Primordial Black Hole Formation. Phys. Rev. D 2011, 83, 124025. [Google Scholar] [CrossRef]
- Mello, M.M.C.; Maciel, A.; Zanchin, V.T. Evolving black holes from conformal transformations of static solutions. Phys. Rev. D 2017, 95, 084031. [Google Scholar] [CrossRef]
- Helou, A.; Musco, I.; Miller, J.C. Causal Nature and Dynamics of Trapping Horizons in Black Hole Collapse. Class. Quant. Grav. 2017, 34, 135012. [Google Scholar] [CrossRef]
- Dafermos, M. Spherically symmetric spacetimes with a trapped surface. Class. Quantum Gravity 2005, 22, 2221–2232. [Google Scholar] [CrossRef]
- Williams, C. Asymptotic Behaviour of Spherically Symmetric Marginally Trapped Tubes. Ann. Henri Poincare 2008, 9, 1029–1067. [Google Scholar] [CrossRef]
- Booth, I.; Brits, L.; Gonzalez, J.A.; Van Den Broeck, C. Marginally trapped tubes and dynamical horizons. Class. Quant. Grav. 2006, 23, 413–440. [Google Scholar] [CrossRef]
- Ashtekar, A.; Krishnan, B. Isolated and dynamical horizons and their applications. Living Rev. Rel. 2004, 7, 10. [Google Scholar] [CrossRef]
- Faraoni, V. Evolving Black Hole Horizons in General Relativity and Alternative Gravity. Galaxies 2013, 1, 114–179. [Google Scholar] [CrossRef]
- Hayward, S.A. General laws of black-hole dynamics. Phys. Rev. D 1994, 49, 6467–6474. [Google Scholar] [CrossRef]
- Jaramillo, J.L.; Macedo, R.P.; Moesta, P.; Rezzolla, L. Black-hole horizons as probes of black-hole dynamics. II. Geometrical insights. Phys. Rev. D 2012, 85, 084031. [Google Scholar] [CrossRef]
- Yoo, C.M.; Okawa, H. Black hole universe with a cosmological constant. Phys. Rev. D 2014, 89, 123502. [Google Scholar] [CrossRef]
- Harada, T.; Carr, B.J. Growth of primordial black holes in a universe containing a massless scalar field. Phys. Rev. D 2005, 71, 104010. [Google Scholar] [CrossRef]
- Custodio, P.S.; Horvath, J.E. Evolution of a primordial black hole population. Phys. Rev. D 1998, 58, 023504. [Google Scholar] [CrossRef]
- Guedens, R.; Clancy, D.; Liddle, A.R. Primordial black holes in braneworld cosmologies: Accretion after formation. Phys. Rev. D 2002, 66, 083509. [Google Scholar] [CrossRef]
- Nayak, B.; Singh, L.P. Accretion, primordial black holes and standard cosmology. Pramana 2011, 76, 173–181. [Google Scholar] [CrossRef]
- Carr, B.; Harada, T.; Maeda, H. Can a primordial black hole or wormhole grow as fast as the universe? Class. Quant. Grav. 2010, 27, 183101. [Google Scholar] [CrossRef]
- Deng, H.; Garriga, J.; Vilenkin, A. Primordial black hole and wormhole formation by domain walls. J. Cosmol. Astropart. Phys. 2017, 2017, 050. [Google Scholar] [CrossRef]
- Kühnel, F.; Rampf, C.; Sandstad, M. Effects of Critical Collapse on Primordial Black-Hole Mass Spectra. Eur. Phys. J. C 2016, 76, 93. [Google Scholar] [CrossRef]
- Baumgarte, T.W.; Shapiro, S.L. Numerical Relativity: Solving Einstein’s Equations on the Computer; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Lehner, L. Numerical relativity: A Review. Class. Quant. Grav. 2001, 18, R25–R86. [Google Scholar] [CrossRef]
- Palenzuela, C. Introduction to Numerical Relativity. Front. Astron. Space Sci. 2020, 7, 58. [Google Scholar] [CrossRef]
- Gourgoulhon, E. 3 + 1 formalism and bases of numerical relativity. arXiv 2007, arXiv:gr-qc/0703035. [Google Scholar]
- Grandclément, P.; Novak, J. Spectral Methods for Numerical Relativity. Living Rev. Relativ. 2009, 12, 1. [Google Scholar] [CrossRef] [PubMed]
- Font, J.A. Numerical hydrodynamics in general relativity. Living Rev. Rel. 2000, 3, 2. [Google Scholar] [CrossRef]
- Clough, K.; Figueras, P.; Finkel, H.; Kunesch, M.; Lim, E.A.; Tunyasuvunakool, S. GRChombo: Numerical Relativity with Adaptive Mesh Refinement. Class. Quant. Grav. 2015, 32, 245011. [Google Scholar] [CrossRef]
- Löffler, F.; Faber, J.; Bentivegna, E.; Bode, T.; Diener, P.; Haas, R.; Laguna, P. The Einstein Toolkit: A Community Computational Infrastructure for Relativistic Astrophysics. Class. Quant. Grav. 2012, 29, 115001. [Google Scholar] [CrossRef]
- Ruchlin, I.; Etienne, Z.B.; Baumgarte, T.W. SENR/NRPy+: Numerical Relativity in Singular Curvilinear Coordinate Systems. Phys. Rev. D 2018, 97, 064036. [Google Scholar] [CrossRef]
- Bloomfield, J.; Bulhosa, D.; Face, S. Formalism for Primordial Black Hole Formation in Spherical Symmetry. arXiv 2015, arXiv:1504.02071. [Google Scholar]
- Albert Escrivà Webpage. 2021. Available online: https://aescriva.wixsite.com/albertescriva (accessed on 15 November 2021).
- Guo, B. Spectral Methods and Their Applications; World Scientific: Shanghai, China, 1998. [Google Scholar] [CrossRef]
- Hussaini, M.Y.; Zang, T.A. Spectral Methods in Fluid Dynamics. Annu. Rev. Fluid Mech. 1987, 19, 339–367. [Google Scholar] [CrossRef]
- Hesthaven, J.S.; Gottlieb, S.; Gottlieb, D.I. Spectral Methods for Time-Dependent Problems; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Santos-Oliván, D.; Sopuerta, C.F. New Features of Gravitational Collapse in Anti–de Sitter Spacetimes. Phys. Rev. Lett. 2016, 116, 041101. [Google Scholar] [CrossRef]
- Canizares, P.; Sopuerta, C.F.; Jaramillo, J.L. Pseudospectral collocation methods for the computation of the self-force on a charged particle: Generic orbits around a Schwarzschild black hole. Phys. Rev. D 2010, 82, 044023. [Google Scholar] [CrossRef]
- Santos-Oliván, D.; Sopuerta, C.F. Numerical Relativity with Arbitrary Precision Arithmetic: Applications to Gravitational Collapse. arXiv 2018, arXiv:1803.00858. [Google Scholar]
- Santos-Oliván, D.; Sopuerta, C.F. Moving closer to the collapse of a massless scalar field in spherically symmetric anti–de Sitter spacetimes. Phys. Rev. D 2016, 93, 104002. [Google Scholar] [CrossRef]
- Meringolo, C.; Servidio, S.; Veltri, P. A spectral method algorithm for numerical simulations of gravitational fields. Class. Quant. Grav. 2021, 38, 075027. [Google Scholar] [CrossRef]
- Bonazzola, S.; Gourgoulhon, E.; Marck, J.A. Spectral methods in general relativistic astrophysics. J. Comput. Appl. Math. 1999, 109, 433–473. [Google Scholar] [CrossRef]
- Sengupta, T.K.; Sundaram, P.; Sengupta, A. Analysis of pseudospectral methods used for numerical simulation of turbulence. arXiv 2021, arXiv:2109.00255. [Google Scholar]
- Moxon, J.; Scheel, M.A.; Teukolsky, S.A.; Deppe, N.; Fischer, N.; Hébert, F.; Kidder, L.E.; Throwe, W. The SpECTRE Cauchy-characteristic evolution system for rapid, precise waveform extraction. arXiv 2021, arXiv:2110.08635. [Google Scholar]
- Alcoforado, M.A.; Aranha, R.F.; Barreto, W.O.; de Oliveira, H.P. Multidomain Galerkin-Collocation method: Spherical collapse of scalar fields II. Class. Quantum Gravity 2021, 38, 225004. [Google Scholar] [CrossRef]
- Alcoforado, M.A.; Barreto, W.O.; de Oliveira, H.P. Multidomain Galerkin-Collocation method: Characteristic spherical collapse of scalar fields. Gen. Rel. Grav. 2021, 53, 42. [Google Scholar] [CrossRef]
- Oltean, M.; Sopuerta, C.F.; Spallicci, A.D.A.M. Particle-without-Particle: A practical pseudospectral collocation method for linear partial differential equations with distributional sources. J. Sci. Comput. 2019, 79, 827. [Google Scholar] [CrossRef]
- Frauendiener, J.; Hennig, J. Fully pseudospectral solution of the conformally invariant wave equation near the cylinder at spacelike infinity. II: Schwarzschild background. Class. Quant. Grav. 2017, 34, 045005. [Google Scholar] [CrossRef]
- Schwabe, B.; Gosenca, M.; Behrens, C.; Niemeyer, J.C.; Easther, R. Simulating mixed fuzzy and cold dark matter. Phys. Rev. D 2020, 102, 083518. [Google Scholar] [CrossRef]
- Edwards, F.; Kendall, E.; Hotchkiss, S.; Easther, R. PyUltraLight: A Pseudo-Spectral Solver for Ultralight Dark Matter Dynamics. J. Cosmol. Astropart. Phys. 2018, 10, 027. [Google Scholar] [CrossRef]
- Musoke, N.; Hotchkiss, S.; Easther, R. Lighting the Dark: Evolution of the Postinflationary Universe. Phys. Rev. Lett. 2020, 124, 061301. [Google Scholar] [CrossRef]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods; DOVER: Mineola, NY, USA, 2000. [Google Scholar]
- Trefethen, L.N. Spectral Methods in MATLAB; SIAM: Mineola, NY, USA, 2000. [Google Scholar]
- Kidder, L.E.; Scheel, M.A.; Teukolsky, S.A.; Carlson, E.D.; Cook, G.B. Black hole evolution by spectral methods. Phys. Rev. D 2000, 62, 084032. [Google Scholar] [CrossRef]
- Atal, V.; Germani, C. The role of non-Gaussianities in Primordial Black Hole formation. Phys. Dark Univ. 2019, 24, 100275. [Google Scholar] [CrossRef]
- Atal, V.; Garriga, J.; Marcos-Caballero, A. Primordial black hole formation with non-Gaussian curvature perturbations. J. Cosmol. Astropart. Phys. 2019, 09, 073. [Google Scholar] [CrossRef]
- Passaglia, S.; Hu, W.; Motohashi, H. Primordial black holes and local non-Gaussianity in canonical inflation. Phys. Rev. D 2019, 99, 043536. [Google Scholar] [CrossRef]
- Cai, Y.F.; Chen, X.; Namjoo, M.H.; Sasaki, M.; Wang, D.G.; Wang, Z. Revisiting non-Gaussianity from non-attractor inflation models. J. Cosmol. Astropart. Phys. 2018, 05, 012. [Google Scholar] [CrossRef]
- Bullock, J.S.; Primack, J.R. NonGaussian fluctuations and primordial black holes from inflation. Phys. Rev. D 1997, 55, 7423–7439. [Google Scholar] [CrossRef]
- Pattison, C.; Vennin, V.; Assadullahi, H.; Wands, D. Quantum diffusion during inflation and primordial black holes. J. Cosmol. Astropart. Phys. 2017, 2017, 046. [Google Scholar] [CrossRef]
- Pina Avelino, P. Primordial black hole constraints on non-Gaussian inflation models. Phys. Rev. D 2005, 72, 124004. [Google Scholar] [CrossRef]
- Riccardi, F.; Taoso, M.; Urbano, A. Solving peak theory in the presence of local non-Gaussianities. J. Cosmol. Astropart. Phys. 2021, 08, 060. [Google Scholar] [CrossRef]
- Young, S.; Byrnes, C.T. Long-short wavelength mode coupling tightens primordial black hole constraints. Phys. Rev. D 2015, 91, 083521. [Google Scholar] [CrossRef]
- Young, S.; Regan, D.; Byrnes, C.T. Influence of large local and non-local bispectra on primordial black hole abundance. J. Cosmol. Astropart. Phys. 2016, 02, 029. [Google Scholar] [CrossRef][Green Version]
- Hidalgo, J.C. The effect of non-Gaussian curvature perturbations on the formation of primordial black holes. arXiv 2007, arXiv:0708.3875. [Google Scholar]
- Atal, V.; Domènech, G. Probing non-Gaussianities with the high frequency tail of induced gravitational waves. J. Cosmol. Astropart. Phys. 2021, 06, 001. [Google Scholar] [CrossRef]
- Kitajima, N.; Tada, Y.; Yokoyama, S.; Yoo, C.M. Primordial black holes in peak theory with a non-Gaussian tail. J. Cosmol. Astropart. Phys. 2021, 10, 053. [Google Scholar] [CrossRef]
- Davies, M.W.; Carrilho, P.; Mulryne, D.J. Non-Gaussianity in inflationary scenarios for primordial black holes. arXiv 2021, arXiv:2110.08189. [Google Scholar]
- Taoso, M.; Urbano, A. Non-Gaussianities for primordial black hole formation. J. Cosmol. Astropart. Phys. 2021, 08, 016. [Google Scholar] [CrossRef]
- Cai, Y.F.; Ma, X.H.; Sasaki, M.; Wang, D.G.; Zhou, Z. One Small Step for an Inflaton, One Giant Leap for Inflation: A novel non-Gaussian tail and primordial black holes. arXiv 2021, arXiv:2112.13836. [Google Scholar]
- Kehagias, A.; Musco, I.; Riotto, A. Non-Gaussian Formation of Primordial Black Holes: Effects on the Threshold. arXiv 2019, arXiv:1906.07135. [Google Scholar] [CrossRef]
- Atal, V.; Cid, J.; Escrivà, A.; Garriga, J. PBH in single field inflation: The effect of shape dispersion and non-Gaussianities. J. Cosmol. Astropart. Phys. 2020, 05, 022. [Google Scholar] [CrossRef]
- Musco, I.; De Luca, V.; Franciolini, G.; Riotto, A. Threshold for primordial black holes. II. A simple analytic prescription. Phys. Rev. D 2021, 103, 063538. [Google Scholar] [CrossRef]
- Deng, H.; Vilenkin, A. Primordial black hole formation by vacuum bubbles. J. Cosmol. Astropart. Phys. 2017, 12, 044. [Google Scholar] [CrossRef]
- Harada, T.; Yoo, C.M.; Kohri, K.; Nakao, K.I. Spins of primordial black holes formed in the matter-dominated phase of the Universe. Phys. Rev. D 2017, 96, 083517, Erratum in Phys. Rev. D 2019, 99, 069904. [Google Scholar] [CrossRef]
- Khlopov, M.Y.; Malomed, B.A.; Zeldovich, Y.B. Gravitational instability of scalar fields and formation of primordial black holes. Mon. Not. R. Astron. Soc. 1985, 215, 575–589. [Google Scholar] [CrossRef]
- Hidalgo, J.C.; De Santiago, J.; German, G.; Barbosa-Cendejas, N.; Ruiz-Luna, W. Collapse threshold for a cosmological Klein Gordon field. Phys. Rev. D 2017, 96, 063504. [Google Scholar] [CrossRef]
- Carr, B.; Tenkanen, T.; Vaskonen, V. Primordial black holes from inflaton and spectator field perturbations in a matter-dominated era. Phys. Rev. D 2017, 96, 063507. [Google Scholar] [CrossRef]
- Carrion, K.; Hidalgo, J.C.; Montiel, A.; Padilla, L.E. Complex Scalar Field Reheating and Primordial Black Hole production. J. Cosmol. Astropart. Phys. 2021, 07, 001. [Google Scholar] [CrossRef]
- Martin, J.; Papanikolaou, T.; Pinol, L.; Vennin, V. Metric preheating and radiative decay in single-field inflation. J. Cosmol. Astropart. Phys. 2020, 05, 003. [Google Scholar] [CrossRef]
- Padilla, L.E.; Hidalgo, J.C.; Malik, K.A. A new mechanism for primordial black hole formation during reheating. arXiv 2021, arXiv:2110.14584. [Google Scholar]
- de Jong, E.; Aurrekoetxea, J.C.; Lim, E.A. Primordial black hole formation with full numerical relativity. arXiv 2021, arXiv:2109.04896. [Google Scholar]
- Khlopov, M.; Polnarev, A. Primordial black holes as a cosmological test of grand unification. Phys. Lett. B 1980, 97, 383–387. [Google Scholar] [CrossRef]
- Harada, T.; Jhingan, S. Spherical and nonspherical models of primordial black hole formation: Exact solutions. Prog. Theor. Exp. Phys. 2016, 2016, 093E04. [Google Scholar] [CrossRef]
- Harada, T.; Goymer, C.; Carr, B.J. Tolman-Bondi collapse in scalar tensor theories as a probe of gravitational memory. Phys. Rev. D 2002, 66, 104023. [Google Scholar] [CrossRef]
- Kokubu, T.; Kyutoku, K.; Kohri, K.; Harada, T. Effect of Inhomogeneity on Primordial Black Hole Formation in the Matter Dominated Era. Phys. Rev. D 2018, 98, 123024. [Google Scholar] [CrossRef]
- Harada, T.; Yoo, C.M.; Kohri, K.; Nakao, K.I.; Jhingan, S. Primordial black hole formation in the matter-dominated phase of the Universe. Astrophys. J. 2016, 833, 61. [Google Scholar] [CrossRef]
- Flores, M.M.; Kusenko, A. Spins of primordial black holes formed in different cosmological scenarios. Phys. Rev. D 2021, 104, 063008. [Google Scholar] [CrossRef]
- Kühnel, F.; Sandstad, M. Ellipsoidal collapse and primordial black hole formation. Phys. Rev. D 2016, 94, 063514. [Google Scholar] [CrossRef]
- Yoo, C.M.; Harada, T.; Okawa, H. Threshold of primordial black hole formation in nonspherical collapse. Phys. Rev. D 2020, 102, 043526. [Google Scholar] [CrossRef]
- He, M.; Suyama, T. Formation threshold of rotating primordial black holes. Phys. Rev. D 2019, 100, 063520. [Google Scholar] [CrossRef]
- Musco, I.; Papanikolaou, T. Primordial black hole formation for an anisotropic perfect fluid: Initial conditions and estimation of the threshold. arXiv 2021, arXiv:2110.05982. [Google Scholar]
- Carr, B.; Clesse, S.; García-Bellido, J. Primordial black holes from the QCD epoch: Linking dark matter, baryogenesis and anthropic selection. Mon. Not. R. Astron. Soc. 2021, 501, 1426–1439. [Google Scholar] [CrossRef]
- Widerin, P.; Schmid, C. Primordial black holes from the QCD transition? arXiv 1998, arXiv:astro-ph/9808142. [Google Scholar]
- Boeckel, T.; Schettler, S.; Schaffner-Bielich, J. The Cosmological QCD Phase Transition Revisited. Prog. Part. Nucl. Phys. 2011, 66, 266–270. [Google Scholar] [CrossRef]
- Jedamzik, K. Primordial black hole formation during the QCD epoch. Phys. Rev. D 1997, 55, 5871–5875. [Google Scholar] [CrossRef]
- Byrnes, C.T.; Hindmarsh, M.; Young, S.; Hawkins, M.R.S. Primordial black holes with an accurate QCD equation of state. J. Cosmol. Astropart. Phys. 2018, 08, 041. [Google Scholar] [CrossRef]
- Gao, F.; Oldengott, I.M. Cosmology meets functional QCD: First-order cosmic QCD transition induced by large lepton asymmetries. arXiv 2021, arXiv:2106.11991. [Google Scholar]
- Abe, K.T.; Tada, Y.; Ueda, I. Induced gravitational waves as a cosmological probe of the sound speed during the QCD phase transition. J. Cosmol. Astropart. Phys. 2021, 06, 048. [Google Scholar] [CrossRef]
- Clesse, S.; Garcia-Bellido, J. GW190425, GW190521 and GW190814: Three candidate mergers of primordial black holes from the QCD epoch. arXiv 2020, arXiv:2007.06481. [Google Scholar]
- Carr, B.; Clesse, S.; García-Bellido, J.; Kühnel, F. Cosmic conundra explained by thermal history and primordial black holes. Phys. Dark Univ. 2021, 31, 100755. [Google Scholar] [CrossRef]
- Sobrinho, J.L.G.; Augusto, P.; Gonçalves, A.L. New thresholds for Primordial Black Hole formation during the QCD phase transition. Mon. Not. R. Astron. Soc. 2016, 463, 2348–2357. [Google Scholar] [CrossRef]
- Borsányi, S.; Fodor, Z.; Guenther, J.; Kampert, K.H.; Katz, S.D.; Kawanai, T.; Kovacs, T.G.; Mages, S.W.; Pasztor, A.; Pittler, F.; et al. Calculation of the axion mass based on high-temperature lattice quantum chromodynamics. Nature 2016, 539, 69–71. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, T.; Buchoff, M.I.; Christ, N.H.; Ding, H.T.; Gupta, R.; Jung, C.; Karsch, F.; Lin, Z.; Mawhinney, R.D.; McGlynn, G.; et al. QCD Phase Transition with Chiral Quarks and Physical Quark Masses. Phys. Rev. Lett. 2014, 113, 082001. [Google Scholar] [CrossRef] [PubMed]
- Kusenko, A.; Shaposhnikov, M.E. Supersymmetric Q balls as dark matter. Phys. Lett. B 1998, 418, 46–54. [Google Scholar] [CrossRef]
- Ballesteros, G.; Rey, J.; Rompineve, F. Detuning primordial black hole dark matter with early matter domination and axion monodromy. J. Cosmol. Astropart. Phys. 2020, 06, 014. [Google Scholar] [CrossRef]
- Cotner, E.; Kusenko, A. Primordial Black Holes from Supersymmetry in the Early Universe. Phys. Rev. Lett. 2017, 119, 031103. [Google Scholar] [CrossRef]
- Cotner, E.; Kusenko, A. Primordial black holes from scalar field evolution in the early universe. Phys. Rev. D 2017, 96, 103002. [Google Scholar] [CrossRef]
- Cotner, E.; Kusenko, A.; Takhistov, V. Primordial Black Holes from Inflaton Fragmentation into Oscillons. Phys. Rev. D 2018, 98, 083513. [Google Scholar] [CrossRef]
- Cotner, E.; Kusenko, A.; Sasaki, M.; Takhistov, V. Analytic Description of Primordial Black Hole Formation from Scalar Field Fragmentation. J. Cosmol. Astropart. Phys. 2019, 10, 077. [Google Scholar] [CrossRef]
- Flores, M.M.; Kusenko, A. Primordial black holes as a dark matter candidate in theories with supersymmetry and inflation. arXiv 2021, arXiv:2108.08416. [Google Scholar]
- Kou, X.X.; Tian, C.; Zhou, S.Y. Oscillon Preheating in Full General Relativity. Class. Quant. Grav. 2021, 38, 045005. [Google Scholar] [CrossRef]
- Nazari, Z.; Cicoli, M.; Clough, K.; Muia, F. Oscillon collapse to black holes. J. Cosmol. Astropart. Phys. 2021, 05, 027. [Google Scholar] [CrossRef]
- Kim, J.; McDonald, J. General Analytical Conditions for Inflaton Fragmentation: Quick and Easy Tests for its Occurrence. arXiv 2021, arXiv:2111.12474. [Google Scholar]
- Gradwohl, B.A.; Frieman, J.A. Dark Matter, Long-Range Forces, and Large-Scale Structure. Astrophys. J. 1992, 398, 407. [Google Scholar] [CrossRef]
- Gubser, S.S.; Peebles, P.J.E. Structure formation in a string inspired modification of the cold dark matter model. Phys. Rev. D 2004, 70, 123510. [Google Scholar] [CrossRef]
- Nusser, A.; Gubser, S.S.; Peebles, P.J.E. Structure formation with a long-range scalar dark matter interaction. Phys. Rev. D 2005, 71, 083505. [Google Scholar] [CrossRef]
- Amendola, L.; Rubio, J.; Wetterich, C. Primordial black holes from fifth forces. Phys. Rev. D 2018, 97, 081302. [Google Scholar] [CrossRef]
- Savastano, S.; Amendola, L.; Rubio, J.; Wetterich, C. Primordial dark matter halos from fifth forces. Phys. Rev. D 2019, 100, 083518. [Google Scholar] [CrossRef]
- Flores, M.M.; Kusenko, A. Primordial Black Holes from Long-Range Scalar Forces and Scalar Radiative Cooling. Phys. Rev. Lett. 2021, 126, 041101. [Google Scholar] [CrossRef]
- Domènech, G.; Sasaki, M. Cosmology of strongly interacting fermions in the early universe. J. Cosmol. Astropart. Phys. 2021, 06, 030. [Google Scholar] [CrossRef]
- Dvali, G.; Kühnel, F.; Zantedeschi, M. Primordial Black Holes from Confinement. Phys. Rev. D 2021, 104, 123507. [Google Scholar] [CrossRef]
- Basu, R.; Guth, A.H.; Vilenkin, A. Quantum creation of topological defects during inflation. Phys. Rev. D 1991, 44, 340–351. [Google Scholar] [CrossRef]
- Ipser, J.; Sikivie, P. Gravitationally repulsive domain wall. Phys. Rev. D 1984, 30, 712–719. [Google Scholar] [CrossRef]
- Liu, J.; Guo, Z.K.; Cai, R.G. Primordial Black Holes from Cosmic Domain Walls. arXiv 2019, arXiv:1908.02662. [Google Scholar] [CrossRef]
- Rubin, S.G.; Khlopov, M.Y.; Sakharov, A.S. Primordial black holes from nonequilibrium second order phase transition. Grav. Cosmol. 2000, 6, 51–58. [Google Scholar]
- Khlopov, M.Y.; Rubin, S.G.; Sakharov, A.S. Primordial structure of massive black hole clusters. Astropart. Phys. 2005, 23, 265. [Google Scholar] [CrossRef]
- Tanahashi, N.; Yoo, C.M. Spherical Domain Wall Collapse in a Dust Universe. Class. Quant. Grav. 2015, 32, 155003. [Google Scholar] [CrossRef]
- Kibble, T.W.B. Topology of cosmic domains and strings. J. Phys. A Math. Gen. 1976, 9, 1387–1398. [Google Scholar] [CrossRef]
- Vilenkin, A. Cosmic strings and domain walls. Phys. Rep. 1985, 121, 263–315. [Google Scholar] [CrossRef]
- Hindmarsh, M.B.; Kibble, T.W.B. Cosmic strings. Rep. Prog. Phys. 1995, 58, 477–562. [Google Scholar] [CrossRef]
- Jenkins, A.C.; Sakellariadou, M. Primordial black holes from cusp collapse on cosmic strings. arXiv 2020, arXiv:2006.16249. [Google Scholar]
- Vilenkin, A.; Levin, Y.; Gruzinov, A. Cosmic strings and primordial black holes. J. Cosmol. Astropart. Phys. 2018, 11, 008. [Google Scholar] [CrossRef]
- James-Turner, C.; Weil, D.P.B.; Green, A.M.; Copeland, E.J. Constraints on the cosmic string loop collapse fraction from primordial black holes. Phys. Rev. D 2020, 101, 123526. [Google Scholar] [CrossRef]
- Özsoy, O.; Parameswaran, S.; Tasinato, G.; Zavala, I. Mechanisms for Primordial Black Hole Production in String Theory. J. Cosmol. Astropart. Phys. 2018, 07, 005. [Google Scholar] [CrossRef]
- Garriga, J.; Vilenkin, A. Black holes from nucleating strings. Phys. Rev. D 1993, 47, 3265–3274. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Casper, P. Formation of black holes from collapsed cosmic string loops. Phys. Rev. D 1996, 53, 3002–3010. [Google Scholar] [CrossRef]
- Polnarev, A.; Zembowicz, R. Formation of primordial black holes by cosmic strings. Phys. Rev. D 1991, 43, 1106–1109. [Google Scholar] [CrossRef]
- Deng, H. Primordial black hole formation by vacuum bubbles. Part II. J. Cosmol. Astropart. Phys. 2020, 09, 023. [Google Scholar] [CrossRef]
- Dymnikova, I.; Koziel, L.; Khlopov, M.; Rubin, S. Quasilumps from first order phase transitions. Grav. Cosmol. 2000, 6, 311–318. [Google Scholar]
- Hawking, S.W.; Moss, I.G.; Stewart, J.M. Bubble collisions in the very early universe. Phys. Rev. D 1982, 26, 2681–2693. [Google Scholar] [CrossRef]
- Jung, T.H.; Okui, T. Primordial black holes from bubble collisions during a first-order phase transition. arXiv 2021, arXiv:2110.04271. [Google Scholar]
- De Luca, V.; Franciolini, G.; Riotto, A. Bubble Correlation in First-Order Phase Transitions. Phys. Rev. D 2021, 104, 123539. [Google Scholar] [CrossRef]
- Lewicki, M.; Vaskonen, V. On bubble collisions in strongly supercooled phase transitions. Phys. Dark Univ. 2020, 30, 100672. [Google Scholar] [CrossRef]
- Baker, M.J.; Breitbach, M.; Kopp, J.; Mittnacht, L. Primordial Black Holes from First-Order Cosmological Phase Transitions. arXiv 2021, arXiv:2105.07481. [Google Scholar]
- Gross, C.; Landini, G.; Strumia, A.; Teresi, D. Dark Matter as dark dwarfs and other macroscopic objects: Multiverse relics? J. High Energy Phys. 2021, 09, 033. [Google Scholar] [CrossRef]
- Garriga, J.; Vilenkin, A.; Zhang, J. Black holes and the multiverse. J. Cosmol. Astropart. Phys. 2016, 02, 064. [Google Scholar] [CrossRef]
- Kusenko, A.; Sasaki, M.; Sugiyama, S.; Takada, M.; Takhistov, V.; Vitagliano, E. Exploring Primordial Black Holes from the Multiverse with Optical Telescopes. Phys. Rev. Lett. 2020, 125, 181304. [Google Scholar] [CrossRef]
- Maeso, D.N.; Marzola, L.; Raidal, M.; Vaskonen, V.; Veermäe, H. Primordial black holes from spectator field bubbles. arXiv 2021, arXiv:2112.01505. [Google Scholar]
- Vallejo-Peña, S.A.; Romano, A.E. Effects of the modification of gravity on the production of primordial black holes. Phys. Lett. B 2021, 817, 136289. [Google Scholar] [CrossRef]
- Kawai, S.; Kim, J. Primordial black holes from Gauss-Bonnet-corrected single field inflation. Phys. Rev. D 2021, 104, 083545. [Google Scholar] [CrossRef]
- Chen, C.Y. Threshold of primordial black hole formation in Eddington-inspired-Born–Infeld gravity. Int. J. Mod. Phys. D 2021, 30, 02. [Google Scholar] [CrossRef]
- Passaglia, S.; Sasaki, M. Primordial Black Holes from CDM Isocurvature. arXiv 2021, arXiv:2109.12824. [Google Scholar]
- Yoo, C.M.; Harada, T.; Hirano, S.; Okawa, H.; Sasaki, M. Primordial black hole formation from massless scalar isocurvature. arXiv 2021, arXiv:2112.12335. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Escrivà, A. PBH Formation from Spherically Symmetric Hydrodynamical Perturbations: A Review. Universe 2022, 8, 66. https://doi.org/10.3390/universe8020066
Escrivà A. PBH Formation from Spherically Symmetric Hydrodynamical Perturbations: A Review. Universe. 2022; 8(2):66. https://doi.org/10.3390/universe8020066
Chicago/Turabian StyleEscrivà, Albert. 2022. "PBH Formation from Spherically Symmetric Hydrodynamical Perturbations: A Review" Universe 8, no. 2: 66. https://doi.org/10.3390/universe8020066
APA StyleEscrivà, A. (2022). PBH Formation from Spherically Symmetric Hydrodynamical Perturbations: A Review. Universe, 8(2), 66. https://doi.org/10.3390/universe8020066





