Statistical Tools for Imaging Atmospheric Cherenkov Telescopes

Abstract

The development of Imaging Atmospheric Cherenkov Telescopes (IACTs) unveiled the sky in the teraelectronvolt regime, initiating the so-called “TeV revolution”, at the beginning of the new millennium. This revolution was also facilitated by the implementation and adaptation of statistical tools for analyzing the shower images collected by these telescopes and inferring the properties of the astrophysical sources that produce such events. Image reconstruction techniques, background discrimination, and signal-detection analyses are just a few of the pioneering studies applied in recent decades in the analysis of IACTs data. This (succinct) review has the intent of summarizing the most common statistical tools that are used for analyzing data collected with IACTs, focusing on their application in the full analysis chain, including references to existing literature for a deeper examination.

1. Introduction

Any scientific experiment would be incomplete if only the collected data were reported. A statistical analysis is needed in order to interpret the data and to draw conclusions from the experiment. This is the case for experiments that are imaging the Cherenkov light emitted by a cascade of secondary particles produced by the interaction of gamma rays and cosmic rays within the Earth’s atmosphere. They are called Imaging Atmospheric Cherenkov telescopes and popular examples are MAGIC [1], HESS [2], VERITAS [3], and CTA [4], which is currently under construction. By “statistic” we mean any function $\mathcal{S}$1 computed from the observed data assuming the truth of a model. Very well-known examples of such functions are the mean, the variance and the ${\chi }^2$. As the observed data consists of random variables, the statistic itself is a random variable whose distribution can be derived either from theoretical considerations or empirically using Monte Carlo (MC) simulations. A statistical analysis is therefore performed by comparing the observed value of the statistic with the frequency distribution of the values of the statistic from hypothetical infinite repetition of the same experiment assuming a given model of interest. This approach is usually called the “classical” or “frequentist” approach. This comparison (referred to as the test statistic) between the observed statistic and its long-run distribution allows the analyzer to draw a conclusion from the observed data with a procedure that is right2 $(1-\alpha )·100\%$ of the time. The value $(1-\alpha )·100\%$ is referred to as the confidence level (CL). It is important to underline that it is the procedure, not the conclusion, which is correct $(1-\alpha )·100\%$ of the time. To better clarify this point we can consider the following claim: “a flux of ${10}^{-13}·{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}$ from the observation of a gamma ray burst is excluded at $95\%$ CL”. Claiming that such a value of the flux is excluded is obviously always wrong in infinite experiments in which the true flux of the observed gamma ray burst is ${10}^{-13}·{\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}$. However, in these infinite experiments, the procedure would lead the analyzer to this wrong conclusion only $5\%$ of the time3. The procedure, i.e., the test statistic and the value $\alpha$ for its significance, is usually dictated by many factors, such as the assumptions about the underlying model, the way the data have been collected and, sometimes, also by the biased conclusions4 one is willing to derive from the experiment. A common principle [6] is to choose the test statistic with the maximum power, where the power of the statistic is the probability of rejecting a hypothesis that is false. According to the Neyman–Pearson lemma the most powerful statistic is the likelihood ratio, usually defined in the literature, for reasons that will be clear soon, as follows

$$-2log\frac{\mathcal{L}\left(\theta \right|D_{obs})}{\mathcal{L}\left(\widehat{\theta }\right|D_{obs})},$$

(1)

which by definition can only take values bigger or equal than zero, since by $\widehat{\theta }$ we have defined the values of the model parameters that maximize the likelihood $\mathcal{L}$. The likelihood is a function of the model parameters $\theta$ defined as the probability of obtaining the observed data $D_{obs}$ assuming $\theta$ to be true:

$$\mathcal{L}\left(\theta \right|D_{obs})=p\left(D_{obs}\right|\theta ).$$

(2)

Searching for the parameter values $\widehat{\theta }$ that maximize the likelihood in Equation (2) is also referred to as fitting the model to the data. If nuisance parameters5 $\pi$ are present in the model, $\pi$ is maximized to the value $\widehat{\widehat{\pi }}$ in the numerator of Equation (1) letting $\theta$ be free, resulting in the so-called likelihood profile

$$\mathcal{L}\left(\theta \right|D_{obs})=\mathcal{L}(\theta ,\widehat{\widehat{\pi }}\left(\theta \right)|D_{obs}).$$

(3)

Taking the log value of the likelihood ratio as done in Equation (1) allows making use of Wilk’s theorem [7], which states that under certain circumstances this random variable has a ${\chi }^2$ distribution with degrees of freedom given by the number of the free parameters. This property makes the likelihood ratio a very appealing statistic, whose usage has a very broad application, and it will indeed appear many times in this manuscript. Yet, it must be used cautiously: the interested reader may refer to Ref. [8] for a critical review of the usage and abuse of the likelihood ratio.

The frequentist theory described so far may be considered unsatisfactory by some [9] with its dependence on long-run distributions from infinite experiments and its arbitrariness in the choice of the statistic. An alternative approach is provided by the “Bayesian” or “probabilistic” approach, in which probabilistic statements about hypotheses and model parameters are made through the Bayes theorem

$$p\left(\theta \right|D_{obs})=\frac{p\left(D_{obs}\right|\theta )p\left(\theta \right)}{p\left(D_{obs}\right)}.$$

(4)

The prior probability $p\left(\theta \right)$ captures the available knowledge about the parameters, or, more generally, about the hypotheses under study. The so-called evidence $p\left(D_{obs}\right)$ can be seen as a normalization factor. It follows from probability theory that

$$p\left(D_{obs}\right)=\sum _{\theta }p\left(D_{obs}\right|\theta )p\left(\theta \right).$$

(5)

In this case nuisance parameters are treated via the marginalization

$$p\left(\theta \right|D_{obs})=\sum _{\pi }p(\theta ,\pi |D_{obs}),$$

(6)

or, in other words, instead of profiling the likelihood by fixing $\pi$ to $\widehat{\widehat{\pi }}\left(\theta \right)$, one marginalizes the likelihood by integrating out $\pi$. Another way of looking at Equation (4) is to consider the odds of a hypothesis defined as the ratio of its probability of being true and not being true

$$o\left(\mathcal{H}\right)=\frac{p\left(\mathcal{H}\right)}{1-p\left(\mathcal{H}\right)}\equiv \frac{p\left(\mathcal{H}\right)}{p\left(\overline{\mathcal{H}}\right)},$$

(7)

where $\overline{\mathcal{H}}$ and $\mathcal{H}$ are mutually exclusive and collectively exhaustive hypotheses. Using the odds formalism the Bayes theorem takes the following form

$$o\left(\mathcal{H}\right|D_{obs})=\mathrm{BF}·o\left(\mathcal{H}\right),\mathrm{with}\mathrm{BF}=\frac{p\left(D_{obs}\right|\mathcal{H})}{p\left(D_{obs}\right|\overline{\mathcal{H}})},$$

(8)

where BF stands for the Bayes Factor, i.e., the likelihood ratio of two competing hypotheses. After the measurement the Bayesian approach leads us to update the odds we assign to a given hypothesis by multiplying it with the BF. Unlike the frequentist approach where the goal is to provide a statement about the long-run performance of a test statistic, in Bayes theory we are not interested in hypothetical infinite experiments but in calculating the probability of hypotheses from the observed data and from our prior knowledge of them.

Going deep into the details of the statistical analysis and the difference between the frequentist and Bayesian theory goes beyond the scope of this paper, the interested readers may refer to Refs. [10,11] and references therein. Yet, this brief introduction of the basic principles and definitions used for performing an inference analysis in both the frequentist and Bayesian approach is necessary for reviewing the statistical tools used in IACTs analysis in the next sections.

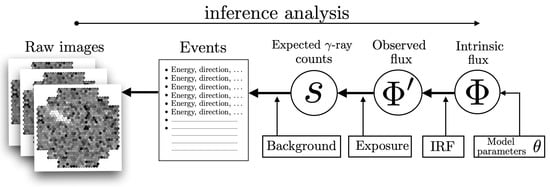
The typical workflow of an IACTs analysis is schematically shown in Figure 1, where, starting from the shower images, the variable s (the expected number of signal events) is derived, which is then used for inferring the flux $\mathrm{\Phi }$ of gamma rays by taking into account the instrument response function (IRF) of the telescopes.

Figure 1. Schematic workflow of the inference analysis performed in order to estimate the intrinsic flux $\mathrm{\Phi }$ of gamma rays (and the values of its parameters $\theta$) from the recorded images. The acronym IRF stands for Instrument Response Function (see Section 4). The bold arrows (going from the right to the left) show the relation of cause and effect. The aim of the inference analysis (shown as a thin arrow going from the left to the right) is to invert such relation.

In the remaining part of this section, the structure of the paper is outlined. First we discuss in Section 2 the most common techniques implemented for performing the event reconstruction from the shower images detected with IACTs. The goal of these techniques’ yields is to obtain a list with the estimated energy, direction, and discriminating variables for each of the candidate gamma ray events.

Using this event list, it is then shown in Section 3 how to estimate the strength of the signal s and how confidently we can claim that a gamma ray source is producing part of the recorded events.

The final result of the statistical analysis is the differential gamma ray flux $\mathrm{\Phi }$, which corresponds to the number $N_{\gamma }$ of expected photons per unit energy (E), time (t), and area (A):

$$\mathrm{\Phi }(E,t,\widehat{\mathbf{n}})=\frac{d{N}_{\gamma }(E,t,\widehat{\mathbf{n}})}{dEdAdt},$$

(9)

where $\widehat{\mathbf{n}}$ is the photon direction. We denote with ${\mathrm{\Phi }}^{\prime }$ the observed flux, i.e., the flux of events actually observed by the telescopes when the IRF of the telescope is included. The expected counts s is connected to ${\mathrm{\Phi }}^{\prime }$ by taking into account the exposure of the observation, i.e., by integrating ${\mathrm{\Phi }}^{\prime }$ over the temporal, energetic and spatial range in which the events have been collected. This is the topic of Section 4, in which the way the source flux and its model parameters are obtained is also discussed.

2. Event Reconstruction Techniques

The first statistical analysis one has to face in IACTs is the reduction of the recorded images in the camera of the telescopes to a few parameters of interest. The Cherenkov light from the shower of secondary particles is reflected by mirrors and focused on a camera with photomultipliers composing the pixels of the shower image (see Figure 2). The event reconstruction consists therefore in extracting from the photo-electron (PhE) counts and arrival time of each pixel the following variables:

• the energy of the primary gamma ray that initiated the shower,
• its arrival direction,
• and one or more discriminating variables.

The role of these discriminating variables is to provide information on how likely one event can be associated with a gamma ray or to the background composed mainly by hadronic cosmic rays. The background estimation and the signal extraction are discussed in Section 3, while for the remaining part of this section the most commonly used event reconstruction tools are reviewed.

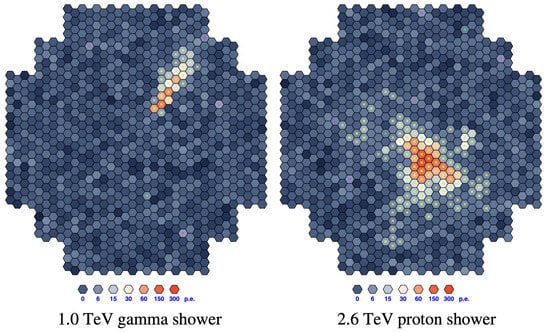
Figure 2. Difference between the images of gamma-induced (left) and hadron-induced (right) showers in the camera of a IACT. Reprinted with permission from Ref. [12]. Copyright 2009 Völk et al.

2.1. Hillas Method

The most common event reconstruction technique is based on the moments (up to the second order) of the pixel amplitudes in the camera, referred to as Hillas parameters [13]. This technique can be thought of as fitting an ellipse to the pixels: a likelihood function that depends on the Hillas parameters is maximized under the assumption that the Cherenkov light from a shower initiated by a gamma ray would produce an elliptical shape in the camera. The set of parameters includes variables such as the total PhE counts in all pixels, the PhE-weighted barycenter of the pixel positions, and the time gradient of the pixel arrival times. If more than one telescope is involved, then these single-image parameters can be combined in order to obtain stereoscopic parameters giving a 3-dimensional reconstruction of the event [14]. The calculation of these parameters is easily affected by image noise and night-sky background, which requires a cleaning procedure in order to remove the pixels that do not contain the shower image. Moreover, the dim and small shower images below 100 GeV can result in parameters values affected by large fluctuations and systematic uncertainties, which is the reason why the instrument response function of IACTs deteriorates at lower energies. Techniques based on Hillas parameters have been implemented since the 1980s and are used in a variety of experiments such as MAGIC [14] and HESS [15], demonstrating the robustness and reliability of the method.

After the parametrization of the event is completed, the gamma ray energy is estimated from the shower impact parameter and from the photon density is measured with each telescope. This is done by constructing look-up tables for different observational conditions, filled with MC information about the true energy of the gamma ray as a function of the simulated image amplitude and impact parameter. The arrival direction is obtained from the crossing point of the main ellipse orientations in the individual cameras. A weighted combination of some Hillas parameters can be used as a discriminating variable [15]. More refined techniques have been developed, aimed at improving the inference analysis on the gamma ray properties starting from the Hillas parameters (see Section 2.5).

2.2. Semi-Analytical Method

Despite the robustness and stability under different conditions of the Hillas method, additional reconstruction procedures have been explored in order to exploit more information from the recorded image. The so-called semi-analytical method consists of fitting to the shower images a model of the Cherenkov light produced by a gamma ray shower as seen by the camera. A first implementation of this method can be found in Ref. [16] from the CAT collaboration in the late 1990s. In this pioneering implementation, the 2D-models are stored in a look-up table and compared to the observed image via a ${\chi }^2$-function of the gamma ray energy, the impact parameter and the source position in the focal plane. This function is defined as the sum of the squared differences over all pixels between the expected PhE content and the actual observed one. This sum is weighted according to the Phe count quadratic error. A ${\chi }^2$ minimization is performed to obtain the best fit parameter of the gamma ray, while the resulting ${\chi }^2$ is then used as a discriminating variable. This method has been re-implemented and subsequently improved by the HESS collaboration [17], where the ${\chi }^2$ minimization has been substituted by the minimization of a log-likelihood defined as

$$ln\mathcal{L}=\sum _{\mathrm{pixels}i}ln{\mathcal{L}}_i=-2\sum _{\mathrm{pixels}i}lnp\left(n_i\right|\theta ).$$

(10)

The variable $n_i$ is the observed PhE count in the pixel i, while $\theta$ are the shower model parameters. This method is referred to as semi-analytical because the template library of shower images is produced with MC simulations which are usually carried out with dedicated software such as KASKADE [18] and CORSIKA [19]. Compared with the Hillas method, a more precise estimation of the energy and direction of the primary gamma ray is provided by this reconstruction technique, especially at low energies.

2.3. 3D-Gaussian Model

An additional approach is given in Refs. [20,21], where the single-pixel PhE counts are fitted to an analytical gaussian air shower model. This method, referred to as a 3D model or 3D Gaussian model, assumes an isotropic angular distribution of the shower, and its rotational symmetry with respect to its incident direction is used to select gamma ray events. As usual a likelihood function is maximized with respect to the shower parameters. This maximization process is rather fast thanks to the simpler assumption of the 3D-Gaussian model. More recently [22] the 3D-model was combined with a multivariate analysis that makes use of the so-called Boosted Decision Tree (see Section 2.5) and adapted to the detection necessity of IACTs, particularly for the discovery of new faint sources.

2.4. MC Template-Based Analysis

The previously mentioned methods in Section 2.2 and Section 2.3 strongly rely on a model fit that becomes more difficult to describe as we reach higher energies. The more energetic the gamma ray, the more particles are produced, and a large fraction of the latter is capable of reaching the ground. This causes strong fluctuations in the fit model above ∼10 TeV. Moreover, in these approaches, the quality of the model fit is inevitably worsened by instrumental effects and atmospheric conditions which require approximations in order to be taken into account. To overcome these issues and improve the accuracy of the analysis, the authors of Ref. [23] proposed an Image Pixel-wise fit for Atmospheric Cherenkov Telescopes (ImPACT). In this approach, the template shower images are produced using more detailed and time consuming MC simulations. The simulation chain consists in simulating the air shower with CORSIKA [19] which is then combined with sim_telarray6 [24] for reproducing the instrumental effects of the telescopes. The sensitivity is improved by a factor of 2 when the ImPACT reconstruction method is implemented, relative to the Hillas-based method (see Section 2.1). Compared with the 2D-model, some improvements were shown at higher energies. A similar implementation for the VERITAS telescopes can be found in Ref. [25]. The role of realistic MC simulations has been very recently emphasized by the authors of Ref. [26], who proposed a new simulation and analysis framework as an alternative to the current way MC templates are obtained. In the existing paradigm, simulations are generated from pre-defined observation and instrument settings, such as the zenith of the observation or the configuration of the camera. Each simulation can be then seen as a grid point in the setting-parameters space. The analyzer willing to use a “run”7 performed with some given settings has to look for the adjacent grid points either by interpolating them or by taking the closest one. Instead in the run-wise simulation approach described in Ref. [26], simulations are generated on a run-by-run basis. In this way observational conditions are fully taken into account, thus leading to more realistic MC simulations that reduce systematic uncertainties and improve the scientific output of the statistical analysis.

2.5. Multivariate Analysis

To date, we described techniques for parametrizing an event detected by IACTs. These parameters are then used for inferring the energy, the arrival direction of the primary gamma ray, and discriminating variables. The latter are used to tell how likely the event can be associated with a gamma ray. The usage of discriminating variables is quite simple: all the events with values of the parameter larger (or smaller, depending on the kind of variable) than a pre-defined threshold are retained and considered to be gamma-like events, i.e., originating from a gamma ray. A different approach that avoids cutting data by exploiting the full probability distribution function (PDF) of the discriminating variable will be discussed in Section 3. Once a discriminating variable is chosen and a fixed threshold is defined, the separation (or discrimination) power can be obtained from the so-called Q value

$$Q=\frac{{ϵ}_{\gamma }}{\sqrt{{ϵ}_h}}.$$

(11)

where ${ϵ}_x$ is the efficiency of the selection procedure given by the fraction of events belonging to the population x surviving the selection (h stands for hadrons which compose the background population). This classification problem becomes considerably more difficult when more than one parameter can be actually used for discriminating signal events from the background population. Multivariate methods consist of combining several of the shower parameters into one single discriminating parameter. The main advantages of these approaches are that

• nonlinear correlations between the parameters are taken into account and
• those parameters with no discrimination power are ignored.

A detailed review and comparison of different multivariate methods for event classification in IACTs can be found in Ref. [27]. In this section, we provide a brief description of the currently most used methods, the Boosted Decision Tree (BDT) and the Random Forest (RF) [28]. The BDT approach, implemented for the HESS [29,30] and VERITAS [31] telescopes, is a binary tree where events are sorted into small subsets by applying a series of cuts until a given condition is fulfilled. This condition might be given by requiring that the number of events in a leaf is smaller than a predefined value or that the signal over the background ratio in a leaf must be large enough. The term “boosted” refers to the fact that more than one individual decision trees are combined in a single classifier by performing a weighted average. The boosting allows improving the stability of the technique with respect to fluctuations in the training sample and is able to considerably enhance the performance of the gamma/hadron separation compared to a single decision tree. Like the BDT approach, the RF method, implemented for the MAGIC telescopes [32], also relies on decision trees, which are built up and combined with some elements of random choice. As for the BDT, training samples of the two classes of population (signal and background) are needed for constructing the decision trees. Once the classifier has been properly8 trained, the algorithm can be used to assign to each event a single discriminating variable whose distribution on a test gamma and hadron population can be seen in Figure 3.

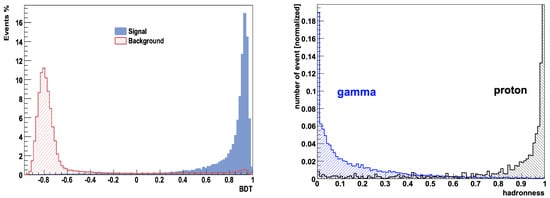
Figure 3. Left panel: distribution for background events (hatched red) and simulated $\gamma$ (blue filled) of the discriminating variable given in output from the BDT method implemented by the HESS collaboration. Reprinted with permission from Ref. [30] Copyright 2010 Fiasson et al. Right panel: distribution for background events (black) and simulated $\gamma$ (blue) of the discriminating variable (called hadronness) given in output from the RF method implemented by the MAGIC collaboration. Reprinted with permission from Ref. [33] Copyright 2009 Colin et al.

2.6. Deep Learning Methods

The multivariate methods described in Section 2.5 for discriminating the signal events from the background have shown a great capability in improving the sensitivity of IACTs. This effort has been recently pushed forward by Deep Learning (DL) [34] techniques for object recognition in images. Such algorithms, which require more computational power, are getting more and more attention thanks to the improvements during recent decades in the usage of CPU and GPUs for matrix operations. When it comes to image processing, the leading DL algorithm is Convolutional Neural Networks (CNNs) whose first application in the context of IACTs can be found in Ref. [35], where a CNN was applied in the simple case of muon-ring events. This work served as a pathfinder for the application of CNNs for gamma/hadron separation from the raw recorded images.

A CNN is made of many connected layers which in turn consist of different nodes. The first layer is the input image whose pixels represent its nodes. The inputs in a new layer are convolved with kernels that have to be trained. Each new layer is in general much smaller than the input one, and allows identifying features in the previous layer. Adding more and more layers, one aims to extract more and more complex features, which can be possibly used to identify those discriminating features in the images that otherwise would not be considered in other event-classifier algorithms. For a more detailed review and description of DL and CNNs algorithms, we refer the reader to Refs. [34,36] and references therein. The training process in CNN can be computationally demanding, due mainly to the very large number of parameters. The main advantages of DL relative to previous event reconstruction methods in IACT is that CNNs do not need the image parameters (such as the Hillas ones), and therefore all the features contained in the image are fully exploited, while they might get lost or suppressed during the parametrization. Recent applications of CNNs in the image processing of IACTs data can be found in Refs. [37,38,39,40], where the algorithm was also implemented for the energy and arrival direction estimation of the gamma rays.

3. Detection Significance and Background Modeling

The final result of the statistical analysis described in Section 2 is a list containing useful information about the candidate gamma ray events, such as their estimated energy and arrival direction. Neglecting any background contamination, the total number n of events in such a list would be a random variable distributed according to the Poisson PMF

$$\mathcal{P}\left(n\right|s)=\frac{s^n}{n!}{e}^{-s},$$

(12)

where s is the expected number of signal counts. The problem is that the majority of the observed events are actually generated by hadronic cosmic rays, while only a small fraction (which for the case of a bright source such as the Crab Nebula is of the order of ${10}^{-3}$) can be associated with gamma rays. By applying a signal extraction selection on the data based on a discrimination variable, it is possible to reduce the background by a factor of 100 or more, thus increasing the signal-to-noise ratio close to 1 for a bright source. In order to infer the gamma ray flux from the resulting event list it is essential to first estimate the remaining background contamination. We can consider three different scenarios (which are the topic of Section 3.1, Section 3.2 and Section 3.3, respectively) where the expected background count b in the target region is:

• zero or negligible relative to the source counts,
• known precisely,
• estimated from an OFF measurement.

The latter case is the most common one and requires the definition of two regions: a region of interest (ROI), also referred to as target, test or ON region, and a background control region, called OFF region. The ON and OFF regions provide, respectively, independent $N_{on}$ and $N_{off}$ counts, where the latter is ideally void of any signal event. A normalization factor $\alpha$ is introduced to account for differences (such as the acceptance and the exposure time) between the ON and OFF region. It can be defined as

$$\alpha =\frac{{\int }_{ON}A(x,t)dxdt}{{\int }_{OFF}A(x,t)dxdt},$$

(13)

where $A(x,t)$ is the instrument acceptance, which is a function of the observation time t and of all observational parameters (such as the FoV position or the zenith angle) here denoted for simplicity with x. The goal of the background modeling analysis is to provide the values of $\alpha$ and $N_{off}$ that are then used for estimating the signal s along with the detection significance.

3.1. The Background Is Zero or Negligible

Although very rare, in some analyses the background b in the ON region may be assumed to be zero or negligible relative to the signal s. Given the simplicity of this case, it is worth dwelling on it, discussing with examples the statistical conclusions that can be drawn from a measurement using the frequentist and Bayesian approach. In this scenario the likelihood function is trivially

$$\mathcal{L}\left(s\right)=\mathcal{P}\left(N_{on}\right|s),$$

(14)

where $\mathcal{P}$ is the Poisson distribution (see Equation (12)) with observed and expected counts $N_{on}$ and s, respectively. Using the likelihood ratio defined in Equation (1) as a statistic, and taking into account that $\widehat{s}=N_{on}$ is the value of s that maximizes the likelihood, we get for any $s>0$ the following statistic

$$\mathcal{S}=2·(s-N_{on})-2N_{on}·\left(logs-log{N}_{on}\right).$$

(15)

Such a statistic, known in the literature as the Cash statistic or C-statistic [41], has a straightforward meaning: if we measured $N_{on}$ counts in the ON region and assumed that the true signal rate is s, then the value obtained from $\mathcal{S}$ according to Wilks’ theorem is a random variable that follows a ${\chi }^2$ distribution with 1 degree of freedom. This can be checked by performing MC simulations as shown in the left plot of Figure 4. The smaller the true value of s the more difficult it is to find an exact distribution for the statistic $\mathcal{S}$ which, due to the discreteness of the Poisson distribution, cannot be assumed anymore to be a ${\chi }^2$ variable. For small expected signal counts s, it is therefore necessary to get the CDF of $\mathcal{S}$ from MC simulations.

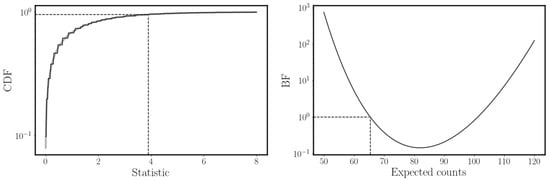
Figure 4. A comparison between the frequentist (left panel) and Bayesian (right panel) conclusion from the experiment result $N_{on}=82$ on the hypothesis that the gamma ray expected counts is 65.4 and no background is present. Left panel: in black the cumulative distribution function (CDF) of the statistic defined in Equation (15) from ${10}^6$ simulations assuming $s=65.4$, while in grey the expected CDF of a ${\chi }^2$ random variable. The step shape of the CDF of the statistic is due to the discrete nature of the Poisson distribution. Dashed lines show the point in which the statistic is 3.9 and the CDF is 0.952. Right panel: evolution of the BF defined in Equation (19) as a function of the expected counts $s_2$, using $s_1=65.4$ and $N_{on}=82$. Dashed lines show the point in which the expected counts are 65.4 and by definition the BF is 1.

We can be interested, for instance, in the hypothesis ${\mathcal{H}}_0$: “the number of expected signal events (for a given temporal and energetic bin and surface area) is $s=65.4$”. After having performed the experiment, we obtain from the measurement $N_{on}=82$ events. In this scenario, by computing the statistic in Equation (15) we get $\mathcal{S}=3.9$. If ${\mathcal{H}}_0$ was true we would have observed a value of the statistic equal or greater than 3.9 only $4.8\%$ of the time (see the left panel of Figure 4). The conclusion of the frequentist approach is therefore that ${\mathcal{H}}_0$ can be excluded with a $95.2\%$ CL or in other words with a 1.98 $\sigma$ significance. The latter is obtained by expressing the CL in multiples of the standard deviation $\sigma$ of a normal distribution via the inverse of the error function9:

$$\sqrt{2}{\mathrm{erf}}^{-1}\left(\mathrm{CL}\right).$$

(16)

The aim of the Bayesian approach is instead to provide a probabilistic statement about s, which is not fixed as in the frequentist approach. By applying the Bayes theorem, we get that the PDF of s is (up to a normalization factor)

$$p\left(s\right|N_{on})\propto \mathcal{P}\left(N_{on}\right|s)·p\left(s\right),$$

(17)

where $p\left(s\right)$ is the prior PDF of s, which encloses the prior knowledge the analyzer has on the source’s signal. In the Bayesian context we can compare two hypotheses $s=s_1$ and $s=s_2$ as follows

$$\frac{p\left(s_1\right|N_{on})}{p\left(s_2\right|N_{on})}=\mathrm{BF}·\frac{p\left(s_1\right)}{p\left(s_2\right)},$$

(18)

where

$$\mathrm{BF}={\left(\frac{s_1}{s_2}\right)}^{N_{on}}{e}^{-s_1+s_2}.$$

(19)

The evolution of the BF as a function of the expected counts $s_2$, using $s_1=65.4$ (which is our hypothesis ${\mathcal{H}}_0$ of interest) and the experiment result $N_{on}=82$ is shown in the right panel of Figure 4. It is worth noticing that the BF is connected to the statistic in Equation (15) via

$$-2logBF=\mathcal{S},$$

(20)

in which $s_1=s$ and $s_2=N_{on}$. Lastly, it can be shown that assuming a uniform prior10 the PDF of s in Equation (17) is

$$p\left(s\right|N_{on})=\mathcal{P}\left(N_{on}\right|s)=\frac{s^{N_{on}}}{N_{on}!}{e}^{-s}.$$

(21)

3.2. The Background Is Known Precisely

This is the case in which we know from theoretical or experimental considerations the true value $\overline{b}$ of the background. This happens for instance in the field-of-view-background model, where the entire FoV (excluding positions where $\gamma$-ray events are expected) is used for modeling the background. Since the OFF region is composed by the entire FoV and the ON region by a small portion of it, we have $\alpha \ll 1$. Therefore the Poissonian fluctuations of the background contamination in the ON region can be neglected, being given by

$$\sigma \left(\alpha N_{off}\right)=\alpha \sqrt{N_{off}}.$$

(22)

Indeed the detection significance of the “known” and “unknown” background cases coincide for $\alpha \ll 1$ (see Section 3.3). Thus, in the field-of-view-background model we can make the assumption of knowing precisely the background, given by the product $\alpha N_{off}$.

The likelihood function is

$$\mathcal{L}\left(s\right)=\mathcal{P}\left(N_{on}\right|s+\overline{b}),$$

(23)

which reaches its maximum value for $\widehat{s}=N_{on}-\overline{b}$. The statistic is obtained from the Cash one defined in Equation (15) in which s has been substituted with $s+\overline{b}$. An important difference between the previous case, in which the background was assumed to be zero, is that now the statistic is also defined for the hypothesis $s=0$. For this no-source hypothesis it is common to slightly modify the Cash statistic by taking the square root of it and by introducing a sign that is arbitrarily chosen to be positive when the excess $N_{on}-\overline{b}$ is positive, yielding

$$\mathcal{S}=\pm \sqrt{2·(\overline{b}-N_{on})-2N_{on}·\left(log\overline{b}-log{N}_{on}\right)}.$$

(24)

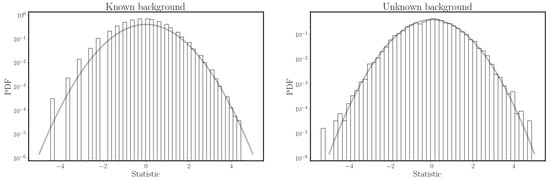
In this way, for large enough counts ($N_{on}\gtrsim 10$) the statistic is a random variable that follows a normal distribution with mean zero and variance 1 (as shown in the left panel of Figure 5). This allows immediately converting the output of $\mathcal{S}$ in a significance level. If for instance we assume $\overline{b}=10$ and we observe $N_{on}=21$ events, then $\mathcal{S}=3.0$ which means that the no-source hypothesis can be excluded with a significance of 3 $\sigma$.

Figure 5. Distribution of the Cash statistic in Equation (24) (left panel) and the Li&Ma statistic in Equation (28) (right panel) from measurements in which the background is known precisely to be $\overline{b}=10$ or must be estimated from the OFF counts $N_{off}$ with $\alpha =1$, respectively. In both simulations, the true values of s and b are 0 and 10, respectively. In both plots, the PDF of a normal distribution with mean zero and variance 1 is shown in grey as reference. In both cases ${10}^6$ simulations were performed. The distribution in the left panel looks to be less populated due to the fact that having the background fixed to 10 (and not estimated from an OFF measurement) limits the number of possible outcomes of the statistic.

3.3. The Background Is Estimated from an OFF Measurement

Let us consider the most common scenario, in which we do not know the background b and therefore need to estimate it by performing OFF measurements, supposedly void of any signal. Such OFF measurements can be performed following one of the below procedures:

• On-Off background: the OFF counts are taken from (usually consecutive) observations made under identical conditions, meaning that $\alpha$ is simply given by $t_{on}/t_{off}$ with $t_{on}$ and $t_{off}$ the exposure time for the ON and OFF observation, respectively. The main advantage of this method is that no assumption is required for the acceptance, except that it is the same for the ON and OFF regions. The drawback of this approach is that dedicated OFF observations are needed, thus “stealing” time from the on-source ones.
• Wobble or reflected-region background: the OFF counts are taken from regions located, on a run-by-run basis, at identical distances from the center of the field of view. Each of the OFF regions is obtained by reflecting the ON region with respect to the FoV center. This is the reason this method is called the reflected-region method. If we have n OFF regions then $\alpha$ is equal to $1/n$. This technique was originally applied to wobble observations [43] and was later on used also in other observation modes.
• Ring background: the OFF counts are taken from a ring around the ROI or around the center of the field of view.
• Template background: the OFF counts are given by those events that have been discarded in the signal extraction selection based on a discriminating variable. In this method, first developed for the HEGRA experiment [44] and more recently refined for HESS [45], the discarded events are used to template the background.

For a more detailed review of the background modeling and comparison of the different methods see Ref. [46].

From one of the above-mentioned procedures, once we obtained the value of $\alpha$ and $N_{off}$, the inference analysis on s is performed using the following likelihood:

$$\begin{array}{cc}\hfill \mathcal{L}(s,b)& =\mathcal{P}\left(N_{on}\right|s+\alpha b)·\mathcal{P}\left(N_{off}\right|b)=\hfill \\ \hfill & =\frac{{(s+\alpha b)}^{N_{on}}}{N_{on}!}{e}^{-(s+\alpha b)}·\frac{b^{N_{off}}}{N_{off}!}{e}^{-b}.\hfill \end{array}$$

(25)

We are not directly interested in knowing the background, which is therefore a nuisance parameter. Thus, in the frequentist approach we have to profile the likelihood (see Equation (3)) by fixing b to the value $\widehat{\widehat{b}}$ that maximizes $\mathcal{L}$ for a given s (see for instance Ref. [47] for a derivation of $\widehat{\widehat{b}}$), i.e.,

$$\widehat{\widehat{b}}=\frac{N+\sqrt{N^2+4(1+1/\alpha )s{N}_{off}}}{2(1+\alpha )},$$

(26)

with $N\equiv N_{on}+N_{off}-(1+1/\alpha )s$. Performing as usual the logarithm of the likelihood ratio we have

$$\begin{array}{cc}\hfill \mathcal{S}=-2log\frac{\mathcal{L}(s,\widehat{\widehat{b}})}{\mathcal{L}(\widehat{s},\widehat{b})}=& 2\left[N_{on}log\left(\frac{N_{on}}{s+\alpha \widehat{\widehat{b}}}\right)+N_{off}log\left(\frac{N_{off}}{\widehat{\widehat{b}}}\right)+\right.\hfill \\ \hfill & \left.+s+(1+\alpha )\widehat{\widehat{b}}-N_{on}-N_{off}\right],\hfill \end{array}$$

(27)

where $\widehat{s}=N_{on}-\alpha N_{off}$ and $\widehat{b}=N_{off}$ are the values11 that maximizes the likelihood in Equation (25), while $\widehat{\widehat{b}}$ is given in Equation (26) and maximizes $\mathcal{L}$ for a given s. The statistic in Equation (27) depends only on the free parameter s and according to Wilks’ theorem it follows a ${\chi }^2$ distribution with 1 degree of freedom. It can then be used for hypothesis testing, in particular the “$s=0$” hypothesis12 from which we can obtain the detection significance. Similarly to Equation (24), we can take the square root of Equation (27) and set $s=0$, yielding the statistic

$$\begin{array}{c}\hfill S=\pm \sqrt{2}{\left[N_{on}log\left(\frac{1}{\alpha }\frac{(\alpha +1)N_{on}}{N_{on}+N_{off}}\right)+N_{off}log\left(\frac{(\alpha +1)N_{off}}{N_{on}+N_{off}}\right)\right]}^{1/2},\end{array}$$

(28)

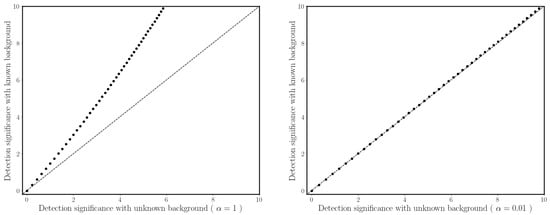
where the sign is arbitrarily chosen to be positive when the excess $N_{on}-\alpha N_{off}$ is positive. This expression is the well-known “Li&Ma” [48] formula for computing the detection significance in ON/OFF measurements. As shown in the right panel of Figure 5 for large enough counts ($N_{on},N_{off}\gtrsim 10$) the statistic in Equation (28) distributes according to a normal distribution with mean zero and variance 1. We can again consider the example in which $N_{on}=21$ counts have been observed in the ON region, but instead of assuming a known background $\overline{b}=10$, our background is instead estimated from the OFF measurement $N_{off}=10$ with $\alpha =1$. Using the statistic in Equation (28) we get a detection significance of 2 $\sigma$, which is smaller than the 3 $\sigma$ obtained from the Cash statistic where the background is assumed to be known precisely. A comparison of different values of $N_{on}$ between the Cash (Equation (24)) and Li&Ma (Equation (28)) statistic is shown in Figure 6, where one can see that the former becomes bigger than the latter as more events are observed in the ON region. This is due to the fact that the Li&Ma statistics account for the Poissonian fluctuations in the observed counts $N_{off}$. These fluctuations make an association with the gamma ray excess with the source signal less likely. When $\alpha \ll 1$ the two statistics give the same result.

Figure 6. Comparison between the Li&Ma statistic in Equation (28) (x-axis) and the Cash statistic in Equation (24) (y-axis). In both plots, each point shows the significance for a different $N_{on}$ ranging from 10 (where the significance is zero in both cases) to 56. For the Cash formula $\overline{b}$ is fixed to 10 in both plots, while for the Li&Ma formula $N_{off}$ is 10 with $\alpha =1$ in the left plot, and $N_{off}=1000$ with $\alpha =0.01$ in the right plot. As a reference the equation $y=x$ (dashed line) is shown. One can see that the Li&Ma statistic converges to the Cash one when $\alpha \ll 1$.

The Li&Ma expression in Equation (28) based on the likelihood ratio is not the only statistic used for rejecting the background-only hypothesis in Poisson counting experiments. One can find in the literature the so-called “signal-to-noise ratio”

$$\mathcal{S}=\frac{N_{on}-\alpha N_{off}}{\sqrt{N_{on}+{\alpha }^2{N}_{off}}},$$

(29)

which has the disadvantages of following a normal distribution only for values of $\alpha$ close to 1 and for large enough counts [48]. Another approach is to compute the p-value from the observed $N_{on}$ counts, i.e., the probability of observing a total count bigger than $N_{on}$ under the assumption of the only-background hypothesis. If we ignore uncertainties in the background we have

$$p-\mathrm{value}=\sum _{n=N_{on}}^{\infty }\mathcal{P}\left(n\right|\alpha b)=\frac{\mathrm{\Gamma }(N_{on},0,\alpha b)}{\mathrm{\Gamma }\left(N_{on}\right)},$$

(30)

written in terms of the incomplete gamma function $\mathrm{\Gamma }$. When we want to include the fact that the background is estimated from an OFF measurement, it is convenient to introduce the variable $N_{tot}=N_{on}+N_{off}$, and it can be shown [49] that the observed quantity $N_{on}$ follows (for a given $N_{tot}$) a binomial distribution $\mathcal{B}$ with success probability $\rho \equiv \alpha /(1+\alpha )$ and total numer of attempts $N_{tot}$. The p-value is

$$p-\mathrm{value}=\sum _{n=N_{on}}^{\infty }\mathcal{B}\left(n\right|N_{tot},\rho )=\frac{\beta (\rho ,N_{on},N_{off}+1)}{\beta (N_{on},N_{off}+1)},$$

(31)

with $\beta$ the incomplete and complete beta functions (distinguished by the number of arguments). Finally the statistic is defined from the above p-values using

$$\mathcal{S}=\sqrt{2}{\mathrm{erf}}^{-1}(1-2·p-\mathrm{value}).$$

(32)

A review and comparison of these statistics applied to the ON/OFF measurement can be found in Refs. [48,49,50,51]. Finally, it is worth mentioning that different extensions and refined versions of the Li&Ma expression in Equation (28) were introduced, each one with its application to a particular problem. The problem of including PSF13 information in the likelihood is addressed in Refs. [52,53,54], while the problem of including the prior knowledge of the source light curve is considered in Ref. [55]. Assessing the role in the detection significance of systematic uncertainties, especially those rising from the normalization factor $\alpha$, is performed in the studies of Refs. [51,56,57].

Following the prescriptions of probability theory, in the Bayesian approach, the signal s is estimated by defining its PDF in which the nuisance parameter b has been marginalized:

$$\begin{array}{c}\hfill p(s|N_{on},N_{off};\alpha )\propto {\int }_0^{\infty }db\mathcal{P}\left(N_{on}\right|s+\alpha b)\mathcal{P}\left(N_{off}\right|b)p\left(b\right)p\left(s\right).\end{array}$$

(33)

Assuming flat priors $p\left(s\right)$ and $p\left(b\right)$ (with $s>0$ and $b>0$) it can be shown [58] that the integral in Equation (33) is

$$p\left(s\right|N_{on},N_{off};\alpha )\propto \sum _{N_s=0}^{N_{on}}\frac{(N_{on}+N_{off}-N_s)!}{{(1+1/\alpha )}^{-N_s}(N_{on}-N_s)!}·\frac{s^{N_s}}{N_s!}{e}^{-s},$$

(34)

where $N_s$ is a bound variable whose physical meaning will be clear soon. Thus, the PDF of the expected signal counts s is given by a weighted sum of Poisson distributions with observed counts ranging from 0 to $N_{on}$. One can recognize (see Refs. [58,59] for a detailed explanation) in Equation (34) a marginalization over the variable $N_s$. The weights in the sum of Equation (34) are indeed the PMF of the number of signal events $N_s$ in the ON region:

$$p\left(N_s\right|N_{on},N_{off};\alpha )\propto \frac{(N_{on}+N_{off}-N_s)!}{{(1+1/\alpha )}^{-N_s}(N_{on}-N_s)!}.$$

(35)

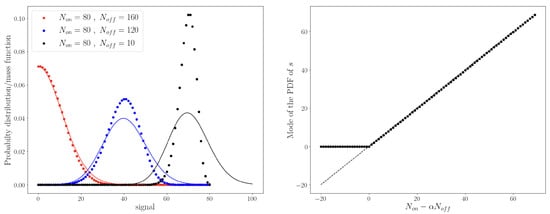
In the left plot of Figure 7 the PDF of s and the PMF of $N_s$ from Equations (34) and (35), respectively, are shown. The best estimate of s can be then obtained from the mode of the PDF in Equation (34). The evolution of the Bayesian estimation of s as a function of the excess $N_{on}-\alpha N_{off}$ can be found in the right plot of Figure 7.

Figure 7. Left panel: Points show the PMF defined in Equation (35) of the number of signal events $N_s$, while lines show the PDF defined in Equation (34) of the expected signal counts s. Different colors are used to distinguish the different counts $N_{off}$ (160 in red, 120 in blue and 10 in black), while $N_{on}$ and $\alpha$ are fixed to 80 and 0.5, respectively. Right panel: The mode of the PDF defined in Equation (34) as a function of the excess $N_{on}-\alpha N_{off}$. As a dashed line the equation $x=y$ is shown for reference.

We can now compare the two hypotheses ${\mathcal{H}}_{s+b}$ and ${\mathcal{H}}_b$, respectively, “the observed counts in the ON region are produced by the source and background” and “the observed counts in the ON region are only produced by the background”. The BF is (see Ref. [60]) in this case (assuming again flat priors for s and b)

$$\mathrm{BF}=\frac{p\left(N_{on}\right|N_{off},\alpha ,{\mathcal{H}}_{s+b})}{p\left(N_{on}\right|N_{off};\alpha ,{\mathcal{H}}_b)}=\frac{1}{s_{max}}\frac{N_{on}!}{(N_{on}+N_{off})!}·\sum _{N_s=0}^{N_{on}}\frac{(N_{on}+N_{off}-N_s)!}{{(1+1/\alpha )}^{-N_s}(N_{on}-N_s)!},$$

(36)

where $s_{max}$ is the maximum prior value of s, i.e., $p\left(s\right)=1/s_{max}$. From the above expression, one can then compute the odds of ${\mathcal{H}}_{s+b}$ following

$$o\left({\mathcal{H}}_{s+b}\right|N_{on},N_{off},\alpha )=\mathrm{BF}·o\left({\mathcal{H}}_{s+b}\right),$$

(37)

with

$$o\left({\mathcal{H}}_{s+b}\right)=\frac{p\left({\mathcal{H}}_{s+b}\right)}{1-p\left({\mathcal{H}}_{s+b}\right)}=\frac{p\left({\mathcal{H}}_{s+b}\right)}{p\left({\mathcal{H}}_b\right)},$$

(38)

and $p\left({\mathcal{H}}_{s+b}\right)$ and $p\left({\mathcal{H}}_b\right)$ the priors of the two competing hypothesis ${\mathcal{H}}_{s+b}$ and ${\mathcal{H}}_b$, respectively. The above odds can be expressed in a “frequentist-fashion” way by converting the posterior probability of ${\mathcal{H}}_b$ in a significance value using the inverse error function:

$$\mathcal{S}=\sqrt{2}·{\mathrm{erf}}^{-1}\left(1-p\left({\mathcal{H}}_b\right|N_{on},N_{off},\alpha )\right)$$

(39)

as shown for instance in Ref. [61] where both constant and Jeffreys’s [62] priors are assumed and a comparison with the Li&Ma significance (see Equation (28)) is shown. More recently this effort has been pushed forward in Ref. [63], where an objective Bayesian solution is proposed and compared to the result of Ref. [61]. The main advantage of these Bayesian solutions is that there are no restrictions in the number of counts $N_{on}$ and $N_{off}$, while the frequentist ones holds only when the counts are large enough. Yet, it is important to not confuse the two approaches, since they aim at finding the solution of two different problems: studying the long-run performance of a statistic in the frequentist approach and deriving the probability of hypotheses in the Bayesian approach.

Lastly, it is worth mentioning that it is possible [59] to extend the PDF of s in Equation (34) by including the information on how the discriminating variables distribute for a signal or background population. The authors of Ref. [59] showed that by performing such extension not only can one avoid discarding data based on a discrimination variable (which inevitably discards also part of the signal events) but one can also increase the resolution of the signal estimation.

3.4. Bounds, Confidence and Credible Intervals

We have shown so far how, given the number of events observed in the ROI, one can estimate the source signal s and its significance. However, the statistical analysis would be incomplete without also reporting lower and upper bounds on the inferred parameters. In the former case they are referred to in the literature as lower limits (LLs), while in the latter as upper limits (ULs), with the interpretation that values of the parameters below the LL or above the UL are more unlikely to be true. They are particularly useful when the detection is not significant, for instance when the source is too dim, and therefore one would like to provide an UL on the strength of the signal s.

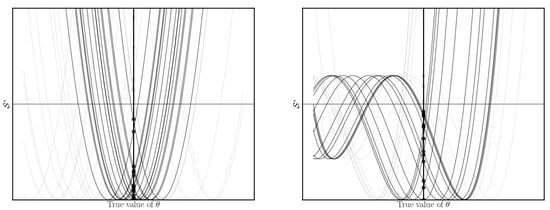
In the frequentist approach, these bounds are obtained by looking at the log-run behavior of the statistic: a threshold value ${\mathcal{S}}^{*}$ of the statistic is defined such that in infinite experiments with fixed parameter $\overline{\theta }$, we would have observed $\mathcal{S}\le {\mathcal{S}}^{*}$ only $x\%$ of the time. The lower or upper bound ${\theta }_x$ is then defined such that $\mathcal{S}\left({\theta }_x\right)={\mathcal{S}}^{*}$. In other words, we look for the values of the parameter that are excluded with a $x\%$ CL. The statistic $\mathcal{S}$ is generally constructed to increase monotonically for values of $\theta$ smaller or bigger than the best estimated value $\widehat{\theta }$, which is by definition the value whose exclusion can be claimed with a $0\%$ CL. For an UL (LL) this means that values of $\theta$ bigger (smaller) than ${\theta }_x$ are excluded with higher CL and they are therefore less likely to be true. This is schematically shown in the left panel of Figure 8 where the statistic $\mathcal{S}$ is shown as a function of the parameter $\theta$ for different experiments in which $\theta$ is fixed to the true value $\overline{\theta }$ (vertical line).

Figure 8. Evolution of the statistic $\mathcal{S}$ as a function of the model parameter $\theta$ from different pseudo-experiments with fixed true value $\overline{\theta }$. Vertical line shows the true value of $\theta$, while the horizontal one shows the threshold ${\mathcal{S}}^{*}$ for the statistic such that $\mathcal{S}\left(\overline{\theta }\right)\le {\mathcal{S}}^{*}$ only $x\%$ of the time. Black curves are those that fulfill this condition while grey ones are those that do not. In the left plot the intersection between the curves and the line $\mathcal{S}={\mathcal{S}}^{*}$ defines CIs which by construction cover the true value of $\theta$ $x\%$ of the time. These CIs cannot be anymore constructed for the curves in the right plot where the statistic has below ${\mathcal{S}}^{*}$ more than one minimum. In both plots the curves shown are not specific on any particular problem but only serve as a schematic representation.

By searching for ${\theta }_x$ such that $\mathcal{S}\left({\theta }_x\right)={\mathcal{S}}^{*}$ we obtain a LL ${\theta }_x^{LL}$ and UL ${\theta }_x^{UL}$. By construction only $x\%$ of these curves have $\mathcal{S}\left(\overline{\theta }\right)\le {\mathcal{S}}^{*}$, which are shown in black in the left plot of Figure 8, while the remaining curves are shown in grey. This implies that the true value $\overline{\theta }$ lies in the interval $\left[{\theta }_x^{LL},{\theta }_x^{UL}\right]$$x\%$ of the time. Such interval is referred to as confidence interval (CI) and it is said to cover the true value of $\theta$ $x\%$ of the time.

The condition that values more extreme than the obtained bounds are rejected with more CL applies for the analysis described in Section 3.1, Section 3.2 and Section 3.3, but in general it is not always true, as shown schematically in the right plot of Figure 8. In such cases LLs, ULs and CIs do not have a straightforward interpretation. This is the reason why it is good practice to report in the result of the statistical analysis also the likelihood shape as a function of the free parameters.

If x is chosen to be 68, the interval between the lower and upper bounds defines the so-called $68\%$ CI. When the background is estimated from an OFF measurement (see Section 3.3) we can use the statistic defined in Equation (27) which is a ${\chi }^2$ random variable with 1 degree of freedom14. By looking for the bounds for which $\mathcal{S}=1$ we obtain the $68\%$ CI of s, that for large count numbers is given by

$$\left[\widehat{s}-\sqrt{N_{on}+{\alpha }^2{N}_{off}},\widehat{s}+\sqrt{N_{on}+{\alpha }^2{N}_{off}}\right]$$

(40)

where $\widehat{s}$ is the estimated signal given by $N_{on}-\alpha N_{off}$.

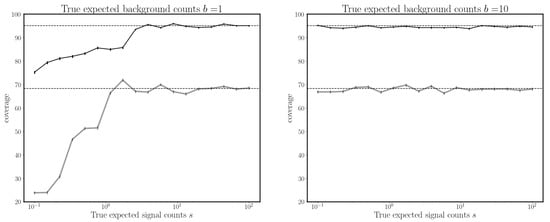
When looking for the UL, the CL is usually set to $95\%$, with other common values being $90\%$ or $99.9\%$. In this case the UL $s_{95}$ is obtained by solving $\mathcal{S}\left(s_{95}\right)=3.84$. The coverage of the $68\%$ and $95\%$ CI is shown in Figure 9 for different true signal and background counts. As one can see from this figure by imposing $\mathcal{S}=$ 1 or 3.84 we have a good coverage (of $68\%$ and $95\%$, respectively) for large enough counts. Although when the counts are too small the CIs tend to undercover the true value of s. Such problem is well-known and it requires ad hoc adjustments [47,64] in order to recover the desired coverage.

Figure 9. Evolution of the coverage of the CIs obtained from solving $\mathcal{S}=$ 1 (grey line) or $\mathcal{S}=$ 3.84 (black line) as a function of the signal s. $\mathcal{S}$ is the statistic defined in Equation (27). The dashed horizontal lines show the expected coverage from the assumption that $\mathcal{S}$ is a ${\chi }^2$-random variable with 1 degree of freedom. In each MC simulation the observed counts $N_{on}$ and $N_{off}$ were simulated from a Poisson distribution with expected counts $s+\alpha b$ and b, respectively. Left panel: the expected background count is fixed to 1. Right panel: the expected background count is fixed to 10. In both plots $\alpha =0.5$ is assumed.

In the Bayesian context, the concept of coverage is meaningless, since the objective of the analysis is not to look for the long-run performance of a given statistic, but to provide a probabilistic statement on the model parameters. In this case, CIs are replaced by credible intervals whose purpose is to provide the analyzer an interval where the model parameter lies with a given probability. Let us assume that we are interested in finding the $68\%$ credible interval $[s_1,s_2]$ of the signal s. By using the PDF of s in Equation (33) such interval is defined as follows

$${\int }_{s_1}^{s_2}p\left(s\right|N_{on},N_{off};\alpha )ds=0.68$$

(41)

where $s_1$ and $s_2$ can be chosen15 to include the values of highest probability density. Similarly the $95\%$ UL $s_{UL}$ on s is obtained from

$${\int }_{s_{UL}}^{\infty }p\left(s\right|N_{on},N_{off};\alpha )ds=0.05.$$

(42)

A comparison between the confidence and credible intervals, computed with the frequentist and Bayesian approach, respectively, can be found in Refs. [59,61,63]. When comparing them it is although important to remember that the two approaches are providing the answer to two completely different questions. In the frequentist case the analyzer is given a procedure for computing the interval that in infinite experiments will cover the true value of the parameters a desired fraction of the time. The parameter is fixed in these infinite experiments and the coverage is usually checked by performing MC simulations. In the Bayesian approach instead the model parameters are not fixed and they lie in the computed interval with a given probability.

4. Flux Estimation and Model Parameter Inference

We have reached the final step of the inference analysis (see Figure 1) which started in Section 2 from the shower image data: estimate the source flux and model parameters. Starting point of this analysis is the expected signal count s, whose estimation from the events list is described in Section 3. Taking into account the exposure of the observation given by the energetic (E), temporal (t) and solid angle ($\mathrm{\Omega }$) range (hereafter denote by $\Delta$) in which the events have been collected we have

$$s={\int }_{\Delta }{\mathrm{\Phi }}^{\prime }(E_r,{\widehat{\mathbf{n}}}_r,t)d{E}_{r}d{\widehat{\mathbf{n}}}_{r}dt$$

(43)

where ${\mathrm{\Phi }}^{\prime }$ is the differential observed flux with units of 1/( solid angle × time × energy), while $E_r$ and ${\widehat{\mathbf{n}}}_r$ are the reconstructed energy and arrival direction (for the time a perfect temporal resolution is assumed being of the order of hundreds of nanoseconds). The observed flux is given by the convolution of the differential source flux $\mathrm{\Phi }$ with the IRF of the telescope:

$${\mathrm{\Phi }}^{\prime }(E_r,{\widehat{\mathbf{n}}}_r,t)={\int }_E{\int }_{\Omega }\mathrm{\Phi }(E,\widehat{\mathbf{n}},t)·\mathrm{IRF}(E_r,{\widehat{\mathbf{n}}}_r,E,\widehat{\mathbf{n}})dEd\widehat{\mathbf{n}}.$$

(44)

The IRF can be though as the probability of detecting a photon with energy E and arrival direction $\widehat{\mathbf{n}}$ and assigning to it a reconstructed energy and arrival direction $E_r$ and ${\widehat{\mathbf{n}}}_r$, respectively. Following the rules of conditional probability the IRF can be expanded as follows:

$$\mathrm{IRF}(E_r,{\widehat{\mathbf{n}}}_r,E,\widehat{\mathbf{n}})=\mathrm{IRF}\left(E_r\right|{\widehat{\mathbf{n}}}_r,E,\widehat{\mathbf{n}})·\mathrm{IRF}\left({\widehat{\mathbf{n}}}_r\right|E,\widehat{\mathbf{n}})·\mathrm{IRF}(E,\widehat{\mathbf{n}}).$$

(45)

Since $E_r$ and ${\widehat{\mathbf{n}}}_r$ are conditional independent variables16 given E and $\widehat{\mathbf{n}}$, the above expression can be rewritten as

$$\mathrm{IRF}(E_r,{\widehat{\mathbf{n}}}_r,E,\widehat{\mathbf{n}})=D\left(E_r\right|E,\widehat{\mathbf{n}})·\mathrm{PSF}\left({\widehat{\mathbf{n}}}_r\right|E,\widehat{\mathbf{n}})·\epsilon (E,\widehat{\mathbf{n}}),$$

(46)

where we have identified the first term with the energy dispersion D, the second one with the point spread function (PSF) and the last term with the collection efficiency $\epsilon$ of the telescopes. To date, we have made the assumption that the observation parameters (such as the zenith angle of the observation) are (or can be assumed to be) constant during the observation.

We can further simplify the IRF expression by ignoring (i.e., by integrating out) the information on the arrival direction $\widehat{\mathbf{n}}$, thus reducing the dimension of the problem from 3 to 1. This assumption is justified if, for instance, the observation is performed on a point-like source, which will be also assumed hereafter to be steady. Having simplified our problem17, Equations (43) and (44) can be then rewritten, respectively, as

$$\begin{array}{cc}\hfill s& ={\int }_{\Delta }{\mathrm{\Phi }}^{\prime }\left(E_r\right)d{E}_r\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill {\mathrm{\Phi }}^{\prime }\left(E_r\right)& ={\int }_E\mathrm{\Phi }\left(E\right)·D\left(E_r\right|E)·\epsilon \left(E\right)dE.\hfill \end{array}$$

(48)

In order to get the flux $\mathrm{\Phi }$ from the expected counts s two approaches are used: unfolding and forward folding.

4.1. Unfolding

If we divide the energy range in bins, the expected counts of gamma ray in the i-th bin ${\Delta }_i$ of reconstructed energy is (when combining Equations (47) and (48))

$$s_i={\int }_{{\Delta }_i}d{E}_r\sum _j{\int }_{{\Delta }_j}dE\mathrm{\Phi }\left(E\right)D\left(E_r\right|E)\epsilon \left(E\right)\equiv \sum _j{R}_{i,j}{\overline{s}}_j,$$

(49)

where ${\overline{s}}_j$ is the expected number of gamma rays from the source flux in the j-th bin ${\Delta }_j$, i.e.,

$${\overline{s}}_j={\int }_{{\Delta }_j}\mathrm{\Phi }\left(E\right)dE.$$

(50)

The matrix $R_{i,j}$ is the response matrix which is the probability of detecting (due to the collection efficiency $\epsilon$) a photon with energy in the range ${\Delta }_j$ and assign to it (due to the energy dispersion D) a different energy bin ${\Delta }_i$. From Equation (49) its expression in formula is given by

$$R_{i,j}=\frac{1}{{\overline{s}}_j}{\int }_{{\Delta }_i}d{E}_r{\int }_{{\Delta }_j}dE\mathrm{\Phi }\left(E\right)D\left(E_r\right|E)\epsilon \left(E\right),$$

(51)

while in practice $R_{i,j}$ is estimated from MC simulations as

$$R_{i,j}=\frac{n_{i,j}^{\gamma }}{N_j^{\gamma }},$$

(52)

where $N_j^{\gamma }$ is the total number of gamma ray events simulated (according to an assumed source flux $\mathrm{\Phi }$) with true energy in the energy range ${\Delta }_j$, and $n_{i,j}^{\gamma }$ the number of those same events that have been detected by the telescope with a reconstructed energy in the energy range ${\Delta }_i$. Clearly, by summing over i we recover the binned collection efficiency

$${\epsilon }_j=\sum _i{R}_{i,j}.$$

(53)

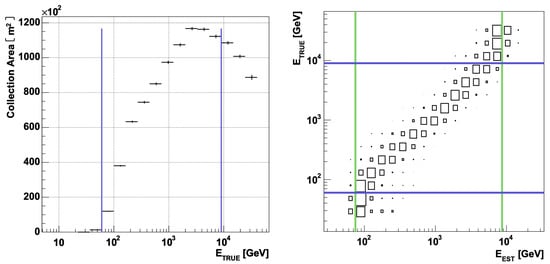
An example of the binned collection efficiency along with the energy dispersion from the same experiment can be found in Figure 10.

Figure 10. Left panel: Evolution in energy of the collection efficiency $\epsilon \left(E\right)$ multiplied by the collection area of the telescope, which for IACTs is generally of the order of ${10}^5{\mathrm{m}}^2$. Right panel: evolution in reconstructed/estimated energy and true energy of the binned dispersion energy (or migration matrix). Both figures are Reprinted with permission from Ref. [67] Copyright 2007 Albert et al.

Goal of the unfolding procedure is to find a solution of Equation (49), by inverting the response matrix

$${\overline{s}}_j=\sum _i{R}_{j,i}^{-1}{s}_i.$$

(54)

Thus, unfolding is basically a deconvolution problem and shares its typical problems, like the fact that the response matrix is, in general, non-invertible. As all ill-posed problems regularization procedures are required in order to find a solution and to prevent overfitting. In the context of IACTs analysis, common regularization procedures are those of Tikhonov [68], Bertero [69] and Schmelling [70]. For a more detailed discussion and comparison of these approaches with applications to data collected with the MAGIC telescopes see Ref. [67]. It is good practice to show the unfolding result with several of these approaches to cross-check the reconstructed flux and to also report along with the reconstructed flux points ${\overline{s}}_j$ their correlation matrix. Such a correlation matrix is needed if one is willing to fit the flux points ${\overline{s}}_j$ with a spectral model.

To date, the unfolding approach has been discussed as a geometrical problem: given a known vector s and a known matrix R, we wish to invert R in order to find the unknown vector $\overline{s}$ as shown in Equation (54). In the Bayesian unfolding approach instead the problem is a probabilistic one: given our prior knowledge I and the expected counts $s_i$ in the reconstructed energy bins, we wish to get the probability distribution of ${\overline{s}}_j$

$$p\left({\overline{s}}_j\right|s_i,I)=\frac{p\left(s_i\right|{\overline{s}}_j,I)·p\left({\overline{s}}_j\right|I)}{{\sum }_{i}p\left(s_i\right|{\overline{s}}_j,I)·p\left({\overline{s}}_j\right|I)}.$$

(55)

The prior $p\left({\overline{s}}_j\right|I)$ is the binned normalized ( ${\sum }_{j}p\left({\overline{s}}_j\right|I)=1$) flux that we initially assumed for the source, while the term $p\left(s_i\right|{\overline{s}}_j,I)$ is the probability of measuring an expected signal count in the reconstructed energy bin ${\Delta }_i$ given the true signal count ${\overline{s}}_j$ in the energy bin ${\Delta }_j$. This term is related to the response matrix defined in Equation (51).

An iterative method for getting the posterior in Equation (55) that takes as a prior $p\left({\overline{s}}_j\right|I)$ the posterior obtained from a previous iteration can be found in Ref. [71] and later on revised and improved by the same author in Ref. [72]. More recently the author of Ref. [73] proposed a fully Bayesian unfolding with applications to numerous examples.

4.2. Forward Folding

The main advantage of the unfolding algorithm is its ability to show a distribution that is as much as possible equivalent to the observed distribution of events with physical and instrumental effects being removed. Although some assumptions about the flux are inevitable as discussed in Section 4.1, the desired outcome of the unfolding procedure is to “interpret” the data as little as possible.

In the total opposite direction, we can find the forward folding approach. In this case, a parametric model for the intrinsic flux is assumed and the final result is to provide an estimate of the free model parameters $\theta$. When it is reasonable to believe that the source flux can be described by one or a family of parametric functions, the forward folding is always preferable to the unfolding one, being easier to implement and free of those problems that are typical of the unfolding methods which are cured by regularization. The problem falls therefore within the realm of “fitting” problems: searching for the values $\widehat{\theta }$ that maximize the likelihood function, defined as the probability of getting the observed data given the model parameters $\theta$. The observed data are the list of $N_{on}$ events (obtained from the shower image as discussed in Section 2) with their reconstructed energy, arrival direction and time (hereafter denoted for simplicity x). If the background is estimated from an OFF region (see Section 3.3) one has to take into account also the observed counts $N_{off}$ in the OFF region and the normalization factor $\alpha$. The likelihood function is

$$\begin{array}{cc}\hfill & \mathcal{L}\left(\theta \right|\pi ,N_{on},N_{off},\alpha ,x_1,\cdots ,x_{N_{on}})=\hfill \\ \hfill & p\left(\pi \right|\theta )·\mathcal{P}\left(N_{on}\right|s+\alpha b)·\mathcal{P}\left(N_{off}\right|b)·\prod _{i=1}^{N_{on}}\left(\frac{f_s\left(x_i\right|\theta ,\pi )+f_b\left(x_i\right)}{s+\alpha b}\right)\hfill \end{array}$$

(56)

where $\pi$ are the nuisance parameters of the model and $p\left(\pi \right|\theta )$ their probability distribution given $\theta$. The function $f_s$ is the differential source flux with the IRF of the telescopes being taken into account, such that

$$\int dx{f}_s\left(x\right|\theta ,\pi )=s,$$

(57)

where s is the expected signal counts in the ON region. The expected background count b in the OFF region is instead provided by

$$\int dx{f}_b\left(x\right)=b$$

(58)

where $f_b$ is the differential background template model. The function $\mathcal{P}$ is the Poisson distribution defined in Equation (12). The likelihood function defined in Equation (56) is usually referred to as “unbinned likelihood” to distinguish it from its binned version

$$\begin{array}{c}\hfill \mathcal{L}\left(\theta \right|\pi ,N_{on}^{\left(1\right)},\cdots ,N_{off}^{\left(1\right)},\cdots ,\alpha )=p\left(\pi \right|\theta )·\prod _{i=1}^{\mathrm{all}\mathrm{bins}}{\mathcal{L}}_i\left(\theta \right|\pi ,N_{on}^{\left(i\right)},N_{off}^{\left(i\right)},\alpha ),\end{array}$$

(59)

where ${\mathcal{L}}_i$ is the likelihood of the single i-th bin (in which $N_{on}^{\left(i\right)}$ and $N_{off}^{\left(i\right)}$ counts have been observed in the ON and OFF region, respectively) given by

$${\mathcal{L}}_i\left(\theta \right|\pi ,N_{on}^{\left(i\right)},N_{off}^{\left(i\right)},\alpha )=\mathcal{P}\left(N_{on}^{\left(i\right)}\right|s_i(\theta ,\pi )+\alpha b_i)·\mathcal{P}\left(N_{off}^{\left(i\right)}\right|b_i).$$

(60)

The variable $b_i$ has to be treated as a nuisance parameter and fixed to the value given in Equation (26) if the frequentist approach is implemented or integrated out in the Bayesian one. The variable $s_i(\theta ,\pi )$ is instead obtained by the integral in Equation (57) with integration limits on x defined by the bin under consideration.

The forward folding procedure applied in IACTs can be found for instance in fundamental physics studies, such as the search for dark matter [74] or tests of the equivalence principle from the time of flight of cosmic gamma rays [75].

5. Discussion

From the discovery of the TeV emission from the Crab nebula in 1989 by the Whipple collaboration [76], IACTs have been able in recent decades to give birth to a mature field of gamma ray astronomy. Instruments such as MAGIC, HESS, and VERITAS discovered numerous astrophysical sources at TeV energies, allowing investigation of the physics of remote cosmic objects. Apart from the technological development needed for the construction and maintenance of these telescopes, a huge effort has been carried out in recent decades to adapt and explore statistical tools aimed at extracting all of the information contained in the collected data.

The most challenging issue in the analysis of IACTs data is the predominant presence of background events that require detailed studies such as the estimation of the background from OFF regions as discussed in Section 3.3. Gamma rays only compose a small fraction of the cosmic flux that hits our atmosphere producing the Cherenkov light observed by the telescopes. Techniques such as the “multivariate analysis” (see Section 2.5) or the CNNs (see Section 2.6 ) are the current state of the art for discriminating gamma rays events from the background.

Another important factor that makes the statistical analysis so important and challenging for these instruments is that unfortunately we do not have a pure source of gamma rays, which is steady and under our control, and can then be used for calibrating the telescopes. The closest we have to a steady and bright gamma ray source is the Crab Nebula [77], which is indeed used as a standard for calibrating the instrument whenever an IACT observatory starts its operations. In order to infer instrumental properties, such as the energy threshold, a signal from the Crab Nebula is collected and then compared with the expected (obtained from MC simulations) response. MC simulations are therefore of huge importance for IACTs and, moreover, they also provide a way for training the BTD and RF algorithms briefly discussed in Section 2.5. The problem is that instrumental effects (such as the reflectance of the mirrors) and the atmospheric conditions have to be taken into account in these MC simulations, which in most cases requires approximations and idealized instrumental parametrizations. This is the reason why different efforts were made as discussed in Section 2.4 for making these MC simulations as realistic as possible.

Once the above issues are overcome, we have to quantify, given the list of detected events, how likely it is that a flux of gamma rays has been detected and how confidently we can set some values to such a flux. This has been discussed in Section 3 where we showed, using the frequentist and Bayesian approach, different solutions to this problem, emphasizing with examples their differences and mentioning some of the most recent developments. Lastly in Section 4, the IRF is taken into account in order to provide a flux estimation which is as much as possible similar to the intrinsic flux of gamma rays.

With the construction of CTA [78], the next generation of IACTs has ten times more sensitivity than the current instruments, and the statistical tools described in this review will become more and more indispensable in order to put the capability of the telescopes at its limits.