Topics in Cosmology—Clearly Explained by Means of Simple Examples
Abstract
:1. Introduction
Conventions
- Planck’s lenght: cm. Compare with Bohr’s radius: cm;
- Planck’s time: s;
- Planck’s mass: g. Compare with the proton mass: g;
- Planck’s temperature: K. The current temperature of our universe is K. The temperature of the solar surface is approximately 6000 K;
- Planck’s energy density erg·. The energy, mass, and temperature are either given in GeV or in terms of . For example, the temperature of the universe one second after the Big Bang is around GeV or , which, in IS units, is approximately K.
2. Big Bang Cosmology
2.1. Hubble’s Law
2.2. The Cosmic Equations
2.3. Singularities
- Type I (Big Rip): For , , , and ;
- Type II (Sudden): For , , , and ;
- Type III (Big Freeze): For , , , and ;
- Type IV (Generalized Sudden): For , , , , and higher-order derivatives of H diverge.
2.3.1. Big Rip Singularity
2.3.2. Sudden Singularity
2.3.3. Big Freeze Singularity
2.3.4. Generalized Sudden Singularity
2.4. Removing Singularities
- Introducing quantum effects (more precisely, holonomy corrections), which could be disregarded at low energy densities, as in loop quantum cosmology (LQC). These quantum effects produce a modification of the FE (the holonomy-corrected FE), which becomes [65,66,67,68]:where is the so-called critical density.Note that now, the modified FE depicts an ellipse in the plane (recall that, in GR, the FE depicts a parabola), which is a bounded curve, so the energy density is always finite. In fact, it is always bounded by the critical one. As a consequence, the singularities such as the BB or the Type I and III do not exist in LQC. About the BB singularity, people say that, in LQC, the Big Bang is replaced by a Big Bounce (the universe bounces from the contracting to the expanding phase).In addition, for low energy densities , the FE in GR (the usual one) is recovered. Thus, singularities of Type II and IV also exist in LQC. Finally, for a non-phantom fluid, the movement throughout the ellipse is clockwise; that is, the universe starts in the contracting phase, with an infinite size, and bounces to enter the expanding one.
- Introducing non-linear effects in the Ricci scalar. We have already seen that, in GR, the Hilbert–Einstein Lagrangian is . Then, the idea is that at high energy densities the Ricci scalar is replaced by a more general function , which satisfies when , in order to recover GR at low energy densities (recall that ) [13,69,70,71].To obtain the Hamiltonian of the system, one has to use the so-called Ostrograski construction, because the Lagrangian contains second derivatives of V. The Hamiltonian constrain leads to the following modified FE in gravity:This is a second-order differential equation with respect to the Hubble rate, which, together with the CE and the EoS, give the dynamics of the universe. However, contrary to the constituent equations in GR, one needs to perform numeric calculations in order to solve the equations in gravity. The most famous model is gravity (sometimes known as the Starobinsky model) given by , which was extensively studied in the Russian literature.
- One can also introduce quantum effects produced by massless fields conformally coupled with gravity, obtaining the so-called semiclassical gravity. If one considers some massless fields conformally coupled with gravity, the vacuum stress tensor acquires an anomalous trace, given by [72]:where R is, once again, the Ricci scalar, and is the Gauss–Bonnet invariant. In terms of the Hubble parameter, one has:The coefficients and are fixed by the regularization process. For instance, using adiabatic regularization, one obtains [11]:while point splitting yields [72]:where is the number of scalar fields, is that of four-component neutrinos, and is the number of electromagnetic fields.Here, it is important to note, as pointed out in [73], that the coefficient is arbitrary, although it is influenced by the regularization method and also by the fields present in the universe, but is independent of the regularization scheme and it is always negative.Now, we are interested in the value of the vacuum energy density, namely, . Since the trace is given by , inserting this expression in the conservation equation , one obtains:a first-order linear differential equation, which can be integrated by using the method of variation of constants, leading to:where C is an integration constant, which vanishes for flat space-time. This can be understood as follows: for a static space-time, reduces to , and the flat space-time reduces to Minkowski, for which , and thus, . Therefore, in semi-classical gravity, the Friedmann equation becomes:Here, we will consider the empty flat case, which corresponds to and . There, since , one has a de Sitter solution . In addition, the Friedmann equation is, in the empty case:and, for , becomes:whose solution is given by ; this shows that, for this model, the branches and decouple, i.e., the universe cannot transition from the expanding to the contracting phase, and vice versa.Next, performing the change of variable (we are here considering that the universe expands), the semi-classical Friedmann equation becomes [74]:where:The corresponding dynamical system can be written as:which can be viewed simply as the dynamics, with friction, of a particle under the action of a potential.There are two different situations (we use the notation ):
- (a)
- Case . Here, the system has two fixed points: is an unstable critical point, and is stable (it is the minimum of the potential). Solutions are only singular at early times. At late times, they oscillate and shrink around a stable point, that is, is a global attractor. In addition, there is a solution that ends at , and only one nonsingular solution that starts at (with zero energy) and ends at ;
- (b)
- Case . This is the famous Starobinsky model [75]. The system has two critical points: is a stable critical point, and is a saddle point (it is the maximum of the potential). There are solutions that do not cross the axis ; these solutions are singular at early and late times: they correspond to the trajectories that cannot pass the top of the potential. There are other solutions that cross the axis twice; they are also singular at early and late times. These trajectories pass the top of the potential, bounce at , and pass once again the top of the potential. There are solutions that cross the axis once. These solutions are singular at early times; however, at late times, the solutions spiral and shrink to the origin. These solutions pass the top of the potential once, and then bounce some number of times about , shrinking to . Finally, there are only two unstable non-singular solutions: one goes from to , and the other is the de Sitter solution . What seems a little bit strange is that the title of Starobinsky’s paper [75] is “A new type of isotropic cosmological models without singularity”. In fact, as we have just shown, in that model, there is only one non-singular solution, but it is unstable, and thus, non-physical.
2.5. Chronology of the Universe
- The energy density is given by , where is the number of degrees of freedom, which for the modes in the standard model are ;
- For a relativistic fluid, pressure is related to energy via the linear relation ;
- The number density of particles is , where is the Riemann zeta function;
- The entropy density is .
- Planck scale. MeV, which means that the Planck scale is reached at seconds after the BB. It is very important to remark that no reliable physical theory can be invoked before this time. This is a crucial, insurmountable constraint that any serious physicist knows well, but that, too often, is kept hidden under the carpet (nobody seems to be interested in proclaiming the shortcomings of present-day fundamental physics). The corresponding redshift has a value of ;
- Grand unification theory (GUT) scale. It enters when the temperature goes down to GeV, i.e., for s or . The three forces of the standard model (electromagnetic, weak, and strong), which constituted a unique force until then, start to become separated forces below this temperature;
- Electroweak epoch. It occurs at – GeV, i.e., when s or . The strong interaction clearly decouples from the electroweak one;
- Radiation-dominated era. It is set up when eV, i.e, s or . The energy density of nearly massless relativistic particles dominates. From then on, the weak and electromagnetic forces become separated so that, finally, during this period, all the different forces decouple and become distinct. Electromagnetic radiation dominates the energy content of the universe at this epoch;
- Matter domination era. It occurs for eV. The energy density of matter dominates, at last. Clusters of galaxies and stars start to be formed during this period due to the omnipresent gravitational force that now overcomes radiation pressure;
- Recombination. This period starts when the temperature goes down to around 3000 K, the redshift being . This happens some 300,000 years after the BB. At this epoch, nearly all free electrons and protons recombine and form neutral hydrogen. Photons decouple from matter and can travel freely, for the first time, throughout the whole universe. They originate what is observed today as cosmic microwave background (CMB) radiation (in that sense, the cosmic background radiation is infrared (and some red) black-body radiation emitted when the universe was at a temperature of some 3000 K, redshifted by a factor of 1100 from the visible spectrum to the microwave spectrum);
- Dark energy era. It starts when the falling temperature reaches eV (correspondingly, ), that is, around 3 billion years ago, and lasts up to present time, extending into the future. The universe is dominated by an unknown sort of energy, called dark energy, and under its influence, it starts to accelerate (the so-called current cosmic acceleration or late-time acceleration).
3. Inflation
3.1. The Problems of BB Cosmology
- The horizon problem: Imagine two observers, A and B, in a circumference of variable radius and separated by an angle . The time it takes for a light signal emitted from A to reach B is . Then, as in natural units the speed of light is 1, we have ; the distance travelled by a signal of light emitted at time and arriving at time is . This is what happens in an expanding universe. Let be the present time, and we take as the singularity, i.e., when the BB occurs. Thus, the distance travelled by a signal emitted at time and received now isThis is the present horizon size (the size of our patch of universe). We cannot see beyond that distance, i.e., we cannot see galaxies which are further away than the present horizon size.To simplify, we will assume that the universe is matter-dominated, that is, , and thus, . We know that our universe is now very homogeneous, so at Planck scales it had to be extremely homogeneous, but at that time the size of our universe was . (Recall that, due to the Hubble law, in an expanding universe, .)This quantity has to be compared with the size of the causal regions (the distance that light travels from the Big Bang to the Planck era), which is . We calculate the ratio:where we have used the adiabatic evolution of the universe, constant, and that, in natural units, .Using that, now, and , we obtainwhich means that, at Planck scales, there are disconnected regions. Then, assuming that inhomogeneities cannot be dissolved by ordinary expansion, how is it possible that our present universe be so homogeneous, and that the cosmic microwave background (CMB) radiation has practically the same temperature in all directions? This seems impossible, if it comes from a patch, which at Planck scales, contains so many regions that have never been in causal contact (they have never exchanged information). This is the well-known horizon problem.An equivalent way to see this problem goes as follows: As we have already explained, the decoupling, or the last scattering, is thought to have occurred at recombination, i.e., about 300,000 years after the Big Bang, or at a redshift of about . We can determine both the size of our universe and the physical size of the particle horizon that had existed at this time.The size of our universe coincides approximately with the size of the last scattering surface, which, currently, is approximately , so that, at recombination, the diameter of the last scattering surface was . At that time, the size of a causally connected region is . Then, we have:Next, taking into account that the energy density of matter scales as , and further, that at recombination the universe is matter-dominated, i.e., , and that at present time , with , one obtains:As a consequence, in the last scattering surface, there are regions which are causally disconnected; however, it turns out that the CMB has practically the same temperature in all directions.To simplify, the horizon size is of the order 14 billion lightyears, which coincides with the age of the universe 14 billion years ago. So, imagine a region that is at a distance of 10 billion lightyears from us, and another region, in the opposite direction, that is at the same distance from us. The question is, how it is possible that both regions, which are about 20 billion lightyears apart, emitted light at the same temperature?This is an apparent “paradox” in a static or decelerating universe, but as we will see in the next section, the paradox is overcome when one assumes a short superluminal expansion phase at early times.
- The flatness problem: Up to now, we have only considered the dynamical equation for flat space, but, in fact, space could have positive or negative curvature. When one considers the general case, the FE becomes:with (open, flat, and closed cases, respectively).This equation can be written as follows:where is the ratio of the energy density to the critical one.Evaluating at the Planck time and at the present time, one obtains:where we have used the adiabatic evolution of the universe.Thus, in order to have (the present observational data), the value of at early times has to be fine-tuned to values amazingly close to zero, but without letting it be exactly zero—this is the flatness problem, which sometimes is also dubbed the fine-tuning problem.To better understand this fine tuning: our very existence depends on the fantastically close balance between the actual density and the critical density in the early universe. If, for instance, the deviation of from one at the time of nucleosynthesis had been one part in 30 thousand, instead of one part in 30 trillion, the universe would have collapsed in a Big Crunch after only a few years. In that case, galaxies, stars, and planets would not have had time to form, and cosmologists would never have existed.
3.2. Inflation: The Basic Idea
3.3. A Simple Way to Produce Inflation
3.4. On the Number of E-Folds
3.5. Different Reheating Mechanisms
- In the case that the potential has a deep well, at the end of inflation, the inflaton field starts to oscillate in this deep well, and releases its energy by creating particles [43,44,76]. This happens in standard inflation, but after the discovery of the current cosmic acceleration, other models containing monotonic potentials appeared, and thus, since the inflaton field cannot oscillate in this case, other mechanisms to reheat the universe were proposed.
- When the potential is a monotonous function, particles could be created via the so-called instant preheating developed by Felder, Kofman, and Linde [46]. In that case, a quantum scalar field with a very light bare mass is coupled with the inflaton, the adiabatic regime breaks after the end of inflation, and particles with an effective very heavy mass are copiously created. The energy density of these particles could never dominate the one of the background, because in that case, another undesirable inflationary period would appear; this is the reason why these particles have to decay in lighter ones well before they can dominate. Once the decay is finished, the universe becomes reheated, at a temperature close to GeV, thus matching with the hot BB model.
- For a monotonous potential, containing an abrupt phase transition from the end of inflation to a regime where all the energy density is kinetic (named kination phase [29] or deflationary phase in [39]), superheavy particles [40,41,77,78] and also lighter ones [30,31,32,33,34,35,36,37,38,42,79,80] can be created via gravitational particle production. The problem of reheating via the production of light particles is that undesirable polarization effects could appear, which would disturb the evolution of the inflaton field during the slow-roll period (see, for a detailed explanation, [46]). On the contrary, these polarization effects, during inflation, can be neglected when one considers the production of superheavy particles, which have to decay in lighter ones, to obtain, after thermalization, a hot radiation-dominated universe.
4. The Current Cosmic Acceleration
4.1. The Cosmological Constant
4.2. Quintessential Inflation
- The power spectrum of scalar perturbations:where the star means that the quantities are evaluated at the horizon crossing;
- The spectral index, . Its central value is ;
- The ratio of tensor to scalar perturbations, . Observational data lead to the constraint .
4.3. Improved Versions of QI
4.3.1. Lorentzian Quintessential Inflation
4.3.2. -Attractors in Quintessential Inflation
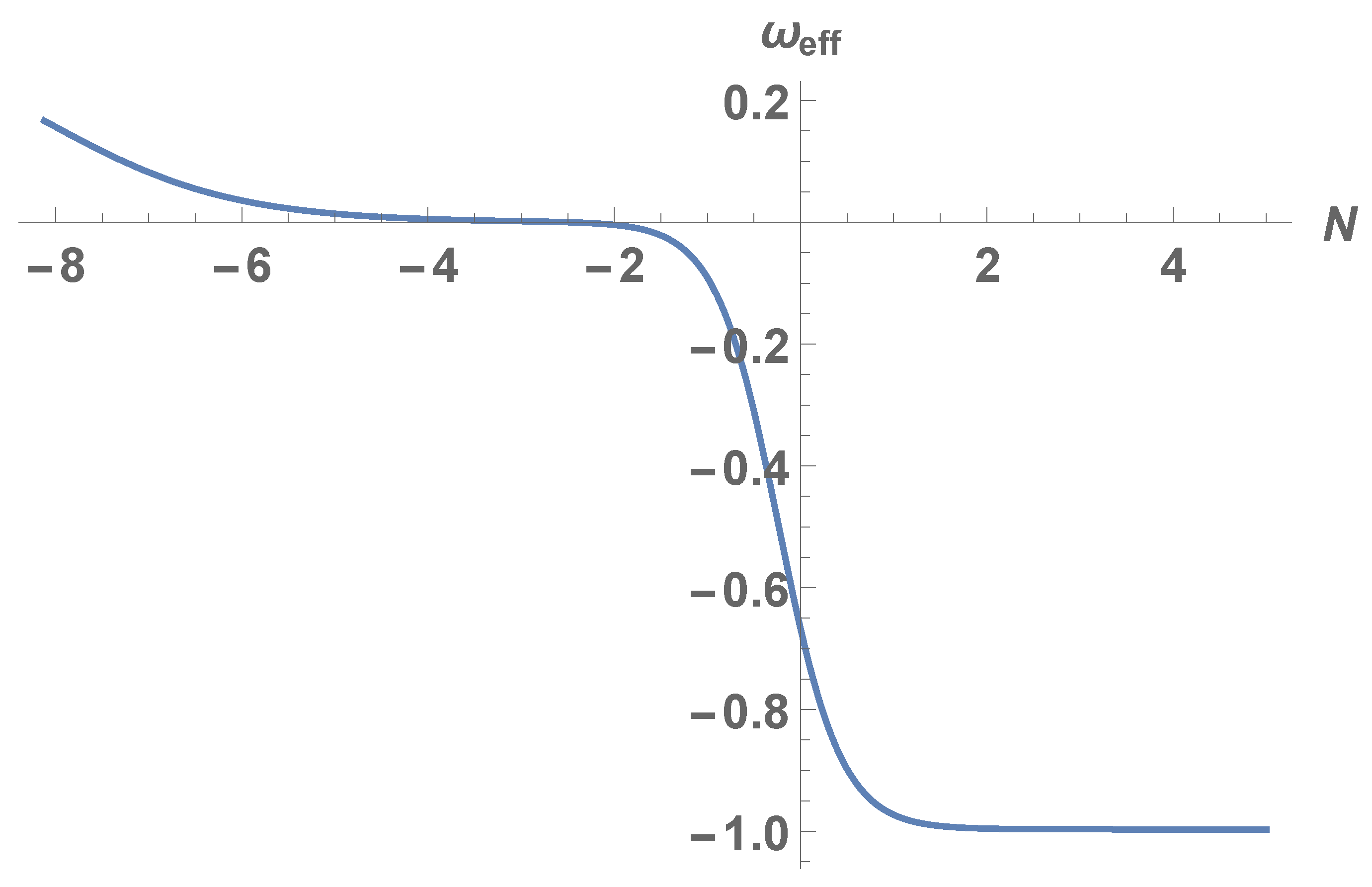
4.4. Evolution of the Dynamical System
The Dynamical System
5. The Reheating Mechanism
5.1. The Harmonic Oscillator
5.2. The Harmonic Oscillator with a Time Dependent Frequency
5.3. Gravitational Particle Production of a Massive Quantum Field Conformally Coupled to Gravity
5.4. Reheating in the Case of -Attractors
- The decay takes place before the end of the kination phase (recall that kination ends when );
- The decay occurs after the end of kination.
5.4.1. Decay Happens before the End of Kination
- The decay occurs after the beginning of kination, i.e., . This value has been obtained numerically in the case of -attractors, and it agrees with the fact that kination starts immediately after the end of inflation, which, in the majority of models, ends at the scale GeV;
- The decay precedes the end of kination, i.e., . Taking into account that the energy density of the background, i.e., the one of the inflaton field, and the one of the relativistic plasma, when the decay is finished, that is, when , will be:one can see that these two constraints bound the decay rate, as follows:
5.4.2. Decay after the End of Kination
6. Historical Notes
- On 20 November 1915, Hilbert gave a talk at the Royal Society of Sciences in Göttingen, which was later published in the Transactions of the Society, in March 1916. There, Hilbert presented the covariant equations for GR. On the other hand, Einstein’s presentation, for the first time, of his equations for GR took place in the Prussian Academy of Sciences in Berlin on 25 November 1915, five days after Hilbert’s.So, at first glance, it would seem that it was Hilbert who first obtained these equations. This was indeed the viewpoint of some scientists contemporary to Einstein and Hilbert, among them Felix Klein, Wolfgang Pauli, and Herman Weyl. In fact, for years there was an ongoing controversy about whether it was Albert Einstein or David Hilbert who had first obtained the GR equations.However, a new document appeared later in Hilbert’s archive at the University of Göttingen: the printing proofs of the first version of Hilbert’s paper, published in March of 1916. These proofs were sent to Hilbert two weeks after his talk (on 6 December 1915), and there, one can check that Hilbert did not present the equations of GR in his talk of November 1915. Quite on the contrary, in these proofs, Hilbert refers explicitly to Einstein’s talk of 25 November, published on 2 December 1915. What really happened is that Hilbert included the GR equations in his publication, which he obtained in an alternative way, but only after reading Einstein’s paper, having made sure to check that the results coincided.More to the point, Einstein wrote to Hilbert: “I had no difficulty finding the general covariance equations of GR. This is easy with the help of the Riemann tensor. What is really difficult is to recognize that these equations constitute a generalization, and even more, a simple and natural generalization of Newton’s laws”.What is also clear is that Hilbert discussed GR in a superficial way only, concentrating on the mathematical structure of the equations and on their Lagrangian formulation, but probably without understanding in depth their physical meaning, quite the opposite of Einstein’s approach to this issue.
- Astronomers who made most important contributions to understand the expansion of our universe were Vesto Slipher, Henrietta Leavitt, and Edwin Hubble. However, the first person who clearly realized that the universe is expanding was a Belgian priest, mathematician, and physicist named Georges Lemaître, who published his results in 1927. We should note that, in those years, everybody believed that the universe was static, and for very strong physical reasons. Indeed, as any ordinary physical system that had more than enough time to evolve (an infinite amount of time, in theory, since the universe was considered to have always existed), it should have necessarily reached the stationary state. It could not be otherwise. However, Lemaître proved reality to be quite the contrary. On the basis of Einstein’s GR and by matching the theory with the astronomical observations of Slipher and Hubble, in a masterful way, he proved that the universe was expanding; later, he observed that it was not eternal, that it had an origin.For many decades (even now, it is still so declared in most places) people believed that the astronomer Edwin Hubble was the person who first discovered the expansion of the universe. Only recently, without denying at all Hubble’s important contributions, have historians put things in the right place. A very detailed account of this thrilling story can be found in a book recently published by one of the authors [1].
- In his calculations, using his table of distances (obtained in part with the help of Leavitt’s law), and Slipher’s table of velocities (obtained as optical Doppler shifts), Hubble obtained a rather large value for the expansion rate, of which is off the presently accepted value by almost one order of magnitude. The reason is that it is extremely difficult to measure cosmological distances. On the contrary, obtaining velocities by means of the Doppler shifts is somehow easier. However, here there is also the problem of appropriately disentangling the recession redshift from other contributions to the observed Doppler shift, coming from the gravitational influence of other massive celestial objects. Even today, there is still a sharp controversy about the right value of (see, e.g., [57] and references therein). Results from astronomical observations by different groups, each one reporting uncertainties of just 1 or 2%, differ by some 5 to 10%, an unpleasant situation that is termed the “Hubble parameter tension” [58,59].
- In 1922, Alexander Friedmann was the first to discover full families of solutions of the EEs, which he rightly interpreted as corresponding to expanding and to contracting universes. In 1922 and 1924, Friedman published two seminal papers in the prestigious German journal Zeitschrift für Physik [7], of which Einstein was an editor. In those papers, Friedmann showed that there were solutions to Einstein’s equations where the universe evolved in an expanding or contracting way. Recall (see above) that, in this epoch, everybody believed that our universe was static. However, Friedmann explicitly declared, in 1924, that, based on some of his solutions, our universe very well might be expanding.Einstein was the ”referee” (this figure did not actually have the same meaning and function at that time) of Friedmann’s first paper and, after having studied it, he wrote a letter to the journal saying that Friedmann’s calculations should not be published since they contained an error. When Friedmann (indirectly) learned of this opinion, he sent all the details of his calculation to Einstein, asking him to check them for himself. After some discussions (described in detail in, e.g., [1,2,3,4]), Einstein finally recognized that Friedmann made no mistake, and hurried to publish another letter recognizing his own error and saying that Friedmann’s paper should be published. Unfortunately, in those days, it took a long time to see an article published after it was finished, and Friedmann died in 1925 before the publication of Einsteins’ retraction.
- During a break at the very famous Solvay meeting of 1927 in Brussels, Einstein said, literally, to Lemaître (as was reported later by the last): “Vos calculs sont corrects, mais votre physique est abominable”. He was referring to Lemaître’s paper of the same year (1927) [9], which he had handed to Einstein during a previous conversation. In the paper (in French), Lemaître had obtained, for the first time ever, the Hubble law, and moreover, he had interpreted it in the right way, as being a proof of the expansion of the universe, of the very fabric of the cosmos (an interpretation that Hubble never admitted, in his whole life). Einstein himself did not accept the expansion of the cosmos until 1932, when he was finally convinced by Richard Tolmann and Willem de Sitter [1,2,3,4].
- In 1956, George Gamow wrote, in Scientific American, that Einstein had told him, long ago, that the idea of the cosmic repulsion associated with the cosmological constant had been “the greatest blunder of his life” (“Die grösste Eselei meines Lebens”, in German). For years to come, this was the only testimony of such a claim, leading many to question it because of Gamow’s well-known imaginative character. Recently, however, it has been discovered by historians of physics ([117] and references therein) that Einstein made a similar statement on at least two more occasions. Indeed, John Wheeler wrote in his book, Exploring Black Holes: Introduction to General Relativity, that he had personally been present when Einstein said the above words to Gamow, outside the hall of the Institute for Advanced Studies in Princeton. Moreover, Ralph Alpher also testified once that he had heard Einstein make such a claim.In addition, it is a proven fact that Einstein never wanted to use the CC again, not even when someone suggested that it might be interesting to put it back, so as to better adjust the age of the universe to the results of observations of the oldest galaxies, which seemed, at one point (erroneously), to clearly exceed the age of the universe. As Einstein explained in a footnote in the appendix to the second edition of his book The Meaning of Relativity [118]: “If Hubble’s expansion had been discovered at the time of the creation of the general theory of relativity, the cosmological constant would never had been added. It now seems much less justified to add a term like this in the field equations, since its introduction loses the only justification it originally had”.Finally, an important consideration, which very few mention, is the following [1]: in taking this position, Einstein was even more radical than Friedmann and Lemaître (the defendants of the expanding universe), since those always included the CC term in their models for the universe; even if such a term was not necessary at all in their equations, contrary to the case of Einstein’s static model, where it was crucial (for an expanding universe solution, such an additional term plays a secondary role). In any case, if there was no reason for its presence, it should not be put there, under any circumstance; this is what Einstein said (please see [1] for additional details).
- Fred Hoyle, an English nuclear physicist and astronomer who formulated the theory of stellar nucleosynthesis (and, with it, the remarkable fact that we are all stardust), was one of the authors of the steady-state theory of the universe, an attempt to maintain a static model for the cosmos that is able to account for Hubble’s empirical law of expansion [1,2,3,4]. Hoyle did not buy Lemaître’s conclusion that the universe had an origin, much less his hypothesis of the primeval atom that latter exploded; he, as a serious nuclear physicist, understood it as lacking any physical rigor. On BBC Radio’s Third Programme broadcast on 28 March 1949, Hoyle explained to the audience that, when comparing Lemaître’s model (by then improved by Gamow) with his steady-state theory (where a smooth creation of matter had to take place in order to compensate for Hubble’s expansion and keep the matter density of the universe constant), in Lemaître’s model a sudden creation of all the matter in the universe had to occur at the very beginning of it. For this to happen, an unbelievably huge expansion (a Big Bang) of the fabric of space was absolutely necessary. However, of course, such a phenomenon was fully impossible, and therefore, he pronounced these famous words in a very disdainful tone (see a much more detailed explanation in [1]). Hoyle anticipated the idea of cosmic inflation very clearly, albeit as an impossible thought, exactly thirty years before Alan Guth, on an inspired night, could formulate it precisely.However, even if Hoyle had spoken these two words, Big Bang, in a disrespectful manner—trying, on purpose, to mock Lemaître’s model (which had, by then, substantially been improved by George Gamow)—from this moment on, everybody, starting with Gamow himself (a very peculiar character, as is well known) began to use this term to refer to the origin of the universe.
- The cosmological horizon problem (aka the homogeneity problem) is a fine-tuning issue that affects classical Big Bang models of the universe. It arises due to the impossibility of explaining the homogeneity reported by astronomical surveys of very distant regions of space—which are causally disconnected in these Big Bang models—unless one invokes a mechanism that sets the same initial conditions everywhere with very high accuracy. This problem was first pointed out by Wolfgang Rindler in 1956. The most commonly accepted solution is cosmic inflation, as we have discussed here, but an explanation in terms of a variable speed of light has been proposed, too.
- The flatness problem is another important issue that appeared in the old, classical Big Bang model of the universe. It was first mentioned by Robert Dicke in 1969, in the Jane Lectures he gave for the American Philosophical Society that year. The total normalized energy density of our present universe has been measured to be very close to 1, with very small uncertainty, which points towards a very flat universe. Any departure from the conditions leading to this value in the past would had been magnified enormously over cosmic time. This leads to the conclusion that one would need an unbelievably accurate fine-tuning in the initial conditions of the universe, with an energy density that should have been incredibly closer to the critical value at the very beginning of the universe. As we have seen, cosmic inflation provides the solution to this problem by making the universe extremely flat, to the needed precision.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Elizalde, E. The True Story of Modern Cosmology: Origins, Protagonists and Breakthroughs; Springer: Berlin/Heidelberg, Germany, 2021; ISBN 978-3-030-80653-8. [Google Scholar]
- Elizalde, E. Zeta functions and the cosmos: A basic brief review. Universe 2021, 7, 5. [Google Scholar] [CrossRef]
- Elizalde, E. Some issues on the foundations of Modern Cosmology, Gravitation and Quantum Physics. Universe 2020, 6, 189. [Google Scholar] [CrossRef]
- Elizalde, E. Reasons in favor of a Hubble-Lemaître-Slipher’s (HLS) law. Symmetry 2019, 11, 35. [Google Scholar] [CrossRef] [Green Version]
- Einstein, A. Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie. Sitz. König. Preuss. Akad. 142–152 (1917). [Cosmological considerations in the general theory of relativity]. In The Principle of Relativity; Lorentz, H.A., Einstein, A., Minskowiski, H., Weyl, H., Sommerfeld, A., Eds.; Dover: Downers Grove, IL, USA, 1952; pp. 175–188. [Google Scholar]
- de Sitter, W. On Einstein’s theory of gravitation and its astronomical consequences. Mon. Not. R. Astron. Soc. 1917, 78, 3–28. [Google Scholar] [CrossRef] [Green Version]
- Friedmann, A. Über die Krümmung des Raumes. [On the curvature of space]. Z. Phys. 1922, 10, 377–386. Available online: https://wwwphy.princeton.edu//~steinh/ph563/friedmann.pdf (accessed on 27 January 2022). [CrossRef]
- Friedmann, A. Über die Möglichkeit einer Welt mit konstanter negativer Krümmung des Raumes. Z. Phys. 1924, 21, 326–332. [Google Scholar] [CrossRef]
- Lemaître, G. Republication of: A homogeneous universe of constant mass and increasing radius accounting for the radial velocity of extra-galactic nebulae. Gen. Rel. Grav. 2013, 45, 1635–1646. [Google Scholar] [CrossRef]
- Lemaître, G. The Beginning of the World from the Point of View of Quantum Theory. Nature 1931, 127, 706. [Google Scholar] [CrossRef]
- Fischetti, M.V.; Hartle, J.B.; Hu, B.L. Quantum Effects in the Early Universe. 1. Influence of Trace Anomalies on Homogeneous, Isotropic, Classical Geometries. Phys. Rev. D 1979, 20, 1757–1771. [Google Scholar] [CrossRef]
- Ashtekar, A.; Singh, P. Loop Quantum Cosmology: A Status Report. Class. Quant. Grav. 2011, 28, 213001. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Method Mod. Phys. 2007, 4, 115–146. [Google Scholar] [CrossRef] [Green Version]
- Sotiriou, T.P.; Faraoni, V. f(R) Theories of Gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef] [Green Version]
- Guth, A. The Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef] [Green Version]
- Linde, A. A new inflationary universe scenario: A possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems. Phys. Lett. B 1982, 108, 389. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P.J. Cosmology for Grand Unified Theories with Radiatively Induced Symmetry Breaking. Phys. Rev. Lett. 1982, 48, 1220. [Google Scholar] [CrossRef]
- Chibisov, G.; Mukhanov, V. Galaxy formation and phonons. Mon. Not. R. Astron. Soc. 1982, 535, 200. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Dynamics of Phase Transition in the New Inflationary Universe Scenario and Generation of Perturbations. Phys. Lett. B 1982, 117, 175. [Google Scholar] [CrossRef]
- Guth, A.H.; Pi, S.-Y. Fluctuations in the New Inflationary universe. Phys. Rev. Lett. 1982, 49, 1110. [Google Scholar] [CrossRef]
- Bardeen, J.M.; Steinhardt, P.J.; Turner, M.S. Spontaneous creation of almost scale-free density perturbations in an inflationary universe. Phys. Rev. D 1983, 28, 679. [Google Scholar] [CrossRef]
- Linde, A.D. Scalar Field Fluctuations in Expanding Universe and the New Inflationary universe Scenario. Phys. Lett. B 1982, 116, 335. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2015 results. XX. Constraints on inflation. Astron. Astrophys. 2016, 594, A20. [Google Scholar] [CrossRef] [Green Version]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef] [Green Version]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 1753, 15. [Google Scholar] [CrossRef] [Green Version]
- Tsujikawa, S. Quintessence: A Review. Class. Quant. Grav. 2013, 214003, 30. [Google Scholar] [CrossRef] [Green Version]
- Peebles, P.J.E.; Vilenkin, A. Quintessential Inflation. Phys. Rev. D 1999, 59, 063505. [Google Scholar] [CrossRef] [Green Version]
- Joyce, M. Electroweak Baryogenesis and the Expansion Rate of the Universe. Phys. Rev. D 1997, 55, 1875. [Google Scholar] [CrossRef] [Green Version]
- Parker, L. Particle creation in expanding universes. Phys. Rev. Lett. 1968, 562, 21. [Google Scholar] [CrossRef]
- Parker, L. Quantized fields and particle creation in expanding universes. I. Phys. Rev. 1969, 1057, 183. [Google Scholar] [CrossRef]
- Parker, L. Quantized fields and particle creation in expanding universes. II. Phys. Rev. D 1970, 3, 346. [Google Scholar] [CrossRef]
- Folov, V.M.; Mamayev, S.G.; Mostepanenko, V.M. On the difference in creation of particles with spin 0 and 1/2 in isotropic cosmologies. Phys. Lett. A 1976, 55, 7. [Google Scholar]
- Grib, A.A.; Levitskii, B.A.; Mostepanenko, V.M. Particle creation from vacuum by a nonstationary gravitational field in the canonical formalism. Theory Math. Fiz. 1974, 59, 19. [Google Scholar] [CrossRef]
- Grib, A.A.; Mamayev, S.G.; Mostepanenko, V.M. Particle creation from vacuum in homogeneous isotropic models of the Universe. Gen. Rel. Grav. 1976, 535, 7. [Google Scholar]
- Grib, A.A.; Mamayev, S.G.; Mostepanenko, V.M. The creation of particles from a vacuum in a non steady isotropic universe. Sov. Phys. J. 1974, 1700, 17. [Google Scholar]
- Ford, L.H. Gravitational particle creation and inflation. Phys. Rev. D 1987, 35, 2955. [Google Scholar] [CrossRef]
- Zeldovich, Y.B.; Starobinsky, A.A. Rate of particle production in gravitational fields. JETP Lett. 1977, 26, 252. [Google Scholar]
- Spokoiny, B. Deflationary Universe Scenario. Phys. Lett. B 1993, 315, 40. [Google Scholar] [CrossRef] [Green Version]
- Hashiba, S.; Yokoyama, J. Gravitational reheating through conformally coupled superheavy scalar particles. JCAP 2019, 8, 1. [Google Scholar] [CrossRef] [Green Version]
- Haro, J.; Yang, W.; Pan, S. Reheating in quintessential inflation via gravitational production of heavy massive particles: A detailed analysis. JCAP 2019, 23, 1. [Google Scholar] [CrossRef] [Green Version]
- Birrell, N.D.; Davies, P.C.W. Massive particle production in anisotropic space-times. J. Phys. A Math. Gen. 1980, 13, 2109. [Google Scholar] [CrossRef]
- Chung, D.J.H.; Kolb, E.W.; Riotto, A. Superheavy dark matter. Phys. Rev. D 1998, 59, 023501. [Google Scholar] [CrossRef] [Green Version]
- Chung, D.J.H.; Crotty, P.; Kolb, E.W.; Riotto, A. On the gravitational production of superheavy dark matter. Phys. Rev. D 2001, 64, 043503. [Google Scholar] [CrossRef] [Green Version]
- Felder, G.; Kofman, L.; Linde, A. Instant Preheating. Phys. Rev. D 1999, 59, 123523. [Google Scholar] [CrossRef] [Green Version]
- Felder, G.; Kofman, L.; Linde, A. Inflation and Preheating in NO models. Phys. Rev. D 1999, 60, 103505. [Google Scholar] [CrossRef] [Green Version]
- Flender, S. Formation of Large-Scale Structure and Its Imprint on the Cosmic Microwave Background. Academic Dissertation, HIP-2014-01. University of Helsinki, Helsinki, Finland, 2014. Available online: https://inspirehep.net/files/b039be17085960901edb8c913f3640c7 (accessed on 27 January 2022).
- Primack, J.R. Dark Matter, Galaxies, and Large Scale Structure in the Universe. In Proceedings of the International School of Physics “Enrico Fermi”, Varenna, Italy, 26 June–6 July 1984; SLAC -PUB - 3387. Available online: https://inspirehep.net/files/bd0d1b777e1e505ad92dacf5731aac64 (accessed on 27 January 2022).
- How Do Stars and Planets form and Evolve? Big Questions, Center for Astrophysics, Harvard & Smithsonian. Available online: https://pweb.cfa.harvard.edu/big-questions/how-do-stars-and-planets-form-and-evolve (accessed on 27 January 2022).
- Gonçalves, R.S.; Carvalho, G.C.; Andrade, U.; Bengaly, C.A.P.; Carvalho, J.C.; Alcaniz, J. Measuring the cosmic homogeneity scale with SDSS-IV DR16 Quasars. JCAP 2021, 3, 29. [Google Scholar] [CrossRef]
- Becker, K. What do “homogeneity” and “isotropy” mean? Ask an Astronomer, Cornell Astronomy. Available online: http://curious.astro.cornell.edu/about-us/101-the-universe/cosmology-and-the-big-bang/general-questions/574-what-do-homogeneity-and-isotropy-mean-intermediate (accessed on 27 January 2022).
- Mo, H.; van den Bosch, F.; White, S. Galaxy Formation and Evolution; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Sagan, C. Cosmos; Chapter 8. Available online: https://www.youtube.com/watch?v=2ktRTHCBBjg (accessed on 27 January 2022).
- Hubble, E. A Relation between Distance and Radial Velocity Among Extra-Galactic Nebulae. Proc. Natl. Acad. Sci. USA 1929, 15, 168–173. [Google Scholar] [CrossRef] [Green Version]
- Huchra, J.P. The Hubble Constant. Available online: https://lweb.cfa.harvard.edu/~dfabricant/huchra/hubble/ (accessed on 27 January 2022).
- Huchra, J.P. Estimates of the Hubble Constant. Available online: https://lweb.cfa.harvard.edu/~dfabricant/huchra/hubble.plot.dat (accessed on 27 January 2022).
- Elizalde, E.; Khurshudyan, M.; Odintsov, S.D.; Myrzakulov, R. An analysis of the H0 tension problem in a universe with a viscous dark fluid. Phys. Rev. D 2020, 102, 123501. [Google Scholar] [CrossRef]
- Verde, L. Exploring the Hubble Tension, CERN Courier, 2 July 2021. Available online: https://cerncourier.com/a/exploring-the-hubble-tension/ (accessed on 27 January 2022).
- Wikipedia. Measurement of the Hubble Constant. Available online: https://en.wikipedia.org/wiki/Hubble%27s_law#Measured_values_of_the_Hubble_constant (accessed on 27 January 2022).
- Nojiri, S.; Odintsov, S.D.; Tsujikawa, S. Properties of singularities in (phantom) dark energy universe. Phys. Rev. D 2005, 71, 063004. [Google Scholar] [CrossRef] [Green Version]
- Barrow, J.D. Sudden future singularities. Class. Quant. Grav. 2004, 21, L79–L82. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D. Inhomogeneous equation of state of the universe: Phantom era, future singularity and crossing the phantom barrier. Phys. Rev. D 2005, 72, 023003. [Google Scholar] [CrossRef] [Green Version]
- Frampton, P.H.; Ludwick, K.J.; Scherrer, R.J. The Little Rip. Phys. Rev. D 2011, 84, 063003. [Google Scholar] [CrossRef] [Green Version]
- Frampton, P.H.; Ludwick, K.J.; Nojiri, S.; Odintsov, S.D.; Scherrer, R.J. Models for Little Rip Dark Energy. Phys. Lett. B 2012, 708, 204–211. [Google Scholar] [CrossRef] [Green Version]
- Singh, P. Loop cosmological dynamics and dualities with Randall-Sundrum braneworlds. Phys. Rev. D 2006, 73, 063508. [Google Scholar] [CrossRef] [Green Version]
- Singh, P.; Vandersloot, K.; Vereshchagin, G. Non-singular bouncing universes in loopquantum cosmology. Phys. Rev. D 2006, 74, 043510. [Google Scholar] [CrossRef] [Green Version]
- Sami, M.; Singh, P.; Tsujikawa, S. Avoidance of future singularities in loop quantum cosmology. Phys. Rev. D 2006, 74, 043514. [Google Scholar] [CrossRef] [Green Version]
- Amorós, J.; de Haro, J.; Odintsov, S.D. Bouncing Loop Quantum Cosmology from F(T) gravity. Phys. Rev. D 2013, 87, 104037. [Google Scholar] [CrossRef] [Green Version]
- Felice, A.D.; Tsujikawa, S. f(R) theories. Living Rev. Rel. 2010, 13, 3. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rep. 2017, 692, 1–104. [Google Scholar] [CrossRef] [Green Version]
- Davies, P.C.W. Singularity Avoidance and Quantum Conformal Anomalies. Phys. Lett. B 1977, 68, 402–404. [Google Scholar] [CrossRef]
- Wald, R.M. Trace Anomaly of a Conformally Invariant Quantum Field in Curved Space-Time. Phys. Rev. D 1978, 17, 1477–1484. [Google Scholar] [CrossRef]
- Azuma, T.; Wada, S. Classification of Spatially Flat Cosmological Solutions in the Presence of the Cosmological Constant and Backreaction of Conformally Invariant Quantum Fields. Prog. Theor. Phys. 1986, 845, 75. [Google Scholar] [CrossRef] [Green Version]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99. [Google Scholar] [CrossRef]
- Kofman, L.; Linde, A.; Starobinsky, A. Towards the Theory of Reheating After Inflation. Phys. Rev. D 1997, 56, 3258–3295. [Google Scholar] [CrossRef] [Green Version]
- Ema, Y.; Nakayama, K.; Tang, Y. Production of Purely Gravitational Dark Matter. JHEP 2018 2018, 09, 135. [Google Scholar] [CrossRef] [Green Version]
- Hashiba, S.; Yokoyama, J. Gravitational particle creation for dark matter and reheating. Phys. Rev. D 2019, 99, 043008. [Google Scholar] [CrossRef] [Green Version]
- Damour, T.; Vilenkin, A. String Theory and Inflation. Phys. Rev. D 1996, 53, 2981. [Google Scholar] [CrossRef] [Green Version]
- Giovannini, M. Gravitational waves constraints on post-inflationary phases stiffer than radiation. Phys. Rev. D 1998, 58, 083504. [Google Scholar] [CrossRef] [Green Version]
- Liddle, A.R.; Urena-Lopez, L.A. Curvaton reheating: An application to braneworld inflation. Phys. Rev. D 2003, 68, 043517. [Google Scholar] [CrossRef] [Green Version]
- Feng, B.; Li, M. Curvaton Reheating in Non-oscillatory Inflationary Models. Phys. Lett. B 2003, 564, 169–174. [Google Scholar] [CrossRef] [Green Version]
- Agarwal, A.; Bekov, S.; Myrzakulov, K. Quintessential Inflation and curvaton reheating. arXiv 2018, arXiv:1807.03629. [Google Scholar]
- Campuzano, C.; del Campo, S.; Herrera, R. Extended Curvaton reheating in inflationary models. JCAP 2006, 17, 606. [Google Scholar] [CrossRef] [Green Version]
- Sanchez, J.C.B.; Dimopoulos, K. Curvaton reheating allows TeV Hubble scale in NO inflation. JCAP 2007, 7, 711. [Google Scholar]
- Bamba, K.; Elizalde, E.; Odintsov, S.D.; Paul, T. Inflationary magnetogenesis with reheating phase from higher curvature coupling. JCAP 2021, 9, 4. [Google Scholar] [CrossRef]
- Maity, D.; Pal, S.; Paul, T. Effective theory of inflationary magnetogenesis and constraints on reheating. JCAP 2021, 45, 5. [Google Scholar] [CrossRef]
- Haque, R.; Maity, D.; Paul, T.; Sriramkumarl, L. Decoding the phases of early and late time reheating through imprints on primordial gravitational waves. Phys. Rev. D 2021, 63513, 104. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D.; Paul, T.; Maity, D. Helical magnetogenesis with reheating phase from higher curvature coupling and baryogenesis. arXiv 2021, arXiv:2107.11524. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Non-singular modified gravity: The unification of the inflation, dark energy and dark mater. AIP Conf. Proc. 2010, 1241, 1094–1099. [Google Scholar]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Unifying Inflation with Early and Late-time Dark Energy in F(R) Gravity. Phys. Dark Universe 2020, 29, 100602. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Nojiri, S.; Odintsov, S.D. f(R,T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef] [Green Version]
- de Haro, J.; Saló, L.A. A review of Quintessential Inflation. Galaxies 2021, 9, 73. [Google Scholar] [CrossRef]
- Giudice, G.F.; Kolb, E.W.; Riotto, A. Largest temperature of the radiation era and its cosmological implications. Phys. Rev. D 2001, 64, 023508. [Google Scholar] [CrossRef] [Green Version]
- Ellis, J.; Nanopoulos, D.V.; Sarkar, S. The cosmology of decaying gravitinos. Nucl. Phys. B 1985, 259, 175. [Google Scholar] [CrossRef] [Green Version]
- Ellis, J.; Linde, A.; Nanopoulos, D. Inflation can save the gravitinon. Phys. Lett. B 1982, 118, 59. [Google Scholar] [CrossRef] [Green Version]
- Haro, J.; Amorós, J.; Pan, S. The Peebles-Vilenkin quintessential inflation model revisited. Eur. Phys. J. C 2019, 79, 505. [Google Scholar] [CrossRef]
- Dimopoulos, K. Towards a model of Quintessential Inflation. Nucl. Phys. Proc. Suppl. 2001, 70, 95. [Google Scholar] [CrossRef] [Green Version]
- Hossain, M.W.; Myrzakulov, R.; Sami, M.; Saridakis, E.N. A class of quintessential inflation models with parameter space consistent with BICEP2. Phys. Rev. D 2014, 123513, 89. [Google Scholar] [CrossRef] [Green Version]
- Hossain, M.W.; Myrzakulov, R.; Sami, M.; Saridakis, E.N. Unification of inflation and dark energy à la quintessential inflation. Int. J. Mod. Phys. D 2015, 24, 1530014. [Google Scholar] [CrossRef] [Green Version]
- de Haro, J.; Amorós, J.; Pan, S. Simple inflationary quintessential model II: Power law potentials. Phys. Rev. D 2016, 94, 064060. [Google Scholar] [CrossRef] [Green Version]
- Geng, C.Q.; Lee, C.C.; Sami, M.; Saridakis, E.N.; Starobinsky, A.A. Observational constraints on successful model of quintessential Inflation. JCAP 2017, 11, 6. [Google Scholar] [CrossRef] [Green Version]
- Haro, J.; Amorós, J.; Pan, S. Scaling solutions in quintessential inflation. Eur. Phys. J. C 2020, 80, 404. [Google Scholar] [CrossRef]
- de Haro, J.; Pan, S.; Saló, L.A. Understanding gravitational particle production in quintessential inflation. JCAP 2019, 056, 06. [Google Scholar] [CrossRef] [Green Version]
- de Haro, J.; Amorós, J.; Pan, S. Simple inflationary quintessential model. Phys. Rev. D 2016, 93, 084018. [Google Scholar] [CrossRef] [Green Version]
- Bettoni, D.; Rubio, J. Quintessential inflation: A tale of emergent and broken symmetries. Galaxies 2022, 10, 22. [Google Scholar] [CrossRef]
- Dimopoulos, K.; Valle, J.W.F. Modeling Quintessential Inflation. Astropart. Phys. 2002, 18, 287–306. [Google Scholar] [CrossRef] [Green Version]
- Benisty, D.; Guendelman, E.I. Lorentzian Quintessential Inflation. Int. J. Mod. Phys. D 2020, 29, 2042002. [Google Scholar] [CrossRef]
- Benisty, D.; Guendelman, E.I. Quintessential Inflation from Lorentzian Slow Roll. Eur. Phys. J. C 2020, 577, 80. [Google Scholar] [CrossRef]
- Saló, L.A.; Benisty, D.; Guendelman, E.I.; de Haro, J. Quintessential inflation and cosmological seesaw Mechanism: Reheating and observational constraints. JCAP 2021, 7, 7. [Google Scholar] [CrossRef]
- Akrami, Y.; Kallosh, R.; Linde, A.; Vardanyan, V. Dark energy, α-attractors, and large-scale structure surveys. JCAP 2018, 41, 1806. [Google Scholar] [CrossRef] [Green Version]
- Dimopoulos, K.; Owen, C. Quintessential Inflation with α-attractors. JCAP 2017, 27, 1706. [Google Scholar] [CrossRef] [Green Version]
- Saló, L.A.; Benisty, D.; Guendelman, E.I.; de Haro, J. α-attractors in Quintessential Inflation motivated by Supergravity. Phys. Rev. D 2021, 103, 123535. [Google Scholar] [CrossRef]
- Grib, A.A.; Mamayev, S.G.; Mostepanenko, V.M. Vaccum Quantum effects in Strong Fields; Friedmann Laboratory Publishing for Theoretical Physics: St. Petersburg, Russia, 1994. [Google Scholar]
- Bunch, T.S. Adiabatic regularisation for scalar fields with arbitrary coupling to the scalar curvature. J. Phys. A 1980, 13, 1297. [Google Scholar] [CrossRef]
- Saló, L.A.; de Haro, J. Gravitational particle production of superheavy massive particles in Quintessential Inflation: A numerical analysis. Phys. Rev. D 2021, 104, 083544. [Google Scholar] [CrossRef]
- O’Raifeartaigh, C. Investigating the legend of Einstein’s “biggest blunder”. Physics Today, 30 October 2018. Available online: https://physicstoday.scitation.org/do/10.1063/PT.6.3.20181030a/full/(accessed on 27 January 2022).
- Einstein, A. The Meaning of Relativity; Four Lectures Delivered at Princeton University, May, 1921; EBook-No. 36276; Project Gutenberg; Mjf Books: Bluffton, SC, USA, 2011. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Haro, J.; Elizalde, E. Topics in Cosmology—Clearly Explained by Means of Simple Examples. Universe 2022, 8, 166. https://doi.org/10.3390/universe8030166
de Haro J, Elizalde E. Topics in Cosmology—Clearly Explained by Means of Simple Examples. Universe. 2022; 8(3):166. https://doi.org/10.3390/universe8030166
Chicago/Turabian Stylede Haro, Jaume, and Emilio Elizalde. 2022. "Topics in Cosmology—Clearly Explained by Means of Simple Examples" Universe 8, no. 3: 166. https://doi.org/10.3390/universe8030166






