Low Energy Supersymmetry Confronted with Current Experiments: An Overview

Abstract

This study provides a brief overview of low energy supersymmetry (SUSY) in light of current experimental constraints, such as collider searches, dark matter searches, and muon $g-2$ measurements. In addition, we survey a variety of low energy supersymmetric models: the phenomenological minimal supersymmetric model (MSSM); the supersymmetric models with cut-off-scale boundary conditions, i.e., the minimal supergravity (mSUGRA) or the constrained MSSM (CMSSM), the gauge mediation of SUSY breaking (GMSB), and the anomaly mediation of SUSY breaking (AMSB), as well as their extensions. The conclusion is that the low energy SUSY can survive all current experimental constraints and remains compelling, albeit suffering from a slight fine-tuning problem. The advanced models such as mSUGRA, GMSB, and AMSB need to be extended if the muon $g-2$ anomaly comes from new physics.

1. Introduction

Despite its remarkable phenomenological success, the standard model (SM) in particle physics still has remaining puzzles, such as the origin of the free parameters, the matter–antimatter asymmetry, the instability of the electroweak scale, or the divergent quantum correction of Higgs boson mass, and the nature of cold dark matter. Searching for new physics beyond the SM is the central theme of today’s and future particle physics. The low energy supersymmetry (SUSY) has been the most appealing framework among various new physics hypotheses. Phenomenologically speaking, the SUSY extension of the SM could solve the hierarchy problem, realize gauge coupling unification, adopt the proper baryogenesis mechanisms, and generate the cold dark matter candidate.

Most notably, SUSY predicts a neutral CP-even Higgs boson upper bounded roughly by 135 GeV, corroborated by the Large Hadron Collider (LHC) discovery of a 125 GeV Higgs boson. In the theoretical view, as a new fundamental symmetry, SUSY is mathematically charming and, unlike other miscellaneous new physics models, SUSY is part of a larger vision of physics, not just a technical solution [1]. SUSY has been in the mainstream of high energy physics for almost half a century. As depicted in Figure 1 in [2], SUSY plays a crucial role in the map of high energy physics and even the whole tree of quantum theory. Indeed, SUSY is needed and predicted by string theory, i.e., the concept of supersymmetry emerged historically, at least in part because of its role in string theory [1]. To date, string theory is the most hopeful candidate for unifying all interactions and such unification is our original intention since our job in physics is to see things simply, to understand a great many complicated phenomena in a unified way [3].

Of course, physics thrives on crisis [4]. Since particle physics is a discipline relying on experiments, the experimental crises or deviations from the SM play a crucial role in searching for new physics. Currently, we are facing two experimental crises: one is the cold dark matter, the other is the muon $g-2$ anomaly. While the former is quite robust evidence of new physics, the latter should be taken with a grain of salt, e.g., there is a 10% chance it is new physics (much more plausible than other anomalies) [5]. In addition, the dark matter direct detection experiment has not found any weakly interactive massive particle (WIMP) dark matter particles. The LHC has not found any particles predicted by new physics (although it found some plausible anomalies in B-decays). Confronted with these experimental results, what is the status of low energy SUSY, is it healthy or does it need to be hospitalized?

In this note, we will briefly review the status of SUSY in light of these experiments, namely the LHC searches, the dark matter, and muon $g-2$ measurements. The SUSY models investigated in the literature are the MSSM, mSUGRA or CMSSM, GMSB, and AMSB, as well as respective extensions. We conclude that the low energy SUSY can survive all these experimental constraints, albeit the advanced models such as mSUGRA, GMSB, and AMSB need to be extended to accommodate the 125 GeV Higgs boson and the muon $g-2$ anomaly.

2. A Brief Description of SUSY

Supersymmetry is an extension of special relativity to include fermionic symmetries [6]. The anticommutative relation of the supercharges $Q_{\alpha }$ is given by [6]

$$Q_{\alpha }{Q}_{\beta }+Q_{\beta }{Q}_{\alpha }={\Gamma }_{\alpha \beta }^{\mu }{P}_{\mu },$$

(1)

with ${\Gamma }^{\mu }$ being the Dirac matrix and $P_{\mu }$ the four-momentum. So, unlike any other internal symmetries which are independent of spacetime symmetry (no-go theorem of Coleman and Mandula [7]: the most general Lie algebra of symmetry operators that commute with S-matrix consists of the generators of the Poincare group and ordinary internal symmetry generators. The latter act on one-particle states with matrices that are diagonal and independent of both momentum and spin), supersymmetry is entangled with spacetime symmetry and is an extension of special relativity (Golfand and Likhtman [8] found that the S-matrix can have Poincare symmetry extended by SUSY algebra, while Haag et al. [9] further proved that SUSY algebra is the only graded Lie algebra of symmetries of the S-matrix consistent with relativistic QFT, which extends the Poincare group by anticommutators). In order words, the spacetime symmetry of QFT is completed by SUSY:

$$\begin{array}{ccc}& & \left[P_{\mu },P_{\nu }\right]=0,\hfill \end{array}$$

(2)

$$\begin{array}{ccc}& & \left[M_{\mu \nu },P_{\lambda }\right]=i\left(P_{\mu }{g}_{\nu \lambda }-P_{\nu }{g}_{\mu \lambda }\right),\hfill \end{array}$$

(3)

$$\begin{array}{ccc}& & \left[M_{\mu \nu },M_{\rho \lambda }\right]=-i\left(M_{\mu \rho }{g}_{\nu \lambda }+M_{\nu \lambda }{g}_{\mu \rho }-M_{\mu \lambda }{g}_{\nu \rho }-M_{\nu \rho }{g}_{\mu \lambda }\right),\hfill \end{array}$$

(4)

$$\begin{array}{ccc}& & \left[P_{\mu },Q_a\right]=0,\hfill \end{array}$$

(5)

$$\begin{array}{ccc}& & \left[M_{\mu \nu },Q_a\right]=-{\left({\sigma }_{\mu \nu }^4\right)}_{ab}{Q}_b,\hfill \end{array}$$

(6)

$$\begin{array}{ccc}& & \left\{Q_a,Q_b\right\}=-2{\left({\gamma }^{\mu }C\right)}_{ab}{P}_{\mu },\hfill \end{array}$$

(7)

$$\begin{array}{ccc}& & \left\{{\overline{Q}}_a,{\overline{Q}}_b\right\}=2{\left(C^{-1}{\gamma }^{\mu }\right)}_{ab}{P}_{\mu },\hfill \end{array}$$

(8)

$$\begin{array}{ccc}& & \left\{Q_a,{\overline{Q}}_b\right\}=2{\left({\gamma }^{\mu }\right)}_{ab}{P}_{\mu },\hfill \end{array}$$

(9)

where $P_{\mu }$ and $M_{\mu \nu }$ are the generators of the Poincare group. At about the same time as Golfand and Likhtman, a string that could be a fermion as well as a boson was introduced and led to the concept of supersymmetry [10,11,12]. When supersymmetry was applied to particle physics (pioneered by Wess and Zumino [13]), it demonstrated remarkable virtues such as [1]: making a “small” Higgs mass natural, surviving electroweak tests, making heavy top mass as needed. Further, when supersymmetry is localized, we obtain supergravity [14].

Since any field representation of SUSY algebra involves fields with different spins and the same mass, SUSY predicts a superpartner for each particle in the SM. If SUSY is unbroken, we will find light sparticles that were ruled out by experiments. So, SUSY must be spontaneously broken in some hidden sector where the breaking effects can be mediated to the observable sector via some interactions. Note that the supertrace sum rule [15,16]

$$\begin{array}{c}\hfill Str{M}^2=\sum _{particles}{(-1)}^{2j}(2j+1)M_j^2=0,\end{array}$$

(10)

with j being the spin, which holds for any renormalizable SUSY Lagrangian, will lead to the mass relation between electron and selectrons

$$\begin{array}{c}\hfill m_{{\tilde{e}}_1}^2+m_{{\tilde{e}}_2}^2=2m_e^2,\end{array}$$

(11)

indicating the existence of a selectron lighter than the electron. Hence, SUSY breaking cannot be merely like the spontaneous breaking of electroweak symmetry in the Higgs sector, which directly couples to the fermion and gauge fields to transfer the breaking effects. Suppose the SUSY breaking in the hidden sector is characterized by the F-term VEV $\langle F\rangle$ and the mediation scale is $M_{med}$, the superpartners in the visible sector obtain a soft mass from SUSY breaking:

$$\begin{array}{c}\hfill M_{soft}\sim \frac{\langle F\rangle }{M_{med}},\end{array}$$

(12)

up to some numerical factor such as the loop factor for gauge mediation. $M_{med}$ can be identified to be the Planck scale $M_{Pl}$ for gravity mediation and the messenger scale $M_{mess}$ for gauge mediation, with $M_{mess}$ possibly being much smaller than the Planck scale $M_{mess}\ll M_{Pl}$. Superpartners of the standard model particles obtain masses both from electroweak symmetry breaking and SUSY breaking. Therefore, it is natural for them to be a bit above the Z, which obtains mass only from electroweak symmetry breaking [1].

Although SUSY predicts numerous sparticles, only the lightest sparticle (LSP) is stable assuming R-parity (without R-parity no sparticles are stable), which is usually assumed to be the lightest neutralino. This lightest neutralino is a good candidate for the WIMP cold dark matter, and at the LHC it appears as missing energy at the end of the decay chain of each produced sparticle.

Another remarkable feature of SUSY is that to give masses for both up and down type quarks, two Higgs doublets with opposite hypercharges are needed since SUSY forbids the appearance of the complex conjugate of the Higgs field in the superpotential. So, SUSY predicts five Higgs bosons: two CP-even ones, one CP-odd one, and a pair of charged ones. The Higgs quartic coupling $\lambda$ arises from D-terms [17]

$$\begin{array}{c}\hfill V_D=\frac{1}{2}\left[D^a{D}^a+{\left(D^{\prime }\right)}^2\right]=\frac{1}{8}(g^2+{g\prime }^2){\left(H_d^{†}{H}_d-H_u^{†}{H}_u\right)}^2+\frac{1}{2}{g}^2{\left(H_d^{†}{H}_u\right)}^2,\end{array}$$

(13)

which are gauge coupling $\lambda \sim g^2$ instead of a free parameter as in the SM. Thus, in the MSSM, the mass of the lightest CP-even Higgs boson must be light $m_h^2\sim \lambda v^2\sim g^2{v}^2$. In detail, its mass is upper bounded by Z-boson mass at the tree level and by about 135 GeV at the loop level:

$$\begin{array}{ccc}& & m_h<m_Z|cos2\beta |<m_Z\left(\mathrm{at}\mathrm{tree}\mathrm{level}\right),\hfill \end{array}$$

(14)

$$\begin{array}{ccc}& & m_h\le \sqrt{m_Z^2+ϵ}\le 135\mathrm{GeV}\left(\mathrm{at}\mathrm{loop}\mathrm{level}\right),\hfill \end{array}$$

(15)

where $ϵ$ is the one-loop effects from top quarks and top squarks given by [18]

$$\begin{array}{c}\hfill ϵ=\frac{3m_t^4}{4{\pi }^2{v}^2}\left[log\frac{M_S^2}{m_t^2}+\frac{X_t^2}{M_S^2}\left(1-\frac{X_t^2}{12M_S^2}\right)\right],\end{array}$$

(16)

with $v=174\mathrm{GeV}$, $X_t\equiv A_t-\mu cot\beta$ ($A_t$ is the trilinear Higgs-stop coupling and $\mu$ is the Higgsino mass parameter), and $M_S=\sqrt{m_{{\tilde{t}}_1}{m}_{{\tilde{t}}_2}}$. As in Figure 1 in the [18] the SM-like Higgs boson mass in the MSSM is more restricted than the SM Higgs boson mass. SM Higgs boson mass is bounded by about 800 GeV if its cut-off scale is 1 TeV.

3. SUSY Confronted with the LHC Searches

At the LHC, the typical signature of SUSY with R-parity is multi-jets or/and multi-leptons plus missing energy since the sparticles must be produced in pairs and each produced sparticle has a cascade decay with the final states containing an odd number of LSPs (the stable neutral LSPs just escape the detector) plus some jets or/and leptons [19,20,21,22]. To date, the CMS and ATLAS collaborations at the LHC have intensively searched for sparticle productions and have failed to find any evidence. For simplified models with significant mass splittings between the LSP and other sparticles, the searches have pushed gluino and first generation squarks above about 2 TeV [23,24] and pushed top squarks above about 1 TeV [25,26], as shown in Figure 1 [27]. while for uncolored sparticles (electroweakinos and sleptons), the bounds are much weaker, only a few hundred GeV due to their small production cross-sections [28,29,30]. As we will discuss later, these relatively light uncolored sparticles are just needed to make sizable contributions to the muon $g-2$.

On the other hand, the LHC discovered a 125 GeV Higgs boson, which is within the range $<135$ GeV predicted by SUSY as shown in Figure 2 in [31], and requires sizable loop effects of top squarks heavier than about TeV for $X_t\equiv A_t-\mu cot\beta$ not much larger than $M_S\equiv \sqrt{m_{{\tilde{t}}_1}{m}_{{\tilde{t}}_2}}$, as shown in Figure 1 [32]. If we believe the stops to be the lightest colored sparticles from the view of renormalization group equation (RGE) runnings, the 125 GeV Higgs mass then requires all colored sparticles above TeV. So, the absence of any colored sparticles and the discovery of a 125 GeV Higgs boson is consistent in the framework of SUSY, both pushing the colored sparticles above TeV. Whereas, since the uncolored sparticles are subject to extremely weak constraints from the LHC searches, their allowed low masses below TeV are just required by the muon $g-2$ discrepancy, as discussed later.

Note that the LHC has not yet discovered any particles predicted by new physics, not just the sparticles predicted by SUSY. Among the new physics models, SUSY remains the most compelling one. Another point we should note is that the LHC bounds on the sparticle masses are usually valid for simplified SUSY models with significant mass splittings between the LSP and other sparticles. If the LSP mass is very close to the relevant sparticles such as the higgsinos [33] or stops [34,35], the LHC bounds on the masses of these sparticles will become much weaker. For example, in the natural SUSY scenario [36,37,38,39,40,41] the higgsinos are light, 100–300 GeV, while the gauginos are heavy, and thus the LSP ${\chi }_1^0$ is higgsino-like and nearly degenerate with the higgsino-like neutralino ${\chi }_2^0$ and the higgsino-like chargino ${\chi }_1^{\pm }$. In this case, the productions of these sparticles ${\chi }_{1,2}^0$ and ${\chi }_1^{\pm }$ at the LHC give missing energy and can only be searched by requiring a hard jet radiated from initial partons, i.e., the signal of monojet plus missing energy [33]. Moreover, global likelihood analysis of the electroweakino sector shows that no range of neutralino or chargino masses can be robustly excluded by current LHC searches [42].

4. SUSY Confronted with the Dark Matter

The cold dark matter can be explained in SUSY by the neutral and stable LSP which can be a weakly interacting massive particle (WIMP), the lightest neutralino, or a superweakly interacting massive particle (superWIMP) such as the pseudo-goldstino or gravitino:

(i)

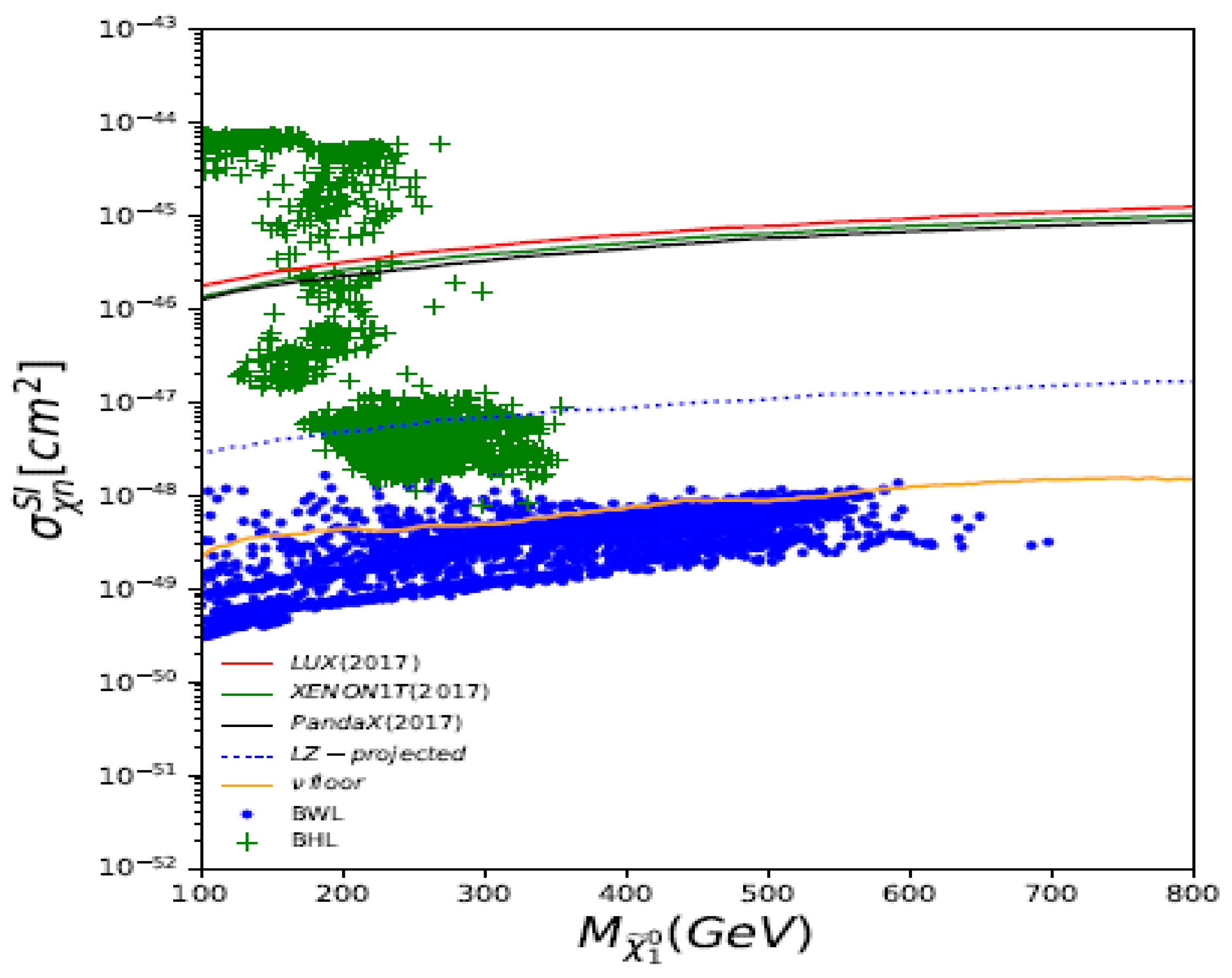
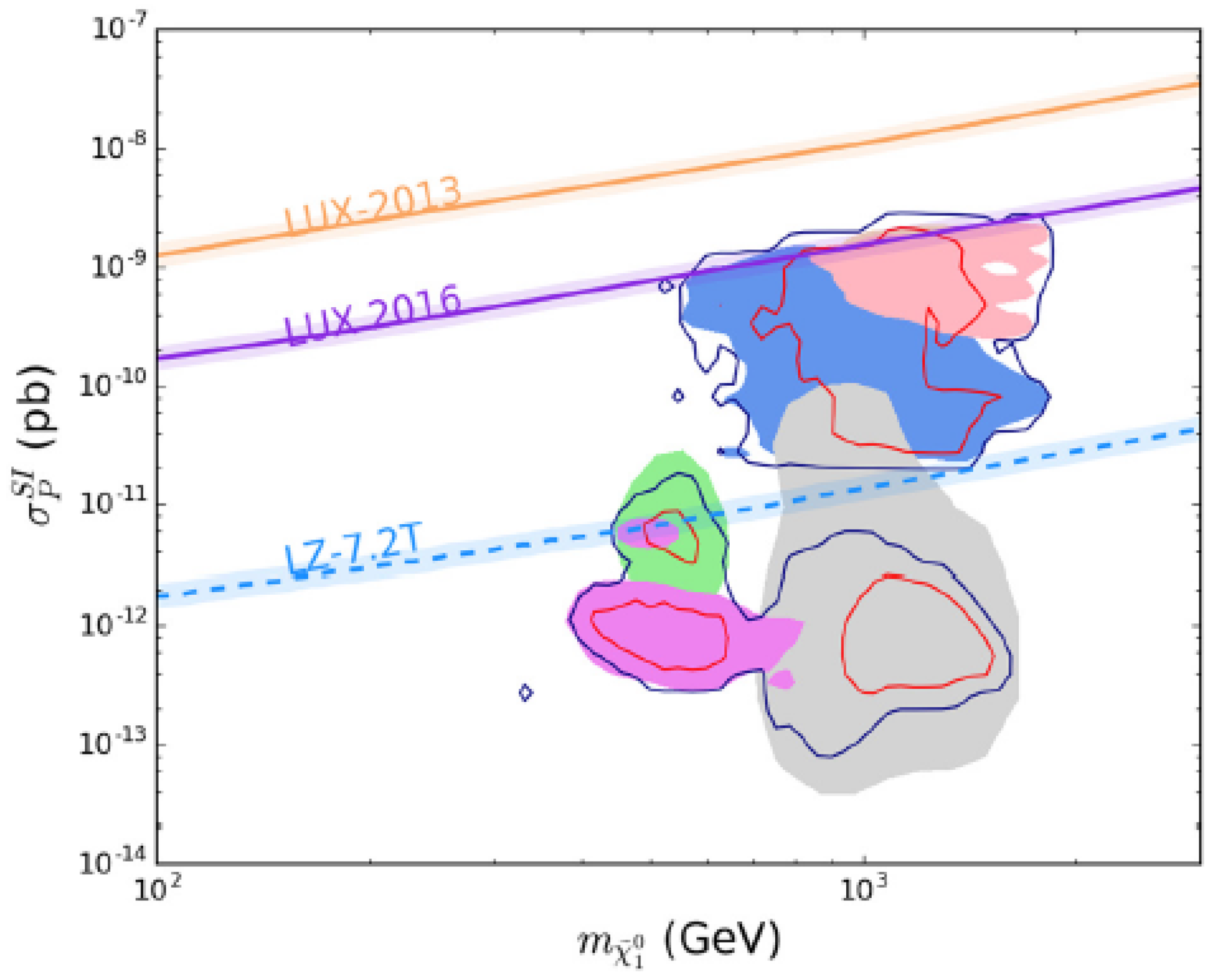
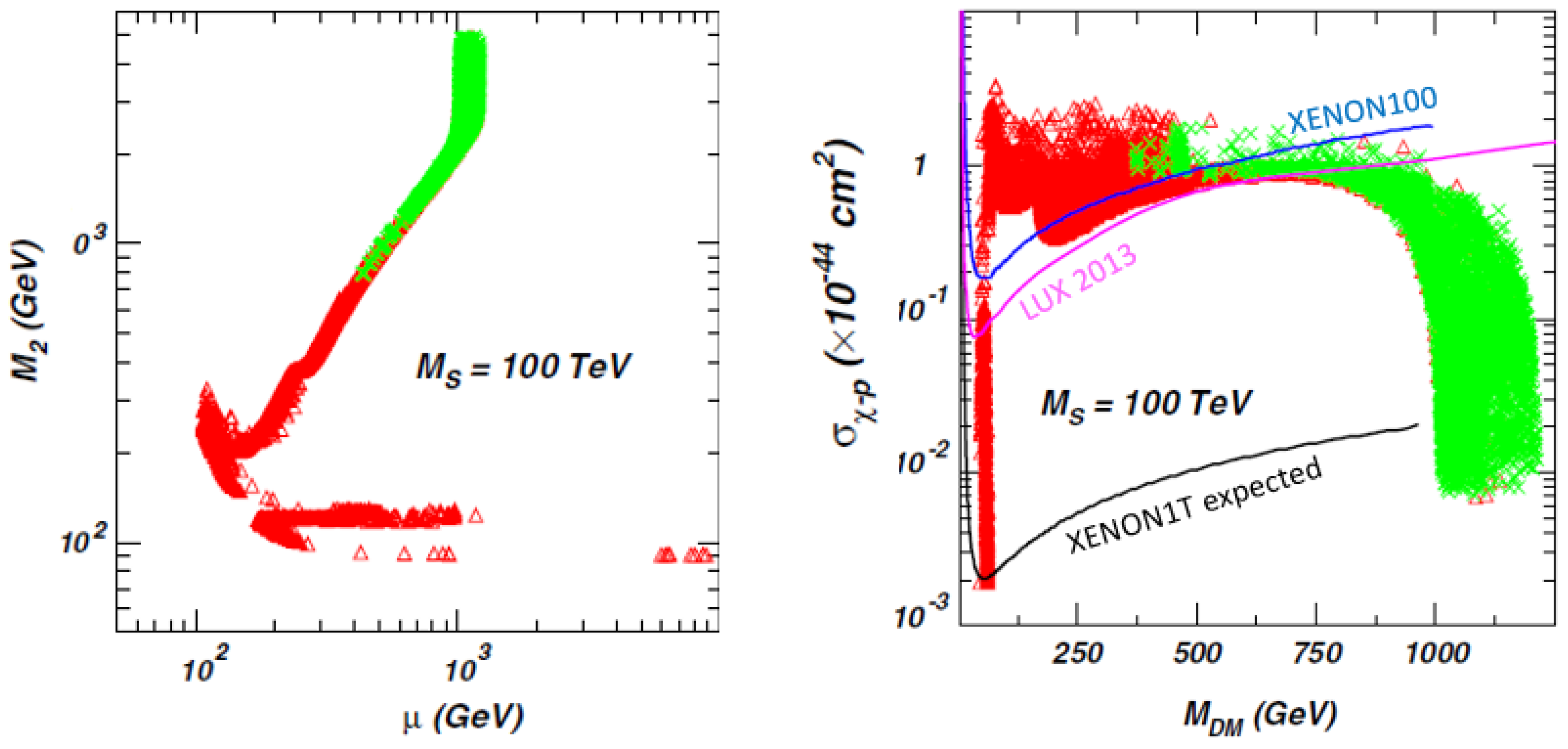
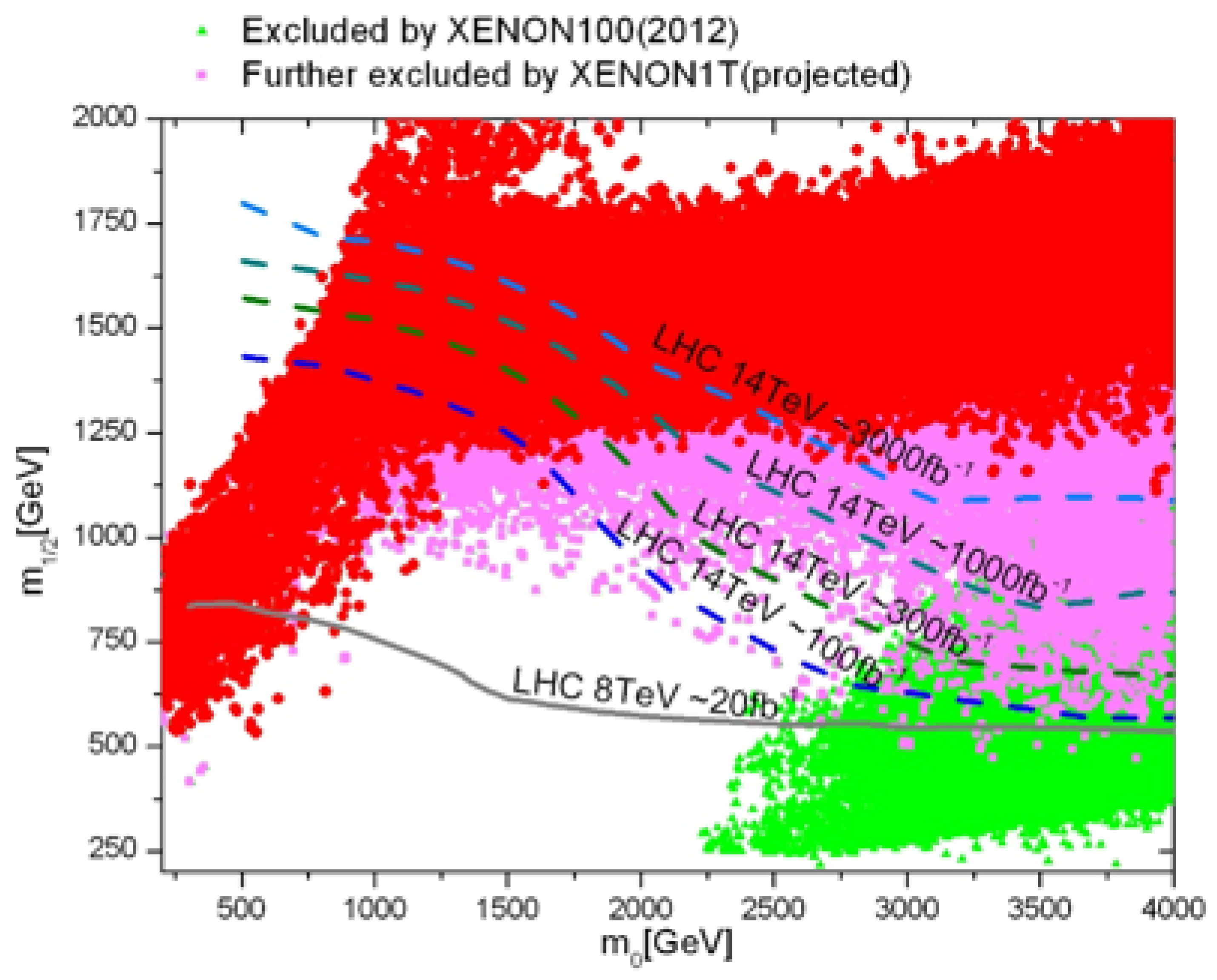
For the lightest neutralino case, it can be bino-like, higgsino-like, or wino-like, depending on its dominant components. The bino-like LSP can easily satisfy the direct detection limits since its scattering with the nucleon is very weak and can also give the correct thermal relic density through the coannihilation with other sparticles like winos [43] or sfermions. For the bino-like dark matter in the MSSM, the parameter space satisfying the relic density at the $2\sigma$ level (and also explaining the muon $g-2$ at the $2\sigma$ level) is displayed in Figure 2 which is taken from [44] (see also [45,46,47,48,49,50]). It has to be heavier than 100 GeV, owing to the LHC direct searches of electroweakino and the DM direct searches [51]. For the bino-like dark matter in the CMSSM/mSUGRA, the $2\sigma$ region from a global fit considering various measurements including the dark matter relic density is shown in Figure 3 taken from [52] (also see [53] for the most updated global fit of CMSSM).

The higgsino-like or wino-like LSP has relatively strong interactions and freezes out rather late from the thermal bath in the early universe, leading to an under-abundance of dark matter if it is light below TeV. To give the sufficient aboundance for the dark matter, the thermal freeze-out higgsino-like (wino-like) LSP must be around $1.0\pm 0.1$ TeV [54,55] ($2.9\pm 0.1$ TeV [55,56,57]), which has been allowed to date by the direct or indirect detections and will be sensitively probed by indirect detections such as the upcoming Cherenkov Telescope Array [58].

The light higgsino-like LSP with an under-abundance can also satisfy the direct detection limits. For example, in natural SUSY the higgsinos are quite light, around 100–300 GeV, and thus the thermal relic density of the higgsino-like LSP is far below the dark matter abundance. If we want to enhance its thermal relic density to the required abundance by mixing bino with higgsino, it may lead to a too large scattering cross-section with the nucleon [59].

(ii)

For the superWIMP pseudo-goldstino or gravitino, it can be produced from the late decay [60,61,62] of the freeze-out lightest neutralino and thus can provide the correct dark matter relic density while easily satisfying the direct detection limits. The pseudo-goldstinos are predicted in multi-sector SUSY breaking with different scales, in which an amount of goldstinos is generated, with one linear combination of these goldstinos being massless and eaten by the gravitino while the orthogonal combinations acquire masses and become the physical states (depending on the messenger masses in the context of gauge mediation, the pseudo-goldstino mass can be from 0.1 GeV to one hundred GeV) [63,64]. Note that if the superWIMP is thermally produced in the reheating period after inflation, its relic density could be over-abundant and hence set an upper bound on the reheating temperature [65]. Such superWIMP dark matter is usually not accessible in direct or indirect detections, but may cause exotic phenomenology at the colliders and may help to alleviate some cosmic problems, such as the Hubble tension [62] or Xenon1T excess [66]. The produced lightest ordinary supersymmetric particle (LOSP) at the colliders, which can possibly be charged, could decay to the superWIMP plus visible particles (photon, Higgs boson, Z-boson etc.) inside or outside the detectors [67,68,69,70,71], depending on the interaction strength of the superWIMP particle.

Therefore, SUSY (both the phenomenological MSSM and the constrained frameworks such as the mSUGRA) can explain the cold dark matter relic density and satisfy the tightened direct detection limits on the WIMP.

5. SUSY Confronted with the Muon $\mathit{g}-\mathbf{2}$

The muon $g-2$ from the Fermilab [72] measurement combined with the BNL result [73] shows a $4.2\sigma$ deviation from the SM prediction [74,75] (however, if the lattice simulation result of the hadronic contribution from the BMW group is taken, the deviation can be reduced to $1.5\sigma$ [76]), which can be readily explained in the phenomenological minimal supersymmetric model (MSSM). The explanation requires relatively light uncolored sparticles (sleptons and electroweakinos). Meanwhile, for the models with boundary conditions at some UV scales for the soft parameters, such as the mSUGRA or GMSB, they need to be extended to account for the muon $g-2$ and the 125 GeV Higgs boson mass.

In SUSY, the smuons, muon sneutrino, and electroweakinos can contribute to muon $g-2$ at the one-loop level. Since the SUSY contribution to muon $g-2$ [77,78] is enhanced by a large $tan\beta$ and suppressed by heavy sparticle masses involved in the loops, to generate the required contribution to explain the muon $g-2$ deviation, a low SUSY mass and a large $tan\beta$ are favored.

(i)

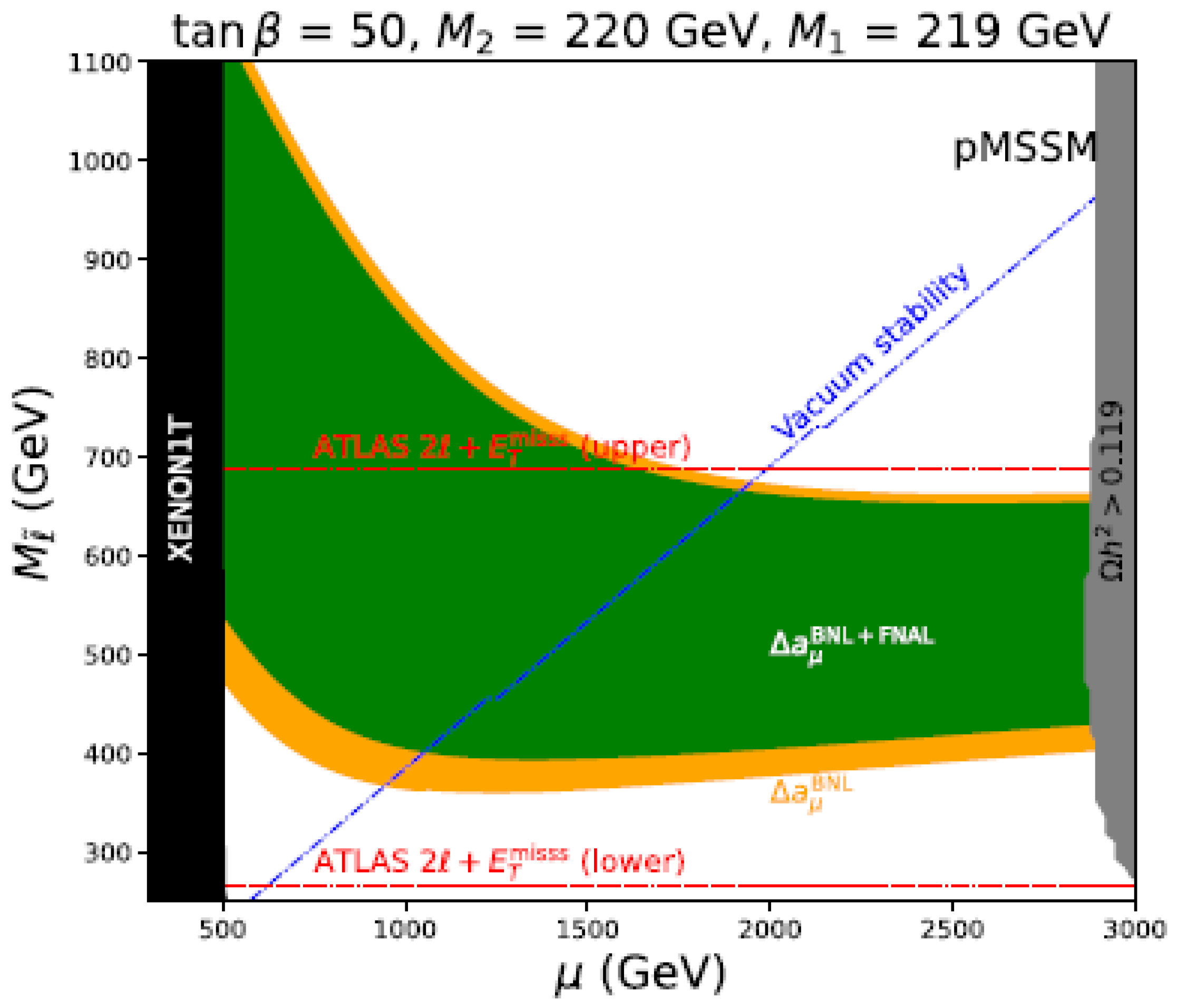
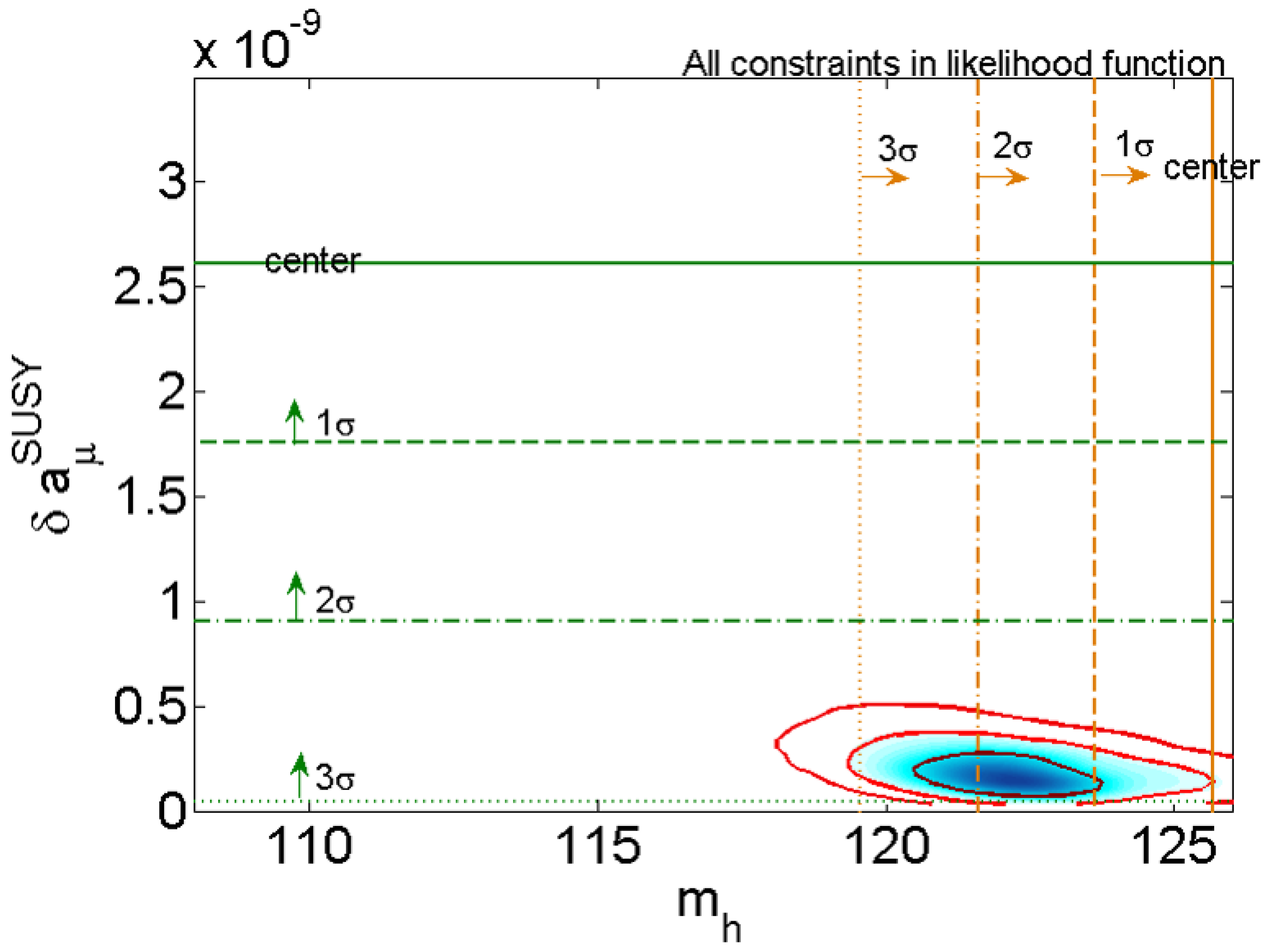
In the low energy effective MSSM, the masses of bino, winos, higgsinos, smuons, and sneutrinos are all independent parameters. As shown in Figure 4 taken from [79] (see also [80,81]), under other constraints including the dark matter, the vacuum stability, and the LHC search for sleptons, there still remains a part of the MSSM parameter space which can explain the muon $g-2$ at the $2\sigma$ level [44,79,80,81].

(ii)

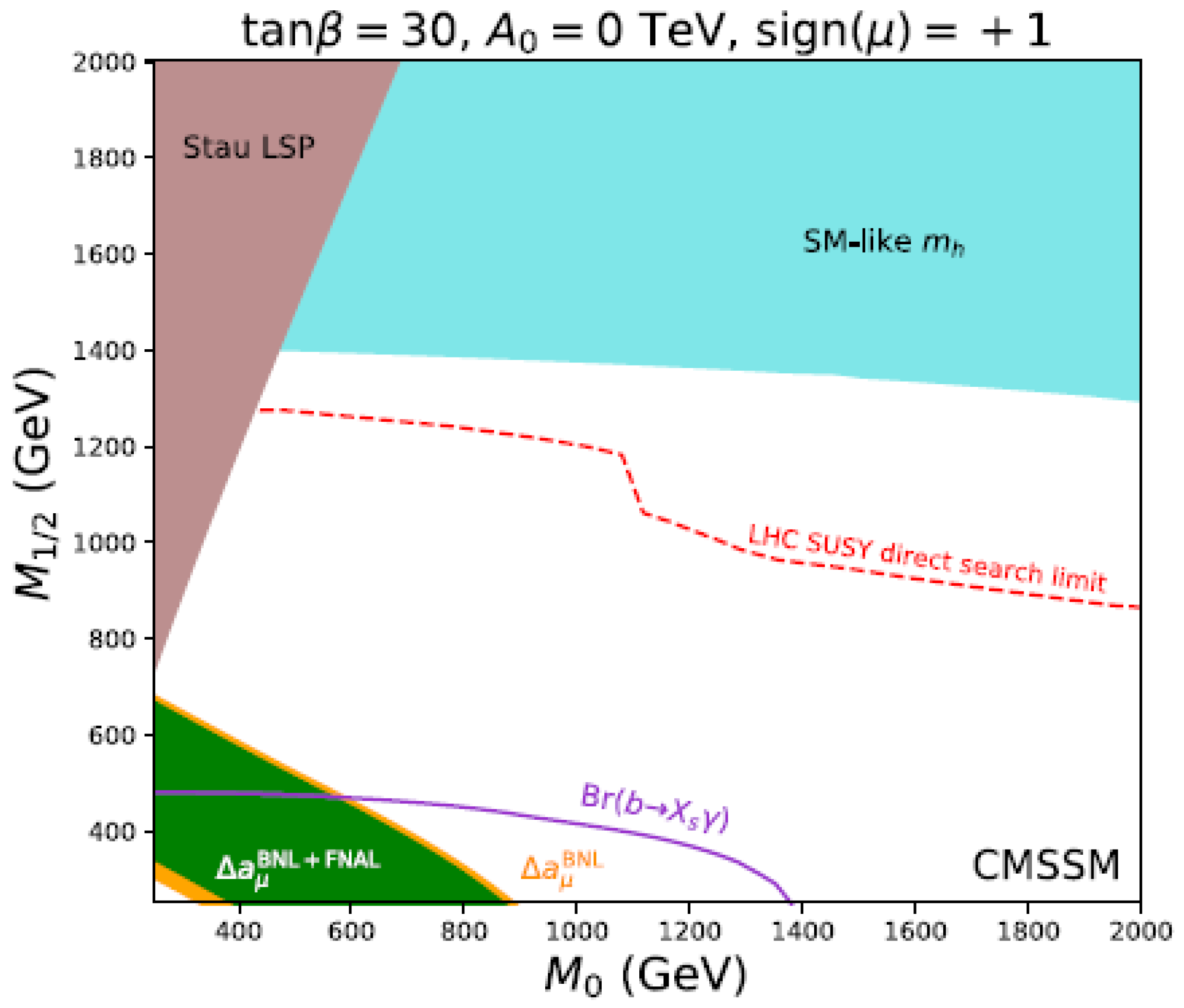
In the constrained models with certain UV boundary conditions for the soft breaking parameters, such as mSUGRA/CMSSM and GMSB, the soft masses at the weak scale are correlated. To give a 125 GeV SM-like Higgs mass, the top squarks must be heavy and the correlated slepton masses cannot be as light as required by the explanation of the muon $g-2$ anomaly. Figure 5 and Figure 6 show the tension between the muon $g-2$ explanation and the 125 GeV SM-like Higgs mass as well as the LHC searches for the CMSSM/mSUGRA [79] with inputs at the GUT scale. To solve such a tension, these models need to be extended, e.g., coupling the messengers with the Higgs doublets to raise the tree-level SM-like Higgs mass [82,83] in gauge mediation or make the colored sparticles much heavier than uncolored sparticles at the weak scale [84,85,86,87,88,89]. In superGUT [90] or subGUT [91] scenarios for SUGRA, which adopts the UV input upon or below the GUT scale, there are still surviving parameter spaces that can account for both the muon $g-2$ anomaly and other constraints, such as the dark matter and collider searches. In the deflected AMSB, which is an elegant extension of AMSB, the muon $g-2$ anomaly can easily be explained [92,93,94,95,96]. The mixed mediation scenarios, such as the mirage mediation, can also successfully account for the muon $g-2$ anomaly [97,98].

(ii)

The non-minimal frameworks of SUSY with more free parameters than the MSSM can easily accommodate the 125 GeV SM-like Higgs mass and the muon $g-2$ at the $2\sigma$ level, e.g., the next-to-minimal SUSY model (NMSSM) extends the MSSM by a singlet Higgs superfield and can satisfy all current constraints [99,100,101,102].

We should also note the electron $g-2$ which shows a slight deviation according to the Berkeley measurement [103]. A joint explanation of such an electron $g-2$ and the muon $g-2$ is feasible in the MSSM [104,105,106,107,108,109]. If we further consider the measurement of electron EDM, its correlation with the muon $g-2$ in the MSSM can set stringent constraints on the CP-phases of the soft parameters [110,111].

In this review, we do not discuss the plausible B-decay anomalies, which are hard to explain in SUSY with minimal flavor violation and the explanation needs non-minimal flavor violation [112].

6. What Is the Problem of SUSY?

The most obvious drawback is simply that SUSY has not been found yet, though we have been hoping for a long time. It is disappointing that we have not found SUSY yet, but for the most part, it is perhaps not too surprising [1]. Although the undiscovery of sparticles at the LHC is not too surprising because sparticles obtain masses from both electroweak symmetry breaking and SUSY breaking and should be significantly heavier than their SM partners, the top squarks which have been pushed above TeV by the direct LHC searches and by the 125 GeV Higgs boson mass will undesirably enlarge the logarithmic divergence in the Higgs boson mass and lead to a slight fine-tuning [113]:

$$\begin{array}{c}\hfill {\Delta }_{\mathrm{HS}}\equiv \frac{\delta m_h^2}{m_h^2}=\frac{3y_t^2}{4{\pi }^2{m}_h^2}(m_{Q_3}^2+m_{U_3}^2+A_t^2)log\frac{\Lambda }{M_{\mathrm{SUSY}}},\end{array}$$

(17)

with $M_{\mathrm{SUSY}}=\sqrt{m_{{\tilde{t}}_1}{m}_{{\tilde{t}}_2}}$, $\Lambda$ being the cut-off scale, $Q_3=({\tilde{t}}_L,{\tilde{b}}_L)$ and $U_3={\tilde{t}}_R$.

The more traditional measure of tuning extent is defined by [114,115]

$${\Delta }_{\mathrm{BG}}\equiv ma{x}_i\left|\frac{p_i}{m_Z^2}\frac{\partial m_Z^2}{\partial p_i}\right|,$$

(18)

with $p_i$ being the independent SUSY parameters at the cut-off scale. In terms of this measure, in the CMSSM the fine-tuning extent is about per mille, as shown in Figure 7 [52]. The fine-tuning can be lower [31] if we use another measure ${\Delta }_{\mathrm{EW}}$ [40,116]:

$${\Delta }_{\mathrm{EW}}\equiv ma{x}_i\left|C_i\right|/(m_Z^2/2),$$

(19)

with [117]

$$\begin{array}{ccc}\hfill C_{H_u}& =& \left|-\frac{m_{H_u}^2{tan}^2\beta }{{tan}^2\beta -1}\right|,C_{H_d}=\left|\frac{m_{H_d}^2}{{tan}^2\beta -1}\right|,C_{\mu }=\left|-{\mu }_{eff}^2\right|,\hfill \\ \hfill C_{{\Sigma }_u^u\left({\tilde{t}}_{1,2}\right)}& =& \frac{{tan}^2\beta }{{tan}^2\beta -1}\left|\frac{3}{16{\pi }^2}F\left(m_{{\tilde{t}}_{1,2}}^2\right)\left[y_t^2-g_Z^2\pm \frac{y_t^2{A}_t^2-8g_Z^2(\frac{1}{4}-\frac{2}{3}{x}_w){\Delta }_t}{m_{{\tilde{t}}_2}^2-m_{{\tilde{t}}_1}^2}\right]\right|,\hfill \\ \hfill C_{{\Sigma }_d^d\left({\tilde{t}}_{1,2}\right)}& =& \frac{1}{{tan}^2\beta -1}\left|\frac{3}{16{\pi }^2}F\left(m_{{\tilde{t}}_{1,2}}^2\right)\left[g_Z^2\pm \frac{y_t^2{\mu }_{eff}^2+8g_Z^2(\frac{1}{4}-\frac{2}{3}{x}_w){\Delta }_t}{m_{{\tilde{t}}_2}^2-m_{{\tilde{t}}_1}^2}\right]\right|,\hfill \end{array}$$

(20)

where $x_w={sin}^2{\theta }_W$ and

$$\begin{array}{ccc}\hfill {\Delta }_t& =& \frac{(m_{{\tilde{t}}_L}^2-m_{{\tilde{t}}_R}^2)}{2}+M_Z^{2}cos2\beta (\frac{1}{4}-\frac{2}{3}{x}_w),\hfill \\ \hfill F\left(m^2\right)& =& m^2\left(log\frac{m^2}{m_{{\tilde{t}}_1}{m}_{{\tilde{t}}_2}}-1\right).\hfill \end{array}$$

(21)

We admit that SUSY has a slight fine-tuning. Note that a solution has been developed to solve such a slight fine-tuning problem [118], in which a framework of supersoft top-squarks is proposed to soften the logarithms to screen the UV-sensitive logs.

Another unpleasant point caused by top-squarks above TeV is that the MSSM can no longer realize the first order electroweak phase transition. However, the NMSSM can do this job (see [119] and refs therein).

Note that in this review we focus on low energy SUSY which helps to solve the naturalness problem in particle physics. It is clear that even with low energy SUSY our particle theory still has a slight tuning, which means we cannot have perfect naturalness. If we give up naturalness and believe simplicity, we may have the fascinating split-SUSY [120,121,122,123], which is emphasized in the recent Witten Reflects [124]. Split-SUSY gives up naturalness and retains the original motivation to explain the dark matter and realize successful gauge coupling unification. Actually, as shown in Figure 8, the dark matter relic density and direct detection limits as well as the gauge coupling unification impose stringent constraints on the parameter space of split-SUSY, i.e., only the higgsino-like dark matter around 1.2 TeV can survive the XENON1T limits assuming the universal GUT input for gaugino masses (which leads to $M_1:M_2:M_3\sim 1:2:6$ at the weak scale). Since in split-SUSY the gauginos and higgsinos are not so heavy, they may be accessible in future colliders [125,126]. This is because the electroweak scale is not natural in the customary sense, but additional particles and forces that would help us understand what is going on exist at an energy not too much above LHC energies [124].

7. The Continual Search for SUSY at HL-LHC

Despite the fact that no sparticles have been discovered to date, SUSY will be actively probed at the High-Luminosity Large Hadron Collider (HL-LHC) as the leading contender for new physics beyond the SM.

As shown above, the MSSM can allow for an explanation for the muon $g-2$ at the $2\sigma$ level while satisfying all other constraints. The light electroweakinos and sleptons required for the muon $g-2$ explanation may be accessible at the HL-LHC. For example, in the scenario where bino-like dark matter annihilates with winos to give the correct dark matter abundance, the light winos required by the muon $g-2$ may be fairly well produced and detected through the signal of soft leptons plus missing energy at the LHC, as shown in Figure 9 [44]. The $2\sigma$ parameter space shown in this figure was allowed by the muon $g-2$, the dark matter relic density, and direct detection limits as well as the LHC Run-2 data [44]. We see that the HL-LHC can cover a sizable part of the MSSM parameter space for the explanation of muon $g-2$ at the $2\sigma$ level. In addition, the precision measurement of the Higgs properties at a lepton collider as a Higgs factory could play a complementary role via detecting the residual effects of SUSY in Higgs couplings [44,127].

Since the muon $g-2$ may not be a real hint of new physics, we consider the CMSSM without explaining the muon $g-2$. As shown in Figure 10, the HL-LHC will continue to narrow down the CMSSM parameter space. The $2\sigma$ parameter space shown in this figure was obtained from a likelihood analysis, taking into account various data including the electroweak precision observables, the B-physics measurements, the LHC Run-1 and Run-2 data of SUSY direct searches, the Planck observation of the dark matter relic density, and the combined LUX Run-3 and Run-4 detection limits [52].

8. Conclusions

We see that the low energy SUSY can generally explain the muon $g-2$ at the $2\sigma$ level and also satisfy other constraints such as the 125 GeV Higgs mass, the dark matter, and the LHC searches. We conclude that low energy SUSY is still a compelling candidate for new physics, though suffering from a slight fine-tuning. The future runs of the LHC will continue to explore SUSY and could bring surprises at any moment.