Theory and Phenomenology of a Four-Dimensional String–Corrected Black Hole
Abstract
:1. Introduction
2. D-Dimensional String-Corrected Black Hole
3. The 4D String Corrected Black Hole
3.1. The ADM Mass
3.2. Hawking Radiation
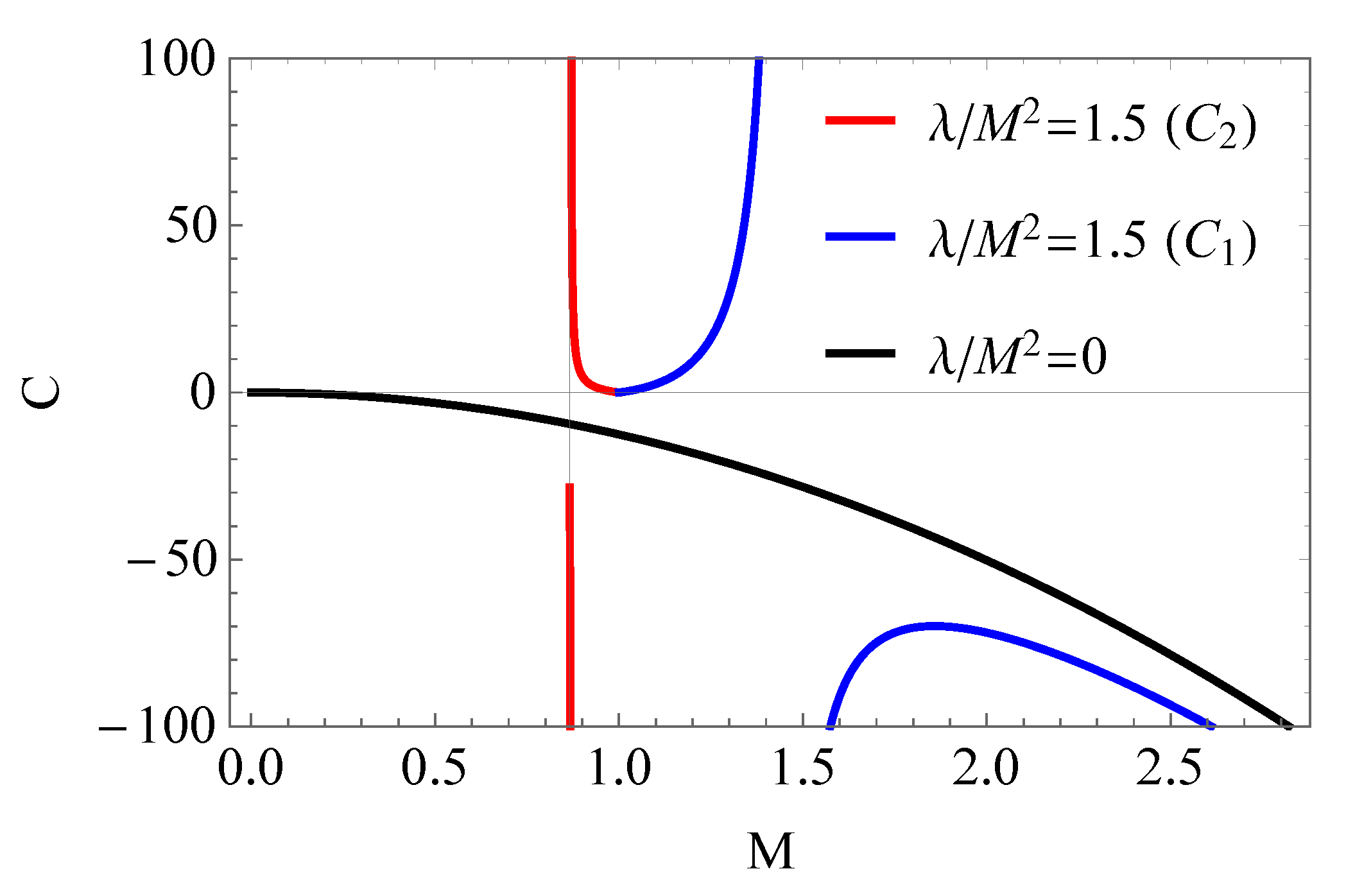
3.3. Can Be a Large Parameter?
4. The S2 Star Orbit
5. Einstein Rings in the Weak Field Regime
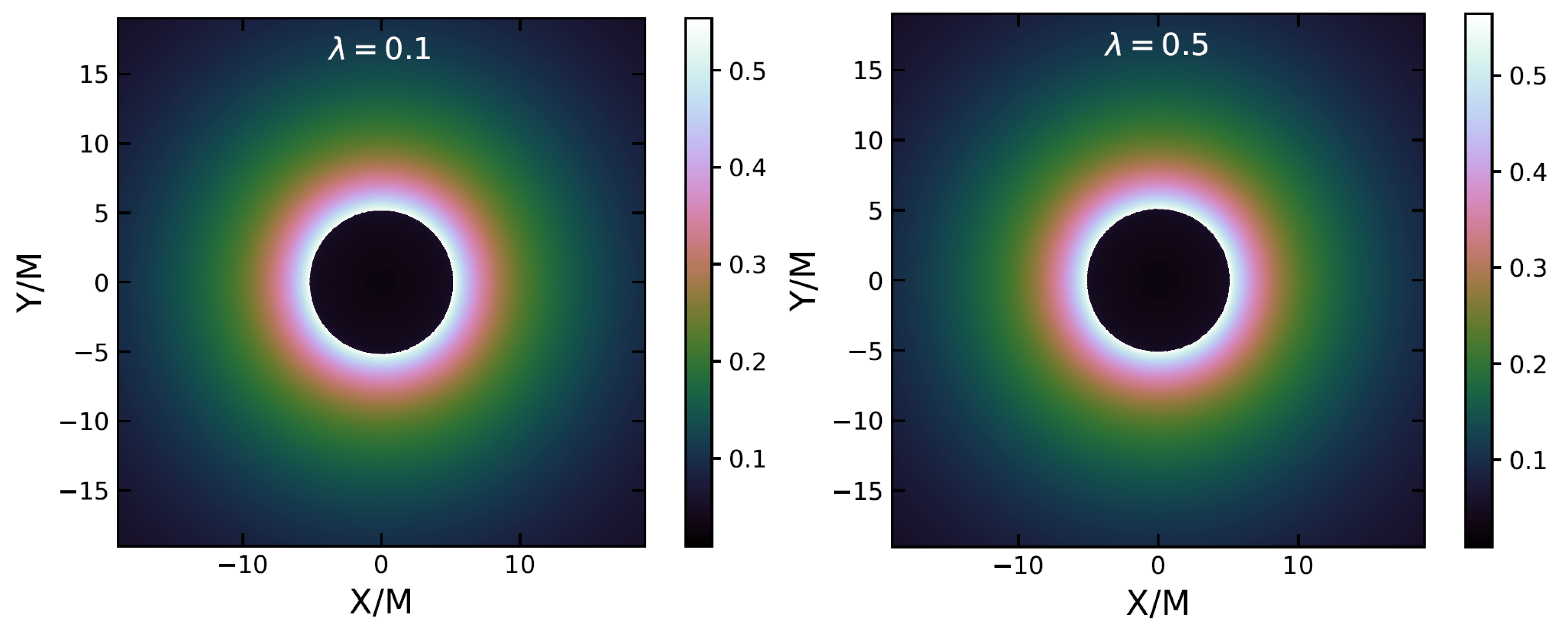
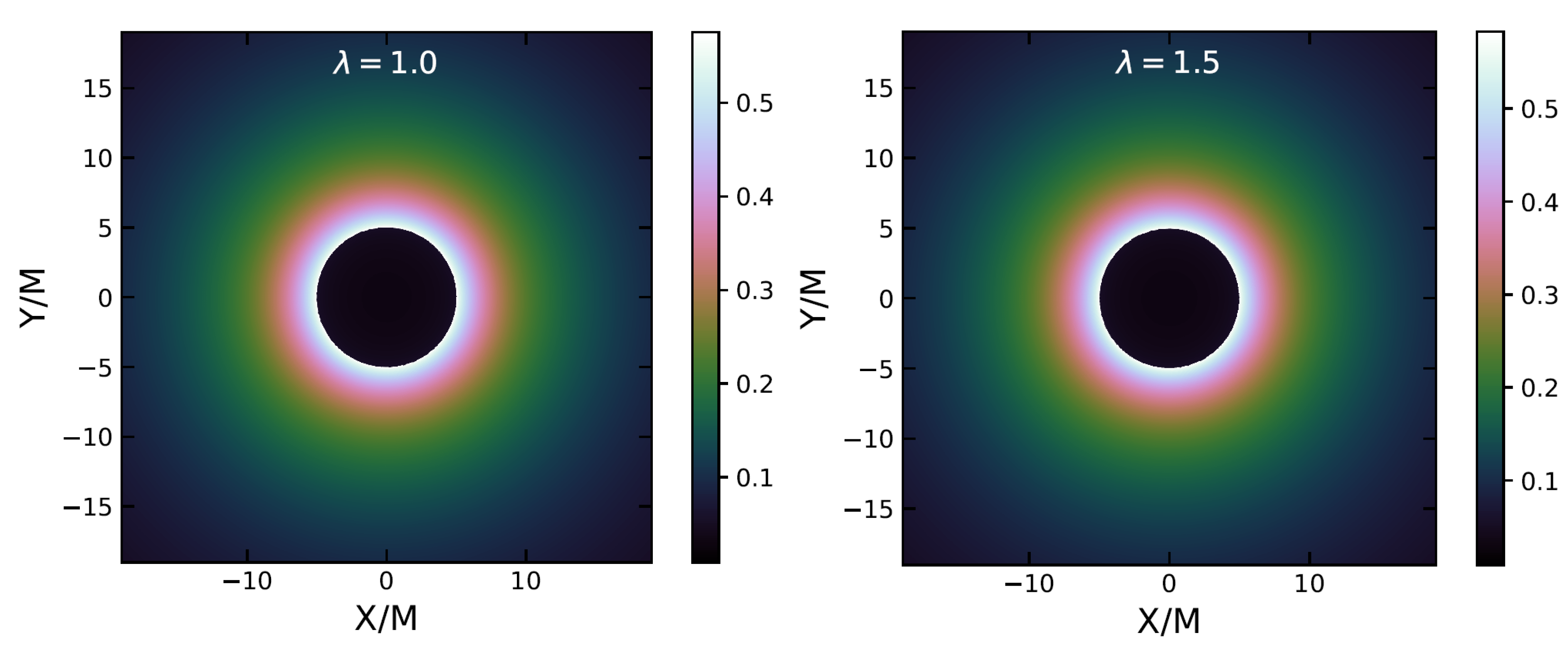
6. Shadow Images of a 4D SCBH
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Akiyama, K. et al. [Event Horizon Telescope Collaboration] First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. 2019, 875, L1. [Google Scholar] [CrossRef]
- Akiyama, K. et al. [Event Horizon Telescope] First M87 Event Horizon Telescope Results. IV. Imaging the Central Supermassive Black Hole. Astrophys. J. 2019, 875, L4. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [LIGO Scientific and Virgo Collaborations] Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Callan, C.G.; Myers, R.C.; Perry, M.J. Black holes in string theory. Nucl. Phys. B 1989, 311, 673. [Google Scholar] [CrossRef]
- Moura, F.; Rodrigues, J. Eikonal quasinormal modes and shadow of string-corrected d-dimensional black holes. Phys. Lett. B 2021, 819, 136407. [Google Scholar] [CrossRef]
- Moura, F. String-corrected dilatonic black holes in d dimensions. Phys. Rev. D 2011, 83, 044002. [Google Scholar] [CrossRef] [Green Version]
- Glavan, D.; Lin, C. Einstein-Gauss–Bonnet gravity in 4-dimensional space-time. Phys. Rev. Lett. 2020, 124, 081301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Konoplya, R.A.; Zhidenko, A. Black holes in the four-dimensional Einstein-Lovelock gravity. Phys. Rev. D 2020, 101, 084038. [Google Scholar] [CrossRef] [Green Version]
- Jusufi, K. Nonlinear magnetically charged black holes in 4D Einstein-Gauss–Bonnet gravity. Ann. Phys. 2020, 421, 168285. [Google Scholar] [CrossRef]
- Jusufi, K.; Banerjee, A.; Ghosh, S.G. Wormholes in 4D Einstein-Gauss–Bonnet Gravity. Eur. Phys. J. C 2020, 80, 698. [Google Scholar] [CrossRef]
- Gürses, M.; Şişman, T.; Tekin, B. Is there a novel Einstein–Gauss–Bonnet theory in four dimensions? Eur. Phys. J. C 2020, 80, 647. [Google Scholar] [CrossRef]
- Gurses, M.; Şişman, T.; Tekin, B. Comment on “Einstein-Gauss–Bonnet Gravity in 4-Dimensional Space-Time. Phys. Rev. Lett. 2020, 125, 149001. [Google Scholar] [CrossRef] [PubMed]
- Ai, W. A note on the novel 4D Einstein-Gauss–Bonnet gravity. Commun. Theor. Phys. 2020, 72, 095402. [Google Scholar] [CrossRef]
- Arrechea, J.; Delhom, A.; Jiménez-Cano, A. Comment on “Einstein-Gauss–Bonnet Gravity in Four-Dimensional Spacetime. Phys. Rev. Lett. 2020, 125, 149002. [Google Scholar] [CrossRef]
- Fernandes, P.G.S. Charged Black Holes in AdS Spaces in 4D Einstein Gauss–Bonnet Gravity. Phys. Lett. B 2020, 805, 135468. [Google Scholar] [CrossRef]
- Clifton, T.; Carrilho, P.; Fernandes, P.G.S.; Mulryne, D.J. Observational Constraints on the Regularized 4D Einstein-Gauss–Bonnet Theory of Gravity. Phys. Rev. D 2020, 102, 084005. [Google Scholar] [CrossRef]
- Fernandes, P.G.S.; Carrilho, P.; Clifton, T.; Mulryne, D.J. Black Holes in the Scalar-Tensor Formulation of 4D Einstein-Gauss–Bonnet Gravity: Uniqueness of Solutions, and a New Candidate for Dark Matter. Phys. Rev. D 2021, 104, 044029. [Google Scholar] [CrossRef]
- Fernandes, P.G.S.; Carrilho, P.; Clifton, T.; Mulryne, D.J. Derivation of Regularized Field Equations for the Einstein-Gauss–Bonnet Theory in Four Dimensions. Phys. Rev. D 2020, 102, 024025. [Google Scholar] [CrossRef]
- Hennigar, R.A.; Kubizňák, D.; Mann, R.B.; Pollack, C. On taking the D → 4 limit of Gauss–Bonnet gravity: Theory and solutions. JHEP 2020, 7, 027. [Google Scholar] [CrossRef]
- Tengherlini, F.R. Schwarzschild field in n dimensions and the dimensionality of space problem. Nuovo C. 1963, 27, 636. [Google Scholar] [CrossRef]
- Shaikh, R. Shadows of rotating wormholes. Phys. Rev. D 2018, 98, 024044. [Google Scholar] [CrossRef] [Green Version]
- Ali, A.F.; Khalil, M.M. Black Hole with Quantum Potential. Nucl. Phys. B 2016, 909, 173–185. [Google Scholar] [CrossRef] [Green Version]
- Carr, B.J.; Mureika, J.; Nicolini, P. Sub-Planckian black holes and the Generalized Uncertainty Principle. JHEP 2015, 7, 052. [Google Scholar] [CrossRef] [Green Version]
- Carr, B.; Mentzer, H.; Mureika, J.; Nicolini, P. Self-complete and GUP-Modified Charged and Spinning Black Holes. Eur. Phys. J. C 2020, 80, 1166. [Google Scholar] [CrossRef]
- Mathur, S.D. The Fuzzball proposal for black holes: An Elementary review. Fortsch. Phys. 2005, 53, 793–827. [Google Scholar] [CrossRef] [Green Version]
- Becerra-Vergara, E.A.; Argüelles, C.R.; Krut, A.; Rueda, J.A.; Ruffini, R. The geodesic motion of S2 and G2 as a test of the fermionic dark matter nature of our galactic core. Astron. Astrophys. 2020, 641, A34. [Google Scholar] [CrossRef]
- Do, T.; Hees, A.; Ghez, A.; Martinez, G.D.; Chu, D.S.; Jia, S.; Sakai, S.; Lu, J.R.; Gautam, A.K.; O’neil, K.K.; et al. Relativistic redshift of the star S0-2 orbiting the Galactic Center supermassive black hole. Science 2019, 365, 664. [Google Scholar] [CrossRef] [Green Version]
- Nampalliwar, S.; Kumar, S.; Jusufi, K.; Wu, Q.; Jamil, M.; Salucci, P. Modeling the Sgr A* Black Hole Immersed in a Dark Matter Spike. Astrophys. J. 2021, 916, 116. [Google Scholar] [CrossRef]
- De Martino, I.; della Monica, R.; de Laurentis, M. f(R) gravity after the detection of the orbital precession of the S2 star around the Galactic Center massive black hole. Phys. Rev. D 2021, 104, L101502. [Google Scholar] [CrossRef]
- Gillessen, S.; Plewa, P.M.; Eisenhauer, F.; Sari, R.E.; Waisberg, I.; Habibi, M.; Pfuhl, O.; George, E.; Dexter, J.; von Fellenberg, S.; et al. An Update on Monitoring Stellar Orbits in the Galactic Center. Astrophys. J. 2017, 837, 30. [Google Scholar] [CrossRef] [Green Version]
- Gibbons, G.W.; Werner, M.C. Applications of the Gauss–Bonnet theorem to gravitational lensing. Class. Quantum Grav. 2008, 25, 235009. [Google Scholar] [CrossRef]
- Belhaj, A.; Benali, M.; Balali, A.E.; Moumni, H.E.; Ennadifi, S.E. Deflection angle and shadow behaviors of quintessential black holes in arbitrary dimensions. Class. Quantum Grav. 2020, 37, 215004. [Google Scholar] [CrossRef]
- Bambi, C.; Freese, K.; Vagnozzi, S.; Visinelli, L. Testing the rotational nature of the supermassive object M87* from the circularity and size of its first image. Phys. Rev. D 2019, 100, 044057. [Google Scholar] [CrossRef] [Green Version]
- Vagnozzi, S.; Visinelli, L. Hunting for extra dimensions in the shadow of M87*. Phys. Rev. D 2019, 100, 024020. [Google Scholar] [CrossRef] [Green Version]
- Atamurotov, F.; Jusufi, K.; Jamil, M.; Abdujabbarov, A.; Azreg-Aïnou, M. Axion-plasmon or magnetized plasma effect on an observable shadow and gravitational lensing of a Schwarzschild black hole. Phys. Rev. D 2021, 104, 064053. [Google Scholar] [CrossRef]
- Papnoi, U.; Atamurotov, F. Rotating charged black hole in 4D Einstein–Gauss–Bonnet gravity: Photon motion and its shadow. Phys. Dark Univ. 2022, 35, 100916. [Google Scholar] [CrossRef]
- Roy, R.; Vagnozzi, S.; Visinelli, L. Superradiance evolution of black hole shadows revisited. arXiv 2021, arXiv:2112.06932. [Google Scholar]
- Yan, S.F.; Li, C.; Xue, L.; Ren, X.; Cai, Y.F.; Easson, D.A.; Yuan, Y.F.; Zhao, H. Testing the equivalence principle via the shadow of black holes. Phys. Rev. Res. 2020, 2, 023164. [Google Scholar] [CrossRef]
- Qi, J.Z.; Zhang, X. A new cosmological probe using super-massive black hole shadows. Chin. Phys. C 2020, 44, 055101. [Google Scholar] [CrossRef]
- Narayan, R.; Johnson, M.D.; Gammie, C.F. The Shadow of a Spherically Accreting Black Hole. Astrophys. J. 2019, 885, L33. [Google Scholar] [CrossRef] [Green Version]
- Saurabh, K.; Jusufi, K. Imprints of dark matter on black hole shadows using spherical accretions. Eur. Phys. J. C 2021, 81, 490. [Google Scholar] [CrossRef]
- Zeng, X.X.; Zhang, H.Q.; Zhang, H. Shadows and photon spheres with spherical accretions in the four-dimensional Gauss–Bonnet black hole. Eur. Phys. J. C 2020, 80, 872. [Google Scholar] [CrossRef]
- Falcke, H.; Melia, F.; Agol, E. Viewing the shadow of the black hole at the galactic center. Astrophys. J. Lett. 2000, 528, L13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bambi, C. Can the supermassive objects at the centers of galaxies be traversable wormholes? The first test of strong gravity for mm/sub-mm very long baseline interferometry facilities. Phys. Rev. D 2013, 87, 107501. [Google Scholar] [CrossRef] [Green Version]
- Perlick, V.; Tsupko, O.Y.; Bisnovatyi-Kogan, G.S. Influence of a plasma on the shadow of a spherically symmetric black hole. Phys. Rev. D 2015, 92, 104031. [Google Scholar] [CrossRef] [Green Version]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jusufi, K.; Stojkovic, D. Theory and Phenomenology of a Four-Dimensional String–Corrected Black Hole. Universe 2022, 8, 194. https://doi.org/10.3390/universe8030194
Jusufi K, Stojkovic D. Theory and Phenomenology of a Four-Dimensional String–Corrected Black Hole. Universe. 2022; 8(3):194. https://doi.org/10.3390/universe8030194
Chicago/Turabian StyleJusufi, Kimet, and Dejan Stojkovic. 2022. "Theory and Phenomenology of a Four-Dimensional String–Corrected Black Hole" Universe 8, no. 3: 194. https://doi.org/10.3390/universe8030194






