Observational Constraints and Some Toy Models in f(Q) Gravity with Bulk Viscous Fluid
Abstract
:1. Introduction
2. Geometrical Overview
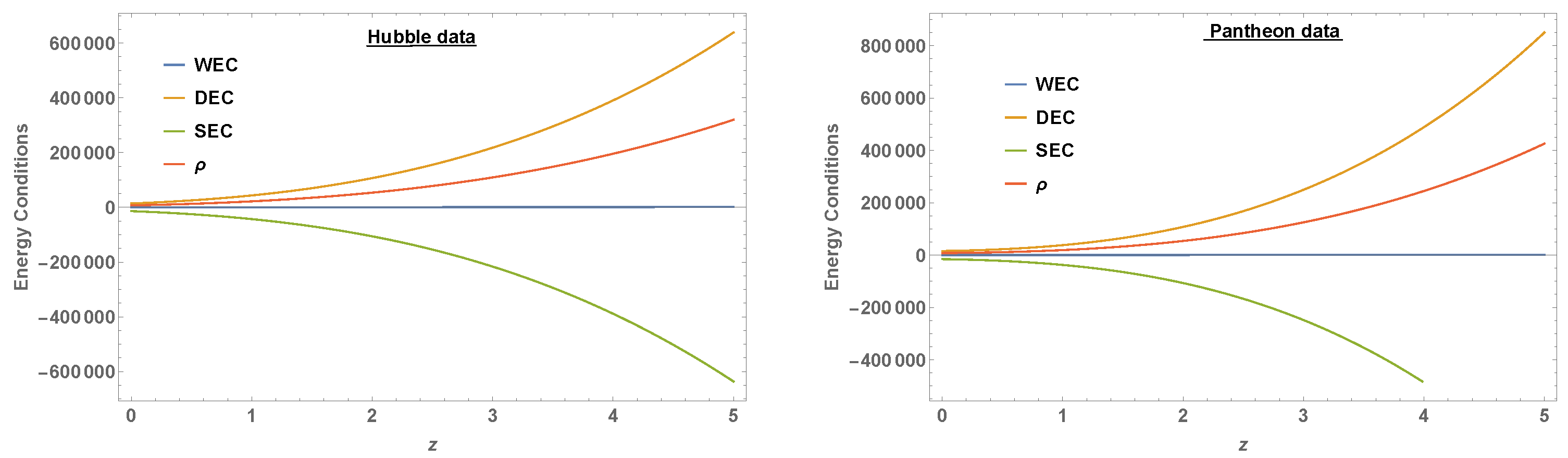
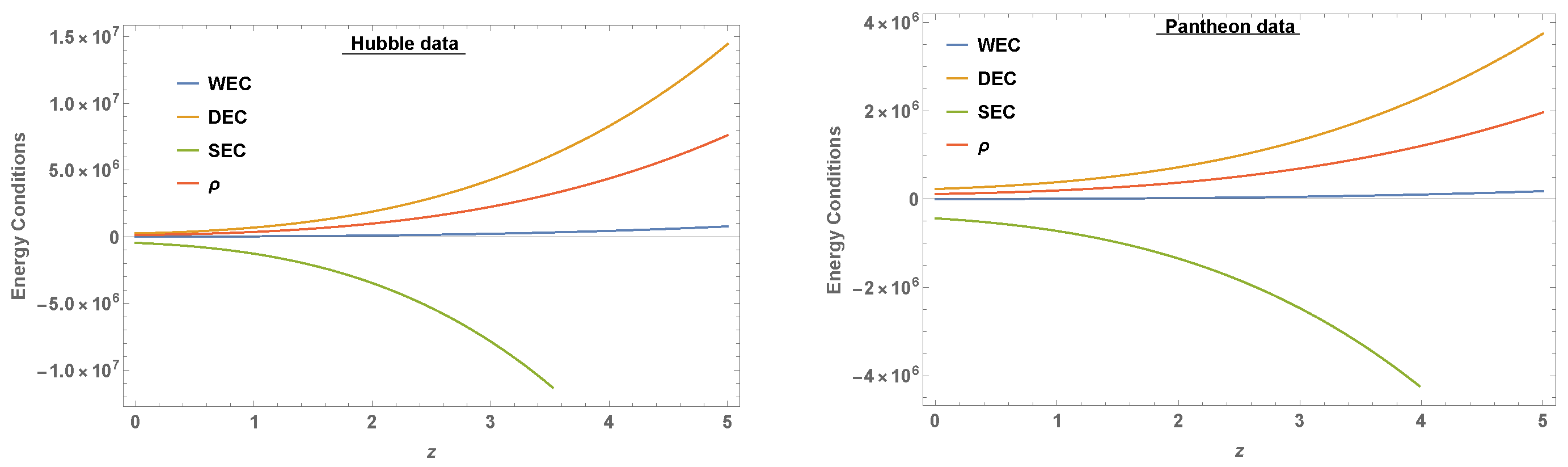
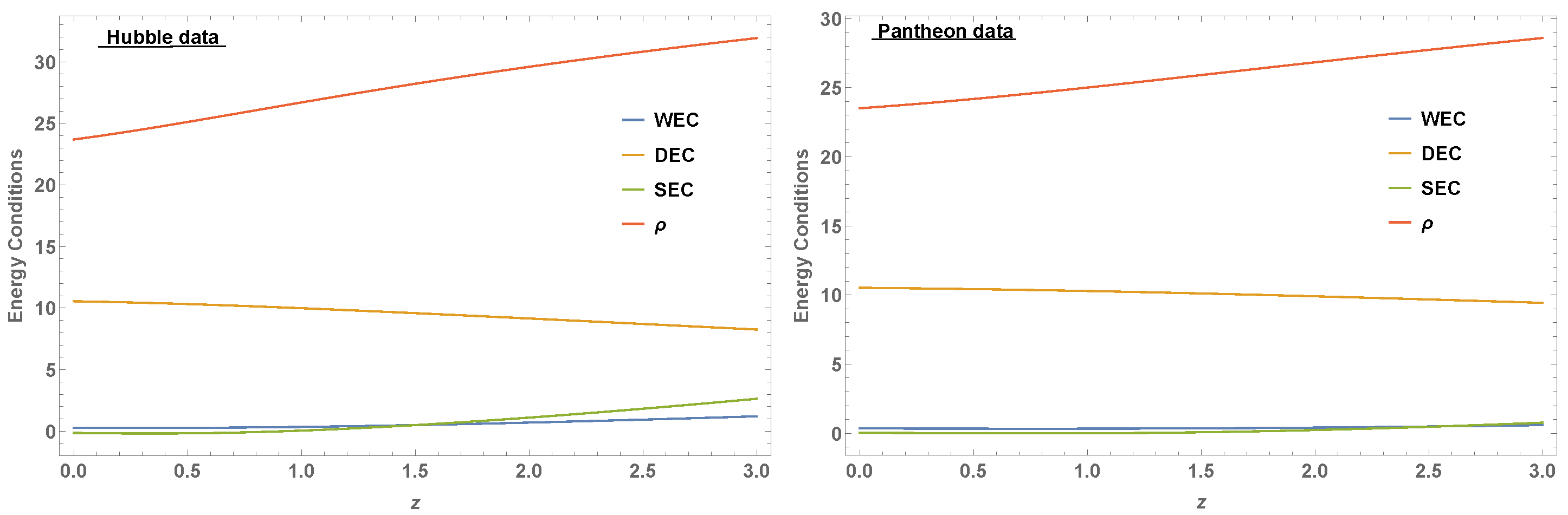
3. Energy Conditions
- Strong energy conditions (SEC) if ;
- Weak energy conditions (WEC) if ;
- Null energy condition (NEC) if ;
- Dominant energy conditions (DEC) if .
- Weak energy conditions (WEC) if ;
- Null energy condition (NEC) if ;
- Dominant energy conditions (DEC) if .
4. Data Interpretation
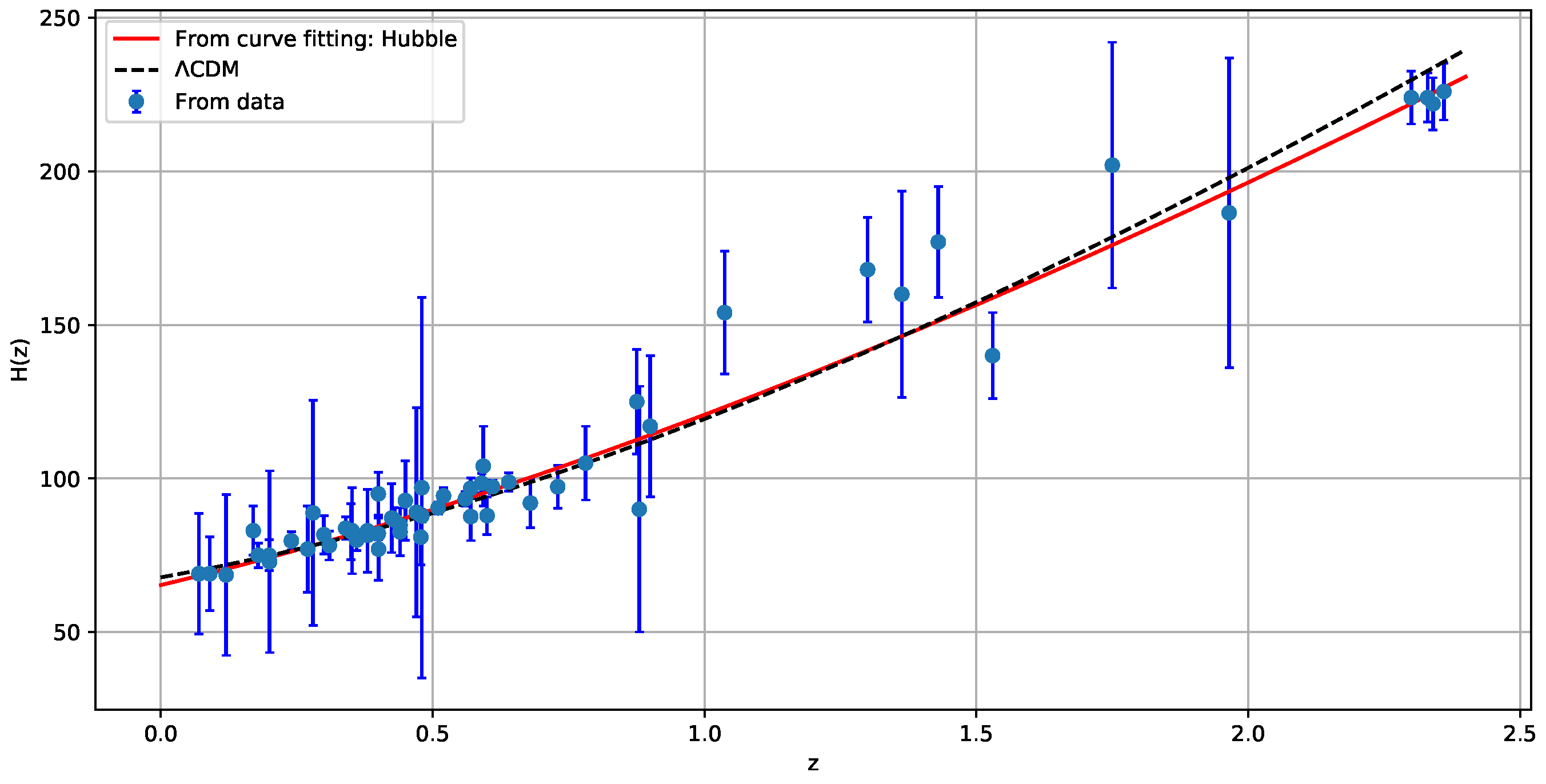
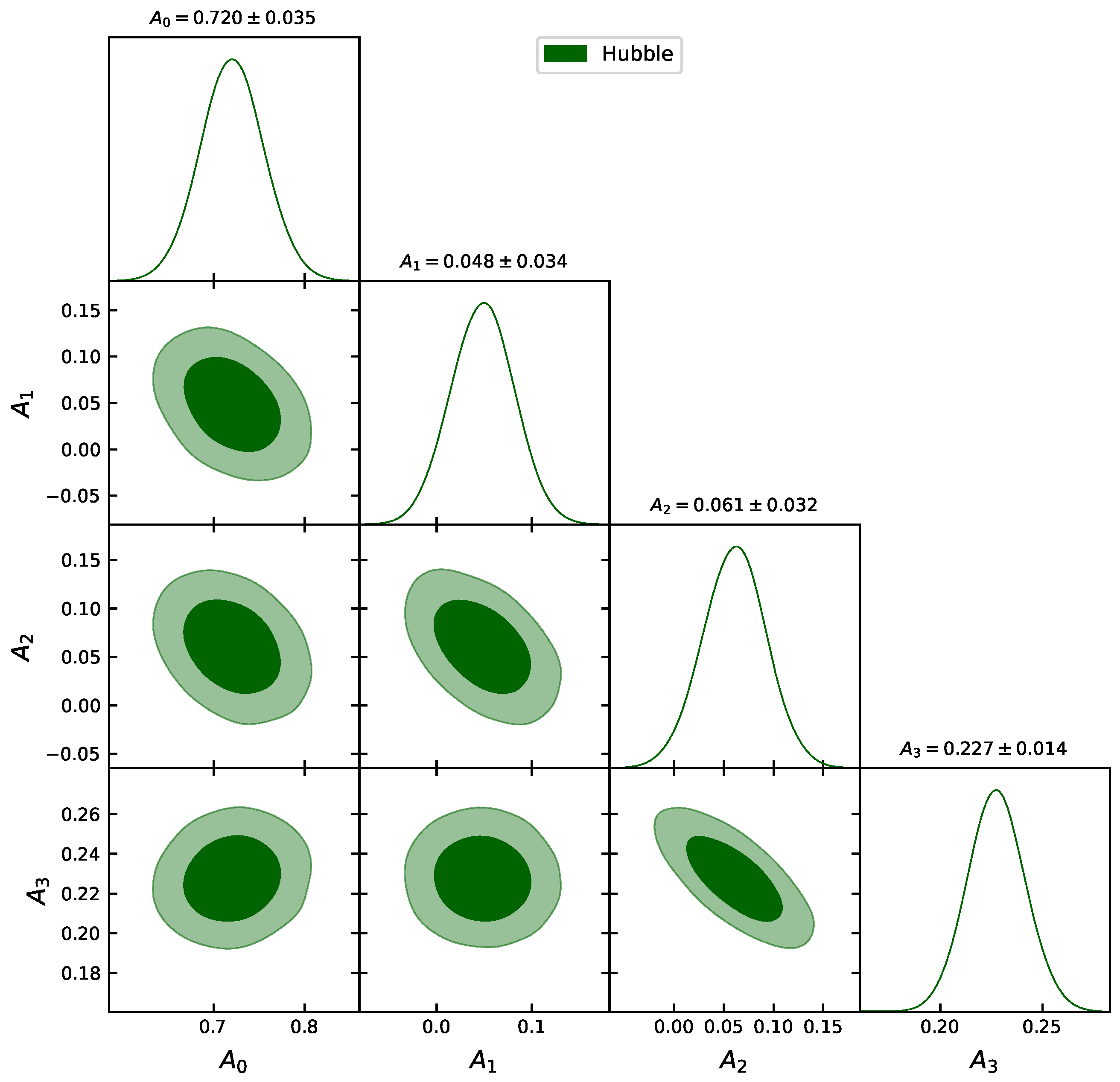
4.1. Hubble Dataset
4.2. Pantheon Dataset
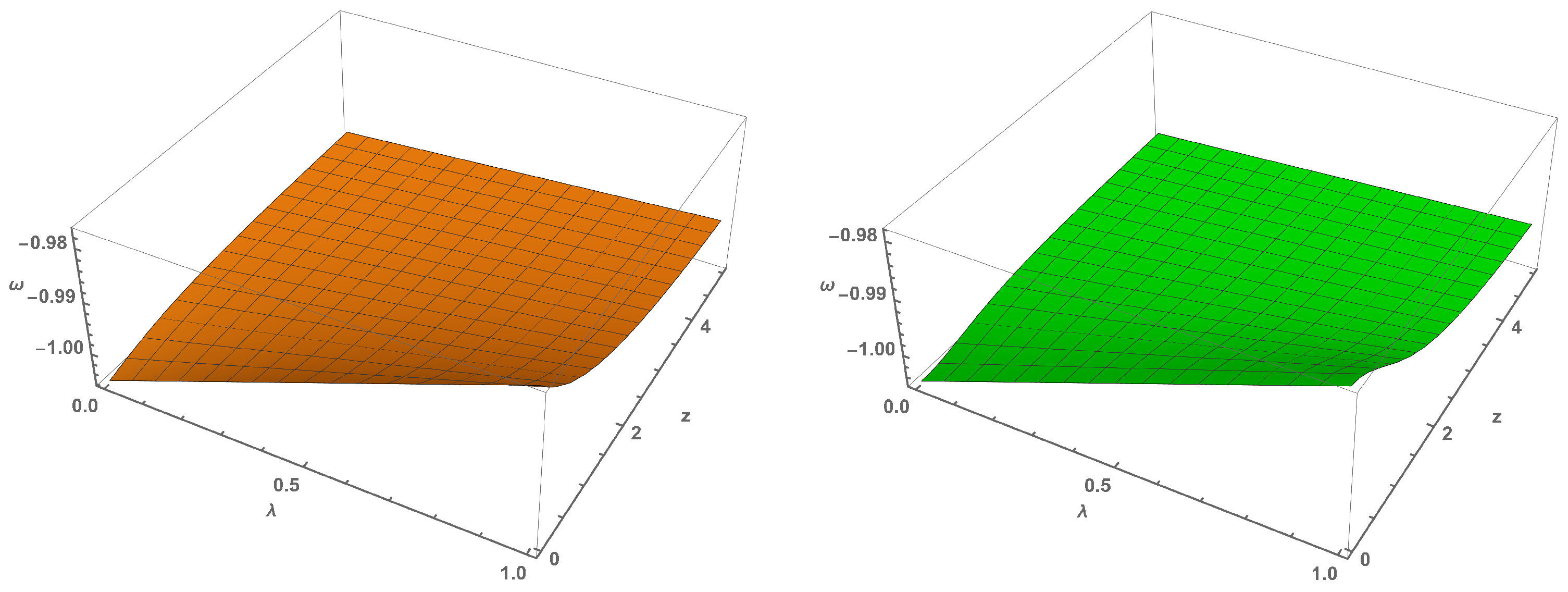
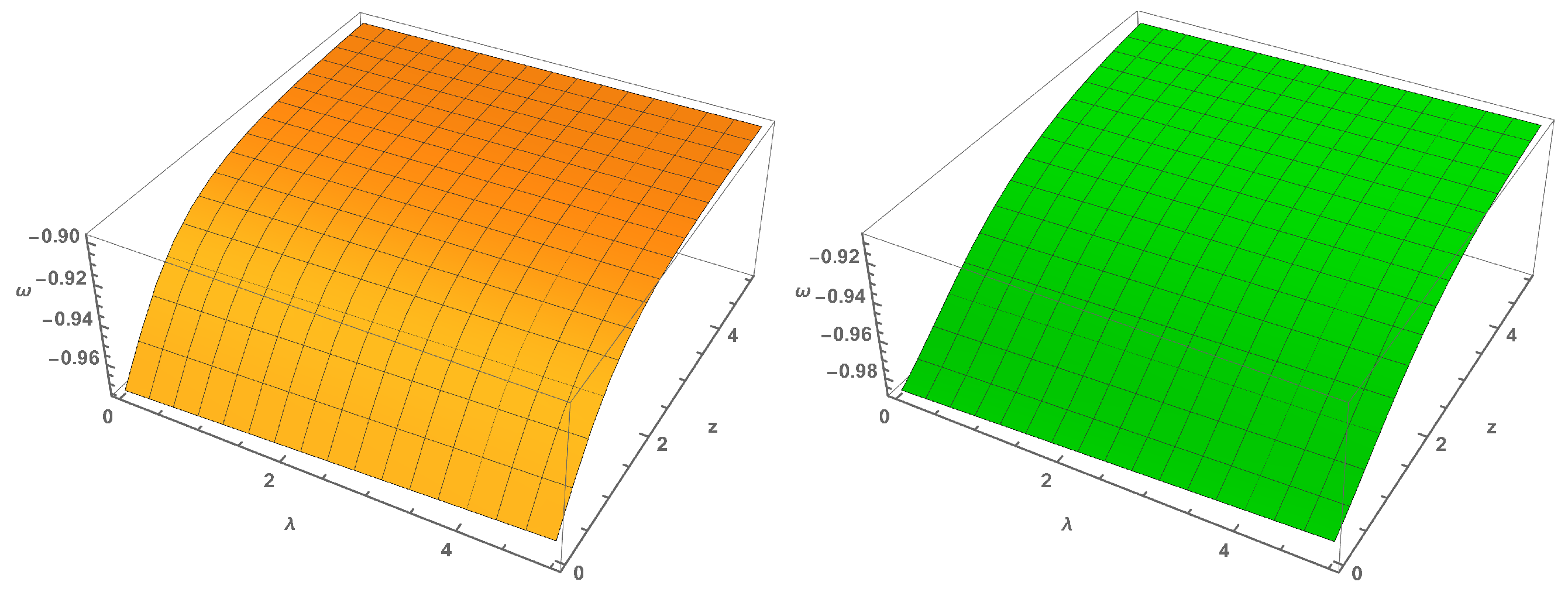
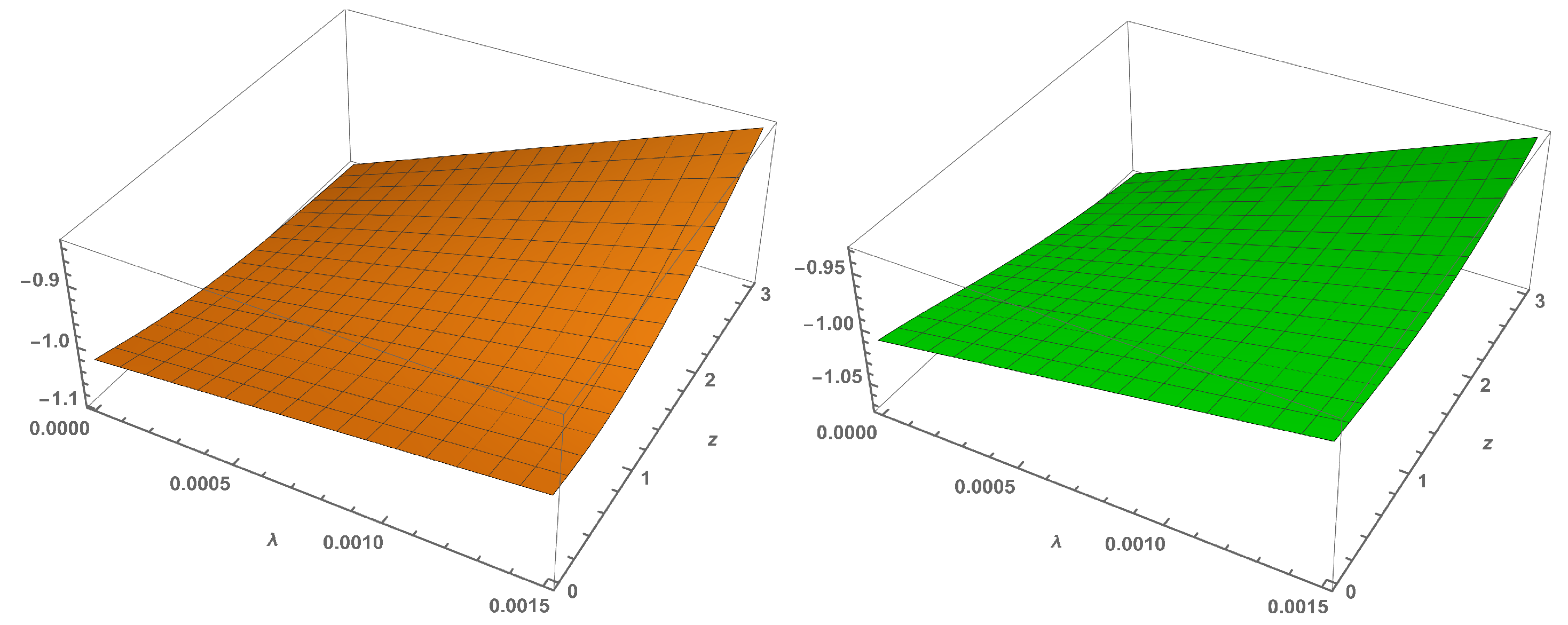
5. Viscous Fluid Models in Gravity
5.1. Model-1:
5.2. Model-2:
5.3. Model-3:
6. Final Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, J.C.; Jha, S.; Kirshner, P.R.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. ApJ 1998, 116, 1009. [Google Scholar] [CrossRef] [Green Version]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. ApJ 1999, 517, 565. [Google Scholar] [CrossRef]
- Hinshaw, G.; Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.L.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; et al. Nine-Year Wilkinson Microwave Anisotropy Probe (Wmap) Observations: Cosmological Parameter Results. ApJ 2013, 208, 19. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, N.; Rubin, D.; Lidman, C.; Aldering, G.; Amanullah, R.; Barbary, K.; Barrientos, L.F.; Botyanszki, J.; Brodwin, M.; Connolly, N.; et al. The Hubble Space Telescope Cluster Supernova Survey. V. Improving the Dark-Energy Constraints Above z > 1 and Building an Early-Type-Hosted Supernova Sample. ApJ 2012, 746, 85. [Google Scholar] [CrossRef] [Green Version]
- Carlip, S. Hiding the Cosmological Constant. Phys. Rev. Lett. 2019, 123, 131302. [Google Scholar] [CrossRef] [Green Version]
- Jimenez, J.B.; Heisenberg, L.; Koivisto, T. Coincident general relativity. Phys. Rev. D 2018, 98, 044048. [Google Scholar] [CrossRef] [Green Version]
- Lazkoz, R.; Lobo, F.S.N.; Ortiz-Baños, M.; Salzano, V. Observational constraints of f(Q) gravity. Phys. Rev. D 2019, 100, 104027. [Google Scholar] [CrossRef] [Green Version]
- Mandal, S.; Sahoo, P.K.; Santos, J.R.L. Energy conditions in f(Q) gravity. Phys. Rev. D 2020, 102, 024057. [Google Scholar] [CrossRef]
- Mandal, S.; Wang, D.; Sahoo, P.K. Cosmography in f(Q) gravity. Phys. Rev. D 2020, 102, 124029. [Google Scholar] [CrossRef]
- Harko, T.; Koivisto, T.S.; Lobo, F.S.N.; Olmo, G.J.; Rubiera-Garcia, D. Coupling matter in modified Q gravity. Phys. Rev. D 2018, 98, 084043. [Google Scholar] [CrossRef] [Green Version]
- Barros, B.J.; Barreiro, T.; Koivisto, T.; Nunes, N.J. Testing F (Q) gravity with redshift space distortions. Phys. Dark Universe 2020, 30, 100616. [Google Scholar] [CrossRef]
- Jimenez, J.B.; Heisenberg, L.; Koivisto, T.; Pekar, S. Cosmology in f(Q) geometry. Phys. Rev. D 2020, 101, 103507. [Google Scholar] [CrossRef]
- Hasan, Z.; Mandal, S.; Sahoo, P.K. Traversable Wormhole Geometries in f(Q) Gravity. Fortschritte Der Phys. 2021, 69, 2100023. [Google Scholar] [CrossRef]
- Solanki, R.; Mandal, S.; Sahoo, P.K. Cosmic acceleration with bulk viscosity in modified f(Q) gravity. Phys. Dark Universe 2021, 32, 100820. [Google Scholar] [CrossRef]
- Eckart, C. The Thermodynamics of Irreversible Processes. III. Relativistic Theory of the Simple Fluid. Phys. Rev. 1940, 58, 919. [Google Scholar] [CrossRef]
- Weinberg, S. Entropy Generation and the Survival of Protogalaxies in an Expanding Universe. Astrophys. J. 1971, 168, 175. [Google Scholar] [CrossRef]
- Treciokas, R.; Ellis, G.F.R. Isotropic solutions of the Einstein-Boltzmann equations. Commun. Math. Phys. 1971, 23, 1–22. [Google Scholar] [CrossRef]
- Misner, C.W. The Isotropy of the Universe. Astrophys. J. 1968, 151, 431. [Google Scholar] [CrossRef]
- Israel, W.; Vardalas, J.N. Transport coefficients of a relativistic quantum gas. Nuovo C. Lett. 1970, 4, 887. [Google Scholar] [CrossRef]
- Murphy, G.L. Big-Bang Model Without Singularities. Phys. Rev. D 1973, 8, 4231. [Google Scholar] [CrossRef]
- Belinskii, V.A.; Kalatnikov, I.M. On the effect of viscosity on the character of the cosmological singularity. Pisma Zh. Eksp. Tekhn. Fiz. 1974, 21, 223. [Google Scholar]
- Hu, M.-G.; Meng, X.-H. Bulk viscous cosmology: Statefinder and entropy. Phys. Lett. B 2006, 635, 186. [Google Scholar] [CrossRef]
- Ren, J.; Meng, X.-H. Cosmological model with viscosity media (dark fluid) described by an effective equation of state. Phys. Lett. B 2006, 633, 1. [Google Scholar] [CrossRef] [Green Version]
- Ren, J.; Meng, X.-H. Modified equation of state, scalar field, and bulk viscosity in Friedmann universe. Phys. Lett. B 2006, 636, 5. [Google Scholar] [CrossRef] [Green Version]
- Gagnon, J.S.; Lesgourgues, J. Dark goo: Bulk viscosity as an alternative to dark energy. J. Cosmol. Astropart. Phys. 2011, 9, 026. [Google Scholar] [CrossRef] [Green Version]
- Diosi, L.; Keszthelyi, B.; Lukacs, B.; Paal, G. Viscosity and the monopole density of the Universe. Acta Phys. Pol. B 1984, 15, 909. [Google Scholar]
- Waga, I.; Falcao, R.C.; Chanda, R. Bulk-viscosity-driven inflationary model. Phys. Rev. D 1986, 15, 1839. [Google Scholar] [CrossRef]
- Barrow, J.D. The deflationary universe: An instability of the de Sitter universe. Phys. Lett. 1986, 180, 335. [Google Scholar] [CrossRef]
- Barrow, J.D. String-driven inflationary and deflationary cosmological models. Nucl. Phys. B 1988, 380, 743. [Google Scholar] [CrossRef]
- Bemfica, F.S.; Disconzi, M.M.; Noronha, J. Causality of the Einstein-Israel-Stewart Theory with Bulk Viscosity. Phys. Rev. Lett. 2019, 122, 221602. [Google Scholar] [CrossRef] [Green Version]
- Chattopadhyay, S. Israel-Stewart Approach to Viscous Dissipative Extended Holographic Ricci Dark Energy Dominated Universe. Adv. High Energy Phys. 2016, 2016, 8515967. [Google Scholar] [CrossRef]
- Olson, T.S. Stability and causality in the Israel-Stewart energy frame theory. Ann. Phys. 1990, 199, 1. [Google Scholar] [CrossRef]
- Ilg, P.; Ottinger, H.C. Nonequilibrium relativistic thermodynamics in bulk viscous cosmology. Phys. Rev. D 1999, 61, 023510. [Google Scholar] [CrossRef]
- Wilson, J.R.; Mathews, G.J.; Fuller, G.M. Bulk viscosity, decaying dark matter, and the cosmic acceleration. Phys. Rev. D 2007, 75, 043521. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.D.; Huang, Z.G.; Zhai, X.H. Generalized Chaplygin gas model with or without viscosity in the w-w′ plane. Astrophys. Space Sci. 2012, 337, 493. [Google Scholar] [CrossRef]
- Feng, C.J.; Li, X.Z. Viscous Ricci dark energy. Phys. Lett. B 2009, 680, 355. [Google Scholar] [CrossRef] [Green Version]
- Capozziello, S.; Cardone, V.F.; Elizalde, E.; Nojiri, S.; Odintsov, S.D. Observational constraints on dark energy with generalized equations of state. Phys. Rev. D 2006, 73, 043512. [Google Scholar] [CrossRef] [Green Version]
- Mohan, N.D.J.; Sasidharan, A.; Mathew, T.K. Bulk viscous matter and recent acceleration of the universe based on causal viscous theory. Eur. Phys. J. C 2017, 77, 849. [Google Scholar] [CrossRef]
- Velten, H.; Schwarz, D.J. Dissipation of dark matter. Phys. Rev. D 2012, 86, 083501. [Google Scholar] [CrossRef] [Green Version]
- Cataldo, M.; Cruz, N.; Lepe, S. Viscous dark energy and phantom evolution. Phys. Lett. B 2005, 619, 5. [Google Scholar] [CrossRef] [Green Version]
- Arora, S.; Meng, X.-H.; Pacif, S.K.J.; Sahoo, P.K. Effective equation of state in modified gravity and observational constraints. Class. Quant. Grav. 2020, 30, 205022. [Google Scholar] [CrossRef]
- Cardenas, V.H.; Cruz, M.; Lepe, S. Cosmic expansion with matter creation and bulk viscosity. Phys. Rev. D 2020, 102, 123543. [Google Scholar] [CrossRef]
- Raychaudhuri, A. Relativistic Cosmology. I. Phys. Rev. D 1955, 98, 1123. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Introduction to Modified Gravity and Gravitational Alternative for Dark Energy. Int. J. Geom. Methods Mod. Phys. 2007, 4, 115. [Google Scholar] [CrossRef] [Green Version]
- Ehlers, J. AK Raychaudhuri and His Equation. IJMPD 2006, 15, 1573. [Google Scholar] [CrossRef] [Green Version]
- Arora, S.; Santos, J.R.L.; Sahoo, P.K. Constraining f(Q, T) gravity from energy conditions. Phys. Dark Universe 2021, 31, 100790. [Google Scholar] [CrossRef]
- Capozziello, S.; Nojiri, S.; Odintsov, S.D. The role of energy conditions in f(R) cosmology. Phys. Lett. B 2018, 781, 99. [Google Scholar] [CrossRef]
- Saini, T.D.; Raychaudhury, S.; Sahni, V.; Starobinsky, A.A. Reconstructing the Cosmic Equation of State from Supernova Distances. Phys. Rev. Lett. 2000, 85, 1162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Capozziello, S.; Cardone, V.F.; Troisi, A. Reconciling dark energy models with f(R) theories. Phys. Rev. D 2005, 71, 043503. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2018 results—VI. Cosmological parameters. A&A 2020, 641, 67. [Google Scholar]
- Sahni, V.; Saini, T.D.; Starobinsky, A.A.; Alam, U. Statefinder—A new geometrical diagnostic of dark energy. JETP Lett. 2003, 77, 201. [Google Scholar] [CrossRef]
- Pourbagher, A.; Amani, A. Thermodynamics and stability of f(T, B) gravity with viscous fluid by observational constraints. Astrophys. Space Sci. 2019, 364, 140. [Google Scholar] [CrossRef] [Green Version]
- Sharov, G.S.; Vasiliev, V.O. How predictions of cosmological models depend on Hubble parameter data sets. Math. Model. Geom. 2018, 6, 1. [Google Scholar] [CrossRef]
- Chuang, C.H.; Wang, Y. Modelling the anisotropic two-point galaxy correlation function on small scales and single-probe measurements of H(z), DA(z) and f(z) σ8(z) from the Sloan Digital Sky Survey DR7 luminous red galaxies. Mon. Not. R. Astron. Soc. 2013, 435, 255. [Google Scholar] [CrossRef] [Green Version]
- Chuang, C.-H.; Prada, F.; Cuesta, A.J.; Eisenstein, D.J.; Kazin, E.; Padmanabhan, N.; Sánchez, A.G.; Xu, X.; Beutler, F.; Manera, M.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Single-probe measurements and the strong power of f(z)σ8(z) on constraining dark energy. Mon. Not. R. Astron. Soc. 2013, 433, 3559. [Google Scholar] [CrossRef]
- Delubac, T.; Bautista, J.E.; Busca, N.G.; Rich, J.; Kirkby, D.; Bailey, S.; Font-Ribera, A.; Slosar, A.; Lee, K.-G.; Pieri, M.M.; et al. Baryon acoustic oscillations in the Lyα forest of BOSS DR11 quasars. Astron. Astrophys. 2015, 574, 17. [Google Scholar] [CrossRef] [Green Version]
- Anderson, L.; Aubourg, E.; Bailey, S.; Beutler, F.; Bhardwaj, V.; Blanton, M.; Bolton, A.S.; Brinkmann, J.; Brownstein, J.R.; Burden, A.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples. Mon. Not. R. Astron. Soc. 2014, 441, 24. [Google Scholar] [CrossRef] [Green Version]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Chuang, C.-H.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. R. Astron. Soc. 2017, 470, 2617. [Google Scholar] [CrossRef] [Green Version]
- Simon, J.; Verde, L.; Jimenez, R. Constraints on the redshift dependence of the dark energy potential. Phys. Rev. D 2005, 71, 123001. [Google Scholar] [CrossRef] [Green Version]
- Stern, D.; Jimenez, R.; Verde, L.; Kamionkowski, M.; Stanford, S.A. Cosmic chronometers: Constraining the equation of state of dark energy. I: H(z) measurements. JCAP 2010, 02, 008. [Google Scholar] [CrossRef] [Green Version]
- Moresco, M. Raising the bar: New constraints on the Hubble parameter with cosmic chronometers at z ∼ 2. Mon. Not. R. Astron. Soc. Lett. 2015, 450, L16. [Google Scholar] [CrossRef] [Green Version]
- Ratsimbazafy, A.L.; Loubser, S.I.; Crawford, S.M.; Cress, C.M.; Bassett, B.A.; Nichol, R.C.; Vaisanen, P. Age-dating luminous red galaxies observed with the Southern African Large Telescope. Mon. Not. R. Astron. Soc. 2017, 467, 3239. [Google Scholar] [CrossRef] [Green Version]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. ApJ 2018, 859, 101. [Google Scholar] [CrossRef]


| Dataset | H(z) Dataset | Pantheon Dataset |
|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mandal, S.; Parida, A.; Sahoo, P.K. Observational Constraints and Some Toy Models in f(Q) Gravity with Bulk Viscous Fluid. Universe 2022, 8, 240. https://doi.org/10.3390/universe8040240
Mandal S, Parida A, Sahoo PK. Observational Constraints and Some Toy Models in f(Q) Gravity with Bulk Viscous Fluid. Universe. 2022; 8(4):240. https://doi.org/10.3390/universe8040240
Chicago/Turabian StyleMandal, Sanjay, Abhishek Parida, and Pradyumn Kumar Sahoo. 2022. "Observational Constraints and Some Toy Models in f(Q) Gravity with Bulk Viscous Fluid" Universe 8, no. 4: 240. https://doi.org/10.3390/universe8040240
APA StyleMandal, S., Parida, A., & Sahoo, P. K. (2022). Observational Constraints and Some Toy Models in f(Q) Gravity with Bulk Viscous Fluid. Universe, 8(4), 240. https://doi.org/10.3390/universe8040240







