A Short Review on the Latest Neutrinos Mass and Number Constraints from Cosmological Observables
Abstract
:1. Introduction
2. Invited Particles to Complement Beta Decay Processes
2.1. Neutrino in the Standard Model of Particle Physics
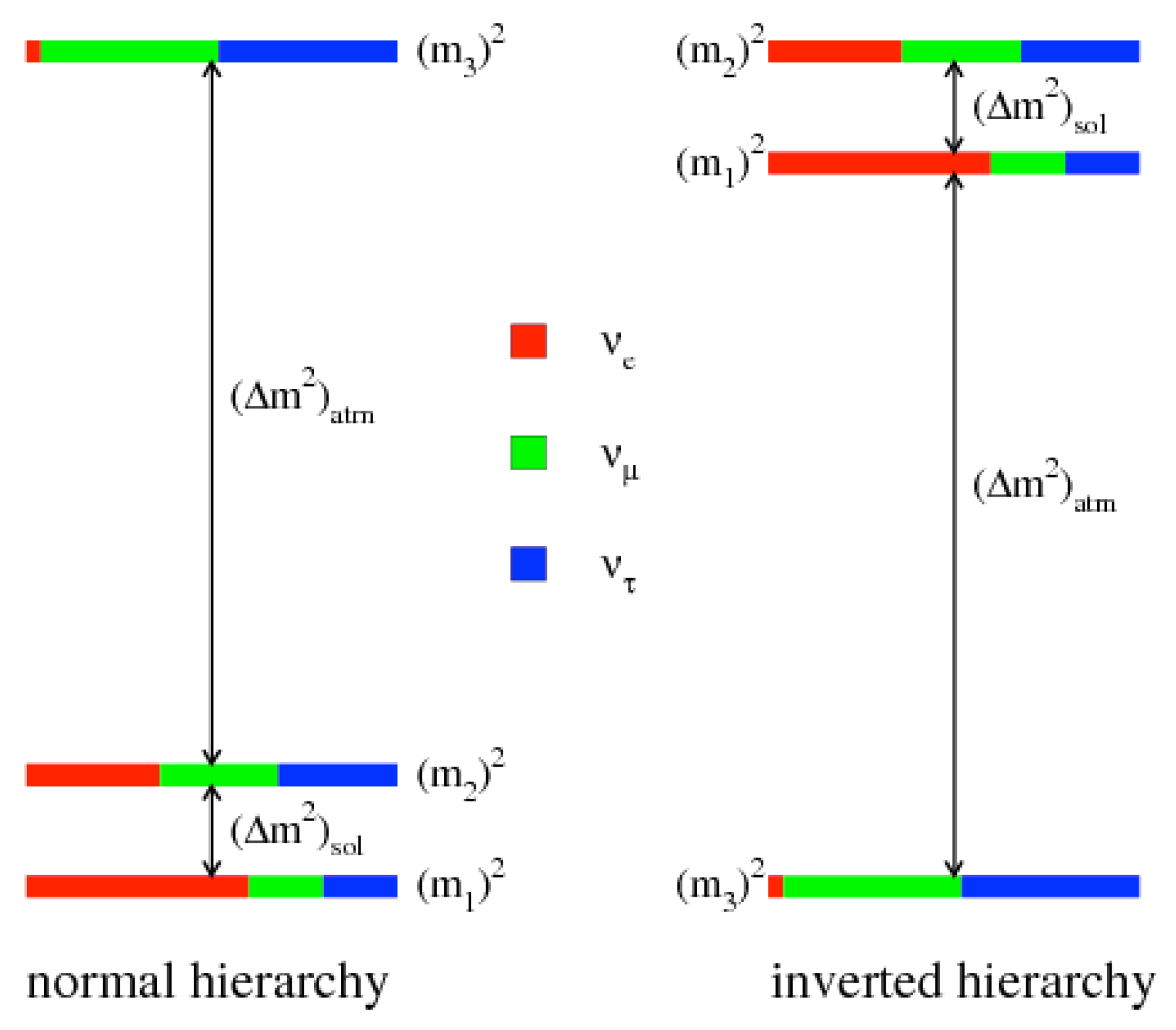
2.2. The Discovery of the Need for a Non-Vanishing Mass for the Neutrinos
2.3. Neutrinos’ Mass from Neutrinoless Double-Beta Decay Rate
3. Neutrino Thermal and Cosmological Density Evolution
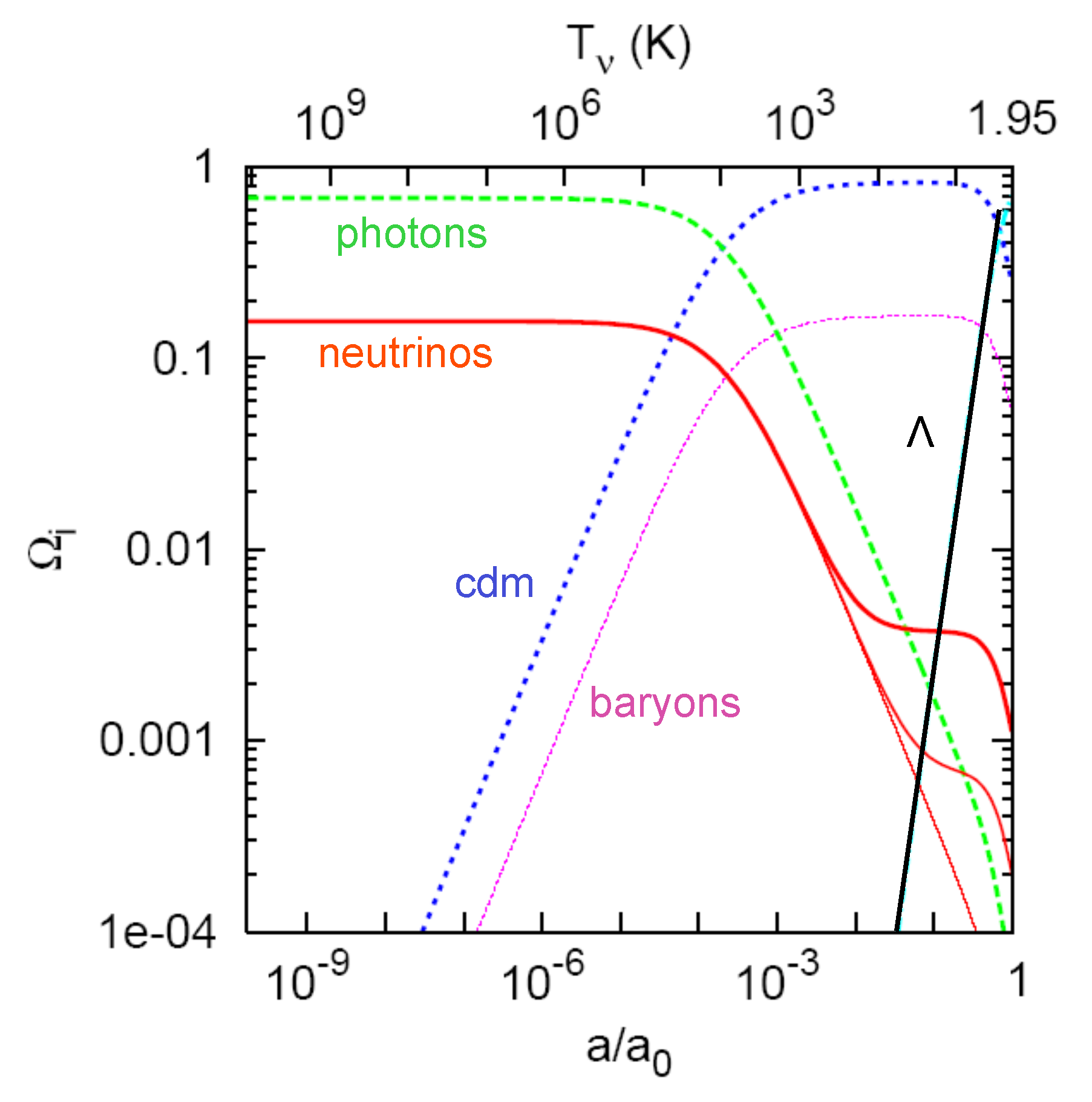
3.1. Neutrino Early-Time History
3.2. Neutrino Late-Time Evolution
4. Impact on Observables
4.1. Neutrino Effects on the CMB Power Spectrum
4.2. Effects of Neutrino on Large-Scale Structure Formation
5. Constraints from Current Cosmo Datasets
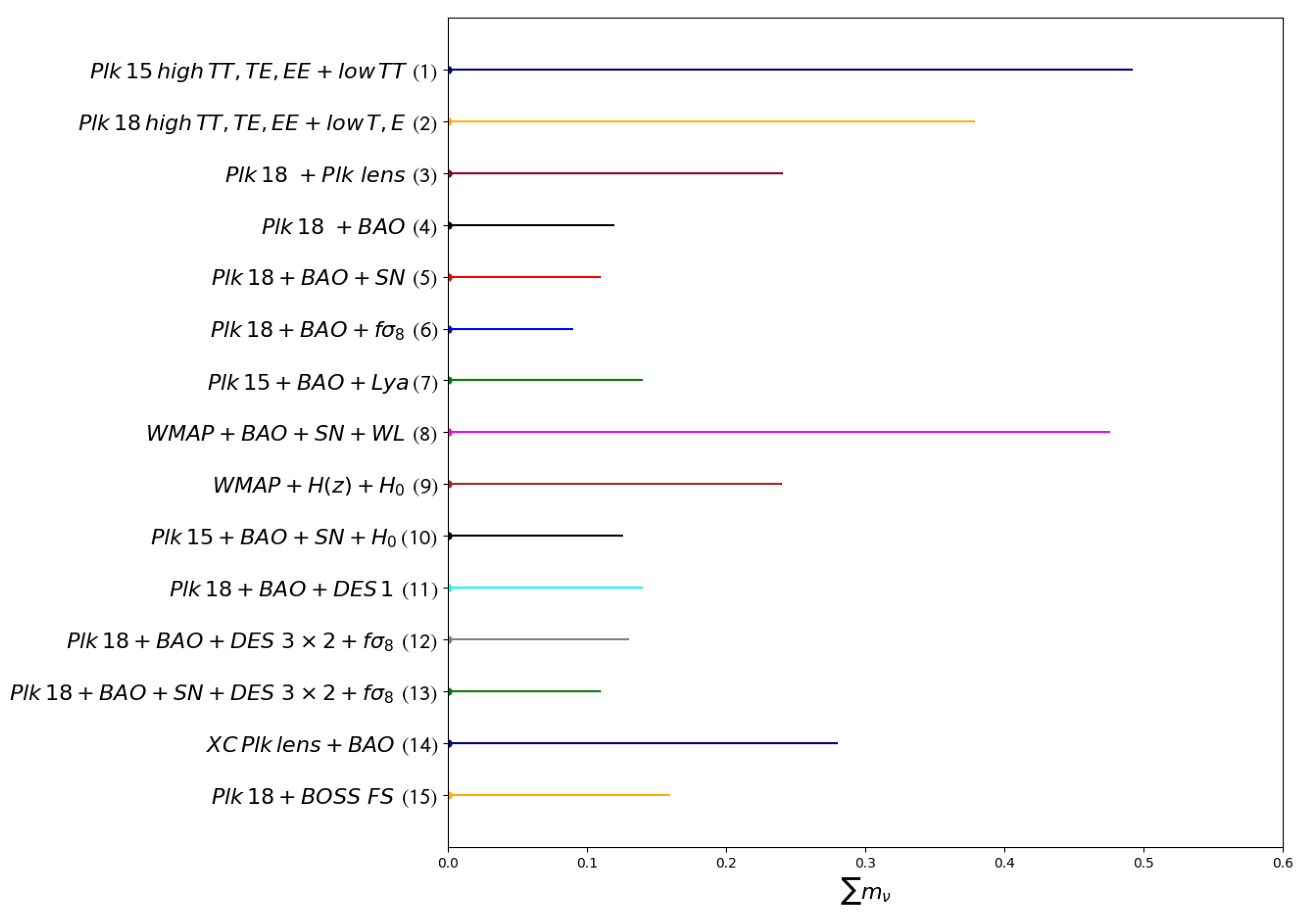
5.1. Neutrino Bounds from CMB and Combination with Other Geometrical Probes
5.2. Constraining a Neutrino from Its Effect on the Growth of LSS
6. Neutrinos and Cosmological Tensions
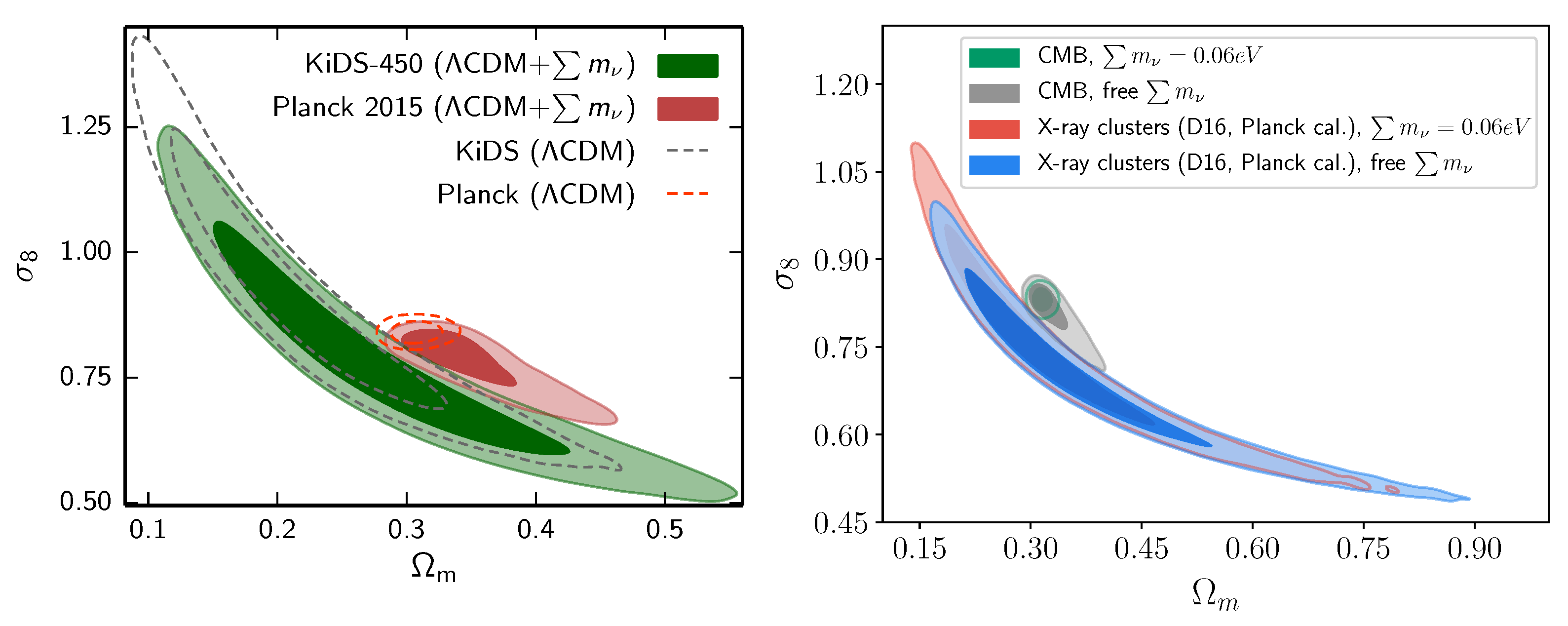
6.1. Neutrinos as Possible Solution to the Cosmological Discrepancies
6.2. Neutrinos’ Inability to Alleviate the Cosmological Tensions
7. A Closure from Next-Generation Surveys?
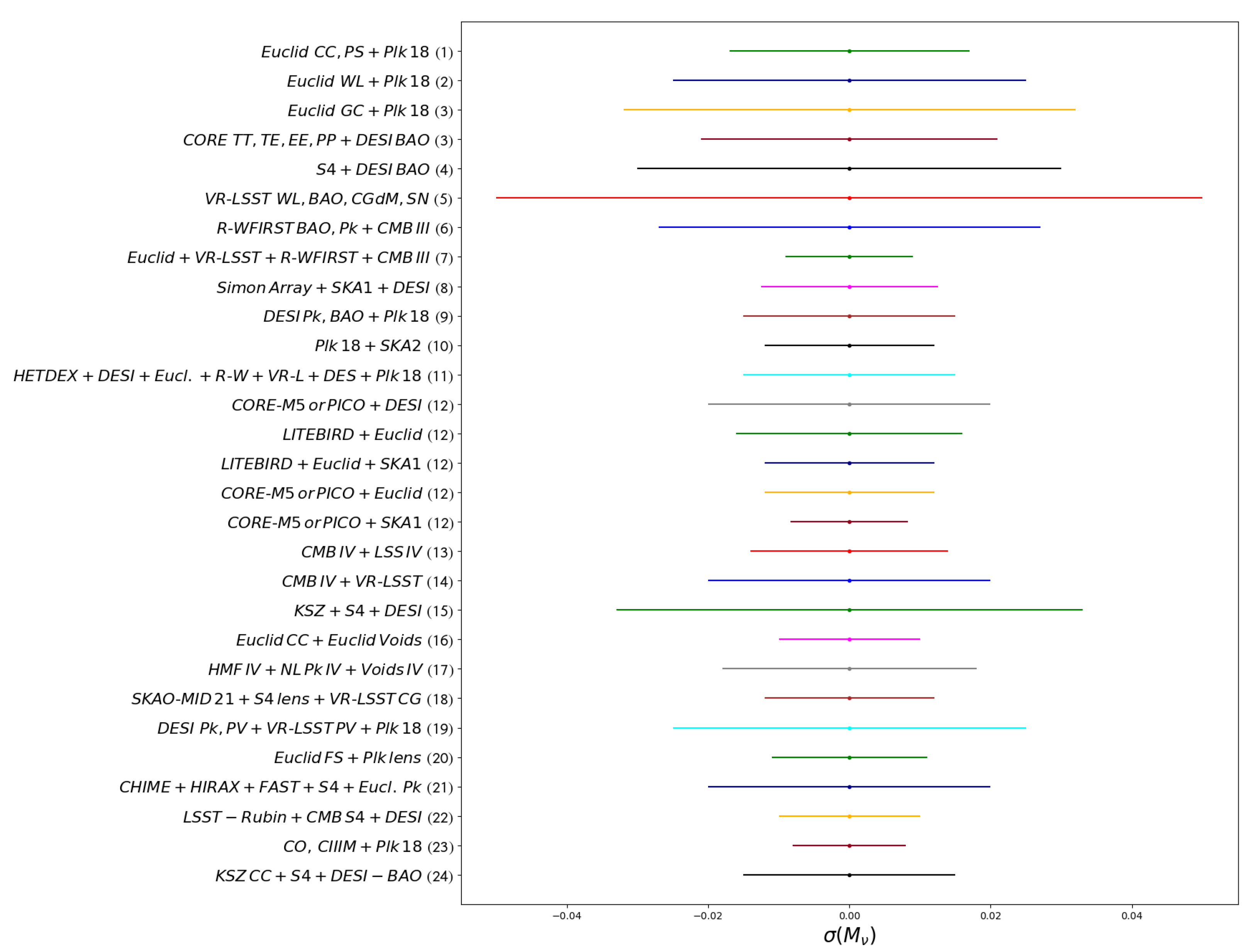
7.1. Review of Forecasts from Next-Generation Surveys on the Mass and Number of Neutrino Species
7.2. Further Forecasts on Bounds from New Probes on the Mass of Neutrino Number of Species
8. Discussion and Conclusions
Funding
Acknowledgments
Conflicts of Interest
| 1 | See [48] for a detailed study on perspectives for neutrino flavor conversions determinations in other astrophysical and cosmological environments. |
| 2 | the power spectrum being the 3D Fourier transform of the correlation function. |
| 3 | similar to the tSZ effect, the kSZ effect is the imprint of galaxy clusters on CMB from peculiar motion and is proportional to the integrated electron momentum along the line-of-sight. |
References
- Capozzi, F.; Lisi, E.; Marrone, A.; Montanino, D.; Palazzo, A. Neutrino masses and mixings: Status of known and unknown 3ν parameters. Nucl. Phys. B 2016, 908, 218–234. [Google Scholar] [CrossRef] [Green Version]
- Robertson, R.G.H.; Bowles, T.J.; Stephenson, G.J.; Wark, D.L.; Wilkerson, J.F.; Knapp, D.A. Limit on anti-electron-neutrino mass from observation of the beta decay of molecular tritium. Phys. Rev. Lett. 1991, 67, 957–960. [Google Scholar] [CrossRef] [PubMed]
- Kraus, C.; Bornschein, B.; Bornschein, L.; Bonn, J.; Flatt, B.; Kovalik, A.; Ostrick, B.; Otten, E.W.; Schall, J.P.; Thümmler, T.; et al. Final results from phase II of the Mainz neutrino mass search in tritium beta decay. Eur. Phys. J. C 2005, 40, 447–468. [Google Scholar] [CrossRef]
- Aseev, V.N.; Belesev, A.I.; Berlev, A.I.; Geraskin, E.V.; Golubev, A.A.; Likhovid, N.A.; Lobashev, V.M.; Nozik, A.A.; Pantuev, V.S.; Parfenov, V.I.; et al. An upper limit on electron antineutrino mass from Troitsk experiment. Phys. Rev. D 2011, 84, 112003. [Google Scholar] [CrossRef] [Green Version]
- Aker, M.; Beglarian, A.; Behrens, J.; Berlev, A.; Besserer, U.; Bieringer, B.; Block, F.; Bobien, S.; Boettcher, M.; Bornschein, B.; et al. Direct neutrino-mass measurement with sub-electronvolt sensitivity. Nat. Phys. 2022, 18, 160–166. [Google Scholar] [CrossRef]
- Alfonso, K. Search for Neutrinoless Double-Beta Decay of 130Te with CUORE-0. Phys. Rev. Lett. 2015, 115, 102502. [Google Scholar] [CrossRef] [Green Version]
- Colgate, S.A.; White, R.H. The Hydrodynamic Behavior of Supernovae Explosions. Astrophys. J. 1966, 143, 626. [Google Scholar] [CrossRef]
- Avrorin, A.D.; Avrorin, A.V.; Aynutdinov, V.M.; Bannash, R.; Belolaptikov, I.A.; Brudanin, V.B.; Budnev, N.M.; Doroshenko, A.A.; Domogatsky, G.V.; Dvornický, R.; et al. Baikal-GVD: Status and prospects. EPJ Web Conf. 2018, 191, 01006. [Google Scholar] [CrossRef]
- Abbasi, R.; Ackermann, M.; Adams, J.; Ahlers, M.; Ahrens, J.; Andeen, K.; Auffenberg, J.; Bai, X.; Baker, M.; Barwick, S.W.; et al. The IceCube Data Acquisition System: Signal Capture, Digitization, and Timestamping. Nucl. Instrum. Meth. A 2009, 601, 294–316. [Google Scholar] [CrossRef] [Green Version]
- Ageron, M.; Aguilar, J.A.; Al Samarai, I.; Albert, A.; Ameli, F.; André, M.; Anton, G.; Anvar, S.; Ardid, M.; Arnaud, K.; et al. ANTARES: The first undersea neutrino telescope. Nucl. Instrum. Meth. A 2011, 656, 11–38. [Google Scholar] [CrossRef]
- Adrian-Martinez, S.; Ageron, M.; Aharonian, F.; Aiello, S.; Albert, A.; Ameli, F.; Anassontzis, E.; Andre, M.; Androulakis, G.; Anghinolfi, M.; et al. Letter of intent for KM3NeT 2.0. J. Phys. G 2016, 43, 084001. [Google Scholar] [CrossRef]
- Di Valentino, E.; Gariazzo, S.; Mena, O. Most constraining cosmological neutrino mass bounds. Phys. Rev. D 2021, 104, 083504. [Google Scholar] [CrossRef]
- Laureijs, R.; Amiaux, J.; Arduini, S.; Augueres, J.L.; Brinchmann, J.; Cole, R.; Cropper, M.; Dabin, C.; Duvet, L.; Ealet, A.; et al. Euclid Definition Study Report. arXiv 2011, arXiv:1110.3193. [Google Scholar]
- LSST Science, Collaboration; Abell, P.A.; Allison, J.; Anderson, S.F.; Andrew, J.R.; Angel, J.R.P.; Armus, L.; Arnett, D.; Asztalos, S.J.; Axelrod, T.S.; et al. LSST Science Book, Version 2.0. arXiv 2009, arXiv:0912.0201. [Google Scholar]
- Spergel, D.; Gehrels, N.; Baltay, C.; Bennett, D.; Breckinridge, J.; Donahue, M.; Dressler, A.; Gaudi, B.S.; Greene, T.; Guyon, O. et al.Wide-Field InfrarRed Survey Telescope-Astrophysics Focused Telescope Assets WFIRST-AFTA 2015 Report. arXiv 2015, arXiv:1503.03757. [Google Scholar]
- Bacon, D.J.; et al.; [Square Kilometre Array Cosmology Science Working Group] Cosmology with Phase 1 of the Square Kilometre Array: Red Book 2018: Technical specifications and performance forecasts. Publ. Astron. Soc. Austral. 2020, 37, e007. [Google Scholar] [CrossRef] [Green Version]
- Abazajian, K.N.; Adshead, P.; Ahmed, Z.; Allen, S.W.; Alonso, D.; Arnold, K.S.; Baccigalupi, C.; Bartlett, J.G.; Battaglia, N.; Benson, B.A.; et al. CMB-S4 Science Book, First Edition. arXiv 2016, arXiv:1610.02743. [Google Scholar]
- Aghamousa, A.; et al.; [DESI Collaboration] The DESI Experiment Part I: Science,Targeting, and Survey Design. arXiv 2016, arXiv:1611.00036. [Google Scholar]
- Hazumi, M.; Ade, P.A.R.; Adler, A.; Allys, E.; Arnold, K.; Auguste, D.; Aumont, J.; Aurlien, R.; Austermann, J.; Baccigalupi, C.; et al. LiteBIRD: JAXA’s new strategic L-class mission for all-sky surveys of cosmic microwave background polarization. Proc. SPIE Int. Soc. Opt. Eng. 2020, 11443, 114432F. [Google Scholar] [CrossRef]
- Di Valentino, E.; Brinckmann, T.; Gerbino, M.; Poulin, V.; Bouchet, F.R.; Lesgourgues, J.; Melchiorri, A.; Chluba, J.; Clesse, S.; Delabrouille, J.; et al. Exploring cosmic origins with CORE: Cosmological parameters. JCAP 2018, 4, 017. [Google Scholar] [CrossRef] [Green Version]
- Archidiacono, M.; Hannestad, S.; Lesgourgues, J. What will it take to measure individual neutrino mass states using cosmology? JCAP 2020, 9, 21. [Google Scholar] [CrossRef]
- Kowalski, M.; Rubin, D.; Aldering, G.; Agostinho, R.J.; Amadon, A.; Amanullah, R.; Balland, C.; Barbary, K.; Blanc, G.; Challis, P.J.; et al. Improved Cosmological Constraints from New, Old and Combined Supernova Datasets. Astrophys. J. 2008, 686, 749–778. [Google Scholar] [CrossRef] [Green Version]
- Aghanim, N.; et al.; [Planck Collaboration] Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2021, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef] [Green Version]
- Scolnic, D.; Brout, D.; Carr, A.; Riess, A.G.; Davis, T.M.; Dwomoh, A.; Jones, D.O.; Ali, N.; Charvu, P.; Chen, R.; et al. The Pantheon+ Type Ia Supernova Sample: The Full Dataset and Light-Curve Release. arXiv 2021, arXiv:2112.03863. [Google Scholar]
- Alam, S.; et al.; [eBOSS Collaboration] Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Cosmological implications from two decades of spectroscopic surveys at the Apache Point Observatory. Phys. Rev. D 2021, 103, 083533. [Google Scholar] [CrossRef]
- Ade, P.A.R.; et al.; [Planck Collaboration] Planck 2015 results. XXIV. Cosmology from Sunyaev-Zeldovich cluster counts. Astron. Astrophys. 2016, 594, A24. [Google Scholar] [CrossRef] [Green Version]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Breuval, L.; Brink, T.G.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km/s/Mpc Uncertainty from the Hubble Space Telescope and the SH0ES Team. arXiv 2021, arXiv:2112.04510. [Google Scholar]
- Dvorkin, C.; Wyman, M.; Rudd, D.H.; Hu, W. Neutrinos help reconcile Planck measurements with both the early and local Universe. Phys. Rev. D 2014, 90, 083503. [Google Scholar] [CrossRef] [Green Version]
- Wyman, M.; Rudd, D.H.; Vanderveld, R.A.; Hu, W. Neutrinos Help Reconcile Planck Measurements with the Local Universe. Phys. Rev. Lett. 2014, 112, 051302. [Google Scholar] [CrossRef] [Green Version]
- Joudaki, S.; Mead, A.; Blake, C.; Choi, A.; de Jong, J.; Erben, T.; Conti, I.F.; Herbonnet, R.; Heymans, C.; Hildebrandt, H.; et al. KiDS-450: Testing extensions to the standard cosmological model. Mon. Not. Roy. Astron. Soc. 2017, 471, 1259–1279. [Google Scholar] [CrossRef] [Green Version]
- Sakr, Z.; Ilić, S.; Blanchard, A.; Bittar, J.; Farah, W. Cluster counts: Calibration issue or new physics? Astron. Astrophys. 2018, 620, A78. [Google Scholar] [CrossRef] [Green Version]
- Archidiacono, M.; Gariazzo, S. Two sides of the same coin: Sterile neutrinos and dark radiation. Status and perspectives. arXiv 2022, arXiv:2201.10319. [Google Scholar]
- Pauli, W. Letter to L. Meitner and her colleagues. Phys. Today 1930, 9, 23. [Google Scholar]
- Fermi, E. Versuch einer Theorie der β-Strahlen. I. Zeitschrift für Physik 1934, 88, 161–177. [Google Scholar] [CrossRef]
- Glashow, S.L. The renormalizability of vector meson interactions. Nucl. Phys. 1959, 10, 107–117. [Google Scholar] [CrossRef]
- Salam, A.; Ward, J.C. Weak and electromagnetic interactions. Nuovo Cim. 1959, 11, 568–577. [Google Scholar] [CrossRef]
- Weinberg, S. A Model of Leptons. Phys. Rev. Lett. 1967, 19, 1264–1266. [Google Scholar] [CrossRef]
- Reines, F.; Cowan, C.L. The neutrino. Nature 1956, 178, 446–449. [Google Scholar] [CrossRef]
- Goldhaber, M.; Grodzins, L.; Sunyar, A.W. Helicity of Neutrinos. Phys. Rev. 1958, 109, 1015–1017. [Google Scholar] [CrossRef] [Green Version]
- Majorana, E. Teoria simmetrica dell’elettrone e del positrone. Il Nuovo Cimento (1924–1942) 1937, 14, 171–184. [Google Scholar] [CrossRef]
- Pontecorvo, B. Mesonium and anti-mesonium. Sov. Phys. JETP 1957, 6, 429. [Google Scholar]
- Maltoni, M.; Schwetz, T.; Tortola, M.A.; Valle, J.W.F. Status of global fits to neutrino oscillations. New J. Phys. 2004, 6, 122. [Google Scholar] [CrossRef]
- Kajita, T. Nobel Lecture: Discovery of atmospheric neutrino oscillations. Rev. Mod. Phys. 2016, 88, 030501. [Google Scholar] [CrossRef] [Green Version]
- McDonald, A.B. Nobel Lecture: The Sudbury Neutrino Observatory: Observation of flavor change for solar neutrinos. Rev. Mod. Phys. 2016, 88, 030502. [Google Scholar] [CrossRef]
- de Salas, P.F.; Forero, D.V.; Ternes, C.A.; Tortola, M.; Valle, J.W.F. Status of neutrino oscillations 2018: 3σ hint for normal mass ordering and improved CP sensitivity. Phys. Lett. B 2018, 782, 633–640. [Google Scholar] [CrossRef]
- Esteban, I.; Gonzalez-Garcia, M.C.; Maltoni, M.; Schwetz, T.; Zhou, A. The fate of hints: Updated global analysis of three-flavor neutrino oscillations. JHEP 2020, 9, 178. [Google Scholar] [CrossRef]
- Formaggio, J.A.; de Gouvêa, A.L.C.; Robertson, R.G.H. Direct Measurements of Neutrino Mass. Phys. Rept. 2021, 914, 1–54. [Google Scholar] [CrossRef]
- Capozzi, F.; Saviano, N. Neutrino Flavor Conversions in High-Density Astrophysical and Cosmological Environments. Universe 2022, 8, 94. [Google Scholar] [CrossRef]
- de Gouvea, A.; Jenkins, J.; Kayser, B. Neutrino mass hierarchy, vacuum oscillations, and vanishing |U(e3)|. Phys. Rev. D 2005, 71, 113009. [Google Scholar] [CrossRef] [Green Version]
- Cappuzzello, F.; Agodi, C.; Cavallaro, M.; Carbone, D.; Tudisco, S.; Presti, D.L.; Oliveira, J.R.B.; Finocchiaro, P.; Colonna, M.; Rifuggiato, D.; et al. The NUMEN project: NUclear Matrix Elements for Neutrinoless double beta decay. Eur. Phys. J. A 2018, 54, 72. [Google Scholar] [CrossRef] [Green Version]
- Albanese, V.; et al.; [SNO+ Collaboration] The SNO+ experiment. JINST 2021, 16, P08059. [Google Scholar] [CrossRef]
- Barabash, A.S. Double Beta Decay: Historical Review of 75 Years of Research. Phys. Atom. Nucl. 2011, 74, 603–613. [Google Scholar] [CrossRef] [Green Version]
- Ejiri, H. Experimental Approaches to Neutrino Nuclear Responses for ββ Decays and Astro-Neutrinos. Front. Phys. 2021, 9, 82. [Google Scholar] [CrossRef]
- Lesgourgues, J.; Pastor, S. Neutrino cosmology and Planck. New J. Phys. 2014, 16, 065002. [Google Scholar] [CrossRef]
- de Salas, P.F.; Pastor, S. Relic neutrino decoupling with flavour oscillations revisited. JCAP 2016, 7, 51. [Google Scholar] [CrossRef]
- Tremaine, S.; Gunn, J.E. Dynamical Role of Light Neutral Leptons in Cosmology. Phys. Rev. Lett. 1979, 42, 407–410. [Google Scholar] [CrossRef]
- Ringwald, A.; Wong, Y.Y.Y. Gravitational clustering of relic neutrinos and implications for their detection. JCAP 2004, 12, 005. [Google Scholar] [CrossRef]
- Alpher, R.A.; Follin, J.W.; Herman, R.C. Physical Conditions in the Initial Stages of the Expanding Universe. Phys. Rev. 1953, 92, 1347–1361. [Google Scholar] [CrossRef]
- Pontecorvo, B.; Smorodinsky, Y. The neutrino and the density of matter in the universe. Z. Eksp. Teor. Fiz. 1961, 41, 239–243. [Google Scholar]
- Gershtein, S.S.; Zeldovich, Y.B. Rest Mass of Muonic Neutrino and Cosmology. JETP Lett. 1966, 4, 120–122. [Google Scholar]
- Gawiser, E.; Silk, J. The Cosmic microwave background radiation. Phys. Rept. 2000, 333, 245–267. [Google Scholar] [CrossRef] [Green Version]
- Sachs, R.K.; Wolfe, A.M. Perturbations of a cosmological model and angular variations of the microwave background. Astrophys. J. 1967, 147, 73–90. [Google Scholar] [CrossRef]
- Hu, W.; White, M.J. CMB anisotropies in the weak coupling limit. Astron. Astrophys. 1996, 315, 33. [Google Scholar]
- Gerbino, M.; Lattanzi, M. Status of neutrino properties and future prospects—Cosmological and astrophysical constraints. Front. Phys. 2018, 5, 70. [Google Scholar] [CrossRef]
- Hu, W.; Eisenstein, D.J.; Tegmark, M. Weighing neutrinos with galaxy surveys. Phys. Rev. Lett. 1998, 80, 5255–5258. [Google Scholar] [CrossRef] [Green Version]
- Costanzi, M.; Villaescusa-Navarro, F.; Viel, M.; Xia, J.Q.; Borgani, S.; Castorina, E.; Sefusatti, E. Cosmology with massive neutrinos III: The halo mass function andan application to galaxy clusters. JCAP 2013, 12, 012. [Google Scholar] [CrossRef]
- Castorina, E.; Sefusatti, E.; Sheth, R.K.; Villaescusa-Navarro, F.; Viel, M. Cosmology with massive neutrinos II: On the universality of the halo mass function and bias. JCAP 2014, 2, 049. [Google Scholar] [CrossRef]
- Ilić, S.; Sakr, Z.; Blanchard, A. Cluster counts. II. Tensions, massive neutrinos, and modified gravity. Astron. Astrophys. 2019, 631, A96. [Google Scholar] [CrossRef]
- Ade, P.A.R.; et al.; [Planck Collaboration] Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef] [Green Version]
- Vagnozzi, S.; Giusarma, E.; Mena, O.; Freese, K.; Gerbino, M.; Ho, S.; Lattanzi, M. Unveiling ν secrets with cosmological data: Neutrino masses and mass hierarchy. Phys. Rev. D 2017, 96, 123503. [Google Scholar] [CrossRef] [Green Version]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Dawson, K.S.; Kneib, J.-P.; Percival, W.J.; Alam, S.; Albareti, F.D.; Anderson, S.F.; Armengaud, E.; Aubourg, E.; Bailey, S.; Bautista, J.E.; et al. The SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Overview and Early Data. Astron. J. 2016, 151, 44. [Google Scholar] [CrossRef]
- Loveday, J.; Pier, J. The Sloan Digital Sky Survey. 1998. Available online: http://xxx.lanl.gov/abs/astro-ph/9809179 (accessed on 19 March 2022).
- Abbott, T.; et al.; [Dark Energy Survey Collaboration] The Dark Energy Survey. 2005. Available online: http://xxx.lanl.gov/abs/astro-ph/0510346 (accessed on 19 March 2022).
- Yèche, C.; Palanque-Delabrouille, N.; Baur, J.; du Mas des Bourboux, H. Constraints on neutrino masses from Lyman-alpha forest power spectrum with BOSS and XQ-100. JCAP 2017, 6, 047. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Wang, Y.F.; Xia, D.M. Constraints on the sum of neutrino masses using cosmological data including the latest extended Baryon Oscillation Spectroscopic Survey DR14 quasar sample. Chin. Phys. C 2018, 42, 065103. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Meng, X.L.; Zhang, T.J.; Shan, H.; Gong, Y.; Tao, C.; Chen, X.; Huang, Y.F. Observational constraints on cosmic neutrinos and dark energy revisited. JCAP 2012, 11, 018. [Google Scholar] [CrossRef] [Green Version]
- Moresco, M.; Verde, L.; Pozzetti, L.; Jimenez, R.; Cimatti, A. New constraints on cosmological parameters and neutrino properties using the expansion rate of the Universe to z~1.75. JCAP 2012, 7, 053. [Google Scholar] [CrossRef] [Green Version]
- Di Valentino, E.; Giusarma, E.; Mena, O.; Melchiorri, A.; Silk, J. Cosmological limits on neutrino unknowns versus low redshift priors. Phys. Rev. D 2016, 93, 083527. [Google Scholar] [CrossRef] [Green Version]
- Wan, H.Y.; Cao, S.L.; Teng, H.Y.; Liu, Y.; Zhang, J.C.; Zhang, T.J. Direct constraint on cosmic neutrino mass using observational Hubble parameter data. Res. Astron. Astrophys. 2018, 18, 124. [Google Scholar] [CrossRef] [Green Version]
- Guo, R.Y.; Zhang, J.F.; Zhang, X. Can the H0 tension be resolved in extensions to ΛCDM cosmology? JCAP 2019, 02, 054. [Google Scholar] [CrossRef] [Green Version]
- Feng, L.; Guo, R.Y.; Zhang, J.F.; Zhang, X. Cosmological search for sterile neutrinos after Planck 2018. Phys. Lett. B 2022, 827, 136940. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; et al.; [DES Collaboration] Dark Energy Survey year 1 results: Cosmological constraints from galaxy clustering and weak lensing. Phys. Rev. D 2018, 98, 043526. [Google Scholar] [CrossRef] [Green Version]
- Abbott, T.M.C.; et al.; [DES Collaboration] Dark Energy Survey Year 3 results: Cosmological constraints from galaxy clustering and weak lensing. Phys. Rev. D 2022, 105, 023520. [Google Scholar] [CrossRef]
- Doux, C.; Penna-Lima, M.; Vitenti, S.D.P.; Tréguer, J.; Aubourg, E.; Ganga, K. Cosmological constraints from a joint analysis of cosmic microwave background and spectroscopic tracers of the large-scale structure. Mon. Not. Roy. Astron. Soc. 2018, 480, 5386–5411. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, M.M.; Simonović, M.; Zaldarriaga, M. Cosmological Parameters and Neutrino Masses from the Final Planck and Full-Shape BOSS Data. Phys. Rev. D 2020, 101, 083504. [Google Scholar] [CrossRef] [Green Version]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—A review of solutions. Class. Quant. Grav. 2021, 38, 153001. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. arXiv 2021, arXiv:2105.05208. [Google Scholar]
- Schöneberg, N.; Lesgourgues, J.; Hooper, D.C. The BAO+BBN take on the Hubble tension. JCAP 2019, 10, 029. [Google Scholar] [CrossRef] [Green Version]
- Leistedt, B.; Peiris, H.V.; Verde, L. No new cosmological concordance with massive sterile neutrinos. Phys. Rev. Lett. 2014, 113, 041301. [Google Scholar] [CrossRef] [Green Version]
- Beutler, F.; Saito, S.; Brownstein, J.R.; Chuang, C.-H.; Cuesta, A.J.; Percival, W.J.; Ross, A.J.; Ross, N.P.; Schneider, D.P.; Samushia, L.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Signs of neutrino mass in current cosmological data sets. Mon. Not. R. Astron. Soc. 2014, 444, 3501–3516. [Google Scholar] [CrossRef] [Green Version]
- Costanzi, M.; Sartoris, B.; Viel, M.; Borgani, S. Neutrino constraints: What large-scale structure and CMB data are telling us? JCAP 2014, 10, 081. [Google Scholar] [CrossRef] [Green Version]
- Emami, R.; Broadhurst, T.; Jimeno, P.; Smoot, G.; Angulo, R.; Lim, J.; Chu, M.C.; Yeung, S.; Zeng, Z.; Lazkoz, R. Evidence of Neutrino Enhanced Clustering in a Complete Sample of Sloan Survey Clusters, Implying ∑mν=0.119±0.034 eV. arXiv 2017, arXiv:1711.05210. [Google Scholar]
- Schaffer, K.K.; Crawford, T.M.; Aird, K.A.; Benson, B.A.; Bleem, L.E.; Carlstrom, J.E.; Chang, C.L.; Cho, H.M.; Crites, A.T.; De Haan, T.; et al. The First Public Release of South Pole Telescope Data: Maps of a 95-square-degree Field from 2008 Observations. Astrophys. J. 2011, 743, 90. [Google Scholar] [CrossRef] [Green Version]
- de Haan, T.; Benson, B.A.; Bleem, L.E.; Allen, S.W.; Applegate, D.E.; Ashby, M.L.N.; Bautz, M.; Bayliss, M.; Bocquet, S.; Brodwin, M.; et al. Cosmological Constraints from Galaxy Clusters in the 2500 square-degree SPT-SZ Survey. Astrophys. J. 2016, 832, 95. [Google Scholar] [CrossRef]
- Giblin, B.; Heymans, C.; Asgari, M.; Hildebrandt, H.; Hoekstra, H.; Joachimi, B.; Kannawadi, A.; Kuijken, K.; Lin, C.-A.; Miller, L.; et al. KiDS-1000 catalogue: Weak gravitational lensing shear measurements. Astron. Astrophys. 2021, 645, A105. [Google Scholar] [CrossRef]
- Sgier, R.; Lorenz, C.; Refregier, A.; Fluri, J.; Zürcher, D.; Tarsitano, F. Combined 13×2-point analysis of the Cosmic Microwave Background and Large-Scale Structure: Implications for the S8-tension and neutrino mass constraints. arXiv 2021, arXiv:2110.03815. [Google Scholar]
- Salvati, L.; Douspis, M.; Aghanim, N. Constraints from thermal Sunyaev-Zel’dovich cluster counts and power spectrum combined with CMB. Astron. Astrophys. 2018, 614, A13. [Google Scholar] [CrossRef] [Green Version]
- Roncarelli, M.; Carbone, C.; Moscardini, L. The effect of massive neutrinos on the Sunyaev–Zel’dovich and X-ray observables of galaxy clusters. Mon. Not. R. Astron. Soc. 2015, 447, 1761–1773. [Google Scholar] [CrossRef] [Green Version]
- Böhringer, H.; Chon, G. Constraints on neutrino masses from the study of the nearby large-scale structure and galaxy cluster counts. Mod. Phys. Lett. A 2016, 31, 1640008. [Google Scholar] [CrossRef] [Green Version]
- Böhringer, H.; Chon, G.; Retzlaff, J.; Trümper, J.; Meisenheimer, K.; Schartel, N. The extended Northern ROSAT Galaxy Cluster Survey (NORAS II) I. Survey Construction and First Results. Astron. J. 2017, 153, 220. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A. Neutrino Mass Bounds in the era of Tension Cosmology. arXiv 2021, arXiv:astro-ph.CO/2112.02993. [Google Scholar]
- Aiola, S.; Calabrese, E.; Maurin, L.; Naess, S.; Schmitt, B.L.; Abitbol, M.H.; Addison, G.E.; Ade, P.A.R.; Alonso, D.; Amiri, M.; et al. The Atacama Cosmology Telescope: DR4 Maps and Cosmological Parameters. JCAP 2020, 12, 047. [Google Scholar] [CrossRef]
- Dutcher, D.; Balkenhol, L.; Ade, P.A.R.; Ahmed, Z.; Anderes, E.; Anderson, A.J.; Archipley, M.; Avva, J.S.; Aylor, K.; Barry, P.S.; et al. Measurements of the E-mode polarization and temperature-E-mode correlation of the CMB from SPT-3G 2018 data. Phys. Rev. D 2021, 104, 022003. [Google Scholar] [CrossRef]
- Kogut, A.J.; Chuss, D.T.; Dotson, J.L.; Fixsen, D.J.; Halpern, M.; Hinshaw, G.F.; Meyer, S.M.; Moseley, S.H.; Seiffert, M.D.; Spergel, D.N.; et al. The Primordial Inflation Explorer (PIXIE) Mission. Proc. SPIE Int. Soc. Opt. Eng. 2010, 7731, 77311S. [Google Scholar] [CrossRef]
- Watts, D.J.; Wang, B.; Ali, A.; Appel, J.W.; Bennett, C.L.; Chuss, D.T.; Dahal, S.; Eimer, J.R.; Essinger-Hileman, T.; Harrington, K.; et al. A Projected Estimate of the Reionization Optical Depth Using the CLASS Experiment’s Sample Variance Limited E-mode Measurement. Astrophys. J. 2018, 863, 121. [Google Scholar] [CrossRef] [Green Version]
- Allison, R.; Caucal, P.; Calabrese, E.; Dunkley, J.; Louis, T. Towards a cosmological neutrino mass detection. Phys. Rev. D 2015, 92, 123535. [Google Scholar] [CrossRef] [Green Version]
- Yu, B.; Knight, R.Z.; Sherwin, B.D.; Ferraro, S.; Knox, L.; Schmittfull, M. Towards Neutrino Mass from Cosmology without Optical Depth Information. arXiv 2018, arXiv:1809.02120. [Google Scholar]
- Errard, J.; Feeney, S.M.; Peiris, H.V.; Jaffe, A.H. Robust forecasts on fundamental physics from the foreground-obscured, gravitationally-lensed CMB polarization. JCAP 2016, 3, 052. [Google Scholar] [CrossRef] [Green Version]
- Alcock, C.; Paczynski, B. An evolution free test for non-zero cosmological constant. Nature 1979, 281, 358–359. [Google Scholar] [CrossRef]
- Percival, W.J.; White, M. Testing cosmological structure formation using redshift-space distortions. MNRAS 2009, 393, 297–308. [Google Scholar] [CrossRef] [Green Version]
- Borm, K.; Reiprich, T.H.; Mohammed, I.; Lovisari, L. Constraining galaxy cluster temperatures and redshifts with eROSITA survey data. Astron. Astrophys. 2014, 567, A65. [Google Scholar] [CrossRef] [Green Version]
- Audren, B.; Lesgourgues, J.; Bird, S.; Haehnelt, M.G.; Viel, M. Neutrino masses and cosmological parameters from a Euclid-like survey: Markov Chain Monte Carlo forecasts including theoretical errors. JCAP 2013, 1, 026. [Google Scholar] [CrossRef] [Green Version]
- Cerbolini, M.C.A.; Sartoris, B.; Xia, J.Q.; Biviano, A.; Borgani, S.; Viel, M. Constraining neutrino properties with a Euclid-like galaxy cluster survey. JCAP 2013, 6, 020. [Google Scholar] [CrossRef] [Green Version]
- Chudaykin, A.; Ivanov, M.M. Measuring neutrino masses with large-scale structure: Euclid forecast with controlled theoretical error. JCAP 2019, 11, 034. [Google Scholar] [CrossRef] [Green Version]
- Oyama, Y.; Kohri, K.; Hazumi, M. Constraints on the neutrino parameters by future cosmological 21 cm line and precise CMB polarization observations. JCAP 2016, 2, 008. [Google Scholar] [CrossRef]
- Sprenger, T.; Archidiacono, M.; Brinckmann, T.; Clesse, S.; Lesgourgues, J. Cosmology in the era of Euclid and the Square Kilometre Array. JCAP 2019, 2, 047. [Google Scholar] [CrossRef] [Green Version]
- Ballardini, M.; Maartens, R. Constraining the neutrino mass using a multi-tracer combination of two galaxy surveys and CMB lensing. arXiv 2021, arXiv:2109.03763. [Google Scholar]
- Obuljen, A.; Castorina, E.; Villaescusa-Navarro, F.; Viel, M. High-redshift post-reionization cosmology with 21 cm intensity mapping. JCAP 2018, 5, 004. [Google Scholar] [CrossRef] [Green Version]
- Newburgh, L.B.; Addison, G.E.; Amiri, M.; Bandura, K.; Bond, J.R.; Connor, L.; Cliche, J.-F.; Davis, G.; Deng, M.; Denman, N.; et al. Calibrating CHIME, A New Radio Interferometer to Probe Dark Energy. Proc. SPIE Int. Soc. Opt. Eng. 2014, 9145, 4V. [Google Scholar] [CrossRef] [Green Version]
- Newburgh, L.B.; Bandura, K.; Bucher, M.A.; Chang, T.-C.; Chiang, H.C.; Cliche, J.F.; Dave, R.; Dobbs, M.; Clarkson, C.; Ganga, K.M.; et al. HIRAX: A Probe of Dark Energy and Radio Transients. Proc. SPIE Int. Soc. Opt. Eng. 2016, 9906, 99065X. [Google Scholar] [CrossRef] [Green Version]
- Bigot-Sazy, M.A.; Ma, Y.Z.; Battye, R.A.; Browne, I.W.A.; Chen, T.; Dickinson, C.; Harper, S.; Maffei, B.; Olivari, L.C.; Wilkinson, P.N. HI intensity mapping with FAST. ASP Conf. Ser. 2016, 502, 41. [Google Scholar]
- Font-Ribera, A.; McDonald, P.; Mostek, N.; Reid, B.A.; Seo, H.J.; Slosar, A. DESI and other dark energy experiments in the era of neutrino mass measurements. JCAP 2014, 5, 023. [Google Scholar] [CrossRef] [Green Version]
- Boyle, A.; Komatsu, E. Deconstructing the neutrino mass constraint from galaxy redshift surveys. JCAP 2018, 03, 035. [Google Scholar] [CrossRef] [Green Version]
- Brinckmann, T.; Hooper, D.C.; Archidiacono, M.; Lesgourgues, J.; Sprenger, T. The promising future of a robust cosmological neutrino mass measurement. JCAP 2019, 1, 059. [Google Scholar] [CrossRef] [Green Version]
- Dvorkin, C.; Gerbino, M.; Alonso, D.; Battaglia, N.; Bird, S.; Rivero, A.D.; Font-Ribera, A.; Fuller, G.; Lattanzi, M.; Loverde, M.; et al. Neutrino Mass from Cosmology: Probing Physics Beyond the Standard Model. arXiv 2019, arXiv:astro-ph.CO/1903.03689. [Google Scholar]
- Mishra-Sharma, S.; Alonso, D.; Dunkley, J. Neutrino masses and beyond- ΛCDM cosmology with LSST and future CMB experiments. Phys. Rev. D 2018, 97, 123544. [Google Scholar] [CrossRef] [Green Version]
- Ansari, R.; et al.; [Cosmic Visions 21 cm Collaboration] Inflation and Early Dark Energy with a Stage II Hydrogen Intensity Mapping experiment. arXiv 2018, arXiv:1810.09572. [Google Scholar]
- Sailer, N.; Castorina, E.; Ferraro, S.; White, M. Cosmology at high redshift—A probe of fundamental physics. JCAP 2021, 12, 049. [Google Scholar] [CrossRef]
- Doré, O.; Bock, J.; Ashby, M.; Capak, P.; Cooray, A.; de Putter, R.; Eifler, T.; Flagey, N.; Gong, Y.; Habib, S.; et al. Cosmology with the SPHEREX All-Sky Spectral Survey. arXiv 2014, arXiv:1412.487. [Google Scholar]
- Babusiaux, C.; et al.; [MSE Science Team] The Detailed Science Case for the Maunakea Spectroscopic Explorer. arXiv 2019, arXiv:1904.04907. [Google Scholar]
- Schlegel, D.J.; Kollmeier, J.A.; Aldering, G.; Bailey, S.; Baltay, C.; Bebek, C.; BenZvi, S.; Besuner, R.; Blanc, G.; Bolton, A.S.; et al. Astro2020 APC White Paper: The MegaMapper: A z > 2 Spectroscopic Instrument for the Study of Inflation and Dark Energy. arXiv 2019, arXiv:1907.11171. [Google Scholar]
- Slosar, A.; Castorina, E.; Connor, L.; Foreman, S.; Green, D.; Karagiannis, D.; Liu, A.; Masui, K.W.; Meerburg, D.; Münchmeyer, M.; et al. Packed Ultra-wideband Mapping Array (PUMA): A Radio Telescope for Cosmology and Transients. Bull. Am. Astron. Soc. 2019, 51, 53. [Google Scholar]
- Visbal, E.; Loeb, A.; Wyithe, J.S.B. Cosmological Constraints from 21 cm Surveys After Reionization. JCAP 2009, 10, 030. [Google Scholar] [CrossRef] [Green Version]
- Mueller, E.M.; de Bernardis, F.; Bean, R.; Niemack, M.D. Constraints on massive neutrinos from the pairwise kinematic Sunyaev-Zel’dovich effect. Phys. Rev. D 2015, 92, 063501. [Google Scholar] [CrossRef] [Green Version]
- Madhavacheril, M.S.; Battaglia, N.; Miyatake, H. Fundamental physics from future weak-lensing calibrated Sunyaev-Zel’dovich galaxy cluster counts. Phys. Rev. D 2017, 96, 103525. [Google Scholar] [CrossRef] [Green Version]
- Bolliet, B.; Brinckmann, T.; Chluba, J.; Lesgourgues, J. Including massive neutrinos in thermal Sunyaev Zeldovich power spectrum and cluster counts analyses. Mon. Not. R. Astron. Soc. 2020, 497, 1332–1347. [Google Scholar] [CrossRef]
- Sahlén, M. Cluster-Void Degeneracy Breaking: Neutrino Properties and Dark Energy. Phys. Rev. D 2019, 99, 063525. [Google Scholar] [CrossRef] [Green Version]
- Bayer, A.E.; Villaescusa-Navarro, F.; Massara, E.; Liu, J.; Spergel, D.N.; Verde, L.; Wandelt, B.D.; Viel, M.; Ho, S. Detecting Neutrino Mass by Combining Matter Clustering, Halos, and Voids. Astrophys. J. 2021, 919, 24. [Google Scholar] [CrossRef]
- Weltman, A.; Bull, P.; Camera, S.; Kelley, K.; Padmanabhan, H.; Pritchard, J.; Raccanelli, A.; Riemer-Sørensen, S.; Shao, L.; Andrianomena, S.; et al. Fundamental physics with the Square Kilometre Array. Publ. Astron. Soc. Austral. 2020, 37, e002. [Google Scholar] [CrossRef] [Green Version]
- Whitford, A.M.; Howlett, C.; Davis, T.M. Using peculiar velocity surveys to constrain neutrino masses. arXiv 2021, arXiv:2112.10302. [Google Scholar] [CrossRef]
- Moradinezhad Dizgah, A.; Keating, G.K.; Karkare, K.S.; Crites, A.; Choudhury, S.R. Neutrino Properties with Ground-Based Millimeter-Wavelength Line Intensity Mapping. arXiv 2021, arXiv:2110.00014. [Google Scholar] [CrossRef]
- Wang, L.F.; Zhang, X.N.; Zhang, J.F.; Zhang, X. Impacts of gravitational-wave standard siren observation of the Einstein Telescope on weighing neutrinos in cosmology. Phys. Lett. B 2018, 782, 87–93. [Google Scholar] [CrossRef]
- Zhao, Z.W.; Wang, L.F.; Zhang, J.F.; Zhang, X. Prospects for improving cosmological parameter estimation with gravitational-wave standard sirens from Taiji. Sci. Bull. 2020, 65, 1340–1348. [Google Scholar] [CrossRef]
- Jin, S.J.; He, D.Z.; Xu, Y.; Zhang, J.F.; Zhang, X. Forecast for cosmological parameter estimation with gravitational-wave standard siren observation from the Cosmic Explorer. JCAP 2020, 3, 051. [Google Scholar] [CrossRef] [Green Version]
- Cao, M.D.; Zheng, J.; Qi, J.Z.; Zhang, X.; Zhu, Z.H. A new way to explore cosmological tensions using gravitational waves and strong gravitational lensing. arXiv 2021, arXiv:2112.14564. [Google Scholar]
- Blanchard, A.; Aubourg, E.; Brax, P.; Castander, F.J.; Codis, S.; Escoffier, S.; Dournac, F.; Ferté, A.; Finelli, F.; Fosalba, P.; et al. Gravitation and the Universe from large scale-structures: The GAUSS mission concept Mapping the cosmic web up to the reionization era. Exp. Astron. 2021, 51, 1623–1640. [Google Scholar] [CrossRef]
- Acciarri, R.; et al.; [DUNE Collaboration] Long-Baseline Neutrino Facility (LBNF) and Deep Underground Neutrino Experiment (DUNE): Conceptual Design Report, Volume 2: The Physics Program for DUNE at LBNF. arXiv 2015, arXiv:1512.06148. [Google Scholar]
- Ternes, C.A.; Gariazzo, S.; Hajjar, R.; Mena, O.; Sorel, M.; Tórtola, M. Neutrino mass ordering at DUNE: An extra ν bonus. Phys. Rev. D 2019, 100, 093004. [Google Scholar] [CrossRef] [Green Version]
- An, F.; An, G.; An, Q.; Antonelli, V.; Baussan, E.; Beacom, J.; Bezrukov, L.; Blyth, S.; Brugnera, R.; Avanzini, M.B.; et al. Neutrino Physics with JUNO. J. Phys. G 2016, 43, 030401. [Google Scholar] [CrossRef]
- Betti, M.G.; et al. [PTOLEMY collaboration]. Neutrino physics with the PTOLEMY project: Active neutrino properties and the light sterile case. JCAP 2019, 7, 047. [Google Scholar] [CrossRef] [Green Version]
- Tegmark, M.; Zaldarriaga, M. The Fast Fourier Transform Telescope. Phys. Rev. D 2009, 79, 083530. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakr, Z. A Short Review on the Latest Neutrinos Mass and Number Constraints from Cosmological Observables. Universe 2022, 8, 284. https://doi.org/10.3390/universe8050284
Sakr Z. A Short Review on the Latest Neutrinos Mass and Number Constraints from Cosmological Observables. Universe. 2022; 8(5):284. https://doi.org/10.3390/universe8050284
Chicago/Turabian StyleSakr, Ziad. 2022. "A Short Review on the Latest Neutrinos Mass and Number Constraints from Cosmological Observables" Universe 8, no. 5: 284. https://doi.org/10.3390/universe8050284
APA StyleSakr, Z. (2022). A Short Review on the Latest Neutrinos Mass and Number Constraints from Cosmological Observables. Universe, 8(5), 284. https://doi.org/10.3390/universe8050284





