Wheeler-DeWitt Equation and the Applicability of Crypto-Hermitian Interaction Representation in Quantum Cosmology
Abstract
:1. Introduction
2. Challenge: Quantum Big Bang Problem
2.1. Could the Degeneracy Survive Quantization? Yes, It Could
2.2. Stationary Theory (Non-Hermitian Schrödinger Picture, NSP)
2.3. Stationary Wheeler-DeWitt Equation
3. Fine-Tuned Nature of the Quantum Big Bang
3.1. The N-Grid-Point Toy Model of Kinematics
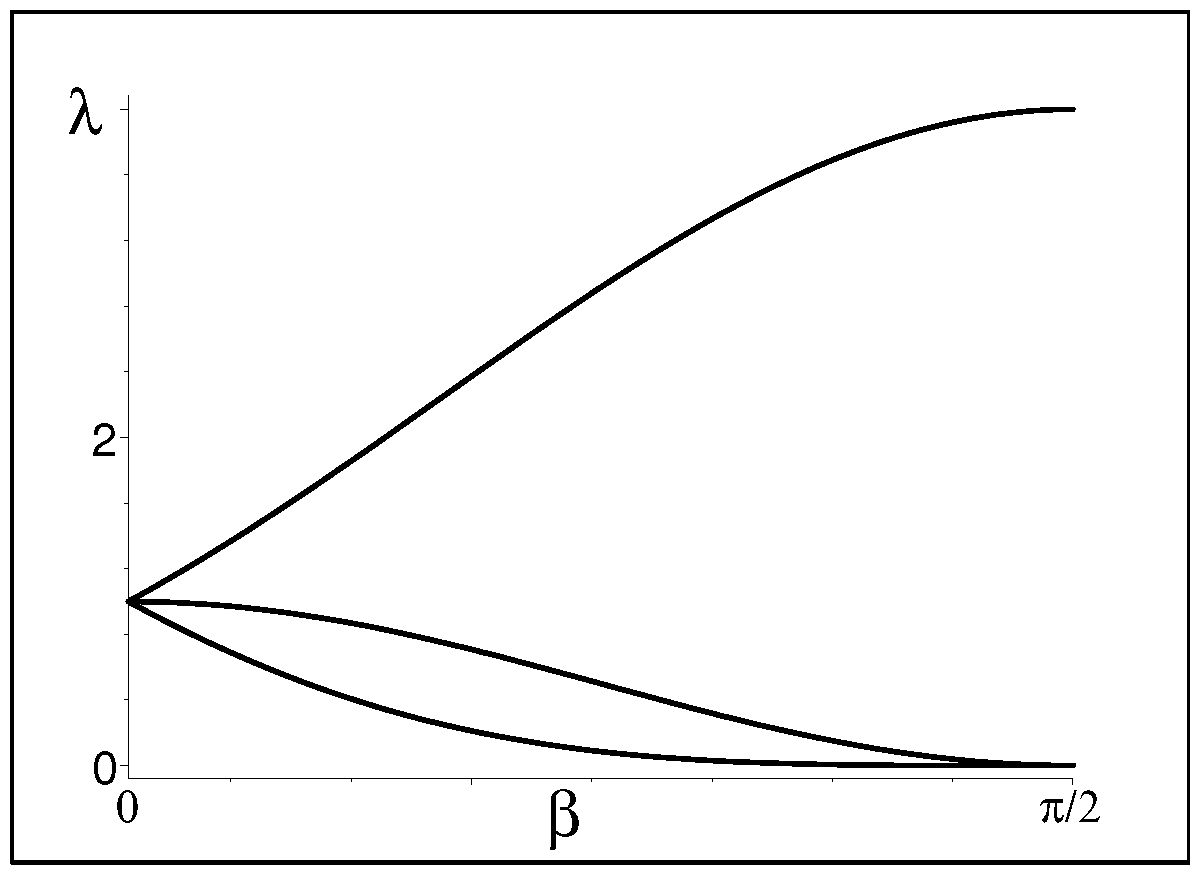
3.2. The Fine-Tuned Nature of the Hilbert-Space Metric
3.2.1. The Eligible Hilbert-Space Metrics at
3.2.2. and the Requirement of Positivity
3.3. Candidates for the Other Observables
4. Mathematics: Non-Hermitian Interaction Picture (NIP)
4.1. Non-Stationary Quantum Systems
4.1.1. Evolution Law for the NIP Ket Vectors
4.1.2. Evolution Law for the NIP Bra Vectors
4.2. Non-Hermitian Operators in Interaction Picture
4.2.1. Evolution Law for the Density Matrices
4.2.2. The Evolution of Observables
5. The Construction of Non-Stationary WDW Universe Admitting Big Bang
5.1. The Evolution of the WDW Ket Vectors
5.2. The Evolution of the WDW Bra Vectors
5.3. Reconstruction of the Metric from the Generator
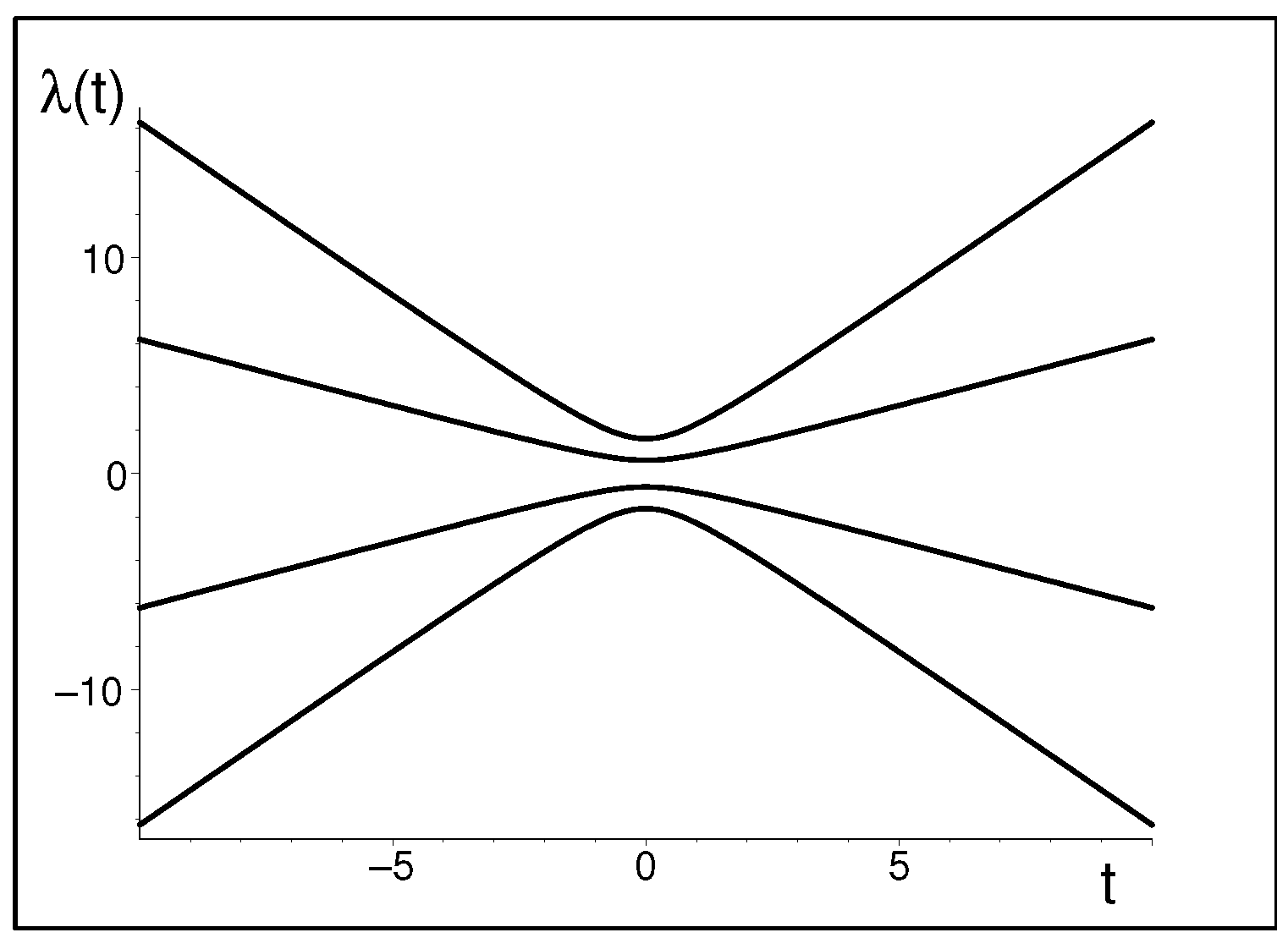
5.3.1. Big Bang Rendered Possible by the Time Dependence of the Metric
5.3.2. The Detailed WDW NIP Recipe
6. Discussion
6.1. The Background Independence Requirement
6.2. Problems with Terminology
6.3. The Danger of an Over-Determination of the Dynamical Input
7. Summary
Funding
Conflicts of Interest
Appendix A. Two Hilbert Spaces in Quantum Mechanics
References
- DeWitt, B.S. Quantum Theory of Gravity. I. The Canonical Theory. Phys. Rev. 1967, 160, 1113–1148. [Google Scholar] [CrossRef] [Green Version]
- Hamber, H.W.; Williams, R.M. Discrete Wheeler-DeWitt Equation. Phys. Rev. 2011, 84, 104033. [Google Scholar] [CrossRef] [Green Version]
- Thiemann, T. Introduction to Modern Canonical Quantum General Relativity; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Rovelli, C.; Smolin, L. Loop space representation of quantum general relativity. Nucl. Phys. B 1990, 331, 80–152. [Google Scholar] [CrossRef]
- Rovelli, C. Quantum Gravity; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ashtekar, A.; Lewandowski, J. Background independent quantum gravity: A status report. Class. Quantum Grav. 2004, 21, R53–R152. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Pseudo-Hermitian Representation of Quantum Mechanics. Int. J. Geom. Meth. Mod. Phys. 2010, 7, 1191–1306. [Google Scholar] [CrossRef] [Green Version]
- Mostafazadeh, A. Quantum mechanics of Klein-Gordon-type fields and quantum cosmology. Ann. Phys. 2004, 309, 1–48. [Google Scholar] [CrossRef] [Green Version]
- Znojil, M. Which operator generates time evolution in Quantum Theory? arXiv 2007, arXiv:0711.0535. [Google Scholar]
- Znojil, M. Time-dependent version of cryptohermitian quantum theory. Phys. Rev. D 2008, 78, 085003. [Google Scholar] [CrossRef] [Green Version]
- Znojil, M. Three-Hilbert-space formulation of Quantum Mechanics. Symm. Integ. Geom. Meth. Appl. SIGMA 2009, 5, 001. [Google Scholar] [CrossRef]
- Znojil, M. Non-Hermitian interaction representation and its use in relativistic quantum mechanics. Ann. Phys. 2017, 385, 162–179. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M. Absence of a singularity in loop quantum cosmology. Phys. Rev. Lett. 2001, 86, 5227–5230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ashtekar, A.; Pawlowski, T.; Singh, P. Quantum nature of the big bang: Improved dynamics. Phys. Rev. D 2006, 74, 084003. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M. Quantum nature of cosmological bounces. Gen. Rel. Grav. 2008, 40, 2659–2683. [Google Scholar] [CrossRef] [Green Version]
- Ashtekar, A.; Corichi, A.; Singh, P. Robustness of key features of loop quantum cosmology. Phys. Rev. D 2008, 77, 024046. [Google Scholar] [CrossRef] [Green Version]
- Malkiewicz, P.; Piechocki, W. Turning Big Bang into Big Bounce: II. Quantum dynamics. Class. Quant. Gravity 2010, 27, 225018. [Google Scholar] [CrossRef] [Green Version]
- Bojowald, M.; Paily, G.M. A no-singularity scenario in loop quantum gravity. Class. Quant. Gravity 2012, 29, 242002. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.-S.; Zhang, C.; Ma, Y.-G. Loop quantum cosmology from an alternative Hamiltonian. Phys. Rev. D 2019, 100, 064026. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Stankiewicz, M. Quantization of time and the big bang via scale-invariant loop gravity. Phys. Lett. B 2020, 800, 135106. [Google Scholar] [CrossRef]
- Messiah, A. Quantum Mechanics; North Holland: Amsterdam, The Netherlands, 1961. [Google Scholar]
- Scholtz, F.G.; Geyer, H.B.; Hahne, F.J.W. Quasi-Hermitian Operators in Quantum Mechanics and the Variational Principle. Ann. Phys. 1992, 213, 74–101. [Google Scholar] [CrossRef]
- Bagarello, F.; Gazeau, J.-P.; Szafraniec, F.; Znojil, M. (Eds.) Non-Selfadjoint Operators in Quantum Physics: Mathematical Aspects; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Bender, C.M. PT Symmetry in Quantum and Classical Physics; World Scientific: Singapore, 2018. [Google Scholar]
- Znojil, M. Feasibility and method of multi-step Hermitization of crypto-Hermitian quantum Hamiltonians. Eur. Phys. J. Plus 2022, 137, 335. [Google Scholar] [CrossRef]
- Rovelli, C.; Smolin, L. Discreteness of area and volume in quantum gravity. Nucl. Phys. B 1995, 442, 593–619. [Google Scholar] [CrossRef] [Green Version]
- Thiemann, T. A length operator for canonical quantum gravity. J. Math. Phys. 1998, 39, 3372–3392. [Google Scholar] [CrossRef] [Green Version]
- Znojil, M. Quantum Big Bang without fine-tuning in a toy-model. J. Phys. Conf. Ser. 2012, 343, 012136. [Google Scholar] [CrossRef] [Green Version]
- Znojil, M. Quantization of Big Bang in crypto-Hermitian Heisenberg picture. In Non-Hermitian Hamiltonians Quantum Physics; Bagarello, F., Passante, R., Trapani, C., Eds.; Springer: Cham, Switzerland, 2016; Volume 184, pp. 383–399. [Google Scholar]
- Brody, D.C.; Hughston, L.P. Quantum measurement of space-time events. J. Phys. A Math. Theor. 2021, 54, 235304. [Google Scholar] [CrossRef]
- Kato, T. Perturbation Theory for Linear Operators; Springer: Berlin/Heidelberg, Germany, 1966. [Google Scholar]
- Znojil, M. Parity-time symmetry and the toy models of gain-loss dynamics near the real Kato’s exceptional points. Symmetry 2016, 8, 52. [Google Scholar] [CrossRef] [Green Version]
- Styer, D.F.; Balkin, M.S.; Becker, K.M.; Burns, M.R.; Dudley, C.E.; Forth, S.T.; Gaumer, J.S.; Kramer, M.A.; Oertel, D.C.; Park, L.H.; et al. Nine formulations of quantum mechanics. Am. J. Phys. 2002, 70, 288–297. [Google Scholar] [CrossRef] [Green Version]
- Moiseyev, N. Non-Hermitian Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Feshbach, H.; Villars, F. Elementary relativistic wave mechanics of spin 0 and spin 1/2 particles. Rev. Mod. Phys. 1958, 30, 24–45. [Google Scholar] [CrossRef]
- Znojil, M. Relativistic supersymmetric quantum mechanics based on Klein-Gordon equation. J. Phys. A Math. Gen. 2004, 37, 9557–9571. [Google Scholar] [CrossRef] [Green Version]
- Pauli, W.; Weisskopf, V. Uber die Quantisierung der skalaren relativistischen Wellengleichung. Helv. Phys. Acta 1934, 7, 709–731. [Google Scholar]
- Bender, C.M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 2007, 70, 947–1118. [Google Scholar] [CrossRef] [Green Version]
- Mostafazadeh, A. Hilbert space structures on the solution space of Klein-Gordon type evolution equations. Class. Quant. Grav. 2003, 20, 155–171. [Google Scholar] [CrossRef] [Green Version]
- Gielen, S.; Turok, N. Perfect Quantum Cosmological Bounce. Phys. Rev. Lett. 2016, 117, 021301. [Google Scholar] [CrossRef] [Green Version]
- Ashtekar, A.; Bianchi, E. A short review of loop quantum gravity. Rep. Prog. Phys. 2021, 84, 042001. [Google Scholar] [CrossRef] [PubMed]
- Znojil, M. Quantum inner-product metrics via recurrent solution of Dieudonne equation. J. Phys. A Math. Theor. 2012, 45, 085302. [Google Scholar] [CrossRef] [Green Version]
- Znojil, M. Tridiagonal PT-symmetric N by N Hamiltonians and a fine-tuning of their observability domains in the strongly non-Hermitian regime. J. Phys. A Math. Theor. 2007, 40, 13131–13148. [Google Scholar] [CrossRef] [Green Version]
- Znojil, M. Maximal couplings in PT-symmetric chain-models with the real spectrum of energies. J. Phys. A Math. Theor. 2007, 40, 4863–4875. [Google Scholar] [CrossRef] [Green Version]
- Znojil, M. N-site-lattice analogues of V(x) = ix3. Ann. Phys. 2012, 327, 893–913. [Google Scholar] [CrossRef] [Green Version]
- Znojil, M. On the role of the normalization factors κn and of the pseudo-metric P in crypto-Hermitian quantum models. Symm. Integ. Geom. Meth. Appl. SIGMA 2008, 4, 001. [Google Scholar] [CrossRef] [Green Version]
- Znojil, M. Non-Hermitian Heisenberg representation. Phys. Lett. A 2015, 379, 2013–2017. [Google Scholar] [CrossRef] [Green Version]
- Miao, Y.-G.; Xu, Z.-M. Investigation of non-Hermitian Hamiltonians in the Heisenberg Picture. Phys. Lett. A 2016, 380, 1805–1810. [Google Scholar] [CrossRef] [Green Version]
- Fring, A.; Moussa, M.H.Y. Unitary quantum evolution for time-dependent quasi-Hermitian systems with non-observable Hamiltonians. Phys. Rev. A 2016, 93, 042114. [Google Scholar] [CrossRef] [Green Version]
- Luiz, F.S.; Pontes, M.A.; Moussa, M.H.Y. Unitarity of the time-evolution and observability of non-Hermitian Hamiltonians for time-dependent Dyson maps. arXiv 2016, arXiv:1611.08286. [Google Scholar] [CrossRef] [Green Version]
- Gong, J.-B.; Wang, Q.-H. Time-dependent PT-symmetric quantum mechanics. J. Phys. A Math. Theor. 2013, 46, 485302. [Google Scholar] [CrossRef] [Green Version]
- Bíla, H. Non-Hermitian Operators in Quantum Physics. Ph.D. Thesis, Charles University, Prague, Czech Republic, 2008. [Google Scholar]
- Bíla, H. Adiabatic time-dependent metrics in PT-symmetric quantum theories. arXiv 2009, arXiv:0902.0474. [Google Scholar]
- Fring, A.; Frith, T. Exact analytical solutions for time-dependent Hermitian Hamiltonian systems from static unobservable non-Hermitian Hamiltonians. Phys. Rev. A 2017, 95, 010102(R). [Google Scholar] [CrossRef] [Green Version]
- Znojil, M. Crypto-unitary forms of quantum evolution operators. Int. J. Theor. Phys. 2013, 52, 2038. [Google Scholar] [CrossRef] [Green Version]
- Znojil, M. Passage through exceptional point: Case study. Proc. Roy. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20190831. [Google Scholar] [CrossRef] [Green Version]
- Znojil, M. Horizons of stability. J. Phys. A Math. Theor. 2008, 41, 44027. [Google Scholar] [CrossRef]
- Mostafazadeh, A.; Batal, A. Physical Aspects of Pseudo-Hermitian and PT-Symmetric Quantum Mechanics. J. Phys. A Math. Gen. 2004, 37, 11645–11679. [Google Scholar] [CrossRef] [Green Version]
- Dieudonne, J. Quasi-Hermitian operators. In Proceedings of the International Symposium on Linear Spaces; Pergamon: Oxford, UK, 1961; pp. 115–122. [Google Scholar]
- Smilga, A.V. Cryptogauge symmetry and cryptoghosts for crypto-Hermitian Hamiltonians. J. Phys. A Math. Theor. 2008, 41, 244026. [Google Scholar] [CrossRef]
- Znojil, M.; Semorádová, I.; Rŭžička, F.; Moulla, H.; Leghrib, I. Problem of the coexistence of several non-Hermitian observables in PT-symmetric quantum mechanics. Phys. Rev. A 2017, 95, 042122. [Google Scholar] [CrossRef] [Green Version]
- Krejčiřík, D.; Lotoreichik, V.; Znojil, M. The minimally anisotropic metric operator in quasi-hermitian quantum mechanics. Proc. Roy. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20180264. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brody, D.C.; Hughston, L.P. Geometric quantum mechanics. J. Geom. Phys. 2001, 38, 19–53. [Google Scholar] [CrossRef] [Green Version]
- Stone, M.H. On one-parameter unitary groups in Hilbert Space. Ann. Math. 1932, 33, 643–648. [Google Scholar] [CrossRef]
- Dyson, F.J. General Theory of Spin-Wave Interactions. Phys. Rev. 1956, 102, 1217. [Google Scholar] [CrossRef]
- Bishop, R.F.; Znojil, M. The coupled-cluster approach to quantum many-body problem in a three-Hilbert-space reinterpretation. Acta Polytech. 2014, 54, 85–92. [Google Scholar] [CrossRef] [Green Version]
- Znojil, M. The cryptohermitian smeared-coordinate representation of wave functions. Phys. Lett. A 2011, 375, 3176–3183. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Znojil, M. Wheeler-DeWitt Equation and the Applicability of Crypto-Hermitian Interaction Representation in Quantum Cosmology. Universe 2022, 8, 385. https://doi.org/10.3390/universe8070385
Znojil M. Wheeler-DeWitt Equation and the Applicability of Crypto-Hermitian Interaction Representation in Quantum Cosmology. Universe. 2022; 8(7):385. https://doi.org/10.3390/universe8070385
Chicago/Turabian StyleZnojil, Miloslav. 2022. "Wheeler-DeWitt Equation and the Applicability of Crypto-Hermitian Interaction Representation in Quantum Cosmology" Universe 8, no. 7: 385. https://doi.org/10.3390/universe8070385
APA StyleZnojil, M. (2022). Wheeler-DeWitt Equation and the Applicability of Crypto-Hermitian Interaction Representation in Quantum Cosmology. Universe, 8(7), 385. https://doi.org/10.3390/universe8070385





