Cosmology from Strong Interactions
Abstract
:1. Introduction and Historical Perspective
2. The Phase Transitions in the Early Universe
2.1. The Phase Transitions in the Standard Model
2.2. Creation of Primordial Black Holes during the Phase Transitions
2.3. Perturbative and Strongly Coupled Regimes of QCD
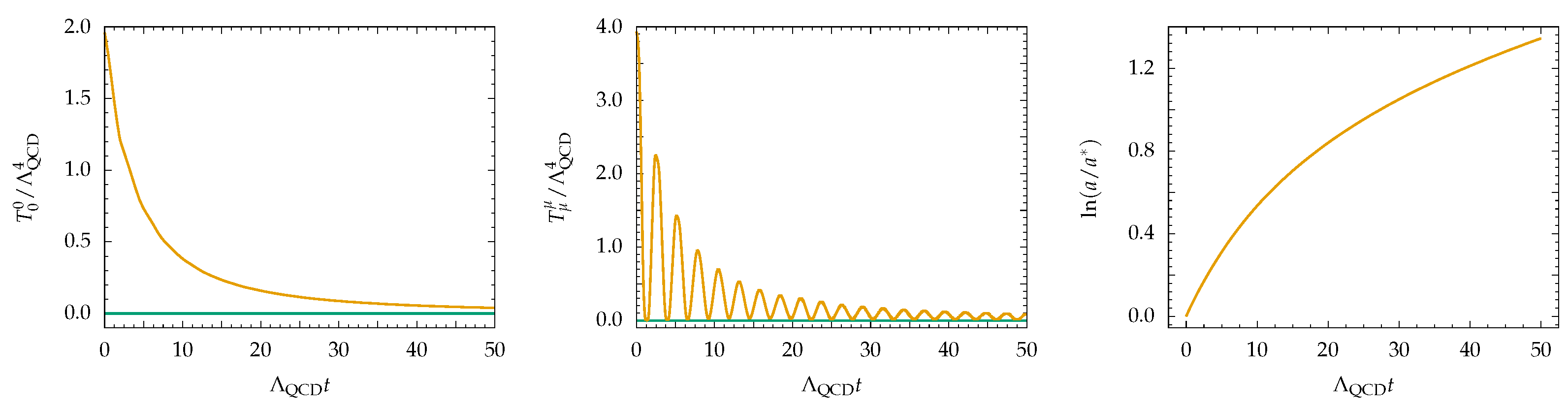
2.4. QCD at High Parton Densities and Saturation
2.5. The Running Couplings of the Standard Model and Their Unification
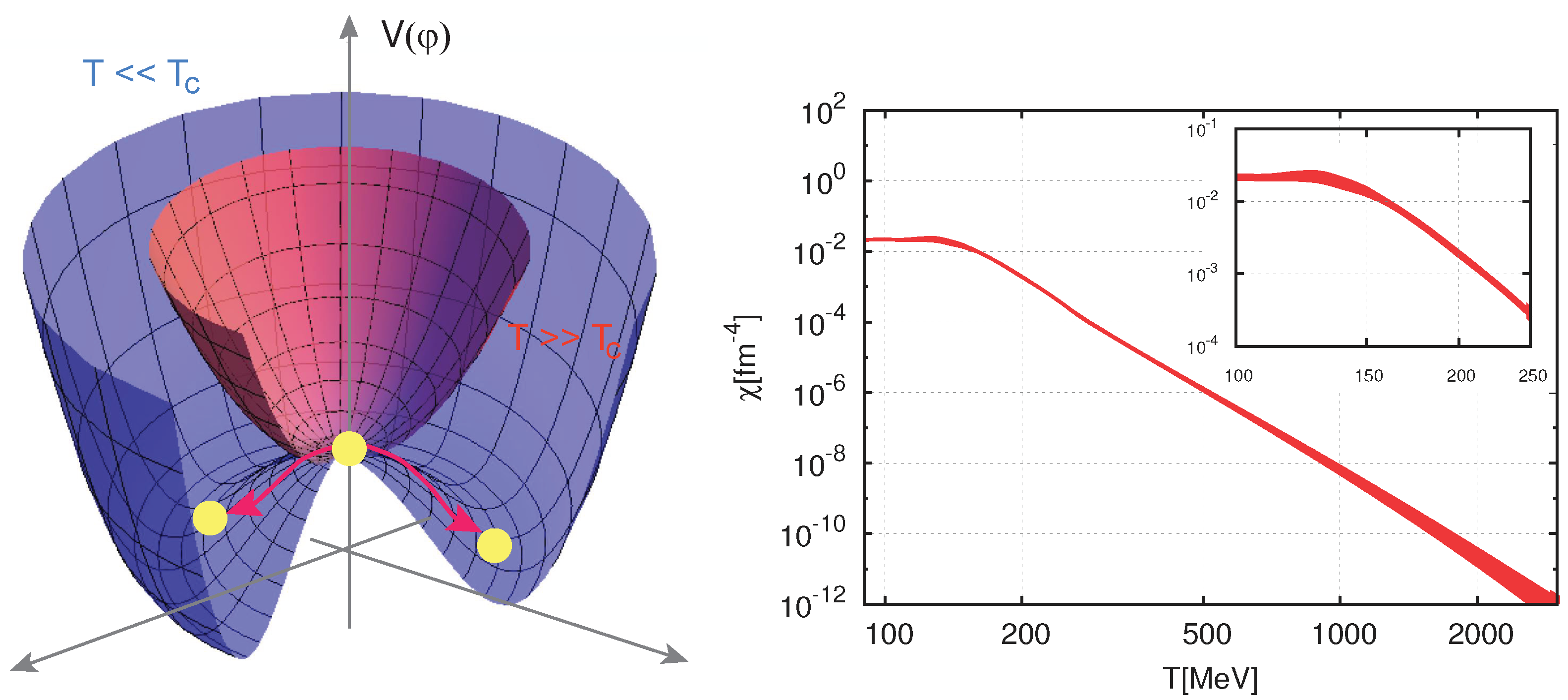
2.6. Axions
3. Dynamics of the Early Universe
3.1. Simple Models with Constant Speed of Sound
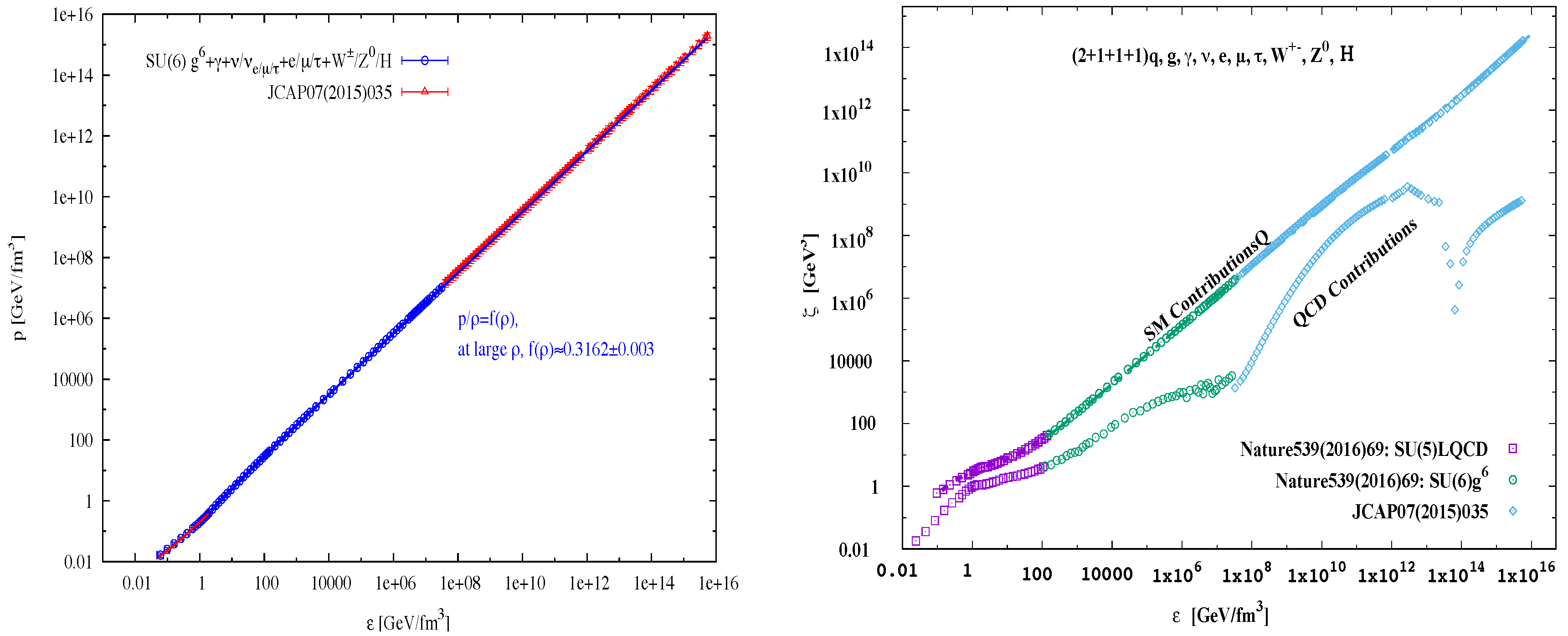
3.2. Equation of State of the Early Universe
3.3. Hydrodynamical Description of Dissipative Effects and the Early Universe
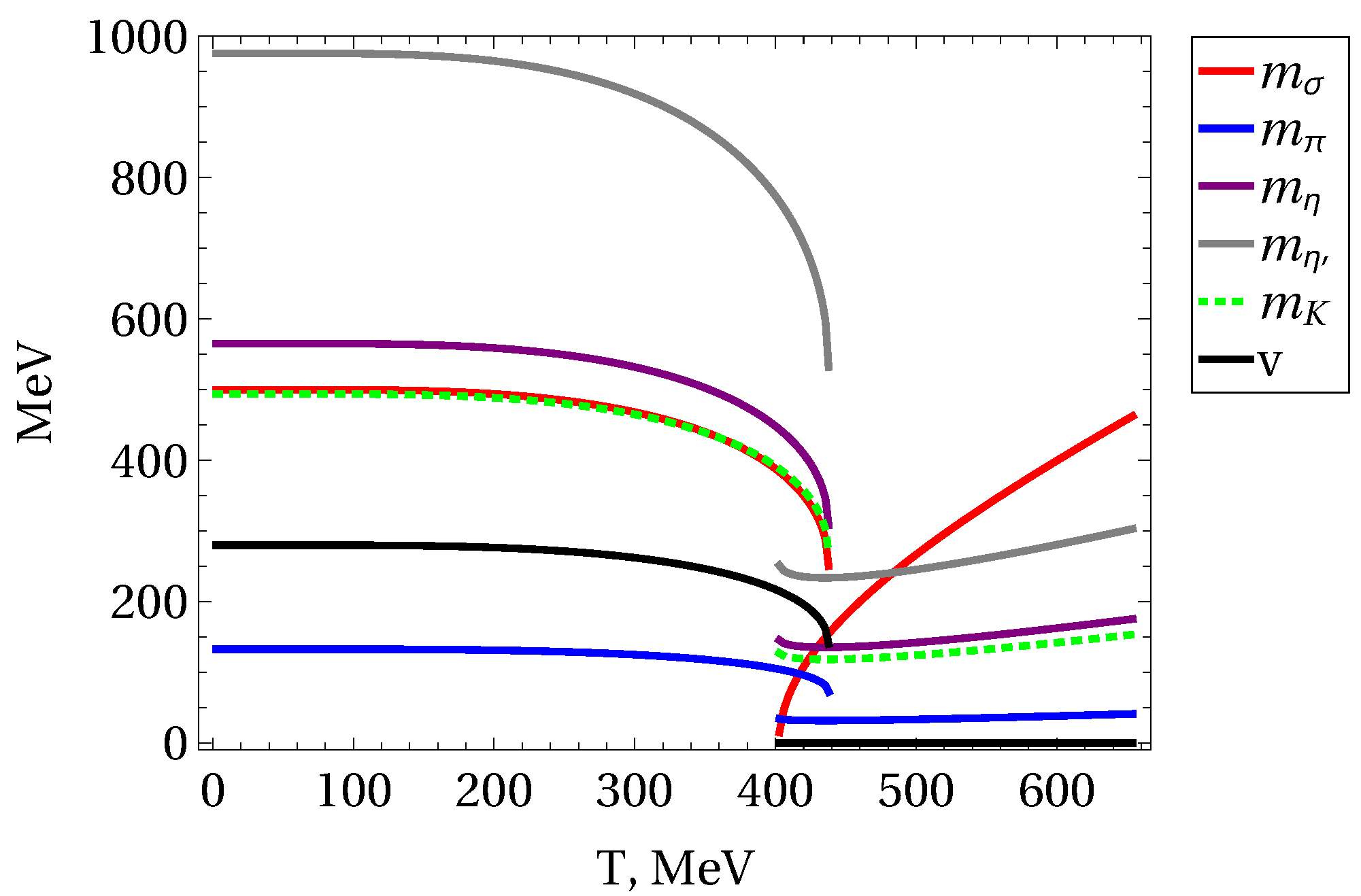
3.4. Theory of Hot Meson Plasma Interacting with the QCD Vacuum
3.5. Cosmological Constant and Vacuum Catastrophe
4. Dynamics of Ground State in YM Theories
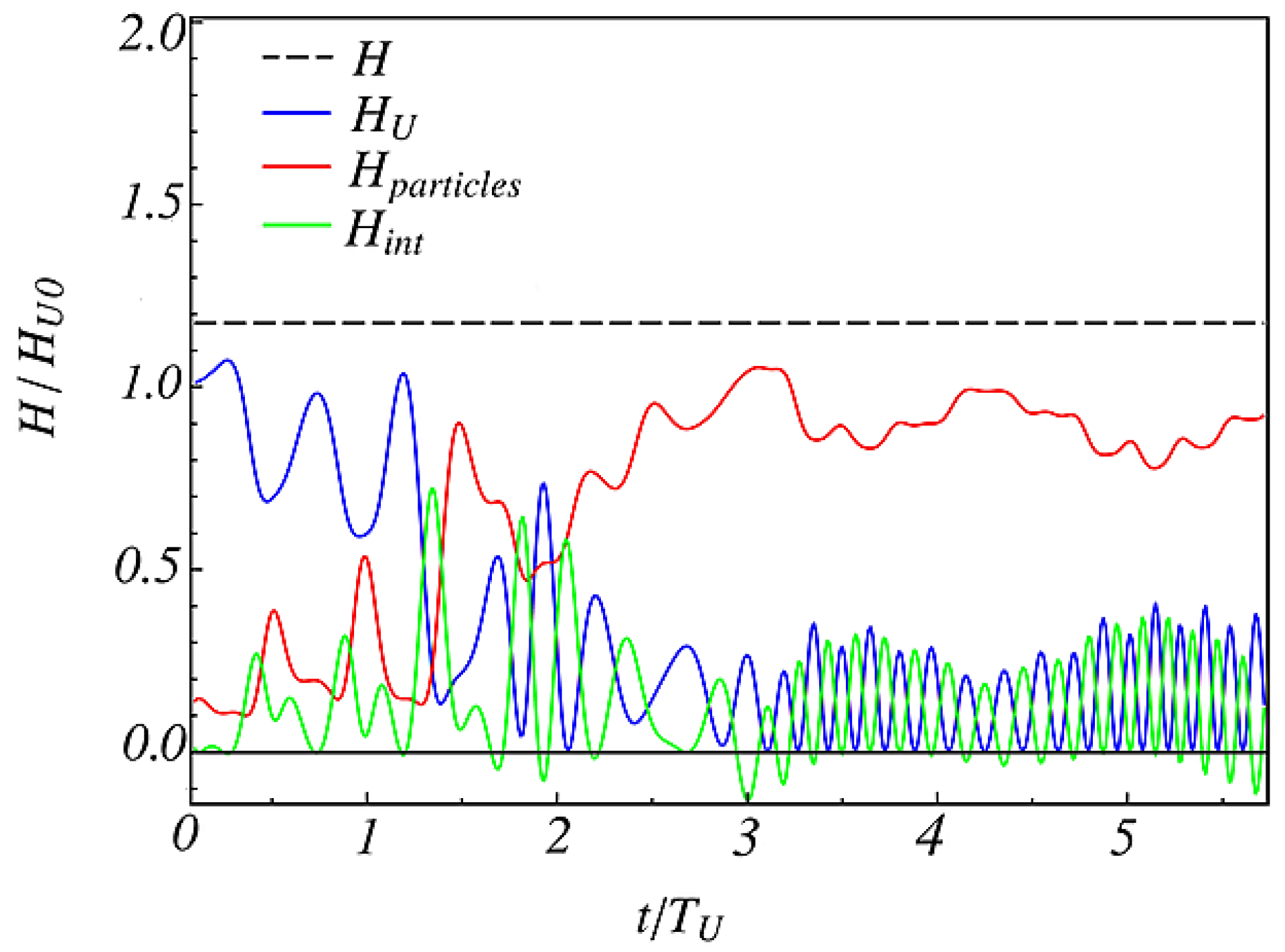
4.1. YM Ground State as a Time Crystal
4.2. Effective Action Approach
4.3. Mirror Symmetry of the Ground-State Solutions
4.4. YM Cosmological Attractors
4.5. SU(N) and the Functional RG Approach
5. Cosmological Implications of Gauge-Fields Driven Inflation
6. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
| 1 | The light cone four-vectors are related to Minkowski four-vectors in a standard way where . The Minkowski dot product in light-cone coordinates is . |
| 2 | In the early universe with , the saturation scale was extremely small. |
| 3 | Let us recall that at the temperatures , most of the gluons are forming the condensate and are thus in the equilibrium but do not participate in two-particle scatterings. |
| 4 | It is worth mentioning that even though a fluid filling a FLRW universe (38) homogeneously is static in the comoving frame , the expanding geometry induces a nonzero fluid expansion rate , where is the determinant of the FLRW metric tensor with . |
| 5 | One of the authors (M.Š.) would like to thank Petr Jizba for pointing out this analogy. |
| 6 | By means of the following ansatz: , the equation for the scale factor can be rewritten as
The scale factor is therefore found in terms of the integral of the solution for as
|
| 7 | For the case of the simple background considered in Section 4.4, , then . |
References
- Shuryak, E.V. Quantum Chromodynamics and the Theory of Superdense Matter. Phys. Rep. 1980, 61, 71–158. [Google Scholar] [CrossRef]
- Kapusta, J.; Muller, B.; Rafelski, J. Quark-Gluon Plasma: Theoretical Foundations; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Polyakov, A.M. Thermal Properties of Gauge Fields and Quark Liberation. Phys. Lett. B 1978, 72, 477–480. [Google Scholar] [CrossRef]
- Olive, K.A. The Thermodynamics of the Quark—Hadron Phase Transition in the Early Universe. Nucl. Phys. B 1981, 190, 483–503. [Google Scholar] [CrossRef]
- Witten, E. Cosmic Separation of Phases. Phys. Rev. D 1984, 30, 272–285. [Google Scholar] [CrossRef]
- Ornik, U.; Weiner, R.M. Expansion of the Early Universe and the Equation of State. Phys. Rev. D 1987, 36, 1263. [Google Scholar] [CrossRef]
- Busza, W.; Rajagopal, K.; van der Schee, W. Heavy Ion Collisions: The Big Picture, and the Big Questions. Ann. Rev. Nucl. Part. Sci. 2018, 68, 339–376. [Google Scholar] [CrossRef]
- Pasechnik, R.; Šumbera, M. Phenomenological Review on Quark–Gluon Plasma: Concepts vs. Observations. Universe 2017, 3, 7. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. The Equation of State of Hot, Dense Matter and Neutron Stars. Phys. Rep. 2016, 621, 127–164. [Google Scholar] [CrossRef]
- Shuryak, E. Strongly coupled quark-gluon plasma in heavy ion collisions. Rev. Mod. Phys. 2017, 89, 035001. [Google Scholar] [CrossRef]
- Yagi, K.; Hatsuda, T.; Miake, Y. Quark-Gluon Plasma: From Big Bang to Little Bang; Cambridge University Press: Cambridge, UK, 2005; Volume 23. [Google Scholar]
- Boyanovsky, D.; de Vega, H.J.; Schwarz, D.J. Phase transitions in the early and the present universe. Ann. Rev. Nucl. Part. Sci. 2006, 56, 441–500. [Google Scholar] [CrossRef] [Green Version]
- Sanches, S.M.; Navarra, F.S.; Fogaça, D.A. The quark gluon plasma equation of state and the expansion of the early Universe. Nucl. Phys. A 2015, 937, 1–16. [Google Scholar] [CrossRef]
- Zhitnitsky, A.R. Dynamical de Sitter phase and nontrivial holonomy in strongly coupled gauge theories in an expanding universe. Phys. Rev. D 2015, 92, 043512. [Google Scholar] [CrossRef]
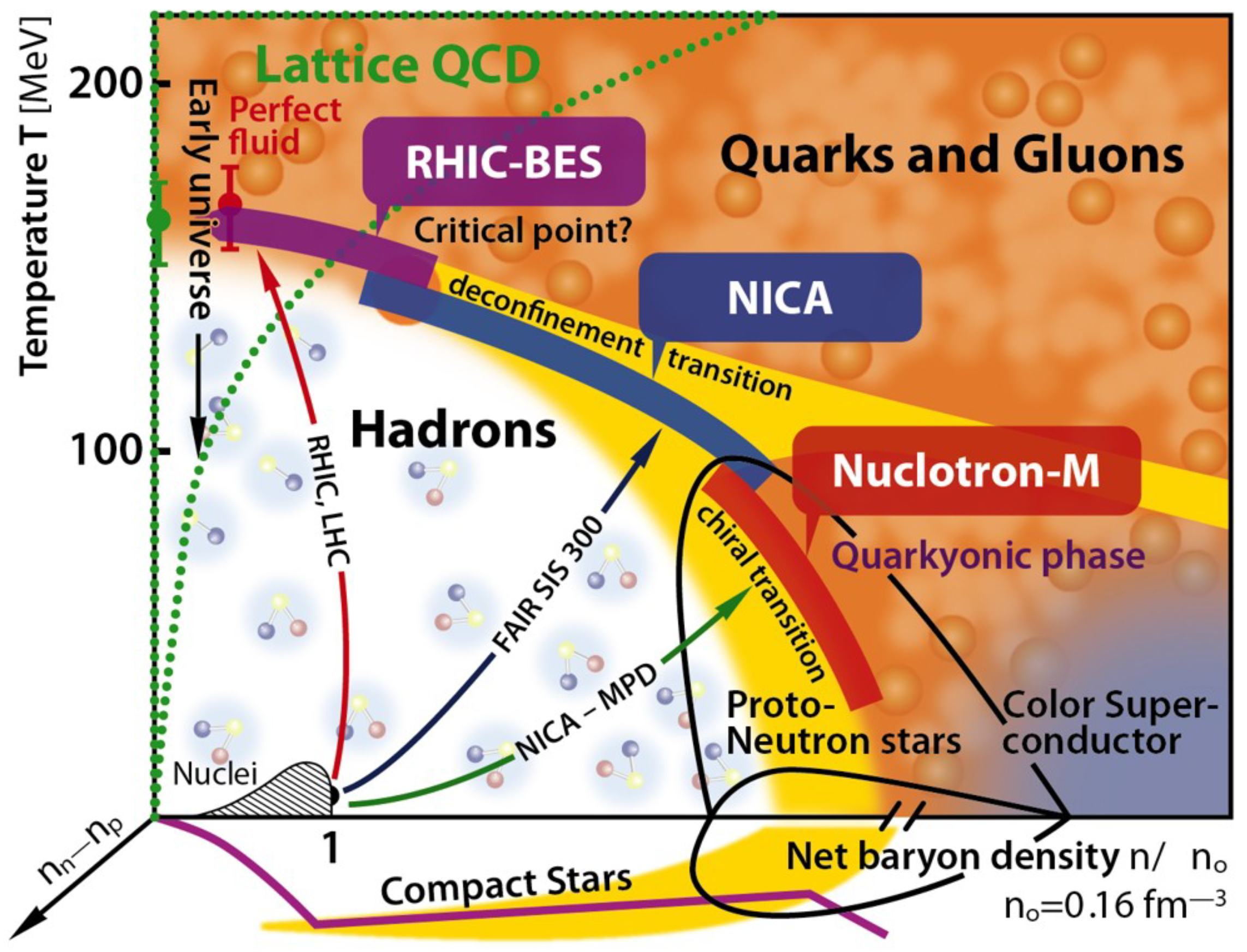
- Braun-Munzinger, P.; Wambach, J. The Phase Diagram of Strongly-Interacting Matter. Rev. Mod. Phys. 2009, 81, 1031–1050. [Google Scholar] [CrossRef]
- McInnes, B. Trajectory of the cosmic plasma through the quark matter phase diagram. Phys. Rev. D 2016, 93, 043544. [Google Scholar] [CrossRef]
- Campbell, J.; Huston, J.; Krauss, F. The Black Book of Quantum Chromodynamics: A Primer for the LHC Era; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Fodor, Z.; Hoelbling, C. Light Hadron Masses from Lattice QCD. Rev. Mod. Phys. 2012, 84, 449. [Google Scholar] [CrossRef]
- Bazavov, A.; Ding, H.-T.; Hegde, P.; Kaczmarek, O.; Karsch, F.; Laermann, E.; Maezawa, Y.; Swagato Mukherjee, H.; Ohno, P.; Petreczky, H.; et al. The QCD Equation of State to O(μB6) from Lattice QCD. Phys. Rev. D 2017, 95, 054504. [Google Scholar] [CrossRef]
- Philipsen, O. Constraining the phase diagram of QCD at finite temperature and density. PoS 2019, 363, 273. [Google Scholar] [CrossRef]
- Shuryak, E. Lectures on nonperturbative QCD (Nonperturbative Topological Phenomena in QCD and Related Theories). arXiv 2018, arXiv:hep-ph/1812.01509. [Google Scholar]
- Pasechnik, R.; Šumbera, M. Different faces of confinement. Universe 2021, 7, 9. [Google Scholar] [CrossRef]
- Poggio, E.C.; Quinn, H.R.; Weinberg, S. Smearing the Quark Model. Phys. Rev. D 1976, 13, 1958. [Google Scholar] [CrossRef]
- Shifman, M.A. Quark hadron duality. In Proceedings of the 8th International Symposium on Heavy Flavor Physics, Southampton, UK, 25–29 July 1999; World Scientific: Singapore, 2000; Volume 3, pp. 1447–1494. [Google Scholar] [CrossRef] [Green Version]
- Romatschke, P.; Romatschke, U. Relativistic Fluid Dynamics In and Out of Equilibrium; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef]
- Lundberg, T.; Pasechnik, R. Thermal Field Theory in real-time formalism: Concepts and applications for particle decays. Eur. Phys. J. A 2021, 57, 71. [Google Scholar] [CrossRef]
- Hofmann, R. The Thermodynamics of Quantum Yang-Mills Theory; World Scientific: Singapore, 2011. [Google Scholar] [CrossRef]
- Aarts, G. Introductory lectures on lattice QCD at nonzero baryon number. J. Phys. Conf. Ser. 2016, 706, 022004. [Google Scholar] [CrossRef]
- Itoh, N. Hydrostatic Equilibrium of Hypothetical Quark Stars. Prog. Theor. Phys. 1970, 44, 291. [Google Scholar] [CrossRef]
- Ivanenko, D.D.; Kurdgelaidze, D.F. Hypothesis concerning quark stars. Astrophysics 1965, 1, 251–252. [Google Scholar] [CrossRef]
- Gross, D.J.; Wilczek, F. Ultraviolet Behavior of Nonabelian Gauge Theories. Phys. Rev. Lett. 1973, 30, 1343–1346. [Google Scholar] [CrossRef]
- Politzer, H.D. Reliable Perturbative Results for Strong Interactions? Phys. Rev. Lett. 1973, 30, 1346–1349. [Google Scholar] [CrossRef]
- Collins, J.C.; Perry, M.J. Superdense Matter: Neutrons Or Asymptotically Free Quarks? Phys. Rev. Lett. 1975, 34, 1353. [Google Scholar] [CrossRef]
- Cabibbo, N.; Parisi, G. Exponential Hadronic Spectrum and Quark Liberation. Phys. Lett. B 1975, 59, 67–69. [Google Scholar] [CrossRef]
- Shuryak, E.V. Theory of Hadronic Plasma. Sov. Phys. JETP 1978, 47, 212–219. [Google Scholar]
- Shuryak, E.V. Quark-Gluon Plasma and Hadronic Production of Leptons, Photons and Psions. Phys. Lett. B 1978, 78, 150. [Google Scholar] [CrossRef]
- Freedman, B.A.; McLerran, L.D. Fermions and Gauge Vector Mesons at Finite Temperature and Density. 3. The Ground State Energy of a Relativistic Quark Gas. Phys. Rev. D 1977, 16, 1169. [Google Scholar] [CrossRef]
- Kapusta, J.I. Quantum Chromodynamics at High Temperature. Nucl. Phys. B 1979, 148, 461–498. [Google Scholar] [CrossRef]
- Ichimaru, S. Strongly coupled plasmas: High-density classical plasmas and degenerate electron liquids. Rev. Mod. Phys. 1982, 54, 1017–1059. [Google Scholar] [CrossRef]
- Braun-Munzinger, P.; Koch, V.; Schäfer, T.; Stachel, J. Properties of hot and dense matter from relativistic heavy ion collisions. Phys. Rep. 2016, 621, 76–126. [Google Scholar] [CrossRef]
- Fukushima, K.; Hatsuda, T. The phase diagram of dense QCD. Rep. Prog. Phys. 2011, 74, 014001. [Google Scholar] [CrossRef]
- Barrois, B.C. Superconducting Quark Matter. Nucl. Phys. B 1977, 129, 390–396. [Google Scholar] [CrossRef]
- Bailin, D.; Love, A. Superfluidity and Superconductivity in Relativistic Fermion Systems. Phys. Rep. 1984, 107, 325. [Google Scholar] [CrossRef]
- Ivanenko, D.; Kurdgelaidze, D.F. Remarks on quark stars. Lett. Nuovo Cim. 1969, 2, 13–16. [Google Scholar] [CrossRef]
- Alford, M.G.; Rajagopal, K.; Wilczek, F. Color flavor locking and chiral symmetry breaking in high density QCD. Nucl. Phys. B 1999, 537, 443–458. [Google Scholar] [CrossRef] [Green Version]
- Becker, W. Neutron Stars and Pulsars; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- McLerran, L.; Pisarski, R.D. Phases of cold, dense quarks at large N(c). Nucl. Phys. A 2007, 796, 83–100. [Google Scholar] [CrossRef]
- McLerran, L.; Reddy, S. Quarkyonic Matter and Neutron Stars. Phys. Rev. Lett. 2019, 122, 122701. [Google Scholar] [CrossRef] [PubMed]
- Migdal, A.B. Pion Fields in Nuclear Matter. Rev. Mod. Phys. 1978, 50, 107–172. [Google Scholar] [CrossRef]
- Pisarski, R.D.; Rennecke, F. Signatures of Moat Regimes in Heavy-Ion Collisions. Phys. Rev. Lett. 2021, 127, 152302. [Google Scholar] [CrossRef] [PubMed]
- Tejeda-Yeomans, M.E. Heavy-ion physics: Freedom to do hot, dense, exciting QCD. CERN Yellow Rep. Sch. Proc. 2021, 2, 137. [Google Scholar] [CrossRef]
- Arsene, I.; Beardeng, I.G.; Beavisa, D.; Besliuj, C.; Budickf, B.; Bøggildg, H.; Chasmana, C.; Christenseng, C.H.; Christianseng, P.; Ciborc, J.; et al. Quark gluon plasma and color glass condensate at RHIC? The Perspective from the BRAHMS experiment. Nucl. Phys. A 2005, 757, 1–27. [Google Scholar] [CrossRef]
- Back, B.B.; PHOBOS Collaboration. The PHOBOS perspective on discoveries at RHIC. Nucl. Phys. A 2005, 757, 28–101. [Google Scholar] [CrossRef]
- Adams, J.; STAR Collaboration. Experimental and theoretical challenges in the search for the quark gluon plasma: The STAR Collaboration’s critical assessment of the evidence from RHIC collisions. Nucl. Phys. A 2005, 757, 102–183. [Google Scholar] [CrossRef]
- Adcox, K.; PHENIX Collaboration. Formation of dense partonic matter in relativistic nucleus-nucleus collisions at RHIC: Experimental evaluation by the PHENIX collaboration. Nucl. Phys. A 2005, 757, 184–283. [Google Scholar] [CrossRef] [Green Version]
- Aprahamian, A.; Robert, A.; Caines, H.; Cates, G.; Cizewski, G.A.; Cirigliano, V.; Dean, D.J.; Deshpande, A.; Ent, R.; Fahey, F.; et al. Reaching for the Horizon: The 2015 Long Range Plan for Nuclear Science. 2015. Available online: https://inspirehep.net/literature/1398831 (accessed on 27 August 2022).
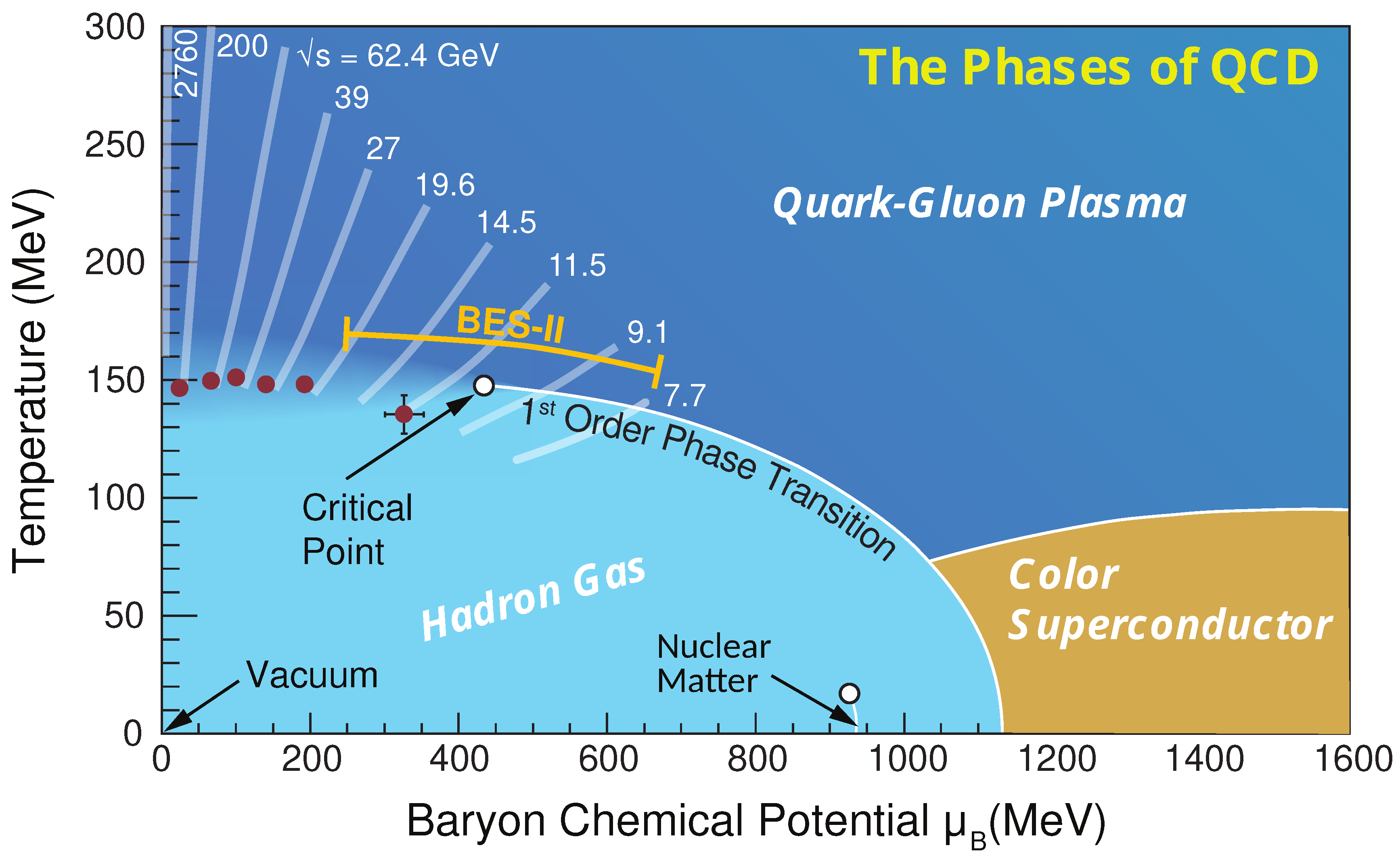
- Bzdak, A.; Esumi, S.; Koch, V.; Liao, J.; Stephanov, M.; Xu, N. Mapping the Phases of Quantum Chromodynamics with Beam Energy Scan. Phys. Rep. 2020, 853, 1–87. [Google Scholar] [CrossRef]
- Wilson, K.G. The renormalization group and critical phenomena. Rev. Mod. Phys. 1983, 55, 583–600. [Google Scholar] [CrossRef]
- Stephanov, M.A.; Rajagopal, K.; Shuryak, E.V. Signatures of the tricritical point in QCD. Phys. Rev. Lett. 1998, 81, 4816–4819. [Google Scholar] [CrossRef]
- Gupta, S.; Luo, X.; Mohanty, B.; Ritter, H.G.; Xu, N. Scale for the Phase Diagram of Quantum Chromodynamics. Science 2011, 332, 1525–1528. [Google Scholar] [CrossRef] [PubMed]
- Sumbera, M. Results from STAR Beam Energy Scan Program. Acta Phys. Polon. Supp. 2013, 6, 429–436. [Google Scholar] [CrossRef]
- Adamczyk, L.; STAR Collaboration. Bulk Properties of the Medium Produced in Relativistic Heavy-Ion Collisions from the Beam Energy Scan Program. Phys. Rev. C 2017, 96, 044904. [Google Scholar] [CrossRef]
- Bellwied, R.; Borsanyi, S.; Fodor, Z.; Günther, J.; Katz, S.D.; Ratti, C.; Szabo, K.K. The QCD phase diagram from analytic continuation. Phys. Lett. B 2015, 751, 559–564. [Google Scholar] [CrossRef]
- Ding, H.T.; Karsch, F.; Mukherjee, S. Thermodynamics of strong-interaction matter from Lattice QCD. Int. J. Mod. Phys. E 2015, 24, 1530007. [Google Scholar] [CrossRef]
- Pasechnik, R.; Beylin, V.; Vereshkov, G. Dark Energy from graviton-mediated interactions in the QCD vacuum. J. Cosmol. Astropart. Phys. 2013, 6, 11. [Google Scholar] [CrossRef]
- Addazi, A.; Marcianò, A.; Pasechnik, R.; Prokhorov, G. Mirror Symmetry of quantum Yang-Mills vacua and cosmological implications. Eur. Phys. J. C 2019, 79, 251. [Google Scholar] [CrossRef]
- Pasechnik, R. Quantum Yang–Mills Dark Energy. Universe 2016, 2, 4. [Google Scholar] [CrossRef]
- Bailin, D.; Love, A. Cosmology in Gauge Field Theory and String Theory; Taylor & Francis: Milton Park, UK, 2004. [Google Scholar]
- Gorbunov, D.S.; Rubakov, V.A. Introduction to the Theory of the Early Universe: Cosmological Perturbations and Inflationary Theory; World Scientific: Singapore, 2011. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rep. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef] [PubMed]
- Bertone, G.; Hooper, D. History of dark matter. Rev. Mod. Phys. 2018, 90, 045002. [Google Scholar] [CrossRef]
- Green, A.M.; Kavanagh, B.J. Primordial Black Holes as a dark matter candidate. J. Phys. G 2021, 48, 043001. [Google Scholar] [CrossRef]
- Addazi, A.; Marcianò, A.; Pasechnik, R. Time-crystal ground state and production of gravitational waves from QCD phase transition. Chin. Phys. C 2019, 43, 065101. [Google Scholar] [CrossRef]
- Yang, C.N.; Mills, R.L. Conservation of Isotopic Spin and Isotopic Gauge Invariance. Phys. Rev. 1954, 96, 191–195. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. 1. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Goldstone, J. Field Theories with Superconductor Solutions. Nuovo Cim. 1961, 19, 154–164. [Google Scholar] [CrossRef]
- Goldstone, J.; Salam, A.; Weinberg, S. Broken Symmetries. Phys. Rev. 1962, 127, 965–970. [Google Scholar] [CrossRef]
- Aad, G.; ATLAS Collaboration. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012, 716, 1–29. [Google Scholar] [CrossRef]
- Chatrchyan, S.; CMS Collaboration. Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC. Phys. Lett. B 2012, 716, 30–61. [Google Scholar] [CrossRef]
- Giacosa, F.; Hofmann, R. Thermal ground state in deconfining Yang-Mills thermodynamics. Prog. Theor. Phys. 2007, 118, 759–767. [Google Scholar] [CrossRef]
- Herbst, U.; Hofmann, R. Asymptotic freedom and compositeness. ISRN High Energy Phys. 2012, 2012, 373121. [Google Scholar] [CrossRef]
- Linde, A.D. Phase Transitions in Gauge Theories and Cosmology. Rep. Prog. Phys. 1979, 42, 389. [Google Scholar] [CrossRef]
- Mukhanov, V. Physical Foundations of Cosmology; Cambridge University Press: Oxford, UK, 2005. [Google Scholar]
- Laine, M.; Vuorinen, A. Basics of Thermal Field Theory; Springer: Berlin/Heidelberg, Germany, 2016; Volume 925. [Google Scholar] [CrossRef]
- Mazumdar, A.; White, G. Review of cosmic phase transitions: Their significance and experimental signatures. Rep. Prog. Phys. 2019, 82, 076901. [Google Scholar] [CrossRef] [PubMed]
- D’Onofrio, M.; Rummukainen, K. Standard model cross-over on the lattice. Phys. Rev. D 2016, 93, 025003. [Google Scholar] [CrossRef]
- Bazavov, A.; HotQCD Collaboration. Chiral crossover in QCD at zero and non-zero chemical potentials. Phys. Lett. B 2019, 795, 15–21. [Google Scholar] [CrossRef]
- Borsanyi, S.; Fodor, Z.; Guenther, J.; Kampert, K.-H.; Katz, S.D.; Kawanai, T.; Kovacs, T.G.; Mages, S.W.; Pasztor, A.; Pittler, F.; et al. Calculation of the axion mass based on high-temperature lattice quantum chromodynamics. Nature 2016, 539, 69–71. [Google Scholar] [CrossRef]
- Laine, M.; Meyer, M. Standard Model thermodynamics across the electroweak crossover. J. Cosmol. Astropart. Phys. 2015, 7, 35. [Google Scholar] [CrossRef]
- Kogut, J.B.; Wyld, H.W.; Karsch, F.; Sinclair, D.K. First Order Chiral Phase Transition in Lattice QCD. Phys. Lett. B 1987, 188, 353–358. [Google Scholar] [CrossRef]
- Aoki, Y.; Endrodi, G.; Fodor, Z.; Katz, S.D.; Szabo, K.K. The Order of the quantum chromodynamics transition predicted by the standard model of particle physics. Nature 2006, 443, 675–678. [Google Scholar] [CrossRef]
- Boeckel, T.; Schettler, S.; Schaffner-Bielich, J. The Cosmological QCD Phase Transition Revisited. Prog. Part. Nucl. Phys. 2011, 66, 266–270. [Google Scholar] [CrossRef]
- Schettler, S.; Boeckel, T.; Schaffner-Bielich, J. Imprints of the QCD Phase Transition on the Spectrum of Gravitational Waves. Phys. Rev. D 2011, 83, 064030. [Google Scholar] [CrossRef]
- Boeckel, T.; Schaffner-Bielich, J. A little inflation in the early universe at the QCD phase transition. Phys. Rev. Lett. 2011, 105, 041301. [Google Scholar] [CrossRef] [PubMed]
- Ayala, A.; Bashir, A.; Cobos-Martinez, J.J.; Hernandez-Ortiz, S.; Raya, A. The effective QCD phase diagram and the critical end point. Nucl. Phys. B 2015, 897, 77–86. [Google Scholar] [CrossRef]
- Cui, Z.F.; Zhang, J.L.; Zong, H.S. Proper time regularization and the QCD chiral phase transition. Sci. Rep. 2017, 7, 45937. [Google Scholar] [CrossRef]
- Burkert, V.D.; Elouadrhiri, L.; Girod, F.X. The pressure distribution inside the proton. Nature 2018, 557, 396–399. [Google Scholar] [CrossRef]
- Diamantini, M.C.; Trugenberger, C.A.; Vinokur, V.M. Confinement and Asymptotic Freedom with Cooper pairs. Commun. Phys. 2018, 1, 77. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Redlich, K.; Stachel, J. Decoding the phase structure of QCD via particle production at high energy. Nature 2018, 561, 321–330. [Google Scholar] [CrossRef]
- Pang, L.G.; Zhou, K.; Su, N.; Petersen, H.; Stöcker, H.; Wang, X.N. An equation-of-state-meter of quantum chromodynamics transition from deep learning. Nat. Commun. 2018, 9, 210. [Google Scholar] [CrossRef]
- Du, Y.L.; Zhou, K.; Steinheimer, J.; Pang, L.G.; Motornenko, A.; Zong, H.S.; Wang, X.N.; Stöcker, H. Identifying the nature of the QCD transition in relativistic collision of heavy nuclei with deep learning. Eur. Phys. J. C 2020, 80, 516. [Google Scholar] [CrossRef]
- Attems, M.; Bea, Y.; Casalderrey-Solana, J.; Mateos, D.; Triana, M.; Zilhão, M. Holographic Collisions across a Phase Transition. Phys. Rev. Lett. 2018, 121, 261601. [Google Scholar] [CrossRef] [PubMed]
- Boiko, V.G.; Jenkovszky, L.L.; Sysoev, V.M. Thermodynamics of phase transitions in nuclear matter. Fiz. Elem. Chast. Atom. Yadra 1991, 22, 675–715. (In Russian) [Google Scholar]
- Bonometto, S.A.; Pantano, O. Physics of the cosmological quark-hadron transition. Phys. Rep. 1993, 228, 175–252. [Google Scholar] [CrossRef]
- Schwarz, D.J. The first second of the universe. Ann. Phys. 2003, 12, 220–270. [Google Scholar] [CrossRef]
- Castorina, P.; Greco, V.; Plumari, S. QCD equation of state and cosmological parameters in the early universe. Phys. Rev. D 2015, 92, 063530. [Google Scholar] [CrossRef]
- Tawfik, A. Cosmological Consequences of QCD Phase Transition(s) in Early Universe. AIP Conf. Proc. 2009, 1115, 239–247. [Google Scholar] [CrossRef]
- Kaczmarek, O.; Karsch, F.; Lahiri, A.; Mazur, L.; Schmidt, C. QCD phase transition in the chiral limit. arXiv 2020, arXiv:2003.07920. [Google Scholar]
- Eidelman, S.; Particle Data Group. Review of particle physics. Particle Data Group. Phys. Lett. B 2004, 592, 1. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Bleicher, M.; Huang, S.L.; Schweda, K.; Stoecker, H.; Xu, N.; Zhuang, P. D anti-D correlations as a sensitive probe for thermalization in high-energy nuclear collisions. Phys. Lett. B 2007, 647, 366–370. [Google Scholar] [CrossRef]
- Hindmarsh, M.B.; Lüben, M.; Lumma, J.; Pauly, M. Phase transitions in the early universe. SciPost Phys. Lect. Notes 2021, 24, 1. [Google Scholar] [CrossRef]
- Weinberg, S. Gauge and Global Symmetries at High Temperature. Phys. Rev. D 1974, 9, 3357–3378. [Google Scholar] [CrossRef]
- Patel, H.H.; Ramsey-Musolf, M.J.; Wise, M.B. Color Breaking in the Early Universe. Phys. Rev. D 2013, 88, 015003. [Google Scholar] [CrossRef]
- Ramsey-Musolf, M.J.; Winslow, P.; White, G. Color Breaking Baryogenesis. Phys. Rev. D 2018, 97, 123509. [Google Scholar] [CrossRef]
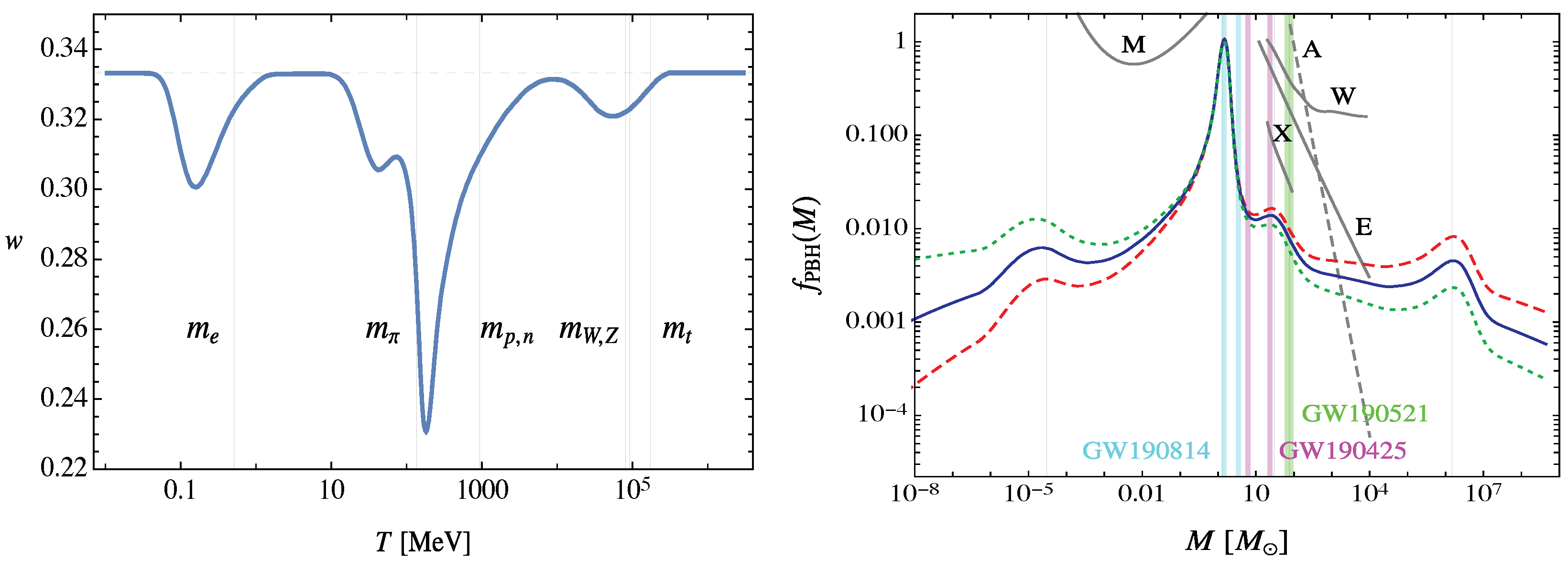
- Byrnes, C.T.; Hindmarsh, M.; Young, S.; Hawkins, M.R.S. Primordial black holes with an accurate QCD equation of state. J. Cosmol. Astropart. Phys. 2018, 8, 41. [Google Scholar] [CrossRef]
- Husdal, L. On Effective Degrees of Freedom in the Early Universe. Galaxies 2016, 4, 78. [Google Scholar] [CrossRef]
- Florkowski, W. The realistic QCD equation of state in relativistic heavy-ion collisions and the early Universe. Nucl. Phys. A 2011, 853, 173–188. [Google Scholar] [CrossRef]
- Guardo, G.L.; Greco, V.; Ruggieri, M. Energy density fluctuations in Early Universe. AIP Conf. Proc. 2014, 1595, 224–227. [Google Scholar] [CrossRef]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Zel’dovich, Y.B.; Novikov, I.D. The Hypothesis of Cores Retarded during Expansion and the Hot Cosmological Model. Sov. Astron. 1967, 10, 602. [Google Scholar]
- Hawking, S. Gravitationally collapsed objects of very low mass. Mon. Not. Roy. Astron. Soc. 1971, 152, 75. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B.P.; LIGO Scientific Collaboration and Virgo Collaboration. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef]
- Carr, B.; Kuhnel, F.; Sandstad, M. Primordial Black Holes as Dark Matter. Phys. Rev. D 2016, 94, 083504. [Google Scholar] [CrossRef]
- Carr, B.; Kuhnel, F. Primordial Black Holes as Dark Matter: Recent Developments. Ann. Rev. Nucl. Part. Sci. 2020, 70, 355–394. [Google Scholar] [CrossRef]
- Biagetti, M.; De Luca, V.; Franciolini, G.; Kehagias, A.; Riotto, A. The formation probability of primordial black holes. Phys. Lett. B 2021, 820, 136602. [Google Scholar] [CrossRef]
- Allahverdi, R.; Osiński, J.K. Early matter domination from long-lived particles in the visible sector. Phys. Rev. D 2022, 105, 023502. [Google Scholar] [CrossRef]
- Carr, B.; Clesse, S.; García-Bellido, J.; Kühnel, F. Cosmic conundra explained by thermal history and primordial black holes. Phys. Dark Univ. 2021, 31, 100755. [Google Scholar] [CrossRef]
- Hung, C.M.; Shuryak, E.V. Hydrodynamics near the QCD phase transition: Looking for the longest lived fireball. Phys. Rev. Lett. 1995, 75, 4003–4006. [Google Scholar] [CrossRef] [PubMed]
- Jedamzik, K. Primordial black hole formation during the QCD epoch. Phys. Rev. D 1997, 55, 5871–5875. [Google Scholar] [CrossRef]
- Jedamzik, K. Could MACHOS be primordial black holes formed during the QCD epoch? Phys. Rep. 1998, 307, 155–162. [Google Scholar] [CrossRef]
- Borsanyi, S.; Endrodi, G.; Fodor, Z.; Jakovac, A.; Katz, S.D.; Krieg, S.; Ratti, C.; Szabo, K.K. The QCD equation of state with dynamical quarks. J. High Energy Phys. 2010, 11, 77. [Google Scholar] [CrossRef] [Green Version]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
- Penrose, R. The Big Bang and its Dark-Matter Content: Whence, Whither, and Wherefore. Found. Phys. 2018, 48, 1177–1190. [Google Scholar] [CrossRef]
- Wysocki, D.; Gerosa, D.; O’Shaughnessy, R.; Belczynski, K.; Gladysz, W.; Berti, E.; Kesden, M.; Holz, D.E. Explaining LIGO’s observations via isolated binary evolution with natal kicks. Phys. Rev. D 2018, 97, 043014. [Google Scholar] [CrossRef]
- Adler, R.J.; Bjorken, J.D.; Chen, P.; Liu, J.S. Simple analytic models of gravitational collapse. Am. J. Phys. 2005, 73, 1148–1159. [Google Scholar] [CrossRef]
- García-Bellido, J.; Carr, B.; Clesse, S. Primordial Black Holes and a Common Origin of Baryons and Dark Matter. Universe 2021, 8, 12. [Google Scholar] [CrossRef]
- Gross, D.J.; Wilczek, F. Asymptotically Free Gauge Theories-I. Phys. Rev. D 1973, 8, 3633–3652. [Google Scholar] [CrossRef]
- CMS Collaboration. Determination of the Strong Coupling Constant from the Measurement of Inclusive Multijet Event Cross Sections in pp Collisions at s = 8 TeV; Technical Report CMS-PAS-SMP-16-008; CERN: Geneva, Switzerland, 2017. [Google Scholar]
- Ghiglieri, J.; Kurkela, A.; Strickland, M.; Vuorinen, A. Perturbative Thermal QCD: Formalism and Applications. Phys. Rep. 2020, 880, 1–73. [Google Scholar] [CrossRef]
- Martin, A.D.; Stirling, W.J.; Thorne, R.S.; Watt, G. Parton distributions for the LHC. Eur. Phys. J. C 2009, 63, 189–285. [Google Scholar] [CrossRef]
- Gelis, F.; Iancu, E.; Jalilian-Marian, J.; Venugopalan, R. The Color Glass Condensate. Ann. Rev. Nucl. Part. Sci. 2010, 60, 463–489. [Google Scholar] [CrossRef]
- Fujii, H.; Kharzeev, D. Long range forces of QCD. Phys. Rev. D 1999, 60, 114039. [Google Scholar] [CrossRef] [Green Version]
- Blaizot, J.P. Weakly and strongly coupled degrees of freedom in the quark-gluon plasma. Acta Phys. Polon. Supp. 2011, 4, 641–646. [Google Scholar] [CrossRef]
- Lacey, R.A.; Ajitanand, N.N.; Alexander, J.M.; Chung, P.; Holzmann, W.G.; Issah, M.; Taranenko, A.; Danielewicz, P.; Stoecker, H. Has the QCD Critical Point been Signaled by Observations at RHIC? Phys. Rev. Lett. 2007, 98, 092301. [Google Scholar] [CrossRef] [PubMed]
- Heinz, U.; Snellings, R. Collective flow and viscosity in relativistic heavy-ion collisions. Ann. Rev. Nucl. Part. Sci. 2013, 63, 123–151. [Google Scholar] [CrossRef]
- Aamodt, K.; ALICE Collaboration. Elliptic flow of charged particles in Pb-Pb collisions at 2.76 TeV. Phys. Rev. Lett. 2010, 105, 252302. [Google Scholar] [CrossRef] [PubMed]
- Aad, G.; ATLAS Collaboration. Measurement of the pseudorapidity and transverse momentum dependence of the elliptic flow of charged particles in lead-lead collisions at sNN=2.76 TeV with the ATLAS detector. Phys. Lett. B 2012, 707, 330–348. [Google Scholar] [CrossRef]
- Chatrchyan, S.; CMS Collaboration. Azimuthal anisotropy of charged particles at high transverse momenta in PbPb collisions at sNN=2.76 TeV. Phys. Rev. Lett. 2012, 109, 022301. [Google Scholar] [CrossRef]
- Gyulassy, M.; Plumer, M. Jet Quenching in Dense Matter. Phys. Lett. B 1990, 243, 432–438. [Google Scholar] [CrossRef]
- Bielčíková, J. Jets and correlations in heavy-ion collisions. PoS 2015, 234, 22. [Google Scholar] [CrossRef]
- Adare, A.; PHENIX Collaboration. Enhanced production of direct photons in Au+Au collisions at sNN=200 GeV and implications for the initial temperature. Phys. Rev. Lett. 2010, 104, 132301. [Google Scholar] [CrossRef]
- Shuryak, E. Physics of Strongly coupled Quark-Gluon Plasma. Prog. Part. Nucl. Phys. 2009, 62, 48–101. [Google Scholar] [CrossRef] [Green Version]
- Thoma, M.H. Complex plasmas as a model for the quark-gluon-plasma liquid. Nucl. Phys. A 2006, 774, 307–314. [Google Scholar] [CrossRef]
- Casalderrey-Solana, J.; Liu, H.; Mateos, D.; Rajagopal, K.; Wiedemann, U.A. Gauge/String Duality, Hot QCD and Heavy Ion Collisions; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 1998, 2, 231–252. [Google Scholar] [CrossRef]
- Susskind, L.; Lindesay, J. An Introduction to Black Holes, Information and the String Theory Revolution: The Holographic Universe; World Scientific: Singapore, 2005. [Google Scholar]
- McGreevy, J. Holographic duality with a view toward many-body physics. Adv. High Energy Phys. 2010, 2010, 723105. [Google Scholar] [CrossRef]
- Altarelli, G.; Parisi, G. Asymptotic Freedom in Parton Language. Nucl. Phys. B 1977, 126, 298–318. [Google Scholar] [CrossRef]
- Dokshitzer, Y.L. Calculation of the Structure Functions for Deep Inelastic Scattering and e+ e- Annihilation by Perturbation Theory in Quantum Chromodynamics. Sov. Phys. JETP 1977, 46, 641–653. [Google Scholar]
- Gribov, V.N.; Lipatov, L.N. Deep inelastic e p scattering in perturbation theory. Sov. J. Nucl. Phys. 1972, 15, 438–450. [Google Scholar]
- Ioffe, B.L.; Fadin, V.S.; Lipatov, L.N. Quantum Chromodynamics: Perturbative and Nonperturbative Aspects; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef]
- Cea, P. The Higgs condensate as a quantum liquid. Int. J. Theor. Phys. 2020, 59, 3310–3323. [Google Scholar] [CrossRef]
- McLerran, L. A Brief Introduction to the Color Glass Condensate and the Glasma. In Proceedings of the 38th International Symposium on Multiparticle Dynamics, Hamburg, Germany, 15–20 September 2008; pp. 3–18. [Google Scholar] [CrossRef]
- Gribov, L.V.; Levin, E.M.; Ryskin, M.G. Semihard Processes in QCD. Phys. Rep. 1983, 100, 1–150. [Google Scholar] [CrossRef]
- Kharzeev, D. Classical chromodynamics of relativistic heavy ion collisions. In Cargese Summer School on QCD Perspectives on Hot and Dense Matter; Springer: Berlin/Heidelberg, Germany, 2002; pp. 207–236. [Google Scholar]
- Berges, J.; Heller, M.P.; Mazeliauskas, A.; Venugopalan, R. QCD thermalization: Ab initio approaches and interdisciplinary connections. Rev. Mod. Phys. 2021, 93, 035003. [Google Scholar] [CrossRef]
- McLerran, L.D.; Venugopalan, R. Computing quark and gluon distribution functions for very large nuclei. Phys. Rev. D 1994, 49, 2233–2241. [Google Scholar] [CrossRef]
- Kovner, A.; McLerran, L.D.; Weigert, H. Gluon production from nonAbelian Weizsacker-Williams fields in nucleus-nucleus collisions. Phys. Rev. D 1995, 52, 6231–6237. [Google Scholar] [CrossRef]
- Tu, Z.; Kharzeev, D.E.; Ullrich, T. Einstein-Podolsky-Rosen Paradox and Quantum Entanglement at Subnucleonic Scales. Phys. Rev. Lett. 2020, 124, 062001. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A.; Corichi, A.; Kesavan, A. Emergence of classical behavior in the early universe. Phys. Rev. D 2020, 102, 023512. [Google Scholar] [CrossRef]
- Vilenkin, A. Quantum Creation of Universes. Phys. Rev. D 1984, 30, 509–511. [Google Scholar] [CrossRef]
- Martin, J.; Vennin, V. Quantum Discord of Cosmic Inflation: Can we Show that CMB Anisotropies are of Quantum-Mechanical Origin? Phys. Rev. D 2016, 93, 023505. [Google Scholar] [CrossRef]
- Green, D.; Porto, R.A. Signals of a Quantum Universe. Phys. Rev. Lett. 2020, 124, 251302. [Google Scholar] [CrossRef] [PubMed]
- Liddle, A.R. An Introduction to Modern Cosmology; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Linde, A. Inflationary Cosmology after Planck 2013; Oxford University Press: Oxford, UK, 2015; pp. 231–316. [Google Scholar] [CrossRef]
- Sethna, J.P. Statistical Mechanics: Entropy, Order Parameters, and Complexity; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Dvali, G.; Gomez, C.; Zell, S. Quantum Break-Time of de Sitter. J. Cosmol. Astropart. Phys. 2017, 6, 28. [Google Scholar] [CrossRef]
- Berezhiani, L.; Zantedeschi, M. Evolution of coherent states as quantum counterpart of classical dynamics. Phys. Rev. D 2021, 104, 085007. [Google Scholar] [CrossRef]
- Langer, S.A.; Sethna, J.P. Entropy of Glasses. Phys. Rev. Lett. 1988, 61, 570–573. [Google Scholar] [CrossRef]
- Carrington, M.E.; Czajka, A.; Mrowczynski, S. The energy-momentum tensor at the earliest stage of relativistic heavy-ion collisions. Eur. Phys. J. A 2022, 58, 5. [Google Scholar] [CrossRef]
- Carrington, M.E.; Czajka, A.; Mrowczynski, S. Physical characteristics of glasma from the earliest stage of relativistic heavy ion collisions. arXiv 2021, arXiv:2105.05327. [Google Scholar]
- Weinberg, S. The Quantum Theory of Fields. Volume 2: Modern Applications; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Degrassi, G.; Di Vita, S.; Elias-Miro, J.; Espinosa, J.R.; Giudice, G.F.; Isidori, G.; Strumia, A. Higgs mass and vacuum stability in the Standard Model at NNLO. J. High Energy Phys. 2012, 8, 98. [Google Scholar] [CrossRef]
- Markkanen, T.; Rajantie, A.; Stopyra, S. Cosmological Aspects of Higgs Vacuum Metastability. Front. Astron. Space Sci. 2018, 5, 40. [Google Scholar] [CrossRef]
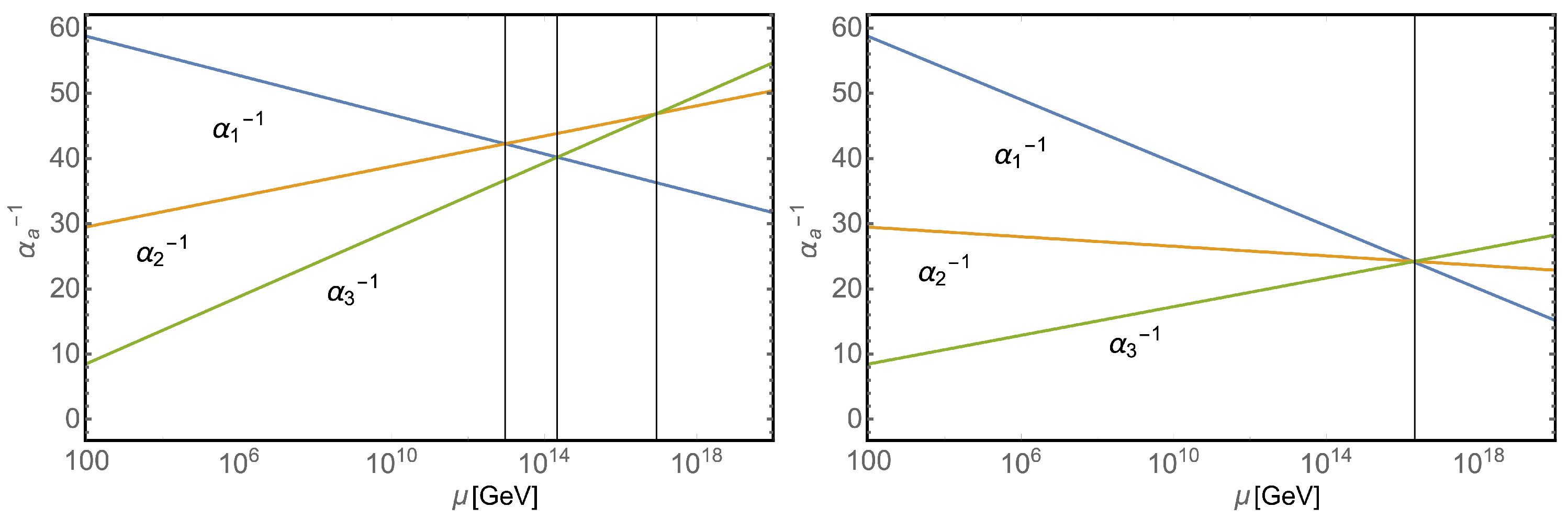
- Georgi, H.; Glashow, S.L. Unity of All Elementary Particle Forces. Phys. Rev. Lett. 1974, 32, 438–441. [Google Scholar] [CrossRef]
- Nishino, H.; Super-Kamiokande Collaboration. Search for Proton Decay via p —> e+ pi0 and p —> mu+ pi0 in a Large Water Cherenkov Detector. Phys. Rev. Lett. 2009, 102, 141801. [Google Scholar] [CrossRef] [PubMed]
- Langacker, P. Grand Unified Theories and Proton Decay. Phys. Rep. 1981, 72, 185. [Google Scholar] [CrossRef]
- Nath, P.; Fileviez Perez, P. Proton stability in grand unified theories, in strings and in branes. Phys. Rep. 2007, 441, 191–317. [Google Scholar] [CrossRef]
- Altarelli, G.; Meloni, D. A non supersymmetric SO(10) grand unified model for all the physics below MGUT. J. High Energy Phys. 2013, 8, 21. [Google Scholar] [CrossRef]
- Morais, A.P.; Pasechnik, R.; Porod, W. Grand Unified origin of gauge interactions and families replication in the Standard Model. Universe 2021, 7, 461. [Google Scholar] [CrossRef]
- Croon, D.; Gonzalo, T.E.; Graf, L.; Košnik, N.; White, G. GUT Physics in the era of the LHC. Front. Phys. 2019, 7, 76. [Google Scholar] [CrossRef]
- Dimopoulos, S.; Raby, S.; Wilczek, F. Supersymmetry and the Scale of Unification. Phys. Rev. D 1981, 24, 1681–1683. [Google Scholar] [CrossRef]
- Linde, A.D. Particle physics and inflationary cosmology. Contemp. Concepts Phys. 1990, 5, 1–362. [Google Scholar]
- Gangui, A. Topological Defects in Cosmology. arXiv 2001, arXiv:astro-ph/0110285. [Google Scholar]
- Caprini, C.; Durrer, R. Gravitational wave production: A Strong constraint on primordial magnetic fields. Phys. Rev. D 2001, 65, 023517. [Google Scholar] [CrossRef]
- Caprini, C.; Durrer, R.; Servant, G. The stochastic gravitational wave background from turbulence and magnetic fields generated by a first-order phase transition. J. Cosmol. Astropart. Phys. 2009, 12, 24. [Google Scholar] [CrossRef]
- Figueroa, D.G.; Hindmarsh, M.; Urrestilla, J. Exact Scale-Invariant Background of Gravitational Waves from Cosmic Defects. Phys. Rev. Lett. 2013, 110, 101302. [Google Scholar] [CrossRef]
- Hindmarsh, M. Sound shell model for acoustic gravitational wave production at a first-order phase transition in the early Universe. Phys. Rev. Lett. 2018, 120, 071301. [Google Scholar] [CrossRef]
- Kamionkowski, M.; Kosowsky, A.; Turner, M.S. Gravitational radiation from first order phase transitions. Phys. Rev. D 1994, 49, 2837–2851. [Google Scholar] [CrossRef]
- Durrer, R.; Neronov, A. Cosmological Magnetic Fields: Their Generation, Evolution and Observation. Astron. Astrophys. Rev. 2013, 21, 62. [Google Scholar] [CrossRef]
- Vilenkin, A.; Shellard, E.P.S. Cosmic Strings and Other Topological Defects; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Espinosa, J.R.; Quiros, M. The Electroweak phase transition with a singlet. Phys. Lett. B 1993, 305, 98–105. [Google Scholar] [CrossRef]
- Iso, S.; Serpico, P.D.; Shimada, K. QCD-Electroweak First-Order Phase Transition in a Supercooled Universe. Phys. Rev. Lett. 2017, 119, 141301. [Google Scholar] [CrossRef] [Green Version]
- Sikivie, P. Axion Cosmology. Lect. Notes Phys. 2008, 741, 19–50. [Google Scholar] [CrossRef]
- Peccei, R.D. The Strong CP problem and axions. Lect. Notes Phys. 2008, 741, 3–17. [Google Scholar] [CrossRef]
- Marsh, D.J.E. Axion Cosmology. Phys. Rep. 2016, 643, 1–79. [Google Scholar] [CrossRef]
- Di Luzio, L.; Giannotti, M.; Nardi, E.; Visinelli, L. The landscape of QCD axion models. Phys. Rep. 2020, 870, 1–117. [Google Scholar] [CrossRef]
- ’t Hooft, G. Computation of the Quantum Effects Due to a Four-Dimensional Pseudoparticle. Phys. Rev. D 1978, 14, 3432–3450. [Google Scholar] [CrossRef]
- Schäfer, T.; Shuryak, E.V. Instantons in QCD. Rev. Mod. Phys. 1998, 70, 323–426. [Google Scholar] [CrossRef]
- Callan, C.G., Jr.; Dashen, R.F.; Gross, D.J. Toward a Theory of the Strong Interactions. Phys. Rev. D 1978, 17, 2717. [Google Scholar] [CrossRef]
- Abel, C.; Afach, S.; Ayres, N.J.; Baker, C.A.; Ban, G.; Bison, G.; Zsigmond, G. Measurement of the permanent electric dipole moment of the neutron. Phys. Rev. Lett. 2020, 124, 081803. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. CP Conservation in the Presence of Instantons. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef]
- Dvali, G.; Zell, S. Classicality and Quantum Break-Time for Cosmic Axions. J. Cosmol. Astropart. Phys. 2018, 7, 64. [Google Scholar] [CrossRef] [Green Version]
- Kawasaki, M.; Nakayama, K. Axions: Theory and Cosmological Role. Ann. Rev. Nucl. Part. Sci. 2013, 63, 69–95. [Google Scholar] [CrossRef]
- Adler, S.L. Axial vector vertex in spinor electrodynamics. Phys. Rev. 1969, 177, 2426–2438. [Google Scholar] [CrossRef]
- Bell, J.S.; Jackiw, R. A PCAC puzzle: π0→γγ in the σ model. Nuovo Cim. A 1969, 60, 47–61. [Google Scholar] [CrossRef]
- Di Vecchia, P.; Veneziano, G. Chiral Dynamics in the Large n Limit. Nucl. Phys. B 1980, 171, 253–272. [Google Scholar] [CrossRef]
- Alles, B.; D’Elia, M.; Di Giacomo, A. Topological susceptibility in full QCD at zero and finite temperature. Phys. Lett. B 2000, 483, 139–143. [Google Scholar] [CrossRef]
- Gattringer, C.; Hoffmann, R.; Schaefer, S. The Topological susceptibility of SU(3) gauge theory near T(c). Phys. Lett. B 2002, 535, 358–362. [Google Scholar] [CrossRef]
- Bernard, V.; Descotes-Genon, S.; Toucas, G. Topological susceptibility on the lattice and the three-flavour quark condensate. J. High Energy Phys. 2012, 6, 051. [Google Scholar] [CrossRef]
- Bonati, C.; D’Elia, M.; Panagopoulos, H.; Vicari, E. Change of θ Dependence in 4D SU(N) Gauge Theories Across the Deconfinement Transition. Phys. Rev. Lett. 2013, 110, 252003. [Google Scholar] [CrossRef]
- Berkowitz, E.; Buchoff, M.I.; Rinaldi, E. Lattice QCD input for axion cosmology. Phys. Rev. D 2015, 92, 034507. [Google Scholar] [CrossRef]
- Kitano, R.; Yamada, N. Topology in QCD and the axion abundance. J. High Energy Phys. 2015, 10, 136. [Google Scholar] [CrossRef] [Green Version]
- Borsanyi, S.; Dierigl, M.; Fodor, Z.; Katz, S.D.; Mages, S.W.; Nogradi, D.; Redondo, J.; Ringwald, A.; Szabo, K.K. Axion cosmology, lattice QCD and the dilute instanton gas. Phys. Lett. B 2016, 752, 175–181. [Google Scholar] [CrossRef]
- Bonati, C.; D’Elia, M.; Mariti, M.; Martinelli, G.; Mesiti, M.; Negro, F.; Sanfilippo, F.; Villadoro, G. Axion phenomenology and θ-dependence from Nf=2+1 lattice QCD. J. High Energy Phys. 2016, 3, 155. [Google Scholar] [CrossRef]
- Taniguchi, Y.; Kanaya, K.; Suzuki, H.; Umeda, T. Topological susceptibility in finite temperature (2+1)-flavor QCD using gradient flow. Phys. Rev. D 2017, 95, 054502. [Google Scholar] [CrossRef]
- Petreczky, P.; Schadler, H.P.; Sharma, S. The topological susceptibility in finite temperature QCD and axion cosmology. Phys. Lett. B 2016, 762, 498–505. [Google Scholar] [CrossRef]
- Grilli di Cortona, G.; Hardy, E.; Pardo Vega, J.; Villadoro, G. The QCD axion, precisely. J. High Energy Phys. 2016, 1, 34. [Google Scholar] [CrossRef]
- Kibble, T.W.B. Topology of Cosmic Domains and Strings. J. Phys. A 1976, 9, 1387–1398. [Google Scholar] [CrossRef]
- Saikawa, K. A review of gravitational waves from cosmic domain walls. Universe 2017, 3, 40. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational collapse: The role of general relativity. Riv. Nuovo Cim. 1969, 1, 252–276. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B. Generation of Waves by a Rotating Body. Zh. Eksp. Teor. Fiz. 1971, 14, 180. [Google Scholar]
- Vinyoles, N.; Serenelli, A.; Villante, F.L.; Basu, S.; Redondo, J.; Isern, J. New axion and hidden photon constraints from a solar data global fit. J. Cosmol. Astropart. Phys. 2015, 10, 15. [Google Scholar] [CrossRef]
- Dent, J.B.; Dutta, B.; Newstead, J.L.; Thompson, A. Inverse Primakoff Scattering as a Probe of Solar Axions at Liquid Xenon Direct Detection Experiments. Phys. Rev. Lett. 2020, 125, 131805. [Google Scholar] [CrossRef] [PubMed]
- Ballesteros, G.; Redondo, J.; Ringwald, A.; Tamarit, C. Standard Model—Axion—Seesaw—Higgs portal inflation. Five problems of particle physics and cosmology solved in one stroke. J. Cosmol. Astropart. Phys. 2017, 8, 1. [Google Scholar] [CrossRef]
- Arcadi, G.; Djouadi, A.; Raidal, M. Dark Matter through the Higgs portal. Phys. Rep. 2020, 842, 1–180. [Google Scholar] [CrossRef]
- Ge, S.; Siddiqui, M.S.R.; Van Waerbeke, L.; Zhitnitsky, A. Impulsive radio events in quiet solar corona and axion quark nugget dark matter. Phys. Rev. D 2020, 102, 123021. [Google Scholar] [CrossRef]
- Ipek, S.; Tait, T.M.P. Early Cosmological Period of QCD Confinement. Phys. Rev. Lett. 2019, 122, 112001. [Google Scholar] [CrossRef]
- Berger, D.; Ipek, S.; Tait, T.M.P.; Waterbury, M. Dark Matter Freeze Out during an Early Cosmological Period of QCD Confinement. J. High Energy Phys. 2020, 7, 192. [Google Scholar] [CrossRef]
- Addazi, A.; Marcianò, A.; Pasechnik, R.; Zeng, K.A. QCD surprises: Strong CP problem, neutrino mass, Dark Matter and Dark Energy. Phys. Dark Univ. 2022, 36, 101007. [Google Scholar] [CrossRef]
- Zee, A. Einstein Gravity in a Nutshell; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Zel’dovich, Y.B. The equation of state at ultrahigh densities and its relativistic limitations. Zh. Eksp. Teor. Fiz. 1961, 41, 1609–1615. [Google Scholar]
- Trojan, E.; Vlasov, G.V. Thermodynamics of exotic matter with constant w=P/E. arXiv 2011, arXiv:1108.0824. [Google Scholar]
- Kapusta, J.I. Finite Temperature Field Theory; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Rhoades, C.E., Jr.; Ruffini, R. Maximum mass of a neutron star. Phys. Rev. Lett. 1974, 32, 324–327. [Google Scholar] [CrossRef]
- Blaschke, D.; Cierniak, M. Studying the onset of deconfinement with multi-messenger astronomy of neutron stars. Astron. Nachr. 2021, 342, 227–233. [Google Scholar] [CrossRef]
- Dutta, S.; Scherrer, R.J. Big Bang nucleosynthesis with a stiff fluid. Phys. Rev. D 2010, 82, 083501. [Google Scholar] [CrossRef]
- Stiele, R.; Boeckel, T.; Schaffner-Bielich, J. Cosmological implications of a Dark Matter self-interaction energy density. Phys. Rev. D 2010, 81, 123513. [Google Scholar] [CrossRef] [Green Version]
- Mathew, T.K.; Aswathy, M.B.; Manoj, M. Cosmology and thermodynamics of FLRW universe with bulk viscous stiff fluid. Eur. Phys. J. C 2014, 74, 3188. [Google Scholar] [CrossRef]
- Banks, T.; Fischler, W. An Holographic cosmology. arXiv 2001, arXiv:hep-th/0111142. [Google Scholar]
- Miguelote, A.Y.; Tomimura, N.A.; Wang, A. Gravitational collapse of selfsimilar perfect fluid in 2+1 gravity. Gen. Rel. Grav. 2004, 36, 1883–1918. [Google Scholar] [CrossRef]
- Dashen, R.; Ma, S.K.; Bernstein, H.J. S Matrix formulation of statistical mechanics. Phys. Rev. 1969, 187, 345–370. [Google Scholar] [CrossRef]
- Welke, G.M.; Venugopalan, R.; Prakash, M. The Speed of sound in an interacting pion gas. Phys. Lett. B 1990, 245, 137–141. [Google Scholar] [CrossRef]
- Lo, P.M. S-matrix formulation of thermodynamics with N-body scatterings. Eur. Phys. J. C 2017, 77, 533. [Google Scholar] [CrossRef]
- Baacke, J. Thermodynamics of a Gas of MIT Bags. Acta Phys. Polon. B 1977, 8, 625. [Google Scholar]
- Fogaca, D.A.; Ferreira Filho, L.G.; Navarra, F.S. Non-linear waves in a Quark Gluon Plasma. Phys. Rev. C 2010, 81, 055211. [Google Scholar] [CrossRef]
- Chodos, A.; Jaffe, R.L.; Johnson, K.; Thorn, C.B.; Weisskopf, V.F. A New Extended Model of Hadrons. Phys. Rev. D 1974, 9, 3471–3495. [Google Scholar] [CrossRef]
- DeTar, C.E.; Donoghue, J.F. BAG MODELS OF HADRONS. Ann. Rev. Nucl. Part. Sci. 1983, 33, 235–264. [Google Scholar] [CrossRef]
- Pisarski, R.D. Effective Theory of Wilson Lines and Deconfinement. Phys. Rev. D 2006, 74, 121703. [Google Scholar] [CrossRef]
- Megias, E.; Ruiz Arriola, E.; Salcedo, L.L. The Quark-antiquark potential at finite temperature and the dimension two gluon condensate. Phys. Rev. D 2007, 75, 105019. [Google Scholar] [CrossRef] [Green Version]
- Zuo, F.; Gao, Y.H. Quadratic thermal terms in the deconfined phase from holography. J. High Energy Phys. 2014, 7, 147. [Google Scholar] [CrossRef]
- Pisarski, R.D. Fuzzy Bags and Wilson Lines. Prog. Theor. Phys. Suppl. 2007, 168, 276–284. [Google Scholar] [CrossRef]
- Schneider, R.A.; Weise, W. On the quasiparticle description of lattice QCD thermodynamics. Phys. Rev. C 2001, 64, 055201. [Google Scholar] [CrossRef]
- Giacosa, F. Analytical study of a gas of gluonic quasiparticles at high temperature: Effective mass, pressure and trace anomaly. Phys. Rev. D 2011, 83, 114002. [Google Scholar] [CrossRef]
- Shuryak, E.V. The QCD Vacuum, Hadrons and the Superdense Matter; World Scientific: Singapore, 2004; Volume 71. [Google Scholar] [CrossRef]
- Castorina, P.; Miller, D.E.; Satz, H. Trace Anomaly and Quasi-Particles in Finite Temperature SU(N) Gauge Theory. Eur. Phys. J. C 2011, 71, 1673. [Google Scholar] [CrossRef]
- Kou, F.F.; The FAST Collaboration. Periodic and Phase-locked Modulation in PSR B1929+10 Observed with FAST. Astrophys. J. 2021, 909, 170. [Google Scholar] [CrossRef]
- Bacon, D.J.; Battye, R.A.; Bull, P.; Camera, S.; Ferreira, P.G.; Harrison, I.; Parkinson, D.; Pourtsidou, A.; Santos, M.G.; Zuntz, J.; et al. Cosmology with Phase 1 of the Square Kilometre Array: Red Book 2018: Technical specifications and performance forecasts. Publ. Astron. Soc. Austral. 2020, 37, e007. [Google Scholar] [CrossRef]
- Abe, K.T.; Tada, Y.; Ueda, I. Induced gravitational waves as a cosmological probe of the sound speed during the QCD phase transition. J. Cosmol. Astropart. Phys. 2021, 6, 48. [Google Scholar] [CrossRef]
- Linde, A.D. Infrared Problem in Thermodynamics of the Yang-Mills Gas. Phys. Lett. B 1980, 96, 289–292. [Google Scholar] [CrossRef] [Green Version]
- Gross, D.J.; Pisarski, R.D.; Yaffe, L.G. QCD and Instantons at Finite Temperature. Rev. Mod. Phys. 1981, 53, 43. [Google Scholar] [CrossRef]
- Gynther, A.; Vepsalainen, M. Pressure of the standard model at high temperatures. J. High Energy Phys. 2006, 1, 60. [Google Scholar] [CrossRef]
- Prokhorov, G.; Pasechnik, R.; Vereshkov, G. Wave fluctuations in the system with some Yang-Mills condensates. Phys. Atom. Nucl. 2016, 79, 1502–1504. [Google Scholar] [CrossRef]
- Pasechnik, R.; Prokhorov, G.; Vereshkov, G. Conformal Evolution of Waves in the Yang-Mills Condensate: The Quasi-Classical Approach. J. Mod. Phys. 2014, 5, 209–229. [Google Scholar] [CrossRef]
- Prokhorov, G.; Pasechnik, R.; Vereshkov, G. Dynamics of wave fluctuations in the homogeneous Yang-Mills condensate. J. High Energy Phys. 2014, 7, 3. [Google Scholar] [CrossRef]
- Prokhorov, G.; Pasechnik, R. Light meson gas in the QCD vacuum and oscillating Universe. J. Cosmol. Astropart. Phys. 2018, 1, 17. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Mishustin, I. Equation of State for Cosmological Matter at and beyond QCD and Electroweak Eras. J. Phys. G 2019, 46, 125201. [Google Scholar] [CrossRef]
- Laine, M.; Schroder, Y. Quark mass thresholds in QCD thermodynamics. Phys. Rev. D 2006, 73, 085009. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Greiner, C. Bulk viscosity in strong and electroweak matter. Int. J. Mod. Phys. E 2021, 30, 2150067. [Google Scholar] [CrossRef]
- Tawfik, A.N.; Greiner, C. Early Universe Thermodynamics and Evolution in Nonviscous and Viscous Strong and Electroweak epochs: Possible Analytical Solutions. Entropy 2021, 23, 295. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O.; Sen, A.A. Generalized Chaplygin gas, accelerated expansion and dark energy matter unification. Phys. Rev. D 2002, 66, 043507. [Google Scholar] [CrossRef]
- Chaplygin, S. On gas jets. Sci. Mem. Mosc. Univ. Math. Phys. 1904, 21, 1. [Google Scholar]
- Kamenshchik, A.Y.; Moschella, U.; Pasquier, V. An Alternative to quintessence. Phys. Lett. B 2001, 511, 265–268. [Google Scholar] [CrossRef]
- Shuryak, E.V.; Schäfer, T. The QCD vacuum as an instanton liquid. Ann. Rev. Nucl. Part. Sci. 1997, 47, 359–394. [Google Scholar] [CrossRef]
- Kolb, E.W.; Turner, M.S. The Early Universe; Addison-Wesley: San Francisco, CA, USA, 1990; Volume 69. [Google Scholar]
- Iorio, A.; Lambiase, G. Thermal relics in cosmology with bulk viscosity. Eur. Phys. J. C 2015, 75, 115. [Google Scholar] [CrossRef]
- Myung, Y.S.; Cho, B.H. Entropy Production in a Hot Heterotic String. Mod. Phys. Lett. A 1986, 1, 37–41. [Google Scholar] [CrossRef]
- Cheng, B. Bulk viscosity in the early universe. Phys. Lett. A 1991, 160, 329–338. [Google Scholar] [CrossRef]
- Brevik, I.; Grøn, O.; de Haro, J.; Odintsov, S.D.; Saridakis, E.N. Viscous Cosmology for Early- and Late-Time Universe. Int. J. Mod. Phys. D 2017, 26, 1730024. [Google Scholar] [CrossRef]
- Carter, G.W.; Ellis, P.J.; Rudaz, S. An Effective Lagrangian with broken scale and chiral symmetry. 3: Mesons at finite temperature. Nucl. Phys. A 1997, 618, 317–329. [Google Scholar] [CrossRef]
- Carter, G.W.; Scavenius, O.; Mishustin, I.N.; Ellis, P.J. An Effective model for hot gluodynamics. Phys. Rev. C 2000, 61, 045206. [Google Scholar] [CrossRef]
- Mocsy, A.; Mishustin, I.N.; Ellis, P.J. Role of fluctuations in the linear sigma model with quarks. Phys. Rev. C 2004, 70, 015204. [Google Scholar] [CrossRef] [Green Version]
- Bowman, E.S.; Kapusta, J.I. Critical Points in the Linear Sigma Model with Quarks. Phys. Rev. C 2009, 79, 015202. [Google Scholar] [CrossRef]
- Chen, H.X.; Imai, S.; Toki, H.; Geng, L.S. Study of hadrons using the Gaussian functional method in the O(4) linear σ model. Chin. Phys. C 2015, 39, 064103. [Google Scholar] [CrossRef]
- Fukushima, K. Chiral effective model with the Polyakov loop. Phys. Lett. B 2004, 591, 277–284. [Google Scholar] [CrossRef]
- Buballa, M. NJL model analysis of quark matter at large density. Phys. Rep. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Blaschke, D.; Dubinin, A.; Buballa, M. Polyakov-loop suppression of colored states in a quark-meson-diquark plasma. Phys. Rev. D 2015, 91, 125040. [Google Scholar] [CrossRef]
- Shifman, M.A.; Vainshtein, A.I.; Zakharov, V.I. QCD and Resonance Physics. Theoretical Foundations. Nucl. Phys. B 1979, 147, 385–447. [Google Scholar] [CrossRef]
- Cornwall, J.M.; Jackiw, R.; Tomboulis, E. Effective Action for Composite Operators. Phys. Rev. D 1974, 10, 2428–2445. [Google Scholar] [CrossRef]
- Norton, R.E.; Cornwall, J.M. On the Formalism of Relativistic Many Body Theory. Ann. Phys. 1975, 91, 106. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Pi, S.Y. Selfconsistent improvement of the finite temperature effective potential. Phys. Rev. D 1993, 47, 2356–2362. [Google Scholar] [CrossRef] [PubMed]
- Gell-Mann, M.; Oakes, R.J.; Renner, B. Behavior of current divergences under SU(3) × SU(3). Phys. Rev. 1968, 175, 2195–2199. [Google Scholar] [CrossRef] [Green Version]
- Ioffe, B.L. Calculation of Baryon Masses in Quantum Chromodynamics. Nucl. Phys. B 1981, 188, 317–341. [Google Scholar] [CrossRef]
- Reinders, L.J.; Rubinstein, H.; Yazaki, S. Hadron Properties from QCD Sum Rules. Phys. Rep. 1985, 127, 1. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Roudier, G.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2021, 641, A6. [Google Scholar] [CrossRef]
- Bull, P.; Akrami, Y.; Adamek, J.; Baker, T.; Bellini, E.; Jimenez, J.B.; Bentivegna, E.; Camera, S.; Clesse, S.; Winther, H.A.; et al. Beyond ΛCDM: Problems, solutions, and the road ahead. Phys. Dark Univ. 2016, 12, 56–99. [Google Scholar] [CrossRef]
- Sakharov, A.D. Early stage of Universe expansion and origin of matter inhomogenities. Sov. Phys. JETP 1966, 22, 241. [Google Scholar]
- Sakharov, A.D. Vacuum quantum fluctuations in curved space and the theory of gravitation. Dokl. Akad. Nauk Ser. Fiz. 1967, 177, 70–71. [Google Scholar] [CrossRef]
- Crewther, R.J. Nonperturbative evaluation of the anomalies in low-energy theorems. Phys. Rev. Lett. 1972, 28, 1421. [Google Scholar] [CrossRef]
- Chanowitz, M.S.; Ellis, J.R. Canonical Trace Anomalies. Phys. Rev. D 1973, 7, 2490–2506. [Google Scholar] [CrossRef]
- Collins, J.C.; Duncan, A.; Joglekar, S.D. Trace and Dilatation Anomalies in Gauge Theories. Phys. Rev. D 1977, 16, 438–449. [Google Scholar] [CrossRef]
- Martin, J. Everything You Always Wanted To Know about the Cosmological Constant Problem (But Were Afraid to Ask). Comptes Rendus Phys. 2012, 13, 566–665. [Google Scholar] [CrossRef]
- Sola, J. Cosmological constant and vacuum energy: Old and new ideas. J. Phys. Conf. Ser. 2013, 453, 012015. [Google Scholar] [CrossRef]
- Pasechnik, R.; Beylin, V.; Vereshkov, G. Possible compensation of the QCD vacuum contribution to the dark energy. Phys. Rev. D 2013, 88, 023509. [Google Scholar] [CrossRef]
- Pasechnik, R.; Prokhorov, G.; Teryaev, O. Mirror QCD and Cosmological Constant. Universe 2017, 3, 43. [Google Scholar] [CrossRef]
- Polchinski, J. The Cosmological Constant and the String Landscape. In Proceedings of the 23rd Solvay Conference in Physics: The Quantum Structure of Space and Time, Brussels, Belgium, 1–3 December 2005; World Scientific: Singapore, 2006; p. 216. [Google Scholar]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef]
- Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Wilczek, F. Foundations and Working Pictures in Microphysical Cosmology. Phys. Rep. 1984, 104, 143. [Google Scholar] [CrossRef]
- Ferroni, L.; Koch, V. Crossover transition in bag-like models. Phys. Rev. C 2009, 79, 034905. [Google Scholar] [CrossRef]
- Novello, M.; Bergliaffa, S.E.P. Bouncing Cosmologies. Phys. Rep. 2008, 463, 127–213. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Brandenberger, R.H. A Nonsingular universe. Phys. Rev. Lett. 1992, 68, 1969–1972. [Google Scholar] [CrossRef]
- Szydlowski, M.; Godlowski, W.; Krawiec, A.; Golbiak, J. Can the initial singularity be detected by cosmological tests? Phys. Rev. D 2005, 72, 063504. [Google Scholar] [CrossRef]
- Dabrowski, M.P. Oscillating Friedman cosmology. Ann. Phys. 1996, 248, 199–219. [Google Scholar] [CrossRef] [Green Version]
- Savvidy, G.K. Infrared Instability of the Vacuum State of Gauge Theories and Asymptotic Freedom. Phys. Lett. B 1977, 71, 133–134. [Google Scholar] [CrossRef]
- Batalin, I.A.; Matinyan, S.G.; Savvidy, G.K. Vacuum Polarization by a Source-Free Gauge Field. Sov. J. Nucl. Phys. 1977, 26, 214. [Google Scholar]
- Nielsen, N.K.; Olesen, P. An Unstable Yang-Mills Field Mode. Nucl. Phys. B 1978, 144, 376–396. [Google Scholar] [CrossRef]
- Olesen, P. On the QCD Vacuum. Phys. Scr. 1981, 23, 1000–1004. [Google Scholar] [CrossRef]
- Shuryak, E.V. Theory and phenomenology of the QCD vacuum. Phys. Rep. 1984, 115, 151. [Google Scholar] [CrossRef]
- Wilczek, F. Quantum Time Crystals. Phys. Rev. Lett. 2012, 109, 160401. [Google Scholar] [CrossRef] [PubMed]
- Wilczek, F. Wilczek Reply. Phys. Rev. Lett. 2013, 110, 118902. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Hess, P.W.; Kyprianidis, A.; Becker, P.; Lee, A.; Smith, J.; Pagano, G.; Potirniche, I.D.; Potter, A.C.; Monroe, C.; et al. Observation A Discret. Time Crystal. Nature 2017, 543, 217–220. [Google Scholar] [CrossRef] [PubMed]
- Sacha, K.; Zakrzewski, J. Time crystals: A review. Rep. Prog. Phys. 2018, 81, 016401. [Google Scholar] [CrossRef]
- Maiani, L.; Testa, M. Final state interactions from Euclidean correlation functions. Phys. Lett. B 1990, 245, 585–590. [Google Scholar] [CrossRef]
- Glimm, J.; Jaffe, A.M. Quantum Physics. A Functional Integral Point of View; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Poland, D.; Rychkov, S.; Vichi, A. The Conformal Bootstrap: Theory, Numerical Techniques, and Applications. Rev. Mod. Phys. 2019, 91, 015002. [Google Scholar] [CrossRef] [Green Version]
- Ferrara, S.; Grillo, A.F.; Gatto, R. Tensor representations of conformal algebra and conformally covariant operator product expansion. Ann. Phys. 1973, 76, 161–188. [Google Scholar] [CrossRef]
- Polyakov, A.M. Nonhamiltonian approach to conformal quantum field theory. Zh. Eksp. Teor. Fiz. 1974, 66, 23–42. [Google Scholar]
- Rychkov, S. EPFL Lectures on Conformal Field Theory in D>= 3 Dimensions. In Springer Briefs in Physics; Springer: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Simmons-Duffin, D. The Conformal Bootstrap. In Theoretical Advanced Study Institute in Elementary Particle Physics: New Frontiers in Fields and Strings; World Scientific: Singapore, 2017; pp. 1–74. [Google Scholar] [CrossRef]
- Rattazzi, R.; Rychkov, V.S.; Tonni, E.; Vichi, A. Bounding scalar operator dimensions in 4D CFT. J. High Energy Phys. 2008, 12, 31. [Google Scholar] [CrossRef]
- Kos, F.; Poland, D.; Simmons-Duffin, D.; Vichi, A. Precision Islands in the Ising and O(N) Models. J. High Energy Phys. 2016, 8, 36. [Google Scholar] [CrossRef]
- Matinyan, S.G.; Savvidy, G.K. Vacuum Polarization Induced by the Intense Gauge Field. Nucl. Phys. B 1978, 134, 539–545. [Google Scholar] [CrossRef]
- Savvidy, G. From Heisenberg–Euler Lagrangian to the discovery of Chromomagnetic Gluon Condensation. Eur. Phys. J. C 2020, 80, 165. [Google Scholar] [CrossRef]
- Callan, C.G., Jr. Broken scale invariance in scalar field theory. Phys. Rev. D 1970, 2, 1541–1547. [Google Scholar] [CrossRef]
- Symanzik, K. Small distance behavior in field theory and power counting. Commun. Math. Phys. 1970, 18, 227–246. [Google Scholar] [CrossRef]
- Agasian, N.O. Low-energy relation for the trace of the energy-momentum tensor in QCD and the gluon condensate in a magnetic field. JETP Lett. 2016, 104, 71–74. [Google Scholar] [CrossRef] [Green Version]
- Aharonov, Y.; Casher, A.; Yankielowicz, S. Instantons and Confinement. Nucl. Phys. B 1978, 146, 256–272. [Google Scholar] [CrossRef]
- Vinciarelli, P. Fluxon Solutions in Nonabelian Gauge Models. Phys. Lett. B 1978, 78, 485–488. [Google Scholar] [CrossRef]
- Ambjorn, J.; Olesen, P. A Color Magnetic Vortex Condensate in QCD. Nucl. Phys. B 1980, 170, 265–282. [Google Scholar] [CrossRef]
- Del Debbio, L.; Faber, M.; Greensite, J.; Olejnik, S. Casimir scaling versus Abelian dominance in QCD string formation. Phys. Rev. D 1996, 53, 5891–5897. [Google Scholar] [CrossRef]
- Del Debbio, L.; Faber, M.; Greensite, J.; Olejnik, S. Center dominance and Z(2) vortices in SU(2) lattice gauge theory. Phys. Rev. D 1997, 55, 2298–2306. [Google Scholar] [CrossRef]
- Faber, M.; Greensite, J.; Olejnik, S. Casimir scaling from center vortices: Towards an understanding of the adjoint string tension. Phys. Rev. D 1998, 57, 2603–2609. [Google Scholar] [CrossRef]
- Engelhardt, M.; Langfeld, K.; Reinhardt, H.; Tennert, O. Interaction of confining vortices in SU(2) lattice gauge theory. Phys. Lett. B 1998, 431, 141–146. [Google Scholar] [CrossRef]
- Greensite, J. An Introduction to the Confinement Problem; Springer: Berlin/Heidelberg, Germany, 2020; Volume 972. [Google Scholar] [CrossRef]
- Wetterich, C. Exact evolution equation for the effective potential. Phys. Lett. B 1993, 301, 90–94. [Google Scholar] [CrossRef]
- Reuter, M.; Wetterich, C. Gluon condensation in nonperturbative flow equations. Phys. Rev. D 1997, 56, 7893–7916. [Google Scholar] [CrossRef] [Green Version]
- Gies, H. Running coupling in Yang-Mills theory: A flow equation study. Phys. Rev. D 2002, 66, 025006. [Google Scholar] [CrossRef]
- Eichhorn, A.; Gies, H.; Pawlowski, J.M. Gluon condensation and scaling exponents for the propagators in Yang-Mills theory. Phys. Rev. D 2011, 83, 045014. [Google Scholar] [CrossRef]
- Khvedelidze, A.M.; Pavel, H.P. Unconstrained Hamiltonian formulation of SU(2) gluodynamics. Phys. Rev. D 1999, 59, 105017. [Google Scholar] [CrossRef]
- Khvedelidze, A.M.; Mladenov, D.M.; Pavel, H.P.; Ropke, G. Unconstrained SU(2) Yang-Mills theory with topological term in the long wavelength approximation. Phys. Rev. D 2003, 67, 105013. [Google Scholar] [CrossRef]
- Cervero, J.; Jacobs, L. Classical Yang-Mills Fields in a Robertson-walker Universe. Phys. Lett. B 1978, 78, 427–429. [Google Scholar] [CrossRef]
- Henneaux, M.; Shepley, L.C. Lagrangians for spherically symmetric potentials. J. Math. Phys. 1982, 23, 2101–2107. [Google Scholar] [CrossRef]
- Hosotani, Y. Exact Solution to the Einstein Yang-Mills Equation. Phys. Lett. B 1984, 147, 44–46. [Google Scholar] [CrossRef]
- Morris, T.R. The Exact renormalization group and approximate solutions. Int. J. Mod. Phys. A 1994, 9, 2411–2450. [Google Scholar] [CrossRef]
- Papenbrock, T.; Wetterich, C. Two loop results from one loop computations and nonperturbative solutions of exact evolution equations. Z. Phys. C 1995, 65, 519–535. [Google Scholar] [CrossRef]
- Fischer, C.S.; Alkofer, R. Infrared exponents and running coupling of SU(N) Yang-Mills theories. Phys. Lett. B 2002, 536, 177–184. [Google Scholar] [CrossRef] [Green Version]
- Fischer, C.S.; Pawlowski, J.M. Uniqueness of infrared asymptotics in Landau gauge Yang-Mills theory. Phys. Rev. D 2007, 75, 025012. [Google Scholar] [CrossRef]
- Fischer, C.S.; Pawlowski, J.M. Uniqueness of infrared asymptotics in Landau gauge Yang-Mills theory II. Phys. Rev. D 2009, 80, 025023. [Google Scholar] [CrossRef]
- Fischer, C.S.; Maas, A.; Pawlowski, J.M. On the infrared behavior of Landau gauge Yang-Mills theory. Ann. Phys. 2009, 324, 2408–2437. [Google Scholar] [CrossRef]
- Ellwanger, U.; Hirsch, M.; Weber, A. Flow equations for the relevant part of the pure Yang-Mills action. Z. Phys. C 1996, 69, 687–698. [Google Scholar] [CrossRef]
- Ellwanger, U.; Hirsch, M.; Weber, A. The Heavy quark potential from Wilson’s exact renormalization group. Eur. Phys. J. C 1998, 1, 563–578. [Google Scholar] [CrossRef]
- Bergerhoff, B.; Wetterich, C. Effective quark interactions and QCD propagators. Phys. Rev. D 1998, 57, 1591–1604. [Google Scholar] [CrossRef]
- Pawlowski, J.M.; Litim, D.F.; Nedelko, S.; von Smekal, L. Infrared behavior and fixed points in Landau gauge QCD. Phys. Rev. Lett. 2004, 93, 152002. [Google Scholar] [CrossRef] [PubMed]
- Donà, P.; Marcianò, A.; Zhang, Y.; Antolini, C. Yang-Mills condensate as dark energy: A nonperturbative approach. Phys. Rev. D 2016, 93, 043012. [Google Scholar] [CrossRef]
- Savvidy, G. Gauge field theory vacuum and cosmological inflation without scalar field. Ann. Phys. 2022, 436, 168681. [Google Scholar] [CrossRef]
- Ford, L.H. Inflation Driven by a Vector Field. Phys. Rev. D 1989, 40, 967. [Google Scholar] [CrossRef]
- Golovnev, A.; Mukhanov, V.; Vanchurin, V. Vector Inflation. J. Cosmol. Astropart. Phys. 2008, 6, 9. [Google Scholar] [CrossRef]
- Maleknejad, A.; Sheikh-Jabbari, M.M.; Soda, J. Gauge Fields and Inflation. Phys. Rep. 2013, 528, 161–261. [Google Scholar] [CrossRef]
- Maleknejad, A.; Sheikh-Jabbari, M.M. Gauge-flation: Inflation From Non-Abelian Gauge Fields. Phys. Lett. B 2013, 723, 224–228. [Google Scholar] [CrossRef]
- Maleknejad, A.; Sheikh-Jabbari, M.M. Non-Abelian Gauge Field Inflation. Phys. Rev. D 2011, 84, 043515. [Google Scholar] [CrossRef]
- Alexander, S.; Marciano, A.; Spergel, D. Chern-Simons Inflation and Baryogenesis. J. Cosmol. Astropart. Phys. 2013, 4, 46. [Google Scholar] [CrossRef]
- Koksma, J.F.; Prokopec, T. Fermion Propagator in Cosmological Spaces with Constant Deceleration. Class. Quant. Grav. 2009, 26, 125003. [Google Scholar] [CrossRef]
- Domcke, V.; von Harling, B.; Morgante, E.; Mukaida, K. Baryogenesis from axion inflation. J. Cosmol. Astropart. Phys. 2019, 10, 32. [Google Scholar] [CrossRef]
- Alexander, S.; Jyoti, D.; Kosowsky, A.; Marciano, A. Dynamics of Gauge Field Inflation. J. Cosmol. Astropart. Phys. 2015, 5, 5. [Google Scholar] [CrossRef]
- Stueckelberg, E.C.G. Interaction forces in electrodynamics and in the field theory of nuclear forces. Helv. Phys. Acta 1938, 11, 299–328. [Google Scholar]
- Adshead, P.; Wyman, M. Chromo-Natural Inflation: Natural inflation on a steep potential with classical non-Abelian gauge fields. Phys. Rev. Lett. 2012, 108, 261302. [Google Scholar] [CrossRef]
- Barvinsky, A.O.; Kamenshchik, A.Y. Cosmological landscape from nothing: Some like it hot. J. Cosmol. Astropart. Phys. 2006, 9, 14. [Google Scholar] [CrossRef] [Green Version]
- Barvinsky, A.O.; Kamenshchik, A.Y. Thermodynamics via Creation from Nothing: Limiting the Cosmological Constant Landscape. Phys. Rev. D 2006, 74, 121502. [Google Scholar] [CrossRef]
- Barvinsky, A.O. Why there is something rather than nothing (out of everything)? Phys. Rev. Lett. 2007, 99, 071301. [Google Scholar] [CrossRef]
- Barvinsky, A.O.; Zhitnitsky, A.R. Inflation and gauge field holonomy. Phys. Rev. D 2018, 98, 045008. [Google Scholar] [CrossRef]
- Zhitnitsky, A.R. Inflaton as an auxiliary topological field in a QCD-like system. Phys. Rev. D 2014, 89, 063529. [Google Scholar] [CrossRef]
- Zhitnitsky, A.R. Cosmological perturbations in \barQCD- inflation. Estimates confronting the observations, including BICEP2. Phys. Rev. D 2014, 90, 043504. [Google Scholar] [CrossRef]
- Hirano, T.; van der Kolk, N.; Bilandzic, A. Hydrodynamics and Flow. Lect. Notes Phys. 2010, 785, 139–178. [Google Scholar] [CrossRef]
- Kovtun, P. Lectures on hydrodynamic fluctuations in relativistic theories. J. Phys. A 2012, 45, 473001. [Google Scholar] [CrossRef]
- Bjorken, J.D. Highly Relativistic Nucleus-Nucleus Collisions: The Central Rapidity Region. Phys. Rev. D 1983, 27, 140–151. [Google Scholar] [CrossRef]
- Chojnacki, M.; Florkowski, W.; Csorgo, T. On the formation of Hubble flow in little bangs. Phys. Rev. C 2005, 71, 044902. [Google Scholar] [CrossRef]
- Csanád, M.; Nagy, M.I.; Jiang, Z.F.; Csörgo, T. A simple family of solutions of relativistic viscous hydrodynamics for fireballs with Hubble flow and ellipsoidal symmetry. In Gribov-90 Memorial Volume; World Scientific: Singapore, 2019; pp. 275–296. [Google Scholar] [CrossRef]
- Csorgo, T.; Kasza, G. New, multipole solutions of relativistic, viscous hydrodynamics. In Gribov-90 Memorial Volume; World Scientific: Singapore, 2020; pp. 297–318. [Google Scholar] [CrossRef]
- Maartens, R. Causal thermodynamics in relativity. arXiv 1996, arXiv:astro-ph/9609119. [Google Scholar]
- Muronga, A. Causal theories of dissipative relativistic fluid dynamics for nuclear collisions. Phys. Rev. C 2004, 69, 034903. [Google Scholar] [CrossRef]
- Hiscock, W.A.; Lindblom, L. Stability and causality in dissipative relativistic fluids. Ann. Phys. 1983, 151, 466–496. [Google Scholar] [CrossRef]
- Gale, C.; Jeon, S.; Schenke, B. Hydrodynamic Modeling of Heavy-Ion Collisions. Int. J. Mod. Phys. A 2013, 28, 1340011. [Google Scholar] [CrossRef]
- Jaiswal, A.; Roy, V. Relativistic hydrodynamics in heavy-ion collisions: General aspects and recent developments. Adv. High Energy Phys. 2016, 2016, 9623034. [Google Scholar] [CrossRef]
- Bravo Medina, S.; Nowakowski, M.; Batic, D. Viscous Cosmologies. Class. Quant. Grav. 2019, 36, 215002. [Google Scholar] [CrossRef]
- Bemfica, F.S.; Disconzi, M.M.; Noronha, J. First-Order General-Relativistic Viscous Fluid Dynamics. Phys. Rev. X 2022, 12, 021044. [Google Scholar] [CrossRef]
- Deur, A.; Brodsky, S.J.; de Teramond, G.F. The QCD Running Coupling. Nucl. Phys. 2016, 90, 1. [Google Scholar] [CrossRef] [Green Version]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Addazi, A.; Lundberg, T.; Marcianò, A.; Pasechnik, R.; Šumbera, M. Cosmology from Strong Interactions. Universe 2022, 8, 451. https://doi.org/10.3390/universe8090451
Addazi A, Lundberg T, Marcianò A, Pasechnik R, Šumbera M. Cosmology from Strong Interactions. Universe. 2022; 8(9):451. https://doi.org/10.3390/universe8090451
Chicago/Turabian StyleAddazi, Andrea, Torbjörn Lundberg, Antonino Marcianò, Roman Pasechnik, and Michal Šumbera. 2022. "Cosmology from Strong Interactions" Universe 8, no. 9: 451. https://doi.org/10.3390/universe8090451
APA StyleAddazi, A., Lundberg, T., Marcianò, A., Pasechnik, R., & Šumbera, M. (2022). Cosmology from Strong Interactions. Universe, 8(9), 451. https://doi.org/10.3390/universe8090451







