Mechanical Properties of Cometary Surfaces
Abstract
1. Introduction
2. Materials and Methods
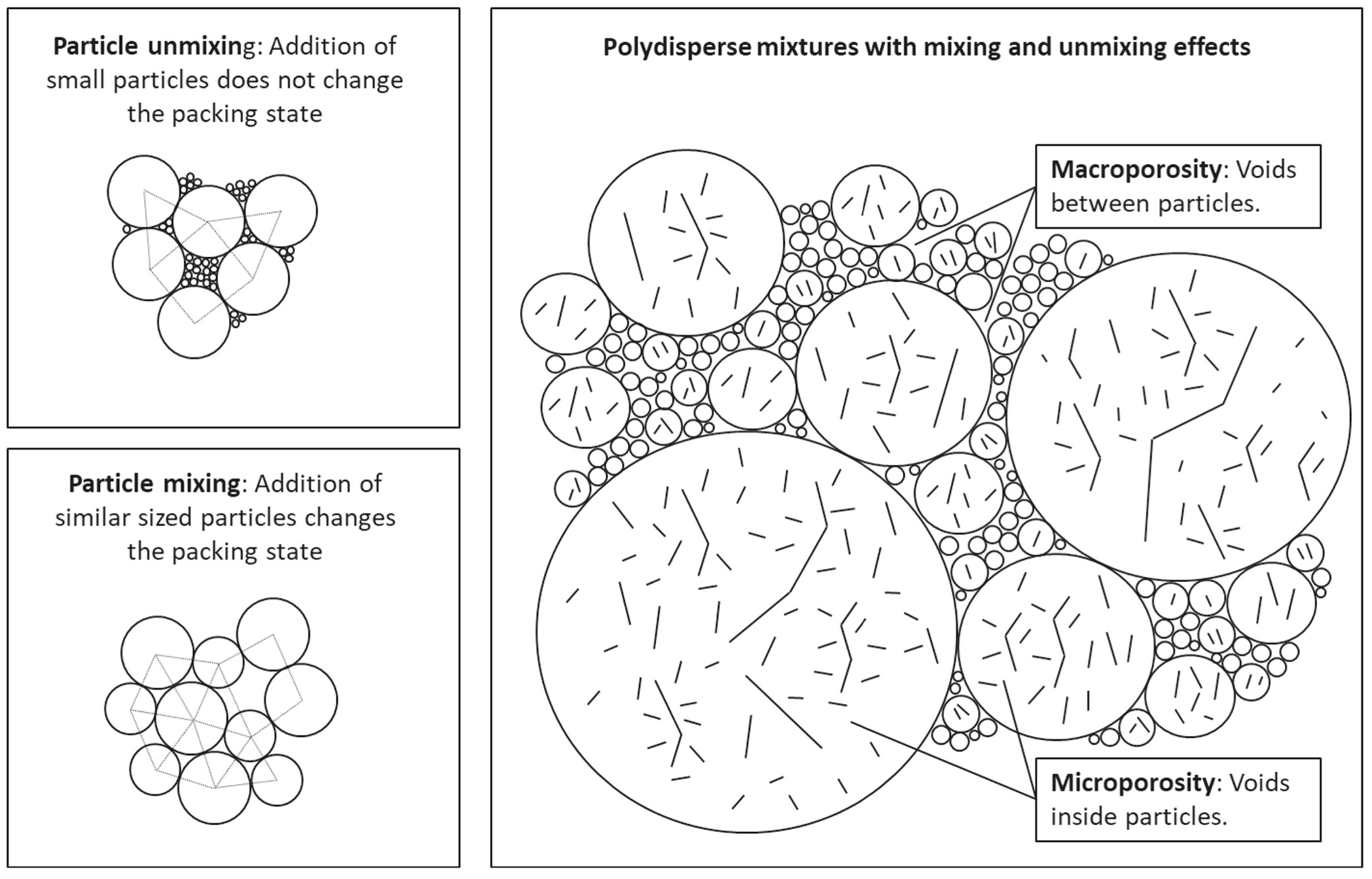
2.1. Definitions: Density, Porosity
2.2. Definition: Bonding
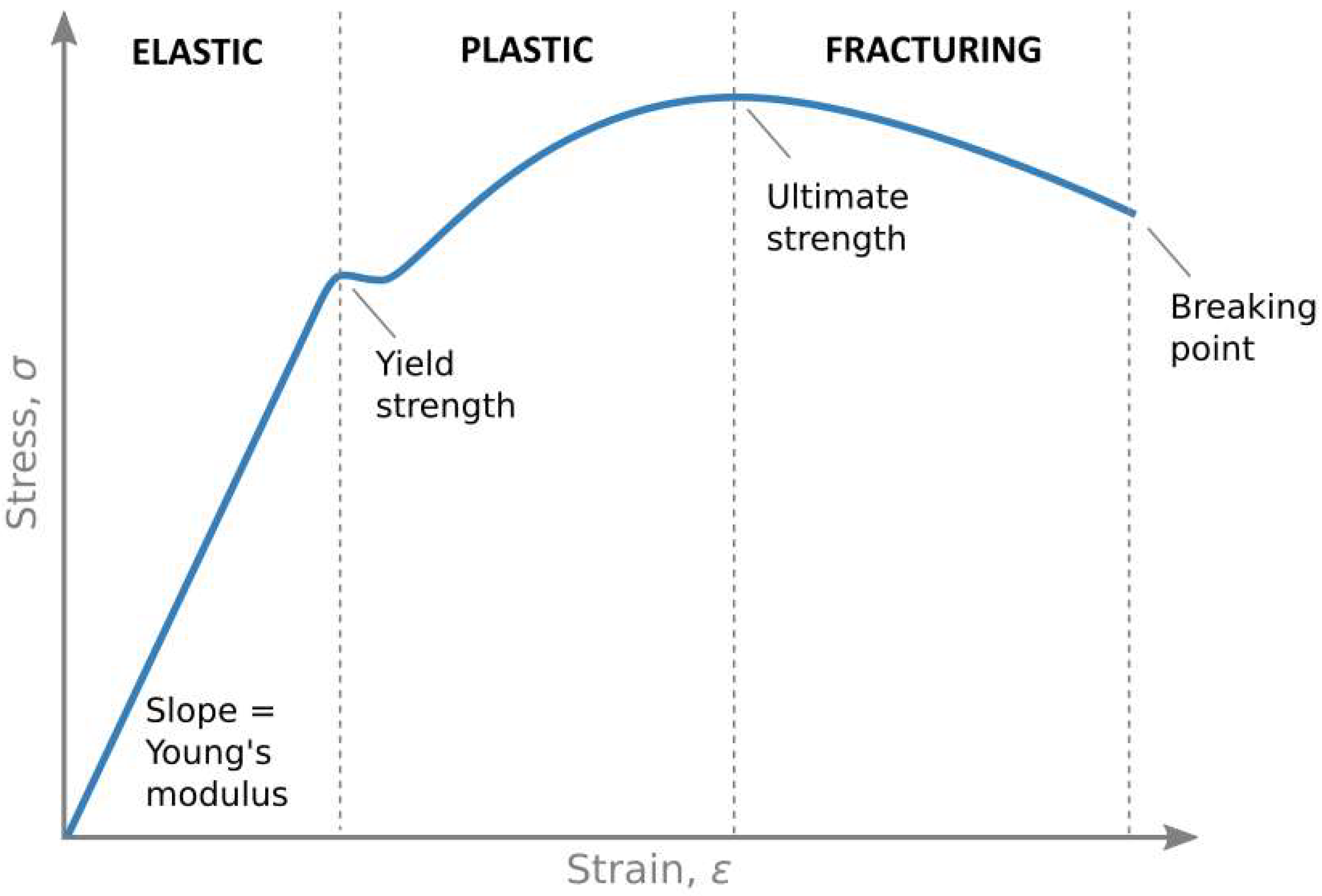
2.3. Definitions: Strength
2.3.1. Strain Rate Dependence of Strength
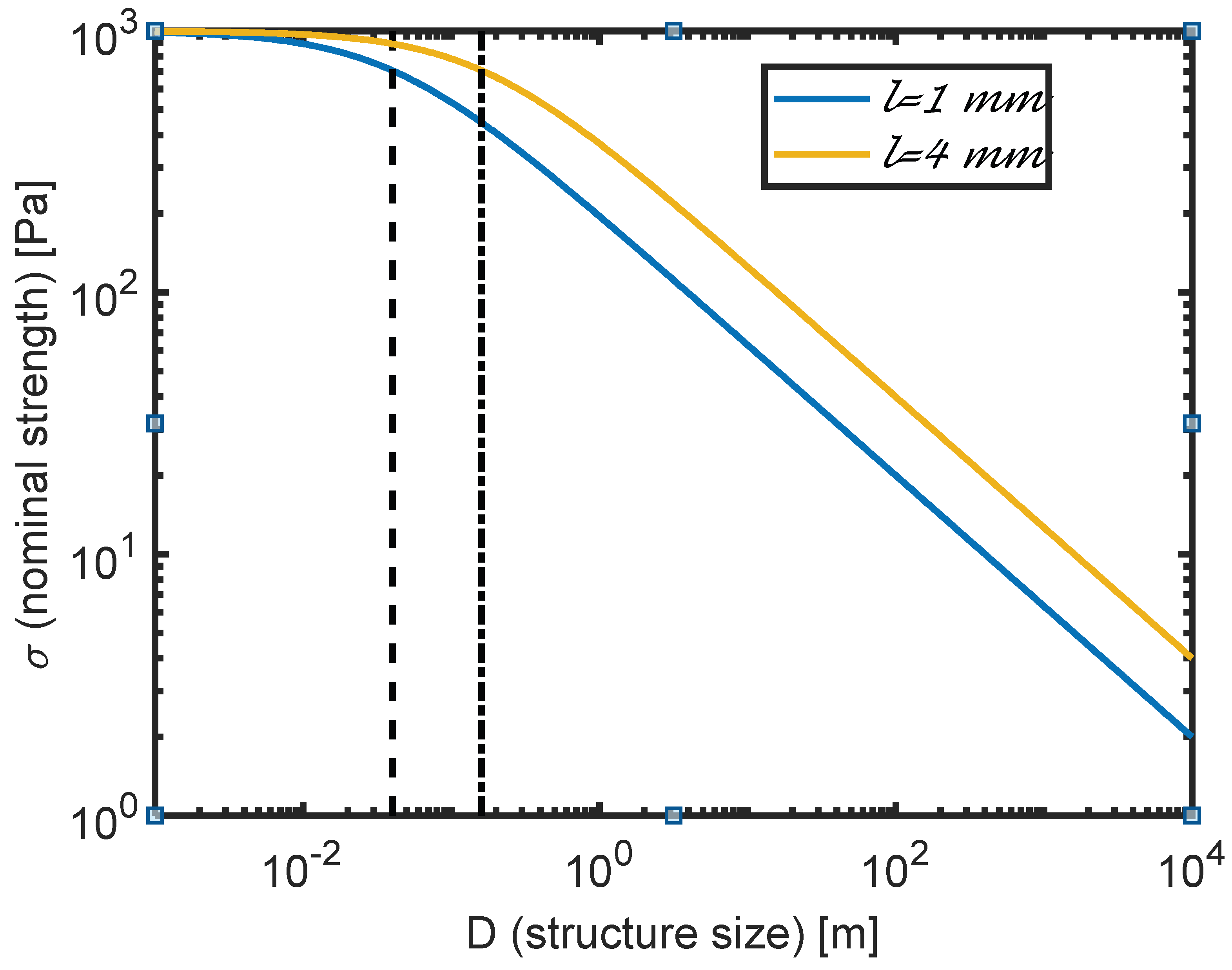
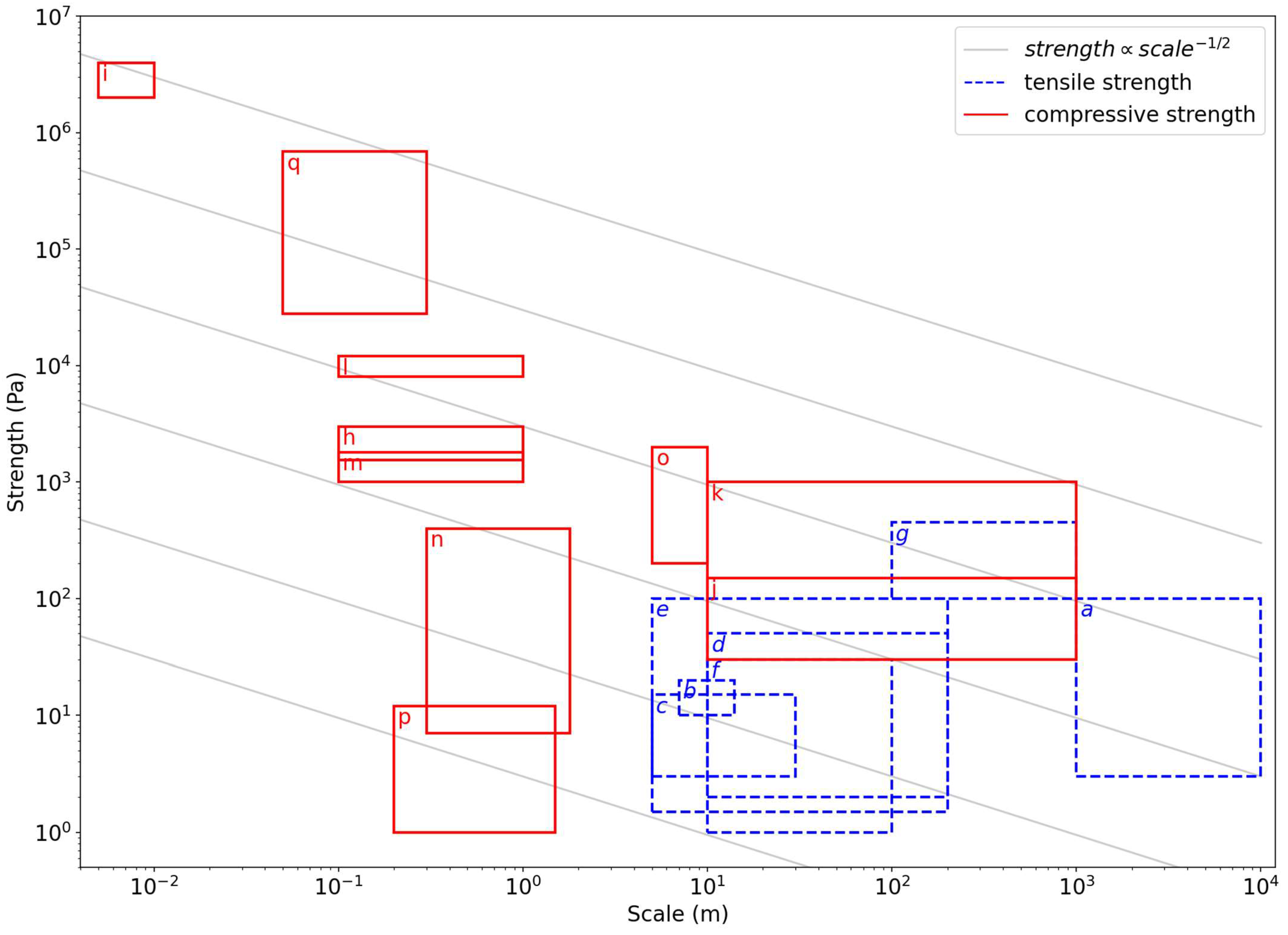
2.3.2. Size Dependence of Strength
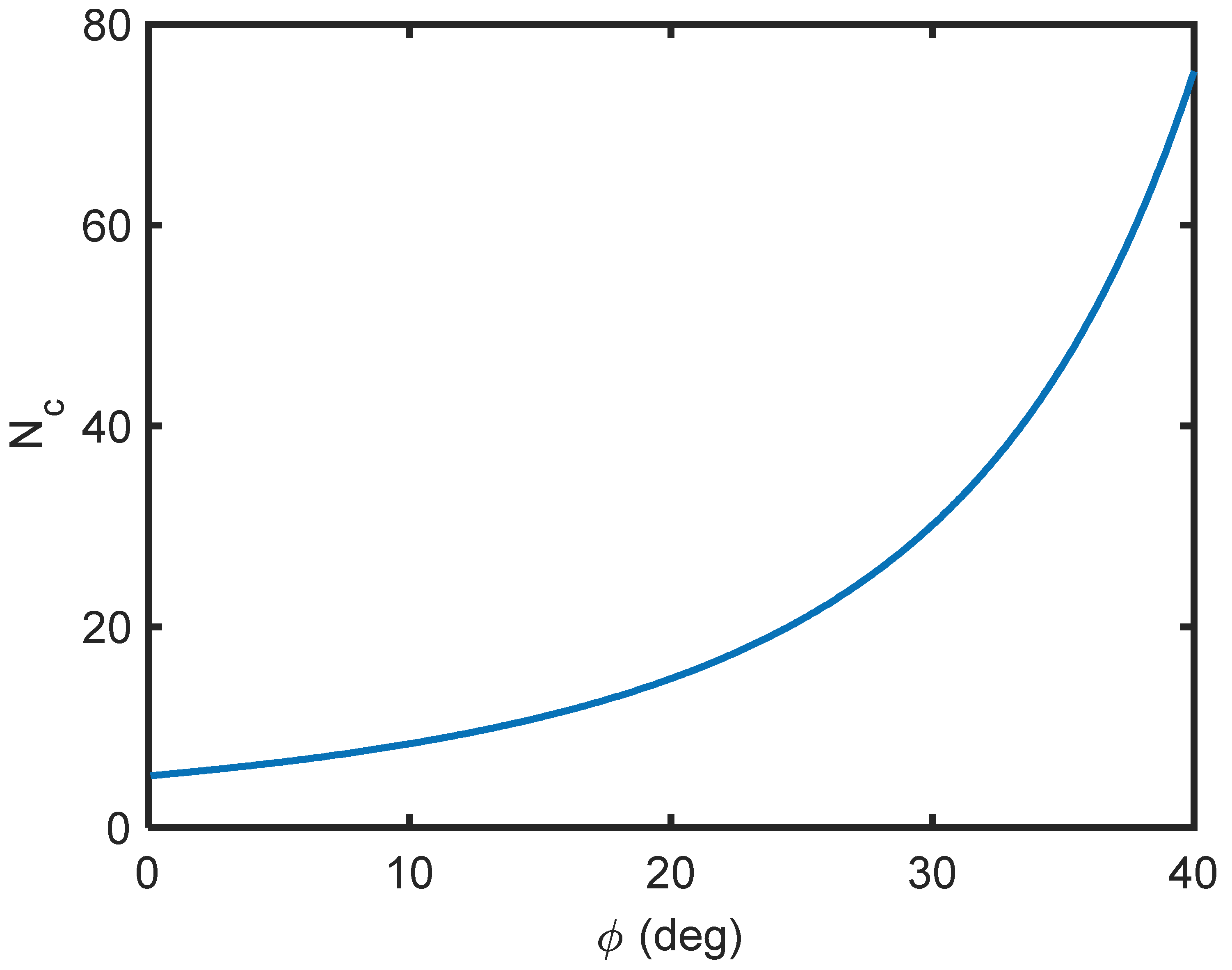
2.3.3. Terminology of Soil Mechanics and Application to Micro-Gravity
3. The Available Data
4. Results from Space Missions (and Telescopic Observations)
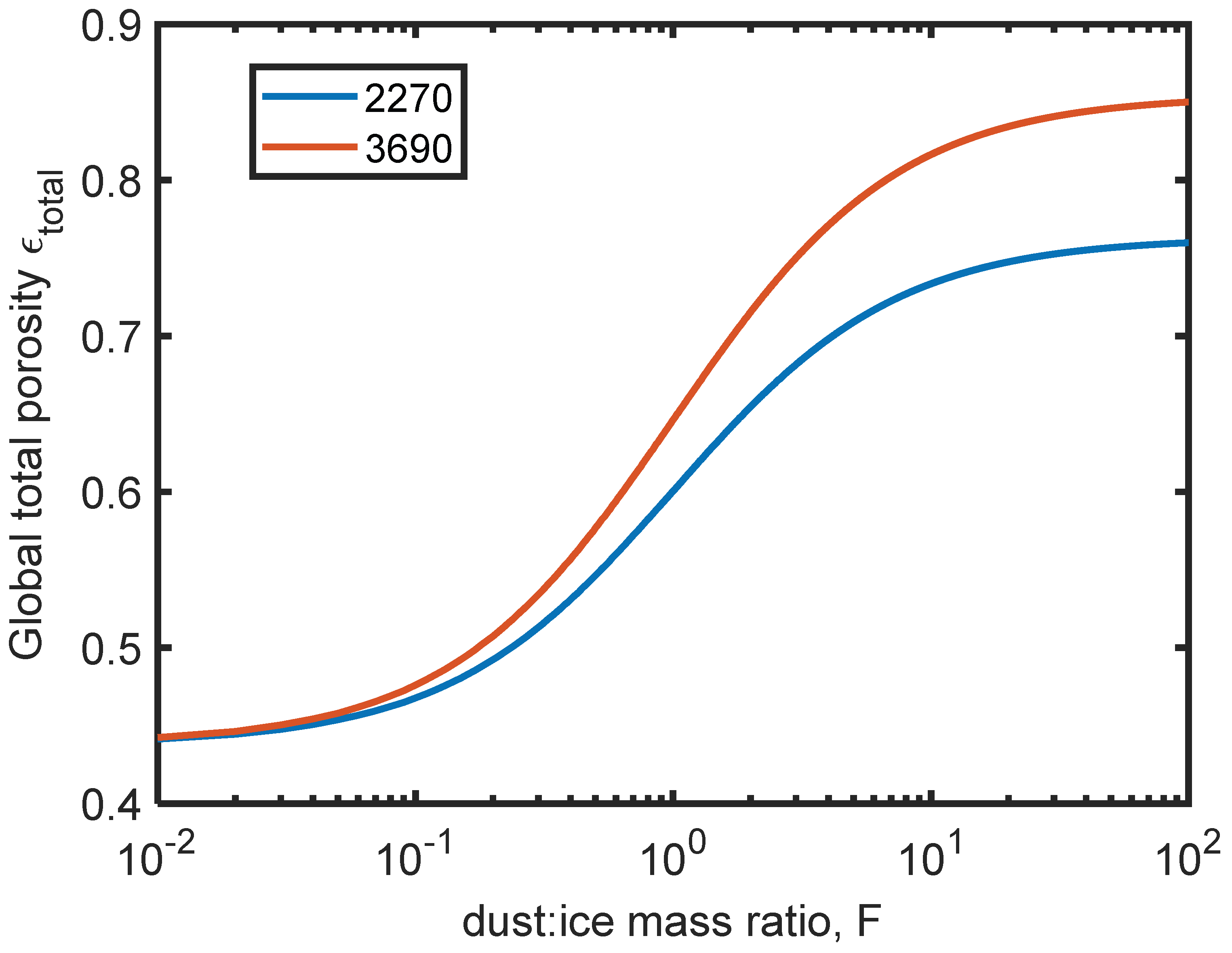
4.1. Porosity
4.2. Strength
4.2.1. Philae’s Collisions: The Putative Ultra-Soft Cometary Material
4.2.2. The Abydos Site of 67P: Review of the Putative Hard Material
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Persson, B.; Biele, J. On the stability of spinning asteroids. Tribol. Lett. 2022, 70, 1–19. [Google Scholar] [CrossRef]
- Groussin, O.; Attree, N.; Brouet, Y.; Ciarletti, V.; Davidsson, B.; Filacchione, G.; Fischer, H.-H.; Gundlach, B.; Knapmeyer, M.; Knollenberg, J. The thermal, mechanical, structural, and dielectric properties of cometary nuclei after Rosetta. Space Sci. Rev. 2019, 215, 29. [Google Scholar] [CrossRef]
- Daniels, K.E. Rubble-pile near Earth objects: Insights from granular physics. In Asteroids; Springer: Berlin/Heidelberg, Germany, 2013; pp. 271–286. [Google Scholar]
- Heiken, G.; Vaniman, D.; French, B.M. Lunar Sourcebook-A User’s Guide to the Moon; Cambridge University Press: Cambridge, UK, 1991; p. 736. [Google Scholar]
- Scott, G.; Kilgour, D. The density of random close packing of spheres. J. Phys. D Appl. Phys. 1969, 2, 863. [Google Scholar] [CrossRef]
- Onoda, G.Y.; Liniger, E.G. Random loose packings of uniform spheres and the dilatancy onset. Phys. Rev. Lett. 1990, 64, 2727–2730. [Google Scholar] [CrossRef]
- Jerkins, M.; Schröter, M.; Swinney, H.L.; Senden, T.J.; Saadatfar, M.; Aste, T. Onset of Mechanical Stability in Random Packings of Frictional Spheres. Phys. Rev. Lett. 2008, 101, 018301. [Google Scholar] [CrossRef]
- Grott, M.; Biele, J.; Michel, P.; Sugita, S.; Schröder, S.; Sakatani, N.; Neumann, W.; Kameda, S.; Michikami, T.; Honda, C. Macroporosity and grain density of rubble pile asteroid (162173) Ryugu. J. Geophys. Res. Planets 2020, 125, e2020JE006519. [Google Scholar] [CrossRef]
- Kiuchi, M.; Nakamura, A.M. Corrigendum to “Relationship between regolith particle size and porosity on small bodies” [Icarus 239 (2014) 291–293]. Icarus 2015, 248, 221. [Google Scholar] [CrossRef]
- Kiuchi, M.; Nakamura, A.M. Relationship between regolith particle size and porosity on small bodies. Icarus 2014, 239, 291–293. [Google Scholar] [CrossRef]
- Thomas, H. Untersuchung der Festigkeit Poröser Eis-Mineral-Körper Kometarer Zusammensetzung. Master’s Thesis, Universität zu Köln, Köln, Germany, 1992. [Google Scholar]
- Molaro, J.L.; Choukroun, M.; Phillips, C.B.; Phelps, E.S.; Hodyss, R.; Mitchell, K.L.; Lora, J.M.; Meirion-Griffith, G. The microstructural evolution of water ice in the solar system through sintering. J. Geophys. Res. Planets 2019, 124, 243–277. [Google Scholar] [CrossRef]
- Kossacki, K.J.; Köinle, N.I.; Kargl, G.; Steiner, G. The influence of grain sintering on the thermoconductivity of porous ice. Planet. Space Sci. 1994, 42, 383–389. [Google Scholar] [CrossRef]
- Holsapple, K.A.; Housen, K.R. Momentum transfer in asteroid impacts. I. Theory and scaling. Icarus 2012, 221, 875–887. [Google Scholar] [CrossRef]
- Housen, K.R.; Sweet, W.J.; Holsapple, K.A. Impacts into porous asteroids. Icarus 2018, 300, 72–96. [Google Scholar] [CrossRef]
- A’Hearn, M.F.; Belton, M.J.S.; Delamere, W.A.; Kissel, J.; Klaasen, K.P.; McFadden, L.A.; Meech, K.J.; Melosh, H.J.; Schultz, P.H.; Sunshine, J.M.; et al. Deep Impact: Excavating Comet Tempel 1. Science 2005, 310, 258–264. [Google Scholar] [CrossRef]
- Watanabe, S.; Tsuda, Y.; Yoshikawa, M.; Tanaka, S.; Saiki, T.; Nakazawa, S. Hayabusa2 mission overview. Space Sci. Rev. 2017, 208, 3–16. [Google Scholar] [CrossRef]
- Cheng, A.F.; Rivkin, A.S.; Michel, P.; Atchison, J.; Barnouin, O.; Benner, L.; Chabot, N.L.; Ernst, C.; Fahnestock, E.G.; Kueppers, M. AIDA DART asteroid deflection test: Planetary defense and science objectives. Planet. Space Sci. 2018, 157, 104–115. [Google Scholar] [CrossRef]
- Rivkin, A.S.; Chabot, N.L.; Stickle, A.M.; Thomas, C.A.; Richardson, D.C.; Barnouin, O.; Fahnestock, E.G.; Ernst, C.M.; Cheng, A.F.; Chesley, S. The double asteroid redirection test (DART): Planetary defense investigations and requirements. Planet. Sci. J. 2021, 2, 173. [Google Scholar] [CrossRef]
- Knollenberg, J. Re-Analysis of MUPUS-TM Thermal Inertia for Abydos; DLR PF: Berlin, Germany, 2020; Unpublished work. [Google Scholar]
- Rüsch, H. Statistische Analyse der Betonfestigkeit; Deutscher Ausschuss für Stahlbeton: Berlin, Germany, 1969. [Google Scholar]
- Spohn, T.; Knollenberg, J.; Ball, A.J.; Banaszkiewicz, M.; Benkhoff, J.; Grott, M.; Grygorczuk, J.; Hüttig, C.; Hagermann, A.; Kargl, G.; et al. Thermal and mechanical properties of the near-surface layers of comet 67P/Churyumov-Gerasimenko. Science 2015, 349, aab0464. [Google Scholar] [CrossRef]
- Biele, J.; Ulamec, S.; Richter, L.; Knollenberg, J.; Kührt, E.; Möhlmann, D. The putative mechanical strength of comet surface material applied to landing on a comet. Acta Astronaut. 2009, 65, 1168–1178. [Google Scholar] [CrossRef]
- Kömle, N.I.; Ball, A.J.; Kargl, G.; Keller, T.; Macher, W.; Thiel, M.; Stöcker, J.; Rohe, C. Impact penetrometry on a comet nucleus—Interpretation of laboratory data using penetration models. Planet. Space Sci. 2001, 49, 575–598. [Google Scholar] [CrossRef]
- Craig, R.F. Craig’s Soil Mechanics; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Ramesh, K.; Hogan, J.D.; Kimberley, J.; Stickle, A. A review of mechanisms and models for dynamic failure, strength, and fragmentation. Planet. Space Sci. 2015, 107, 10–23. [Google Scholar] [CrossRef]
- Housen, K.R.; Holsapple, K.A. Scale effects in strength-dominated collisions of rocky asteroids. Icarus 1999, 142, 21–33. [Google Scholar] [CrossRef]
- Bryson, K.L.; Ostrowski, D.R.; Blasizzo, A. Meteorite flaws and scaling for atmospheric entry. Planet. Space Sci. 2018, 164, 85–90. [Google Scholar] [CrossRef]
- Weibull, W. A statistical theory of strength of materials. Ingeniörs Vetenskaps. Akad. 1939, 151, 1–45. [Google Scholar]
- Trustrum, K.; Jayatilaka, A.D.S. Applicability of Weibull analysis for brittle materials. J. Mater. Sci. 1983, 18, 2765–2770. [Google Scholar] [CrossRef]
- Bažant, Z.P. Size effect on structural strength: A review. Arch. Appl. Mech. 1999, 69, 703–725. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Yu, Q. Universal size effect law and effect of crack depth on quasi-brittle structure strength. J. Eng. Mech. 2009, 135, 78–84. [Google Scholar] [CrossRef]
- Pohl, L. The Physical Properties of Asteroids; University of Central Florida: Orlando, FL, USA, 2020. [Google Scholar]
- Pohl, L.; Britt, D.T. Strengths of meteorites—An overview and analysis of available data. Meteorit. Planet. Sci. 2020, 55, 962–987. [Google Scholar] [CrossRef]
- Poulet, F.; Lucchetti, A.; Bibring, J.-P.; Carter, J.; Gondet, B.; Jorda, L.; Langevin, Y.; Pilorget, C.; Capanna, C.; Cremonese, G. Origin of the local structures at the Philae landing site and possible implications on the formation and evolution of 67P/Churyumov-Gerasimenko. Mon. Not. R. Astron. Soc. 2016, 462, S23–S32. [Google Scholar] [CrossRef]
- García-Triñanes, P.; Luding, S.; Shi, H. Tensile strength of cohesive powders. Adv. Powder Technol. 2019, 30, 2868–2880. [Google Scholar] [CrossRef]
- Reissner, H. Zum Erddruckproblem. In Proceedings of the First International Congress for Applied Mechanics, Delft, The Netherlands, 22–26 April 1924; pp. 295–311. [Google Scholar]
- Terzaghi, K.; Mesri, G.; Peck, R.B. Soil Mechanics in Engineering Practice; Wiley: Hoboken, NJ, USA, 1996. [Google Scholar]
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley and Sons Inc.: New York, NY, USA, 1943; Volume 314. [Google Scholar]
- Meyerhof, G. The ultimate bearing capacity of foudations. Geotechnique 1951, 2, 301–332. [Google Scholar] [CrossRef]
- Lorenz, R.D. Titan’s surface bearing strength: Contact force models for the Dragonfly rotorcraft lander. Planet. Space Sci. 2022, 214, 105449. [Google Scholar] [CrossRef]
- Biele, J.; Ulamec, S.; Richter, L.; Kührt, E.; Knollenberg, J.; Möhlmann, D. The Strength of Cometary Surface Material: Relevance of Deep Impact Results for Philae Landing on a Comet. In Deep Impact as a World Observatory Event: Synergies in Space, Time, and Wavelength; Springer: Berlin/Heidelberg, Germany, 2009; pp. 285–300. [Google Scholar]
- Rosetta Lander Mission Analysis Working Group. Comet Surface Engineering Model; RO-ESC-RP-5006; ESA: Noordwijk, The Netherlands, 1999. [Google Scholar]
- Blum, J.; Schräpler, R.; Davidsson, B.J.; Trigo-Rodriguez, J.M. The physics of protoplanetesimal dust agglomerates. I. Mechanical properties and relations to primitive bodies in the solar system. Astrophys. J. 2006, 652, 1768. [Google Scholar] [CrossRef]
- Biele, J.; Ulamec, S. Capabilities of Philae, the Rosetta Lander. Space Sci. Rev. 2007, 138, 275–289. [Google Scholar] [CrossRef]
- Biele, J.; Ulamec, S.; Feuerbacher, B.; Rosenbauer, H.; Mugnolo, D.; Moura, D.; Bibring, J.P. Current status and scientific capabilities of the ROSETTA Lander payload. Adv. Space Res. 2002, 29, 1199–1208. [Google Scholar] [CrossRef]
- Kömle, N.I.; Ball, A.J.; Kargl, G.; Stöcker, J.; Thiel, M.; Jolly, H.S.; Dziruni, M.; Zarnecki, J.C. Using the anchoring device of a comet lander to determine surface mechanical properties. Planet. Space Sci. 1997, 45, 1515–1538. [Google Scholar] [CrossRef]
- Mellor, M. A review of basic snow mechanics. In Proceedings of the Grindelwald Symposium, International Symposium of Snow Mechanics, Grindelwald, Switzerland, 1–5 April 1974; pp. 251–291. [Google Scholar]
- Petrovic, J. Review mechanical properties of ice and snow. J. Mater. Sci. 2003, 38, 1–6. [Google Scholar] [CrossRef]
- Litwin, K.L.; Zygielbaum, B.R.; Polito, P.J.; Sklar, L.S.; Collins, G.C. Influence of temperature, composition, and grain size on the tensile failure of water ice: Implications for erosion on Titan. J. Geophys. Res. 2012, 117, E08013. [Google Scholar] [CrossRef]
- Schulson, E.M.; Duval, P. Creep and Fracture of Ice; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Schulson, E. The structure and mechanical behavior of ice. JOM 1999, 51, 21–27. [Google Scholar] [CrossRef]
- Jessberger, H.; Kotthaus, M. Compressive strength of synthetic comet nucleus samples. In Proceedings of the Physics and Mechanics of Cometary Materials, Munster, Germany, 9–11 October 1989. [Google Scholar]
- Bar-Nun, A.; Laufer, D. First experimental studies of large samples of gas-laden amorphous “cometary” ices. Icarus 2003, 161, 157–163. [Google Scholar] [CrossRef]
- Pätzold, M.; Andert, T.; Hahn, M.; Asmar, S.W.; Barriot, J.P.; Bird, M.K.; Häusler, B.; Peter, K.; Tellmann, S.; Grün, E.; et al. A homogeneous nucleus for comet 67P/Churyumov–Gerasimenko from its gravity field. Nature 2016, 530, 63–65. [Google Scholar] [CrossRef]
- Richardson, J.E.; Melosh, H.J.; Lisse, C.M.; Carcich, B.J.I. A ballistics analysis of the Deep Impact ejecta plume: Determining Comet Tempel 1’s gravity, mass, and density. Icarus 2007, 191, 176–209. [Google Scholar] [CrossRef]
- Pätzold, M.; Andert, T.P.; Hahn, M.; Barriot, J.-P.; Asmar, S.W.; Häusler, B.; Bird, M.K.; Tellmann, S.; Oschlisniok, J.; Peter, K. The Nucleus of comet 67P/Churyumov-Gerasimenko—Part I: The global view—nucleus mass, mass-loss, porosity, and implications. Mon. Not. R. Astron. Soc. 2019, 483, 2337–2346. [Google Scholar] [CrossRef]
- Britt, D.; Yeomans, D.; Housen, K.; Consolmagno, G. Asteroid density, porosity, and structure. In Asteroids III; The University of Arizona: Tucson, AZ, USA, 2002. [Google Scholar]
- Kofman, W.; Herique, A.; Barbin, Y.; Barriot, J.-P.; Ciarletti, V.; Clifford, S.; Edenhofer, P.; Elachi, C.; Eyraud, C.; Goutail, J.-P. Properties of the 67P/Churyumov-Gerasimenko interior revealed by CONSERT radar. Science 2015, 349, aab0639. [Google Scholar] [CrossRef] [PubMed]
- Brouet, Y.; Levasseur-Regourd, A.C.; Sabouroux, P.; Neves, L.; Encrenaz, P.; Poch, O.; Pommerol, A.; Thomas, N.; Kofman, W.; Le Gall, A.; et al. A porosity gradient in 67P/C-G nucleus suggested from CONSERT and SESAME-PP results: An interpretation based on new laboratory permittivity measurements of porous icy analogues. Mon. Not. R. Astron. Soc. 2016, 462, S89–S98. [Google Scholar] [CrossRef]
- Herique, A.; Kofman, W.; Zine, S.; Blum, J.; Vincent, J.-B.; Ciarletti, V. Homogeneity of 67P/Churyumov-Gerasimenko as seen by CONSERT: Implication on composition and formation. Astron. Astrophys. 2019, 630, A6. [Google Scholar] [CrossRef]
- Marschall, R.; Markkanen, J.; Gerig, S.-B.; Pinzón-Rodríguez, O.; Thomas, N.; Wu, J.-S. The dust-to-gas ratio, size distribution, and dust fall-back fraction of comet 67p/Churyumov-Gerasimenko: Inferences from linking the optical and dynamical properties of the inner comae. Front. Phys. 2020, 8, 227. [Google Scholar] [CrossRef]
- Fulle, M.; Blum, J.; Rotundi, A.; Gundlach, B.; Güttler, C.; Zakharov, V. How comets work: Nucleus erosion versus dehydration. Mon. Not. R. Astron. Soc. 2020, 493, 4039–4044. [Google Scholar] [CrossRef]
- Choukroun, M.; Altwegg, K.; Kührt, E.; Biver, N.; Bockelée-Morvan, D.; Drążkowska, J.; Hérique, A.; Hilchenbach, M.; Marschall, R.; Pätzold, M. Dust-to-gas and refractory-to-ice mass ratios of comet 67P/Churyumov-Gerasimenko from Rosetta observations. Space Sci. Rev. 2020, 216, 1–38. [Google Scholar] [CrossRef]
- Davidsson, B.J.R. Tidal Splitting and Rotational Breakup of Solid Biaxial Ellipsoids. Icarus 2001, 149, 375–383. [Google Scholar] [CrossRef]
- Asphaug, E.; Benz, W. Size, Density, and Structure of Comet Shoemaker-Levy 9 Inferred from the Physics of Tidal Breakup. Icarus 1996, 121, 225–248. [Google Scholar] [CrossRef]
- Klinger, J.; Espinasse, S.; Schmidt, B. Some considerations on cohesive forces in sun-grazing comets. In Physics and Mechanics of Cometary Materials; Hunt, J.J., Guyenne, T.D., Eds.; ESA Special Publication: Noordwijk, The Netherlands, 1989; Volume 302, pp. 197–200. [Google Scholar]
- Vincent, J.-B.; Bodewits, D.; Besse, S.; Sierks, H. Large heterogeneities in comet 67P as revealed by active pits from sinkhole collapse. Nature 2015, 523, 63–66. [Google Scholar] [CrossRef]
- Vincent, J.-B.; Hviid, S.F.; Mottola, S.; Kührt, E.; Kuehrt, E.; Preusker, F.; Scholten, F.; Keller, H.U.; Oklay, N.; de Niem, D.; et al. Constraints on cometary surface evolution derived from a statistical analysis of 67P’s topography. Mon. Not. R. Astron. Soc. 2017, 469, S329–S338. [Google Scholar] [CrossRef]
- Groussin, O.; Jorda, L.; Auger, A.-T.; Kührt, E.; Gaskell, R.; Capanna, C.; Scholten, F.; Preusker, F.; Lamy, P.; Hviid, S.; et al. Gravitational slopes, geomorphology, and material strengths of the nucleus of comet 67P/Churyumov-Gerasimenko from OSIRIS observations. Astron. Astrophys. 2015, 583, A32. [Google Scholar] [CrossRef]
- Attree, N.; Groussin, O.; Jorda, L.; Nébouy, D.; Thomas, N.; Brouet, Y.; Kührt, E.; Preusker, F.; Scholten, F.; Knollenberg, J.; et al. Tensile strength of 67P/Churyumov-Gerasimenko nucleus material from overhangs. Astron. Astrophys. 2018, 611, A33. [Google Scholar] [CrossRef]
- Basilevsky, A.T.; Krasil’nikov, S.S.; Shiryaev, A.A.; Mall, U.; Keller, H.U.; Skorov, Y.V.; Mottola, S.; Hviid, S.F. Estimating the strength of the nucleus material of comet 67P Churyumov-Gerasimenko. Sol. Syst. Res. 2016, 50, 225–234. [Google Scholar] [CrossRef]
- Thomas, N.; Sierks, H.; Barbieri, C.; Lamy, P.L.; Rodrigo, R.; Rickman, H.; Koschny, D.; Keller, H.U.; Agarwal, J.; A’Hearn, M.F. The morphological diversity of comet 67P/Churyumov-Gerasimenko. Science 2015, 347, aaa0440. [Google Scholar] [CrossRef]
- Holsapple, K.A.; Housen, K.R. A crater and its ejecta: An interpretation of Deep Impact. Icarus 2007, 187, 345–356. [Google Scholar] [CrossRef]
- Pajola, M.; Vincent, J.-B.; Güttler, C.; Lee, J.-C.; Bertini, I.; Massironi, M.; Simioni, E.; Marzari, F.; Giacomini, L.; Lucchetti, A.; et al. Size-frequency distribution of boulders ≥7 m on comet 67P/Churyumov-Gerasimenko. Astron. Astrophys. 2015, 583, A37. [Google Scholar] [CrossRef]
- Pajola, M.; Oklay, N.; La Forgia, F.; Giacomini, L.; Massironi, M.; Bertini, I.; El-Maarry, M.R.; Marzari, F.; Preusker, F.; Scholten, F.; et al. Aswan site on comet 67P/Churyumov-Gerasimenko: Morphology, boulder evolution, and spectrophotometry. Astron. Astrophys. 2016, 592, A69. [Google Scholar] [CrossRef]
- El-Maarry, M.R.; Groussin, O.; Thomas, N.; Pajola, M.; Auger, A.-T.; Davidsson, B.; Hu, X.; Hviid, S.F.; Knollenberg, J.; Güttler, C.; et al. Surface changes on comet 67P/Churyumov-Gerasimenko suggest a more active past. Science 2017, 355, 1392–1395. [Google Scholar] [CrossRef]
- Vincent, J.-B.; Birch, S.; Hayes, A.; Zacny, K.; Oklay, N.; Cambianica, P. Bouncing boulders on comet 67P. In Proceedings of the EPSC-DPS Joint Meeting 2019, Geneva, Switzerland, 15–20 September 2019; p. EPSC-DPS2019-2502. [Google Scholar]
- Richardson, J.E.; Jay Melosh, H. An examination of the Deep Impact collision site on Comet Tempel 1 via Stardust-NExT: Placing further constraints on cometary surface properties. Icarus 2013, 222, 492–501. [Google Scholar] [CrossRef]
- Biele, J.; Ulamec, S.; Maibaum, M.; Roll, R.; Witte, L.; Jurado, E.; Munoz, P.; Arnold, W.; Auster, H.U.; Casas, C.; et al. The Landing(s) of Philae and Inferences on Comet Surface Mechanical Properties. Science 2015, 349, aaa9816. [Google Scholar] [CrossRef] [PubMed]
- Roll, R.; Witte, L. ROSETTA lander Philae: Touch-down reconstruction. Planet. Space Sci. 2016, 125, 12–19. [Google Scholar] [CrossRef]
- Roll, R.; Witte, L.; Arnold, W. ROSETTA lander Philae–soil strength analysis. Icarus 2016, 280, 359–365. [Google Scholar] [CrossRef]
- Jurado, E.; Martin, T.; Canalias, E.; Blazquez, A.; Garmier, R.; Ceolin, T.; Gaudon, P.; Delmas, C.; Biele, J.; Ulamec, S.; et al. Rosetta lander Philae: Flight Dynamics analyses for landing site selection and post-landing operations. Acta Astronaut. 2016, 125, 65–79. [Google Scholar] [CrossRef]
- Heinisch, P.; Auster, H.U.; Gundlach, B.; Blum, J.; Güttler, C.; Tubiana, C.; Sierks, H.; Hilchenbach, M.; Biele, J.; Richter, I.; et al. Compressive strength of comet 67P/Churyumov-Gerasimenko derived from Philae surface contacts. Astron. Astrophys. 2019, 630, A2. [Google Scholar] [CrossRef]
- Heinisch, P.; Auster, H.-U.; Richter, I.; Hercik, D.; Jurado, E.; Garmier, R.; Güttler, C.; Glassmeier, K.-H. Attitude reconstruction of ROSETTA’s Lander PHILAE using two-point magnetic field observations by ROMAP and RPC-MAG. Acta Astronaut. 2016, 125, 174–182. [Google Scholar] [CrossRef]
- O’Rourke, L.; Heinisch, P.; Blum, J.; Fornasier, S.; Filacchione, G.; Van Hoang, H.; Ciarniello, M.; Raponi, A.; Gundlach, B.; Blasco, R.A.; et al. The Philae lander reveals low-strength primitive ice inside cometary boulders. Nature 2020, 586, 697–701. [Google Scholar] [CrossRef]
- Knapmeyer, M.; Fischer, H.H.; Knollenberg, J.; Seidensticker, K.J.; Thiel, K.; Arnold, W.; Faber, C.; Möhlmann, D. Structure and elastic parameters of the near surface of Abydos site on comet 67P/Churyumov-Gerasimenko, as obtained by SESAME/CASSE listening to the MUPUS insertion phase. Icarus 2018, 310, 165–193. [Google Scholar] [CrossRef]
- Sunday, C.; Murdoch, N.; Wilhelm, A.; Drilleau, M.; Zhang, Y.; Tardivel, S.; Michel, P. The influence of gravity on granular impacts-II. A gravity-scaled collision model for slow interactions. Astron. Astrophys. 2022, 658, A118. [Google Scholar] [CrossRef]
- Faug, T. Macroscopic force experienced by extended objects in granular flows over a very broad Froude-number range. Eur. Phys. J. E 2015, 38, 34. [Google Scholar] [CrossRef]
- Rumpf, H. The strength of granules and agglomerates. In Proceedings of the Agglomeration—Proceedings of the First International Symposium on Agglomeration, Philadelphia, PA, USA, 12–14 April 1961; pp. 379–418. [Google Scholar]
- Bika, D.G.; Gentzler, M.; Michaels, J.N. Mechanical properties of agglomerates. Powder Technol. 2001, 117, 98–112. [Google Scholar] [CrossRef]
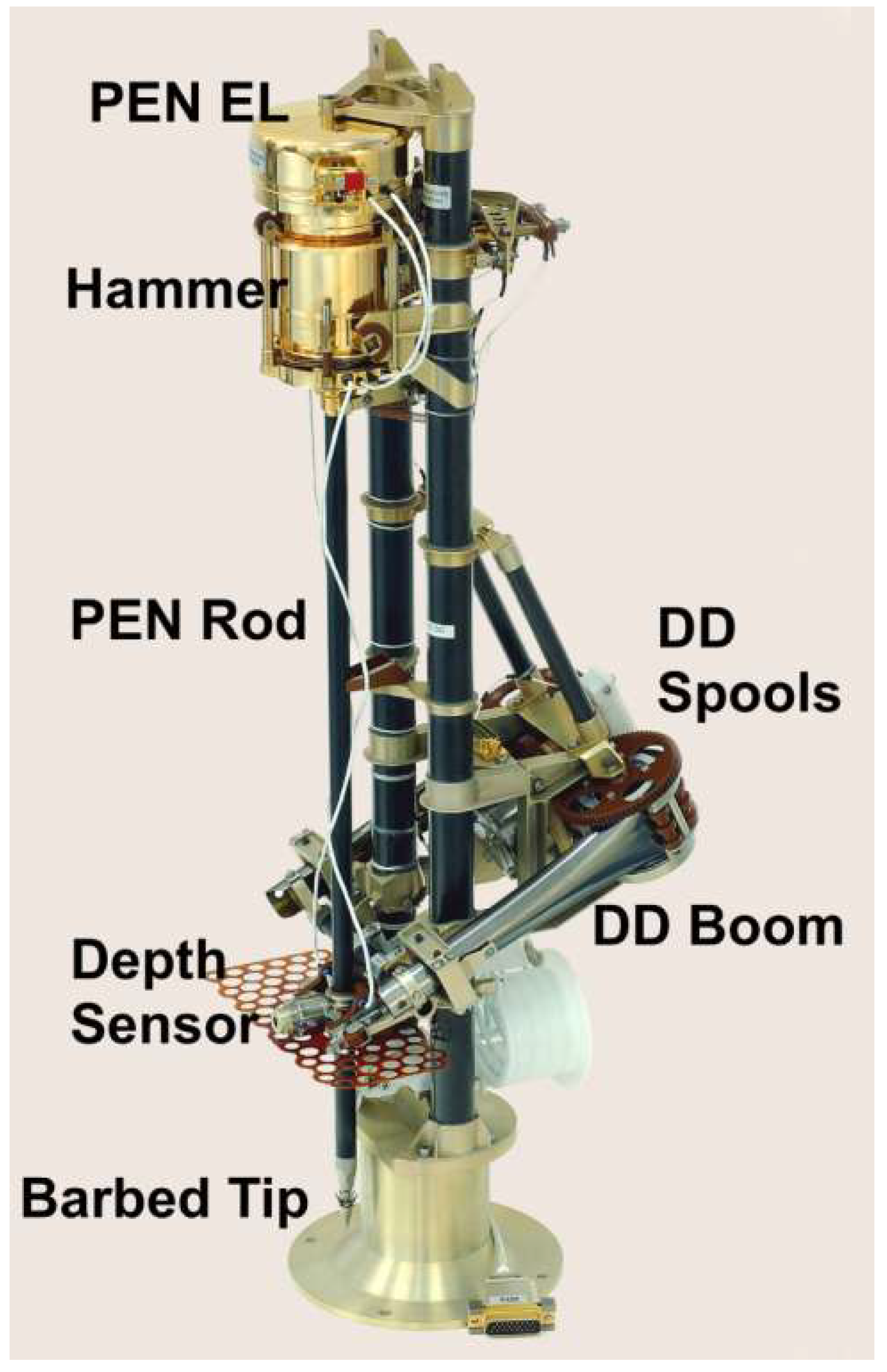
- Spohn, T.; Seiferlin, K.; Hagermann, A.; Knollenberg, J.; Ball, A.J.; Banaszkiewicz, M.; Benkhoff, J.; Gadomski, S.; Gregorczyk, W.; Grygorczuk, J. MUPUS—A thermal and mechanical properties probe for the Rosetta lander Philae. Space Sci. Rev. 2007, 128, 339–362. [Google Scholar] [CrossRef]
- Seidensticker, K.J.; Möhlmann, D.; Apathy, I.; Schmidt, W.; Thiel, K.; Arnold, W.; Fischer, H.-H.; Kretschmer, M.; Madlener, D.; Péter, A. Sesame—An experiment of the rosetta lander philae: Objectives and general design. Space Sci. Rev. 2007, 128, 301–337. [Google Scholar] [CrossRef]
- Ulamec, S.; O’Rourke, L.; Biele, J.; Grieger, B.; Andrés, R.; Lodiot, S.; Muñoz, P.; Charpentier, A.; Mottola, S.; Knollenberg, J. Rosetta Lander-Philae: Operations on comet 67P/Churyumov-Gerasimenko, analysis of wake-up activities and final state. Acta Astronaut. 2017, 137, 38–43. [Google Scholar] [CrossRef]
- Grygorczuk, J.; Banaszkiewicz, M.; Seweryn, K.; Spoin, T. MUPUS insertion device for the Rosetta mission. J. Telecommun. Inf. Technol. 2007, 1, 50–53. [Google Scholar]
- Schröder, S.; Mottola, S.; Arnold, G.; Grothues, H.-G.; Jaumann, R.; Keller, H.; Michaelis, H.; Bibring, J.-P.; Pelivan, I.; Koncz, A. Close-up images of the final Philae landing site on comet 67P/Churyumov-Gerasimenko acquired by the ROLIS camera. Icarus 2017, 285, 263–274. [Google Scholar] [CrossRef][Green Version]
- Biele, J.; Kührt, E.; Senshu, H.; Sakatani, N.; Ogawa, K.; Hamm, M.; Grott, M.; Okada, T.; Arai, T. Effects of dust layers on thermal emission from airless bodies. Prog. Earth Planet. Sci. 2019, 6, 48. [Google Scholar] [CrossRef]
- Biele, J.; Grott, M.; Zolensky, M.E.; Benisek, A.; Dachs, E. The specific heat capacity of astro-material I: Review of theoretical concepts, materials and techniques. Int. J. Thermophys. 2022, 43, 143. [Google Scholar] [CrossRef]
- Schloerb, F.P.; Keihm, S.; Von Allmen, P.; Choukroun, M.; Lellouch, E.; Leyrat, C.; Beaudin, G.; Biver, N.; Bockelée-Morvan, D.; Crovisier, J. MIRO observations of subsurface temperatures of the nucleus of 67P/Churyumov-Gerasimenko. Astron. Astrophys. 2015, 583, A29. [Google Scholar] [CrossRef]
- Sakatani, N.; Ogawa, K.; Iijima, Y.; Arakawa, M.; Honda, R.; Tanaka, S. Thermal conductivity model for powdered materials under vacuum based on experimental studies. AIP Adv. 2017, 7, 015310. [Google Scholar] [CrossRef]
- Digby, P. The effective elastic moduli of porous granular rocks. J. Appl. Mech. 1981, 48, 803–808. [Google Scholar] [CrossRef]
- Grott, M.; Knollenberg, J.; Hamm, M.; Ogawa, K.; Jaumann, R.; Otto, K.A.; Delbo, M.; Michel, P.; Biele, J.; Neumann, W. Low thermal conductivity boulder with high porosity identified on C-type asteroid (162173) Ryugu. Nat. Astron. 2019, 3, 971–976. [Google Scholar] [CrossRef]
- Andersson, O.; Suga, H. Thermal conductivity of the Ih and XI phases of ice. Phys. Rev. B 1994, 50, 6583–6588. [Google Scholar] [CrossRef]
- Andersson, O.; Inaba, A. Thermal conductivity of crystalline and amorphous ices and its implications on amorphization and glassy water. Phys. Chem. Chem. Phys. 2005, 7, 1441–1449. [Google Scholar] [CrossRef] [PubMed]
- Hobbs, P.V. Ice Physics; Clarendon: New York, NY, USA, 1974; p. 837. [Google Scholar]
- Lintzén, N.; Edeskär, T. Uniaxial strength and deformation properties of machine-made snow. J. Cold Reg. Eng. 2015, 29, 04014020. [Google Scholar] [CrossRef]
- Karagianni, A.; Karoutzos, G.; Ktena, S.; Vagenas, N.; Vlachopoulos, I.; Sabatakakis, N.; Koukis, G. Elastic properties of rocks. Bull. Geol. Soc. Greece 2010, 43, 1165–1168. [Google Scholar] [CrossRef]
- Sun, W.-J.; Kothari, S.; Sun, C.C. The relationship among tensile strength, Young’s modulus, and indentation hardness of pharmaceutical compacts. Powder Technol. 2018, 331, 1–6. [Google Scholar] [CrossRef]
- Matonti, C.; Attree, N.; Groussin, O.; Jorda, L.; Viseur, S.; Hviid, S.F.; Bouley, S.; Nébouy, D.; Auger, A.-T.; Lamy, P.L.; et al. Bilobate comet morphology and internal structure controlled by shear deformation. Nat. Geosci. 2019, 12, 157–162. [Google Scholar] [CrossRef]
- Möhlmann, D.; Seidensticker, K.J.; Fischer, H.-H.; Faber, C.; Flandes, A.; Knapmeyer, M.; Krüger, H.; Roll, R.; Scholten, F.; Thiel, K.; et al. Compressive strength and elastic modulus at Agilkia on comet 67P/Churyumov-Gerasimenko derived from the SESAME/CASSE touchdown signals. Icarus 2018, 303, 251–264. [Google Scholar] [CrossRef]

| Material | Tensile Strength/kPa (Depth If Sintered from Top) | Comments | Ref. |
|---|---|---|---|
| Snow | 0.3–2000 | in air | [49] |
| H2O ice, porous (73%), sintered | 1000 (0...0.1 m) 100 (0.1...0.5 m) 500 (0.5...0.65 m) 1000 (>0.65 m) | ρ0 = 261 kgm−3, strongly sintered (compact ice crust of a few cm, below texture of well-sintered snow) | [24] |
| CO2 ice, porous (48%) | 2400 (crust) 200...500 (below) | CO2 ice powder, sintered. ρ0 = 806 kgm−3 | [24] |
| Solid ice | 700–3000 | −15 °C, increases moderately for lower temperatures | [49,50] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biele, J.; Vincent, J.-B.; Knollenberg, J. Mechanical Properties of Cometary Surfaces. Universe 2022, 8, 487. https://doi.org/10.3390/universe8090487
Biele J, Vincent J-B, Knollenberg J. Mechanical Properties of Cometary Surfaces. Universe. 2022; 8(9):487. https://doi.org/10.3390/universe8090487
Chicago/Turabian StyleBiele, Jens, Jean-Baptiste Vincent, and Jörg Knollenberg. 2022. "Mechanical Properties of Cometary Surfaces" Universe 8, no. 9: 487. https://doi.org/10.3390/universe8090487
APA StyleBiele, J., Vincent, J.-B., & Knollenberg, J. (2022). Mechanical Properties of Cometary Surfaces. Universe, 8(9), 487. https://doi.org/10.3390/universe8090487






