The Higgs Trilinear Coupling and the Scale of New Physics for the SM-Axion-Seesaw-Higgs Portal Inflation (SMASH) Model
Abstract
:1. Introduction
2. Theory
3. Methods
- Allow the quartic and Yukawa couplings of the theory to remain positive and perturbative up to the Planck scale;
- Utilize a threshold correction mechanism to via ;
- Avoid the overproduction of dark radiation via the cosmic axion background (requiring );
- Produce a significant contribution matter–antimatter asymmetry via leptogenesis (requiring hierarchy between the heavy neutrinos);
- Produce a ∼5% correction to triple Higgs coupling .
4. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | We integrate out at the tree level and then compute loop corrections to the triple Higgs coupling in the resulting effective theory with integrated out. By construction, the effective theory is just the SM plus higher-dimensional operators suppressed by inverse powers of . Deviations from the SM triple Higgs coupling can then only come from the effects of the higher-dimensional operators, and so these deviations should involve the inverse powers of which are in Equation (17). In other words, in the limit , one should recover the SM result, which Equation (17) does satisfy. |
| 2 | We acknowledge that neutrino Yukawa coupling matrix should be complex in order to allow the leptogenesis scenario to work. The vacuum stability analysis, however, is unaffected by this, and we can safely ignore the imaginary parts of the Yukawa couplings in this part of the analysis. |
| 3 | https://pdg.lbl.gov/2022/reviews/rpp2022-rev-higgs-boson.pdf, page 29–30, chapter 11, Section 3.4.2 and page 66, chapter 11, Section 6.2.5. |
References
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdelalim, A.A.; Aben, R.; Abi, B.; Abolins, M.; AbouZeid, O.S.; et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012, 716, 1–29. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; et al. Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC. Phys. Lett. B 2012, 716, 30–61. [Google Scholar] [CrossRef]
- Workman, R.L.; Burkert, V.D.; Crede, V.; Klempt, E.; Thoma, U.; Tiator, L.; Agashe, K.; Aielli, G.; Allanach, B.C.; Amsler, C.; et al. Review of Particle Physics. PTEP 2022, 2022, 083C01. [Google Scholar] [CrossRef]
- Bass, S.D.; De Roeck, A.; Kado, M. The Higgs boson implications and prospects for future discoveries. Nat. Rev. Phys. 2021, 3, 608–624. [Google Scholar] [CrossRef]
- Alekhin, S.; Djouadi, A.; Moch, S. The top quark and Higgs boson masses and the stability of the electroweak vacuum. Phys. Lett. B 2012, 716, 214–219. [Google Scholar] [CrossRef]
- Nielsen, H.B.; Froggatt, C.D. Anomalies from Non-Perturbative Standard Model Effects. arXiv 2019, arXiv:1905.00070. [Google Scholar]
- Arbuzov, B.A.; Zaitsev, I.V. Calculation of the contribution to muon g − 2 due to the effective anomalous three boson interaction and the new experimental result. Int. J. Mod. Phys. A 2021, 36, 2150223. [Google Scholar] [CrossRef]
- Arbuzov, B.A. The discrepancy in the muon g − 2 is a non-perturbative effect of the Standard Model. arXiv 2013, arXiv:1304.7090. [Google Scholar]
- Wang, J.; Wen, X.G. Nonperturbative definition of the standard models. Phys. Rev. Res. 2020, 2, 023356. [Google Scholar] [CrossRef]
- Arbuzov, B.A. Non-perturbative Effective Interactions in the Standard Model. In De Gruyter Studies in Mathematical Physics; De Gruyter: Berlin, Germany; Boston, MA, USA, 2014; Volume 23. [Google Scholar] [CrossRef]
- Bednyakov, A.V. An advanced precision analysis of the SM vacuum stability. Phys. Part. Nucl. 2017, 48, 698–703. [Google Scholar] [CrossRef] [Green Version]
- Abel, S.; Spannowsky, M. Observing the fate of the false vacuum with a quantum laboratory. PRX Quantum 2021, 2, 010349. [Google Scholar] [CrossRef]
- Markkanen, T.; Rajantie, A.; Stopyra, S. Cosmological Aspects of Higgs Vacuum Metastability. Front. Astron. Space Sci. 2018, 5, 40. [Google Scholar] [CrossRef]
- Lorenz, C.S.; Funcke, L.; Calabrese, E.; Hannestad, S. Time-varying neutrino mass from a supercooled phase transition: Current cosmological constraints and impact on the Ωm-σ8 plane. Phys. Rev. D 2019, 99, 023501. [Google Scholar] [CrossRef] [Green Version]
- Landim, R.G.; Abdalla, E. Metastable dark energy. Phys. Lett. B 2017, 764, 271–276. [Google Scholar] [CrossRef] [Green Version]
- Kohri, K.; Matsui, H. Electroweak Vacuum Instability and Renormalized Vacuum Field Fluctuations in Friedmann-Lemaitre-Robertson-Walker Background. Phys. Rev. D 2018, 98, 103521. [Google Scholar] [CrossRef] [Green Version]
- Masina, I. Higgs boson and top quark masses as tests of electroweak vacuum stability. Phys. Rev. D 2013, 87, 053001. [Google Scholar] [CrossRef] [Green Version]
- Fritzsch, H.; Gell-Mann, M.; Minkowski, P. Vecto—Like Weak Currents and New Elementary Fermions. Phys. Lett. B 1975, 59, 256–260. [Google Scholar] [CrossRef]
- Minkowski, P. μ→eγ at a Rate of One Out of 109 Muon Decays? Phys. Lett. B 1977, 67, 421–428. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Ramond, P.; Slansky, R. Complex Spinors and Unified Theories. Conf. Proc. C 1979, 790927, 315–321. [Google Scholar]
- Yanagida, T. Horizontal Symmetry and Masses of Neutrinos. Prog. Theor. Phys. 1980, 64, 1103. [Google Scholar] [CrossRef] [Green Version]
- Mohapatra, R.N.; Senjanovic, G. Neutrino Mass and Spontaneous Parity Nonconservation. Phys. Rev. Lett. 1980, 44, 912. [Google Scholar] [CrossRef] [Green Version]
- Mohapatra, R.N.; Senjanovic, G. Neutrino Masses and Mixings in Gauge Models with Spontaneous Parity Violation. Phys. Rev. D 1981, 23, 165. [Google Scholar] [CrossRef]
- Schechter, J.; Valle, J.W.F. Neutrino Masses in SU(2) × U(1) Theories. Phys. Rev. D 1980, 22, 2227. [Google Scholar] [CrossRef]
- Magg, M.; Wetterich, C. Neutrino Mass Problem and Gauge Hierarchy. Phys. Lett. B 1980, 94, 61–64. [Google Scholar] [CrossRef] [Green Version]
- Glashow, S.L. The Future of Elementary Particle Physics. NATO Sci. Ser. B 1980, 61, 687. [Google Scholar] [CrossRef]
- Lazarides, G.; Shafi, Q. Neutrino Masses in SU(5). Phys. Lett. B 1981, 99, 113–116. [Google Scholar] [CrossRef] [Green Version]
- Gelmini, G.B.; Roncadelli, M. Left-Handed Neutrino Mass Scale and Spontaneously Broken Lepton Number. Phys. Lett. B 1981, 99, 411–415. [Google Scholar] [CrossRef]
- Bambhaniya, G.; Bhupal Dev, P.S.; Goswami, S.; Khan, S.; Rodejohann, W. Naturalness, Vacuum Stability and Leptogenesis in the Minimal Seesaw Model. Phys. Rev. D 2017, 95, 095016. [Google Scholar] [CrossRef] [Green Version]
- Abbott, L.F.; Sikivie, P. A Cosmological Bound on the Invisible Axion. Phys. Lett. B 1983, 120, 133–136. [Google Scholar] [CrossRef]
- Preskill, J.; Wise, M.B.; Wilczek, F. Cosmology of the Invisible Axion. Phys. Lett. B 1983, 120, 127–132. [Google Scholar] [CrossRef] [Green Version]
- Dine, M.; Fischler, W. The Not So Harmless Axion. Phys. Lett. B 1983, 120, 137–141. [Google Scholar] [CrossRef]
- Bertolini, S.; Di Luzio, L.; Kolešová, H.; Malinský, M. Massive neutrinos and invisible axion minimally connected. Phys. Rev. D 2015, 91, 055014. [Google Scholar] [CrossRef]
- Salvio, A. A Simple Motivated Completion of the Standard Model below the Planck Scale: Axions and Right-Handed Neutrinos. Phys. Lett. B 2015, 743, 428–434. [Google Scholar] [CrossRef] [Green Version]
- Elias-Miro, J.; Espinosa, J.R.; Giudice, G.F.; Lee, H.M.; Strumia, A. Stabilization of the Electroweak Vacuum by a Scalar Threshold Effect. J. High Energy Phys. 2012, 6, 031. [Google Scholar] [CrossRef] [Green Version]
- Lebedev, O. On Stability of the Electroweak Vacuum and the Higgs Portal. Eur. Phys. J. C 2012, 72, 2058. [Google Scholar] [CrossRef] [Green Version]
- He, S.P.; Zhu, S.H. One-loop radiative correction to the triple Higgs coupling in the Higgs singlet model. Phys. Lett. B 2017, 764, 31–37, Erratum in Phys. Lett. B 2019, 797, 134782. [Google Scholar] [CrossRef] [Green Version]
- Arhrib, A.; Benbrik, R.; El Falaki, J.; Jueid, A. Radiative corrections to the Triple Higgs Coupling in the Inert Higgs Doublet Model. J. High Energy Phys. 2015, 12, 007. [Google Scholar] [CrossRef] [Green Version]
- Arhrib, A.; Benbrik, R.; Chiang, C.W. Probing triple Higgs couplings of the Two Higgs Doublet Model at Linear Collider. Phys. Rev. D 2008, 77, 115013. [Google Scholar] [CrossRef] [Green Version]
- Cepeda, M.; Gori, S.; Ilten, P.; Kado, M.; Riva, F.; Abdul Khalek, R.; Aboubrahim, A.; Alimena, J.; Alioli, S.; Alves, A.; et al. Report from Working Group 2: Higgs Physics at the HL-LHC and HE-LHC. CERN Yellow Rep. Monogr. 2019, 7, 221–584. [Google Scholar] [CrossRef]
- Adhikary, A.; Banerjee, S.; Barman, R.K.; Bhattacherjee, B.; Niyogi, S. Higgs Self-Coupling at the HL-LHC and HE-LHC. Springer Proc. Phys. 2022, 277, 27–31. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Han, T.; Mangano, M.; Wang, L.T. Physics opportunities of a 100 TeV proton–proton collider. Phys. Rept. 2016, 652, 1–49. [Google Scholar] [CrossRef] [Green Version]
- Baglio, J.; Djouadi, A.; Quevillon, J. Prospects for Higgs physics at energies up to 100 TeV. Rept. Prog. Phys. 2016, 79, 116201. [Google Scholar] [CrossRef] [PubMed]
- Contino, R.; Curtin, D.; Katz, A.; Mangano, M.L.; Panico, G.; Ramsey-Musolf, M.J.; Zanderighi, G.; Anastasiou, C.; Astill, W.; Bambhaniya, G.; et al. Physics at a 100 TeV pp collider: Higgs and EW symmetry breaking studies. arXiv 2016, arXiv:1606.09408. [Google Scholar]
- Myers, S. The Future Circular Collider: Its potential and lessons learnt from the LEP and LHC experiments. Res. Outreach 2022. [Google Scholar] [CrossRef]
- Benedikt, M.; Blondel, A.; Janot, P.; Mangano, M.; Zimmermann, F. Future Circular Colliders succeeding the LHC. Nat. Phys. 2020, 16, 402–407. [Google Scholar] [CrossRef] [Green Version]
- Blondel, A.; Janot, P. FCC-ee overview: New opportunities create new challenges. Eur. Phys. J. Plus 2022, 137, 92. [Google Scholar] [CrossRef]
- Myers, S. FCC: Building on the shoulders of giants. Eur. Phys. J. Plus 2021, 136, 1076. [Google Scholar] [CrossRef]
- Aleksa, M.; Allport, P.P.; Asai, S.; Ball, A.; Besana, M.I.; Bielert, E.R.; Bologna, S.; Boos, E.; Borgonovi, L.; Bosley, R.; et al. Conceptual design of an experiment at the FCC-hh, a future 100 TeV hadron collider. CERN Yellow Rep. Monogr. 2022, 2/2022, 1–304. [Google Scholar] [CrossRef]
- Baglio, J.; Weiland, C. Heavy neutrino impact on the triple Higgs coupling. Phys. Rev. D 2016, 94, 013002. [Google Scholar] [CrossRef] [Green Version]
- Baglio, J.; Weiland, C. Impact of heavy sterile neutrinos on the triple Higgs coupling. PoS 2017, EPS-HEP2017, 143. [Google Scholar] [CrossRef] [Green Version]
- Baglio, J.; Weiland, C. The triple Higgs coupling: A new probe of low-scale seesaw models. J. High Energy Phys. 2017, 4, 038. [Google Scholar] [CrossRef] [Green Version]
- Dubinin, M.N.; Semenov, A.V. Triple and quartic interactions of Higgs bosons in the general two Higgs doublet model. arXiv 1998, arXiv:hep-ph/9812246. [Google Scholar]
- Dubinin, M.N.; Semenov, A.V. Triple and quartic interactions of Higgs bosons in the two Higgs doublet model with CP violation. Eur. Phys. J. C 2003, 28, 223–236. [Google Scholar] [CrossRef]
- Kanemura, S.; Kikuchi, M.; Yagyu, K. Radiative corrections to the Higgs boson couplings in the model with an additional real singlet scalar field. Nucl. Phys. B 2016, 907, 286–322. [Google Scholar] [CrossRef]
- Kanemura, S.; Kikuchi, M.; Yagyu, K. One-loop corrections to the Higgs self-couplings in the singlet extension. Nucl. Phys. B 2017, 917, 154–177. [Google Scholar] [CrossRef]
- Aoki, M.; Kanemura, S.; Kikuchi, M.; Yagyu, K. Radiative corrections to the Higgs boson couplings in the triplet model. Phys. Rev. D 2013, 87, 015012. [Google Scholar] [CrossRef] [Green Version]
- Ballesteros, G.; Redondo, J.; Ringwald, A.; Tamarit, C. Standard Model—Axion—Seesaw—Higgs portal inflation. Five problems of particle physics and cosmology solved in one stroke. J. Cosmol. Astropart. Phys. 2017, 8, 001. [Google Scholar] [CrossRef] [Green Version]
- Ballesteros, G.; Redondo, J.; Ringwald, A.; Tamarit, C. Unifying inflation with the axion, dark matter, baryogenesis and the seesaw mechanism. Phys. Rev. Lett. 2017, 118, 071802. [Google Scholar] [CrossRef] [Green Version]
- Ballesteros, G.; Redondo, J.; Ringwald, A.; Tamarit, C. Several Problems in Particle Physics and Cosmology Solved in One SMASH. Front. Astron. Space Sci. 2019, 6, 55. [Google Scholar] [CrossRef] [Green Version]
- Fukugita, M.; Yanagida, T. Baryogenesis Without Grand Unification. Phys. Lett. B 1986, 174, 45–47. [Google Scholar] [CrossRef]
- Buchmuller, W.; Di Bari, P.; Plumacher, M. Cosmic microwave background, matter–antimatter asymmetry and neutrino masses. Nucl. Phys. B 2002, 643, 367–390, Erratum in Nucl. Phys. B 2008, 793, 362. [Google Scholar] [CrossRef] [Green Version]
- Davidson, S.; Ibarra, A. A Lower bound on the right-handed neutrino mass from leptogenesis. Phys. Lett. B 2002, 535, 25–32. [Google Scholar] [CrossRef] [Green Version]
- Buchmuller, W.; Di Bari, P.; Plumacher, M. Leptogenesis for pedestrians. Ann. Phys. 2005, 315, 305–351. [Google Scholar] [CrossRef] [Green Version]
- Buchmüller, W. Leptogenesis: Theory and Neutrino Masses. Nucl. Phys. B Proc. Suppl. 2013, 235–236, 329–335. [Google Scholar] [CrossRef]
- Buchmüller, W. Leptogenesis. Scholarpedia 2014, 9, 11471. [Google Scholar] [CrossRef]
- Esteban, I.; Gonzalez-Garcia, M.C.; Maltoni, M.; Schwetz, T.; Zhou, A. The fate of hints: Updated global analysis of three-flavor neutrino oscillations. J. High Energy Phys. 2020, 9, 178. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef] [Green Version]
- Goobar, A.; Hannestad, S.; Mortsell, E.; Tu, H. A new bound on the neutrino mass from the sdss baryon acoustic peak. J. Cosmol. Astropart. Phys. 2006, 6, 019. [Google Scholar] [CrossRef]
- Di Valentino, E.; Gariazzo, S.; Mena, O. Most constraining cosmological neutrino mass bounds. Phys. Rev. D 2021, 104, 083504. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Giusarma, E.; Mena, O.; Freese, K.; Gerbino, M.; Ho, S.; Lattanzi, M. Unveiling ν secrets with cosmological data: Neutrino masses and mass hierarchy. Phys. Rev. D 2017, 96, 123503. [Google Scholar] [CrossRef] [Green Version]
- Hut, P.; Olive, K.A. A Cosmological Upper Limit on the Mass of Heavy Neutrinos. Phys. Lett. B 1979, 87, 144–146. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A. Neutrino Mass Bounds in the Era of Tension Cosmology. Astrophys. J. Lett. 2022, 931, L18. [Google Scholar] [CrossRef]
- Li, E.K.; Zhang, H.; Du, M.; Zhou, Z.H.; Xu, L. Probing the Neutrino Mass Hierarchy beyond ΛCDM Model. J. Cosmol. Astropart. Phys. 2018, 8, 042. [Google Scholar] [CrossRef] [Green Version]
- Naidoo, K.; Massara, E.; Lahav, O. Cosmology and neutrino mass with the minimum spanning tree. Mon. Not. R. Astron. Soc. 2022, 513, 3596–3609. [Google Scholar] [CrossRef]
- Mishra-Sharma, S.; Alonso, D.; Dunkley, J. Neutrino masses and beyond-ΛCDM cosmology with LSST and future CMB experiments. Phys. Rev. D 2018, 97, 123544. [Google Scholar] [CrossRef] [Green Version]
- Gariazzo, S. Neutrino Properties and the Cosmological Tensions in the ΛCDM Model. In Proceedings of the 15th Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity, Astrophysics, and Relativistic Field Theories, Rome, Italy, 1–7 July 2018. [Google Scholar]
- Zhao, M.M.; Li, Y.H.; Zhang, J.F.; Zhang, X. Constraining neutrino mass and extra relativistic degrees of freedom in dynamical dark energy models using Planck 2015 data in combination with low-redshift cosmological probes: Basic extensions to ΛCDM cosmology. Mon. Not. R. Astron. Soc. 2017, 469, 1713–1724. [Google Scholar] [CrossRef] [Green Version]
- Denton, P.B.; Friend, M.; Messier, M.D.; Tanaka, H.A.; Böser, S.; Coelho, J.a.A.B.; Perrin-Terrin, M.; Stuttard, T. Snowmass Neutrino Frontier: NF01 Topical Group Report on Three-Flavor Neutrino Oscillations. arXiv 2022, arXiv:2212.00809. [Google Scholar]
- Jegerlehner, F.; Kalmykov, M.Y.; Kniehl, B.A. On the difference between the pole and the masses of the top quark at the electroweak scale. Phys. Lett. B 2013, 722, 123–129. [Google Scholar] [CrossRef] [Green Version]
- Hamaguchi, K.; Murayama, H.; Yanagida, T. Leptogenesis from N dominated early universe. Phys. Rev. D 2002, 65, 043512. [Google Scholar] [CrossRef] [Green Version]
- He, H.J.; Ren, J.; Yao, W. Probing new physics of cubic Higgs boson interaction via Higgs pair production at hadron colliders. Phys. Rev. D 2016, 93, 015003. [Google Scholar] [CrossRef] [Green Version]
- Abdullahi, A.M.; Alzas, P.B.; Batell, B.; Boyarsky, A.; Carbajal, S.; Chatterjee, A.; Crespo-Anadon, J.I.; Deppisch, F.F.; De Roeck, A.; Drewes, M.; et al. The Present and Future Status of Heavy Neutral Leptons. In Proceedings of the 2022 Snowmass Summer Study, Seattle, WA, USA, 17–26 July 2022. [Google Scholar]
- Alimena, J.; Beacham, J.; Borsato, M.; Cheng, Y.; Vidal, X.C.; Cottin, G.; Curtin, D.; De Roeck, A.; Desai, N.; Evans, J.A.; et al. Searching for long-lived particles beyond the Standard Model at the Large Hadron Collider. J. Phys. G 2020, 47, 090501. [Google Scholar] [CrossRef]
- Gao, J. Snowmass2021 White Paper AF3-CEPC. arXiv 2022, arXiv:2203.09451. [Google Scholar]
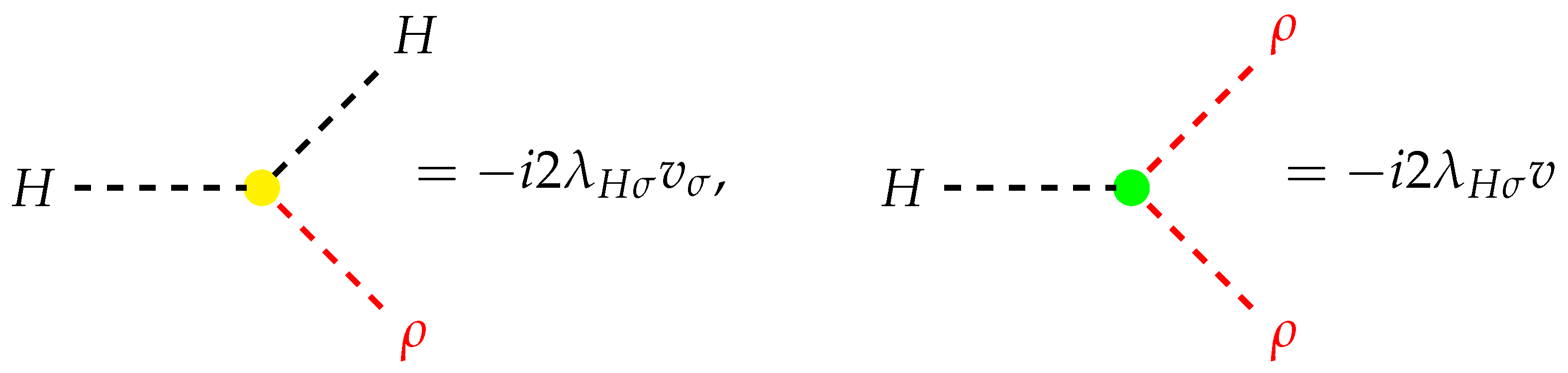
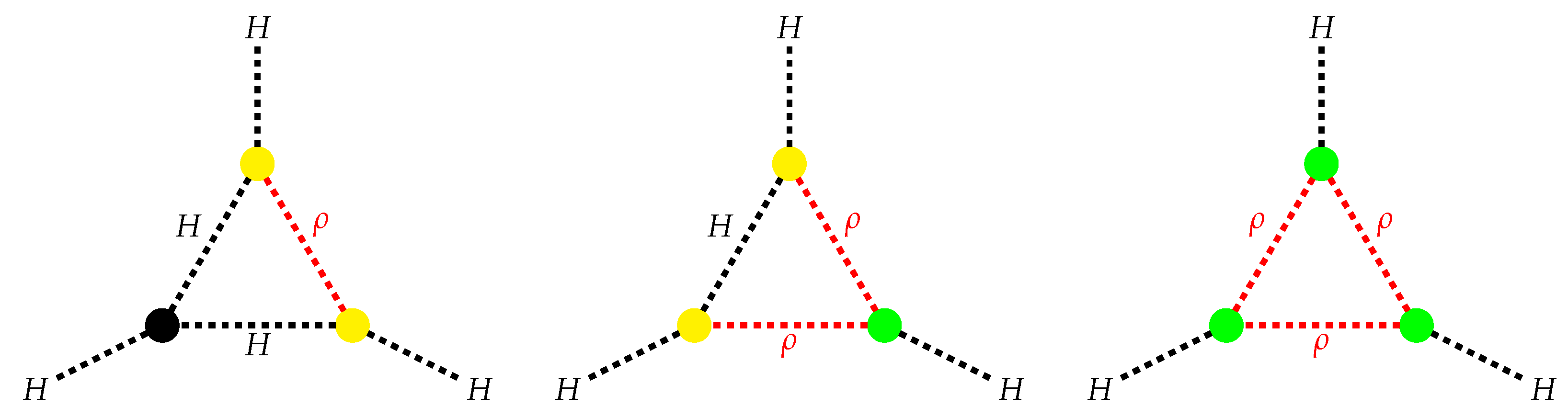
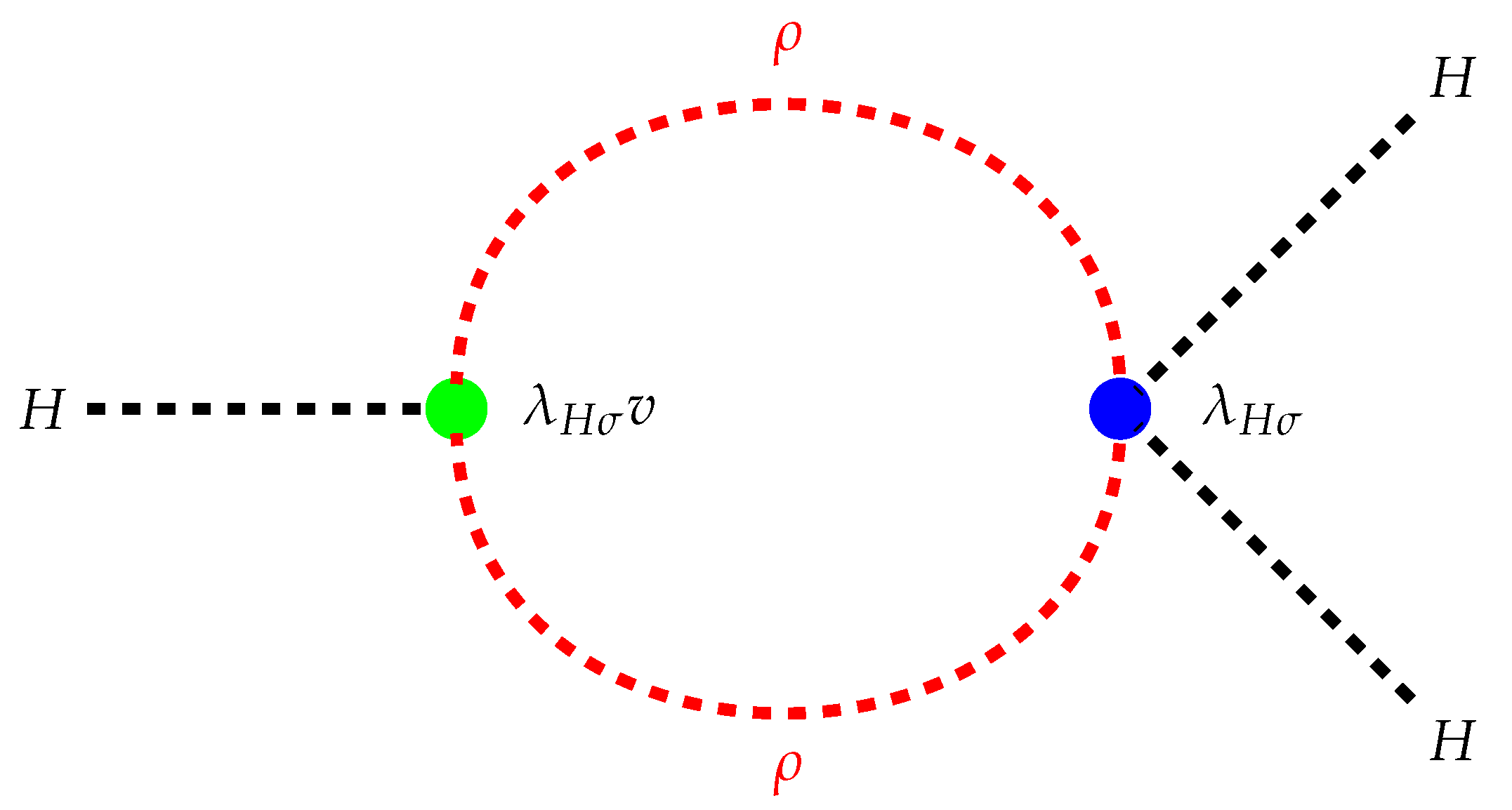

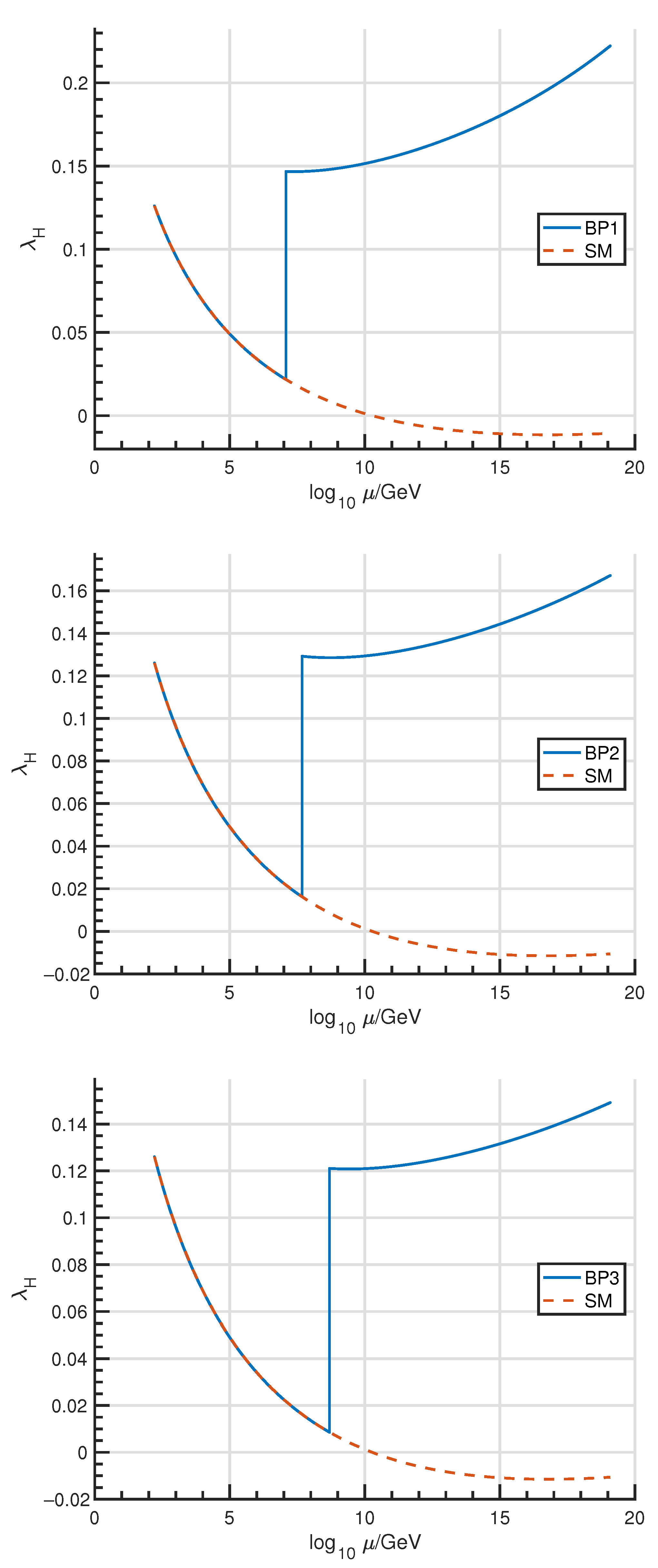
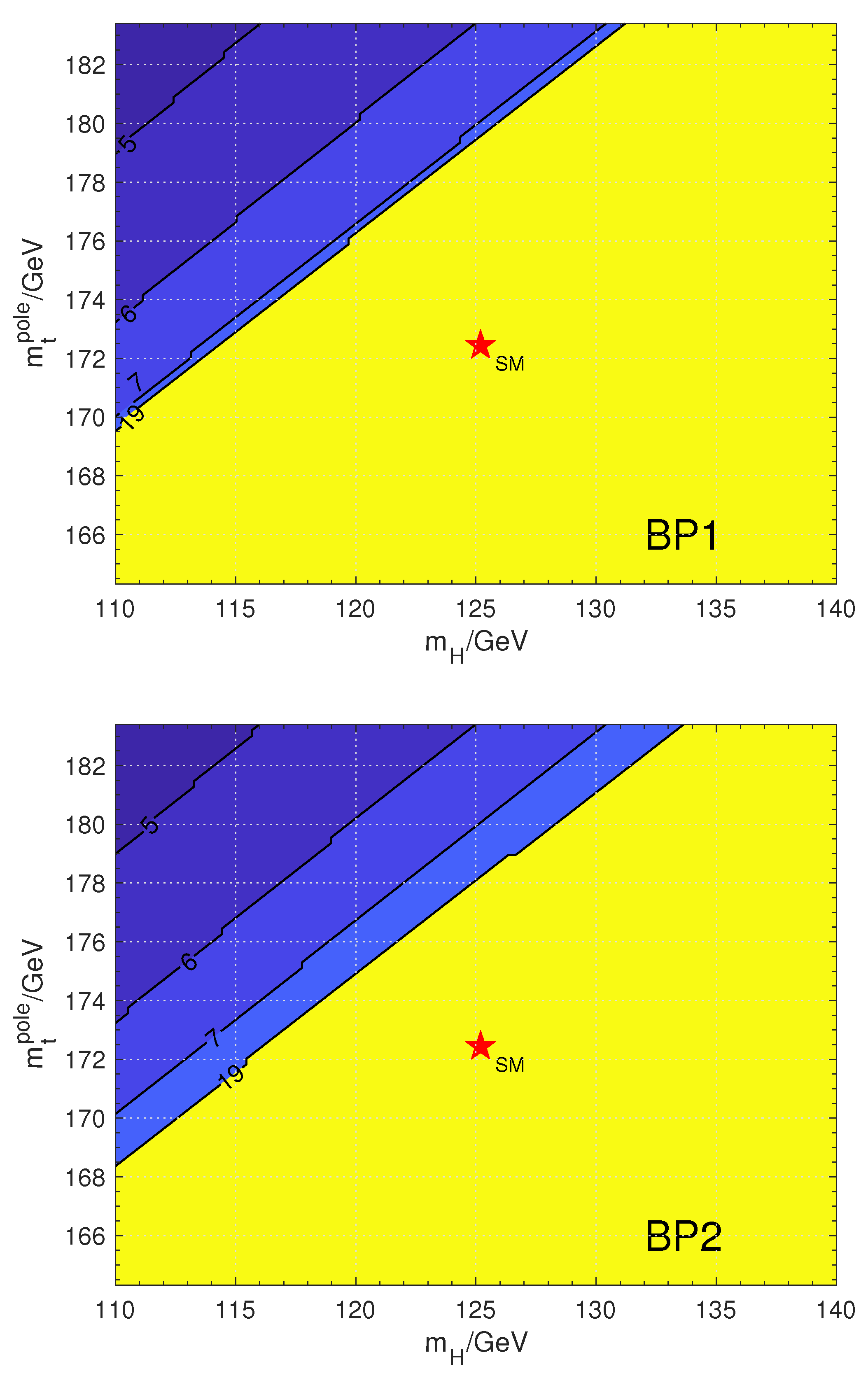
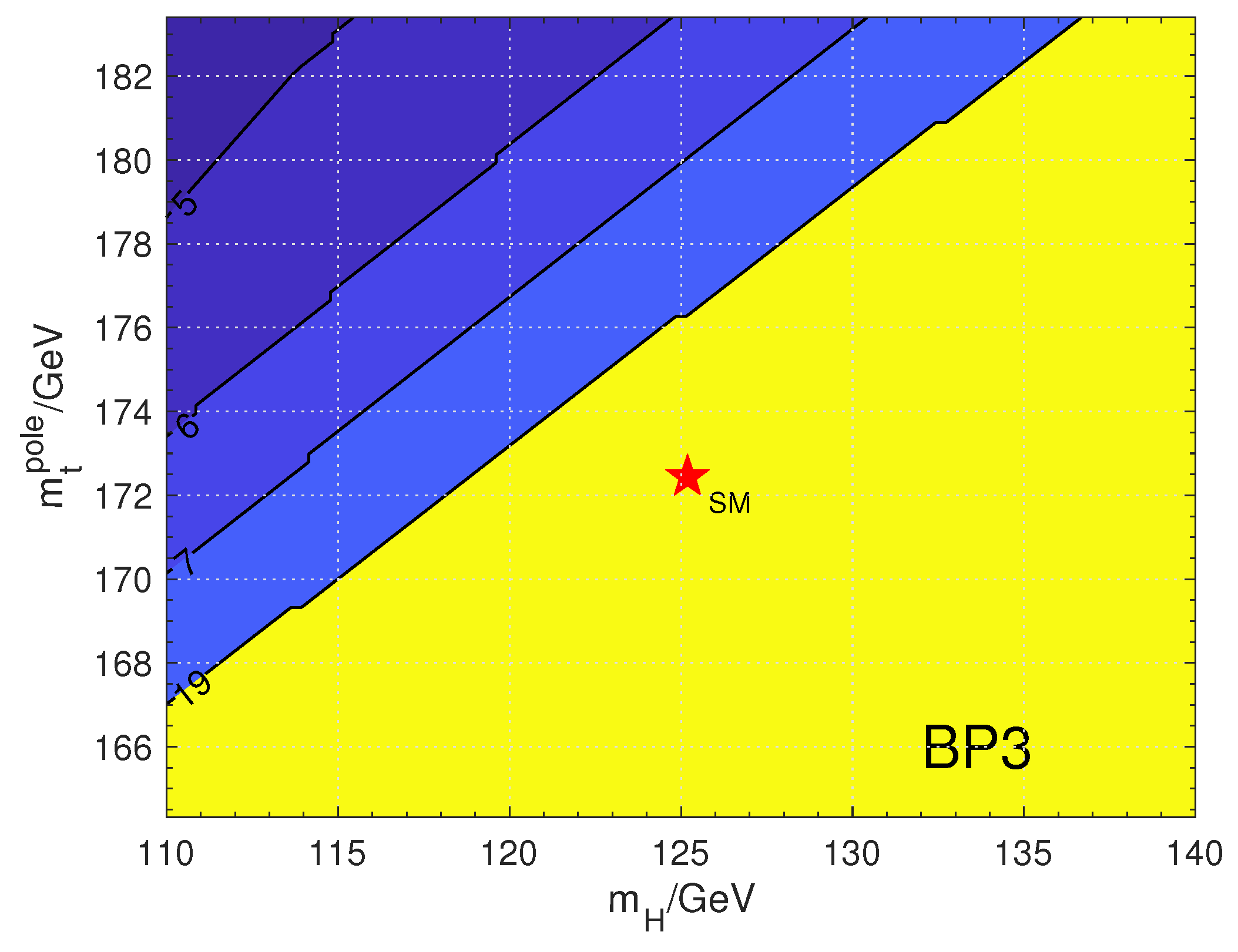
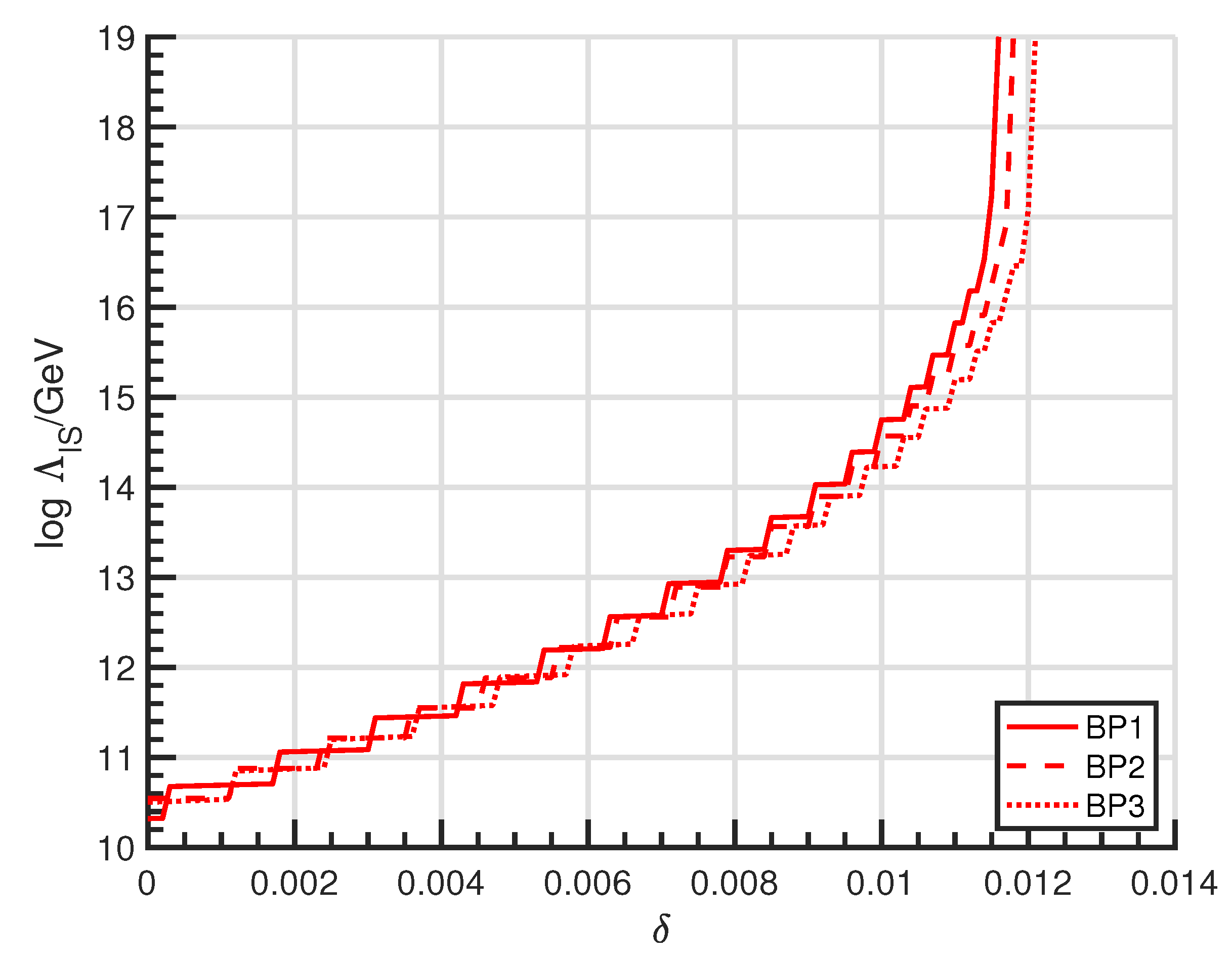
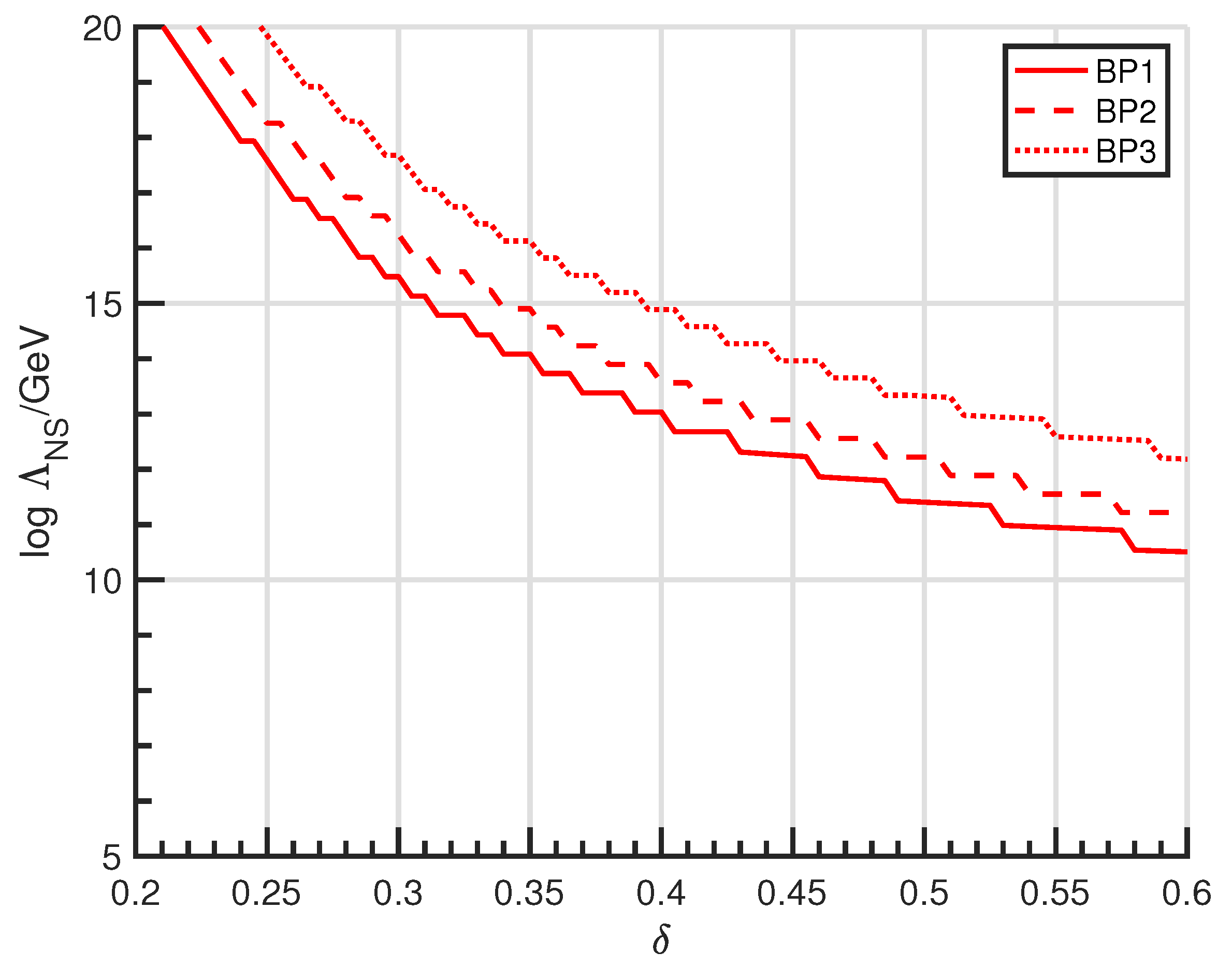
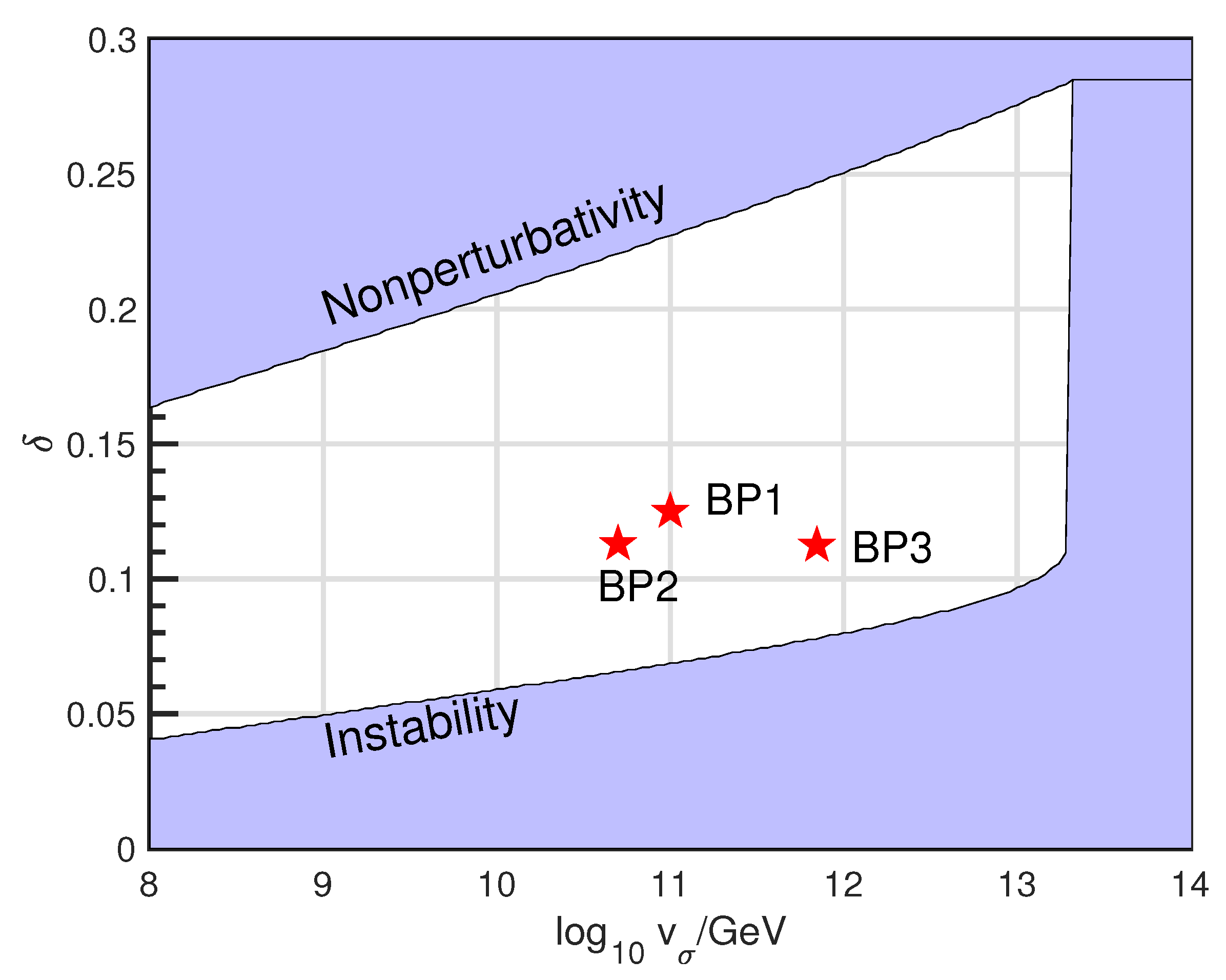
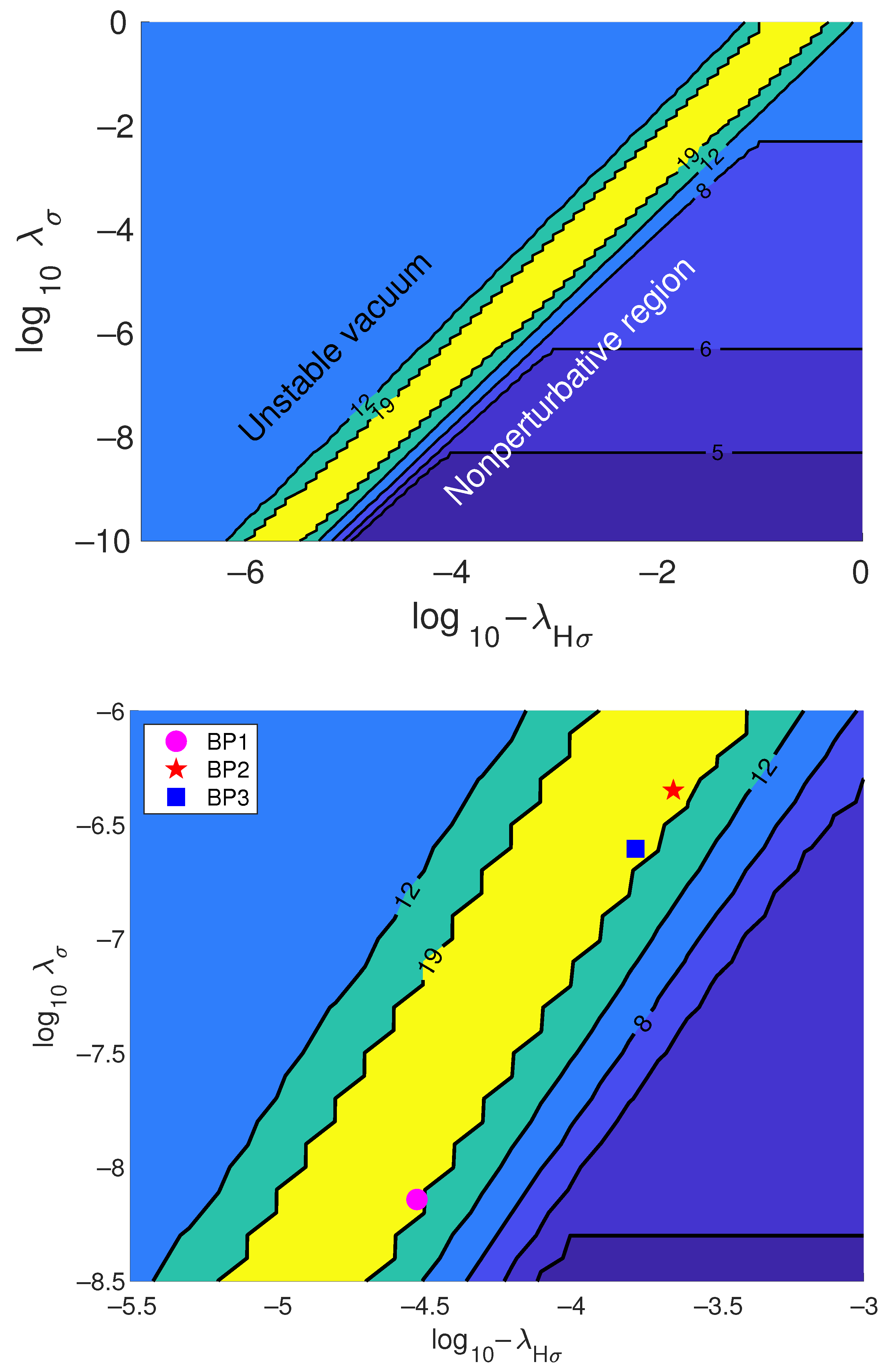

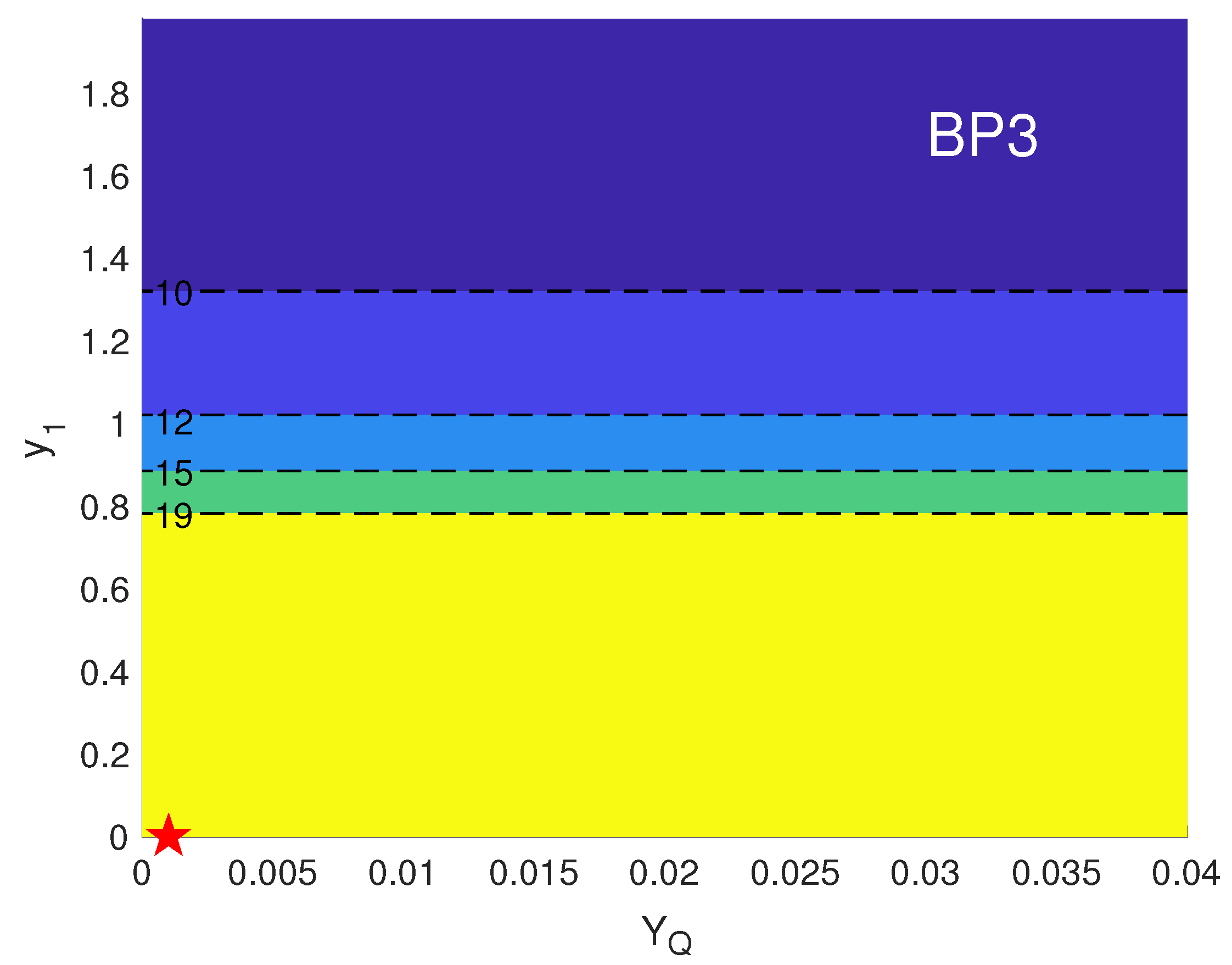
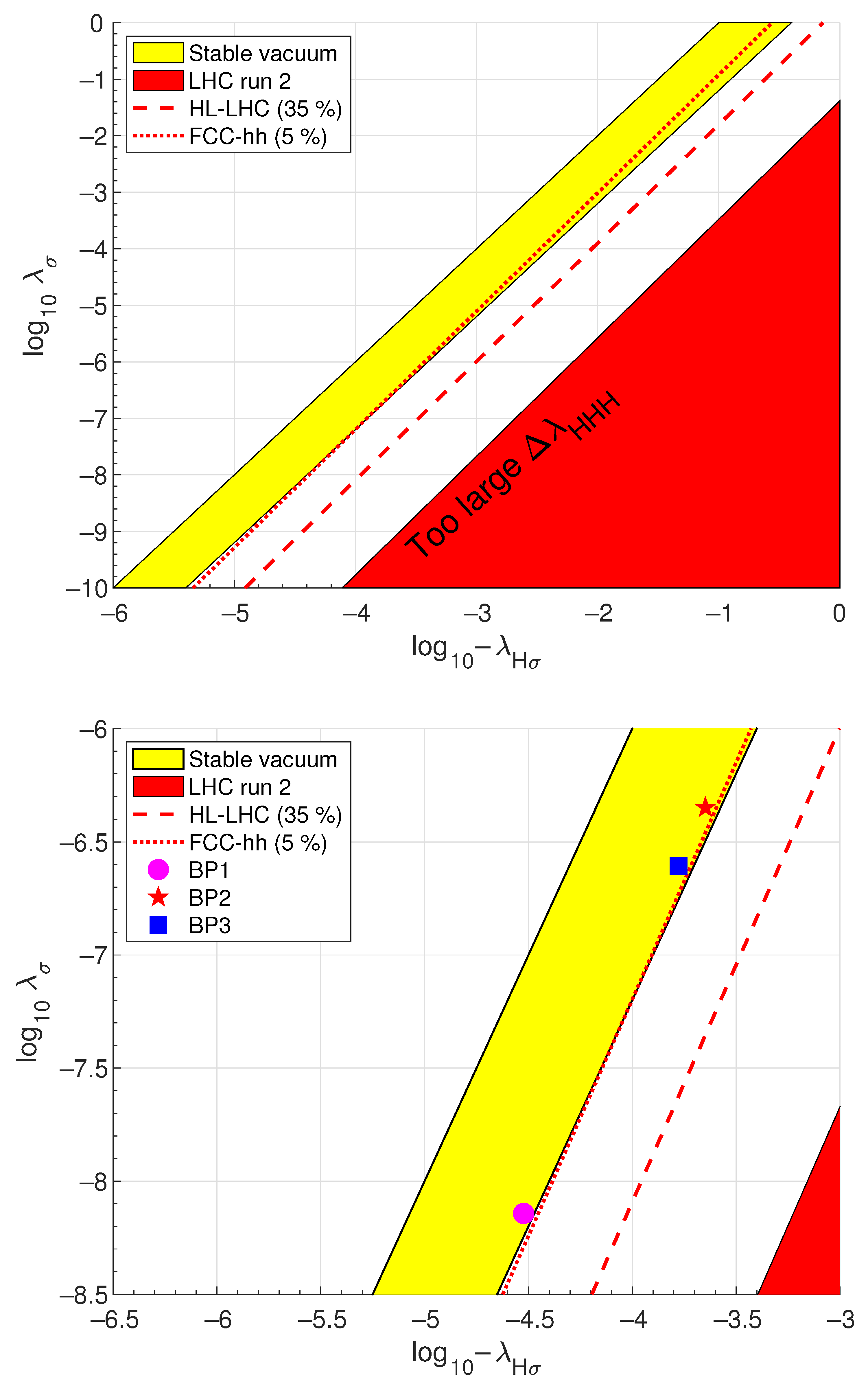
| Benchmarks | BP1 | BP2 | BP3 |
|---|---|---|---|
| (GeV) | |||
| Benchmarks | BP1 | BP2 | BP3 | Experimental Values |
|---|---|---|---|---|
| (meV) | 0.015 | ≲55 (Equations (10) & (11) and Figure 1 of [74] | ||
| (meV) | 8.64 | 8.50 | 8.68 | with mass bound from [68]) |
| (meV) | 50.67 | 50.93 | 50.88 | ≲60 (Equation (12) and Figure 1 of [74] |
| with mass bound from [68]) | ||||
| (meV) | 59.30 | 59.45 | 59.57 | <120 [68,70] |
| but, ⪆60 (Equation (13) of [74]) | ||||
| ( eV) | 7.46 | 7.22 | 7.54 | 6.79–8.0 [67,79] |
| ( eV) | 2.57 | 2.59 | 2.59 | 2.412–2.625 [67,79] |
| (GeV) | Unknown | |||
| (GeV) |
| Parameter | v | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Value | 164.0 | 4.18 | 125.25 | 1.777 | 246.22 | 0.357 | 0.652 | 1.221 | 0.126 |
| Benchmarks | BP1 | BP2 | BP3 | Experimental Values |
|---|---|---|---|---|
| 0.125 | 0.113 | 0.113 | None | |
| (eV) | Model-dependent | |||
| (GeV) | ||||
| ∼ | ∼ | ∼ | ||
| 0.222 | 0.166 | 0.149 | None | |
| % | −5% | % | <1400% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, C.R.; Huitu, K.; Kärkkäinen, T.J. The Higgs Trilinear Coupling and the Scale of New Physics for the SM-Axion-Seesaw-Higgs Portal Inflation (SMASH) Model. Universe 2023, 9, 43. https://doi.org/10.3390/universe9010043
Das CR, Huitu K, Kärkkäinen TJ. The Higgs Trilinear Coupling and the Scale of New Physics for the SM-Axion-Seesaw-Higgs Portal Inflation (SMASH) Model. Universe. 2023; 9(1):43. https://doi.org/10.3390/universe9010043
Chicago/Turabian StyleDas, C.R., Katri Huitu, and Timo J. Kärkkäinen. 2023. "The Higgs Trilinear Coupling and the Scale of New Physics for the SM-Axion-Seesaw-Higgs Portal Inflation (SMASH) Model" Universe 9, no. 1: 43. https://doi.org/10.3390/universe9010043
APA StyleDas, C. R., Huitu, K., & Kärkkäinen, T. J. (2023). The Higgs Trilinear Coupling and the Scale of New Physics for the SM-Axion-Seesaw-Higgs Portal Inflation (SMASH) Model. Universe, 9(1), 43. https://doi.org/10.3390/universe9010043








