Effects of Background Turbulence on the Relaxation of Ion Temperature Anisotropy Firehose Instability in Space Plasmas
Abstract
:1. Introduction
2. Method: Macroscopic Quasilinear Equations
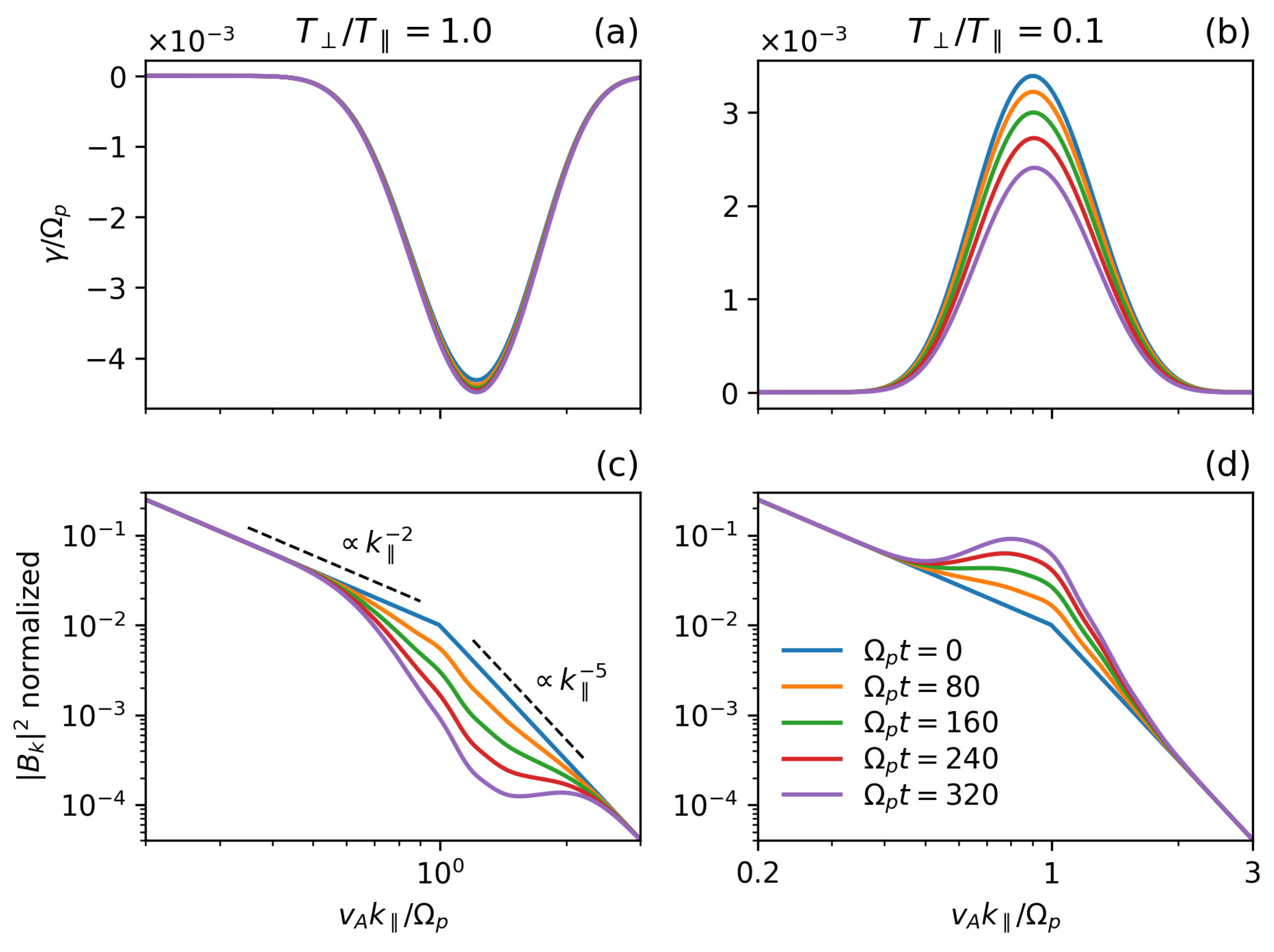
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FHI | Firehose instability |
| VDF | Velocity distribution function |
References
- Krall, N.A.; Trivelpiece, A.W. Principle of Plasma Physics; San Francisco Press Inc.: San Francisco, CA, USA, 1986. [Google Scholar]
- Stix, T. Waves in Plasmas; American Institute of Physics: College Park, MD, USA, 1992. [Google Scholar]
- Gary, S.P. Theory of Space Plasma Microinstabilities; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar] [CrossRef]
- Seough, J.; Yoon, P.H.; Kim, K.H.; Lee, D.H. Solar-Wind Proton Anisotropy Versus Beta Relation. Phys. Rev. Lett. 2013, 110, 071103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yoon, P.H. Kinetic instabilities in the solar wind driven by temperature anisotropies. Rev. Mod. Plasma Phys. 2017, 1, 4. [Google Scholar] [CrossRef]
- Hellinger, P.; Trávníček, P.; Kasper, J.C.; Lazarus, A.J. Solar wind proton temperature anisotropy: Linear theory and WIND/SWE observations. Geophys. Res. Lett. 2006, 33, 2–5. [Google Scholar] [CrossRef] [Green Version]
- Bale, S.D.; Kasper, J.C.; Howes, G.G.; Quataert, E.; Salem, C.; Sundkvist, D. Magnetic Fluctuation Power Near Proton Temperature Anisotropy Instability Thresholds in the Solar Wind. Phys. Rev. Lett. 2009, 103, 211101. [Google Scholar] [CrossRef] [Green Version]
- Adrian, M.L.; Viñas, A.F.; Moya, P.S.; Wendel, D.E. Solar Wind Magnetic Fluctuations and Electron Non-thermal Temperature Anisotropy: Survey of Wind-SWE-VEIS Observations. Astrophys. J. 2016, 833, 49. [Google Scholar] [CrossRef] [Green Version]
- Matteini, L.; Landi, S.; Hellinger, P.; Pantellini, F.; Maksimovic, M.; Velli, M.; Goldstein, B.E.; Marsch, E. Evolution of the solar wind proton temperature anisotropy from 0.3 to 2.5 AU. Geophys. Res. Lett. 2007, 34, L20105. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Kasper, J.C.; Vech, D.; Klein, K.G.; Stevens, M.; Martinović, M.M.; Alterman, B.L.; Ďurovcová, T.; Paulson, K.; Maruca, B.A.; et al. Proton Temperature Anisotropy Variations in Inner Heliosphere Estimated with the First Parker Solar Probe Observations. Astrophys. J. 2020, 246, 70. [Google Scholar] [CrossRef] [Green Version]
- Chew, G.F.; Goldberger, M.L.; Low, F.E.; Chandrasekhar, S. The Boltzmann equation an d the one-fluid hydromagnetic equations in the absence of particle collisions. Proc. R. Soc. Lond. A Math. Phys. Sci. 1956, 236, 112–118. [Google Scholar] [CrossRef]
- Woodham, L.D.; Wicks, R.T.; Verscharen, D.; Owen, C.J.; Maruca, B.A.; Alterman, B.L. Parallel-propagating Fluctuations at Proton-kinetic Scales in the Solar Wind Are Dominated By Kinetic Instabilities. Astrophys. J. Lett. 2019, 884, L53. [Google Scholar] [CrossRef]
- Gomberoff, L.; Elgueta, R. Resonant acceleration of a-particles by ion-cyclotron waves in the solar wind. J. Geophys. Res. 1991, 96, 9801–9804. [Google Scholar] [CrossRef]
- Gary, S.P.; McKean, M.E.; Winske, D.; Anderson, B.J.; Denton, R.E.; Fuselier, S.A. The proton cyclotron instability and the anisotropy/β inverse correlation. J. Geophys. Res. 1994, 99, 5903–5914. [Google Scholar] [CrossRef]
- Gomberoff, L.; Valdivia, J.A. Ion cyclotron instability due to the thermal anisotropy of drifting ion species. J. Geophys. Res. 2003, 108, 1050. [Google Scholar] [CrossRef]
- Yoon, P.H.; Seough, J.J.; Khim, K.K.; Kim, H.; Kwon, H.J.; Park, J.; Parkh, S.; Park, K.S. Analytic model of electromagnetic ion-cyclotron anisotropy instability. Phys. Plasmas 2010, 17, 082111. [Google Scholar] [CrossRef]
- Navarro, R.E.; Muñoz, V.; Araneda, J.; Viñas, A.F.; Moya, P.S.; Valdivia, J.A. Magnetic Alfvén-cyclotron fluctuations of anisotropic nonthermal plasmas. J. Geophys. Res. 2015, 120, 2382–2396. [Google Scholar] [CrossRef]
- Gary, S.P.; Li, H.; O’Rourke, S.; Winske, D. Proton resonant firehose instability: Temperature anisotropy and fluctuating field constraints. J. Geophys. Res. 1998, 103, 14567–14574. [Google Scholar] [CrossRef]
- Seough, J.; Yoon, P.H.; Hwang, J. Simulation and quasilinear theory of proton firehose instability. Phys. Plasmas 2015, 22, 012303. [Google Scholar] [CrossRef]
- Navarro, R.E.; Muñoz, V.; Valdivia, J.A.; Moya, P.S. Feasibility of Ion-cyclotron Resonant Heating in the Solar Wind. Astrophys. J. 2020, 898, L9. [Google Scholar] [CrossRef]
- Markovskii, S.A.; Vasquez, B.J. The Effect of Solar Wind Turbulence on Parallel and Oblique Firehose Instabilities. Astrophys. J. 2022, 924, 111. [Google Scholar] [CrossRef]
- Opie, S.; Verscharen, D.; Owen, C.J.; Isenberg, P.A. Conditions for proton temperature anisotropy to drive instabilities in the solar wind. Astrophys. J. 2022, 941, 176. [Google Scholar] [CrossRef]
- Bandyopadhyay, R.; Qudsi, R.A.; Gary, S.P.; Matthaeus, W.H.; Parashar, T.N.; Maruca, B.A.; Roytershteyn, V.; Chasapis, A.; Giles, B.L.; Gershman, D.J.; et al. Interplay of turbulence and proton-microinstability growth in space plasmas. Phys. Plasmas 2022, 29, 102107. [Google Scholar] [CrossRef]
- Andrés, N.; Clark di Leoni, P.; Mininni, P.D.; Dmitruk, P.; Sahraoui, F.; Matthaeus, W.H. Interplay between Alfvén and magnetosonic waves in compressible magnetohydrodynamics turbulence. Phys. Plasmas 2017, 24, 102314. [Google Scholar] [CrossRef]
- Svidzinski, V.A.; Li, H.; Rose, H.A.; Albright, B.J.; Bowers, K.J. Particle in cell simulations of fast magnetosonic wave turbulence in the ion cyclotron frequency range. Phys. Plasmas 2009, 16, 122310. [Google Scholar] [CrossRef]
- Chandran, B.D.G. Weak Compressible Magnetohydrodynamic Turbulence in the Solar Corona. Phys. Rev. Lett. 2005, 95, 265004. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cho, J.; Lazarian, A. Compressible magnetohydrodynamic turbulence: Mode coupling, scaling relations, anisotropy, viscosity-damped regime and astrophysical implications. Mon. Not. R. Astron. Soc. 2003, 345, 325–339. [Google Scholar] [CrossRef] [Green Version]
- Sharma, R.P.; Kumar, S. Nonlinear coupling of kinetic Alfvén waves and magnetosonic waves in plasma. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Moya, P.S.; Navarro, R.E. Effects of the Background Turbulence on the Relaxation of Ion Temperature Anisotropy in Space Plasmas. Front. Phys. 2021, 9, 1–12. [Google Scholar] [CrossRef]
- Hellinger, P.; Trávníček, P. Parallel and oblique proton fire hose instabilities in the presence of alpha/proton drift: Hybrid simulations. J. Geophys. Res. 2006, 111, A01107. [Google Scholar] [CrossRef] [Green Version]
- Servidio, S.; Osman, K.T.; Valentini, F.; Perrone, D.; Califano, F.; Chapman, S.; Matthaeus, W.H.; Veltri, P. Proton Kinetic Effects in Vlasov and Solar Wind Turbulence. Astrophys. J. Lett. 2014, 781, L27. [Google Scholar] [CrossRef] [Green Version]
- Moya, P.S.; Viñas, A.F.; Muñoz, V.; Valdivia, J.A. Computational and Theoretical study of the wave-particle interaction of protons and waves. Ann. Geophys. 2012, 30, 1361–1369. [Google Scholar] [CrossRef]
- Gomberoff, L.; Muñoz, V.; Valdivia, J.A. Ion cyclotron instability triggered by drifting minor ion species: Cascade effect and exact results. Planet. Space Sci. 2004, 52, 679–684. [Google Scholar] [CrossRef]
- Gary, S.P.; Tokar, R.L. The second-order theory of electromagnetic hot ion beam instabilities. J. Geophys. Res. 1985, 90, 65–72. [Google Scholar] [CrossRef]
- Fried, B.D.; Conte, S.D. The Plasma Dispersion Function; Academic: San Diego, CA, USA, 1961. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [Green Version]
- Yoon, P.H. Quasilinear evolution of Alfvén-ion-cyclotron and mirror instabilities driven by ion temperature anisotropy. Phys. Fluids B 1992, 4, 3627–3637. [Google Scholar] [CrossRef]
- Isenberg, P.A.; Vasquez, B.J. Preferential perpendicular heating of coronal hole minor ions by the Fermi mechanism. Astrophys. J. 2007, 668, 546–556. [Google Scholar] [CrossRef]
- Azevedo, J.C.d.A.; Vianna, M.L. Theory of Waves in Inhomogeneous Warm Plasmas. Phys. Rev. 1969, 177, 300–305. [Google Scholar] [CrossRef]
- Sharma, R.P.; Goyal, R.; Gaur, N.; Scime, E.E. Linear kinetic Alfvén waves in inhomogeneous plasma: Effects of Landau damping. EPL 2016, 113, 25001. [Google Scholar] [CrossRef] [Green Version]
- Noreen, N.; Yoon, P.H.; Zaheer, S. Cyclotron instabilities driven by temperature anisotropy in the solar wind. Phys. Plasmas 2017, 24, 102902. [Google Scholar] [CrossRef]
- Moya, P.S.; Navarro, R.; Viñas, A.F.; Muñoz, V.; Valdivia, J.A. Weak Turbulence Cascading Effects in the Acceleration and Heating of Ions in the Solar Wind. Astrophys. J. 2014, 781, 76. [Google Scholar] [CrossRef] [Green Version]
- Lazar, M.; Yoon, P.H.; López, R.A.; Moya, P.S. Electromagnetic Electron Cyclotron Instability in the Solar Wind. J. Geophys. Res. Space Phys. 2018, 123, 6–19. [Google Scholar] [CrossRef]
- Shaaban, S.M.; Lazar, M.; Yoon, P.H.; Poedts, S. Quasilinear approach of the cumulative whistler instability in fast solar wind: Constraints of electron temperature anisotropy. Astron. Astrophys. 2019, 627. [Google Scholar] [CrossRef]
- Sarfraz, M.; Yoon, P.H.; Saeed, S.; Abbas, G.; Shah, H.A. Macroscopic quasilinear theory of parallel electron firehose instability associated with solar wind electrons. Phys. Plasmas 2017, 24, 012907. [Google Scholar] [CrossRef]
- Ali, Z.; Sarfraz, M.; Yoon, P.H. Combined electron firehose and electromagnetic ion cyclotron instabilities: Quasilinear approach. Mon. Not. R. Astron. Soc. 2020, 499, 659–667. [Google Scholar] [CrossRef]
- Moya, P.S.; Muñoz, V.; Rogan, J.; Valdivia, J.A. Study of the Cascading Effect During the Acceleration and Heating of Ions in the Solar Wind. J. Atmos. Solar-Terr. Phys. 2011, 73, 1390–1397. [Google Scholar] [CrossRef]
- Seough, J.; Yoon, P.H. Quasilinear theory of anisotropy-beta relations for proton cyclotron and parallel firehose instabilities. J. Geophys. Res. 2012, 117, A08101. [Google Scholar] [CrossRef]
- Navarro, R.E.; Moya, P.S.; Muñoz, V.; Araneda, J.A.; Viñas, A.F.; Valdivia, J.A. Solar wind thermally induced magnetic fluctuations. Phys. Rev. Lett. 2014, 112, 1–5. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Wang, L.; Tu, C.; Marsch, E.; Zong, Q. Evidence of Landa and Cyclotron Resonance Between Protons and Kinetic Waves in Solar Wind Turbulence. Astrophys. J. 2015, 800, L31. [Google Scholar] [CrossRef] [Green Version]
- Malaspina, D.M.; Halekas, J.; Berčič, L.; Larson, D.; Whittlesey, P.; Bale, S.D.; Bonnell, J.W.; de Wit, T.D.; Ergun, R.E.; Howes, G.; et al. Plasma Waves near the Electron Cyclotron Frequency in the Near-Sun Solar Wind. Astrophys. J. Suppl. Ser. 2020, 246, 21. [Google Scholar] [CrossRef] [Green Version]
- Muller, D.E. A Method for Solving Algebraic Equations Using an Automatic Computer. Math. Tables Other Aids Comput. 1956, 10, 208–215. [Google Scholar] [CrossRef]
- Astudillo, H.F. High-order modes of left-handed electromagnetic waves in a solar-wind-like plasma. J. Geophys. Res. 1996, 101, 24433. [Google Scholar] [CrossRef]
- Alexandrova, O.; Mangeney, A.; Maksimovic, M.; Cornilleau-Wehrlin, N.; Bosqued, J.M.; André, M. Alfvén vortex filaments observed in magnetosheath downstream of a quasi-perpendicular bow shock. J. Geophys. Res. Space Phys. 2006, 111, A12208. [Google Scholar] [CrossRef] [Green Version]
- Alexandrova, O.; Lacombe, C.; Mangeney, A. Spectra and anisotropy of magnetic fluctuations in the Earth’s magnetosheath: Cluster observations. Ann. Geophys. 2008, 26, 3585–3596. [Google Scholar] [CrossRef] [Green Version]
- Rakhmanova, L.; Riazantseva, M.; Zastenker, G. Plasma and Magnetic Field Turbulence in the Earth’s Magnetosheath at Ion Scales. Front. Astron. Space Sci. 2021, 7, 115. [Google Scholar] [CrossRef]
- Alexandrova, O.; Carbone, V.; Veltri, P.; Sorriso-Valvo, L. Small-Scale Energy Cascade of the Solar Wind Turbulence. Astrophys. J. 2008, 674, 1153–1157. [Google Scholar] [CrossRef] [Green Version]
- Boldyrev, S.; Perez, J.C. Spectrum of Kinetic-Alfvén Turbulence. Astrophys. J. 2012, 758, L44. [Google Scholar] [CrossRef] [Green Version]
- Chaston, C.C.; Bonnell, J.W.; Wygant, J.R.; Mozer, F.; Bale, S.D.; Kersten, K.; Breneman, A.W.; Kletzing, C.A.; Kurth, W.S.; Hospodarsky, G.B.; et al. Observations of kinetic scale field line resonances. Geophys. Res. Lett. 2014, 41, 209–215. [Google Scholar] [CrossRef]
- Moya, P.S.; Pinto, V.A.; Viñas, A.F.; Sibeck, D.G.; Kurth, W.S.; Hospodarsky, G.B.; Wygant, J.R. Weak kinetic Alfvén waves turbulence during the 14 November 2012 geomagnetic storm: Van Allen Probes observations. J. Geophys. Res. Space Phys. 2015, 120, 5504–5523. [Google Scholar] [CrossRef]
- Gamayunov, K.V.; Engebretson, M.J.; Zhang, M.; Rassoul, H.K. Source of seed fluctuations for electromagnetic ion cyclotron waves in Earth’s magnetosphere. Adv. Space Res. 2015, 55, 2573–2583. [Google Scholar] [CrossRef]
- Goldstein, M.L.; Wicks, R.T.; Perri, S.; Sahraoui, F. Kinetic scale turbulence and dissipation in the solar wind: Key observational results and future outlook. Phil. Trans. R. Soc. A 2015, 373, 20140147. [Google Scholar] [CrossRef] [Green Version]
- Franci, L.; Landi, S.; Matteini, L.; Verdini, A.; Hellinger, P. High-Resolution Hybrid Simulations of Kinetic Plasma Turbulence at Proton Scales. Astrophys. J. 2015, 812, 21. [Google Scholar] [CrossRef]
- Arzamasskiy, L.; Kunz, M.W.; Chandran, B.D.G.; Quataert, E. Hybrid-kinetic Simulations of Ion Heating in Alfvénic Turbulence. Astrophys. J. 2019, 879, 53. [Google Scholar] [CrossRef] [Green Version]
- Cerri, S.S.; Grošelj, D.; Franci, L. Kinetic Plasma Turbulence: Recent Insights and Open Questions From 3D3V Simulations. Front. Astron. Space Sci. 2019, 6, 64. [Google Scholar] [CrossRef] [Green Version]
- Franci, L.; Sarto, D.D.; Papini, E.; Giroul, A.; Stawarz, J.E.; Burgess, D.; Hellinger, P.; Landi, S.; Bale, S.D. Evidence of a “current-mediated” turbulent regime in space and astrophysical plasmas. arXiv 2020, arXiv:2010.05048. [Google Scholar]
- Bowen, T.A.; Bale, S.D.; Bonnell, J.W.; Dudok de Wit, T.; Goetz, K.; Goodrich, K.; Gruesbeck, J.; Harvey, P.R.; Jannet, G.; Koval, A.; et al. A Merged Search-Coil and Fluxgate Magnetometer Data Product for Parker Solar Probe FIELDS. J. Geophys. Res. Space Phys. 2020, 125, e2020JA027813. [Google Scholar] [CrossRef]
- Wilson, L.B.; Stevens, M.L.; Kasper, J.C.; Klein, K.G.; Maruca, B.A.; Bale, S.D.; Bowen, T.A.; Pulupa, M.P.; Salem, C.S. The Statistical Properties of Solar Wind Temperature Parameters Near 1 AU. Astrophys. J. Suppl. Ser. 2018, 236, 41. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navarro, R.E.; Moya, P.S. Effects of Background Turbulence on the Relaxation of Ion Temperature Anisotropy Firehose Instability in Space Plasmas. Universe 2023, 9, 8. https://doi.org/10.3390/universe9010008
Navarro RE, Moya PS. Effects of Background Turbulence on the Relaxation of Ion Temperature Anisotropy Firehose Instability in Space Plasmas. Universe. 2023; 9(1):8. https://doi.org/10.3390/universe9010008
Chicago/Turabian StyleNavarro, Roberto E., and Pablo S. Moya. 2023. "Effects of Background Turbulence on the Relaxation of Ion Temperature Anisotropy Firehose Instability in Space Plasmas" Universe 9, no. 1: 8. https://doi.org/10.3390/universe9010008




