Classification of Solar Radio Spectrum Based on Swin Transformer
Abstract
1. Introduction
2. Solar Radio Spectrum and Preprocessing
2.1. Dataset Introduction
2.2. Normalization of Channels
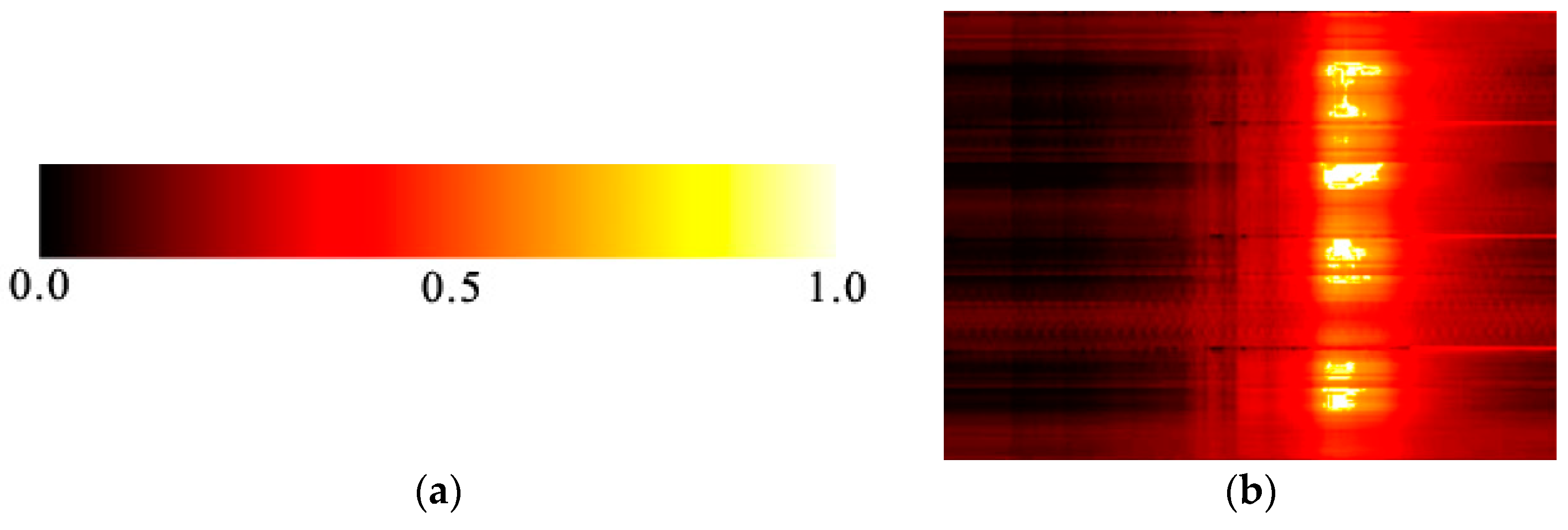
2.3. Pseudocolor Conversion and Dimensional Transformation of the Solar Radio Spectrum
3. Method
3.1. Transfer Learning
3.2. Solar Radio Spectrum Classification Based on Swin Transformer
4. Experimentation and Discussion
4.1. Experimental Evaluation Metrics
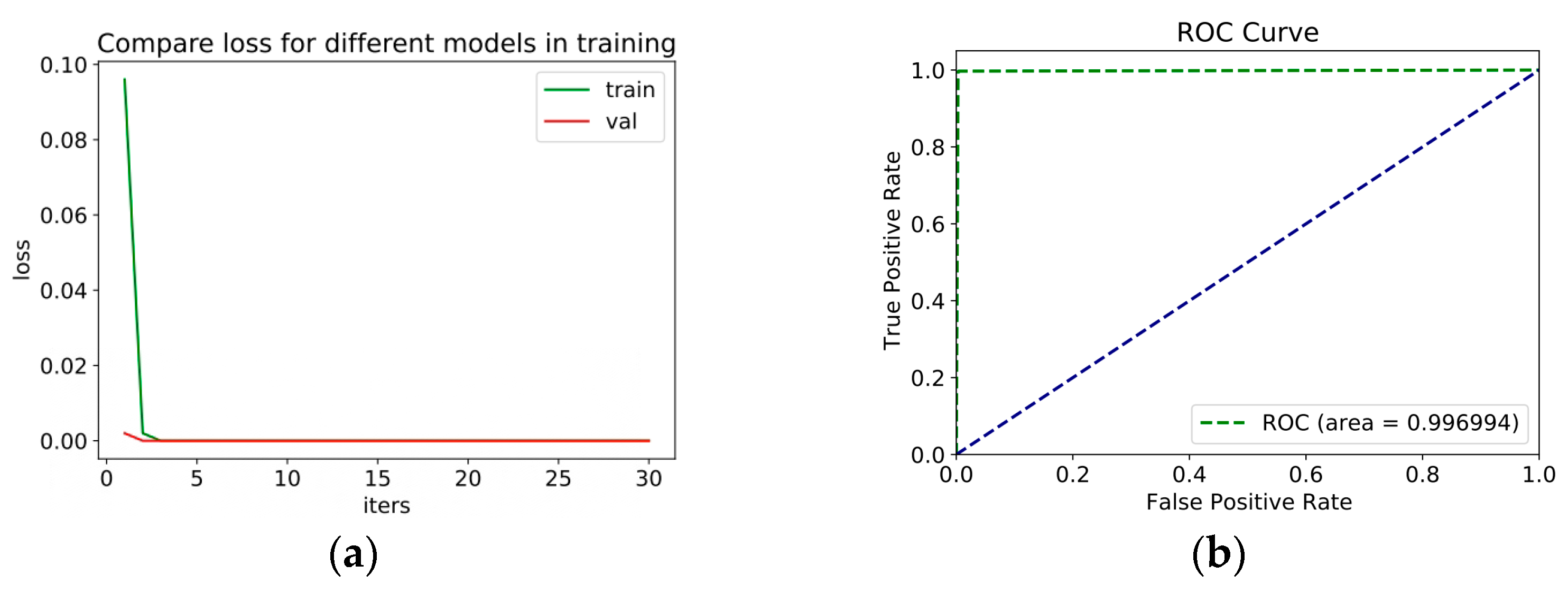
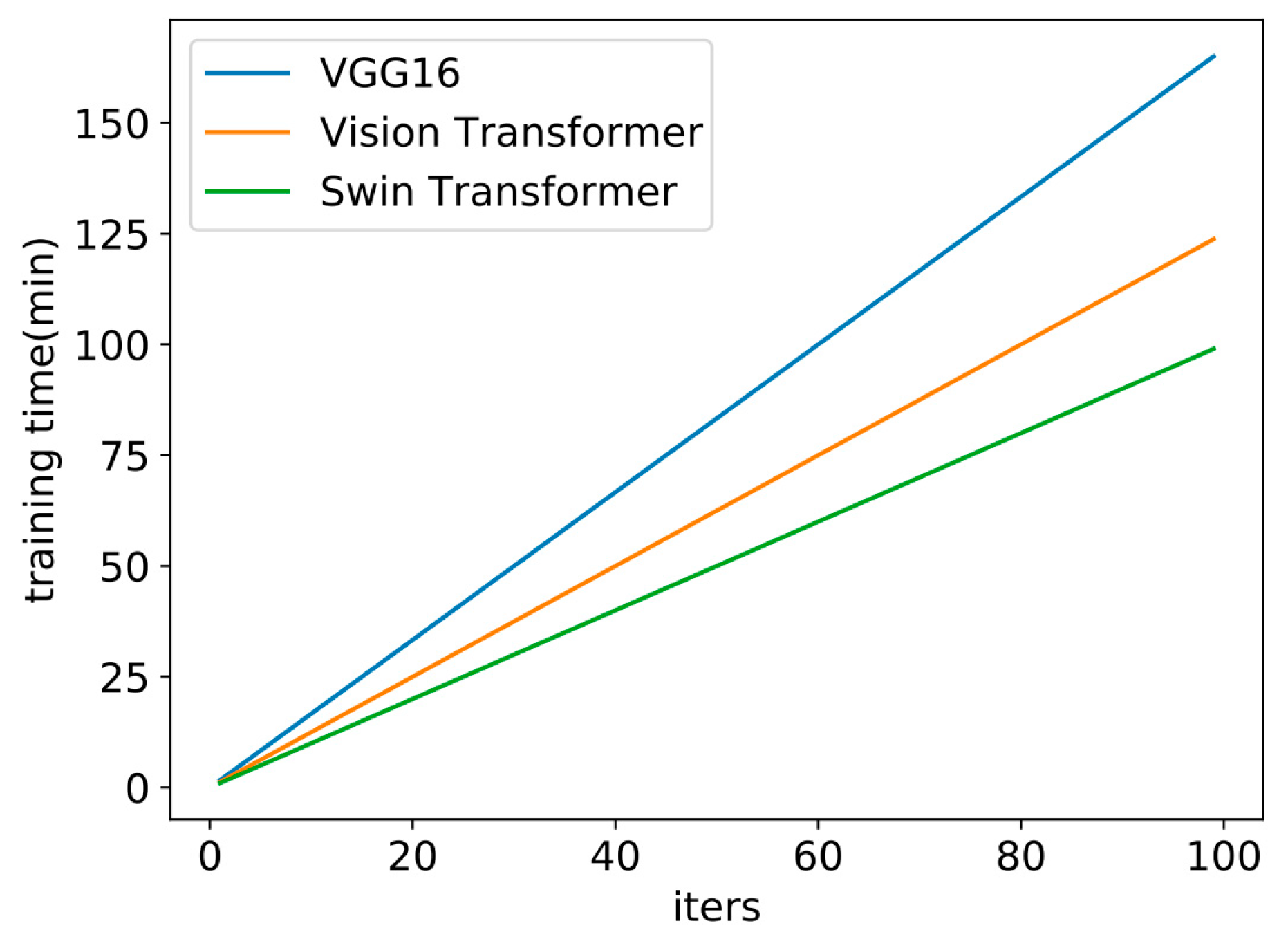
4.2. Experimental Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, R.; Hu, Z. Wavelet NeighShrink Method for Grid Texture Removal in Image of Solar Radio Bursts. Spectrosc. Spectr. Anal. 2007, 27, 4. (In Chinese) [Google Scholar]
- Yan, Y.; Tan, C.; Xu, L.; Ji, H.; Fu, Q.; Song, G. Nonlinear Relative Calibration Methods and Data Processing for Solar Radio Bursts. Sci. China Math. 2001, 45, 89–96. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, Y.; Yan, Y.; Tan, C.; Zhao, C. Automatic Contour Detection and Information Extraction of Solar Radio Spectrogram. Mod. Electron. Technol. 2011, 34, 4. (In Chinese) [Google Scholar]
- Tan, C.; Yan, Y.; Tan, B.; Liu, Y. Design of A Data Processing System for Solar Radio Spectral Observations. Astron. Res. Technol. 2011. (In Chinese) [Google Scholar]
- White, S.M. Solar Radio Bursts and Space Weather. Asian J. Phys. 2007, 16, 189–207. (In Chinese) [Google Scholar]
- Preminger, D.G.; Walton, S.R.; Chapman, G.A. Solar Feature Identification using Contrasts and Contiguity. Sol. Phys. 2001, 202, 53–62. [Google Scholar] [CrossRef]
- Iwai, K.; Tsuchiya, F.; Morioka, A.; Misawa, H. IPRT/AMATERAS: A new metric spectrum observation system for solar radio bursts. Sol. Phys. 2012, 277, 447–457. [Google Scholar] [CrossRef]
- Liu, H.; Yuan, G.; Yang, L.; Liu, K.; Zhou, H. An Appearance Defect Detection Method for Cigarettes Based on C-CenterNet. Electronics 2022, 11, 2182. [Google Scholar] [CrossRef]
- Yang, L.; Yuan, G.; Zhou, H.; Liu, H.; Chen, J.; Wu, H. RS-YOLOX: A High-Precision Detector for Object Detection in Satellite Remote Sensing Images. Appl. Sci. 2022, 12, 8707. [Google Scholar] [CrossRef]
- Lobzin, V.V.; Cairns, I.H.; Robinson, P.A.; Steward, G.; Patterson, G. Automatic recognition of type III solar radio bursts: Automated Radio Burst Identification System method and first observations. Space Weather. Int. J. Res. Appl. 2009, 7, S04002. [Google Scholar] [CrossRef]
- Lobzin, V.V.; Cairns, I.H.; Robinson, P.A.; Steward, G.; Patterson, G. Automatic 19 recognition of coronal type II radio bursts: The automated radio burst identification system method and first observations. Astrophys. J. Lett. 2010, 710, 58–62. [Google Scholar] [CrossRef]
- Guo, J.-C.; Yan, F.-B.; Wan, G.; Hu, X.-J.; Wang, S. A deep learning method for the recognition of solar radio burst spectrum. PeerJ Comput. Sci. 2022, 8, e855. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Yan, F.; Han, F.; He, R.; Li, E.; Wu, Z.; Chen, Y. Auto recognition of solar radio bursts using the C-DCGAN method. Front. Phys. 2021, 9, 646556. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Wang, S.; Yang, K. Research and implementation of image scaling algorithm based on bilinear interpolation. Autom. Technol. Appl. 2008, 27, 44–45. (In Chinese) [Google Scholar]
- Chen, S. Research on Classification Algorithm of Solar Radio Spectrum Based on Convolutional Neural Network; Shenzhen University: Shenzhen, China, 2018. (In Chinese) [Google Scholar]
- Trockman, A.; Kolter, J.Z. Patches Are All You Need? arXiv 2022, arXiv:2201.09792. [Google Scholar]
- Chen, M.; Yuan, G.; Zhou, H.; Cheng, R.; Xu, L.; Tan, C. Classification of Solar Radio Spectrum Based on VGG16 Transfer Learning. In Chinese Conference on Image and Graphics Technologies; Springer: Singapore, 2021; pp. 35–48. [Google Scholar]




| Spectrum Type | Burst | Nonburst | Calibration | Total |
|---|---|---|---|---|
| Spectrum number | 579 | 3335 | 494 | 4408 |
| Dataset | Burst | Nonburst | Calibration | Total |
|---|---|---|---|---|
| Training set | 200 | 1200 | 200 | 1600 |
| Validation set | 179 | 935 | 94 | 1208 |
| Test set | 200 | 1200 | 200 | 1600 |
| Model | Swin Transformer | Swin Transformer+ Transfer Learning | ||
|---|---|---|---|---|
| TPR (%) | FPR (%) | TPR (%) | FPR (%) | |
| Burst | 98.9 | 0 | 100 | 0 |
| Nonburst | 100 | 0.5 | 100 | 0 |
| Calibration | 99.5 | 0.1 | 100 | 0 |
| Model | Swin Transformer+ Transfer Learning | VGG16+ Transfer Learning | ||
|---|---|---|---|---|
| TPR (%) | FPR (%) | TPR (%) | FPR (%) | |
| Burst | 100 | 0 | 96.8 | 1.4 |
| Nonburst | 100 | 0 | 97.1 | 1.3 |
| Calibration | 100 | 0 | 99.6 | 1.8 |
| Parameters | 27, 550, 473 | 139, 357, 544 | ||
| Method | Swin Transformer+ Transfer Learning | Vision Transformer | ||
|---|---|---|---|---|
| TPR (%) | FPR (%) | TPR (%) | FPR (%) | |
| Burst | 100 | 0 | 99.5 | 0 |
| Nonburst | 100 | 0 | 100 | 0 |
| Calibration | 100 | 0 | 100 | 0.1 |
| Parameters | 27, 550, 473 | 85, 800, 963 | ||
| Model | Burst | Nonburst | Calibration | |
|---|---|---|---|---|
| Swin transformer | TPR (%) | 100 | 100 | 100 |
| FPR (%) | 0 | 0 | 0 | |
| Vision transformer | TPR (%) | 99.5 | 100 | 100 |
| FPR (%) | 0 | 0 | 0.1 | |
| CGRU | TPR (%) | 96.8 | 99.5 | 99.9 |
| FPR (%) | 0 | 1.5 | 0.3 | |
| VGG16 | TPR (%) | 96.8 | 97.1 | 99.6 |
| FPR (%) | 1.4 | 1.3 | 1.8 | |
| CNN | TPR (%) | 84.6 | 90 | 99 |
| FPR (%) | 9.7 | 8.7 | 0.7 | |
| Multimodel | TPR (%) | 70.9 | 80.9 | 96.8 |
| FPR (%) | 15.6 | 13.9 | 3.2 | |
| DBN | TPR (%) | 67.4 | 86.4 | 95.7 |
| FPR (%) | 3.2 | 14.1 | 0.4 | |
| PCA+SVM | TPR (%) | 52.7 | 0.1 | 68.3 |
| FPR (%) | 2.6 | 16.6 | 72.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Yuan, G.; Zhou, H.; Tan, C.; Yang, L.; Li, S. Classification of Solar Radio Spectrum Based on Swin Transformer. Universe 2023, 9, 9. https://doi.org/10.3390/universe9010009
Chen J, Yuan G, Zhou H, Tan C, Yang L, Li S. Classification of Solar Radio Spectrum Based on Swin Transformer. Universe. 2023; 9(1):9. https://doi.org/10.3390/universe9010009
Chicago/Turabian StyleChen, Jian, Guowu Yuan, Hao Zhou, Chengming Tan, Lei Yang, and Siqi Li. 2023. "Classification of Solar Radio Spectrum Based on Swin Transformer" Universe 9, no. 1: 9. https://doi.org/10.3390/universe9010009
APA StyleChen, J., Yuan, G., Zhou, H., Tan, C., Yang, L., & Li, S. (2023). Classification of Solar Radio Spectrum Based on Swin Transformer. Universe, 9(1), 9. https://doi.org/10.3390/universe9010009









