Neutron Dark Decay
Abstract
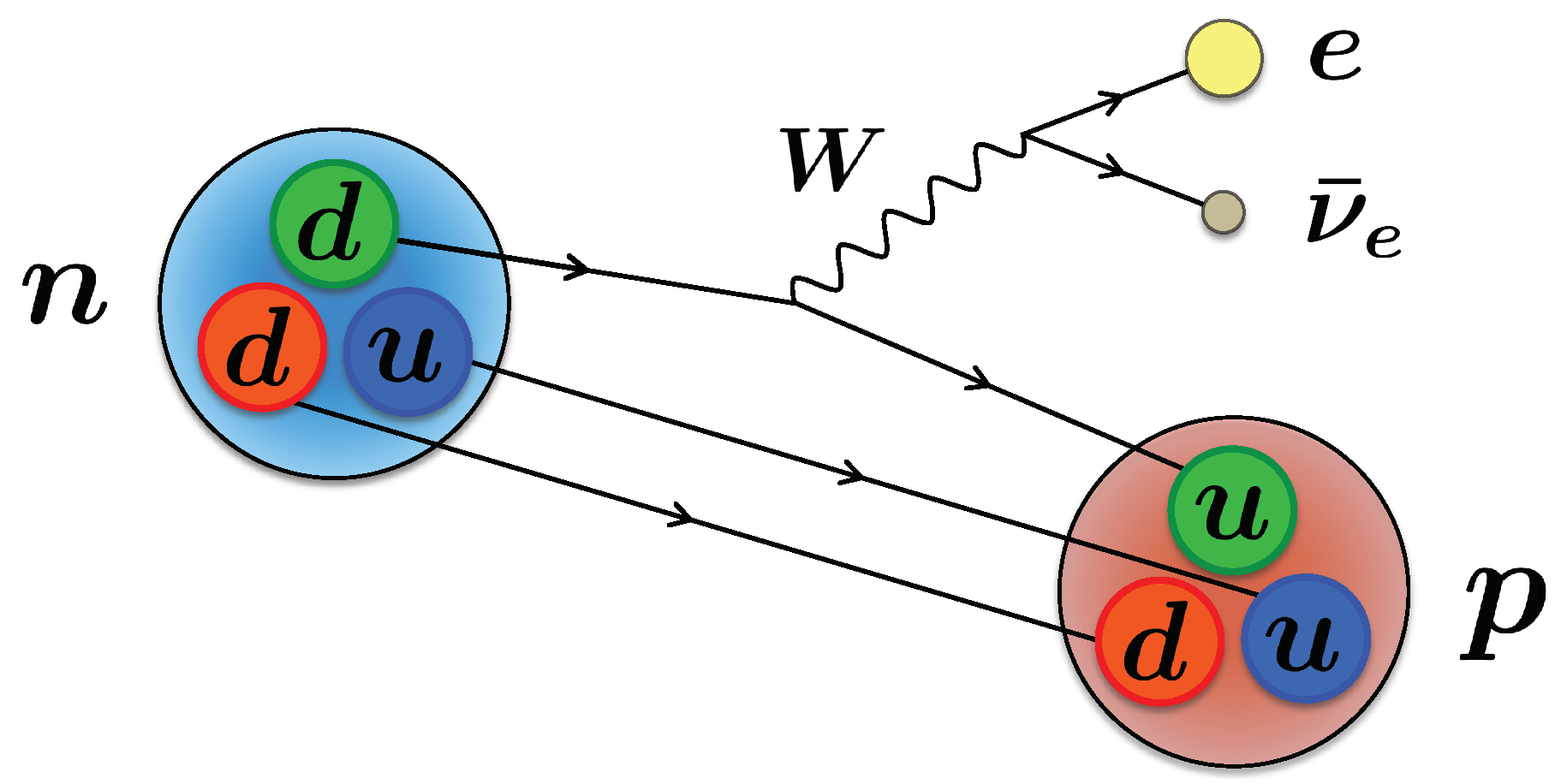
:1. Introduction
2. Effective Picture of Neutron Dark Decay
2.1. Stability of Nuclei
2.2. Neutron Dark Decay Channels
2.3. Neutron Dark Fermion + Photon
2.4. Neutron Dark Fermion + Dark Scalar
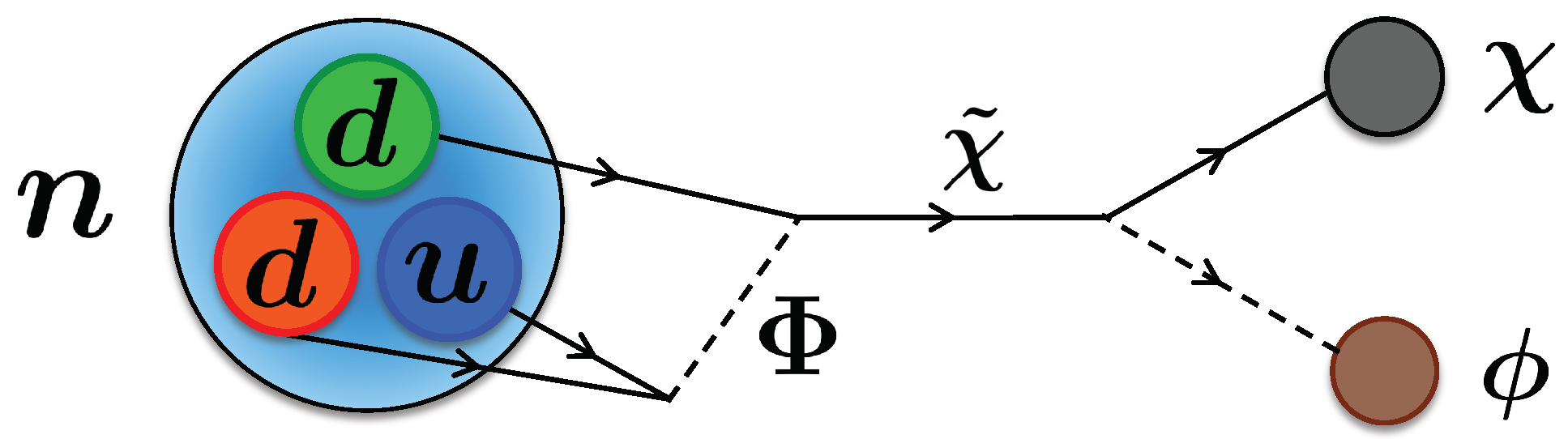
3. Particle Physics Models
3.1. Model 1
3.2. Model 2
4. Experimental Progress
4.1. Search for
4.2. Search for
4.3. Search for Nuclear Dark Decays
4.3.1. Dark Decay
4.3.2. Dark Decay
4.4. Beam and Bottle Experiments
4.5. Neutron Lifetime from Decay Parameters
4.6. Space Missions
4.7. Colliders
5. Theoretical Developments
5.1. Neutron Star Masses
5.2. Self-Interactions in the Dark Sector
5.3. Dark Matter–Neutron Repulsion
5.4. Stability of Hydrogen
5.5. Dark Matter Nuclear Capture
5.6. Dark Matter–Neutron Annihilation
- Model 1: ;
- Model 2: .
5.7. Hadron Dark Decays
5.8. Neutron–Mirror Neutron Oscillations
5.9. Other Theoretical Progress
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thomson, J.J. Cathode Rays. Philos. Mag. 1897, 44, 293–316. [Google Scholar] [CrossRef]
- Rutherford, E. Collision of α Particles with Light Atoms. IV. An Anomalous Effect in Nitrogen. Philos. Mag. Ser. 6 1919, 37, 581–587. [Google Scholar] [CrossRef]
- Joliot-Curie, I.; Joliot-Curie, F. Emission de Protons de Grande Vitesse par les Substances Hydrogenees sous l’Influence des Rayons γ Tres Penetrants [Emission of High-Speed Protons by Hydrogenated Substances under the Influence of Very Penetrating γ-Rays]. C. R. Seances L’Academie Sci. 1932, 194, 273. [Google Scholar]
- Chadwick, J. The Existence of a Neutron. Proc. R. Soc. Lond. Ser. 1932, 136, 692–708. [Google Scholar] [CrossRef]
- Joliot-Curie, I.; Joliot-Curie, F. Mass of the Neutron. Nature 1934, 133, 721. [Google Scholar] [CrossRef]
- Bales, M.J.; Alarcon, R.; Bass, C.D.; Beise, E.J.; Breuer, H.; Byrne, J.; Chupp, T.E.; Coakley, K.J.; Cooper, R.L.; Dewey, M.S.; et al. Precision Measurement of the Radiative β Decay of the Free Neutron. Phys. Rev. Lett. 2016, 116, 242501. [Google Scholar] [CrossRef] [PubMed]
- Faber, M.; Ivanov, A.N.; Ivanova, V.A.; Marton, J.; Pitschmann, M.; Serebrov, A.P.; Troitskaya, N.I.; Wellenzohn, M. On Continuum-State and Bound-State Beta Decay Rates of the Neutron. Phys. Rev. C 2009, 80, 035503. [Google Scholar] [CrossRef]
- Glashow, S.L. Partial Symmetries of Weak Interactions. Nucl. Phys. 1961, 22, 579–588. [Google Scholar] [CrossRef]
- Higgs, P.W. Broken Symmetries and the Masses of Gauge Bosons. Phys. Rev. Lett. 1964, 13, 508–509. [Google Scholar] [CrossRef]
- Englert, F.; Brout, R. Broken Symmetry and the Mass of Gauge Vector Mesons. Phys. Rev. Lett. 1964, 13, 321–323. [Google Scholar] [CrossRef]
- Weinberg, S. A Model of Leptons. Phys. Rev. Lett. 1967, 19, 1264–1266. [Google Scholar] [CrossRef]
- Salam, A. Weak and Electromagnetic Interactions. Conf. Proc. C 1968, 680519, 367–377. [Google Scholar]
- Fritzsch, H.; Gell-Mann, M.; Leutwyler, H. Advantages of the Color Octet Gluon Picture. Phys. Lett. B 1973, 47, 365–368. [Google Scholar] [CrossRef]
- Gross, D.J.; Wilczek, F. Ultraviolet Behavior of Nonabelian Gauge Theories. Phys. Rev. Lett. 1973, 30, 1343–1346. [Google Scholar] [CrossRef]
- Politzer, H.D. Reliable Perturbative Results for Strong Interactions? Phys. Rev. Lett. 1973, 30, 1346–1349. [Google Scholar] [CrossRef]
- Marciano, W.J.; Sirlin, A. Improved Calculation of Electroweak Radiative Corrections and the Value of Vud. Phys. Rev. Lett. 2006, 96, 032002. [Google Scholar] [CrossRef]
- Czarnecki, A.; Marciano, W.J.; Sirlin, A. Neutron Lifetime and Axial Coupling Connection. Phys. Rev. Lett. 2018, 120, 202002. [Google Scholar] [CrossRef]
- Hardy, J.C.; Towner, I.S. Superallowed 0+→0+ Nuclear β Decays: 2014 Critical Survey, with Precise Results for Vud and CKM Unitarity. Phys. Rev. C 2015, 91, 025501. [Google Scholar] [CrossRef]
- Workman, R.L. et al. [Particle Data Group] Review of Particle Physics. Prog. Theor. Exp. Phys. 2022, 2022, 083C01. [Google Scholar] [CrossRef]
- Chang, C.C.; Nicholson, A.N.; Rinaldi, E.; Berkowitz, E.; Garron, N.; Brantley, D.A.; Monge-Camacho, H.; Monahan, C.J.; Bouchard, C.; Clark, M.A.; et al. A Per-Cent-Level Determination of the Nucleon Axial Coupling from Quantum Chromodynamics. Nature 2018, 558, 91–94. [Google Scholar] [CrossRef]
- Dubbers, D.; Schmidt, M.G. The Neutron and its Role in Cosmology and Particle Physics. Rev. Mod. Phys. 2011, 83, 1111–1171. [Google Scholar] [CrossRef]
- Wietfeldt, F.E.; Greene, G.L. The Neutron Lifetime. Rev. Mod. Phys. 2011, 83, 1173–1192. [Google Scholar] [CrossRef]
- Byrne, J.; Dawber, P.G. A Revised Value for the Neutron Lifetime Measured Using a Penning Trap. Europhys. Lett. 1996, 33, 187. [Google Scholar] [CrossRef]
- Nico, J.S.; Dewey, M.S.; Gilliam, D.M.; Wietfeldt, F.E.; Fei, X.; Snow, W.M.; Greene, G.L.; Pauwels, J.; Eykens, R.; Lamberty, A.; et al. Measurement of the Neutron Lifetime by Counting Trapped Protons in a Cold Neutron Beam. Phys. Rev. C 2005, 71, 055502. [Google Scholar] [CrossRef]
- Yue, A.T.; Dewey, M.S.; Gilliam, D.M.; Greene, G.L.; Laptev, A.B.; Nico, J.S.; Snow, W.M.; Wietfeldt, F.E. Improved Determination of the Neutron Lifetime. Phys. Rev. Lett. 2013, 111, 222501. [Google Scholar] [CrossRef] [PubMed]
- Hirota, K.; Ichikawa, G.; Ieki, S.; Ino, T.; Iwashita, Y.; Kitaguchi, M.; Kitahara, R.; Koga, J.; Mishima, K.; Mogi, T.; et al. Neutron Lifetime Measurement with Pulsed Cold Neutrons. Prog. Theor. Exp. Phys. 2020, 2020, 123C02. [Google Scholar] [CrossRef]
- Serebrov, A.; Varlamov, V.; Kharitonov, A.; Fomin, A.; Pokotilovski, Y.; Geltenbort, P.; Butterworth, J.; Krasnoschekova, I.; Lasakov, M.; Tal’daev, R.; et al. Measurement of the Neutron Lifetime Using a Gravitational Trap and a Low-Temperature Fomblin Coating. Phys. Lett. B 2005, 605, 72–78. [Google Scholar] [CrossRef]
- Pichlmaier, A.; Varlamov, V.; Schreckenbach, K.; Geltenbort, P. Neutron Lifetime Measurement with the UCN Trap-in-Trap MAMBO II. Phys. Lett. B 2010, 693, 221–226. [Google Scholar] [CrossRef]
- Steyerl, A.; Pendlebury, J.M.; Kaufman, C.; Malik, S.S.; Desai, A.M. Quasielastic Scattering in the Interaction of Ultracold Neutrons with a Liquid Wall and Application in a Reanalysis of the Mambo I Neutron Lifetime Experiment. Phys. Rev. C 2012, 85, 065503. [Google Scholar] [CrossRef]
- Arzumanov, S.; Bondarenko, L.; Chernyavsky, S.; Geltenbort, P.; Morozov, V.; Nesvizhevsky, V.V.; Panin, Y.; Strepetov, A. A Measurement of the Neutron Lifetime Using the Method of Storage of Ultracold Neutrons and Detection of Inelastically Up-Scattered Neutrons. Phys. Lett. B 2015, 745, 79–89. [Google Scholar] [CrossRef]
- Serebrov, A.P.; Kolomensky, E.A.; Fomin, A.K.; Krasnoshchekova, I.A.; Vassiljev, A.V.; Prudnikov, D.M.; Shoka, I.V.; Chechkin, A.V.; Chaikovskiy, M.E.; Varlamov, V.E.; et al. Neutron Lifetime Measurements with a Large Gravitational Trap for Ultracold Neutrons. Phys. Rev. C 2018, 97, 055503. [Google Scholar] [CrossRef]
- Pattie, R.W., Jr.; Callahan, N.B.; Cude-Woods, C.; Adamek, E.R.; Broussard, L.J.; Clayton, S.M.; Currie, S.A.; Dees, E.B.; Ding, X.; Zeck, B.A.; et al. Measurement of the Neutron Lifetime Using a Magneto-Gravitational Trap and In Situ Detection. Science 2018, 360, 627–632. [Google Scholar] [CrossRef] [PubMed]
- Ezhov, V.F.; Andreev, A.Z.; Ban, G.; Bazarov, B.A.; Geltenbort, P.; Glushkov, A.G.; Knyazkov, V.A.; Kovrizhnykh, N.A.; Krygin, G.B.; Ryabov, V.L.; et al. Measurement of the Neutron Lifetime with Ultra-Cold Neutrons Stored in a Magneto-Gravitational Trap. J. Exp. Theor. Phys. Lett. 2018, 107, 671–675. [Google Scholar] [CrossRef]
- Gonzalez, F.M.; Fries, E.M.; Cude-Woods, C.; Bailey, T.; Blatnik, M.; Broussard, L.J.; Callahan, N.B.; Choi, J.H.; Clayton, S.M.; Young, A.R.; et al. Improved Neutron Lifetime Measurement with UCNτ. Phys. Rev. Lett. 2021, 127, 162501. [Google Scholar] [CrossRef] [PubMed]
- Fornal, B.; Grinstein, B. Dark Matter Interpretation of the Neutron Decay Anomaly. Phys. Rev. Lett. 2018, 120, 191801, Erratum in Phys. Rev. Lett. 2020, 124, 219901. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, S.N.; Anthony, A.E.; Beier, E.W.; Bellerive, A.; Biller, S.D.; Boger, J.; Boulay, M.G.; Bowler, M.G.; Bowles, T.J.; Brice, S.J.; et al. Constraints on Nucleon Decay via Invisible Modes from the Sudbury Neutrino Observatory. Phys. Rev. Lett. 2004, 92, 102004. [Google Scholar] [CrossRef]
- Araki, T.; Enomoto, S.; Furuno, K.; Gando, Y.; Ichimura, K.; Ikeda, H.; Inoue, K.; Kishimoto, Y.; Koga, M.; Koseki, Y.; et al. Search for the Invisible Decay of Neutrons with KamLAND. Phys. Rev. Lett. 2006, 96, 101802. [Google Scholar] [CrossRef]
- Pfutzner, M.; Riisager, K. Examining the Possibility to Observe Neutron Dark Decay in Nuclei. Phys. Rev. C 2018, 97, 042501. [Google Scholar] [CrossRef]
- Tang, Z.; Blatnik, M.; Broussard, L.J.; Choi, J.H.; Clayton, S.M.; Cude-Woods, C.; Currie, S.; Fellers, D.E.; Fries, E.M.; Geltenbort, P.; et al. Search for the Neutron Decay n → X + γ where X is a Dark Matter Particle. Phys. Rev. Lett. 2018, 121, 022505. [Google Scholar] [CrossRef]
- Aoki, Y.; Izubuchi, T.; Shintani, E.; Soni, A. Improved Lattice Computation of Proton Decay Matrix Elements. Phys. Rev. 2017, D96, 014506. [Google Scholar] [CrossRef]
- Gustafson, J.; Abe, K.; Haga, Y.; Hayato, Y.; Ikeda, M.; Iyogi, K.; Kameda, J.; Kishimoto, Y.; Miura, M.; Moriyama, S.; et al. Search for Dinucleon Decay into Pions at Super-Kamiokande. Phys. Rev. D 2015, 91, 072009. [Google Scholar] [CrossRef]
- Abe, K.; Hayato, Y.; Iida, T.; Ishihara, K.; Kameda, J.; Koshio, Y.; Minamino, A.; Mitsuda, C.; Miura, M.; Moriyama, S.; et al. The Search for n − n Oscillation in Super-Kamiokande I. Phys. Rev. D 2015, 91, 072006. [Google Scholar] [CrossRef]
- McKeen, D.; Pospelov, M. How Long Does the Hydrogen Atom Live? arXiv 2020, arXiv:2003.02270. [Google Scholar]
- Agostini, M.; Appel, S.; Bellini, G.; Benziger, J.; Bick, D.; Bonfini, G.; Bravo, D.; Caccianiga, B.; Calaprice, F.; Caminata, A.; et al. A Test of Electric Charge Conservation with Borexino. Phys. Rev. Lett. 2015, 115, 231802. [Google Scholar] [CrossRef] [PubMed]
- McKeen, D.; Pospelov, M.; Raj, N. Cosmological and Astrophysical Probes of Dark Baryons. Phys. Rev. D 2021, 103, 115002. [Google Scholar] [CrossRef]
- Sun, X.; Adamek, E.; Allgeier, B.; Blatnik, M.; Bowles, T.J.; Broussard, L.J.; Brown, M.A.-P.; Carr, R.; Clayton, S.; Cude-Woods, C.; et al. Search for Dark Matter Decay of the Free Neutron from the UCNA Experiment: n → χ + e+e−. Phys. Rev. C 2018, 97, 052501. [Google Scholar] [CrossRef]
- Klopf, M.; Jericha, E.; Markisch, B.; Saul, H.; Soldner, T.; Abele, H. Constraints on the Dark Matter Interpretation n → χ + e+e− of the Neutron Decay Anomaly with the PERKEO II Experiment. Phys. Rev. Lett. 2019, 122, 222503. [Google Scholar] [CrossRef]
- Borge, M.J.G.; Fraile, L.M.; Fynbo, H.O.U.; Jonson, B.; Kirsebom, O.S.; Nilsson, T.; Nyman, G.; Possnert, G.; Riisager, K.; Tengblad, O. Rare βp decays in light nuclei. J. Phys. Nucl. Part. Phys. 2013, 40, 035109. [Google Scholar] [CrossRef]
- Riisager, K.; Forstner, O.; Borge, M.J.G.; Briz, J.A.; Carmona-Gallardo, M.; Fraile, L.M.; Fynbo, H.O.U.; Giles, T.; Gottberg, A.; Heinz, A.; et al. 11Be(βp), a Quasi-Free Neutron Decay? Phys. Lett. B 2014, 732, 305–308. [Google Scholar] [CrossRef]
- Ejiri, H.; Vergados, J.D. Neutron Disappearance Inside the Nucleus. J. Phys. G 2019, 46, 025104. [Google Scholar] [CrossRef]
- CERN-ISOLDE Schedule. 2018. Available online: https://isolde.web.cern.ch/isolde-schedule (accessed on 26 July 2020).
- Ayyad, Y.; Olaizola, B.; Mittig, W.; Potel, G.; Zelevinsky, V.; Horoi, M.; Beceiro-Novo, S.; Alcorta, M.; Andreoiu, C.; Ahn, T.; et al. Direct Observation of Proton Emission in 11Be. Phys. Rev. Lett. 2019, 123, 082501, Erratum in Phys. Rev. Lett. 2020, 124, 129902. [Google Scholar] [CrossRef] [PubMed]
- Ayyad, Y.; Mittig, W.; Tang, T.; Olaizola, B.; Potel, G.; Rijal, N.; Watwood, N.; Alvarez-Pol, H.; Bazin, D.; Chen, J.; et al. Evidence of a Near-Threshold Resonance in 11B Relevant to the β-Delayed Proton Emission of 11Be. Phys. Rev. Lett. 2022, 129, 012501. [Google Scholar] [CrossRef] [PubMed]
- Lopez-Saavedra, E.; Almaraz-Calderon, S.; Asher, B.W.; Baby, L.T.; Gerken, N.; Hanselman, K.; Kemper, K.W.; Kuchera, A.N.; Morelock, A.B.; Perello, J.F.; et al. Observation of a Near-Threshold Proton Resonance in 11B. Phys. Rev. Lett. 2022, 129, 012502. [Google Scholar] [CrossRef] [PubMed]
- Okolowicz, J.; Ploszajczak, M.; Nazarewicz, W. Convenient Location of a Near-Threshold Proton-Emitting Resonance in 11B. Phys. Rev. Lett. 2020, 124, 042502. [Google Scholar] [CrossRef]
- Anh, N.L.; Loc, B.M.; Auerbach, N.; Zelevinsky, V. Single-Particle Properties of the Near-Threshold Proton-Emitting Resonance in 11B. Phys. Rev. C 2022, 106, L051302. [Google Scholar] [CrossRef]
- Riisager, K.; Borge, M.J.G.; Briz, J.A.; Carmona-Gallardo, M.; Forstner, O.; Fraile, L.M.; Fynbo, H.O.U.; Camacho, A.G.; Johansen, J.G.; Jonson, B.; et al. Search for Beta-Delayed Proton Emission from 11Be. Eur. Phys. J. A 2020, 56, 100. [Google Scholar] [CrossRef]
- Le Joubioux, M.; Savajols, H.; Mittig, W.; Fléchard, X.; Penionzhkevich, Y.E.; Ackermann, D.; Borcea, C.; Caceres, L.; Delahaye, P.; Didierjean, F.; et al. Is There a Dark Decay of Neutrons in 6He? arXiv 2023, arXiv:2308.16536. [Google Scholar]
- Anthony, D.; Buchmann, L.; Bergbusch, P.; D’Auria, J.M.; Dombsky, M.; Giesen, U.; Jackson, K.P.; King, J.D.; Powell, J.; Barker, F.C. β-Delayed Deuteron Emission from 6He. Phys. Rev. C 2002, 65, 034310. [Google Scholar] [CrossRef]
- Raabe, R.; Büscher, J.; Ponsaers, J.; Aksouh, F.; Huyse, M.; Ivanov, O.; Lesher, S.R.; Mukha, I.; Pauwels, D.; Sawicka, M.; et al. Measurement of the Branching Ratio of the 6He β-Decay Channel into the α + d Continuum. Phys. Rev. C 2009, 80, 054307. [Google Scholar] [CrossRef]
- Pfutzner, M.; Dominik, W.; Janas, Z.; Mazzocchi, C.; Pomorski, M.; Bezbakh, A.A.; Borge, M.J.G.; Chrapkiewicz, K.; Chudoba, V.; Frederickx, R.; et al. β Decay of 6He into the α + d Continuum. Phys. Rev. C 2015, 92, 014316. [Google Scholar] [CrossRef]
- Dewey, M.; Coakley, K.; Gilliam, D.; Greene, G.; Laptev, A.; Nico, J.; Snow, W.; Wietfeldt, F.; Yue, A. Prospects for a New Cold Neutron Beam Measurement of the Neutron Lifetime. Nucl. Instrum. Methods A 2009, 611, 189. [Google Scholar] [CrossRef]
- Hoogerheide, S.F.; Caylor, J.; Adamek, E.R.; Anderson, E.S.; Biswas, R.; Chavali, S.M.; Crawford, B.; DeAngelis, C.; Dewey, M.S.; Yue, A.T.; et al. Progress on the BL2 Beam Measurement of the Neutron Lifetime. EPJ Web Conf. 2019, 219, 03002. [Google Scholar] [CrossRef]
- Nagakura, N.; Hirota, K.; Ieki, S.; Ino, T.; Iwashita, Y.; Kitaguchi, M.; Kitahara, R.; Mishima, K.; Morishita, A.; Oide, H.; et al. Precise Neutron Lifetime Experiment Using Pulsed Neutron Beams at J-PARC. arXiv 2017, arXiv:1702.03099. [Google Scholar] [CrossRef]
- Nagakura, N.; Hirota, K.; Ieki, S.; Ino, T.; Iwashita, Y.; Kitaguchi, M.; Kitahara, R.; Koga, J.; Mishima, K.; Morishita, A.; et al. New Project for Precise Neutron Lifetime Measurement at J-PARC. EPJ Web Conf. 2019, 219, 03003. [Google Scholar] [CrossRef]
- Sumi, N.; Hirota, K.; Ichikawa, G.; Ino, T.; Iwashita, Y.; Kajiwara, S.; Kato, Y.; Kitaguchi, M.; Mishima, K.; Morikawa, K.; et al. Precise Neutron Lifetime Measurement Using Pulsed Neutron Beams at J-PARC. JPS Conf. Proc. 2021, 33, 011056. [Google Scholar] [CrossRef]
- Nelsen, A.W.; Ballantyne, E.G.; Calvert, R.E.; Crawford, C.B.; Greene, G.L.; Vickers, S.E.; Wietfeldt, F.E. Geometric Optimization of a Neutron Detector for In-Flight Measurement of the Neutron Lifetime. arXiv 2020, arXiv:2010.11250. [Google Scholar]
- Fomin, N.; BL3 Collaboration. BL3: Next Generation Beam Experiment to Measure the Neutron Lifetime. In Proceedings of the APS April Meeting Abstracts, Virtual, 16–19 April 2021; Volume 2021, p. T11.008. [Google Scholar]
- Wietfeldt, F.; BL3 Collaboration Team. The BL3 Beam Neutron Lifetime Experiment. In Proceedings of the APS April Meeting Abstracts, New York, NY, USA, 9–12 April 2022; Volume 2022, p. T12.004. [Google Scholar]
- Fry, J. BL3: The Next Generation Neutron Lifetime Measurement Using the Beam Method. In Proceedings of the Talk at the APS Southeastern Section Meeting 2022, Oxford, MS, USA, 3–5 November 2022; Available online: https://meetings.aps.org/Meeting/SES22/Session/K03.3 (accessed on 27 June 2023).
- Fornal, B.; Grinstein, B. Dark Side of the Neutron? EPJ Web Conf. 2019, 219, 05005. [Google Scholar] [CrossRef]
- Tang, Z.; Cude-Woods, C.; Clayton, S.; Morris, C.; Ito, T.; Makela, M.; Saunders, A.; Choi, J.H.; Lambert, J.; Liu, C.-Y.; et al. Ultra-Cold Neutron Measurement of Proton Branching Ratio in Neutron Beta Decay (UCNProBe). In Proceedings of the Talk at the APS Meeting 2019, Denver, CO, USA, 13–16 April 2019; Available online: http://meetings.aps.org/Meeting/APR19/Session/H14.5 (accessed on 27 June 2023).
- Hassan, M.; Floyd, N.; Tang, Z.; UCNProBe Team. The Current Status of the UCNProBe Experiment. In Proceedings of the APS Division of Nuclear Physics Meeting Abstracts, Virtual, 11–14 October 2021; Volume 2021, p. QJ.008. [Google Scholar]
- Markisch, B.; Mest, H.; Saul, H.; Wang, X.; Abele, H.; Dubbers, D.; Klopf, M.; Petoukhov, A.; Roick, C.; Soldner, T.; et al. Measurement of the Weak Axial-Vector Coupling Constant in the Decay of Free Neutrons Using a Pulsed Cold Neutron Beam. Phys. Rev. Lett. 2019, 122, 242501. [Google Scholar] [CrossRef]
- Beck, M.; Ayala Guardia, F.; Borg, M.; Kahlenberg, J.; Muñoz Horta, R.; Schmidt, C.; Wunderle, A.; Heil, W.; Maisonobe, R.; Simson, M.; et al. Improved Determination of the β − νe Angular Correlation Coefficient a in Free Neutron Decay with the aSPECT Spectrometer. Phys. Rev. C 2020, 101, 055506. [Google Scholar] [CrossRef]
- Hassan, M.T.; Byron, W.A.; Darius, G.; DeAngelis, C.; Wietfeldt, F.E.; Collett, B.; Jones, G.L.; Komives, A.; Noid, G.; Stephenson, E.J.; et al. Measurement of the Neutron Decay Electron-Antineutrino Angular Correlation by the aCORN Experiment. Phys. Rev. C 2021, 103, 045502. [Google Scholar] [CrossRef]
- Dubbers, D.; Markisch, B. Precise Measurements of the Decay of Free Neutrons. Ann. Rev. Nucl. Part. Sci. 2021, 71, 139–163. [Google Scholar] [CrossRef]
- Wilson, J.T.; Lawrence, D.J.; Peplowski, P.N.; Eke, V.R.; Kegerreis, J.A. Space-Based Measurement of the Neutron Lifetime Using Data from the Neutron Spectrometer on NASA’s MESSENGER Mission. Phys. Rev. Res. 2020, 2, 023316. [Google Scholar] [CrossRef]
- Wilson, J.T.; Lawrence, D.J.; Peplowski, P.N.; Eke, V.R.; Kegerreis, J.A. Measurement of the Free Neutron Lifetime Using the Neutron Spectrometer on NASA’s Lunar Prospector Mission. Phys. Rev. C 2021, 104, 045501. [Google Scholar] [CrossRef]
- Abada, A.; Abbrescia, M.; AbdusSalam, S.S.; Abdyukhanov, I.; Fernandez, J.A.; Abramov, A.; Aburaia, M.; Acar, A.O.; Adzic, P.R.; Agrawal, P.; et al. FCC Physics Opportunities: Future Circular Collider Conceptual Design Report Volume 1. Eur. Phys. J. C 2019, 79, 474. [Google Scholar] [CrossRef]
- Baym, G.; Beck, D.H.; Geltenbort, P.; Shelton, J. Testing Dark Decays of Baryons in Neutron Stars. Phys. Rev. Lett. 2018, 121, 061801. [Google Scholar] [CrossRef]
- McKeen, D.; Nelson, A.E.; Reddy, S.; Zhou, D. Neutron Stars Exclude Light Dark Baryons. Phys. Rev. Lett. 2018, 121, 061802. [Google Scholar] [CrossRef]
- Motta, T.F.; Guichon, P.A.M.; Thomas, A.W. Implications of Neutron Star Properties for the Existence of Light Dark Matter. J. Phys. G 2018, 45, 05LT01. [Google Scholar] [CrossRef]
- Grinstein, B.; Kouvaris, C.; Nielsen, N.G. Neutron Star Stability in Light of the Neutron Decay Anomaly. Phys. Rev. Lett. 2019, 123, 091601. [Google Scholar] [CrossRef]
- Spergel, D.N.; Steinhardt, P.J. Observational Evidence for Self-Interacting Cold Dark Matter. Phys. Rev. Lett. 2000, 84, 3760–3763. [Google Scholar] [CrossRef]
- Cline, J.M.; Cornell, J.M. Dark Decay of the Neutron. J. High Energy Phys. 2018, 07, 081. [Google Scholar] [CrossRef]
- Bringmann, T.; Cline, J.M.; Cornell, J.M. Baryogenesis from Neutron–Dark Matter Oscillations. Phys. Rev. D 2019, 99, 035024. [Google Scholar] [CrossRef]
- Karananas, G.K.; Kassiteridis, A. Small-Scale Structure from Neutron Dark Decay. J. Cosmol. Astropart. Phys. 2018, 09, 036. [Google Scholar] [CrossRef]
- Elahi, F.; Mohammadi Najafabadi, M. Neutron Decay to a Non-Abelian Dark Sector. Phys. Rev. 2020, 102, 035011. [Google Scholar] [CrossRef]
- Berezhiani, Z. Neutron Lifetime Puzzle and Neutron—Mirror Neutron Oscillation. Eur. Phys. J. C 2019, 79, 484. [Google Scholar] [CrossRef]
- Fornal, B.; Grinstein, B.; Zhao, Y. Dark Matter Capture by Atomic Nuclei. Phys. Lett. B 2020, 811, 135869. [Google Scholar] [CrossRef]
- Cao, X.; Chen, X.; Chen, Y.; Cui, X.; Fang, D.; Fu, C.; Giboni, K.L.; Gong, H.; Guo, G.; He, M.; et al. PandaX: A Liquid Xenon Dark Matter Experiment at CJPL. Sci. China Phys. Mech. Astron. 2014, 57, 1476–1494. [Google Scholar] [CrossRef]
- Aprile, E.; Abe, K.; Agostini, F.; Ahmed Maouloud, S.; Althueser, L.; Andrieu, B.; Angelino, E.; Angevaare, J.R.; Antochi, V.C.; Antón Martin, D.; et al. Search for New Physics in Electronic Recoil Data from XENONnT. Phys. Rev. Lett. 2022, 129, 161805. [Google Scholar] [CrossRef]
- Murphy, A. et al. [The LUX-ZEPLIN (LZ) Collaboration] The LUX-ZEPLIN (LZ) Experiment. Nucl. Instrum. Methods A 2020, 953, 163047. [Google Scholar] [CrossRef]
- Abi, B.; Acciarri, R.; Acero, M.A.; Adamov, G.; Adams, D.; Adinolfi, M.; Ahmad, Z.; Ahmed, J.; Alion, T.; Monsalve, S.A.; et al. Deep Underground Neutrino Experiment (DUNE), Far Detector Technical Design Report. arXiv 2020, arXiv:2002.03005. [Google Scholar]
- Hostert, M.; McKeen, D.; Pospelov, M.; Raj, N. Dark Sectors in Neutron-Shining-Through-a-Wall and Nuclear-Absorption Signals. Phys. Rev. D 2023, 107, 075034. [Google Scholar] [CrossRef]
- Jin, M.; Gao, Y. Nucleon—Light Dark Matter Annihilation through Baryon Number Violation. Phys. Rev. D 2018, 98, 075026. [Google Scholar] [CrossRef]
- Keung, W.Y.; Marfatia, D.; Tseng, P.Y. Annihilation Signatures of Neutron Dark Decay Models in Neutron Oscillation and Proton Decay Searches. J. High Energy Phys. 2019, 09, 053. [Google Scholar] [CrossRef]
- Davoudiasl, H.; Morrissey, D.E.; Sigurdson, K.; Tulin, S. Hylogenesis: A Unified Origin for Baryonic Visible Matter and Antibaryonic Dark Matter. Phys. Rev. Lett. 2010, 105, 211304. [Google Scholar] [CrossRef] [PubMed]
- Davoudiasl, H.; Morrissey, D.E.; Sigurdson, K.; Tulin, S. Baryon Destruction by Asymmetric Dark Matter. Phys. Rev. D 2011, 84, 096008. [Google Scholar] [CrossRef]
- Fukuda, S.; Fukuda, Y.; Hayakawa, T.; Ichihara, E.; Ishitsuka, M.; Itow, Y.; Kajita, T.; Kameda, J.; Kaneyuki, K.; Kasuga, S.; et al. The Super-Kamiokande Detector. Nucl. Instrum. Methods A 2003, 501, 418–462. [Google Scholar] [CrossRef]
- Fajfer, S.; Susic, D. Colored Scalar Mediated Nucleon Decays to an Invisible Fermion. Phys. Rev. D 2021, 103, 055012. [Google Scholar] [CrossRef]
- Barducci, D.; Fabbrichesi, M.; Gabrielli, E. Neutral Hadrons Disappearing into the Darkness. Phys. Rev. D 2018, 98, 035049. [Google Scholar] [CrossRef]
- Heeck, J. Light Particles with Baryon and Lepton Numbers. Phys. Lett. B 2021, 813, 136043. [Google Scholar] [CrossRef]
- Alonso-Alvarez, G.; Elor, G.; Escudero, M.; Fornal, B.; Grinstein, B.; Martin Camalich, J. Strange Physics of Dark Baryons. Phys. Rev. D 2022, 105, 115005. [Google Scholar] [CrossRef]
- Ablikim, M.; Achasov, M.N.; Adlarson, P.; Ahmed, S.; Albrecht, M.; Aliberti, R.; Amoroso, A.; An, M.R.; An, Q.; Bai, X.H.; et al. Search for Invisible Decays of the Λ Baryon. Phys. Rev. D 2022, 105, L071101. [Google Scholar] [CrossRef]
- Berezhiani, Z. Neutron Lifetime and Dark Decay of the Neutron and Hydrogen. Lett. High Energy Phys. 2019, 2, 118. [Google Scholar] [CrossRef]
- Fornal, B.; Grinstein, B. Comment on “Neutron lifetime and dark decay of the neutron and hydrogen”. arXiv 2019, arXiv:1902.08975. [Google Scholar]
- Tan, W. Neutron Oscillations for Solving Neutron Lifetime and Dark Matter Puzzles. Phys. Lett. B 2019, 797, 134921. [Google Scholar] [CrossRef]
- McKeen, D.; Pospelov, M.; Raj, N. Neutron Star Internal Heating Constraints on Mirror Matter. Phys. Rev. Lett. 2021, 127, 061805. [Google Scholar] [CrossRef] [PubMed]
- Broussard, L.J.; Barrow, J.L.; DeBeer-Schmitt, L.; Dennis, T.; Fitzsimmons, M.R.; Frost, M.J.; Gilbert, C.E.; Gonzalez, F.M.; Heilbronn, L.; Iverson, E.B.; et al. Experimental Search for Neutron to Mirror Neutron Oscillations as an Explanation of the Neutron Lifetime Anomaly. Phys. Rev. Lett. 2022, 128, 212503. [Google Scholar] [CrossRef] [PubMed]
- Strumia, A. Dark Matter Interpretation of the Neutron Decay Anomaly. J. High Energy Phys. 2022, 2, 067. [Google Scholar] [CrossRef]
- Husain, W.; Thomas, A.W. Novel Neutron Decay Mode Inside Neutron Stars. J. Phys. G 2023, 50, 015202. [Google Scholar] [CrossRef]
- McKeen, D.; Pospelov, M.; Raj, N. Hydrogen Portal to Exotic Radioactivity. Phys. Rev. Lett. 2020, 125, 231803. [Google Scholar] [CrossRef]
- Aprile, E.; Aalbers, J.; Agostini, F.; Alfonsi, M.; Althueser, L.; Amaro, F.D.; Antochi, V.C.; Angelino, E.; Angevaare, J.R.; Arneodo, F.; et al. Observation of Excess Electronic Recoil Events in XENON1T. arXiv 2020, arXiv:2006.09721. [Google Scholar]
- Tien Du, P.; Ai Viet, N.; Van Dat, N. Decay of Neutron with Participation of the Light Vector Boson X17. J. Phys. Conf. Ser. 2020, 1506, 012004. [Google Scholar] [CrossRef]
- Krasznahorkay, A.J.; Csatlós, M.; Csige, L.; Gácsi, Z.; Gulyás, J.; Hunyadi, M.; Kuti, I.; Nyakó, B.M.; Stuhl, L.; Timár, J.; et al. Observation of Anomalous Internal Pair Creation in 8Be: A Possible Indication of a Light, Neutral Boson. Phys. Rev. Lett. 2016, 116, 042501. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.L.; Fornal, B.; Galon, I.; Gardner, S.; Smolinsky, J.; Tait, T.M.P.; Tanedo, P. Protophobic Fifth-Force Interpretation of the Observed Anomaly in 8Be Nuclear Transitions. Phys. Rev. Lett. 2016, 117, 071803. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, A.N.; Hollwieser, R.; Troitskaya, N.I.; Wellenzohn, M.; Berdnikov, Y.A. Neutron Dark Matter Decays. arXiv 2018, arXiv:1806.10107. [Google Scholar]
- Giacosa, F.; Pagliara, G. Measurement of the Neutron Lifetime and Inverse Quantum Zeno Effect. Phys. Rev. D 2020, 101, 056003. [Google Scholar] [CrossRef]
- Byrne, J.; Worcester, D.L. The Neutron Lifetime Anomaly and Charge Exchange Collisions of Trapped Protons. J. Phys. G 2019, 46, 085001. [Google Scholar] [CrossRef]
- Serebrov, A.P.; Chaikovskii, M.E.; Klyushnikov, G.N.; Zherebtsov, O.M.; Chechkin, A.V. Search for Explanation of the Neutron Lifetime Anomaly. Phys. Rev. D 2021, 103, 074010. [Google Scholar] [CrossRef]
- Byrne, J.; Worcester, D.L. The Neutron Lifetime Anomaly: Analysis of Charge Exchange and Molecular Reactions in a Proton Trap. Eur. Phys. J. A 2022, 58, 151. [Google Scholar] [CrossRef]
- Fornal, B.; Garcia, K.; Pierre, E. Testing Unification and Dark Matter with Gravitational Waves. Phys. Rev. D 2023, 108, 055022. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fornal, B. Neutron Dark Decay. Universe 2023, 9, 449. https://doi.org/10.3390/universe9100449
Fornal B. Neutron Dark Decay. Universe. 2023; 9(10):449. https://doi.org/10.3390/universe9100449
Chicago/Turabian StyleFornal, Bartosz. 2023. "Neutron Dark Decay" Universe 9, no. 10: 449. https://doi.org/10.3390/universe9100449
APA StyleFornal, B. (2023). Neutron Dark Decay. Universe, 9(10), 449. https://doi.org/10.3390/universe9100449






