Uniform Asymptotic Approximation Method with Pöschl–Teller Potential
Abstract
1. Introduction
2. The Uniform Asymptotic Approximation Method
2.1. The UAA Method
2.1.1. The Liouville Transformations
2.1.2. Minimization of Errors
2.1.3. Choice of
2.2. UAA Method for Two Turning Points
- and are two distinct real roots of ;
- , a double real root of ;
- and are two complex roots of . Since is real, in this case, these two roots must be complex conjugate, .
- When far away from any of the two turning points, we require
- When near any of these two points, we requireprovided that the two turning points are far away from each other: that is, when .
- If the two turning points are close to each other, , then near these points, we require
2.2.1. When Are Real
2.2.2. When Are Complex Conjugate
2.2.3. The First-Order Approximate Solutions
3. UAA Solutions with the Pöschl–Teller Potential
3.1.
3.2.
3.2.1.
3.2.2.
3.3.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Upper Bounds of Errors
Appendix B. Exact Solutions with the Pöschl–Teller Potential
Appendix C. Computing the Error Control Function
Appendix C.1. g < 0
Appendix C.2. g > 0
| 1 | It should be noted that the first application of the UAA method to cosmological perturbations in GR was carried out by Habib et al. |
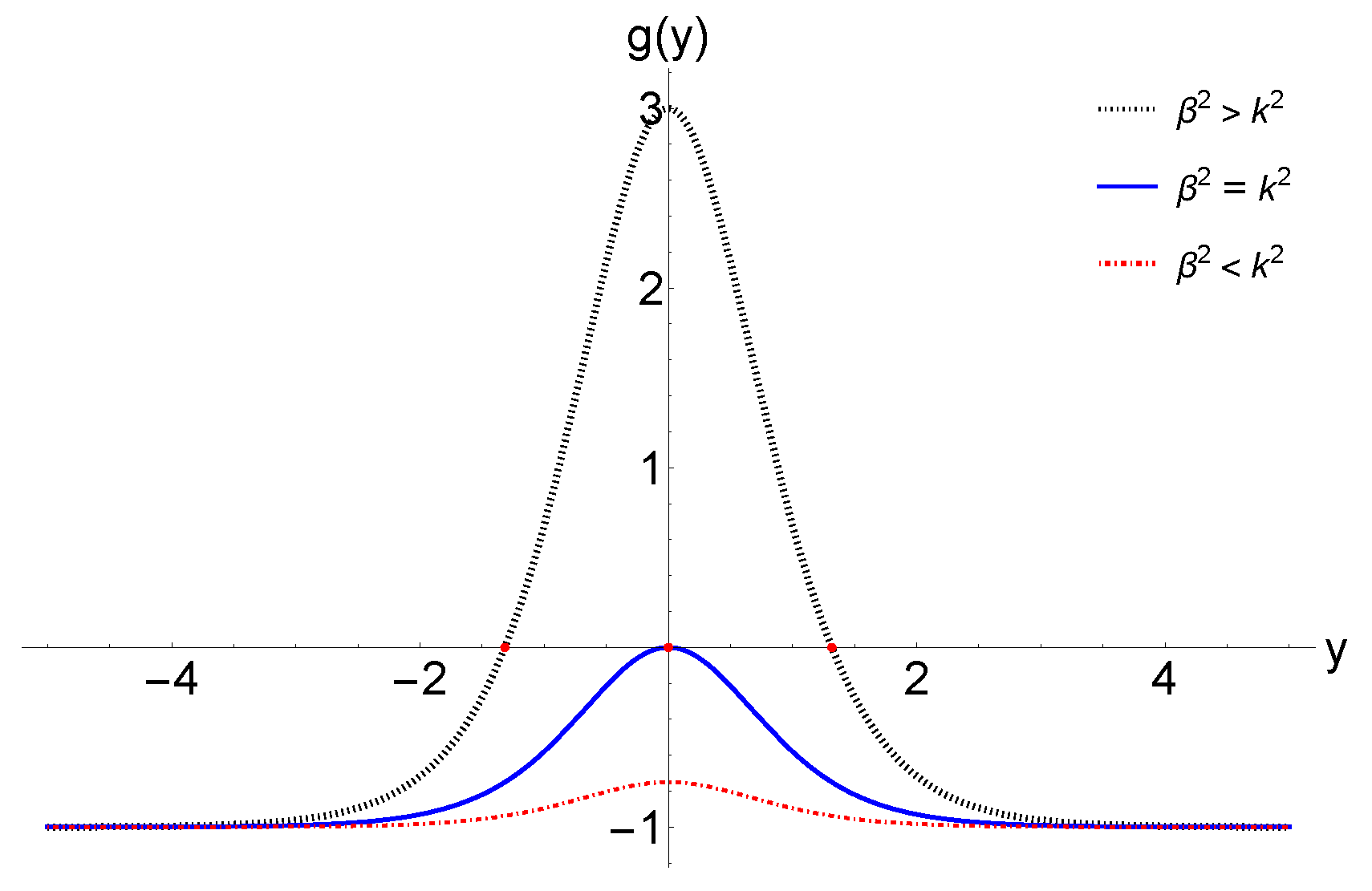
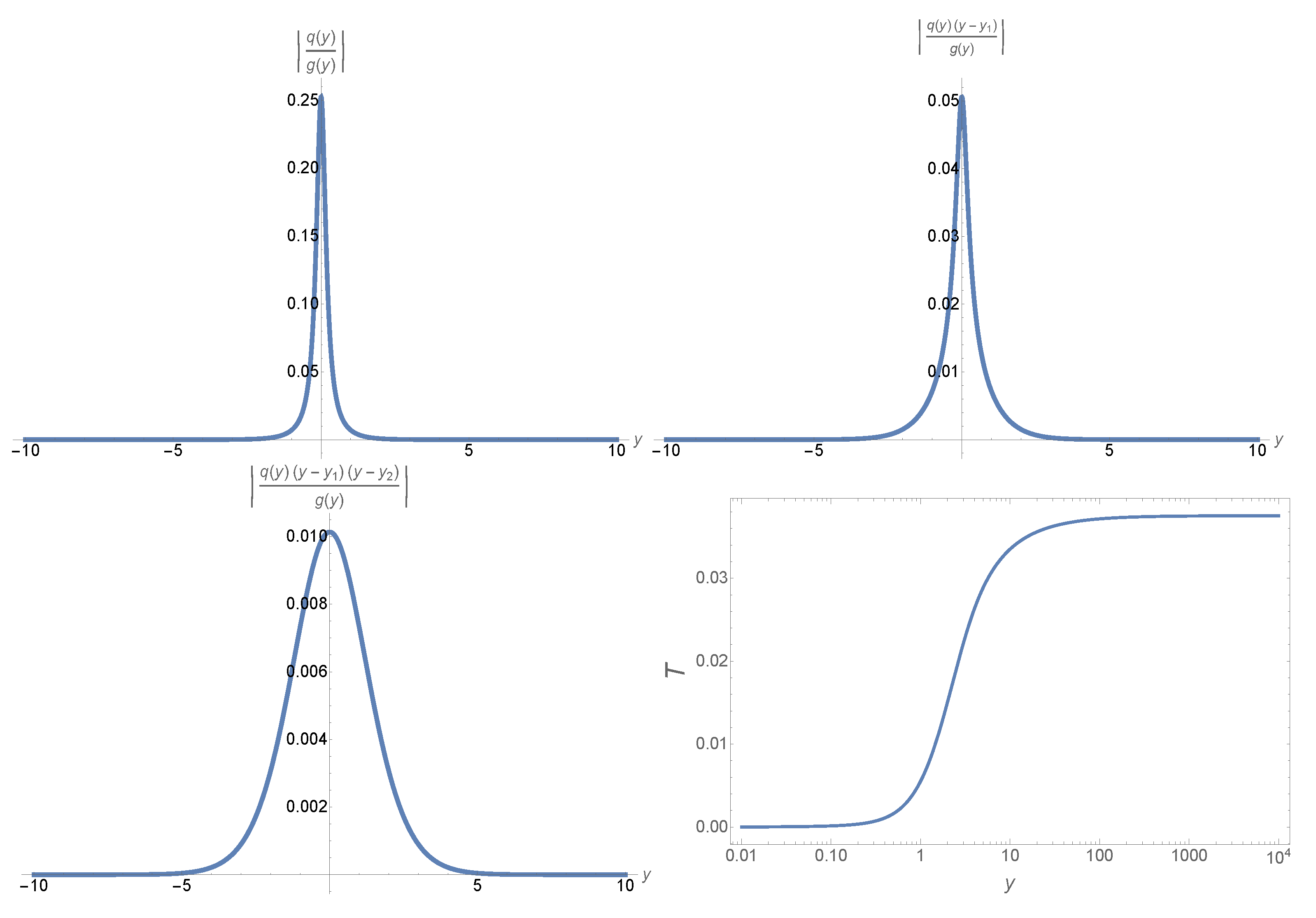
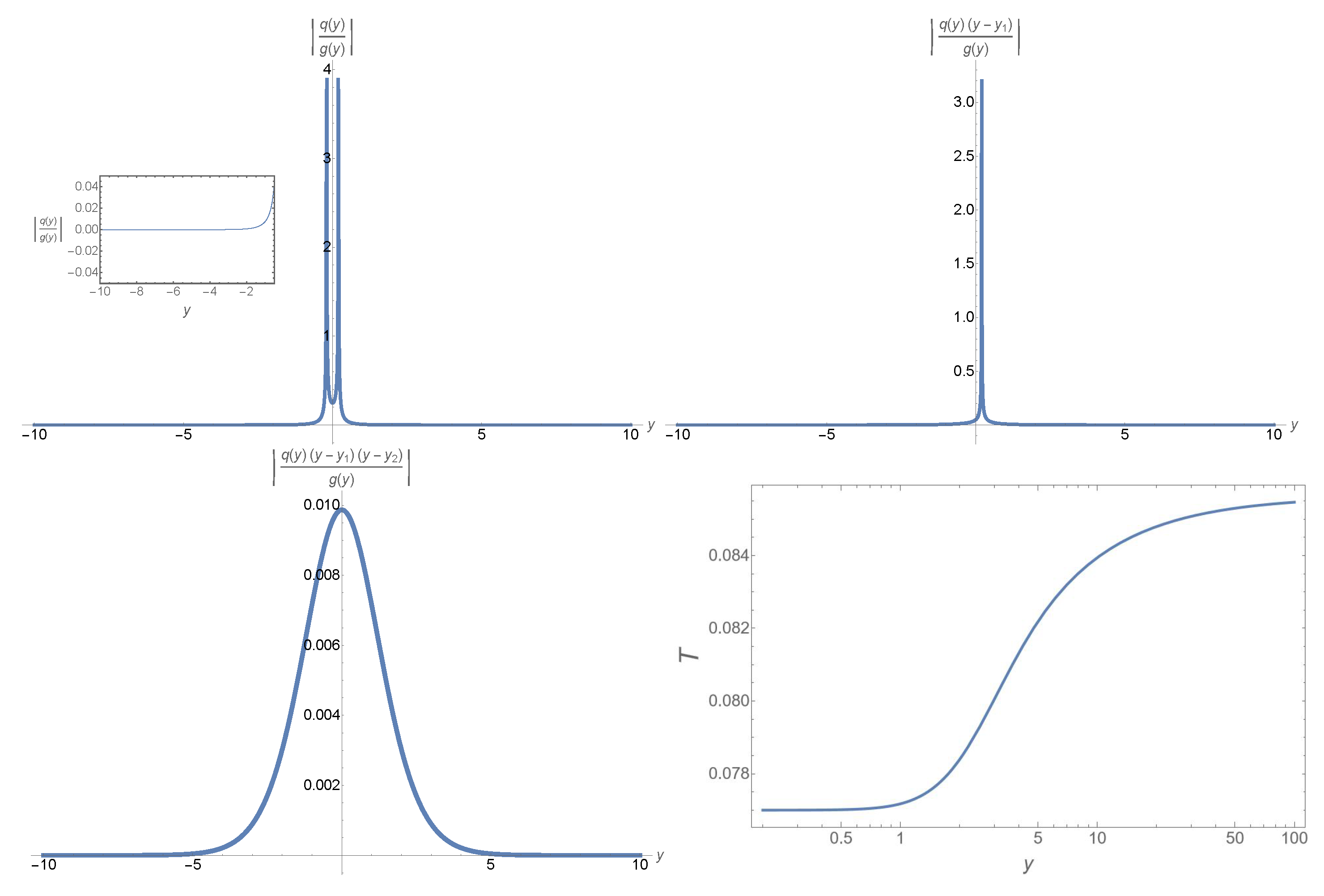
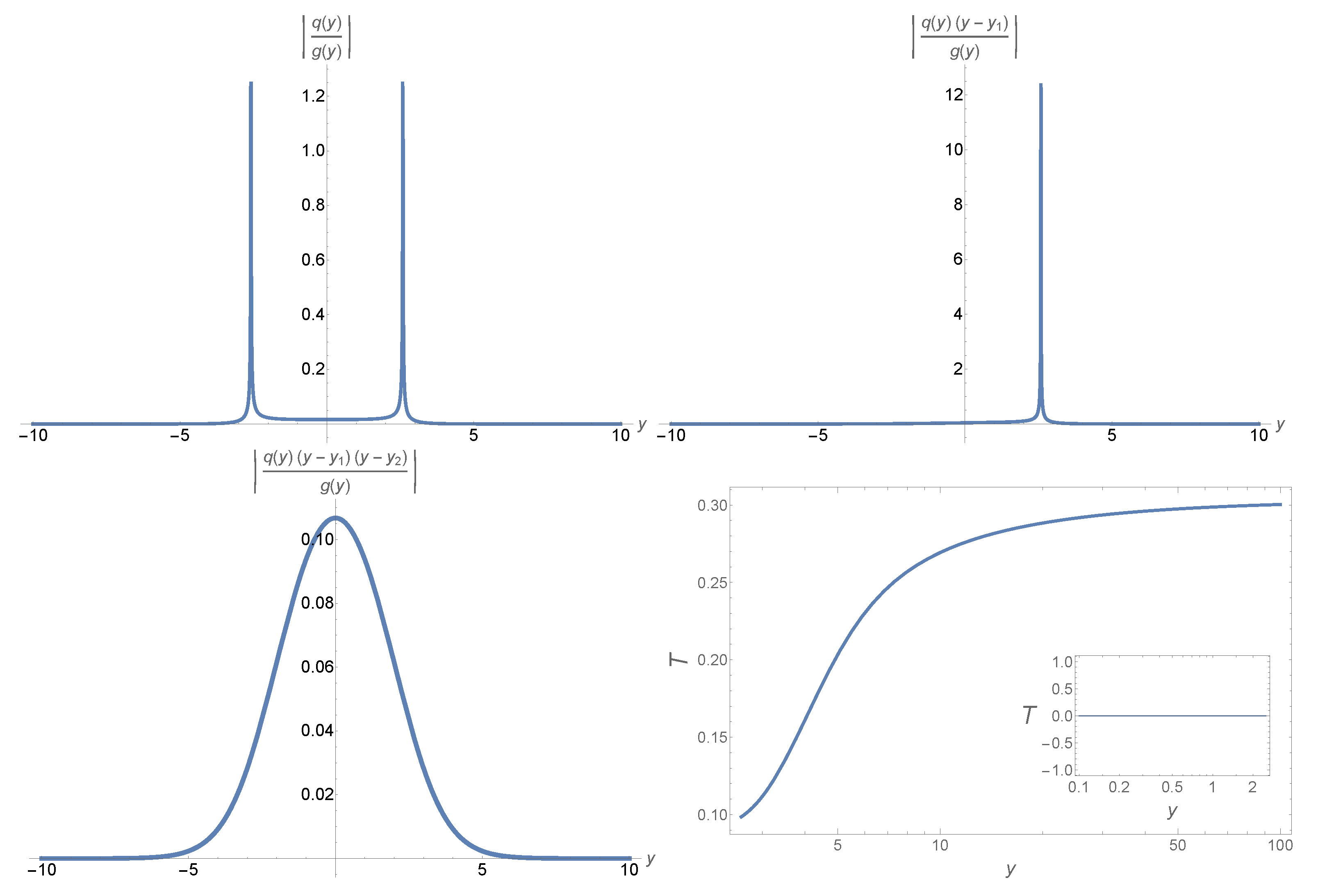
| 2 | In this case, the associated error control function is for any given , where [64]. In this paper, we choose , so the integrations will be carried out over the interval , corresponding to . Due to the symmetry of the equation, one can easily obtain the solutions for the region by simply replacing y by (or by )) |
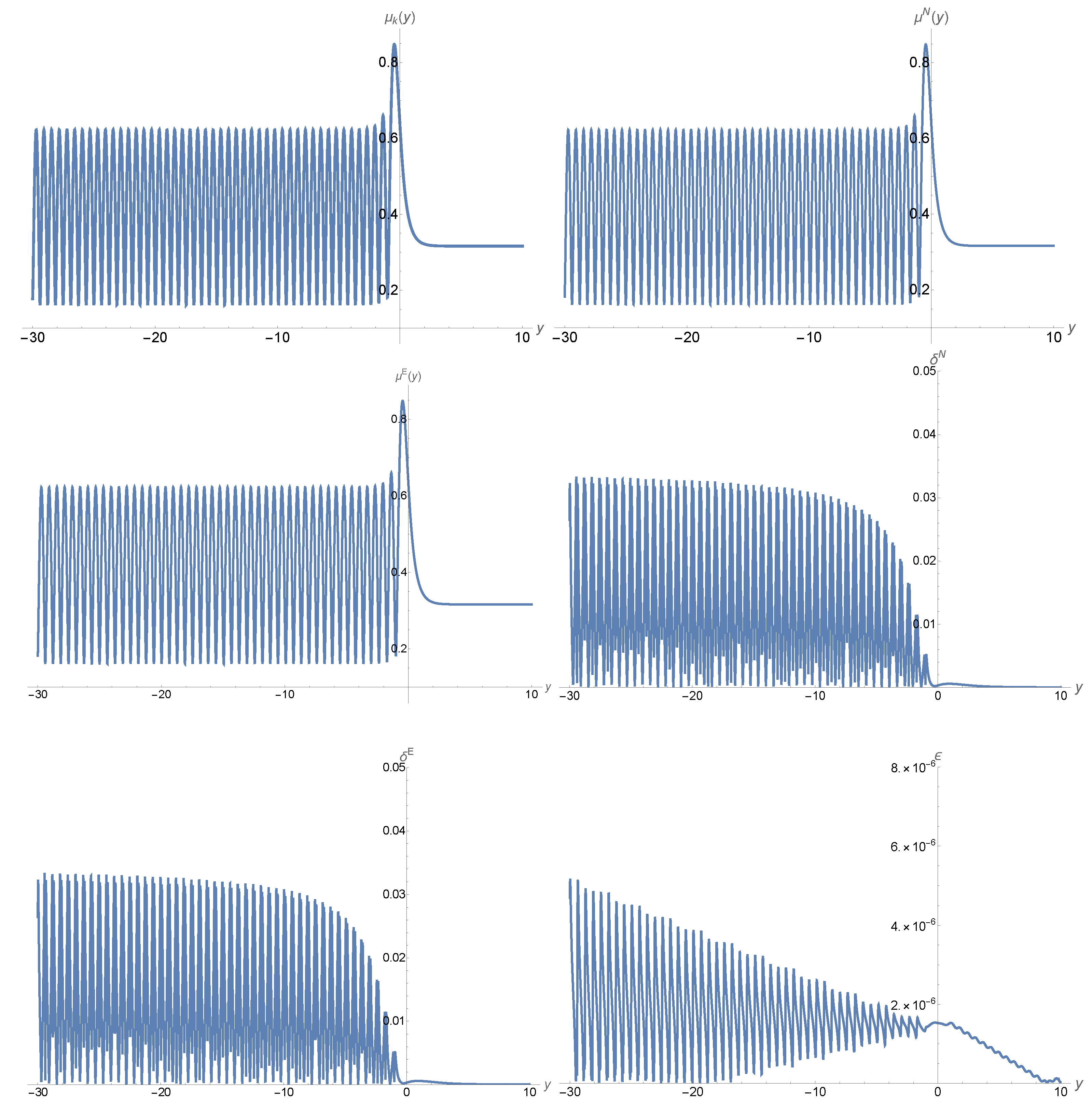
| 3 | Recall the inner boundaries of black hole perturbations are the horizons, at which the potentials are usually finite and non-singular. |
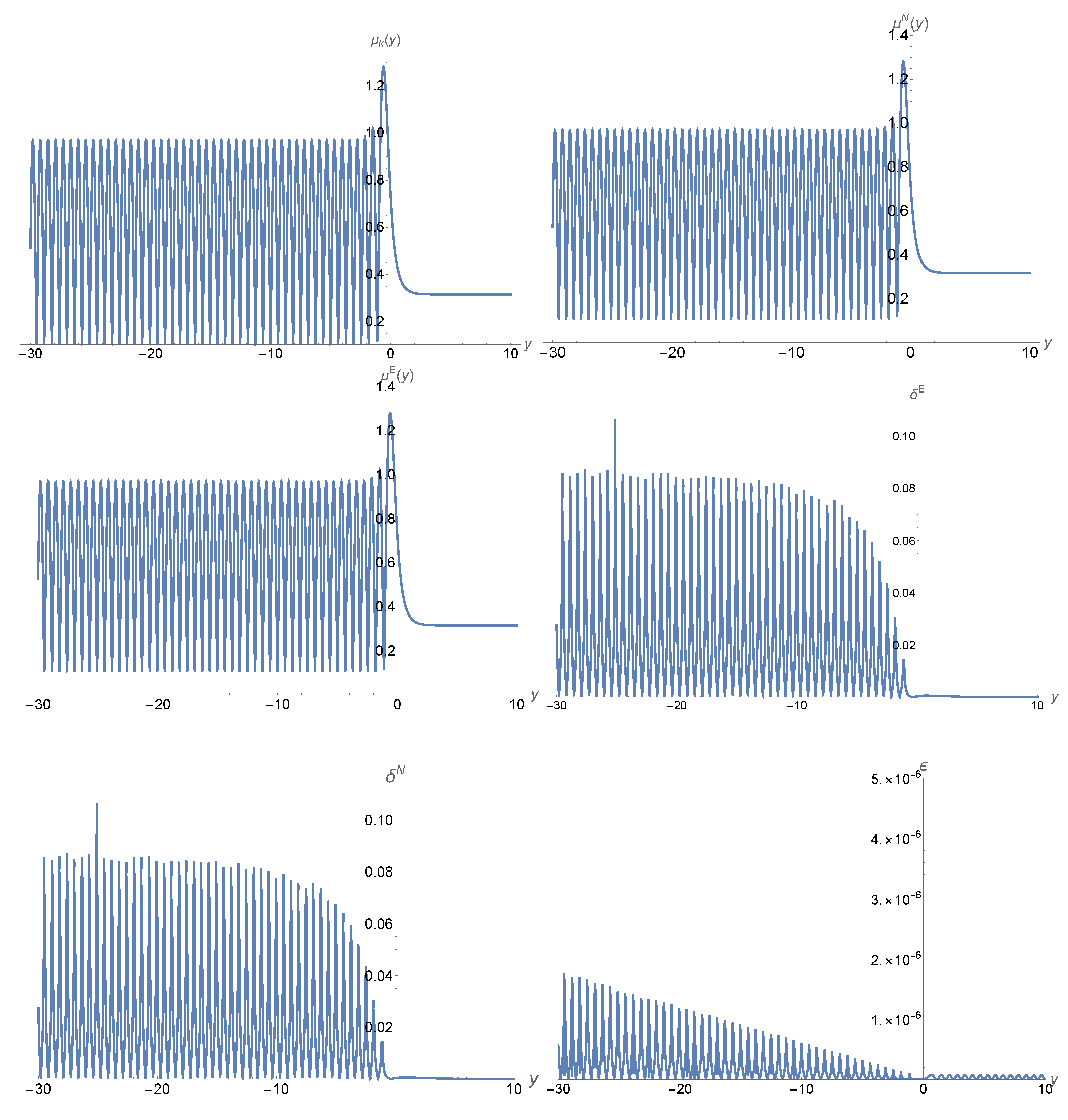
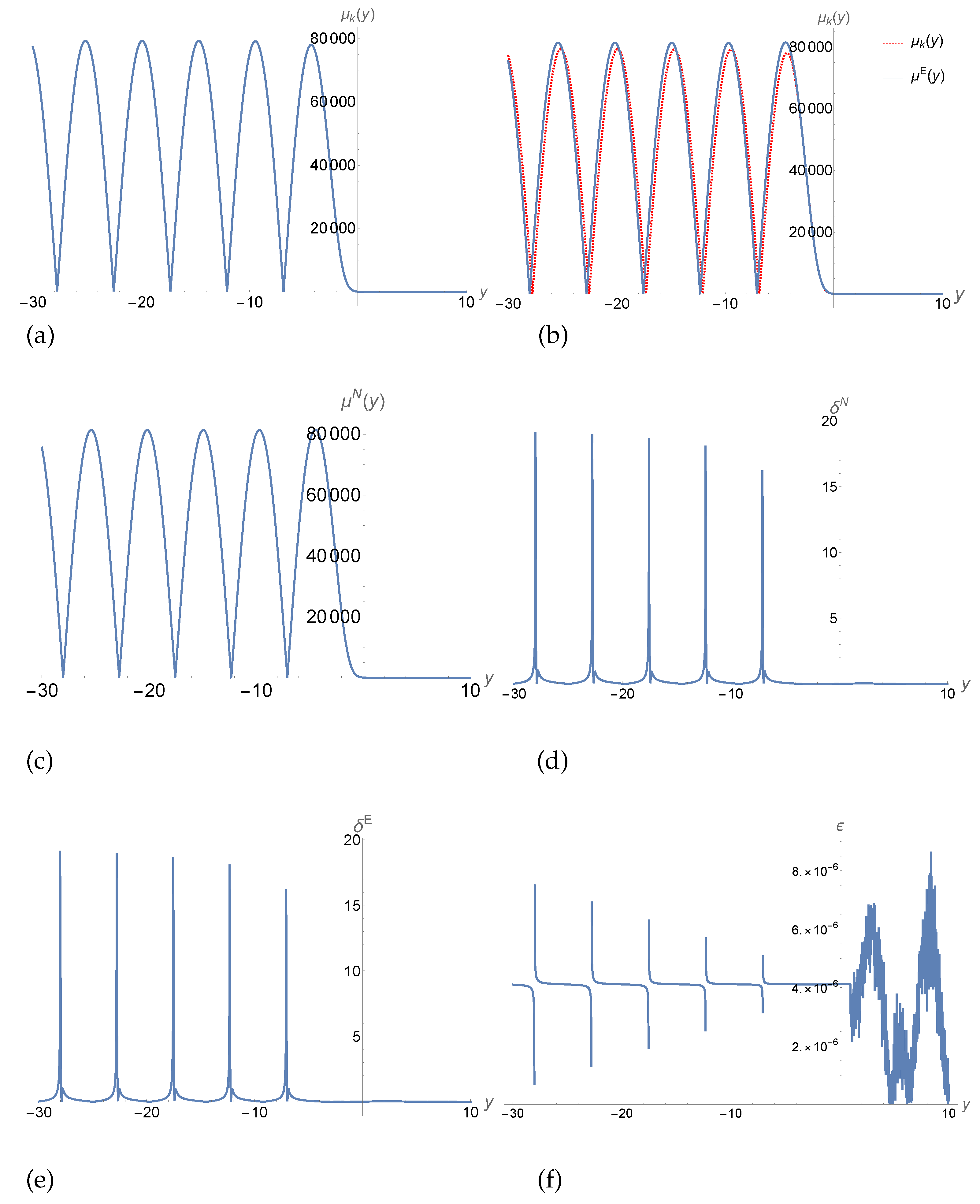
| 4 |
References
- Kiefer, C. Quantum Gravity, 3rd ed.; Oxford Science Publications, Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Hamber, H.W. Quantum Gravity, the Feynman Path Integral Approach; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Green, M.B.; Schwarz, J.H.; Witten, E. Superstring Theory; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 1999; Volumes 1–2. [Google Scholar]
- Polchinski, J. String Theory; Cambridge University Press: Cambridge, UK, 2001; Volumes 1–2. [Google Scholar]
- Johson, C.V. D-Branes; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Becker, K.; Becker, M.; Schwarz, J.H. String Theory and M-Theory; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Ashtekar, A.; Lewandowski, J. Background independent quantum gravity: A status report. Class. Quant. Grav. 2004, 21, R53. [Google Scholar] [CrossRef]
- Thiemann, T. Modern Canonical Quantum General Relativity; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Rovelli, C. Quantum Gravity; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Bojowald, M. Canonical Gravity and Applications: Cosmology, Black Holes, and Quantum Gravity; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Gambini, R.; Pullin, J. A First Course in Loop Quantum Gravity; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Rovelli, C.; Vidotto, F. Covariant Loop Quantum Gravity; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Ashtekar, A.; Pullin, J. Loop Quantum Gravity, the First 30 Years; World Scientific: Singapore, 2017. [Google Scholar]
- Thiemann, T. The LQG String—loop quantum gravity quantization of string theory: I. Flat target space. Class. Quamtum Grav. 2006, 23, 1923. [Google Scholar] [CrossRef]
- Helling, R.C.; Giuseppe, P. String quantization: Fock vs. LQG representations. arXiv 2004, arXiv:hep-th/0409182. [Google Scholar]
- Witt, B.S.D. Quantum Theory of Gravity. I. The Canonical Theory. Phys. Rev. 1967, 160, 1113. [Google Scholar]
- Wheeler, J.A. Relativity, Groups and Topology; Witt, C.M.D., Wheeler, J.A., Eds.; Benjamin: New York, NY, USA, 1968. [Google Scholar]
- Ashtekar, A. New variables for classical and quantum gravity. Phys. Rev. Lett. 1986, 57, 2244. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A. New Hamiltonian formulation of general relativity. Phys. Rev. D 1987, 36, 1587. [Google Scholar] [CrossRef] [PubMed]
- Bojowald, M. Loop Quantum Cosmology. Living Rev. Relativ. 2008, 11, 4. [Google Scholar] [CrossRef]
- Bojowald, M. Quantum cosmology: A review. Rep. Prog. Phys. 2015, 78, 023901. [Google Scholar] [CrossRef]
- Ashtekar, A.; Singh, P. Loop Quantum Cosmology: A Status Report. Class. Quant. Grav. 2011, 28, 213001. [Google Scholar] [CrossRef]
- Ashtekar, A.; Barrau, A. Loop quantum cosmology: From pre-inflationary dynamics to observations. Class. Quant. Grav. 2015, 32, 234001. [Google Scholar] [CrossRef]
- Singh, P. Loop Quantum Cosmology. Int. J. Mod. Phys. D 2016, 25, 8. [Google Scholar]
- Agullo, I.; Singh, P. Loop Quantum Cosmology. In Loop Quantum Gravity: The First 30 Years; Ashtekar, A., Pullin, J., Eds.; World Scientific: Singapore, 2017. [Google Scholar]
- Wilson-Ewing, E. Testing loop quantum cosmology. Comptes Rendus Phys. 2017, 18, 207. [Google Scholar] [CrossRef]
- Navascués, B.E.; Marugán, G.A.M. Hybrid Loop Quantum Cosmology: An Overview. Front. Astron. Space Sci. 2021, 8, 624824. [Google Scholar] [CrossRef]
- Ashtekar, A.; Bianchi, E. A short review of loop quantum gravity. Rep. Prog. Phys. 2021, 84, 042001. [Google Scholar] [CrossRef] [PubMed]
- Agullo, I.; Wang, A.; Wilson-Ewing, E. Loop quantum cosmology: Relation between theory and observations. In Handbook of Quantum Gravity; Bambi, C., Modesto, L., Shapiro, I., Eds.; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Li, B.-F.; Singh, P. Loop Quantum Cosmology: Physics of Singularity Resolution and its Implications. In Handbook of Quantum Gravity; Bambi, C., Modesto, L., Shapiro, I., Eds.; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Taveras, V. Corrections to the Friedmann Equations from LQG for a Universe with a Free Scalar Field. Phys. Rev. D 2008, 78, 064072. [Google Scholar] [CrossRef]
- Ashtekar, A.; Gupt, B. Generalized effective description of loop quantum cosmology. Phys. Rev. D 2015, 92, 084060. [Google Scholar] [CrossRef]
- Agullo, I.; Ashtekar, A.; Gupt, B. Phenomenology with fluctuating quantum geometries in loop quantum cosmology. Class. Quantum Grav. 2017, 34, 074003. [Google Scholar] [CrossRef]
- Singh, P. Glimpses of Space-Time Beyond the Singularities Using Supercomputers. Comput. Sci. Eng. 2018, 20, 26. [Google Scholar] [CrossRef]
- Diener, P.; Joe, A.; Megevand, M.; Singh, P. Numerical simulations of loop quantum Bianchi-I spacetimes. Class. Quant. Grav. 2017, 34, 094004. [Google Scholar] [CrossRef]
- Diener, P.; Gupt, B.; Megevand, M.; Singh, P. Numerical evolution of squeezed and non-Gaussian states in loop quantum cosmology. Class. Quant. Grav. 2014, 31, 165006. [Google Scholar] [CrossRef]
- Diener, P.; Gupt, B.; Singh, P. Numerical simulations of a loop quantum cosmos: Robustness of the quantum bounce and the validity of effective dynamics. Class. Quant. Grav. 2014, 31, 105015, and references therein. [Google Scholar] [CrossRef]
- Kaminski, W.; Kolanowski, M.; Lewandowski, J. Dressed metric predictions revisited. Class. Quantum Grav. 2020, 37, 095001. [Google Scholar] [CrossRef]
- Singh, P. Are loop quantum cosmos never singular? Class. Quant. Grav. 2009, 26, 125005. [Google Scholar] [CrossRef]
- Singh, P. Curvature invariants, geodesics and the strength of singularities in Bianchi-I loop quantum cosmology. Phys. Rev. D 2012, 85, 104011. [Google Scholar] [CrossRef]
- Saini, S.; Singh, P. Geodesic completeness and the lack of strong singularities in effective loop quantum Kantowski-Sachs spacetime. Class. Quant. Grav. 2016, 33, 245019. [Google Scholar] [CrossRef]
- Resolution of strong singularities and geodesic completeness in loop quantum Bianchi-II spacetimes. Class. Quant. Grav. 2017, 34, 235006. [CrossRef]
- Generic absence of strong singularities in loop quantum Bianchi-IX spacetimes. Class. Quant. Grav. 2018, 35, 065014. [CrossRef]
- Singh, P.; Vandersloot, K.; Vereshchagin, G.V. Nonsingular bouncing universes in loop quantum cosmology. Phys. Rev. D 2006, 74, 043510. [Google Scholar] [CrossRef]
- Zhang, X.; Ling, Y. Inflationary universe in loop quantum cosmology. J. Cosmol. Astropart. Phys. 2007, 08, 012. [Google Scholar] [CrossRef]
- Ashtekar, A.; Sloan, D. Loop quantum cosmology and slow roll inflation. Phys. Lett. B 2010, 694, 108. [Google Scholar] [CrossRef]
- Ashtekar, A.; Sloan, D. Probability of inflation in loop quantum cosmology. Gen. Relativ. Gravit. 2011, 43, 3619. [Google Scholar] [CrossRef]
- Chen, L.; Zhu, J.-Y. Loop quantum cosmology: The horizon problem and the probability of inflation. Phys. Rev. D 2015, 92, 084063. [Google Scholar] [CrossRef]
- Agullo, I.; Ashtekar, A.; Nelson, W. Quantum Gravity Extension of the Inflationary Scenario. Phys. Rev. Lett. 2012, 109, 251301. [Google Scholar] [CrossRef] [PubMed]
- Agullo, I.; Ashtekar, A.; Nelson, W. Extension of the quantum theory of cosmological perturbations to the Planck era. Phys. Rev. D 2013, 87, 043507. [Google Scholar] [CrossRef]
- Agullo, I.; Ashtekar, A.; Nelson, W. The pre-inflationary dynamics of loop quantum cosmology: Confronting quantum gravity with observations. Class. Quant. Grav. 2013, 30, 085014. [Google Scholar] [CrossRef]
- Fernandez-Mendez, M.; Marugán, G.A.M.; Olmedo, J. Hybrid quantization of an inflationary universe. Phys. Rev. D 2012, 86, 024003. [Google Scholar] [CrossRef]
- Fernández-Méndez, M.; Marugán, G.A.M.; Olmedo, J. Effective dynamics of scalar perturbations in a flat Friedmann-Robertson-Walker spacetime in loop quantum cosmology. Phys. Rev. D 2014, 89, 044041. [Google Scholar] [CrossRef]
- Martínez, F.B.; Olmedo, J. Primordial tensor modes of the early Universe. Phys. Rev. D 2016, 93, 124008. [Google Scholar] [CrossRef]
- Bojowald, M.; Hossain, G.M. Cosmological vector modes and quantum gravity effects. Class. Quant. Grav. 2007, 24, 4801. [Google Scholar] [CrossRef][Green Version]
- Bojowald, M.; Hossain, G.M. Loop quantum gravity corrections to gravitational wave dispersion. Phys. Rev. D 2008, 77, 023508. [Google Scholar] [CrossRef]
- Bojowald, M.; Hossain, G.M.; Kagan, M.; Shankaranarayanan, S. Anomaly freedom in perturbative loop quantum gravity. Phys. Rev. D 2008, 78, 063547. [Google Scholar] [CrossRef]
- Bojowald, M.; Hossain, G.M.; Kagan, M.; Shankaranarayanan, S. Gauge invariant cosmological perturbation equations with corrections from loop quantum gravity. Phys. Rev. D 2009, 79, 043505, Erratum in Phys. Rev. D 2010, 82, 109903. [Google Scholar] [CrossRef]
- Wilson-Ewing, E. Lattice loop quantum cosmology: Scalar perturbations. Class. Quant. Grav. 2012, 29, 215013. [Google Scholar] [CrossRef]
- Wilson-Ewing, E. Separate universes in loop quantum cosmology: Framework and applications. Int. J. Mod. Phys. D 2016, 25, 1642002. [Google Scholar] [CrossRef]
- Agullo, I.; Morris, N.A. Detailed analysis of the predictions of loop quantum cosmology for the primordial power spectra. Phys. Rev. D 2015, 92, 124040. [Google Scholar] [CrossRef]
- Olver, F.W.J. Asymptotics and Special Functions; AKP Classics: Wellesley, MA, USA, 1997. [Google Scholar]
- Olver, F.W.J. The asymptotic solution of linear differential equations of the second order in a domain containing one transition point. Philos. Trans. Roy. Soc. London A 1956, 249, 65–97. [Google Scholar]
- Olver, F.W.J. Second-order linear differential equations with two turning points. Philos. Trans. Roy. Soc. London A 1975, 278, 137–174. [Google Scholar]
- Wang, A. Vector and tensor perturbations in Horava-Lifshitz cosmology. Phys. Rev. D 2010, 82, 124063. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Cleaver, G.; Kirsten, K.; Sheng, Q. Constructing analytical solutions of linear perturbations of inflation with modified dispersion relations. Int. J. Mod. Phys. A 2014, 29, 1450142. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Cleaver, G.; Kirsten, K.; Sheng, Q. Inflationary cosmology with nonlinear dispersion relations. Phys. Rev. D 2014, 89, 043507. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A. Gravitational quantum effects in the light of BICEP2 results. Phys. Rev. D 2014, 90, 027304. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Cleaver, G.; Kirsten, K.; Sheng, Q. Gravitational quantum effects on power spectra and spectral indices with higher-order corrections. Phys. Rev. D 2014, 90, 063503. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Cleaver, G.; Kirsten, K.; Sheng, Q. Power spectra and spectral indices of k-inflation: High-order corrections. Phys. Rev. D 2014, 90, 103517. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Cleaver, G.; Kirsten, K.; Sheng, Q.; Wu, Q. Detecting quantum gravitational effects of loop quantum cosmology in the early universe? Astrophy. J. Lett. 2015, 807, L17. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Cleaver, G.; Kirsten, K.; Sheng, Q.; Wu, Q. Scalar and tensor perturbations in loop quantum cosmology: High-order corrections. JCAP 2015, 10, 052. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Kirsten, K.; Cleaver, G.; Sheng, Q.; Wu, Q. Inflationary spectra with inverse-volume corrections in loop quantum cosmology and their observational constraints from Planck 2015 data. JCAP 2016, 3, 46. [Google Scholar] [CrossRef][Green Version]
- Zhu, T.; Wang, A.; Kirsten, K.; Cleaver, G.; Sheng, Q. High-order Primordial Perturbations with Quantum Gravitational Effects. Phys. Rev. D 2016, 93, 123525. [Google Scholar] [CrossRef]
- Wu, Q.; Zhu, T.; Wang, A. Primordial Spectra of slow-roll inflation at second-order with the Gauss-Bonnet correction. Phys. Rev. D 2018, 97, 103502. [Google Scholar] [CrossRef]
- Qiao, J.; Ding, G.-H.; Wu, Q.; Zhu, T.; Wang, A. Inflationary perturbation spectrum in extended effective field theory of inflation. JCAP 2019, 9, 64. [Google Scholar] [CrossRef]
- Zhu, T.; Wu, Q.; Wang, A. An analytical approach to the field amplification and particle production by parametric resonance during inflation and reheating. Phys. Dark Universe 2019, 26, 100373. [Google Scholar] [CrossRef]
- Li, B.-F.; Zhu, T.; Wang, A.; Kirsten, K.; Cleaver, G.; Sheng, Q. Preinflationary perturbations from the closed algebra approach in loop quantum cosmology. Phys. Rev. D 2019, 99, 103536. [Google Scholar] [CrossRef]
- Ding, G.-H.; Qiao, J.; Wu, Q.; Zhu, T.; Wang, A. Inflationary perturbation spectra at next-to-leading slow-roll order in effective field theory of inflation. Eur. Phys. J. C 2019, 79, 976. [Google Scholar] [CrossRef]
- Li, B.-F.; Zhu, T.; Wang, A. Langer Modification, Quantization condition and Barrier Penetration in Quantum Mechanics. Universe 2020, 6, 90. [Google Scholar] [CrossRef]
- Qiao, J.; Zhu, T.; Zhao, W.; Wang, A. Polarized primordial gravitational waves in the ghost-free parity-violating gravity. Phys. Rev. D 2020, 101, 043528. [Google Scholar] [CrossRef]
- Zhu, T.; Zhao, W.; Wang, A. Polarized primordial gravitational waves in spatial covariant gravities. Phys. Rev. D 2023, 107, 024031. [Google Scholar] [CrossRef]
- Li, T.C.; Zhu, T.; Wang, A. Power spectra of slow-roll inflation in the consistent D→4 Einstein-Gauss-Bonnet gravity. JCAP 2023, 5, 6. [Google Scholar] [CrossRef]
- Habib, S.; Heitmann, K.; Jungman, G.; Molina-Paris, C. The Inflationary perturbation spectrum. Phys. Rev. Lett. 2002, 89, 281301. [Google Scholar] [CrossRef]
- Habib, S.; Heinen, A.; Heitmann, K.; Jungman, G.; Molina-Paris, C. Characterizing inflationary perturbations: The Uniform approximation. Phys. Rev. D 2004, 70, 083507. [Google Scholar] [CrossRef]
- Dong, S.-H. Wave Equations in Higher Dimensions; Springer: New York, NY, USA, 2011. [Google Scholar]
- Zhu, T.; Wang, A.; Cleaver, G.; Kirsten, K.; Sheng, Q. Pre-inflationary universe in loop quantum cosmology. Phys. Rev. D 2017, 96, 083520. [Google Scholar] [CrossRef]
- Wu, Q.; Zhu, T.; Wang, A. Nonadiabatic evolution of primordial perturbations and non-Gaussinity in hybrid approach of loop quantum cosmology. Phys. Rev. D 2018, 98, 103528. [Google Scholar] [CrossRef]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Berti, E.; Cardoso, V.; Starinets, A.O. Quasinormal modes of black holes and black branes. Class. Quant. Grav. 2009, 26, 163001. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Quasinormal modes of black holes: From astrophysics to string theory. Rev. Mod. Phys. 2011, 83, 793. [Google Scholar] [CrossRef]
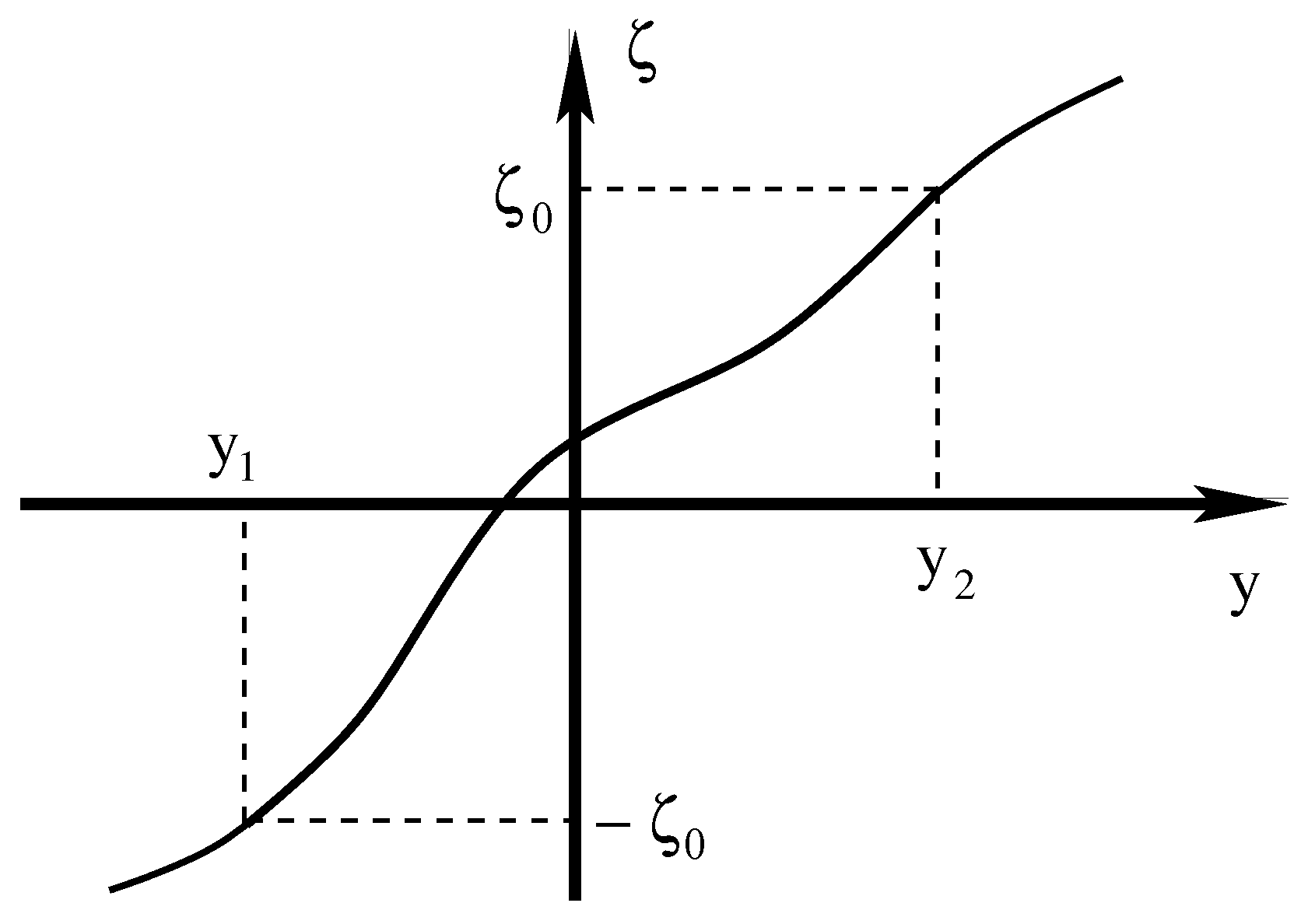


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, R.; Marchetta, J.J.; Saeed, J.; Cleaver, G.; Li, B.-F.; Wang, A.; Zhu, T. Uniform Asymptotic Approximation Method with Pöschl–Teller Potential. Universe 2023, 9, 471. https://doi.org/10.3390/universe9110471
Pan R, Marchetta JJ, Saeed J, Cleaver G, Li B-F, Wang A, Zhu T. Uniform Asymptotic Approximation Method with Pöschl–Teller Potential. Universe. 2023; 9(11):471. https://doi.org/10.3390/universe9110471
Chicago/Turabian StylePan, Rui, John Joseph Marchetta, Jamal Saeed, Gerald Cleaver, Bao-Fei Li, Anzhong Wang, and Tao Zhu. 2023. "Uniform Asymptotic Approximation Method with Pöschl–Teller Potential" Universe 9, no. 11: 471. https://doi.org/10.3390/universe9110471
APA StylePan, R., Marchetta, J. J., Saeed, J., Cleaver, G., Li, B.-F., Wang, A., & Zhu, T. (2023). Uniform Asymptotic Approximation Method with Pöschl–Teller Potential. Universe, 9(11), 471. https://doi.org/10.3390/universe9110471








