Gauge Couplings Evolution from the Standard Model, through Pati–Salam Theory, into E₈ Unification of Families and Forces

Abstract

We explore the potential of ultimate unification of the Standard Model matter and gauge sectors into a single $E_8$ superfield in ten dimensions via an intermediate Pati–Salam gauge theory. Through a consistent realisation of a ${\mathbb{T}}^6/({\mathbb{Z}}_6\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2)$ orbifolding procedure and renormalisation group evolution of gauge couplings, we establish several novel benchmark scenarios for New Physics that are worth further phenomenological exploration.

1. Introduction

Grand Unified Theories (GUTs) aim to unify the three independent gauge interactions of the Standard Model (SM) into a single one. Among the simplest ways to achieve this is via an $SU\left(5\right)$ gauge symmetry [1]. One can also extend the gauge symmetry to unify all the SM fermions of a single family into one $SO\left(10\right)$ representation [2]. Enlarging the gauge group even further into $E_6$, one could unify the SM Higgs sector and a full family of fermions into a single representation [3] by means of the simple $\mathcal{N}=1$ supersymmetry (SUSY).

Such a step-by-step enlarging of the gauge symmetry group can be studied through its Dynkin diagram and is known to follow the exceptional chain [4,5],

$$SU{\left(3\right)}_C\times SU{\left(2\right)}_L\times U{\left(1\right)}_Y\subset SU\left(5\right)\subset SO\left(10\right)\subset E_6\subset E_7\subset E_8.$$

(1)

Note the group $E_8$ is the largest group of the chain and is especially relevant as its adjoint representation $\left(\mathbf{248}\right)$ is the same as the fundamental one [6]. This suggests that the SM gauge fields can be in principle unified with the SM fermions provided that a maximal $\mathcal{N}=4$ SUSY is realised. Furthermore, it also provides an $SU\left(3\right)$ flavor (or family) symmetry as a cost of $E_8$ to $E_6$ reduction.

There is a plethora of models in the literature that aim to build GUTs including flavor symmetries [7,8,9,10,11,12,13,14,15,16,17,18,19,20] and extra dimensions (EDs) [21,22,23,24,25,26,27,28,29,30,31]). In order to achieve viability, most require a number of independent groups and quite a large number of fields. As alluded above, the group $E_8$ seems to be a good bet for a complete unification of SM vectors, fermions and scalars and has indeed been widely studied both in the context of string theory [32,33] and within the framework of quantum field theory (QFT) [18,34,35,36,37,38,39,40,41,42,43,44,45,46].

The first challenge posed by $E_8$ is that it is a real group (as is extended SUSY), while the SM requires chiral representations. A way forward is to assume the existence of extra dimensions which are orbifolded in such a way that, after their compactification, the massless chiral representations containing the SM fermion sectors remain. Furthermore, extended SUSY can also be generated from the EDs [47,48]. A big challenge is to avoid the presence of too many massless states in the low-energy limit of the theory typically originating by an orbifolding procedure of $E_8$. A consistent resolution may be found by a combination of orbifolding and the Wilson line symmetry-breaking mechanism, also associated to the specific orbifold structure, providing a reduction of the symmetry group and generation of large masses for many of the unobserved states [49,50,51].

One of the main requirements for a consistent GUT is gauge couplings unification, i.e., when the SM gauge couplings are evolved from their measured values at the electroweak (EW) scale up to the high-energy scales, and they match into a single coupling of a unified gauge group. Recently [52,53], some of us presented a framework where the $E_8$ gauge symmetry with $\mathcal{N}=1$ SUSY is considered in 10d corresponding to an extended $\mathcal{N}=4$ SUSY in 4d, where the EDs are orbifolded so that after the compactification stage, only simple SUSY and Pati–Salam symmetry remain [54]. For an alternative example considering an $E_6$ SUSY GUT with 6d orbifold breaking via an intermediate Pati–Salam symmetry, see [55].

In this paper, we study for the first time a particular realisation of the GUT with $E_8$ gauge symmetry in 10d, where the full SM (Higgs, gauge, fermion) field content is unified into a single $E_8$ gauge superfield. Through the ${\mathbb{T}}^6/({\mathbb{Z}}_6\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2)$ orbifold, the $E_8$ symmetry is broken down into $SU{\left(4\right)}_{PS}\times SU{\left(2\right)}_L\times SU{\left(2\right)}_R\times U{\left(1\right)}_X\times U{\left(1\right)}_F\times SU{\left(2\right)}_F$, with no remaining SUSY. In order to consistently derive the 4d Pati–Salam theory from $E_8$ in 10d, the ED compactification procedure invokes the presence of several extra fields for the model to be anomaly free at every step1. Thus, we assume the existence of additional chiral superfields, consistent with the $E_8$ symmetry, so that the anomalies are manifestly cancelled at the Pati–Salam level. The symmetry is further broken down to the SM one through Wilson lines and VEVs of the extra fields of the model, thus leaving only the SM field content as massless.

The SM gauge and matter sectors originate from a single gauge superfield and remain massless up to the EW symmetry breaking scale. The additional chiral fields have arbitrary masses and thus may be chosen to not be present at low energies. In this work, we study different benchmark scenarios of New Physics where some of the fields survive below the compactification scale and provide important contributions to the renormalization group (RG) evolution of the gauge couplings necessary to achieve the exact gauge couplings unification below the Planck scale.

The layout of the paper is as follows: In Section 2, we show the basics of the orbifolding mechanism employed in this work. In Section 3, we demonstrate how the specific ${\mathbb{T}}_6/({\mathbb{Z}}_6\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2)$ orbifold breaks the $E_8$ gauge symmetry and SUSY in 10d. In Section 4, we introduce the extra superfields that are needed to cancel anomalies at the Pati–Salam level. In Section 5, we present the benchmark scenarios relevant for further explorations of New Physics phenomenology where the exact gauge couplings unification is achieved. Finally, in Section 6 the basic conclusions are summarised.

2. Orbifolding

Let us start by considering a theory in 10d spacetime with $\mathcal{N}=1$ SUSY. Six extra spatial dimensions are assumed to be orbifolded as ${\mathbb{T}}^6/F$, where F is a discrete subgroup of the extra dimensional Poincarè symmetry $O\left(6\right)⋉T^6$, such that $O\left(6\right)\simeq SO\left(6\right)\times {\mathbb{Z}}_2\simeq SU\left(4\right)\times {\mathbb{Z}}_2$ is the rotation group, while $T^6$ is the translation group. The translation group is molded by the lattice vectors $\mathrm{\Gamma }={\mathbb{Z}}^6$ compactifying it as ${\mathbb{R}}^6\to {\mathbb{T}}^6\simeq {\mathbb{R}}^6/\mathrm{\Gamma }$ into a 6d torus. The group F must leave the lattice invariant, i.e., $F\mathrm{\Gamma }=\mathrm{\Gamma }$. If the discrete subgroup of the rotations is such that $F\subset SU\left(3\right)$, it would preserve simple $\mathcal{N}=1$ SUSY, leaving an invariant $U\left(1\right)$ [56,57]. The remaining SUSY must be broken in order to generate a realistic theory. It could be broken by orbifolding through a larger discrete group $F\in SU\left(4\right)$ or through Wilson lines. In the next section it will be shown that the latter is preferable. Therefore, in the considered model, simple SUSY is preserved by the rotation subgroup F but broken by the translation one via Wilson lines at the compactification scale.

A simple orbifolding that preserves $\mathcal{N}=1$ SUSY reads

$$F\simeq {\mathbb{Z}}_N\subset SU\left(3\right),$$

(2)

with a positive integer N, where a generic ${\mathbb{Z}}_N$ orbifolding can be defined by identifying

$$\begin{array}{ccc}\hfill & & \hfill (x,z_1,z_2,z_3)\sim (x,{\omega }_1{z}_1,{\omega }_2{z}_2,{\omega }_3{z}_3),{\omega }_i\equiv e^{2i\pi n_i/N},\hfill \\ & & \hfill \mathcal{V}(x,z_1,z_2,z_3)=R({\omega }_1,{\omega }_2,{\omega }_3)\mathcal{V}(x,{\omega }_1{z}_1,{\omega }_2{z}_2,{\omega }_3{z}_3).\hfill \end{array}$$

(3)

Here, R corresponds to a representation of the ${\mathbb{Z}}_N$ rotation acting on the 10d vector superfield $\mathcal{V}$. Such a transformation would belong to $SU\left(3\right)$ and preserve SUSY as long as

$$n_1+n_2+n_3=0mod2N,$$

(4)

as fermions rotate twice as slow [58].

Considering only an Abelian orbifolding that preserves $\mathcal{N}=1$ SUSY, the most general one reads as $F\simeq {\mathbb{Z}}_N\times {\mathbb{Z}}_M\subset SU\left(3\right)$, where $N,M$ are positive integers [59,60,61]. If the boundary condition that breaks the gauge group is imposed, the orbifolding must be accompanied by an $E_8\supset U{\left(1\right)}_f\supset {\mathbb{Z}}_N$ transformation. As a result, the decomposed 10d superfield is transformed as follows

$$\begin{array}{cc}\hfill V(x,z_1,z_2,z_3)& \hfill =e^{2i\pi q_a^f/N}V(x,{\omega }_1{z}_1,{\omega }_2{z}_2,{\omega }_3{z}_3),\hfill \\ \hfill {\varphi }^i(x,z_1,z_2,z_3)& \hfill ={\omega }_i{e}^{2i\pi q_a^f/N}{\varphi }^i(x,{\omega }_1{z}_1,{\omega }_2{z}_2,{\omega }_3{z}_3),\hfill \end{array}$$

(5)

where $q_a^f$ is the $U{\left(1\right)}_f$ charge of the corresponding representation. Here, V lies in the adjoint representation of the unbroken gauge group, while the light chiral superfields ${\varphi }_i$ belong to the corresponding fundamental representation with charge $q_a^f=-n_{i}modN$. The desired light fields are then specified by an appropriate choice of $n_i$. This fully determines the orbifolding procedure.

The underlined gauge symmetry can be broken and its rank reduced by adding a gauge transformation to the EDs translations through the so-called Wilson line mechanism. The latter generates a mass splitting similar to the one a Vacuum Expectation Value (VEVs) would generate. It is therefore usual to parametrize this symmetry breaking by an effective VEV. It should be remembered that it is not actually a VEV, as it does not come from the minimization of a potential, but from the ED profiles of the fields, determined by boundary conditions. Consistent with the orbifold boundary conditions, the effective VEVs should obey the rotation–translation commutation relations coming from the Poincarè algebra and hence emerge in chiral supermultiplets that have a zero mode. An effective potential for the fields is obtained by integrating out all the other fields (for more details, see, e.g., Refs. [62,63,64,65,66,67]).

The full $\mathcal{R}$ symmetry without orbifolding is $SU{\left(4\right)}_{\mathcal{R}}$ of the effective $\mathcal{N}=4$ SUSY. We can add a further orbifolding ${\mathbb{Z}}_2\subset SU{\left(4\right)}_{\mathcal{R}}$ but ${\mathbb{Z}}_2\not\subset SU{\left(3\right)}_{\mathcal{R}}$. Let us define $S_i$ as the complex scalar field inside the chiral superfield ${\varphi }_i$ (up to a phase $e^{i{\xi }_i}$ which depends on the definition of the base) and ${\psi }_i$ the chiral fermion (up to the same phase $e^{i{\xi }_i}$). Let us also define as $A_{\mu }$ the vector field inside the gauge superfield and $\lambda$ as the gaugino inside it.

The fermions transform as a $\mathbf{4}$ of $SU{\left(4\right)}_{\mathcal{R}}$, and they can be written as a 4 vector

$${({\psi }_1,{\psi }_2,{\psi }_3,\lambda )}^T,$$

(6)

while the real scalars transform as a $\mathbf{6}$ of $SU{\left(4\right)}_{\mathcal{R}}$, and it can be written as a $4\times 4$ antisymmetric matrix

$$\left(\begin{array}{cccc}0& \Re S_3& \Im S_2& \Re S_1\\ -\Re S_3& 0& \Im S_1& \Re S_2\\ -\Im S_2& -\Im S_1& 0& \Im S_3\\ -\Re S_1& -\Re S_2& -\Im S_3& 0\end{array}\right).$$

(7)

This would break the remaining SUSY.

3. The ${\mathbb{T}}^6/({\mathbb{Z}}_6\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2)$ Orbifold with $E_8$

Now, we consider an $E_8$ gauge theory in 10d spacetime. The $E_8$ gauge symmetry has rank 8, and the orbifolding must preserve the rank-4 SM gauge symmetry, $SU{\left(3\right)}_C\times SU{\left(2\right)}_L\times U{\left(1\right)}_Y$. In this work, we employ the following decomposition [6]

$$\begin{array}{cc}\hfill E_8& \supset SO\left(10\right)\times U{\left(1\right)}_{X^{\prime }}\times SU{\left(3\right)}_F\hfill \\ \hfill & \supset SO\left(10\right)\times U{\left(1\right)}_{X^{\prime }}\times U{\left(1\right)}_F\times SU{\left(2\right)}_F\hfill \\ \hfill & \supset G_{PS}\equiv SU{\left(4\right)}_{PS}\times SU{\left(2\right)}_L\times SU{\left(2\right)}_R\times U{\left(1\right)}_{X^{\prime }}\times U{\left(1\right)}_F\times SU{\left(2\right)}_F,\hfill \end{array}$$

(8)

and consider the $T^6/({\mathbb{Z}}_6\times {\mathbb{Z}}_2)$ orbifold whose compactification triggers the breaking $E_8\to G_{PS}$, i.e., featuring an intermediate Pati–Salam SUSY theory and a flavor $U{\left(1\right)}_F\times SU{\left(2\right)}_F$ symmetry in 4d. Subsequent reduction of this symmetry occurs in the following steps,

$$\begin{array}{cc}\hfill & \hfill SU{\left(4\right)}_{PS}\to SU{\left(3\right)}_C\times U{\left(1\right)}_{B-L},SU{\left(2\right)}_R\to U{\left(1\right)}_{T_3^R},\hfill \\ \hfill & \hfill SU{\left(4\right)}_{PS}\times SU{\left(2\right)}_R\to SU{\left(3\right)}_C\times U{\left(1\right)}_Y\times U{\left(1\right)}_X,\hfill \end{array}$$

(9)

with

$$q_Y=6q_{T_3^R}+3q_{B-L},q_X=4Q_{T_3^R}-3q_{B-L},$$

(10)

where one recovers the color $SU{\left(3\right)}_C$ and hypercharge $U{\left(1\right)}_Y$ groups of the SM.

The orbifold boundary conditions which provide such a breaking pattern read

$${\mathbb{Z}}_6:\varphi \to e^{2i\pi q_{X^{\prime }}/6}\varphi ,{\mathbb{Z}}_2:\varphi \to e^{2i\pi (q_Y+q_{T_8^F})/2}\varphi ,$$

(11)

with the orbifold transformations

$$\begin{array}{cc}\hfill (x,z_1,z_2,z_3)& \hfill \sim (x,{\alpha }^2{z}_1,{\alpha }^5{z}_2,{\alpha }^5{z}_3),\hfill \\ \hfill (x,z_1,z_2,z_3)& \hfill \sim (x,-z_1,-z_2,{(-1)}^2{z}_3),\hfill \end{array}$$

(12)

where $\alpha =e^{2i\pi /6}$, and $-1=e^{2i\pi /2}$. The breaking described in the first line of Equation (8) is achieved by the boundary condition given by $q_{X^{\prime }}/6$. It is further broken to the second line by the boundary condition $q_{T_8^F}/2$. The third line is achieved by further applying $q_Y/2$. The above conditions enable us to decompose the $\mathbf{248}$ representation of $E_8$ into the representations of unbroken $G_{PS}$ symmetry summarised in

Table 1. The ${\mathbb{Z}}_6\times {\mathbb{Z}}_2$ orbifold charges of each $G_{PS}$$\mathcal{N}=1$ superfield. Only the superfields with both charges equal to unity (the singlets $1,1$) have zero modes. The colors indicate where the different fields of interest are contained: SM fermions, right handed neutrinos, SM Higgses, gauge fields in the adjoint, mirror fermions, mirror Higgses, flavons, leptoquarks and vector-like triplets.

	V	${\mathit{\varphi }}_1$	${\mathit{\varphi }}_2$	${\mathit{\varphi }}_3$
${\mathcal{V}}_{(\mathbf{15},\mathbf{1},\mathbf{1},0,0,\mathbf{1})}$	$1,1$	${\alpha }^2,-1$	${\alpha }^5,-1$	${\alpha }^5,1$
${\mathcal{V}}_{(\mathbf{1},\mathbf{3},\mathbf{1},0,0,\mathbf{1})}$	$1,1$	${\alpha }^2,-1$	${\alpha }^5,-1$	${\alpha }^5,1$
${\mathcal{V}}_{(\mathbf{1},\mathbf{1},\mathbf{3},0,0,\mathbf{1})}$	$1,1$	${\alpha }^2,-1$	${\alpha }^5,-1$	${\alpha }^5,1$
${\mathcal{V}}_{(\mathbf{1},\mathbf{1},\mathbf{1},0,0,\mathbf{1})}$	$1,1$	${\alpha }^2,-1$	${\alpha }^5,-1$	${\alpha }^5,1$
${\mathcal{V}}_{(\mathbf{1},\mathbf{1},\mathbf{1},0,0,\mathbf{3})}$	$1,1$	${\alpha }^2,-1$	${\alpha }^5,-1$	${\alpha }^5,1$
${\mathcal{V}}_{(\mathbf{1},\mathbf{1},\mathbf{1},0,0,\mathbf{1})}$	$1,1$	${\alpha }^2,-1$	${\alpha }^5,-1$	${\alpha }^5,1$
${\mathcal{V}}_{(\mathbf{1},\mathbf{1},\mathbf{1},0,-3,\mathbf{2})}$	$1,-1$	${\alpha }^2,1$	${\alpha }^5,1$	${\alpha }^5,-1$
${\mathcal{V}}_{(\mathbf{1},\mathbf{1},\mathbf{1},3,0,\mathbf{2})}$	$1,-1$	${\alpha }^2,1$	${\alpha }^5,1$	${\alpha }^5,-1$
${\mathcal{V}}_{(\mathbf{6},\mathbf{2},\mathbf{2},0,0,\mathbf{1})}$	$1,-1$	${\alpha }^2,1$	${\alpha }^5,1$	${\alpha }^5,-1$
${\mathcal{V}}_{(\mathbf{4},\mathbf{2},\mathbf{1},-3,0,\mathbf{1})}$	${\alpha }^3,-1$	${\alpha }^5,1$	${\alpha }^2,1$	${\alpha }^2,-1$
${\mathcal{V}}_{(\overline{\mathbf{4}},\mathbf{1},\mathbf{2},-3,0,\mathbf{1})}$	${\alpha }^3,1$	${\alpha }^5,-1$	${\alpha }^2,-1$	${\alpha }^2,1$
${\mathcal{V}}_{(\overline{\mathbf{4}},\mathbf{2},\mathbf{1},3,0,\mathbf{1})}$	${\alpha }^3,-1$	${\alpha }^5,1$	${\alpha }^2,1$	${\alpha }^2,-1$
${\mathcal{V}}_{(\mathbf{4},\mathbf{1},\mathbf{2},3,0,\mathbf{1})}$	${\alpha }^3,1$	${\alpha }^5,-1$	${\alpha }^2,-1$	${\alpha }^2,1$
${\mathcal{V}}_{(\mathbf{6},\mathbf{1},\mathbf{1},-2,1,\mathbf{2})}$	${\alpha }^4,-1$	$1,1$	${\alpha }^3,1$	${\alpha }^3,-1$
${\mathcal{V}}_{(\mathbf{6},\mathbf{1},\mathbf{1},-2,-2,\mathbf{1})}$	${\alpha }^4,1$	$1,-1$	${\alpha }^3,-1$	${\alpha }^3,1$
${\mathcal{V}}_{(\mathbf{6},\mathbf{1},\mathbf{1},2,-1,\mathbf{2})}$	${\alpha }^2,-1$	${\alpha }^4,1$	$\alpha ,1$	$\alpha ,-1$
${\mathcal{V}}_{(\mathbf{6},\mathbf{1},\mathbf{1},2,2,\mathbf{1})}$	${\alpha }^2,1$	${\alpha }^4,-1$	$\alpha ,-1$	$\alpha ,1$
${\mathcal{V}}_{(\mathbf{4},\mathbf{2},\mathbf{1},1,1,\mathbf{2})}$	$\alpha ,1$	${\alpha }^3,-1$	$1,-1$	$1,1$
${\mathcal{V}}_{(\mathbf{4},\mathbf{2},\mathbf{1},1,-2,\mathbf{1})}$	$\alpha ,-1$	${\alpha }^3,1$	$1,1$	$1,-1$
${\mathcal{V}}_{(\overline{\mathbf{4}},\mathbf{1},\mathbf{2},1,1,\mathbf{2})}$	$\alpha ,-1$	${\alpha }^3,1$	$1,1$	$1,-1$
${\mathcal{V}}_{(\overline{\mathbf{4}},\mathbf{1},\mathbf{2},1,-2,\mathbf{1})}$	$\alpha ,1$	${\alpha }^3,-1$	$1,-1$	$1,1$
${\mathcal{V}}_{(\mathbf{1},\mathbf{2},\mathbf{2},-2,1,\mathbf{2})}$	${\alpha }^4,1$	$1,-1$	${\alpha }^3,-1$	${\alpha }^3,1$
${\mathcal{V}}_{(\mathbf{1},\mathbf{2},\mathbf{2},-2,-2,\mathbf{1})}$	${\alpha }^4,-1$	$1,1$	${\alpha }^3,1$	${\alpha }^3,-1$
${\mathcal{V}}_{(\mathbf{1},\mathbf{1},\mathbf{1},4,1,\mathbf{2})}$	${\alpha }^4,-1$	$1,1$	${\alpha }^3,1$	${\alpha }^3,-1$
${\mathcal{V}}_{(\mathbf{1},\mathbf{1},\mathbf{1},4,-2,\mathbf{1})}$	${\alpha }^4,1$	$1,-1$	${\alpha }^3,-1$	${\alpha }^3,1$
${\mathcal{V}}_{(\overline{\mathbf{4}},\mathbf{2},\mathbf{1},-1,-1,\mathbf{2})}$	${\alpha }^5,1$	$\alpha ,-1$	${\alpha }^4,-1$	${\alpha }^4,1$
${\mathcal{V}}_{(\overline{\mathbf{4}},\mathbf{2},\mathbf{1},-1,2,\mathbf{1})}$	${\alpha }^5,-1$	$\alpha ,1$	${\alpha }^4,1$	${\alpha }^4,-1$
${\mathcal{V}}_{(\mathbf{4},\mathbf{1},\mathbf{2},-1,-1,\mathbf{2})}$	${\alpha }^5,-1$	$\alpha ,1$	${\alpha }^4,1$	${\alpha }^4,-1$
${\mathcal{V}}_{(\mathbf{4},\mathbf{1},\mathbf{2},-1,2,\mathbf{1})}$	${\alpha }^5,1$	$\alpha ,-1$	${\alpha }^4,-1$	${\alpha }^4,1$
${\mathcal{V}}_{(\mathbf{1},\mathbf{2},\mathbf{2},2,-1,\mathbf{2})}$	${\alpha }^2,1$	${\alpha }^4,-1$	$\alpha ,-1$	$\alpha ,1$
${\mathcal{V}}_{(\mathbf{1},\mathbf{2},\mathbf{2},2,2,\mathbf{1})}$	${\alpha }^2,-1$	${\alpha }^4,1$	$\alpha ,1$	$\alpha ,-1$
${\mathcal{V}}_{(\mathbf{1},\mathbf{1},\mathbf{1},-4,-1,\mathbf{2})}$	${\alpha }^2,-1$	${\alpha }^4,1$	$\alpha ,1$	$\alpha ,-1$
${\mathcal{V}}_{(\mathbf{1},\mathbf{1},\mathbf{1},-4,2,\mathbf{1})}$	${\alpha }^2,1$	${\alpha }^4,-1$	$\alpha ,-1$	$\alpha ,1$

, together with the corresponding charges 2 (for a better presentation we color code the representations containing SM fermions, right handed neutrinos, SM Higgses, gauge fields in the adjoint, mirror fermions, mirror Higgses, flavons, leptoquarks and vector-like triplets).

The zero modes have the following representations of the residual symmetry group (recall they correspond to those with $1,1$ charges in Table 1):

$$\begin{array}{cc}\hfill V_{\mu }& :(\mathbf{15},\mathbf{1},\mathbf{1},0,0,\mathbf{1})+(\mathbf{1},\mathbf{3},\mathbf{1},0,0,\mathbf{1})+(\mathbf{1},\mathbf{1},\mathbf{3},0,0,\mathbf{1})\hfill \\ \hfill & +(\mathbf{1},\mathbf{1},\mathbf{1},0,0,\mathbf{1})+(\mathbf{1},\mathbf{1},\mathbf{1},0,0,\mathbf{1})+(\mathbf{1},\mathbf{1},\mathbf{1},0,0,\mathbf{3}),\hfill \\ \hfill {\varphi }_1& :(\mathbf{6},\mathbf{1},\mathbf{1},-2,1,\mathbf{2})+(\mathbf{1},\mathbf{2},\mathbf{2},-2,-2,\mathbf{1})+(\mathbf{1},\mathbf{1},\mathbf{1},4,1,\mathbf{2}),\hfill \\ \hfill {\varphi }_2& :(\mathbf{4},\mathbf{2},\mathbf{1},1,-2,\mathbf{1})+(\overline{\mathbf{4}},\mathbf{1},\mathbf{2},1,1,\mathbf{2}),\hfill \\ \hfill {\varphi }_3& :(\mathbf{4},\mathbf{2},\mathbf{1},1,1,\mathbf{2})+(\overline{\mathbf{4}},\mathbf{1},\mathbf{2},1,-2,\mathbf{1}).\hfill \end{array}$$

(13)

which can be named as

$$\begin{array}{cc}\hfill V_{\mu }& :G_{\mu }+W_{\mu }^L+W_{\mu }^R+Z_{\mu }^{{}^{\prime }}+Z_{\mu }^F+W_{\mu }^F,\hfill \\ \hfill {\varphi }_1& :T+h+\mathrm{\Phi },\hfill \\ \hfill {\varphi }_2& :f+F^c,\hfill \\ \hfill {\varphi }_3& :F+f^c,\hfill \end{array}$$

(14)

where uppercase letters $T,F,\mathrm{\Phi }$ are used to denote $SU{\left(2\right)}_F$ doublets, and lowercase letters $f,h$ correspond to $SU{\left(2\right)}_F$ singlets.

In order to further break the intermediate symmetry group down to the SM, one could use each Wilson line to give an effective VEV to the SM singlet fields. If they are not available, there are extra fields described below that can provide such breaking.

We now analyze each field to find the SM singlets. The field $T_{1,2}$ contains a color triplet and antitriplet; therefore, it has no SM singlets. The field

$$\begin{array}{c}\hfill h\sim \left(\begin{array}{c}{H}_u\\ H_d\end{array}\right),\end{array}$$

(15)

only contains the Higgs $SU{\left(2\right)}_L$ doublets and cannot obtain a Wilson line VEV. Otherwise, the electroweak symmetry would be broken at the compactification scale. The fields

$$\begin{array}{c}\hfill F,f\sim (Q_{1,2,3}^r,Q_{1,2,3}^g,Q_{1,2,3}^b,L_{1,2,3}),\end{array}$$

(16)

contain the quark and lepton $SU{\left(2\right)}_L$ doublets (where the $r,g,b$ are the color indices) and cannot obtain a Wilson line VEV, as it would break the SM symmetry. Finally,

$$F^c,f^c\sim \left(\begin{array}{cccc}{u}_{1,2,3}^{cr}& u_{1,2,3}^{cg}& u_{1,2,3}^{cb}& {\nu }_{1,2,3}^c\\ d_{1,2,3}^{cr}& d_{1,2,3}^{cg}& d_{1,2,3}^{cb}& e_{1,2,3}^c\end{array}\right),$$

(17)

where the $v_{1,2,3}^c$ are SM singlets, and the sneutrino can obtain a VEV. They are charged under $SU{\left(4\right)}_{PS}\times SU{\left(2\right)}_R\times U{\left(1\right)}_{X^{\prime }}\times U{\left(1\right)}_F\times SU{\left(2\right)}_F$ so their VEVs break it. A VEV in a $\mathbf{4}$ dimensional representation of $SU{\left(4\right)}_{PS}$ would break $SU{\left(4\right)}_{PS}\to SU{\left(3\right)}_C$, while a VEV in a $\mathbf{2}$ dimensional representation of $SU{\left(2\right)}_R$ would break it completely. Together, both sneutrino VEVs break $SU{\left(4\right)}_{PS}\times SU{\left(2\right)}_R\times U{\left(1\right)}_{X^{\prime }}\times U{\left(1\right)}_F\times SU{\left(2\right)}_F\to SU{\left(3\right)}_C\times SU{\left(2\right)}_L\times U{\left(1\right)}_Y\times U{\left(1\right)}_N$, where it preserves an extra $U{\left(1\right)}_N$ whose charge is defined by

$$q_N=q_X+5q_{X^{\prime }}.$$

(18)

The field $\mathrm{\Phi }\sim {\phi }_{1,2}$ contains two SM singlets and can get a Wilson line VEV. Note that the VEV $\langle \mathrm{\Phi }\rangle =(\langle {\mathrm{\phi }}_2\rangle ,\langle {\mathrm{\phi }}_3\rangle )$ has a non-zero $q_N$ charge and hence breaks the remaining $U{\left(1\right)}_N$ symmetry yielding the SM gauge symmetry at low energies.

Note that the symmetry breaking is triggered by the geometry of the orbifold. This means that the original symmetries (both the $E_8$ and SUSY) are not exact as they are broken explicitly on the singular points of the orbifold. Therefore, after compactification, all effective calculations are performed without SUSY and $E_8$.

In this model, we can impose an extra rotational ${\mathbb{Z}}_2$ boundary condition

$$P_{\mathrm{SS}}=\mathrm{diag}(-1,1,1,-1),$$

(19)

which would only leave as massless modes the gauge vectors (but not the gauginos), the scalars of ${\varphi }_1$ (which lie in the $T,h,\mathrm{\Phi }$ representations) and the chiral fermions ${\varphi }_{2,3}$ (which lie in the representations $f,f^c,F,F^c$). Therefore, the whole SM field content lies in the zero modes. As the right-handed sneutrinos now do not have a zero mode, there can not be a Wilson line aligned with them; therefore, the Pati–Salam symmetry is unbroken. One may safely assume that the fields in Section 4 can break the remaining symmetry.

The sneutrino effective VEV does break the usual R-parity. It affects the phenomenology by generating the R-parity violating (RPV) terms $\sim \langle \tilde{\nu }\rangle {\tilde{H}}_{u}L$. The latter can be effectively “rotated” away by a unitary transformation which then generates terms such as $\sim y_{\mathrm{RPV}}^{ijk}{Q}_i{L}_j{d}_k^c$. The strongest experimental bound on this type of interactions implies that $y_{\mathrm{RPV}}^{111}<0.001$ [68,69]. As such, an interaction term is proportional to the first-family neutrino Yukawa couplin; it is expected to be well below this bound.

4. Anomaly-Cancelling Sector

In the previous section, we have shown that the orbifold can break $E_8$ into the SM directly, leaving no remaining SUSY. We have also shown that the full SM field content arises from the single gauge supermultiplet. Therefore, the full low energy phenomenology is determined by the orbifold compactification. However, one has to ensure that any potential anomalies are cancelled at every symmetry breaking step. While this may require the addition of new fields, we will assume that they do not survive at low energies, so that the predictivity shown in the previous section is not spoiled. Let us discuss the anomaly cancellation in more detail.

The rotation boundary conditions split the masses of different representations by integer multiples of the compactification scale $n\mathrm{\Lambda }$. The Wilson lines split the masses by an effective VEV with scale $y\mathrm{\Lambda }$, where y is an arbitrary real parameter. The latter can, in principle, be as small as desired, generating a certain hierarchy between the scales. Therefore, one could think of the subsequential breaking $E_8\to G_{\mathrm{PS}}\to G_{\mathrm{SM}}$ at well-separated energy scales as a New Physics scenario potentially relevant for phenomenology.

The field content in the Pati–Salam phase would be composed of zero modes from Equation (13). However, we can easily notice that this phase is not fully consistent as the field content generates gauge anomalies, while the SM phase is anomaly free. In order to resolve this issue, one can add more fields so that the considered two-step breaking is consistently realised in an anomaly-free way.

There are two sets of fields that cancel the anomalies generated by the zero modes. First, one would add 27 copies of the pair of representations $(\mathbf{1},\mathbf{1},\mathbf{1},0,-1,\mathbf{2})+(\mathbf{1},\mathbf{1},\mathbf{1},0,2,\mathbf{1})$ as the 4d chiral superfields located at the $z_i=0$ origin brane. These would cancel the flavor-specific anomalies. Note that they are all SM singlets and do not affect the low energy phenomenology. The second set of fields consists of 5 copies of 10d chiral superfields in the bulk living in the $\mathbf{248}$ representation of $E_8$. They have the charges under the orbifold rotations $(1,\pm 1),({\alpha }^4,\pm 1),({\alpha }^2,-1)$. These will add a bunch of zero-mode chiral superfields (51 in total) which are either the real representations (i.e., vector-like pairs) or the chiral representations $(\mathbf{6},\mathbf{1},\mathbf{1},-2,-2,\mathbf{1})+(\mathbf{1},\mathbf{2},\mathbf{2},-2,-2,\mathbf{1})+(\mathbf{1},\mathbf{1},\mathbf{1},4,-2,\mathbf{1})$, as summarised in

Table 2. The ${\mathbb{Z}}_6\times {\mathbb{Z}}_2$ orbifold charges of each $G_{PS}$$\mathcal{N}=1$ superfield. Only the superfields with highlighted charges have zero modes from the 10d chiral superfields. The same colored highlighted fields would come from the same 10d chiral superfield.

	${\mathit{\varphi }}_0$	${\mathit{\varphi }}_1$	${\mathit{\varphi }}_2$	${\mathit{\varphi }}_3$
${\mathrm{\Phi }}_{(\mathbf{15},\mathbf{1},\mathbf{1},0,0,\mathbf{1})}$	$1,1$	${\alpha }^2,-1$	${\alpha }^5,-1$	${\alpha }^5,1$
${\mathrm{\Phi }}_{(\mathbf{1},\mathbf{3},\mathbf{1},0,0,\mathbf{1})}$	$1,1$	${\alpha }^2,-1$	${\alpha }^5,-1$	${\alpha }^5,1$
${\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{3},0,0,\mathbf{1})}$	$1,1$	${\alpha }^2,-1$	${\alpha }^5,-1$	${\alpha }^5,1$
${\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},0,0,\mathbf{1})}$	$1,1$	${\alpha }^2,-1$	${\alpha }^5,-1$	${\alpha }^5,1$
${\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},0,0,\mathbf{3})}$	$1,1$	${\alpha }^2,-1$	${\alpha }^5,-1$	${\alpha }^5,1$
${\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},0,0,\mathbf{1})}$	$1,1$	${\alpha }^2,-1$	${\alpha }^5,-1$	${\alpha }^5,1$
${\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},0,-3,\mathbf{2})}$	$1,-1$	${\alpha }^2,1$	${\alpha }^5,1$	${\alpha }^5,-1$
${\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},0,3,\mathbf{2})}$	$1,-1$	${\alpha }^2,1$	${\alpha }^5,1$	${\alpha }^5,-1$
${\mathrm{\Phi }}_{(\mathbf{6},\mathbf{2},\mathbf{2},0,0,\mathbf{1})}$	$1,-1$	${\alpha }^2,1$	${\alpha }^5,1$	${\alpha }^5,-1$
${\mathrm{\Phi }}_{(\mathbf{4},\mathbf{2},\mathbf{1},-3,0,\mathbf{1})}$	${\alpha }^3,-1$	${\alpha }^5,1$	${\alpha }^2,1$	${\alpha }^2,-1$
${\mathrm{\Phi }}_{(\overline{\mathbf{4}},\mathbf{1},\mathbf{2},-3,0,\mathbf{1})}$	${\alpha }^3,1$	${\alpha }^5,-1$	${\alpha }^2,-1$	${\alpha }^2,1$
${\mathrm{\Phi }}_{(\overline{\mathbf{4}},\mathbf{2},\mathbf{1},3,0,\mathbf{1})}$	${\alpha }^3,-1$	${\alpha }^5,1$	${\alpha }^2,1$	${\alpha }^2,-1$
${\mathrm{\Phi }}_{(\mathbf{4},\mathbf{1},\mathbf{2},3,0,\mathbf{1})}$	${\alpha }^3,1$	${\alpha }^5,-1$	${\alpha }^2,-1$	${\alpha }^2,1$
${\mathrm{\Phi }}_{(\mathbf{6},\mathbf{1},\mathbf{1},-2,1,\mathbf{2})}$	${\alpha }^4,-1$	$1,1$	${\alpha }^3,1$	${\alpha }^3,-1$
${\mathrm{\Phi }}_{(\mathbf{6},\mathbf{1},\mathbf{1},-2,-2,\mathbf{1})}$	${\alpha }^4,1$	$1,-1$	${\alpha }^3,-1$	${\alpha }^3,1$
${\mathrm{\Phi }}_{(\mathbf{6},\mathbf{1},\mathbf{1},2,-1,\mathbf{2})}$	${\alpha }^2,-1$	${\alpha }^4,1$	$\alpha ,1$	$\alpha ,-1$
${\mathrm{\Phi }}_{(\mathbf{6},\mathbf{1},\mathbf{1},2,2,\mathbf{1})}$	${\alpha }^2,1$	${\alpha }^4,-1$	$\alpha ,-1$	$\alpha ,1$
${\mathrm{\Phi }}_{(\mathbf{4},\mathbf{2},\mathbf{1},1,1,\mathbf{2})}$	$\alpha ,1$	${\alpha }^3,-1$	$1,-1$	$1,1$
${\mathrm{\Phi }}_{(\mathbf{4},\mathbf{2},\mathbf{1},1,-2,\mathbf{1})}$	$\alpha ,-1$	${\alpha }^3,1$	$1,1$	$1,-1$
${\mathrm{\Phi }}_{(\overline{\mathbf{4}},\mathbf{1},\mathbf{2},1,1,\mathbf{2})}$	$\alpha ,-1$	${\alpha }^3,1$	$1,1$	$1,-1$
${\mathrm{\Phi }}_{(\overline{\mathbf{4}},\mathbf{1},\mathbf{2},1,-2,\mathbf{1})}$	$\alpha ,1$	${\alpha }^3,-1$	$1,-1$	$1,1$
${\mathrm{\Phi }}_{(\mathbf{1},\mathbf{2},\mathbf{2},-2,1,\mathbf{2})}$	${\alpha }^4,1$	$1,-1$	${\alpha }^3,-1$	${\alpha }^3,1$
${\mathrm{\Phi }}_{(\mathbf{1},\mathbf{2},\mathbf{2},-2,-2,\mathbf{1})}$	${\alpha }^4,-1$	$1,1$	${\alpha }^3,1$	${\alpha }^3,-1$
${\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},4,1,\mathbf{2})}$	${\alpha }^4,-1$	$1,1$	${\alpha }^3,1$	${\alpha }^3,-1$
${\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},4,-2,\mathbf{1})}$	${\alpha }^4,1$	$1,-1$	${\alpha }^3,-1$	${\alpha }^3,1$
${\mathrm{\Phi }}_{(\overline{\mathbf{4}},\mathbf{2},\mathbf{1},-1,-1,\mathbf{2})}$	${\alpha }^5,1$	$\alpha ,-1$	${\alpha }^4,-1$	${\alpha }^4,1$
${\mathrm{\Phi }}_{(\overline{\mathbf{4}},\mathbf{2},\mathbf{1},-1,2,\mathbf{1})}$	${\alpha }^5,-1$	$\alpha ,1$	${\alpha }^4,1$	${\alpha }^4,-1$
${\mathrm{\Phi }}_{(\mathbf{4},\mathbf{1},\mathbf{2},-1,-1,\mathbf{2})}$	${\alpha }^5,-1$	$\alpha ,1$	${\alpha }^4,1$	${\alpha }^4,-1$
${\mathrm{\Phi }}_{(\mathbf{4},\mathbf{1},\mathbf{2},-1,2,\mathbf{1})}$	${\alpha }^5,1$	$\alpha ,-1$	${\alpha }^4,-1$	${\alpha }^4,1$
${\mathrm{\Phi }}_{(\mathbf{1},\mathbf{2},\mathbf{2},2,-1,\mathbf{2})}$	${\alpha }^2,1$	${\alpha }^4,-1$	$\alpha ,-1$	$\alpha ,1$
${\mathrm{\Phi }}_{(\mathbf{1},\mathbf{2},\mathbf{2},2,2,\mathbf{1})}$	${\alpha }^2,-1$	${\alpha }^4,1$	$\alpha ,1$	$\alpha ,-1$
${\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},-4,-1,\mathbf{2})}$	${\alpha }^2,-1$	${\alpha }^4,1$	$\alpha ,1$	$\alpha ,-1$
${\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},-4,2,\mathbf{1})}$	${\alpha }^2,1$	${\alpha }^4,-1$	$\alpha ,-1$	$\alpha ,1$

.

The full SM field content comes from the gauge superfield. While one can add a symmetry to restrict the couplings, they will not change the couplings to the gauge superfield. This does not reduce the predictivity of the setup. The added fields will have arbitrary couplings, and since they live in real representations, they also have explicit arbitrary masses. The extra fields in the bulk have real representations and therefore allow explicit mass terms. They are naturally heavy, and no hierarchies between them will be assumed; thus they do not affect the low energy physics.

Below the compactification scale, we have the chiral multiplets

$$\begin{array}{cccc}2\times {\mathrm{\Phi }}_{(\mathbf{15},\mathbf{1},\mathbf{1},0,0,\mathbf{1})},\hfill & 1\times {\mathrm{\Phi }}_{(\mathbf{6},\mathbf{2},\mathbf{2},0,0,\mathbf{1})},\hfill & 3\times {\mathrm{\Phi }}_{(\mathbf{4},\mathbf{2},\mathbf{1},1,1,\mathbf{2})},\hfill & 2\times {\mathrm{\Phi }}_{(\overline{\mathbf{4}},\mathbf{2},\mathbf{1},-1,-1,\mathbf{2})},\hfill \\ 2\times {\mathrm{\Phi }}_{(\mathbf{1},\mathbf{3},\mathbf{1},0,0,\mathbf{1})},\hfill & 0\times {\mathrm{\Phi }}_{(\mathbf{4},\mathbf{2},\mathbf{1},-3,0,\mathbf{1})},\hfill & 3\times {\mathrm{\Phi }}_{(\mathbf{4},\mathbf{2},\mathbf{1},1,-2,\mathbf{1})},\hfill & 2\times {\mathrm{\Phi }}_{(\overline{\mathbf{4}},\mathbf{2},\mathbf{1},-1,2,\mathbf{1})},\hfill \\ 2\times {\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{3},0,0,\mathbf{1})},\hfill & 0\times {\mathrm{\Phi }}_{(\overline{\mathbf{4}},\mathbf{1},\mathbf{2},-3,0,\mathbf{1})},\hfill & 3\times {\mathrm{\Phi }}_{(\overline{\mathbf{4}},\mathbf{1},\mathbf{2},1,1,\mathbf{2})},\hfill & 2\times {\mathrm{\Phi }}_{(\mathbf{4},\mathbf{1},\mathbf{2},-1,-1,\mathbf{2})},\hfill \\ 2\times {\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},0,0,\mathbf{1})},\hfill & 0\times {\mathrm{\Phi }}_{(\overline{\mathbf{4}},\mathbf{2},\mathbf{1},3,0,\mathbf{1})},\hfill & 3\times {\mathrm{\Phi }}_{(\overline{\mathbf{4}},\mathbf{1},\mathbf{2},1,-2,\mathbf{1})},\hfill & 2\times {\mathrm{\Phi }}_{(\mathbf{4},\mathbf{1},\mathbf{2},-1,2,\mathbf{1})},\hfill \\ 2\times {\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},0,0,\mathbf{3})},\hfill & 0\times {\mathrm{\Phi }}_{(\mathbf{4},\mathbf{1},\mathbf{2},3,0,\mathbf{1})},\hfill & 2\times {\mathrm{\Phi }}_{(\mathbf{1},\mathbf{2},\mathbf{2},-2,1,\mathbf{2})},\hfill & 1\times {\mathrm{\Phi }}_{(\mathbf{1},\mathbf{2},\mathbf{2},2,-1,\mathbf{2})},\hfill \\ 2\times {\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},0,0,\mathbf{1})},\hfill & 3\times {\mathrm{\Phi }}_{(\mathbf{6},\mathbf{1},\mathbf{1},-2,1,\mathbf{2})},\hfill & 3\times {\mathrm{\Phi }}_{(\mathbf{1},\mathbf{2},\mathbf{2},-2,-2,\mathbf{1})},\hfill & 2\times {\mathrm{\Phi }}_{(\mathbf{1},\mathbf{2},\mathbf{2},2,2,\mathbf{1})},\hfill \\ 1\times {\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},0,-3,\mathbf{2})},\hfill & 2\times {\mathrm{\Phi }}_{(\mathbf{6},\mathbf{1},\mathbf{1},-2,-2,\mathbf{1})},\hfill & 3\times {\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},4,1,\mathbf{2})},\hfill & 2\times {\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},-4,-1,\mathbf{2})},\hfill \\ 1\times {\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},0,3,\mathbf{2})},\hfill & 2\times {\mathrm{\Phi }}_{(\mathbf{6},\mathbf{1},\mathbf{1},2,-1,\mathbf{2})},\hfill & 2\times {\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},4,-2,\mathbf{1})},\hfill & 1\times {\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},-4,2,\mathbf{1})},\hfill \\ & 1\times {\mathrm{\Phi }}_{(\mathbf{6},\mathbf{1},\mathbf{1},2,2,\mathbf{1})},\hfill & 27\times {\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},0,-1,\mathbf{2})}\hfill & 27\times {\mathrm{\Phi }}_{(\mathbf{1},\mathbf{1},\mathbf{1},0,2,\mathbf{1})},\hfill \end{array}$$

(20)

where all the vector-like pairs have an arbitrary mass determined by the abovementioned parameters. The unpaired fields contain the SM sectors plus SM singlets as we further discuss below in Section 5. While the masses of the KK modes are fixed by the compactification scale, the ones in Equation (20) are determined by the arbitrary parameters of the superpotential. Furthermore, aWilson line VEV does not preserve SUSY; therefore, the chiral multiplets will be split into their scalar and fermion components.

For completeness, let us also show the branching rules of the Pati–Salam blue representations in terms of the SM gauge group identifying them with standard chiral matter and right-handed neutrinos,

$$\begin{array}{cc}\hfill & (\mathbf{4},\mathbf{2},\mathbf{1},1,1,\mathbf{2})\to (\mathbf{3},\mathbf{2},-{\displaystyle \frac{1}{6}})+(\mathbf{1},\mathbf{2},{\displaystyle \frac{1}{2}})\equiv {\mathrm{Q}}_{1,2}+{\mathrm{L}}_{1,2}\hfill \\ \hfill & (\mathbf{4},\mathbf{2},\mathbf{1},1,-2,\mathbf{1})\to (\mathbf{3},\mathbf{2},-{\displaystyle \frac{1}{6}})+(\mathbf{1},\mathbf{2},{\displaystyle \frac{1}{2}})\equiv {\mathrm{Q}}_3+{\mathrm{L}}_3\hfill \\ \hfill & (\overline{\mathbf{4}},\mathbf{1},\mathbf{2},1,1,\mathbf{2})\to (\overline{\mathbf{3}},\mathbf{1},-{\displaystyle \frac{2}{3}})+(\overline{\mathbf{3}},\mathbf{1},{\displaystyle \frac{1}{3}})+(\mathbf{1},\mathbf{1},1)+(\mathbf{1},\mathbf{1},0)\equiv {\mathrm{u}}_{1,2}^c+{\mathrm{d}}_{1,2}^c+{\mathrm{e}}_{1,2}^c+{\nu }_{1,2}^c\hfill \\ \hfill & (\overline{\mathbf{4}},\mathbf{1},\mathbf{2},1,-2,\mathbf{1})\to (\overline{\mathbf{3}},\mathbf{1},-{\displaystyle \frac{2}{3}})+(\overline{\mathbf{3}},\mathbf{1},{\displaystyle \frac{1}{3}})+(\mathbf{1},\mathbf{1},1)+(\mathbf{1},\mathbf{1},0)\equiv {\mathrm{u}}_3^c+{\mathrm{d}}_3^c+{\mathrm{e}}_3^c+{\nu }_3^c\hfill \end{array}$$

(21)

with the labels $1,2,3$ denoting the three families.

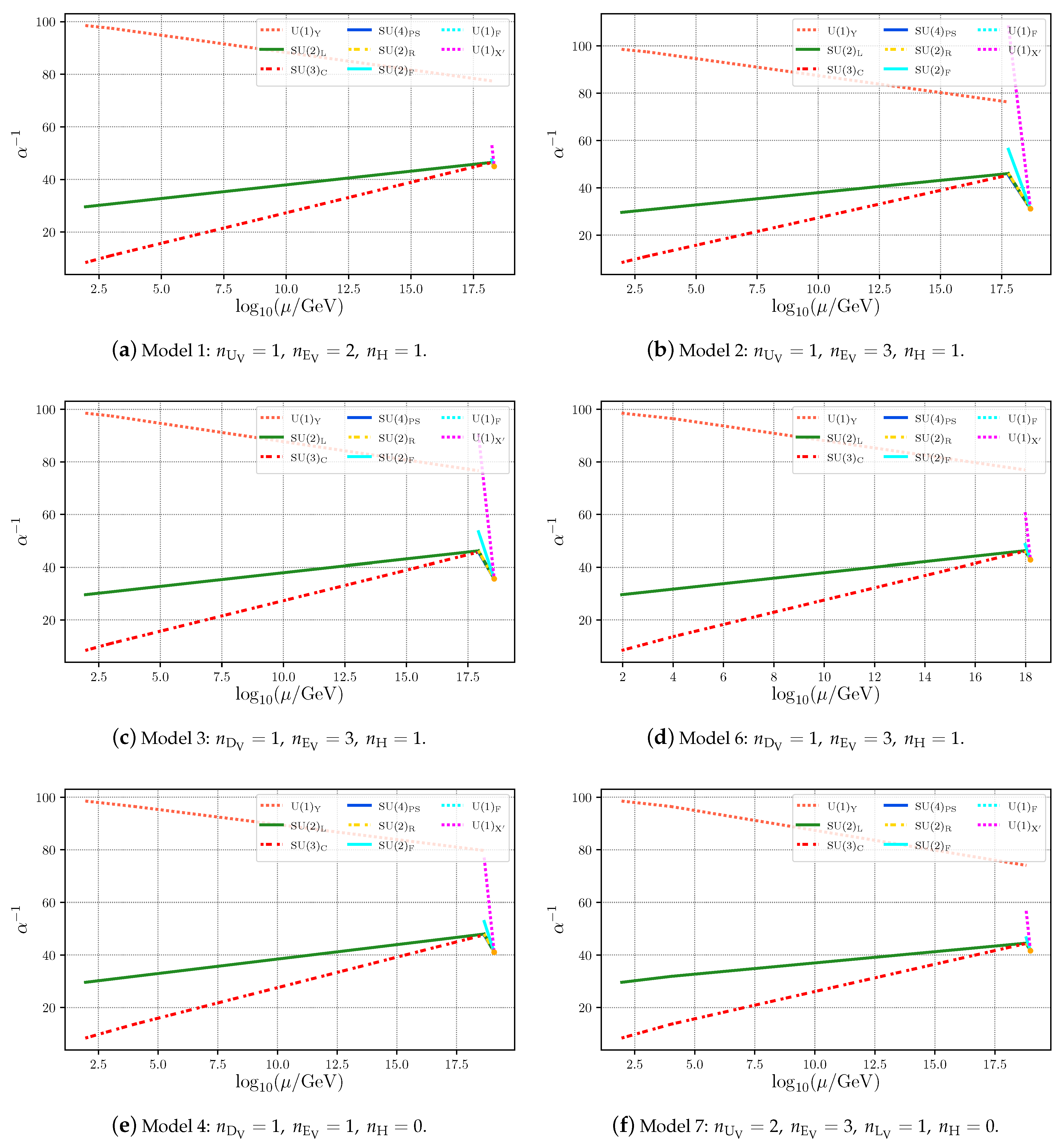
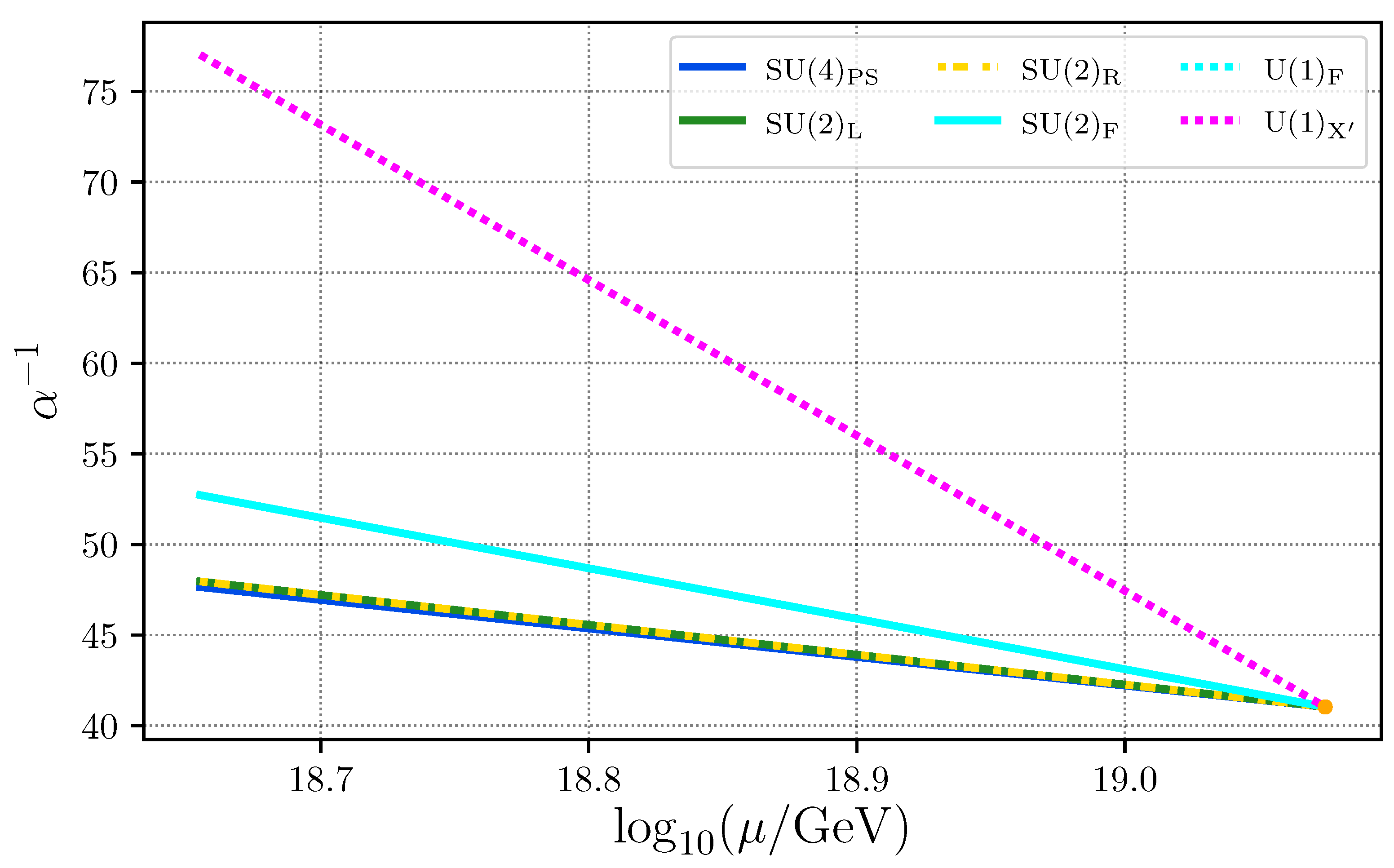
5. RG Evolution of Gauge Couplings

In this section, we study the RG evolution of the gauge couplings in our model with the purpose of finding possible low-energy scale scenarios compatible with an exact unification of all forces, including flavour, into ${\mathrm{E}}_8$. Our strategy for the current analysis consists of searching for those extensions of the SM with a minimal field content. Note that for a consistent SM-like fermion mass spectrum, one needs two Higgs doublets. The need for two Higgs doublets comes from the holomorphicity of the superpotential when there is SUSY. In this model, SUSY is broken through a non-vanishing $<D>$ which provides specific soft SUSY breaking terms. As $<\mathcal{D}>$ also breaks Pati–Salam and flavor symmetry, the structure of the SUSY breaking terms is also determined by their GUT representations. These do not allow non-holomorphic Yukawa couplings; therefore, two Higgs doublets are needed. While one is responsible for giving masses to up-type quarks, the other is needed for their down-type partners. Therefore, the minimal framework to consider contains two Higgs doublets, commonly dubbed two-Higgs doublet model (2HDM) (for a detailed review, see, e.g., refs. [70,71,72]). The SUSY breaking mechanism, coming from the Wilson line effective VEVs, may decouple one of the Higgs doublets and create large mass difference between the two doublets. A precise analysis of their masses and their running lies beyond the scope of this paper. Due to the large amount of parameters coming from the extra fields, it will be assumed that there are scenarios where they can be tuned to bring down the scale of some extra Higgs doublets.

In what follows, we study whether a 2HDM scenario is already consistent with gauge couplings unification under ${\mathrm{E}}_8$, and if not, how many extra Higgs doublets or generations of vector-like fermions are needed to fulfil the unification condition. As we discuss below, we will only consider low-scale scenarios with up to a maximum of three generations of vector-like quarks (VLQ) and vector-like leptons (VLL) that can be either $\mathrm{SU}{\left(2\right)}_{\mathrm{L}}$ doublets or singlets. We also allow up to one additional Higgs doublet in the low-energy scale theory on top of the two doublets already mentioned above.

In this work, the unification scale is assumed to be below the compactification scale through a simplifying assumption of a small Wilson line scale. Therefore, unification of gauge couplings will be studied before the KK modes enter into effect. The running of the gauge couplings is calculated at one-loop order where the value of the inverse structure constants at a given scale $\mu$ is given by

$${\alpha }_{\mathrm{A}}^{-1}\left(\mu \right)={\alpha }_0^{-1}+\frac{b_{\mathrm{A}}}{2\pi }log\left(\frac{\mu }{{\mu }_0}\right),$$

(22)

where a label $\mathrm{A}$ identifies a given gauge group and ${\alpha }_{\mathrm{A}}=g_{\mathrm{A}}^2/\left(4\pi \right)$, while ${\alpha }_0^{-1}$ denotes the value of the inverse structure constant at the initial energy-scale ${\mu }_0$. The value of the $b_{\mathrm{A}}$ coefficients will determine how fast a given gauge coupling evolves between any two scales. For non-Abelian gauge groups, these are given by

$$b_{\mathrm{A}}=\frac{11}{3}{C}_2\left(G\right)-\frac{4}{3}\kappa T\left(F\right)-\frac{1}{3}T\left(S\right),$$

(23)

where $\kappa =\frac{1}{2}$ for Weyl fermions, $C_2\left(G\right)$ is a group Casimir in the adjoint representation, $T\left(F\right)$ and $T\left(S\right)$ are the Dynkin indices for fermions and complex scalars, respectively. For the case of U(1) symmetries, the beta-function coefficients read as

$$b_{\mathrm{A}}^{\prime }=-\frac{4}{3}\kappa \sum _f{\left(\frac{Q_f}{2}\right)}^2-\frac{1}{3}\sum _s{\left(\frac{Q_s}{2}\right)}^2,$$

(24)

with $Q_f$ and $Q_s$ the Abelian charges of the fermions and scalars in the theory.

In our RG analysis, we consider three distinct regions:

1.

The first one corresponds to the running of the gauge couplings of the $G_{PS}$ symmetry emergent from the orbifold compactification of the 10-dimensional ${\mathrm{E}}_8$ theory as described above. In such a region, we label the beta-function coefficients as $b_{\mathrm{A}}^{\mathrm{I}}$ and denote the universal ${\mathrm{E}}_8$ inverse structure constant at the GUT scale as ${\alpha }_8^{-1}$. At this stage, all representations identified in Equation (20) contribute to the $b_{\mathrm{A}}^{\mathrm{I}}$ coefficients with the indicated multiplicity. Knowing that for $\mathrm{SU}{\left(4\right)}_{}$ we have

$$T\left(\mathbf{15}\right)=C_2\left(\mathbf{15}\right)=4,T\left(\mathbf{6}\right)=1,T\left(\mathbf{4}\right)=\frac{1}{2},$$

(25)

and that for $\mathrm{SU}{\left(2\right)}_{}$

$$T\left(\mathbf{3}\right)=C_2\left(\mathbf{3}\right)=2,T\left(\mathbf{2}\right)=\frac{1}{2},$$

(26)

we obtain the coefficients

$$b_{\mathrm{PS}}^{\mathrm{I}}=-43,b_{\mathrm{L}}^{\mathrm{I}}=b_{\mathrm{R}}^{\mathrm{I}}=-45,b_{\mathrm{F}}^{\mathrm{I}}=-76.$$

(27)

Taking into account the U(1)${}_{X^{\prime }}$ and U(1)${}_F$ charges and respective multiplicities also in Equation (20), the slopes of the RGEs of the Abelian inverse structure constants read as

$$b_{{\mathrm{X}}^{\prime }}^{{}^{\prime }\mathrm{I}}=b_{\mathrm{F}}^{{}^{\prime }\mathrm{I}}=-234.$$

(28)

while U(1)${}_{X^{\prime }}$ and U(1)${}_F$ are considered to be trivially embedded into ${\mathrm{E}}_8$.

2.

The second region corresponds to the stage after the three Wilson lines $<{\varphi }_{1,2,3}>$ give VEVs to the SM singlet directions. The gauge group after this stage is that of the SM, and as discussed above, we only study the following possibilities:

• A scalar sector with either two or three Higgs doublets that we denote as $\mathrm{H}$ in what follows;
• New exotic quarks containing either none or up to three generations of $\mathrm{SU}{\left(2\right)}_{\mathrm{L}}$ doublet VLQs denoted as ${\mathrm{Q}}_{\mathrm{V}}$;
• New exotic up-type quarks containing either none or up to three generations of $\mathrm{SU}{\left(2\right)}_{\mathrm{L}}$ singlet VLQs and denoted as ${\mathrm{U}}_{\mathrm{V}}$;
• New exotic down-type quarks containing either none or up to three generations of $\mathrm{SU}{\left(2\right)}_{\mathrm{L}}$ singlet VLQs and denoted as ${\mathrm{D}}_{\mathrm{V}}$;
• New exotic leptons containing either none or up to three generations of $\mathrm{SU}{\left(2\right)}_{\mathrm{L}}$ doublet VLLs denoted as ${\mathrm{L}}_{\mathrm{V}}$;
• New exotic leptons containing either none or up to three generations of $\mathrm{SU}{\left(2\right)}_{\mathrm{L}}$ singlet VLLs denoted as ${\mathrm{E}}_{\mathrm{V}}$.

Note that the choice of including up to three generations of vector-like fermions in the low-energy spectrum is not arbitrary. To see this, let us consider the possible bilinear terms involving the red and blue fields in Equation (20) that can be cast as

$$\begin{array}{cc}\hfill \sum _{i=1}^3\sum _{k=1}^2& \hfill \left({\mu }_{ik}{F}_i{\overline{F}}_k+{\mu }_{ik}^{\prime }{f}_i{\overline{f}}_k+{\mu }_{ik}^{″}{F}_i^c{\overline{F}}_k^c+{\mu }_{ik}^{‴}{f}_i^c{\overline{f}}_k^c\right).\hfill \end{array}$$

(29)

If we specialize on the first term, we can write a $5\times 5$ mass matrix in the basis $\left\{F_1,F_2,F_3,{\overline{F}}_1,{\overline{F}}_2\right\}$ as

$${\mathit{m}}_{\mathrm{F}}=\left(\begin{array}{ccccc}0& 0& 0& {\mu }_{11}& {\mu }_{12}\\ 0& 0& 0& {\mu }_{21}& {\mu }_{22}\\ 0& 0& 0& {\mu }_{31}& {\mu }_{32}\\ {\mu }_{11}& {\mu }_{21}& {\mu }_{31}& 0& 0\\ {\mu }_{12}& {\mu }_{22}& {\mu }_{32}& 0& 0\end{array}\right),$$

(30)

whose rank is 4. Furthermore, and assuming ${\mu }_{ik}$ real for illustration purposes, we see that $m_{\mathrm{F}}^2=m_{\mathrm{F}}·m_{\mathrm{F}}^{†}$ has two degenerate eigenvalues which means that in the mass basis, we end up with one massless chiral fermion F as well as two vector-like states $F_{\mathrm{V}}^1$ and $F_{\mathrm{V}}^2$. Inspired by the unified origin of our model under ${\mathrm{E}}_8$, in the limit where all ${\mu }_{ik}$ can be thought as approximately degenerate, one can write

$${\mu }_{ik}=\mu +ϵm_{ik},$$

(31)

where for $ϵ\ll 1$ the squared masses read as

$$m_F^2=0m_{F_{\mathrm{V}}^1}^2=0+\mathcal{O}\left({ϵ}^2\right)m_{F_{\mathrm{V}}^2}^2=6{\mu }^2+\mathcal{O}\left(ϵ\right).$$

(32)

This implies that, for a $\mu$ of the order of the compactification scale and for sufficiently small $ϵ$, we can have $m_{F_{\mathrm{V}}^1}\ll m_{F_{\mathrm{V}}^2}$. In turn, it may result in up to two generations of vector-like fermions of the type $F_{\mathrm{V}}^1$ not far from the TeV scale. Note that both $F_i$ and ${\overline{F}}_k$ are $\mathrm{SU}{\left(2\right)}_{\mathrm{F}}$ doublets and so is $F_{\mathrm{V}}^1$. The exact same reasoning can be applied to the ${\mu }_{ik}^{\prime }$, ${\mu }_{ik}^{″}$ and ${\mu }_{ik}^{‴}$ yielding up to two generations of the Pati–Salam fermions $F_{\mathrm{V}}^{1c}$ and up to one generation of $f_{\mathrm{V}}^1$ and $f_{\mathrm{V}}^{1c}$, motivating our choices in the bullet points above. Note that the $\mathrm{SU}{\left(2\right)}_{\mathrm{L}}$ doublet VLQs, ${\mathrm{Q}}_{\mathrm{V}}$, and VLLs ${\mathrm{L}}_{\mathrm{V}}$ belong to $F_{\mathrm{V}}$ (two generations) and $f_{\mathrm{V}}$ (one generation), while their singlet counterparts, ${\mathrm{U}}_{\mathrm{V}}$, ${\mathrm{D}}_{\mathrm{V}}$ and ${\mathrm{E}}_{\mathrm{V}}$ are embedded in $F_{\mathrm{V}}^c$ and $f_{\mathrm{V}}^c$. Similarly, all chiral matter belongs to the massless eigenstates and transforms according to the blue quantum numbers in Equation (20).

With this in mind, the coefficients of the $G_{SM}$ RGEs read as

$$\begin{array}{cc}\hfill b_{\mathrm{C}}^{\mathrm{II}}& =11-\frac{2}{3}\left(6+n_{\mathrm{Q}}\mathrm{V}+\frac{n_{\mathrm{D}}\mathrm{V}}{2}+\frac{n_{\mathrm{U}}\mathrm{V}}{2}\right),\hfill \\ \hfill b_{\mathrm{L}}^{\mathrm{II}}& =\frac{22}{3}-\frac{1}{3}\left(\frac{n_{\mathrm{H}}}{2}+1\right)-\frac{2}{3}\left(6+\frac{n_{\mathrm{L}}\mathrm{V}}{2}+3\frac{n_{\mathrm{Q}}\mathrm{V}}{2}\right),\hfill \\ \hfill b_{\mathrm{Y}}^{\mathrm{II}}& =-\frac{1}{3}\left(\frac{11}{4}+\frac{n_{\mathrm{H}}}{16}\right)-\frac{2}{3}\left(\frac{11}{4}+\frac{n_{\mathrm{D}}\mathrm{V}}{36}+\frac{n_{\mathrm{E}}\mathrm{V}}{4}+\frac{n_{\mathrm{L}}\mathrm{V}}{16}+\frac{n_{\mathrm{Q}}\mathrm{V}}{144}+\frac{n_{\mathrm{U}}\mathrm{V}}{9}\right),\hfill \end{array}$$

(33)

with the various $n_{\mathrm{X}}$, encoding the number of extra Higgs and vector-like fermions at the low scale according to the label $\mathrm{X}=\mathrm{H},{\mathrm{Q}}_{\mathrm{V}},{\mathrm{U}}_{\mathrm{V}},{\mathrm{D}}_{\mathrm{V}},{\mathrm{L}}_{\mathrm{V}},{\mathrm{E}}_{\mathrm{V}}$.

3.

Finally, we consider a third region below the mass threshold of the vector-like fermions and where the only New Physics states are either one or two additional Higgs doublets, i.e., a 2HDM or a 3HDM EW-scale theory. Note that the presence of three Higgs doublets can be advantageous for the generation of a realistic CKM mixing in the quark sector as discussed in refs. [16,17]. With this in mind, the beta-function coefficients in this region are

$$\begin{array}{cc}\hfill b_{\mathrm{C}}^{\mathrm{III}}& =7,\hfill \\ \hfill b_{\mathrm{L}}^{\mathrm{III}}& =\frac{10}{3}-\frac{1}{3}\left(\frac{n_{\mathrm{H}}}{2}+1\right),\hfill \\ \hfill b_{\mathrm{Y}}^{\mathrm{III}}& =-\frac{11}{6}-\frac{1}{3}\left(\frac{n_{\mathrm{H}}}{16}+\frac{11}{4}\right).\hfill \end{array}$$

(34)

The U(1)${}_Y$ generators and the inverse structure constants matched at tree-level with those of the Pati–Salam theory read as

$${\mathrm{T}}_{\mathrm{Y}}=\sqrt{\frac{2}{3}}{\mathrm{T}}_{\mathrm{PS}}^{15}-{\mathrm{T}}_{\mathrm{R}}^3{\alpha }_{\mathrm{Y}}^{-1}={\displaystyle \frac{2}{3}}{\alpha }_{\mathrm{PS}}^{-1}+{\alpha }_{\mathrm{R}}^{-1},$$

(35)

resulting in the RGEs

$$\begin{array}{cc}\hfill {\alpha }_{\mathrm{Y}}^{-1}\left(\mu \right)& =\frac{2}{3}{\alpha }_{\mathrm{PS}}^{-1}\left({\mu }_8\right)+{\alpha }_{\mathrm{R}}^{-1}\left({\mu }_8\right)+\left(\frac{b_{\mathrm{PS}}^{\mathrm{I}}}{3\pi }+\frac{b_{\mathrm{R}}^{\mathrm{I}}}{2\pi }\right)log\left(\frac{{\mu }_{{}_{\mathrm{PS}}}}{{\mu }_8}\right)+\frac{b_{\mathrm{Y}}^{\mathrm{II}}}{2\pi }log\left(\frac{{\mu }_{{}_{\mathrm{VLF}}}}{{\mu }_{{}_{\mathrm{PS}}}}\right)\hfill \\ \hfill & +\frac{b_{\mathrm{Y}}^{\mathrm{III}}}{2\pi }log\left(\frac{\mu }{{\mu }_{{}_{\mathrm{VLF}}}}\right),\hfill \\ \hfill {\alpha }_{\mathrm{L}}^{-1}\left(\mu \right)& ={\alpha }_{\mathrm{L}}^{-1}\left({\mu }_8\right)+\frac{b_{\mathrm{L}}^{\mathrm{I}}}{2\pi }log\left(\frac{{\mu }_{{}_{\mathrm{PS}}}}{{\mu }_8}\right)+\frac{b_{\mathrm{L}}^{\mathrm{II}}}{2\pi }log\left(\frac{{\mu }_{{}_{\mathrm{VLF}}}}{{\mu }_{{}_{\mathrm{PS}}}}\right)+\frac{b_{\mathrm{L}}^{\mathrm{III}}}{2\pi }log\left(\frac{\mu }{{\mu }_{{}_{\mathrm{VLF}}}}\right),\hfill \\ \hfill {\alpha }_{\mathrm{C}}^{-1}\left(\mu \right)& ={\alpha }_{\mathrm{PS}}^{-1}\left({\mu }_8\right)+\frac{b_{\mathrm{PS}}^{\mathrm{I}}}{2\pi }log\left(\frac{{\mu }_{{}_{\mathrm{PS}}}}{{\mu }_8}\right)+\frac{b_{\mathrm{C}}^{\mathrm{II}}}{2\pi }log\left(\frac{\mu }{{\mu }_{{}_{\mathrm{VLF}}}}\right)+\frac{b_{\mathrm{C}}^{\mathrm{III}}}{2\pi }log\left(\frac{\mu }{{\mu }_{{}_{\mathrm{VLF}}}}\right),\hfill \end{array}$$

(36)

where ${\mu }_8\equiv \mathrm{\Lambda }$ is the orbifold compactification scale, ${\mu }_{{}_{\mathrm{PS}}}$ represents the Pati–Salam breaking scale via the Wilson line mechanismm whereas ${\mu }_{{}_{\mathrm{VLF}}}$ is the mass threshold scale at which all vector-like fermions are integrated out.

We have performed a scan over the number of vector-like fermion generations such that $0\le n_{\mathrm{X}}\le 3$ for $\mathrm{X}={\mathrm{Q}}_{\mathrm{V}},{\mathrm{U}}_{\mathrm{V}},{\mathrm{D}}_{\mathrm{V}},{\mathrm{L}}_{\mathrm{V}},{\mathrm{E}}_{\mathrm{V}}$ and additional Higgs doublets $0\le n_{\mathrm{H}}\le 1$, i.e., considering a scalar $(n_{\mathrm{H}}+2)$ HDM sector. In addition, we have selected two possible cases: one where ${\mu }_{{}_{\mathrm{VLF}}}=1\mathrm{TeV}$ and so the new VLLs and VLQs may be at the reach of the LHC (see ref. [73] for a recent study on VLLs phenomenology in the GUT context) and another where ${\mu }_{{}_{\mathrm{VLF}}}=10\mathrm{TeV}$, which may only be accessible at future colliders. Defining as valid low-scale models (we call each set of $(n_{\mathrm{X}},n_H,{\mu }_{{}_{\mathrm{VLF}}})$ a “model”) those that are compatible with an exact unification of all gauge interactions at the ${\mathrm{E}}_8$ breaking scale ${\mu }_8$, we have found that there are only 17 such models ($(n_{\mathrm{X}},n_H,{\mu }_{{}_{\mathrm{VLF}}})$ sets). Of those, 3 work for the case where ${\mu }_{{}_{\mathrm{VLF}}}=1\mathrm{TeV}$, while only 4 do so for the case where ${\mu }_{{}_{\mathrm{VLF}}}=10\mathrm{TeV}$. Our results are presented in

Table 3. Benchmark models consistent with the unification of gauge couplings at ${\mu }_8$ for ${\mu }_{{}_{\mathrm{VLF}}}=1\mathrm{TeV}$. All three viable scenarios have $n_{\mathrm{Q}}\mathrm{V}=0$ and $n_{\mathrm{H}}=1$.

Model	${log}_{10}\frac{{\mathit{\mu }}_8}{\mathbf{GeV}}$	${log}_{10}\frac{{\mathit{\mu }}_{{}_{\mathbf{PS}}}}{\mathbf{GeV}}$	${\mathit{\alpha }}_8^{-1}\left({\mathit{\mu }}_8\right)$	${\mathit{n}}_{\mathbf{H}}$	${\mathit{n}}_{{\mathbf{U}}_{\mathbf{V}}}$	${\mathit{n}}_{{\mathbf{D}}_{\mathbf{V}}}$	${\mathit{n}}_{{\mathbf{L}}_{\mathbf{V}}}$	${\mathit{n}}_{{\mathbf{E}}_{\mathbf{V}}}$
1	$18.33$	$18.24$	$44.96$	1	1	0	0	2
2	$18.68$	$17.77$	$31.12$	1	1	0	0	3
3	$18.56$	$17.93$	$35.64$	1	0	1	0	3

and

Table 4. Benchmark models consistent with the unification of gauge couplings at ${\mu }_8$ for ${\mu }_{{}_{\mathrm{VLF}}}=10\mathrm{TeV}$. All viable scenarios have $n_{\mathrm{Q}}\mathrm{V}=0$. Models 5 and 6 share the same field content as Models 2 and 3 in Table 3.

Model	${log}_{10}\frac{{\mathit{\mu }}_8}{\mathbf{GeV}}$	${log}_{10}\frac{{\mathit{\mu }}_{{}_{\mathbf{PS}}}}{\mathbf{GeV}}$	${\mathit{\alpha }}_8^{-1}\left({\mathit{\mu }}_8\right)$	${\mathit{n}}_{\mathbf{H}}$	${\mathit{n}}_{{\mathbf{U}}_{\mathbf{V}}}$	${\mathit{n}}_{{\mathbf{D}}_{\mathbf{V}}}$	${\mathit{n}}_{{\mathbf{L}}_{\mathbf{V}}}$	${\mathit{n}}_{{\mathbf{E}}_{\mathbf{V}}}$
4	$19.07$	$18.66$	$41.03$	0	0	1	0	1
5	$18.30$	$17.84$	$38.54$	1	1	0	0	3
6	$18.19$	$17.98$	$42.77$	1	0	1	0	3
7	$18.98$	$18.80$	$41.58$	0	2	0	1	3

.

We limit the scan to solutions where gauge coupling unification happens below the Planck scale $M_P=1.22\times {10}^{19}\mathrm{GeV}$, to avoid potentially significant corrections from quantum gravity.

We have found that at least one generation of $\mathrm{SU}{\left(2\right)}_{\mathrm{L}}$ singlet VLQs and VLLs is needed (Model 4), while none of the viable scenarios allow for $\mathrm{SU}{\left(2\right)}_{\mathrm{L}}$ doublet VLQs and only one (Model 7) do so for doublet VLLs in the low-energy scale spectrum. Model 7 is also the only one with more than one generation of ${\mathrm{U}}_{\mathrm{V}}$ VLQs. The compactification scale always satisfies ${\mu }_8>{10}^{18}\mathrm{GeV}$, while the Wilson line scale ${\mu }_{{}_{\mathrm{PS}}}>{10}^{17.7}\mathrm{GeV}$, not too far from ${\mu }_8$. The value of the universal ${\mathrm{E}}_8$ gauge coupling is also limited to a small range $33\lesssim {\alpha }_8^{-1}\left({\mu }_8\right)\lesssim 45$. Finally, we show in Figure 1 six representative examples of Models 1, 2 and 3 for the case of ${\mu }_{{}_{\mathrm{VLF}}}=1\mathrm{TeV}$ and Models 4, 6 and 7 for the case of ${\mu }_{{}_{\mathrm{VLF}}}=10\mathrm{TeV}$, whereas in Figure 2, we show how the gauge couplings evolve between the $E_8$ and the $G_{PS}$ scales. Notice that in such a region, the only difference resides in the starting ${\mu }_8$ and stopping ${\mu }_{\mathrm{PS}}$ scales as shown in Table 3 and Table 4, while the coefficients of the beta functions are the same for all considered models. In particular, the coefficient of the $\mathrm{SU}{\left(2\right)}_{\mathrm{L}}$ and $\mathrm{SU}{\left(2\right)}_{\mathrm{R}}$ gauge couplings are identical $b_{\mathrm{L}}^{\mathrm{I}},\mathrm{R}=-45$, while that of $\mathrm{SU}{\left(4\right)}_{\mathrm{PS}}$ is $b_{\mathrm{PS}}^{\mathrm{I}}=-43$, thus closely superimposed with the latter two.

6. Conclusions

In this paper, as a further development of the previous work by some of the authors [52], we have classified for the first time possible anomaly-free realisations of non-minimal Pati–Salam GUts emerging in four dimensions and studied the corresponding gauge couplings’ unification under the ${\mathrm{E}}_8$ symmetry in ten dimensions. The 10-dimensional theory contains one vector $\mathbf{248}$ as well as five chiral $\mathbf{248}$-plets. The four-dimensional limit of the ${\mathrm{E}}_8$ theory upon ${\mathbb{Z}}_6\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2$ orbifold compactification contains massless zero modes that can describe all SM gauge fields, chiral matter and right-handed neutrinos. We have shown that in the limit of approximately degenerate superpotential mass parameters, our Pati–Salam GUT can naturally contain vector-like fermions at low-energy scales and at the reach of LHC or future collider experiments. In particular, the unification of the gauge couplings under ${\mathrm{E}}_8$ requires that such exotic fermions can either be $\mathrm{SU}{\left(2\right)}_{\mathrm{L}}$ singlet VLQs or both singlet and doublet VLLs. In total, we have found 7 viable models with New Physics manifest at $1\mathrm{TeV}$ or at $10\mathrm{TeV}$, making our model falsifiable at the LHC or future colliders.