Inextensible Flows of Null Cartan Curves in Minkowski Space
Abstract
1. Introduction
2. The Geometric Concepts of Null Curves in Minkowski Space
- .
- .
3. Main Results
4. The Method of Construction Family of Inextensible Null Cartan Curves in
- Step 1.
- We choose specific values of the velocity functions (certain values of velocities are based on physical phenomena, such as the motion of vortex filaments, where the normal velocity equals the curvature of the curve). Then, we substitute these values of the velocity functions into (38) to obtain the general solution that represents the torsion of the (NCC).
- Step 2.
- As soon as we determine the torsion, we substitute it into (3) and solve the system numerically with specific initial conditions for .
- Step 3.
- Solve the (PDEs) systems (20) numerically by using specific initial conditions that are given as the numerical results obtained from Step. 2 for .
- Step 4.
- To validate the solutions, we can use the Cartan frame properties provided by Definition 4.
- Step 5.
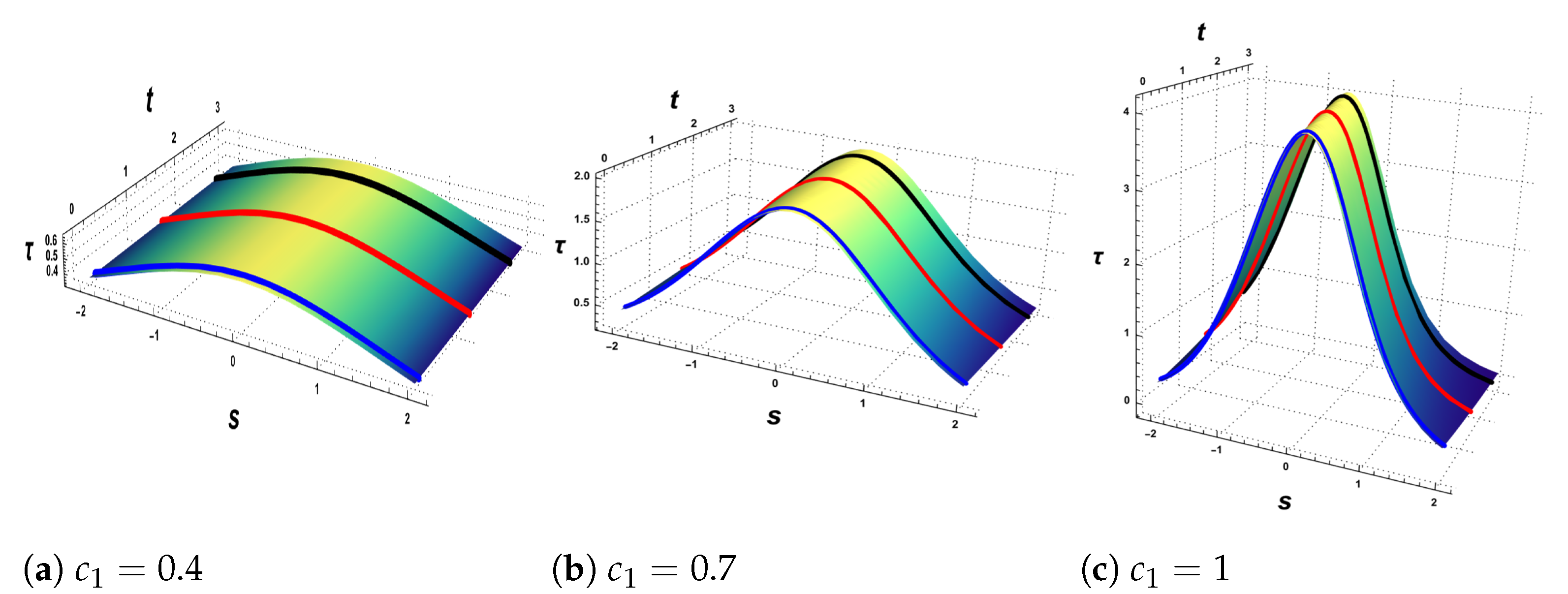
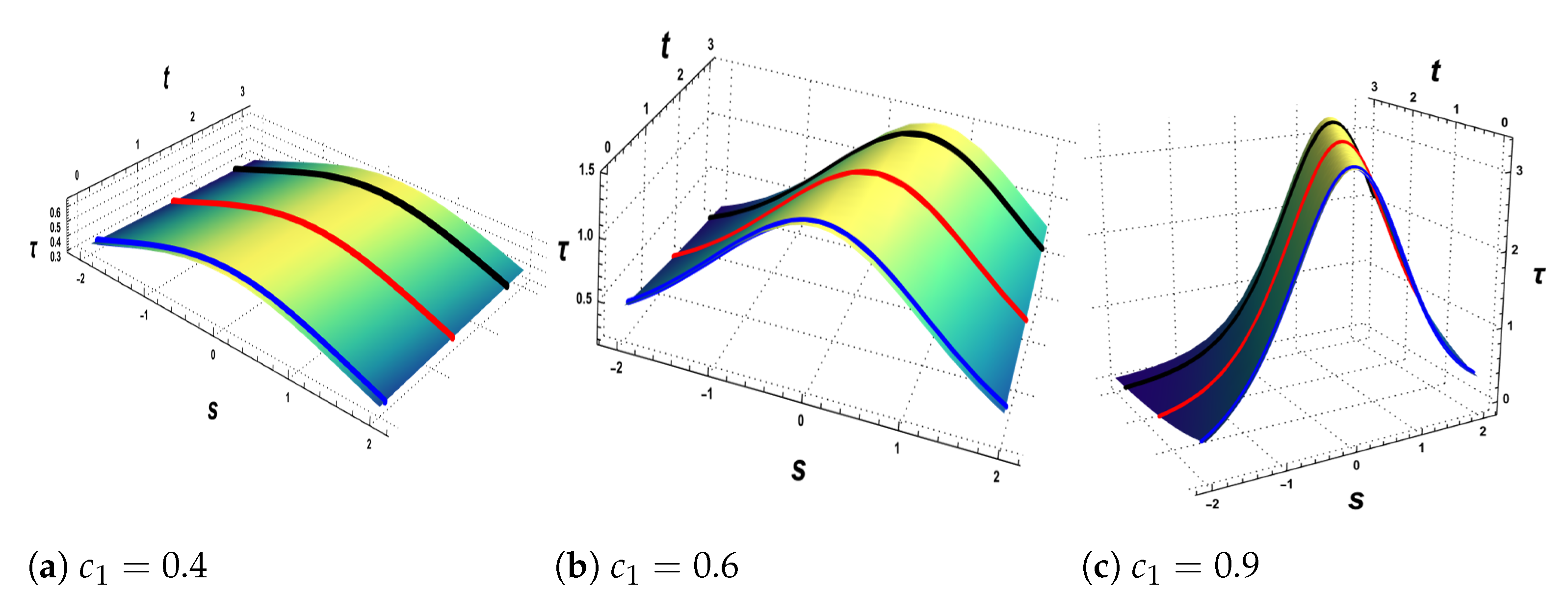
- Now, we have the null Cartan curve at every point , then we can graph the family of (IFNCC) and visualize the surface generated by this family.
- Step 6.
A Model of Construction of the Family of Inextensible Null Cartan Curves
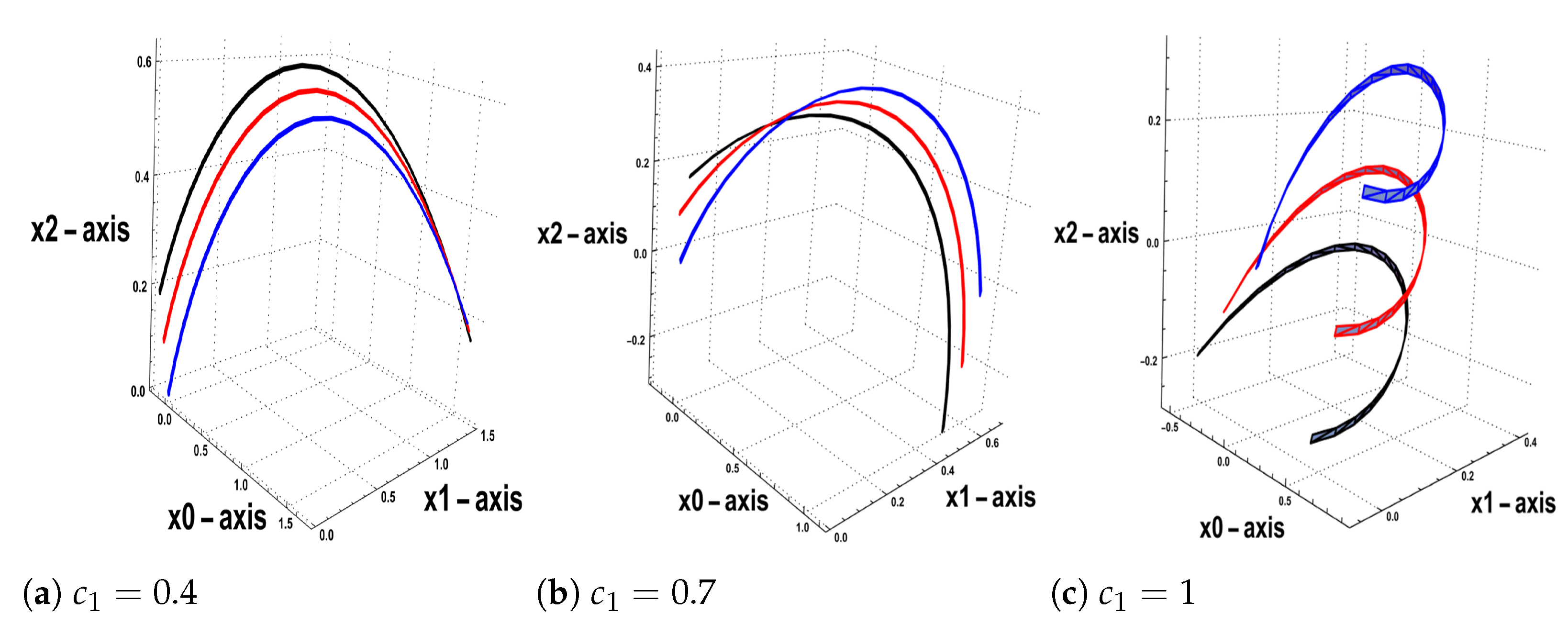
5. Graphical Interpretations
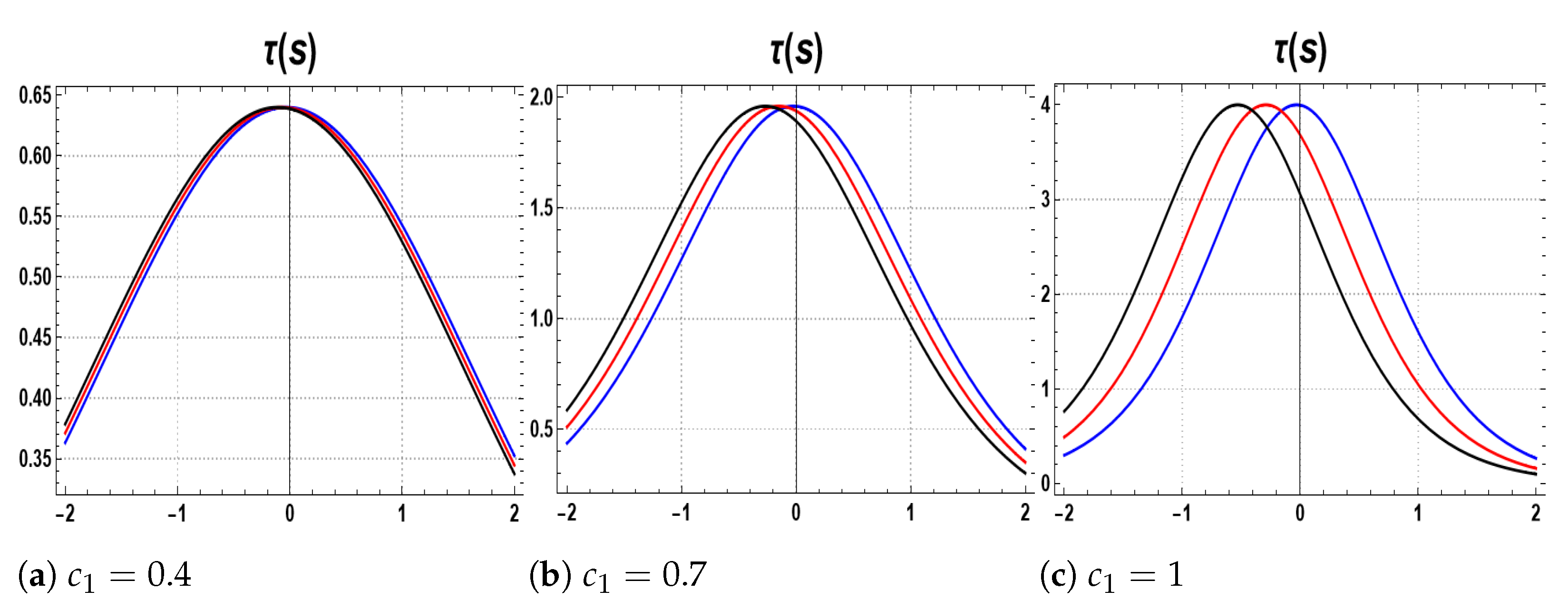
- Case 1: Consider the binormal velocity . The shape in Figure 1a for the soliton solutions with does not vary for different values of the time at . The shape in Figure 1b, for the soliton solutions with does not change at different values of the time , but there is a little shift to the left while as time increases. The shape in Figure 1c, for the soliton solutions with for does not change by increasing the time , respectively, and there is a slight shift to the left. The soliton solutions represent the torsion of the family of (NCC) and by increasing the amplitude, the torsion will increase, and it has the following maximum values:
- (a)
- For , the torsion has maximum value at and .
- (b)
- For , the torsion has maximum value at and .
- (c)
- For , the torsion has maximum value at and .
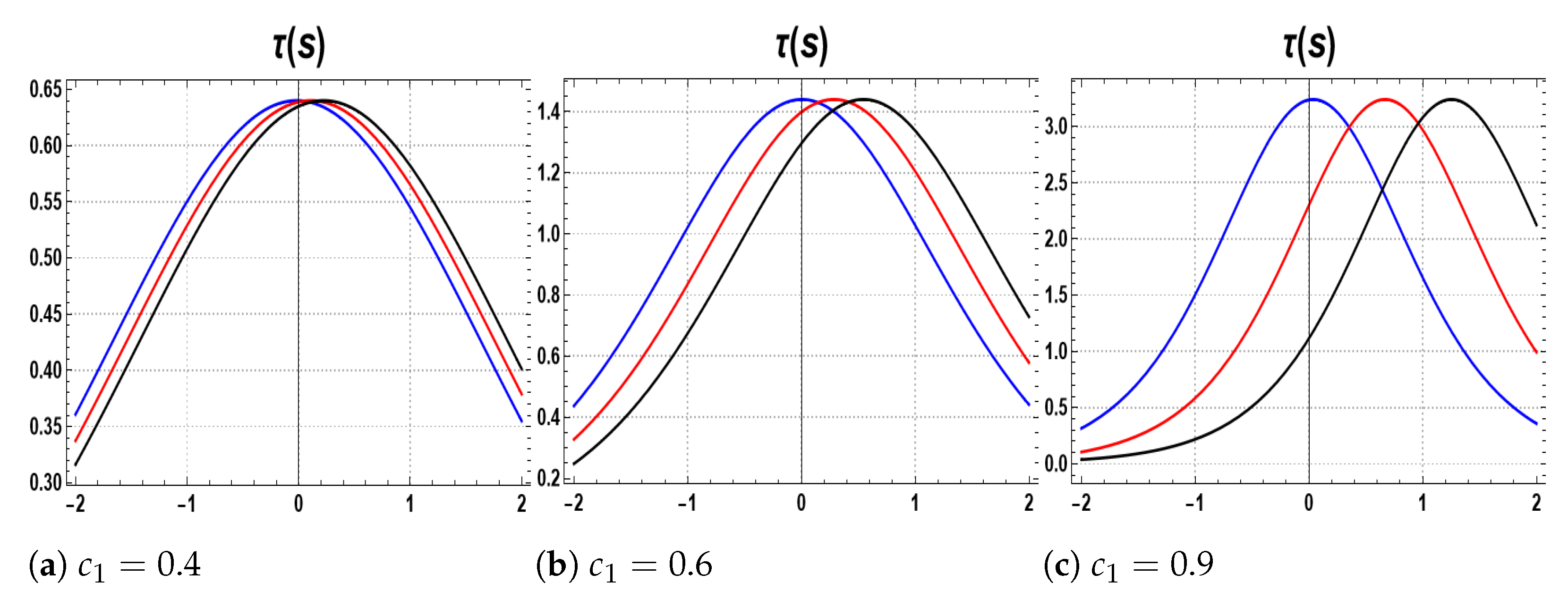
- Case 2: Consider the binormal velocity . The shape in Figure 2a, of the soliton solutions at does not change for different values of the time at . The shape in Figure 2b for the soliton solutions at does not change at different values of the time , respectively, but there is a slight shift to the right while the time increases. In Figure 2c, for , the shape does not vary with increasing the time , respectively, and there is a slight shift to the right. The soliton solutions represent the torsion of the family of the (NCC) and by increasing the amplitude, the torsion will increase, and it has the following maximum values:
- (a)
- For , the torsion has maximum value at and .
- (b)
- For , the torsion has maximum value at and .
- (c)
- For , the torsion has maximum value at and .
- The choice of the value of the amplitude affects the properties of the vectors T, N, and B for the Cartan frame, where it can be used to verify the numerical solutions.
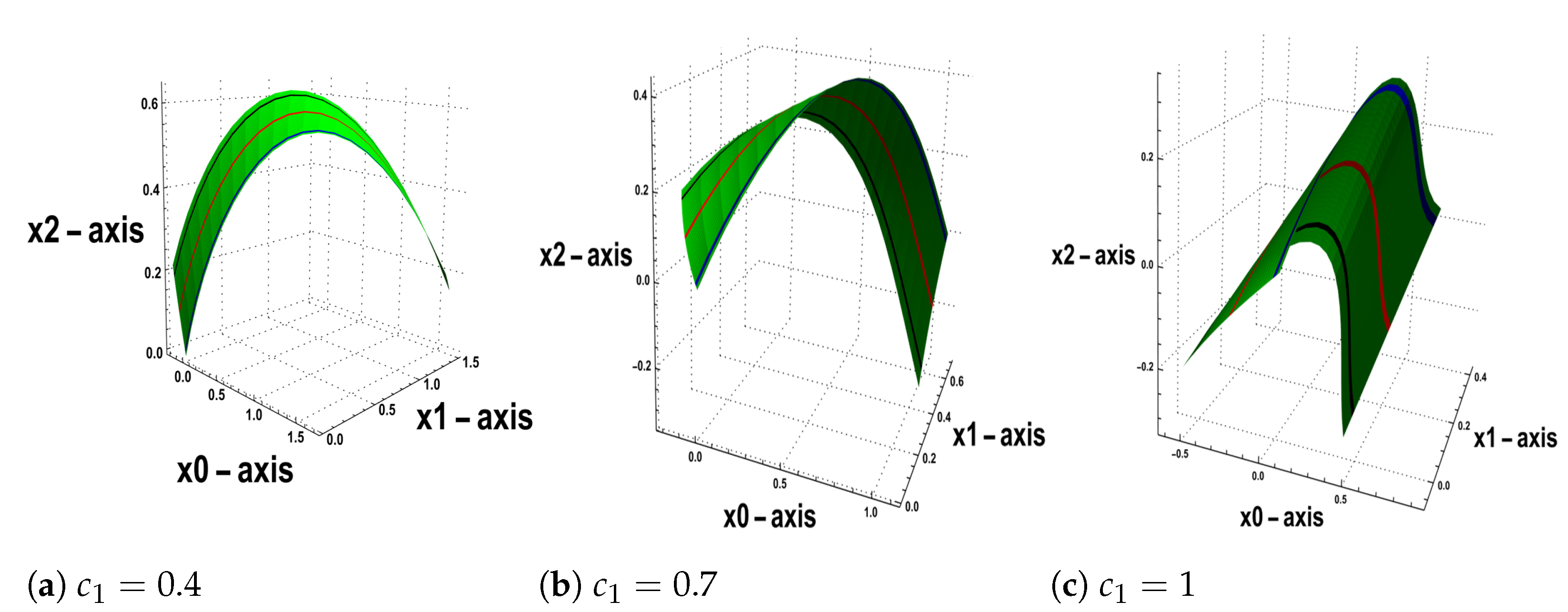
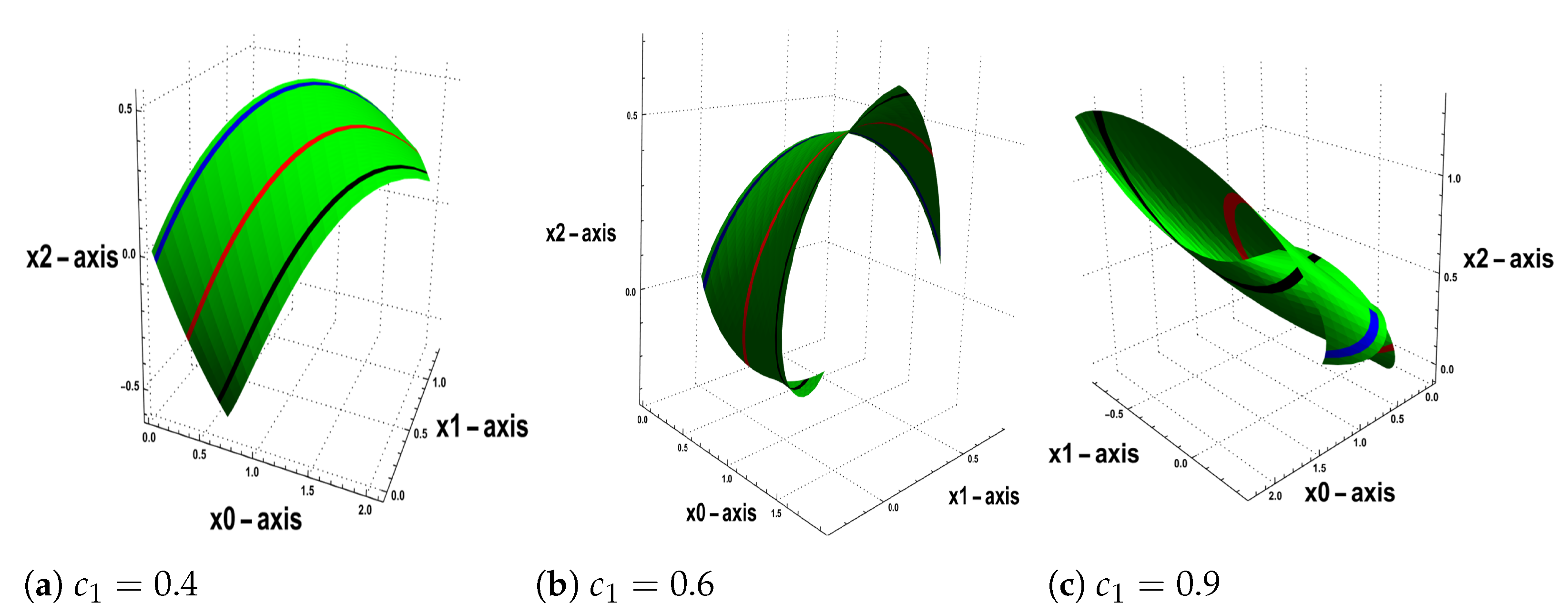
6. The Geometric Description of the Constructed Surface
7. Inextensible Flows of Null Cartan Curve Specified by Acceleration Fields
8. Application on Inextensible Flows of Null Cartan Curve Specified by Normal Acceleration
9. Discussion
10. Conclusions
- The (TEE) for the pseudo arclength of the null Cartan curve is obtained, and the necessary and sufficient conditions for the null Cartan curve (NCC) to be inextensible are derived. These conditions show that the tangential velocity () and the normal velocity () are dependent on the binormal velocity () and on the torsion () by (16).
- The (TEE) for the torsion is obtained in terms of the velocities (38).
- The flows of inextensible (NCC) is constructed, and we present a novel model to describe the process of constructing this family of (IFNCC) with velocities and . In this model, the (TEE) of the torsion of the inextensible (NCC) appears in the form of the Korteweg-de Vries (K-dV) equation. We obtain the soliton solutions for the (K-dV) equation, and we graph these solitons for different time values with certain amplitudes. By using the value of the torsion, we visualize the flows of the initial (NCC), then we visualize the generated surface of these flows for different values of the constant velocity and various amplitudes. Additionally, we compute the first and second fundamental quantities for the generated surface, as well as the Gaussian curvature G and mean curvature H (49), (50) and (51), respectively.
- We provided an application for the inextensible flows of (NCC) with constant normal acceleration. In this application, the time evolution equation of torsion arising as a first order (PDE) given by (59). It is known as the transport equation, and it has the general solution given (60). In addition, in this application, the flows of the (NCC) satisfy (PDE) (61), and it represents a one-dimensional wave equation, and it has the general solution of the form (62).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IF | Inextensible Flows |
| IFC | Inextensible Flow(s) of Curve(s) |
| IFNCC | Inextensible Flows of Null Cartan Curve |
| NCC | Null Cartan Curve |
| PDE(s) | Partial Differential Equation(s) |
| TEE(s) | Time Evolution Equation(s) |
References
- Balakrishnan, R.; Blumenfeld, R. Transformation of general curve evolution to a modified Belavin–Polyakov equation. J. Math. Phys. 1997, 38, 5878. [Google Scholar] [CrossRef]
- Lakshmanan, M.; Ruijgrok, T.W.; Thompson, C.J. On the dynamics of a continuum spin system. Phys. A Stat. Mech. Its Appl. 1976, 84, 577–590. [Google Scholar] [CrossRef]
- Frédéric, C. Geometric Curve Evolution and Image Processing; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Chirikjian, G.S.; Burdick, J.W. Kinematics of hyper-redundant manipulation. In Proceedings of the ASME Mechanisms Conference, Chicago, IL, USA, 16–19 September 1990; pp. 391–396. [Google Scholar]
- Desbrun, M.; Cani, M.-P. Active implicit surface for animation. In Proceedings of the Graphics Interface 1998 Conference, Vancouver, BC, Canada, 18–20 June 1998; pp. 143–150. [Google Scholar]
- Kass, M.; Witkin, A.; Terzopoulos, D. Snakes: Active contour models. Int. J. Comput. Vision 1988, 1, 321–331. [Google Scholar] [CrossRef]
- Schief, W.K.; Rogers, C. Binormal motion of curves of constant curvature and torsion, generation of soliton surfaces. Proc. R. Soc. Lond. A 1999, 455, 3163–3188. [Google Scholar] [CrossRef]
- Baş, S.; Körpınar, T. Inextensible flows of spacelike curves on spacelike surfaces according to Darboux Frame in . Bol. Soc. Paran. Mat. 2013, 31, 9–17. [Google Scholar] [CrossRef]
- Abdel-All, N.H.; Gaber, S.; Al-Dossary, M.T. Evolution of a generalized Space Curve as a function of Its Local Geometry. Appl. Math. 2014, 5, 2381–2392. [Google Scholar] [CrossRef]
- Gaber, S. Explicit Examples of Motions of Inextensible Curves in Spherical Space S3. Appl. Math. Inf. Sci. Lett. 2014, 2, 77–83. [Google Scholar]
- Gaber, S. Inextensible flows of spacelike curves in De-Sitter Space S2,1. Appl. Math. Inf. Sci. Lett. 2018, 6, 75–83. [Google Scholar]
- Gürbüzü, N. Inextensible Flows of spacelike, timelike and null curves. Int. J. Contemp. Math. Sci. 2009, 4, 1599–1604. [Google Scholar]
- Körpinar, T. A New method for inextensible flows of timelike curves in Minkowski Space-Time . Int. J. Partial. Differ. Equations 2014, 2014, 517070. [Google Scholar] [CrossRef]
- Uçum, A.; Erdem, H.A.; Ílarslan, K. Inextensible flows of partially null and pseudo null curves in semi-Euclidean 4-space with index 2. Novi Sad J. Math. 2016, 46, 115–129. [Google Scholar] [CrossRef]
- Yıldız, Ö.G.; Tosun, M. A Note on evolution of curves in the Minkowski Spaces. Adv. Appl. Clifford Algebras 2017, 27, 2873–2884. [Google Scholar] [CrossRef]
- Yoon, D.W.; Yüzbaşi, Z.K.; Aslan, E.C. Evolution of space-like curves and special time-like ruled surfaces in the Minkowski space. Indian J. Phys. 2019, 96, 995–999. [Google Scholar] [CrossRef]
- Gaber, S. New models of normal motions of the inextensible curves according to type-1 Bishop frame in . Int. J. Geom. Methods Mod. Phys. 2021, 18, 2150009. [Google Scholar] [CrossRef]
- Körpinar, T. On the Fermi–Walker derivative for inextensible flows. Zeitschrift FÜr Naturforschung A 2015, 70, 477–482. [Google Scholar] [CrossRef]
- Körpinar, T. Bianchi Type-I Cosmological Models for Inextensible Flows of Biharmonic Particles by Using Curvature Tensor Field in Spacetime. Int. J. Theor. Phys. 2015, 54, 1762–1774. [Google Scholar] [CrossRef]
- Körpinar, Z.; Tuz, M.; Körpinar, T. New Electromagnetic Fluids Inextensible Flows of Spacelike Particles and some Wave Solutions in Minkowski Space-time. Int. J. Theor. Phys. 2016, 55, 8–16. [Google Scholar] [CrossRef]
- Körpinar, T. Tangent bimagnetic curves in terms of inextensible flows in space. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1950018. [Google Scholar] [CrossRef]
- Körpinar, T.; Baş, S. A new approach for inextensible flows of binormal spherical indicatrices of magnetic curves. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1950020. [Google Scholar] [CrossRef]
- Körpinar, T.; Demirkol, R.C.; Körpinar, Z. Approximate solutions for the inextensible Heisenberg antiferromagnetic flow and solitonic magnetic flux surfaces in the normal direction in Minkowski space. Optik 2021, 238, 166403. [Google Scholar] [CrossRef]
- Körpinar, T.; Demirkol, R.C.; Körpinar, Z. New analytical solutions for the inextensible Heisenberg ferromagnetic flow and solitonic magnetic flux surfaces in the binormal direction. Phys. Scr. 2021, 96, 085219. [Google Scholar] [CrossRef]
- Körpinar, T.; Demirkol, R.C.; Asil, V.; Körpinar, Z. Magnetic flux surfaces by the fractional Heisenberg antiferromagnetic flow of magnetic b-lines in binormal direction in Minkowski space. J. Magn. Magn. Mater. 2022, 549, 168952. [Google Scholar] [CrossRef]
- Körpinar, T.; Körpinar, Z.; Asil, V. Electric flux fibers with spherical antiferromagnetic approach with electroosmotic velocity. Optik 2022, 252, 168108. [Google Scholar] [CrossRef]
- Körpinar, T.; Sazak, A.; Körpinar, Z. Optical modeling of Hasimoto map for antiferromagnetic timelike optical fiber. Optik 2022, 251, 168302. [Google Scholar] [CrossRef]
- López, R.l. Differential geometry of curves and surfaces in Lorentz-Minkowski space. Int. Electron. J. Geom. 2014, 7, 44–107. [Google Scholar] [CrossRef]
- Muhammad, I.; Mihriban, K. A study on null cartan curve in Minkowski 3-space. Appl. Math. Nonlinear Sci. 2020, 5, 413–424. [Google Scholar] [CrossRef]
- Yavuz, A.; Erdoğdu, M. Some new properties of surfaces generated by Null Cartan curves. Int. Electron. J. Geom. 2022, 15, 116–131. [Google Scholar] [CrossRef]
- Honda, K.; Inoguchi, J.I. Deformations of Cartan framed null curves preserving the torsion. Differ. Geom. Dyn. Syst. 2003, 5, 31–37. [Google Scholar]
- Ekici, C.; Korpınar, T.; Unluturk, Y. An approach to characterizations of null curves lying in timelike ruled surfaces. Soft Comput. 2022. [Google Scholar] [CrossRef]
- Roshid, H.O. Novel solitary wave solution in shallow water and ion acoustic plasma waves in-terms of two nonlinear models via MSE method. J. Ocean. Eng. Sci. 2017, 2, 196–202. [Google Scholar] [CrossRef]
- Chen, Y.X.; Xiao, X.; Mei, Z.L. Optical soliton solutions of the (1+1)-dimensional space-time fractional single and coupled nonlinear Schrödinger equations. Results Phys. 2020, 18, 103211. [Google Scholar] [CrossRef]
- Bhowmik, R.K.; Al-Asad, M.F.; Karim, M.R. Soliton Solution of Korteweg-de Vries Equation. Int. J. Appl. Math. Stat. 2020, 4, 45–48. [Google Scholar]
- Xu, B.; Zhang, Y.; Zhang, S. Line Soliton Interactions for Shallow Ocean Waves and Novel Solutions with Peakon, Ring, Conical, Columnar, and Lump Structures Based on Fractional KP Equation. Adv. Math. Phys. 2021, 2021, 6664039. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaber, S.; Al Elaiw, A.
Inextensible Flows of Null Cartan Curves in Minkowski Space
Gaber S, Al Elaiw A.
Inextensible Flows of Null Cartan Curves in Minkowski Space
Gaber, Samah, and Abeer Al Elaiw.
2023. "Inextensible Flows of Null Cartan Curves in Minkowski Space
Gaber, S., & Al Elaiw, A.
(2023). Inextensible Flows of Null Cartan Curves in Minkowski Space




