Probing Modified Gravity Theories with Scalar Fields Using Black-Hole Images
Abstract
:1. Introduction
2. Shadow Radius of Compact Objects
2.1. Black Holes
2.2. Wormholes
3. The EHT Bounds
4. The Einstein-Scalar-GB Theory
4.1. Black Holes
4.1.1.
4.1.2.
4.1.3.
4.2. Wormholes
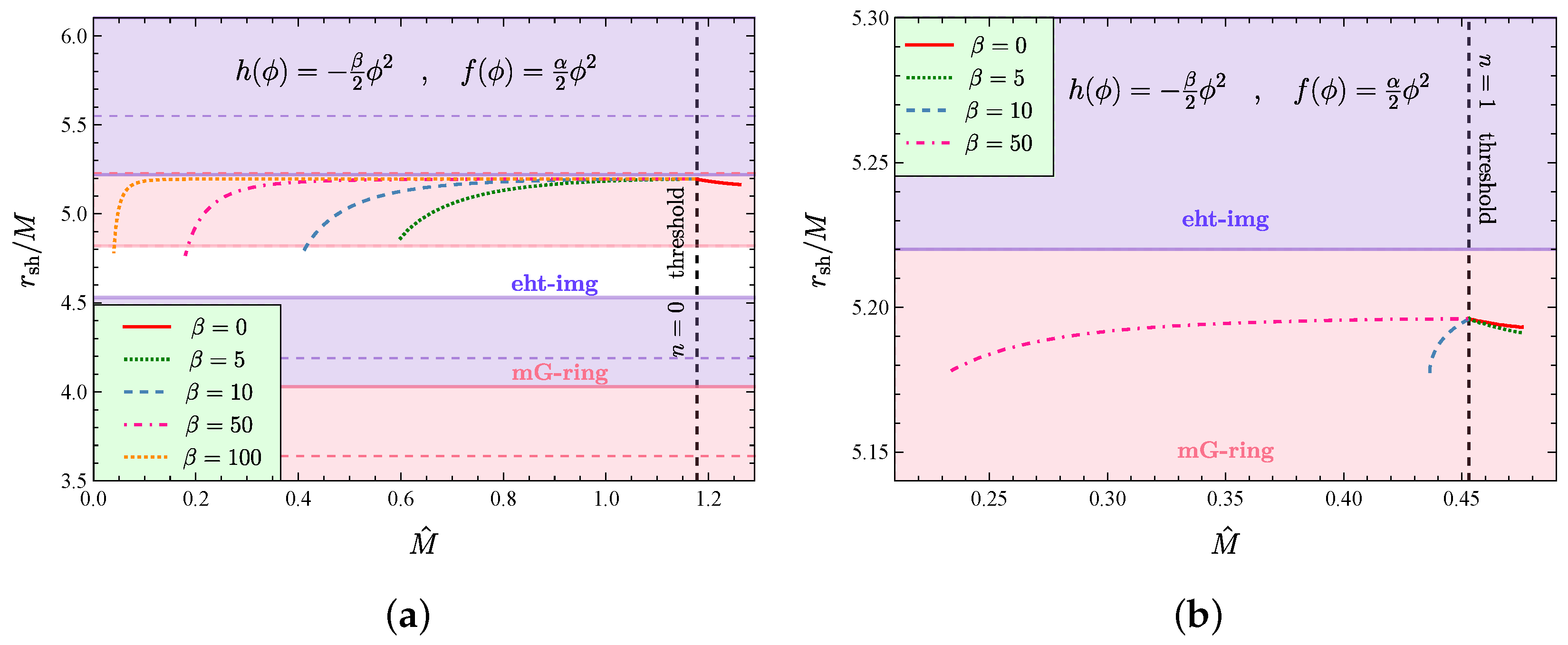
5. Curvature-Induced Spontaneous Scalarization
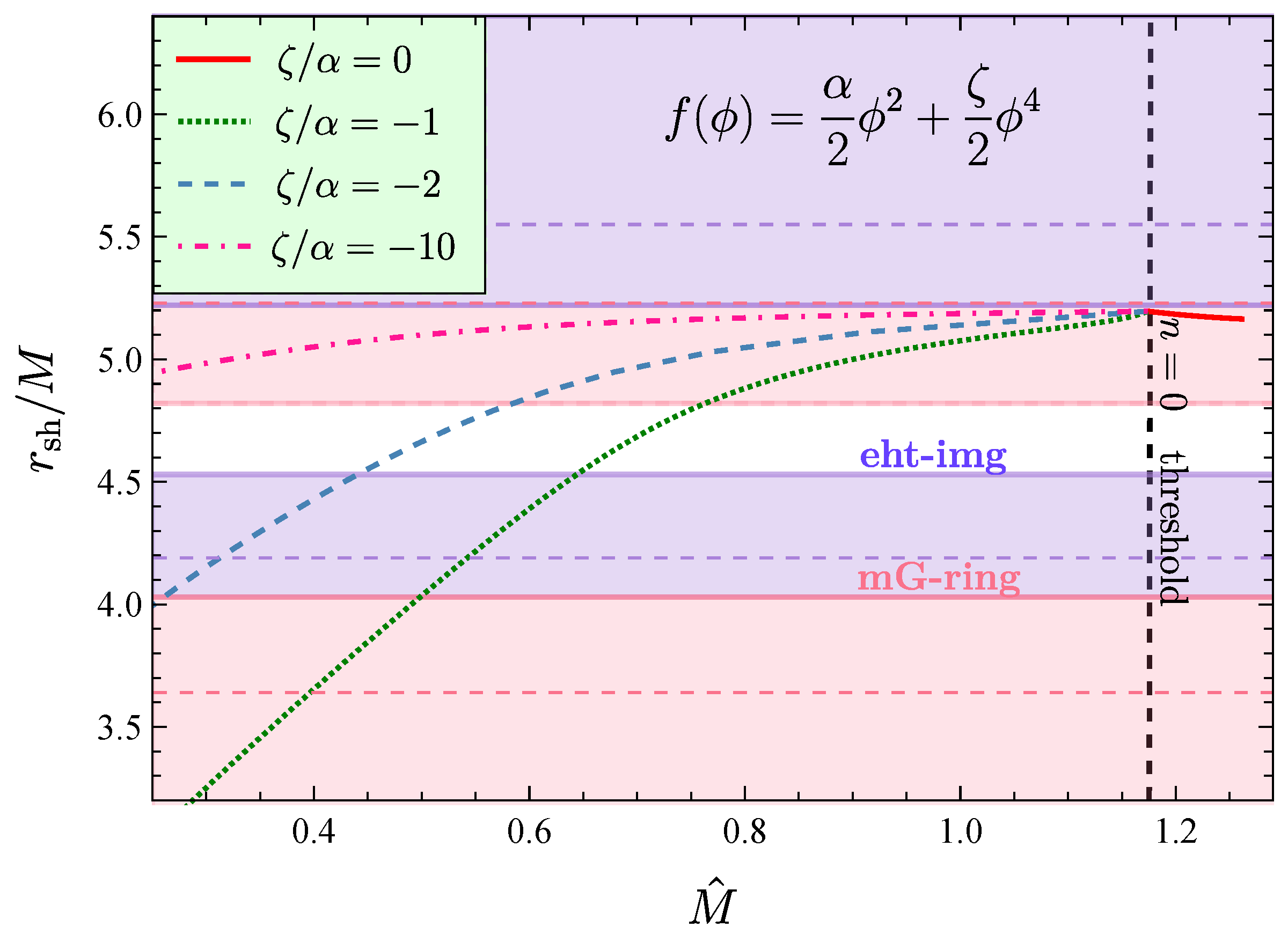
5.1. Minimal Model
5.2. Quartic sGB Coupling
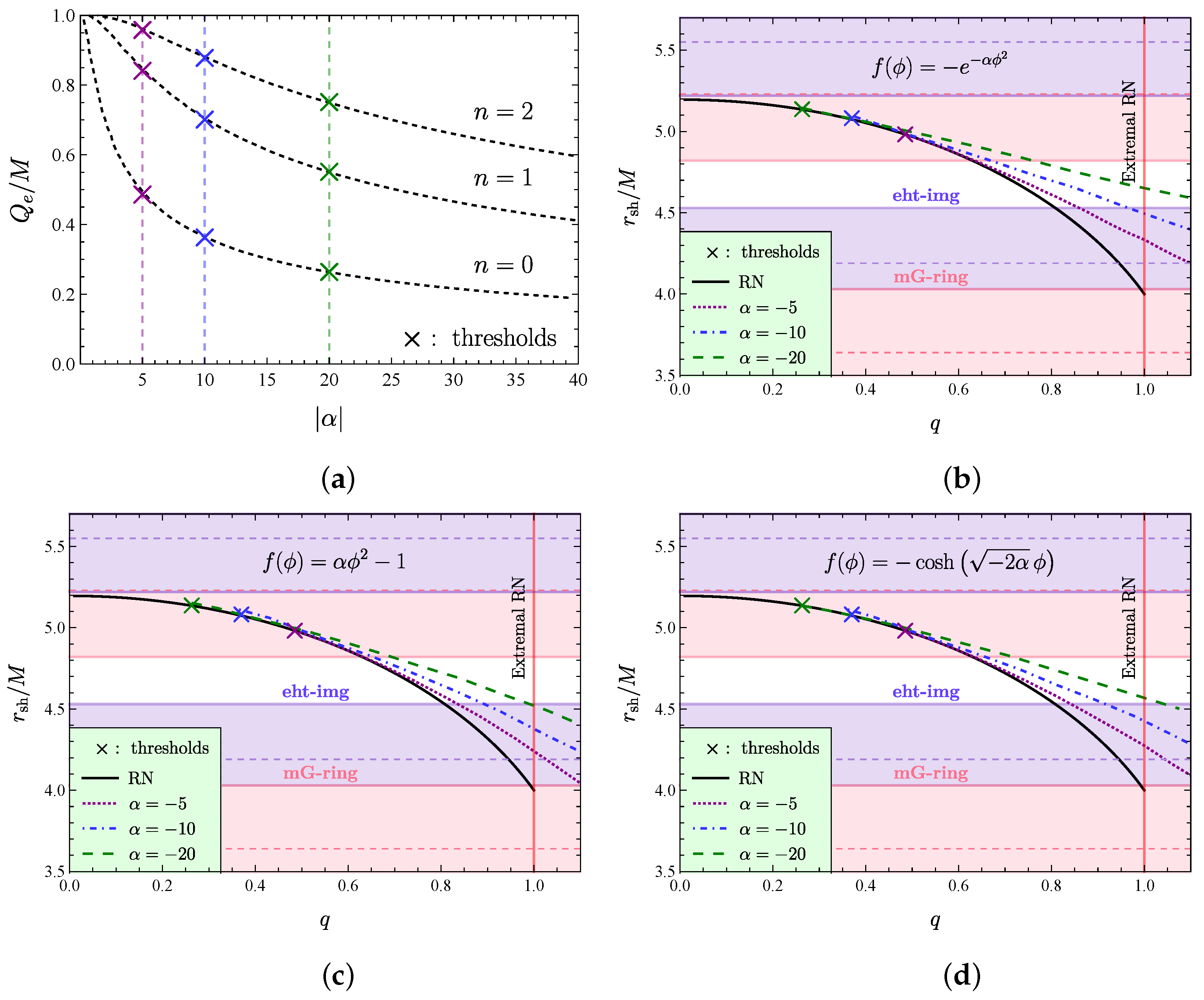
6. The Einstein–Maxwell-Scalar Theory
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Equations in EsRGB Theory
Appendix B. Equations in EMS Theory
| 1 |
References
- Bertotti, B.; Iess, L.; Tortora, P. A test of general relativity using radio links with the Cassini spacecraft. Nature 2003, 425, 374–376. [Google Scholar] [CrossRef] [PubMed]
- Stairs, I.H. Testing general relativity with pulsar timing. Living Rev. Rel. 2003, 6, 5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Verma, A.; Fienga, A.; Laskar, J.; Manche, H.; Gastineau, M. Use of messenger radioscience data to improve planetary ephemeris and to test general relativity. Astron. Astrophys. 2014, 561, A115. [Google Scholar] [CrossRef]
- Lambert, S.B.; Le Poncin-Lafitte, C. Improved determination of gamma by VLBI. Astron. Astrophys. 2011, 529, A70. [Google Scholar] [CrossRef] [Green Version]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; Wex, N.; Deller, A.T.; Coles, W.A.; Ali, M.; Burgay, M.A.R.T.A.; Camilo, F.; Cognard, I.; et al. Strong-Field Gravity Tests with the Double Pulsar. Phys. Rev. X 2021, 11, 041050. [Google Scholar] [CrossRef]
- Will, C.M. The Confrontation between General Relativity and Experiment. Living Rev. Rel. 2014, 17, 4. [Google Scholar] [CrossRef] [Green Version]
- Berti, E.; Barausse, E.; Cardoso, V.; Gualtieri, L.; Pani, P.; Sperhake, U.; Stein, L.C.; Wex, N.; Yagi, K.; Baker, T.; et al. Testing General Relativity with Present and Future Astrophysical Observations. Class. Quant. Grav. 2015, 32, 243001. [Google Scholar] [CrossRef] [Green Version]
- Ishak, M. Testing General Relativity in Cosmology. Living Rev. Rel. 2019, 22, 1. [Google Scholar] [CrossRef] [Green Version]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rept. 2011, 509, 167–321. [Google Scholar] [CrossRef] [Green Version]
- Burgess, C.P. Quantum gravity in everyday life: General relativity as an effective field theory. Living Rev. Rel. 2004, 7, 5–56. [Google Scholar] [CrossRef] [Green Version]
- Donoghue, J.F. General relativity as an effective field theory: The leading quantum corrections. Phys. Rev. D 1994, 50, 3874–3888. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luckock, H.; Moss, I. Black holes have skyrmion hair. Phys. Lett. B 1986, 176, 341–345. [Google Scholar] [CrossRef]
- Bizon, P. Colored black holes. Phys. Rev. Lett. 1990, 64, 2844–2847. [Google Scholar] [CrossRef]
- Campbell, B.A.; Duncan, M.J.; Kaloper, N.; Olive, K.A. Axion hair for Kerr black holes. Phys. Lett. B 1990, 251, 34–38. [Google Scholar] [CrossRef] [Green Version]
- Campbell, B.A.; Kaloper, N.; Olive, K.A. Classical hair for Kerr-Newman black holes in string gravity. Phys. Lett. B 1992, 285, 199–205. [Google Scholar] [CrossRef] [Green Version]
- Maeda, K.I.; Tachizawa, T.; Torii, T.; Maki, T. Stability of nonAbelian black holes and catastrophe theory. Phys. Rev. Lett. 1994, 72, 450–453. [Google Scholar] [CrossRef] [Green Version]
- Kanti, P.; Mavromatos, N.E.; Rizos, J.; Tamvakis, K.; Winstanley, E. Dilatonic black holes in higher curvature string gravity. Phys. Rev. D 1996, 54, 5049–5058. [Google Scholar] [CrossRef] [Green Version]
- Kanti, P.; Tamvakis, K. Colored black holes in higher curvature string gravity. Phys. Lett. B 1997, 392, 30–38. [Google Scholar] [CrossRef] [Green Version]
- Kanti, P.; Mavromatos, N.E.; Rizos, J.; Tamvakis, K.; Winstanley, E. Dilatonic black holes in higher curvature string gravity. 2: Linear stability. Phys. Rev. D 1998, 57, 6255–6264. [Google Scholar] [CrossRef] [Green Version]
- Torii, T.; Yajima, H.; Maeda, K.i. Dilatonic black holes with Gauss-Bonnet term. Phys. Rev. D 1997, 55, 739–753. [Google Scholar] [CrossRef] [Green Version]
- Barack, L.; Cardoso, V.; Nissanke, S.; Sotiriou, T.P.; Askar, A.; Belczynski, C.; Bertone, G.; Bon, E.; Blas, D.; Brito, R.; et al. Black holes, gravitational waves and fundamental physics: A roadmap. Class. Quant. Grav. 2019, 36, 143001. [Google Scholar] [CrossRef] [Green Version]
- Tretyakova, D.A.; Latosh, B.N. Scalar-Tensor Black Holes Embedded in an Expanding Universe. Universe 2018, 4, 26. [Google Scholar] [CrossRef] [Green Version]
- Kerr, R.P. Gravitational field of a spinning mass as an example of algebraically special metrics. Phys. Rev. Lett. 1963, 11, 237–238. [Google Scholar] [CrossRef]
- Israel, W. Event horizons in static vacuum space-times. Phys. Rev. 1967, 164, 1776–1779. [Google Scholar] [CrossRef]
- Israel, W. Event horizons in static electrovac space-times. Commun. Math. Phys. 1968, 8, 245–260. [Google Scholar] [CrossRef]
- Carter, B. Global structure of the Kerr family of gravitational fields. Phys. Rev. 1968, 174, 1559–1571. [Google Scholar] [CrossRef] [Green Version]
- Carter, B. Axisymmetric Black Hole Has Only Two Degrees of Freedom. Phys. Rev. Lett. 1971, 26, 331–333. [Google Scholar] [CrossRef]
- Hawking, S.W. Black holes in general relativity. Commun. Math. Phys. 1972, 25, 152–166. [Google Scholar] [CrossRef]
- Price, R.H. Nonspherical perturbations of relativistic gravitational collapse. 1. Scalar and gravitational perturbations. Phys. Rev. D 1972, 5, 2419–2438. [Google Scholar] [CrossRef]
- Price, R.H. Nonspherical Perturbations of Relativistic Gravitational Collapse. II. Integer-Spin, Zero-Rest-Mass Fields. Phys. Rev. D 1972, 5, 2439–2454. [Google Scholar] [CrossRef]
- Robinson, D.C. Uniqueness of the Kerr black hole. Phys. Rev. Lett. 1975, 34, 905–906. [Google Scholar] [CrossRef]
- Teitelboim, C. Nonmeasurability of the quantum numbers of a black hole. Phys. Rev. D 1972, 5, 2941–2954. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Nonexistence of baryon number for static black holes. Phys. Rev. D 1972, 5, 1239–1246. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Nonexistence of baryon number for black holes. ii. Phys. Rev. D 1972, 5, 2403–2412. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Novel ‘‘no-scalar-hair’’ theorem for black holes. Phys. Rev. D 1995, 51, R6608. [Google Scholar] [CrossRef]
- Guo, Z.K.; Ohta, N.; Torii, T. Black Holes in the Dilatonic Einstein-Gauss-Bonnet Theory in Various Dimensions. I. Asymptotically Flat Black Holes. Prog. Theor. Phys. 2008, 120, 581–607. [Google Scholar] [CrossRef] [Green Version]
- Pani, P.; Cardoso, V. Are black holes in alternative theories serious astrophysical candidates? The Case for Einstein-Dilaton-Gauss-Bonnet black holes. Phys. Rev. D 2009, 79, 084031. [Google Scholar] [CrossRef] [Green Version]
- Pani, P.; Macedo, C.F.B.; Crispino, L.C.B.; Cardoso, V. Slowly rotating black holes in alternative theories of gravity. Phys. Rev. D 2011, 84, 087501. [Google Scholar] [CrossRef] [Green Version]
- Kleihaus, B.; Kunz, J.; Radu, E. Rotating Black Holes in Dilatonic Einstein-Gauss-Bonnet Theory. Phys. Rev. Lett. 2011, 106, 151104. [Google Scholar] [CrossRef] [Green Version]
- Yagi, K.; Yunes, N.; Tanaka, T. Slowly Rotating Black Holes in Dynamical Chern-Simons Gravity: Deformation Quadratic in the Spin. Phys. Rev. D 2012, 86, 044037. [Google Scholar] [CrossRef] [Green Version]
- Sotiriou, T.P.; Zhou, S.Y. Black hole hair in generalized scalar-tensor gravity. Phys. Rev. Lett. 2014, 112, 251102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sotiriou, T.P.; Zhou, S.Y. Black hole hair in generalized scalar-tensor gravity: An explicit example. Phys. Rev. D 2014, 90, 124063. [Google Scholar] [CrossRef] [Green Version]
- Kleihaus, B.; Kunz, J.; Mojica, S.; Radu, E. Spinning black holes in Einstein–Gauss-Bonnet–dilaton theory: Nonperturbative solutions. Phys. Rev. D 2016, 93, 044047. [Google Scholar] [CrossRef] [Green Version]
- Blázquez-Salcedo, J.L.; Macedo, C.F.B.; Cardoso, V.; Ferrari, V.; Gualtieri, L.; Khoo, F.S.; Kunz, J.; Pani, P. Perturbed black holes in Einstein-dilaton-Gauss-Bonnet gravity: Stability, ringdown, and gravitational-wave emission. Phys. Rev. D 2016, 94, 104024. [Google Scholar] [CrossRef] [Green Version]
- Antoniou, G.; Bakopoulos, A.; Kanti, P. Evasion of No-Hair Theorems and Novel Black-Hole Solutions in Gauss-Bonnet Theories. Phys. Rev. Lett. 2018, 120, 131102. [Google Scholar] [CrossRef] [Green Version]
- Antoniou, G.; Bakopoulos, A.; Kanti, P. Black-Hole Solutions with Scalar Hair in Einstein-Scalar-Gauss-Bonnet Theories. Phys. Rev. D 2018, 97, 084037. [Google Scholar] [CrossRef] [Green Version]
- Doneva, D.D.; Yazadjiev, S.S. New Gauss-Bonnet Black Holes with Curvature-Induced Scalarization in Extended Scalar-Tensor Theories. Phys. Rev. Lett. 2018, 120, 131103. [Google Scholar] [CrossRef] [Green Version]
- Silva, H.O.; Sakstein, J.; Gualtieri, L.; Sotiriou, T.P.; Berti, E. Spontaneous scalarization of black holes and compact stars from a Gauss-Bonnet coupling. Phys. Rev. Lett. 2018, 120, 131104. [Google Scholar] [CrossRef] [Green Version]
- Brihaye, Y.; Hartmann, B.; Urrestilla, J. Solitons and black hole in shift symmetric scalar-tensor gravity with cosmological constant. JHEP 2018, 6, 074. [Google Scholar] [CrossRef] [Green Version]
- Doneva, D.D.; Kiorpelidi, S.; Nedkova, P.G.; Papantonopoulos, E.; Yazadjiev, S.S. Charged Gauss-Bonnet black holes with curvature induced scalarization in the extended scalar-tensor theories. Phys. Rev. D 2018, 98, 104056. [Google Scholar] [CrossRef] [Green Version]
- Bakopoulos, A.; Antoniou, G.; Kanti, P. Novel Black-Hole Solutions in Einstein-Scalar-Gauss-Bonnet Theories with a Cosmological Constant. Phys. Rev. D 2019, 99, 064003. [Google Scholar] [CrossRef] [Green Version]
- Witek, H.; Gualtieri, L.; Pani, P.; Sotiriou, T.P. Black holes and binary mergers in scalar Gauss-Bonnet gravity: Scalar field dynamics. Phys. Rev. D 2019, 99, 064035. [Google Scholar] [CrossRef] [Green Version]
- Minamitsuji, M.; Ikeda, T. Scalarized black holes in the presence of the coupling to Gauss-Bonnet gravity. Phys. Rev. D 2019, 99, 044017. [Google Scholar] [CrossRef] [Green Version]
- Macedo, C.F.B.; Sakstein, J.; Berti, E.; Gualtieri, L.; Silva, H.O.; Sotiriou, T.P. Self-interactions and Spontaneous Black Hole Scalarization. Phys. Rev. D 2019, 99, 104041. [Google Scholar] [CrossRef] [Green Version]
- Doneva, D.D.; Staykov, K.V.; Yazadjiev, S.S. Gauss-Bonnet black holes with a massive scalar field. Phys. Rev. D 2019, 99, 104045. [Google Scholar] [CrossRef] [Green Version]
- Zou, D.C.; Myung, Y.S. Scalarized charged black holes with scalar mass term. Phys. Rev. D 2019, 100, 124055. [Google Scholar] [CrossRef] [Green Version]
- Cunha, P.V.P.; Herdeiro, C.A.R.; Radu, E. Spontaneously Scalarized Kerr Black Holes in Extended Scalar-Tensor–Gauss-Bonnet Gravity. Phys. Rev. Lett. 2019, 123, 011101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brihaye, Y.; Hartmann, B.; Aprile, N.P.; Urrestilla, J. Scalarization of asymptotically anti–de Sitter black holes with applications to holographic phase transitions. Phys. Rev. D 2020, 101, 124016. [Google Scholar] [CrossRef]
- Ellis, H.G. Ether flow through a drainhole: A particle model in general relativity. J. Math. Phys. 1973, 14, 104. [Google Scholar] [CrossRef]
- Bronnikov, K.A. Scalar-tensor theory and scalar charge. Acta Phys. Polon. B 1973, 4, 251–266. [Google Scholar]
- Visser, M.; Kar, S.; Dadhich, N. Traversable wormholes with arbitrarily small energy condition violations. Phys. Rev. Lett. 2003, 90, 201102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bronnikov, K.A. Extra dimensions, nonminimal couplings, horizons and wormholes. Grav. Cosmol. 1996, 2, 221–226. [Google Scholar]
- Bronnikov, K.A.; Fabris, J.C. Weyl space-times and wormholes in D-dimensional Einstein and dilaton gravity. Class. Quant. Grav. 1997, 14, 831–842. [Google Scholar] [CrossRef] [Green Version]
- Armendariz-Picon, C. On a class of stable, traversable Lorentzian wormholes in classical general relativity. Phys. Rev. D 2002, 65, 104010. [Google Scholar] [CrossRef] [Green Version]
- Bronnikov, K.A.; Grinyok, S.V. Conformal continuations and wormhole instability in scalar-tensor gravity. Grav. Cosmol. 2004, 10, 237. [Google Scholar]
- Lobo, F.S.N. Phantom energy traversable wormholes. Phys. Rev. D 2005, 71, 084011. [Google Scholar] [CrossRef] [Green Version]
- Lobo, F.S.N. Chaplygin traversable wormholes. Phys. Rev. D 2006, 73, 064028. [Google Scholar] [CrossRef] [Green Version]
- Lobo, F.S.N.; Oliveira, M.A. Wormhole geometries in f(R) modified theories of gravity. Phys. Rev. D 2009, 80, 104012. [Google Scholar] [CrossRef] [Green Version]
- Bronnikov, K.A.; Skvortsova, M.V.; Starobinsky, A.A. Notes on wormhole existence in scalar-tensor and F(R) gravity. Grav. Cosmol. 2010, 16, 216–222. [Google Scholar] [CrossRef] [Green Version]
- Garcia, N.M.; Lobo, F.S.N. Wormhole geometries supported by a nonminimal curvature-matter coupling. Phys. Rev. D 2010, 82, 104018. [Google Scholar] [CrossRef] [Green Version]
- Kanti, P.; Kleihaus, B.; Kunz, J. Wormholes in Dilatonic Einstein-Gauss-Bonnet Theory. Phys. Rev. Lett. 2011, 107, 271101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kanti, P.; Kleihaus, B.; Kunz, J. Stable Lorentzian Wormholes in Dilatonic Einstein-Gauss-Bonnet Theory. Phys. Rev. D 2012, 85, 044007. [Google Scholar] [CrossRef] [Green Version]
- Bolokhov, S.V.; Bronnikov, K.A.; Skvortsova, M.V. Magnetic black universes and wormholes with a phantom scalar. Class. Quant. Grav. 2012, 29, 245006. [Google Scholar] [CrossRef] [Green Version]
- Bronnikov, K.A.; Galiakhmetov, A.M. Wormholes without exotic matter in Einstein–Cartan theory. Grav. Cosmol. 2015, 21, 283–288. [Google Scholar] [CrossRef] [Green Version]
- Shaikh, R. Lorentzian wormholes in Eddington-inspired Born-Infeld gravity. Phys. Rev. D 2015, 92, 024015. [Google Scholar] [CrossRef] [Green Version]
- Mehdizadeh, M.R.; Kord Zangeneh, M.; Lobo, F.S.N. Einstein-Gauss-Bonnet traversable wormholes satisfying the weak energy condition. Phys. Rev. D 2015, 91, 084004. [Google Scholar] [CrossRef] [Green Version]
- Kuhfittig, P.K.F. Wormholes in f(R) gravity with a noncommutative-geometry background. Indian J. Phys. 2018, 92, 1207–1212. [Google Scholar] [CrossRef] [Green Version]
- Ibadov, R.; Kleihaus, B.; Kunz, J.; Murodov, S. Wormhole solutions with NUT charge in higher curvature theories. Arabian J. Math. 2021, 11, 31–41. [Google Scholar] [CrossRef]
- Karakasis, T.; Papantonopoulos, E.; Vlachos, C. f(R) gravity wormholes sourced by a phantom scalar field. Phys. Rev. D 2022, 105, 024006. [Google Scholar] [CrossRef]
- Ghosh, B.; Mitra, S. Wormhole solutions in f(R) gravity theory for Chaplygin gas scenario. Int. J. Mod. Phys. A 2021, 36, 18. [Google Scholar] [CrossRef]
- Fisher, I.Z. Scalar mesostatic field with regard for gravitational effects. Zh. Eksp. Teor. Fiz. 1948, 18, 636–640. [Google Scholar]
- Janis, A.I.; Newman, E.T.; Winicour, J. Reality of the Schwarzschild Singularity. Phys. Rev. Lett. 1968, 20, 878–880. [Google Scholar] [CrossRef]
- Wyman, M. Static Spherically Symmetric Scalar Fields in General Relativity. Phys. Rev. D 1981, 24, 839–841. [Google Scholar] [CrossRef]
- Agnese, A.G.; La Camera, M. GRAVITATION WITHOUT BLACK HOLES. Phys. Rev. D 1985, 31, 1280–1286. [Google Scholar] [CrossRef] [PubMed]
- Roberts, M.D. Scalar Field Counterexamples to the Cosmic Censorship Hypothesis. Gen. Rel. Grav. 1989, 21, 907–939. [Google Scholar] [CrossRef]
- Kleihaus, B.; Kunz, J.; Kanti, P. Particle-like ultracompact objects in Einstein-scalar-Gauss-Bonnet theories. Phys. Lett. B 2020, 804, 135401. [Google Scholar] [CrossRef]
- Kleihaus, B.; Kunz, J.; Kanti, P. Properties of ultracompact particlelike solutions in Einstein-scalar-Gauss-Bonnet theories. Phys. Rev. D 2020, 102, 024070. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [Green Version]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GWTC-2: Compact Binary Coalescences Observed by LIGO and Virgo During the First Half of the Third Observing Run. Phys. Rev. X 2020, 11, 021053. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. II. Array and Instrumentation. Astrophys. J. Lett. 2019, 875, L2. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. III. Data Processing and Calibration. Astrophys. J. Lett. 2019, 875, L3. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. IV. Imaging the Central Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L4. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. V. Physical Origin of the Asymmetric Ring. Astrophys. J. Lett. 2019, 875, L5. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. VI. The Shadow and Mass of the Central Black Hole. Astrophys. J. Lett. 2019, 875, L6. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. VII. Polarization of the Ring. Astrophys. J. Lett. 2021, 910, L12. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 Event Horizon Telescope Results. VIII. Magnetic Field Structure near The Event Horizon. Astrophys. J. Lett. 2021, 910, L13. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way. Astrophys. J. Lett. 2022, 930, L12. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First Sagittarius A* Event Horizon Telescope Results. II. EHT and Multiwavelength Observations, Data Processing, and Calibration. Astrophys. J. Lett. 2022, 930, L13. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First Sagittarius A* Event Horizon Telescope Results. III. Imaging of the Galactic Center Supermassive Black Hole. Astrophys. J. Lett. 2022, 930, L14. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First Sagittarius A* Event Horizon Telescope Results. IV. Variability, Morphology, and Black Hole Mass. Astrophys. J. Lett. 2022, 930, L15. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First Sagittarius A* Event Horizon Telescope Results. V. Testing Astrophysical Models of the Galactic Center Black Hole. Astrophys. J. Lett. 2022, 930, L16. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First Sagittarius A* Event Horizon Telescope Results. VI. Testing the Black Hole Metric. Astrophys. J. Lett. 2022, 930, L17. [Google Scholar] [CrossRef]
- Virbhadra, K.S.; Ellis, G.F.R. Schwarzschild black hole lensing. Phys. Rev. D 2000, 62, 084003. [Google Scholar] [CrossRef] [Green Version]
- Claudel, C.M.; Virbhadra, K.S.; Ellis, G.F.R. The Geometry of photon surfaces. J. Math. Phys. 2001, 42, 818–838. [Google Scholar] [CrossRef] [Green Version]
- Virbhadra, K.S.; Ellis, G.F.R. Gravitational lensing by naked singularities. Phys. Rev. D 2002, 65, 103004. [Google Scholar] [CrossRef]
- Zakharov, A.F.; De Paolis, F.; Ingrosso, G.; Nucita, A.A. Direct measurements of black hole charge with future astrometrical missions. Astron. Astrophys. 2005, 442, 795–799. [Google Scholar] [CrossRef] [Green Version]
- Virbhadra, K.S.; Keeton, C.R. Time delay and magnification centroid due to gravitational lensing by black holes and naked singularities. Phys. Rev. D 2008, 77, 124014. [Google Scholar] [CrossRef] [Green Version]
- Virbhadra, K.S. Relativistic images of Schwarzschild black hole lensing. Phys. Rev. D 2009, 79, 083004. [Google Scholar] [CrossRef] [Green Version]
- Johannsen, T.; Psaltis, D. A Metric for Rapidly Spinning Black Holes Suitable for Strong-Field Tests of the No-Hair Theorem. Phys. Rev. D 2011, 83, 124015. [Google Scholar] [CrossRef] [Green Version]
- Zakharov, A.F. Constraints on a charge in the Reissner-Nordström metric for the black hole at the Galactic Center. Phys. Rev. D 2014, 90, 062007. [Google Scholar] [CrossRef] [Green Version]
- Psaltis, D.; Wex, N.; Kramer, M. A Quantitative Test of the No-Hair Theorem with Sgr A* using stars, pulsars, and the Event Horizon Telescope. Astrophys. J. 2016, 818, 121. [Google Scholar] [CrossRef] [Green Version]
- Ezquiaga, J.M.; Zumalacárregui, M. Dark Energy After GW170817: Dead Ends and the Road Ahead. Phys. Rev. Lett. 2017, 119, 251304. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baker, T.; Bellini, E.; Ferreira, P.G.; Lagos, M.; Noller, J.; Sawicki, I. Strong constraints on cosmological gravity from GW170817 and GRB 170817A. Phys. Rev. Lett. 2017, 119, 251301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Creminelli, P.; Vernizzi, F. Dark Energy after GW170817 and GRB170817A. Phys. Rev. Lett. 2017, 119, 251302. [Google Scholar] [CrossRef] [Green Version]
- Sakstein, J.; Jain, B. Implications of the Neutron Star Merger GW170817 for Cosmological Scalar-Tensor Theories. Phys. Rev. Lett. 2017, 119, 251303. [Google Scholar] [CrossRef] [Green Version]
- Cunha, P.V.P.; Herdeiro, C.A.R. Shadows and strong gravitational lensing: A brief review. Gen. Rel. Grav. 2018, 50, 42. [Google Scholar] [CrossRef] [Green Version]
- Khodadi, M.; Allahyari, A.; Vagnozzi, S.; Mota, D.F. Black holes with scalar hair in light of the Event Horizon Telescope. JCAP 2020, 9, 026. [Google Scholar] [CrossRef]
- Psaltis, D.; Medeiros, L.; Christian, P.; Özel, F.; Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Ball, D.; et al. Gravitational Test Beyond the First Post-Newtonian Order with the Shadow of the M87 Black Hole. Phys. Rev. Lett. 2020, 125, 141104. [Google Scholar] [CrossRef]
- Psaltis, D.; Talbot, C.; Payne, E.; Mandel, I. Probing the Black Hole Metric. I. Black Hole Shadows and Binary Black-Hole Inspirals. Phys. Rev. D 2021, 103, 104036. [Google Scholar] [CrossRef]
- Oikonomou, V.K.; Fronimos, F.P. Reviving non-minimal Horndeski-like theories after GW170817: Kinetic coupling corrected Einstein–Gauss–Bonnet inflation. Class. Quant. Grav. 2021, 38, 035013. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K.; Fronimos, F.P. Rectifying Einstein-Gauss-Bonnet Inflation in View of GW170817. Nucl. Phys. B 2020, 958, 115135. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Swampland implications of GW170817-compatible Einstein-Gauss-Bonnet gravity. Phys. Lett. B 2020, 805, 135437. [Google Scholar] [CrossRef]
- Oikonomou, V.K. A refined Einstein–Gauss–Bonnet inflationary theoretical framework. Class. Quant. Grav. 2021, 38, 195025. [Google Scholar] [CrossRef]
- Kocherlakota, P.; Rezzolla, L.; Falcke, H.; Fromm, C.M.; Kramer, M.; Mizuno, Y.; Nathanail, A.; Olivares, H.; Younsi, Z.; Akiyama, K.; et al. Constraints on black-hole charges with the 2017 EHT observations of M87*. Phys. Rev. D 2021, 103, 104047. [Google Scholar] [CrossRef]
- Völkel, S.H.; Barausse, E.; Franchini, N.; Broderick, A.E. EHT tests of the strong-field regime of general relativity. Class. Quant. Grav. 2021, 38, 21LT01. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Roy, R.; Tsai, Y.D.; Visinelli, L. Horizon-scale tests of gravity theories and fundamental physics from the Event Horizon Telescope image of Sagittarius A*. arXiv 2022, arXiv:2205.07787. [Google Scholar]
- Falcke, H.; Melia, F.; Agol, E. Viewing the shadow of the black hole at the galactic center. Astrophys. J. Lett. 2000, 528, L13. [Google Scholar] [CrossRef] [Green Version]
- Psaltis, D. Testing General Metric Theories of Gravity with Bursting Neutron Stars. Phys. Rev. D 2008, 77, 064006. [Google Scholar] [CrossRef] [Green Version]
- Antoniou, G.; Bakopoulos, A.; Kanti, P.; Kleihaus, B.; Kunz, J. Novel Einstein–scalar-Gauss-Bonnet wormholes without exotic matter. Phys. Rev. D 2020, 101, 024033. [Google Scholar] [CrossRef] [Green Version]
- Perlick, V.; Tsupko, O.Y. Calculating black hole shadows: Review of analytical studies. Phys. Rept. 2022, 947, 1–39. [Google Scholar] [CrossRef]
- Abuter, R.; Amorim, A.; Anugu, N.; Bauböck, M.; Benisty, M.; Berger, J.P.; Blind, N.; Bonnet, H.; Brandner, W.; Buron, A.; et al. Detection of the gravitational redshift in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2018, 615, L15. [Google Scholar] [CrossRef] [Green Version]
- Amorim, A.; Bauböck, M.; Berger, J.P.; Brandner, W.; Clénet, Y.; Du Foresto, V.C.; de Zeeuw, P.T.; Dexter, J.; Duvert, G.; Ebert, M.; et al. Test of the Einstein Equivalence Principle near the Galactic Center Supermassive Black Hole. Phys. Rev. Lett. 2019, 122, 101102. [Google Scholar] [CrossRef] [Green Version]
- Abuter, R.; Amorim, A.; Bauböck, M.; Berger, J.P.; Bonnet, H.; Brandner, W.; Cardoso, V.; Clénet, Y.; De Zeeuw, P.T.; Dexter, J.; et al. Detection of the Schwarzschild precession in the orbit of the star S2 near the Galactic centre massive black hole. Astron. Astrophys. 2020, 636, L5. [Google Scholar] [CrossRef] [Green Version]
- Do, T.; Hees, A.; Ghez, A.; Martinez, G.D.; Chu, D.S.; Jia, S.; Sakai, S.; Lu, J.R.; Gautam, A.K.; O’neil, K.K.; et al. Relativistic redshift of the star S0-2 orbiting the Galactic center supermassive black hole. Science 2019, 365, 664–668. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hees, A.; Dehghanfar, A.; Do, T.; Ghez, A.M.; Martinez, G.D.; Campbell, R.; Lu, J.R. An adaptive scheduling tool to optimize measurements to reach a scientific objective: Methodology and application to the measurements of stellar orbits in the Galactic Center. Astrophys. J. 2019, 880, 87. [Google Scholar] [CrossRef]
- Della Monica, R.; de Martino, I.; de Laurentis, M. Orbital precession of the S2 star in Scalar–Tensor–Vector Gravity. Mon. Not. Roy. Astron. Soc. 2022, 510, 4757–4766. [Google Scholar] [CrossRef]
- de Martino, I.; della Monica, R.; de Laurentis, M. f(R) gravity after the detection of the orbital precession of the S2 star around the Galactic Center massive black hole. Phys. Rev. D 2021, 104, L101502. [Google Scholar] [CrossRef]
- Fragione, G.; Loeb, A. Implication of Spin Constraints by the Event Horizon Telescope on Stellar Orbits in the Galactic Center. Astrophys. J. Lett. 2022, 932, L17. [Google Scholar] [CrossRef]
- Lee, B.H.; Lee, W.; Ro, D. Expanded evasion of the black hole no-hair theorem in dilatonic Einstein-Gauss-Bonnet theory. Phys. Rev. D 2019, 99, 024002. [Google Scholar] [CrossRef] [Green Version]
- Papageorgiou, A.; Park, C.; Park, M. Rectifying no-hair theorems in Gauss-Bonnet theory. Phys. Rev. D 2022, 106, 084024. [Google Scholar] [CrossRef]
- Arnowitt, R.L.; Deser, S.; Misner, C.W. The Dynamics of general relativity. Gen. Rel. Grav. 2008, 40, 1997–2027. [Google Scholar] [CrossRef] [Green Version]
- Popova, A.D.; Petrov, A.N. Exact Dynamic Theories on a Given Background in Gravitation. Int. J. Mod. Phys. A 1988, 3, 2651–2679. [Google Scholar] [CrossRef]
- Petrov, A.N.; Lompay, R.R. Covariantized Noether identities and conservation laws for perturbations in metric theories of gravity. Gen. Rel. Grav. 2013, 45, 545–579. [Google Scholar] [CrossRef] [Green Version]
- Alexeyev, S.O.; Petrov, A.N.; Latosh, B.N. Maeda-Dadhich Solutions as Real Black Holes. Phys. Rev. D 2015, 92, 104046. [Google Scholar] [CrossRef] [Green Version]
- Perkins, S.E.; Nair, R.; Silva, H.O.; Yunes, N. Improved gravitational-wave constraints on higher-order curvature theories of gravity. Phys. Rev. D 2021, 104, 024060. [Google Scholar] [CrossRef]
- Gross, D.J.; Sloan, J.H. The Quartic Effective Action for the Heterotic String. Nucl. Phys. B 1987, 291, 41–89. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Doneva, D.D.; Kunz, J.; Yazadjiev, S.S. Radial perturbations of the scalarized Einstein-Gauss-Bonnet black holes. Phys. Rev. D 2018, 98, 084011. [Google Scholar] [CrossRef] [Green Version]
- Antoniou, G.; Macedo, C.F.B.; McManus, R.; Sotiriou, T.P. Stable spontaneously-scalarized black holes in generalized scalar-tensor theories. Phys. Rev. D 2022, 106, 024029. [Google Scholar] [CrossRef]
- Andreou, N.; Franchini, N.; Ventagli, G.; Sotiriou, T.P. Spontaneous scalarization in generalised scalar-tensor theory. Phys. Rev. D 2019, 99, 124022. [Google Scholar] [CrossRef] [Green Version]
- Silva, H.O.; Macedo, C.F.B.; Sotiriou, T.P.; Gualtieri, L.; Sakstein, J.; Berti, E. Stability of scalarized black hole solutions in scalar-Gauss-Bonnet gravity. Phys. Rev. D 2019, 99, 064011. [Google Scholar] [CrossRef] [Green Version]
- Ventagli, G.; Lehébel, A.; Sotiriou, T.P. Onset of spontaneous scalarization in generalized scalar-tensor theories. Phys. Rev. D 2020, 102, 024050. [Google Scholar] [CrossRef]
- Antoniou, G.; Bordin, L.; Sotiriou, T.P. Compact object scalarization with general relativity as a cosmic attractor. Phys. Rev. D 2021, 103, 024012. [Google Scholar] [CrossRef]
- Ventagli, G.; Antoniou, G.; Lehébel, A.; Sotiriou, T.P. Neutron star scalarization with Gauss-Bonnet and Ricci scalar couplings. Phys. Rev. D 2021, 104, 124078. [Google Scholar] [CrossRef]
- Antoniou, G.; Lehébel, A.; Ventagli, G.; Sotiriou, T.P. Black hole scalarization with Gauss-Bonnet and Ricci scalar couplings. Phys. Rev. D 2021, 104, 044002. [Google Scholar] [CrossRef]
- Herdeiro, C.A.R.; Radu, E.; Sanchis-Gual, N.; Font, J.A. Spontaneous Scalarization of Charged Black Holes. Phys. Rev. Lett. 2018, 121, 101102. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, P.G.S.; Herdeiro, C.A.R.; Pombo, A.M.; Radu, E.; Sanchis-Gual, N. Spontaneous Scalarisation of Charged Black Holes: Coupling Dependence and Dynamical Features. Class. Quant. Grav. 2019, 36, 134002. [Google Scholar] [CrossRef] [Green Version]
- Blázquez-Salcedo, J.L.; Herdeiro, C.A.R.; Kunz, J.; Pombo, A.M.; Radu, E. Einstein-Maxwell-scalar black holes: The hot, the cold and the bald. Phys. Lett. B 2020, 806, 135493. [Google Scholar] [CrossRef]
- Zajaček, M.; Tursunov, A.; Eckart, A.; Britzen, S. On the charge of the Galactic centre black hole. Mon. Not. Roy. Astron. Soc. 2018, 480, 4408–4423. [Google Scholar] [CrossRef] [Green Version]
- Zajaček, M.; Tursunov, A.; Eckart, A.; Britzen, S.; Hackmann, E.; Karas, V.; Stuchlík, Z.; Czerny, B.; Zensus, J.A. Constraining the charge of the Galactic centre black hole. J. Phys. Conf. Ser. 2019, 1258, 012031. [Google Scholar] [CrossRef]
- Blackburn, L.; Doeleman, S.; Dexter, J.; Gómez, J.L.; Johnson, M.D.; Palumbo, D.C.; Weintroub, J.; Bouman, K.L.; Chael, A.A.; Zhao, G.; et al. Studying Black Holes on Horizon Scales with VLBI Ground Arrays. arXiv 2019, arXiv:1909.01411. [Google Scholar]
- Doeleman, S. Black Hole Imaging: First Results and Future Vision. In Proceedings of the American Astronomical Society Meeting Abstracts, virtual. 7–9 June 2021; Volume 53, p. 221.01. [Google Scholar]
- Misner, C.W.; Sharp, D.H. Relativistic Equations for Adiabatic, Spherically Symmetric Gravitational Collapse. Phys. Rev. 1964, 136, B571–B576. [Google Scholar] [CrossRef]

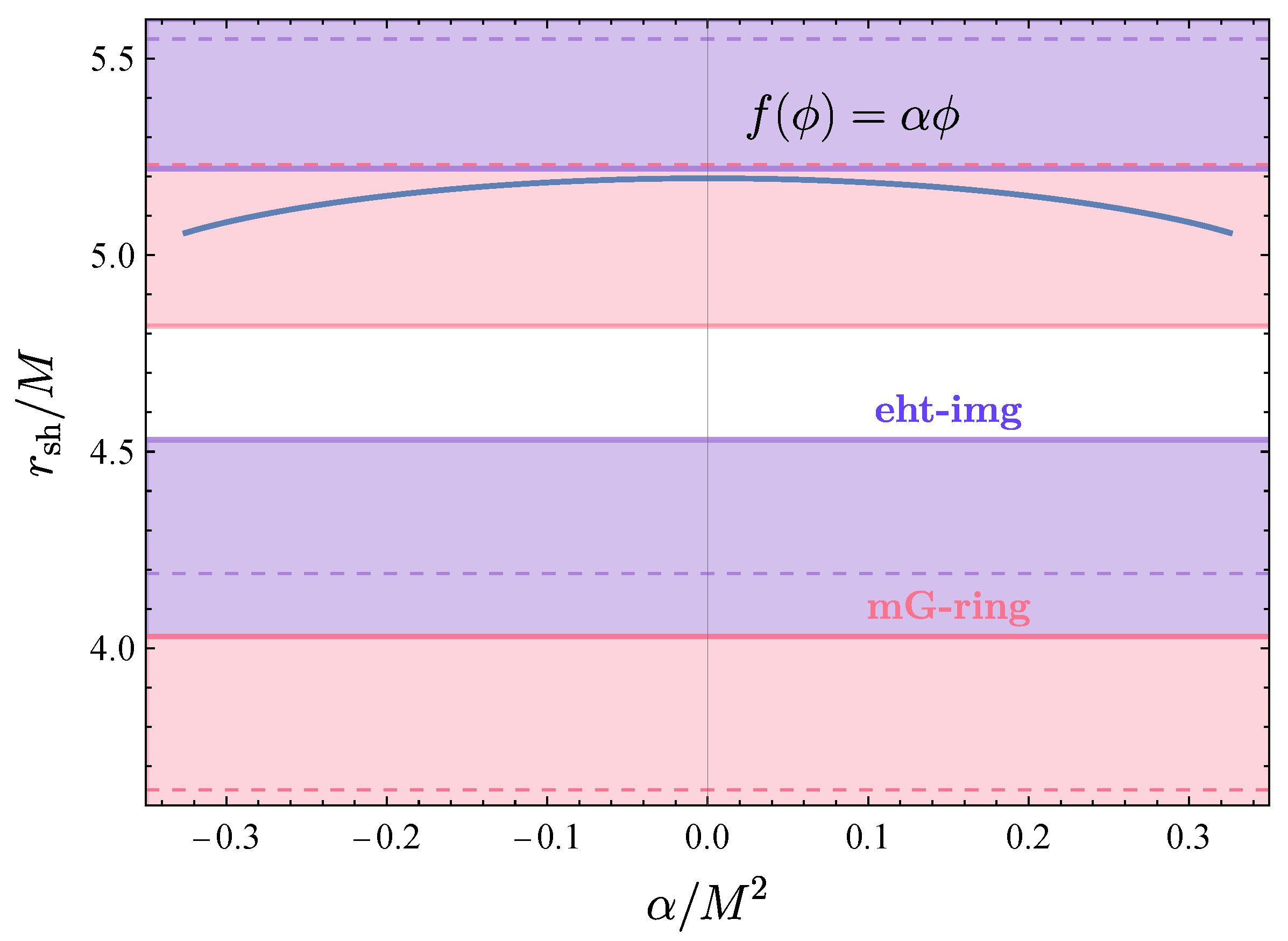
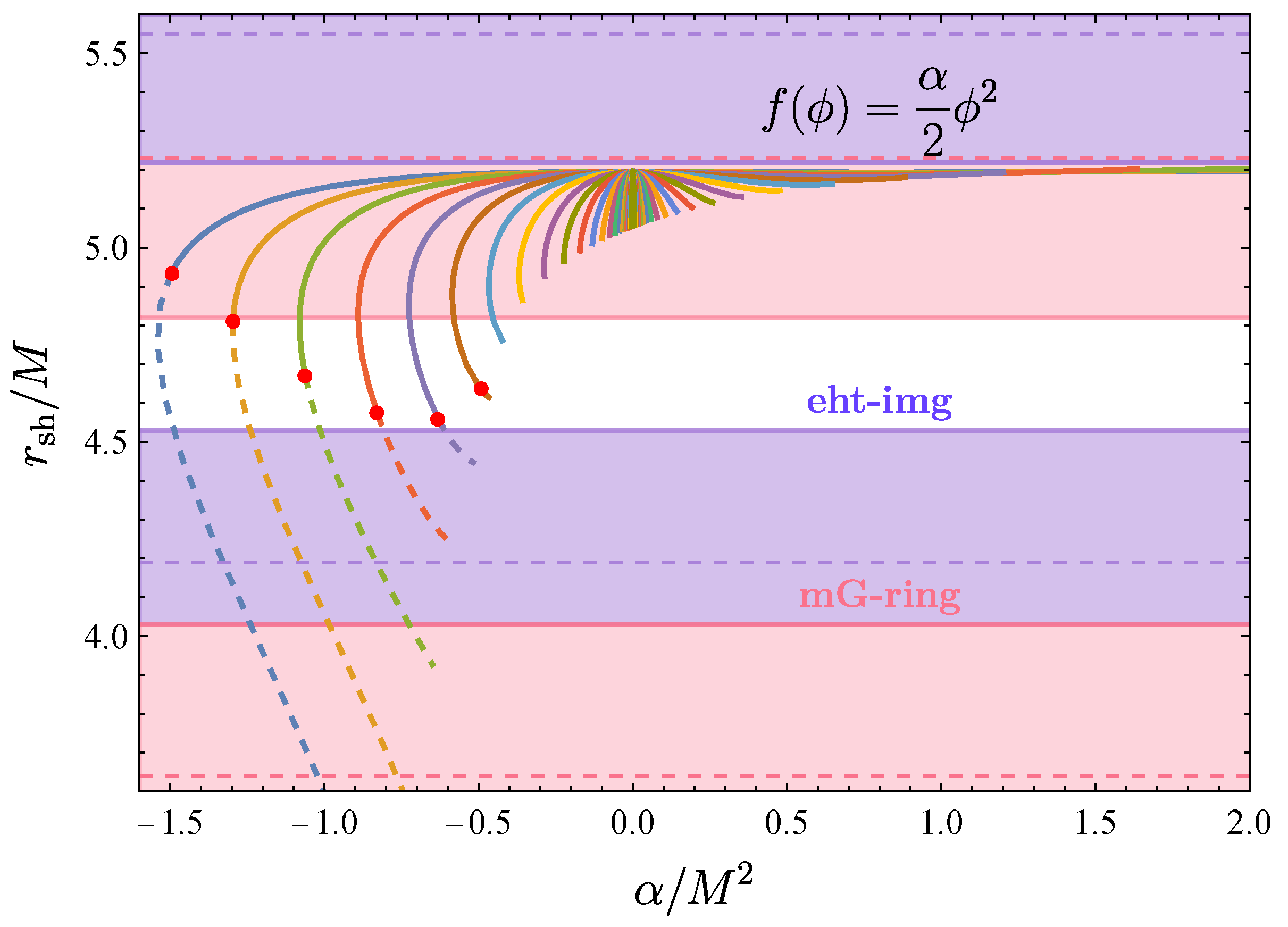
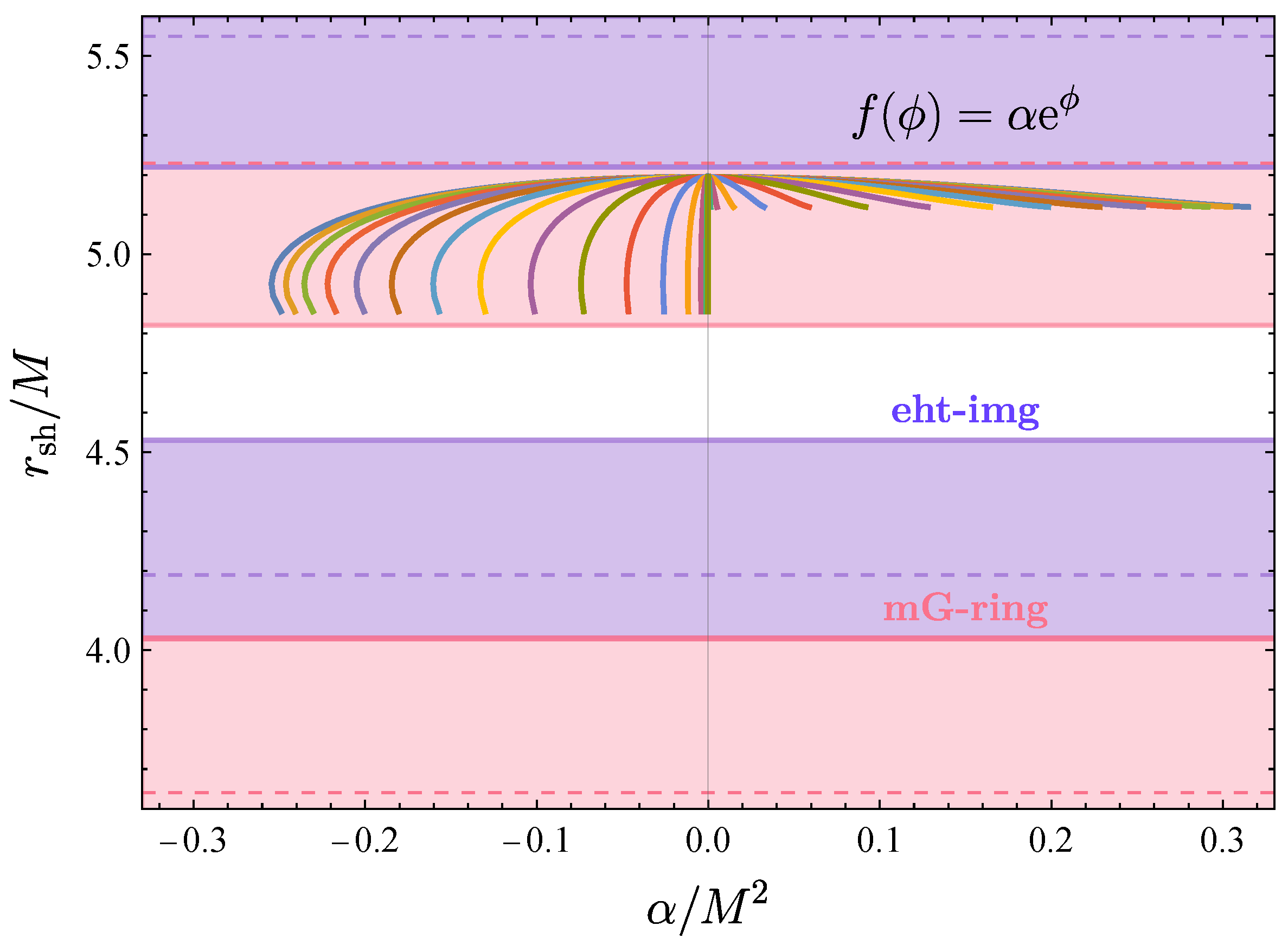

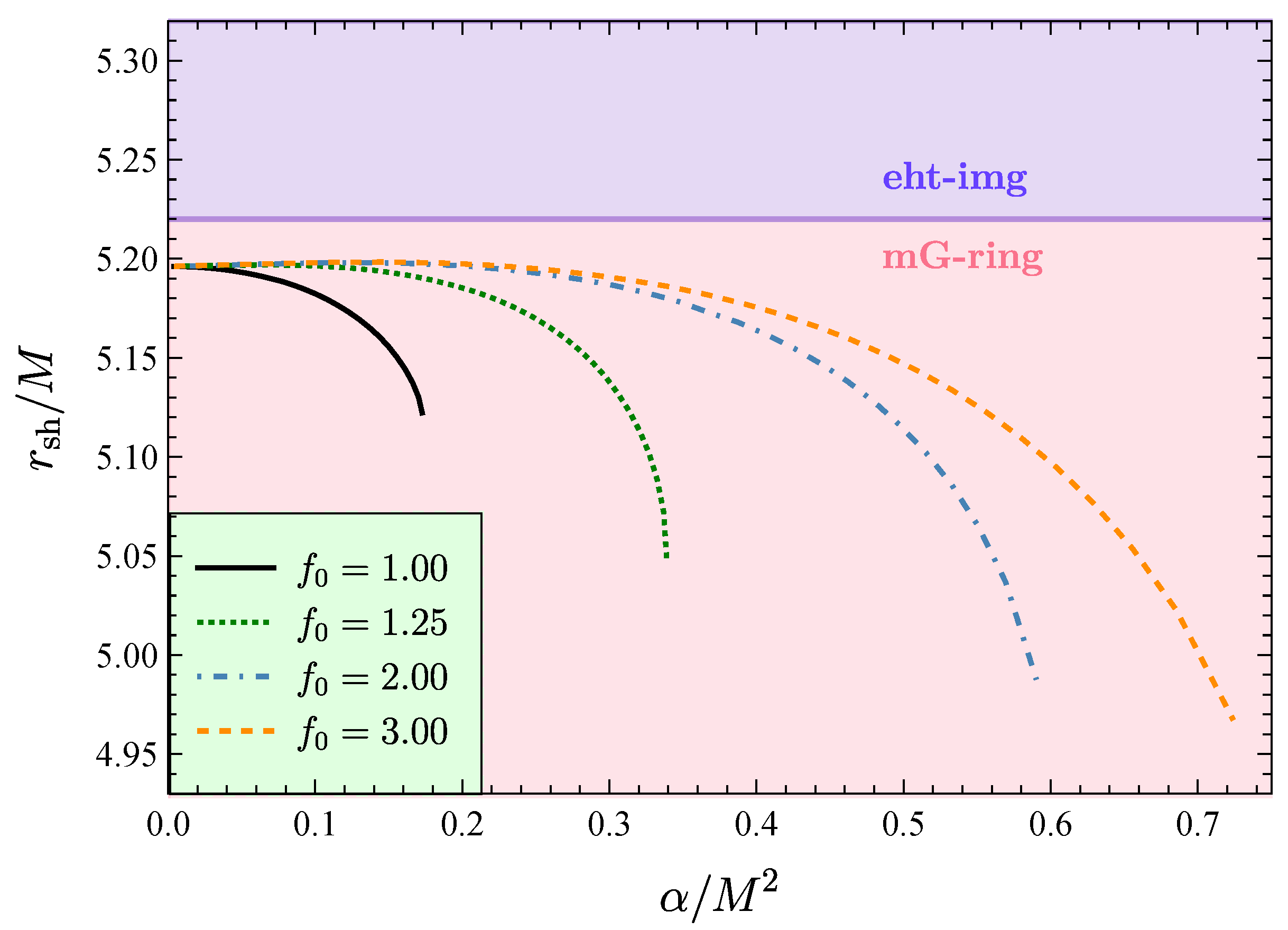
| Sgr Estimates | ||||
|---|---|---|---|---|
| Deviation | 1- Bounds | 2- Bounds | ||
| eht-img | VLTI | |||
| Keck | ||||
| SMILI | VLTI | |||
| Keck | ||||
| DIFMAP | VLTI | |||
| Keck | ||||
| mG-ring | VLTI | |||
| Keck | ||||
| M Estimates | |||
|---|---|---|---|
| Deviation | 1- Bounds | 2- Bounds | |
| EHT | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antoniou, G.; Papageorgiou, A.; Kanti, P. Probing Modified Gravity Theories with Scalar Fields Using Black-Hole Images. Universe 2023, 9, 147. https://doi.org/10.3390/universe9030147
Antoniou G, Papageorgiou A, Kanti P. Probing Modified Gravity Theories with Scalar Fields Using Black-Hole Images. Universe. 2023; 9(3):147. https://doi.org/10.3390/universe9030147
Chicago/Turabian StyleAntoniou, Georgios, Alexandros Papageorgiou, and Panagiota Kanti. 2023. "Probing Modified Gravity Theories with Scalar Fields Using Black-Hole Images" Universe 9, no. 3: 147. https://doi.org/10.3390/universe9030147
APA StyleAntoniou, G., Papageorgiou, A., & Kanti, P. (2023). Probing Modified Gravity Theories with Scalar Fields Using Black-Hole Images. Universe, 9(3), 147. https://doi.org/10.3390/universe9030147






