Modelling Neutron-Star Ocean Dynamics
Abstract
:1. Context
1.1. Observations
1.2. Theory
2. Ocean Oscillations
The Traditional Approximation
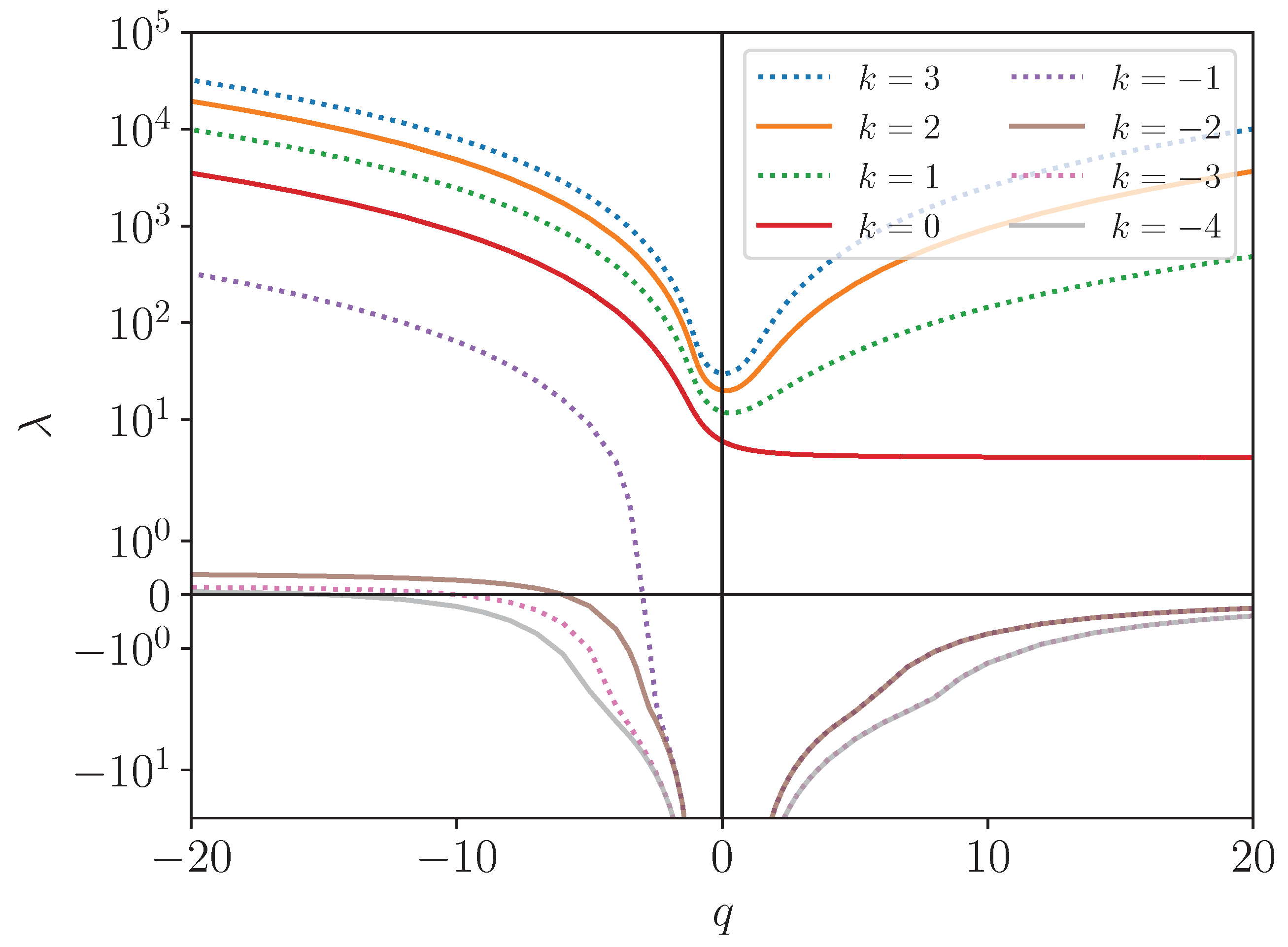
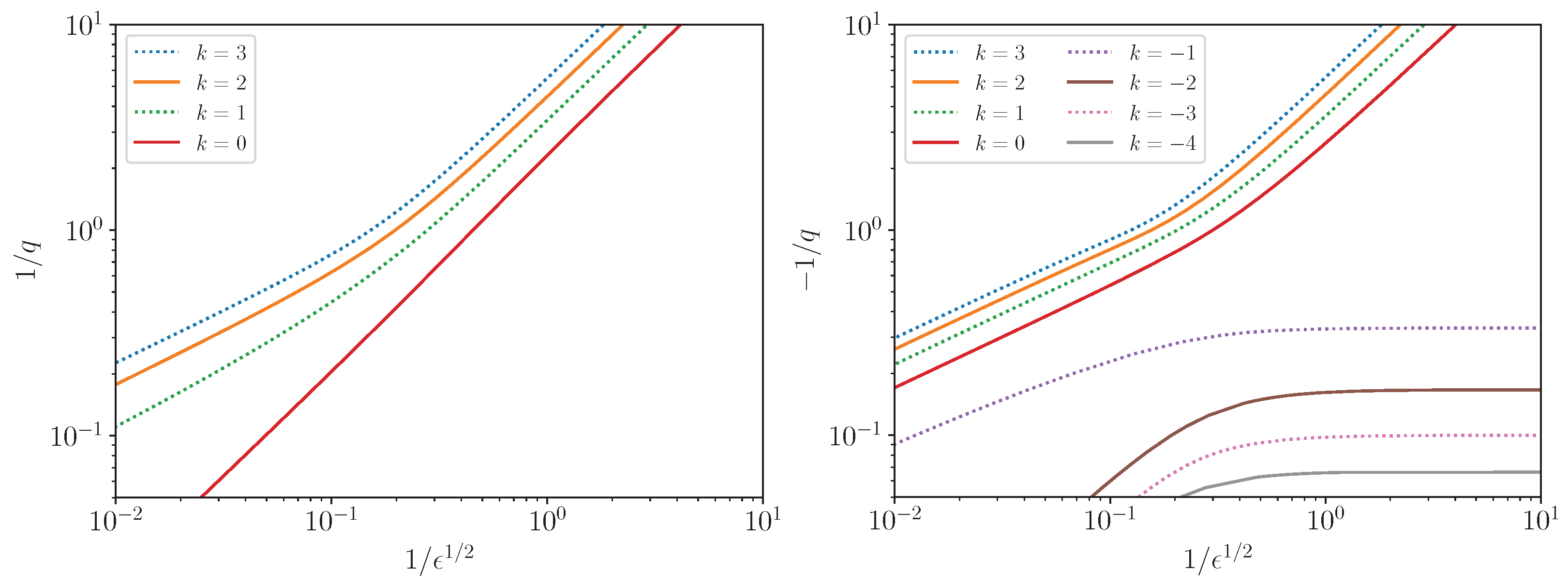
3. Solutions of Laplace’s Tidal Equation
3.1. The Shallow-Water Problem
4. Relativistic Ocean Modes
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Plane-Wave Analysis
| 1 | This turns out not to be an overly restrictive constraint, since for a canonical , neutron star, while the fastest known pulsar spin is just above . |
| 2 | The r-modes are a subset of the inertial modes. In general, an inertial mode has comparable radial and horizontal motion, whereas an r-mode is unique in that it is axial at leading order (see, e.g., Ref. [32]). When a fluid is strongly stratified, the r-modes are the only inertial modes that exist. |
| 3 | At this point, it is worth noting that the traditional approximation relies on the Cowling approximation. In relaxing the Cowling approximation, the linearised gravitational potential must be determined from Poisson’s equation, which spoils the radial and angular separation that we have arrived at. |
| 4 | In the geophysics literature, these particular solutions are referred to as “gravity waves” (see, e.g., Ref. [25]). In fluids that are uniform density and incompressible, it is common in asteroseismology to refer to such perturbations as f-modes. The connection between the mode families is, in fact, easy to understand. If we impose a no-penetration condition on the fluid velocity at some fixed depth h then the standard f-mode solution (see Ref. [21] for a pedagogical derivation) limits to that of surface gravity waves when . |
| 5 | As we “integrate out” the radial dependence, we lose any information about stratification in the fluid. In principle, this may still be accounted for by introducing an “equivalent depth” (see, e.g., Ref. [46]), but it is not clear to what extent this notion is useful in practice. |
| 6 | The results obtained here agree with a direct derivation starting from the general-relativistic version of the traditional-approximation equations [29]. |
References
- Jahoda, K.; Markwardt, C.B.; Radeva, Y.; Rots, A.H.; Stark, M.J.; Swank, J.H.; Strohmayer, T.E.; Zhang, W. Calibration of the Rossi X-ray Timing Explorer Proportional Counter Array. Astrophys. J. Suppl. Ser. 2006, 163, 401. [Google Scholar] [CrossRef]
- Gendreau, K.C.; Arzoumanian, Z.; Adkins, P.W.; Albert, C.L.; Anders, J.F.; Aylward, A.T.; Baker, C.L.; Balsamo, E.R.; Bamford, W.A.; Benegalrao, S.S.; et al. The Neutron star Interior Composition Explorer (NICER): Design and development. Proc. SPIE 2016, 9905, 99051H. [Google Scholar] [CrossRef]
- Agrawal, P.C. A broad spectral band Indian Astronomy satellite ‘Astrosat’. Adv. Space Res. 2006, 38, 2989. [Google Scholar] [CrossRef]
- Singh, K.P. The AstroSat Observatory. In Handbook of X-ray and Gamma-ray Astrophysics; Bambi, C., Santangelo, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2022; p. 83. [Google Scholar] [CrossRef]
- Chambers, F.R.N.; Watts, A.L. Relativistic ocean r-modes during type-I X-ray bursts. Mon. Not. R. Astron. Soc. 2020, 491, 6032. [Google Scholar] [CrossRef]
- Patruno, A.; Watts, A.L. Accreting Millisecond X-ray Pulsars. In Timing Neutron Stars: Pulsations, Oscillations and Explosions; Belloni, T.M., Méndez, M., Zhang, C., Eds.; Astrophysics and Space Science Library Book Series; Springer: Berlin/Heidelberg, Germany, 2021; Volume 461, p. 143. [Google Scholar] [CrossRef]
- Galloway, D.K.; Keek, L. Thermonuclear X-ray Bursts. In Timing Neutron Stars: Pulsations, Oscillations and Explosions; Belloni, T.M., Méndez, M., Zhang, C., Eds.; Astrophysics and Space Science Library Book Series; Springer: Berlin/Heidelberg, Germany, 2021; Volume 461, p. 209. [Google Scholar] [CrossRef]
- Bhattacharyya, S. Nuclear-Powered X-ray Millisecond Pulsars. In Millisecond Pulsars; Bhattacharyya, S., Papitto, A., Bhattacharya, D., Eds.; Astrophysics and Space Science Library Book Series; Springer: Berlin/Heidelberg, Germany, 2022; Volume 465, p. 125. [Google Scholar] [CrossRef]
- Strohmayer, T.E.; Jahoda, K.; Giles, A.B.; Lee, U. Millisecond Pulsations from a Low-Mass X-ray Binary in the Galactic Center Region. Astrophys. J. 1997, 486, 355. [Google Scholar] [CrossRef]
- Strohmayer, T.E.; Zhang, W.; Swank, J.H. 363 HZ Oscillations during the Rising Phase of Bursts from 4U 1728-34: Evidence for Rotational Modulation. Astrophys. J. 1997, 487, L77. [Google Scholar] [CrossRef]
- Strohmayer, T.E.; Zhang, W.; Swank, J.H.; Lapidus, I. The Long-Term Stability of Oscillations during Thermonuclear X-ray Bursts: Constraining the Binary X-ray Mass Function. Astrophys. J. 1998, 503, L147. [Google Scholar] [CrossRef]
- Chakrabarty, D.; Morgan, E.H.; Muno, M.P.; Galloway, D.K.; Wijnands, R.; van der Klis, M.; Markwardt, C.B. Nuclear-powered millisecond pulsars and the maximum spin frequency of neutron stars. Nature 2003, 424, 42. [Google Scholar] [CrossRef]
- Watts, A.L.; Kini, Y. Thermonuclear Burst Oscillations from Accreting Neutron Stars: Catalogue of Confirmed Sources. 2021. Available online: https://zenodo.org/record/5513798#.ZF2cEHYzaUk (accessed on 1 April 2023).
- Strohmayer, T.E.; Markwardt, C.B.; Swank, J.H.; in’t Zand, J. X-ray Bursts from the Accreting Millisecond Pulsar XTE J1814-338. Astrophys. J. 2003, 596, L67. [Google Scholar] [CrossRef]
- Altamirano, D.; Watts, A.; Linares, M.; Markwardt, C.B.; Strohmayer, T.; Patruno, A. Type I X-ray bursts and burst oscillations in the accreting millisecond X-ray pulsar IGR J17511-3057. Mon. Not. R. Astron. Soc. 2010, 409, 1136. [Google Scholar] [CrossRef]
- Chakraborty, M.; Bhattacharyya, S. Thermonuclear X-ray bursts from the 401-Hz accreting pulsar IGR J17498-2921: Indication of burning in confined regions. Mon. Not. R. Astron. Soc. 2012, 422, 2351. [Google Scholar] [CrossRef]
- Beri, A.; Sharma, R.; Roy, P.; Gaur, V.; Altamirano, D.; Andersson, N.; Gittins, F.; Celora, T. AstroSat and NuSTAR observations of XTE J1739-285 during the 2019–2020 outburst. Mon. Not. R. Astron. Soc. 2023, 521, 5904. [Google Scholar] [CrossRef]
- Galloway, D.K.; Chakrabarty, D.; Muno, M.P.; Savov, P. Discovery of a 270 Hertz X-ray Burst Oscillation in the X-ray Dipper 4U 1916-053. Astrophys. J. 2001, 549, L85. [Google Scholar] [CrossRef]
- Wijnands, R.; Strohmayer, T.; Franco, L.M. Discovery of Nearly Coherent Oscillations with a Frequency of ~567 HZ during Type I X-ray Bursts of the X-ray Transient and Eclipsing Binary X1658-298. Astrophys. J. 2001, 549, L71. [Google Scholar] [CrossRef]
- Watts, A.L. Thermonuclear Burst Oscillations. Annu. Rev. Astron. Astrophys. 2012, 50, 609. [Google Scholar] [CrossRef]
- Andersson, N. Gravitational-Wave Astronomy: Exploring the Dark Side of the Universe; Oxford University Press: Oxford, UK, 2019. [Google Scholar] [CrossRef]
- Eckart, C. Hydrodynamics of Oceans and Atmospheres; Pergamon Press: Oxford, UK, 1960. [Google Scholar] [CrossRef]
- Bildsten, L.; Ushomirsky, G.; Cutler, C. Ocean g-Modes on Rotating Neutron Stars. Astrophys. J. 1996, 460, 827. [Google Scholar] [CrossRef]
- Heyl, J.S. r-Modes on Rapidly Rotating, Relativistic Stars. I. Do Type I Bursts Excite Modes in the Neutron Star Ocean? Astrophys. J. 2004, 600, 939. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. The Eigenfunctions of Laplace’s Tidal Equations over a Sphere. Philos. Trans. R. Soc. Lond. Ser. A 1968, 262, 511. [Google Scholar] [CrossRef]
- Lee, U. Surface r-Modes and Burst Oscillations of Neutron Stars. Astrophys. J. 2004, 600, 914. [Google Scholar] [CrossRef]
- Piro, A.L.; Bildsten, L. Surface Modes on Bursting Neutron Stars and X-ray Burst Oscillations. Astrophys. J. 2005, 629, 438. [Google Scholar] [CrossRef]
- Chambers, F.R.N.; Watts, A.L.; Keek, L.; Cavecchi, Y.; Garcia, F. Burning in the Tail: Implications for a Burst Oscillation Model. Astrophys. J. 2019, 871, 61. [Google Scholar] [CrossRef]
- Maniopoulou, A.; Andersson, N. The traditional approximation in general relativity. Mon. Not. R. Astron. Soc. 2004, 351, 1349. [Google Scholar] [CrossRef]
- Pedlosky, J. Geophysical Fluid Dynamics; Springer: New York, NY, USA, 1987. [Google Scholar] [CrossRef]
- Unno, W.; Osaki, Y.; Ando, H.; Saio, H.; Shibahashi, H. Nonradial Oscillations of Stars; University of Tokyo Press: Tokyo, Japan, 1989. [Google Scholar]
- Lockitch, K.H.; Friedman, J.L. Where are the R-Modes of Isentropic Stars? Astrophys. J. 1999, 521, 764. [Google Scholar] [CrossRef]
- Lee, U.; Saio, H. Low-Frequency Nonradial Oscillations in Rotating Stars. I. Angular Dependence. Astrophys. J. 1997, 491, 839. [Google Scholar] [CrossRef]
- Chamel, N.; Haensel, P. Physics of Neutron Star Crusts. Living Rev. Relativ. 2008, 11, 10. [Google Scholar] [CrossRef]
- Hough, S.S. On the Application of Harmonic Analysis to the Dynamical Theory of the Tides. Part II: On the General Integration of Laplace’s Dynamical Equations. Philos. Trans. R. Soc. Lond. Ser. A 1898, 191, 139. [Google Scholar] [CrossRef]
- Love, A.E.H. Notes on the Dynamical Theory of the Tides. Proc. Lond. Math. Soc. 1913, s2-12, 309. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. Planetary Waves on a Rotating Sphere. Proc. R. Soc. Lond. Ser. A 1964, 279, 446. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. Planetary Waves on a Rotating Sphere. II. Proc. R. Soc. Lond. Ser. A 1965, 284, 40. [Google Scholar] [CrossRef]
- Zaqarashvili, T.V.; Albekioni, M.; Ballester, J.L.; Bekki, Y.; Biancofiore, L.; Birch, A.C.; Dikpati, M.; Gizon, L.; Gurgenashvili, E.; Heifetz, E.; et al. Rossby Waves in Astrophysics. Space Sci. Rev. 2021, 217, 15. [Google Scholar] [CrossRef]
- Phillips, N.A. The Equations of Motion for a Shallow Rotating Atmosphere and the “Traditional Approximation”. J. Atmos. Sci. 1966, 23, 626. [Google Scholar] [CrossRef]
- Holton, J.R.; Hakim, G.J. An Introduction to Dynamic Meteorology; Academic Press: Boston, MA, USA, 2013. [Google Scholar] [CrossRef]
- Vallis, G.K. Atmospheric and Oceanic Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
- Papaloizou, J.; Pringle, J.E. Non-radial oscillations of rotating stars and their relevance to the short-period oscillations of cataclysmic variables. Mon. Not. R. Astron. Soc. 1978, 182, 423. [Google Scholar] [CrossRef]
- Provost, J.; Berthomieu, G.; Rocca, A. Low Frequency Oscillations of a Slowly Rotating Star—Quasi Toroidal Modes. Astron. Astrophys. 1981, 94, 126. [Google Scholar]
- Saio, H. R-mode oscillations in uniformly rotating stars. Astrophys. J. 1982, 256, 717. [Google Scholar] [CrossRef]
- Taylor, G.I. The Oscillations of the Atmosphere. Proc. R. Soc. Lond. Ser. A 1936, 156, 318. [Google Scholar] [CrossRef]
- Andersson, N.; Gittins, F. Formulating the r-mode Problem for Slowly Rotating Neutron Stars. Astrophys. J. 2023, 945, 139. [Google Scholar] [CrossRef]
- Gittins, F.; Andersson, N. The r-modes of slowly rotating, stratified neutron stars. Mon. Not. R. Astron. Soc. 2023, 521, 3043. [Google Scholar] [CrossRef]
- Abramowicz, M.A.; Rezzolla, L.; Yoshida, S. General relativistic Rossby-Haurwitz waves of a slowly and differentially rotating fluid shell. Classical Quant. Grav. 2002, 19, 191. [Google Scholar] [CrossRef]
- Hartle, J.B. Slowly Rotating Relativistic Stars. I. Equations of Structure. Astrophys. J. 1967, 150, 1005. [Google Scholar] [CrossRef]
- Mathis, S.; Prat, V. The traditional approximation of rotation, including the centrifugal acceleration for slightly deformed stars. Astron. Astrophys. 2019, 631, A26. [Google Scholar] [CrossRef]
- Van Baal, B.F.A.; Chambers, F.R.N.; Watts, A.L. Waves in thin oceans on oblate neutron stars. Mon. Not. R. Astron. Soc. 2020, 496, 2098–2106. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gittins, F.; Celora, T.; Beri, A.; Andersson, N. Modelling Neutron-Star Ocean Dynamics. Universe 2023, 9, 226. https://doi.org/10.3390/universe9050226
Gittins F, Celora T, Beri A, Andersson N. Modelling Neutron-Star Ocean Dynamics. Universe. 2023; 9(5):226. https://doi.org/10.3390/universe9050226
Chicago/Turabian StyleGittins, Fabian, Thomas Celora, Aru Beri, and Nils Andersson. 2023. "Modelling Neutron-Star Ocean Dynamics" Universe 9, no. 5: 226. https://doi.org/10.3390/universe9050226
APA StyleGittins, F., Celora, T., Beri, A., & Andersson, N. (2023). Modelling Neutron-Star Ocean Dynamics. Universe, 9(5), 226. https://doi.org/10.3390/universe9050226





