Even and Odd Self-Similar Solutions of the Diffusion Equation for Infinite Horizon
Abstract
:1. Introduction
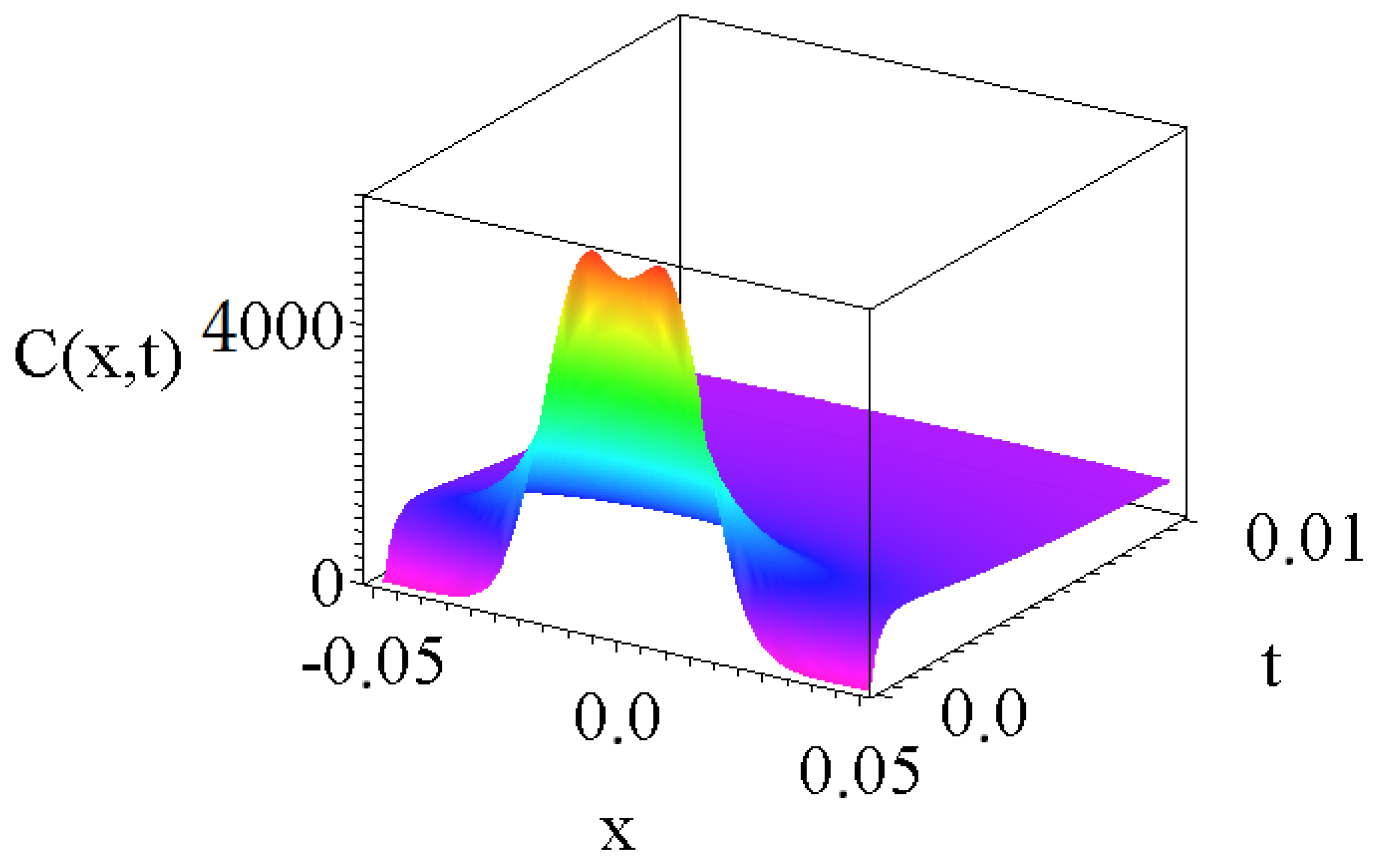
2. Theory and Results
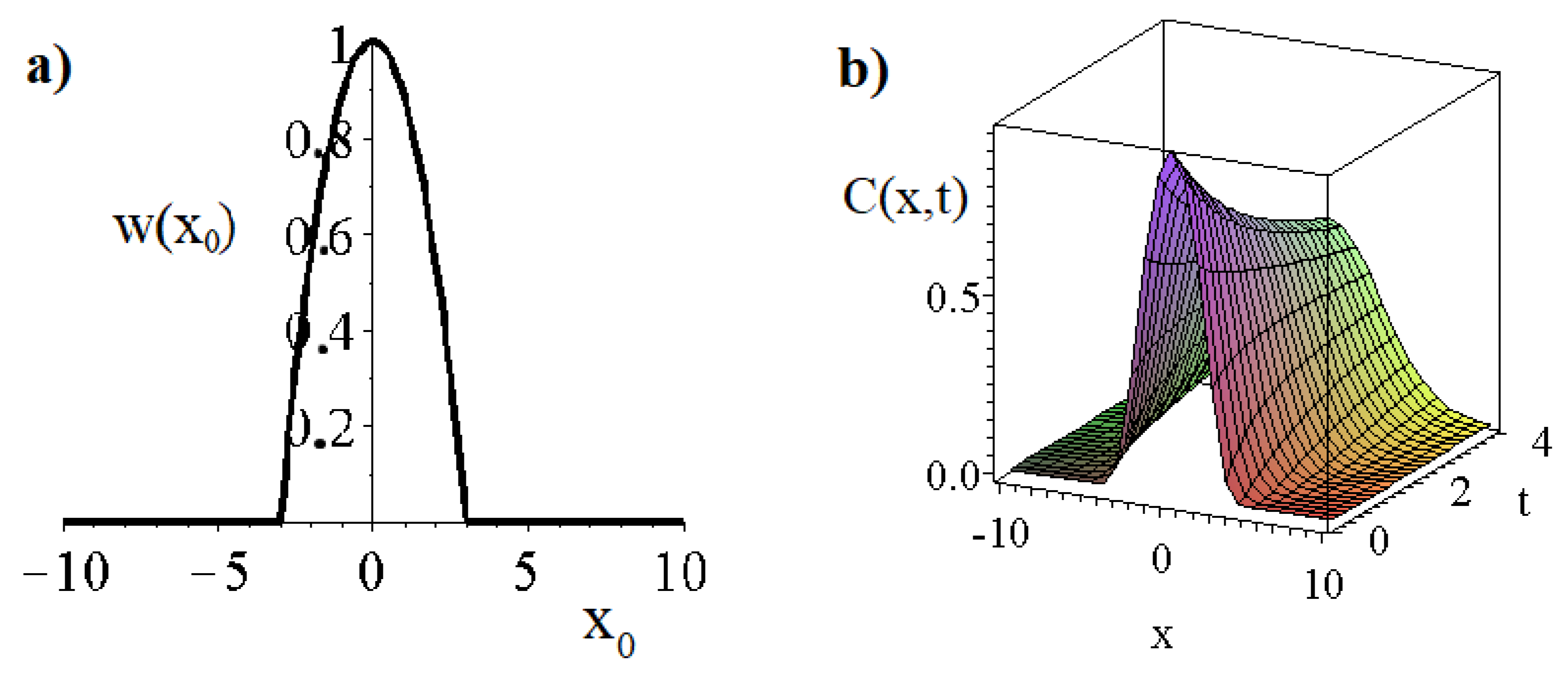
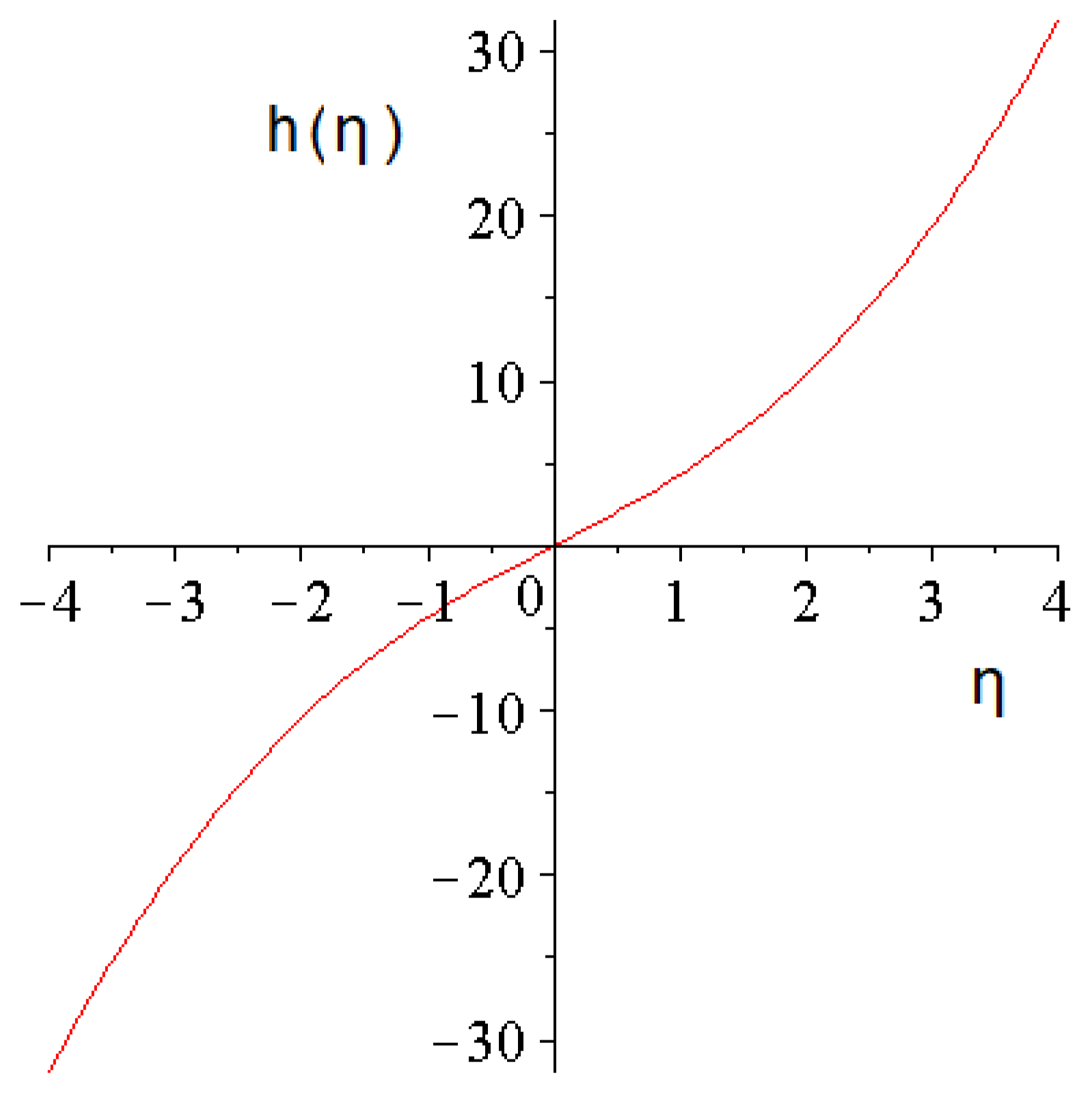
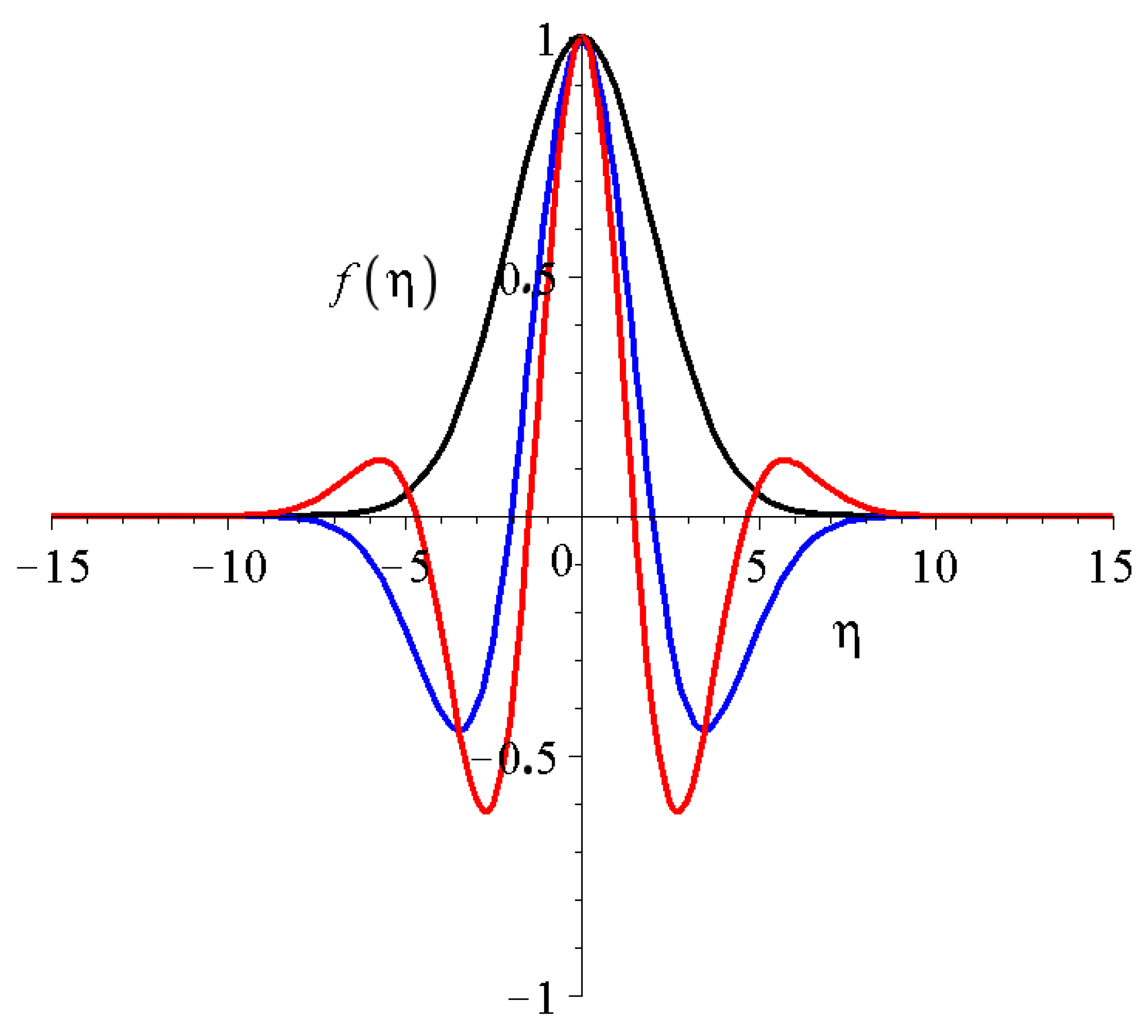
3. The Properties of the Shape Functions and Solutions
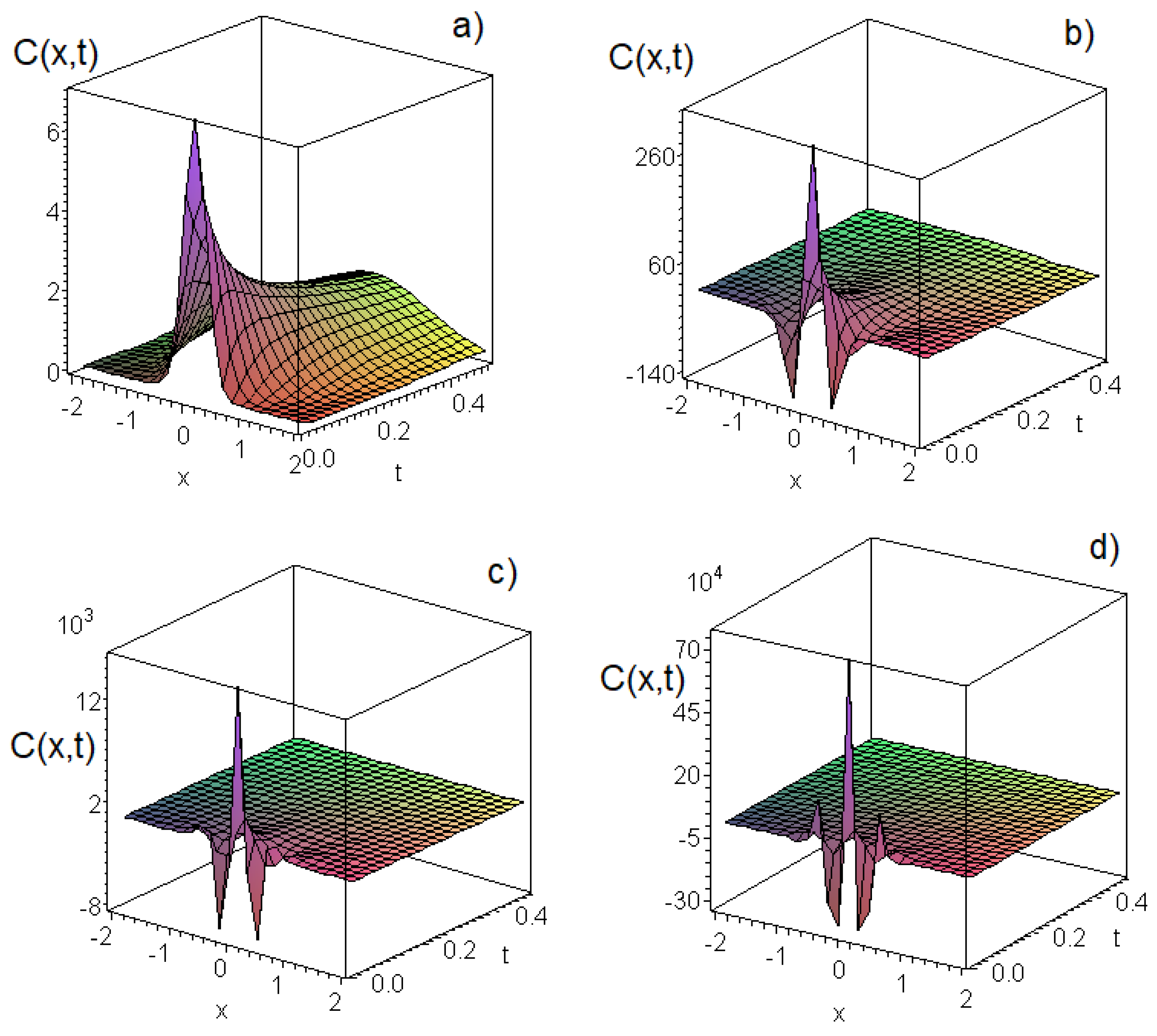
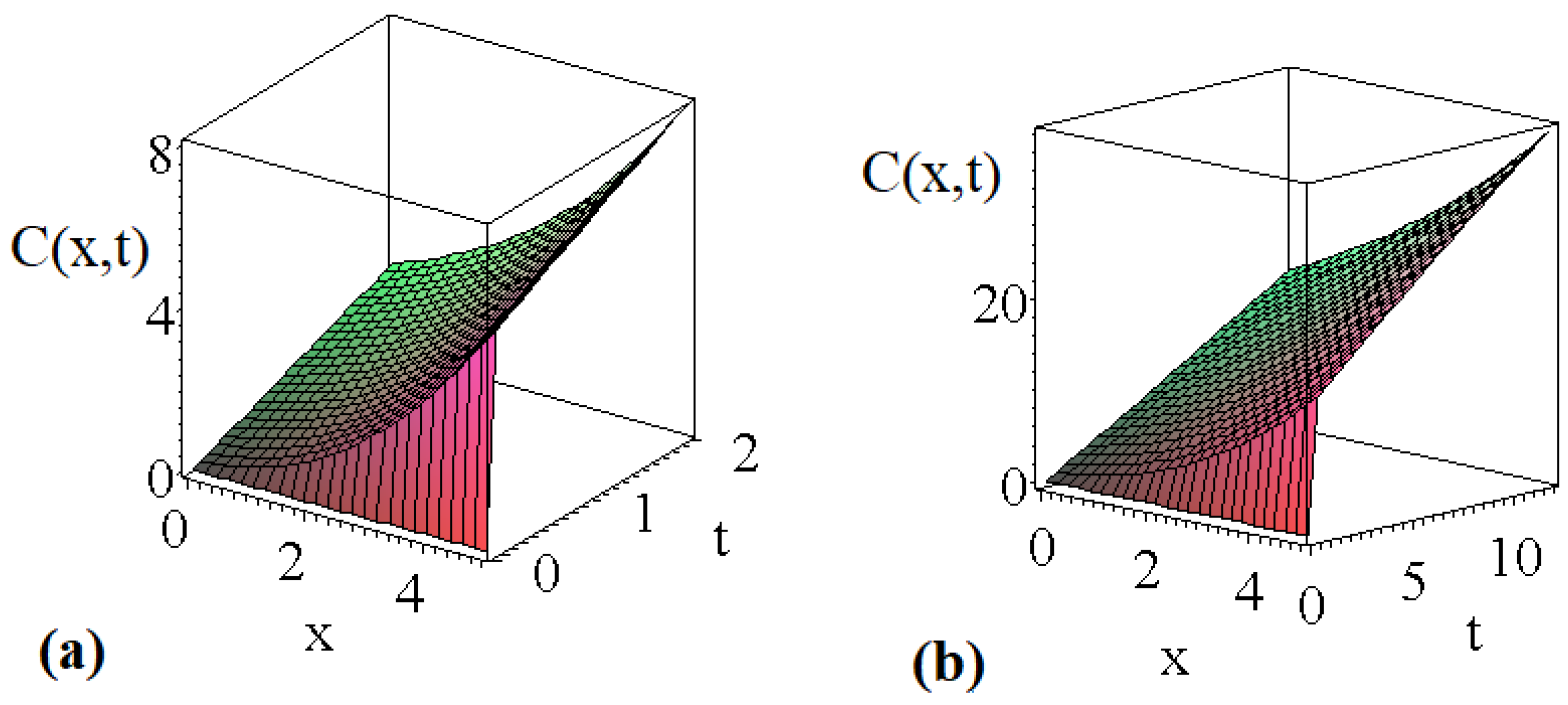
4. The Diffusion Equation with Constant Source
5. Summary and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Crank, J. The Mathematics of Diffusion; Clarendon Press: Oxford, UK, 1956. [Google Scholar]
- Ghez, R. Diffusion Phenomena; Dover Publication: Mineola, NY, USA, 2001. [Google Scholar]
- Bennett, T.D. Transport by Advection and Diffusion: Momentum, Heat and Mass Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Lienhard, J.H., IV; Lienhard, J.H., V. A Heat Transfer Textbook, 4th ed.; Phlogiston Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Newman, J.; Battaglia, V. The Newman Lectures on Transport Phenomena; Jenny Stanford Publishing: Dubai, United Arab Emirates, 2021. [Google Scholar]
- Kardar, M.; Parisi, G.; Zhang, Y.-C. Dynamic scaling of growing interfaces. Phys. Rev. Lett. 1986, 56, 889. [Google Scholar] [CrossRef]
- Barna, I.F.; Bognár, G.; Guedda, M.; Hriczó, K.; Mátyás, L. Analytic self-similar solutions of the Kardar-Parisi-Zhang interface growing equation with various noise terms. Math. Model. Anal. 2020, 25, 241. [Google Scholar] [CrossRef]
- Barabási, A.L.; Stanley, E. Fractal Concepts in Surface Growth; Cambridge University Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Mátyás, L.; Gaspard, P. Entropy production in diffusion-reaction systems: The reactive random Lorentz gas. Phys. Rev. E 2005, 71, 036147. [Google Scholar] [CrossRef] [PubMed]
- Mátyás, L.; Barna, I.F. General self-similar solutions of diffusion equation and related constructions. Rom. J. Phys. 2022, 67, 101. [Google Scholar]
- Barna, I.F.; Mátyás, L. Advanced Analytic Self-Similar Solutions of Regular and Irregular Diffusion Equations. Mathematics 2022, 10, 3281. [Google Scholar] [CrossRef]
- Cannon, J.R. The One-Dimensional Heat Equation; Addison-Wesley Publishing: Reading, MA, USA, 1984. [Google Scholar]
- Cole, K.D.; Beck, J.V.; Haji-Sheikh, A.; Litkouhi, B. Heat Conduction Using Green’s Functions; Series in Computational and Physical Processes in Mechanics and Thermal Sciences (2nd ed); CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Mátyás, L.; Tél, T.; Vollmer, J. Thermodynamic cross effects from dynamical systems. Phys. Rev. E 2000, 61, R3295. [Google Scholar] [CrossRef]
- Thambynayagam, R.K.M. The Diffusion Handbook: Applied Solutions for Engineers; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Michaud, G.; Alecian, G.; Richer, G. Atomic Diffusion in Stars; Springer: New York, NY, USA, 2013; Volume 70. [Google Scholar]
- Murray, J.D. Mathematical Biology II: Spatial Models and Biomedical Applications, 3rd ed.; Springer: New York, NY, USA, 2003. [Google Scholar]
- Alebraheem, J. Predator interference in a predator-prey model with mixed functional and numerical responses. Hindawi J. Math. 2023, 2023, 4349573. [Google Scholar] [CrossRef]
- Perthame, B. Parabolic Equations in Biology; Springer International Publishing: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Szép, R.; Mateescu, E.; Nechifor, A.C.; Keresztesi, Á. Chemical characteristics and source analysis on ionic composition of rainwater collected in the Charpatians “Cold Pole”, Ciuc basin, Eastern Carpatians, Romania. Environ. Sci. Pollut. Res. 2017, 24, 27288. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, D.T.; Seitaridou, E. Simple Brownian Diffusion; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Tálos, K.; Páger, C.; Tonk, S.; Majdik, C.; Kocsis, B.; Kilár, F.; Pernyeszi, T. Cadmium biosorption on native Saccharomyces cerevisiae cells in aqueous suspension. Acta Univ. Sapientiae Agric. Environ. 2009, 1, 20. [Google Scholar]
- Nechifor, G.; Voicu, S.I.; Nechifor, A.C.; Garea, S. Nanostructured hybrid membrane polysulfone-carbon nanotubes for hemodialysis. Desalination 2009, 241, 342. [Google Scholar] [CrossRef]
- Lv, J.; Ren, K.; Chen, Y. CO2 diffusion in various carbonated beverages: A molecular dynamic study. Phys. Chem. 2018, 122, 1655. [Google Scholar] [CrossRef]
- Hägerstrand, T. Innovation Diffusion as a Spatial Process; The University of Chicago Press: Chicago, IL, USA, 1967. [Google Scholar]
- Rogers, E.M. Diffusion of Innovations; The Free Press: Los Angeles, CA, USA, 1983. [Google Scholar]
- Nakicenovic, N.; Griübler, A. Diffusion of Technologies and Social Behavior; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Bunde, A.; Kärger, J.C.; Vogl, G. Diffusive Spreading in Nature, Technology and Society; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Vogel, G. Adventure Diffusion; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Mazzoni, T. A First Course in Quantitative Finance; Cambridge University Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Lázár, E. Quantifying the economic value of warranties: A survey. Acta Univ. Sapientiae Econ. Bus. 2014, 2, 75. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Rogolino, P.; Kovács, R.; Ván, P.; Cimmelli, V.A. Generalized heat-transport equations: Parabolic and hyperbolic models. Contin. Mech. Thermodyn. 2018, 30, 1245. [Google Scholar] [CrossRef]
- Jalghaf, H.K.; Kovács, E.; Majár, J.; Nagy, A.; Askar, A.H. Explicit stable finite difference methods for diffusion-reaction type equations. Mathematics 2021, 9, 3308. [Google Scholar] [CrossRef]
- Nagy, A.; Saleh, M.; Omle, I.; Kareem, H.; Kovács, E. New stable, explicit shifted-hopscotch algoritms for the heat equation. Math. Comput. Appl. 2021, 26, 61. [Google Scholar]
- Ezzahri, Y.; Ordonez-Miranda, J.; Joulain, K. Heat transport in semiconductor crystals under large temperature gradients. Int. J. Heat Mass Transf. 2017, 108, 1357. [Google Scholar] [CrossRef]
- Cussler, E.L. Diffusion: Mass Transfer in Fluid Systems, 3rd ed.; Cambridge University Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Bluman, G.W.; Cole, J.D. The general similarity solution of the heat equation. J. Math. Mech. 1969, 18, 1025. [Google Scholar]
- Sedov, L. Similarity and Dimensional Methods in Mechanics; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Zel’dovich, Y.B.; Raizer, Y.P. Physics of Shock Waves and High Temperature Hydrodynamic Phenomena; Academic Press: New York, NY, USA, 1966. [Google Scholar]
- Baraneblatt, G.I. Similarity, Self-Similarity, and Intermediate Asymptotics; Consultants Bureau: New York, NY, USA, 1979. [Google Scholar]
- Barna, I.F.; Mátyás, L. Analytic solutions for the three dimensional compressible Navier-Stokes equation. Fluid Dyn. Res. 2014, 46, 055508. [Google Scholar] [CrossRef]
- Barna, I.F.; Pocsai, M.A.; Lökös, S.; Mátyás, L. Rayleigh-Benard convection in the generalized Oberbeck-Boussinesq system. Chaos Solitons Fractals 2017, 103, 336. [Google Scholar] [CrossRef]
- Barna, I.F.; Pocsai, M.A.; Barnaföldi, G.G. Self-similar solutions of a gravitating dark fluid. Mathematics 2022, 10, 3220. [Google Scholar] [CrossRef]
- Barna, I.F.; Pocsai, M.A.; Mátyás, L. Analytic solutions of the Madelung equation. J. Gen. Lie Theory Appl. 2017, 11, 1000271. [Google Scholar]
- Csanád, M.; Vargyas, M. Observables from a solution of (1+3)-dimensional relativistic hydrodynamics. Eur. Phys. J. A 2010, 44, 473. [Google Scholar] [CrossRef]
- Barna, I.F.; Mátyás, L. Analytic solutions for the one-dimensional compressible Euler equation with heat conduction closed with different kind of equation of states. Miskolc Math. Notes 2013, 14, 785. [Google Scholar] [CrossRef]
- Nath, G.; Singh, S. Approximate analytical solution for shock wave in rotational axisymetric perfect gas with azimutal magnetic field: Isotermal flow. J. Astrophys. Astron. 2019, 40, 50. [Google Scholar] [CrossRef]
- Sahu, P.K. Shock wave driven out by a piston in a mixture of a non-ideal gas and small solid particles under the influence of azimuthal or axial magnetic field. Braz. J. Phys. 2020, 50, 548. [Google Scholar] [CrossRef]
- Kanchana, C.; Su, Y.; Zhao, Y. Primary and secondary instabilities in Rayleigh-Benard convention of water-copper nanoliquid. Commun. Nonlinear Sci. Numer. Simul. 2020, 83, 105129. [Google Scholar] [CrossRef]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Kythe, P.K. Green’s Functions and Linear Differential Equations; Chapman & Hall/CRC Applied Mathematics and Nonliner Science; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Rother, T. Green’s Functions in Classical Physics; Lecture Notes in Physics; Springer International Publishing: New York, NY, USA, 2017; Volume 938. [Google Scholar]
- Bronshtein, I.N.; Semendyayev, K.A.; Musiol, G.; Mühlig, H. Handbook of Mathematics; Springer: Wiesbaden, Germany, 2007. [Google Scholar]
- Greiner, W.; Reinhardt, J. Quantum Electrodynamics; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Claus, I.; Gaspard, P. Fractals and dynamical chaos in a two-dimensional Lorentz gas with sinks. Phys. Rev. E 2001, 63, 036227. [Google Scholar] [CrossRef]
- Rápó, E.; Tonk, S. Factors affecting synthetic dye adsorption; desorption studies: A review of results from the last five years (2017–2021). Molecules 2021, 26, 5419. [Google Scholar] [CrossRef]
- Boltzmann, L. Zur Intergration der Diffusionsgleichung bei variabeln Diffusionscoefficienten. Ann. Phys. 1894, 53, 959. [Google Scholar] [CrossRef]
- Lonngren, K.E. Self similar solution of plasma equations. Proc. Indian Acad. Sci. 1977, 86, 125. [Google Scholar] [CrossRef]
- Mehrer, H.; Stolwijk, N.A. Heroes and highlights in the history of diffusion. Diffus. Fundam. 2009, 11, 1. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mátyás, L.; Barna, I.F. Even and Odd Self-Similar Solutions of the Diffusion Equation for Infinite Horizon. Universe 2023, 9, 264. https://doi.org/10.3390/universe9060264
Mátyás L, Barna IF. Even and Odd Self-Similar Solutions of the Diffusion Equation for Infinite Horizon. Universe. 2023; 9(6):264. https://doi.org/10.3390/universe9060264
Chicago/Turabian StyleMátyás, László, and Imre Ferenc Barna. 2023. "Even and Odd Self-Similar Solutions of the Diffusion Equation for Infinite Horizon" Universe 9, no. 6: 264. https://doi.org/10.3390/universe9060264
APA StyleMátyás, L., & Barna, I. F. (2023). Even and Odd Self-Similar Solutions of the Diffusion Equation for Infinite Horizon. Universe, 9(6), 264. https://doi.org/10.3390/universe9060264