Study of Hidden-Charm and Hidden-Bottom Pentaquark Resonances in the Quark Model
Abstract
:1. Introduction
2. Quark Model and Wave Functions
2.1. The Quark Delocalization Color Screening Model
2.2. Wave Functions
3. The Results and Discussions
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Resonating Group Method for Bound-State and Scattering Problems
References
- Aaij, R.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; et al. Observation of J/ψp resonances consistent with pentaquark states in →J/ψK−p decays. Phys. Rev. Lett. 2015, 115, 072001. [Google Scholar]
- Chen, R.; Liu, X.; Li, X.Q.; Zhu, S.L. Identifying exotic hidden-charm pentaquarks. Phys. Rev. Lett. 2015, 115, 132002. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.X.; Chen, W.; Liu, X.; Steele, T.G.; Zhu, S.L. Towards exotic hidden-charm pentaquarks in QCD. Phys. Rev. Lett. 2015, 115, 172001. [Google Scholar] [CrossRef]
- Roca, L.; Nieves, J.; Oset, E. LHCb pentaquark as a molecular state. Phys. Rev. D 2015, 92, 094003. [Google Scholar] [CrossRef]
- He, J. and interactions and the LHCb hidden-charmed pentaquarks. Phys. Lett. B 2016, 753, 547–551. [Google Scholar] [CrossRef]
- Huang, H.X.; Deng, C.R.; Ping, J.L.; Wang, F. Possible pentaquarks with heavy quarks. Eur. Phys. J. C 2016, 76, 624. [Google Scholar] [CrossRef]
- Yang, G.; Ping, J.L.; Wang, F. The structure of pentaquarks in the chiral quark model. Phys. Rev. D 2017, 95, 014010. [Google Scholar] [CrossRef]
- Meissner, U.G.; Oller, J.A. Testing the χc1p composite nature of the Pc(4450). Phys. Lett. B 2015, 751, 59–62. [Google Scholar] [CrossRef]
- Xiao, C.W.; Meissner, U.G. J/ψ(ηc)N and Υ(ηb)N cross-sections. Phys. Rev. D 2015, 92, 114002. [Google Scholar] [CrossRef]
- Chen, R.; Liu, X.; Zhu, S.L. Hidden-charm molecular pentaquarks and their charm-strange partners. Nucl. Phys. A 2016, 954, 406–421. [Google Scholar] [CrossRef]
- Chen, H.X.; Cui, E.L.; Chen, W.; Liu, X.; Steele, T.G.; Zhu, S.L. QCD sum rule study of hidden-charm pentaquarks. Eur. Phys. J. C 2016, 76, 572. [Google Scholar] [CrossRef]
- Azizi, K.; Sarac, Y.; Sundu, H. Analysis of (4380) and (4450) as pentaquark states in the molecular picture with QCD sum rules. Phys. Rev. D 2017, 95, 094016. [Google Scholar] [CrossRef]
- Lebed, R.F. The pentaquark candidates in the dynamical diquark picture. Phys. Lett. B 2015, 749, 454–457. [Google Scholar] [CrossRef]
- Zhu, R.L.; Qiao, C.F. Pentaquark states in a diquark–triquark model. Phys. Lett. B 2016, 756, 259–264. [Google Scholar] [CrossRef]
- Maiani, L.; Polosa, A.D.; Riquer, V. The new pentaquarks in the diquark model. Phys. Lett. B 2015, 749, 289–291. [Google Scholar] [CrossRef]
- Anisovich, V.V.; Matveev, M.A.; Nyiri, J.; Sarantsev, A.V.; Semenova, A.N. Pentaquarks and resonances in the pJ/ψ spectrum. arXiv 2015, arXiv:1507.07652. [Google Scholar]
- Ghosh, R.; Bhattacharya, A.; Chakrabarti, B. A study on (4380) and in the quasi particle diquark model. Phys. Part. Nucl. Lett. 2017, 14, 550–552. [Google Scholar] [CrossRef]
- Wang, Z.G. Analysis of Pc(4380) and Pc(4450) as pentaquark states in the diquark model with QCD sum rules. Eur. Phys. J. C 2016, 76, 70. [Google Scholar] [CrossRef]
- Mironov, A.; Morozov, A. Is the pentaquark doublet a hadronic molecule? JETP Lett. 2015, 102, 271–273. [Google Scholar] [CrossRef]
- Scoccola, N.N.; Riska, D.O.; Rho, M. Pentaquark candidates (4380) and (4450) within the soliton picture of baryons. Phys. Rev. D 2015, 92, 051501. [Google Scholar] [CrossRef]
- Guo, F.K.; Meissner, U.G.; Wang, W.; Yang, Z. How to reveal the exotic nature of the Pc(4450). Phys. Rev. D 2015, 92, 071502. [Google Scholar] [CrossRef]
- Liu, X.H.; Wang, Q.; Zhao, Q. Understanding the newly observed heavy pentaquark candidates. Phys. Lett. B 2016, 757, 231–236. [Google Scholar] [CrossRef]
- Mikhasenko, M. A triangle singularity and the LHCb pentaquarks. arXiv 2015, arXiv:1507.06552. [Google Scholar]
- Skerbis, U.; Prelovsek, S. Nucleon-J/ψ and nucleon-ηc scattering in Pc pentaquark channels from LQCD. Phys. Rev. D 2019, 99, 094505. [Google Scholar] [CrossRef]
- Aaij, R.; Abellan Beteta, C.; Adeva, B.; Adinolfi, M.; Aidala, C.A.; Ajaltouni, Z.; Akar, S.; Albicocco, P.; Albrecht, J.; Alessio, F.; et al. Observation of a narrow pentaquark state, Pc(4312)+, and of two-peak structure of the Pc(4450)+. Phys. Rev. Lett. 2019, 122, 222001. [Google Scholar] [PubMed]
- Chen, H.X.; Chen, W.; Zhu, S.L. Possible interpretations of the Pc(4312), Pc(4440), and Pc(4457). Phys. Rev. D 2019, 100, 051501. [Google Scholar] [CrossRef]
- Chen, R.; Sun, Z.F.; Liu, X.; Zhu, S.L. Strong LHCb evidence supporting the existence of the hidden-charm molecular pentaquarks. Phys. Rev. D 2019, 100, 011502. [Google Scholar] [CrossRef]
- Liu, M.Z.; Pan, Y.W.; Peng, F.Z.; Sanchez, M.S.; Geng, L.S.; Hosaka, A.; Valderrama, P. Emergence of a complete heavy-quark spin symmetry multiplet: Seven molecular pentaquarks in light of the latest LHCb analysis. Phys. Rev. Lett. 2019, 122, 242001. [Google Scholar] [CrossRef]
- He, J. Study of Pc(4457), Pc(4440), and Pc(4312) in a quasipotential Bethe-Salpeter equation approach. Eur. Phys. J. C 2019, 79, 393. [Google Scholar] [CrossRef]
- Guo, F.K.; Jing, H.J.; Meissner, U.-G.; Sakai, S. Isospin breaking decays as a diagnosis of the hadronic molecular structure of the Pc(4457). Phys. Rev. D 2019, 99, 091501. [Google Scholar] [CrossRef]
- Wu, J.J.; Molina, R.; Oset, E.; Zou, B.S. Prediction of narrow N* and Λ* resonances with hidden charm above 4 GeV. Phys. Rev. Lett. 2010, 105, 232001. [Google Scholar] [CrossRef]
- Yang, Z.C.; Sun, Z.F.; He, J.; Liu, X.; Zhu, S.L. The possible hidden-charm molecular baryons composed of anti-charmed meson and charmed baryon. Chin. Phys. C 2012, 36, 6–13. [Google Scholar] [CrossRef]
- Chen, H.X.; Chen, W.; Liu, X.; Zhu, S.L. The hidden-charm pentaquark and tetraquark states. Phys. Rep. 2016, 639, 1–121. [Google Scholar] [CrossRef]
- Liu, Y.R.; Chen, H.X.; Chen, W.; Liu, X.; Zhu, S.L. Pentaquark and tetraquark states. Prog. Part. Nucl. Phys. 2019, 107, 237–320. [Google Scholar] [CrossRef]
- Yang, G.; Ping, J.L.; Segovia, J. Tetra- and penta-quark structures in the constituent quark model. Symmetry 2020, 12, 1869. [Google Scholar] [CrossRef]
- Aoki, S. Nucleon-nucleon interactions via Lattice QCD: Methodology: HAL QCD approach to extract hadronic interactions in lattice QCD. Eur. Phys. J. A 2013, 49, 81. [Google Scholar] [CrossRef]
- Wang, F.; Wu, G.H.; Teng, L.J.; Goldman, T. Quark delocalization, color screening, and nuclear intermediate range attraction. Phys. Rev. Lett. 1992, 69, 2901–2904. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.H.; Teng, L.J.; Ping, J.L.; Wang, F.; Goldman, T. Quark delocalization, color screening, and N N intermediate range attraction: P waves. Phys. Rev. C 1996, 53, 1161–1166. [Google Scholar] [CrossRef] [PubMed]
- Ping, J.L.; Wang, F.; Goldman, T. Effective baryon baryon potentials in the quark delocalization and color screening model. Nucl. Phys. A 1999, 657, 95–109. [Google Scholar] [CrossRef]
- Wu, G.H.; Ping, J.L.; Teng, L.J.; Wang, F.; Goldman, T. Quark delocalization, color screening model and nucleon baryon scattering. Nucl. Phys. A 2000, 673, 279–297. [Google Scholar] [CrossRef]
- Ping, J.L.; Huang, H.X.; Pang, H.R.; Wang, F.; Wong, C.W. Quark models of dibaryon resonances in nucleon-nucleon scattering. Phys. Rev. C 2009, 79, 024001. [Google Scholar] [CrossRef]
- Huang, H.X.; Ping, J.L. Investigating the hidden-charm and hidden-bottom pentaquark resonances in scattering process. Phys. Rev. D 2019, 99, 014010. [Google Scholar] [CrossRef]
- Valcarce, A.; Garcilazo, H.; Fernandez, F.; Gonzalez, P. Quark-model study of few-baryon systems. Rep. Prog. Phys. 2005, 68, 965–1042. [Google Scholar] [CrossRef]
- Vijande, J.; Fernandez, F.; Valcarce, A. Constituent quark model study of the meson spectra. J. Phys. G 2005, 31, 481. [Google Scholar] [CrossRef]
- Laermann, E.; Langhammer, F.; Schmitt, I.; Zerwas, P.M. The interquark potential: SU(2) color gauge theory with fermions. Phys. Lett. B 1986, 173, 437–442. [Google Scholar] [CrossRef]
- Born, K.D.; Laermann, E.; Pirch, N.; Walsh, T.F.; Zerwas, P.M. Hadron properties in lattice QCD with dynamical fermions. Phys. Rev. D 1989, 40, 1653–1663. [Google Scholar] [CrossRef]
- Xu, M.M.; Yu, M.L.; Liu, L.S. Examining the crossover from hadronic to partonic phase in QCD. Phys. Rev. Lett. 2008, 100, 092301. [Google Scholar] [CrossRef]
- Kamimura, M. Chapter V. A Coupled Channel Variational Method for Microscopic Study of Reactions between Complex Nuclei M. Suppl. Prog. Theor. Phys. 1977, 62, 236. [Google Scholar] [CrossRef]
- Wu, J.J.; Molina, R.; Oset, E.; Zou, B.S. Dynamically generated N* and Λ* resonances in the hidden charm sector around 4.3 GeV. Phys. Rev. C 2011, 84, 015202. [Google Scholar]
- Wu, J.J.; Zhao, L.; Zou, B.S. Prediction of super-heavy N* and Λ* resonances with hidden beauty. Phys. Lett. B 2012, 709, 70–76. [Google Scholar] [CrossRef]
- Abazov, V.M.; Abbott, B.; Acharya, B.S.; Adams, M.; Adams, T.; Agnew, J.P.; Alexeev, G.D.; Alkhazov, G.; Altona, A.; Askew, A.; et al. Inclusive production of the Pc resonances in collisions. arXiv 2019, arXiv:1910.11767. [Google Scholar]
- Ali, A.; Amaryan, M.; Anassontzis, E.G.; Austregesilo, A.; Baalouch, M.; Barbosa, F.; Barlow, J.; Barnes, A.; Barriga, E.; Beattie, T.D.; et al. First Measurement of Near-Threshold J/ψ Exclusive Photoproduction off the Proton. Phys. Rev. Lett. 2019, 123, 072001. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, S.; Afzal, F.; Akondi, C.S.; Albrecht, M.; Amaryan, M.; Arroyave, V.; Asaturyan, A.; Austregesilo, A.; Baldwin, Z.; Barbosa, F.; et al. Measurement of the J/ψ photoproduction cross-section over the full near-threshold kinematic region. arXiv 2023, arXiv:2304.03845. [Google Scholar]
- Hiller Blin, A.N.; Fernandez-Ramirez, C.; Jackura, A.; Mathieu, V.; Mokeev, V.I.; Pilloni, A.; Szczepaniak, A.P. Studying the Pc(4450) resonance in J/ψ photoproduction off protons. Phys. Rev. D 2016, 94, 034002. [Google Scholar]
- Kubarovsky, V.; Voloshin, M.B. Search for hidden-charm pentaquark with CLAS12. arXiv 2016, arXiv:1609.00050. [Google Scholar]
- Mezianin, Z.E.; Joostenn, S.; Paolonen, M.; Chudakovm, E.; Jonesm, M.; Adhikarig, K.; Aniold, K.; Armstrongb, W.; Arringtonb, J.; Asaturyan, A.; et al. A Search for the LHCb charmed ’pentaquark’ using photo-production of J/ψ at threshold in Hall C at Jefferson Lab. arXiv 2016, arXiv:1609.00676. [Google Scholar]
- Erni, W.; Keshelashvili, I.; Krusche, B.; Steinacher, M.; Heng, Y.; Liu, Z.; Liu, H.; Shen, X.; Wang, O.; Xu, H.; et al. Physics Performance Report for PANDA: Strong Interaction Studies with Antiprotons. arXiv 2009, arXiv:0903.3905. [Google Scholar]
- Ptitsyn, V. Polarized beams at EICs. AIP Conf. Proc. 2009, 1149, 735–740. [Google Scholar]
- Joosten, S.; Meziani, Z.E. Heavy quarkonium production at threshold: From JLab to EIC. arXiv 2018, arXiv:1802.02616. [Google Scholar]
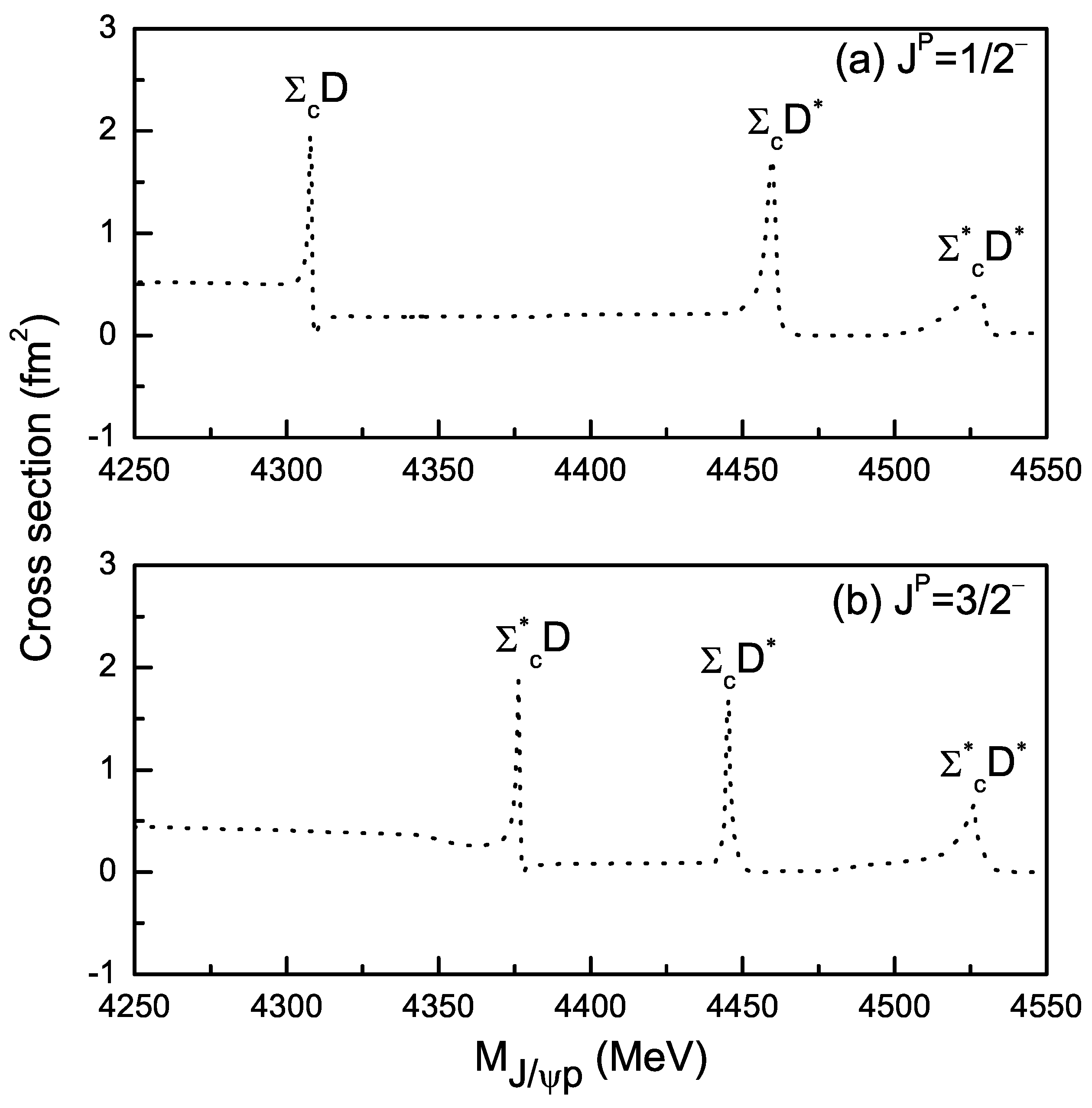
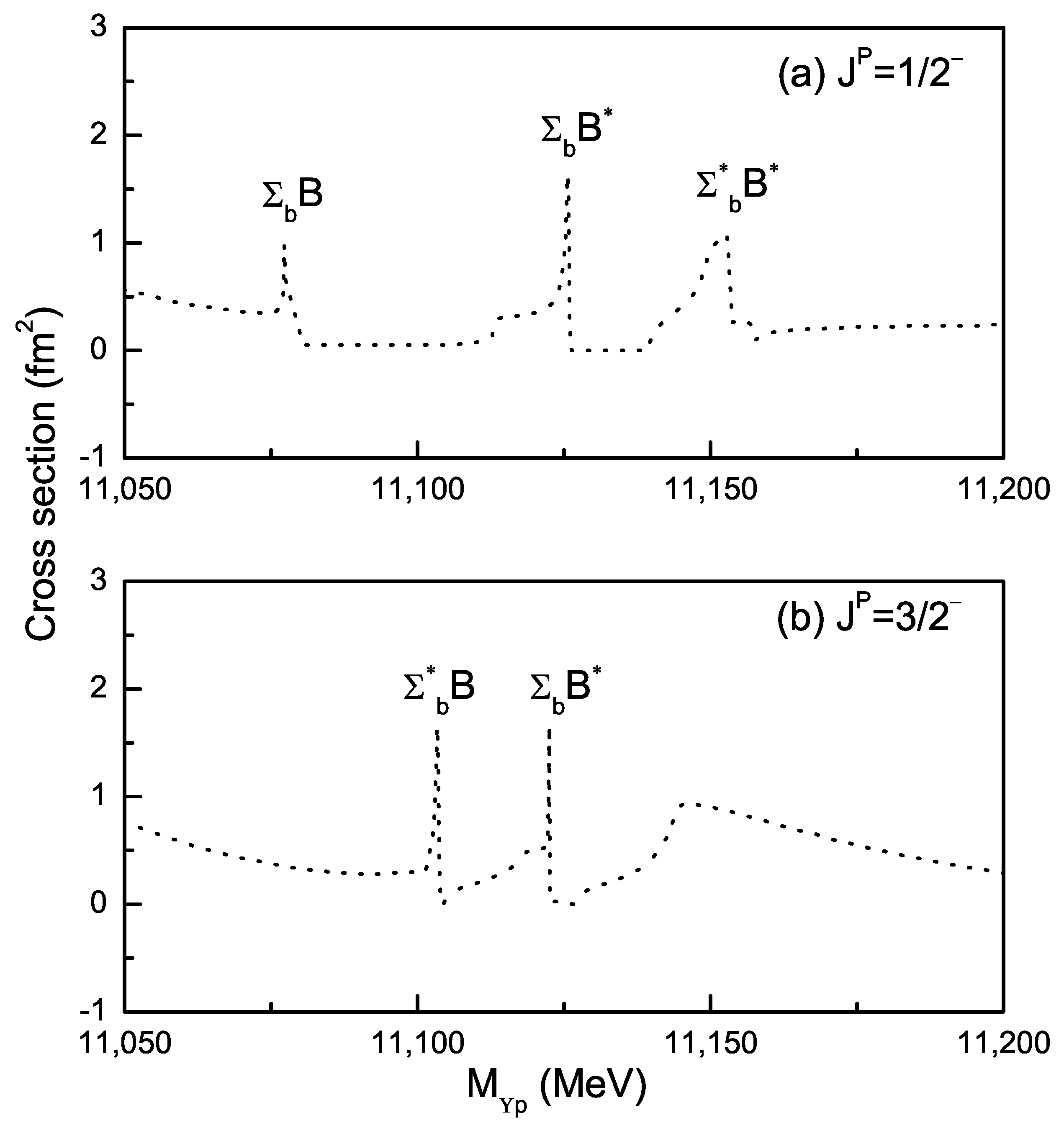
| Channels | |||||
|---|---|---|---|---|---|
| hidden charm | |||||
| hidden bottom | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Wu, Y.; Huang, H.; Ping, J.; Yang, Y. Study of Hidden-Charm and Hidden-Bottom Pentaquark Resonances in the Quark Model. Universe 2023, 9, 265. https://doi.org/10.3390/universe9060265
Zhu X, Wu Y, Huang H, Ping J, Yang Y. Study of Hidden-Charm and Hidden-Bottom Pentaquark Resonances in the Quark Model. Universe. 2023; 9(6):265. https://doi.org/10.3390/universe9060265
Chicago/Turabian StyleZhu, Xinmei, Yuheng Wu, Hongxia Huang, Jialun Ping, and Youchang Yang. 2023. "Study of Hidden-Charm and Hidden-Bottom Pentaquark Resonances in the Quark Model" Universe 9, no. 6: 265. https://doi.org/10.3390/universe9060265
APA StyleZhu, X., Wu, Y., Huang, H., Ping, J., & Yang, Y. (2023). Study of Hidden-Charm and Hidden-Bottom Pentaquark Resonances in the Quark Model. Universe, 9(6), 265. https://doi.org/10.3390/universe9060265







