Compact Stars in the vBag Model and Its f-Mode Oscillations
Abstract
:1. Introduction
2. EoS and Macrostructure of Compact Stars
2.1. Hadronic Phase
2.2. Quark Phase
2.3. Mixed Phase: Gibbs Construction
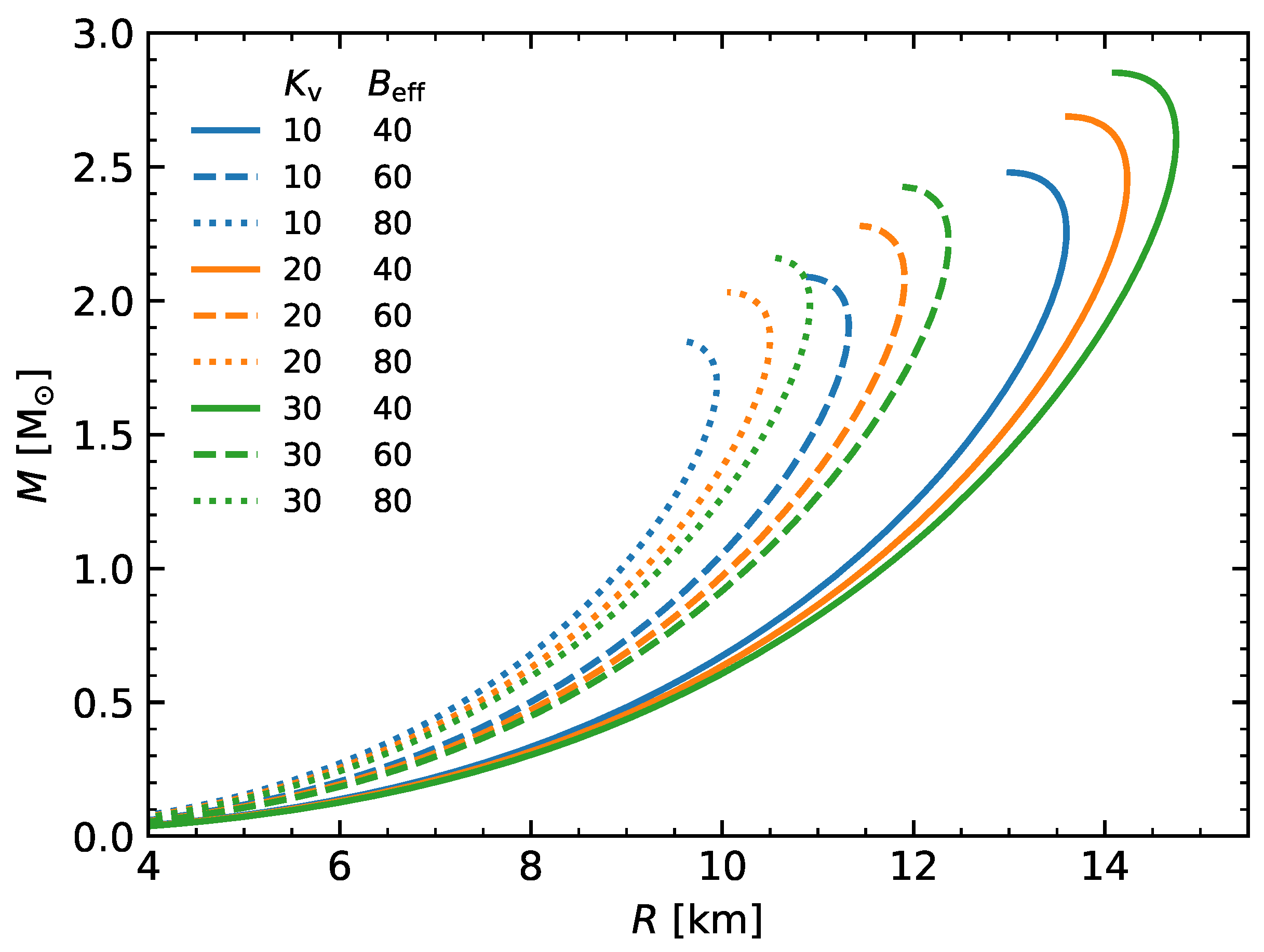
2.4. Macroscopic Structure of Compact Stars
3. Constraints on the EoS of Quark Matter in the vBag Model
- Current bounds for the effective tidal deformability as reported by the LIGO–Virgo collaboration have been placed at at a 90% confidence for low-spin priors [45]. Furthermore, the dimensionless tidal deformability of a star at the Chandrasekhar mass has been reported at under the same conditions [4,69].
4. The f-Mode Oscillations and Related Universal Relations of Hybrid Stars in the vBag Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blaschke, D.; Chamel, N. Phases of Dense Matter in Compact Stars. In The Physics and Astrophysics of Neutron Stars; Rezzolla, L., Pizzochero, P., Jones, D.I., Rea, N., Vidaña, I., Eds.; Astrophysics and Space Science Library; Springer: Cham, Switzerland, 2018; Volume 457, p. 337. [Google Scholar] [CrossRef] [Green Version]
- Endo, T. Appearance of a quark matter phase in hybrid stars. J. Phys. Conf. Ser. 2014, 509, 012075. [Google Scholar] [CrossRef]
- Buballa, M. Phase diagram of quark matter under compact star conditions. In Quark Confinement and the Hadron Spectrum VII; Ribeiro, J.E.F.T., Brambilla, N., Vairo, A., Maung, K., Prosperi, G.M., Eds.; American Institute of Physics Conference Series; American Institute of Physics: Melville, NY, USA, 2007; Volume 892, pp. 476–478. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Radice, D.; Perego, A.; Zappa, F.; Bernuzzi, S. GW170817: Joint Constraint on the Neutron Star Equation of State from Multimessenger Observations. Astrophys. J. Lett. 2018, 852, L29. [Google Scholar] [CrossRef] [Green Version]
- Chatziioannou, K.; Haster, C.J.; Zimmerman, A. Measuring the neutron star tidal deformability with equation-of-state-independent relations and gravitational waves. Phys. Rev. D 2018, 97, 104036. [Google Scholar] [CrossRef] [Green Version]
- Malik, T.; Alam, N.; Fortin, M.; Providência, C.; Agrawal, B.K.; Jha, T.K.; Kumar, B.; Patra, S.K. GW170817: Constraining the nuclear matter equation of state from the neutron star tidal deformability. Phys. Rev. C 2018, 98, 035804. [Google Scholar] [CrossRef]
- Tews, I.; Margueron, J.; Reddy, S. Critical examination of constraints on the equation of state of dense matter obtained from GW170817. Phys. Rev. C 2018, 98, 045804. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.Y.; Zhou, E.P.; Li, A. Neutron Star Equation of State from the Quark Level in Light of GW170817. Astrophys. J. 2018, 862, 98. [Google Scholar] [CrossRef] [Green Version]
- Paschalidis, V.; Yagi, K.; Alvarez-Castillo, D.; Blaschke, D.B.; Sedrakian, A. Implications from GW170817 and I-Love-Q relations for relativistic hybrid stars. Phys. Rev. D 2018, 97, 084038. [Google Scholar] [CrossRef] [Green Version]
- Nandi, R.; Char, P. Hybrid Stars in the Light of GW170817. Astrophys. J. 2018, 857, 12. [Google Scholar] [CrossRef]
- Christian, J.E.; Zacchi, A.; Schaffner-Bielich, J. Signals in the tidal deformability for phase transitions in compact stars with constraints from GW170817. Phys. Rev. D 2019, 99, 023009. [Google Scholar] [CrossRef] [Green Version]
- Demorest, P.B.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 448. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72–76. [Google Scholar] [CrossRef] [Green Version]
- Fonseca, E.; Cromartie, H.T.; Pennucci, T.T.; Ray, P.S.; Kirichenko, A.Y.; Ransom, S.M.; Demorest, P.B.; Stairs, I.H.; Arzoumanian, Z.; Guillemot, L.; et al. Refined Mass and Geometric Measurements of the High-mass PSR J0740+6620. Astrophys. J. Lett. 2021, 915, L12. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef] [Green Version]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef] [Green Version]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Cottam, J.; Paerels, F.; Mendez, M. Gravitationally redshifted absorption lines in the X-ray burst spectra of a neutron star. Nature 2002, 420, 51–54. [Google Scholar] [CrossRef]
- Özel, F. Soft equations of state for neutron-star matter ruled out by EXO 0748-676. Nature 2006, 441, 1115–1117. [Google Scholar] [CrossRef] [Green Version]
- Chodos, A.; Jaffe, R.L.; Johnson, K.; Thorn, C.B.; Weisskopf, V.F. New extended model of hadrons. Phys. Rev. D 1974, 9, 3471–3495. [Google Scholar] [CrossRef] [Green Version]
- Rüster, S.B.; Rischke, D.H. Effect of color superconductivity on the mass and radius of a quark star. Phys. Rev. D 2004, 69, 045011. [Google Scholar] [CrossRef] [Green Version]
- Horvath, J.E.; Lugones, G. Self-bound CFL stars in binary systems: Are they “hidden” among the black hole candidates? Astron. Astrophys. 2004, 422, L1–L4. [Google Scholar] [CrossRef] [Green Version]
- Farhi, E.; Jaffe, R.L. Strange matter. Phys. Rev. D 1984, 30, 2379–2390. [Google Scholar] [CrossRef]
- Fraga, E.S.; Pisarski, R.D.; Schaffner-Bielich, J. Small, dense quark stars from perturbative QCD. Phys. Rev. D 2001, 63, 121702. [Google Scholar] [CrossRef] [Green Version]
- Klähn, T.; Fischer, T. Vector Interaction Enhanced Bag Model for Astrophysical Applications. Astrophys. J. 2015, 810, 134. [Google Scholar] [CrossRef] [Green Version]
- Gomes, R.O.; Char, P.; Schramm, S. Constraining Strangeness in Dense Matter with GW170817. Astrophys. J. 2019, 877, 139. [Google Scholar] [CrossRef] [Green Version]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef] [Green Version]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. II. Phys. Rev. 1961, 124, 246–254. [Google Scholar] [CrossRef] [Green Version]
- Alford, M.; Blaschke, D.; Drago, A.; Klähn, T.; Pagliara, G.; Schaffner-Bielich, J. Astrophysics: Quark matter in compact stars? Nature 2007, 445, 7–8. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, H.; Duarte, S.B.; Oliveira, J.C.T. EXO 0748-676 as a Quark Star. Int. J. Mod. Phys. D 2010, 19, 1447–1454. [Google Scholar] [CrossRef]
- Sotani, H.; Yasutake, N.; Maruyama, T.; Tatsumi, T. Signatures of hadron-quark mixed phase in gravitational waves. Phys. Rev. D 2011, 83, 024014. [Google Scholar] [CrossRef] [Green Version]
- Sotani, H.; Maruyama, T.; Tatsumi, T. Shear oscillations in the hadron-quark mixed phase. Nucl. Phys. A 2013, 906, 37–49. [Google Scholar] [CrossRef] [Green Version]
- Brillante, A.; Mishustin, I.N. Radial oscillations of neutral and charged hybrid stars. EPL (Europhys. Lett.) 2014, 105, 39001. [Google Scholar] [CrossRef] [Green Version]
- Vásquez Flores, C.; Lugones, G. Non-radial fluid oscillation modes of color superconducting self-bound stars. Astron. Nachrichten 2014, 335, 769. [Google Scholar] [CrossRef]
- Wei, W.; Irving, B.; Salinas, M.; Klähn, T.; Jaikumar, P. Camouflage of the Phase Transition to Quark Matter in Neutron Stars. Astrophys. J. 2019, 887, 151. [Google Scholar] [CrossRef]
- Wei, W.; Salinas, M.; Klähn, T.; Jaikumar, P.; Barry, M. Lifting the Veil on Quark Matter in Compact Stars with Core g-mode Oscillations. Astrophys. J. 2020, 904, 187. [Google Scholar] [CrossRef]
- Andersson, N.; Kokkotas, K.D. Towards gravitational wave asteroseismology. Mon. Not. R. Astron. Soc. 1998, 299, 1059–1068. [Google Scholar] [CrossRef] [Green Version]
- Kokkotas, K.D.; Schmidt, B.G. Quasi-Normal Modes of Stars and Black Holes. Living Rev. Relativ. 1999, 2, 2. [Google Scholar] [CrossRef] [Green Version]
- Kokkotas, K.D.; Apostolatos, T.A.; Andersson, N. The inverse problem for pulsating neutron stars: A ‘fingerprint analysis’ for the supranuclear equation of state. Mon. Not. R. Astron. Soc. 2001, 320, 307–315. [Google Scholar] [CrossRef] [Green Version]
- Punturo, M.; Abernathy, M.; Acernese, F.; Allen, B.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. The Einstein Telescope: A third-generation gravitational wave observatory. Class. Quantum Gravity 2010, 27, 194002. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Ackley, K.; Adams, C.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Exploring the sensitivity of next generation gravitational wave detectors. Class. Quantum Gravity 2017, 34, 044001. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Properties of the Binary Neutron Star Merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar] [CrossRef] [Green Version]
- Benhar, O.; Berti, E.; Ferrari, V. The imprint of the equation of state on the axial w-modes of oscillating neutron stars. Mon. Not. R. Astron. Soc. 1999, 310, 797–803. [Google Scholar] [CrossRef] [Green Version]
- Benhar, O.; Ferrari, V.; Gualtieri, L. Gravitational wave asteroseismology reexamined. Phys. Rev. D 2004, 70, 124015. [Google Scholar] [CrossRef]
- Tsui, L.K.; Leung, P.T. Universality in quasi-normal modes of neutron stars. Mon. Not. R. Astron. Soc. 2005, 357, 1029–1037. [Google Scholar] [CrossRef] [Green Version]
- Chan, T.K.; Sham, Y.H.; Leung, P.T.; Lin, L.M. Multipolar universal relations between f -mode frequency and tidal deformability of compact stars. Phys. Rev. D 2014, 90, 124023. [Google Scholar] [CrossRef] [Green Version]
- Zhao, T.; Lattimer, J.M. Universal relations for neutron star f -mode and g -mode oscillations. Phys. Rev. D 2022, 106, 123002. [Google Scholar] [CrossRef]
- Aziz, A.; Ray, S.; Rahaman, F.; Khlopov, M.; Guha, B.K. Constraining values of bag constant for strange star candidates. Int. J. Mod. Phys. D 2019, 28, 1941006. [Google Scholar] [CrossRef] [Green Version]
- Das, S.; Ray, S.; Khlopov, M.; Nandi, K.K.; Parida, B.K. Anisotropic compact stars: Constraining model parameters to account for physical features of tidal Love numbers. Ann. Phys. 2021, 433, 168597. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. Neutron Star Structure and the Equation of State. Astrophys. J. 2001, 550, 426–442. [Google Scholar] [CrossRef] [Green Version]
- Glendenning, N.K. First-order phase transitions with more than one conserved charge: Consequences for neutron stars. Phys. Rev. D 1992, 46, 1274–1287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baym, G.; Bethe, H.A.; Pethick, C.J. Neutron star matter. Nucl. Phys. A 1971, 175, 225–271. [Google Scholar] [CrossRef]
- Baym, G.; Pethick, C.; Sutherland, P. The Ground State of Matter at High Densities: Equation of State and Stellar Models. Astrophys. J. 1971, 170, 299. [Google Scholar] [CrossRef]
- Fuchs, C. The Relativistic Dirac-Brueckner Approach to Nuclear Matter. In Extended Density Functionals in Nuclear Structure Physics; Lalazissis, G.A., Ring, P., Vretenar, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 641, pp. 119–146. [Google Scholar]
- van Dalen, E.N.E.; Fuchs, C.; Faessler, A. The relativistic Dirac-Brueckner approach to asymmetric nuclear matter. Nucl. Phys. A 2004, 744, 227–248. [Google Scholar] [CrossRef] [Green Version]
- Klähn, T.; Blaschke, D.; Typel, S.; van Dalen, E.N.E.; Faessler, A.; Fuchs, C.; Gaitanos, T.; Grigorian, H.; Ho, A.; Kolomeitsev, E.E.; et al. Constraints on the high-density nuclear equation of state from the phenomenology of compact stars and heavy-ion collisions. Phys. Rev. C 2006, 74, 035802. [Google Scholar] [CrossRef] [Green Version]
- Glendenning, N.K. Compact Stars. Nuclear Physics, Particle Physics, and General Relativity; Springer: New York, NY, USA, 1997. [Google Scholar]
- Tolman, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef] [Green Version]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Flanagan, É.É.; Hinderer, T. Constraining neutron-star tidal Love numbers with gravitational-wave detectors. Phys. Rev. D 2008, 77, 021502. [Google Scholar] [CrossRef] [Green Version]
- Hinderer, T. Tidal Love Numbers of Neutron Stars. Astrophys. J. 2008, 677, 1216–1220. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A. Relativistic tidal properties of neutron stars. Phys. Rev. D 2009, 80, 084035. [Google Scholar] [CrossRef] [Green Version]
- Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.J.; Crawford, F.; Thankful Cromartie, H.; et al. The NANOGrav 11-year Data Set: High-precision Timing of 45 Millisecond Pulsars. Astrophys. J. Suppl. Ser. 2018, 235, 37. [Google Scholar] [CrossRef] [Green Version]
- Romani, R.W.; Kandel, D.; Filippenko, A.V.; Brink, T.G.; Zheng, W. PSR J1810+1744: Companion Darkening and a Precise High Neutron Star Mass. Astrophys. J. Lett. 2021, 908, L46. [Google Scholar] [CrossRef]
- Romani, R.W.; Kandel, D.; Filippenko, A.V.; Brink, T.G.; Zheng, W. PSR J0952-0607: The Fastest and Heaviest Known Galactic Neutron Star. Astrophys. J. Lett. 2022, 934, L17. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Witten, E. Cosmic separation of phases. Phys. Rev. D 1984, 30, 272–285. [Google Scholar] [CrossRef]
- Weissenborn, S.; Sagert, I.; Pagliara, G.; Hempel, M.; Schaffner-Bielich, J. Quark Matter in Massive Compact Stars. Astrophys. J. Lett. 2011, 740, L14. [Google Scholar] [CrossRef]
- Lindblom, L.; Detweiler, S.L. The quadrupole oscillations of neutron stars. Astrophys. J. 1983, 53, 73–92. [Google Scholar] [CrossRef]
- Detweiler, S.; Lindblom, L. On the nonradial pulsations of general relativistic stellar models. Astrophys. J. 1985, 292, 12–15. [Google Scholar] [CrossRef]
- Press, W.H. Long Wave Trains of Gravitational Waves from a Vibrating Black Hole. Astrophys. J. Lett. 1971, 170, L105. [Google Scholar] [CrossRef]
- Leaver, E.W. Spectral decomposition of the perturbation response of the Schwarzschild geometry. Phys. Rev. D 1986, 34, 384–408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ching, E.S.C.; Leung, P.T.; Suen, W.M.; Young, K. Wave propagation in gravitational systems: Completeness of quasinormal modes. Phys. Rev. D 1996, 54, 3778–3791. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chirenti, C.; de Souza, G.H.; Kastaun, W. Fundamental oscillation modes of neutron stars: Validity of universal relations. Phys. Rev. D 2015, 91, 044034. [Google Scholar] [CrossRef] [Green Version]
- Lioutas, G.; Bauswein, A.; Stergioulas, N. Frequency deviations in universal relations of isolated neutron stars and postmerger remnants. Phys. Rev. D 2021, 104, 043011. [Google Scholar] [CrossRef]
- Lioutas, G.; Stergioulas, N. Universal and approximate relations for the gravitational-wave damping timescale of f-modes in neutron stars. Gen. Relativ. Gravit. 2018, 50, 12. [Google Scholar] [CrossRef] [Green Version]







| 8.162 × 10 | 2.760 × 10 | 1.116 | 2.318 × 10 | −3.641 | ... | ... | ... | 0.9994 | |
| −2.514 × 10 | −9.301 × 10 | 3.172 × 10 | −9.566 × 10 | 8.581 × 10 | −4.117 × 10 | 6.562 × 10 | −4.655 × 10 | 0.9997 | |
| 1.827 × 10 | −7.219 × 10 | −4.172 × 10 | 5.311 × 10 | −1.957 × 10 | ... | ... | ... | 0.999995 | |
| 1.963 × 10 | 5.749 × 10 | −1.850 × 10 | 1.972 × 10 | −7.147 × 10 | ... | ... | ... | 0.999976 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.-Y.; Wei, W.; Zhou, X. Compact Stars in the vBag Model and Its f-Mode Oscillations. Universe 2023, 9, 285. https://doi.org/10.3390/universe9060285
Zhou H-Y, Wei W, Zhou X. Compact Stars in the vBag Model and Its f-Mode Oscillations. Universe. 2023; 9(6):285. https://doi.org/10.3390/universe9060285
Chicago/Turabian StyleZhou, Heng-Yi, Wei Wei, and Xia Zhou. 2023. "Compact Stars in the vBag Model and Its f-Mode Oscillations" Universe 9, no. 6: 285. https://doi.org/10.3390/universe9060285
APA StyleZhou, H.-Y., Wei, W., & Zhou, X. (2023). Compact Stars in the vBag Model and Its f-Mode Oscillations. Universe, 9(6), 285. https://doi.org/10.3390/universe9060285






