Structure of the Medium Formed in Heavy Ion Collisions
Abstract
:1. Introduction
2. Models
2.1. Color String Percolation Model
2.2. Core–Shell-Color String Percolation Model
2.3. Color Glass Condensate
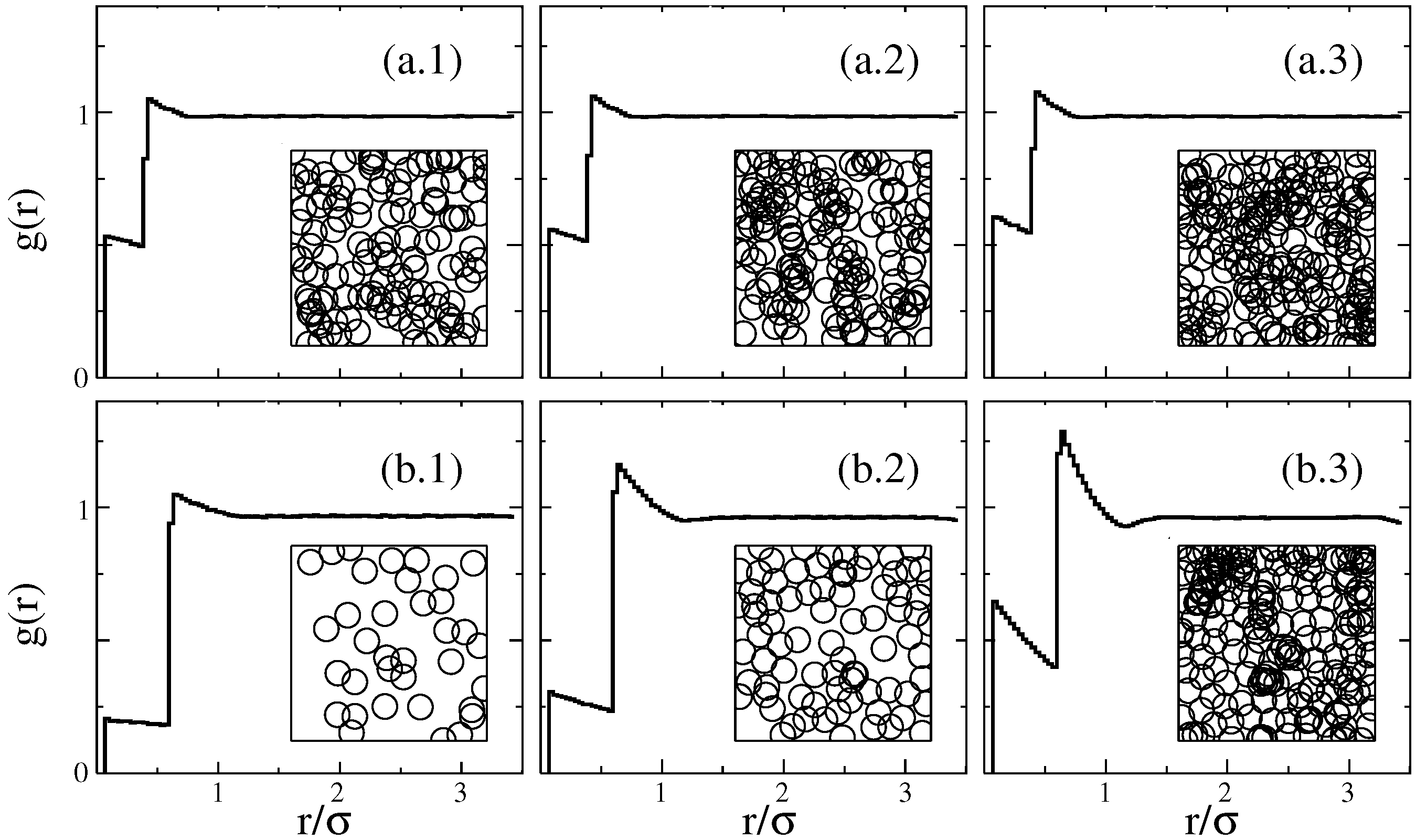
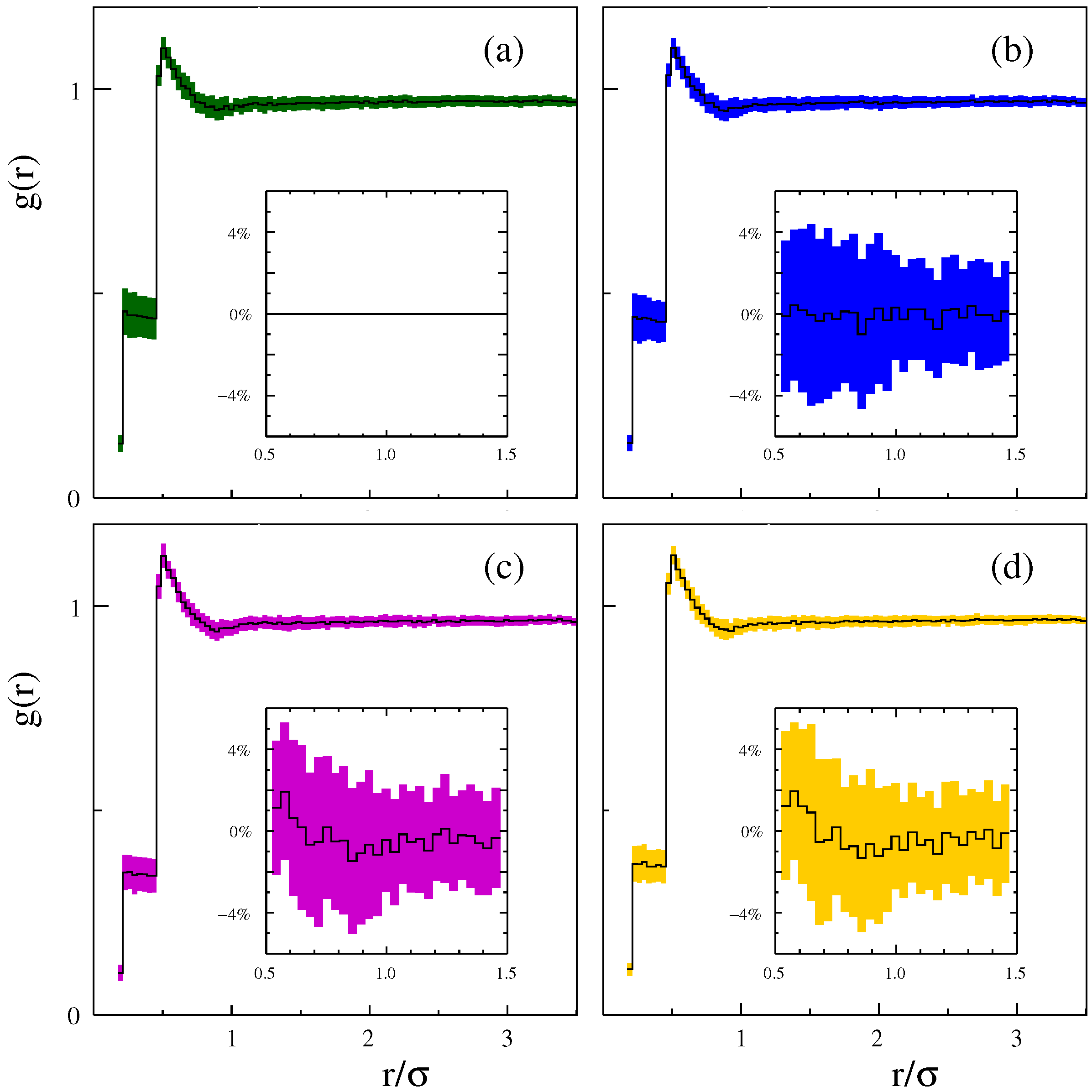
3. Simulation Methods and Data Analysis
3.1. Color String Percolation Model
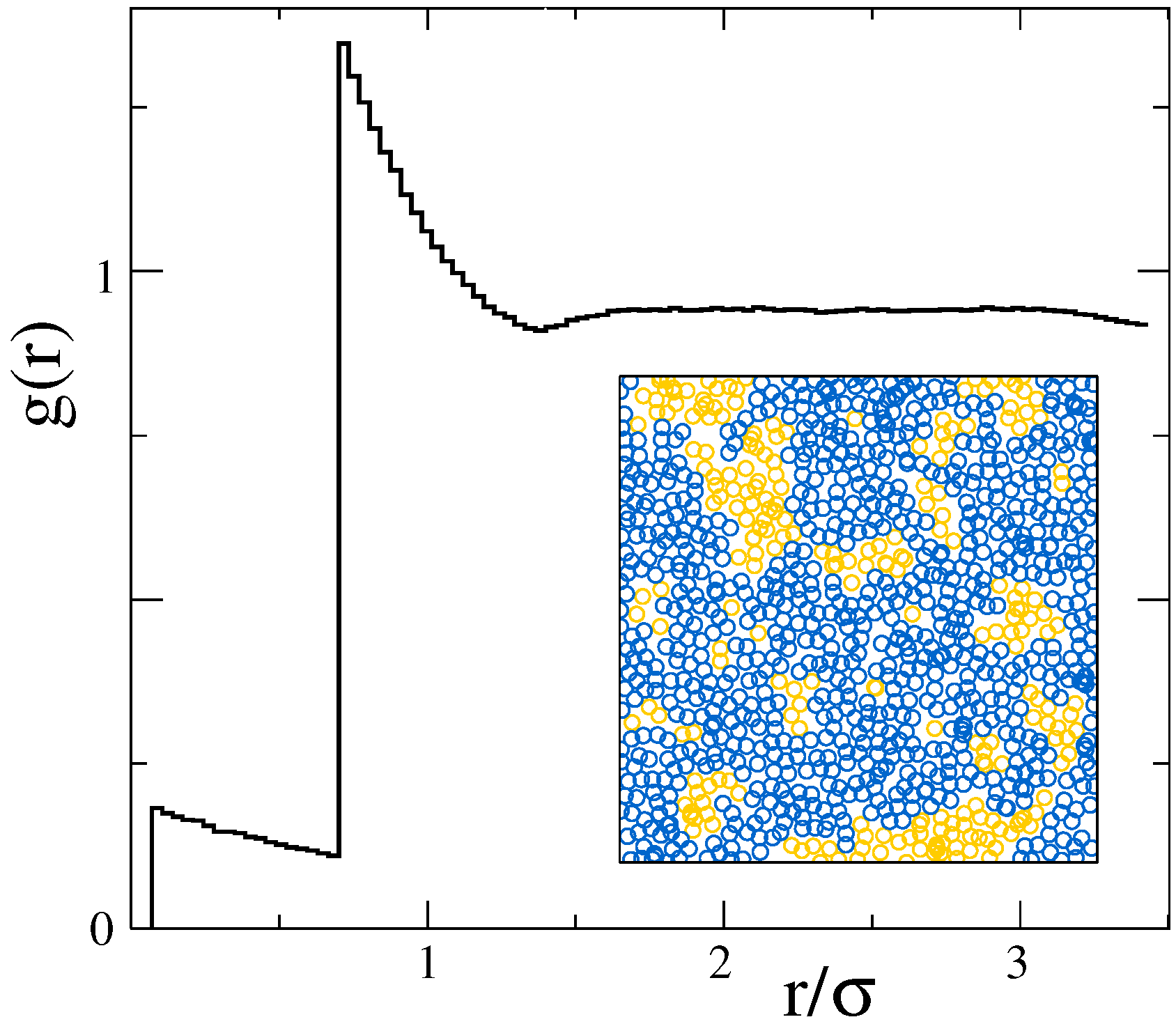
3.2. Core–Shell-Color String Percolation Model
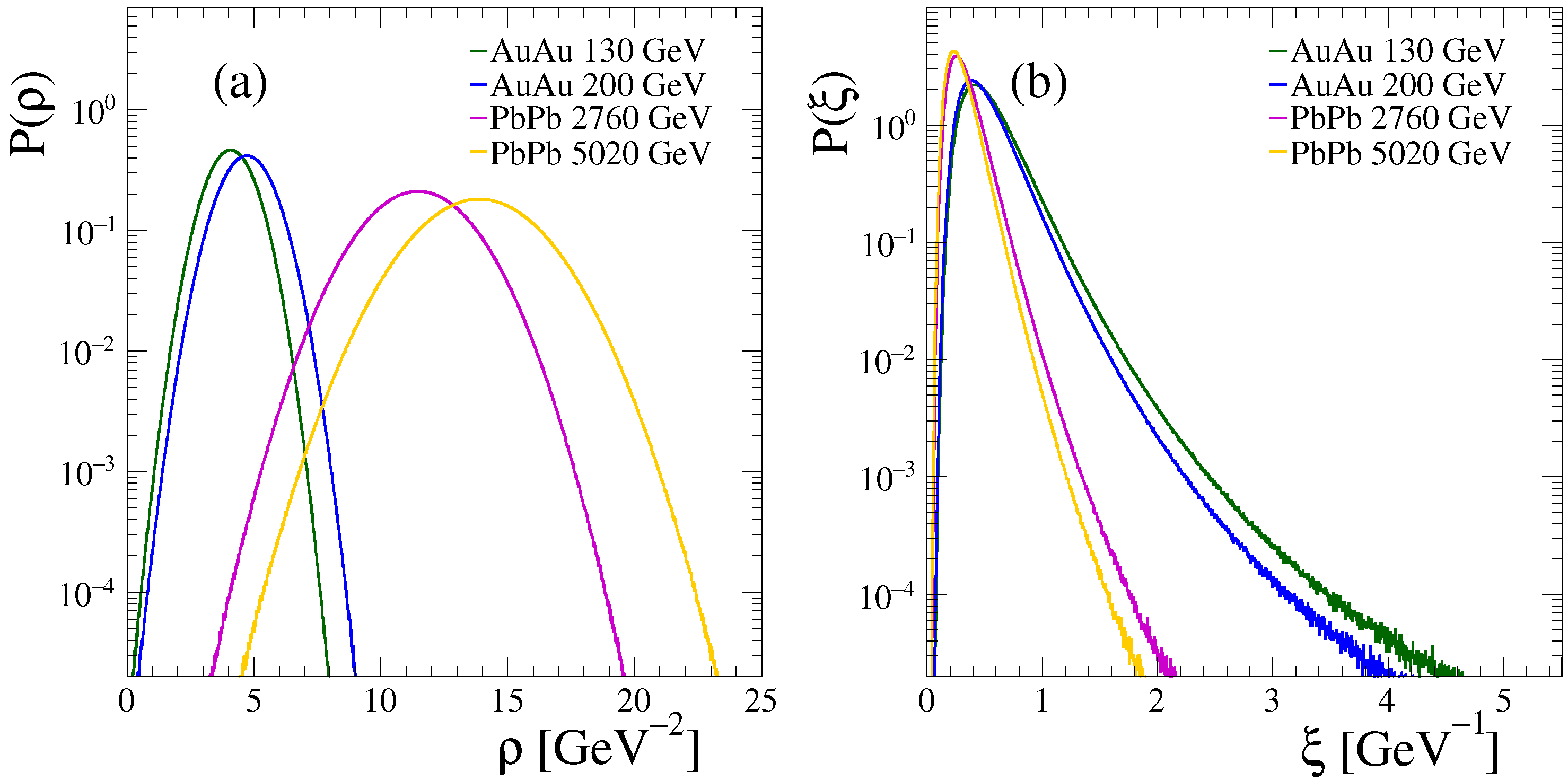
3.3. Color Glass Condensate
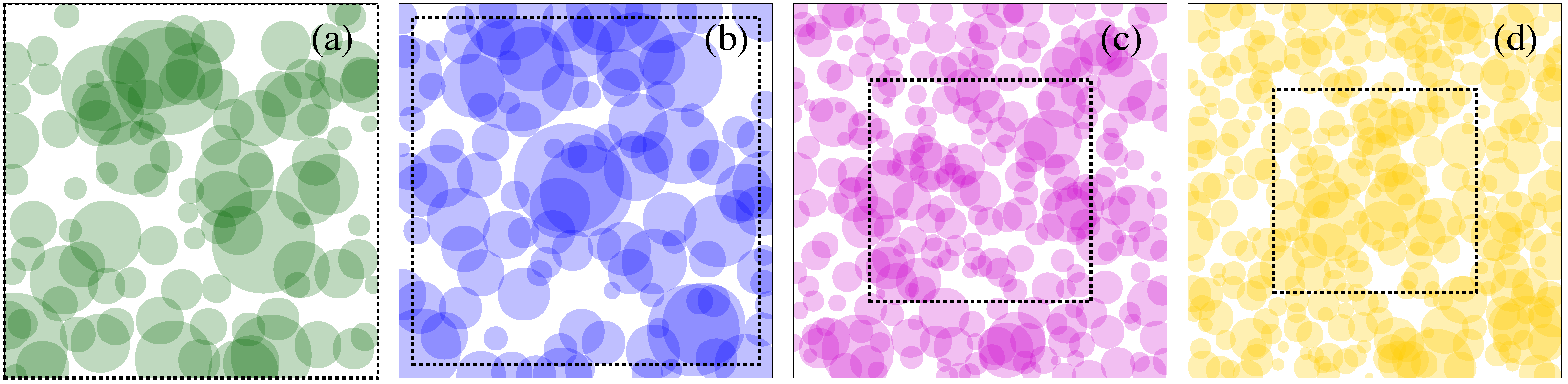
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shuryak, E. Quark-gluon plasma and hadronic production of leptons, photons and psions. Phys. Lett. B 1978, 78, 150–153. [Google Scholar] [CrossRef]
- McLerran, L.D.; Svetitsky, B. Quark liberation at high temperature: A Monte Carlo study of SU(2) gauge theory. Phys. Rev. D 1981, 24, 450–460. [Google Scholar] [CrossRef]
- Bjorken, J.D. Highly relativistic nucleus-nucleus collisions: The central rapidity region. Phys. Rev. D 1983, 27, 140–151. [Google Scholar] [CrossRef]
- Gyulassy, M.; McLerran, L. New forms of QCD matter discovered at RHIC. Nucl. Phys. A 2005, 750, 30–63. [Google Scholar] [CrossRef] [Green Version]
- Adams, J.; Aggarwal, M.M.; Ahammed, Z.; Amonett, J.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Badyal, S.K.; Bai, Y.; Balewski, J.; et al. Experimental and theoretical challenges in the search for the quark–gluon plasma: The STAR Collaboration’s critical assessment of the evidence from RHIC collisions. Nucl. Phys. A 2005, 757, 102–183. [Google Scholar] [CrossRef] [Green Version]
- Adcox, K.; Adler, S.S.; Afanasiev, S.; Aidala, C.; Ajitan, N.N.; Akiba, Y.; Al-Jamel, A.; Alexer, J.; Amirikas, R.; Aoki, K.; et al. Formation of dense partonic matter in relativistic nucleus–nucleus collisions at RHIC: Experimental evaluation by the PHENIX Collaboration. Nucl. Phys. A 2005, 757, 184–283. [Google Scholar] [CrossRef] [Green Version]
- Aamodt, K.; Abelev, B.; Quintana, A.A.; Adamova, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agocs, A.G.; Salazar, S.A.; Ahammed, Z.; et al. Elliptic Flow of Charged Particles in Pb-Pb Collisions at TeV. Phys. Rev. Lett. 2010, 105, 252302. [Google Scholar] [CrossRef] [Green Version]
- Aad, G.; Abbott, B.; Abdallah, J.; Abdelalim, A.A.; Abdesselam, A.; Abi, B.; Abolins, M.; Abramowicz, H.; Abreu, H.; Acerbi, E.; et al. Measurement of the pseudorapidity and transverse momentum dependence of the elliptic flow of charged particles in lead–lead collisions at TeV with the ATLAS detector. Phys. Lett. B 2012, 707, 330–348. [Google Scholar] [CrossRef]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Friedl, M. Centrality dependence of dihadron correlations and azimuthal anisotropy harmonics in PbPb collisions at TeV. Eur. Phys. J. C 2012, 72, 10052. [Google Scholar] [CrossRef] [Green Version]
- Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; et al. Observation of long-range, near-side angular correlations in pPb collisions at the LHC. Phys. Lett. B 2013, 718, 795–814. [Google Scholar] [CrossRef]
- Aidala, C. Creation of quark-gluon plasma droplets with three distinct geometries. Nat. Phys. 2019, 15, 214–220. [Google Scholar] [CrossRef] [Green Version]
- Braun, M.; Dias de Deus, J.; Hirsch, A.; Pajares, C.; Scharenberg, R.; Srivastava, B. De-confinement and clustering of color sources in nuclear collisions. Phys. Rep. 2015, 599, 1–50. [Google Scholar] [CrossRef] [Green Version]
- Bautista, I.; Pajares, C.; Ramírez, J.E. String percolation in AA and p+ p collisions. Rev. Mex. Fis. 2019, 65, 197–223. [Google Scholar] [CrossRef] [Green Version]
- Braun, M.A.; Pajares, C. Implications of color-string percolation on multiplicities, correlations, and the transverse momentum. Eur. Phys. J. C 2000, 16, 349–359. [Google Scholar] [CrossRef]
- Armesto, N.; Braun, M.A.; Ferreiro, E.G.; Pajares, C. Percolation Approach to Quark-Gluon Plasma and J/ψ Suppression. Phys. Rev. Lett. 1996, 77, 3736–3738. [Google Scholar] [CrossRef] [Green Version]
- Tribedy, P.; Venugopalan, R. Saturation models of HERA DIS data and inclusive hadron distributions in p+p collisions at the LHC. Nucl. Phys. A 2011, 850, 136–156. [Google Scholar] [CrossRef]
- Tribedy, P.; Venugopalan, R. QCD saturation at the LHC: Comparisons of models to p + p and A + A data and predictions for p + Pb collisions. Phys. Lett. B 2012, 710, 125–133. [Google Scholar] [CrossRef] [Green Version]
- Ramírez, J.E.; Díaz, B.; Pajares, C. Interacting color strings as the origin of the liquid behavior of the quark-gluon plasma. Phys. Rev. D 2021, 103, 094029. [Google Scholar] [CrossRef]
- Aste, T.; di Matteo, T. 2—Nanometric architectures: Emergence of efficient non-crystalline atomic organization in nanostructures. In Nanostructure Control of Materials; Hannink, R., Hill, A., Eds.; Woodhead Publishing: Boca Raton, FL, USA, 2006; pp. 32–56. [Google Scholar] [CrossRef]
- Dias de Deus, J.; Hirsch, A.S.; Pajares, C.; Scharenberg, R.P.; Srivastava, B.K. Transport coefficient to trace anomaly in the clustering of color sources approach. Phys. Rev. C 2016, 93, 024915. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, P.; Tiwari, S.K.; De, S.; Sahoo, R.; Scharenberg, R.P.; Srivastava, B.K. Thermodynamic and transport properties in Au + Au collisions at RHIC energies from the clustering of color strings. Mod. Phys. Lett. A 2019, 34, 1950034. [Google Scholar] [CrossRef] [Green Version]
- Texca García, J.C.; Rosales Herrera, D.; Ramírez, J.E.; Fernández Téllez, A.; Pajares, C. Percolation leads to finite-size effects on the transition temperature and center-of-mass energy required for quark-gluon plasma formation. Phys. Rev. D 2022, 106, L031503. [Google Scholar] [CrossRef]
- Amelin, N.S.; Braun, M.A.; Pajares, C. Multiple production in the Monte Carlo string fusion model. Phys. Lett. B 1993, 306, 312–318. [Google Scholar] [CrossRef]
- Dias de Deus, J.; Pajares, C. Percolation of color sources and critical temperature. Phys. Lett. B 2006, 642, 455–458. [Google Scholar] [CrossRef] [Green Version]
- Chandler, D. Introduction to Modern Statistical Mechanics; Oxford University Press: New York, NY, USA, 1987. [Google Scholar]
- Myroshnychenko, V.; Brosseau, C. Possible manifestation of nonuniversality in some continuum percolation systems. J. Phys. D 2008, 41, 095401. [Google Scholar] [CrossRef]
- Myroshnychenko, V.; Brosseau, C. Effective complex permittivity and continuum percolation analysis of two-phase composite media. IEEE Trans. Dielectr. Electr. Insul. 2009, 16, 1209–1222. [Google Scholar] [CrossRef]
- Halperin, B.I.; Feng, S.; Sen, P.N. Differences between Lattice and Continuum Percolation Transport Exponents. Phys. Rev. Lett. 1985, 54, 2391–2394. [Google Scholar] [CrossRef] [PubMed]
- Mertens, S.; Moore, C. Continuum percolation thresholds in two dimensions. Phys. Rev. E 2012, 86, 061109. [Google Scholar] [CrossRef] [Green Version]
- Albacete, J.L.; Marquet, C. Gluon saturation and initial conditions for relativistic heavy ion collisions. Prog. Part. Nucl. Phys. 2014, 76, 1–42. [Google Scholar] [CrossRef] [Green Version]
- Gribov, L.V.; Levin, E.M.; Ryskin, M.G. Semihard Processes in QCD. Phys. Rept. 1983, 100, 1–150. [Google Scholar] [CrossRef]
- Mueller, A.H. Small x Behavior and Parton Saturation: A QCD Model. Nucl. Phys. B 1990, 335, 115–137. [Google Scholar] [CrossRef]
- Blaizot, J.P.; Mueller, A.H. The Early Stage of Ultrarelativistic Heavy Ion Collisions. Nucl. Phys. B 1987, 289, 847–860. [Google Scholar] [CrossRef] [Green Version]
- McLerran, L.D.; Venugopalan, R. Green’s functions in the color field of a large nucleus. Phys. Rev. D 1994, 50, 2225–2233. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Balitsky, I. Operator expansion for high-energy scattering. Nucl. Phys. B 1996, 463, 99–160. [Google Scholar] [CrossRef] [Green Version]
- Kovchegov, Y.V. Small x F(2) structure function of a nucleus including multiple pomeron exchanges. Phys. Rev. D 1999, 60, 034008. [Google Scholar] [CrossRef] [Green Version]
- Jalilian-Marian, J.; Kovner, A.; Leonidov, A.; Weigert, H. The Wilson renormalization group for low x physics: Towards the high density regime. Phys. Rev. D 1998, 59, 014014. [Google Scholar] [CrossRef] [Green Version]
- Jalilian-Marian, J.; Kovner, A.; Leonidov, A.; Weigert, H. The BFKL equation from the Wilson renormalization group. Nucl. Phys. B 1997, 504, 415–431. [Google Scholar] [CrossRef] [Green Version]
- Iancu, E.; Leonidov, A.; McLerran, L.D. The Renormalization group equation for the color glass condensate. Phys. Lett. B 2001, 510, 133–144. [Google Scholar] [CrossRef] [Green Version]
- Iancu, E.; Leonidov, A.; McLerran, L.D. Nonlinear gluon evolution in the color glass condensate. 1. Nucl. Phys. A 2001, 692, 583–645. [Google Scholar] [CrossRef] [Green Version]
- Weigert, H. Unitarity at small Bjorken x. Nucl. Phys. A 2002, 703, 823–860. [Google Scholar] [CrossRef] [Green Version]
- Dumitru, A.; Kharzeev, D.E.; Levin, E.M.; Nara, Y. Gluon Saturation in pA Collisions at the LHC: KLN Model Predictions For Hadron Multiplicities. Phys. Rev. C 2012, 85, 044920. [Google Scholar] [CrossRef] [Green Version]
- Dumitru, A.; Nara, Y. KNO scaling of fluctuations in pp and pA, and eccentricities in heavy-ion collisions. Phys. Rev. C 2012, 85, 034907. [Google Scholar] [CrossRef] [Green Version]
- Kowalski, H.; Teaney, D. An Impact parameter dipole saturation model. Phys. Rev. D 2003, 68, 114005. [Google Scholar] [CrossRef] [Green Version]
- Schenke, B.; Tribedy, P.; Venugopalan, R. Fluctuating Glasma initial conditions and flow in heavy ion collisions. Phys. Rev. Lett. 2012, 108, 252301. [Google Scholar] [CrossRef] [Green Version]
- Schenke, B.; Tribedy, P.; Venugopalan, R. Event-by-event gluon multiplicity, energy density, and eccentricities in ultrarelativistic heavy-ion collisions. Phys. Rev. C 2012, 86, 034908. [Google Scholar] [CrossRef] [Green Version]
- McLerran, L.D.; Venugopalan, R. Computing quark and gluon distribution functions for very large nuclei. Phys. Rev. D 1994, 49, 2233–2241. [Google Scholar] [CrossRef] [Green Version]
- McLerran, L.D.; Venugopalan, R. Gluon distribution functions for very large nuclei at small transverse momentum. Phys. Rev. D 1994, 49, 3352–3355. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gelis, F.; Iancu, E.; Jalilian-Marian, J.; Venugopalan, R. The Color Glass Condensate. Ann. Rev. Nucl. Part. Sci. 2010, 60, 463–489. [Google Scholar] [CrossRef] [Green Version]
- Schenke, B.; Tribedy, P.; Venugopalan, R. Multiplicity distributions in p+p, p+A and A+A collisions from Yang-Mills dynamics. Phys. Rev. C 2014, 89, 024901. [Google Scholar] [CrossRef] [Green Version]
- Gale, C.; Jeon, S.; Schenke, B.; Tribedy, P.; Venugopalan, R. Event-by-event anisotropic flow in heavy-ion collisions from combined Yang-Mills and viscous fluid dynamics. Phys. Rev. Lett. 2013, 110, 012302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dusling, K.; Venugopalan, R. Azimuthal collimation of long range rapidity correlations by strong color fields in high multiplicity hadron-hadron collisions. Phys. Rev. Lett. 2012, 108, 262001. [Google Scholar] [CrossRef] [Green Version]
- McLerran, L.; Tribedy, P. Intrinsic Fluctuations of the Proton Saturation Momentum Scale in High Multiplicity p+p Collisions. Nucl. Phys. A 2016, 945, 216–225. [Google Scholar] [CrossRef] [Green Version]
- Schenke, B.; Shen, C.; Tribedy, P. Running the gamut of high energy nuclear collisions. Phys. Rev. C 2020, 102, 044905. [Google Scholar] [CrossRef]
- Kovchegov, Y.V. NonAbelian Weizsacker-Williams field and a two-dimensional effective color charge density for a very large nucleus. Phys. Rev. D 1996, 54, 5463–5469. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kharzeev, D.; Levin, E.; Nardi, M. Color glass condensate at the LHC: Hadron multiplicities in pp, pA and AA collisions. Nucl. Phys. A 2005, 747, 609–629. [Google Scholar] [CrossRef] [Green Version]
- Kharzeev, D.; Nardi, M. Hadron production in nuclear collisions at RHIC and high density QCD. Phys. Lett. B 2001, 507, 121–128. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, P.; Tiwari, S.K.; Sahoo, R. Electrical conductivity of hot and dense QCD matter created in heavy-ion collisions: A color string percolation approach. Phys. Rev. D 2018, 98, 054005. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, P.; Sahoo, R.; Tiwari, S.K. Wiedemann-Franz law for hot QCD matter in a color string percolation scenario. Phys. Rev. D 2019, 100, 051503. [Google Scholar] [CrossRef] [Green Version]
- Ramírez, J.E.; Pajares, C. Area covered by disks in small-bounded continuum percolating systems: An application to the string percolation model. Phys. Rev. E 2019, 100, 022123. [Google Scholar] [CrossRef]
- Patrignani, C. Review of Particle Physics. Chin. Phys. C 2016, 40, 100001. [Google Scholar] [CrossRef] [Green Version]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alvarado García, J.R.; Rosales Herrera, D.; Fernández Téllez, A.; Díaz, B.; Ramírez, J.E. Structure of the Medium Formed in Heavy Ion Collisions. Universe 2023, 9, 291. https://doi.org/10.3390/universe9060291
Alvarado García JR, Rosales Herrera D, Fernández Téllez A, Díaz B, Ramírez JE. Structure of the Medium Formed in Heavy Ion Collisions. Universe. 2023; 9(6):291. https://doi.org/10.3390/universe9060291
Chicago/Turabian StyleAlvarado García, J. R., D. Rosales Herrera, A. Fernández Téllez, Bogar Díaz, and J. E. Ramírez. 2023. "Structure of the Medium Formed in Heavy Ion Collisions" Universe 9, no. 6: 291. https://doi.org/10.3390/universe9060291
APA StyleAlvarado García, J. R., Rosales Herrera, D., Fernández Téllez, A., Díaz, B., & Ramírez, J. E. (2023). Structure of the Medium Formed in Heavy Ion Collisions. Universe, 9(6), 291. https://doi.org/10.3390/universe9060291






