Characterizing Low-Energy Charged Particles in the Magnetosphere with the LEM CubeSat Spectrometer Project: Detector Concept and Hardware Characterisation †
Abstract
1. Introduction
2. Investigation of the Magnetosphere: Correlation between Particle Precipitations and Seismic Events
3. The Current Landscape of Space-Based Particle Detectors
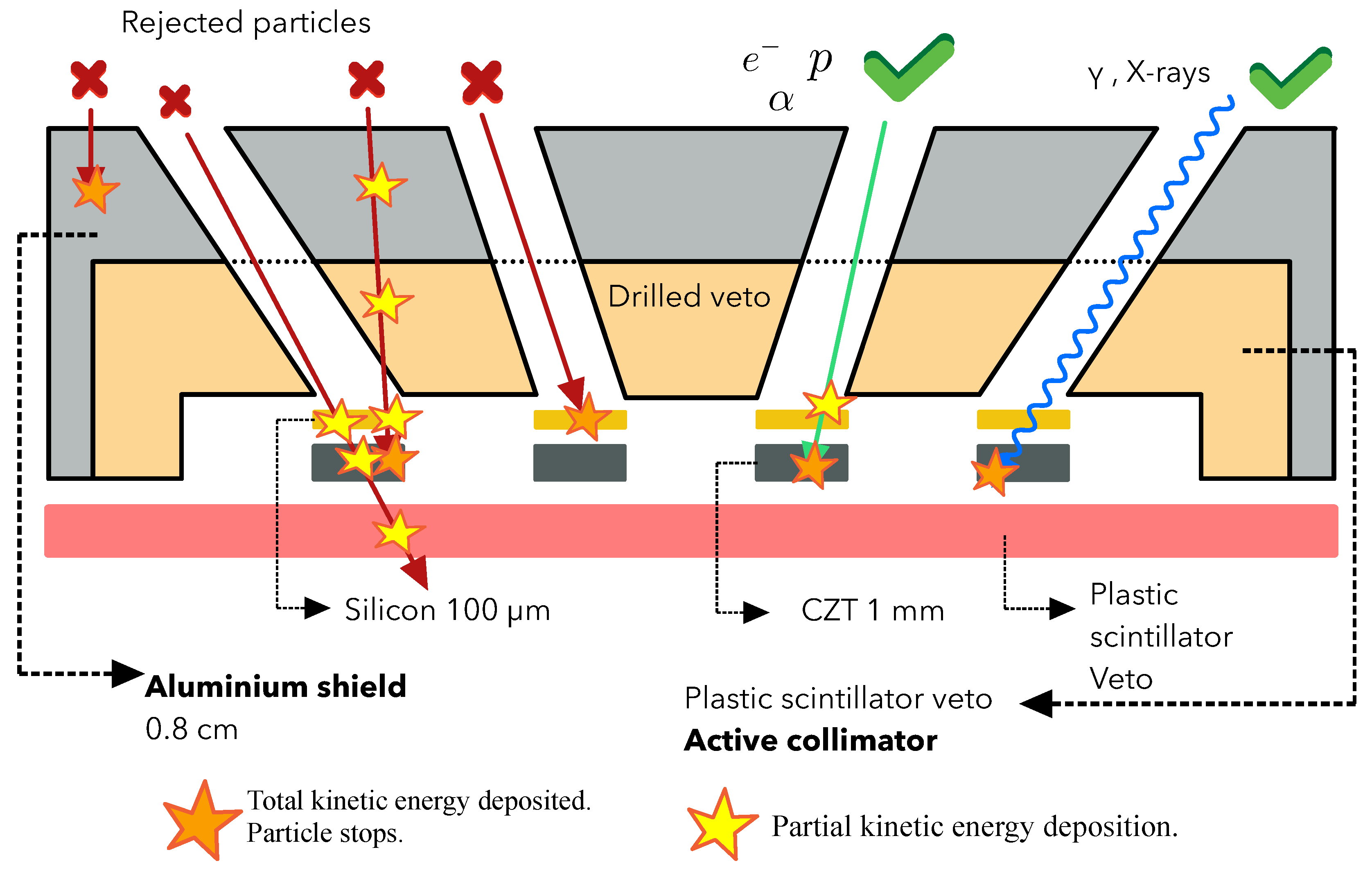
4. The LEM Concept: The Active Collimation Technique
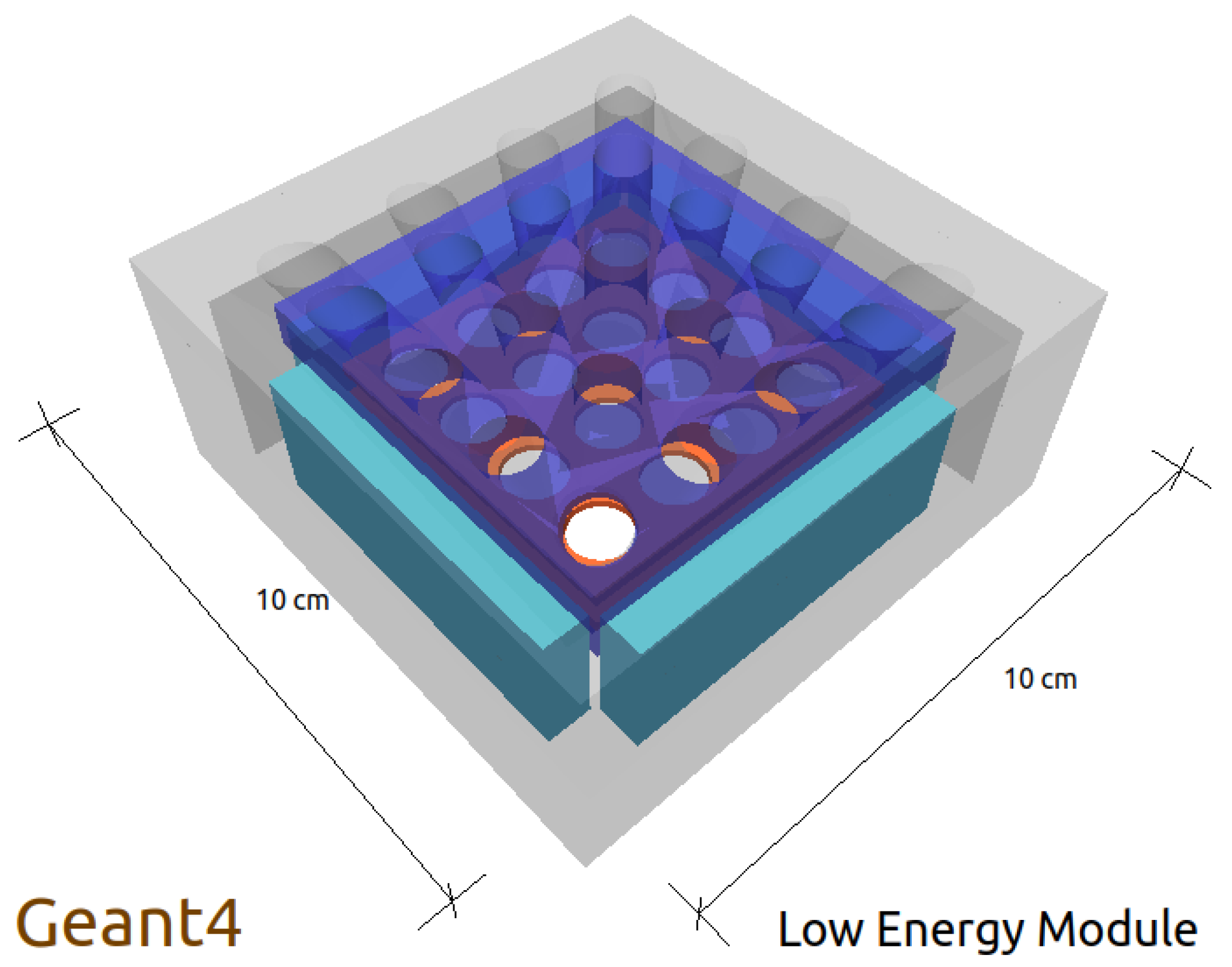
5. Performance Characterisation with GEANT 4 Simulation
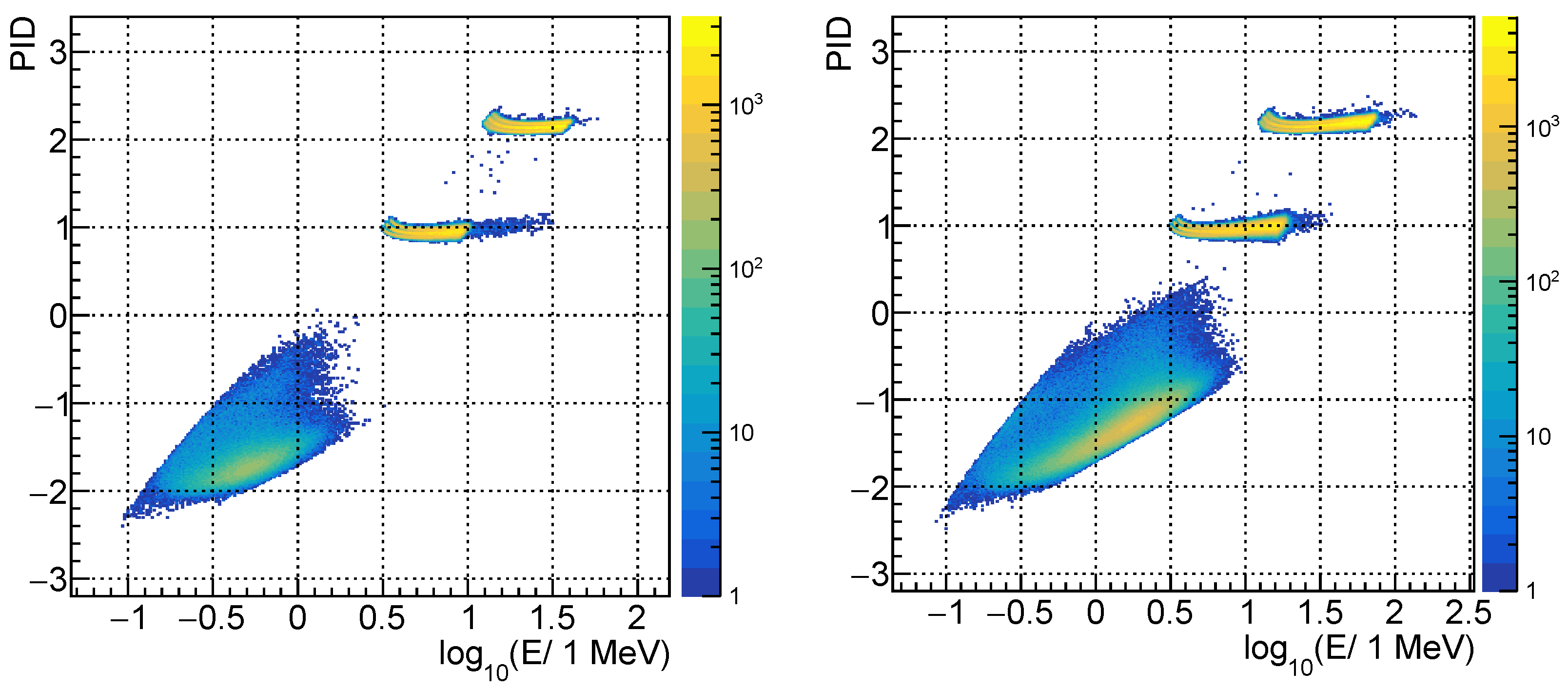
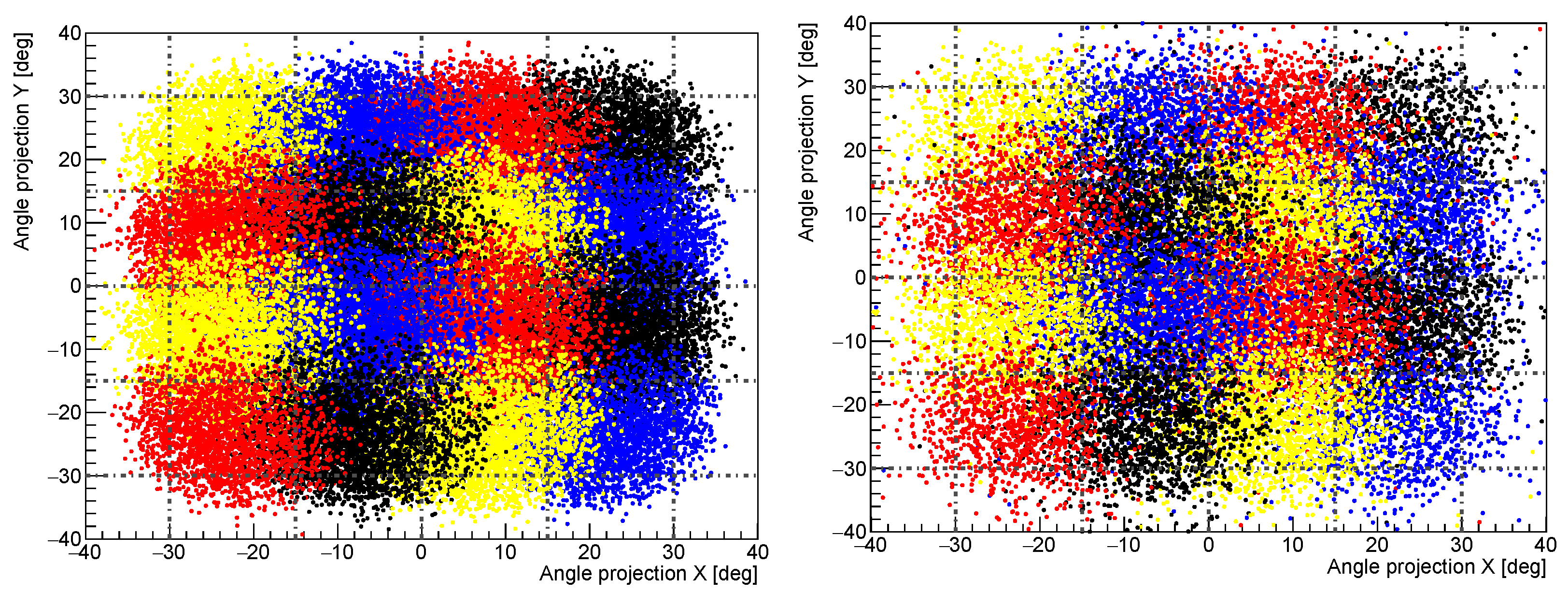
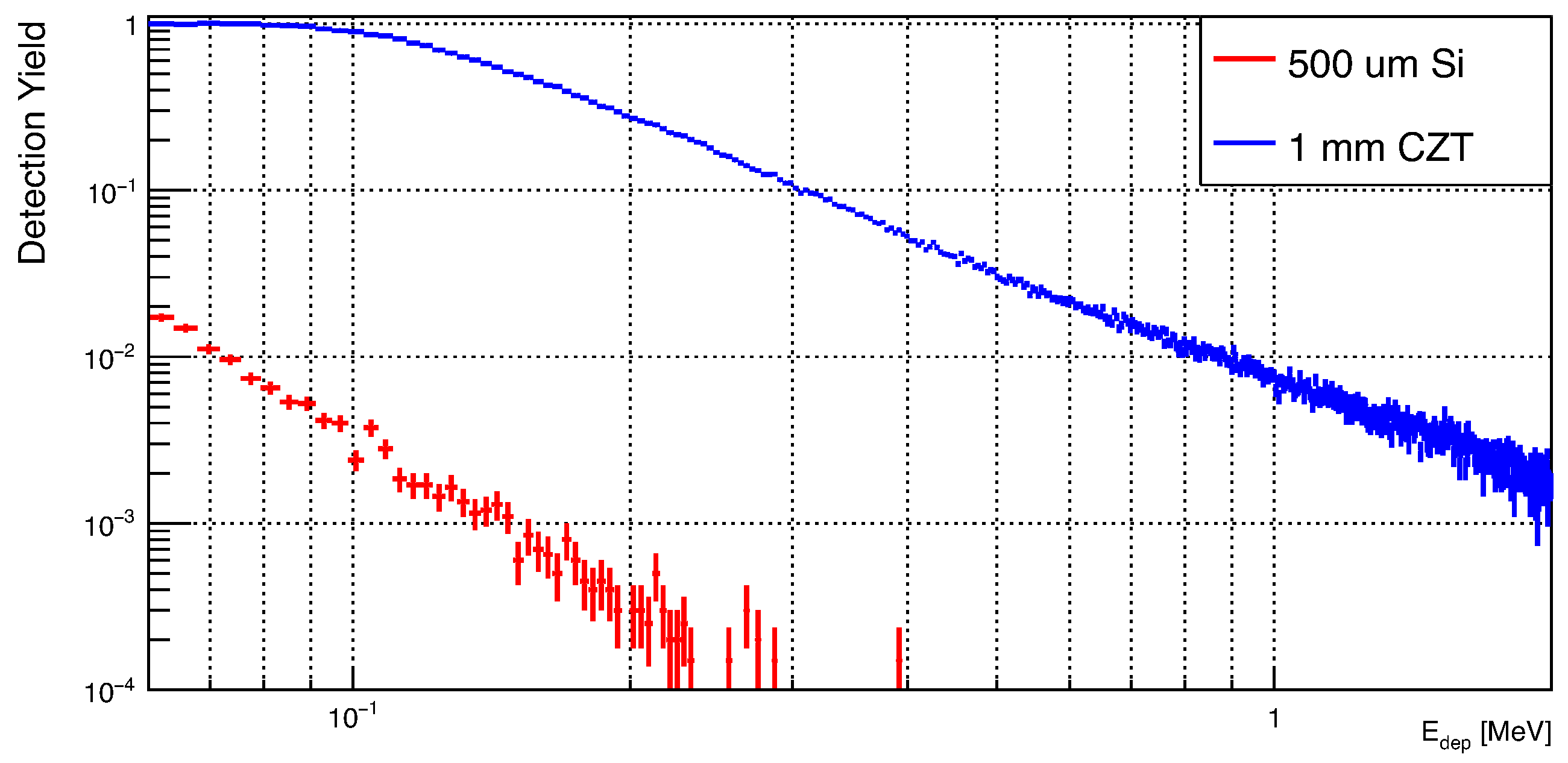
5.1. Expected Performance for Low-Energy Charged Particles
5.2. Expected Performance for Gamma Rays
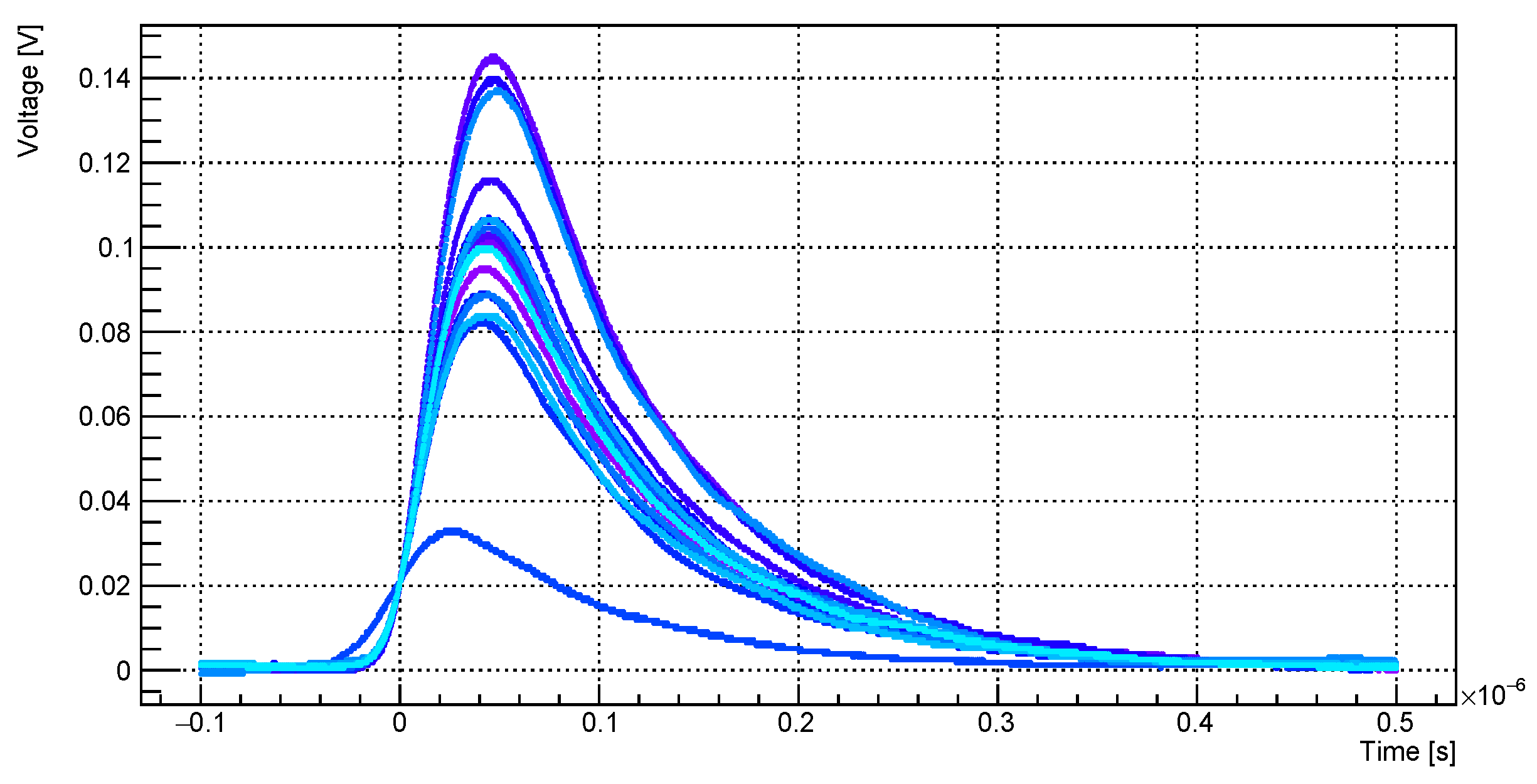
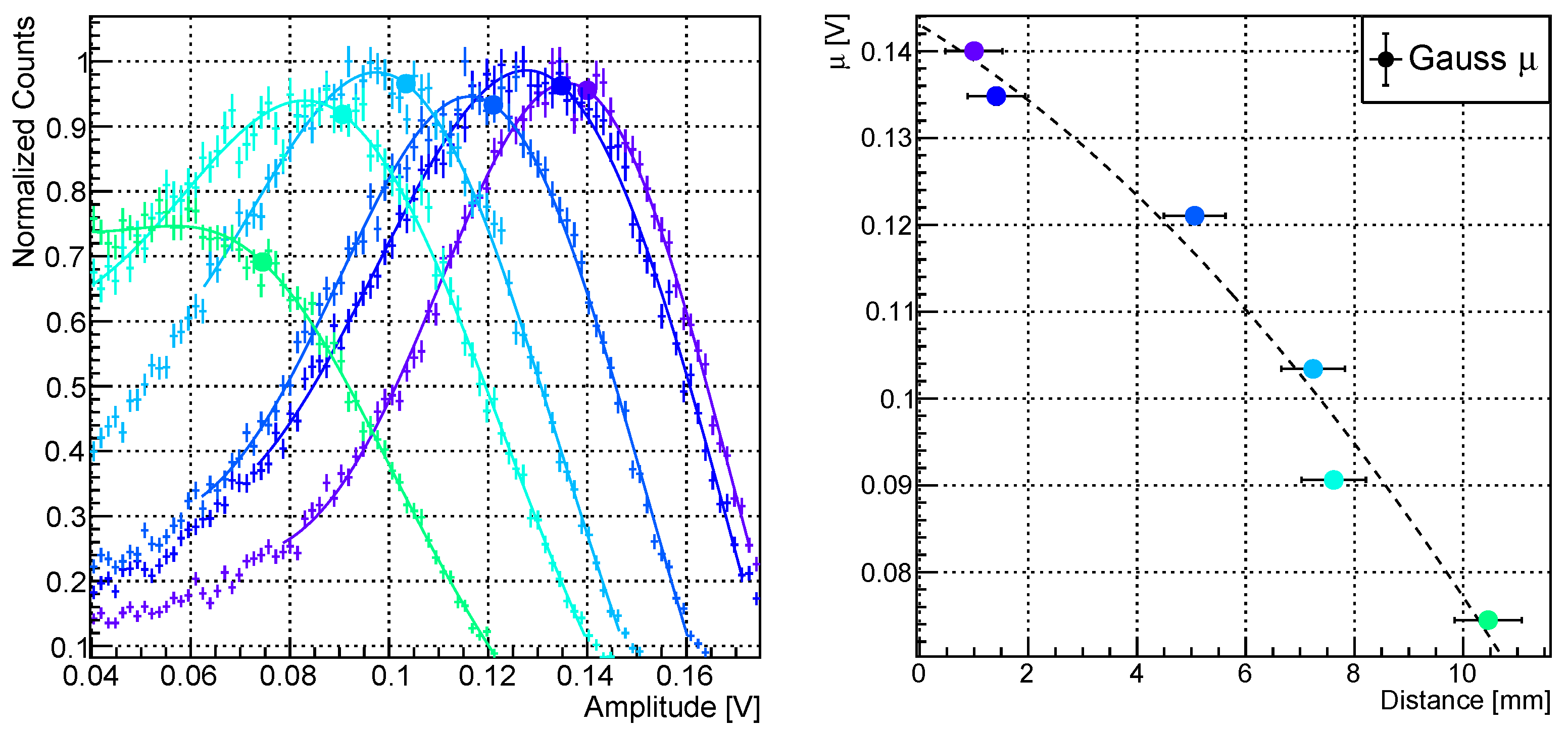
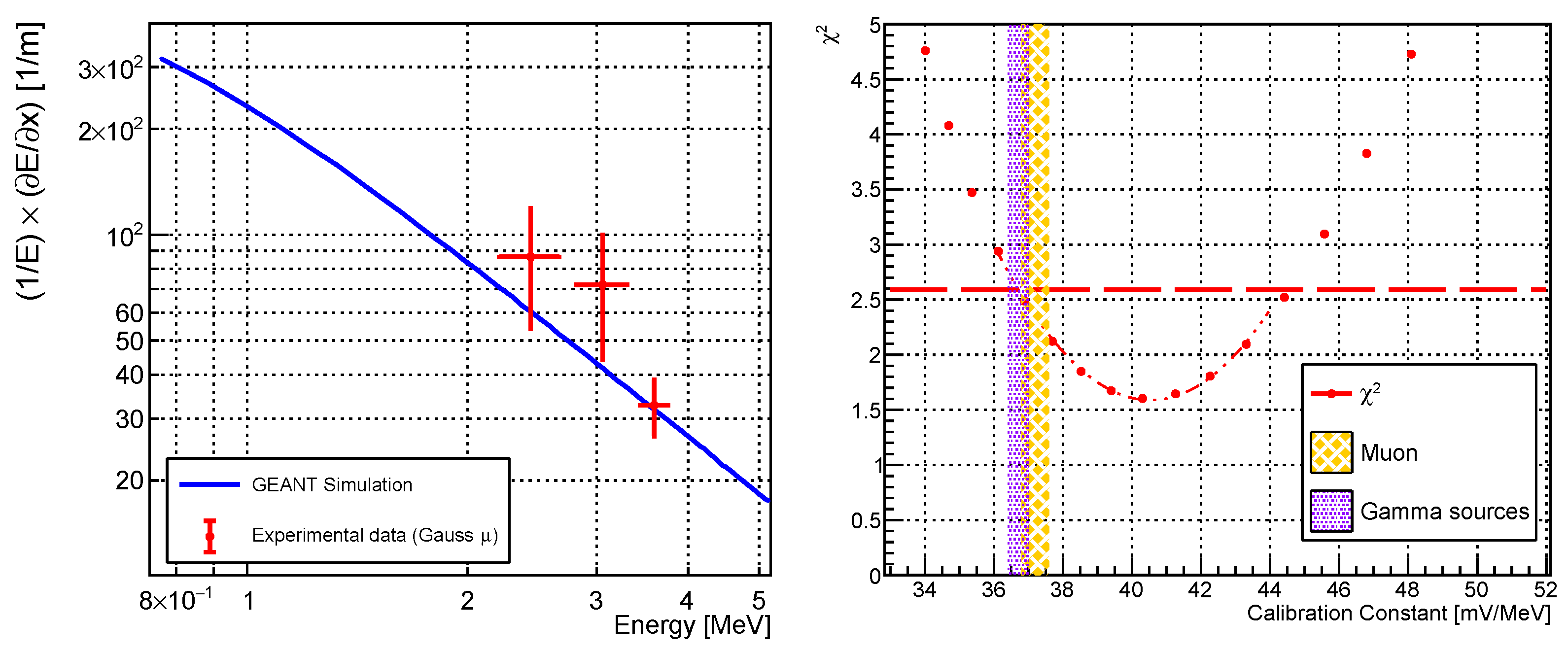
6. Characterisation of Fully Depleted Silicon Detector Prototypes
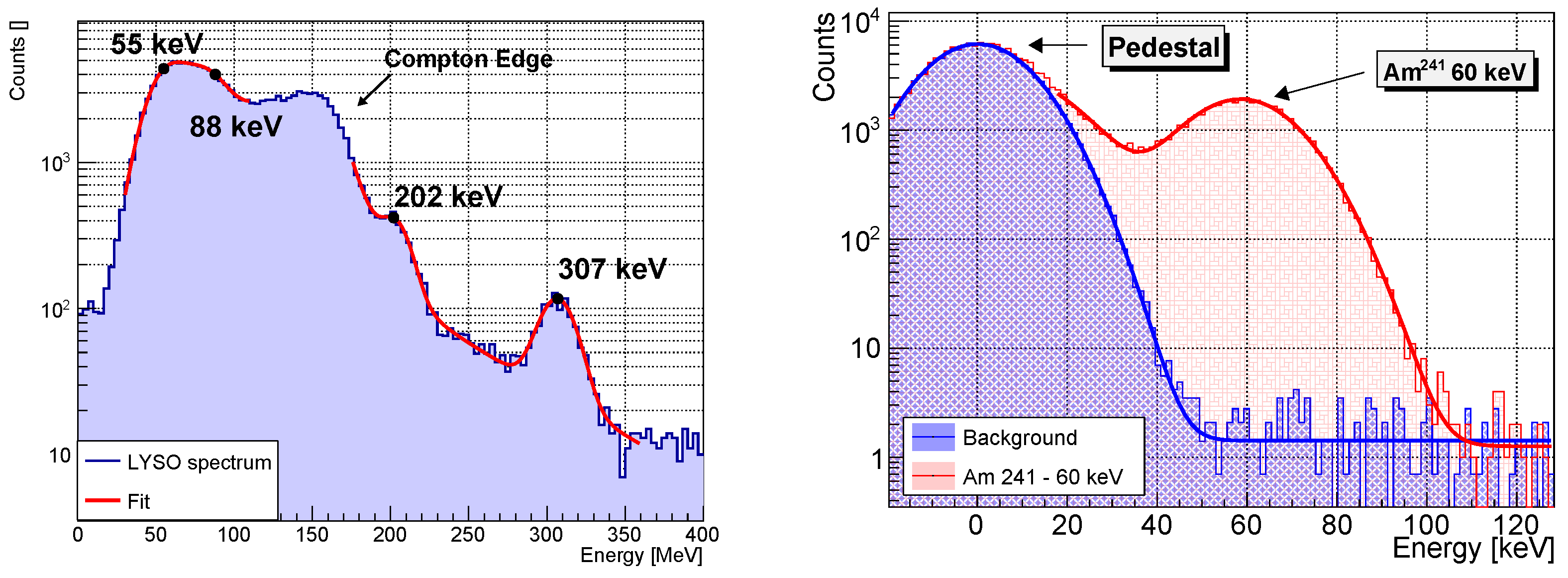
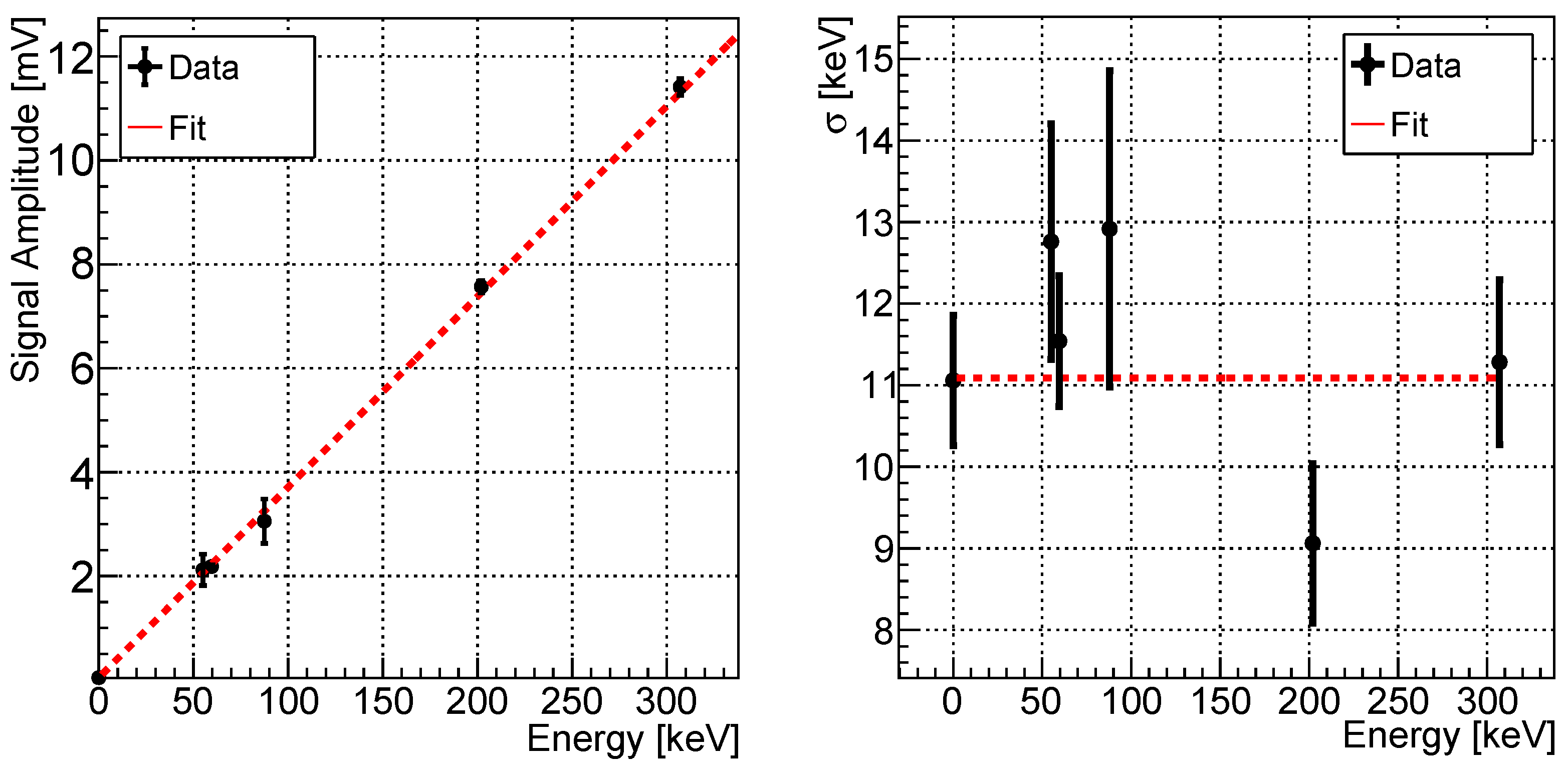
6.1. Calibration with -Ray Sources
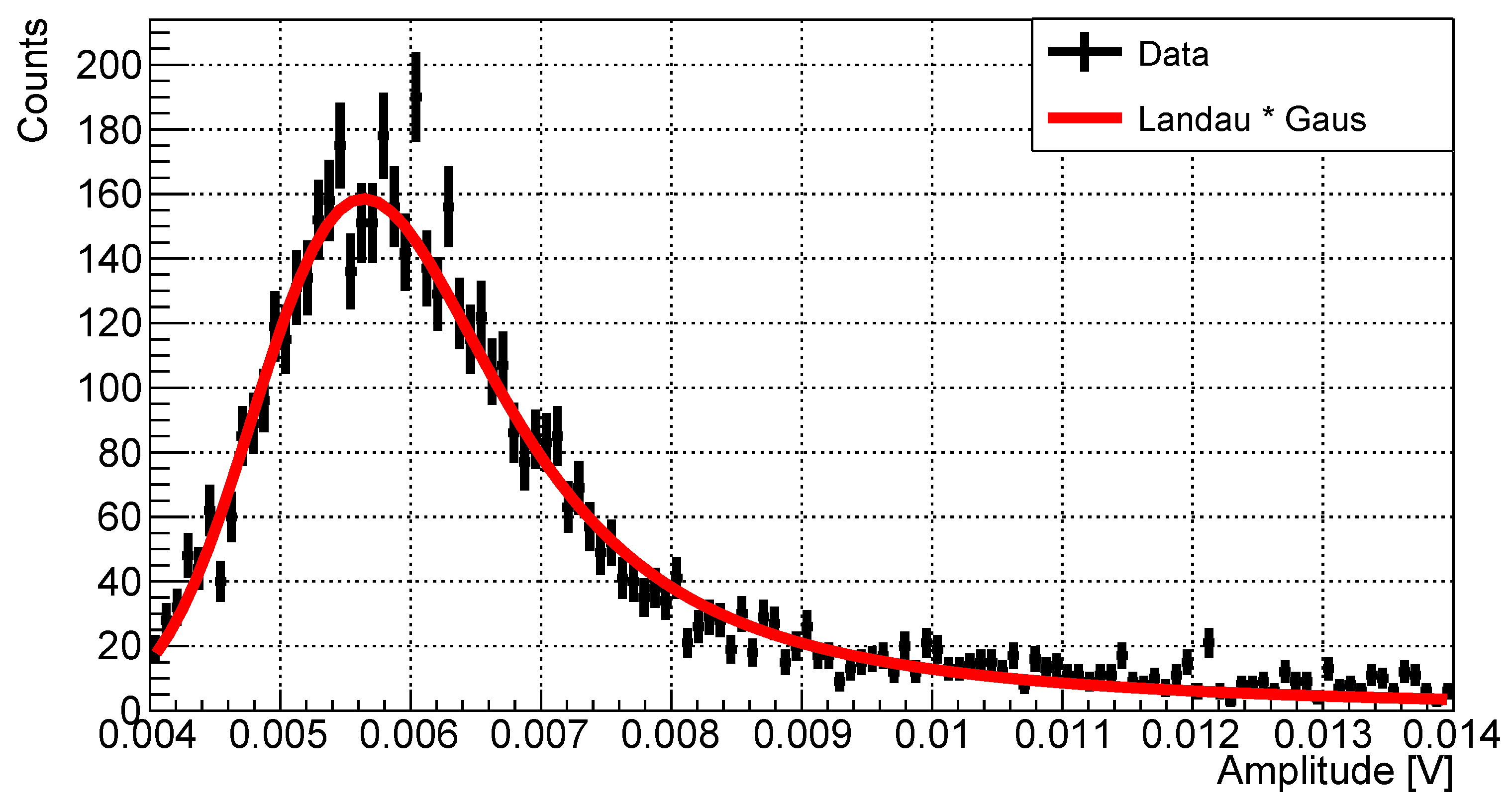
6.2. Calibration with Cosmic Muons (MIP)
6.3. Characterisation with -Particles Emitted by Am
7. Conclusions and Outlooks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACD | Anti-coincidence detector |
| CSA | Charge sensitive amplifier |
| CSES | China seismo-electromagnetic satellite |
| CZT | Cadmium zing telluride (CdZnTe) |
| DSSSD | Double-sided silicon strip detector |
| GEANT | Geometrty and tracking |
| GRB | Gamma-ray burst |
| LAIM | Lithosphere atmosphere ionosphere magnetosphere |
| EM | Low-energy module |
| LEO | Low earth orbit |
| LYSO | Lutetium–yttrium oxyorthoSilicate |
| MILC | Magnetosphere ionosphere lithosphere coupling |
| MIP | Minimum ionising particle |
| MPV | Most probable value |
| PID | Particle identification |
| PIPS | Passivated implanted planar silicon |
| TGF | Terrestrial gamma-ray flash |
References
- Battiston, R.; Vitale, V. First evidence for correlations between electron fluxes measured by NOAA-POES satellites and large seismic events. Nucl. Phys. Proc. Suppl. 2013, 243, 249–257. [Google Scholar] [CrossRef]
- Walt, M. Introduction to geomagnetically trapped radiation. Camb. Atmos. Space Sci. Ser. 1994, 10, 1–10. [Google Scholar]
- De Santis, A.; De Franceschi, G.; Spogli, L.; Perrone, L.; Alfonsi, L.; Qamili, E.; Cianchini, G.; Di Giovambattista, R.; Salvi, S.; Filippi, E.; et al. Geospace perturbations induced by the Earth: The state of the art and future trends. Phys. Chem. Earth Parts A/B/C 2015, 85, 17–33. [Google Scholar] [CrossRef]
- Piersanti, M.; Materassi, M.; Battiston, R.; Carbone, V.; Cicone, A.; D’Angelo, G.; Diego, P.; Ubertini, P. Magnetospheric–ionospheric–lithospheric coupling model. 1: Observations during the 5 August 2018 Bayan Earthquake. Remote Sens. 2020, 12, 3299. [Google Scholar] [CrossRef]
- D’Angelo, G.; Piersanti, M.; Battiston, R.; Bertello, I.; Carbone, V.; Cicone, A.; Diego, P.; Papini, E.; Parmentier, A.; Picozza, P.; et al. Haiti Earthquake (Mw 7.2): Magnetospheric–Ionospheric–Lithospheric Coupling during and after the Main Shock on 14 August 2021. Remote Sens. 2022, 14, 5340. [Google Scholar] [CrossRef]
- Parrot, M.; Li, M. Demeter results related to seismic activity. Ursi Radio Sci. Bull. 2015, 2015, 18–25. [Google Scholar]
- Sauvaud, J.; Moreau, T.; Maggiolo, R.; Treilhou, J.P.; Jacquey, C.; Cros, A.; Coutelier, J.; Rouzaud, J.; Penou, E.; Gangloff, M. High-energy electron detection onboard DEMETER: The IDP spectrometer, description and first results on the inner belt. Planet. Space Sci. 2006, 54, 502–511. [Google Scholar] [CrossRef]
- Dubourg, V.; Kainov, V.; Thoby, M.; Silkin, O.; Solovey, V. The DEMETER micro satellite launch campaign: A cheap access to space. Adv. Space Res. 2006, 37, 754–760. [Google Scholar] [CrossRef]
- Xu, Y.B.; Wang, H.Y.; Meng, X.C.; Wang, H.; Lu, H.; Ma, Y.Q.; Li, X.Q.; Shi, F.; Wang, P.; Zhao, X.Y.; et al. Design and simulations for the detector based on DSSSD. Chin. Phys. C 2010, 34, 1846. [Google Scholar] [CrossRef]
- Wu, F.; Wang, H.Y.; Zhao, X.Y.; Meng, X.C.; Xu, Y.B.; Wang, H.; Ma, Y.Q.; Lu, H.; Wang, P.; Shi, F.; et al. Design and performance study of the LEPD silicon tracker onboard the CSES satellite. Chin. Phys. C 2013, 37, 026004. [Google Scholar] [CrossRef]
- Li, X.; Xu, Y.; An, Z.; Liang, X.; Wang, P.; Zhao, X.; Wang, H.; Lu, H.; Ma, Y.; Shen, X.; et al. The high-energy particle package onboard CSES. Radiat. Detect. Technol. Methods 2019, 3, 22. [Google Scholar] [CrossRef]
- Nan, Y.F.; An, Z.H.; Li, H.X.; Zhao, X.Y.; Wen, X.Y.; Zhang, D.L.; Cheng, S.G.; Li, X.Q.; Wang, H.; Liang, X.H.; et al. Design and performance study of the HEPP-H calorimeter onboard the CSES satellite. Res. Astron. Astrophys. 2018, 18, 154. [Google Scholar] [CrossRef]
- Li, C.; Tang, S.; Hu, X.; Qian, Y.; Wang, Y.; Zhao, H.; Fu, Q.; Sun, Z.; He, H.; Yu, Y.; et al. Design and realization of China Tianwen-1 energetic particle analyzer. Space Sci. Rev. 2021, 217, 26. [Google Scholar] [CrossRef]
- Tang, S.; Wang, Y.; Zhao, H.; Fang, F.; Qian, Y.; Zhang, Y.; Yang, H.; Li, C.; Fu, Q.; Kong, J.; et al. Calibration of Mars energetic particle analyzer (MEPA). Earth Planet. Phys. 2020, 4, 355–363. [Google Scholar] [CrossRef]
- Zou, Y.; Zhu, Y.; Bai, Y.; Wang, L.; Jia, Y.; Shen, W.; Fan, Y.; Liu, Y.; Wang, C.; Zhang, A.; et al. Scientific objectives and payloads of Tianwen-1, China’s first Mars exploration mission. Adv. Space Res. 2021, 67, 812–823. [Google Scholar] [CrossRef]
- Hassler, D.M.; Zeitlin, C.; Wimmer-Schweingruber, R.; Böttcher, S.; Martin, C.; Andrews, J.; Böhm, E.; Brinza, D.; Bullock, M.; Burmeister, S.; et al. The radiation assessment detector (RAD) investigation. Space Sci. Rev. 2012, 170, 503–558. [Google Scholar] [CrossRef]
- Zeitlin, C.; Hassler, D.; Wimmer-Schweingruber, R.; Ehresmann, B.; Appel, J.; Berger, T.; Böhm, E.; Böttcher, S.; Brinza, D.; Burmeister, S.; et al. Calibration and characterization of the radiation assessment detector (RAD) on curiosity. Space Sci. Rev. 2016, 201, 201–233. [Google Scholar] [CrossRef]
- Ehresmann, B.; Zeitlin, C.; Hassler, D.M.; Wimmer-Schweingruber, R.F.; Böhm, E.; Böttcher, S.; Brinza, D.E.; Burmeister, S.; Guo, J.; Köhler, J.; et al. Charged particle spectra obtained with the Mars Science Laboratory Radiation Assessment Detector (MSL/RAD) on the surface of Mars. J. Geophys. Res. Planets 2014, 119, 468–479. [Google Scholar] [CrossRef]
- Ehresmann, B.; Hassler, D.M.; Zeitlin, C.; Guo, J.; Köhler, J.; Wimmer-Schweingruber, R.F.; Appel, J.K.; Brinza, D.E.; Rafkin, S.C.; Böttcher, S.I.; et al. Charged particle spectra measured during the transit to Mars with the Mars Science Laboratory Radiation Assessment Detector (MSL/RAD). Life Sci. Space Res. 2016, 10, 29–37. [Google Scholar] [CrossRef]
- Guo, J.; Zeitlin, C.; Wimmer-Schweingruber, R.F.; Hassler, D.M.; Ehresmann, B.; Köhler, J.; Böhm, E.; Böttcher, S.; Brinza, D.; Burmeister, S.; et al. MSL-RAD radiation environment measurements. Radiat. Prot. Dosim. 2015, 166, 290–294. [Google Scholar] [CrossRef]
- Takahashi, T.; Watanabe, S. Recent progress in CdTe and CdZnTe detectors. IEEE Trans. Nucl. Sci. 2001, 48, 950–959. [Google Scholar] [CrossRef]
- Sordo, S.D.; Abbene, L.; Caroli, E.; Mancini, A.M.; Zappettini, A.; Ubertini, P. Progress in the development of CdTe and CdZnTe semiconductor radiation detectors for astrophysical and medical applications. Sensors 2009, 9, 3491–3526. [Google Scholar] [CrossRef]
- Piran, T. The physics of gamma-ray bursts. Rev. Mod. Phys. 2005, 76, 1143. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.a.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. GEANT4—A simulation toolkit. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Scarduelli, V.; Gasques, L.; Chamon, L.; Lépine-Szily, A. A method to optimize mass discrimination of particles identified in ΔE − E silicon surface barrier detector systems. Eur. Phys. J. A 2020, 56, 24. [Google Scholar] [CrossRef]
- Evensen, L.; Westgaard, T.; Avdeichikov, V.; Carlen, L.; Jakobsson, B.; Murin, Y.; Martensson, J.; Oskarsson, A.; Siwek, A.; Whitlow, H.; et al. Thin detectors for the CHICSi/spl Delta/EE telescope. IEEE Trans. Nucl. Sci. 1997, 44, 629–634. [Google Scholar] [CrossRef]
- Carboni, S.; Barlini, S.; Bardelli, L.; Le Neindre, N.; Bini, M.; Borderie, B.; Bougault, R.; Casini, G.; Edelbruck, P.; Olmi, A.; et al. Particle identification using the ΔE − E technique and pulse shape discrimination with the silicon detectors of the FAZIA project. Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2012, 664, 251–263. [Google Scholar] [CrossRef]
- Li, H.; Ma, B.Q. Lorentz invariance violation induced threshold anomaly versus very-high energy cosmic photon emission from GRB 221009A. Astropart. Phys. 2023, 148, 102831. [Google Scholar] [CrossRef]
- Bietenholz, W. Cosmic rays and the search for a Lorentz Invariance Violation. Phys. Rep. 2011, 505, 145–185. [Google Scholar] [CrossRef]
- Petitjean, P.; Wang, F.; Wu, X.; Wei, J. Grbs and fundamental physics. Space Sci. Rev. 2016, 202, 195–234. [Google Scholar] [CrossRef]
- Dutta, S.; Moharana, R.; Kumar, M. Generalized Linear Models of T _{90}-T _{50} relation to classify GRBs. arXiv 2023, arXiv:2305.03947. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.B.; et al. GW170817: Observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbasi, R.; Ackermann, M.; Adams, J.; Aguilar, J.; Ahlers, M.; Ahrens, M.; Alameddine, J.; Alves, A.; Amin, N.; Andeen, K.; et al. Searches for Neutrinos from Gamma-Ray Bursts Using the IceCube Neutrino Observatory. Astrophys. J. 2022, 939, 116. [Google Scholar] [CrossRef]
- Fiore, F.; Werner, N.; Behar, E. Distributed Architectures and Constellations for γ-ray Burst Science. Galaxies 2021, 9, 120. [Google Scholar] [CrossRef]
- Battiston, R.; Neubüser, C.; Follega, F.; Iuppa, R.; Vitale, V.; Ammendola, R.; Badoni, D.; Bartocci, S.; Bazzano, A.; Beolè, S.; et al. Observation of Anomalous Electron Fluxes Induced by GRB221009A on CSES-01 Low-energy Charged Particle Detector. Astrophys. J. Lett. 2023, 946, L29. [Google Scholar] [CrossRef]
- Agapitov, O.; Balikhin, M.; Hull, A.; Hobara, Y.; Angelopoulos, V.; Mozer, F. First Detection of the Powerful Gamma-Ray Burst GRB 221009A by the THEMIS ESA and SST Particle Detectors on 2022 October 9. Astrophys. J. Lett. 2023, 948, L21. [Google Scholar] [CrossRef]
- Dwyer, J.R.; Smith, D.M.; Cummer, S.A. High-energy atmospheric physics: Terrestrial gamma-ray flashes and related phenomena. Space Sci. Rev. 2012, 173, 133–196. [Google Scholar] [CrossRef]
- Tavani, M.; Marisaldi, M.; Labanti, C.; Fuschino, F.; Argan, A.; Trois, A.; Giommi, P.; Colafrancesco, S.; Pittori, C.; Palma, F.; et al. Terrestrial gamma-ray flashes as powerful particle accelerators. Phys. Rev. Lett. 2011, 106, 018501. [Google Scholar] [CrossRef]
- Alva-Sánchez, H.; Zepeda-Barrios, A.; Díaz-Martínez, V.; Murrieta-Rodríguez, T.; Martínez-Dávalos, A.; Rodríguez-Villafuerte, M. Understanding the intrinsic radioactivity energy spectrum from 176Lu in LYSO/LSO scintillation crystals. Sci. Rep. 2018, 8, 17310. [Google Scholar] [CrossRef]
- Group, P.D.; Zyla, P.; Barnett, R.; Beringer, J.; Dahl, O.; Dwyer, D.; Groom, D.; Lin, C.J.; Lugovsky, K.; Pianori, E.; et al. Review of particle physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Pommé, S.; Marroyo, B.C. Improved peak shape fitting in alpha spectra. Appl. Radiat. Isot. 2015, 96, 148–153. [Google Scholar] [CrossRef] [PubMed]
| Instrument | Size | Directions | Angular | Energy | PID | Detector |
|---|---|---|---|---|---|---|
| Weight | Resolution | Range | Elements | |||
| IDP DEMETER | 525 g | 1 | FOV 32 deg. | e: (0.07, 0.8) MeV | No | Silicon diode |
| RAD Curiosity | ∼10 × 10 | Complex | FOV 36.7 deg. | e: (0.1, 20) MeV | Yes | PIPS (3 segments) |
| × 10 cm | segmentation | p: (5, 200) MeV | CsI(Tl) | |||
| : (5, 200) MeV | Plast. scint. | |||||
| l.Z: (10, 300) MeV | ||||||
| HEPP-L | Large | 5 Narrow | FOV 6.5 deg. | e: (0.1, 3) MeV | Yes | Si det. (2 layers) |
| collimators | 4 Wide | FOV 15 deg. | p: (2, 20) MeV | Plast. scint. | ||
| HEPP-H | DSSSDs | Silicon tracker | e: 3.2 degs. | e:(1.5, 50) MeV | Yes | DSSSDs |
| 100 cm | with DSSSDs | p: 2.94 degs. | p:(15, 200) MeV | DSSSDs | ||
| 5 CsI(Tl): | CsI | |||||
| 120 × 120 | ||||||
| × 30 mm | ||||||
| Mars-EPA | 270 × 180 | 1 | FOV 60 deg. | e: (0.1, 12) MeV | Yes | PIPS (2 layers) |
| × 148 cm | p: (2, 100) MeV | CsI(Tl) | ||||
| : (25, 400) MeV | ||||||
| l.Z: (25, 400) MeV |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nicolaidis, R.; Nozzoli, F.; Pepponi, G.; Bellutti, P.; Demenev, E.; Follega, F.M.; Iuppa, R.; Vilona, V. Characterizing Low-Energy Charged Particles in the Magnetosphere with the LEM CubeSat Spectrometer Project: Detector Concept and Hardware Characterisation. Universe 2023, 9, 331. https://doi.org/10.3390/universe9070331
Nicolaidis R, Nozzoli F, Pepponi G, Bellutti P, Demenev E, Follega FM, Iuppa R, Vilona V. Characterizing Low-Energy Charged Particles in the Magnetosphere with the LEM CubeSat Spectrometer Project: Detector Concept and Hardware Characterisation. Universe. 2023; 9(7):331. https://doi.org/10.3390/universe9070331
Chicago/Turabian StyleNicolaidis, Riccardo, Francesco Nozzoli, Giancarlo Pepponi, Pierluigi Bellutti, Evgeny Demenev, Francesco Maria Follega, Roberto Iuppa, and Veronica Vilona. 2023. "Characterizing Low-Energy Charged Particles in the Magnetosphere with the LEM CubeSat Spectrometer Project: Detector Concept and Hardware Characterisation" Universe 9, no. 7: 331. https://doi.org/10.3390/universe9070331
APA StyleNicolaidis, R., Nozzoli, F., Pepponi, G., Bellutti, P., Demenev, E., Follega, F. M., Iuppa, R., & Vilona, V. (2023). Characterizing Low-Energy Charged Particles in the Magnetosphere with the LEM CubeSat Spectrometer Project: Detector Concept and Hardware Characterisation. Universe, 9(7), 331. https://doi.org/10.3390/universe9070331











