Abstract
The Hubble tension has now grown to a level of significance which can no longer be ignored and calls for a solution which, despite a huge number of attempts, has so far eluded us. Significant efforts in the literature have focused on early-time modifications of CDM, introducing new physics operating prior to recombination and reducing the sound horizon. In this opinion paper I argue that early-time new physics alone will always fall short of fully solving the Hubble tension. I base my arguments on seven independent hints, related to (1) the ages of the oldest astrophysical objects, (2) considerations on the sound horizon-Hubble constant degeneracy directions in cosmological data, (3) the important role of cosmic chronometers, (4) a number of “descending trends” observed in a wide variety of low-redshift datasets, (5) the early integrated Sachs-Wolfe effect as an early-time consistency test of CDM, (6) early-Universe physics insensitive and uncalibrated cosmic standard constraints on the matter density, and finally (7) equality wavenumber-based constraints on the Hubble constant from galaxy power spectrum measurements. I argue that a promising way forward should ultimately involve a combination of early- and late-time (but non-local—in a cosmological sense, i.e., at high redshift) new physics, as well as local (i.e., at ) new physics, and I conclude by providing reflections with regards to potentially interesting models which may also help with the tension.
1. Introduction
The concordance CDM model has been extremely successful in describing cosmological and astrophysical observations across a wide range of times and scales, such as anisotropies in the Cosmic Microwave Background (CMB), the clustering of the large-scale structure (LSS), weak lensing of the CMB and the LSS (cosmic shear), the magnitude-redshift relation of distant Type Ia Supernovae (SNeIa), and light element abundances [1,2,3,4,5,6,7,8,9,10]. Nonetheless, we know that CDM cannot be the end of the story: at best, it is a phenomenological placeholder for our ignorance about the fundamental nature of dark matter (DM), dark energy (DE), and the origin of primordial perturbations. Theory considerations aside, possible observational hints for new physics have recently emerged, in the form of tensions between independent inferences of cosmological parameters assuming CDM.
Among these discrepancies, a special position is held by the “Hubble tension”: the mismatch between several early- and late-time inferences of the Hubble constant . One of the most precise early-time inferences is obtained from CMB temperature, polarization, and lensing measurements by the Planck satellite, which assuming CDM yield [4], improving to once combined with Baryon Acoustic Oscillation (BAO) and Hubble flow SNeIa data [4]. In contrast, one of the most precise local measurements (model-independent in a cosmological sense, although dependent on the underlying models for a variety of astrophysical effects), provided by the SH0ES team via a distance ladder making use of Cepheid-calibrated SNeIa, yields [11]. Depending on the dataset considered (see e.g., Refs. [12,13,14,15,16,17,18,19,20,21] for other local measurements), the significance of the tension falls between and , making it one of the most exciting open problems in cosmology (see Refs. [22,23,24,25,26,27,28,29,30,31] for reviews).
While systematics-based explanations (e.g., Refs. [32,33,34,35,36]) are not yet completely excluded (but are admittedly becoming increasingly unlikely), the possibility of the Hubble tension calling for new physics, potentially related to the dark sector, is now taken very seriously, with a wide range of proposals having been put forward: with no claims as to completeness, see e.g., Refs. [37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195,196,197,198,199,200,201,202,203,204,205,206,207,208,209,210,211,212,213,214,215,216,217,218,219,220,221,222,223,224,225,226,227,228,229,230,231,232,233,234,235,236,237,238,239,240,241,242,243,244,245,246,247,248,249,250,251,252,253,254,255,256,257,258,259,260,261,262,263,264,265,266,267,268,269,270,271,272,273,274,275,276,277,278,279,280,281,282,283,284,285,286,287,288,289,290,291,292,293,294,295,296,297,298,299,300,301,302,303,304,305,306,307,308,309,310,311,312,313,314,315,316,317,318,319,320,321,322,323,324,325,326,327,328,329,330,331,332,333,334,335,336,337,338,339,340,341,342,343,344,345,346,347,348,349,350,351,352,353,354,355,356,357,358,359,360,361,362,363,364,365,366,367,368,369,370,371,372,373,374,375,376,377,378,379,380,381,382,383,384,385,386,387,388,389,390,391,392,393,394,395,396,397,398,399,400,401,402,403,404,405,406,407,408,409,410,411,412,413,414,415,416,417,418,419,420,421,422,423,424,425,426,427,428,429,430,431,432,433,434,435,436,437,438,439,440,441,442,443,444,445,446,447,448,449,450,451,452,453,454,455,456,457,458,459,460,461,462,463,464,465,466,467,468,469,470,471,472,473,474,475,476,477,478,479,480,481,482,483,484,485,486,487,488,489,490,491,492,493,494,495,496,497,498,499,500,501,502,503,504,505,506,507,508,509,510,511,512,513,514,515,516,517,518,519,520,521,522,523,524,525,526,527,528,529,530,531,532,533,534,535,536,537,538,539,540,541,542,543,544,545,546,547,548,549,550,551,552,553,554,555,556] for examples of the rich variety of discussions in this context, as well as approaches adopted, with varying degrees of success. Cosmological solutions (involving new physics in the Hubble flow and not in the local Universe) usually feature modifications to CDM either prior to recombination, or in the late Universe, which I shall refer to as early-time and late-time modifications respectively. It is now well understood that late-time models are less effective in addressing the Hubble tension, because of their worsened fit to BAO and Hubble flow SNeIa data when is increased, due to the fact that the sound horizon at baryon drag is not altered [557,558,559,560,561,562,563,564,565,566]. In fact, the focus is now mostly towards early-time modifications, which aim to reduce by ≈7% to accommodate a higher while keeping the angular size of the sound horizon to the CMB value, and not running afoul of late-time BAO and SNeIa constraints. Examples in this sense include but are not limited to models raising the pre-recombination expansion rate, or modifying the recombination history.
Nevertheless, it is fair to say that we remain far from a compelling solution to the Hubble tension. Leaving aside their theoretical motivation, none of the models proposed so far have succeeded in accommodating a higher while maintaining a good fit to all available data, or not worsening other tensions (e.g., the “ discrepancy” [567,568,569,570,571]). Tongue-in-cheek, I would say that the statement “the Hubble tension calls for early-time new physics” may have been elevated to somewhat of a mantra in the community, and more often than not interpreted a bit too literally.1 My goal here is to argue that solving the Hubble tension will ultimately require more than just early-time new physics. I stress that this is not an original paper in a strict sense: to build my case, I will review results from a number of earlier works, at first glance perhaps unrelated to each other. When viewed more broadly, these results paint a coherent picture with a clear message: early-time new physics alone is not sufficient to solve the Hubble tension. “Alone” is the key word here: there is no question that an important fraction of the “tension-solving job” needs to come from early-time physics (and that late-time new physics alone definitely cannot do the job), but the point is that something more, e.g., some amount of late-time or local new physics, is required. As a clarification, the terms “local” and “non-local” here are used not in the field theory sense of the principle of locality, but to distinguish physics in the local Universe () from physics taking place at sufficiently high redshift. My case is built upon seven hints,2 some more theoretical in nature, others more data-driven, and others seemingly unrelated to the Hubble tension!
The rest of this paper is then organized as follows. The seven hints mentioned above are presented in Section 2. The latter is divided into seven subsections, each devoted to discussing one of these hints. In Section 3, I speculate about promising model building directions towards solving the Hubble tension and possibly other tensions (such as the discrepancy) simultaneously, building upon the lessons learned from these seven hints. Finally, in Section 4 I draw concluding remarks.
2. Seven Hints
In what follows, I present the seven hints upon which my case is built. In hopes that this will help committing them to memory, I have developed an “ABCDEFG” mnemonic for the hints as follows:
- ges of the oldest astrophysical objects;
- aryon Acoustic Oscillations sound horizon-Hubble constant degeneracy slope (compared to the same slope in the CMB);
- osmic chronometers;
- escending trends observed in a wide range of low-redshift data;
- arly integrated Sachs-Wolfe effect and the restrictions it imposes on early-time new physics;
- ractional matter density constraints from early-Universe physics insensitive and uncalibrated cosmic standards;
- alaxy power spectrum sound horizon- and equality wavenumber-based determinations of the Hubble constant.
In the following subsections, the hints will be presented in the above order, though I note that this is not necessarily the order which I would adopt to present them, say, in a talk.
2.1. Ages of the Oldest Astrophysical Objects
This first hint is, in principle, unrelated to the Hubble tension. The existence of old astrophysical objects (OAO) at high redshift has historically played an important role in cosmology, particularly with regards to hinting towards the existence of a cosmological constant-like component, and thus cosmic acceleration, way before the latter was actually discovered through SNeIa in 1998. The usefulness of OAO as a cosmological test is based on the following simple, incontrovertible fact: at any given redshift, the Universe must be at least as old as the oldest objects it contains at that redshift. Being the age-redshift of the Universe a model-dependent function, this statement can be turned around into a cosmological test, which can be used to exclude those models (or parameters) leading to the Universe being paradoxically younger than its oldest objects.3
To set the stage, the age of the Universe at any redshift, , is given by the following integral:
where is the normalized expansion rate, and in what follows I will denote the age of the Universe today by . Three comments are in order about Equation (1):
- the age of the Universe at any given redshift is self-evidently inversely proportional to the Hubble constant, ;
- the age integral picks up most of its contributions at late times, , since increases faster than in the early Universe (see e.g., Ref. [286])—for all intents and purposes, it is therefore basically insensitive to pre-recombination (new) physics;4
- it is possible for different cosmological models to lead to the same value of (at ), while predicting a completely different evolution at high redshift.
As myself, Pacucci and Loeb recently noted [575], the first two points above indicate that OAO can play an important role in further uncovering the origin of the Hubble tension, if due to new physics. In particular, OAO can be used as an early-time-independent consistency test of late-time physics, as follows [575]:
- create an OAO age-redshift catalog;
- choose a given model for the late-time expansion (the “null hypothesis” which will be the subject of the consistency test);
- impose (in a statistical sense) that the age of the Universe at any redshift within the chosen model exceeds the OAO ages—given the previous point 1), this will lead to an upper limit on ;
- the derived upper limit being in tension with local measurements would indicate an inconsistency in the chosen cosmological model and thus the need for at least some amount of late-time new physics (“new” relative to the chosen model)—conversely, absence of tension is at best an indication that there is no inconsistency yet, since it is in principle possible that OAO older than those present in the catalog may not yet have been identified.
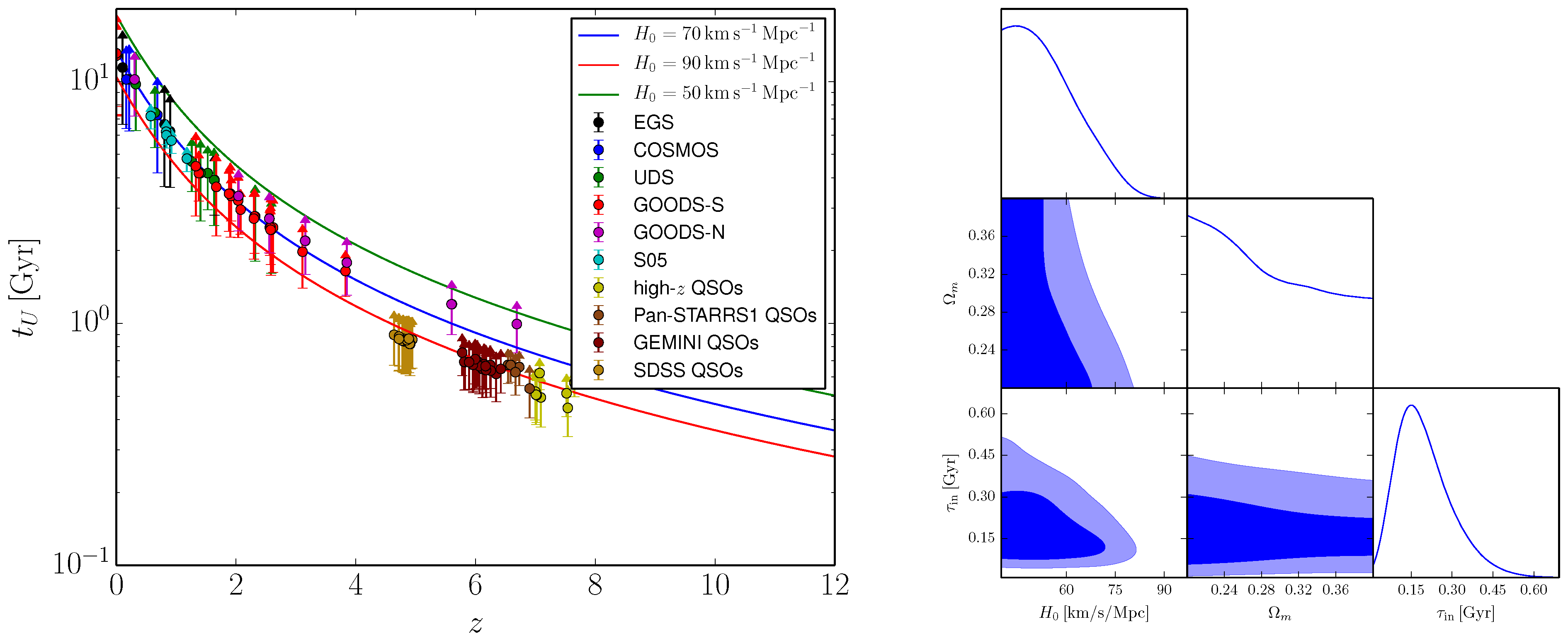
Before moving on, I note that an important caveat to results involving OAO concerns the reliability of their ages, which are notoriously difficult to estimate. Nonetheless, significant progress is being made with regard to these issues (see e.g., Refs. [576,577,578,579,580]), and more progress can be expected along these lines thanks to the recent launch of the James Webb Space Telescope. With these caveats in mind, in Ref. [575], I led an analysis following the above recipe, selecting CDM as the baseline model for the late-time expansion. In Ref. [575], myself, Pacucci and Loeb constructed an age-redshift catalog of 114 OAO up to , considering both galaxies, most of which identified within the CANDELS observing program, and quasars (QSOs) identified within various surveys. Most galaxy ages were estimated via photometric spectral energy distribution fits, whereas the QSOs ages were estimated via Monte Carlo realizations of the growth model proposed by Pacucci et al. [581]. I refer the reader to Section 3 of Ref. [575] for further details on the adopted galaxies and QSOs data, as well as on the age estimate methodology. The resulting OAO age-redshift diagram is shown in the left panel of Figure 1, alongside the predicted age-redshift relationship for three CDM cosmologies with and three different values of .
Figure 1.
(Left panel) age-redshift diagram of the OAO considered in Ref. [575], with the curves showing the age-redshift relationship for three CDM cosmologies with and different values of as per the color coding. (Right panel) corner plot for , , and in light of the OAO age-redshift diagram. Reproduced from Figure 1 and 2 of Vagnozzi, Pacucci & Loeb, “Implications for the Hubble tension from the ages of the oldest astrophysical objects”, Journal of High Energy Astrophysics, Volume 36, Pages 27–35, doi:10.1016/j.jheap.2022.07.004, published 4 August 2022 [575]. © (2022) Elsevier BV. Reproduced by permission of Elsevier and the first author. All rights reserved.
To obtain (Bayesian) upper limit on from the OAO age-redshift diagram, Markov Chain Monte Carlo (MCMC) methodswere used, considering a 3-dimensional parameter space described by , , and [575]. The latter is referred to as “incubation time” and accounts for the time elapsed between the Big Bang and the formation of the OAO, or in other words the fact that no OAO formed right at the Big Bang. From general considerations, we expect [582,583], but to be as conservative as possible was marginalized upon, imposing the so-called J19 prior, using the fitting function provided in Appendix G of Ref. [584]: this approach was argued to be conservative, as it assumes that the OAO descend from the oldest generation of galaxies (had they been assumed to descended from a later generation of galaxies, more stringent but less conservative upper limits on would have been obtained), see Refs. [575,582] for further details.
For the baseline analysis adopting flat priors on and , and the J19 prior on , regarded as the most balanced one in terms of equilibrium between conservative and aggressive assumptions, in Ref. [575] myself, Pacucci and Loeb found the 95% confidence level (C.L.) upper limit : see the right panel of Figure 1 for the corresponding contour plot. The concordance/discordance between this upper limit and the then-current local Cepheid-calibrated SNeIa distance ladder measurement was estimated to be at the level, certainly not high enough to be alarming, but still worthy of attention. This limit was found to be relatively stable against different analysis assumptions (particularly concerning priors on and ), with most of these assumptions actually resulting in more stringent upper limits on , and hence stronger conclusions. Other analysis assumptions were further explored by Wei and Melia [585], and their effect on the resulting upper limits on were found to be small (see however Ref. [586]).
If we take this discrepancy seriously, what consequences follow? Assuming that the OAO ages have been correctly estimated, essentially only two further assumptions can be questioned: the validity of the CDM model for the late-time expansion, and the validity of the local Cepheid-calibrated SNeIa estimate of . Going down the first route requires introducing new (cosmological) physics which makes the Universe older at all redshifts: this can be achieved if new physics results in the expansion rate lowering relative to CDM at (as in the case of a phantom-like component), in such a way to accommodate a higher , of course to an extent which is compatible with BAO and Hubble flow SNeIa constraints—more on this will be discussed in Section 3. Going down the second route opens the increasingly unlikely door of systematics (already amply discussed in the literature, as noted in Section 1), or the possibility of new local physics affecting the distance ladder measurements, more precisely lowering it. While I will return to these points in much more detail in Section 3, in the meantime I simply note that the possibilities of new late-time (cosmological) and local physics are not mutually exclusive, as the two can well act simultaneously (in addition to early-time new physics), the former to raise the cosmological estimate, the latter to lower the local estimate, bringing the two into better agreement. Of course, these results come with the caveats discussed earlier, pertaining to the difficulty of reliably estimating OAO ages. In particular, if mismodelled astrophysical or galaxy evolution effects cause the OAO ages to be systematically overestimated, this would directly result in a systematic underestimation of the upper limit on , therefore artificially worsening the tension with local measurements.
Before moving on, a comment on related works is in order, as Ref. [575] was not to the only one to recently appreciate the role of galaxy ages in the quest towards arbitrating the Hubble tension. Similar arguments, albeit limited to the age of the Universe today , were recently put forward [286,582,587]. In essence these works pointed out that, should (lower limits on) the age of the Universe as obtained from old stars and galaxies confirm the high value of indicated by Planck assuming CDM (given the preferred low value of , and the fact that ), this would at the very least require introducing either some late-time new physics, or some local new physics: to put it differently, early-time new physics alone would not be sufficient to solve the Hubble tension in this case. A stronger version of this argument was put forward by Bernal et al. [587], who pointed out the key role of (alongside ) in arbitrating the Hubble tension, highlighting the usefulness of “cosmic triangles” related to , , , and the sound horizon , i.e., ternary plots simultaneously visualizing independent constraints on these parameters (which are over-constrained given the precision of current cosmological measurements). Similarly, Krishnan et al. [286] instead argued that recent constraints on from old globular clusters, when analyzed in conjunction with a minimal parametrization for the late-time expansion while treating as a free parameter, indicate that early-time new physics can at best bring up to ≈71, confirming empirical findings that no early-time model so far has been able to do better than this. The results of Ref. [575], which this first hint build upon, essentially constitute a stronger version of these arguments, built upon rather than alone (recall that different cosmological models can lead to the same while predicting a completely different evolution), and providing the first direct indication that OAO ages may indeed be in slight tension with local measurements. Finally, I note that the importance of OAO ages in arbitrating the Hubble tension was also discussed later by Borghi et al. [579], Wei and Melia [585], and Moresco et al. [588]. For further related works, see Refs. [589,590,591], and Ref. [592] for a discussion in the context of the related look-back time quantity.
In closing, I think it is important to stress once more that this first hint is in principle completely unrelated to the Hubble tension. In essence, it constitutes of a consistency test whose failure indicates the need for some new physics at late times or on local scales, independently any assumed model for the early Universe. Of course, one would hope that this late-time and/or local new physics would go in the direction of helping with (or at the very least not worsen!) the Hubble tension, beyond the (lion’s share?) of the job inevitably done by early-time new physics.
2.2. BAO Sound Horizon-Hubble Constant Degeneracy Slope
The physics of acoustic oscillations, whose associated distance scale(s) provides a standard ruler through which distances at high redshift can be inferred, is cleanly imprinted in two classes of observations: in the CMB through the location of the acoustic peaks (particularly the first ones), and in the Baryon Acoustic Oscillation BAO peaks observed in correlators of tracers of the large-scale structure, such as galaxies. In the case of the CMB, the location of the acoustic peaks and their spacing determines , the angular size of the comoving sound horizon at recombination:
where is the comoving sound horizon at the epoch of recombination, occurring at redshift , and is the comoving distance to recombination. Since essentially only depends on the Hubble constant or equivalently the reduced Hubble constant , as well as the physical matter density parameter , measurements of can be used to infer once and are known (or, in the case of , calibrated given a model).
On the other hand, BAO measurements at a certain redshift (typically ) carry the imprint of , the sound horizon at baryon drag. The latter is the epoch when baryons were released from the drag of photons, and takes place at a redshift slightly lower than , making slightly larger than as a result: in essentially all reasonable modified recombination scenarios, holds. Focusing for simplicity on transverse BAO measurements, these constrain the BAO angular scale ,5 given by the following:
where once again is the comoving distance to the (effective, survey-averaged) redshift at which the BAO feature is observed. Observing the BAO feature at several redshifts allows one to constrain and the product , or equivalently , given the assumed relation between and . Equations (2) and (3) together with the assumed - relation are the starting point for the work of Jedamzik, Pogosian and Zhao [593], which investigated the effect of early-time new physics decreasing (and thereby ), treating the latter as a free parameter to be as model-independent as possible, while assuming that the post-recombination Universe is described by CDM.
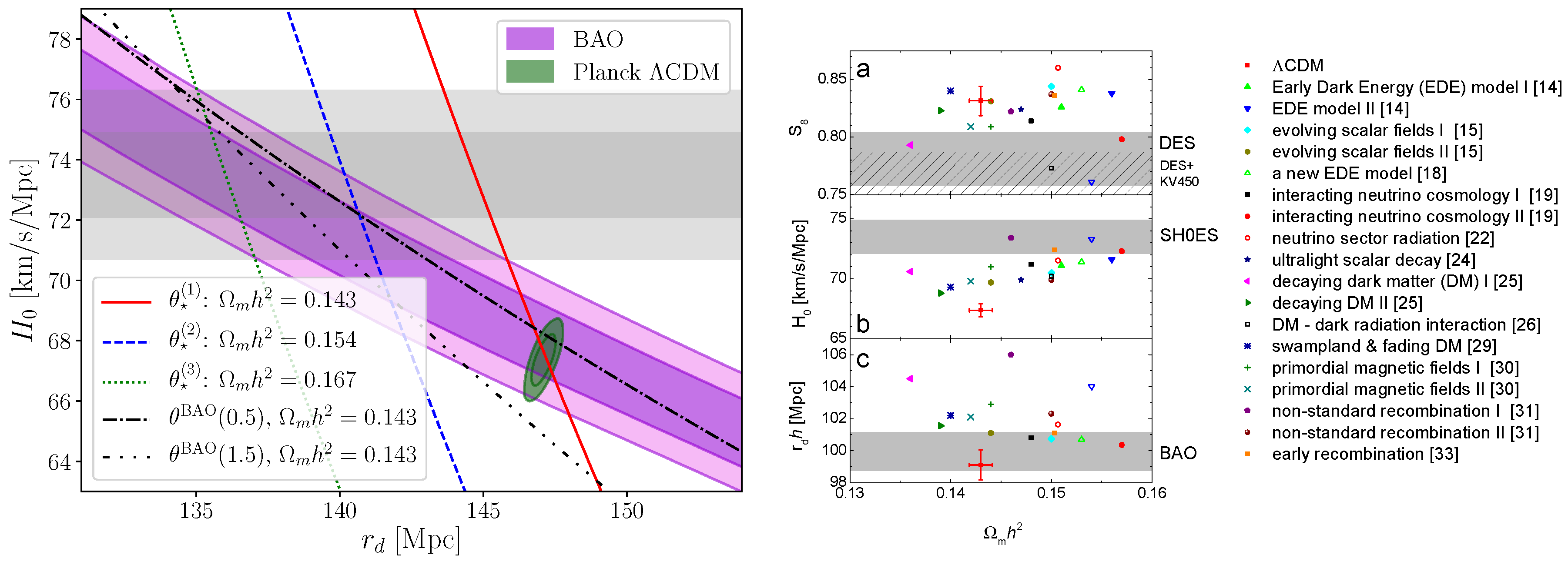
The key observation of Ref. [593] is that, given a value of , both CMB and BAO measurements define a degeneracy line in the - plane, along which the corresponding and are constant (it is in this sense that I adopt the qualifier “degeneracy”). Importantly, given the enormous difference between and , the redshifts at which the acoustic feature is observed in BAO and CMB measurements, the corresponding degeneracy slopes are very different, as shown in the left panel of Figure 2. Placing and on the horizontal and vertical axes respectively, the - degeneracy lines get steeper with increasing observation redshift, and are therefore steepest when considering the CMB measurements of . Along the same plane, as shown in the left panel of Figure 2, increasing moves the degeneracy lines towards the left, keeping the degeneracy slope fixed.
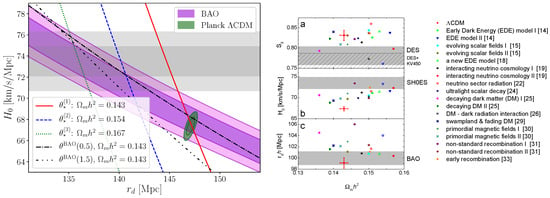
Figure 2.
(Left panel) degeneracy lines in the - plane defined by constant and (the latter at different redshifts), and for different values of in the case of , alongside constraints from (Planck) CMB data (within CDM), then-current BAO data, and the SH0ES measurement. (Right panel) best-fit values of , , , and for a compilation of models aiming to solve the Hubble tension, alongside 68% constraints on the corresponding parameters from different surveys (grey bands). No single model manages to solve the Hubble tension while remaining consistent with all other external measurements. Reproduced from Figure 2 and 3 of Jedamzik, Pogosian & Zhao, “Why reducing the cosmic sound horizon alone can not fully resolve the Hubble tension”, Communications Physics, Volume 4, article number 123, doi:10.1038/s42005-021-00628-x, published 8 June 2021 [593], with permission from the authors. Both figures are licensed under a Creative Commons Attribution 4.0 International License, and no changes were made.
The difference between the BAO and CMB - degeneracy slopes plays a key role in assessing the ability to solve the Hubble tension of new physics which only lowers . To see this, consider again the left panel of Figure 2, where the solid red line has been plotted assuming the best-fit value of determined by the Planck satellite (whose constraints in the - plane are given by the green contours, and are in agreement with BAO data—purple bands—for low values of ). Clearly, for Planck and SH0ES measurements (grey bands) to be brought into agreement, one has to move along one of the - degeneracy lines: if this is done along the red line (“low” , Planck best-fit), one clearly sees that it is impossible to obtain complete consistency between CMB, SH0ES, and BAO data, given that the point where the red line and the grey bands meet is outside the purple bands.
The only way for a CMB - degeneracy line to meet both BAO and SH0ES measurements is for this line to be obtained at a higher value of : see for instance the green dotted line (in the example of Figure 2, “high” ). However, in this minimal scenario where the effect of new physics is only that of reducing , the increase in quickly bring a tension with WL data, worsening the already existing discrepancy. Recall that, along with , the parameter best constrained by WL measurements is , where is the present day linear theory amplitude of matter fluctuations averaged in spheres of radius Mpc, and quantifies the variance of fluctuations on this scale. The clustering amplitude depends both on the amplitude of the primordial power spectrum (fixed by the CMB), as well as the net growth of matter perturbations, which increases as is increased. Therefore raising , which is required to achieve consistency between CMB, SH0ES, and BAO measurements as argued earlier, comes at the price of increasing : this exacerbates the discrepancy, as the values of preferred by WL surveys such as DES and KiDS are already lower than that inferred from Planck, with the significance of this discrepancy lying between 2 and depending on the underlying assumptions (see Ref. [569]).
The overall observation of Jedamzik, Pogosian and Zhao [593] is therefore that early-time new physics which reduces the sound horizon alone cannot completely resolve the Hubble tension, as it will always create additional tensions: with BAO data if operating at lower , and with WL data (worsening the discrepancy) if operating at higher . These problems were first explicitly noted in the context of early dark energy (EDE) models, which introduce a dark energy-like component dynamically relevant around matter-radiation equality, and where the necessity of operating at higher is related to the enhanced early integrated Sachs-Wolfe effect predicted by such models (which will become relevant in discussing my fifth hint in Section 2.5). Surveying a compilation of models introduced to solve the Hubble tension, Jedamzik, Pogosian and Zhao [593] confirmed that the features discussed previously are indeed generically observed, in some cases more strongly than others (see the right panel of Figure 2).
To conclude, this second hint indicates that early-time new physics whose only effect is to reduce the sound horizon cannot fully solve the Hubble tension. It is worth noting that the vast majority of early-time new physics models introduced in this context were introduced precisely to lower the sound horizon: one notable exception is the strongly interacting neutrino model, which however is now severely constrained by CMB polarization data. Clearly, a full solution to the Hubble tension which does not introduce additional tensions requires extra ingredients beyond the -lowering ones. While I will discuss in more detail some possibilities in this direction in Section 3, here I simply note that including additional early-time new physics is highly non-trivial due to the necessity of maintaining a good fit to all features in the CMB temperature and polarization spectra, beyond just the acoustic peaks. I believe a much more promising direction involves additional late-time new physics, which “decouples” itself from the early-time effects, and possibly predominantly operating at the perturbation level in order not to spoil CDM’s fit to late-time background measurements.
2.3. Cosmic Chronometers
To further arbitrate the Hubble tension or, as in our case, shed light on which epochs may require new physics, it is helpful to consider cosmological datasets which are as model-independent as possible.6 In order to identify whether late-time new physics may be required, it is helpful to consider probes which carry little or no dependence on early-time physics, as with the OAO considered earlier. Should such a probe return a value of consistent with the high-redshift ones (e.g., the Planck low value of assuming CDM), the resulting (persisting) tension with the local measurements of is, by construction, one that may not be resolved by early-time new physics.
Cosmic chronometers (CC) are interesting in this sense, as they are able to provide a direct, cosmology-independent estimate of the Hubble rate . They were first proposed by Jiménez and Loeb [594], and rely on inverting the time-redshift relation within a Friedmann-Lemaître-Robertson-Walker (FLRW) Universe:
valid for a FLRW Universe and assuming only homogeneity, isotropy, and a metric theory of gravity, with no further assumptions on the functional form of the expansion rate or the spatial geometry. Using Equation (4) requires identifying a class of “cosmic chronometers” to estimate as the look-back time differential change with redshift: as redshifts (and hence ) can easily be measured via spectroscopy, the difficulty is in finding a trustworthy estimator for look-back time (and hence ).
The question of which objects are best suited for use as CC has been the subject of much study over the past two decades. It is now understood that extremely massive (), early, passively-evolving galaxies (i.e., evolving on a timescale much larger than their differential ages) are an excellent choice [595]. The reason is that these galaxies formed and assembled their mass at high redshift ( 2–3) and over a very short period of time (), after which they quickly exhaust their gas reservoir and evolve passively. With a suitable CC sample at hand, the age difference between two passively-evolving CC formed approximately at the same time and separated by a small redshift interval around can be used to obtain , and thus via Equation (4). While not unrelated to the OAO discussed in Section 2.1, the crucial difference is that CC rely on differential rather than absolute age measurements, and hence are affected to a much lesser degree by systematics, which are expected to (at least partially) cancel when considering age differences.
The appeal of CC lies in their providing a determination of free from cosmological model assumptions. To infer from CC data, one can proceed non-parametrically (e.g., as done by Yu, Ratra and Wang [596], Gómez-Valent and Amendola [597], and many other works), or assuming a specific model. Two important points are worth noting now:
- regardless of whether one goes parametric or non-parametric, the value of inferred from CC is the cosmological (as opposed to local) one;
- as CC directly measure the late-time () expansion rate, a parametric analysis thereof requires no assumption whatsoever about early Universe physics (this is actually true for a non-parametric inference as well).
Focusing on the parametric approach, which is the one we shall follow later, two immediate corollaries of the above are:
- should the value of inferred from CC within a certain model be in tension with local measurements, such a conclusion would be completely independent of whatever happened in the early Universe, including before and around recombination;
- assuming such a (residual) tension is physical (i.e., not due to systematics), resolving it would require introducing new (relative to the assumed parametric model) late-time ingredients to alter the cosmological value of , and/or new local physics to alter the local value of .
The above points suggest that CC can be used as a late-time consistency test of CDM, much as the OAO discussed in Section 2.1, by comparing the value of inferred from CC assuming CDM to local measurements, and assessing whether there is a (residual) tension between the two. Of course, CC data come with several caveats pertaining to their reliability similar to those of OAO (although less severe, given the fact that the CC galaxies are passively evolving), and inevitably carry dependence on assumed astrophysical galaxy evolution models. The fact that CC are differential rather than absolute age measurements somewhat mitigates these potential systematics, which have nevertheless been studied and quantified in detail in various works, including several by Moresco et al. [588,598,599]: therefore, at the current stage of things, CC data are significantly more trustworthy than OAO.
I perform this analysis on the latest compilation of 32 CC measurements, comprising the 31 measurements listed in Table 1 of Ref. [583] and the latest measurement of Borghi et al. [579], including systematics and off-diagonal covariance terms as discussed in detail in various recent works (e.g., Ref. [588]).7 Assuming CDM, I infer and : both values are in excellent agreement with the values inferred from the Planck satellite assuming CDM, although the uncertainties are a factor of respectively 6 and 8 bigger, which should not come as a surprise, given that I have analyzed CC data on their own. One could of course try and sharpen these inferences using additional external datasets (e.g., a prior on from weak lensing or cluster count measurements), but here I choose to be as conservative as possible and use no data other than CC, in order to keep the picture as clean as possible.
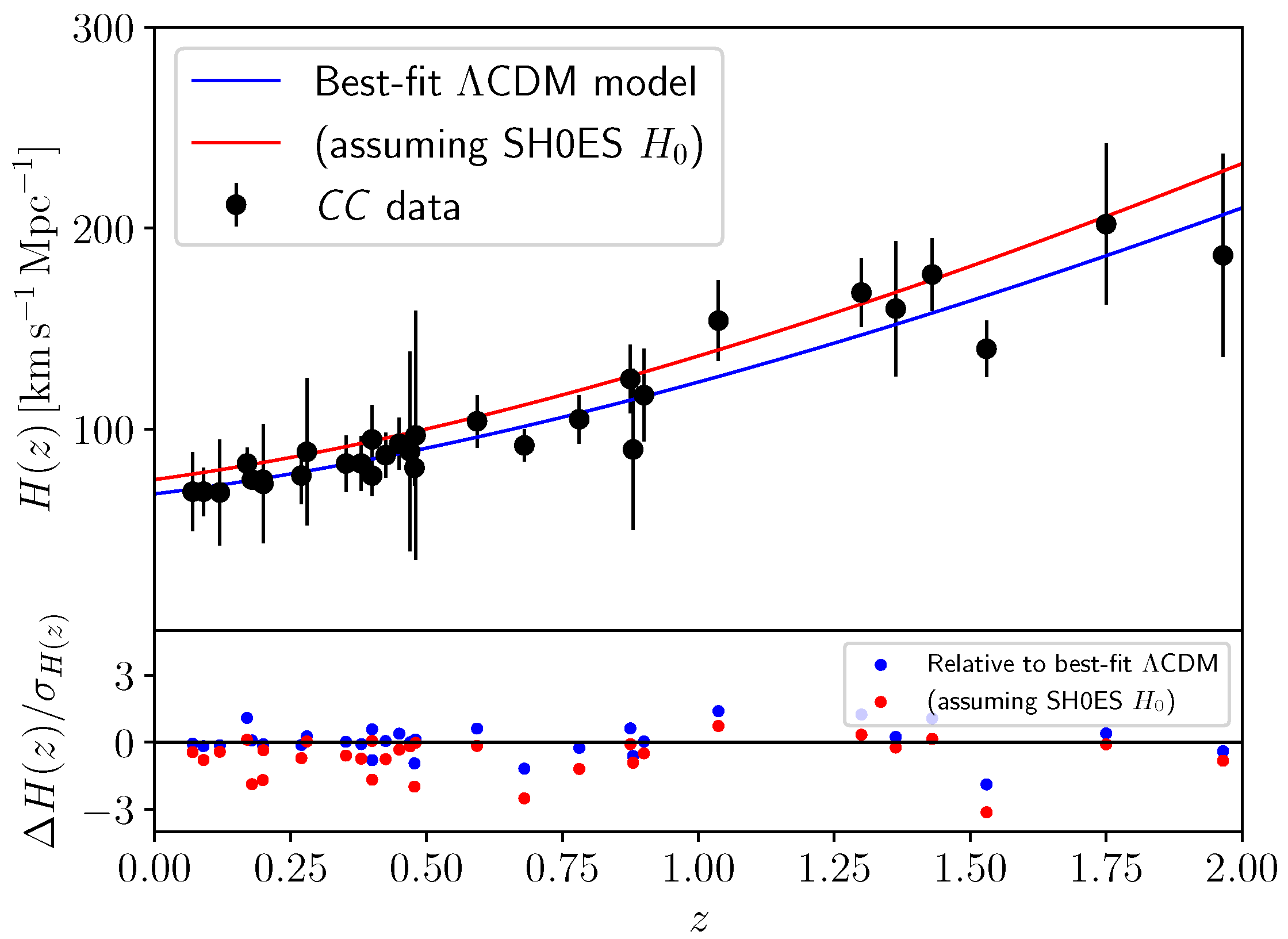
While the uncertainty on is relatively large, it is intriguing that the central value is in remarkable agreement with the Planck’s central value (). Moreover, despite the size of the uncertainty, a tension with the local determination from Cepheid-calibrated SNeIa remains. As with the case of OAO earlier, this residual tension is not high enough to be alarming, but nonetheless worthy of attention. It is worth examining which part(s) of the CC dataset prevent a high determination. To show this, in Figure 3 I plot the CC dataset alongside the CDM prediction for the expansion rate (upper panel blue curve), with the best-fit values for the parameters obtained by analyzing the CC dataset alone, and with the corresponding residuals (data minus theory, in units of data uncertainties) shown in the lower panel. Then, I plot the same functional form for the expansion rate, but with fixed to the local SH0ES value (red curve). From the lower panel (red points), it is clear that there is no single point driving the preference for low (or rather disfavoring high ). Rather, there are a number of points (especially for , as well as a point around ) for which the high fit is noticeably worse than the low one, with the high theory prediction in some cases being nearly off from the data.

Figure 3.
(Upper panel) CC measurements (black datapoints), alongside the predicted expansion rate given the best-fit CDM cosmological parameters from a fit to CC data alone (blue curve), and the same cosmology but with fixed to the SH0ES value. (Lower panel) residuals (CC data minus theory predictions) in units of datapoint uncertainties, for the two cosmologies considered in the upper panel, with the same color coding.
If we therefore take this residual tension seriously, and eliminate the possibility of systematics, once more we are left with the options of questioning the validity of CDM at late times, and/or the validity of local determination(s). Should one pursue the first route, new late-time physics should again go in the direction of lowering the expansion rate relative to CDM at (similar to the effect of a phantom component), compatibly with BAO and high-z SNeIa constraints. As with the earlier discussion on OAO, I once more note that the possibilities of new late-time (cosmological) and local physics are not mutually exclusive: the two can act simultaneously (together with early-time new physics), the former to raise the cosmological value, the latter to lower the local value, to bring the two into better agreement and meet along the way. In closing, it is intriguing that both absolute (Section 2.1) and relative (Section 2.3) galaxy ages independently8 appear to disfavor high (≳73) values of and, when used as consistency tests of CDM, indicate the need for new physics at late times and/or local scales, if the residual tension with local measurements is taken seriously.
2.4. Descending Trends in Low-Redshift Data
The CDM model is a dynamical model (i.e., one which describes the evolution of a system over time or, equivalently, redshift), equipped with a number of fitting parameters. In science, including physics and by extension cosmology, it is a non-negotiable (mathematical) fact that dynamical models break down when fitting parameters which are supposed to be constant actually evolve with time—more precisely, when their inferred values evolve depending on the time when they are inferred. In the case of CDM, this would correspond to the inferred values of otherwise constant parameters taking different values depending on the redshift of the data used to infer the parameters themselves. Let me now be more specific and focus on as the parameter of interest. Within an FLRW Universe, from the mathematical point of view is none other than an integration constant: therefore, by definition, it should be constant regardless of the redshift at which it is inferred. More specifically, as shown by Krishnan et al. [602], under the assumptions of homogeneity and isotropy, and once a theoretical in the form of an effective equation of state ,9 the Friedmann equations can be integrated to give:
While Equation (5) is a mathematical identity, from the observational point of view an useful interpretation is as follows. An input , appearing in the right-hand side of Equation (5) is specified in the form of a underlying model fit to the data, the latter corresponding to appearing on the same side of the equation.10 This is used to infer on the left-hand side of the equation. If the input [] and the data [] “agree”, the value of inferred as a function of the redshift of the data should be consistent (within uncertainties) across redshift. On the other hand, if and disagree beyond the uncertainties, picks up z dependence and “runs”. Note that this statement can also be made for other parameters beyond (e.g., and ) which are either integration constants, or are directly related to integration constants.
Overall, it would appear that inferring running constants is a telltale signature of a model’s death. In some way, the tension (and other tensions) can be thought of as a primitive example of such running, in the simplest case between two (extreme) redshifts. However, if the tension is physical (i.e., not due to systematics) and calls for some amount of late-time new physics,11 redshift evolution at some other intermediate redshift is non-negotiable. If such a redshift evolution is not observed, one is left with the conclusion that either systematics are to blame, and/or that the assumption of FLRW itself [underlying the derivation of Equation (5)] should be dropped. This is a mathematical statement, and amounts to the observation that there cannot be contradictions between mathematics and observations. This leads to the following questions:
- Has such a redshift evolution already been observed in current data?
- Has it been observed across different independent datasets, and if so is there a common trend across these independent datasets?
- Are the size and/or direction of this trend inconsistent with what one would expect if no new physics were at play, i.e., can it be attributed to new physics?
With a few caveats, the answers to the above three questions are positive: hints of running have now been observed in multiple datasets, and in all of these decreases with increasing redshift, which is why I will refer to these as “descending trends”.
The first, and perhaps most famous, example of descending trend was reported by the H0LiCOW collaboration, who in Wong et al. [14] performed a joint analysis of six gravitationally lensed quasars with measured time delays to infer . The strong lensing approach is a one-step technique, which unlike the distance ladder approach requires no external calibration, although the absence of a ladder is traded for the dependence on assumptions concerning the lens and line-of-sight mass distribution [603,604,605]. As such, the method is completely independent of and complementary to the CMB and distance ladder approaches. Nevertheless, the inferred value of is still cosmological model-dependent, as it is related to the so-called “time-delay distance” . The time-delay distance combines information on the lens redshift as well as the angular diameter distances to the lens, source, and between lens and source. Therefore, interpreting measurements requires adopting an underlying cosmological model, which in the case of H0LiCOW was chosen to be the CDM model.
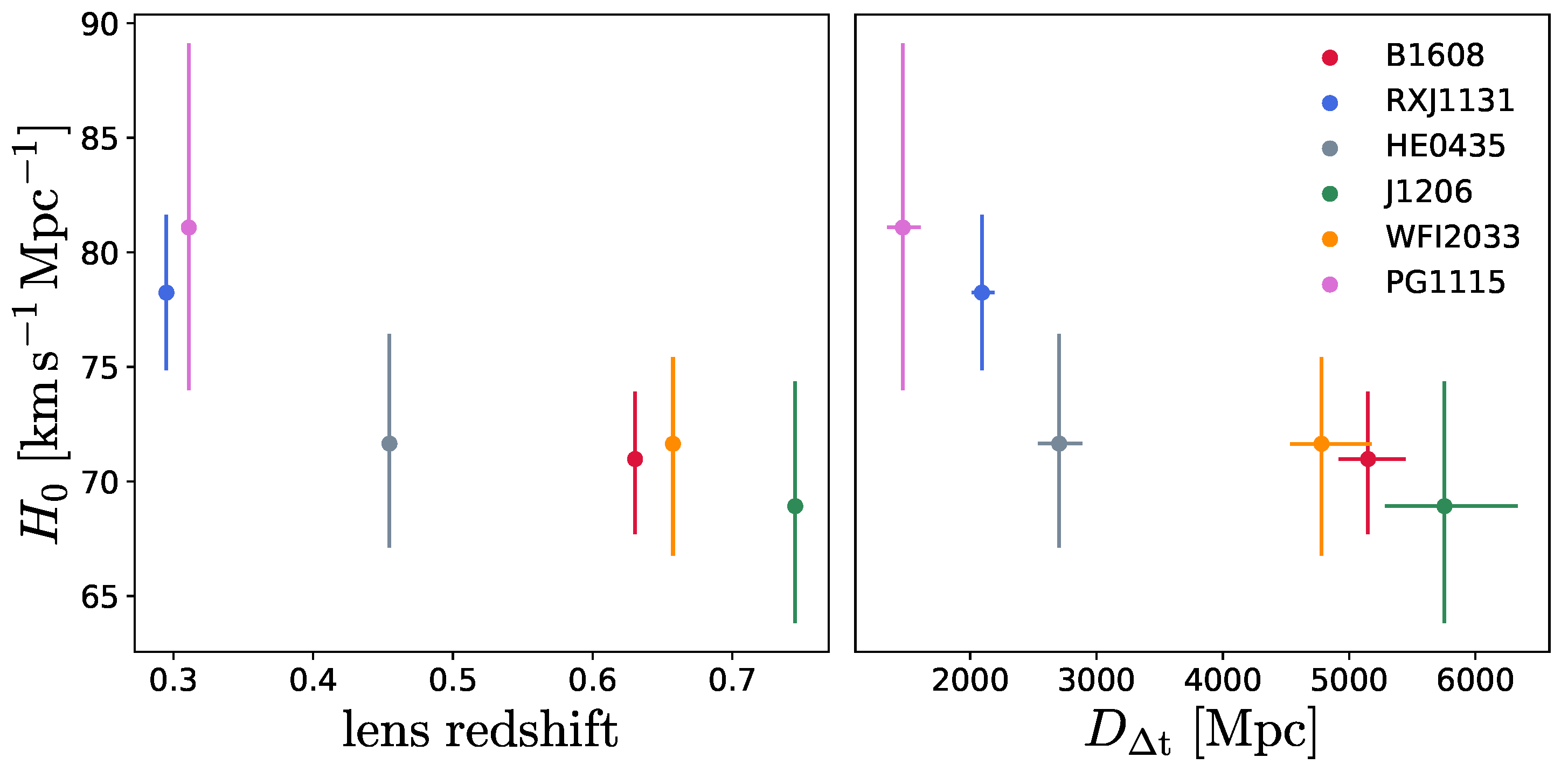
Albeit relegated to an Appendix, the H0LiCOW collaboration [14] noted a curious trend where the value of inferred from each of the single lenses decreased with increasing redshift lens. This trend, in the redshift range , is reported in the left panel of Figure 4, whereas the right panel reports a similar trend observed with the time-delay distance. In particular, the central value of evolves from when inferred from the lens PG1115 at redshift 0.3, to ∼68 when inferred from the lens J1206 at redshift ∼0.7. Using mock data, the trend was found to deviate from the null hypothesis (where does not run with redshift) at an equivalent Gaussian significance level of nearly [14]. Albeit intriguing, the trend and its possible physical origin were not discussed further, possibly also due to its moderate significance. A similar trend was confirmed by the TDCOSMO collaboration when revisiting the analysis including stellar kinematics measurements to break the mass-sheet degeneracy and thereby jointly infer and lens density profiles [606]. The key point, however, is that this trend is inferred without making any assumptions on early-Universe physics, since the interpretation of the time-delay distance measurements is essentially only sensitive to late-time physics (and, in this case, the assumption of CDM). Therefore, if not due to systematics or astrophysical mismodeling, “fixing” this trend12 can only be achieved by fiddling around with late-time new physics.
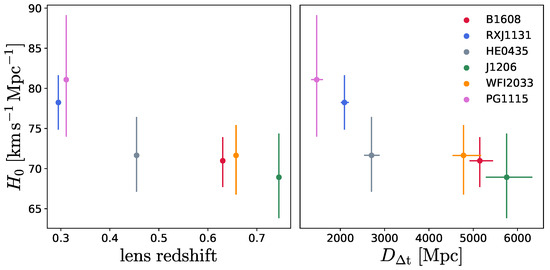
Figure 4.
(Left panel) constraints on from the individual H0LiCOW lenses as a function of lens redshift. (Right panel) same as for the left panel, but as a function of the lens time-delay distances. Reproduced from Figure A1 of Wong et al., “H0LiCOW—XIII. A 2.4 per cent measurement of from lensed quasars: 5.3σ tension between early- and late-Universe probes”, Monthly Notices of the Royal Astronomical Society, Volume 498, Issue 1, Pages 1420–1439, doi:10.1093/mnras/stz3094, published 16 September 2019 [14]. © (2019) The Authors. Reproduced by permission of Oxford University Press on behalf of the Royal Astronomical Society. All rights reserved.
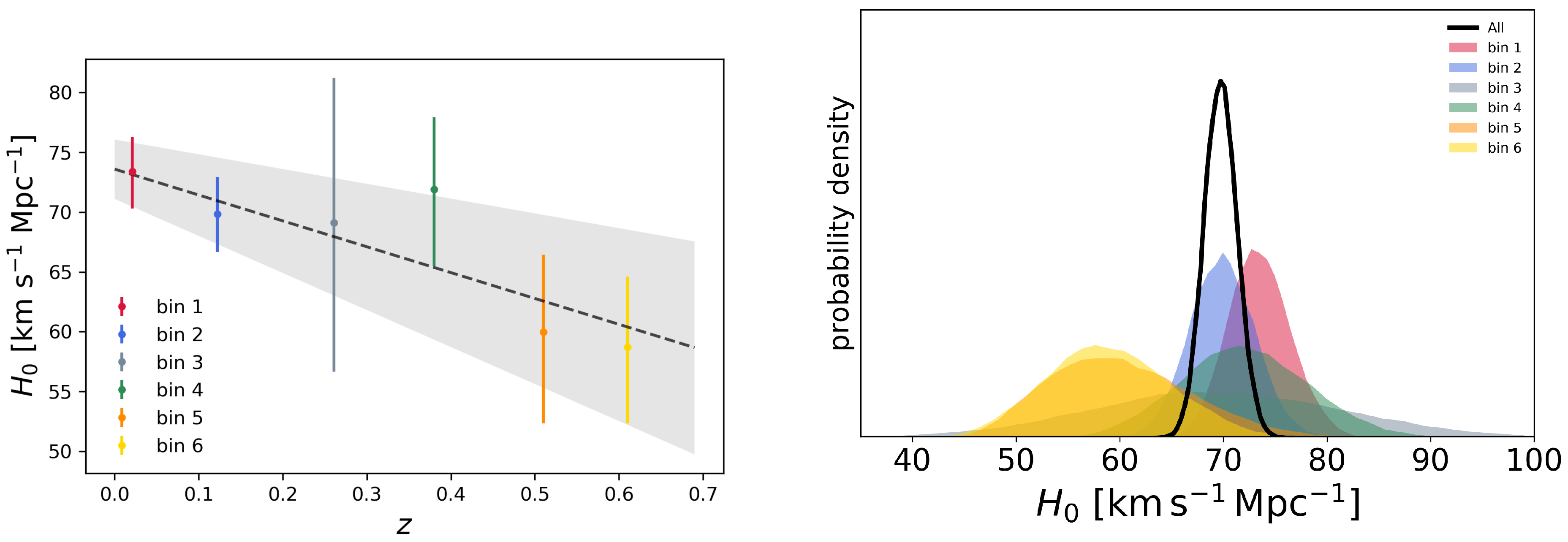
Inspired by the H0LiCOW results, Krishnan et al. [607] considered a low-redshift () dataset which overall indicates an intermediate (∼70) value of , and used previously by Dutta et al. [151], to examine whether this intermediate value actually hides a similar trend once the data is divided in redshift bins. The adopted dataset included distances to 6 megamaser-hosting galaxies [18,608,609], CC data restricted to the range , BAO data from 6dFGS, SDSS-MGS, and BOSS DR12 (only isotropic measurements, without including measurements), and Pantheon SNeIa in the range . Krishnan et al. [607] then divided the data into 6 redshift bins, and inferred from each bin via an MCMC where a number of additional nuisance parameters were also varied (see Ref. [607] for more details). Note that the presence of CC data, which directly constrain , allows for the use of BAO data without having to impose any external prior on the sound horizon at baryon drag , which is instead treated as a free parameter. Therefore, the determinations of are free of any early-Universe physics assumption, and the same is true for any trend that may be inferred. The result of this analysis is shown in Figure 5, where a descending trend broadly similar to the H0LiCOW one is clearly seen. Intriguingly, the slope of the two trends are consistent, albeit the two intercepts differ slightly. Using the same approach as H0LiCOW to establish the significance of the trend, this was found to deviate from the null hypothesis at an equivalent Gaussian significance level of [607]. As with the H0LiCOW trend, this is by construction one which cannot be fixed by invoking early-time new physics which alters , since such modifications will only push the trend up and down without removing it. In fact, Krishnan et al. [607] used this observation to argue that the Hubble tension calls for something more than just early-time new physics.
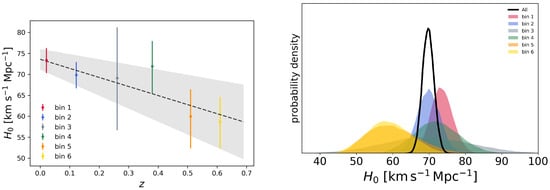
Figure 5.
(Left panel) binned constraints on obtained from the late-time dataset combination considered in Ref. [607]. (Right panel) probability distribution functions for as inferred from each bin, together with the overall constraint obtained from the complete dataset. Reproduced from Figure 1 and 2 of Krishnan et al., “Is there an early Universe solution to Hubble tension?”, Physical Review D, Volume 102, Issue 10, article number 103525, doi:10.1103/PhysRevD.102.103525, published 20 November 2020 [607]. © (2020) American Physical Society. Reproduced by permission of the American Physical Society and the authors. All rights reserved.
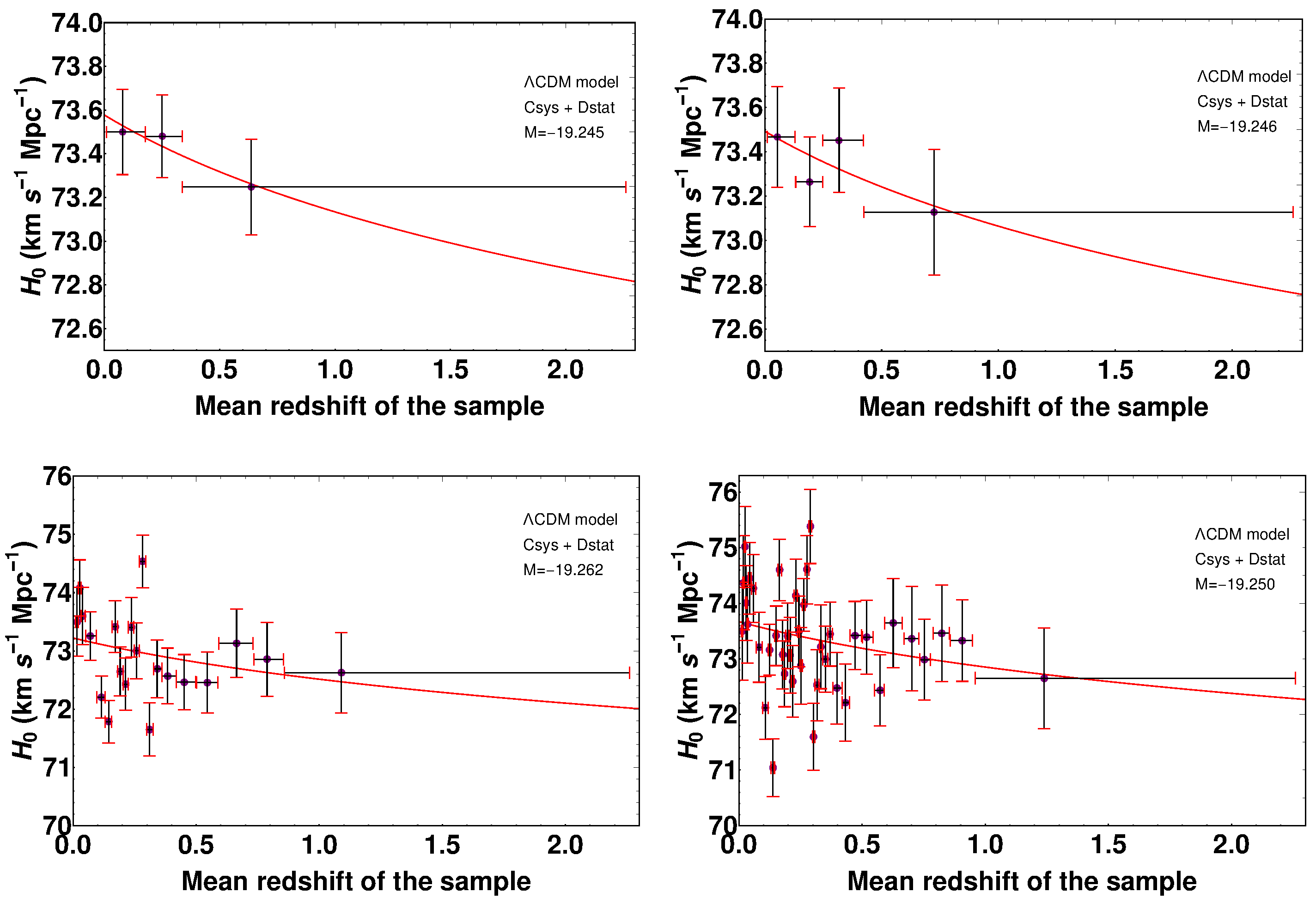
Another notable example, and the last one I will discuss to a similar level of detail as the previous two, is the Pantheon SNeIa sample. The analysis of Dainotti et al. [610] considered the full Pantheon sample and binned the SNeIa into respectively 3, 4, 20, and 40 redshift bins, each containing the same number of SNeIa. Within each bin a value for was then inferred, both assuming the CDM model, as well as the CDM model where the DE equation of state (EoS) is described by the so-called Chevallier-Polarski-Linder parametrization . The results, as far as the CDM model is concerned, are shown in Figure 6, with each panel corresponding to a different choice of number of bins. Albeit visually less clear than the previous two, a trend is visible in this case as well, with significance estimated to be up to by Dainotti et al. [610]. When instead assuming the CDM model, the trend was found to persist, albeit at a lower significance. The authors then fit the inferred values of with a function of the form , where , inferring values of differing from 0 at up to . Various possible astrophysical causes for such a redshift evolution of were discussed (in fact, the proposed fitting function is routinely used in modelling astrophysical evolution effects in Gamma-Ray Bursts an Active Galactic Nuclei studies), ranging from correlations between SNeIa luminosities, progenitor ages, and metallicities, to intrinsic evolution of SNeIa luminosities, to Malmquist bias. However, none of these effects could be convincingly narrowed down as the underlying explanation for the trend. As with the H0LiCOW trend and the trend found by Krishnan et al. [607], this is one which cannot be fixed by new physics in the early Universe, but only at low redshifts. Finally, while consistent in direction with the previous two trends, the slope in this case is much lower.
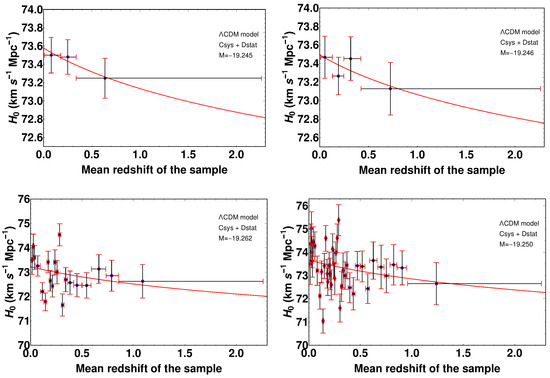
Figure 6.
Binned constraints on obtained from the Pantheon SNeIa sample in Ref. [610], considering 3 redshift bins (upper left panel), 4 redshift bins (upper right panel), 20 redshift bins (lower left panel), and 40 redshift bins (lower right panel). Reproduced from Figure 5 and 6 of Dainotti et al., “On the Hubble Constant Tension in the SNe Ia Pantheon Sample”, The Astrophysical Journal, Volume 912, Number 2, article number 150, doi:10.3847/1538-4357/abeb73, published 17 May 2021 [610]. © (2021) American Astronomical Society. Reproduced by permission of the American Astronomical Society and the authors. All rights reserved.
Besides these three examples, similar trends have been observed in several other late-time datasets. For instance, Jia, Hu and Wang [611] performed an analysis of the latest Pantheon+ SNeIa sample in combination with BAO and CC data, finding a similar trend of decreasing with increasing redshift, with significance of up to depending on the binning strategy, and explicitly arguing that this strongly indicates the need for new late-time physics. Importantly, in their analysis Jia, Hu and Wang [611] for the first time removed the correlations between different redshift bins, making use of the transformation matrix discussed by Huterer and Cooray [612]. A similar trend was also found in the Pantheon+ SNeIa sample (without making use of the SH0ES calibrator sample) by Malekjani et al. [613],13 who argued in favor of possible evidence for negative dark energy density (or equivalently ). While not directly focusing on but rather attempting to infer the proper motion of the Solar System from the Pantheon SNeIa, Horstmann, Pietschke and Schwarz [614] also found an interesting trend of slightly decreasing with redshift and thereby slightly increasing with redshift (see Figure 6 in Ref. [614]): this inverse correlation is a direct reflection of the - degeneracy at the level of low-redshift distances (within CDM), as one can keep the distance to a certain redshift fixed by decreasing [increasing] one parameter and simultaneously increasing [decreasing] the other. For the same reason, observed increasing trends in from QSOs data (see e.g., Refs. [615,616,617]), which appear to prefer at high redshift, can directly be translated into a decreasing trend in (although not always explicitly reported). A combination of CC, Pantheon SNeIa, and QSOs data was also used by Ó Colgáin et al. to report a similar trend [618].14
Having reported all these trends, the natural questions to ask are to what extent they could have been expected, and what are their implications for the Hubble tension. Let me start from the latter question. Since all these trends were obtained making no assumptions on early-Universe physics, their implication is quite clear: some amount of late-time new physics is clearly needed to “fix” these trends, which intriguingly all go in the same direction and show a good compatibility between each other (although not all show the same level of significance). Taking these trends seriously would require this new physics to work in the same direction as that inferred from OAO and CC, i.e., in the direction of lowering the expansion rate relative to CDM at , similar to the effect of a phantom component.
As for whether similar trends may be expected even within CDM, the answer is positive, although somewhat surprising. Naïvely, one would guess that, because in CDM DE dies quickly and matter becomes quickly dominant as one moves to high redshift, probes at higher redshift should indicate higher values of , and thereby lower values of . This expectation, while reasonable, does not appear to be confirmed in analyses of mock data. Specifically, Ó Colgáin et al. [618] and Ó Colgáin, Sheikh-Jabbai and Solomon [630] considered mock distance and expansion rate data matching the expected sensitivity of DESI. After binning this mock data, it was found that as one moves to higher redshifts the and posterior distributions develop non-Gaussian tails in the low and high directions, but the peaks of the distributions actually move in the opposite direction (high and low ). This was explained in terms of projection effects in combination with the non-Gaussian tails [618,630] (see also Ref. [631]). The surprising conclusion is therefore that one should indeed expect some evolution in and , but in the opposite direction compared to what is seen in data. Perhaps more relevant is the fact that the expected size of this “running” effect, even at the sensitivity of DESI, is small - far smaller than what is actually observed in data. In fact, as both Figure 4 and Figure 5 show, the size of the trend is quite significant even at redshifts , where DE is still dominant and one would not expect any evolution within CDM, regardless of the direction of the evolution (see e.g., Figure 2 of Ref. [618]).
Taken in conjunction, all these considerations suggest that the descending trends observed in data are not consistent, neither in terms of size nor direction, with what is expected within CDM. If we take them seriously, they appear to be the telltale signature of the breakdown of CDM at late times—or, to put it differently, a disagreement between mathematics and observations. Importantly, this problem cannot simply be fixed by changing a length scale (such as reducing , as is achieved by most early-time new physics models), but require a other than the CDM one at late times, and therefore call for late-time new physics. Of course, it is also possible that astrophysical systematics may be the cause of these descending trends. One way to eliminate this possibility would be to observe such trends in as many independent datasets as possible, and ascertain whether these independent trends are consistent among each other: should this be the case, it would be extremely hard to make a convincing case for systematics, as different astrophysical systematics would somehow have to conspire to make the trend consistent across independent probes. Current results are indeed moving in this direction, which is why I believe these descending trends should be taken seriously as an indication for new late-time physics.
In closing, I also note that a trend of increasing with redshift was recently reported by Adil et al. [632] based on an analysis of measurements. Moreover, Esposito et al. [633] analyzed SZ-identified galaxy cluster number counts from the South Pole Telescope, and Lyman- spectra from the MIKE/HIRES and X-shooter spectrographs, and inferred a tension between the low value of preferred by low-redshift cluster count data and the high value of inferred from high-redshift Lyman- data. While the latter was not discussed in light of evolving trends, it can indeed be read in terms of increasing with redshift. If one believes the decreasing /increasing trends, this result should not be unexpected, as , and therefore one should expect the inferred to increase with redshift within CDM. If substantiated, this trend would suggest that the and tensions are connected, and that further evolution in may be detected with the improvement in precision of WL data.
2.5. Early Integrated Sachs-Wolfe Effect
This fifth hint originates from the following question I first explicitly raised in Ref. [634]: “If solving the Hubble tension requires a significant amount of early-time new physics, why do we not see clear signs of it in CMB data alone”? Or, equivalently, “Why does ΛCDM appear to fit CMB data so well”? These queries were driven by the apparently puzzling contradiction between the significant amount of new physics required to solve the Hubble tension, and the lack of detection thereof when analyzing CMB data alone, without the use of any late-time prior. For instance, this is exemplified by the EDE solution to the Hubble tension, which requires of the energy budget of the Universe at matter-radiation equality to have been in the form of an exotic EDE component, raising the question as to how such a significant amount of new physics may have escaped detection in CMB-only analyses.15 As a caveat, hereafter I will focus my discussion on CMB data from Planck in order to follow the analysis I performed in Ref. [634].
The key observation I made in Ref. [634] is that for what concerns CMB data, a non-insignificant amount of early-time new physics would first be expected to appear in conjunction with the so-called early integrated Sachs-Wolfe (eISW) effect. The eISW effect is a contribution to CMB anisotropies sourced by time-varying gravitational potentials at early times. In the standard picture, the eISW effect is driven by the fact that the CMB forms when the Universe is not entirely matter dominated, since only in a matter-dominated Universe are gravitational potentials constant in time. The potential decay driven by the non-negligible residual radiation fraction is then responsible for sourcing the eISW effect, which is particularly prominent around the first acoustic peak. To linear order in temperature perturbations, the eISW contribution to the ℓth temperature anisotropy multipole, , is given by:
where and are the two scalar potentials in Newtonian gauge, is conformal time (with denoting the conformal time today), is the optical depth to a given conformal time, is the order-ℓ spherical Bessel function, , and is the conformal time at an arbitrary point deep inside the matter-domination era (as long as this point is chosen deep inside the matter-domination era, e.g., , the exact value of is irrelevant). The observation I made in Ref. [634] is then that early-Universe new physics altering the expansion rate around recombination will inevitably modify the evolution of the gravitational potentials, and hence the terms and in Equation (6), which in turn alters the prediction for the eISW contribution to the CMB anisotropies. This would result in a mismatch between the CDM prediction for the eISW effect, and that of new physics,16 which can be tested in a relatively model-agnostic way via an eISW-based consistency test of CDM (similar in spirit to the OAO test of Section 2.1, but restricted to early times).
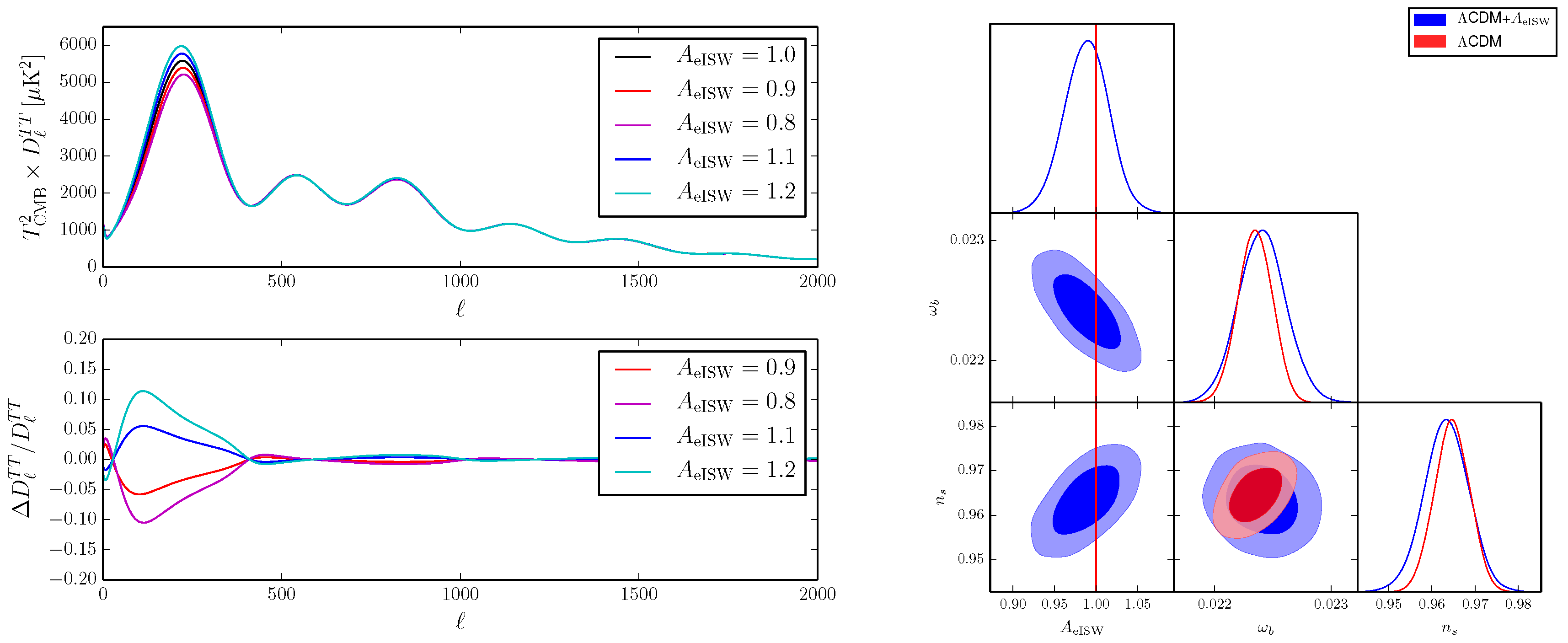
To proceed, in Ref. [634] I isolated the eISW contribution to the CMB power spectra by introducing a phenomenological scaling parameter/fudge factor, the “eISW amplitude” , which multiplies Equation (6). This parameter is reminiscent of the phenomenological lensing parameter introduced by Calabrese et al. [635] as a consistency test of the amplitude of CMB lensing (see also Refs. [636,637] for recent reassessments pertaining to the problem), and is part of a more general class of phenomenological scaling parameters discussed by Kable, Addison and Bennett [638], and Ruiz-Granda and Vielva [639]. Note that should not be viewed as a standard cosmological parameter, but rather as a phenomenological consistency test parameter: corresponds to the prediction of the underlying “null hypothesis” model (in this case CDM), whereas could be an indication for discrepancy at the level of the eISW effect between the underlying model and data. The effect on the CMB temperature power spectrum of varying is shown in the left panel of Figure 7. Clearly, the effect is most prominent around the first peak (with / respectively enhancing/reducing the amplitude of the first peak), as one could have expected from purely theoretical considerations [634].
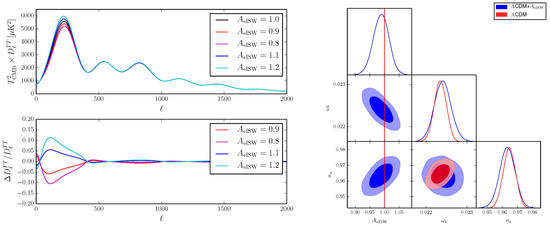
Figure 7.
(Left panel) impact of varying on the CMB temperature power spectrum (upper sub-panel), and relative differences in with respect to the CDM model (lower sub-panel). (Right panel) corner plot for , , and , within the CDM (red contours) and CDM+ (blue contours) models, from Planck data. Reproduced from Figure 1 and 2 of Vagnozzi, “Consistency tests of ΛCDM from the early integrated Sachs-Wolfe effect: Implications for early-time new physics and the Hubble tension”, Physical Review D, Volume 104, Issue 6, article number 063524, doi:10.1103/PhysRevD.104.063524, published 15 September 2021 [634]. © (2021) American Physical Society. Reproduced by permission of the American Physical Society and the author. All rights reserved.
In Ref. [634], I then fit a 7-parameter CDM+ cosmological model to Planck CMB temperature and polarization data, resulting in the inference of at 68% C.L., in perfect agreement with the CDM value . In addition, the fact that introducing leads to negligible shifts in the 6 cosmological parameters reinforces the conclusion that CDM’s prediction for the amplitude of the eISW effect agrees perfectly with Planck data. The most “significant” (to use an euphemism) parameter shifts induced by freeing up were observed in the scalar spectral index and the physical baryon density , which as expected are the two parameters most strongly correlated with [634]: however, both of these parameters shift by less than (see the right panel of Figure 7). This result was found to be stable against the use of the CamSpec likelihood in place of the Plik one, as well as the inclusion of additional datasets, such as a Big Bang Nucleosynthesis (BBN) prior on , and constraints on the late-time expansion rate (which can further stabilize constraints on ) from BAO and uncalibrated SNeIa [634]. Moreover, the same result was found to be very stable against further parameter space extensions, including cases where the effective number of neutrinos , Helium fraction , lensing amplitude , running and running of the running of the spectral index were allowed to vary [634]. Therefore, when adopting Planck CMB data, the inferred amplitude of the eISW effect is perfectly in agreement with the expectation from CDM.
I used this result in Ref. [634] to argue against the presence of a significant amount of early-time new physics which can fit cosmological observations as well as CDM. Taking as example the EDE solution to the Hubble tension [106,640,641], which requires ≳10% of the energy budget of the Universe at matter-radiation equality to have been in the form of an exotic EDE component, in Ref. [634] I explicitly showed that, if all other parameters are kept fixed to their CDM best-fits, the amplitude of the eISW effect of a Hubble tension-solving EDE cosmology (with ≈12% EDE fraction at its maximum) is ≈20% higher compared to CDM, corresponding to , and hence completely excluded by the previous analysis. One way of fixing this is to absorb the excess eISW power through parameter shifts, the simplest of which being an increase in the DM density (and a further more moderate increase in ): in fact, such an increase makes matter-radiation equality occur earlier, thereby decreasing the time over which the radiation-driven decay of gravitational potentials can source the eISW effect. However, an increase in comes with the deleterious effect of exacerbating the tension, as a larger amount of DM naturally enhances the growth of structure, worsening the tension between CMB and WL probes: this has explicitly been noted in the context of EDE and first emphasized by Hill et al. [194] (whereas other recent works, such as Goldstein et al. [494], discussed related issues pertaining to the scalar spectral index and its inconsistency with measurements from the one-dimensional Lyman- forest flux power spectrum). I further argued that such a problem, namely an increase in the eISW amplitude which then needs to be compensated in some other way, is not limited to EDE, but quite generally applies to most models which decrease the sound horizon by increasing the pre-recombination expansion rate, i.e., a significant fraction of early-time models invoked to solve the Hubble tension [634]. These models would need to reduce the excess eISW power, the most direct of which involves an increase in , which has indeed been observed in several early-time models: note that this increase in goes precisely in the same direction of the increase in discussed in the context of the second hint (Section 2.2), but has a completely different physical origin. At the same time, I caution against generalizing to all early-time models, given that some of these may possess model-dependent ingredients which ameliorate the eISW-related problem (explicitly discussing the cases of Refs. [231,266]), and therefore the prospects of specific models should be judged on a case-by-case basis [634].
In conclusion the eISW effect, and in particular the high level of consistency between its expected amplitude within the CDM model and Planck CMB data, places important restrictions on the leeway of early-time models which raise the expansion rate around recombination (and thereby enhance the eISW effect), most of which pay the eISW price by increasing and thereby worsening the tension. Of course, the conclusions I reached in Ref. [634] discussed in this hint hinge upon the use of Planck CMB data. Although such an analysis has not been explicitly performed in the literature, it is conceivable that the adoption of a different CMB dataset, for instance from the Atacama Cosmology Telescope (ACT), could lead to different conclusions for what concerns . In fact, ACT DR4 data [6] is known to be in slight tension with Planck for what concerns the extrapolated height of the first acoustic peak, and thus of parameters whose determination is closely tied to the latter, such as , , and [642,643,644,645,646]: by extension, one would expect these conclusions to extend to as well, although I stress that such a conclusion has yet to be checked explicitly. In fact, if interpreted within an EDE framework, ACT data at face value lead to a detection of non-zero EDE fraction [320,322,383], although the “CMB tension” between ACT and Planck calls for a deeper scrutiny of possible systematics involved. Until these are better understood, or clarified by future CMB data (e.g., Refs. [647,648,649]), the most conservative stand one can take is to view Planck’s results as placing (upper) guard rails on the amount of early-time new physics which affects the amplitude of the eISW effect.
2.6. (Fractional) Matter Density Constraints from Early-Universe Physics Insensitive and Uncalibrated Cosmic Standards
As the reader has hopefully been able to appreciate so far in the context of OAO (Section 2.1), CC (Section 2.3), and descending trends in low-redshift data (Section 2.4), re-analyses of observations relaxing strong assumptions, or alternative analyses which do not depend on these strong assumptions, are very important. If the results of the re-analyses of alternative analyses are consistent with the original/baseline results, new physics attempting to solve tensions by modifying those assumptions cannot be completely successful. In the cases discussed earlier, alternative analyses carrying absolutely no dependence on early-Universe physics systematically uncovered a residual ≈2 tension between CDM and late-time probes which cannot, by construction, be fixed by early-time new physics. However, all the resulting constraints were not as competitive as those adopting using CMB data under the assumption of CDM: this is not surprising, given the enormous constraining power carried by CMB observations, which however have long been thought to depend strongly on early-Universe physics. These observations are the starting point for the discussion of the sixth hint, which relies on a re-analysis of CMB data (in combination with other low-redshift observations) performed by Lin, Chen and Mack [650] with little to no dependence on early-Universe physics, while remaining competitive with the original analysis at least as far as the inferred value of is concerned.
As noted in earlier by Lin, Mack and Hou [651], the Hubble tension is normally presented comparing constraints on only, or sometimes and , and this has strenghtened the pre-recombination vs post-recombination narrative. However, besides the age of the Universe as noted elsewhere, a very important role in the Hubble tension discussion can be played by the (fractional) matter density parameter , and Lin, Mack and Hou [651] advocated for comparing constraints between different probes in the - plane, as this allows for a much more complete assessment of the compatibility between different probes, the model-dependence of each, and the ability of non-standard models to truly reconcile all constraints (as referring exclusively to projected information along the direction may obscure the full picture).
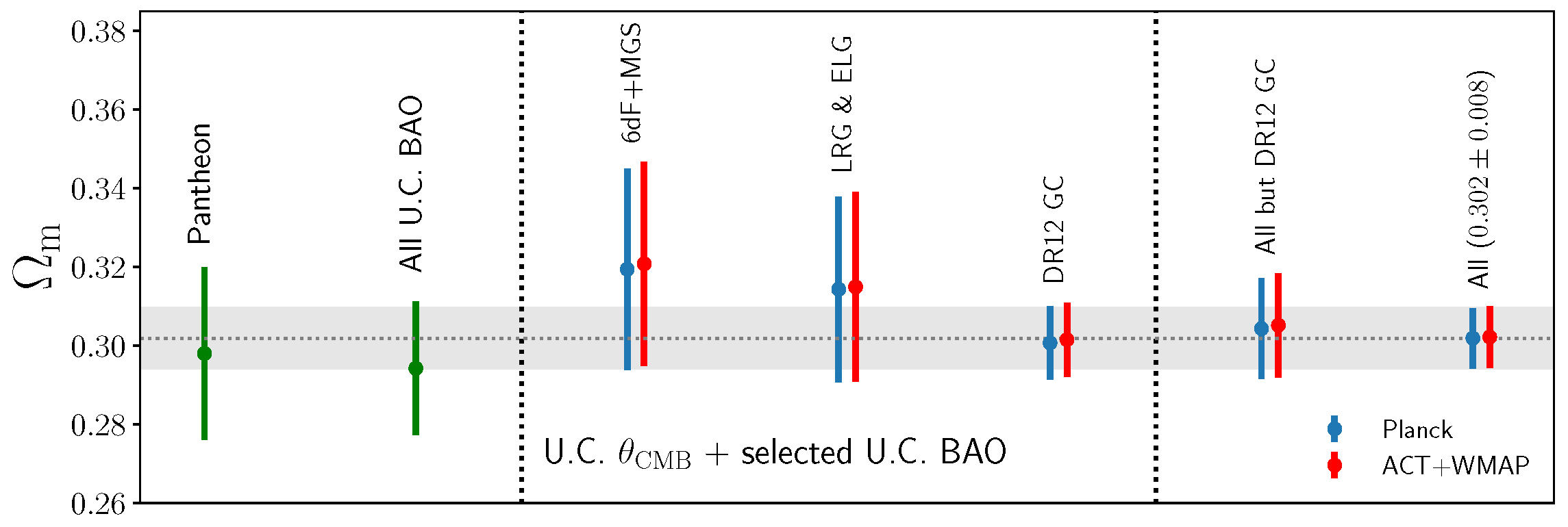
CMB observations can set strong constraints on , although these have long been thought to depend strongly on the assumed early-Universe physics model (usually CDM). On the other hand, combined uncalibrated BAO and SNeIa data can constrain the -normalized background evolution of the late-time Universe: in the case of BAO, this requires treating as a free parameter, which will therefore be completely degenerate with .17 This dataset combination, which essentially constrains (and in particular the slope thereof), can constrain , although such constraints are not as strong as the model-dependent CMB ones. Finally, there exist plenty of low-redshift probes only involving post-recombination physics (CC are an excellent example), but their precision on is relatively low, because of their own astrophysical uncertainties and their inherent - degeneracy. Is it possible to get the best of all three worlds, i.e., determinations of and which are as free from early-Universe assumptions as possible, while remaining competitive with the CMB determinations? Lin, Chen and Mack [650] show that this is indeed possible, through a particular combination of the CMB acoustic peak scale 18 with uncalibrated BAO and SNeIa data, plus other late-time probes which are completely insensitive to early-Universe physics, which together deliver constraints on and competitive with Planck’s CDM ones. Lin, Chen and Mack [650] denoted this combination “early Universe physics insensitive and uncalibrated cosmic standards”, or simply “uncalibrated cosmic standards” (UCS).
Earlier in Section 2.2, I argued that the two distance scales imprinted in CMB and BAO observations, respectively the comoving sound horizon at recombination and at baryon drag , are closely related, with . This simple observation is the key behind the UCS approach—Lin, Chen and Mack [650] argued that the difference between the two sound horizons normalized by the Hubble distance, denoted by , is very small and almost completely insensitive to early-Universe physics:
where is the sound speed of the photon-baryon fluid and . The near insensitivity to early-Universe physics of is a direct consequence of the narrow separation in redshift between the epochs of recombination and baryon drag. On the other hand, the two epochs leave their imprints (respectively in the CMB acoustic peaks and the BAO feature observed in the clustering of the large-scale structure) at widely separated redshifts, , and this provides the extremely long lever arm required to constrain with a precision comparable to that of CMB data alone when working within a specific model (for instance CDM).
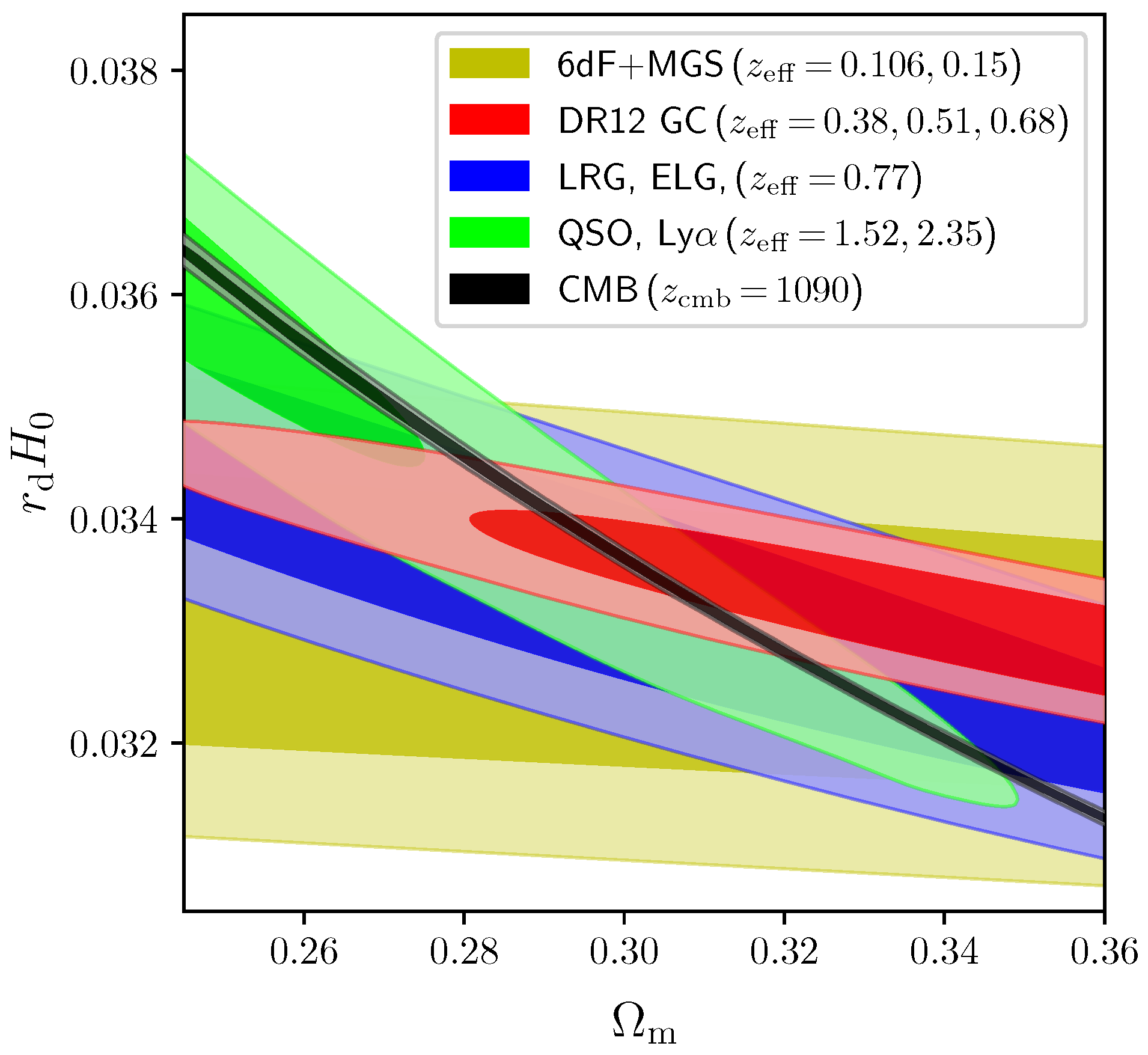
With these premises, the initial UCS dataset combination considered by Lin, Chen and Mack [650] includes measurements of the CMB acoustic peak scale obtained from Planck and ACT+WMAP, alongside uncalibrated BAO distance and expansion rate measurements from the 6dFGS, SDSS-MGS, SDSS DR12, and SDSS DR16 galaxy samples, as well as from the eBOSS DR16 quasars and Lyman- (including their cross-correlations), and finally uncalibrated SNeIa distance moduli measurements from the Pantheon sample. The free parameters varied are , the SNeIa absolute magnitude , and the combination , whereas a BBN prior is set on (required to compute the sound speed of the photon-baryon fluid), and Planck-driven priors are set on the redshift of recombination and the redshift separation between recombination and the epoch of baryon drag . The priors on and fix via Equation (7), through which can be inferred given the values of and : this essentially makes another measurement of at , well above the redshift range probed by BAO measurements (), providing a powerfully constraining anchor at high redshift and the extremely long lever arm required to tighten constraints on relative changes in and thereby constrain at the same level as in CDM, but without assuming any specific early-Universe model. The underlying reason is closely related to our earlier discussion in Section 2.2 in the context of the - degeneracy slopes: in this case, the slope of the - degeneracy gets steeper as the redshift of the measurements is increased, and it is the fact that which allows for a precise determination of , as shown in Figure 8 making use of a number of actual datasets.
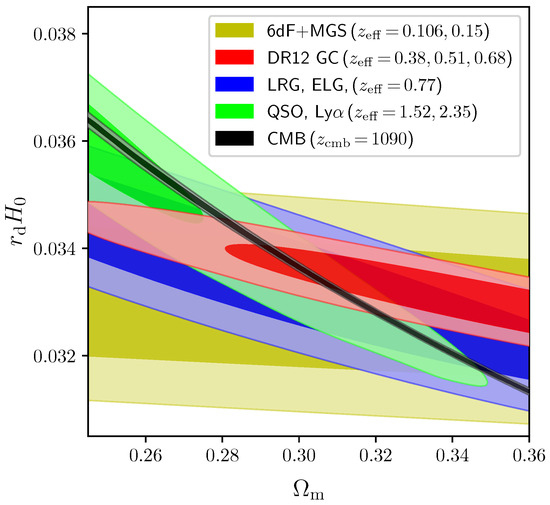
Figure 8.
Degeneracy contours in the - plane from different BAO and CMB (geometrical) probes. Reproduced from Figure 2 of Lin, Chen & Mack, “Early Universe Physics Insensitive and Uncalibrated Cosmic Standards: Constraints on and Implications for the Hubble Tension”, The Astrophysical Journal, Volume 920, Number 2, article number 159, doi:10.3847/1538-4357/ac12cf, published 25 October 2021 [650]. © (2021) American Astronomical Society. Reproduced by permission of the American Astronomical Society and the authors. All rights reserved.
From the previous combination and assuming the validity of CDM post-recombination (but without making any assumption on the pre-recombination expansion history), Lin, Chen and Mack [650] infer , only slightly looser than the value obtained from a full analysis of the same data within CDM (including all CMB information, and not just the location of the first peak), where is inferred. The obtained constraints only makes use of geometrical information on the CMB, and makes almost no assumptions on early-Universe physics, while being also insensitive to degeneracies between and by which a full-shape CMB analysis is instead affected (and which in turn can carry imprints of the slight large-versus-small angular scales discrepancy in Planck and therefore potential systematics). Lin, Chen and Mack [650] studied in detail the impact of various assumptions in the choice of UCS datasets and priors (especially for what concerns Planck vs ACT+WMAP as well as the inclusion of certain BAO measurements), with the results shown in Figure 9 indicating that the previous constraint is very robust against these assumptions.
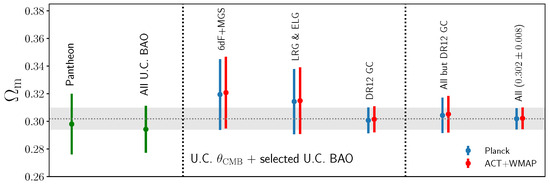
Figure 9.
Constraints on obtained from different combinations of uncalibrated cosmic standards, with the shaded grey band representing the result to the far right obtained including all UCS measurements. Reproduced from Figure 3 of Lin, Chen & Mack, “Early Universe Physics Insensitive and Uncalibrated Cosmic Standards: Constraints on and Implications for the Hubble Tension”, The Astrophysical Journal, Volume 920, Number 2, article number 159, doi:10.3847/1538-4357/ac12cf, published 25 October 2021 [650]. © (2021) American Astronomical Society. Reproduced by permission of the American Astronomical Society and the authors. All rights reserved.
The above analysis delivers a constraint in the - plane which is not exactly along the direction, but rather exhibits a small positive correlation described by the following:
This suggests that the baseline UCS dataset combination can be further supplemented with additional late-time, but non-local, datasets to break the - background evolution degeneracy and thereby determine . If these late-time datasets are chosen within the same philosophy of ensuring their independence/insensitivity to early-Universe physics, the resulting inference will be equally insensitive to early-Universe physics and will therefore be extremely valuable in arbitrating the source of the Hubble tension. Lin, Chen and Mack [650] consider many such examples of late-time datasets, ranging from CC, to -ray optical depth measurements, to cosmic age measurements via the ages of old globular clusters (see Section 4 of Ref. [650] for further details). While in doing so one is trading the dependence on early-Universe physics for a dependence on other astrophysical effects and thereby potential systematics, the idea is that by choosing a range of late-time measurements as wide and independent as possible one can try to reduce the effects of these systematics as much as possible.
Combining the baseline UCS dataset with all the chosen late-time, non-local observations, Lin, Chen and Mack [650] infer , in tension with the local Cepheid-calibrated SNeIa distance ladder measurement. This inference was obtained by modelling the latest available systematic error estimates for all non-local probes, and was found to be extremely stable against the exclusion of one or more of such probes (most notably the cosmic age estimates, given its dependence on the prior for the formation time of the globular cluster). Remarkably, despite having only assumed the validity of CDM at late times and introducing almost no early-Universe assumptions, the inferred value of is in excellent agreement with the CDM-based value obtained from a full analysis of CMB and BAO data, only with uncertainty a factor of ≈2 wider.
What are the implications of these results for the Hubble tension? Clearly the UCS analysis has identified a residual ≳ 2 tension which has nothing to do with early-Universe new physics, since virtually any information whatsoever on early-Universe physics has been removed in the analysis. Therefore, such a tension may only be solved by post-recombination non-local new physics (recall that this UCS analysis assumed that the post-recombination expansion history is described by CDM), and/or local new physics, and/or systematics in either or both the local measurements or the non-local datasets which have been combined with the UCS dataset. However, at least for what concerns the latter, the mutual consistency between the all the UCS+non-local results (see Table 1 in Ref. [650] for a complete assessment) suggests that systematics in the latter are unlikely to be an important driver of this residual tension. Leaving aside systematics in general leaves us contemplating either or both late-time (non-local) and local new physics as the most natural avenue for resolving this residual tension. While local new physics would have to go in the direction of lowering the local determinations, late-time (non-local) new physics would once more have to work in the same direction as that inferred from the OAO, CC, and descending trends hints, i.e., in the direction of lowering the expansion rate relative to CDM at , similar to the effect of a phantom component. Intriguingly, the size of the “residual tension” uncovered by all these probes is consistently in the ballpark which is not high enough to be alarming, but worthy of attention. Overall, the UCS-based analysis strengthens the case for the pre-recombination versus post-recombination narrative not being the end of the story, and strongly makes the case for focusing more on a tension between non-local (pre-recombination and post-recombination) and local measurements, in light of the consistency between UCS+non-local measurements and a full CDM-based CMB analysis.
Finally, one may wonder whether this UCS analysis is truly free of any early-Universe assumption, a question which Lin, Chen and Mack [650] addressed in detail. From the data side, it was argued that the choice of adopting CDM-based priors for and , as well as the use of the CDM-based determination of , have virtually no effect on the results, as does the choice of computing the sound speed as in CDM once a prior on the physical baryon density is given. From the physics side, Lin, Chen and Mack [650] argued that there are basically three ways the connection, or more precisely the value of , could come to depend on early-Universe new physics: (a) some unknown mechanism changing the integrand of relative to (or viceversa) at —else, the fact that the two share the same integrand at this epoch is the reason why the integral in Equation (7) only runs between and ; (b) new physics which very significantly affects the normalized expansion rate and/or sound speed in the narrow window ; (c) a very substantial change in . While none of these three ingredients can be definitively excluded, all of them are very hard to achieve, particularly in the context of well-motivated fundamental models. It is more likely that the post-recombination and/or local Universe may need some tweaking to fix the residual early-Universe-independent UCS tension.
2.7. Galaxy Power Spectrum Sound Horizon- and Equality Wavenumber-Based Determinations of the Hubble Constant
As discussed in detail earlier, most attempts at resolving the Hubble tension do so by reducing the sound horizon at recombination . The reason is that it is this (acoustic) scale which serves as a standard ruler to calibrate the BAO feature observed both in the CMB and in the clustering of the LSS.19 Indeed, comparing the angular size of the BAO feature extracted from galaxy clustering data to the expected theoretical value of (or more precisely , see Section 2.2 and Section 2.6) has been instrumental in “stabilizing” CMB-only constraints on and shedding further light on where new physics should act to reduce the Hubble tension. However, is not the only scale imprinted in galaxy surveys, which also contain information on the “equality scale” , defined as the wavenumber of a perturbation entering the horizon at the epoch of matter-radiation equality at redshift . The galaxy power spectrum features a turnaround at , with modes on smaller scales () exhibiting a suppression compared to their large-scale () counterparts. The reason is that the modes of the DM overdensity field entered the horizon in the radiation domination era, where the large radiation pressure prevented them from growing as much as if they had entered during the matter domination era. This results in a small-scale suppression whose scaling is well approximated as (but is highly degenerate with and , and therefore relies on a precise determination thereof from CMB data, see Ref. [652]), whereas modes on larger scales are unsuppressed and directly trace the primordial spectrum of scalar perturbations presumably set up during inflation.
The value of the equality scale depends on the balance between energy components with pressure support (typically referred to as “radiation”) and pressureless matter. This makes the conclusions related to the present hint somewhat dependent on early-time new physics (see also Ref. [652]), and this hint should therefore be used more as a consistency test of CDM rather than a means of excluding specific models of early-time new physics, as I will also discuss in more detail later. With these important caveats in mind, in standard scenarios where no extra components with pressure support are present, the equality scale is given by:
and can therefore be used as a standard ruler, provided its value can be inferred from galaxy clustering observations. From Equation (9) one sees that, since , a measurement of in is sensitive to the combination . Supplying an external measurement/prior for can therefore break the degeneracy and lead to an equality-based inference of . Besides its intrinsic value as an independent inference, why should this be of particular interest in the context of the Hubble tension? The reason is due to the fact that matter-radiation equality () occurs much earlier than recombination (): as a result, most models of early-Universe new physics invoked to solve the Hubble tension predict significant differences at one epoch versus the other (see e.g., Figure 2 of Ref. [194] for an example in the context of EDE). This observation provides an avenue for a valuable consistency test of CDM: since the - and -based determinations of from galaxy surveys originate from vastly different epochs and underlying physical phenomena, an inconsistency between the two would provide evidence for early-time new physics at redshifts beyond that of recombination, whereas consistency between the two could potentially cause difficulties for models which substantially modify that expansion history immediately prior to recombination (but not necessarily around matter-radiation equality).
After a first exploration in CMB lensing data (where the equality scale enters in a projected way) by Baxter and Sherwin [653], the above idea was pursued in detail in two works by Philcox et al. [654,655] in the context of galaxy power spectrum measurements. In particular, Philcox et al. [654,655] developed methods to “marginalize over the sound horizon” or, more precisely, ensure that the constraints on resulting from galaxy power spectrum measurements contain as little information about as possible, but result only from information. In the first work, Philcox et al. [655] proceeded by removing any informative prior on (e.g., from BBN): as the latter is required to calibrate , this operation effectively removes any information on at least given the precision of current data, where the -induced small-scale Jeans suppression cannot be detected at high enough significance to effectively calibrated the sound horizon. Using mock data, Fisher analyses, and scale cuts, the method was demonstrated to efficiently remove sound horizon information in galaxy clustering data, and to capture information from from the full shape of the galaxy power spectrum around the peak (even though the peak itself is difficult to resolve in galaxy surveys). Later Farren et al. [656] refined this method to more robustly marginalize over and avoid unnecessarily degrading the constraints, by directly marginalizing over templates capturing the power spectrum features related to (i.e., the BAO features and Jeans suppression). This allows one to add direct information (e.g., a BBN prior) while still ensuring that the resulting constraints retain only information from the equality scale.
An application of this method to the latest available cosmological data was presented by Philcox et al. [654], who considered CMB lensing power spectrum measurements from Planck, measurements of the power spectrum monopole, quadrupole, and hexadecapole from the BOSS DR12 galaxy sample, SNeIa measurements from the Pantheon+ sample (in the form of a Gaussian prior on ), and a BBN prior on . The constraints from various combinations of these datasets are shown in Figure 10. Including the Pantheon+ prior on , Philcox et al. [654] find , which shifts (slightly) to when removing this prior. Both inferences are in significant tension with the SH0ES results at the ≳3 level. Importantly, this residual tension cannot be solved by altering alone, since such a modification would alter the -based but not -based value of . These results were argued to provide an important null test for the model at early times (as the -free constraints are in excellent agreement with those based on discussed elsewhere), and to disfavor new physics models which affect the sound horizon and equality scale in a very different way. Taken at face value, this suggests the need for new ingredients beyond the “standard” -reducing ones.
Figure 10.
Sound horizon-independent constraints on and other parameters from various recent cosmological probes. Reproduced from Figure 1 of Philcox et al., “Determining the Hubble constant without the sound horizon: A 3.6% constraint on from galaxy surveys, CMB lensing, and supernovae”, Physical Review D, Volume 106, Issue 6, article number 063530, doi:10.1103/PhysRevD.106.063530, published 26 September 2022 [654]. © (2022) American Physical Society. Reproduced by permission of the American Physical Society and the authors. All rights reserved.
There are, however, a few important caveats, as already alluded to earlier. Firstly, this analysis is mainly a null test of CDM, and cannot directly be used to exclude specific models. Moreover, the limited sensitivity of current LSS clustering data prevents one from making strong statements in this direction, and implies that priors could play an important role. These points were explored in much more detail by Smith, Poulin and Simon [652] where, focusing on three specific beyond-CDM models, it was shown that:
- the constraints on obtained from -marginalized analyses are model-dependent, although not to a large extent;
- the results depend to some extent on the assumed priors on , , and ;
- models which introduce additional energy density with significant pressure support (such as EDE or models increasing the effective number of relativistic species ) can lead to higher values even in -free analyses (for such models the -based value of is actually slightly lower than the -based value, although the error bars are huge).
Overall, the conclusion reached by Smith, Poulin and Simon [652] is that current -free analyses are not strong enough to draw strong conclusions in favor of or against beyond-CDM models, and therefore that the consistency test proposed by Philcox et al. [654] is inconclusive given the precision of current data, with no strong indication that beyond-CDM models are in tension with data. However, the forecasts of Philcox et al. [654,655] indicate that the precision of -free determinations of will improve significantly with future galaxy clustering data [657,658,659,660,661], and at that point it will be possible to put significant pressure on early-Universe new physics models which alter alone. In fact, it is conceivable that the difference between the - and -based values of , currently consistent within uncertainties, will remain approximately constant, while the error bars will shrink considerably: in this case, the resulting tension between the two determinations may be able to put specific early-time modifications under significant pressure. At the current stage of things, however, drawing strong conclusions does not seem possible, although the consistency (within large error bars) between - and -based values of certainly disfavors there being an enormous amount of new physics between equality and recombination.
3. Reflections on Promising Scenarios Moving Forward
Hopefully by now I have managed to convince the reader that pre-recombination physics alone (and I stress that “alone” is the keyword here) is not sufficient to solve the Hubble tension: in fact, whatever one does will leave a “residual” - tension which will require new physics at either or both late times and local scales. This has been made especially clear by the first (OAO), third (CC), fourth (descending trends), and sixth (UCS) hints discussed earlier. It is somewhat fair to say that one could have reached such a conclusion empirically: in fact, in the absence of (high) external local priors on , most early-time modifications struggle to reach , and many actually fall short of the 70 threshold. Clearly this is far from satisfactory if one is to claim a solution to the Hubble tension. One can of course discuss whether or not it is acceptable or even desirable to include an external prior when assessing the viability of a model in addressing the tension (in which case the previous figures all increase), but I do not believe this is the appropriate place, and I refer the reader to e.g., Section VA of Ref. [641] for a very recent and detailed discussion on the matter. How to make progress from here then? The “simplest” scenario which comes to my mind involves a combination of two or three ingredients: early-time new physics, late-time but non-local (i.e., cosmological) new physics, and finally possibly local new physics as well. I would expect each of these three ingredients to contribute in a different way. With the caveat that what follows is my opinion and needs to be corroborated by explicit analyses (which I encourage), I now discuss more in detail this scenario.
There is no question that early-time (pre-recombination) new physics would need to do the lion’s share of the job in this context, consistently with earlier “no-go theorems” excluding late-time new physics alone [557,558,559,560,561,562,563,564,565,566]. One could envisage considering a particularly successful (relatively speaking) early-time model, such as EDE and variants, varying electron mass (potentially in a curved Universe) resulting in an earlier recombination, self-interacting dark radiation, and so on (see e.g., Table 1 in Ref. [561]). Empirically, in the absence of external priors, this should bring up to ∼70–71 in the best-case scenario. In addition to this, a completely decoupled model of late-time (post-recombination, but non-local) new physics could help further push up. In what direction would this late-time new physics need to go? As discussed for several earlier hints, we would require a model which lowers the normalized expansion rate relative to CDM. Examples in this sense include phantom DE or phantom-like models: this includes so-called interacting DE models, where non-gravitational interactions between DM and DE result in energy exchange between the two. In the case of energy flow from DM to DE, this results in an effective non-zero positive EoS for DM, while making the DE EoS more negative (i.e., moving towards the phantom regime). These models are only mentioned for concreteness, and by no means constitute the only possibilities in this sense.
The question I can already hear the reader asking is whether such a model would even be viable—after all, isn’t it already established that late-time new physics alone cannot solve the Hubble tension [557,558,559,560,561,562,563,564,565,566]? True, but here I am far from requiring such an ambitious goal for late-time new physics! Rather, all that I require is for the latter to give a further “push” in the right direction to the cosmological value of , already partially raised by early-time new physics. In other words, I am not asking for late-time new physics to produce a (which is definitely not allowed once BAO and Hubble flow SNeIa data are taken into account), but a much more modest value, say ∼1.5–2 at most.
Something along the lines of what I proposed above should definitely be possible, and let me defend this statement with an empirical argument, in the context of phantom DE. It is often stated that late-time datasets are consistent with a cosmological constant, and do not tolerate large deviations in the DE EoS from . This is broadly speaking true (although it is worth noting that some of the hints for parameter evolution discussed earlier only emerge once one bins data, which is not done in standard analyses), but at the same time (a) there is certainly room within the error bars for reaching values of w as low as ∼−1.07 (or even ∼−1.10), and (b) the central value of the DE EoS w inferred by combining CMB data with several late-time probes which are efficient in breaking the geometrical degeneracy actually falls slightly in the phantom regime ( 1.03–1.05 or so)20—in this sense, there is already some room within current data for late-time new physics to help in the right direction. Adimensional multipliers quantifying the correlation between and w when confronted against the latest CMB, BAO, and Hubble flow SNeIa data have been estimated in earlier works (see e.g., Refs. [141,447]), and indicate that even a modest phantom model with , by all means tolerated by data, can help as much as . Still from an empirical point of view, the most successful interacting DE models, once confronted against CMB, BAO, and Hubble flow SNeIa data, have been found to give , which again could be sufficient to bring the Hubble tension to an acceptable level once combined with early-time new physics which has already done the lion’s share of the job in raising .
The above considerations hinge upon an important point: loosely speaking, it would be desirable for early-time and late-time new physics to contribute “in phase”/“constructively” towards . This should be possible if the two models “decouple” their tension-solving effects, in other words both raise through completely decoupled physical mechanisms which do not interfere between each other. One might naïvely guess that early- and late-time new physics should not interfere as they operate at completely different epochs. Such a reasoning however misses one subtle point: parameter shifts induced by one of the two models can limit the tension-solving ability of the other, and viceversa. I already discussed in the second and fifth hints how early-time modifications which only reduce the sound horizon will inevitably induced some parameter shifts. The only way to assess whether these shifts would interfere with the tension-solving ability of additional late-time modifications is to choose a specific combination of models and perform a concrete analysis, and I hope the considerations I have drawn above will encourage others to carry out such an analysis. However, if one were to find two (or more) early- and late-time new physics models which could combine constructively to raise , the Hubble tension may well be reduced to an acceptable level, more so than can be achieved with early-time new physics alone (a model which could potentially be interesting in this sense has been presented, albeit in a different context, by Oikonomou [681], based on an axion-Higgs portal and enabling multiple stages of non-standard accelerated expansion both prior to and after recombination, see also Refs. [682,683,684,685,686] for related works).
The above considerations, however, may not be the end of the story. In fact, the scenarios proposed so far would have the only effect of raising the cosmological value of , while leaving the local value(s) untouched. In principle there is no reason to entertain such an asymmetry from the model point of view. For instance, what if new physics on local scales were able to reduce the local value of ? In this case, the cosmological and local values would not need to meet at ∼74, but perhaps at a slightly lower value, making the task of early-plus-late-time new physics in bringing the Hubble tension to an acceptable level less demanding. It is worth noting that there is a rich literature on local effects which could lead to an overestimate of the distance ladder value of , including physical effects such as a local void (the “Hubble bubble” [174,249,460]), ultra-late transitions in the gravitational constant [253], screened fifth forces [137], and so on. None of these models on their own have proven able to completely address the Hubble tension. In light of the previous discussion, however, such an ambitious goal may no longer be required! Even a small push down by 0.5–1 (certainly well within the range of what can be achieved with local new physics!) could be more than sufficient for the combined early-plus-late-plus-local new physics scenario to bring the Hubble tension to an acceptable level. In passing let me mention that a breakdown of the Friedmann-Lemaître-Robertson-Walker framework, and more generally of the cosmological principle, may be a scenario particularly worthy of consideration.
The combined early-plus-late-plus-local new physics scenario I have discussed in words above is perhaps best summarized pictorially in Figure 11. I hope that this helps convey the idea that early-time new physics (the yellow person) still needs to carry the lion’s share of the task, but with a little help from late-time new physics (the orange person) and local new physics (the green person with the SH0ES), the task of solving the Hubble tension or at least bringing it to an acceptable level may be made less daunting. There are three obvious objections to this otherwise arguably nice picture:
Figure 11.
Pictorial representation of my proposed approach towards promising solutions to the Hubble tension, discussed in Section 3. The grey band at the bottom of the picture represents the CDM baseline. The yellow person illustrates the effect of early-time new physics, which is still required to do the lion’s share of the job. A smaller but non-negligible contribution from late-time new physics, represented by the orange person, pushes the cosmological value of further up. Finally, local new physics, corresponding to the green person holding the SH0ES, can help bringing the local value of slightly down, and make the job of new cosmological physics less demanding. Picture drawn by Cristina Ghirardini.
- What about Occam’s razor? True, such a scenario may be viewed as unnecessary complicated, and aesthetically unpleasing, to the eyes of some. My view on this point is that, in the field of cosmology, Occam’s razor (and with it the concept of Bayesian evidence) is sometimes overused/abused. Not always is the simplest model the “most correct” one just because it fits the data better or with less parameters. Think, for example, about the many parameters for which we need to impose physical priors in cosmological analyses, to avoid inferring unphysical values thereof (the sum of the neutrino masses is an excellent example), which would otherwise be preferred by the data. If the true model chosen by Nature is actually as complicated as shown in Figure 11... then so be it! With a bit of poetic liberty, allow me to paraphrase Neil de Grasse Tyson and state that “Nature [the universe] is under no obligation to appear beautiful or simple in our eyes [make sense to you]”.
- You haven’t mentioned any concrete combination of early-plus-late-plus-local new physics models which does what you advocate. True once more, and this is left as an exercise to the reader and to aspiring Hubble tension solvers (including myself—so I hope to report on this in future work).
- Can all these early-plus-late-plus-local new physics ingredients come from one single underlying microphysical model, thus reducing the overall complexity? Maybe, why not? But once more, I am leaving this as an exercise to the reader and to aspiring Hubble tension solvers (this time likely not including myself).
Granted, the above objections remain, but I hope the reader now finds them less worrisome.
Before concluding, let me address the remaining elephant in the room: the tension. It would be preferable if the scenario depicted in Figure 11 were to ameliorate the tension as well. It is now becoming increasingly clearer to the community that simultaneously addressing the and tensions requires multiple modifications to CDM at multiple epochs, not unlike the picture shown in Figure 11. In particular, it is likely that addressing the tension will require some physical mechanism to suppress small-scale power [687], rather than playing around with (although complete consensus has yet to be reached on this matter). It would of course be desirable if the physical mechanism responsible for ameliorating the tension does not do so at the expense of the tension, i.e., does not interfere with the tension-solving abilities of the other models. In this respect, there is a class of models I find extremely interesting, which I will call “dark scattering” models.
The dark scattering class of models involves elastic (pure momentum) scattering-type interactions between dark components (DM, DE, or some other additional dark component), or between dark components and baryons.21 The attractive feature of these interactions is that, at linear level in cosmological perturbations, they only affect the evolution of perturbations, but not that of the background. In other words, these interactions only exchange momentum, but not energy (in an appropriate reference frame, e.g., the frame where one of the two scattering fluids is at rest). Such a feature is attractive because it can ensure that whatever mechanism is responsible for suppressing small-scale power does not alter the background expansion, and therefore the quality of the fit to BAO and Hubble flow SNeIa data. While this is not a guarantee of such a model not interfering with the tension-solving abilities of whatever other ingredients are solving the Hubble tension, it can certainly be a fairly important step in the right direction. Therefore, even if the scenario depicted in Figure 11 were not to solve the tension, one could envisage adding further scattering-type ingredients to ameliorate the situation, ideally without significantly affecting the successes obtained with . For instance, Poulin et al. [713] recently proposed DM-DE scattering as a potential solution to the tension, precisely due to the features discussed above. It would be interesting to further combine this model with a decoupled successful early-time model, e.g., EDE, to assess the potential of this combination in solving both the Hubble and tensions without the two models “interfering distructively”.
Is it natural, however, to consider ingredients which only modify the evolution of perturbations but not the background? There is, in fact, a very natural example of such an ingredient within the CDM model: Thomson scattering between photons and baryons. At the level of first-order Boltzmann equations, Thomson scattering only affects the evolution of perturbations, and more precisely the photon and baryon velocity divergences and (without affecting the photon and baryon overdensities and ), whereas the background expansion remains unchanged while the two components scatter, with their energy densities evolving as and respectively. In the case of dark components, it has actually been argued that at linear order in perturbations a scenario with only momentum exchange can actually be constructed even at the microphysical level by a particular choice of interaction Lagrangian, which within the classification of coupled DE models first discussed by Pourtsidou, Skordis and Copeland [748] and later by Skordis, Pourtsidou and Copeland [749], was termed Type 3 model: this model involves couplings of the covariant derivative of the DE scalar field to the velocity field of the scattering species and was shown to lead to a coupling current vector whose time component, in the DE rest frame, is null, ensuring the absence of energy exchange (thus featuring pure momentum exchange) at least up to linear order. This is of course no guarantee that the resulting model is well-motivated from the microphysical point of view, but is certainly of interest from the perspective of model-builders.
4. Conclusions
I have argued the Hubble tension, which at the time of writing remains unsolved, will ultimately require more than just early-time new physics alone. My claim is not based on a proof in a strict sense, but rather on a number of independent hints, at first glance somewhat unrelated, but which paint a more coherent picture once viewed from a holistic perspective. In a nutshell, these seven hints can be summarized as follows:
- the CDM Universe appears a bit too young to accommodate the oldest astrophysical objects at high redshift, and this is a problem which cannot be fixed by new physics in the early Universe, but requires new physics at late times or in the local Universe;
- early-Universe new physics which only reduces the sound horizon cannot simultaneously agree with CMB, BAO, local , and WL data, and will necessarily introduce new tensions (or worsen existing ones) involving some of these observations;
- cosmic chronometers show a residual ≈2 tension with local measurements within CDM, a conclusion which is completely independent of early-Universe physics, and which therefore cannot be addressed by invoking the latter;
- if the tension is physical (in the sense of not being due to systematics) and calls for some amount of late-time new physics, evolving trends should be seen at intermediate redshifts between the CMB and local scales, and by now several independent hints thereof have appeared;
- the early ISW effect places very restrictive guard rails on what early-Universe physics may or may not do, and for models enhancing the pre-recombination expansion rate this often results in fixing the otherwise overpredicted eISW amplitude at the expense of worsening other tensions;
- early-Universe-independent uncalibrated cosmic standard constraints on and show a residual ≈2 tension with local measurements which cannot, by construction, be fixed by early-time new physics, but most involve late-time or local new physics;
- the good agreement between sound horizon- and equality wavenumber-based constraints on from galaxy power spectra measurements makes it relatively unlikely that a significant amount of new physics operating before recombination can be at play.
As I stressed earlier alone is the keyword here, as there is no question (given the important role of BAO and Hubble flow SNeIa data) that early-time new physics will have to play an important role in solving the Hubble tension. However, on its own, I have argued that early-time new physics will not be able to achieve the task. I believe that an ultimately promising scenario may be the one depicted in Figure 11: early-time new physics doing an important job in raising can further be helped (in a smaller proportion) by late-time new physics, and by local new physics which lowers the local value of , easing the task of ensuring the cosmological and local values of meet halfway. It would be intriguing if the late-time contribution were also to help with the tension without affecting the Hubble tension-solving ingredients of the early-time part. In this sense, I have argued that late-time dark scattering-type models with pure momentum exchange, which to linear order in perturbations do not alter the background evolution, are particularly promising and worth exploring much more in the context of cosmological tensions.
Despite significant efforts from the theoretical and observational sides, the solution to the Hubble tension has so far eluded us. However, I believe there is reason to be optimistic, especially in light of upcoming Stage-IV cosmological data which may contain key evidence for beyond-CDM physics. These may potentially confirm some or all of the hints I have presented here which, I hope, can play a small role in guiding the community towards a building a new concordance model of cosmology.
Funding
This research received no external funding.
Acknowledgments
I thank Cristina Ghirardini for producing Figure 11. This publication is based upon work from the COST Action CA21136 “Addressing observational tensions in cosmology with systematics and fundamental physics (CosmoVerse), supported by COST (European Cooperation in Science and Technology).
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ACT | Atacama Cosmology Telescope |
| BBN | Big Bang Nucleosynthesis |
| BAO | Baryon Acoustic Oscillations |
| CC | Cosmic Chronometers |
| C.L. | Confidence Level |
| CMB | Cosmic Microwave Background |
| DE | Dark Energy |
| DM | Dark Matter |
| EDE | Early Dark Energy |
| EdS | Einstein-de Sitter |
| eISW | early Integrated Sachs-Wolfe |
| EoS | Equation of State |
| FLRS | Friedmann-Lemaître-Robertson-Walker |
| ISW | Integrated Sachs-Wolfe |
| LSS | Large-Scale Structure |
| MCMC | Markov Chain Monte Carlo |
| OAO | Old Astrophysical Objects |
| QSOs | Quasars |
| SNeIa | Type Ia Supernovae |
| UCS | Uncalibrated Cosmic Standards |
| WL | Weak Lensing |
Notes
| 1 | Or with an added, uncalled for, adverb “exclusively” between “calls” and “for”. |
| 2 | It has been argued that the number of objects an average human can hold in short-term memory is , a finding sometimes referred to as Miller’s law. Together with the many special and symbolic properties of the number seven, this is the reason behind my choice of focusing on seven hints. |
| 3 | Prior to 1998, and particularly in the 1980s, the leading cosmological model envisaged an Einstein-de Sitter (EdS) Universe, with a vanishing cosmological constant and no spatial curvature. The existence of old galaxies at high redshift (in conjunction with increasingly precise measurements of ), seemingly older than the EdS Universe, gave rise to an important “age crisis” [572,573,574], whose resolution eventually came with the discovery of cosmic acceleration in 1998. In fact, compared to an EdS Universe with the same total energy density, a CDM Universe where part of the matter content is replaced by dark energy naturally leads to an older Universe at any redshift, thus accommodating the otherwise puzzling OAO. |
| 4 | Note that, although Equation (1) is formally integrated up to , since in practice OAO can only form after recombination, the upper limit of the integral can be set to , the redshift of recombination. This prevents it from being sensitive to huge pre-BBN modifications to which could make arbitrarily large, although such modifications are not of interest in the discussion on the Hubble tension. |
| 5 | Note that in Ref. [593] and in Figure 2 is denoted by . |
| 6 | Here by “model-independent” I really mean independent of any assumed underlying cosmological model, where the cosmological model-dependence of the “standard” CMB, BAO, SNeIa probes may be traded for dependence on other models, e.g., of more astrophysical/astronomical nature. |
| 7 | I follow the procedure outlined in gitlab.com/mmoresco/CCcovariance, accessed on 18 May 2023. |
| 8 | The OAO and CC datasets are mostly independent, except for 8 CC measurements with relatively large uncertainties [600], whose relative statistical weight in the conclusions is therefore low. Note that the reliability of these measurements has also been recently questioned by Kjerrgren and Mörtsell [601]. Given their low statistical weight in reaching my conclusions, a posteriori this should not present a concern. |
| 9 | This effective equation of state directly enters the second Friedmann equation (the acceleration equation) and includes contributions from all species, not only dark energy. |
| 10 | Of course the data need not be exactly in the form of , but other types of data (e.g., distance measurements) can be brought into this form, or conversely Equation (5) can be generalized to account for other types of data. |
| 11 | In principle, if some early-time new physics raised the CMB value of to be perfectly in agreement with the local value, and the late-time Universe were completely described by CDM, there should be no evolving trend at intermediate redshifts. |
| 12 | At this point there is no reason not to refer to this trend as a tension where, if one wants, the tension is with the mathematical requirement that be a (integration) constant. |
| 13 | In this case, rather than binning the data in redshift, the choice was to only use data above a certain redshift and examine the effect of the lower redshift cutoff. |
| 14 | The reliability of Hubble diagrams constructed out of QSOs data has been questioned (see e.g., Refs. [619,620]), but methods to overcome selection biases and astrophysical evolution in the QSOs parameters have also been tested [621,622,623,624,625]. Similar considerations hold for Gamma Ray Bursts as a cosmological probe [334,626,627,628,629]. |
| 15 | Tongue-in-cheek, one could say that this is the Hubble tension equivalent of the much more famous Fermi paradox. |
| 16 | In particular in Ref. [634] I argued that models raising the pre-recombination expansion rate, of which EDE can be considered a prototype (but certainly not the only example), naturally boost the eISW effect due to the enhanced potential decay. |
| 17 | In the case of SNeIa one simply needs to treat the SNeIa absolute magnitude as a free parameter to be marginalized over: however, this is what is routinely done anyway when analyzing uncalibrated SNeIa data (whereas it is much less common to analyze BAO data treating as a free parameter, rather an early-Universe model is usually assumed). |
| 18 | Note that in Ref. [650] and in Figure 9 is denoted by . |
| 19 | In what follows, I will focus on galaxies as tracers of the LSS, and will therefore refer to “galaxy clustering”, although the subsequent discussion can apply to any LSS tracer. |
| 20 | See e.g., Refs. [4,7,240,575,583,588,621,662,663,664,665,666,667,668,669,670,671,672,673,674,675,676,677,678,679] for examples of recent analyses in these directions whose inferred central values of w (in some cases depending on the specific dataset combination or underlying model considered) lie slightly within the phantom regime, arising from a wide range of dataset combinations, mostly involving combinations of Planck CMB data with other external late-time measurements, and see Ref. [680] for a recent reassessment of this point. |
| 21 | Dark scattering-type scenarios studied in the literature include DM-DE scattering [293,688,689,690,691,692,693,694,695,696,697,698,699,700,701,702,703,704,705,706,707,708,709,710,711,712,713,714,715,716], DM-photon scattering [83,717,718,719], DM-neutrino scattering [71,720,721,722,723,724], DM-baryon scattering [725,726,727,728,729,730,731,732,733,734,735], DM self-scattering and scattering with dark radiation [66,136,736,737,738,739,740,741], “multi-interacting DM” scenarios featuring multiple similar interactions simultaneously [742], and DE-baryon scattering [743,744,745,746,747]. |
References
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Troxel, M.A.; MacCrann, N.; Zuntz, J.; Eifler, T.F.; Krause, E.; Dodelson, S.; Gruen, D.; Blazek, J.; Friedrich, O.; Samuroff, S.; et al. Dark Energy Survey Year 1 results: Cosmological constraints from cosmic shear. Phys. Rev. D 2018, 98, 43528. [Google Scholar] [CrossRef]
- Aghanim, N. et al. [Planck Collaboration] Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar]
- Bianchini, F.; Wu, W.L.K.; Ade, P.A.R.; Anderson, A.J.; Austermann, J.E.; Avva, J.S.; Beall, J.A.; Bender, A.N.; Benson, B.A.; Bleem, L.E.; et al. Constraints on Cosmological Parameters from the 500 deg2 SPTpol Lensing Power Spectrum. Astrophys. J. 2020, 888, 119. [Google Scholar] [CrossRef]
- Aiola, S.; Calabrese, E.; Maurin, L.; Naess, S.; Schmitt, B.L.; Abitbol, M.H.; Addison, G.E.; Ade, P.A.R.; Alonso, D.; Amiri, M.; et al. The Atacama Cosmology Telescope: DR4 Maps and Cosmological Parameters. JCAP 2020, 12, 47. [Google Scholar] [CrossRef]
- Alam, S.; Aubert, M.; Avila, S.; Balland, C.; Bautista, J.E.; Bershady, M.A.; Bizyaev, D.; Blanton, M.R.; Bolton, A.S.; Bovy, J.; et al. Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Cosmological implications from two decades of spectroscopic surveys at the Apache Point Observatory. Phys. Rev. D 2021, 103, 83533. [Google Scholar] [CrossRef]
- Asgari, M.; Lin, C.-A.; Joachimi, B.; Giblin, B.; Heymans, C.; Hildebrandt, H.; Kannawadi, A.; Stolzner, B.; Troster, T.; van den Busch, J.L.; et al. KiDS-1000 Cosmology: Cosmic shear constraints and comparison between two point statistics. Astron. Astrophys. 2021, 645, A104. [Google Scholar] [CrossRef]
- Mossa, V.; Stockel, K.; Cavanna, F.; Ferraro, F.; Aliotta, M.; Barile, F.; Bemmerer, D.; Best, A.; Boeltzig, A.; Broggini, C.; et al. The baryon density of the Universe from an improved rate of deuterium burning. Nature 2020, 587, 210–213. [Google Scholar] [CrossRef]
- Brout, D.; Scolnic, D.; Popovic, B.; Riess, A.G.; Zuntz, J.; Kessler, R.; Carr, A.; Davis, T.M.; Hinton, S.; Jones, D.; et al. The Pantheon+ Analysis: Cosmological Constraints. Astrophys. J. 2022, 938, 110. [Google Scholar] [CrossRef]
- Riess, A.G.; Yuan, W.L.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Anand, G.S.; Breuval, L.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km s−1 Mpc−1 Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Fernández Arenas, D.; Terlevich, E.; Terlevich, R.; Melnick, J.; Chávez, R.; Bresolin, F.; Telles, E.; Plionis, M.; Basilakos, S. An independent determination of the local Hubble constant. Mon. Not. R. Astron. Soc. 2018, 474, 1250–1276. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. Astrophys. J. 2019, 876, 85. [Google Scholar]
- Wong, K.C.; Suyu, S.H.; Chen, G.C.F.; Rusu, C.E.; Millon, M.; Sluse, D.; Bonvin, V.; Fassnacht, C.D.; Taubenberger, S.; Auger, M.W.; et al. H0LiCOW–XIII. A 2.4 per cent measurement of H0 from lensed quasars: 5.3σ tension between early- and late-Universe probes. Mon. Not. R. Astron. Soc. 2020, 498, 1420–1439. [Google Scholar]
- Freedman, W.L.; Madore, B.F.; Hatt, D.; Hoyt, T.J.; Jang, I.-S.; Beaton, R.L.; Burns, C.R.; Lee, M.G.; Monson, A.J.; Neeley, J.R.; et al. The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch. Astrophys. J. 2019, 882, 34. [Google Scholar] [CrossRef]
- Yuan, W.; Riess, A.G.; Macri, L.M.; Casertano, S.; Scolnic, D. Consistent Calibration of the Tip of the Red Giant Branch in the Large Magellanic Cloud on the Hubble Space Telescope Photometric System and a Re-determination of the Hubble Constant. Astrophys. J. 2019, 886, 61. [Google Scholar] [CrossRef]
- Huang, C.D.; Riess, A.G.; Yuan, W.; Macri, L.M.; Zakamska, N.L.; Casertano, S.; Whitelock, P.A.; Hoffmann, S.L.; Filippenko, A.V.; Scolnic, D. Hubble Space Telescope Observations of Mira Variables in the Type Ia Supernova Host NGC 1559: An Alternative Candle to Measure the Hubble Constant. Astrophys. J. 2020, 889, 5. [Google Scholar]
- Pesce, D.W.; Braatz, J.A.; Reid, M.J.; Riess, A.G.; Scolnic, D.; Condon, J.J.; Gao, F.; Henkel, C.; Impellizzeri, C.M.V.; Kuo, C.Y.; et al. The Megamaser Cosmology Project. XIII. Combined Hubble constant constraints. Astrophys. J. Lett. 2020, 891, L1. [Google Scholar] [CrossRef]
- de Jaeger, T.; Stahl, B.E.; Zheng, W.; Filippenko, A.V.; Riess, A.G.; Galbany, L. A measurement of the Hubble constant from Type II supernovae. Mon. Not. R. Astron. Soc. 2020, 496, 3402–3411. [Google Scholar]
- Schombert, J.; McGaugh, S.; Lelli, F. Using the Baryonic Tully–Fisher Relation to Measure H o. Astron. J. 2020, 160, 71. [Google Scholar] [CrossRef]
- Blakeslee, J.P.; Jensen, J.B.; Ma, C.P.; Milne, P.A.; Greene, J.E. The Hubble Constant from Infrared Surface Brightness Fluctuation Distances. Astrophys. J. 2021, 911, 65. [Google Scholar]
- Verde, L.; Treu, T.; Riess, A.G. Tensions between the Early and the Late Universe. Nat. Astron. 2019, 3, 891. [Google Scholar] [CrossRef]
- Riess, A.G. The Expansion of the Universe is Faster than Expected. Nat. Rev. Phys. 2019, 2, 10–12. [Google Scholar] [CrossRef]
- Di Valentino, E.; Anchordoqui, L.A.; Akarsu, O.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Asgari, M.; Ballardini, M.; Basilakos, S.; Battistelli, E.; et al. Snowmass2021—Letter of interest cosmology intertwined II: The hubble constant tension. Astropart. Phys. 2021, 131, 102605. [Google Scholar]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—A review of solutions. Class. Quant. Grav. 2021, 38, 153001. [Google Scholar]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. New Astron. Rev. 2022, 95, 101659. [Google Scholar]
- Schöneberg, N.; Franco Abellán, G.; Pérez Sánchez, A.; Witte, S.J.; Poulin, V.; Lesgourgues, J. The H0 Olympics: A fair ranking of proposed models. Phys. Rept. 2022, 984, 1–55. [Google Scholar]
- Shah, P.; Lemos, P.; Lahav, O. A buyer’s guide to the Hubble constant. Astron. Astrophys. Rev. 2021, 29, 9. [Google Scholar]
- Abdalla, E.; Abellan, G.F.; Aboubrahim, A.; Agnello, A.; Akarsu, O.; Akrami, Y.; Alestas, G.; Aloni, D.; Amendola, L.; Anchordoqui, L.A.; et al. Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies. JHEAp 2022, 34, 49–211. [Google Scholar]
- Di Valentino, E. Challenges of the Standard Cosmological Model. Universe 2022, 8, 399. [Google Scholar] [CrossRef]
- Hu, J.P.; Wang, F.Y. Hubble Tension: The Evidence of New Physics. Universe 2023, 9, 94. [Google Scholar]
- Efstathiou, G. A Lockdown Perspective on the Hubble Tension (with comments from the SH0ES team). arXiv 2020, arXiv:2007.10716. [Google Scholar]
- Mortsell, E.; Goobar, A.; Johansson, J.; Dhawan, S. Sensitivity of the Hubble Constant Determination to Cepheid Calibration. Astrophys. J. 2022, 933, 212. [Google Scholar]
- Mortsell, E.; Goobar, A.; Johansson, J.; Dhawan, S. The Hubble Tension Revisited: Additional Local Distance Ladder Uncertainties. Astrophys. J. 2022, 935, 58. [Google Scholar] [CrossRef]
- Freedman, W.L. Measurements of the Hubble Constant: Tensions in Perspective. Astrophys. J. 2021, 919, 16. [Google Scholar]
- Wojtak, R.; Hjorth, J. Intrinsic tension in the supernova sector of the local Hubble constant measurement and its implications. Mon. Not. R. Astron. Soc. 2022, 515, 2790–2799. [Google Scholar] [CrossRef]
- Berezhiani, Z.; Dolgov, A.D.; Tkachev, I.I. Reconciling Planck results with low redshift astronomical measurements. Phys. Rev. D 2015, 92, 61303. [Google Scholar] [CrossRef]
- Sola, J.; Gomez-Valent, A.; de Cruz Pérez, J. Hints of dynamical vacuum energy in the expanding Universe. Astrophys. J. Lett. 2015, 811, L14. [Google Scholar] [CrossRef]
- Solà, J.; Gómez-Valent, A.; de Cruz Pérez, J. First evidence of running cosmic vacuum: Challenging the concordance model. Astrophys. J. 2017, 836, 43. [Google Scholar] [CrossRef]
- Solà Peracaula, J.; de Cruz Pérez, J.; Gómez-Valent, A. Dynamical dark energy vs. Λ = const in light of observations. EPL 2018, 121, 39001. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Silk, J. Reconciling Planck with the local value of H0 in extended parameter space. Phys. Lett. B 2016, 761, 242–246. [Google Scholar] [CrossRef]
- Huang, Q.G.; Wang, K. How the dark energy can reconcile Planck with local determination of the Hubble constant. Eur. Phys. J. C 2016, 76, 506. [Google Scholar] [CrossRef]
- Tram, T.; Vallance, R.; Vennin, V. Inflation Model Selection meets Dark Radiation. JCAP 2017, 1, 46. [Google Scholar] [CrossRef][Green Version]
- Ko, P.; Tang, Y. Light dark photon and fermionic dark radiation for the Hubble constant and the structure formation. Phys. Lett. B 2016, 762, 462–466. [Google Scholar] [CrossRef]
- Karwal, T.; Kamionkowski, M. Dark energy at early times, the Hubble parameter, and the string axiverse. Phys. Rev. D 2016, 94, 103523. [Google Scholar] [CrossRef]
- Kumar, S.; Nunes, R.C. Probing the interaction between dark matter and dark energy in the presence of massive neutrinos. Phys. Rev. D 2016, 94, 123511. [Google Scholar] [CrossRef]
- Xia, D.M.; Wang, S. Constraining interacting dark energy models with latest cosmological observations. Mon. Not. R. Astron. Soc. 2016, 463, 952–956. [Google Scholar] [CrossRef]
- Ko, P.; Tang, Y. Residual Non-Abelian Dark Matter and Dark Radiation. Phys. Lett. B 2017, 768, 12–17. [Google Scholar] [CrossRef]
- Chacko, Z.; Cui, Y.; Hong, S.; Okui, T.; Tsai, Y. Partially Acoustic Dark Matter, Interacting Dark Radiation, and Large Scale Structure. JHEP 2016, 12, 108. [Google Scholar] [CrossRef]
- Prilepina, V.; Tsai, Y. Reconciling Large And Small-Scale Structure In Twin Higgs Models. JHEP 2017, 9, 33. [Google Scholar] [CrossRef]
- Zhao, G.B.; Raveri, M.; Pogosian, L.; Wang, Y.T.; Crittenden, R.G.; Handley, W.J.; Percival, W.J.; Beutler, F.; Brinkmann, J.; Chuang, C.-H.; et al. Dynamical dark energy in light of the latest observations. Nat. Astron. 2017, 1, 627–632. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Giusarma, E.; Mena, O.; Freese, K.; Gerbino, M.; Ho, S.; Lattanzi, M. Unveiling ν secrets with cosmological data: Neutrino masses and mass hierarchy. Phys. Rev. D 2017, 96, 123503. [Google Scholar] [CrossRef]
- Kumar, S.; Nunes, R.C. Echo of interactions in the dark sector. Phys. Rev. D 2017, 96, 103511. [Google Scholar] [CrossRef]
- Benetti, M.; Graef, L.L.; Alcaniz, J.S. Do joint CMB and HST data support a scale invariant spectrum? JCAP 2017, 4, 3. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, J.F.; Zhang, X. A search for sterile neutrinos with the latest cosmological observations. Eur. Phys. J. C 2017, 77, 418. [Google Scholar] [CrossRef]
- Solà Peracaula, J.; de Cruz Pérez, J.; Gomez-Valent, A. Possible signals of vacuum dynamics in the Universe. Mon. Not. R. Astron. Soc. 2018, 478, 4357–4373. [Google Scholar] [CrossRef]
- Zhao, M.M.; He, D.Z.; Zhang, J.F.; Zhang, X. Search for sterile neutrinos in holographic dark energy cosmology: Reconciling Planck observation with the local measurement of the Hubble constant. Phys. Rev. D 2017, 96, 43520. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Linder, E.V.; Silk, J. Constraining Dark Energy Dynamics in Extended Parameter Space. Phys. Rev. D 2017, 96, 23523. [Google Scholar] [CrossRef]
- Dirian, Y. Changing the Bayesian prior: Absolute neutrino mass constraints in nonlocal gravity. Phys. Rev. D 2017, 96, 83513. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Mena, O. Can interacting dark energy solve the H0 tension? Phys. Rev. D 2017, 96, 43503. [Google Scholar] [CrossRef]
- Solà, J.; Gómez-Valent, A.; de Cruz Pérez, J. The H0 tension in light of vacuum dynamics in the Universe. Phys. Lett. B 2017, 774, 317–324. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Barrow, J.D. Large-scale Stability and Astronomical Constraints for Coupled Dark-Energy Models. Phys. Rev. D 2018, 97, 43529. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, J.F.; Zhang, X. Searching for sterile neutrinos in dynamical dark energy cosmologies. Sci. China Phys. Mech. Astron. 2018, 61, 50411. [Google Scholar] [CrossRef]
- Renk, J.; Zumalacárregui, M.; Montanari, F.; Barreira, A. Galileon gravity in light of ISW, CMB, BAO and H0 data. JCAP 2017, 10, 20. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Paliathanasis, A. Latest astronomical constraints on some non-linear parametric dark energy models. Mon. Not. R. Astron. Soc. 2018, 475, 2605–2613. [Google Scholar] [CrossRef]
- Buen-Abad, M.A.; Schmaltz, M.; Lesgourgues, J.; Brinckmann, T. Interacting Dark Sector and Precision Cosmology. JCAP 2018, 1, 8. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Mota, D.F. Novel approach toward the large-scale stable interacting dark-energy models and their astronomical bounds. Phys. Rev. D 2017, 96, 123508. [Google Scholar] [CrossRef]
- Raveri, M.; Hu, W.; Hoffman, T.; Wang, L.T. Partially Acoustic Dark Matter Cosmology and Cosmological Constraints. Phys. Rev. D 2017, 96, 103501. [Google Scholar] [CrossRef]
- Solà, J.; Gómez-Valent, A.; de Cruz Pérez, J. Vacuum dynamics in the Universe versus a rigid Λ=const. Int. J. Mod. Phys. A 2017, 32, 1730014. [Google Scholar] [CrossRef]
- Di Valentino, E.; Linder, E.V.; Melchiorri, A. Vacuum phase transition solves the H0 tension. Phys. Rev. D 2018, 97, 43528. [Google Scholar] [CrossRef]
- Di Valentino, E.; Bøehm, C.; Hivon, E.; Bouchet, F.R. Reducing the H0 and σ8 tensions with Dark Matter-neutrino interactions. Phys. Rev. D 2018, 97, 43513. [Google Scholar] [CrossRef]
- Khosravi, N.; Baghram, S.; Afshordi, N.; Altamirano, N. H0 tension as a hint for a transition in gravitational theory. Phys. Rev. D 2019, 99, 103526. [Google Scholar] [CrossRef]
- Santos, M.A.; Benetti, M.; Alcaniz, J.; Brito, F.A.; Silva, R. CMB constraints on β-exponential inflationary models. JCAP 2018, 3, 23. [Google Scholar] [CrossRef]
- Nunes, R.C.; Bonilla, A. Probing the properties of relic neutrinos using the cosmic microwave background, the Hubble Space Telescope and galaxy clusters. Mon. Not. R. Astron. Soc. 2018, 473, 4404–4409. [Google Scholar] [CrossRef]
- Benetti, M.; Graef, L.L.; Alcaniz, J.S. The H0 and σ8 tensions and the scale invariant spectrum. JCAP 2018, 7, 66. [Google Scholar] [CrossRef]
- Binder, T.; Gustafsson, M.; Kamada, A.; Sandner, S.M.R.; Wiesner, M. Reannihilation of self-interacting dark matter. Phys. Rev. D 2018, 97, 123004. [Google Scholar] [CrossRef]
- Bolejko, K. Emerging spatial curvature can resolve the tension between high-redshift CMB and low-redshift distance ladder measurements of the Hubble constant. Phys. Rev. D 2018, 97, 103529. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, J.F.; Zhang, X. Search for sterile neutrinos in a universe of vacuum energy interacting with cold dark matter. Phys. Dark Univ. 2019, 23, 100261. [Google Scholar] [CrossRef]
- Mörtsell, E.; Dhawan, S. Does the Hubble constant tension call for new physics? JCAP 2018, 9, 25. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Dhawan, S.; Gerbino, M.; Freese, K.; Goobar, A.; Mena, O. Constraints on the sum of the neutrino masses in dynamical dark energy models with w(z) ≥ −1 are tighter than those obtained in ΛCDM. Phys. Rev. D 2018, 98, 83501. [Google Scholar] [CrossRef]
- Nunes, R.C. Structure formation in f(T) gravity and a solution for H0 tension. JCAP 2018, 5, 52. [Google Scholar] [CrossRef]
- Poulin, V.; Boddy, K.K.; Bird, S.; Kamionkowski, M. Implications of an extended dark energy cosmology with massive neutrinos for cosmological tensions. Phys. Rev. D 2018, 97, 123504. [Google Scholar] [CrossRef]
- Kumar, S.; Nunes, R.C.; Yadav, S.K. Cosmological bounds on dark matter-photon coupling. Phys. Rev. D 2018, 98, 43521. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Xu, L.; Mota, D.F. Effects of anisotropic stress in interacting dark matter–Dark energy scenarios. Mon. Not. R. Astron. Soc. 2019, 482, 1858–1871. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Alam, U.; Pandey, K.L.; Das, S.; Pal, S. Are H0 and σ8 tensions generic to present cosmological data? Astrophys. J. 2019, 876, 143. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Di Valentino, E.; Nunes, R.C.; Vagnozzi, S.; Mota, D.F. Tale of stable interacting dark energy, observational signatures, and the H0 tension. JCAP 2018, 9, 19. [Google Scholar] [CrossRef]
- Poulin, V.; Smith, T.L.; Grin, D.; Karwal, T.; Kamionkowski, M. Cosmological implications of ultralight axionlike fields. Phys. Rev. D 2018, 98, 83525. [Google Scholar] [CrossRef]
- Akarsu, O.; Katirci, N.; Kumar, S.; Nunes, R.C.; Sami, M. Cosmological implications of scale-independent energy-momentum squared gravity: Pseudo nonminimal interactions in dark matter and relativistic relics. Phys. Rev. D 2018, 98, 63522. [Google Scholar] [CrossRef]
- Ócolgáin, E.; van Putten, M.H.P.M.; Yavartanoo, H. de Sitter Swampland, H0 tension & observation. Phys. Lett. B 2019, 793, 126–129. [Google Scholar]
- Yang, W.; Pan, S.; Herrera, R.; Chakraborty, S. Large-scale (in) stability analysis of an exactly solved coupled dark-energy model. Phys. Rev. D 2018, 98, 43517. [Google Scholar] [CrossRef]
- Banihashemi, A.; Khosravi, N.; Shirazi, A.H. Phase transition in the dark sector as a proposal to lessen cosmological tensions. Phys. Rev. D 2020, 101, 123521. [Google Scholar] [CrossRef]
- Dutta, K.; Ruchika; Roy, A.; Sen, A.A.; Sheikh-Jabbari, M.M. Beyond ΛCDM with low and high redshift data: Implications for dark energy. Gen. Rel. Grav. 2020, 52, 15. [Google Scholar] [CrossRef]
- D’Eramo, F.; Ferreira, R.Z.; Notari, A.; Bernal, J.L. Hot Axions and the H0 tension. JCAP 2018, 11, 14. [Google Scholar] [CrossRef]
- Guo, R.Y.; Zhang, J.F.; Zhang, X. Can the H0 tension be resolved in extensions to ΛCDM cosmology? JCAP 2019, 2, 54. [Google Scholar] [CrossRef]
- Graef, L.L.; Benetti, M.; Alcaniz, J.S. Primordial gravitational waves and the H0-tension problem. Phys. Rev. D 2019, 99, 43519. [Google Scholar] [CrossRef]
- Visinelli, L.; Vagnozzi, S. Cosmological window onto the string axiverse and the supersymmetry breaking scale. Phys. Rev. D 2019, 99, 63517. [Google Scholar] [CrossRef]
- Yang, W.; Mukherjee, A.; Di Valentino, E.; Pan, S. Interacting dark energy with time varying equation of state and the H0 tension. Phys. Rev. D 2018, 98, 123527. [Google Scholar] [CrossRef]
- El-Zant, A.; El Hanafy, W.; Elgammal, S. H0 Tension and the Phantom Regime: A Case Study in Terms of an Infrared f(T) Gravity. Astrophys. J. 2019, 871, 210. [Google Scholar] [CrossRef]
- Lin, M.X.; Raveri, M.; Hu, W. Phenomenology of Modified Gravity at Recombination. Phys. Rev. D 2019, 99, 43514. [Google Scholar] [CrossRef]
- Bengaly, C.A.P.; Andrade, U.; Alcaniz, J.S. How does an incomplete sky coverage affect the Hubble Constant variance? Eur. Phys. J. C 2019, 79, 768. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Di Valentino, E.; Saridakis, E.N.; Chakraborty, S. Observational constraints on one-parameter dynamical dark-energy parametrizations and the H0 tension. Phys. Rev. D 2019, 99, 43543. [Google Scholar] [CrossRef]
- Bonilla, A.; Nunes, R.C.; Abreu, E.M.C. Forecast on lepton asymmetry from future CMB experiments. Mon. Not. R. Astron. Soc. 2019, 485, 2486–2491. [Google Scholar] [CrossRef]
- Yang, W.; Shahalam, M.; Pal, B.; Pan, S.; Wang, A. Constraints on quintessence scalar field models using cosmological observations. Phys. Rev. D 2019, 100, 23522. [Google Scholar] [CrossRef]
- Banihashemi, A.; Khosravi, N.; Shirazi, A.H. Ginzburg-Landau Theory of Dark Energy: A Framework to Study Both Temporal and Spatial Cosmological Tensions Simultaneously. Phys. Rev. D 2019, 99, 83509. [Google Scholar] [CrossRef]
- Sola Peracaula, J.; Gomez-Valent, A.; de Cruz Pérez, J. Signs of Dynamical Dark Energy in Current Observations. Phys. Dark Univ. 2019, 25, 100311. [Google Scholar] [CrossRef]
- Poulin, V.; Smith, T.L.; Karwal, T.; Kamionkowski, M. Early Dark Energy Can Resolve The Hubble Tension. Phys. Rev. Lett. 2019, 122, 221301. [Google Scholar] [CrossRef] [PubMed]
- Farrugia, C.R.; Sultana, J.; Mifsud, J. Endowing Λ with a dynamic nature: Constraints in a spatially curved universe. Phys. Rev. D 2020, 102, 24013. [Google Scholar] [CrossRef]
- Carneiro, S.; de Holanda, P.C.; Pigozzo, C.; Sobreira, F. Is the H0 tension suggesting a fourth neutrino generation? Phys. Rev. D 2019, 100, 23505. [Google Scholar] [CrossRef]
- Kumar, S.; Nunes, R.C.; Yadav, S.K. Testing the warmness of dark matter. Mon. Not. R. Astron. Soc. 2019, 490, 1406–1414. [Google Scholar] [CrossRef]
- Kenworthy, W.D.; Scolnic, D.; Riess, A. The Local Perspective on the Hubble Tension: Local Structure Does Not Impact Measurement of the Hubble Constant. Astrophys. J. 2019, 875, 145. [Google Scholar] [CrossRef]
- Kreisch, C.D.; Cyr-Racine, F.Y.; Doré, O. Neutrino puzzle: Anomalies, interactions, and cosmological tensions. Phys. Rev. D 2020, 101, 123505. [Google Scholar] [CrossRef]
- Pandey, K.L.; Karwal, T.; Das, S. Alleviating the H0 and σ8 anomalies with a decaying dark matter model. JCAP 2020, 7, 26. [Google Scholar] [CrossRef]
- Martinelli, M.; Hogg, N.B.; Peirone, S.; Bruni, M.; Wands, D. Constraints on the interacting vacuum–geodesic CDM scenario. Mon. Not. R. Astron. Soc. 2019, 488, 3423–3438. [Google Scholar] [CrossRef]
- Kumar, S.; Nunes, R.C.; Yadav, S.K. Dark sector interaction: A remedy of the tensions between CMB and LSS data. Eur. Phys. J. C 2019, 79, 576. [Google Scholar] [CrossRef]
- Vattis, K.; Koushiappas, S.M.; Loeb, A. Dark matter decaying in the late Universe can relieve the H0 tension. Phys. Rev. D 2019, 99, 121302. [Google Scholar] [CrossRef]
- Pan, S.; Yang, W.; Singha, C.; Saridakis, E.N. Observational constraints on sign-changeable interaction models and alleviation of the H0 tension. Phys. Rev. D 2019, 100, 83539. [Google Scholar] [CrossRef]
- Akarsu, O.; Barrow, J.D.; Board, C.V.R.; Uzun, N.M.; Vazquez, J.A. Screening Λ in a new modified gravity model. Eur. Phys. J. C 2019, 79, 846. [Google Scholar] [CrossRef]
- Li, X.; Shafieloo, A.; Sahni, V.; Starobinsky, A.A. Revisiting Metastable Dark Energy and Tensions in the Estimation of Cosmological Parameters. Astrophys. J. 2019, 887, 153. [Google Scholar] [CrossRef]
- Alexander, S.; McDonough, E. Axion-Dilaton Destabilization and the Hubble Tension. Phys. Lett. B 2019, 797, 134830. [Google Scholar] [CrossRef]
- Agrawal, P.; Cyr-Racine, F.Y.; Pinner, D.; Randall, L. Rock ’n’ Roll Solutions to the Hubble Tension. arXiv 2019, arXiv:1904.01016. [Google Scholar]
- Yang, W.; Pan, S.; Paliathanasis, A.; Ghosh, S.; Wu, Y. Observational constraints of a new unified dark fluid and the H0 tension. Mon. Not. R. Astron. Soc. 2019, 490, 2071–2085. [Google Scholar] [CrossRef]
- Hooper, D.; Krnjaic, G.; McDermott, S.D. Dark Radiation and Superheavy Dark Matter from Black Hole Domination. JHEP 2019, 8, 1. [Google Scholar] [CrossRef]
- Adhikari, S.; Huterer, D. Super-CMB fluctuations and the Hubble tension. Phys. Dark Univ. 2020, 28, 100539. [Google Scholar] [CrossRef]
- Colgáin, E.O.; Yavartanoo, H. Testing the Swampland: H0 tension. Phys. Lett. B 2019, 797, 134907. [Google Scholar] [CrossRef]
- Blinov, N.; Kelly, K.J.; Krnjaic, G.Z.; McDermott, S.D. Constraining the Self-Interacting Neutrino Interpretation of the Hubble Tension. Phys. Rev. Lett. 2019, 123, 191102. [Google Scholar] [CrossRef]
- Keeley, R.E.; Joudaki, S.; Kaplinghat, M.; Kirkby, D. Implications of a transition in the dark energy equation of state for the H0 and σ8 tensions. JCAP 2019, 12, 35. [Google Scholar] [CrossRef]
- Lin, M.X.; Benevento, G.; Hu, W.; Raveri, M. Acoustic Dark Energy: Potential Conversion of the Hubble Tension. Phys. Rev. D 2019, 100, 63542. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Di Valentino, E.; Paliathanasis, A.; Lu, J. Challenging bulk viscous unified scenarios with cosmological observations. Phys. Rev. D 2019, 100, 103518. [Google Scholar] [CrossRef]
- Agrawal, P.; Obied, G.; Vafa, C. H0 tension, swampland conjectures, and the epoch of fading dark matter. Phys. Rev. D 2021, 103, 43523. [Google Scholar] [CrossRef]
- Li, X.; Shafieloo, A. A Simple Phenomenological Emergent Dark Energy Model can Resolve the Hubble Tension. Astrophys. J. Lett. 2019, 883, L3. [Google Scholar] [CrossRef]
- Martinelli, M.; Tutusaus, I. CMB tensions with low-redshift H0 and S8 measurements: Impact of a redshift-dependent type-Ia supernovae intrinsic luminosity. Symmetry 2019, 11, 986. [Google Scholar] [CrossRef]
- Gelmini, G.B.; Kusenko, A.; Takhistov, V. Possible Hints of Sterile Neutrinos in Recent Measurements of the Hubble Parameter. JCAP 2021, 6, 2. [Google Scholar] [CrossRef]
- Rossi, M.; Ballardini, M.; Braglia, M.; Finelli, F.; Paoletti, D.; Starobinsky, A.A.; Umiltà, C. Cosmological constraints on post-Newtonian parameters in effectively massless scalar-tensor theories of gravity. Phys. Rev. D 2019, 100, 103524. [Google Scholar] [CrossRef]
- Di Valentino, E.; Ferreira, R.Z.; Visinelli, L.; Danielsson, U. Late time transitions in the quintessence field and the H0 tension. Phys. Dark Univ. 2019, 26, 100385. [Google Scholar] [CrossRef]
- Yang, W.; Mena, O.; Pan, S.; Di Valentino, E. Dark sectors with dynamical coupling. Phys. Rev. D 2019, 100, 83509. [Google Scholar] [CrossRef]
- Archidiacono, M.; Hooper, D.C.; Murgia, R.; Bohr, S.; Lesgourgues, J.; Viel, M. Constraining Dark Matter-Dark Radiation interactions with CMB, BAO, and Lyman-α. JCAP 2019, 10, 55. [Google Scholar] [CrossRef]
- Desmond, H.; Jain, B.; Sakstein, J. Local resolution of the Hubble tension: The impact of screened fifth forces on the cosmic distance ladder. Phys. Rev. D 2019, 100, 43537, Erratum in Phys. Rev. D 2020, 101, 069904, Erratum in Phys. Rev. D 2020, 101, 129901. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Vagnozzi, S.; Di Valentino, E.; Mota, D.F.; Capozziello, S. Dawn of the dark: Unified dark sectors and the EDGES Cosmic Dawn 21-cm signal. JCAP 2019, 11, 44. [Google Scholar] [CrossRef]
- Nesseris, S.; Sapone, D.; Sypsas, S. Evaporating primordial black holes as varying dark energy. Phys. Dark Univ. 2020, 27, 100413. [Google Scholar] [CrossRef]
- Pan, S.; Yang, W.; Di Valentino, E.; Saridakis, E.N.; Chakraborty, S. Interacting scenarios with dynamical dark energy: Observational constraints and alleviation of the H0 tension. Phys. Rev. D 2019, 100, 103520. [Google Scholar] [CrossRef]
- Vagnozzi, S. New physics in light of the H0 tension: An alternative view. Phys. Rev. D 2020, 102, 23518. [Google Scholar] [CrossRef]
- Visinelli, L.; Vagnozzi, S.; Danielsson, U. Revisiting a negative cosmological constant from low-redshift data. Symmetry 2019, 11, 1035. [Google Scholar] [CrossRef]
- Hardy, E.; Parameswaran, S. Thermal Dark Energy. Phys. Rev. D 2020, 101, 23503. [Google Scholar] [CrossRef]
- Cai, Y.F.; Khurshudyan, M.; Saridakis, E.N. Model-independent reconstruction of f(T) gravity from Gaussian Processes. Astrophys. J. 2020, 888, 62. [Google Scholar] [CrossRef]
- Pan, S.; Yang, W.; Di Valentino, E.; Shafieloo, A.; Chakraborty, S. Reconciling H0 tension in a six parameter space? JCAP 2020, 6, 62. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Silk, J. Cosmological constraints in extended parameter space from the Planck 2018 Legacy release. JCAP 2020, 1, 13. [Google Scholar] [CrossRef]
- Xiao, L.; Zhang, L.; An, R.; Feng, C.; Wang, B. Fractional Dark Matter decay: Cosmological imprints and observational constraints. JCAP 2020, 1, 45. [Google Scholar] [CrossRef]
- Panpanich, S.; Burikham, P.; Ponglertsakul, S.; Tannukij, L. Resolving Hubble Tension with Quintom Dark Energy Model. Chin. Phys. C 2021, 45, 15108. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Mena, O.; Vagnozzi, S. Interacting dark energy in the early 2020s: A promising solution to the H0 and cosmic shear tensions. Phys. Dark Univ. 2020, 30, 100666. [Google Scholar] [CrossRef]
- Benetti, M.; Miranda, W.; Borges, H.A.; Pigozzo, C.; Carneiro, S.; Alcaniz, J.S. Looking for interactions in the cosmological dark sector. JCAP 2019, 12, 23. [Google Scholar] [CrossRef]
- Dutta, K.; Roy, A.; Ruchika; Sen, A.A.; Sheikh-Jabbari, M.M. Cosmology with low-redshift observations: No signal for new physics. Phys. Rev. D 2019, 100, 103501. [Google Scholar] [CrossRef]
- Ghosh, S.; Khatri, R.; Roy, T.S. Can dark neutrino interactions phase out the Hubble tension? Phys. Rev. D 2020, 102, 123544. [Google Scholar] [CrossRef]
- Solà Peracaula, J.; Gomez-Valent, A.; de Cruz Pérez, J.; Moreno-Pulido, C. Brans–Dicke Gravity with a Cosmological Constant Smoothes Out ΛCDM Tensions. Astrophys. J. Lett. 2019, 886, L6. [Google Scholar] [CrossRef]
- Escudero, M.; Witte, S.J. A CMB search for the neutrino mass mechanism and its relation to the Hubble tension. Eur. Phys. J. C 2020, 80, 294. [Google Scholar] [CrossRef]
- Yan, S.F.; Zhang, P.; Chen, J.W.; Zhang, X.Z.; Cai, Y.F.; Saridakis, E.N. Interpreting cosmological tensions from the effective field theory of torsional gravity. Phys. Rev. D 2020, 101, 121301. [Google Scholar] [CrossRef]
- Banerjee, S.; Benisty, D.; Guendelman, E.I. Running Dark Energy and Dark Matter from Dynamical Spacetime. Bulg. J. Phys. 2021, 48, 117–137. [Google Scholar]
- Liu, M.; Huang, Z. Band-limited Features in the Primordial Power Spectrum Do Not Resolve the Hubble Tension. Astrophys. J. 2020, 897, 166. [Google Scholar] [CrossRef]
- Anchordoqui, L.A.; Perez Bergliaffa, S.E. Hot thermal universe endowed with massive dark vector fields and the Hubble tension. Phys. Rev. D 2019, 100, 123525. [Google Scholar] [CrossRef]
- Lunardini, C.; Perez-Gonzalez, Y.F. Dirac and Majorana neutrino signatures of primordial black holes. JCAP 2020, 8, 14. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Nunes, R.C.; Mota, D.F. Dark calling Dark: Interaction in the dark sector in presence of neutrino properties after Planck CMB final release. JCAP 2020, 4, 8. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Mena, O.; Vagnozzi, S. Nonminimal dark sector physics and cosmological tensions. Phys. Rev. D 2020, 101, 63502. [Google Scholar] [CrossRef]
- Niedermann, F.; Sloth, M.S. New early dark energy. Phys. Rev. D 2021, 103, L041303. [Google Scholar] [CrossRef]
- Cheng, G.; Ma, Y.Z.; Wu, F.; Zhang, J.; Chen, X. Testing interacting dark matter and dark energy model with cosmological data. Phys. Rev. D 2020, 102, 43517. [Google Scholar] [CrossRef]
- Berghaus, K.V.; Karwal, T. Thermal Friction as a Solution to the Hubble Tension. Phys. Rev. D 2020, 101, 83537. [Google Scholar] [CrossRef]
- Sakstein, J.; Trodden, M. Early Dark Energy from Massive Neutrinos as a Natural Resolution of the Hubble Tension. Phys. Rev. Lett. 2020, 124, 161301. [Google Scholar] [CrossRef]
- Liu, M.; Huang, Z.; Luo, X.; Miao, H.; Singh, N.K.; Huang, L. Can Non-standard Recombination Resolve the Hubble Tension? Sci. China Phys. Mech. Astron. 2020, 63, 290405. [Google Scholar] [CrossRef]
- Anchordoqui, L.A.; Antoniadis, I.; Lüst, D.; Soriano, J.F.; Taylor, T.R. H0 tension and the String Swampland. Phys. Rev. D 2020, 101, 83532. [Google Scholar] [CrossRef]
- Hart, L.; Chluba, J. Updated fundamental constant constraints from Planck 2018 data and possible relations to the Hubble tension. Mon. Not. R. Astron. Soc. 2020, 493, 3255–3263. [Google Scholar] [CrossRef]
- Wang, K.; Huang, Q.G. Implications for cosmology from Ground-based Cosmic Microwave Background observations. JCAP 2020, 6, 45. [Google Scholar] [CrossRef]
- Alcaniz, J.; Bernal, N.; Masiero, A.; Queiroz, F.S. Light dark matter: A common solution to the lithium and H 0 problems. Phys. Lett. B 2021, 812, 136008. [Google Scholar] [CrossRef]
- Gehrlein, J.; Pierre, M. A testable hidden-sector model for Dark Matter and neutrino masses. JHEP 2020, 2, 68. [Google Scholar] [CrossRef]
- Akarsu, O.; Barrow, J.D.; Escamilla, L.A.; Vazquez, J.A. Graduated dark energy: Observational hints of a spontaneous sign switch in the cosmological constant. Phys. Rev. D 2020, 101, 63528. [Google Scholar] [CrossRef]
- Mazo, B.Y.D.V.; Romano, A.E.; Quintero, M.A.C. Combining gravitational and electromagnetic waves observations to investigate local structure and the Hubble tension. arXiv 2019, arXiv:1912.12465. [Google Scholar]
- Ding, Q.; Nakama, T.; Wang, Y. A gigaparsec-scale local void and the Hubble tension. Sci. China Phys. Mech. Astron. 2020, 63, 290403. [Google Scholar] [CrossRef]
- Ye, G.; Piao, Y.S. Is the Hubble tension a hint of AdS phase around recombination? Phys. Rev. D 2020, 101, 83507. [Google Scholar] [CrossRef]
- Pan, S.; Sharov, G.S.; Yang, W. Field theoretic interpretations of interacting dark energy scenarios and recent observations. Phys. Rev. D 2020, 101, 103533. [Google Scholar] [CrossRef]
- Amirhashchi, H.; Yadav, A.K.; Ahmad, N.; Yadav, V. Interacting dark sectors in anisotropic universe: Observational constraints and H0 tension. Phys. Dark Univ. 2022, 36, 101043. [Google Scholar] [CrossRef]
- Yang, W.; Di Valentino, E.; Pan, S.; Basilakos, S.; Paliathanasis, A. Metastable dark energy models in light of Planck 2018 data: Alleviating the H0 tension. Phys. Rev. D 2020, 102, 63503. [Google Scholar] [CrossRef]
- Li, X.; Shafieloo, A. Evidence for Emergent Dark Energy. Astrophys. J. 2020, 902, 58. [Google Scholar] [CrossRef]
- Beradze, R.; Gogberashvili, M. Can the quasi-molecular mechanism of recombination decrease the Hubble tension? Phys. Dark Univ. 2021, 32, 100841. [Google Scholar] [CrossRef]
- Perez, A.; Sudarsky, D.; Wilson-Ewing, E. Resolving the H0 tension with diffusion. Gen. Rel. Grav. 2021, 53, 7. [Google Scholar] [CrossRef]
- Lyu, M.Z.; Haridasu, B.S.; Viel, M.; Xia, J.Q. H0 Reconstruction with Type Ia Supernovae, Baryon Acoustic Oscillation and Gravitational Lensing Time-Delay. Astrophys. J. 2020, 900, 160. [Google Scholar] [CrossRef]
- Yang, W.; Di Valentino, E.; Mena, O.; Pan, S.; Nunes, R.C. All-inclusive interacting dark sector cosmologies. Phys. Rev. D 2020, 101, 83509. [Google Scholar] [CrossRef]
- Choi, G.; Suzuki, M.; Yanagida, T.T. Degenerate Sub-keV Fermion Dark Matter from a Solution to the Hubble Tension. Phys. Rev. D 2020, 101, 75031. [Google Scholar] [CrossRef]
- Dutta, B.; Ghosh, S.; Kumar, J. Contributions to ΔNeff from the dark photon of U(1)T3R. Phys. Rev. D 2020, 102, 15013. [Google Scholar] [CrossRef]
- Pan, S.; Yang, W.; Paliathanasis, A. Non-linear interacting cosmological models after Planck 2018 legacy release and the H0 tension. Mon. Not. R. Astron. Soc. 2020, 493, 3114–3131. [Google Scholar] [CrossRef]
- Sharov, G.S.; Sinyakov, E.S. Cosmological models, observational data and tension in Hubble constant. arXiv 2020, arXiv:2002.03599. [Google Scholar] [CrossRef]
- Lucca, M.; Hooper, D.C. Shedding light on dark matter-dark energy interactions. Phys. Rev. D 2020, 102, 123502. [Google Scholar] [CrossRef]
- D’Agostino, R.; Nunes, R.C. Measurements of H0 in modified gravity theories: The role of lensed quasars in the late-time Universe. Phys. Rev. D 2020, 101, 103505. [Google Scholar] [CrossRef]
- Hogg, N.B.; Bruni, M.; Crittenden, R.; Martinelli, M.; Peirone, S. Latest evidence for a late time vacuum–geodesic CDM interaction. Phys. Dark Univ. 2020, 29, 100583. [Google Scholar] [CrossRef]
- Benevento, G.; Hu, W.; Raveri, M. Can Late Dark Energy Transitions Raise the Hubble constant? Phys. Rev. D 2020, 101, 103517. [Google Scholar] [CrossRef]
- Barker, W.E.V.; Lasenby, A.N.; Hobson, M.P.; Handley, W.J. Systematic study of background cosmology in unitary Poincaré gauge theories with application to emergent dark radiation and H0 tension. Phys. Rev. D 2020, 102, 24048. [Google Scholar] [CrossRef]
- Zumalacarregui, M. Gravity in the Era of Equality: Towards solutions to the Hubble problem without fine-tuned initial conditions. Phys. Rev. D 2020, 102, 23523. [Google Scholar] [CrossRef]
- Hill, J.C.; McDonough, E.; Toomey, M.W.; Alexander, S. Early dark energy does not restore cosmological concordance. Phys. Rev. D 2020, 102, 43507. [Google Scholar] [CrossRef]
- Desmond, H.; Sakstein, J. Screened fifth forces lower the TRGB-calibrated Hubble constant too. Phys. Rev. D 2020, 102, 23007. [Google Scholar] [CrossRef]
- Benisty, D.; Guendemlan, E.I.; Nissimov, E.; Pacheva, S. ΛCDM as a Noether Symmetry in Cosmology. Int. J. Mod. Phys. D 2020, 26, 2050104. [Google Scholar] [CrossRef]
- Gómez-Valent, A.; Pettorino, V.; Amendola, L. Update on coupled dark energy and the H0 tension. Phys. Rev. D 2020, 101, 123513. [Google Scholar] [CrossRef]
- Akarsu, O.; Katırcı, N.; Kumar, S.; Nunes, R.C.; Öztürk, B.; Sharma, S. Rastall gravity extension of the standard ΛCDM model: Theoretical features and observational constraints. Eur. Phys. J. C 2020, 80, 1050. [Google Scholar] [CrossRef]
- Ballesteros, G.; Notari, A.; Rompineve, F. The H0 tension: ΔGN vs. ΔNeff. JCAP 2020, 11, 24. [Google Scholar] [CrossRef]
- Blinov, N.; Keith, C.; Hooper, D. Warm Decaying Dark Matter and the Hubble Tension. JCAP 2020, 6, 5. [Google Scholar] [CrossRef]
- Haridasu, B.S.; Viel, M. Late-time decaying dark matter: Constraints and implications for the H0-tension. Mon. Not. R. Astron. Soc. 2020, 497, 1757–1764. [Google Scholar] [CrossRef]
- Alestas, G.; Kazantzidis, L.; Perivolaropoulos, L. H0 tension, phantom dark energy, and cosmological parameter degeneracies. Phys. Rev. D 2020, 101, 123516. [Google Scholar] [CrossRef]
- Jedamzik, K.; Pogosian, L. Relieving the Hubble tension with primordial magnetic fields. Phys. Rev. Lett. 2020, 125, 181302. [Google Scholar] [CrossRef] [PubMed]
- Braglia, M.; Ballardini, M.; Emond, W.T.; Finelli, F.; Gumrukcuoglu, A.E.; Koyama, K.; Paoletti, D. Larger value for H0 by an evolving gravitational constant. Phys. Rev. D 2020, 102, 23529. [Google Scholar] [CrossRef]
- Chudaykin, A.; Gorbunov, D.; Nedelko, N. Combined analysis of Planck and SPTPol data favors the early dark energy models. JCAP 2020, 8, 13. [Google Scholar] [CrossRef]
- Izaurieta, F.; Lepe, S.; Valdivia, O. The Spin Tensor of Dark Matter and the Hubble Parameter Tension. Phys. Dark Univ. 2020, 30, 100662. [Google Scholar] [CrossRef]
- Ballardini, M.; Braglia, M.; Finelli, F.; Paoletti, D.; Starobinsky, A.A.; Umiltà, C. Scalar-tensor theories of gravity, neutrino physics, and the H0 tension. JCAP 2020, 10, 44. [Google Scholar] [CrossRef]
- Di Valentino, E.; Gariazzo, S.; Mena, O.; Vagnozzi, S. Soundness of Dark Energy properties. JCAP 2020, 7, 45. [Google Scholar] [CrossRef]
- Ivanov, M.M.; Ali-Haïmoud, Y.; Lesgourgues, J. H0 tension or T0 tension? Phys. Rev. D 2020, 102, 63515. [Google Scholar] [CrossRef]
- Gogoi, A.; Sharma, R.K.; Chanda, P.; Das, S. Early Mass-varying Neutrino Dark Energy: Nugget Formation and Hubble Anomaly. Astrophys. J. 2021, 915, 132. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mukherjee, A.; Sen, A.A. Dark Energy with Phantom Crossing and the H0 Tension. Entropy 2021, 23, 404. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, A.; Cai, H.; Heisenberg, L.; Colgáin, E.O.; Sheikh-Jabbari, M.M.; Yang, T. Hubble sinks in the low-redshift swampland. Phys. Rev. D 2021, 103, L081305. [Google Scholar] [CrossRef]
- Elizalde, E.; Khurshudyan, M.; Odintsov, S.D.; Myrzakulov, R. Analysis of the H0 tension problem in the Universe with viscous dark fluid. Phys. Rev. D 2020, 102, 123501. [Google Scholar] [CrossRef]
- Clark, S.J.; Vattis, K.; Koushiappas, S.M. Cosmological constraints on late-universe decaying dark matter as a solution to the H0 tension. Phys. Rev. D 2021, 103, 43014. [Google Scholar] [CrossRef]
- Solà Peracaula, J.; Gómez-Valent, A.; de Cruz Pérez, J.; Moreno-Pulido, C. Brans–Dicke cosmology with a Λ-term: A possible solution to ΛCDM tensions. Class. Quant. Grav. 2020, 37, 245003. [Google Scholar] [CrossRef]
- Niedermann, F.; Sloth, M.S. Resolving the Hubble tension with new early dark energy. Phys. Rev. D 2020, 102, 63527. [Google Scholar] [CrossRef]
- Ivanov, M.M.; McDonough, E.; Hill, J.C.; Simonović, M.; Toomey, M.W.; Alexander, S.; Zaldarriaga, M. Constraining Early Dark Energy with Large-Scale Structure. Phys. Rev. D 2020, 102, 103502. [Google Scholar] [CrossRef]
- D’Amico, G.; Senatore, L.; Zhang, P.; Zheng, H. The Hubble Tension in Light of the Full-Shape Analysis of Large-Scale Structure Data. JCAP 2021, 5, 72. [Google Scholar] [CrossRef]
- Elizalde, E.; Khurshudyan, M. Constraints on cosmic opacity from Bayesian machine learning: The hidden side of the H0 tension problem. Phys. Dark Univ. 2022, 37, 101114. [Google Scholar] [CrossRef]
- Di Valentino, E.; Linder, E.V.; Melchiorri, A. H0 ex machina: Vacuum metamorphosis and beyond H0. Phys. Dark Univ. 2020, 30, 100733. [Google Scholar] [CrossRef]
- Gonzalez, M.; Hertzberg, M.P.; Rompineve, F. Ultralight Scalar Decay and the Hubble Tension. JCAP 2020, 10, 28. [Google Scholar] [CrossRef]
- Capozziello, S.; Benetti, M.; Spallicci, A.D.A.M. Addressing the cosmological H0 tension by the Heisenberg uncertainty. Found. Phys. 2020, 50, 893–899. [Google Scholar] [CrossRef]
- Yang, W.; Di Valentino, E.; Pan, S.; Mena, O. Emergent Dark Energy, neutrinos and cosmological tensions. Phys. Dark Univ. 2021, 31, 100762. [Google Scholar] [CrossRef]
- Sekiguchi, T.; Takahashi, T. Early recombination as a solution to the H0 tension. Phys. Rev. D 2021, 103, 83507. [Google Scholar] [CrossRef]
- Nunes, R.C.; Bernui, A. BAO signatures in the 2-point angular correlations and the Hubble tension. Eur. Phys. J. C 2020, 80, 1025. [Google Scholar] [CrossRef]
- Berechya, D.; Leonhardt, U. Lifshitz cosmology: Quantum vacuum and Hubble tension. Mon. Not. R. Astron. Soc. 2021, 507, 3473–3485. [Google Scholar] [CrossRef]
- Benaoum, H.B.; Yang, W.; Pan, S.; Di Valentino, E. Modified emergent dark energy and its astronomical constraints. Int. J. Mod. Phys. D 2022, 31, 2250015. [Google Scholar] [CrossRef]
- Calderón, R.; Gannouji, R.; L’Huillier, B.; Polarski, D. Negative cosmological constant in the dark sector? Phys. Rev. D 2021, 103, 23526. [Google Scholar] [CrossRef]
- Ye, G.; Piao, Y.S. T0 censorship of early dark energy and AdS vacua. Phys. Rev. D 2020, 102, 83523. [Google Scholar] [CrossRef]
- Flores, M.M.; Kusenko, A. Primordial Black Holes from Long-Range Scalar Forces and Scalar Radiative Cooling. Phys. Rev. Lett. 2021, 126, 41101. [Google Scholar] [CrossRef]
- Niedermann, F.; Sloth, M.S. New Early Dark Energy is compatible with current LSS data. Phys. Rev. D 2021, 103, 103537. [Google Scholar] [CrossRef]
- Vázquez, J.A.; Tamayo, D.; Sen, A.A.; Quiros, I. Bayesian model selection on scalar ϵ-field dark energy. Phys. Rev. D 2021, 103, 43506. [Google Scholar] [CrossRef]
- Akarsu, O.; Barrow, J.D.; Uzun, N.M. Screening anisotropy via energy-momentum squared gravity: ΛCDM model with hidden anisotropy. Phys. Rev. D 2020, 102, 124059. [Google Scholar] [CrossRef]
- Pogosian, L.; Zhao, G.B.; Jedamzik, K. Recombination-independent determination of the sound horizon and the Hubble constant from BAO. Astrophys. J. Lett. 2020, 904, L17. [Google Scholar] [CrossRef]
- Smith, T.L.; Poulin, V.; Bernal, J.L.; Boddy, K.K.; Kamionkowski, M.; Murgia, R. Early dark energy is not excluded by current large-scale structure data. Phys. Rev. D 2021, 103, 123542. [Google Scholar] [CrossRef]
- Murgia, R.; Abellán, G.F.; Poulin, V. Early dark energy resolution to the Hubble tension in light of weak lensing surveys and lensing anomalies. Phys. Rev. D 2021, 103, 63502. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Di Valentino, E.; Gariazzo, S.; Melchiorri, A.; Mena, O.; Silk, J. The galaxy power spectrum take on spatial curvature and cosmic concordance. Phys. Dark Univ. 2021, 33, 100851. [Google Scholar] [CrossRef]
- Anchordoqui, L.A. Decaying dark matter, the H0 tension, and the lithium problem. Phys. Rev. D 2021, 103, 35025. [Google Scholar] [CrossRef]
- Hashim, M.; El Hanafy, W.; Golovnev, A.; El-Zant, A.A. Toward a concordance teleparallel cosmology. Part I. Background dynamics. JCAP 2021, 7, 52. [Google Scholar] [CrossRef]
- Di Valentino, E. A combined analysis of the H0 late time direct measurements and the impact on the Dark Energy sector. Mon. Not. R. Astron. Soc. 2021, 502, 2065–2073. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Sáez-Chillón Gómez, D.; Sharov, G.S. Analyzing the H0 tension in F(R) gravity models. Nucl. Phys. B 2021, 966, 115377. [Google Scholar] [CrossRef]
- Carrillo González, M.; Liang, Q.; Sakstein, J.; Trodden, M. Neutrino-Assisted Early Dark Energy: Theory and Cosmology. JCAP 2021, 4, 63. [Google Scholar] [CrossRef]
- Das, A.; Ghosh, S. Flavor-specific interaction favors strong neutrino self-coupling in the early universe. JCAP 2021, 7, 38. [Google Scholar] [CrossRef]
- Braglia, M.; Ballardini, M.; Finelli, F.; Koyama, K. Early modified gravity in light of the H0 tension and LSS data. Phys. Rev. D 2021, 103, 43528. [Google Scholar] [CrossRef]
- Adi, T.; Kovetz, E.D. Can conformally coupled modified gravity solve the Hubble tension? Phys. Rev. D 2021, 103, 23530. [Google Scholar] [CrossRef]
- Banihashemi, A.; Khosravi, N.; Shafieloo, A. Dark energy as a critical phenomenon: A hint from Hubble tension. JCAP 2021, 6, 3. [Google Scholar] [CrossRef]
- Roy Choudhury, S.; Hannestad, S.; Tram, T. Updated constraints on massive neutrino self-interactions from cosmology in light of the H0 tension. JCAP 2021, 3, 84. [Google Scholar] [CrossRef]
- Mavromatos, N.E.; Solà Peracaula, J. Stringy-running-vacuum-model inflation: From primordial gravitational waves and stiff axion matter to dynamical dark energy. Eur. Phys. J. Special Top. 2021, 230, 2077–2110. [Google Scholar] [CrossRef]
- Cai, R.G.; Ding, J.F.; Guo, Z.K.; Wang, S.J.; Yu, W.W. Do the observational data favor a local void? Phys. Rev. D 2021, 103, 123539. [Google Scholar] [CrossRef]
- Haridasu, B.S.; Viel, M.; Vittorio, N. Sources of H0-tension in dark energy scenarios. Phys. Rev. D 2021, 103, 63539. [Google Scholar] [CrossRef]
- Shimon, M. Possible resolution of the Hubble tension with Weyl invariant gravity. JCAP 2022, 4, 48. [Google Scholar] [CrossRef]
- Brinckmann, T.; Chang, J.H.; LoVerde, M. Self-interacting neutrinos, the Hubble parameter tension, and the cosmic microwave background. Phys. Rev. D 2021, 104, 63523. [Google Scholar] [CrossRef]
- Alestas, G.; Kazantzidis, L.; Perivolaropoulos, L. w—M phantom transition at zt < 0.1 as a resolution of the Hubble tension. Phys. Rev. D 2021, 103, 83517. [Google Scholar]
- Yin, L. Reducing the H0 tension with exponential acoustic dark energy. Eur. Phys. J. C 2022, 82, 78. [Google Scholar] [CrossRef]
- Moshafi, H.; Baghram, S.; Khosravi, N. CMB lensing in a modified ΛCDM model in light of the H0 tension. Phys. Rev. D 2021, 104, 63506. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Di Valentino, E.; Mena, O.; Melchiorri, A. 2021-H0 odyssey: Closed, phantom and interacting dark energy cosmologies. JCAP 2021, 10, 8. [Google Scholar] [CrossRef]
- Seto, O.; Toda, Y. Comparing early dark energy and extra radiation solutions to the Hubble tension with BBN. Phys. Rev. D 2021, 103, 123501. [Google Scholar] [CrossRef]
- Sinha, S. Differentiating dark interactions with perturbation. Phys. Rev. D 2021, 103, 123547. [Google Scholar] [CrossRef]
- Gao, L.Y.; Zhao, Z.W.; Xue, S.S.; Zhang, X. Relieving the H 0 tension with a new interacting dark energy model. JCAP 2021, 7, 5. [Google Scholar] [CrossRef]
- Cai, R.G.; Guo, Z.K.; Li, L.; Wang, S.J.; Yu, W.W. Chameleon dark energy can resolve the Hubble tension. Phys. Rev. D 2021, 103, 121302. [Google Scholar] [CrossRef]
- Di Valentino, E.; Pan, S.; Yang, W.; Anchordoqui, L.A. Touch of neutrinos on the vacuum metamorphosis: Is the H0 solution back? Phys. Rev. D 2021, 103, 123527. [Google Scholar] [CrossRef]
- Marra, V.; Perivolaropoulos, L. Rapid transition of Geff at zt ≃0.01 as a possible solution of the Hubble and growth tensions. Phys. Rev. D 2021, 104, L021303. [Google Scholar] [CrossRef]
- Solà Peracaula, J.; Gómez-Valent, A.; de Cruz Perez, J.; Moreno-Pulido, C. Running vacuum against the H0 and σ8 tensions. EPL 2021, 134, 19001. [Google Scholar] [CrossRef]
- Kumar, S. Remedy of some cosmological tensions via effective phantom-like behavior of interacting vacuum energy. Phys. Dark Univ. 2021, 33, 100862. [Google Scholar] [CrossRef]
- Ren, X.; Wong, T.H.T.; Cai, Y.F.; Saridakis, E.N. Data-driven Reconstruction of the Late-time Cosmic Acceleration with f(T) Gravity. Phys. Dark Univ. 2021, 32, 100812. [Google Scholar] [CrossRef]
- Escudero, M.; Witte, S.J. The hubble tension as a hint of leptogenesis and neutrino mass generation. Eur. Phys. J. C 2021, 81, 515. [Google Scholar] [CrossRef]
- Levi Said, J.; Mifsud, J.; Sultana, J.; Adami, K.Z. Reconstructing teleparallel gravity with cosmic structure growth and expansion rate data. JCAP 2021, 6, 15. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Saez-Chillon Gomez, D.; Sharov, G.S. Modeling and testing the equation of state for (Early) dark energy. Phys. Dark Univ. 2021, 32, 100837. [Google Scholar] [CrossRef]
- Ye, G.; Hu, B.; Piao, Y.S. Implication of the Hubble tension for the primordial Universe in light of recent cosmological data. Phys. Rev. D 2021, 104, 63510. [Google Scholar] [CrossRef]
- Elizalde, E.; Gluza, J.; Khurshudyan, M. An approach to cold dark matter deviation and the H0 tension problem by using machine learning. arXiv 2021, arXiv:2104.01077. [Google Scholar]
- Dhawan, S.; Alsing, J.; Vagnozzi, S. Non-parametric spatial curvature inference using late-Universe cosmological probes. Mon. Not. R. Astron. Soc. 2021, 506, L1–L5. [Google Scholar] [CrossRef]
- Acquaviva, G.; Akarsu, O.; Katirci, N.; Vazquez, J.A. Simple-graduated dark energy and spatial curvature. Phys. Rev. D 2021, 104, 23505. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Aresté Saló, L.; de Haro, J. Theoretical and observational bounds on some interacting vacuum energy scenarios. Phys. Rev. D 2021, 103, 83520. [Google Scholar] [CrossRef]
- Paul, A.; Chatterjee, A.; Ghoshal, A.; Pal, S. Shedding light on dark matter and neutrino interactions from cosmology. JCAP 2021, 10, 17. [Google Scholar] [CrossRef]
- Geng, C.Q.; Hsu, Y.T.; Lu, J.R.; Yin, L. A Dark Energy model from Generalized Proca Theory. Phys. Dark Univ. 2021, 32, 100819. [Google Scholar] [CrossRef]
- Hashim, M.; El-Zant, A.A.; El Hanafy, W.; Golovnev, A. Toward a concordance teleparallel cosmology. Part II. Linear perturbation. JCAP 2021, 7, 53. [Google Scholar] [CrossRef]
- Alestas, G.; Antoniou, I.; Perivolaropoulos, L. Hints for a Gravitational Transition in Tully–Fisher Data. Universe 2021, 7, 366. [Google Scholar] [CrossRef]
- Fung, L.W.H.; Li, L.; Liu, T.; Luu, H.N.; Qiu, Y.C.; Tye, S.H.H. Hubble constant in the axi-Higgs universe. Phys. Rev. Res. 2023, 5, L022059. [Google Scholar] [CrossRef]
- Mavromatos, N.E.; Solà Peracaula, J. Inflationary physics and trans-Planckian conjecture in the stringy running vacuum model: From the phantom vacuum to the true vacuum. Eur. Phys. J. Plus 2021, 136, 1152. [Google Scholar] [CrossRef]
- Teng, Y.P.; Lee, W.; Ng, K.W. Constraining the dark-energy equation of state with cosmological data. Phys. Rev. D 2021, 104, 83519. [Google Scholar] [CrossRef]
- Thiele, L.; Guan, Y.; Hill, J.C.; Kosowsky, A.; Spergel, D.N. Can small-scale baryon inhomogeneities resolve the Hubble tension? An investigation with ACT DR4. Phys. Rev. D 2021, 104, 63535. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, G.; Mu, Y.; Xu, L. Can phantom transition at z ∼ 1 restore the Cosmic concordance? Mon. Not. R. Astron. Soc. 2022, 511, 595–606. [Google Scholar] [CrossRef]
- Linares Cedeño, F.X.; Roy, N.; Ureña López, L.A. Tracker phantom field and a cosmological constant: Dynamics of a composite dark energy model. Phys. Rev. D 2021, 104, 123502. [Google Scholar] [CrossRef]
- Gu, Y.; Wu, L.; Zhu, B. Axion dark radiation: Hubble tension and the Hyper-Kamiokande neutrino experiment. Phys. Rev. D 2022, 105, 95008. [Google Scholar] [CrossRef]
- Lucca, M. Dark energy–dark matter interactions as a solution to the S8 tension. Phys. Dark Univ. 2021, 34, 100899. [Google Scholar] [CrossRef]
- Krishnan, C.; Mohayaee, R.; Colgáin, E.O.; Sheikh-Jabbari, M.M.; Yin, L. Does Hubble tension signal a breakdown in FLRW cosmology? Class. Quant. Grav. 2021, 38, 184001. [Google Scholar] [CrossRef]
- Okamatsu, F.; Sekiguchi, T.; Takahashi, T. H0 tension without CMB data: Beyond the ΛCDM. Phys. Rev. D 2021, 104, 23523. [Google Scholar] [CrossRef]
- Jin, S.J.; Wang, L.F.; Wu, P.J.; Zhang, J.F.; Zhang, X. How can gravitational-wave standard sirens and 21-cm intensity mapping jointly provide a precise late-universe cosmological probe? Phys. Rev. D 2021, 104, 103507. [Google Scholar] [CrossRef]
- Krishnan, C.; Mohayaee, R.; Colgáin, E.O.; Sheikh-Jabbari, M.M.; Yin, L. Hints of FLRW breakdown from supernovae. Phys. Rev. D 2022, 105, 63514. [Google Scholar] [CrossRef]
- Dinda, B.R. Cosmic expansion parametrization: Implication for curvature and H0 tension. Phys. Rev. D 2022, 105, 63524. [Google Scholar] [CrossRef]
- Adil, S.A.; Gangopadhyay, M.R.; Sami, M.; Sharma, M.K. Late-time acceleration due to a generic modification of gravity and the Hubble tension. Phys. Rev. D 2021, 104, 103534. [Google Scholar] [CrossRef]
- de Araujo, J.C.N.; De Felice, A.; Kumar, S.; Nunes, R.C. Minimal theory of massive gravity in the light of CMB data and the S8 tension. Phys. Rev. D 2021, 104, 104057. [Google Scholar] [CrossRef]
- Beltrán Jiménez, J.; Bettoni, D.; Figueruelo, D.; Teppa Pannia, F.A.; Tsujikawa, S. Probing elastic interactions in the dark sector and the role of S8. Phys. Rev. D 2021, 104, 103503. [Google Scholar] [CrossRef]
- Karwal, T.; Raveri, M.; Jain, B.; Khoury, J.; Trodden, M. Chameleon early dark energy and the Hubble tension. Phys. Rev. D 2022, 105, 63535. [Google Scholar] [CrossRef]
- Lucca, M. Multi-interacting dark energy and its cosmological implications. Phys. Rev. D 2021, 104, 83510. [Google Scholar] [CrossRef]
- Bag, S.; Sahni, V.; Shafieloo, A.; Shtanov, Y. Phantom Braneworld and the Hubble Tension. Astrophys. J. 2021, 923, 212. [Google Scholar] [CrossRef]
- Jiang, J.Q.; Piao, Y.S. Testing AdS early dark energy with Planck, SPTpol, and LSS data. Phys. Rev. D 2021, 104, 103524. [Google Scholar] [CrossRef]
- Ghosh, S.; Kumar, S.; Tsai, Y. Free-streaming and coupled dark radiation isocurvature perturbations: Constraints and application to the Hubble tension. JCAP 2022, 5, 14. [Google Scholar] [CrossRef]
- Nunes, R.C.; Di Valentino, E. Dark sector interaction and the supernova absolute magnitude tension. Phys. Rev. D 2021, 104, 63529. [Google Scholar] [CrossRef]
- Gómez-Valent, A.; Zheng, Z.; Amendola, L.; Pettorino, V.; Wetterich, C. Early dark energy in the pre- and postrecombination epochs. Phys. Rev. D 2021, 104, 83536. [Google Scholar] [CrossRef]
- Li, B.; Shapiro, P.R. Precision cosmology and the stiff-amplified gravitational-wave background from inflation: NANOGrav, Advanced LIGO-Virgo and the Hubble tension. JCAP 2021, 10, 24. [Google Scholar] [CrossRef]
- Hart, L.; Chluba, J. Varying fundamental constants principal component analysis: Additional hints about the Hubble tension. Mon. Not. R. Astron. Soc. 2022, 510, 2206–2227. [Google Scholar] [CrossRef]
- Pogosian, L.; Raveri, M.; Koyama, K.; Martinelli, M.; Silvestri, A.; Zhao, G.B.; Li, J.; Peirone, S.; Zucca, A. Imprints of cosmological tensions in reconstructed gravity. Nat. Astron. 2022, 6, 1484–1490. [Google Scholar] [CrossRef]
- Cyr-Racine, F.Y.; Ge, F.; Knox, L. Symmetry of Cosmological Observables, a Mirror World Dark Sector, and the Hubble Constant. Phys. Rev. Lett. 2022, 128, 201301. [Google Scholar] [CrossRef] [PubMed]
- Ye, G.; Zhang, J.; Piao, Y.S. Alleviating both H0 and S8 tensions: Early dark energy lifts the CMB-lockdown on ultralight axion. Phys. Lett. B 2023, 839, 137770. [Google Scholar] [CrossRef]
- Normann, B.D.; Brevik, I.H. Can the Hubble tension be resolved by bulk viscosity? Mod. Phys. Lett. A 2021, 36, 2150198. [Google Scholar] [CrossRef]
- Anchordoqui, L.A.; Di Valentino, E.; Pan, S.; Yang, W. Dissecting the H0 and S8 tensions with Planck + BAO + supernova type Ia in multi-parameter cosmologies. JHEAp 2021, 32, 28–64. [Google Scholar] [CrossRef]
- Staicova, D.; Benisty, D. Constraining the dark energy models using Baryon Acoustic Oscillations: An approach independent of H0·rd. Astron. Astrophys. 2022, 668, A135. [Google Scholar] [CrossRef]
- Chang, C.F. Imprint of early dark energy in stochastic gravitational wave background. Phys. Rev. D 2022, 105, 23508. [Google Scholar] [CrossRef]
- Drees, M.; Zhao, W. U(1)Lμ−Lτ for Light Dark Matter, gμ-2, the 511 keV excess and the Hubble Tension. Phys. Lett. B 2022, 827, 136948. [Google Scholar] [CrossRef]
- Rashkovetskyi, M.; Muñoz, J.B.; Eisenstein, D.J.; Dvorkin, C. Small-scale clumping at recombination and the Hubble tension. Phys. Rev. D 2021, 104, 103517. [Google Scholar] [CrossRef]
- Qiu, X.W.; Zhao, Z.W.; Wang, L.F.; Zhang, J.F.; Zhang, X. A forecast of using fast radio burst observations to constrain holographic dark energy. JCAP 2022, 2, 6. [Google Scholar] [CrossRef]
- Liu, W.; Anchordoqui, L.A.; Di Valentino, E.; Pan, S.; Wu, Y.; Yang, W. Constraints from high-precision measurements of the cosmic microwave background: The case of disintegrating dark matter with Λ or dynamical dark energy. JCAP 2022, 2, 12. [Google Scholar] [CrossRef]
- Rezaei, M.; Solà Peracaula, J.; Malekjani, M. Cosmographic approach to Running Vacuum dark energy models: New constraints using BAOs and Hubble diagrams at higher redshifts. Mon. Not. R. Astron. Soc. 2021, 509, 2593–2608. [Google Scholar] [CrossRef]
- Nilsson, N.A.; Park, M.I. Tests of standard cosmology in Hořava gravity, Bayesian evidence for a closed universe, and the Hubble tension. Eur. Phys. J. C 2022, 82, 873. [Google Scholar] [CrossRef]
- Akarsu, O.; Kumar, S.; Özülker, E.; Vazquez, J.A. Relaxing cosmological tensions with a sign switching cosmological constant. Phys. Rev. D 2021, 104, 123512. [Google Scholar] [CrossRef]
- Luongo, O.; Muccino, M.; Colgáin, E.O.; Sheikh-Jabbari, M.M.; Yin, L. Larger H0 values in the CMB dipole direction. Phys. Rev. D 2022, 105, 103510. [Google Scholar] [CrossRef]
- Mawas, E.; Street, L.; Gass, R.; Wijewardhana, L.C.R. Interacting dark energy axions in light of the Hubble tension. arXiv 2021, arXiv:2108.13317. [Google Scholar]
- Perivolaropoulos, L.; Skara, F. Hubble tension or a transition of the Cepheid SnIa calibrator parameters? Phys. Rev. D 2021, 104, 123511. [Google Scholar] [CrossRef]
- Hill, J.C.; Calabrese, E.; Aiola, S.; Battaglia, N.; Bolliet, B.; Choi, S.K.; Devlin, M.J.; Duivenvoorden, A.J.; Dunkley, J.; Ferraro, S.; et al. Atacama Cosmology Telescope: Constraints on prerecombination early dark energy. Phys. Rev. D 2022, 105, 123536. [Google Scholar] [CrossRef]
- Feng, L.; Guo, R.Y.; Zhang, J.F.; Zhang, X. Cosmological search for sterile neutrinos after Planck 2018. Phys. Lett. B 2022, 827, 136940. [Google Scholar] [CrossRef]
- Poulin, V.; Smith, T.L.; Bartlett, A. Dark energy at early times and ACT data: A larger Hubble constant without late-time priors. Phys. Rev. D 2021, 104, 123550. [Google Scholar] [CrossRef]
- Theodoropoulos, A.; Perivolaropoulos, L. The Hubble Tension, the M Crisis of Late Time H(z) Deformation Models and the Reconstruction of Quintessence Lagrangians. Universe 2021, 7, 300. [Google Scholar] [CrossRef]
- Hogg, N.B.; Bruni, M. Shan–Chen interacting vacuum cosmology. Mon. Not. R. Astron. Soc. 2022, 511, 4430–4443. [Google Scholar] [CrossRef]
- Drepanou, N.; Lymperis, A.; Saridakis, E.N.; Yesmakhanova, K. Kaniadakis holographic dark energy and cosmology. Eur. Phys. J. C 2022, 82, 449. [Google Scholar] [CrossRef]
- Khosravi, N.; Farhang, M. Phenomenological gravitational phase transition: Early and late modifications. Phys. Rev. D 2022, 105, 63505. [Google Scholar] [CrossRef]
- Aghababaei, S.; Moradpour, H.; Vagenas, E.C. Hubble tension bounds the GUP and EUP parameters. Eur. Phys. J. Plus 2021, 136, 997. [Google Scholar] [CrossRef]
- Petronikolou, M.; Basilakos, S.; Saridakis, E.N. Alleviating H0 tension in Horndeski gravity. Phys. Rev. D 2022, 106, 124051. [Google Scholar] [CrossRef]
- Guo, R.Y.; Feng, L.; Yao, T.Y.; Chen, X.Y. Exploration of interacting dynamical dark energy model with interaction term including the equation-of-state parameter: Alleviation of the H0 tension. JCAP 2021, 12, 36. [Google Scholar] [CrossRef]
- Di Valentino, E.; Gariazzo, S.; Giunti, C.; Mena, O.; Pan, S.; Yang, W. Minimal dark energy: Key to sterile neutrino and Hubble constant tensions? Phys. Rev. D 2022, 105, 103511. [Google Scholar] [CrossRef]
- Castello, S.; Högås, M.; Mörtsell, E. A cosmological underdensity does not solve the Hubble tension. JCAP 2022, 7, 3, Erratum in JCAP 2022, 09, E01. [Google Scholar] [CrossRef]
- Bansal, S.; Kim, J.H.; Kolda, C.; Low, M.; Tsai, Y. Mirror twin Higgs cosmology: Constraints and a possible resolution to the H0 and S8 tensions. JHEP 2022, 5, 50. [Google Scholar] [CrossRef]
- Alestas, G.; Camarena, D.; Di Valentino, E.; Kazantzidis, L.; Marra, V.; Nesseris, S.; Perivolaropoulos, L. Late-transition versus smooth H(z)-deformation models for the resolution of the Hubble crisis. Phys. Rev. D 2022, 105, 63538. [Google Scholar] [CrossRef]
- De Simone, B.; Nielson, V.; Rinaldi, E.; Dainotti, M.G. A new perspective on cosmology through Supernovae Ia and Gamma Ray Bursts. In Proceedings of the 16th Marcel Grossmann Meeting on Recent Developments in Theoretical and Experimental General Relativity, Astrophysics and Relativistic Field Theories, Online, 5–10 July 2021. [Google Scholar]
- Clark, S.J.; Vattis, K.; Fan, J.; Koushiappas, S.M. H0 and S8 tensions necessitate early and late time changes to ΛCDM. Phys. Rev. D 2023, 107, 83527. [Google Scholar] [CrossRef]
- Aloni, D.; Berlin, A.; Joseph, M.; Schmaltz, M.; Weiner, N. A Step in understanding the Hubble tension. Phys. Rev. D 2022, 105, 123516. [Google Scholar] [CrossRef]
- Luu, H.N. Axion-Higgs cosmology: Cosmic microwave background and cosmological tensions. Phys. Rev. D 2023, 107, 23513. [Google Scholar] [CrossRef]
- Tiwari, P.; Kothari, R.; Jain, P. Superhorizon Perturbations: A Possible Explanation of the Hubble–Lemaître Tension and the Large-scale Anisotropy of the Universe. Astrophys. J. Lett. 2022, 924, L36. [Google Scholar] [CrossRef]
- Gariazzo, S.; Di Valentino, E.; Mena, O.; Nunes, R.C. Late-time interacting cosmologies and the Hubble constant tension. Phys. Rev. D 2022, 106, 23530. [Google Scholar] [CrossRef]
- Benetti, M.; Graef, L.L.; Vagnozzi, S. Primordial gravitational waves from NANOGrav: A broken power-law approach. Phys. Rev. D 2022, 105, 43520. [Google Scholar] [CrossRef]
- Belgacem, E.; Prokopec, T. Quantum origin of dark energy and the Hubble tension. Phys. Lett. B 2022, 831, 137174. [Google Scholar] [CrossRef]
- Duan, W.F.; Li, S.P.; Li, X.Q.; Yang, Y.D. Linking anomalies to Hubble tension via a single right-handed neutrino *. Chin. Phys. C 2023, 47, 33102. [Google Scholar] [CrossRef]
- Dialektopoulos, K.; Said, J.L.; Mifsud, J.; Sultana, J.; Adami, K.Z. Neural network reconstruction of late-time cosmology and null tests. JCAP 2022, 2, 23. [Google Scholar] [CrossRef]
- Gómez-Valent, A. Measuring the sound horizon and absolute magnitude of SNIa by maximizing the consistency between low-redshift data sets. Phys. Rev. D 2022, 105, 43528. [Google Scholar] [CrossRef]
- Corona, M.A.; Murgia, R.; Cadeddu, M.; Archidiacono, M.; Gariazzo, S.; Giunti, C.; Hannestad, S. Pseudoscalar sterile neutrino self-interactions in light of Planck, SPT and ACT data. JCAP 2022, 6, 10. [Google Scholar] [CrossRef]
- Niedermann, F.; Sloth, M.S. Hot new early dark energy: Towards a unified dark sector of neutrinos, dark energy and dark matter. Phys. Lett. B 2022, 835, 137555. [Google Scholar] [CrossRef]
- Niedermann, F.; Sloth, M.S. Hot new early dark energy. Phys. Rev. D 2022, 105, 63509. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A. Neutrino Mass Bounds in the Era of Tension Cosmology. Astrophys. J. Lett. 2022, 931, L18. [Google Scholar] [CrossRef]
- Renzi, F.; Hogg, N.B.; Giarè, W. The resilience of the Etherington–Hubble relation. Mon. Not. R. Astron. Soc. 2022, 513, 4004–4014. [Google Scholar] [CrossRef]
- Takahashi, F.; Yin, W. Cosmological implications of ns ≈ 1 in light of the Hubble tension. Phys. Lett. B 2022, 830, 137143. [Google Scholar] [CrossRef]
- Spallicci, A.D.A.M.; Benetti, M.; Capozziello, S. The Heisenberg Limit at Cosmological Scales. Found. Phys. 2022, 52, 23. [Google Scholar] [CrossRef]
- Akarsu, O.; Di Valentino, E.; Kumar, S.; Ozyigit, M.; Sharma, S. Testing spatial curvature and anisotropic expansion on top of the ΛCDM model. Phys. Dark Univ. 2023, 39, 101162. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Yang, W.; Pan, S.; Anagnostopoulos, F.K.; Basilakos, S. Observational constraints on soft dark energy and soft dark matter: Challenging ΛCDM cosmology. Nucl. Phys. B 2023, 986, 116042. [Google Scholar] [CrossRef]
- McDonough, E.; Lin, M.X.; Hill, J.C.; Hu, W.; Zhou, S. Early dark sector, the Hubble tension, and the swampland. Phys. Rev. D 2022, 106, 43525. [Google Scholar] [CrossRef]
- Sen, A.A.; Adil, S.A.; Sen, S. Do cosmological observations allow a negative Λ? Mon. Not. R. Astron. Soc. 2022, 518, 1098–1105. [Google Scholar] [CrossRef]
- La Posta, A.; Louis, T.; Garrido, X.; Hill, J.C. Constraints on prerecombination early dark energy from SPT-3G public data. Phys. Rev. D 2022, 105, 83519. [Google Scholar] [CrossRef]
- Greene, K.L.; Cyr-Racine, F.Y. Hubble distancing: Focusing on distance measurements in cosmology. JCAP 2022, 6, 2. [Google Scholar] [CrossRef]
- Herold, L.; Ferreira, E.G.M.; Komatsu, E. New Constraint on Early Dark Energy from Planck and BOSS Data Using the Profile Likelihood. Astrophys. J. Lett. 2022, 929, L16. [Google Scholar] [CrossRef]
- Sakr, Z.; Sapone, D. Can varying the gravitational constant alleviate the tensions? JCAP 2022, 3, 34. [Google Scholar] [CrossRef]
- Cao, M.D.; Zheng, J.; Qi, J.Z.; Zhang, X.; Zhu, Z.H. A New Way to Explore Cosmological Tensions Using Gravitational Waves and Strong Gravitational Lensing. Astrophys. J. 2022, 934, 108. [Google Scholar] [CrossRef]
- Solomon, R.; Agarwal, G.; Stojkovic, D. Environment dependent electron mass and the Hubble constant tension. Phys. Rev. D 2022, 105, 103536. [Google Scholar] [CrossRef]
- Colaço, L.R.; Holanda, R.F.L.; Nunes, R.C. Varying-α in scalar-tensor theory: Implications in light of the supernova absolute magnitude tension and forecast from GW standard sirens. arXiv 2022, arXiv:2201.04073. [Google Scholar]
- Banihashemi, A.; Khosravi, N. Fluctuations in the Ginzburg–Landau Theory of Dark Energy: Internal (In)consistencies in the Planck Data Set. Astrophys. J. 2022, 931, 148. [Google Scholar] [CrossRef]
- Alestas, G.; Perivolaropoulos, L.; Tanidis, K. Constraining a late time transition of Geff using low-z galaxy survey data. Phys. Rev. D 2022, 106, 23526. [Google Scholar] [CrossRef]
- Wang, H.; Piao, Y.S. Testing dark energy after pre-recombination early dark energy. Phys. Lett. B 2022, 832, 137244. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Did the Universe experience a pressure non-crushing type cosmological singularity in the recent past? EPL 2022, 137, 39001. [Google Scholar] [CrossRef]
- Perivolaropoulos, L. Is the Hubble Crisis Connected with the Extinction of Dinosaurs? Universe 2022, 8, 263. [Google Scholar] [CrossRef]
- Roy, N.; Goswami, S.; Das, S. Quintessence or phantom: Study of scalar field dark energy models through a general parametrization of the Hubble parameter. Phys. Dark Univ. 2022, 36, 101037. [Google Scholar] [CrossRef]
- Dainotti, M.G.; De Simone, B.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G.; Bogdan, M.; Ugale, S. On the Evolution of the Hubble Constant with the SNe Ia Pantheon Sample and Baryon Acoustic Oscillations: A Feasibility Study for GRB-Cosmology in 2030. Galaxies 2022, 10, 24. [Google Scholar] [CrossRef]
- Heisenberg, L.; Villarrubia-Rojo, H.; Zosso, J. Simultaneously solving the H0 and σ8 tensions with late dark energy. Phys. Dark Univ. 2023, 39, 101163. [Google Scholar] [CrossRef]
- Hazra, D.K.; Antony, A.; Shafieloo, A. One spectrum to cure them all: Signature from early Universe solves major anomalies and tensions in cosmology. JCAP 2022, 8, 63. [Google Scholar] [CrossRef]
- Wang, Y.J.; Qi, J.Z.; Wang, B.; Zhang, J.F.; Cui, J.L.; Zhang, X. Cosmological model-independent measurement of cosmic curvature using distance sum rule with the help of gravitational waves. Mon. Not. R. Astron. Soc. 2022, 516, 5187–5195. [Google Scholar] [CrossRef]
- Heisenberg, L.; Villarrubia-Rojo, H.; Zosso, J. Can late-time extensions solve the H0 and σ8 tensions? Phys. Rev. D 2022, 106, 43503. [Google Scholar] [CrossRef]
- Qi, J.Z.; Cui, Y.; Hu, W.H.; Zhang, J.F.; Cui, J.L.; Zhang, X. Strongly lensed type Ia supernovae as a precise late-Universe probe of measuring the Hubble constant and cosmic curvature. Phys. Rev. D 2022, 106, 23520. [Google Scholar] [CrossRef]
- Sharma, R.K.; Pandey, K.L.; Das, S. Implications of an Extended Dark Energy Model with Massive Neutrinos. Astrophys. J. 2022, 934, 113. [Google Scholar] [CrossRef]
- Lee, B.H.; Lee, W.; Colgáin, E.O.; Sheikh-Jabbari, M.M.; Thakur, S. Is local H 0 at odds with dark energy EFT? JCAP 2022, 4, 4. [Google Scholar] [CrossRef]
- Benisty, D.; Mifsud, J.; Levi Said, J.; Staicova, D. On the robustness of the constancy of the Supernova absolute magnitude: Non-parametric reconstruction & Bayesian approaches. Phys. Dark Univ. 2023, 39, 101160. [Google Scholar]
- Aboubrahim, A.; Klasen, M.; Nath, P. Analyzing the Hubble tension through hidden sector dynamics in the early universe. JCAP 2022, 4, 42. [Google Scholar] [CrossRef]
- Hoshiya, K.; Toda, Y. Electron mass variation from dark sector interactions and compatibility with cosmological observations. Phys. Rev. D 2023, 107, 43505. [Google Scholar] [CrossRef]
- Sabla, V.I.; Caldwell, R.R. Microphysics of early dark energy. Phys. Rev. D 2022, 106, 63526. [Google Scholar] [CrossRef]
- Heeck, J.; Thapa, A. Explaining lepton-flavor non-universality and self-interacting dark matter with Lμ−Lτ. Eur. Phys. J. C 2022, 82, 480. [Google Scholar] [CrossRef]
- Benevento, G.; Kable, J.A.; Addison, G.E.; Bennett, C.L. An Exploration of an Early Gravity Transition in Light of Cosmological Tensions. Astrophys. J. 2022, 935, 156. [Google Scholar] [CrossRef]
- Smith, T.L.; Lucca, M.; Poulin, V.; Abellan, G.F.; Balkenhol, L.; Benabed, K.; Galli, S.; Murgia, R. Hints of early dark energy in Planck, SPT, and ACT data: New physics or systematics? Phys. Rev. D 2022, 106, 43526. [Google Scholar] [CrossRef]
- Ye, G.; Piao, Y.S. Improved constraints on primordial gravitational waves in light of the H0 tension and BICEP/Keck data. Phys. Rev. D 2022, 106, 43536. [Google Scholar] [CrossRef]
- Mazo, B.Y.D.V.; Romano, A.E.; Quintero, M.A.C. H0 tension or M overestimation? Eur. Phys. J. C 2022, 82, 610. [Google Scholar] [CrossRef]
- Jin, S.J.; Li, T.N.; Zhang, J.F.; Zhang, X. Precisely measuring the Hubble constant and dark energy using only gravitational-wave dark sirens. arXiv 2022, arXiv:2202.11882. [Google Scholar]
- Cai, R.G.; Guo, Z.K.; Wang, S.J.; Yu, W.W.; Zhou, Y. No-go guide for late-time solutions to the Hubble tension: Matter perturbations. Phys. Rev. D 2022, 106, 63519. [Google Scholar] [CrossRef]
- Jiang, J.Q.; Piao, Y.S. Toward early dark energy and ns=1 with Planck, ACT, and SPT observations. Phys. Rev. D 2022, 105, 103514. [Google Scholar] [CrossRef]
- Mehrabi, A.; Levi Said, J. Gaussian discriminators between ΛCDM and wCDM cosmologies using expansion data. Eur. Phys. J. C 2022, 82, 806. [Google Scholar] [CrossRef]
- Ren, X.; Yan, S.F.; Zhao, Y.; Cai, Y.F.; Saridakis, E.N. Gaussian processes and effective field theory of f(T) gravity under the H0 tension. Astrophys. J. 2022, 932, 2. [Google Scholar] [CrossRef]
- Anchordoqui, L.A.; Barger, V.; Marfatia, D.; Soriano, J.F. Decay of multiple dark matter particles to dark radiation in different epochs does not alleviate the Hubble tension. Phys. Rev. D 2022, 105, 103512. [Google Scholar] [CrossRef]
- Adhikari, S. The Hubble tension in the non-flat Super-ΛCDM model. Phys. Dark Univ. 2022, 36, 101005. [Google Scholar] [CrossRef]
- Simon, T.; Franco Abellán, G.; Du, P.; Poulin, V.; Tsai, Y. Constraining decaying dark matter with BOSS data and the effective field theory of large-scale structures. Phys. Rev. D 2022, 106, 23516. [Google Scholar] [CrossRef]
- Nunes, R.C.; Vagnozzi, S.; Kumar, S.; Di Valentino, E.; Mena, O. New tests of dark sector interactions from the full-shape galaxy power spectrum. Phys. Rev. D 2022, 105, 123506. [Google Scholar] [CrossRef]
- Harko, T.; Asadi, K.; Moshafi, H.; Sheikhahmadi, H. Observational constraints on the interacting dark energy — Dark matter (IDM) cosmological models. Phys. Dark Univ. 2022, 38, 101131. [Google Scholar] [CrossRef]
- Davari, Z.; Khosravi, N. Can decaying dark matter scenarios alleviate both H0 and σ8 tensions? Mon. Not. R. Astron. Soc. 2022, 516, 4373–4382. [Google Scholar] [CrossRef]
- Qi, J.Z.; Hu, W.H.; Cui, Y.; Zhang, J.F.; Zhang, X. Cosmological Parameter Estimation Using Current and Future Observations of Strong Gravitational Lensing. Universe 2022, 8, 254. [Google Scholar] [CrossRef]
- Fondi, E.; Melchiorri, A.; Pagano, L. No evidence for EDE from Planck data in extended scenarios. Astrophys. J. Lett. 2022, 931, L18. [Google Scholar] [CrossRef]
- Hu, J.P.; Wang, F.Y. Revealing the late-time transition of H0: Relieve the Hubble crisis. Mon. Not. R. Astron. Soc. 2022, 517, 576–581. [Google Scholar] [CrossRef]
- Gómez-Valent, A. Fast test to assess the impact of marginalization in Monte Carlo analyses and its application to cosmology. Phys. Rev. D 2022, 106, 63506. [Google Scholar] [CrossRef]
- Jin, S.J.; Zhu, R.Q.; Wang, L.F.; Li, H.L.; Zhang, J.F.; Zhang, X. Impacts of gravitational-wave standard siren observations from Einstein Telescope and Cosmic Explorer on weighing neutrinos in interacting dark energy models. Commun. Theor. Phys. 2022, 74, 105404. [Google Scholar] [CrossRef]
- Archidiacono, M.; Castorina, E.; Redigolo, D.; Salvioni, E. Unveiling dark fifth forces with linear cosmology. JCAP 2022, 10, 74. [Google Scholar] [CrossRef]
- Berghaus, K.V.; Karwal, T. Thermal friction as a solution to the Hubble and large-scale structure tensions. Phys. Rev. D 2023, 107, 103515. [Google Scholar] [CrossRef]
- Yusofi, E.; Ramzanpour, M.A. Cosmological Constant Problem and H0 Tension in Void-dominated Cosmology. arXiv 2022, arXiv:2204.12180. [Google Scholar]
- Carneiro, S.; Pigozzo, C.; Alcaniz, J.S. Redshift systematics and the H0 tension problem. Eur. Phys. J. Plus 2022, 137, 537. [Google Scholar] [CrossRef]
- Ye, G.; Jiang, J.Q.; Piao, Y.S. Toward inflation with ns=1 in light of the Hubble tension and implications for primordial gravitational waves. Phys. Rev. D 2022, 106, 103528. [Google Scholar] [CrossRef]
- Kumar, S.; Nunes, R.C.; Yadav, P. Updating non-standard neutrinos properties with Planck-CMB data and full-shape analysis of BOSS and eBOSS galaxies. JCAP 2022, 9, 60. [Google Scholar] [CrossRef]
- Camarena, D.; Marra, V.; Sakr, Z.; Clarkson, C. A void in the Hubble tension? The end of the line for the Hubble bubble. Class. Quant. Grav. 2022, 39, 184001. [Google Scholar] [CrossRef]
- Alvi, S.; Brinckmann, T.; Gerbino, M.; Lattanzi, M.; Pagano, L. Do you smell something decaying? Updated linear constraints on decaying dark matter scenarios. JCAP 2022, 11, 15. [Google Scholar] [CrossRef]
- Garcia-Arroyo, G.; Cervantes-Cota, J.L.; Nucamendi, U. Neutrino mass and kinetic gravity braiding degeneracies. JCAP 2022, 8, 9. [Google Scholar] [CrossRef]
- Aljaf, M.; Elizalde, E.; Khurshudyan, M.; Myrzakulov, K.; Zhadyranova, A. Solving the H0 tension in f(T) gravity through Bayesian machine learning. Eur. Phys. J. C 2022, 82, 1130. [Google Scholar] [CrossRef]
- Schiavone, T.; Montani, G.; Dainotti, M.G.; De Simone, B.; Rinaldi, E.; Lambiase, G. Running Hubble Constant from the SNe Ia Pantheon Sample? In Proceedings of the 17th Italian-Korean Symposium on Relativistic Astrophysics, Online, 2–6 August 2022. [Google Scholar]
- Vagnozzi, S.; Roy, R.; Tsai, Y.D.; Visinelli, L.; Afrin, M.; Allahyari, A.; Bambhaniya, P.; Dey, D.; Ghosh, S.G.; Joshi, P.S.; et al. Horizon-scale tests of gravity theories and fundamental physics from the Event Horizon Telescope image of Sagittarius A. Class. Quant. Grav. 2023, 40, 165007. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Integral F(R) gravity and saddle point condition as a remedy for the H0-tension. Nucl. Phys. B 2022, 980, 115850. [Google Scholar] [CrossRef]
- Sandoval-Orozco, R.; Escamilla-Rivera, C. Cosmological piecewise functions to treat the local Hubble tension. Eur. Phys. J. Plus 2022, 137, 819. [Google Scholar] [CrossRef]
- Kojima, K.; Okubo, Y. Early dark energy from a higher-dimensional gauge theory. Phys. Rev. D 2022, 106, 63540. [Google Scholar] [CrossRef]
- Yao, Y.H.; Meng, X.H. A new coupled three-form dark energy model and implications for the H0 tension. Phys. Dark Univ. 2020, 30, 100729. [Google Scholar] [CrossRef]
- Mohseni Sadjadi, H.; Anari, V. Early dark energy and the screening mechanism. Eur. Phys. J. Plus 2023, 138, 84. [Google Scholar] [CrossRef]
- Oikonomou, V.K.; Lymperiadou, E.C. Effects of a Geometrically Realized Early Dark Energy Era on the Spectrum of Primordial Gravitational Waves. Symmetry 2022, 14, 1143. [Google Scholar] [CrossRef]
- Hernández-Jiménez, R.; Moreno, C.; Bellini, M.; Ortiz, C. Cosmological Boundary Flux Parameter. Phys. Dark Univ. 2022, 38, 101137. [Google Scholar] [CrossRef]
- Schöneberg, N.; Franco Abellán, G. A step in the right direction? Analyzing the Wess Zumino Dark Radiation solution to the Hubble tension. JCAP 2022, 12, 1. [Google Scholar] [CrossRef]
- Seto, O.; Toda, Y. Big bang nucleosynthesis constraints on varying electron mass solution to the Hubble tension. Phys. Rev. D 2023, 107, 83512. [Google Scholar] [CrossRef]
- Reeves, A.; Herold, L.; Vagnozzi, S.; Sherwin, B.D.; Ferreira, E.G.M. Restoring cosmological concordance with early dark energy and massive neutrinos? Mon. Not. R. Astron. Soc. 2023, 520, 3688–3695. [Google Scholar] [CrossRef]
- Zhai, Z.; Percival, W.J. Sample variance for supernovae distance measurements and the Hubble tension. Phys. Rev. D 2022, 106, 103527. [Google Scholar] [CrossRef]
- Joseph, M.; Aloni, D.; Schmaltz, M.; Sivarajan, E.N.; Weiner, N. A Step in Understanding the S8 Tension. arXiv 2022, arXiv:2207.03500. [Google Scholar] [CrossRef]
- Aluri, P.K.; Cea, P.; Chingangbam, P.; Chu, M.-C.; Clowes, R.G.; Hutsemekers, D.; Kochappan, J.P.; Lopez, A.M.; Liu, L.; Martens, N.C.; et al. Is the observable Universe consistent with the cosmological principle? Class. Quant. Grav. 2023, 40, 94001. [Google Scholar] [CrossRef]
- Adil, A.; Albrecht, A.; Knox, L. Quintessential cosmological tensions. Phys. Rev. D 2023, 107, 63521. [Google Scholar] [CrossRef]
- Trivedi, O. Another look on the connections of Hubble tension with the Heisenberg Uncertainty Principle. Phys. Dark Univ. 2023, 39, 101150. [Google Scholar] [CrossRef]
- Akarsu, O.; Colgain, E.O.; Özulker, E.; Thakur, S.; Yin, L. Inevitable manifestation of wiggles in the expansion of the late Universe. Phys. Rev. D 2023, 107, 123526. [Google Scholar] [CrossRef]
- Wang, D. Pantheon+ tomography and Hubble tension. arXiv 2022, arXiv:2207.10927. [Google Scholar]
- Rezaei, M.; Sola Peracaula, J. Running vacuum versus holographic dark energy: A cosmographic comparison. Eur. Phys. J. C 2022, 82, 765. [Google Scholar] [CrossRef]
- Gómez-Valent, A.; Zheng, Z.; Amendola, L.; Wetterich, C.; Pettorino, V. Coupled and uncoupled early dark energy, massive neutrinos, and the cosmological tensions. Phys. Rev. D 2022, 106, 103522. [Google Scholar] [CrossRef]
- El Bourakadi, K. Hubble tension and Reheating: Hybrid Inflation Implications. arXiv 2022, arXiv:2208.01162. [Google Scholar]
- Moshafi, H.; Firouzjahi, H.; Talebian, A. Multiple Transitions in Vacuum Dark Energy and H 0 Tension. Astrophys. J. 2022, 940, 121. [Google Scholar] [CrossRef]
- Simon, T.; Zhang, P.; Poulin, V.; Smith, T.L. Updated constraints from the effective field theory analysis of the BOSS power spectrum on early dark energy. Phys. Rev. D 2023, 107, 63505. [Google Scholar] [CrossRef]
- Buen-Abad, M.A.; Chacko, Z.; Kilic, C.; Marques-Tavares, G.; Youn, T. Stepped partially acoustic dark matter, large scale structure, and the Hubble tension. JHEP 2023, 6, 12. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Dissimilar donuts in the sky? Effects of a pressure singularity on the circular photon orbits and shadow of a cosmological black hole. EPL 2022, 139, 59003. [Google Scholar] [CrossRef]
- Rezazadeh, K.; Ashoorioon, A.; Grin, D. Cascading Dark Energy. arXiv 2022, arXiv:2208.07631. [Google Scholar]
- Perivolaropoulos, L.; Skara, F. A Reanalysis of the Latest SH0ES Data for H0: Effects of New Degrees of Freedom on the Hubble Tension. Universe 2022, 8, 502. [Google Scholar] [CrossRef]
- Escudero, H.G.; Kuo, J.L.; Keeley, R.E.; Abazajian, K.N. Early or phantom dark energy, self-interacting, extra, or massive neutrinos, primordial magnetic fields, or a curved universe: An exploration of possible solutions to the H0 and σ8 problems. Phys. Rev. D 2022, 106, 103517. [Google Scholar] [CrossRef]
- Banerjee, S.; Petronikolou, M.; Saridakis, E.N. Alleviating the H0 tension with new gravitational scalar tensor theories. Phys. Rev. D 2023, 108, 24012. [Google Scholar] [CrossRef]
- Cruz, J.S.; Niedermann, F.; Sloth, M.S. A grounded perspective on new early dark energy using ACT, SPT, and BICEP/Keck. JCAP 2023, 2, 41. [Google Scholar] [CrossRef]
- Oikonomou, V.K.; Tsyba, P.; Razina, O. Probing Our Universe’s Past Using Earth’s Geological and Climatological History and Shadows of Galactic Black Holes. Universe 2022, 8, 484. [Google Scholar] [CrossRef]
- Naidoo, K.; Jaber, M.; Hellwing, W.A.; Bilicki, M. A dark matter solution to the H0 and σ8 tensions, and the integrated Sachs-Wolfe void anomaly. arXiv 2022, arXiv:2209.08102. [Google Scholar]
- Wang, H.; Piao, Y.S. A fraction of dark matter faded with early dark energy? arXiv 2022, arXiv:2209.09685. [Google Scholar]
- Kumar, S.; Nunes, R.C.; Yadav, P. New cosmological constraints on f(T) gravity in light of full Planck-CMB and type Ia supernovae data. Phys. Rev. D 2023, 107, 63529. [Google Scholar] [CrossRef]
- de Sá, R.; Benetti, M.; Graef, L.L. An empirical investigation into cosmological tensions. Eur. Phys. J. Plus 2022, 137, 1129. [Google Scholar] [CrossRef]
- Di Valentino, E.; Giarè, W.; Melchiorri, A.; Silk, J. Health checkup test of the standard cosmological model in view of recent cosmic microwave background anisotropies experiments. Phys. Rev. D 2022, 106, 103506. [Google Scholar] [CrossRef]
- Secco, L.F.; Karwal, T.; Hu, W.; Krause, E. Role of the Hubble scale in the weak lensing versus CMB tension. Phys. Rev. D 2023, 107, 83532. [Google Scholar] [CrossRef]
- Schöneberg, N.; Verde, L.; Gil-Marín, H.; Brieden, S. BAO+BBN revisited—Growing the Hubble tension with a 0.7 km/s/Mpc constraint. JCAP 2022, 11, 39. [Google Scholar] [CrossRef]
- Jusufi, K.; Sheykhi, A. Entropic corrections to Friedmann equations and bouncing universe due to the zero-point length. Phys. Lett. B 2023, 836, 137621. [Google Scholar] [CrossRef]
- Jiang, J.Q.; Ye, G.; Piao, Y.S. Return of Harrison-Zeldovich spectrum in light of recent cosmological tensions. arXiv 2022, arXiv:2210.06125. [Google Scholar]
- Zhou, Z.; Mu, Y.; Liu, G.; Xu, L.; Lu, J. Equality scale-based and sound horizon-based analysis of the Hubble tension. Phys. Rev. D 2023, 107, 63536. [Google Scholar] [CrossRef]
- Zhao, Z.W.; Wang, L.F.; Zhang, J.G.; Zhang, J.F.; Zhang, X. Probing the interaction between dark energy and dark matter with future fast radio burst observations. arxiv 2022, arXiv:2210.07162. [Google Scholar] [CrossRef]
- Yang, W.; Giarè, W.; Pan, S.; Di Valentino, E.; Melchiorri, A.; Silk, J. Revealing the effects of curvature on the cosmological models. Phys. Rev. D 2023, 107, 63509. [Google Scholar] [CrossRef]
- Cardona, W.; Sabogal, M.A. Holographic energy density, dark energy sound speed, and tensions in cosmological parameters: H0 and S8. JCAP 2023, 2, 45. [Google Scholar] [CrossRef]
- Herold, L.; Ferreira, E.G.M. Resolving the Hubble tension with Early Dark Energy. arXiv 2022, arXiv:2210.16296. [Google Scholar] [CrossRef]
- Holm, E.B.; Herold, L.; Hannestad, S.; Nygaard, A.; Tram, T. Decaying dark matter with profile likelihoods. Phys. Rev. D 2023, 107, L021303. [Google Scholar] [CrossRef]
- Akarsu, O.; Kumar, S.; Özülker, E.; Vazquez, J.A.; Yadav, A. Relaxing cosmological tensions with a sign switching cosmological constant: Improved results with Planck, BAO and Pantheon data. arXiv 2022, arXiv:2211.05742. [Google Scholar] [CrossRef]
- Cai, T.; Ding, Q.; Wang, Y. Reconciling cosmic dipolar tensions with a gigaparsec void. arXiv 2022, arXiv:2211.06857. [Google Scholar]
- Pan, S.; Yang, W.; Di Valentino, E.; Mota, D.F.; Silk, J. IWDM: The fate of an interacting non-cold dark matter—Vacuum scenario. arXiv 2022, arXiv:2211.11047. [Google Scholar] [CrossRef]
- Gangopadhyay, M.R.; Pacif, S.K.J.; Sami, M.; Sharma, M.K. Generic Modification of Gravity, Late Time Acceleration and Hubble Tension. Universe 2023, 9, 83. [Google Scholar] [CrossRef]
- Kuzmichev, V.E.; Kuzmichev, V.V. The Hubble tension from the standpoint of quantum cosmology. arXiv 2022, arXiv:2211.16394. [Google Scholar]
- Schiavone, T.; Montani, G.; Bombacigno, F. f(R) gravity in the Jordan frame as a paradigm for the Hubble tension. Mon. Not. R. Astron. Soc. 2023, 522, L72–L77. [Google Scholar] [CrossRef]
- Bernardo, R.C.; Lee, Y.R. Hubble constant by natural selection: Evolution chips in the Hubble tension. arXiv 2022, arXiv:2212.02203. [Google Scholar] [CrossRef]
- Bansal, S.; Barron, J.; Curtin, D.; Tsai, Y. Precision Cosmological Constraints on Atomic Dark Matter. arXiv 2022, arXiv:2212.02487. [Google Scholar]
- Lee, N.; Ali-Haïmoud, Y.; Schöneberg, N.; Poulin, V. What It Takes to Solve the Hubble Tension through Modifications of Cosmological Recombination. Phys. Rev. Lett. 2023, 130, 161003. [Google Scholar] [CrossRef] [PubMed]
- Di Valentino, E.; Nilsson, N.A.; Park, M.I. A new test of dynamical dark energy models and cosmic tensions in Hořava gravity. Mon. Not. R. Astron. Soc. 2023, 519, 5043–5058. [Google Scholar] [CrossRef]
- Lin, M.X.; McDonough, E.; Hill, J.C.; Hu, W. Dark matter trigger for early dark energy coincidence. Phys. Rev. D 2023, 107, 103523. [Google Scholar] [CrossRef]
- Haridasu, B.S.; Khoraminezhad, H.; Viel, M. Scrutinizing Early Dark Energy models through CMB lensing. arXiv 2022, arXiv:2212.09136. [Google Scholar]
- Brinckmann, T.; Chang, J.H.; Du, P.; LoVerde, M. Confronting interacting dark radiation scenarios with cosmological data. Phys. Rev. D 2023, 107, 123517. [Google Scholar] [CrossRef]
- Gao, L.Y.; Xue, S.S.; Zhang, X. Dark energy and matter interacting scenario can relieve H0 and S8 tensions. arXiv 2022, arXiv:2212.13146. [Google Scholar]
- de Jesus, A.S.; Pinto-Neto, N.; Queiroz, F.S.; Silk, J.; da Silva, D.R. The hubble rate trouble: An effective field theory of dark matter. Eur. Phys. J. C 2023, 83, 203. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. On the homogeneity of SnIa absolute magnitude in the Pantheon+ sample. Mon. Not. R. Astron. Soc. 2023, 520, 5110–5125. [Google Scholar] [CrossRef]
- Bouchè, F.; Capozziello, S.; Salzano, V. Addressing Cosmological Tensions by Non-Local Gravity. Universe 2023, 9, 27. [Google Scholar] [CrossRef]
- Brissenden, L.; Dimopoulos, K.; Sánchez López, S. Non-oscillating Early Dark Energy and Quintessence from Alpha-Attractors. arXiv 2023, arXiv:2301.03572. [Google Scholar]
- Dahmani, S.; Bouali, A.; Bojaddaini, I.E.; Errahmani, A.; Ouali, T. Smoothing the H0 tension with a dynamical dark energy model. arXiv 2023, arXiv:2301.04200. [Google Scholar] [CrossRef]
- Khodadi, M.; Schreck, M. Hubble tension as a guide for refining the early Universe: Cosmologies with explicit local Lorentz and diffeomorphism violation. Phys. Dark Univ. 2023, 39, 101170. [Google Scholar] [CrossRef]
- Bernui, A.; Di Valentino, E.; Giarè, W.; Kumar, S.; Nunes, R.C. Exploring the H0 tension and the evidence for dark sector interactions from 2D BAO measurements. Phys. Rev. D 2023, 107, 103531. [Google Scholar] [CrossRef]
- Thakur, R.K.; Gupta, S.; Nigam, R.; Thiruvikraman, P. Investigating the Hubble Tension Through Hubble Parameter Data. Res. Astron. Astrophys. 2023, 23, 65017. [Google Scholar] [CrossRef]
- Mandal, S.; Sokoliuk, O.; Mishra, S.S.; Sahoo, P.K. H0 tension in torsion-based modified gravity. Nucl. Phys. B 2023, 993, 116285. [Google Scholar] [CrossRef]
- Jin, S.J.; Xing, S.S.; Shao, Y.; Zhang, J.F.; Zhang, X. Joint constraints on cosmological parameters using future multi-band gravitational wave standard siren observations*. Chin. Phys. C 2023, 47, 65104. [Google Scholar] [CrossRef]
- Kumar, S.; Nunes, R.C.; Pan, S.; Yadav, P. New late-time constraints on f(R) gravity. Phys. Dark Univ. 2023, 42, 101281. [Google Scholar] [CrossRef]
- Tiwari, Y.; Ghosh, B.; Jain, R.K. Horndeski Helping Hubble: Towards a possible solution to the Hubble tension with Horndeski gravity. arXiv 2023, arXiv:2301.09382. [Google Scholar]
- Dainotti, M.; De Simone, B.; Montani, G.; Schiavone, T.; Lambiase, G. The Hubble constant tension: Current status and future perspectives through new cosmological probes. In Proceedings of the CORFU2022: 22th Hellenic School and Workshops on Elementary Particle Physics and Gravity, Corfu, Greece, 28 August–1 October 2022. [Google Scholar]
- Bassi, A.; Adil, S.A.; Rajvanshi, M.P.; Sen, A.A. Cosmological evolution in bimetric gravity: Observational constraints and LSS signatures. Eur. Phys. J. C 2023, 83, 525. [Google Scholar] [CrossRef]
- Ben-Dayan, I.; Kumar, U. Emergent Unparticles Dark Energy can restore cosmological concordance. arXiv 2023, arXiv:2302.00067. [Google Scholar]
- de Cruz Perez, J.; Sola Peracaula, J.; Singh, C.P. Running vacuum in Brans-Dicke theory: A possible cure for the σ8 and H0 tensions. arXiv 2023, arXiv:2302.04807. [Google Scholar]
- Ballardini, M.; Ferrari, A.G.; Finelli, F. Phantom scalar-tensor models and cosmological tensions. JCAP 2023, 4, 29. [Google Scholar] [CrossRef]
- Giani, L.; Piattella, O.F. Induced non-local cosmology. Phys. Dark Univ. 2023, 40, 101219. [Google Scholar] [CrossRef]
- Rebouças, J.A.; Gordon, J.; de Souza, D.H.F.; Zhong, K.; Miranda, V.; Rosenfeld, R.; Eifler, T.; Krause, E. Early dark energy constraints with late-time expansion marginalization. arXiv 2023, arXiv:2302.07333. [Google Scholar]
- Cruz, J.S.; Hannestad, S.; Holm, E.B.; Niedermann, F.; Sloth, M.S.; Tram, T. Profiling Cold New Early Dark Energy. arXiv 2023, arXiv:2302.07934. [Google Scholar] [CrossRef]
- Carrillo González, M.; Liang, Q.; Sakstein, J.; Trodden, M. Neutrino-Assisted Early Dark Energy is a Natural Resolution of the Hubble Tension. arXiv 2023, arXiv:2302.09091. [Google Scholar]
- Goldstein, S.; Hill, J.C.; Iršič, V.; Sherwin, B.D. Canonical Hubble-Tension-Resolving Early Dark Energy Cosmologies are Inconsistent with the Lyman-α Forest. arXiv 2023, arXiv:2303.00746. [Google Scholar]
- Yao, Y.H.; Wang, J.C.; Meng, X.H. Observational constraints on non-cold dark matter and phenomenological emergent dark energy. arXiv 2023, arXiv:2303.00961. [Google Scholar]
- Borges, H.A.; Pigozzo, C.; Hepp, P.; Baraúna, L.O.; Benetti, M. Testing the growth rate in homogeneous and inhomogeneous interacting vacuum models. JCAP 2023, 6, 9. [Google Scholar] [CrossRef]
- Das, A.; Ghosh, S. The magnificent ACT of flavor-specific neutrino self-interaction. arXiv 2023, arXiv:2303.08843. [Google Scholar]
- Staicova, D. Model selection results from different BAO datasets—DE models and ΩKCDM. arXiv 2023, arXiv:2303.11271. [Google Scholar]
- Jiang, J.Q.; Ye, G.; Piao, Y.S. Impact of the Hubble tension on the r-ns contour. arXiv 2023, arXiv:2303.12345. [Google Scholar]
- Högås, M.; Mörtsell, E. Impact of symmetron screening on the Hubble tension: New constraints using cosmic distance ladder data. Phys. Rev. D 2023, 108, 24007. [Google Scholar] [CrossRef]
- Jusufi, K.; Sheykhi, A.; Capozziello, S. Apparent dark matter as a non-local manifestation of emergent gravity. Phys. Dark Univ. 2023, 42, 101270. [Google Scholar] [CrossRef]
- Hill, J.C.; Bolliet, B. Did the Universe Reheat After Recombination? arXiv 2023, arXiv:2304.03750. [Google Scholar]
- Nojiri, S.; Odintsov, S.D.; Sáez-Chillón Gómez, D. Unifying inflation with early and late dark energy in Einstein–Gauss–Bonnet gravity. Phys. Dark Univ. 2023, 41, 101238. [Google Scholar] [CrossRef]
- Sola Peracaula, J.; Gomez-Valent, A.; de Cruz Perez, J.; Moreno-Pulido, C. Running Vacuum in the Universe: Phenomenological Status in Light of the Latest Observations, and Its Impact on the σ8 and H0 Tensions. Universe 2023, 9, 262. [Google Scholar] [CrossRef]
- Sakr, Z. Extensions to ΛCDM at Intermediate Redshifts to Solve the Tensions? In Proceedings of the CORFU2022: 22th Hellenic School and Workshops on Elementary Particle Physics and Gravity, Corfu, Greece, 28 August–1 October 2022. [Google Scholar]
- Sakr, Z. One matter density discrepancy to alleviate them all or further trouble for ΛCDM model. arXiv 2023, arXiv:2305.02846. [Google Scholar]
- Cruz, J.S.; Niedermann, F.; Sloth, M.S. Cold New Early Dark Energy pulls the trigger on the H0 and S8 tensions: A simultaneous solution to both tensions without new ingredients. arXiv 2023, arXiv:2305.08895. [Google Scholar]
- Perivolaropoulos, L. On the isotropy of SnIa absolute magnitudes in the Pantheon+ and SH0ES samples. arXiv 2023, arXiv:2305.12819. [Google Scholar]
- Allali, I.J.; Rompineve, F.; Hertzberg, M.P. Dark Sectors with Mass Thresholds Face Cosmological Datasets. arXiv 2023, arXiv:2305.14166. [Google Scholar] [CrossRef]
- Dialektopoulos, K.F.; Mukherjee, P.; Levi Said, J.; Mifsud, J. Neural network reconstruction of scalar-tensor cosmology. arXiv 2023, arXiv:2305.15500. [Google Scholar]
- Dialektopoulos, K.F.; Mukherjee, P.; Levi Said, J.; Mifsud, J. Neural network reconstruction of cosmology using the Pantheon Compilation. arXiv 2023, arXiv:2305.15499. [Google Scholar]
- Gómez-Valent, A.; Mavromatos, N.E.; Solà Peracaula, J. Stringy Running Vacuum Model and current Tensions in Cosmology. arXiv 2023, arXiv:2305.15774. [Google Scholar]
- Bisnovatyi-Kogan, G.S.; Nikishin, A.M. Eliminating the Hubble Tension in the Presence of the Interconnection between Dark Energy and Matter in the Modern Universe. Astron. Rep. 2023, 67, 115–124. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K.; Sharov, G.S. Early dark energy with power-law F(R) gravity. Phys. Lett. B 2023, 843, 137988. [Google Scholar] [CrossRef]
- Ye, G.; Jiang, J.Q.; Piao, Y.S. Shape of CMB lensing in the early dark energy cosmology. arXiv 2023, arXiv:2305.18873. [Google Scholar]
- Jin, S.J.; Zhang, Y.Z.; Song, J.Y.; Zhang, J.F.; Zhang, X. The Taiji-TianQin-LISA network: Precisely measuring the Hubble constant using both bright and dark sirens. arXiv 2023, arXiv:2305.19714. [Google Scholar]
- Takahashi, T.; Toda, Y. Impact of big bang nucleosynthesis on the H0 tension. arXiv 2023, arXiv:2306.00454. [Google Scholar]
- Li, Y.H.; Zhang, X. IDECAMB: An implementation of interacting dark energy cosmology in CAMB. arXiv 2023, arXiv:2306.01593. [Google Scholar]
- Buen-Abad, M.A.; Chacko, Z.; Kilic, C.; Marques-Tavares, G.; Youn, T. Stepped Partially Acoustic Dark Matter: Likelihood Analysis and Cosmological Tensions. arXiv 2023, arXiv:2306.01844. [Google Scholar]
- Flores, M.M.; Kouvaris, C.; Kusenko, A. Defrosting and Blast Freezing Dark Matter. arXiv 2023, arXiv:2306.04056. [Google Scholar]
- Ruchika; Rathore, H.; Roy Choudhury, S.; Rentala, V. A gravitational constant transition within cepheids as supernovae calibrators can solve the Hubble tension. arXiv 2023, arXiv:2306.05450. [Google Scholar]
- Greene, K.; Cyr-Racine, F.Y. Thomson scattering: One rate to rule them all. arXiv 2023, arXiv:2306.06165. [Google Scholar]
- Adil, S.A.; Akarsu, O.; Di Valentino, E.; Nunes, R.C.; Ozulker, E.; Sen, A.A.; Specogna, E. Omnipotent dark energy: A phenomenological answer to the Hubble tension. arXiv 2023, arXiv:2306.08046. [Google Scholar]
- Montani, G.; De Angelis, M.; Bombacigno, F.; Carlevaro, N. Metric f(R) gravity with dynamical dark energy as a paradigm for the Hubble Tension. arXiv 2023, arXiv:2306.11101. [Google Scholar]
- Schöneberg, N.; Franco Abellán, G.; Simon, T.; Bartlett, A.; Patel, Y.; Smith, T.L. The weak, the strong and the ugly—A comparative analysis of interacting stepped dark radiation. arXiv 2023, arXiv:2306.12469. [Google Scholar]
- Farhang, M.; Khosravi, N. Reconstruction of A Scale-Dependent Gravitational Phase Transition. arXiv 2023, arXiv:2306.14014. [Google Scholar]
- Escamilla-Rivera, C.; de Albornoz-Caratozzolo, J.M.; Nájera, S. Fab-Four cosmography to tackle the Hubble tension. arXiv 2023, arXiv:2306.14855. [Google Scholar] [CrossRef]
- Yadav, V. Measuring Hubble constant in an anisotropic extension of ΛCDM model. arXiv 2023, arXiv:2306.16135. [Google Scholar]
- Lombriser, L. Cosmology in Minkowski space. Class. Quant. Grav. 2023, 40, 155005. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C.; Wang, Z.; Cui, M.; Tsai, Y.L.S.; Yuan, Q.; Fan, Y.Z. Primordial magnetic field as a common solution of nanohertz gravitational waves and Hubble tension. arXiv 2023, arXiv:2306.17124. [Google Scholar]
- Singh, N.K.; Kashyap, G. Unimodular Theory of Gravity in Light of the Latest Cosmological Data. arXiv 2023, arXiv:2306.17754. [Google Scholar]
- Nygaard, A.; Holm, E.B.; Tram, T.; Hannestad, S. Decaying Dark Matter and the Hubble Tension. arXiv 2023, arXiv:2307.00418. [Google Scholar]
- Sarkar, A.; Ghosh, B. Early Dark Energy Motivated Quintessential α-Attractor Inflaton Potential. arXiv 2023, arXiv:2307.00603. [Google Scholar]
- Sengupta, R.; Paul, P.; Paul, B.C.; Kalam, M. Can extended Chaplygin gas source a Hubble tension resolved emergent universe? arXiv 2023, arXiv:2307.02602. [Google Scholar]
- Ferrari, A.G.; Ballardini, M.; Finelli, F.; Paoletti, D.; Mauri, N. Cosmological effects of the Galileon term in Scalar-Tensor Theories. arXiv 2023, arXiv:2307.02987. [Google Scholar]
- Patil, T.; Ruchika; Panda, S. Coupled Quintessence scalar field model in light of observational datasets. arXiv 2023, arXiv:2307.03740. [Google Scholar]
- Benaoum, H.B.; García, L.A.; Castañeda, L. Early dark energy induced by non-linear electrodynamics. arXiv 2023, arXiv:2307.05917. [Google Scholar]
- Frion, E.; Camarena, D.; Giani, L.; Miranda, T.; Bertacca, D.; Marra, V.; Piattella, O.F. Bayesian analysis of Unified Dark Matter models with fast transition: Can they alleviate the H0 tension? arXiv 2023, arXiv:2307.06320. [Google Scholar]
- Brax, P.; Ouazzani, A. Two-field Screening and its Cosmological Dynamics. arXiv 2023, arXiv:2307.06781. [Google Scholar]
- Liu, G.; Zhou, Z.; Mu, Y.; Xu, L. Alleviating Cosmological Tensions with a Coupled Scalar Fields Model. arXiv 2023, arXiv:2307.07228. [Google Scholar]
- D’Agostino, R.; Nunes, R.C. Cosmographic view on the H0 and σ8 tensions. Phys. Rev. D 2023, 108, 23523. [Google Scholar] [CrossRef]
- Lu, Z.; Imtiaz, B.; Zhang, D.; Cai, Y.F. Testing the coupling of dark radiations in light of the Hubble tension. arXiv 2023, arXiv:2307.09863. [Google Scholar]
- Akarsu, O.; Di Valentino, E.; Kumar, S.; Nunes, R.C.; Vazquez, J.A.; Yadav, A. ΛsCDM model: A promising scenario for alleviation of cosmological tensions. arXiv 2023, arXiv:2307.10899. [Google Scholar]
- Bousder, M.; Riadsolh, A.; Fatimy, A.E.; Belkacemi, M.E.; Ez-Zahraouy, H. Implications of the NANOGrav results for primordial black holes and Hubble tension. arXiv 2023, arXiv:2307.10940. [Google Scholar]
- Kable, J.A.; Benevento, G.; Addison, G.E.; Bennett, C.L. Cosmological Tensions and the Transitional Planck Mass Model. arXiv 2023, arXiv:2307.12174. [Google Scholar]
- Adil, S.A.; Mukhopadhyay, U.; Sen, A.A.; Vagnozzi, S. Dark energy in light of the early JWST observations: Case for a negative cosmological constant? arXiv 2023, arXiv:2307.12763. [Google Scholar]
- Das, S.; Nasiri, A.; Yazdi, Y.K. Aspects of Everpresent Λ (II): Cosmological Tests of Current Models. arXiv 2023, arXiv:2307.13743. [Google Scholar]
- Kalita, S.; Rabha, C. Possible combinations of early and late time cosmologies through BAO scales. Eur. Phys. J. C 2023, 83, 671. [Google Scholar] [CrossRef]
- Peng, Z.Y.; Piao, Y.S. Testing the ns—H0 scaling relation with Planck-independent CMB data. arXiv 2023, arXiv:2308.01012. [Google Scholar]
- Basilakos, S.; Lymperis, A.; Petronikolou, M.; Saridakis, E.N. Alleviating both H0 and σ8 tensions in Tsallis cosmology. arXiv 2023, arXiv:2308.01200. [Google Scholar]
- Banerjee, T.; Mandal, G.; Biswas, A.; Biswas, S.K. Gravitationally induced matter creation and cosmological consequences. arXiv 2023, arXiv:2308.00804. [Google Scholar]
- M, N.K.; Nelleri, S.; Poonthottathil, N. Testing the dynamical stability and validity of generalized second law within the phantom dynamical dark energy model. arXiv 2023, arXiv:2308.03084. [Google Scholar]
- Santana, Z.C.; Holanda, R.F.L.; Silva, R. Non-Parametric Analysis for the Dark Matter Density Evolution. arXiv 2023, arXiv:2308.05165. [Google Scholar]
- Wei, J.J.; Melia, F. Investigating Cosmological Models and the Hubble Tension using Localized Fast Radio Bursts. arXiv 2023, arXiv:2308.05918. [Google Scholar]
- Hoerning, G.A.; Landim, R.G.; Ponte, L.O.; Rolim, R.P.; Abdalla, F.B.; Abdalla, E. Constraints on interacting dark energy revisited: Alleviating the Hubble tension. arXiv 2023, arXiv:2308.05807. [Google Scholar]
- Harada, J. Dark energy in conformal Killing gravity. arXiv 2023, arXiv:2308.07634. [Google Scholar]
- Bernal, J.L.; Verde, L.; Riess, A.G. The trouble with H0. JCAP 2016, 10, 19. [Google Scholar] [CrossRef]
- Addison, G.E.; Watts, D.J.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Weiland, J.L. Elucidating ΛCDM: Impact of Baryon Acoustic Oscillation Measurements on the Hubble Constant Discrepancy. Astrophys. J. 2018, 853, 119. [Google Scholar] [CrossRef]
- Lemos, P.; Lee, E.; Efstathiou, G.; Gratton, S. Model independent H(z) reconstruction using the cosmic inverse distance ladder. Mon. Not. R. Astron. Soc. 2019, 483, 4803–4810. [Google Scholar] [CrossRef]
- Aylor, K.; Joy, M.; Knox, L.; Millea, M.; Raghunathan, S.; Wu, W.L.K. Sounds Discordant: Classical Distance Ladder & ΛCDM -based Determinations of the Cosmological Sound Horizon. Astrophys. J. 2019, 874, 4. [Google Scholar]
- Schöneberg, N.; Lesgourgues, J.; Hooper, D.C. The BAO+BBN take on the Hubble tension. JCAP 2019, 10, 29. [Google Scholar] [CrossRef]
- Knox, L.; Millea, M. Hubble constant hunter’s guide. Phys. Rev. D 2020, 101, 43533. [Google Scholar] [CrossRef]
- Arendse, N.; Wojtak, R.J.; Agnello, A.; Chen, G.C.F.; Fassnacht, C.D.; Sluse, D.; Hilbert, S.; Millon, M.; Bonvin, V.; Wong, K.C.; et al. Cosmic dissonance: Are new physics or systematics behind a short sound horizon? Astron. Astrophys. 2020, 639, A57. [Google Scholar] [CrossRef]
- Efstathiou, G. To H0 or not to H0? Mon. Not. R. Astron. Soc. 2021, 505, 3866–3872. [Google Scholar] [CrossRef]
- Cai, R.G.; Guo, Z.K.; Wang, S.J.; Yu, W.W.; Zhou, Y. No-go guide for the Hubble tension: Late-time solutions. Phys. Rev. D 2022, 105, L021301. [Google Scholar] [CrossRef]
- Keeley, R.E.; Shafieloo, A. Ruling Out New Physics at Low Redshift as a solution to the H0 Tension. arXiv 2022, arXiv:2206.08440. [Google Scholar]
- Di Valentino, E.; Bridle, S. Exploring the Tension between Current Cosmic Microwave Background and Cosmic Shear Data. Symmetry 2018, 10, 585. [Google Scholar] [CrossRef]
- Di Valentino, E.; Anchordoqui, L.A.; Akarsu, O.; Ali-Haimoud, Y.; Amendola, L.; Arendse, N.; Asgari, M.; Ballardini, M.; Basilakos, S.; Battistelli, E.; et al. Cosmology Intertwined III: fσ8 and S8. Astropart. Phys. 2021, 131, 102604. [Google Scholar] [CrossRef]
- Nunes, R.C.; Vagnozzi, S. Arbitrating the S8 discrepancy with growth rate measurements from redshift-space distortions. Mon. Not. R. Astron. Soc. 2021, 505, 5427–5437. [Google Scholar] [CrossRef]
- Huterer, D. Growth of cosmic structure. Astron. Astrophys. Rev. 2023, 31, 2. [Google Scholar] [CrossRef]
- Sakr, Z. Untying the Growth Index to Relieve the σ8 Discomfort. Universe 2023, 9, 366. [Google Scholar] [CrossRef]
- Jaffe, A.H. H0 and odds on cosmology. Astrophys. J. 1996, 471, 24. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Steinhardt, P.J. The Observational case for a low density universe with a nonzero cosmological constant. Nature 1995, 377, 600–602. [Google Scholar] [CrossRef]
- Dunlop, J.; Peacock, J.; Spinrad, H.; Dey, A.; Jimenez, R.; Stern, D.; Windhorst, R. A 3.5-Gyr-old galaxy at redshift 1.55. Nature 1996, 381, 581. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Pacucci, F.; Loeb, A. Implications for the Hubble tension from the ages of the oldest astrophysical objects. JHEAp 2022, 36, 27–35. [Google Scholar] [CrossRef]
- Pacucci, F.; Baldassare, V.; Cappelluti, N.; Fan, X.H.; Ferrara, A.; Haiman, Z.; Natarajan, P.; Ozel, F.; Schneider, R.; Tremblay, G.R.; et al. Detecting the Birth of Supermassive Black Holes Formed from Heavy Seeds. Bull. Am. Astron. Soc. 2019, 51, 117. [Google Scholar]
- Valcin, D.; Jimenez, R.; Verde, L.; Bernal, J.L.; Wandelt, B.D. The age of the Universe with globular clusters: Reducing systematic uncertainties. JCAP 2021, 8, 17. [Google Scholar] [CrossRef]
- Borghi, N.; Moresco, M.; Cimatti, A.; Huchet, A.; Quai, S.; Pozzetti, L. Toward a Better Understanding of Cosmic Chronometers: Stellar Population Properties of Passive Galaxies at Intermediate Redshift. Astrophys. J. 2022, 927, 164. [Google Scholar] [CrossRef]
- Borghi, N.; Moresco, M.; Cimatti, A. Toward a Better Understanding of Cosmic Chronometers: A New Measurement of H(z) at z ∼ 0.7. Astrophys. J. Lett. 2022, 928, L4. [Google Scholar] [CrossRef]
- Pacucci, F.; Loeb, A. The search for the farthest quasar: Consequences for black hole growth and seed models. Mon. Not. R. Astron. Soc. 2021, 509, 1885–1891. [Google Scholar] [CrossRef]
- Pacucci, F.; Natarajan, P.; Volonteri, M.; Cappelluti, N.; Urry, C.M. Conditions for Optimal Growth of Black Hole Seeds. Astrophys. J. Lett. 2017, 850, L42. [Google Scholar] [CrossRef]
- Jimenez, R.; Cimatti, A.; Verde, L.; Moresco, M.; Wandelt, B. The local and distant Universe: Stellar ages and H0. JCAP 2019, 3, 43. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Loeb, A.; Moresco, M. Eppur è piatto? The Cosmic Chronometers Take on Spatial Curvature and Cosmic Concordance. Astrophys. J. 2021, 908, 84. [Google Scholar] [CrossRef]
- Valcin, D.; Bernal, J.L.; Jimenez, R.; Verde, L.; Wandelt, B.D. Inferring the Age of the Universe with Globular Clusters. JCAP 2020, 12, 2. [Google Scholar] [CrossRef]
- Wei, J.J.; Melia, F. Exploring the Hubble Tension and Spatial Curvature from the Ages of Old Astrophysical Objects. Astrophys. J. 2022, 928, 165. [Google Scholar] [CrossRef]
- Costa, A.A.; Ren, Z.; Yin, Z. A bias using the ages of the oldest astrophysical objects to address the Hubble tension. arXiv 2023, arXiv:2306.01234. [Google Scholar]
- Bernal, J.L.; Verde, L.; Jimenez, R.; Kamionkowski, M.; Valcin, D.; Wandelt, B.D. The trouble beyond H0 and the new cosmic triangles. Phys. Rev. D 2021, 103, 103533. [Google Scholar] [CrossRef]
- Moresco, M.; Amati, L.; Amendola, L.; Birrer, S.; Blakeslee, J.P.; Cantiello, M.; Cimatti, A.; Darling, J.; Della Valle, M.; Fishbach, M.; et al. Unveiling the Universe with emerging cosmological probes. Living Rev. Rel. 2022, 25, 6. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Weisz, D.R. Uncertain times: The redshift–time relation from cosmology and stars. Mon. Not. R. Astron. Soc. 2021, 505, 2764–2783. [Google Scholar] [CrossRef]
- Cimatti, A.; Moresco, M. Revisiting oldest stars as cosmological probes: New constraints on the Hubble constant. arXiv 2023, arXiv:2302.07899. [Google Scholar] [CrossRef]
- Jimenez, R.; Moresco, M.; Verde, L.; Wandelt, B.D. Cosmic Chronometers with Photometry: A new path to H(z). arXiv 2023, arXiv:2306.11425. [Google Scholar]
- Capozziello, S.; Sarracino, G.; Spallicci, A.D.A.M. Questioning the H0 tension via the look-back time. Phys. Dark Univ. 2023, 40, 101201. [Google Scholar] [CrossRef]
- Jedamzik, K.; Pogosian, L.; Zhao, G.B. Why reducing the cosmic sound horizon alone can not fully resolve the Hubble tension. Commun. in Phys. 2021, 4, 123. [Google Scholar] [CrossRef]
- Jimenez, R.; Loeb, A. Constraining cosmological parameters based on relative galaxy ages. Astrophys. J. 2002, 573, 37–42. [Google Scholar] [CrossRef]
- Thomas, D.; Maraston, C.; Schawinski, K.; Sarzi, M.; Silk, J. Environment and self-regulation in galaxy formation. Mon. Not. R. Astron. Soc. 2010, 404, 1775. [Google Scholar] [CrossRef]
- Yu, H.; Ratra, B.; Wang, F.Y. Hubble Parameter and Baryon Acoustic Oscillation Measurement Constraints on the Hubble Constant, the Deviation from the Spatially Flat ΛCDM Model, the Deceleration–Acceleration Transition Redshift, and Spatial Curvature. Astrophys. J. 2018, 856, 3. [Google Scholar] [CrossRef]
- Gómez-Valent, A.; Amendola, L. H0 from cosmic chronometers and Type Ia supernovae, with Gaussian Processes and the novel Weighted Polynomial Regression method. JCAP 2018, 4, 51. [Google Scholar] [CrossRef]
- Moresco, M.; Jimenez, R.; Verde, L.; Pozzetti, L.; Cimatti, A.; Citro, A. Setting the Stage for Cosmic Chronometers. I. Assessing the Impact of Young Stellar Populations on Hubble Parameter Measurements. Astrophys. J. 2018, 868, 84. [Google Scholar] [CrossRef]
- Moresco, M.; Jimenez, R.; Verde, L.; Cimatti, A.; Pozzetti, L. Setting the Stage for Cosmic Chronometers. II. Impact of Stellar Population Synthesis Models Systematics and Full Covariance Matrix. Astrophys. J. 2020, 898, 82. [Google Scholar] [CrossRef]
- Simon, J.; Verde, L.; Jimenez, R. Constraints on the redshift dependence of the dark energy potential. Phys. Rev. D 2005, 71, 123001. [Google Scholar] [CrossRef]
- Kjerrgren, A.A.; Mortsell, E. On the use of galaxies as clocks and the universal expansion. Mon. Not. R. Astron. Soc. 2022, 518, 585–591. [Google Scholar]
- Krishnan, C.; Colgáin, E.O.; Sheikh-Jabbari, M.M.; Yang, T. Running Hubble Tension and a H0 Diagnostic. Phys. Rev. D 2021, 103, 103509. [Google Scholar] [CrossRef]
- Birrer, S.; Amara, A.; Refregier, A. The mass-sheet degeneracy and time-delay cosmography: Analysis of the strong lens RXJ1131-1231. JCAP 2016, 8, 20. [Google Scholar] [CrossRef]
- Kochanek, C.S. Overconstrained gravitational lens models and the Hubble constant. Mon. Not. R. Astron. Soc. 2020, 493, 1725–1735. [Google Scholar] [CrossRef]
- Blum, K.; Castorina, E.; Simonović, M. Could Quasar Lensing Time Delays Hint to a Core Component in Halos, Instead of H0 Tension? Astrophys. J. Lett. 2020, 892, L27. [Google Scholar] [CrossRef]
- Birrer, S.; Shajib, A.J.; Galan, A.; Millon, M.; Treu, T.; Agnello, A.; Auger, M.; Chen, G.C.F.; Christensen, L.; Collett, T.; et al. TDCOSMO—IV. Hierarchical time-delay cosmography – joint inference of the Hubble constant and galaxy density profiles. Astron. Astrophys. 2020, 643, A165. [Google Scholar] [CrossRef]
- Krishnan, C.; Colgáin, E.O.; Ruchika; Sen, A.A.; Sheikh-Jabbari, M.M.; Yang, T. Is there an early Universe solution to Hubble tension? Phys. Rev. D 2020, 102, 103525. [Google Scholar] [CrossRef]
- Reid, M.J.; Pesce, D.W.; Riess, A.G. An Improved Distance to NGC 4258 and its Implications for the Hubble Constant. Astrophys. J. Lett. 2019, 886, L27. [Google Scholar] [CrossRef]
- Pesce, D.W.; Braatz, J.A.; Reid, M.J.; Condon, J.J.; Gao, F.; Henkel, C.; Kuo, C.Y.; Lo, K.Y.; Zhao, W. The Megamaser Cosmology Project. XI. A geometric distance to CGCG 074-064. Astrophys. J. 2020, 890, 118. [Google Scholar] [CrossRef]
- Dainotti, M.G.; De Simone, B.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G. On the Hubble constant tension in the SNe Ia Pantheon sample. Astrophys. J. 2021, 912, 150. [Google Scholar] [CrossRef]
- Jia, X.D.; Hu, J.P.; Wang, F.Y. Evidence of a decreasing trend for the Hubble constant. Astron. Astrophys. 2023, 674, A45. [Google Scholar] [CrossRef]
- Huterer, D.; Cooray, A. Uncorrelated estimates of dark energy evolution. Phys. Rev. D 2005, 71, 23506. [Google Scholar] [CrossRef]
- Malekjani, M.; Conville, R.M.; Colgáin, E.O.; Pourojaghi, S.; Sheikh-Jabbari, M.M. Negative Dark Energy Density from High Redshift Pantheon+ Supernovae. arXiv 2023, arXiv:2301.12725. [Google Scholar]
- Horstmann, N.; Pietschke, Y.; Schwarz, D.J. Inference of the cosmic rest-frame from supernovae Ia. Astron. Astrophys. 2022, 668, A34. [Google Scholar] [CrossRef]
- Risaliti, G.; Lusso, E. Cosmological constraints from the Hubble diagram of quasars at high redshifts. Nat. Astron. 2019, 3, 272–277. [Google Scholar] [CrossRef]
- Lusso, E.; Risaliti, G.; Nardini, E.; Bargiacchi, G.; Benetti, M.; Bisogni, S.; Capozziello, S.; Civano, F.; Eggleston, L.; Elvis, M.; et al. Quasars as standard candles III. Validation of a new sample for cosmological studies. Astron. Astrophys. 2020, 642, A150. [Google Scholar] [CrossRef]
- Colgáin, E.O.; Sheikh-Jabbari, M.M.; Solomon, R.; Bargiacchi, G.; Capozziello, S.; Dainotti, M.G.; Stojkovic, D. Revealing intrinsic flat ΛCDM biases with standardizable candles. Phys. Rev. D 2022, 106, L041301. [Google Scholar] [CrossRef]
- Colgáin, E.O.; Sheikh-Jabbari, M.M.; Solomon, R.; Dainotti, M.G.; Stojkovic, D. Putting Flat ΛCDM In The (Redshift) Bin. arXiv 2022, arXiv:2206.11447. [Google Scholar]
- Velten, H.; Gomes, S. Is the Hubble diagram of quasars in tension with concordance cosmology? Phys. Rev. D 2020, 101, 43502. [Google Scholar] [CrossRef]
- Mehrabi, A.; Basilakos, S. Does ΛCDM really be in tension with the Hubble diagram data? Eur. Phys. J. C 2020, 80, 632. [Google Scholar] [CrossRef]
- Bargiacchi, G.; Benetti, M.; Capozziello, S.; Lusso, E.; Risaliti, G.; Signorini, M. Quasar cosmology: Dark energy evolution and spatial curvature. Mon. Not. R. Astron. Soc. 2022, 515, 1795–1806. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Bardiacchi, G.; Lenart, A.L.; Capozziello, S.; Colgain, E.O.; Solomon, R.; Stojkovic, D.; Sheikh-Jabbari, M.M. Quasar Standardization: Overcoming Selection Biases and Redshift Evolution. Astrophys. J. 2022, 931, 106. [Google Scholar] [CrossRef]
- Lenart, A.L.; Bargiacchi, G.; Dainotti, M.G.; Nagataki, S.; Capozziello, S. A Bias-free Cosmological Analysis with Quasars Alleviating H 0 Tension. Astrophys. J. Suppl. 2023, 264, 46. [Google Scholar] [CrossRef]
- Bargiacchi, G.; Dainotti, M.G.; Nagataki, S.; Capozziello, S. Gamma-Ray Bursts, Quasars, Baryonic Acoustic Oscillations, and Supernovae Ia: New statistical insights and cosmological constraints. Mon. Not. R. Astron. Soc. 2023, 521, 3909–3924. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Bargiacchi, G.; Bogdan, M.; Lenart, A.L.; Iwasaki, K.; Capozziello, S.; Zhang, B.; Fraija, N. Reducing the Uncertainty on the Hubble Constant up to 35% with an Improved Statistical Analysis: Different Best-fit Likelihoods for Type Ia Supernovae, Baryon Acoustic Oscillations, Quasars, and Gamma-Ray Bursts. Astrophys. J. 2023, 951, 63. [Google Scholar] [CrossRef]
- Wei, J.J.; Wu, X.F. Gamma-ray burst cosmology: Hubble diagram and star formation history. Int. J. Mod. Phys. D 2016, 26, 1730002. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Nielson, V.; Sarracino, G.; Rinaldi, E.; Nagataki, S.; Capozziello, S.; Gnedin, O.Y.; Bargiacchi, G. Optical and X-ray GRB Fundamental Planes as cosmological distance indicators. Mon. Not. R. Astron. Soc. 2022, 514, 1828–1856. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Sarracino, G.; Capozziello, S. Gamma-ray bursts, supernovae Ia, and baryon acoustic oscillations: A binned cosmological analysis. Publ. Astron. Soc. Jap. 2022, 74, 1095–1113. [Google Scholar] [CrossRef]
- Dainotti, M.G.; Lenart, A.L.; Chraya, A.; Sarracino, G.; Nagataki, S.; Fraija, N.; Capozziello, S.; Bogdan, M. The Gamma-ray Bursts fundamental plane correlation as a cosmological tool. Mon. Not. R. Astron. Soc. 2023, 518, 2201–2240. [Google Scholar] [CrossRef]
- Colgáin, E.O.; Sheikh-Jabbari, M.M.; Solomon, R. High redshift ΛCDM cosmology: To bin or not to bin? Phys. Dark Univ. 2023, 40, 101216. [Google Scholar] [CrossRef]
- Colgáin, E.O.; Pourojaghi, S.; Sheikh-Jabbari, M.M.; Sherwin, D. MCMC Marginalisation Bias and ΛCDM tensions. arXiv 2023, arXiv:2307.16349. [Google Scholar]
- Adil, S.A.; Akarsu, O.; Malekjani, M.; Colgáin, E.O.; Pourojaghi, S.; Sen, A.A.; Sheikh-Jabbari, M.M. S8 increases with effective redshift in ΛCDM cosmology. arXiv 2023, arXiv:2303.06928. [Google Scholar]
- Esposito, M.; Iršič, V.; Costanzi, M.; Borgani, S.; Saro, A.; Viel, M. Weighing cosmic structures with clusters of galaxies and the intergalactic medium. Mon. Not. R. Astron. Soc. 2022, 515, 857–870. [Google Scholar] [CrossRef]
- Vagnozzi, S. Consistency tests of ΛCDM from the early integrated Sachs-Wolfe effect: Implications for early-time new physics and the Hubble tension. Phys. Rev. D 2021, 104, 63524. [Google Scholar] [CrossRef]
- Calabrese, E.; Slosar, A.; Melchiorri, A.; Smoot, G.F.; Zahn, O. Cosmic Microwave Weak lensing data as a test for the dark universe. Phys. Rev. D 2008, 77, 123531. [Google Scholar] [CrossRef]
- Specogna, E.; Di Valentino, E.; Levi Said, J.; Nguyen, N.M. Exploring the Growth Index γL: Insights from Different CMB Dataset Combinations and Approaches. arXiv 2023, arXiv:2305.16865. [Google Scholar]
- Giarè, W.; Mena, O.; Di Valentino, E. On the lensing impact on cosmic relics & tensions. arXiv 2023, arXiv:2307.14204. [Google Scholar]
- Kable, J.A.; Addison, G.E.; Bennett, C.L. Deconstructing the Planck TT Power Spectrum to Constrain Deviations from ΛCDM. Astrophys. J. 2020, 905, 164. [Google Scholar] [CrossRef]
- Ruiz-Granda, M.; Vielva, P. Constraining CMB physical processes using Planck 2018 data. JCAP 2022, 11, 43. [Google Scholar] [CrossRef]
- Kamionkowski, M.; Riess, A.G. The Hubble Tension and Early Dark Energy. arXiv 2022, arXiv:2211.04492. [Google Scholar] [CrossRef]
- Poulin, V.; Smith, T.L.; Karwal, T. The Ups and Downs of Early Dark Energy solutions to the Hubble tension: A review of models, hints and constraints circa 2023. arXiv 2023, arXiv:2302.09032. [Google Scholar]
- Handley, W.; Lemos, P. Quantifying the global parameter tensions between ACT, SPT and Planck. Phys. Rev. D 2021, 103, 63529. [Google Scholar] [CrossRef]
- Giarè, W.; Renzi, F.; Mena, O.; Di Valentino, E.; Melchiorri, A. Is the Harrison-Zel’dovich spectrum coming back? ACT preference for ns ∼ 1 and its discordance with Planck. Mon. Not. R. Astron. Soc. 2023, 521, 2911–2918. [Google Scholar] [CrossRef]
- Zhai, Y.; Giarè, W.; van de Bruck, C.; Di Valentino, E.; Mena, O.; Nunes, R.C. A consistent view of interacting dark energy from multiple CMB probes. JCAP 2023, 7, 32. [Google Scholar] [CrossRef]
- Di Valentino, E.; Gariazzo, S.; Giarè, W.; Mena, O. Weighing neutrinos at the damping tail. arXiv 2023, arXiv:2305.12989. [Google Scholar]
- Giarè, W.; Pan, S.; Di Valentino, E.; Yang, W.; de Haro, J.; Melchiorri, A. Inflationary Potential as seen from Different Angles: Model Compatibility from Multiple CMB Missions. arXiv 2023, arXiv:2305.15378. [Google Scholar]
- Abazajian, K.N.; Adshead, P.; Ahmed, Z.; Allen, S.W.; Alonso, D.; Arnold, K.S.; Baccigalupi, C.; Bartlett, J.G.; Battaglia, N.; Benson, B.A.; et al. CMB-S4 Science Book, First Edition. arXiv 2016, arXiv:1610.02743. [Google Scholar]
- Ade, P.; Aguirre, J.; Ahmed, Z.; Aiola, S.; Ali, A.; Alonso, D.; Alvarez, M.A.; Arnold, K.; Ashton, P.; Austermann, J.; et al. The Simons Observatory: Science goals and forecasts. JCAP 2019, 2, 56. [Google Scholar] [CrossRef]
- Abitbol, M.H.; Adachi, S.; Ade, P.; Aguirre, J.; Ahmed, Z.; Aiola, S.; Ali, A.; Alonso, D.; Alvarez, M.A.; Arnold, K.; et al. The Simons Observatory: Astro2020 Decadal Project Whitepaper. Bull. Am. Astron. Soc. 2019, 51, 147. [Google Scholar]
- Lin, W.; Chen, X.; Mack, K.J. Early Universe Physics Insensitive and Uncalibrated Cosmic Standards: Constraints on Ωm and Implications for the Hubble Tension. Astrophys. J. 2021, 920, 159. [Google Scholar] [CrossRef]
- Lin, W.; Mack, K.J.; Hou, L. Investigating the Hubble Constant Tension—Two Numbers in the Standard Cosmological Model. Astrophys. J. Lett. 2020, 904, L22. [Google Scholar] [CrossRef]
- Smith, T.L.; Poulin, V.; Simon, T. Assessing the robustness of sound horizon-free determinations of the Hubble constant. arXiv 2022, arXiv:2208.12992. [Google Scholar]
- Baxter, E.J.; Sherwin, B.D. Determining the Hubble Constant without the Sound Horizon Scale: Measurements from CMB Lensing. Mon. Not. R. Astron. Soc. 2021, 501, 1823–1835. [Google Scholar] [CrossRef]
- Philcox, O.H.E.; Farren, G.S.; Sherwin, B.D.; Baxter, E.J.; Brout, D.J. Determining the Hubble constant without the sound horizon: A 3.6% constraint on H0 from galaxy surveys, CMB lensing, and supernovae. Phys. Rev. D 2022, 106, 63530. [Google Scholar] [CrossRef]
- Philcox, O.H.E.; Sherwin, B.D.; Farren, G.S.; Baxter, E.J. Determining the Hubble Constant without the Sound Horizon: Measurements from Galaxy Surveys. Phys. Rev. D 2021, 103, 23538. [Google Scholar] [CrossRef]
- Farren, G.S.; Philcox, O.H.E.; Sherwin, B.D. Determining the Hubble constant without the sound horizon: Perspectives with future galaxy surveys. Phys. Rev. D 2022, 105, 63503. [Google Scholar] [CrossRef]
- Ivezić, V.; Kahn, S.M.; Tyson, J.A.; Abel, B.; Acosta, E.; Allsman, R.; Alonso, D.; AlSayyad, Y.; Anderson, S.F.; Andrew, J.; et al. LSST: From Science Drivers to Reference Design and Anticipated Data Products. Astrophys. J. 2019, 873, 111. [Google Scholar] [CrossRef]
- Amendola, L.; Appleby, S.; Bacon, D.; Baker, T.; Baldi, M.; Bartolo, N.; Blanchard, A.; Bonvin, C.; Borgani, S.; Branchini, E.; et al. Cosmology and fundamental physics with the Euclid satellite. Living Rev. Rel. 2013, 16, 6. [Google Scholar] [CrossRef]
- Spergel, D.; Gehrels, N.; Baltay, C.; Bennett, D.; Breckinridge, J.; Donahue, M.; Dressler, A.; Gaudi, B.S.; Greene, T.; Guyon, O.; et al. Wide-Field InfrarRed Survey Telescope-Astrophysics Focused Telescope Assets WFIRST-AFTA 2015 Report. arXiv 2015, arXiv:1503.03757. [Google Scholar]
- Aghamousa, A.; Aguilar, J.; Ahlen, S.; Alam, S.; Allen, L.E.; Allende Prieto, C.; Annis, J.; Bailey, S.; Balland, C.; Ballester, O.; et al. The DESI Experiment Part I: Science, Targeting, and Survey Design. arXiv 2016, arXiv:1611.00036. [Google Scholar]
- Bacon, D.J.; Battye, R.A.; Bull, P.; Camera, S.; Ferreira, P.G.; Harrison, I.; Parkinson, D.; Pourtsidou, A.; Santos, M.G.; Wolz, L.; et al. Cosmology with Phase 1 of the Square Kilometre Array: Red Book 2018: Technical specifications and performance forecasts. Publ. Astron. Soc. Austral. 2020, 37, e007. [Google Scholar]
- D’Amico, G.; Senatore, L.; Zhang, P. Limits on wCDM from the EFTofLSS with the PyBird code. JCAP 2021, 1, 6. [Google Scholar] [CrossRef]
- Chudaykin, A.; Dolgikh, K.; Ivanov, M.M. Constraints on the curvature of the Universe and dynamical dark energy from the Full-shape and BAO data. Phys. Rev. D 2021, 103, 23507. [Google Scholar] [CrossRef]
- Brieden, S.; Gil-Marín, H.; Verde, L. Model-agnostic interpretation of 10 billion years of cosmic evolution traced by BOSS and eBOSS data. JCAP 2022, 8, 24. [Google Scholar] [CrossRef]
- Carrilho, P.; Moretti, C.; Pourtsidou, A. Cosmology with the EFTofLSS and BOSS: Dark energy constraints and a note on priors. JCAP 2023, 1, 28. [Google Scholar] [CrossRef]
- Semenaite, A.; Sánchez, A.G.; Pezzotta, A.; Hou, J.; Eggemeier, A.; Crocce, M.; Zhao, C.; Brownstein, J.R.; Rossi, G.; Schneider, D.P. Beyond – ΛCDM constraints from the full shape clustering measurements from BOSS and eBOSS. Mon. Not. R. Astron. Soc. 2023, 521, 5013–5025. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Abdalla, F.B.; Avila, S.; Banerji, M.; Baxter, E.; Bechtol, K.; Becker, M.R.; Bertin, E.; Blazek, J.; Bridle, S.L.; et al. Dark Energy Survey Year 1 Results: Constraints on Extended Cosmological Models from Galaxy Clustering and Weak Lensing. Phys. Rev. D 2019, 99, 123505. [Google Scholar] [CrossRef]
- Tröster, T.; Asgari, M.; Blake, C.; Cataneo, M.; Heymans, C.; Hildebrandt, H.; Joachimi, B.; Lin, C.-A.; Sanchez, A.G.; Wright, A.H.; et al. KiDS-1000 Cosmology: Constraints beyond flat ΛCDM. Astron. Astrophys. 2021, 649, A88. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Aguena, M.; Alarcon, A.; Alves, O.; Amon, A.; Annis, J.; Avila, S.; Bacon, D.; Baxter, E.; Bechtol, K.; et al. Dark Energy Survey Year 3 results: Constraints on extensions to ΛCDM with weak lensing and galaxy clustering. Phys. Rev. D 2023, 107, 83504. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed SNe Ia from Pan-STARRS1 and Cosmological Constraints from the Combined Pantheon Sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Moresco, M.; Jimenez, R.; Verde, L.; Cimatti, A.; Pozzetti, L.; Maraston, C.; Thomas, D. Constraining the time evolution of dark energy, curvature and neutrino properties with cosmic chronometers. JCAP 2016, 12, 39. [Google Scholar] [CrossRef]
- Yang, W.; Di Valentino, E.; Pan, S.; Wu, Y.; Lu, J. Dynamical dark energy after Planck CMB final release and H0 tension. Mon. Not. R. Astron. Soc. 2021, 501, 5845–5858. [Google Scholar] [CrossRef]
- Grillo, C.; Rosati, P.; Suyu, S.H.; Caminha, G.B.; Mercurio, A.; Halkola, A. On the accuracy of time-delay cosmography in the Frontier Fields Cluster MACS J1149.5+2223 with supernova Refsdal. Astrophys. J. 2020, 898, 87. [Google Scholar] [CrossRef]
- Cao, S.; Ryan, J.; Ratra, B. Cosmological constraints from H ii starburst galaxy, quasar angular size, and other measurements. Mon. Not. R. Astron. Soc. 2022, 509, 4745–4757. [Google Scholar] [CrossRef]
- Khadka, N.; Ratra, B. Using quasar X-ray and UV flux measurements to constrain cosmological model parameters. Mon. Not. R. Astron. Soc. 2020, 497, 263–278. [Google Scholar] [CrossRef]
- Khadka, N.; Ratra, B. Determining the range of validity of quasar X-ray and UV flux measurements for constraining cosmological model parameters. Mon. Not. R. Astron. Soc. 2021, 502, 6140–6156. [Google Scholar] [CrossRef]
- Cao, S.; Ryan, J.; Ratra, B. Using Pantheon and DES supernova, baryon acoustic oscillation, and Hubble parameter data to constrain the Hubble constant, dark energy dynamics, and spatial curvature. Mon. Not. R. Astron. Soc. 2021, 504, 300–310. [Google Scholar] [CrossRef]
- Khadka, N.; Ratra, B. Do quasar X-ray and UV flux measurements provide a useful test of cosmological models? Mon. Not. R. Astron. Soc. 2022, 510, 2753–2772. [Google Scholar] [CrossRef]
- Cao, S.; Ratra, B. H0 = 69.8 ± 1.3 km s−1 Mpc−1, Ωm0 = 0.288 ± 0.017, and other constraints from lower-redshift, non-CMB, expansion-rate data. Phys. Rev. D 2023, 107, 103521. [Google Scholar] [CrossRef]
- Escamilla, L.A.; Giarè, W.; Di Valentino, E.; Nunes, R.C.; Vagnozzi, S. The state of the dark energy equation of state circa 2023. arXiv 2023, arXiv:2307.14802. [Google Scholar]
- Oikonomou, V.K. Effects of the axion through the Higgs portal on primordial gravitational waves during the electroweak breaking. Phys. Rev. D 2023, 107, 64071. [Google Scholar] [CrossRef]
- Espinosa, J.R.; Grojean, C.; Panico, G.; Pomarol, A.; Pujolàs, O.; Servant, G. Cosmological Higgs-Axion Interplay for a Naturally Small Electroweak Scale. Phys. Rev. Lett. 2015, 115, 251803. [Google Scholar] [CrossRef]
- Dev, P.S.B.; Ferrer, F.; Zhang, Y.; Zhang, Y. Gravitational Waves from First-Order Phase Transition in a Simple Axion-Like Particle Model. JCAP 2019, 11, 6. [Google Scholar] [CrossRef]
- Im, S.H.; Jeong, K.S. Freeze-in Axion-like Dark Matter. Phys. Lett. B 2019, 799, 135044. [Google Scholar] [CrossRef]
- Bauer, M.; Rostagni, G.; Spinner, J. Axion-Higgs portal. Phys. Rev. D 2023, 107, 15007. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Flat energy spectrum of primordial gravitational waves versus peaks and the NANOGrav 2023 observation. Phys. Rev. D 2023, 108, 43516. [Google Scholar] [CrossRef]
- Amon, A.; Efstathiou, G. A non-linear solution to the S8 tension? Mon. Not. R. Astron. Soc. 2022, 516, 5355–5366. [Google Scholar] [CrossRef]
- Simpson, F. Scattering of dark matter and dark energy. Phys. Rev. D 2010, 82, 83505. [Google Scholar] [CrossRef]
- Xu, X.D.; Wang, B.; Abdalla, E. The signature of the scattering between dark sectors in large scale cosmic microwave background anisotropies. Phys. Rev. D 2012, 85, 83513. [Google Scholar] [CrossRef]
- Richarte, M.G.; Xu, L. Interacting parametrized post-Friedmann method. Gen. Rel. Grav. 2016, 48, 39. [Google Scholar] [CrossRef]
- Boehmer, C.G.; Tamanini, N.; Wright, M. Interacting quintessence from a variational approach Part II: Derivative couplings. Phys. Rev. D 2015, 91, 123003. [Google Scholar] [CrossRef]
- Tamanini, N. Phenomenological models of dark energy interacting with dark matter. Phys. Rev. D 2015, 92, 43524. [Google Scholar] [CrossRef]
- Koivisto, T.S.; Saridakis, E.N.; Tamanini, N. Scalar-Fluid theories: Cosmological perturbations and large-scale structure. JCAP 2015, 9, 47. [Google Scholar] [CrossRef]
- Pourtsidou, A.; Tram, T. Reconciling CMB and structure growth measurements with dark energy interactions. Phys. Rev. D 2016, 94, 43518. [Google Scholar] [CrossRef]
- Dutta, J.; Khyllep, W.; Tamanini, N. Scalar-Fluid interacting dark energy: Cosmological dynamics beyond the exponential potential. Phys. Rev. D 2017, 95, 23515. [Google Scholar] [CrossRef]
- Kumar, S.; Nunes, R.C. Observational constraints on dark matter–dark energy scattering cross section. Eur. Phys. J. C 2017, 77, 734. [Google Scholar] [CrossRef]
- Linton, M.S.; Pourtsidou, A.; Crittenden, R.; Maartens, R. Variable sound speed in interacting dark energy models. JCAP 2018, 4, 43. [Google Scholar] [CrossRef]
- Bose, B.; Baldi, M.; Pourtsidou, A. Modelling Non-Linear Effects of Dark Energy. JCAP 2018, 4, 32. [Google Scholar] [CrossRef]
- Bose, B.; Taruya, A. The one-loop matter bispectrum as a probe of gravity and dark energy. JCAP 2018, 10, 19. [Google Scholar] [CrossRef]
- Asghari, M.; Beltrán Jiménez, J.; Khosravi, S.; Mota, D.F. On structure formation from a small-scales-interacting dark sector. JCAP 2019, 4, 42. [Google Scholar] [CrossRef]
- Kase, R.; Tsujikawa, S. Scalar-Field Dark Energy Nonminimally and Kinetically Coupled to Dark Matter. Phys. Rev. D 2020, 101, 63511. [Google Scholar] [CrossRef]
- Kase, R.; Tsujikawa, S. Weak cosmic growth in coupled dark energy with a Lagrangian formulation. Phys. Lett. B 2020, 804, 135400. [Google Scholar] [CrossRef]
- Chamings, F.N.; Avgoustidis, A.; Copeland, E.J.; Green, A.M.; Pourtsidou, A. Understanding the suppression of structure formation from dark matter-dark energy momentum coupling. Phys. Rev. D 2020, 101, 43531. [Google Scholar] [CrossRef]
- Asghari, M.; Khosravi, S.; Mollazadeh, A. Perturbation level interacting dark energy model and its consequence on late-time cosmological parameters. Phys. Rev. D 2020, 101, 43503. [Google Scholar] [CrossRef]
- Amendola, L.; Tsujikawa, S. Scaling solutions and weak gravity in dark energy with energy and momentum couplings. JCAP 2020, 6, 20. [Google Scholar] [CrossRef]
- De Felice, A.; Nakamura, S.; Tsujikawa, S. Suppressed cosmic growth in coupled vector-tensor theories. Phys. Rev. D 2020, 102, 63531. [Google Scholar] [CrossRef]
- Beltrán Jiménez, J.; Bettoni, D.; Figueruelo, D.; Teppa Pannia, F.A.; Tsujikawa, S. Velocity-dependent interacting dark energy and dark matter with a Lagrangian description of perfect fluids. JCAP 2021, 3, 85. [Google Scholar] [CrossRef]
- Figueruelo, D.; Aparicio Resco, M.; Teppa Pannia, F.A.; Beltran Jimenez, J.; Bettoni, D.; Maroto, A.L.; Abramo, L.R.; Alcaniz, J.; Benitez, N.; Bonoli, S.; et al. J-PAS: Forecasts for dark matter—Dark energy elastic couplings. JCAP 2021, 7, 22. [Google Scholar] [CrossRef]
- Carrilho, P.; Moretti, C.; Bose, B.; Markovič, K.; Pourtsidou, A. Interacting dark energy from redshift-space galaxy clustering. JCAP 2021, 10, 4. [Google Scholar] [CrossRef]
- Linton, M.S.; Crittenden, R.; Pourtsidou, A. Momentum transfer models of interacting dark energy. JCAP 2022, 8, 75. [Google Scholar] [CrossRef]
- Mancini Spurio, A.; Pourtsidou, A. KiDS-1000 cosmology: Machine learning–Accelerated constraints on interacting dark energy with CosmoPower. Mon. Not. R. Astron. Soc. 2022, 512, L44–L48. [Google Scholar] [CrossRef]
- Carrilho, P.; Carrion, K.; Bose, B.; Pourtsidou, A.; Hidalgo, J.C.; Lombriser, L.; Baldi, M. On the road to per cent accuracy VI: The non-linear power spectrum for interacting dark energy with baryonic feedback and massive neutrinos. Mon. Not. R. Astron. Soc. 2022, 512, 3691–3702. [Google Scholar] [CrossRef]
- Poulin, V.; Bernal, J.L.; Kovetz, E.D.; Kamionkowski, M. Sigma-8 tension is a drag. Phys. Rev. D 2023, 107, 123538. [Google Scholar] [CrossRef]
- Cardona, W.; Figueruelo, D. Momentum transfer in the dark sector and lensing convergence in upcoming galaxy surveys. JCAP 2022, 12, 10. [Google Scholar] [CrossRef]
- Piga, L.; Marinucci, M.; D’Amico, G.; Pietroni, M.; Vernizzi, F.; Wright, B.S. Constraints on modified gravity from the BOSS galaxy survey. JCAP 2023, 4, 38. [Google Scholar] [CrossRef]
- Jiménez, J.B.; Di Dio, E.; Figueruelo, D. A smoking gun from the power spectrum dipole for elastic interactions in the dark sector. arXiv 2022, arXiv:2212.08617. [Google Scholar]
- Wilkinson, R.J.; Lesgourgues, J.; Boehm, C. Using the CMB angular power spectrum to study Dark Matter-photon interactions. JCAP 2014, 4, 26. [Google Scholar] [CrossRef]
- Stadler, J.; Bœhm, C. Constraints on γ-CDM interactions matching the Planck data precision. JCAP 2018, 10, 9. [Google Scholar] [CrossRef]
- Yadav, S.K. Constraints on dark matter-photon coupling in the presence of time-varying dark energy. Mod. Phys. Lett. A 2019, 35, 1950358. [Google Scholar] [CrossRef]
- Serra, P.; Zalamea, F.; Cooray, A.; Mangano, G.; Melchiorri, A. Constraints on neutrino—Dark matter interactions from cosmic microwave background and large scale structure data. Phys. Rev. D 2010, 81, 43507. [Google Scholar] [CrossRef]
- Wilkinson, R.J.; Boehm, C.; Lesgourgues, J. Constraining Dark Matter-Neutrino Interactions using the CMB and Large-Scale Structure. JCAP 2014, 5, 11. [Google Scholar] [CrossRef]
- Escudero, M.; Mena, O.; Vincent, A.C.; Wilkinson, R.J.; Bœhm, C. Exploring dark matter microphysics with galaxy surveys. JCAP 2015, 9, 34. [Google Scholar] [CrossRef]
- Stadler, J.; Bœhm, C.; Mena, O. Comprehensive Study of Neutrino-Dark Matter Mixed Damping. JCAP 2019, 8, 14. [Google Scholar] [CrossRef]
- Hooper, D.C.; Lucca, M. Hints of dark matter-neutrino interactions in Lyman-α data. Phys. Rev. D 2022, 105, 103504. [Google Scholar] [CrossRef]
- Dvorkin, C.; Blum, K.; Kamionkowski, M. Constraining Dark Matter-Baryon Scattering with Linear Cosmology. Phys. Rev. D 2014, 89, 23519. [Google Scholar] [CrossRef]
- Gluscevic, V.; Boddy, K.K. Constraints on Scattering of keV–TeV Dark Matter with Protons in the Early Universe. Phys. Rev. Lett. 2018, 121, 81301. [Google Scholar] [CrossRef]
- Boddy, K.K.; Gluscevic, V. First Cosmological Constraint on the Effective Theory of Dark Matter-Proton Interactions. Phys. Rev. D 2018, 98, 83510. [Google Scholar] [CrossRef]
- Xu, W.L.; Dvorkin, C.; Chael, A. Probing sub-GeV Dark Matter-Baryon Scattering with Cosmological Observables. Phys. Rev. D 2018, 97, 103530. [Google Scholar] [CrossRef]
- Boddy, K.K.; Gluscevic, V.; Poulin, V.; Kovetz, E.D.; Kamionkowski, M.; Barkana, R. Critical assessment of CMB limits on dark matter-baryon scattering: New treatment of the relative bulk velocity. Phys. Rev. D 2018, 98, 123506. [Google Scholar] [CrossRef]
- Ali-Haïmoud, Y. Testing dark matter interactions with CMB spectral distortions. Phys. Rev. D 2021, 103, 43541. [Google Scholar] [CrossRef]
- Buen-Abad, M.A.; Essig, R.; McKeen, D.; Zhong, Y.M. Cosmological constraints on dark matter interactions with ordinary matter. Phys. Rept. 2022, 961, 1–35. [Google Scholar] [CrossRef]
- Nguyen, D.V.; Sarnaaik, D.; Boddy, K.K.; Nadler, E.O.; Gluscevic, V. Observational constraints on dark matter scattering with electrons. Phys. Rev. D 2021, 104, 103521. [Google Scholar] [CrossRef]
- Rogers, K.K.; Dvorkin, C.; Peiris, H.V. Limits on the Light Dark Matter–Proton Cross Section from Cosmic Large-Scale Structure. Phys. Rev. Lett. 2022, 128, 171301. [Google Scholar] [CrossRef]
- Driskell, T.; Nadler, E.O.; Mirocha, J.; Benson, A.; Boddy, K.K.; Morton, T.D.; Lashner, J.; An, R.; Gluscevic, V. Structure formation and the global 21-cm signal in the presence of Coulomb-like dark matter-baryon interactions. Phys. Rev. D 2022, 106, 103525. [Google Scholar] [CrossRef]
- He, A.; Ivanov, M.M.; An, R.; Gluscevic, V. S8 Tension in the Context of Dark Matter-Baryon Scattering. arXiv 2023, arXiv:2301.08260. [Google Scholar]
- Foot, R.; Vagnozzi, S. Dissipative hidden sector dark matter. Phys. Rev. D 2015, 91, 23512. [Google Scholar] [CrossRef]
- Foot, R.; Vagnozzi, S. Diurnal modulation signal from dissipative hidden sector dark matter. Phys. Lett. B 2015, 748, 61–66. [Google Scholar] [CrossRef]
- Cyr-Racine, F.Y.; Sigurdson, K.; Zavala, J.; Bringmann, T.; Vogelsberger, M.; Pfrommer, C. ETHOS—An effective theory of structure formation: From dark particle physics to the matter distribution of the Universe. Phys. Rev. D 2016, 93, 123527. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Zavala, J.; Cyr-Racine, F.Y.; Pfrommer, C.; Bringmann, T.; Sigurdson, K. ETHOS–An effective theory of structure formation: Dark matter physics as a possible explanation of the small-scale CDM problems. Mon. Not. R. Astron. Soc. 2016, 460, 1399–1416. [Google Scholar] [CrossRef]
- Foot, R.; Vagnozzi, S. Solving the small-scale structure puzzles with dissipative dark matter. JCAP 2016, 7, 13. [Google Scholar] [CrossRef]
- Archidiacono, M.; Bohr, S.; Hannestad, S.; Jørgensen, J.H.; Lesgourgues, J. Linear scale bounds on dark matter–dark radiation interactions and connection with the small scale crisis of cold dark matter. JCAP 2017, 11, 10. [Google Scholar] [CrossRef][Green Version]
- Becker, N.; Hooper, D.C.; Kahlhoefer, F.; Lesgourgues, J.; Schöneberg, N. Cosmological constraints on multi-interacting dark matter. JCAP 2021, 2, 19. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Visinelli, L.; Mena, O.; Mota, D.F. Do we have any hope of detecting scattering between dark energy and baryons through cosmology? Mon. Not. R. Astron. Soc. 2020, 493, 1139–1152. [Google Scholar] [CrossRef]
- Jiménez, J.B.; Bettoni, D.; Figueruelo, D.; Teppa Pannia, F.A. On cosmological signatures of baryons-dark energy elastic couplings. JCAP 2020, 8, 20. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Visinelli, L.; Brax, P.; Davis, A.C.; Sakstein, J. Direct detection of dark energy: The XENON1T excess and future prospects. Phys. Rev. D 2021, 104, 63023. [Google Scholar] [CrossRef]
- Benisty, D.; Davis, A.C. Dark energy interactions near the Galactic Center. Phys. Rev. D 2022, 105, 24052. [Google Scholar] [CrossRef]
- Ferlito, F.; Vagnozzi, S.; Mota, D.F.; Baldi, M. Cosmological direct detection of dark energy: Non-linear structure formation signatures of dark energy scattering with visible matter. Mon. Not. R. Astron. Soc. 2022, 512, 1885–1905. [Google Scholar] [CrossRef]
- Pourtsidou, A.; Skordis, C.; Copeland, E.J. Models of dark matter coupled to dark energy. Phys. Rev. D 2013, 88, 83505. [Google Scholar] [CrossRef]
- Skordis, C.; Pourtsidou, A.; Copeland, E.J. Parametrized post-Friedmannian framework for interacting dark energy theories. Phys. Rev. D 2015, 91, 83537. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).