DPQP: A Detection Pipeline for Quasar Pair Candidates Based on QSO Photometric Images and Spectra
Abstract
:1. Introduction
2. Data
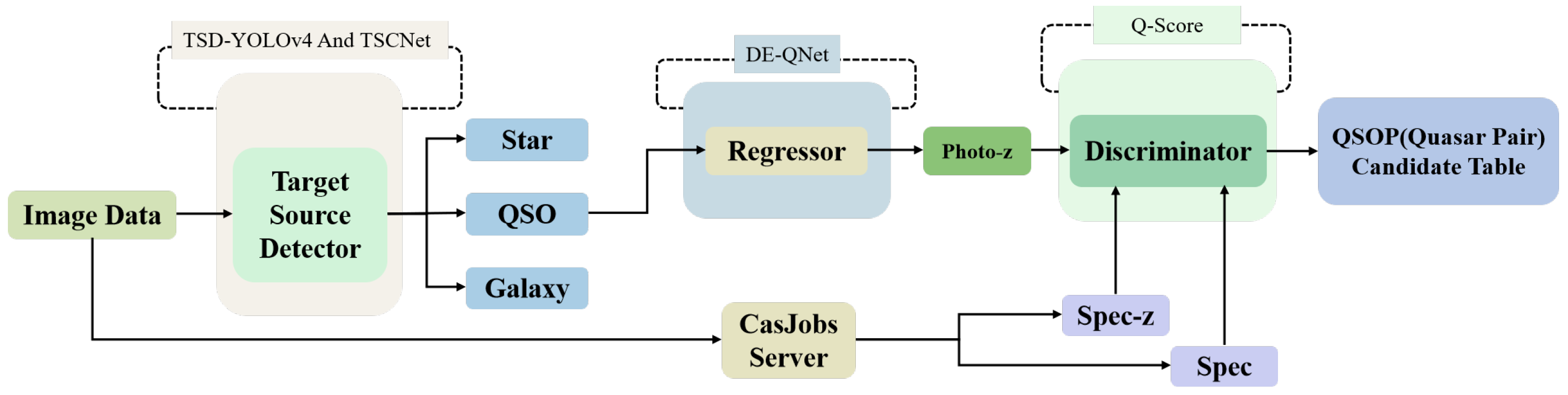
3. Method
3.1. Target Source Detector
3.2. Regressor
3.2.1. Redshift Estimation Network: DE-QNet
3.2.2. Network Training Strategy
4. Discriminator
4.1. Q-Score Indicator
| Emission Lines | |
|---|---|
| Ly | 1031.48 |
| Ly | 1215.86 |
| O I | 1305.31 |
| Si IV | 1398.16 |
| C IV | 1545.57 |
| C III | 1903.61 |
| Mg II | 2800.14 |
4.2. Spectral Analysis Process
4.2.1. Spectral Analysis Process
4.2.2. Filtering
4.2.3. Searching for Absorption Lines
5. Results and Discussion
5.1. Evaluation Metrics
5.2. Comparison and Analysis of DE-QNet
5.3. DPQP Processing
- Step 1: Detecting the target sources in the image, with the detection of quasars as the .
- Step 2: The CasJobs Server obtains quasars with spectra in this image as (red boxes in Figure 11) and matches these with from Step 1 within 60 arcseconds. No quasar is detected within 60 arcseconds from the center of (red boxes on the left side of Figure 11, ra = 181.09295, dec = 2.37135, = 2.0368) on the left side of Figure 11. A quasar is detected within 60 arcseconds from the center of (red boxes on right side of Figure 11, ra = 181.06953, dec = 2.35055, = 2.5320) on the right side of Figure 11.
- Step 3: DE-QNet is used to estimate the redshift of the matching quasar by Step 2, and the estimated value () is 2.412.
- Step 4: Because the MAE of DE-QNet is 0.316, in order to accurately match emission lines and absorption lines, the redshift should fluctuate within a certain range. The range restriction for this redshift fluctuation, given by Equations (9) and (10), is provided as follows. The redshift fluctuation range for = 2.412 is 2.100 < < 2.532.Generally, are smaller than . According to Equation = (1+) ×, when the emission line () is fixed, the observed wavelength () can be calculated from the estimated redshift (). is the lower limit of the redshift range. is the upper limit of the redshift range. The MAE of DE-QNet is 0.316. is the estimated redshift of quasars. is the redshift of background quasars obtained from the CasJobs Server in Step 2. None means that if exceeds , it will be discarded.
- Step 5: Bring the Zpre from Step 4 into Equation (1), calculate the corresponding Q-Scores for different , and output the maximum Q-Score.


5.4. DPQP Testing
6. Conclusions
- Proposes a quasar pair candidate detection pipeline.
- Proposes an accurate redshift regression network based on photometric images.
- A new table with 1025 QP candidates is provided (refer to Appendix A).
- We plan to incorporate a neighboring image stitching algorithm to address the issue of two quasars being QP but not present in the same image. By aligning and stitching these neighboring images together, we can create a larger composite image.
- Since high-redshift samples are scarce, the scope of this study is currently limited to a redshift range of 0.0–4.0. Our next step is to expand the redshift range and utilize high-redshift quasars as probes to search for other high-redshift quasar pairs. By including a wider range of redshift values, we can explore and analyze the properties and characteristics of high-redshift quasars more comprehensively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | Linear dichroism |
Appendix A
| Quasar Pair | Q-Score | |||||
| J1301 + 0013 | J130142.41 + 00136.7 | J130139.93 + 001310.35 | 3.095716 | 2.365087748 | 37.14735264 | 27.283 |
| J0045 + 0014 | J004527.66 + 001410.26 | J004524.94 + 001456.01 | 2.424207 | 2.196105719 | 61.40756165 | 100.924 |
| J0919 + 5404 | J091925.21 + 540,459.83 | J091921.14 + 540,534.4 | 2.174495 | 2.203944683 | 50.45078615 | 98.932 |
| J0942 + 0817 | J094212.56 + 081737.25 | J094215.03 + 081815.44 | 3.161636 | 3.011915207 | 53.32757725 | 93.822 |
| J0019 + 1415 | J001911.49 + 14,158.03 | J00199.54 + 141,428.87 | 3.003208 | 2.844203472 | 48.19299423 | 84.906 |
| J2159 − 0816 | J215944.02 − 081634.34 | J215948.24 − 08169.95 | 3.736069 | 2.407644749 | 67.62501206 | 50.141 |
| … | ||||||
| … | ||||||
| … | ||||||
| 1025 | ||||||
| … | ||||||
| … | ||||||
| … | ||||||
| J0217 − 0817 | J021719.39 − 081728.87 | J021719.94 − 081655.24 | 2.742388 | 2.731396675 | 34.94623331 | 93.822 |
| J1233 + 0616 | J123323.8 + 06168.42 | J123321.25 + 061552.18 | 2.680345 | 2.610152483 | 41.23386367 | 90.016 |
| J1518 + 2603 | J151823.17 + 260,353.36 | J151822.83 + 26,033.64 | 3.65314 | 2.468950987 | 49.90493798 | 86.199 |
| 1 | Fiber collisions occur when the positions of two or more astronomical objects in the survey field are so close to each other that the fibers cannot be positioned without overlapping or conflicting. |
References
- Peterson, B.M. An Introduction to Active Galactic Nuclei; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Prochaska, J.X.; Hennawi, J.F.; Lee, K.G.; Cantalupo, S.; Bovy, J.; Djorgovski, S.; Ellison, S.L.; Lau, M.W.; Martin, C.L.; Myers, A.; et al. Quasars probing quasars. VI. Excess H i absorption within one proper Mpc of z 2 quasars. Astrophys. J. 2013, 776, 136. [Google Scholar] [CrossRef]
- Hennawi, J.F.; Prochaska, J.X.; Burles, S.; Strauss, M.A.; Richards, G.T.; Schlegel, D.J.; Fan, X.; Schneider, D.P.; Zakamska, N.L.; Oguri, M.; et al. Quasars probing quasars. I. Optically thick absorbers near luminous quasars. Astrophys. J. 2006, 651, 61. [Google Scholar] [CrossRef]
- Prochaska, J.X.; Hennawi, J.F. Quasars probing quasars. III. New clues to feedback, quenching, and the physics of massive galaxy formation. Astrophys. J. 2008, 690, 1558. [Google Scholar] [CrossRef]
- Hennawi, J.F.; Prochaska, J.X. Quasars probing quasars. IV. Joint constraints on the circumgalactic medium from absorption and emission. Astrophys. J. 2013, 766, 58. [Google Scholar] [CrossRef]
- Cox, T.; Di Matteo, T.; Hernquist, L.; Hopkins, P.F.; Robertson, B.; Springel, V. X-ray emission from hot gas in galaxy mergers. Astrophys. J. 2006, 643, 692. [Google Scholar] [CrossRef]
- Sijacki, D.; Springel, V.; Di Matteo, T.; Hernquist, L. A unified model for AGN feedback in cosmological simulations of structure formation. Mon. Not. R. Astron. Soc. 2007, 380, 877–900. [Google Scholar] [CrossRef]
- Hopkins, P.F.; Cox, T.J.; Kereš, D.; Hernquist, L. A cosmological framework for the co-evolution of Quasars, supermassive black holes, and elliptical galaxies. II. Formation of red ellipticals. Astrophys. J. Suppl. Ser. 2008, 175, 390. [Google Scholar] [CrossRef]
- Findlay, J.R.; Prochaska, J.X.; Hennawi, J.F.; Fumagalli, M.; Myers, A.D.; Bartle, S.; Chehade, B.; DiPompeo, M.A.; Shanks, T.; Lau, M.W.; et al. Quasars Probing Quasars. X. The Quasar Pair Spectral Database. Astrophys. J. Suppl. Ser. 2018, 236, 44. [Google Scholar] [CrossRef]
- Alam, S.; Aubert, M.; Avila, S.; Balland, C.; Bautista, J.E.; Bershady, M.A.; Bizyaev, D.; Blanton, M.R.; Bolton, A.S.; Bovy, J.; et al. Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Cosmological implications from two decades of spectroscopic surveys at the Apache Point Observatory. Phys. Rev. D 2021, 103, 083533. [Google Scholar] [CrossRef]
- Kaiser, N.; Burgett, W.; Chambers, K.; Denneau, L.; Heasley, J.; Jedicke, R.; Magnier, E.; Morgan, J.; Onaka, P.; Tonry, J. The Pan-STARRS wide-field optical/NIR imaging survey. In Proceedings of the Ground-Based and Airborne Telescopes III; SPIE: San Diego, CA, USA, 2010; Volume 7733, pp. 159–172. [Google Scholar]
- Perez, S.J.A.; Nichol, B.; Percival, W.; Thomas, D.B.; Collaboration, D.; DES Collaboration. The Dark Energy Survey: Data Release 1. Astrophys. J. Suppl. Ser. 2018, 239, 18. [Google Scholar]
- Jakobsen, P.; Ferruit, P.; de Oliveira, C.A.; Arribas, S.; Bagnasco, G.; Barho, R.; Beck, T.; Birkmann, S.; Böker, T.; Bunker, A.; et al. The near-infrared spectrograph (nirspec) on the james webb space telescope-i. overview of the instrument and its capabilities. Astron. Astrophys. 2022, 661, A80. [Google Scholar] [CrossRef]
- Jarolim, R.; Veronig, A.; Hofmeister, S.; Heinemann, S.; Temmer, M.; Podladchikova, T.; Dissauer, K. Multi-channel coronal hole detection with convolutional neural networks. Astron. Astrophys. 2021, 652, A13. [Google Scholar] [CrossRef]
- Wang, S.; Chen, B.; Ma, J.; Long, Q.; Yuan, H.; Liu, D.; Zhou, Z.; Liu, W.; Chen, J.; He, Z. Identification of new M 31 star cluster candidates from PAndAS images using convolutional neural networks. Astron. Astrophys. 2022, 658, A51. [Google Scholar] [CrossRef]
- He, Z.; Qiu, B.; Luo, A.L.; Shi, J.; Kong, X.; Jiang, X. Deep learning applications based on SDSS photometric data: Detection and classification of sources. Mon. Not. R. Astron. Soc. 2021, 508, 2039–2052. [Google Scholar] [CrossRef]
- Shi, J.H.; Qiu, B.; Luo, A.L.; He, Z.D.; Kong, X.; Jiang, X. A photometry pipeline for SDSS images based on convolutional neural networks. Mon. Not. R. Astron. Soc. 2022, 516, 264–278. [Google Scholar] [CrossRef]
- Soo, J.Y.; Moraes, B.; Joachimi, B.; Hartley, W.; Lahav, O.; Charbonnier, A.; Makler, M.; Pereira, M.E.; Comparat, J.; Erben, T.; et al. Morpho-z: Improving photometric redshifts with galaxy morphology. Mon. Not. R. Astron. Soc. 2018, 475, 3613–3632. [Google Scholar] [CrossRef]
- Hong, S.; Zou, Z.; Luo, A.L.; Kong, X.; Yang, W.; Chen, Y. PhotoRedshift-MML: A multimodal machine learning method for estimating photometric redshifts of quasars. Mon. Not. R. Astron. Soc. 2023, 518, 5049–5058. [Google Scholar] [CrossRef]
- Schuldt, S.; Suyu, S.; Cañameras, R.; Taubenberger, S.; Meinhardt, T.; Leal-Taixé, L.; Hsieh, B. Photometric redshift estimation with a convolutional neural network: NetZ. Astron. Astrophys. 2021, 651, A55. [Google Scholar] [CrossRef]
- Margony, B. The Sloan digital sky survey. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1999, 357, 93–103. [Google Scholar] [CrossRef]
- D’Isanto, A.; Polsterer, K.L. Photometric redshift estimation via deep learning-generalized and pre-classification-less, image based, fully probabilistic redshifts. Astron. Astrophys. 2018, 609, A111. [Google Scholar] [CrossRef]
- Huang, L.; Zhou, Y.; Wang, T.; Luo, J.; Liu, X. Delving into the estimation shift of batch normalization in a network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 763–772. [Google Scholar]
- Smee, S.A.; Gunn, J.E.; Uomoto, A.; Roe, N.; Schlegel, D.; Rockosi, C.M.; Carr, M.A.; Leger, F.; Dawson, K.S.; Olmstead, M.D.; et al. The multi-object, fiber-fed spectrographs for the sloan digital sky survey and the baryon oscillation spectroscopic survey. Astron. J. 2013, 146, 32. [Google Scholar] [CrossRef]
- Berk, D.E.V.; Richards, G.T.; Bauer, A.; Strauss, M.A.; Schneider, D.P.; Heckman, T.M.; York, D.G.; Hall, P.B.; Fan, X.; Knapp, G.; et al. Composite quasar spectra from the sloan digital sky survey. Astron. J. 2001, 122, 549. [Google Scholar] [CrossRef]
- Xiang, G.; Chen, J.; Qiu, B.; Lu, Y. Estimating Stellar Atmospheric Parameters from the LAMOST DR6 Spectra with SCDD Model. Publ. Astron. Soc. Pac. 2021, 133, 024504. [Google Scholar] [CrossRef]










| Layer | Output Size | Input Channels | Output Channels | Kernel Size | Stride | Padding | Activation |
|---|---|---|---|---|---|---|---|
| P1 | 64 × 64 | 5 | 32 | 3 | 1 | 1 | Hardswish |
| P2 | 32 × 32 | 32 | 64 | 3 | 2 | 1 | Hardswish |
| P3 | 32 × 32 | 64 | 64 | 3 | 1 | 1 | Hardswish |
| P4 | 16 × 16 | 64 | 64 | 2 | - | - | - |
| P5 | 16 × 16 | 64 | 128 | 3 | 1 | 1 | Hardswish |
| P6 | 16 × 16 | 128 | 256 | - | - | - | - |
| P7 | 8 × 8 | 256 | 256 | - | - | - | - |
| P8 | 8 × 8 | 256 | 64 | 1 | 1 | 1 | Hardswish |
| Fully connected | - | 4096 | 1024 | - | - | - | Hardswish |
| Fully connected | - | 1024 | 32 | - | - | - | Hardswish |
| Fully connected | - | 32 | 1 | - | - | - | Hardswish |
| Configuration | DE-QNet |
|---|---|
| Optimizer | Adam |
| Batch size | 8 |
| Totale poch | 300 |
| Learn rate | 1 × 10 |
| Resize shape | 64 |
| Method | MSE | MAE | Bias | NMAD | |||
|---|---|---|---|---|---|---|---|
| DCMDN | 0.387 | 0.389 | −0.052 | 0.299 | 0.117 | 0.682 | 0.894 |
| NetZ | 0.299 | 0.367 | −0.048 | 0.267 | 0.124 | 0.680 | 0.868 |
| DE-QNet | 0.284 | 0.316 | −0.048 | 0.264 | 0.081 | 0.771 | 0.888 |
| Quasar Pair | Q-Score | |||||||
|---|---|---|---|---|---|---|---|---|
| J0023 − 0106 | J023946.45 − 010644.2 | J023946.43 − 010640.5 | 3.129 | 2.591 | 2.307 | 2.324 | 3.7 | 102.133 |
| J | J025039.82 − 004749.6 | J025038.68 − 004739.2 | 2.448 | 2.192 | - | - | - | - |
| J075259.14 + 401118.2 | J075259.81 + 401,128.2 | 2.121 | 2.008 | 1.881 | 2.334 | 12.6 | 0.000 | |
| J081419.58 + 325018.7 | J081420.37 + 325,016.1 | - | - | 2.178 | - | - | - | |
| J083757.13 + 383,722.4 | J083757.91 + 383,727.1 | - | - | 2.059 | - | - | - | |
| J0841 + 3921 | J084159.26 + 392,140.0 | J084158.47 + 392,121.0 | 2.213 | 2.209 | 2.04 | 2.046 | 21.1 | 51.985 |
| J085656.05 + 115,802.7 | J085655.75 + 115,802.0 | - | - | 1.767 | - | - | - | |
| J093804.84 + 531,743.1 | J093804.22 + 531,743.9 | 2.320 | 2.111 | 2.068 | 2.455 | 5.6 | 0.000 | |
| J100627.10 + 480,429.9 | J100627.47 + 480,420.0 | 2.591 | 2.378 | - | - | - | - | |
| J1025 + 5820 | J102554.77 + 582,017.0 | J102553.47 + 582,012.0 | 2.567 | 2.357 | 1.956 | 2.266 | 11.4 | 60.899 |
| J1041 + 5630 | J104129.27 + 563,023.5 | J104121.90 + 563,001.3 | 2.266 | 2.262 | 2.043 | 1.968 | 65.0 | 77.273 |
| J104506.39 + 435,115.3 | J104508.88 + 435,118.2 | - | - | 2.423 | - | - | - | |
| J1204 + 0221 | J120416.69 + 022111.0 | J120417.47 + 022104.7 | 2.529 | 2.438 | 2.436 | 2.412 | 13.3 | 92.008 |
| J130603.55 + 615,835.2 | J130605.19 + 615,823.7 | - | - | 2.109 | - | - | - | |
| J135849.54 + 273,756.9 | J135849.71 + 273,806.9 | 2.113 | 2.380 | 1.899 | 2.64 | 10.2 | 0.000 | |
| J1427 − 0121 | J142758.74 − 012136.2 | J142758.89 − 012130.4 | 2.353 | 2.346 | 2.271 | 2.256 | 6.2 | 84.207 |
| J1442 + 0137 | J144231.91 + 013734.8 | J144232.92 + 013730.4 | 2.273 | 1.882 | 1.803 | 2.179 | 15.7 | 98.920 |
| J150812.80 + 363,530.3 | J150814.06 + 363,529.4 | - | - | 1.837 | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Qiu, B.; Luo, A.-l.; Jiang, X.; Yao, L.; Wang, K.; Zhao, G. DPQP: A Detection Pipeline for Quasar Pair Candidates Based on QSO Photometric Images and Spectra. Universe 2023, 9, 425. https://doi.org/10.3390/universe9090425
Liu Y, Qiu B, Luo A-l, Jiang X, Yao L, Wang K, Zhao G. DPQP: A Detection Pipeline for Quasar Pair Candidates Based on QSO Photometric Images and Spectra. Universe. 2023; 9(9):425. https://doi.org/10.3390/universe9090425
Chicago/Turabian StyleLiu, Yuanbo, Bo Qiu, A-li Luo, Xia Jiang, Lin Yao, Kun Wang, and Guiyu Zhao. 2023. "DPQP: A Detection Pipeline for Quasar Pair Candidates Based on QSO Photometric Images and Spectra" Universe 9, no. 9: 425. https://doi.org/10.3390/universe9090425






